A Bilevel Optimization Approach for Tuning a Neuro-Fuzzy Controller

Abstract

This work presents a methodology to solve optimization problems with dynamic-size solution vectors containing continuous and integer variables. It is achieved by reformulating the original problem through a bilevel optimization approach and implementing metaheuristic techniques to solve it. In the selected case study, the optimization problem corresponds to tuning a neuro-fuzzy controller (NFC) that operates in a biodiesel production system for controlling temperature. The NFC performs well and is especially robust to disturbances, but due to its complexity, it is difficult to determine the best set of parameters for its use. This has led to biased searches based on criteria such as the experiences of designers. With the proposed method, it was possible to obtain a tuning that—when implemented in a simulation—led to results that surpassed those documented in the literature. Finally, the proposal offers flexibility for implementation with other controllers that have similar architectures and can be integrated into various other plants or processes.

1. Introduction

Metaheuristics have gained popularity in various engineering fields due to the advantages these algorithms provide for addressing optimization problems when analytical or classical methods are not viable. This non-viability mainly occurs if the objective function to be optimized is not derivable or when there are insufficient computing resources to use analytical methods.

However, solving real-world engineering problems that involve mixed variables (integer and continuous) is challenging, even for metaheuristic algorithms. This makes it necessary to modify the algorithms themselves or their application. In this type of problem, where integer and real variables coexist, highly complex search spaces are generated. Another limitation of metaheuristics is related to the operations performed on the candidate solutions to update them and eventually find a better solution, which implies that all solution vectors must have the same dimension. When the optimization problem involves candidate solutions with differing numbers of variables, metaheuristic algorithms are limited to exploring subsets of the search spaces at a time. In this work, the concept of bilevel optimization is employed to tackle this issue. It refers to a type of optimization in which one problem is embedded within another (the lower problem), such that the solution to this first problem sets a constraint for the upper problem [1].

According to [2], optimization cases that are both non-convex and non-differentiable are considered hard problems. An alternative for addressing them involves formulating these as bilevel optimization problems and solving them using metaheuristics. In [3], a bilevel mixed-integer linear problem was formulated to determine the optimal distribution of measurement devices across an electrical network. Another example was detailed in [4], where a bilevel problem was formulated to avoid air conflicts by establishing a distance threshold between planes, which implies an underlying problem for each pair of planes in a traffic control system. The authors in [5] proposed tuning the hyperparameters of a neural network by formulating a bilevel optimization problem, which was solved using the differential evolution algorithm (DE). Although the present work also focuses on parameter tuning, its nature and the bilevel problem formulated differ due to the use of solution vectors of different sizes, an aspect not contemplated in the aforementioned works.

Nowadays, research efforts in automatic control theory are focused on developing more efficient modern controllers with strong mathematical properties. These controllers are designed to guarantee adequate solutions that meet the control objectives set by the user, even in the presence of disturbances and the inherent uncertainties of dynamical systems, particularly in real-world problems. This focus has led to collaboration across various areas to complement and enhance these solutions with controllers based on bio-inspired algorithms, such as neural networks, expert systems, fuzzy logic, and neuro-fuzzy systems, among others. The performance of this type of controller strongly depends on the initialization of the hyperparameters for their operation, which are typically selected randomly. Metaheuristics can help reduce this dependency and optimize controller performance by generating good setup parameters. Neuro-fuzzy controllers combine the learning plasticity of neural networks with the method of harnessing human knowledge through fuzzy logic. This type of controller is particularly attractive for solving real-world problems in the industrial sector, as it can adapt to changing environmental conditions over time while considering human operators who have worked for a long time with the process, accumulating vast experience.

Various works have addressed the tuning of different controllers through experimentation, using random combinations [6,7,8]. Another example of a challenging optimization problem is the tuning of a neuro-fuzzy controller (NFC). According to [9], this controller is a hybridization between controllers based on fuzzy networks [10,11] and those that use neural networks [12]. A fuzzy logic system uses if–then rules to determine the appropriate course of action based on input data. The programmer initially proposes these rules and uses their expertise to create them; they are further refined by integrating a machine learning algorithm. The rules are based on the experience of the programmer as well as on how the system learns from the data. Therefore, this process involves tuning both the hyperparameters of the neural network and the elements associated with the inference laws of fuzzy logic.

In [13], a specific case of tuning an NFC applied to a biodiesel production process was presented. Its architecture requires a series of initial values (weights) to operate, where the number of weights is exponential to the number of membership functions. Optimal tuning involved determining the appropriate membership functions and then the number of initial weights. In fact, the final behavior of the controller was quite susceptible to the initial values despite the training of its neural network. A metaheuristic technique was used to select the optimal initialization values, with the restriction of a fixed number of membership functions. Remarkably, the same task in the biodiesel production process was presented in [14], but using a proportional–integral–derivative (PID) controller tuned with analytical methods. However, its performance was widely surpassed by the system implemented with the NFC.

It is worth noting that designing robust controllers capable of dealing with unexpected situations during the process implies increasing difficulty due to their tuning. For example, a PID controller only requires the tuning of three variables in a continuous space, while the NFC in this work requires determining a discrete variable that defines its architecture and the number of continuous variables, N. This is calculated using (1), where m is the number of membership functions, $m^2$ corresponds to the number of initial weights, and an additional term (in this specific case, 5) relates to the learning constants and additional parameters used to define the membership functions.

$$N=m^2+m+5$$

(1)

The NFC used as a case study in this work has various advantages, such as the ability to adapt itself online to both fulfill the trajectory tracking task and to be robust to disturbances. Despite this, it is necessary to initialize it with a configuration good enough to avoid overreactions to disturbances. In addition to the hyperparameters that define the neural network, the NFC is also sensitive to the initial value of the weights in the network. This aspect limits the application of other proposals such as [15], where the authors tuned the epochs, the number of layers, and neurons of a neural network using DE, but omitted the tuning of the initial weights. In other developments [16,17], different heuristic techniques (harmony search and genetic algorithm) were used for tuning NNs with additional parameters like the learning rate or a pool of activation functions, but the weights were not considered, as they were initialized randomly or followed a normal distribution.

The use of an optimization approach to determine the best tuning parameters of the NFC (including the initial values of its weights) involves solving an unconventional problem in the sense that the candidate solutions have different sizes. The novelty of the proposal in this work is the reinterpretation of the tuning problem as a bilevel optimization problem, where each single problem uses fixed-size solution vectors. Because of this modeling, a variety of metaheuristic algorithms can be applied to solve it, since dealing with variable-size candidate solutions is not required. Additionally, it is proposed to implement the repulsion strategy described in [18] to obtain the integer type variable, to avoid problems such as the loss of diversification in scenarios with mixed variables, which has been reported in various developments [19,20,21]. Using the proposed process, it is possible to determine the complete tuning of the NFC without depending on the experience or intuition of the designers to determine its architecture (number of membership functions and weights), with results that surpassed those in [13], where the exploration was biased.

In summary, the contributions of this work are as follows:

• The modeling of an optimization problem for tuning an NFC, applied to a case study from the related literature, with dynamic-size solution vectors containing continuous and integer variables.
• The reformulation of the optimization problem as a bilevel optimization problem to be solved using metaheuristic algorithms, allowing for unbiased tuning of the NFC without fixing the size of weights or membership functions.
• The simulation of the case study, focusing on temperature control with the NFC as part of a biodiesel generation process, using the best setting found by the proposed method and comparing it with other approaches reported in the literature.

This paper is organized as follows: Section 2, describes the NFC as a case study; Section 3 presents the concept of optimization and some classifications of optimization problems that are useful for the approach. Section 4 explains the stages in which the tuning problem for the NFC is transformed into a bilevel optimization problem. Section 5 presents the experiments and results. Section 6 corresponds to the final discussion, which includes conclusions and future work.

2. Neuro-Fuzzy Controller

The neuro-fuzzy controller, considered as a case study in this work, is an improved version of the definition presented in [22]. It represents an important alternative to on–off systems and PID controllers that are used in industrial processes such as biodiesel production but often perform poorly due to their inadequate handling of disturbances over time [13].

There are two inputs in this NFC, E and $\Delta E$, corresponding to the error and the increment of the error over time, respectively. These signals are calculated using (2) and (3), where $SP\left(k\right)$ and $PV\left(k\right)$ denote the set point and the value of the process variable in the instant k, $E(k-1)$ represents a delay in the time of $E\left(k\right)$, and $Ts$ is the sampling time.

$$E\left(k\right)=SP\left(k\right)-PV\left(k\right)$$

(2)

$$\Delta E\left(k\right)=\frac{E\left(k\right)-E(k-1)}{Ts}$$

(3)

Sampling a signal in process control is a common practice in the industry. Although there is no analytical method to determine the exact value of the sampling rate, it is possible to establish a limit to ensure no loss of information when discretizing a continuous signal from the real world. The Shannon–Nyquist theorem [23] establishes that the sample rate, $f_s$, must be higher than twice the highest frequency component of interest in the signal, known as the Nyquist frequency, $f_N$, as expressed in (4):

$$f_s>2\ast f_N$$

(4)

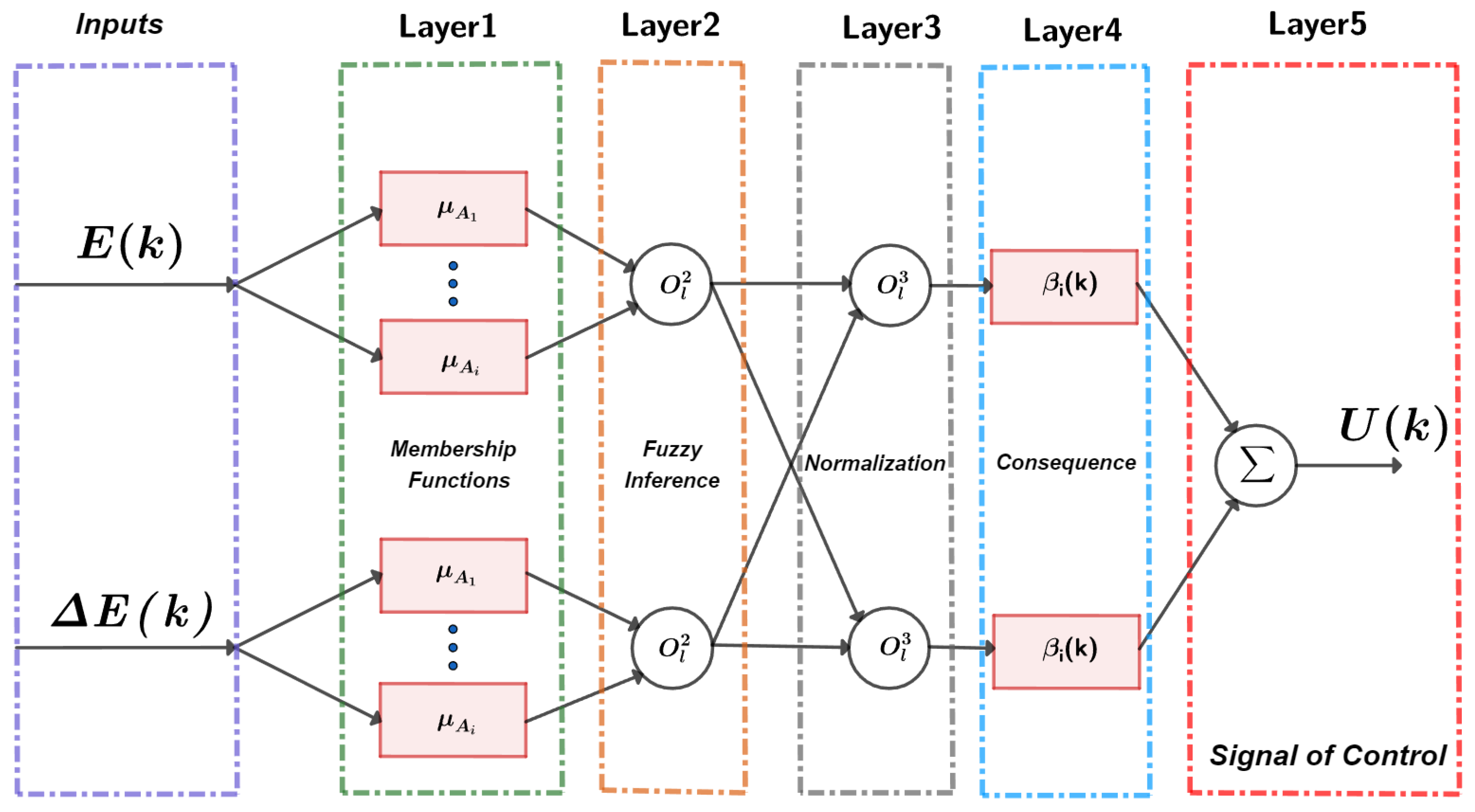
Figure 1 shows the five layers of the network architecture in the NFC. The first one provides the input vector $X\left(k\right)$ for the fuzzification, considering $E\left(k\right)$ and $\Delta E\left(k\right)$. The second layer is used to make the inferences using a fuzzy rule base, whereas the third to fifth layers are used in the defuzzification process to formulate the output $u\left(k\right)$.

The first layer maps the real values of the input vector $X\left(k\right)$ to the linguistics applied to make the fuzzification, according to the Takagi–Sugeno method [24]. The structure of this step is defined by (5):

$${\mu }_{A_{j,k}}={\mathsf{\Gamma }}_j({\mathsf{\Lambda }}_j\left(k\right),X_i\left(k\right))$$

(5)

where ${\mu }_{A_{j,k}}$ denotes the number of membership functions selected for the vector $X\left(k\right)$, which is normally set by the designer through a trial and error process. The last value of the index, j, corresponds to the number of membership functions. The terms ${\mathsf{\Gamma }}_j(·)$ and ${\mathsf{\Lambda }}_j\left(k\right)$ describe the function selected to make the fuzzification and its parameters, respectively. As an example, for the Gaussian bell described by (6), the ${\mathsf{\Lambda }}_j\left(k\right)$ set contains the parameters ${\varphi }_{j,k}$ and ${\sigma }_{j,k}$, representing the position and spread of the Gaussian function [13].

$${\mu }_{A_{j,k}}\left(X_i\left(k\right)\right)=e^{0.5{\left(\frac{X_i\left(k\right){\varphi }_{j,k}}{{\sigma }_{j,k}}\right)}^2}$$

(6)

The second layer makes inferences based on the if–then statements to generate fuzzy sets using the vector $X\left(k\right)$ for subsequent membership. In this way, the functions are interconnected, enabling the classification and determination of possible scenarios in the behavior of the system. Subsequently, they propose an output value according to each of the cases established by the set of fuzzy rules denoted by (7), where the index $p=2,3$ corresponds to the second or third layer, respectively [13].

$$O^p=w\left(k\right)={\mu }_{A_{j,k}}{\left(X_i\left(k\right)\right)}^T\ast {\mu }_{A_{j,k}}\left(X_i\left(k\right)\right)$$

(7)

The output of the third layer should be normalized according to (8), where the index $l=1,2,\dots ,R$ is defined by the number of fuzzy rules n since $R=n\times n$ [13].

$$\overline{w}\left(k\right)=\frac{w\left(k\right)}{{\sum }_{l=1}^R{w}_l\left(k\right)}$$

(8)

The output of the fourth layer ($O^4$) is composed of the products of the normalized firing strength and the parameter $r_l={\gamma }_j\left({\lambda }_j\left(k\right)\right)$. This output is calculated using (9), where ${\beta }_n\left(k\right)\in {\mathfrak{R}}^n$, ${\gamma }_j\left({\lambda }_j\left(k\right)\right)$ corresponds to the membership function and its parameters that describe the action of the controller by considering the output of the third layer, and ${\overline{w}}_{n,:}\left(k\right)$ represents each row of the matrix [13].

$$O^4={\beta }_n\left(k\right)={\overline{w}}_{n,:}\left(k\right)\ast {\gamma }_j\left({\lambda }_j\left(k\right)\right)$$

(9)

The output of the fifth layer is the scalar value of the control signal that is obtained by the sum function described by (10),

$$U\left(k\right)=\sum \beta \left(k\right)$$

(10)

A hybridization with neural networks was introduced to the control system to impart a learning property, enabling it to adapt as time progresses and the system encounters various operating conditions, including disturbances, as mentioned in [25]. The gradient descent (GD) method [23] was adapted for tuning the membership functions (Gaussian bells) of the neuro-fuzzy network, following (11) and (12) for the fuzzification and defuzzification stages, respectively [13].

$${\mathsf{\Lambda }}_j(k+1)={\mathsf{\Lambda }}_j\left(k\right)-{\eta }_{{\mathsf{\Lambda }}_i}\frac{\partial E\left(k\right)}{\partial {\mu }_{A_{j,k}}\left(X_i\left(k\right)\right)}$$

(11)

$${\lambda }_j(k+1)={\lambda }_j\left(k\right)-{\eta }_{{\lambda }_i}\frac{\partial E\left(k\right)}{\partial w_l\left(k\right)}$$

(12)

The update parameters for the Gaussian bells are described in (13) and (14), according to [13,22]

$$\varphi (k+1)=\varphi \left(k\right)-{\left(E\left(k\right)\right)}^3\ast {\eta }_{\varphi }\ast {\mu }_{A_{j,k}}\ast \left(\frac{{\varphi }_{i,k}}{{\sigma }_{i,k}}\right)\ast D$$

(13)

$$\sigma (k+1)=\sigma \left(k\right)-{\left(E\left(k\right)\right)}^4\ast {\eta }_{\sigma }\ast {\mu }_{A_{j,k}}\ast \left(\frac{{\left({\varphi }_{i,k}\right)}^2}{{\sigma }_{i,k}^3}\right)\ast D$$

(14)

where

$$D=\frac{diag\left({\gamma }_j\left({\lambda }_j\left(k\right)\right)\right)-{\beta }_{n,i}\left(k\right)}{\sum w_l\left(k\right)}$$

Finally, the gradient $r_j\left(k\right)$ is updated following (15), where ${\eta }_{\varphi },{\eta }_{\sigma }$, and ${\eta }_r$ are known as the constants of the learning rate that define the learning speed of the control system. These constants are normally chosen by trial and error in the range $0<\eta \le 1$. Figure 2 presents the diagram of the complete NFC, including the described hybridization [13].

$$r_j(k+1)=r_j\left(k\right)-{\eta }_r\ast E\left(k\right)\ast \overline{w_l}\left(k\right)$$

(15)

3. Optimization

In general terms, optimization can be defined as the process of obtaining the best selection between a set of items available, according to some criteria. In a mathematical form, an optimization problem consists of finding a set of values $\overrightarrow{x}$, as follows:

$$\min /\max f_m\left(\overrightarrow{x}\right)$$

(16)

subject to:

$$g_i\left(\overrightarrow{x}\right)\le 0,i=1,\dots ,n_i$$

(17)

$$h_j\left(\overrightarrow{x}\right)=0,j=1,\dots ,n_j$$

(18)

$$x_k^L\le x_k\le x_k^U,k=1,\dots ,n_k$$

(19)

where $f_m\left(\overrightarrow{x}\right)$ represents the mth objective function to minimize/maximize, $g_i\left(\overrightarrow{x}\right)$ is the ith inequality constraint, $h_j\left(\overrightarrow{x}\right)$ is the jth equality constraint, and $x_k^L$, $x_k^U$ delimit the search space of the $x_k$ element in $\overrightarrow{x}$. The optimization problem is considered mono-objective if it only has one objective function.

There are different categories of optimization problems, according to specific characteristics of the objective functions, types of constraints, or the size and shape of the search space. One of these categories is the bilevel optimization problems, where for its solution, the optimization cases are divided into two sequential problems.

In this work, a bilevel optimization is implemented to solve a special problem. The solution set $\overrightarrow{x}$ in the first problem includes continuous variables as well as at least one integer variable, categorizing it among mixed optimization problems as described in [26]. Also, it can be considered a noisy optimization problem, applying the concepts in [27], where this type of optimization problem is described as one where the objective function is affected by a noise function, as shown in (20), where $N(0,1)$ is the normal distribution with a mean of 0 and a variance of 1.

$$\min f\left(\overrightarrow{x}\right)+N(0,1)$$

(20)

For this work, the optimization function is denoted by (21), where the set $\overrightarrow{w}$ corresponds to the weights of the NFC, whose size can vary in number depending on its architecture. It prevents the direct implementation of a metaheuristic, so in the first level of optimization, these weights are treated as noise elements. Different initialization values can lead to varying results, despite the learning component of the network. A uniform normal distribution is used to generate $\overrightarrow{w}$ in each evaluation of the function at the first level, considering that the gradient descent method mitigates the variance in the results. This consideration is used in diverse developments where the architecture is tuned without taking into account the initial value of the weights.

$$\min f(\overrightarrow{x},\overrightarrow{w})$$

(21)

On the other hand, the second optimization problem has an order constraint, and this means that any subset of $\overrightarrow{x}$ must satisfy the following: (22),

$$x_{k+1}\le x_{k+2}\le \dots \le x_{k+n}$$

(22)

In general, these definitions will be used to model an optimization problem that, when solved, results in the tuning of an NFC to perform the task of trajectory tracking in the transesterification process.

4. Bilevel Optimization for Tuning a NFC

In this work, the parameter tuning of an NFC is approached as a bilevel optimization problem to minimize an error function. In order to evaluate this proposal, it is compared with the method described in [13] using the same error function. This function is presented in (23), where e is calculated as the difference between a signal control and the behavior result of applying the NFC to a system.

$$f\left(\overrightarrow{x}\right)=\sum _{i=1}^k\left(\right|e_i\left(\overrightarrow{x}\right)|+L|\dot{e_i}\left(\overrightarrow{x}\right)\left|\right)$$

(23)

In (23), the decision variables in $\overrightarrow{x}$ include the number of membership functions (m), which must be an integer; the continuous variables are the weights of the neural network [$w_1,w_2,\dots ,w_n$], where $n=m^2$; the parameters of the membership functions (${\varphi }_{j,k}$) and (${\sigma }_{j,k}$); and the learning rate constants ${\eta }_{\varphi },{\eta }_{\sigma }$ and ${\eta }_r$. L is a scalar used to manipulate the change over time that the control applies to the system.

One of the main contributions of this paper is the formulation of an optimization problem to apply a metaheuristic algorithm for solving the complete tuning of the NFC. The differential evolution (DE) algorithm was selected as the base metaheuristic for this proposal because it has been successfully applied in diverse optimization scenarios and has demonstrated competitive performance [28,29,30]. However, a significant challenge arises in this specific optimization problem due to the variability in the size of the weight vector [$w_1,w_2,\dots ,w_n$] since n changes according to the number of membership functions. This variability conflicts with the fixed-size solution vectors required by DE. To overcome this challenge, a bilevel optimization approach [31] is proposed, where the objective of the first or lower level is to determine the number of membership functions and perform a preliminary tuning of the NFC. The second (upper) level improves the tuning and finds the weights set randomly in the lower level (noise).

4.1. First Level

In the first-level optimization problem, the weights are excluded from the decision variables, resulting in a solution vector and a noise vector structured as in (24) and (25), respectively.

$$\overrightarrow{x}=[m,{\sigma }_1,{\sigma }_2,{\eta }_{\varphi },{\eta }_{\sigma },{\eta }_r]$$

(24)

$$\overrightarrow{w}=[w_1,w_2,\dots ,w_{n=m^2},{\varphi }_1,{\varphi }_2,\dots ,{\varphi }_m]$$

(25)

This separation ensures that the size of the solution vector ($\overrightarrow{x}$) is fixed. However, the vector needs to be complemented with weight values. To achieve this, each solution vector is combined with 10 randomly generated sets of weights of size $m^2$, and the combination that produces the lowest objective function is selected as the fitness for the solution vector. In the next optimization level, the elements in the noise vector are tuned, as they were undetermined in the lower level. An additional algorithm could be used at the first level to tune them, but this would increase computational costs. On the other hand, due to the learning capability of the NFC, different random sets have the potential to be good solutions, although not necessarily the optimum. An example of the same parameter set but with different noise vectors for a randomly selected system is shown in Figure 3.

Furthermore, an elitist selection mechanism has been incorporated to mitigate the effect of the noise, in that for new executions, the noise vector $\overrightarrow{w}$ that generates the lowest objective function is preserved. It is important to remember that this subset will be refined in the second-level problem.

The previous procedure addresses the challenge that not all variables can be simultaneously handled in this optimization process. Therefore, in the first-level optimization, the aim is to find the solution that best works with the randomly generated weight vectors. In other words, the goal is to identify the solution with the best performance when combined with the random weights. Similar concepts have been explored in the context of cooperative co-evolution [32,33,34].

Another important consideration is that the number of membership functions (m) is limited to integer values, whereas the remaining variables are real. Therefore, a mixed-variable optimization problem is carried out at the first-level optimization. Several authors have emphasized the performance issues of evolutionary algorithms in such scenarios, where the loss of population diversity leads to fast stagnation at integer values [19,20,21]. To prevent this premature convergence, the repulsion strategy proposed by Liu et al. 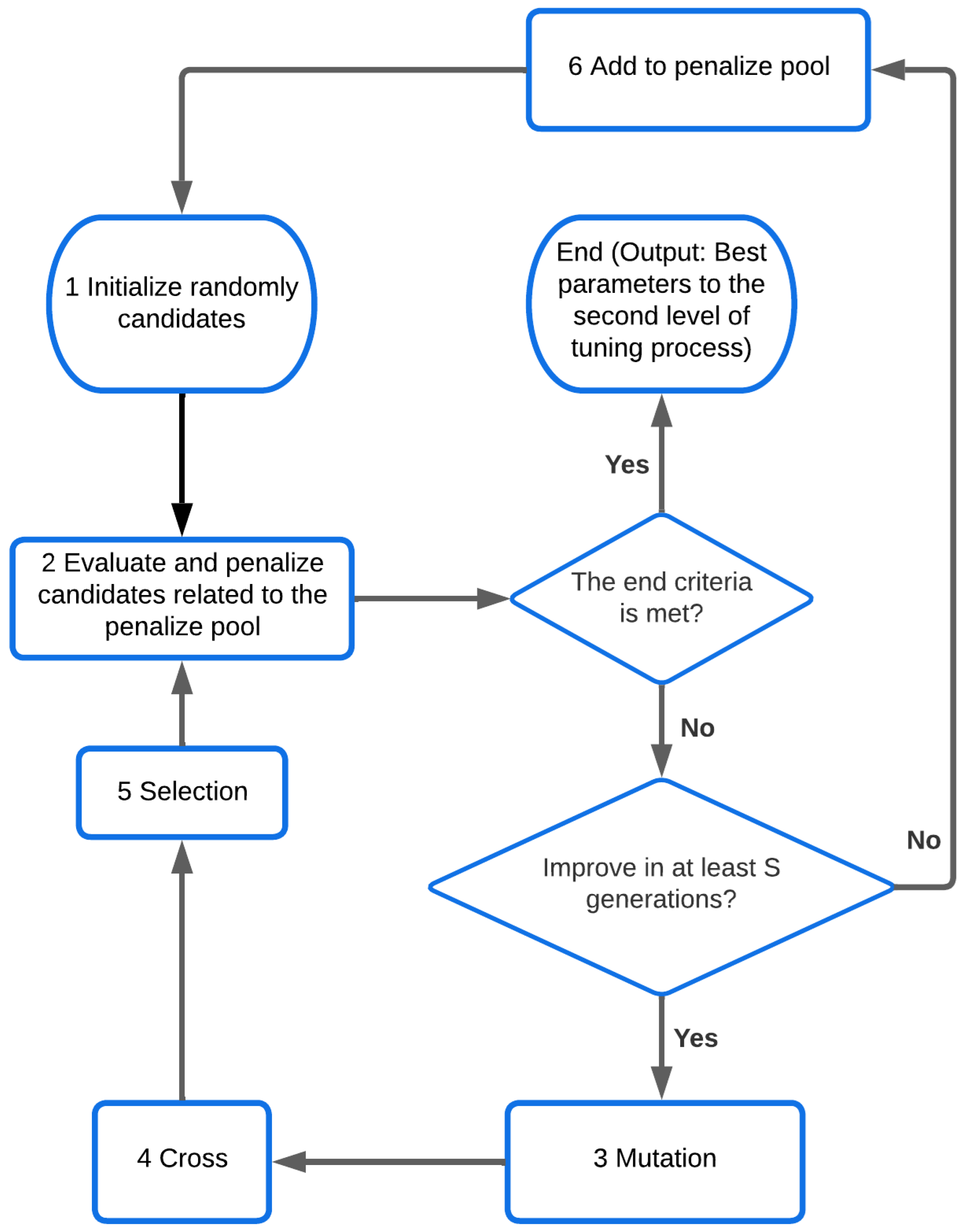[18] is employed in the low-level problem. In mixed-variable problems, the integer variables define several discontinuous feasible parts where the integer constraints are fulfilled. The repulsion strategy assumes that the population is trapped in one of these discontinuous feasible parts when there is no fitness improvement for a predefined number of consecutive generations. Under this condition, the population is reset, and the explored discontinuous feasible part is penalized to avoid attracting the population again.

The general process is shown in Figure 4, and the operations for the mutation, cross, and selection are described by (26), (27), and (28), respectively.

$$Mutant{x}^j=x^{r1}+F(x^{r2}-x^{r3})$$

(26)

$$New{x}_i=\left\{\begin{array}{cc}Mutant{x}_i,\hfill & rand(0,1)\le CR\hfill \\ Father{x}_i,\hfill & rand(0,1)>CR.\hfill \end{array}\right.$$

(27)

$$x^{g+1}=\left\{\begin{array}{cc}New{x}_i,\hfill & f\left(New{x}_i\right)\le f\left(x^g\right)\hfill \\ x^g,\hfill & other.\hfill \end{array}\right.$$

(28)

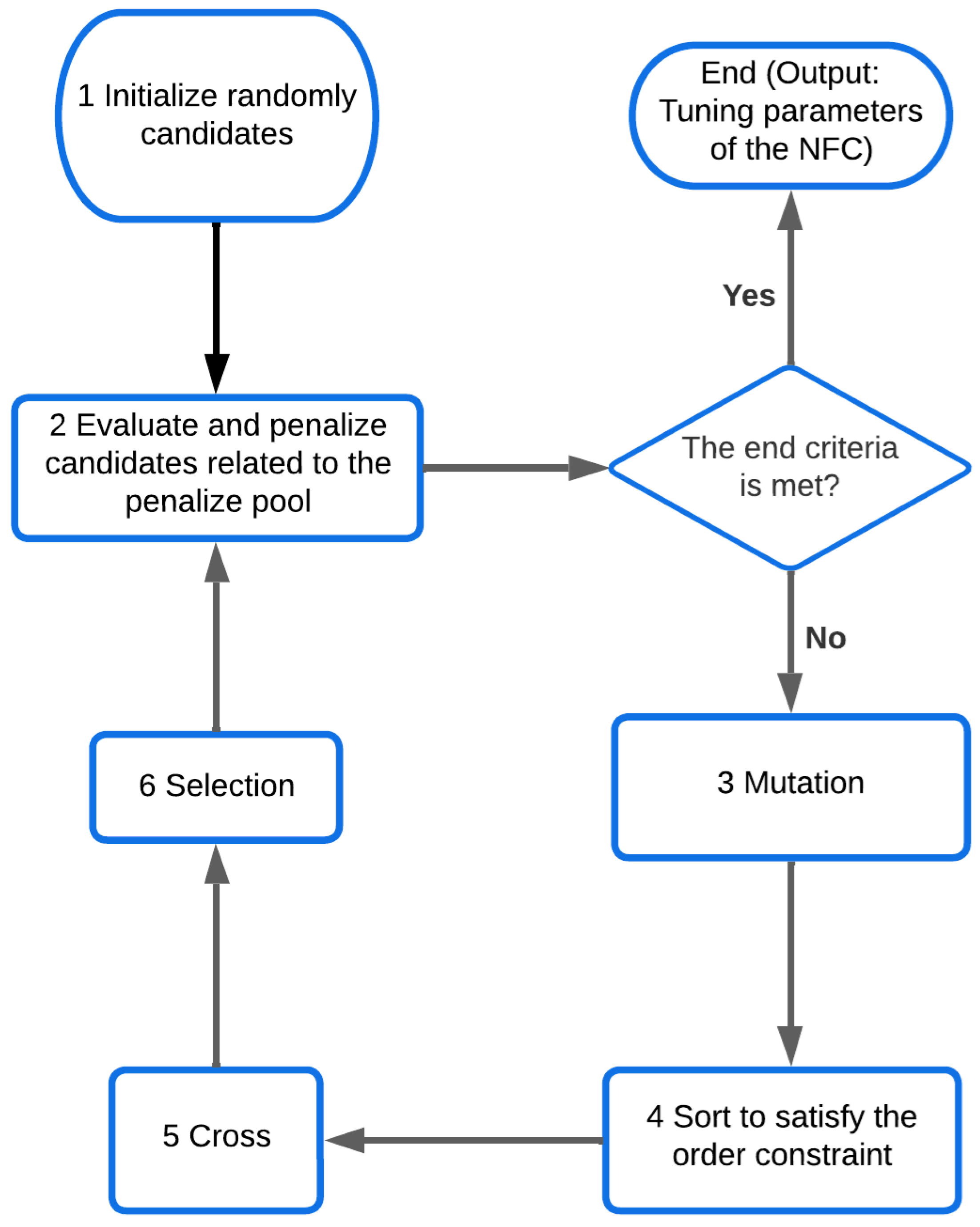
4.2. Second Level

The solution obtained in the first optimization level is transferred to the second level, where the weights of the NFC are tuned. The solution vector is structured as in (29), where m is fixed and taken from the solution in the previous level. In the second level, some elements of the solution vector are retaken considering that—although additional emphasis will be placed on the weights—it is possible that a different configuration would be better for the tracking task.

$$\overrightarrow{x}=[{\sigma }_1,{\sigma }_2,{\eta }_{\varphi },{\eta }_{\sigma },{\eta }_r,w_1,\dots ,w_{n=m^2},{\varphi }_1,\dots ,{\varphi }_m]$$

(29)

The original version of DE was employed for this stage, only with the inclusion of a sorting algorithm to address the ordering constraint for the elements in $w_i$. Figure 5 shows the process carried out in the second level.

5. Experiments and Results

In order to validate the proposed bilevel optimization method, the temperature model of the industrial plant for the biodiesel process described in [14] was used as a case study. As mentioned before, the results from the proposed method were compared with the tuning obtained in [13], where an NFC was applied to control a system with a disturbance.

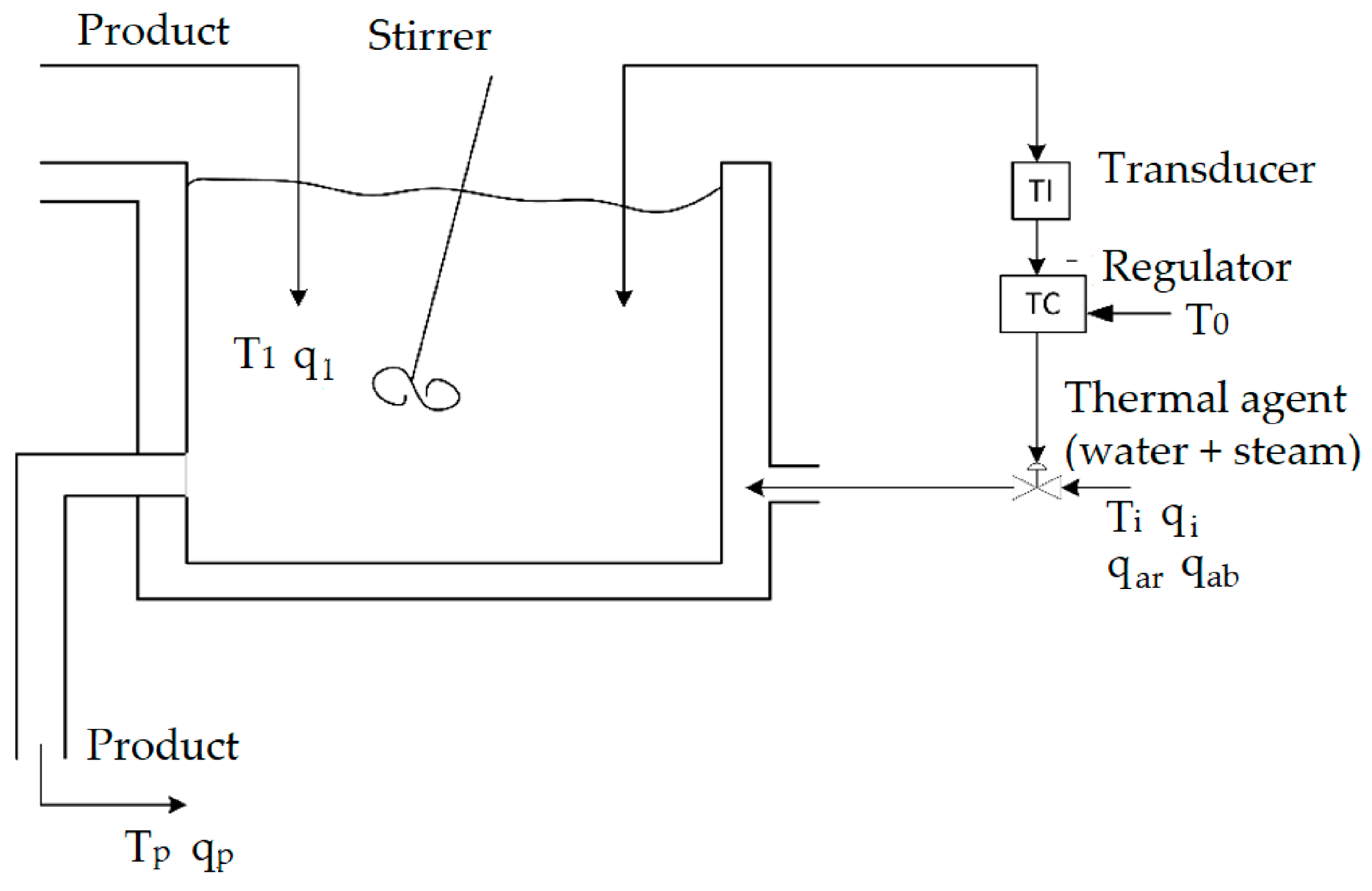
The plant shown in Figure 6 represents the system to be controlled. In the scheme, $TC$ corresponds to the temperature of the thermal agent, $Tp$ corresponds to the temperature of the output product, and $T1$ corresponds to the temperature of the product. The system was designed to maintain the temperature of the product $\left(T1\right)$ equal to $T0$, which is the reference temperature. This is achieved through a control system that uses a transducer to receive information from the tank. Mathematical modeling of the reversible chemical reactions that occur during the transesterification process is required before designing a biodiesel reactor, in order to establish a relationship between the control system and the process variables. In [35], the authors consider the transesterification reaction in three stages, with each intermediate reaction as a second-order reaction. The reaction of this process is described by (30), where $k_1-k_8$ denote the reaction speed constants.

$$\mathrm{Tg}+3{\mathrm{CH}}_3\mathrm{OH}\stackrel{{\mathrm{k}}_1-{\mathrm{k}}_8}{\leftrightarrow }\stackrel{\mathrm{k}7}{\leftrightarrow }3{\mathrm{RCOOCH}}_3+\mathrm{Gl}$$

(30)

This model considers the stirring intensity and the temperature effect on the conversion rate. It also quantifies the activation energy for the transesterification simulation at different temperatures and stirring rates [13]. Also, Komers’ model [36] takes into consideration the modeling of the reaction, the saponification, and the water content effect. It is the most complex model found in the literature and is described by (31), where Uv is the oil used in the reaction.

$$\mathrm{Uv}+3\mathrm{ROH}=\mathrm{Gl}+3\mathrm{Bd}$$

(31)

A serial array of three transfer functions is used to calculate the transfer function for the tank temperature. Equation (32) corresponds to the execution element where $KE=2$ and $TE=360$, (33) applies to the process with $Tp=1143$, $Kp=1$, and (34) denotes a gain. These parameters physically represent system properties and differentiate it from other systems that also produce biodiesel but with different production volumes. An explanation of how to find the numerical parameters of the system is included in [14].

$$G_E=\frac{K_E}{T_{E}s+1};$$

(32)

$$G_P=\frac{K_p}{T_{p}s+1};$$

(33)

$$G_T=2.$$

(34)

According to the data, (35) is the resultant transfer function of the system:

$$G_f=\frac{4}{\left(360s+1\right)\left(1143s+1\right)}.$$

(35)

The system can be treated as a batch process due to its characteristics, as mentioned in [14], and it is also possible to find a detailed explanation of the mathematical model developed in that work.

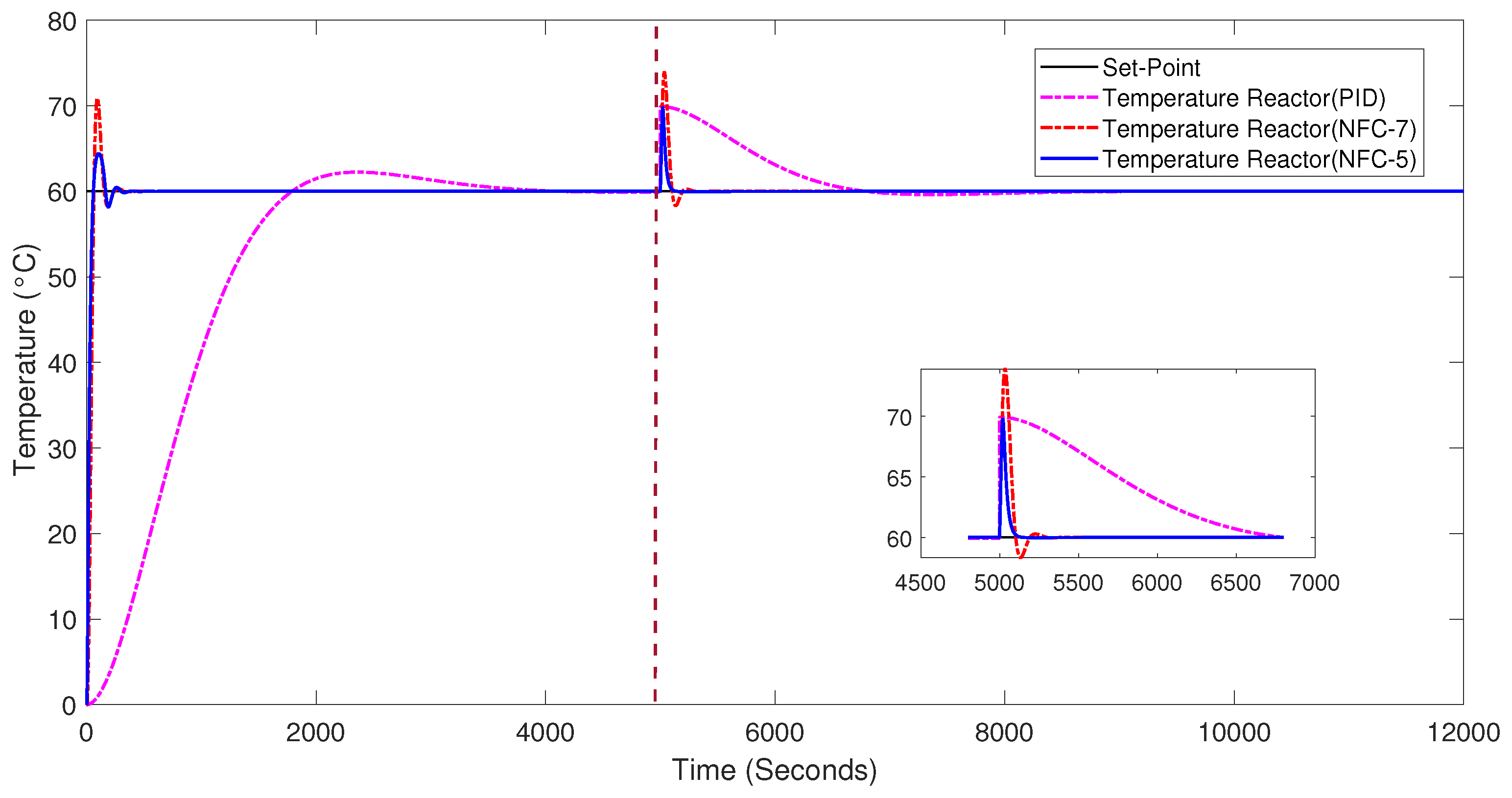
The tuning optimization algorithm and the equations for the NFC were programmed in MATLAB R2020a, which was also used for simulating the temperature control. The computing platform employed had the following specifications: Intel i7 processor @3.70 GHz, 16 GB RAM, and a Windows 11 operating system. The simulation shows 12,000 seconds of the controller’s behavior using the parameter sets generated by the proposed method. The task involves tracking a set point (60 °C) that suffers a disturbance at a time t = 5000 s. In both levels of optimization, the parameters for DE were set as follows, using the same settings as in [13]: scaling factor $F=0.6$, crossover rate $Cr=0.5$, and population size $NP=20$. In the first level of optimization, a stagnation criterion was employed, considering 400 consecutive generations without fitness improvement.

Table 1. List and range of tuned parameters for the NFC.

Parameter	Range
Parameter of the membership functions (${\varphi }_{j,k}$ and ${\sigma }_{j,k}$)	${\varphi }_{j,k},{\sigma }_{j,k}$ $\in \left[-100,100\right]$
Learning rate constants ${\eta }_{\varphi },{\eta }_{\sigma },{\eta }_r$	${\eta }_{\varphi },{\eta }_{\sigma },{\eta }_r$ $\in \left[0.0001,3\right]$
Number of member functions m	$m\in \mathbb{Z}\cap \left[3,15\right]$
Initial weights $\overrightarrow{w}$ referred to as $r_j$	$w_i\in \left[0.0001,50\right]$

shows the range of each variable.

This parameter selection meets the recommendations in [37] and the results documented in [38], indicating that the optimal search capacity and convergence speed are sensitive to the control parameter choice. In particular, for $F=0.6$, it is suggested that a value of $CR$ be in the range of $[0.3,0.9]$. $CR=0.5$ has been used as a fixed value or as a starting point for diverse DE variants in [39,40], respectively, producing good results.

The stop criterion was the maximum number of evaluations of the objective function. For the lower problem, it was set at 500,000, while in the upper level, 50,000 evaluations were carried out. This is because, in the first level, 10 noise samples were considered in each evaluation to obtain the final value used for DE. The resulting number of membership functions and the optimization function value in the first level of the tuning process are shown in

Table 2. Objective function values obtained in the first level of the tuning.

	Number of Membership	Noisy Optimization
Run	Functions $\mathit{m}$	Function Values
1	8	$5766.2$
2	7	$5567.9$
3	5	$5875.4$
4	5	$5796.7$
5	13	$5968.0$
6	11	$5962.3$
7	5	$5800.3$
8	5	$6016.5$
9	5	$5272.5$
10	5	$5748.8$
Average	$6.9$	$5777.5$
Standard deviation	$2.9231$	$220.5$

, also including their average and standard deviation.

Five different values for the number of membership functions, m, were obtained from the lower problem. The value with the best performance (and also the one that appeared most frequently), m = 5, was used in the second level to determine the best configuration for the NFC. The final results are shown in

Table 3. Objective function values using five membership functions.

Run	Optimization Function Values
1	$4824.6$
2	$4949.8$
3	$4785.3$
4	$4918.3$
5	$4877.5$
6	$5081.2$
7	$4804.4$
8	$4878.1$
9	$4799.0$
10	$4961.8$
Average	$4888.0$
Standard deviation	$92.6$

. The best result from the upper-level optimization was simulated for the tracking task of the controller. Additionally, the results obtained in [13,14] were simulated, corresponding to an NFC controller with a different architecture than that obtained by the bilevel optimization approach in this work and to an analytically tuned PID controller, respectively (see Figure 7). In quantitative terms, to evaluate the performance of the controllers, Equation (23) was used, which is a function that penalizes the error in the monitoring task. So, the closer the value is to zero, the better the controller is considered. The best performance was obtained by the NFC with the tuning in this work through the bilevel optimization approach with a value of $f_{NFC5}\left(\overrightarrow{x}\right)=4785.3$, followed by the NFC reported in [13] with a value of $f_{NFC7}\left(\overrightarrow{x}\right)=5641.9$, and finally, the PID controller reported in [14] with a value of $f_{PID}\left(\overrightarrow{k}\right)=\mathrm{59,076.6},$. The function $f_{PID}\left(\overrightarrow{k}\right)$ refers to Equation (23) in the sense that error metrics between the obtained signal and the desired value are used to evaluate the performance of the controllers, but in the case of the PID controller, these would be subject to the gains of the PID controller $\overrightarrow{k}$ instead of the architecture and values of the NFC $\overrightarrow{w}$.

The simulation begins at 0 °C due to the characteristics of the transfer function with zero initial conditions. However, in the real world, it must start from the ambient temperature of the place where the process is located. The disturbances are generated by agents that are external to the process or by failures in the system itself. They normally cannot be measured and are unknown. Figure 7 shows an upward and abrupt change in the reactor temperature at 5000 s, which is rejected by the proposed controller. In the simulation, it is interpreted as an external source described by a step function, which is added to the output of the system’s transfer function. According to the process described in Figure 6, this increase in temperature may have originated, for instance, because the system was operating on a very hot day combined with a failure in the operation of the valve responsible for supplying water and steam, which opened for an instant to its maximum capacity. It could also be caused by more than one factor. Designing a controller that can respond to a disturbance is essential in optimizing the performance of production processes.

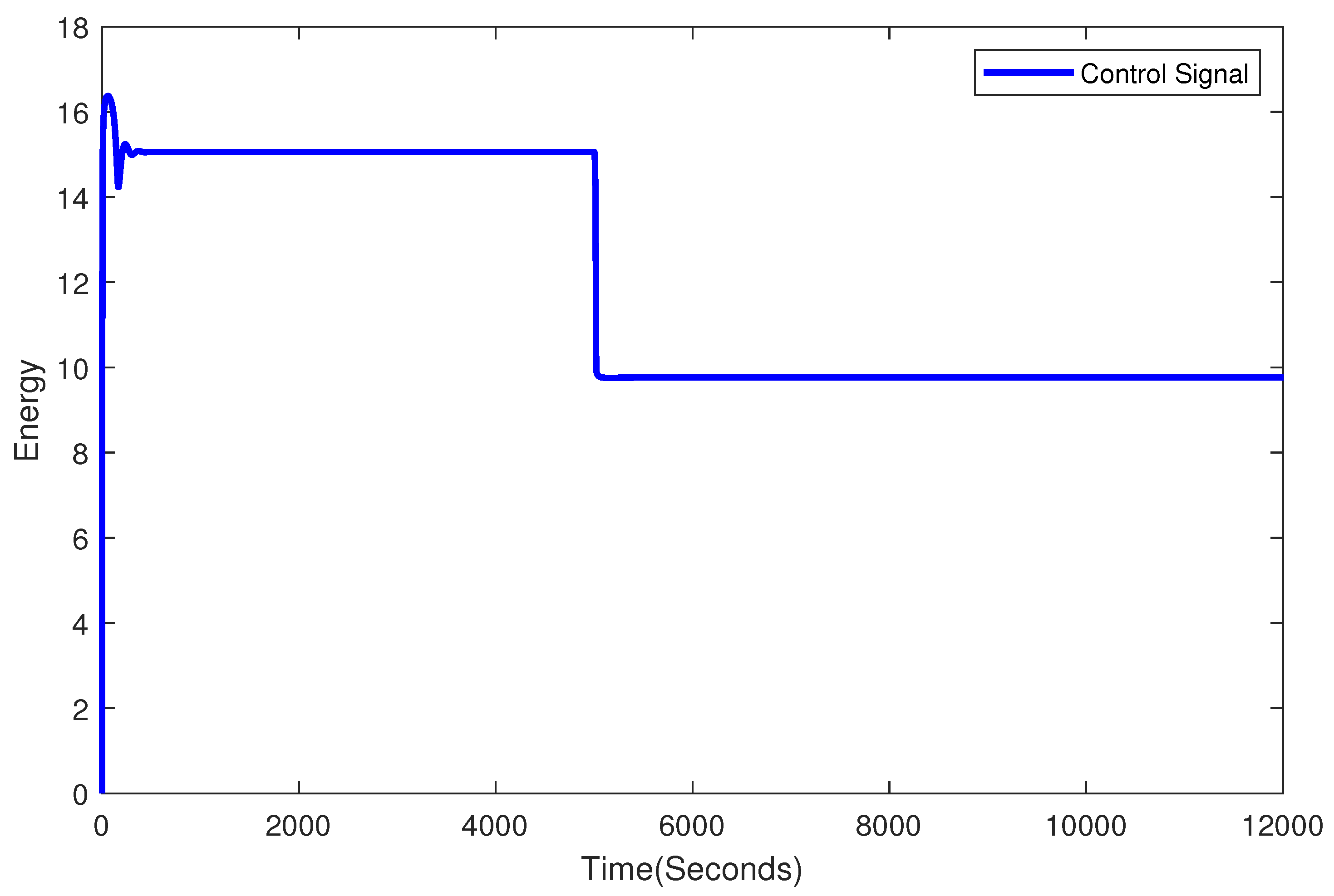
Figure 8 presents a brief example of how the control signal exerted on the manipulated variable of the system can be interpreted. It shows the control signal produced by the proposed controller (NFC-5), which in turn generates the corresponding dynamic presented in Figure 7 along with the results from other proposals in the literature. It should be noted that this corresponds to the case study presented in [14], which entails the restrictions mentioned in that work. However, it allows us to clarify the inherent and important relationship of the control action with the elements and components of a real system. According to the control action, it should be noted that the stabilization of the system and its fast convergence occur due to the dynamic process of the system where the control action signal is divided into two parts. The first one refers to the heating of the reactor, in this case, governed by a control valve that allows the passage of water and steam to the tank jacket. The second part refers to a cooling process through a natural action of the system to dissipate heat due to its design characteristics or by a subsystem. For example, a cooling tower lowers the temperature of the service water for water supply to the reactor jacket through a valve alignment process, which initiates a reverse action in the control signal. The ability of a system to achieve the conditions found in a simulation will depend exclusively on the design characteristics of the system. However, this does not mean that the control actions cannot be achieved. It may even involve a process of reengineering or modifying the current process to optimize the industrial process.

In the literature on automatic control theory, it is possible to find a wide variety of approaches and techniques aimed at solving theoretical problems with real-world applications. An approach that relies on human experience and can adapt over time to different operating conditions, considering the environment in which it is situated, could represent a desirable situation for its implementation.

5.1. Applying the Proposed Method in a Real-World Scenario

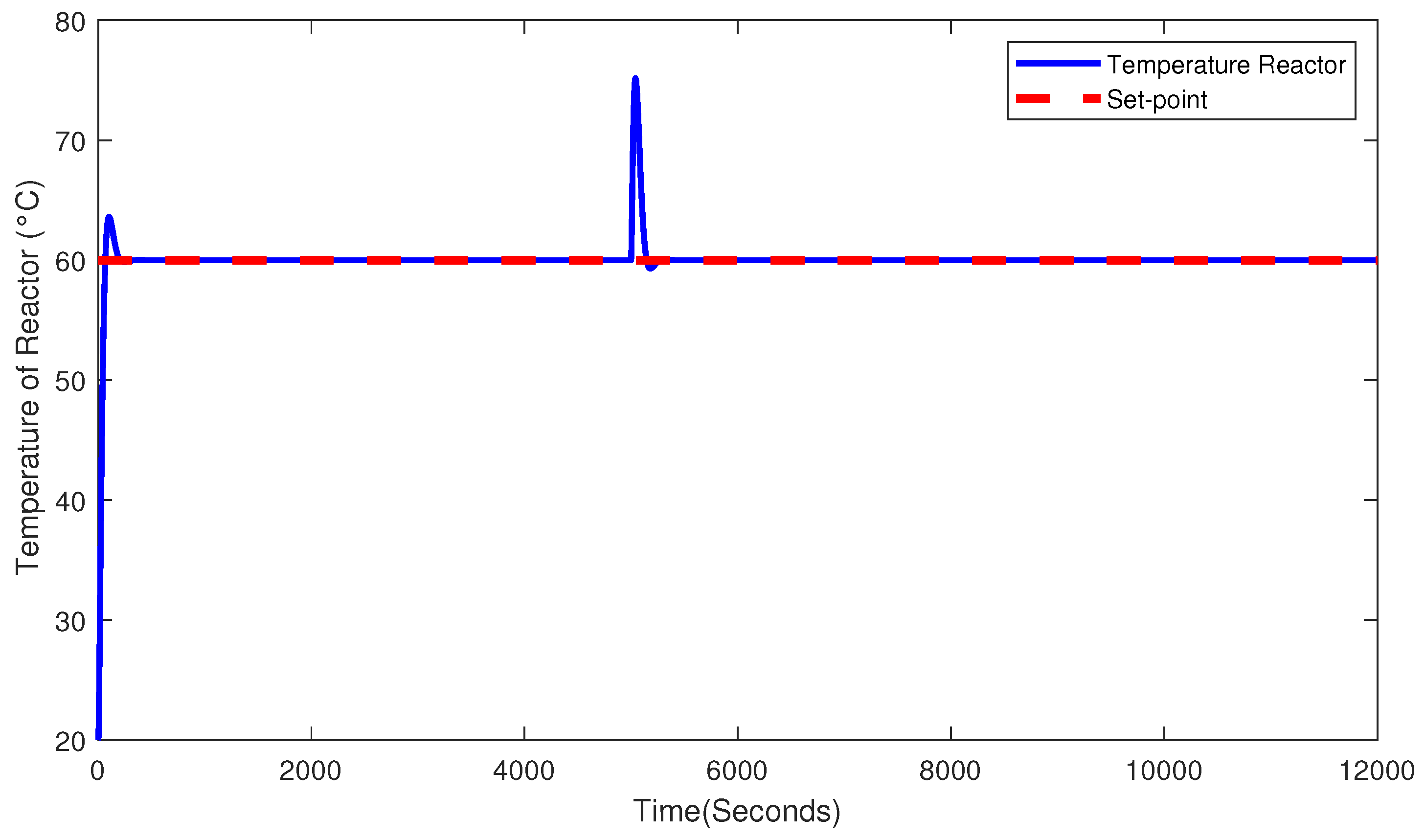
The simulations in Figure 7 were carried out by considering an initial temperature of 0 °C, as used in [13,14]. In order to show the flexibility of the method in different scenarios, the optimal tuning parameters were obtained for a given assumption, in which the ambient temperature was 20 °C and must reach 60 °C. The dynamics of the temperature reactor considering this condition with the NFC5 and the PID controller are shown in Figure 9. In this simulation, the optimization function was $f_{NFC5}\left(\overrightarrow{x}\right)=4618.1$, which is slightly lower than what was obtained in the previous simulations. This is mainly due to the initial starting condition because, in the first seconds of the simulation, the error is smaller. This is an expected result since the performance should improve by finding and implementing adequate tuning for the NFC in a more favorable scenario.

5.2. Discussion

The results reported in [13] show that the NFC performs the task of the case study efficiently. Those results are presented in

Table 4. Objective function values using seven membership functions [13].

Run	Optimization Function Values
1	$6762.7$
2	$7218.1$
3	$5888.4$
4	$5956.0$
5	$5641.9$
6	$5768.8$
7	$5959.0$
8	$6007.2$
9	$5979.6$
10	$6039.6$
Average	$6122.1$
Standard deviation	$484.8$

. However, in that work, the authors began modeling the architecture of the controller by biasing the tuning, using an initial configuration based on the experience of a designer who suggested using seven membership functions. On the other hand, the main goal of the proposed method in this paper was to tune the NFC without any bias while trying to improve the response of the controller. The results of both approaches were compared to evaluate the performance of this proposal.

From the information in Table 2, Table 3 and Table 4, it can be observed that after applying the bilevel-optimization tuning algorithm, the number of membership functions was reduced to five, contrasting with the seven in the original development. This parameter (m = 5) was used as a constant to determine the rest of the optimal tuning parameters, which obtained better performance than those generated with seven membership functions. The worst solution of the tuned parameters obtained with the proposed method (Run 6, Table 3) is better than the best solution reported in the original work (Run 5, Table 4).

It should also be mentioned that the lower level achieved competitive results without the need for refining the noise parameters since some with varying numbers of membership functions obtained preliminary results that were better than those reported in Table 4. The difference in the standard deviation of the objective function between the lower and upper levels can be attributed to the noise vectors and the architecture of the controllers, as a result of the variation in the number of membership functions.

A direct consequence of using fewer membership functions is that it simplifies the design problem and, from a control perspective, allows for easier implementation. Despite the proposed approach yielding better results, it has a drawback: it uses more computational time because the first level of the tuning algorithm requires a considerable number of executions. However, in cases where the possible behaviors of the controller under specific conditions are unknown, using this algorithm is recommended to generate candidate parameters and subsequently refine them using processes such as metaheuristic algorithms. This approach is a safety measure to prevent potential overreactions due to poor tuning. It is advisable to establish a good initial setting, like the one calculated with this proposal, to enable the NFC to handle potential events such as overheating in the reactor, which was considered in the simulation.

A common practice in the literature is to report the results of the tuning process and claim that one controller is better than another based on the final results (but without mentioning the sensitivity of the controller). In the case of the NFC, it may not be well-tuned because there are many solution vectors ($\overrightarrow{x}$) that produce similar behaviors. The objective function computed with those vectors using MATLAB software can produce an infinite value as output, as the difference between the control point and the controller output is very large. 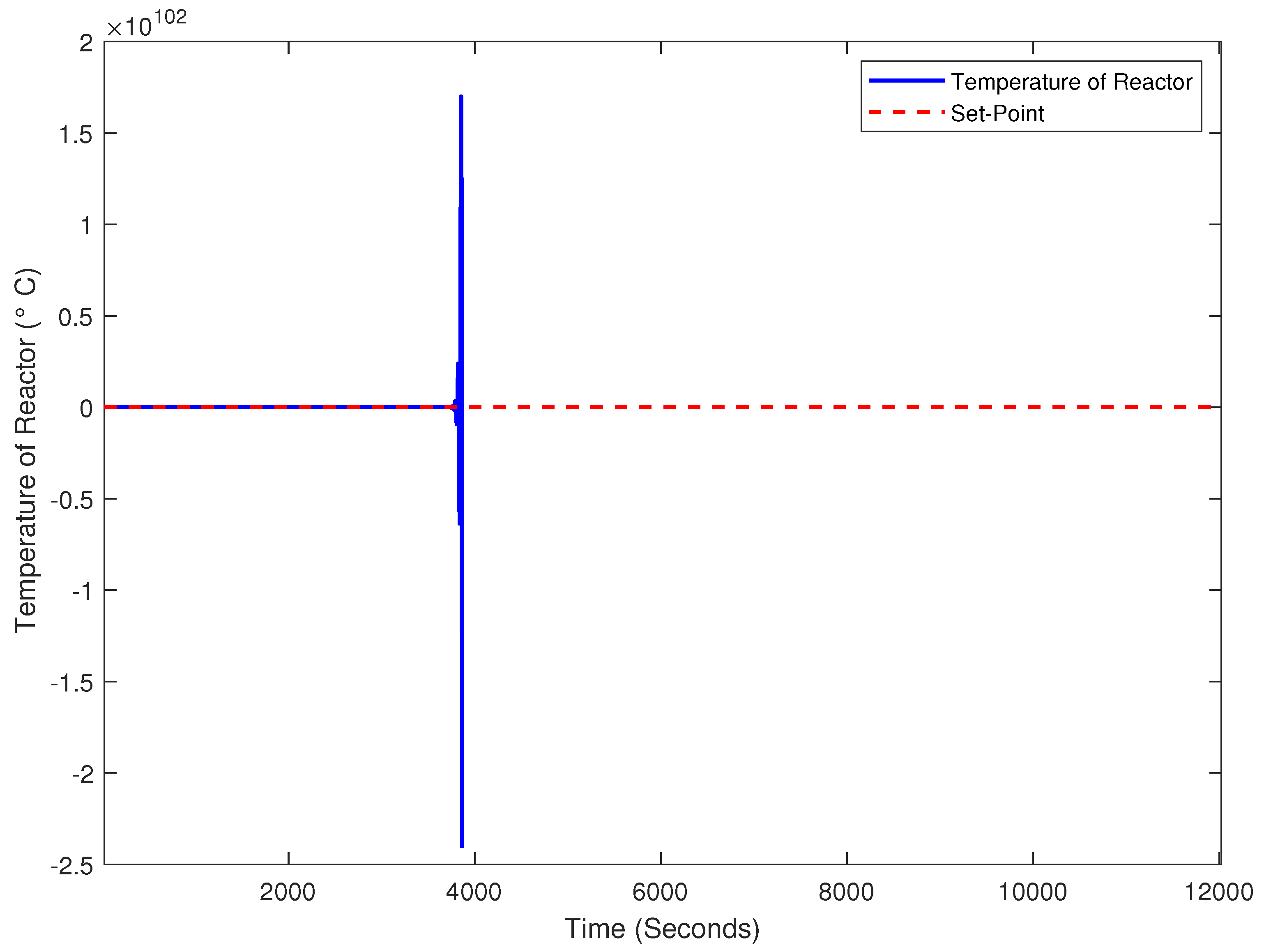Figure 10 shows the dynamics of the mathematical model of the reactor temperature using one of the worst possible settings for the NFC. The graphic presents temperature magnitudes in the order of ${10}^{102}$. While this is not realistic, it corresponds to the overreaction that a poorly tuned NFC has to a disturbance in the mathematical model used for the plant (which maps to infinite values). In real life, although the simulation would not be compatible with the real world because the temperature exceeds the melting point of the tank material, the system actuator would not be able to handle what was requested by the controller, and the behavior of the plant would become unpredictable due to different failures. So, this simulation serves as an example to highlight the importance of properly tuning the NFC.

This information is relevant for the methodology, particularly for selecting the metaheuristic and providing a reference for future works that may explore other solution algorithms. DE works with a set of solutions (a population), so if at least one solution in the initialization has an objective function with a computable output (not infinite), the other individuals will eventually be attracted to the neighborhood of that solution. For this reason, algorithms that work with a single solution face the problem that if the first attempt results in an infinite value, and the next solution does as well, it becomes a complicated task to decide which is better.

6. Conclusions

In this work, a bilevel optimization method applied to a tuning process was presented to determine the best operating parameters of a neuro-fuzzy controller. The case study is relevant because it represents a difficult optimization problem, with candidate solutions being vectors of different dimensions containing both integer and continuous variables. In addition, the search space includes vectors mapping to infinite values, which must be considered unfeasible solutions. Consequently, this creates an incompatibility with most metaheuristic techniques that require vectors to be of the same dimension to perform operations that explore and improve candidate solutions. The approach involves transforming the main problem into a sequence of a noisy mixed-variable optimization problem followed by an optimization problem with order constraints and adjustments to the metaheuristics used for its solution. From this approach, it is possible to obtain a better tuning NFC compared to the biased tuning by the criteria of human experience, presented in previous works.

The NFC configuration obtained by the proposed method not only demonstrated better performance according to an error-based metric but is also simpler to implement because it uses fewer membership functions. This reduction translates into fewer weights and operations required to calculate the control signal. Additionally, the proposal offers flexibility by tuning the optimal parameters of the controller based on its behavior in a particular system, making the methodology replicable for other plants.

As part of future work, other metaheuristics and search strategies can be applied to evaluate their performance in order to achieve better tuning and find ways to reduce the number of evaluations for individuals with non-computable objective functions. From the point of view of controller design, it is necessary to carry out an exhaustive analysis of the mathematical model to limit the configuration space and avoid overreaction.