Adaptive-Dynamic-Programming-Based Robust Control for a Quadrotor UAV with External Disturbances and Parameter Uncertainties
Abstract
:1. Introduction
- (1)
- Two fixed-time NN-based observers (FTNNOBs) were developed to compensate the control inputs of quadrotor UAV, which can estimate external disturbances and parameter uncertainties in a fixed time. Different from the traditional NN approximators designed in [33,34,35], the FTNNOBs only need to adjust the scalar parameters rather than the weight vectors or matrices. They provided a simple structure and inexpensive computation.
- (2)
- A novel ADP-based robust control scheme is proposed by combining the ADP technique with the estimated information from FTNNOBs, which improves the tracking control accuracy and optimizes the control cost consumption. Different from the existing weight update laws of AC NNs [16,25], two novel weight update laws were introduced in this work. They not only have a simple structure, but are also independent of the PE condition. Moreover, two auxiliary terms related to the system states were introduced to improve the data utilization efficiency of the AC NNs and make the training results more effective.
2. Model Description and Transformation
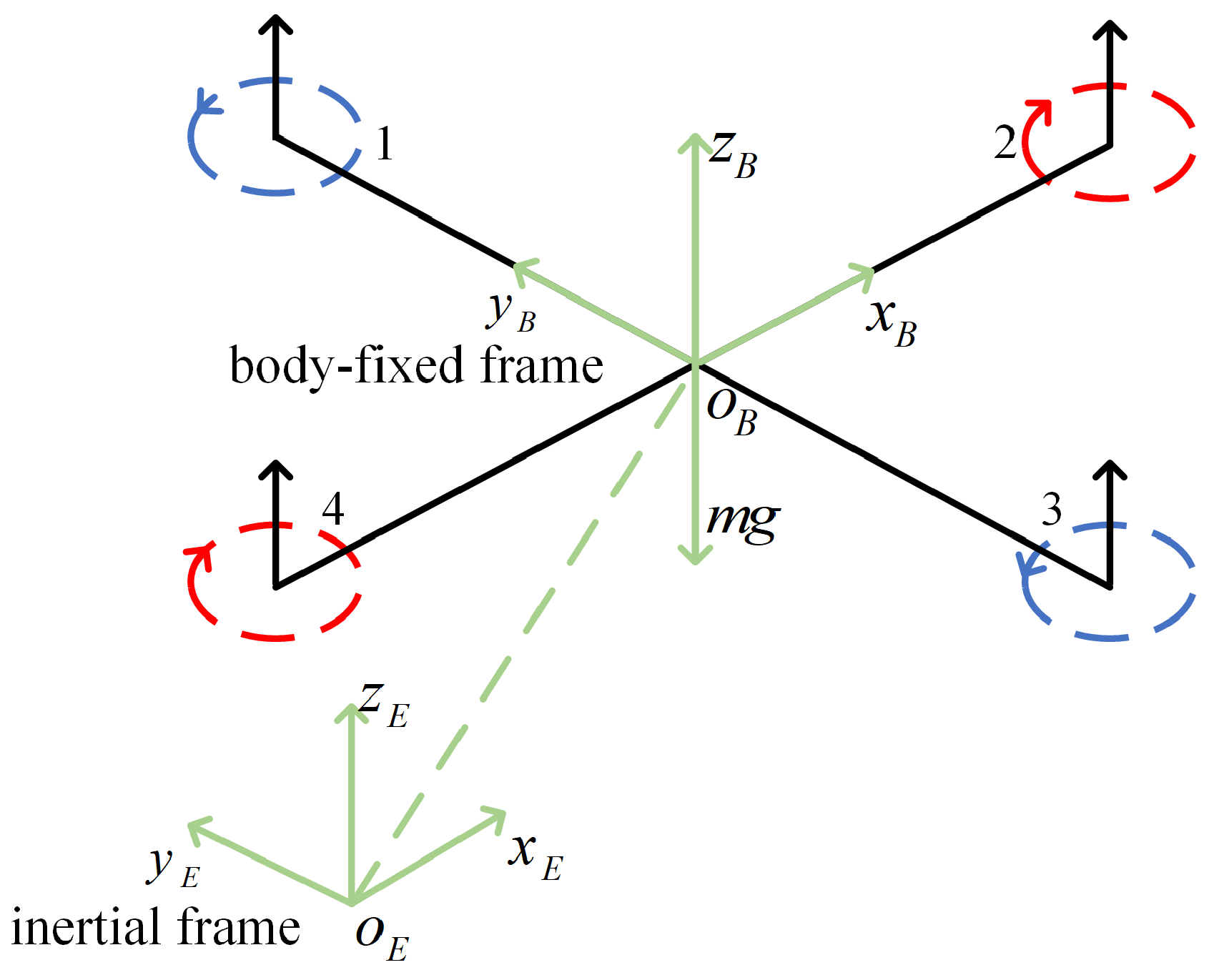
2.1. Dynamics Model
2.2. Model Transformation
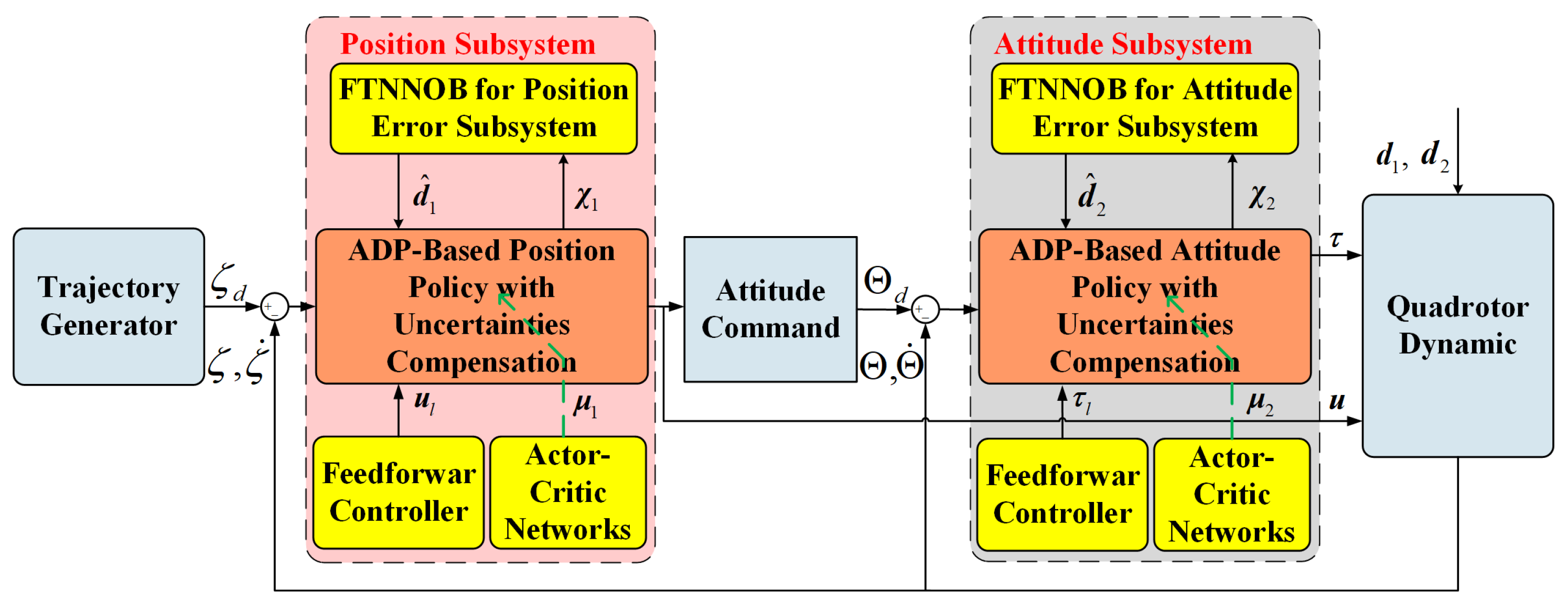
3. Adaptive-Dynamic-Programming-Based Robust Control Design
3.1. Online-Uncertainty-Compensation-Based Fixed-Time NN-Based Observers
3.2. ADP-Based Nominal Optimal Control Design
3.3. Adaptive-Dynamic-Programming-Based Robust Control Law Design
4. Simulation
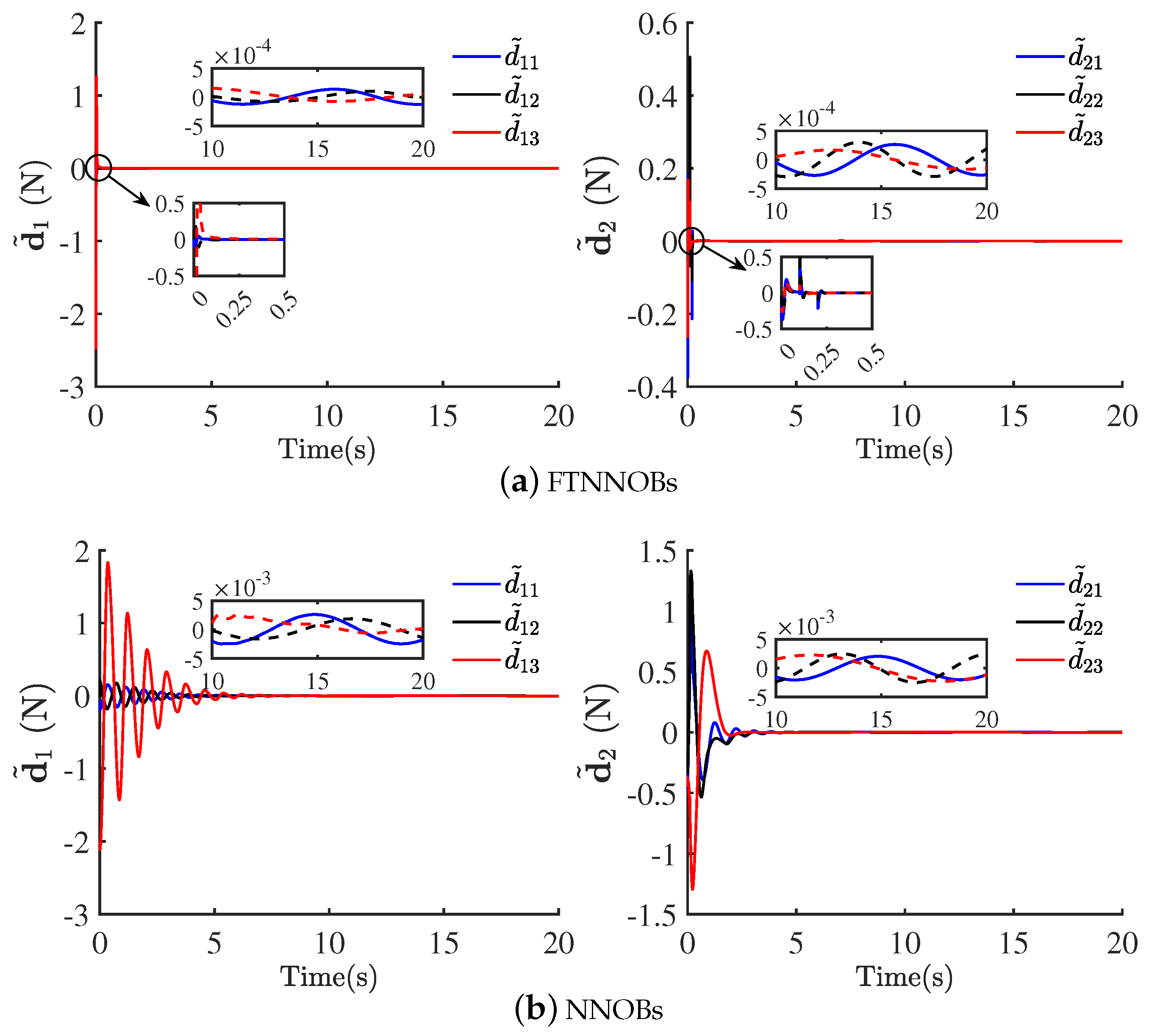
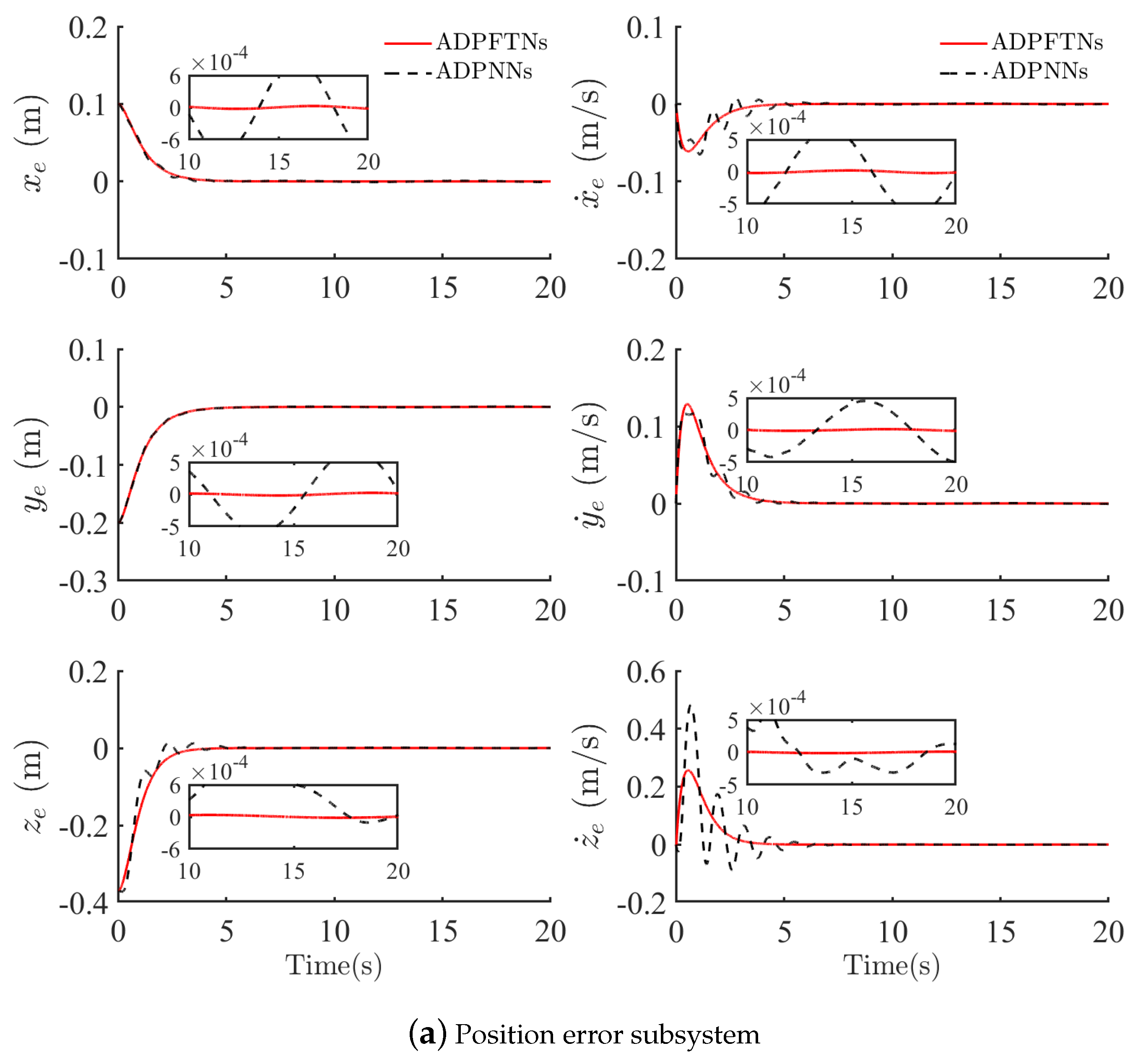
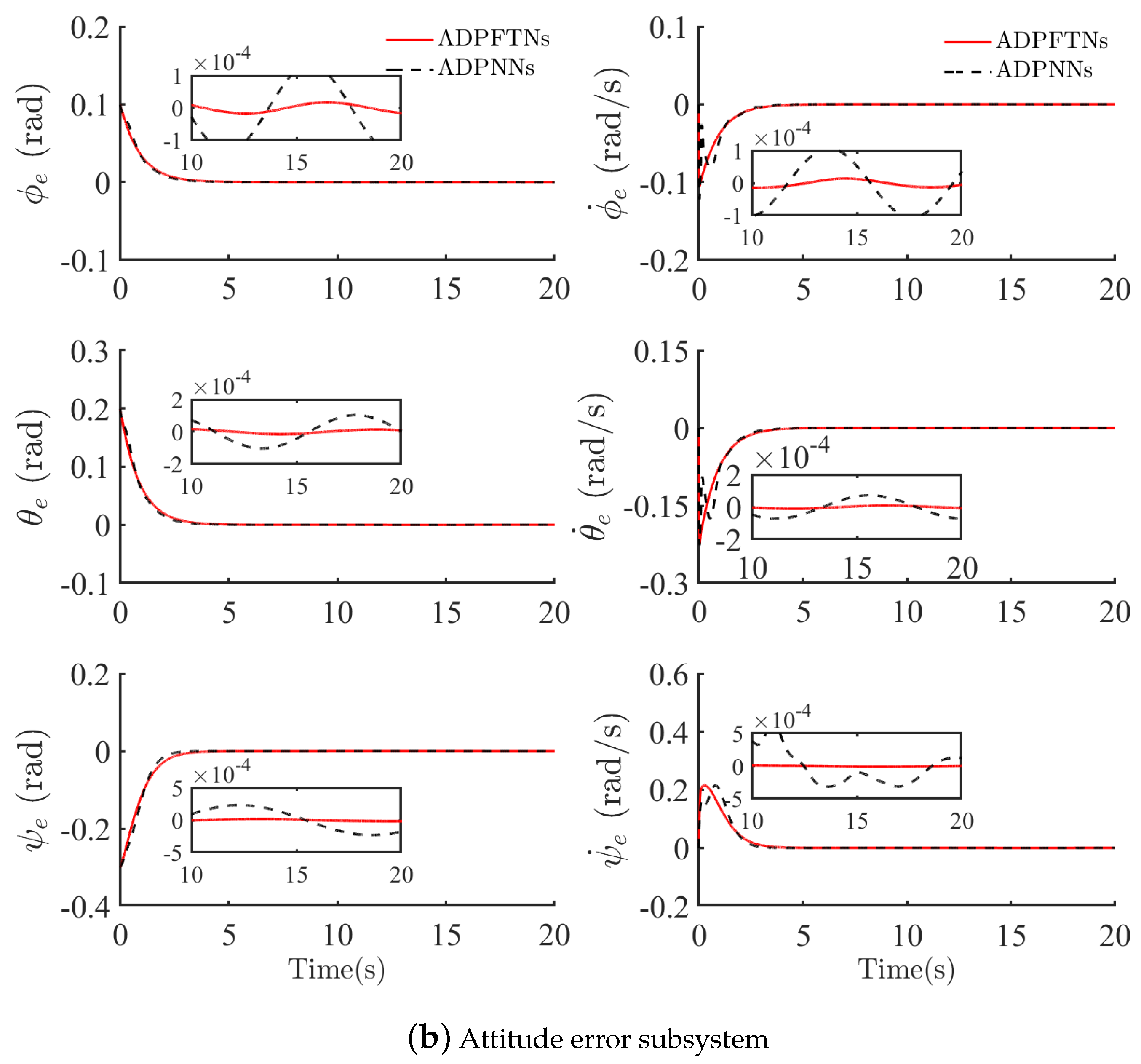
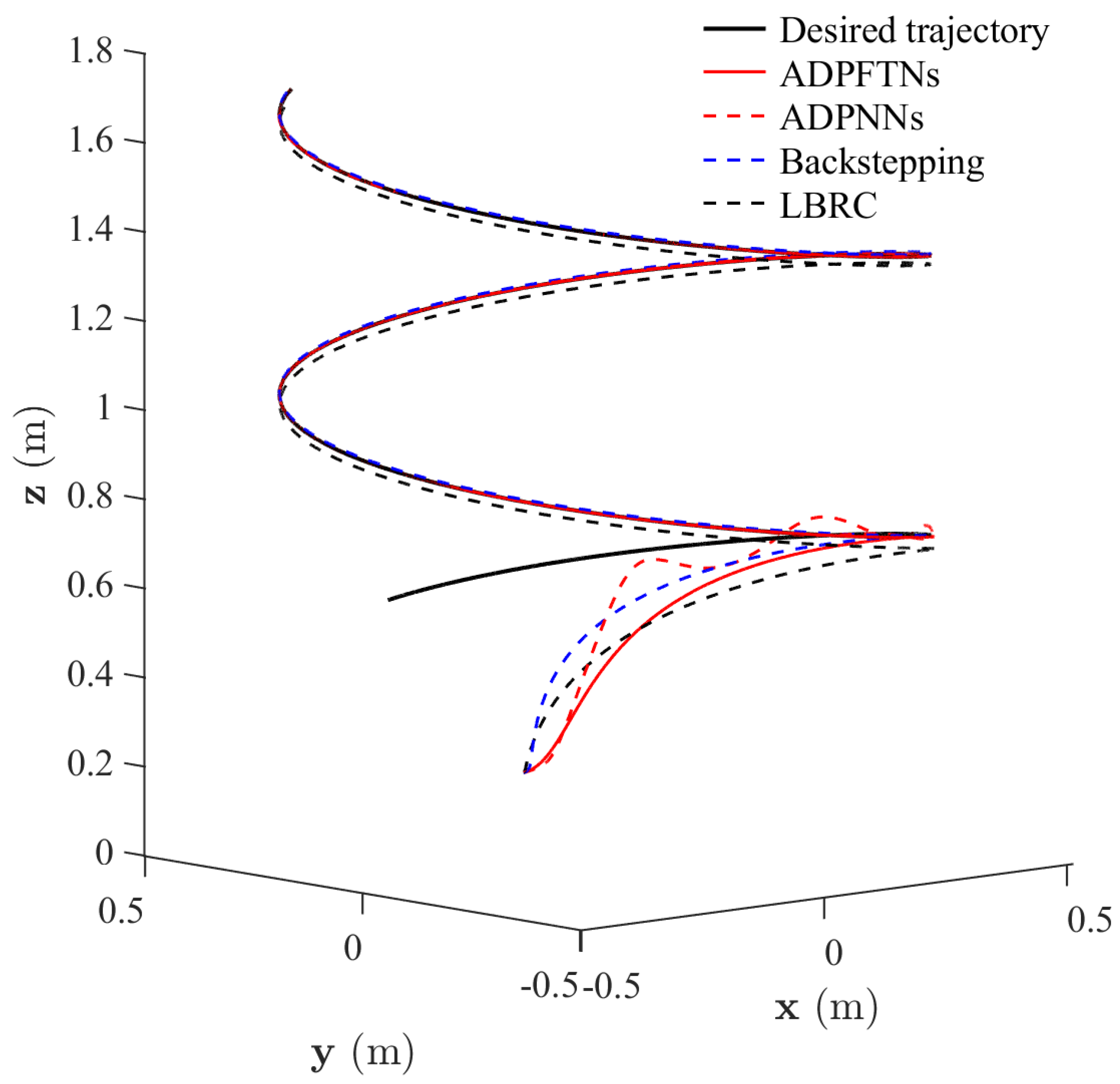
4.1. Robust Tracking Control Performances with Uncertainty
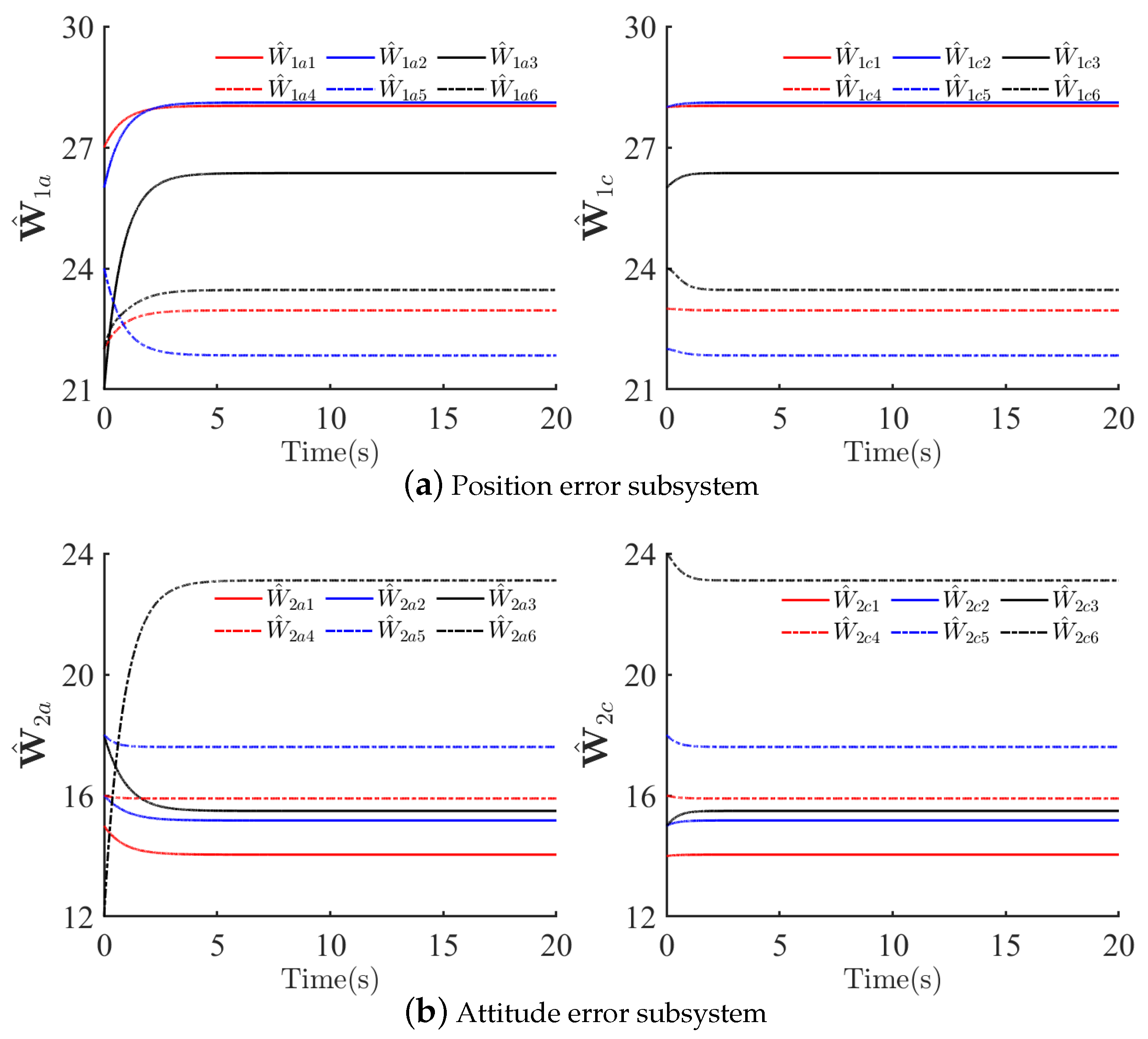
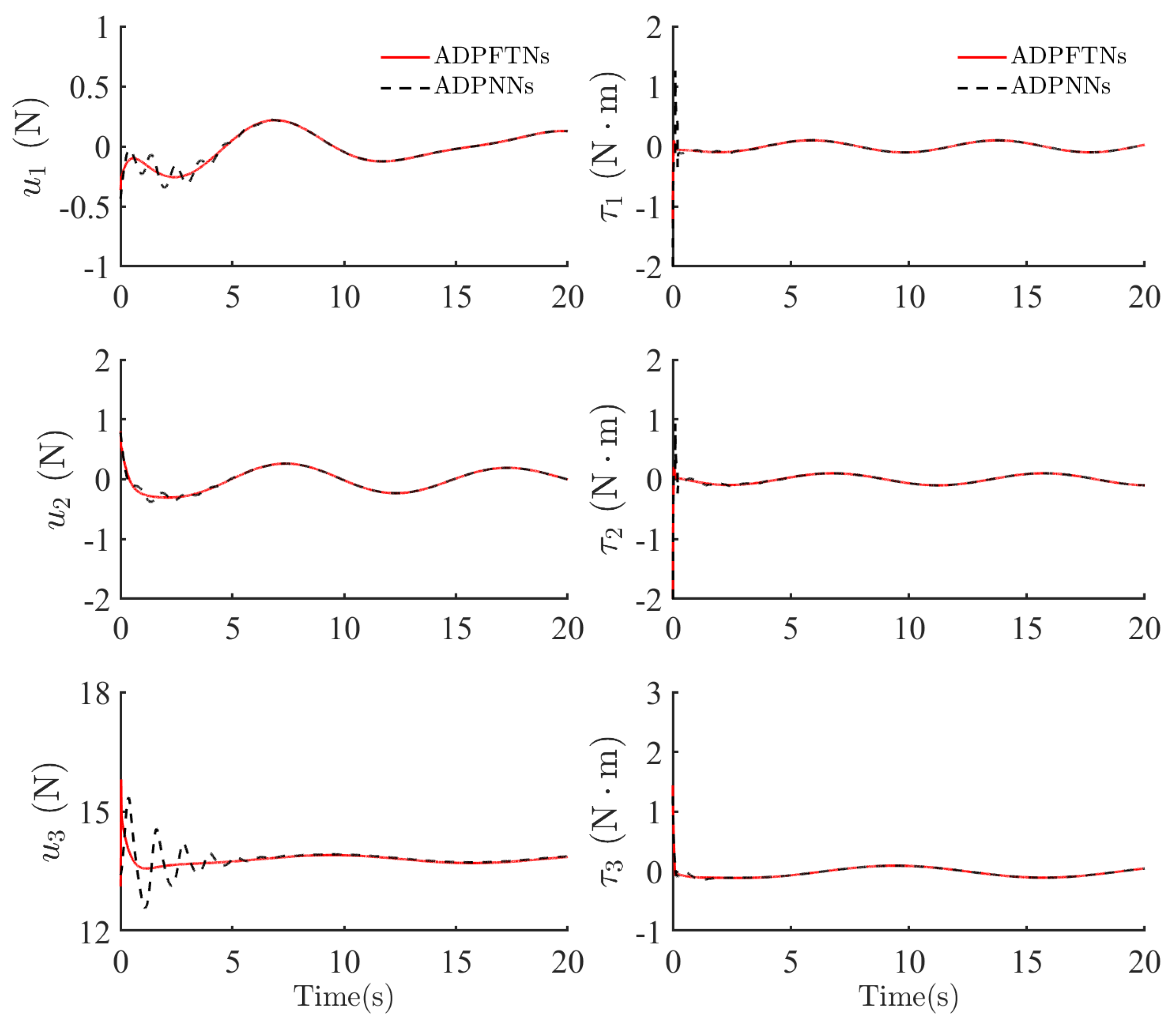
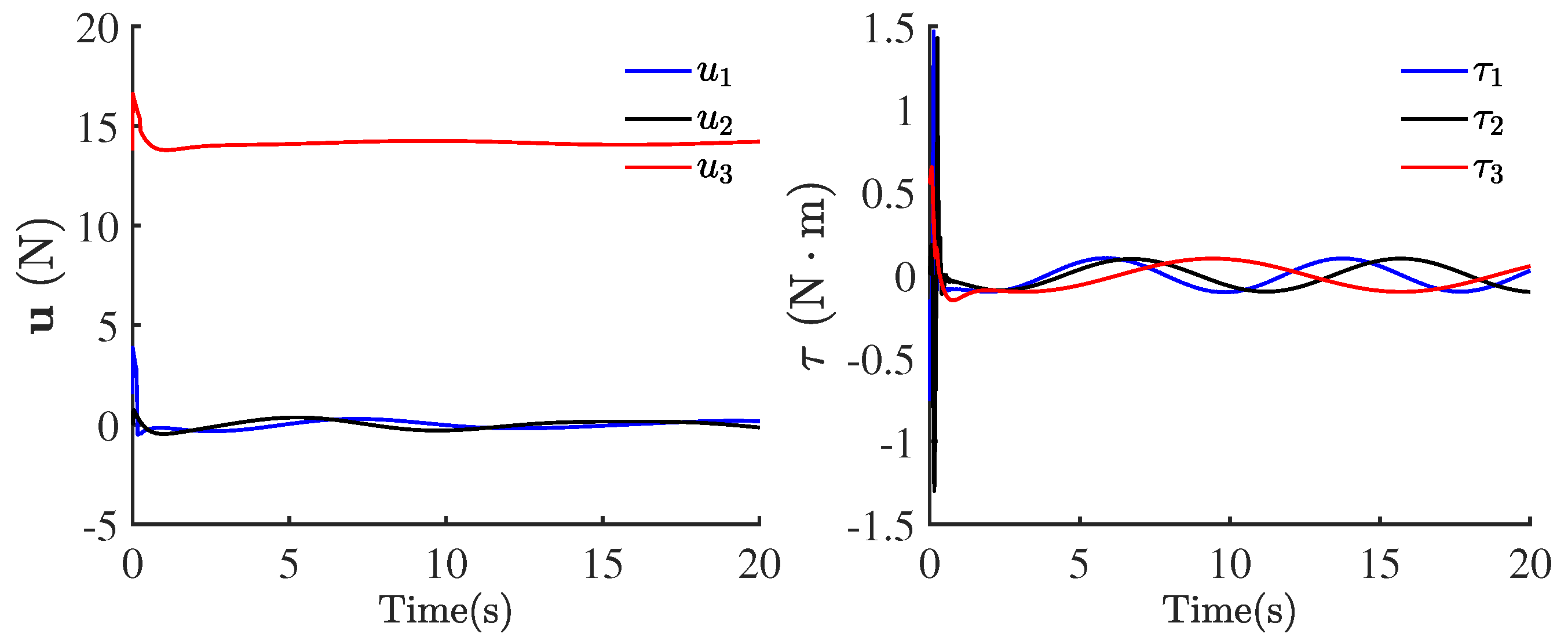
4.2. Tracking Control Performances and Cost
4.3. Matlab/Simscape Simulation Results
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, N.; Shao, X. Desired compensation RISE-based IBVS control of quadrotors for tracking a moving target. Nonlinear Dyn. 2019, 95, 2605–2624. [Google Scholar] [CrossRef]
- Das, D.N.; Sewani, R.; Wang, J.; Tiwari, M.K. Synchronized truck and drone routing in package delivery logistics. IEEE Trans. Intell. Transp. Syst. 2021, 22, 5772–5782. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, S.B.; Hu, X.T. Cooperative path planning of UAVs & UGVs for a persistent surveillance task in urban environments. IEEE Internet Things J. 2021, 8, 4906–4919. [Google Scholar]
- Gajbhiye, S.; Cabecinhas, D.; Silvestre, C.; Cunha, R. Geometric finite-time inner-outer loop trajectory tracking control strategy for quadrotor slung-load transportation. Nonlinear Dyn. 2022, 107, 2291–2308. [Google Scholar] [CrossRef]
- Li, B.; Gong, W.Q.; Yang, Y.S.; Xiao, B. Distributed fixed-time leader-following formation control for multi-quadrotors with prescribed performance and collision avoidance. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 7281–7294. [Google Scholar] [CrossRef]
- Labbadi, M.; Cherkaoui, M. Robust adaptive backstepping fast terminal sliding mode controller for uncertain quadrotor UAV. Aerosp. Sci. Technol. 2019, 93, 105306. [Google Scholar] [CrossRef]
- Michael, N.; Mellinger, D.; Lindsey, Q.; Kumar, V. The GRASP Multiple Micro-UAV Testbed. IEEE Robot Autom. Mag. 2010, 17, 56–65. [Google Scholar] [CrossRef]
- Sun, Y.B.; Xian, N.; Duan, H.B. Linear-quadratic regulator controller design for quadrotor based on pigeon-inspired optimization. Aircr. Eng. Aerosp. Tec. 2016, 88, 761–770. [Google Scholar] [CrossRef]
- Li, B.; Gong, W.Q.; Yang, Y.S.; Xiao, B.; Ran, D.C. Appointed Fixed Time Observer-Based Sliding Mode Control for a Quadrotor UAV Under External Disturbances. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 290–303. [Google Scholar] [CrossRef]
- Zhao, Z.; Cao, D.; Yang, J.; Wang, H. High-order sliding mode observer-based trajectory tracking control for a quadrotor UAV with uncertain dynamics. Nonlinear Dyn. 2020, 102, 2583–2596. [Google Scholar] [CrossRef]
- Xiao, B.; Yin, S. A New Disturbance Attenuation Control Scheme for Quadrotor Unmanned Aerial Vehicles. IEEE Trans. Industr. Inform. 2017, 13, 2922–2932. [Google Scholar] [CrossRef]
- Tran, V.P.; Santoso, F.; Garratt, M.A. Adaptive Trajectory Tracking for Quadrotor Systems in Unknown Wind Environments Using Particle Swarm Optimization-Based Strictly Negative Imaginary Controllers. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 1742–1752. [Google Scholar] [CrossRef]
- Alifbek, K.K.; Stepan, D.; Murodbek, S.; Dmitry, A.P.; Anvari, G.; Javod, A. Expert system application for reactive power compensation in isolated electric power systems. Int. J. Electr. Comput. Eng. 2021, 11, 3682–3691. [Google Scholar]
- Martyushev, N.V.; Malozyomov, B.V.; Khalikov, I.H.; Kukartsev, V.A.; Kukartsev, V.V.; Tynchenko, V.S.; Tynchenko, Y.A.; Qi, M. Review of Methods for Improving the Energy Efficiency of Electrified Ground Transport by Optimizing Battery Consumption. Energies 2023, 16, 729. [Google Scholar] [CrossRef]
- Werbos, P.J. Consistency of HDP applied to a simple reinforcement learning problem. Neural Netw. 1990, 3, 179–189. [Google Scholar] [CrossRef]
- Vamvoudakis, K.G.; Lewis, F.L. Online actor–Ccritic algorithm to solve the continuous-time infinite horizon optimal control problem. Automatica 2010, 46, 878–888. [Google Scholar] [CrossRef]
- Kamalapurkar, R.; Dinh, H.; Bhasin, S.; Dixon, W.E. Approximate optimal trajectory tracking for continuous-time nonlinear systems. Automatica 2015, 51, 40–48. [Google Scholar] [CrossRef]
- Wang, D.; Liu, D.R.; Li, H.L. Policy Iteration Algorithm for Online Design of Robust Control for a Class of Continuous-Time Nonlinear Systems. IEEE Trans. Autom. Sci. Eng. 2014, 11, 627–632. [Google Scholar] [CrossRef]
- Wen, G.X.; Ge, S.S.; Tu, F.W. Optimized Backstepping for Tracking Control of Strict-Feedback Systems. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 13. [Google Scholar]
- Zhao, B.; Liu, D.R.; Li, Y.C. Observer based adaptive dynamic programming for fault tolerant control of a class of nonlinear systems. Inf. Sci. 2017, 384, 21–33. [Google Scholar] [CrossRef]
- Wei, Q.L.; Liu, D.R.; Lin, Q.; Song, R.Z. Adaptive Dynamic Programming for Discrete-Time Zero-Sum Games. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 957–969. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, H.; Lewis, F.L. Data-Driven Fault-Tolerant Control for Attitude Synchronization of Nonlinear Quadrotors. IEEE Trans. Automat. Control 2021, 66, 5584–5591. [Google Scholar] [CrossRef]
- Chowdhary, G.; Yucelen, T.; Mühlegg, M.; Johnson, E.N. Concurrent learning adaptive control of linear systems with exponentially convergent bounds. Int. J. Adapt. Control Signal Process. 2013, 27, 280–301. [Google Scholar] [CrossRef]
- Yang, X.; He, H. Self-learning robust optimal control for continuous-time nonlinear systems with mismatched disturbances. Neural Netw. 2018, 99, 19–30. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.Y.; Zhao, X.W.; Yang, H.Y. Reinforcement Learning-Based Approximate Optimal Control for Attitude Reorientation Under State Constraints. IEEE Trans. Control Syst. Technol. 2021, 29, 1664–1673. [Google Scholar] [CrossRef]
- Liu, H.; Li, B.; Xiao, B.; Ran, D.C.; Zhang, C.X. Reinforcement learning© tracking control for a quadrotor unmanned aerial vehicle under external disturbances. Int. J. Robust Nonlinear Control. 2022, 33, 10360–10377. [Google Scholar] [CrossRef]
- Sun, J.L.; Liu, C.S. Disturbance observer-based robust missile autopilot design with full-state constraints via adaptive dynamic programming. J. Frankl. Inst. 2018, 355, 2344–2368. [Google Scholar] [CrossRef]
- Zhao, B.; Xu, S.Y.; Guo, J.Q.; Jiang, R.M.; Zhou, J. Integrated strapdown missile guidance and control based on neural network disturbance observer. Aerosp. Sci. Technol. 2019, 84, 170–181. [Google Scholar] [CrossRef]
- Zhang, R.; Xu, B.; Shi, P. Finite time observer© output feedback control of MEMS gyroscopes with input saturation. Int. J. Robust Nonlinear Control. 2022, 32, 4300–4317. [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Jin, X.Z. Adaptive neural network-based sliding mode tracking control for agricultural quadrotor with variable payload. Comput. Electr. Eng. 2022, 103, 108336. [Google Scholar] [CrossRef]
- Wang, D.D.; Zong, Q.; Tian, B.L.; Shao, S.K.; Zhang, X.Y.; Zhao, X.Y. Neural network disturbance observer-based distributed finite-time formation tracking control for multiple unmanned helicopters. ISA Trans. 2018, 73, 208–226. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Wang, R.J.; Wang, X.D.; Wang, X.X. Anti-saturation adaptive finite-time neural network based fault-tolerant tracking control for a quadrotor UAV with external disturbances. Aerosp. Sci. Technol. 2021, 115, 106790. [Google Scholar] [CrossRef]
- Fan, Q.Y.; Yang, G.H. Adaptive Actor–Ccritic design-based integral sliding-mode control for partially unknown nonlinear systems with input disturbances. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 165–177. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhao, B.; Liu, D.R. Fault tolerant tracking control for nonlinear systems with actuator failures through particle swarm optimization-based adaptive dynamic programming. Appl. Soft Comput. 2020, 97, 106766. [Google Scholar] [CrossRef]
- Adhyaru, D.M. State observer design for nonlinear systems using neural network. Appl. Soft Comput. 2012, 12, 2530–2537. [Google Scholar] [CrossRef]
- Farid, K.; Zhen Yu, Y.; Kenzo, N. Guidance and nonlinear control system for autonomous flight of minirotorcraft unmanned aerial vehicles. J. Field Robot. 2010, 27, 311–334. [Google Scholar]
- Abeywardena, D.; Kodagoda, S.; Dissanayake, G.; Munasinghe, R. Improved State Estimation in Quadrotor MAVs: A Novel Drift-Free Velocity Estimator. IEEE Robot. Autom. Mag. 2013, 20, 32–39. [Google Scholar] [CrossRef]
- Tang, P.; Zhang, F.B.; Ye, J.C.; Lin, D.F. An integral TSMC-based adaptive fault-tolerant control for quadrotor with external disturbances and parametric uncertainties. Aerosp. Sci. Technol. 2021, 109, 106415. [Google Scholar] [CrossRef]
- Xiao, B.; Yin, S. Exponential Tracking Control of Robotic Manipulators With Uncertain Dynamics and Kinematics. IEEE Trans. Industr. Inform. 2019, 15, 689–698. [Google Scholar] [CrossRef]
- Li, B.; Zhang, H.C.; Xiao, B.; Wang, C.H.; Yang, Y.S. Fixed-time integral sliding mode control of a high-order nonlinear system. Nonlinear Dyn. 2022, 107, 909–920. [Google Scholar] [CrossRef]
- Zhao, L.; Yu, J.P.; Lin, C.; Yu, H.S. Distributed adaptive fixed-time consensus tracking for second-order multi-agent systems using modified terminal sliding mode. Appl. Math. Comput. 2017, 312, 23–35. [Google Scholar] [CrossRef]
- Yu, S.H.; Yu, X.H.; Shirinzadeh, B.; Man, Z.H. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Shao, K.; Zheng, J.C.; Huang, K.; Wang, H.; Man, Z.H.; Fu, M.Y. Finite-time control of a linear motor positioner using adaptive recursive terminal sliding mode. IEEE Trans. Ind. Electron. 2020, 67, 6659–6668. [Google Scholar] [CrossRef]
- Song, Y.D.; Huang, X.C.; Wen, C.Y. Tracking Control for a Class of Unknown Nonsquare MIMO Nonaffine Systems: A Deep-Rooted Information Based Robust Adaptive Approach. IEEE Trans. Automat. Control 2016, 61, 3227–3233. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Girosi, F.; Poggio, T. Networks and the best approximation property. Biol. Cybern. 1990, 63, 169–176. [Google Scholar] [CrossRef]
- Zhang, D.H.; Kong, L.H.; Zhang, S.; Li, Q.; Fu, Q. Neural networks-based fixed-time control for a robot with uncertainties and input deadzone. Neurocomputing 2020, 390, 139–147. [Google Scholar] [CrossRef]
- Wen, G.X.; Chen, C.L.P.; Ge, S.S. Simplified Optimized Backstepping Control for a Class of Nonlinear Strict-Feedback Systems With Unknown Dynamic Functions. IEEE Trans. Cybern. 2021, 51, 4567–4580. [Google Scholar] [CrossRef]
- Li, K.W.; Li, Y.M. Adaptive NN optimal consensus fault-tolerant control for stochastic nonlinear multiagent systems. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 947–957. [Google Scholar] [CrossRef]
- Mu, C.X.; Zhang, Y. Learning-Based Robust Tracking Control of Quadrotor With Time-Varying and Coupling Uncertainties. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 259–273. [Google Scholar] [CrossRef]
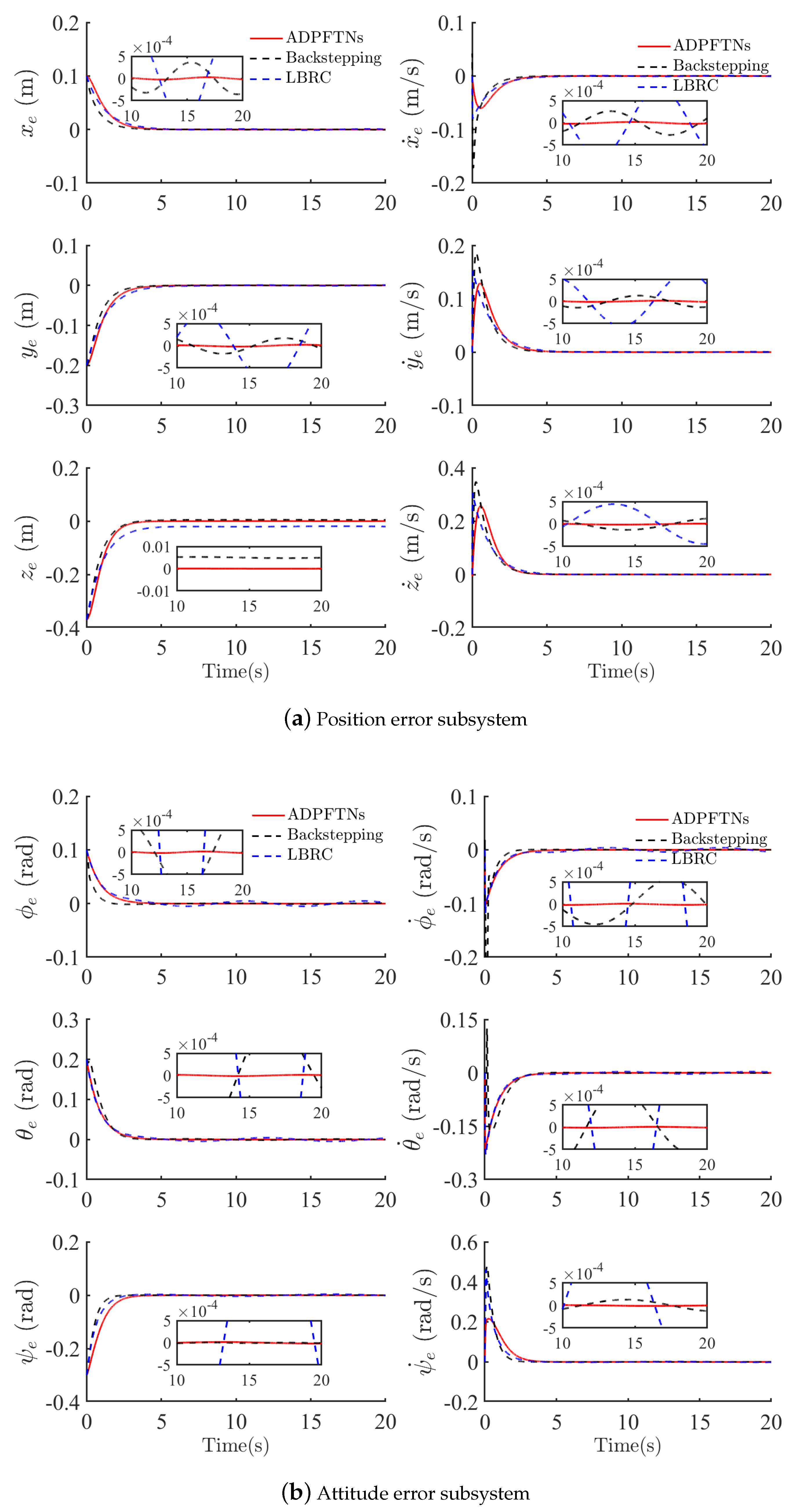
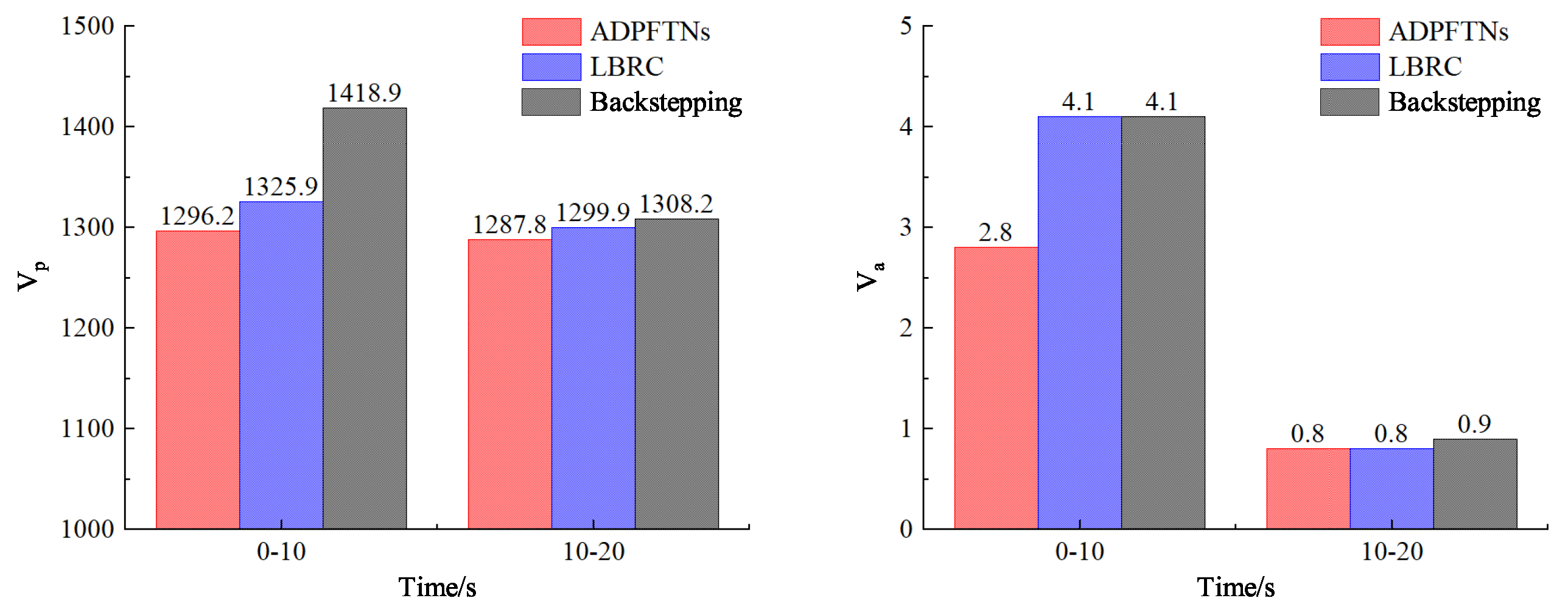
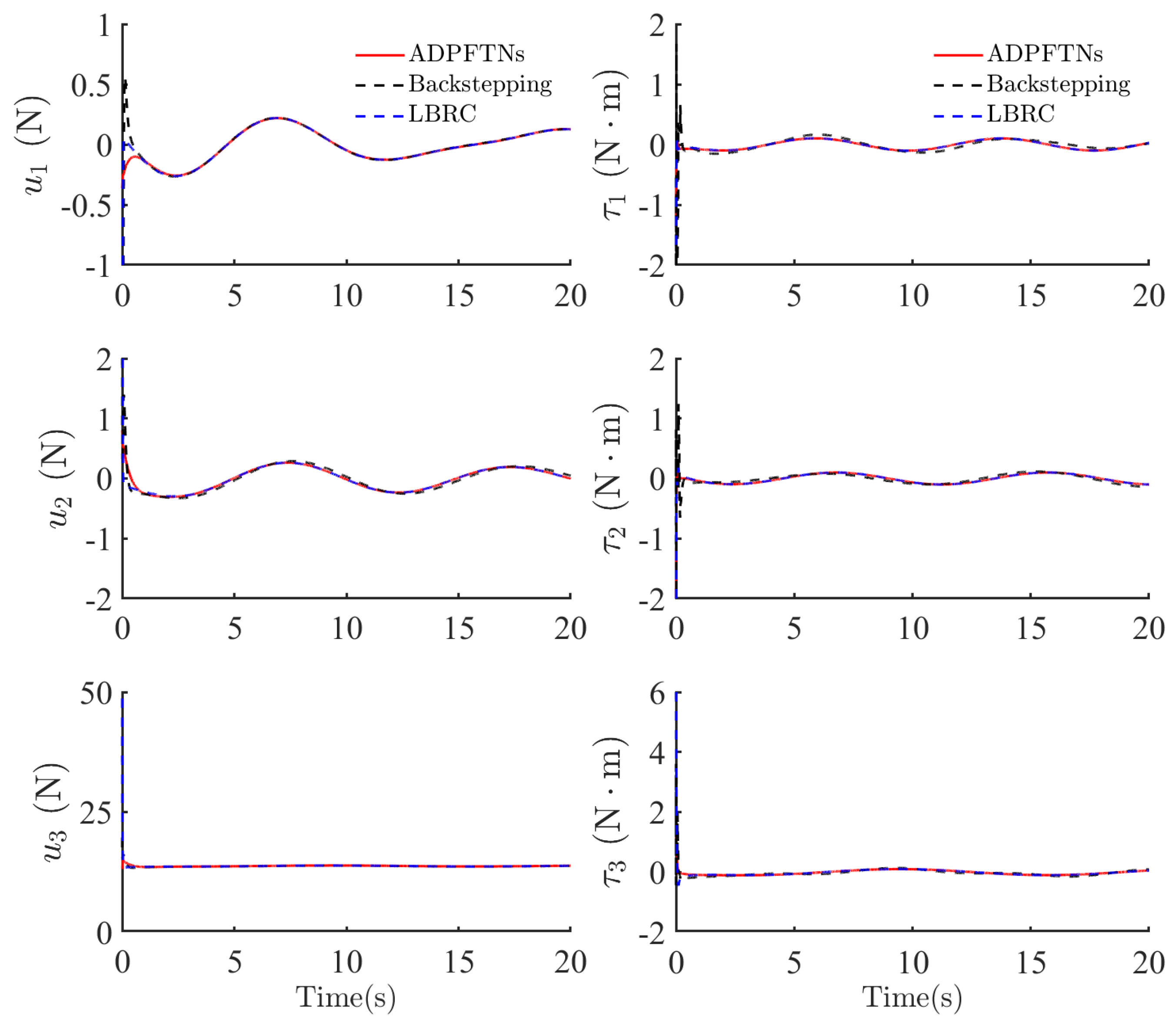
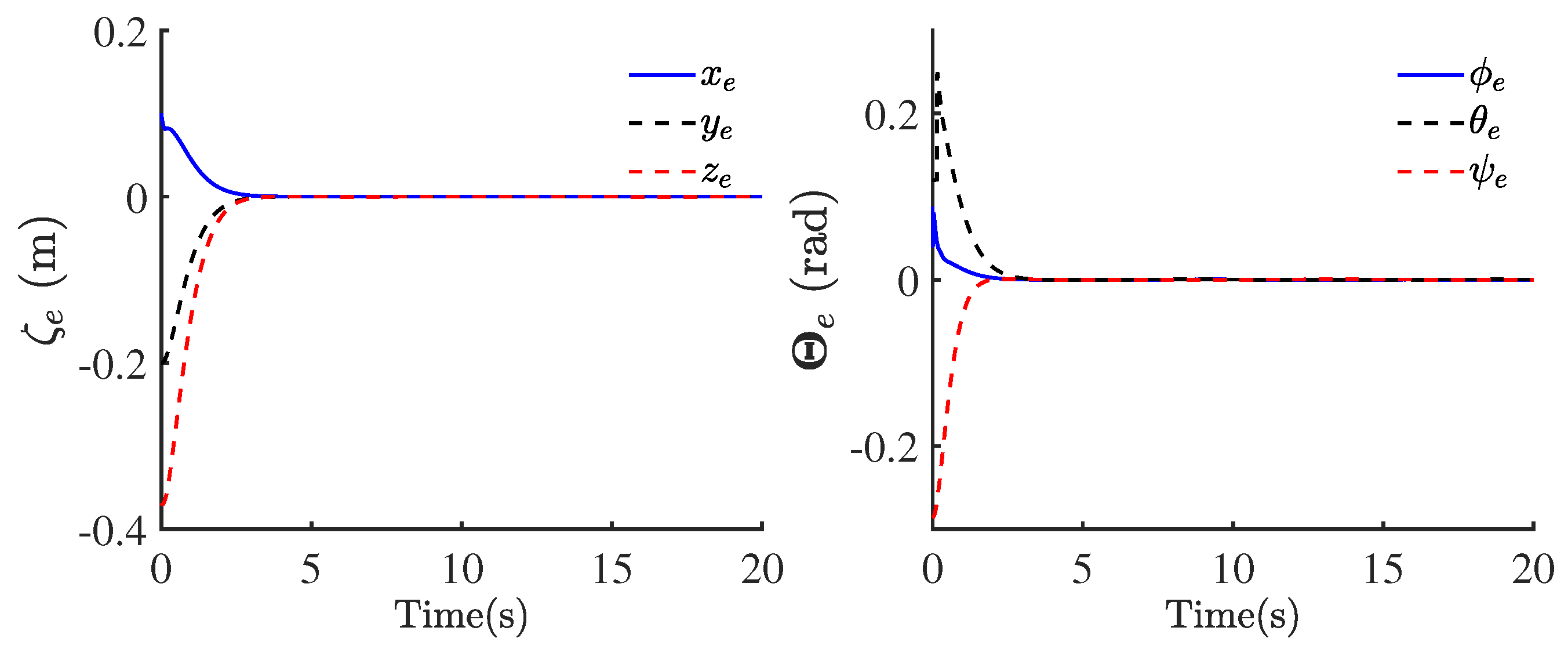
| Variable | Position Error System (i = 1) | Attitude Error System (i = 2) |
|---|---|---|
| 200 | 700 | |
| 97 | 99 | |
| 99 | 101 | |
| 105 | 105 | |
| 99 | 101 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Yu, F.; Liu, H.; Ma, H.; Zhang, H. Adaptive-Dynamic-Programming-Based Robust Control for a Quadrotor UAV with External Disturbances and Parameter Uncertainties. Appl. Sci. 2023, 13, 12672. https://doi.org/10.3390/app132312672
Yang S, Yu F, Liu H, Ma H, Zhang H. Adaptive-Dynamic-Programming-Based Robust Control for a Quadrotor UAV with External Disturbances and Parameter Uncertainties. Applied Sciences. 2023; 13(23):12672. https://doi.org/10.3390/app132312672
Chicago/Turabian StyleYang, Shaoyu, Fang Yu, Hui Liu, Hongyue Ma, and Haichao Zhang. 2023. "Adaptive-Dynamic-Programming-Based Robust Control for a Quadrotor UAV with External Disturbances and Parameter Uncertainties" Applied Sciences 13, no. 23: 12672. https://doi.org/10.3390/app132312672
APA StyleYang, S., Yu, F., Liu, H., Ma, H., & Zhang, H. (2023). Adaptive-Dynamic-Programming-Based Robust Control for a Quadrotor UAV with External Disturbances and Parameter Uncertainties. Applied Sciences, 13(23), 12672. https://doi.org/10.3390/app132312672





