A Three-Coil Constant Output Wireless Power Transfer System Based on Parity–Time Symmetry Theory
Abstract
:1. Introduction
2. Modeling and Analysis of the Three-Coil PT-WPT System
2.1. Circuit Model of the Three-Coil PT-WPT System
2.2. Transmission Characteristics
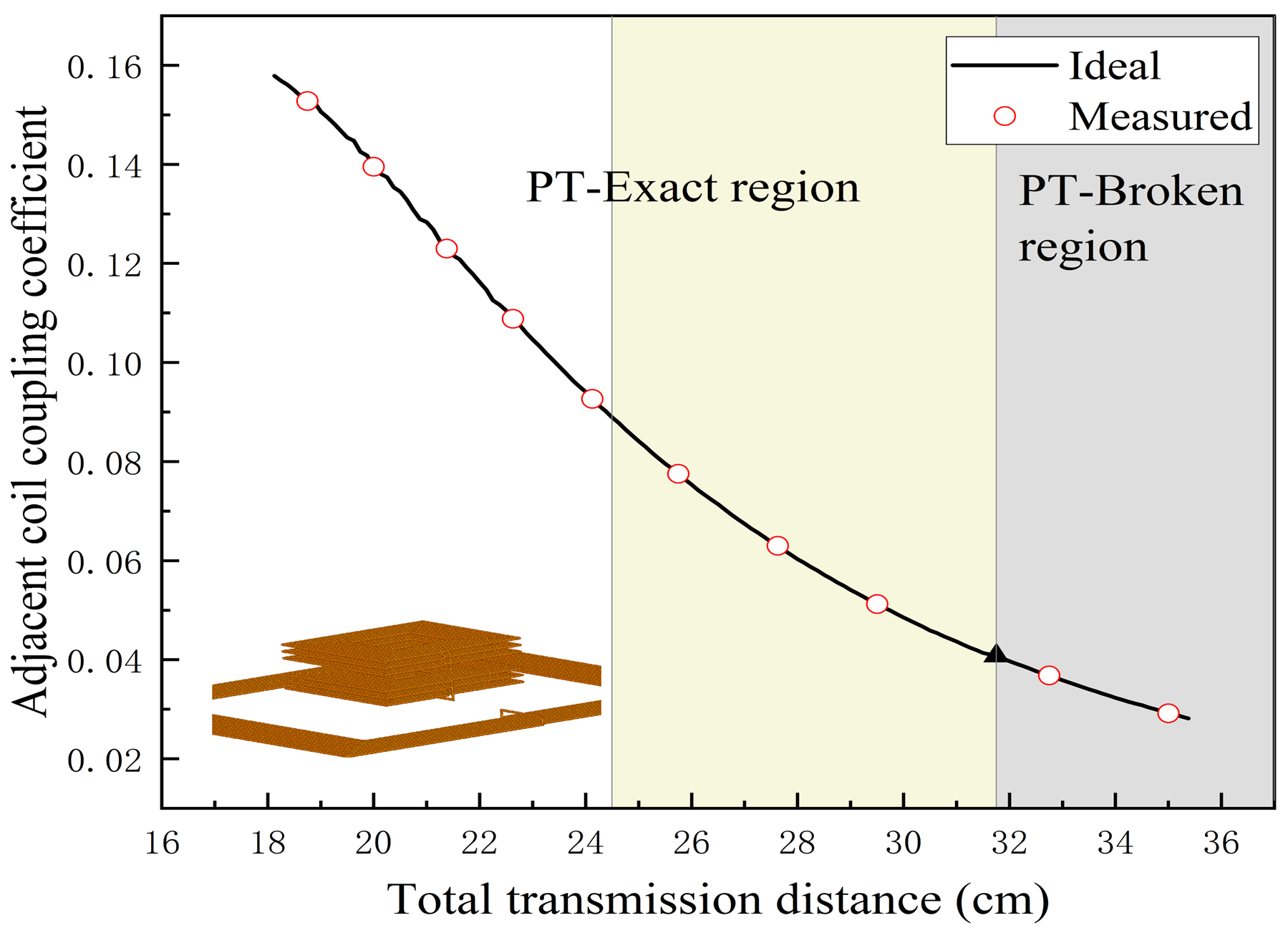
2.2.1. In the PT-Exact Symmetry State
2.2.2. In the PT-Broken State
2.2.3. In the Resonant State
3. Proposed Three-Coil PT-WPT System
3.1. With Boost Converter and Receiver Side Rectifier Model
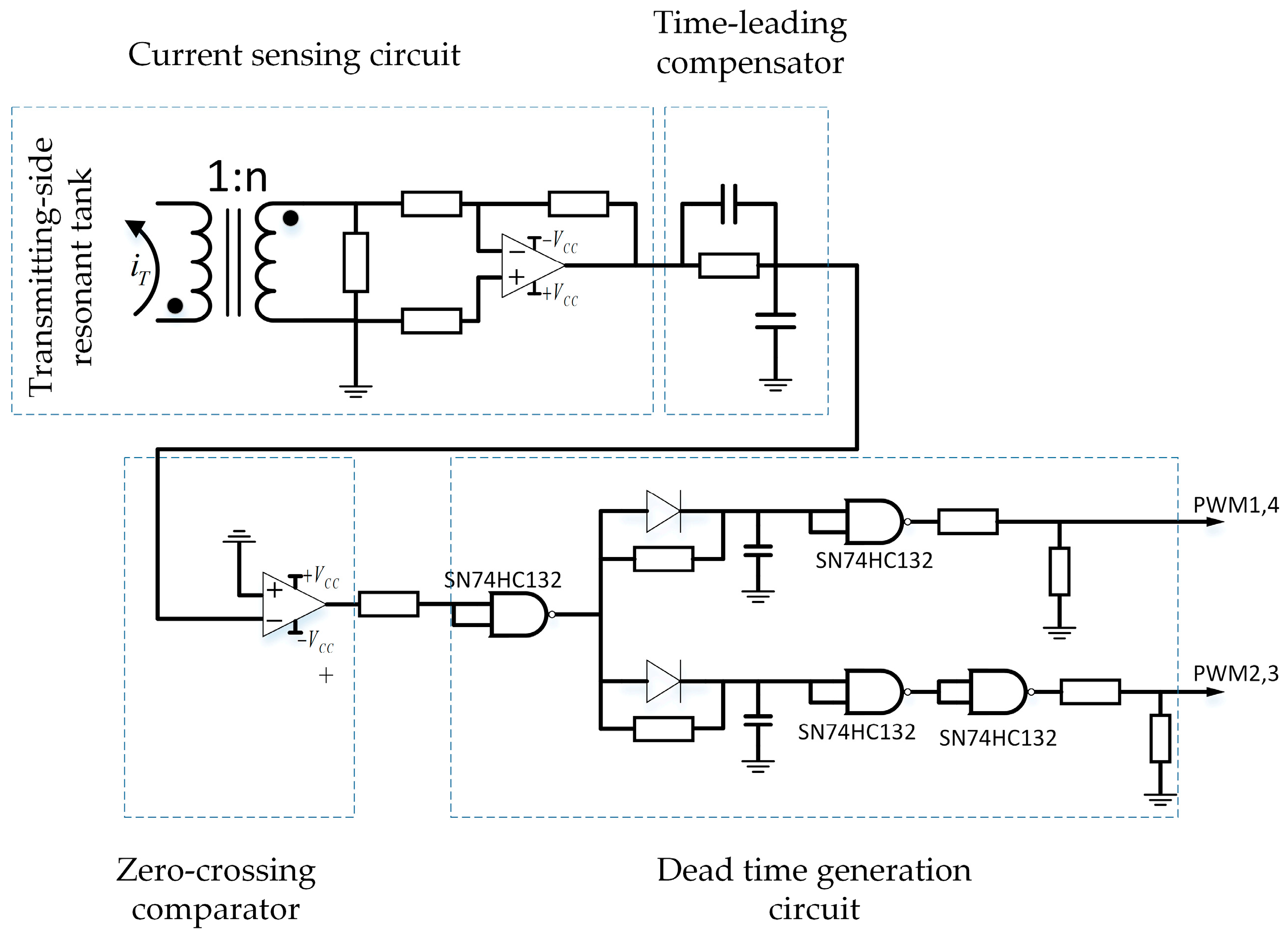
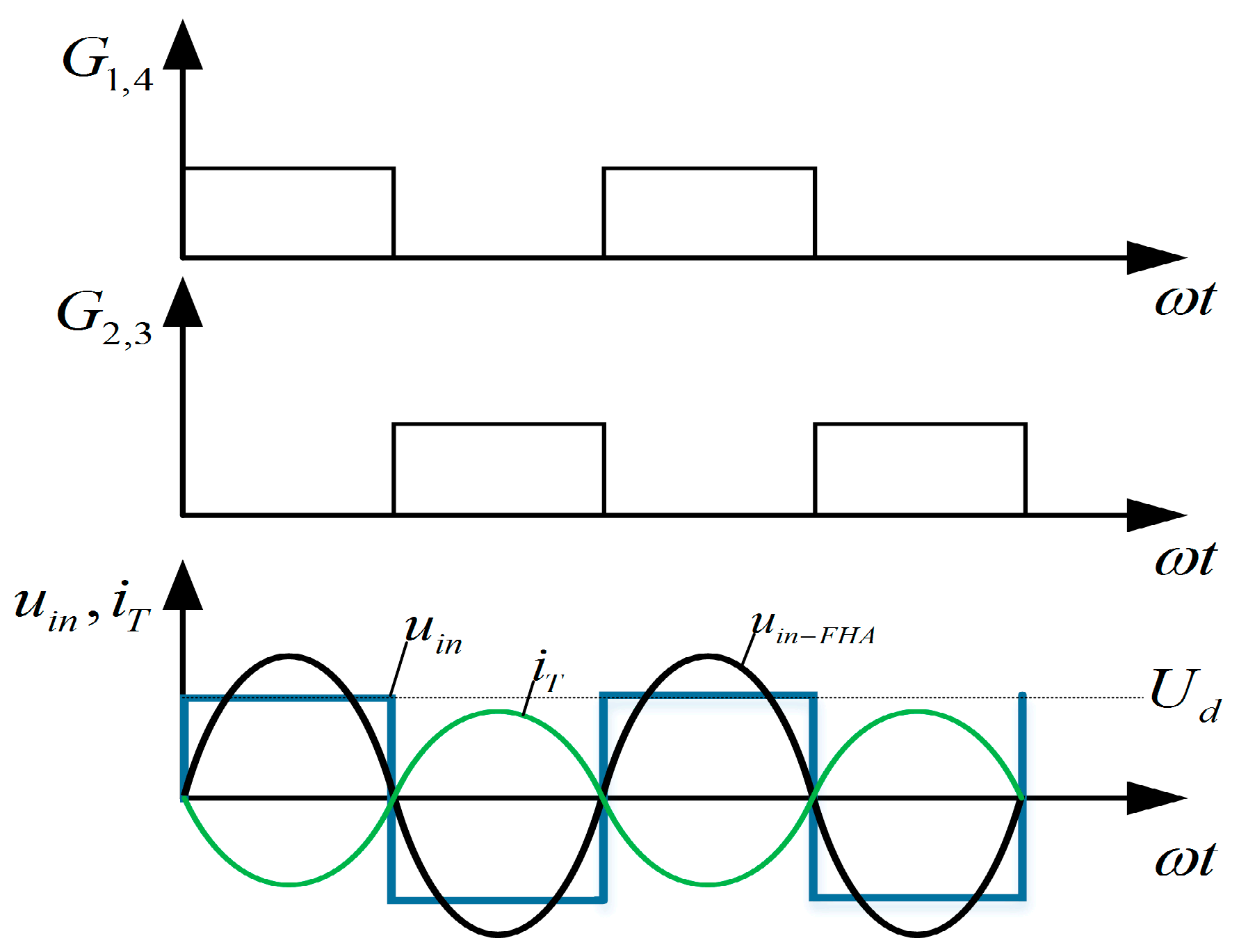
3.2. Self-Oscillation Control Strategy for Achieving Constant Output
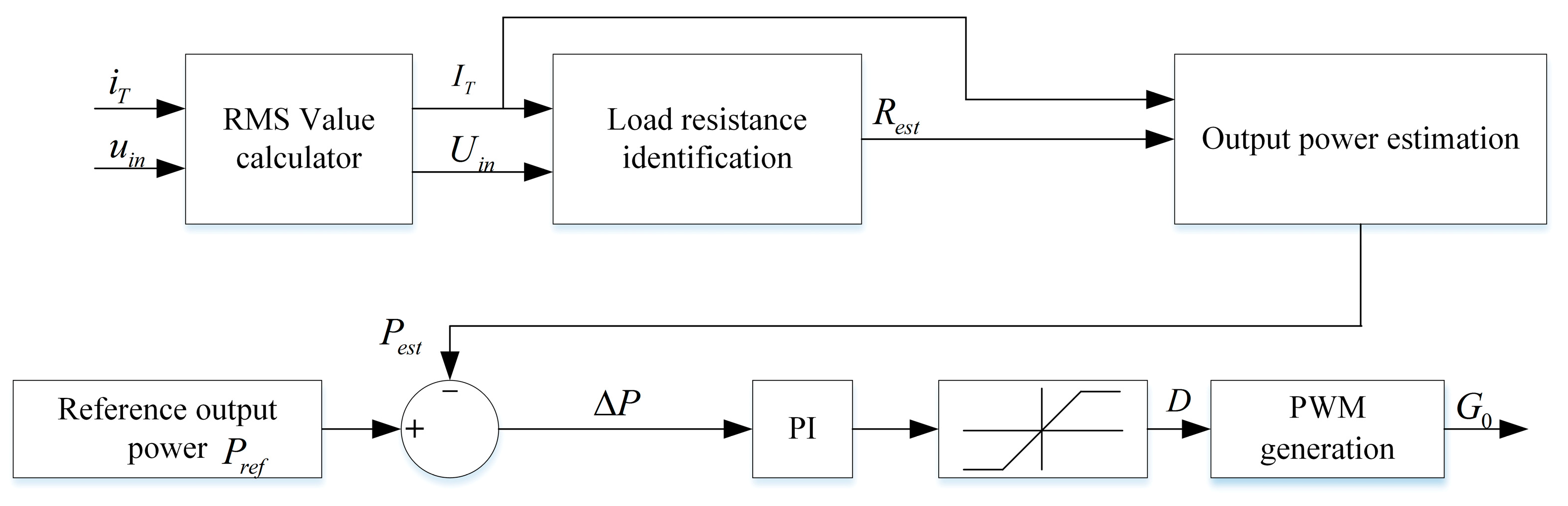
3.3. Online Load Resistance Identification and System Status Detection
3.4. Variable Negative Resistance Control Strategy Based on Primary Side Regulation
4. Experimental Verification
4.1. Coupling Coil Structure Design and Simulation
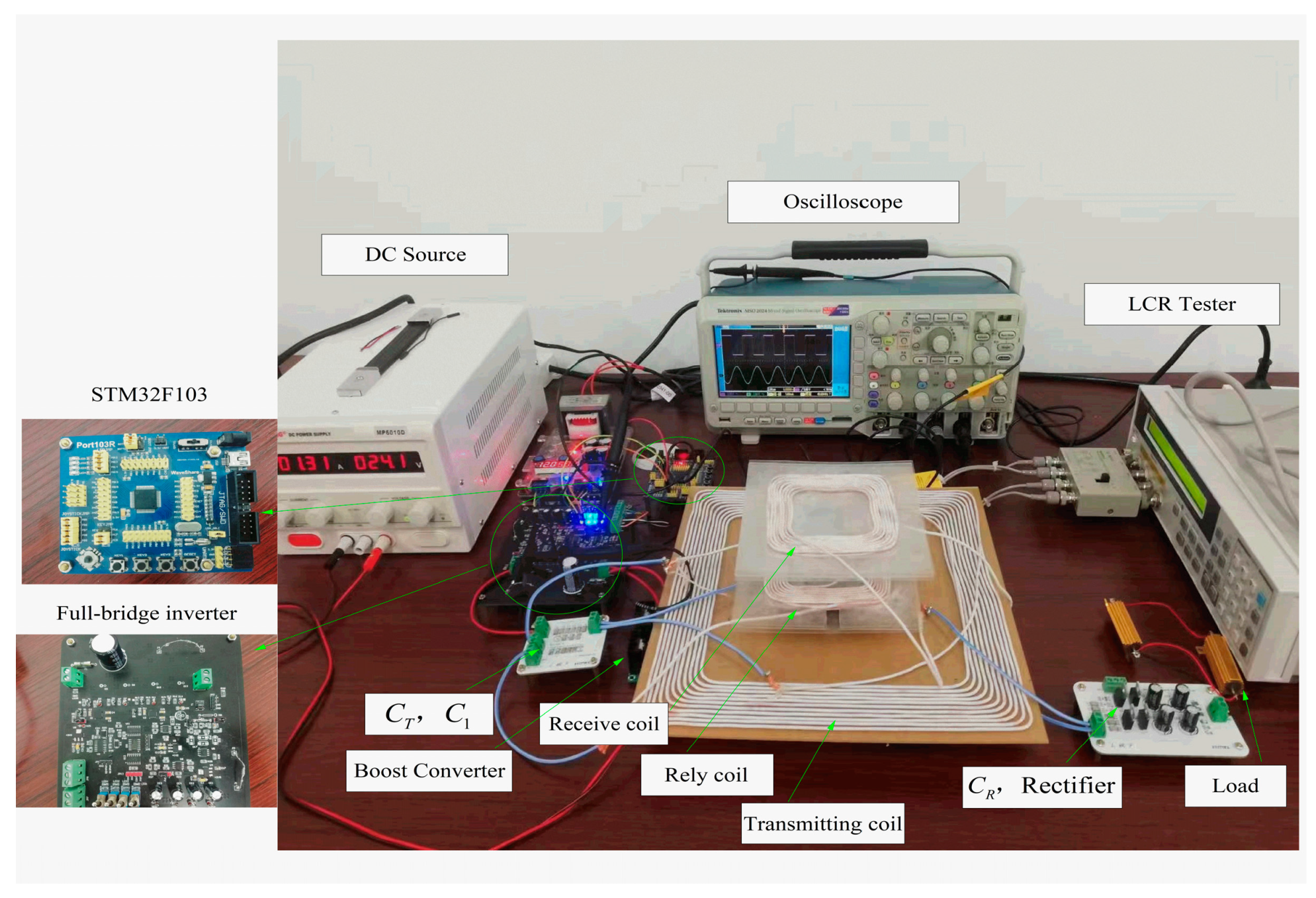
4.2. Experimental Construction
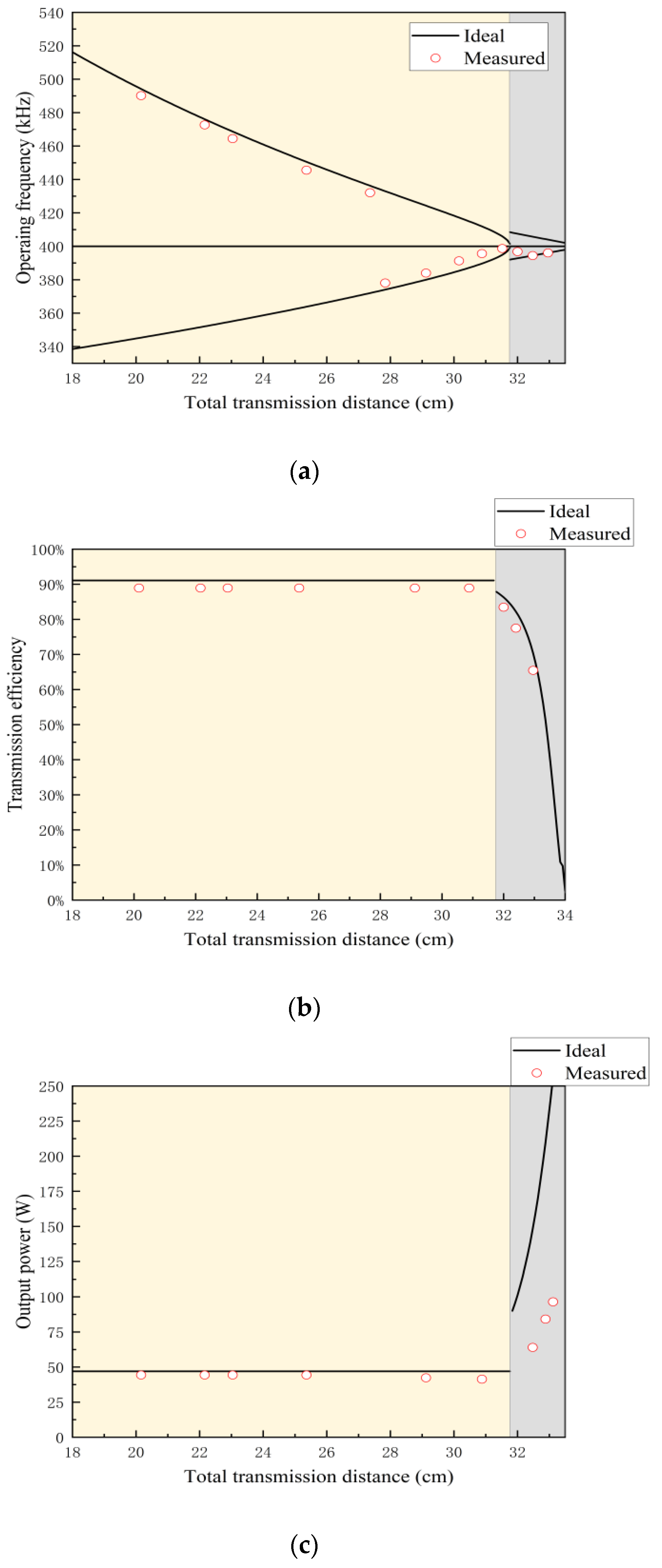
4.3. Experimental Results
4.3.1. Steady-State Performance of the System
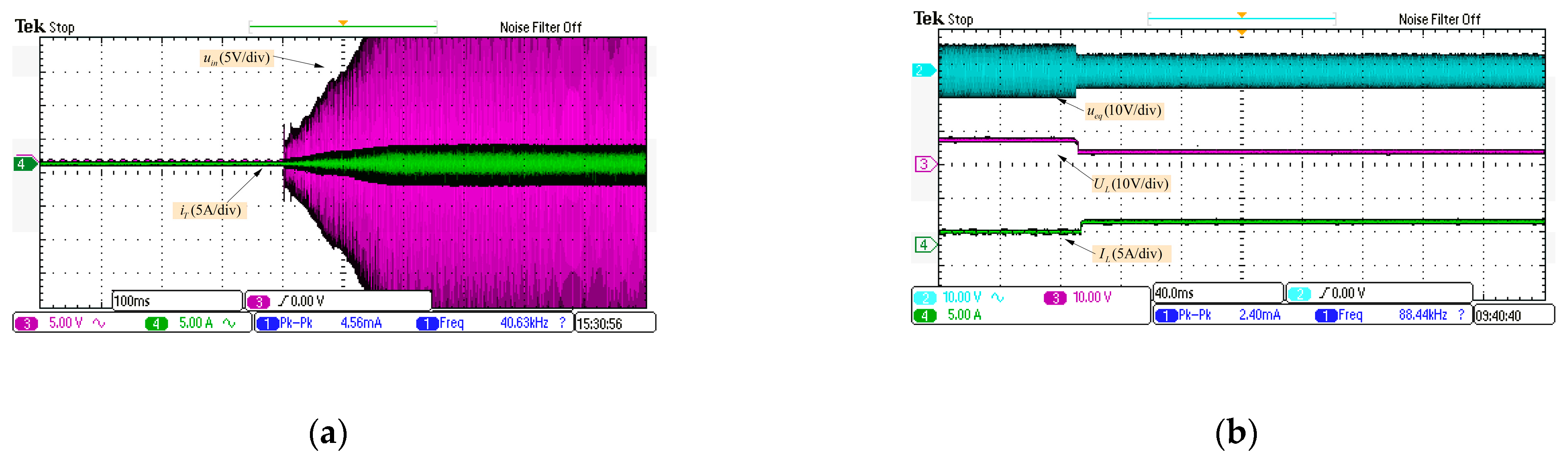
4.3.2. Experimental Results of the Proposed Control Strategy
4.3.3. Dynamic Performance of the Proposed Three-Coil PT-WPT System
4.3.4. Error Analysis
4.3.5. Comparison with Other WPT Systems
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fu, Y.; Shi, Z.; Zhu, Y.; Lv, K.; Peng, Z. PT Symmetry-Based AUV Dual Transmission Coil Wireless Power Transfer System Design. Machines 2023, 11, 146. [Google Scholar] [CrossRef]
- Rong, C.; Zhang, B.; Wei, Z.; Wu, L.; Shu, X. A Wireless Power Transfer System for Spinal Cord Stimulation Based on Generalized Parity–Time Symmetry Condition. IEEE Trans. Ind. Appl. 2022, 58, 1330–1339. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, B.; Jiang, Y.; Zhou, J. A Robust Parity-Time-Symmetric WPT System With Extended Constant-Power Range for Cordless Kitchen Appliances. IEEE Trans. Ind. Appl. 2022, 58, 1179–1189. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, B. Omnidirectional and Efficient Wireless Power Transfer System for Logistic Robots. IEEE Access 2020, 8, 13683–13693. [Google Scholar] [CrossRef]
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljacic, M. Wireless power transfer via strongly coupled magnetic resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef]
- Zhaksylyk, Y.; Hanke, U.; Azadmehr, M. Single-Sided Interspiraled Inductive Impedance Matching for Magnetic Resonance Wireless Power Transfer. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 2189–2200. [Google Scholar] [CrossRef]
- Chen, Z.; Sun, X.; Ren, B.; Wang, Z.; Liu, J. Analysis of four-coil magnetic resonance coupling wireless power transfer system based on LCC-SSS compensation network. Energy Rep. 2023, 9, 419–427. [Google Scholar] [CrossRef]
- Assawaworrarit, S.; Yu, X.; Fan, S. Robust wireless power transfer using a nonlinear parity-time-symmetric circuit. Nature 2017, 546, 387–390. [Google Scholar] [CrossRef]
- Wei, Z.; Zhang, B. Transmission Range Extension of PT-Symmetry-Based Wireless Power Transfer System. IEEE Trans. Power Electron. 2021, 36, 11135–11147. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, B.; Xiao, W.; Qiu, D.; Chen, Y. Nonlinear Parity-Time-Symmetric Model for Constant Efficiency Wireless Power Transfer: Application to a Drone-in-Flight Wireless Charging Platform. IEEE Trans. Ind. Electron. 2019, 66, 4097–4107. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, B.; Zhou, J. Efficiency Improvement of the Parity-Time-Symmetric Wireless Power Transfer System for Electric Vehicle Charging. IEEE Trans. Power Electron. 2020, 35, 12497–12508. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, B.; Wu, L. Output Power Stabilization for Wireless Power Transfer System Employing Primary-Side-Only Control. IEEE Access 2020, 8, 63735–63747. [Google Scholar] [CrossRef]
- Chen, J.; Xie, F.; Zhang, B.; Chen, Y.; Xiao, W. Transmission range extension strategy of parity-time-symmetry-based wireless power transfer system by a boost converter. Int. J. Circuit Theory Appl. 2022, 51, 510–524. [Google Scholar] [CrossRef]
- Cheng, C.; Zhou, Z.; Li, W.; Zhu, C.; Deng, Z.; Mi, C.C. A Multi-Load Wireless Power Transfer System With Series-Parallel-Series Compensation. IEEE Trans. Power Electron. 2019, 34, 7126–7130. [Google Scholar] [CrossRef]
- Cheng, C.; Lu, F.; Zhou, Z.; Li, W.; Zhu, C.; Zhang, H.; Deng, Z.; Chen, X.; Mi, C.C. Load-Independent Wireless Power Transfer System for Multiple Loads Over a Long Distance. IEEE Trans. Power Electron. 2019, 34, 9279–9288. [Google Scholar] [CrossRef]
- Cheng, C.; Li, W.; Zhou, Z.; Deng, Z.; Mi, C. A Load-Independent Wireless Power Transfer System With Multiple Constant Voltage Outputs. IEEE Trans. Power Electron. 2020, 35, 3328–3331. [Google Scholar] [CrossRef]
- Shu, X.; Zhang, B.; Wei, Z.; Rong, C.; Sun, S. Extended-Distance Wireless Power Transfer System With Constant Output Power and Transfer Efficiency Based on Parity-Time-Symmetric Principle. IEEE Trans. Power Electron. 2021, 36, 8861–8871. [Google Scholar] [CrossRef]
- Wang, Z.; Qiu, D.; Zhang, B.; Xiao, W.; Chen, Y.; Xie, F. Extended-Range Wireless Power Transfer System Based on High-Order PT Symmetric Principle. In Proceedings of the 2021 IEEE 1st International Power Electronics and Application Symposium (PEAS), Shanghai, China, 12–15 November 2021; pp. 1–6. [Google Scholar]
- Qu, Y.; Zhang, B.; Gu, W.; Shu, X. Wireless Power Transfer System with High-Order Compensation Network Based on Parity-Time-Symmetric Principle and Relay Coil. IEEE Trans. Power Electron. 2023, 38, 1314–1323. [Google Scholar] [CrossRef]
- Wei, Z.; Zhang, B.; Shu, X.; Rong, C. A wireless power transfer system with hybrid control for constant current and voltage output. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 6317–6331. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, B.; Jiang, Y. Position-Independent Constant Current or Constant Voltage Wireless Electric Vehicles Charging System Without Dual-Side Communication and DC–DC Converter. IEEE Trans. Ind. Electron. 2022, 69, 7930–7939. [Google Scholar] [CrossRef]
- Wu, L.; Zhang, B.; Jiang, Y. Robust Parity-Time-Symmetric WPT System with Reduced Switching-Frequency and Improved Step-Down Conversion Ratio. IEEE Trans. Transp. Electrif. 2022, 9, 2090–2103. [Google Scholar] [CrossRef]
- Luo, C.; Qiu, D.; Gu, W.; Zhang, B.; Chen, Y.; Xiao, W. Multiload Wireless Power Transfer System With Constant Output Power and Efficiency. IEEE Trans. Ind. Appl. 2022, 58, 1101–1114. [Google Scholar] [CrossRef]
- Liu, F.; Yang, Y.; Jiang, D.; Ruan, X.; Chen, X. Modeling and optimization of magnetically coupled resonant wireless power transfer system with varying spatial scales. IEEE Trans. Power Electron. 2016, 32, 3240–3250. [Google Scholar] [CrossRef]
- Hu, X.; Wang, Y.; Jiang, Y.; Lei, W.; Dong, X. Maximum efficiency tracking for dynamic wireless power transfer system using LCC compensation topology. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 1992–1996. [Google Scholar]
- Tan, L.; Guo, J.; Huang, X.; Liu, H.; Wang, W.; Yan, C.; Zhang, M. Coordinated source control for output power stabilization and efficiency optimization in WPT systems. IEEE Trans. Power Electron. 2017, 33, 3613–3621. [Google Scholar] [CrossRef]


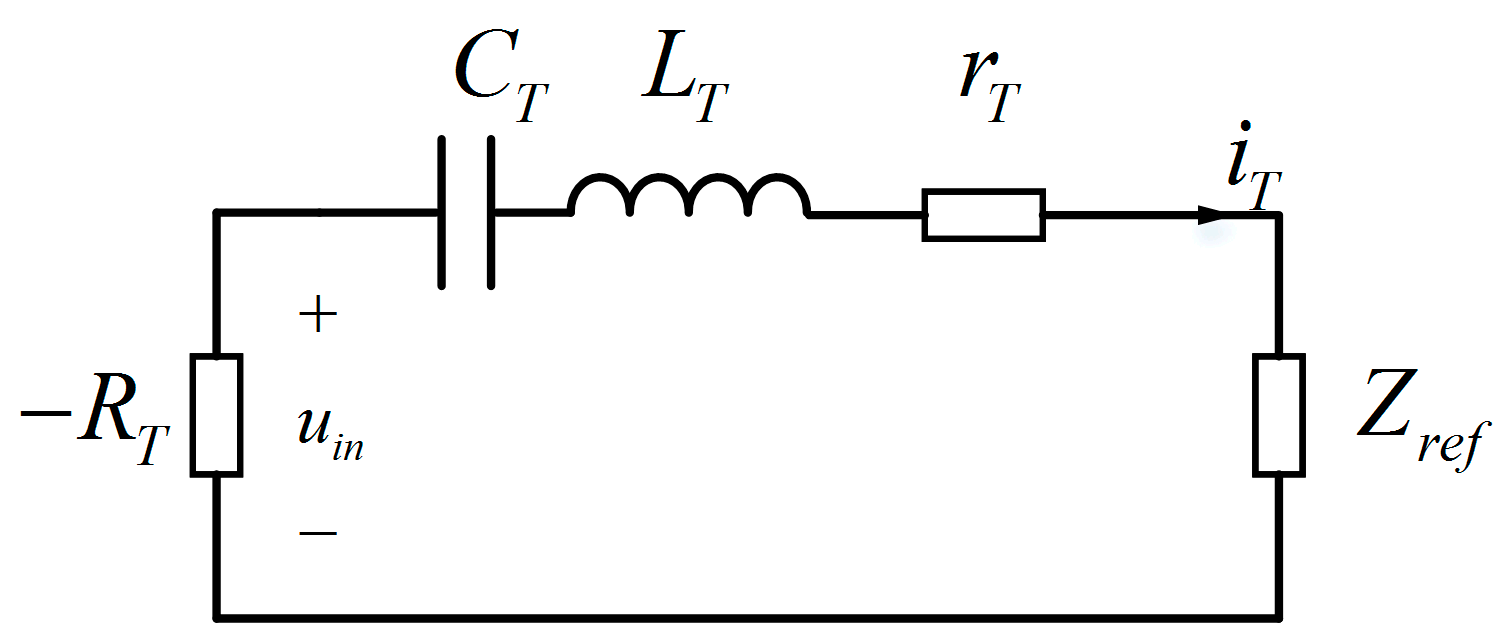

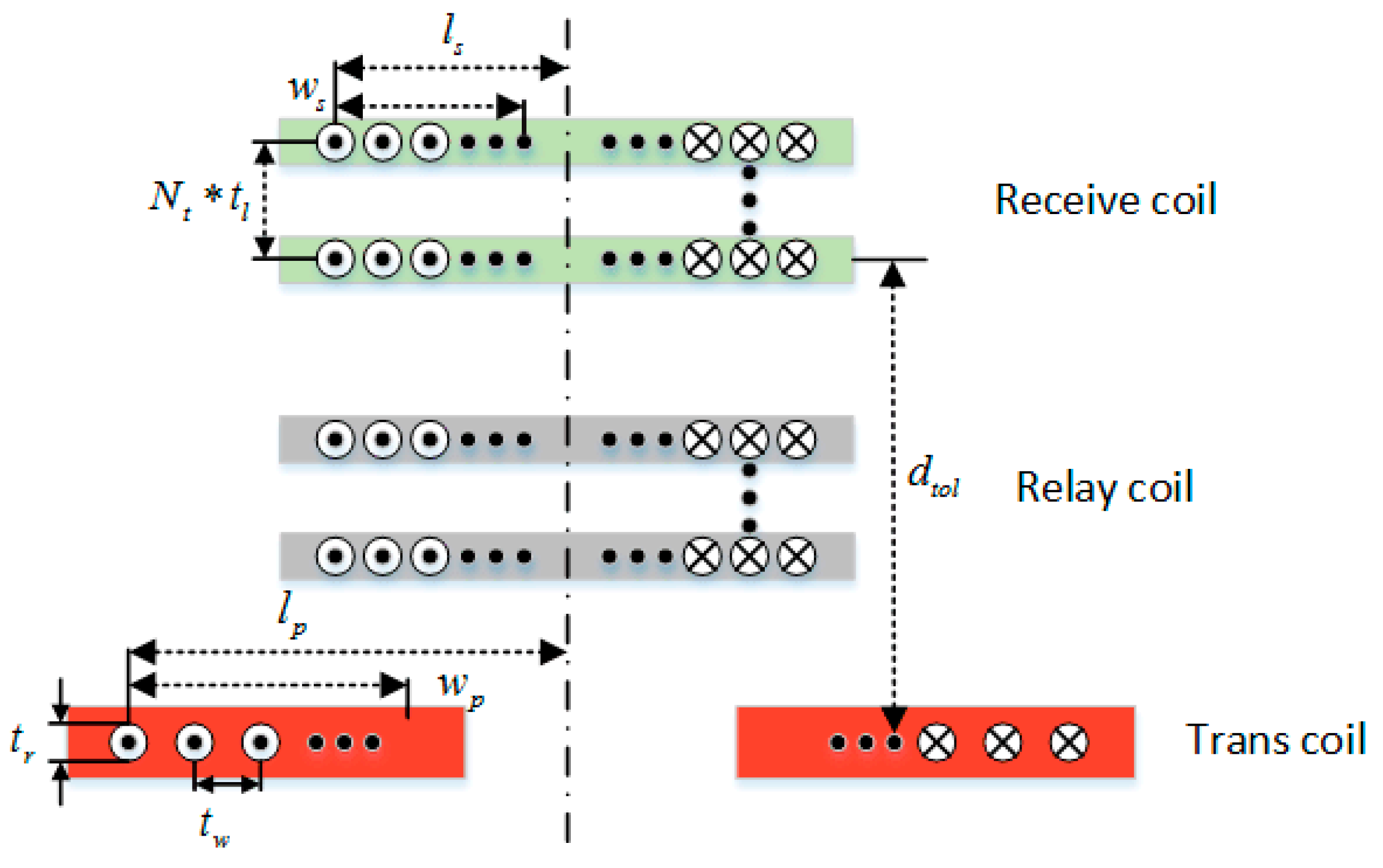

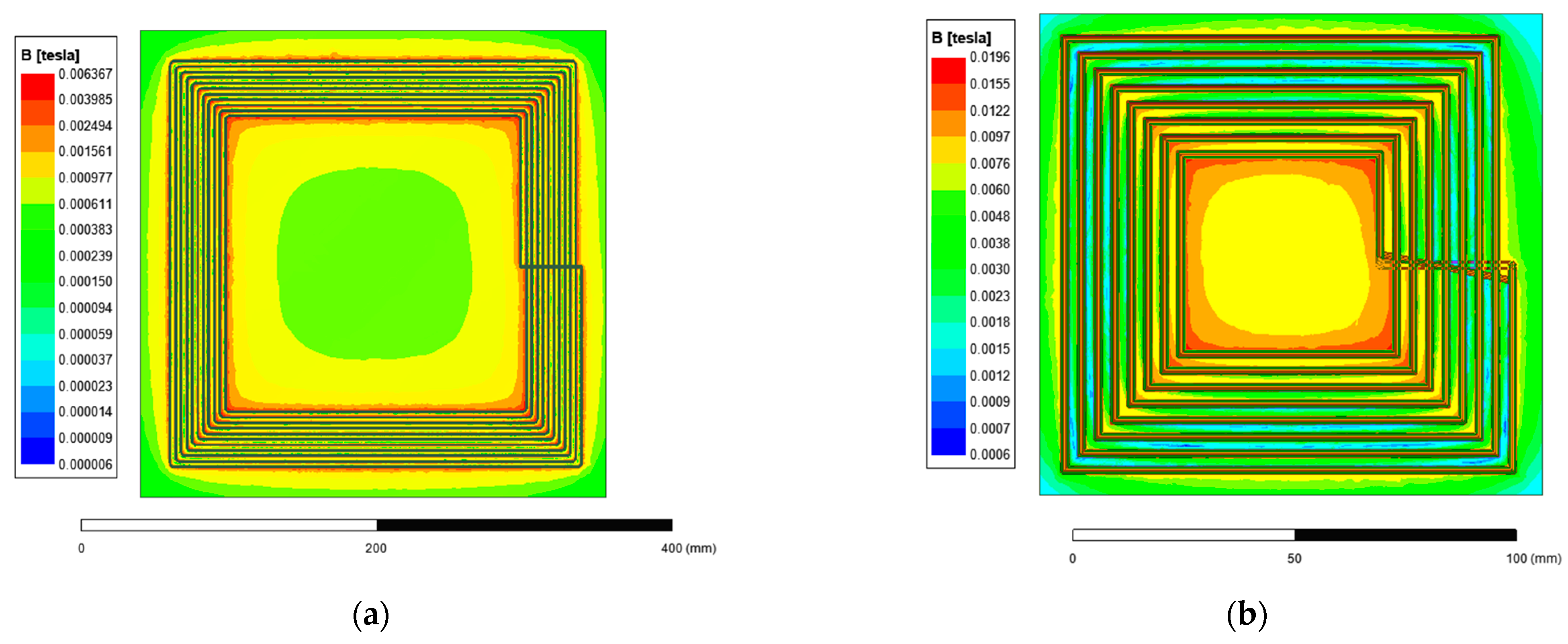


| Structure Parameters | Parameters Values |
|---|---|
| Outside diameter of transmitting coil | 14 cm |
| Number of turns of transmitting coil | 11 |
| Multilayer coil outer diameter | 5 cm |
| Number of turns of multilayer coils | 8 |
| Winding width | 1.5 mm |
| Turn spacing of coils | 3.78 mm |
| Multilayer coil layer spacing | 5.5 mm |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Load Resistance | Total Transmission Distance (Coupling Coefficient of Adjacent Coils) | |||
|---|---|---|---|---|
| 10 | 10.41 | 4.10% | 10.37 | 3.70% |
| 12 | 12.44 | 3.67% | 12.41 | 3.417% |
| 14 | 14.49 | 3.50% | 14.45 | 3.214% |
| 16 | 16.54 | 3.375% | 16.56 | 3.50% |
| Reference Output Power | Total Transmission Distance (Coupling Coefficient of Adjacent Coils) | |||
|---|---|---|---|---|
| 10 | 46.17 | 3.819% | 46.11 | 3.935% |
| 12 | 46.33 | 3.47% | 46.34 | 3.453% |
| 14 | 46.45 | 3.23% | 46.44 | 3.247% |
| 16 | 46.5 | 3.126% | 46.4395 | 3.251% |
| Reference | Freq | Power Control | Control Method | Output Power |
|---|---|---|---|---|
| [25] | 100 kHz | Controllable | Transmitter control and Communication needed | Unstable |
| [26] | 108 kHz | Controllable | Dual Transmitter control and no communication required | Unstable |
| [19] | 371.1 kHz | Uncontrollable | None | Constant |
| This work | 400 kHz | Controllable | Transmitter control and Communication needed | Constant |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, Y.; Yang, J.; Li, R. A Three-Coil Constant Output Wireless Power Transfer System Based on Parity–Time Symmetry Theory. Appl. Sci. 2023, 13, 12188. https://doi.org/10.3390/app132212188
Yue Y, Yang J, Li R. A Three-Coil Constant Output Wireless Power Transfer System Based on Parity–Time Symmetry Theory. Applied Sciences. 2023; 13(22):12188. https://doi.org/10.3390/app132212188
Chicago/Turabian StyleYue, Yuntao, Jiahui Yang, and Ruofan Li. 2023. "A Three-Coil Constant Output Wireless Power Transfer System Based on Parity–Time Symmetry Theory" Applied Sciences 13, no. 22: 12188. https://doi.org/10.3390/app132212188
APA StyleYue, Y., Yang, J., & Li, R. (2023). A Three-Coil Constant Output Wireless Power Transfer System Based on Parity–Time Symmetry Theory. Applied Sciences, 13(22), 12188. https://doi.org/10.3390/app132212188






