The Data-Driven Homogenization of Mohr–Coulomb Parameters Based on a Bayesian Optimized Back Propagation Artificial Neural Network (BP-ANN)
Abstract
:1. Introduction
2. Methodology
2.1. Back Propagation Artificial Neural Networks
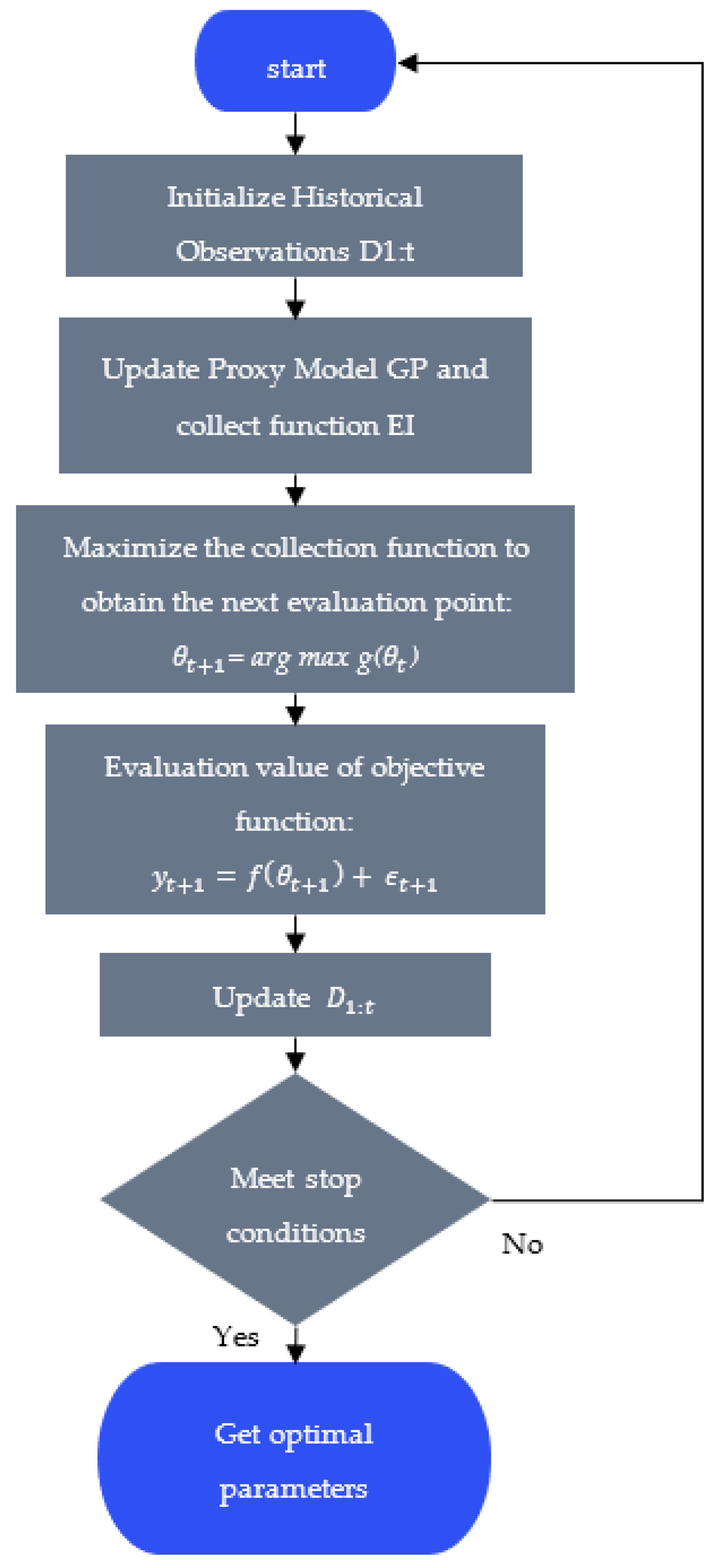
2.2. Bayesian Optimization
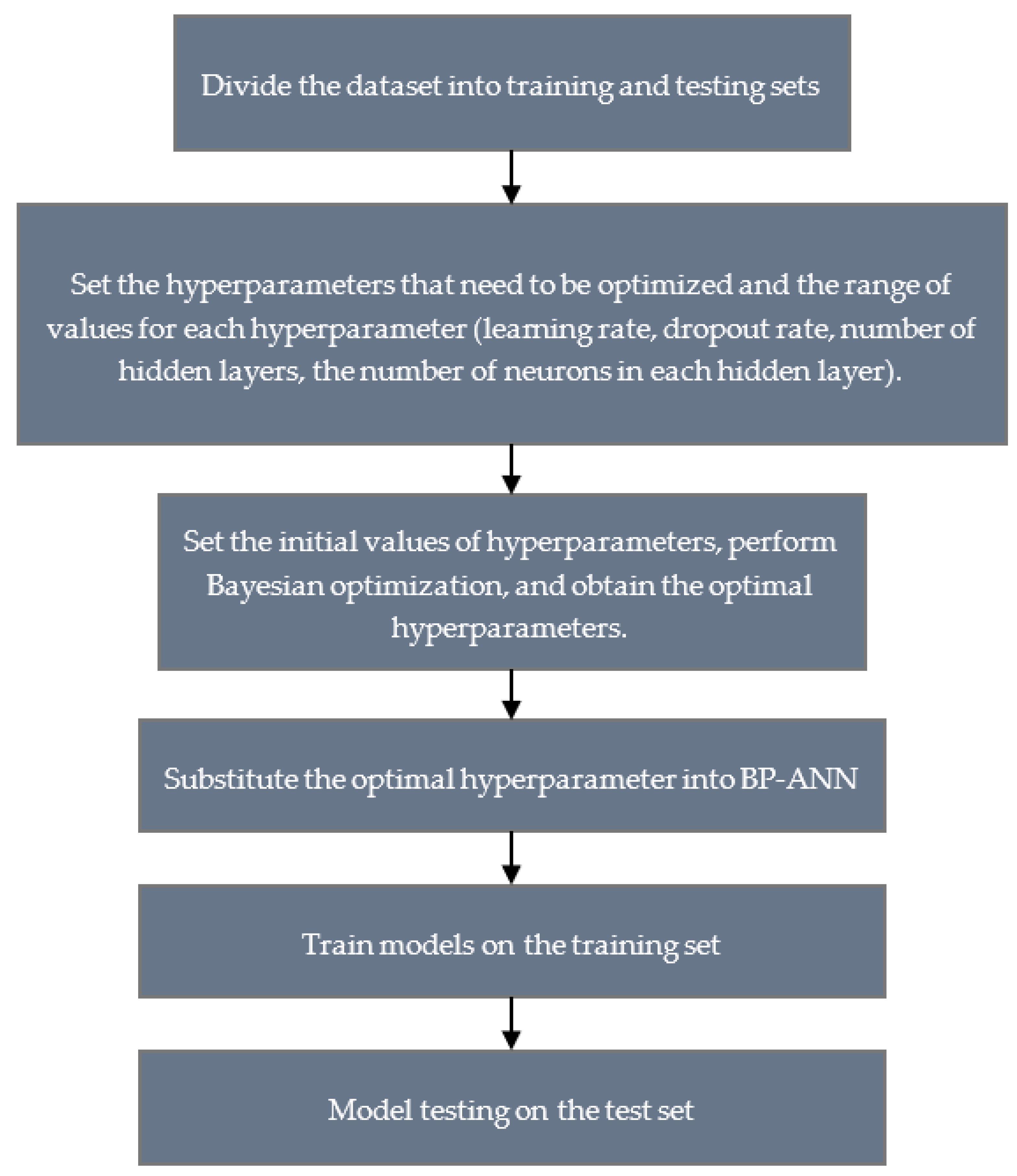
2.3. Back Propagation Artificial Neural Network Based on Bayesian Optimization
- (1)
- Divide the dataset into training and testing sets.
- (2)
- Set the hyperparameters that need to be optimized and the range of values for each hyperparameter. In this work, we selected hyperparameters such as learning rate, dropout rate, the number of hidden layers, and the number of neurons in each hidden layer.
- (3)
- Set the initial values of hyperparameters, perform Bayesian optimization, and obtain the optimal hyperparameters.
- (4)
- Substitute the optimal hyperparameters into the back propagation artificial neural network to determine the final architecture of the back propagation artificial neural network.
- (5)
- Train models on the training set.
- (6)
- Test the model on the test set.
3. Generation of the Training Dataset
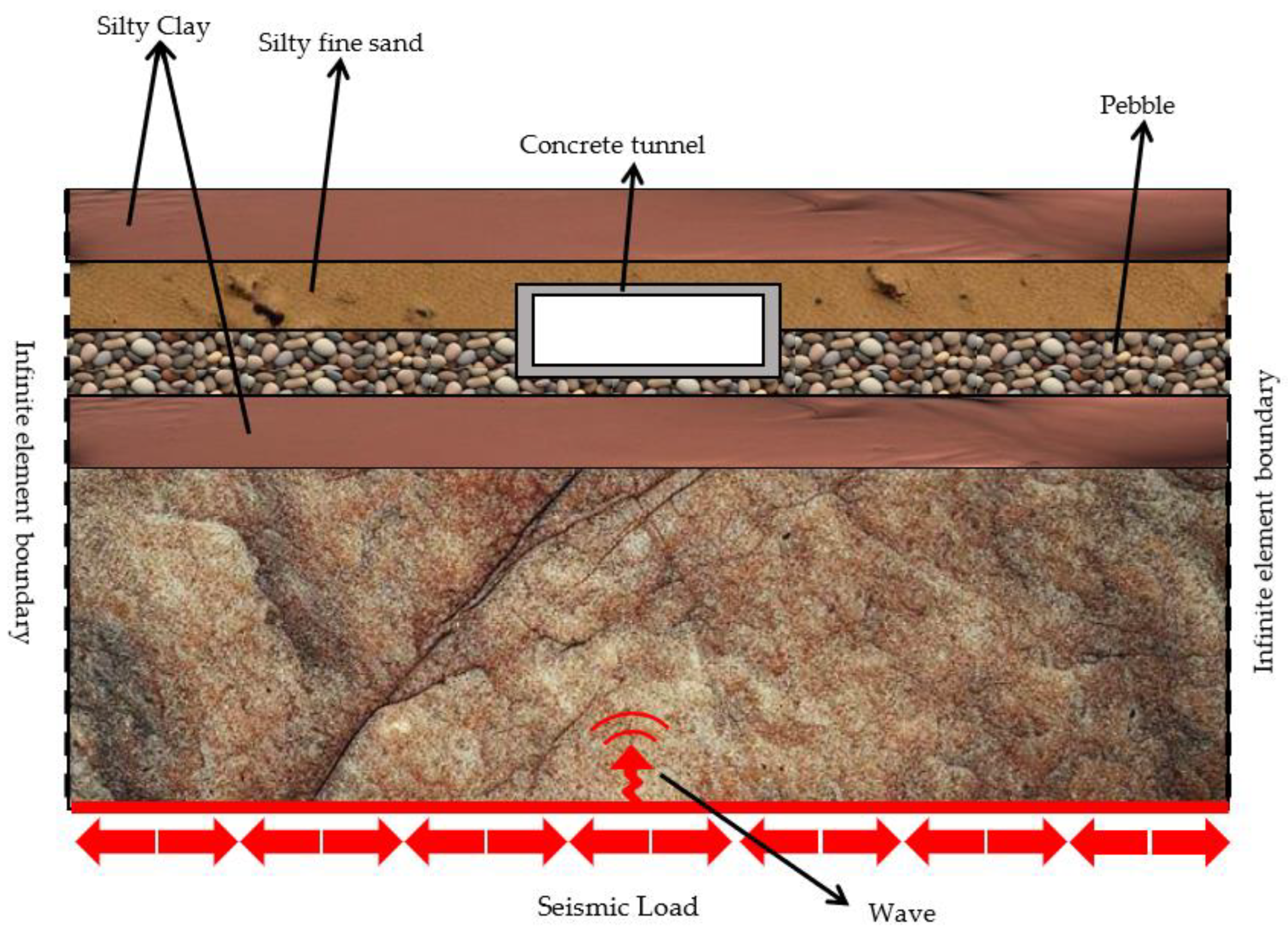
3.1. Problem Formulation
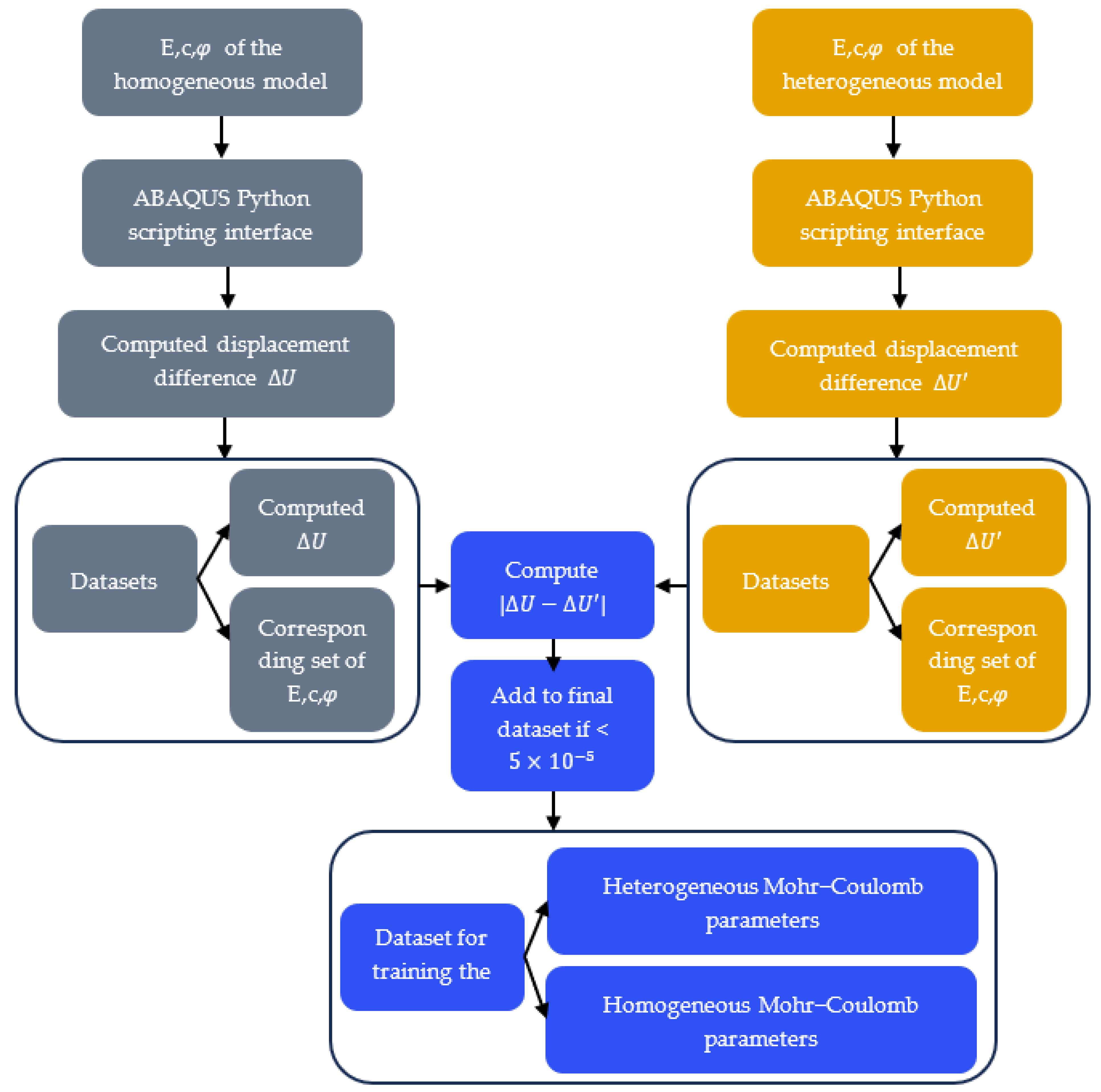
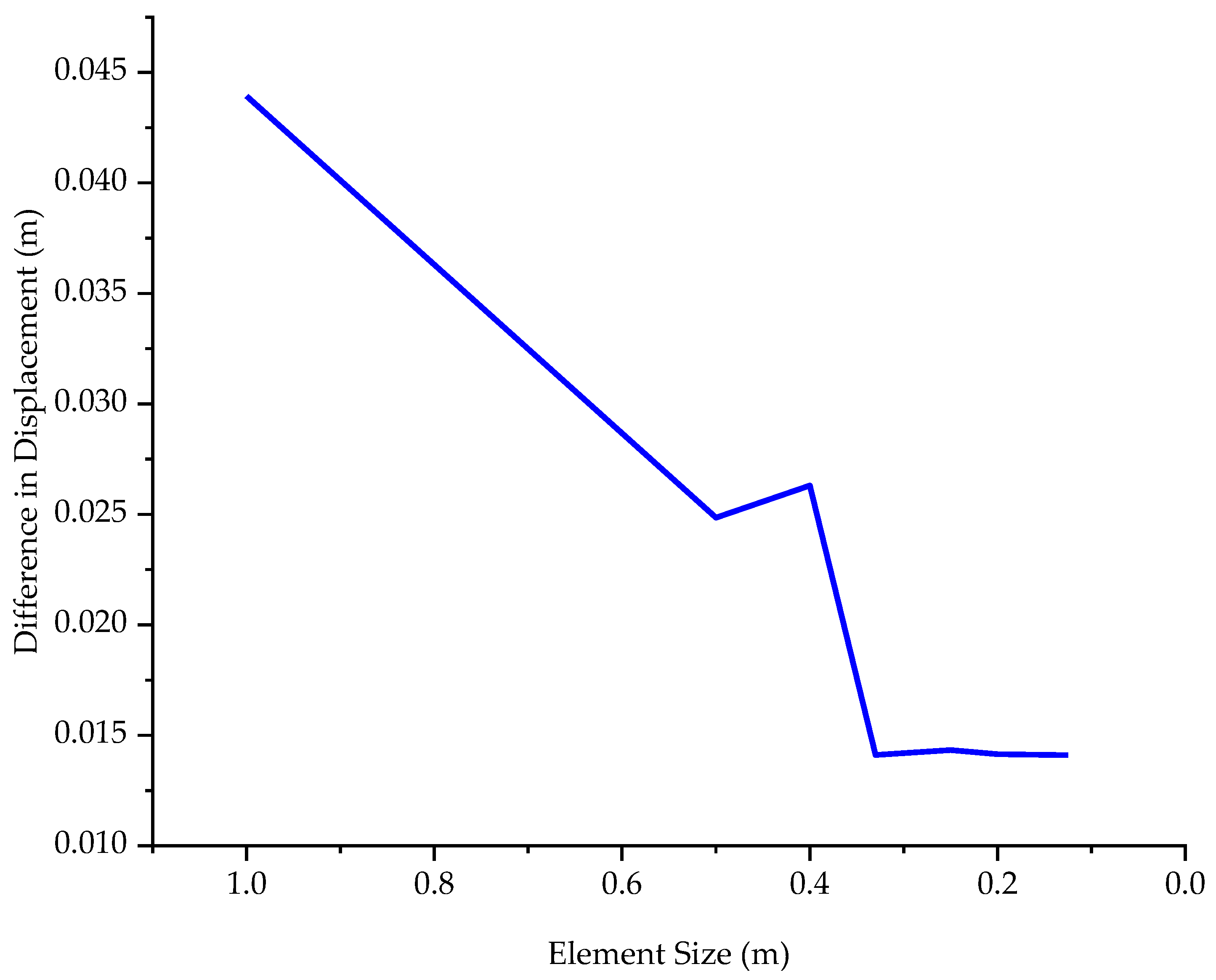
3.2. Finite Element Simulation of the Heterogeneous Model
3.3. Finite Element Simulation of the Homogenized Model
3.4. Matching the Homogenized Parameters to the Heterogeneous Parameters
4. Network Architecture and Parameter Optimization
4.1. Data Pre-Processing
4.2. Dataset Partitioning
4.3. The Bayesian Optimized Neural Network
5. Results
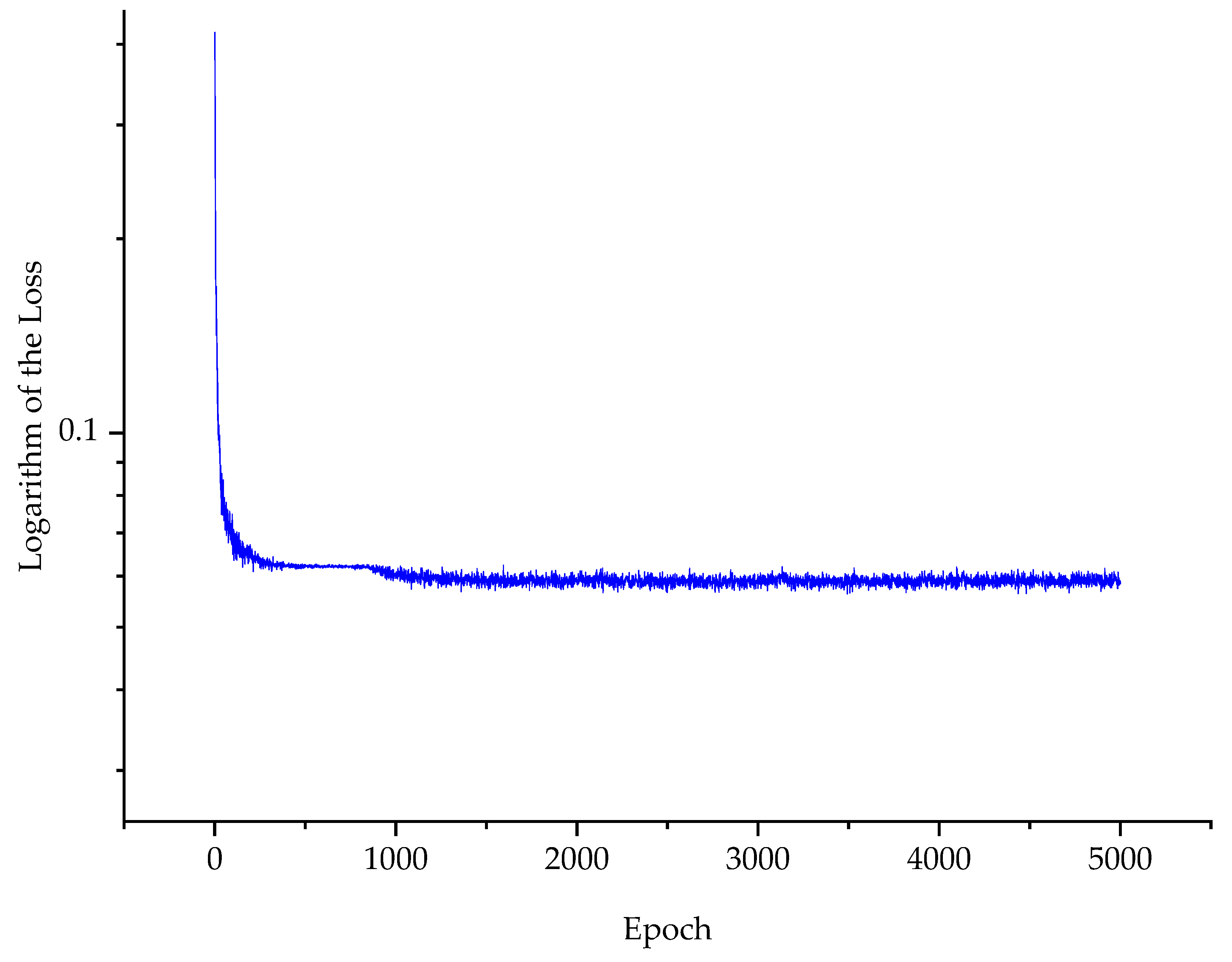
5.1. Training Loss of the BP-ANN Model
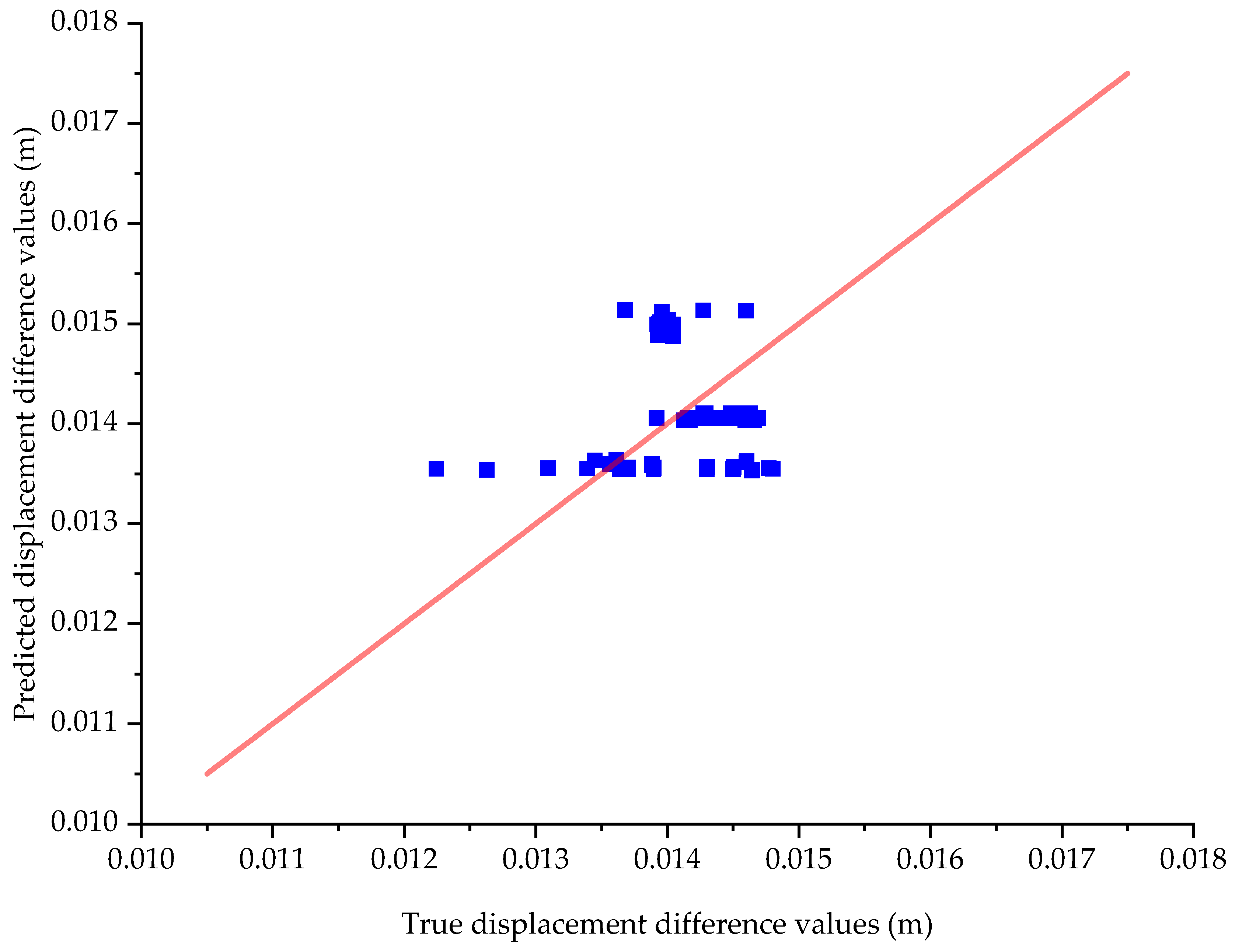
5.2. Verification of Our Model on an Independent Dataset
5.3. Discussion
- (1)
- The proposed method exhibits generalizability and can be applied in various fields of geotechnical mechanics.
- (2)
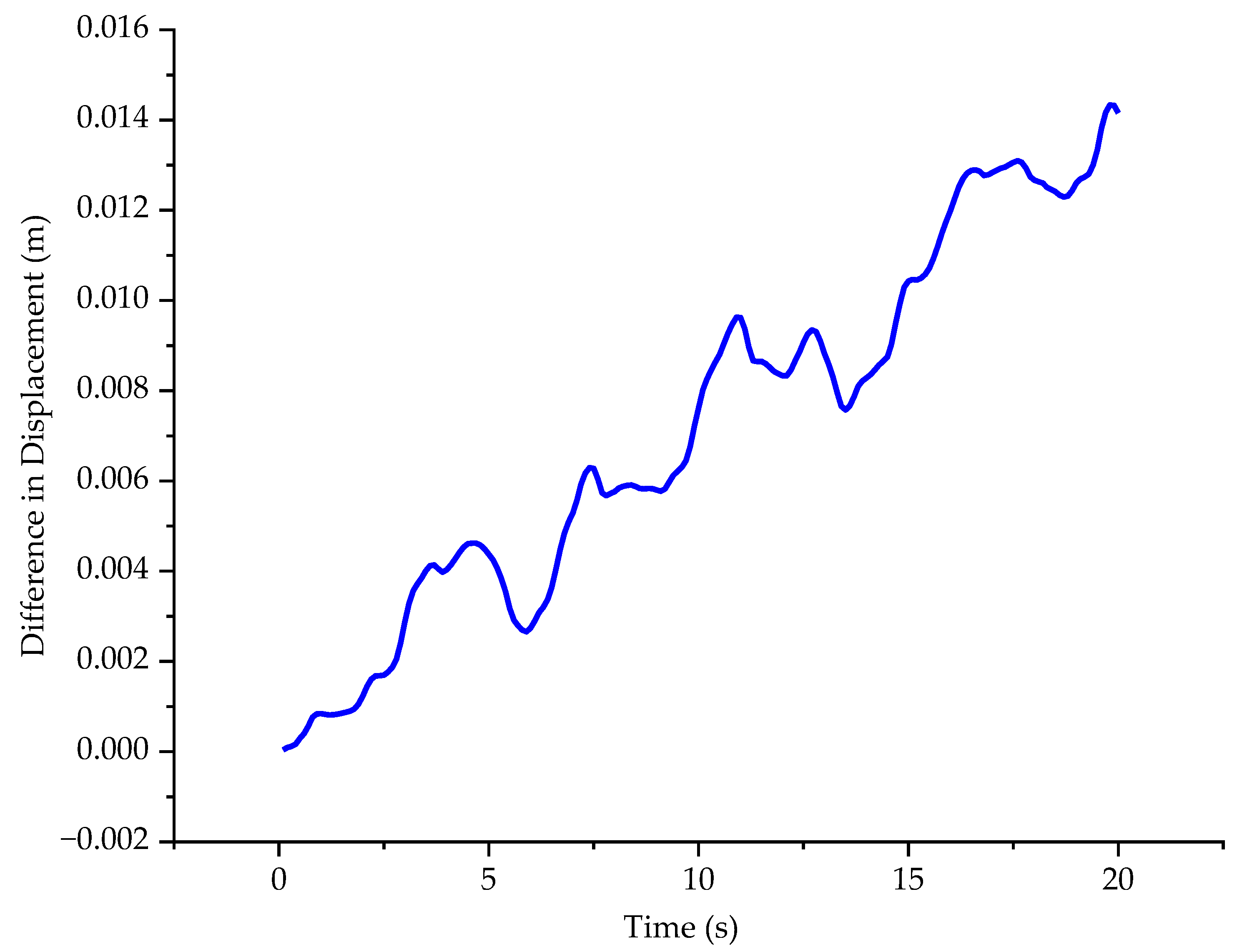
- The established model accurately predicts the displacement difference. The mean absolute percentage error (MAPE) between the predicted and actual displacement difference is only 5.3% for the test set, and 2.6% for the independent validation set. This again demonstrates the model’s strong generalization ability for the geotechnical problems examined in this study.
- (3)
- Utilizing the trained model for practical geotechnical problems significantly reduces the need for computational resources and time costs when compared to traditional approaches.
6. Conclusions
- Bayesian optimization, in our work, managed to optimize our network architecture as well as the hyperparameters.
- Applying the BP-ANN to predict the yields of the corresponding sets of predicted parameters and the good agreement between the difference in displacement computed using the predicted parameters and the simulation data of the heterogeneous model verify the superiority of our model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chang, D.; Lai, Y.; Zhang, M. A meso-macroscopic constitutive model of frozen saline sandy soil based on homogenization theory. Sciences 2019, 159, 246–259. [Google Scholar] [CrossRef]
- Gasmi, H.; Hamdi, E.; Bouden Romdhane, N. Numerical homogenization of jointed rock masses using wave propagation simulation. Rock Mech. Rock Eng. 2014, 47, 1393–1409. [Google Scholar] [CrossRef]
- Shi, F.; Fantuzzi, N.; Li, Y.; Trovalusci, P.; Wei, Z. Modeling of dilatancy effect in layered rock with rough interfaces using micropolar continuum. Res. Commun. 2022, 125, 1039944. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Logarzo, H.J.; Capuano, G.; Rimoli, J.J. Smart constitutive laws: Inelastic homogenization through machine learning. Comput. Methods Appl. Mech. Eng. 2021, 373, 113482. [Google Scholar] [CrossRef]
- Rodríguez, C.A.; Rodríguez-Pérez, A.M.; López, R.; Hernández-Torres, J.A.; Caparrós-Mancera, J.J. A Finite Element Method Integrated with Terzaghi’s Principle to Estimate Settlement of a Building Due to Tunnel Construction. Buildings 2023, 13, 1343. [Google Scholar] [CrossRef]
- Ismail, Y.; Wan, L.; Chen, J.Y.; Ye, J.Q.; Yang, D.M. An ABAQUS (R) plug-in for generating virtual data required for inverse analysis of unidirectional composites using artificial neural networks. Eng. Comput. 2022, 38, 4323–4335. [Google Scholar] [CrossRef]
- Peng, G.C.Y.; Alber, M.; Tepole, A.B.; Cannon, W.; De, S.; Dura-Bernal, S.; Garikipati, K.; Karniadakis, G.; Lytton, W.W.; Perdikaris, P.; et al. Multiscale Modeling Meets Machine Learning: What Can We Learn? Arch. Comput. Methods Eng. 2021, 28, 1017–1037. [Google Scholar] [CrossRef]
- Eidgahee, D.R.; Jahangir, H.; Solatifar, N.; Fakharian, P.; Rezaeemanesh, M. Data-driven estimation models of asphalt mixtures dynamic modulus using ANN, GP and combinatorial GMDH approaches. Neural Comput. Appl. 2022, 34, 17289–17314. [Google Scholar] [CrossRef]
- Frankel, A.L.; Jones, R.E.; Alleman, C.; Templeton, J.A. Predicting the mechanical response of oligocrystals with deep learning. Comput. Mater. Sci. 2019, 169, 109099. [Google Scholar] [CrossRef]
- Zhang, W.G.; Li, H.R.; Li, Y.Q.; Liu, H.L.; Chen, Y.M.; Ding, X.M. Application of deep learning algorithms in geotechnical engineering: A short critical review. Artif. Intell. Rev. 2021, 54, 5633–5673. [Google Scholar] [CrossRef]
- Rehman, Z.U.; Khalid, U.; Ijaz, N.; Mujtaba, H.; Haider, A.; Farooq, K.; Ijaz, Z. Machine learning-based intelligent modeling of hydraulic conductivity of sandy soils considering a wide range of grain sizes. Eng. Geol. 2022, 311, 106899. [Google Scholar] [CrossRef]
- Khalid, U.; Rehman, Z.U.; Mujtaba, H.; Farooq, K. 3D response surface modeling based in-situ assessment of physico-mechanical characteristics of alluvial soils using dynamic cone penetrometer. Transp. Geotech. 2022, 36, 100781. [Google Scholar] [CrossRef]
- Onyelowe, K.C.; Mojtahedi, F.F.; Ebid, A.M.; Rezaei, A.; Osinubi, K.J.; Eberemu, A.O.; Salahudeen, B.; Gadzama, E.W.; Rezazadeh, D.; Jahangir, H.; et al. Selected AI optimization techniques and applications in geotechnical engineering. Cogent Eng. 2023, 10, 2153419. [Google Scholar] [CrossRef]
- Labuz, J.F.; Zang, A. Mohr-Coulomb Failure Criterion. Rock Mech. Rock Eng. 2012, 45, 975–979. [Google Scholar] [CrossRef]
- Yonggang, H.; Xueyan, Z.; Xuezhen, L.; Yunzhang, R. Contrastive application of neural network and fuzzy comprehensive evaluation to slope stability analysis. J. Nonferrous Met. Sci. Eng. 2016, 7, 94–99. [Google Scholar] [CrossRef]
- Zhongyang, L.; Bingyang, L.; Yimiao, H.; Hao, W.; Wei, C.; Weisu, W. Research on prediction of ultimate moment capacity of beam-to-column flush end-plate connection joint via BP-ANN model. J. Build. Struct. 2023, 53, 119–126. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Dubey, S.R.; Singh, S.K.; Chaudhuri, B.B.J.N. Activation functions in deep learning: A comprehensive survey and benchmark. Neurocomputing 2022, 503, 92–108. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Nevitt, J.M.; Warren, J.M.; Kumamoto, K.M.; Pollard, D.D. Using geologic structures to constrain constitutive laws not accessible in the laboratory. J. Struct. Geol. 2019, 125, 55–63. [Google Scholar] [CrossRef]
- Rehman, Z.U.; Luo, F.Y.; Wang, T.; Zhang, G. Large-Scale Test Study on the Three-Dimensional Behavior of the Gravel-Concrete Interface of a CFR Dam. Int. J. Geomech. 2020, 20, 04020046. [Google Scholar] [CrossRef]
- Rehman, Z.U.; Zhang, G. Three-dimensional elasto-plastic damage model for gravelly soil-structure interface considering the shear coupling effect. Comput. Geotech. 2021, 129, 103868. [Google Scholar] [CrossRef]
- Berdychowski, M.; Talaska, K.; Malujda, I.; Kukla, M. Application of the Mohr-Coulomb model for simulating the biomass compaction process. IOP Conf. Ser. Mater. Sci. Eng. 2020, 776, 012066. [Google Scholar] [CrossRef]
- Sui, C.Y.; Shen, Y.S.; Wen, Y.M.; Gao, B. Application of the Modified Mohr-Coulomb Yield Criterion in Seismic Numerical Simulation of Tunnels. Shock Vib. 2021, 2021, 9968935. [Google Scholar] [CrossRef]
- Wang, Y.W.; Li, S.Y.; Ma, Q.; Li, W. A Comparative Study of Artificial Boundary Conditions in ABAQUS. In Proceedings of the International Conference on Structures and Building Materials (ICSBM 2013), Guizhou, China, 9–10 March 2013; Volume 9, pp. 1386–1389. [Google Scholar] [CrossRef]
- Asheghabadi, M.S.; Ali, Z. Infinite element boundary conditions for dynamic models under seismic loading. Indian J. Phys. 2020, 94, 907–917. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A. Data Mining: Practical Machine Learning Tools and Techniques, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Chao, Z.M.; Dang, Y.B.; Pan, Y.; Wang, F.Y.; Wang, M.; Zhang, J.; Yang, C.X. Prediction of the shale gas permeability: A data mining approach. Geomech. Energy Environ. 2023, 33, 100435. [Google Scholar] [CrossRef]
| Parameter | Min | Max | Avg | STD |
|---|---|---|---|---|
| 15.00 | 20.00 | 17.63 | 2.50 | |
| 15.00 | 20.00 | 17.65 | 2.50 | |
| 8.00 | 48.00 | 34.50 | 11.86 |
| Neuron | Dropout_Rate | Learning_Rate | Hidden Layers |
|---|---|---|---|
| 25 | 0.6 | 0.006 | 7 |
| MSE | RMSE | MAE | |
|---|---|---|---|
| E | 0.06 | 0.24 | 0.18 |
| 0.036 | 0.19 | 0.14 | |
| C | 0.10 | 0.32 | 0.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Huang, G.; Li, Y.; Zhang, J.; Yang, Z.; Wang, M. The Data-Driven Homogenization of Mohr–Coulomb Parameters Based on a Bayesian Optimized Back Propagation Artificial Neural Network (BP-ANN). Appl. Sci. 2023, 13, 11966. https://doi.org/10.3390/app132111966
Gao Y, Huang G, Li Y, Zhang J, Yang Z, Wang M. The Data-Driven Homogenization of Mohr–Coulomb Parameters Based on a Bayesian Optimized Back Propagation Artificial Neural Network (BP-ANN). Applied Sciences. 2023; 13(21):11966. https://doi.org/10.3390/app132111966
Chicago/Turabian StyleGao, Yunfei, Guogui Huang, Yinxi Li, Junyuan Zhang, Zeng Yang, and Meng Wang. 2023. "The Data-Driven Homogenization of Mohr–Coulomb Parameters Based on a Bayesian Optimized Back Propagation Artificial Neural Network (BP-ANN)" Applied Sciences 13, no. 21: 11966. https://doi.org/10.3390/app132111966
APA StyleGao, Y., Huang, G., Li, Y., Zhang, J., Yang, Z., & Wang, M. (2023). The Data-Driven Homogenization of Mohr–Coulomb Parameters Based on a Bayesian Optimized Back Propagation Artificial Neural Network (BP-ANN). Applied Sciences, 13(21), 11966. https://doi.org/10.3390/app132111966






