Abstract
Charged particle beams driven to ultra-high dose rates (UHDRs) have been shown to offer potential benefits for future clinical applications, particularly in the reduction of normal-tissue toxicity. Studies of the so-called FLASH effect have shown promise, generating huge interest in high dose rate radiation studies. With laser-driven proton beams, where the duration of the proton burst delivered to a sample can be as short as hundreds of picoseconds, the instantaneous dose rates are several orders of magnitude higher than those used for conventional radiotherapy. The dosimetry of these beam modalities is not trivial, with conventional active detectors, such as ionisation chambers, experiencing saturation effects making them unusable at the extremely high dose rates. Calorimeters, measuring the radiation-induced temperature rise in an absorber, offer an ideal candidate for the dosimetry of UHDR beams. However, their application in the measurement of laser-driven UHDR beams has so far not been trialled, and their effective suitability to work with the quasi-instantaneous and inhomogeneous dose deposition patterns and the harsh environment of a laser-plasma experiment has not been tested. The measurement of the absorbed dose of laser-driven proton beams was conducted in a first-of-its-kind investigation, employing the VULCAN-PW laser system of the Central Laser Facility (CLF) at the Rutherford Appleton Laboratory (RAL), using a small-body portable graphite calorimeter (SPGC) developed at the National Physical Laboratory (NPL) and radiochromic films. A small number of shots were recorded, with the corresponding absorbed dose measurements resulting from the induced temperature rise. The effect of the electromagnetic pulse (EMP) generated during laser–target interaction was assessed on the system, showing no significant effects on the derived signal-to-noise ratio. These proof-of-principle tests highlight the ability of calorimetry techniques to measure the absorbed dose for laser-driven proton beams.
1. Introduction
Radiotherapy is responsible for approximately 60% of cured cancer cases [1], although the treatments are limited by the maximum radiation dose that can be delivered to the tumour without damaging the healthy surrounding tissue [2,3]. Innovative strategies have recently been investigated, through delivering the dose in a single or limited number of pulses at high dose rates, which show a reduction in normal tissue toxicities whilst maintaining levels of tumour control in line with conventional techniques [4]. This is possible through the so-called FLASH effect at rates in excess of 40 Gy/s [5,6]. The ability to operate at regimes with even higher dose rates per pulse has further fuelled research interest into UHDR beams. This includes exploring alternative mechanisms of particle acceleration, such as the laser-driven approach, which typically leads to pulse dose rates several orders of magnitude higher than the threshold characterised as the FLASH regime [7,8,9].
The laser-driven acceleration of protons has successfully resulted in the generation of beams with energies lying within the range of interest for medical applications [10,11,12], with recent demonstrations of the generation of proton beams up to ~100 MeV [13]. Since laser-driven proton beams can reach dose rates in excess of 109 Gy/s, dosimetry becomes increasingly complicated, with conventional detectors, such as ionisation chambers, often unusable because of ion recombination effects [14,15,16], which leads to increased levels of uncertainty. Furthermore, for laser-driven beams, additional complications arise from the harsh experimental environment, where a large electromagnetic pulse (EMP) can be generated during the laser–target interaction, in addition to non-ideal beam parameters, such as beam inhomogeneity and wide energy spread. For potential applications, accurate dosimetric methods and new approaches must be investigated [17,18,19].
Despite the significant metrological challenges faced when performing dosimetry measurements of UHDR beams, potential solutions have been proposed, and a number of these have already been explored. This includes dosimetry based on the use of Faraday cups [20,21] and ionisation chambers, although the latter of these detectors cannot be used satisfactorily due to recombination effects [22]. Passive detectors such as radiochromic films also have an extensive history of use in the measurement of laser-accelerated beams [23]. Furthermore, a number of measurements have been demonstrated and reported using calorimeters, including in the dosimetry of very high energy electron (VHEE) beams to characterise ion collection losses in ionisation chambers [18]. The National Research Council Canada (NRC) also developed a portable calorimeter that has been tested with UHDR electron beams, aiming to eliminate inhomogeneities in the absorber material by constructing this of pure aluminium [24]. Additionally, a Graphite Probe Calorimeter (GPC) known as ‘Aerrow’ [25,26] was built with a waterproof design, allowing its use in a conventional water phantom. The Aerrow has so far been utilised within high-energy photon and electron beams, suggesting its potential usage with ultra-high dose per pulse beams [24,25,26]. Furthermore, the ion recombination losses experienced in ionisation chambers were addressed through the development of a prototype secondary standard calorimeter [27]. Developed at the NPL, this device utilises a single sensing core thermistor encased within a 3D-printed body mimicking the shape of a standard Roos-type chamber.
Calorimeters have several advantages which make them ideally suited for UHDR dosimetry. They can provide instant readout, have a dose-rate independent response and allow for direct determination of the absorbed dose from fundamental principles. Calorimeters rely on measuring the radiation-induced temperature rise in an absorber material as the initial energy of the impinging particle degrades to heat. Through knowledge of the material properties, including the specific heat capacity of the absorber, the rise in temperature can be converted to a measure of the absorbed dose. Although various formats and applications are available, graphite calorimeters have an already well-established usage as primary standard level instruments for conventional radiotherapy treatments [28,29,30,31,32,33].
Calorimetry techniques have been tested with proton beams at dose rates up to 60 Gy/s using clinical scanning beams [33,34], but have so far not been employed to conduct measurements of the absorbed dose generated by laser-driven proton beams at UHDRs. Within the EURAMET UHDpulse project (The name of EURAMET research project UHDpulse, shorthand for ultra-high dose pulse (http://uhdpulse-empir.eu/, accessed on 18 September 2023)) [15,35], investigations were carried out to establish calorimetry techniques for the measurement of UHDR beams, including laser-driven beams. These include the initial characterisation of a small-body portable graphite calorimeter (SPGC), originally developed and optimised at the NPL for the measurement of low-energy clinical proton beams [31]. The SPGC has since been refurbished in preparation for the absorbed dose measurement of laser-driven proton beams. The aim of this investigation was to assess the feasibility of providing traceable dose standards through the SPGC and back to the NPL primary standard level proton calorimeter. The initial tests reported here focus on the characterisation of the operation of the SPGC. The tests were carried out on a VULCAN-PW laser system at the Central Laser Facility (CLF) of the Rutherford Appleton Laboratory (RAL), UK.
2. Materials and Methods
2.1. Calorimetry
The small-body portable graphite calorimeter (SPGC, National Physical Laboratory, NPL, Teddington, UK) is a smaller derivative of the previous portable graphite calorimeter reported in the literature [31,36], with both devices developed from the same materials at the NPL. The intended purpose for the SPGC was the measurement of low energy, clinical proton beams, but more recently it has been refurbished to enable use with laser-driven protons.
A schematic of the graphite components of the SPGC is shown in Figure 1. The SPGC comprises a cylindrical arrangement of graphite structures, with the innermost component, the core, containing thermistors used to detect the radiation-induced temperature rise from which the absorbed dose is measured. The core has a 20 mm diameter and 2 mm thickness and is separated from a jacket of 30 mm external diameter and 4 mm depth by a 1 mm air cavity. Both the core and jacket are composed almost exclusively of graphite. This graphite arrangement of components is enclosed within a Styrofoam structure, with the outer surface of the graphite lid exposed to the incoming radiation beam. These two outermost components (graphite jacket and Styrofoam enclosure) are designed to enhance thermal isolation of the core by reducing heat exchange with the surrounding environment. The structure of the small portable graphite calorimeter, in addition to its placement within the irradiation pipe, are shown in Figure 2, Figure 3 and Figure 4.
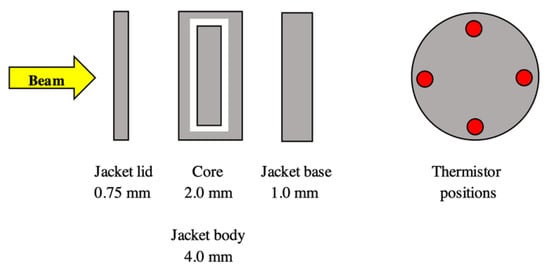
Figure 1.
Configuration of the graphite components of the SPGC for measurements within a radiation beam. The red dots on the right indicate the relative locations of the thermistors within the body of the calorimeter. Dimensional metrology of the graphite components was carried out during the refurbishment of the calorimeter. The SPGC prepared for use with the VULCAN-PW system can be seen in Figure 2a.
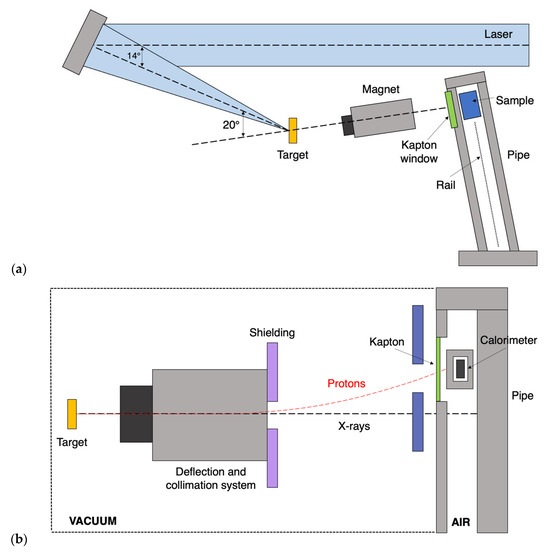
Figure 2.
(a). Schematic showing the layout and components of the VULCAN-PW beamline at CLF (RAL) used in the irradiation of both biological sample/calorimeter system. The rail and re-entrance pipe connecting the sample to be irradiated to the interaction chamber are identified as the furthermost right components. (b). Alternative perspective of the beamline at RAL, with the small portable graphite calorimeter positioned at the irradiation point through the use of the pipe and rail system. The dashed lines indicate the relative paths of the X-rays (black) and protons (red), respectively.

Figure 3.
(a). The NPL small portable graphite calorimeter mounted in a custom-made holder alongside the associated electronics. This was attached to a specially made carriage so that it could be fitted onto the rail system and slide along the pipe to the irradiation point. (b). The SPGC being attached to the rail and inserted within the re-entrance pipe.
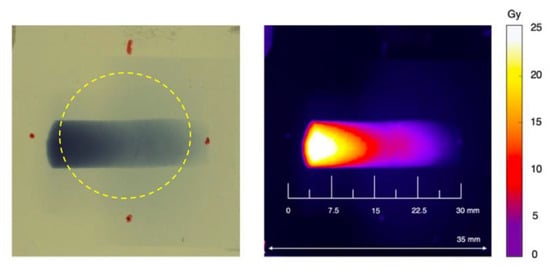
Figure 4.
Irradiated film which was attached to the front surface of the SPGC. The dose is integrated over a region corresponding to that of the total core area (highlighted in dashed yellow), giving a measurement of the average dose deposited over the entirety of the core. The red marked regions indicate the rough relative positions of the calorimeter circumference (left). Reference dose and spatial scales are included in the analysed image (right).
The first recorded measurements of the absorbed dose of a laser-driven proton beam using the calorimeter system as reported here were conducted with the high-power VULCAN-PW laser system at the CLF, Rutherford Appleton Laboratory, United Kingdom. This system is capable of producing pulses with wavelength λ = 1.054 µm duration ~500–700 ps and energy up to 600 J. The laser pulses were focused with an f/3 Off Axis Parabola onto the surface of thin foils at an intensity of ~5 1020 W/cm2. Upon irradiation, protons were accelerated from the rear of the foils through the target normal sheath acceleration (TNSA) process [11]. As shown in Figure 2a, a dipole magnet system was placed downstream of the target within the interaction chamber, generating a magnetic field of 0.9 T, thus allowing for the energy dispersion of the protons before they reach a sample located in a re-entrance tube. This setup, designed for radiobiology measurements [37], was adapted to fit the SPGC system within the in-air irradiation pipe, as shown in the schematic included in Figure 2b.
Proton bunches are generated through intense laser–target interactions impinging on the SPGC core, inducing a temperature rise in the graphite which is detected by the embedded thermistors. The temperature of the core thermistors was remotely monitored via instrumentation controlled by a LabVIEW program (LabVIEW software version 2010, National Instruments, www.ni.com/; accessed 18 September 2023) running on a computer located within the control area.
The energy delivered by the laser system during the sequence of 5 shots was 556.0, 592.0, 582.4, 620.9 and 617.7 J. The laser was operated at full power with ~500 fs duration pulses focused onto 15 µm gold targets (with the exception of shot 2, in which 1 µm CH plastic was used) [38]. The calorimeter operates in adiabatic mode, which allows the temperature of the calorimeter components to drift so energy deposited through impinging radiation will translate to an induced temperature rise in the graphite components. It was expected that a significant electromagnetic pulse (EMP) would be generated through the laser–target interaction, a typical feature of high-power laser systems [12]. As a result, precautions, such as (i) strategic placement of the instrumentation, (ii) protection of the electronics through implementation of electronic circuitry consisting of discrete components that were designed to sit externally alongside the current DC Wheatstone bridge connection, and (iii) operation of the SPGC in a full adiabatic mode, aimed to limit such effects.
Out of the 5 shots, 4 adopted the previously described setup (Figure 2b), with the SPGC placed at the irradiation point. The system was retracted from the beam path in the remaining shot, allowing for a simple assessment of the EMP-induced effects by monitoring the temperature drift in the absence of incident particles. The temperature drift data are analysed by observing a 30 s pre- and post-irradiation window, with a quadratic fit applied to best extrapolate the temperature data to mid-run. This interval allows the absorbed dose to be calculated whilst minimising the impact from changes in the environment surrounding the calorimeter. The rise in temperature at the mid-run position is then calculated and converted to the absorbed dose to the core through prior knowledge of the specific heat capacity of the absorber material.
2.2. Radiochromic Film
Corresponding film measurements were simultaneously performed for each of the calorimeter irradiations by placing a single RCF on the front surface of the calorimeter jacket—i.e., the surface which was directly exposed to the incoming proton beam. Singular sheets of GafChromic EBT3 films [39] were cut to approximate dimensions of 3 cm × 3 cm, sufficient to fully encompass the entirety of the sensitive region of the SPGC core. Prior to irradiation, the outer circumference of the calorimeter jacket was marked on the attached film, allowing the volume averaged dose region to be analysed. This is highlighted in Figure 4.
As observed from Figure 4, the dose distribution deposited on the EBT3 film is the result of the magnetic dispersion system that was employed, giving a horizontal spread of energy components. The deflection of proton kinetic energies is demonstrated in the schematic shown in Figure 5. The least energetic protons should experience the greatest deflection corresponding to those deposited leftmost on the film shown in Figure 4, with the most energetic being deposited further across the horizontal direction.
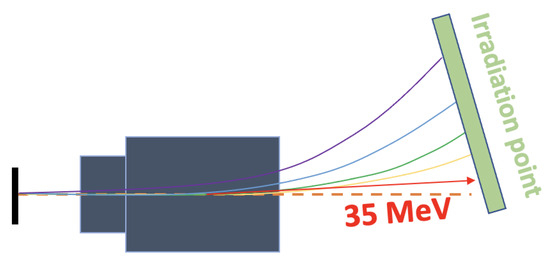
Figure 5.
Schematic showing the deflection of protons contained within the laser-accelerated beam, with the degree of deflection dependent on the incident particle kinetic energy. The colours highlight the fact that particles are deflected onto the irradiation point according to their energy, with the higher energies (red) deflecting least and the lower energies (purple) the most.
The significant darkening on the left-hand side of the dose profile on the EBT3 film in Figure 4 indicates that the least energetic protons are the most populous and are being stopped by the film. A “line-out” of the dose profile was calculated and examined from the irradiated RCF, as shown in Figure 6. This is taken as a line directly across the horizontal geometrical distance of the irradiated region, from which the dose is analysed.
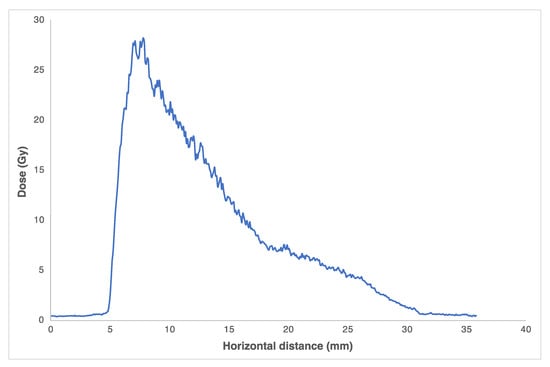
Figure 6.
Horizontal dose profile taken from the EBT3 layer attached to the SPGC for the first shot. The blue line indicates the dose line-out taking across the film horizontal. As seen, the different kinetic energy components of the proton bunch, which are contained in differing proportions, are magnetically dispersed, leading to an inhomogeneous dose deposition on the film.
The proton energy dispersion was investigated through Monte Carlo simulations using the Geant4 code (applying the QGSP_BERT_HP physics list for all processes) [39,40,41]. A proton source, variable in its distribution of particle kinetic energy (ranging from 0 to 45 MeV at the source), was simulated using Geant4. Through the use of particle scoring, the cartesian coordinates in addition to the initial kinetic energy of each component of this simulated proton beam were recorded at a position corresponding to that of the exact entrance of the jacket of the small-body portable graphite calorimeter. This setup was simulated to replicate that of the calorimeter system within the beamline at the RAL.
The plot shown in Figure 7, in addition to that in Figure 8, highlights that within the proton bunch accelerated from the laser system, the particle kinetic energies at the lower end of the spectrum (~0–10 MeV) are the most populous. It was anticipated that this lower end of the spectrum would comprise those particles that are stopped within the initial RCF and graphite jacket. This was confirmed through calculations performed with the LISE++ software (Michigan State University, https://lise.nscl.msu.edu/lise.html, accessed on 18 September 2023) [42]. Using this toolkit, the proton energy required to penetrate a structure composed of 350 m water equivalent thickness RCF (EBT3) material, followed immediately by 0.75 mm of graphite of density 2 g/cm3, was obtained. Proton energies of between 12.1 and 12.2 MeV were calculated with the LISE++ setup, indicating this energy is required to reach the SPGC core after initially traversing both the film and jacket layers.
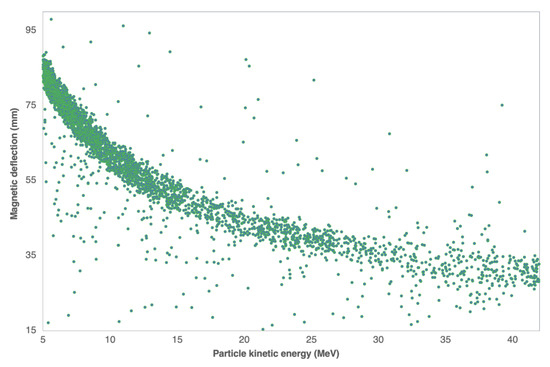
Figure 7.
Simulation conducted in Geant4 of the particle kinetic energy spectrum scored against their deposited positions on the front surface of the constructed calorimeter. The green dots represent the individual particles scored in the Monte Carlo simulation.
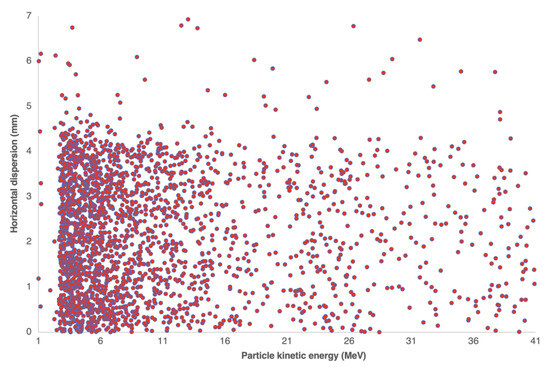
Figure 8.
Simulated spectrum of the incident proton kinetic energy values scored along their horizontal displacement. The red dots again represent the scored particles, similar to that in Figure 7. The protons at the lower end of the energetic spectrum are higher in quantity than those at higher energies.
The dose deposited on each film was retrieved more than 24 h post irradiation to avoid any effects related to film development in the first 24 h [43]. The films were scanned using an EPSON 12000 XL 48-bit (Seiko Epson, Nagano, Japan, https://www.epson.co.uk/en_GB, accessed on 1 August 2019) flat-bed photo scanner (300 dpi resolution with the red channel) [44]. A suitable region of interest (ROI) was defined on each film from which the absorbed dose was calculated. The ImageJ analysis software (National Institutes on Health, https://imagej.nih.gov/ij/download.html, accessed on 15 July 2019) was used for dose analysis [45]. The ROI within the analysis is matched to that of the SPGC core area. An EBT3 film calibration enables a conversion of the pixel value optical density to the absorbed dose. The deposited dose was integrated over the ROI (SPGC core equivalent area) using the ImageJ analysis software for each of the irradiated EBT3 films [45]. This is shown in Figure 4, with further information on the dose analysis highlighted in Figure 9.
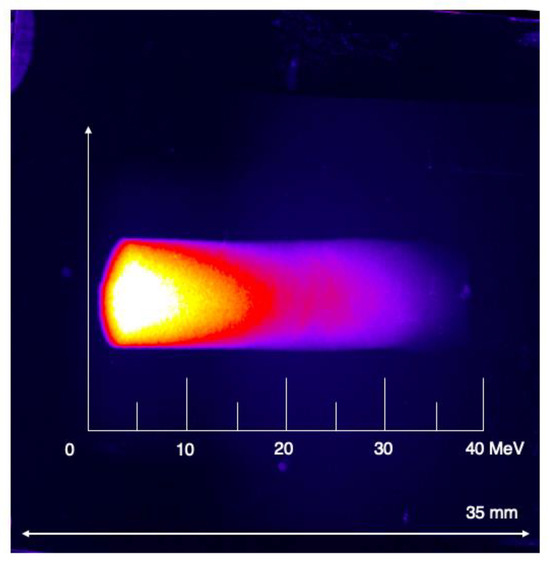
Figure 9.
Digitised RCF layer from which the deposited dose was integrated over the core area. The dimensions of the film are shown, along with an energy scale highlighting the dispersion of kinetic energy components identified through Monte Carlo simulation.
3. Results
The temperature drift curves for each shot were analysed offline, converting the radiation-induced temperature rise (measured in K) into a measure of the absorbed dose through the specific heat capacity of the absorber material, cg. Calibration of the core thermistors was carried out at the NPL using a CTR3000 thermometer and PRT probe system, traceable to national standards allowing the bridge-out-of-balance voltage to be converted to the temperature in the thermistors. For every shot taken, the temperature rise resulting from the impinging proton beam was converted to the absorbed dose deposited in the calorimeter core. The data taken for the dose from each shot, in addition to the target and film parameters, are outlined in Table 1.

Table 1.
Summary of the mean values of absorbed dose measured with the three correctly operating thermistors within the small-body portable graphite calorimeter using the VULCAN-PW laser system at CLF, calculated from the radiation-induced temperature rise in the core. The data from core thermistor 4 are omitted as they were not consistent with the other 3 due to an issue with a poor electrical connection within the measurement electronics. For comparison, the dose deposited on the RCF placed on the front face of the SPGC for each shot is also included.
Given the relatively low levels of dose encountered, thermistors T1, T2 and T3 showed remarkably good levels of consistency. For example, within shot 1, absorbed dose values of 2.018 Gy, 2.048 Gy and 2.035 Gy were found from core thermistors 1, 2 and 3, respectively. The uncertainty of the dose values found from the temperature rise in the SPGC core thermistors was estimated to be ~12.7%. This analysis was performed through consideration of the fluctuation in temperature drift of the data acquisition and dose deposition over the sensitive area of the calorimeter. An upper and lower bound was set for the temperature drift curves pre- and post irradiation and the variation analysed. This is a conservative estimation taking into consideration only the systematic error of the measurement, as the statistics cannot be considered due to the low number of shots performed. It is important to note that the absorbed dose measurement with a calorimeter is independent of the pulse width, instead depending only on the amount of energy that is transferred to the system during irradiation. It is thus possible that different pulses may deposit exactly the same energy with the same corresponding absorbed dose. This represents a great advantage of calorimeters, which are dose-rate and/or dose-per-pulse independent, unlike ionisation chambers, which are routinely used in clinical dosimetry.
The GafChromic EBT3 film layers attached to the SPGC during each shot (see Figure 3 and Figure 4) provided an additional measurement of the dose. From these measurements, it was found that the dose deposited on the RCF was greater than that retrieved from the calorimeter, as shown in Table 1. The greater RCF dose is a consequence of the energy spectrum of the laser-accelerated proton bunch (typically exponential, as per [11]), with lower proton energies present in higher proportions. From the LISE++ calculations mentioned previously, a proton energy of 12.1–12.2 MeV is needed to traverse both the film and graphite jacket layers, meaning that the dose contributions of energy components below this threshold will be absent from the absorbed dose measured in the calorimeter core. From these calculations, it is also estimated that 1.96 MeV protons are stopped in the initial RCF, with the remaining 10.24 MeV lost in the jacket. This dose decrease was further investigated through Monte Carlo simulation of the setup with the particle simulation toolkit TOPAS [46,47]. Separate simulations were used to retrieve the dose within this initial jacket and film region, followed by that in the SPGC core, with a decrease in the absorbed dose of 49% indicated. These were performed using the entirety of the exponential energy spectrum. This clearly highlights the effect of the insulating jacket layer on the measured dose, outlining the minimum energy requirements needed from proton sources.
For the irradiation in which the calorimeter was withdrawn from the irradiation point, the online analysis software was monitored for any potential signal disruption that may occur as a result of EMP generation. Such distortion would affect the resolution of the system and, hence, the final dose value obtained from the temperature rise in the core. This initial concern was alleviated through the very good signal–noise ratio evident in the temperature drift signals. This is further supported by the radiation-induced temperature signals shown in Figure 10, detected with the calorimeter placed in the beamline. When removed from the irradiation point, no change in the background drift of the calorimeter signal was observed.
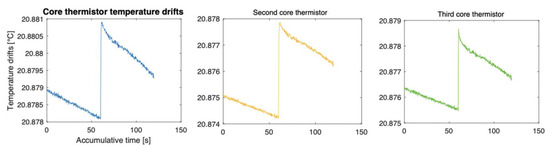
Figure 10.
Temperature drift curves for the core thermistors used in the determination of the absorbed dose for the first laser shot. An excellent signal–noise ratio is apparent, indicating the absence of electronic distortion deriving from effects such as the EMP generation in the target chamber. The different colours simply indicate that the temperature drift curves shown in the relative plots have been taken from different thermistors (1, 2, 3) in the calorimeter core.
Table 1 presents the values of the absorbed dose to the core measured with the calorimeter in the different shots. The variations observed are due to the deposited dose being dependent to some extent on the stability of the laser parameters (which will affect the proton spectrum), as well as the characteristics of the target from which the beam is accelerated. The laser instability contributes to this effect to a lesser effect than that of the target material, which plays a major role particularly within the target normal sheath acceleration (TNSA) mechanism [11]. From the data displayed in Table 1, the higher dose values were measured in shots 1 and 3, where the TNSA protons were accelerated from a 15 µm thick gold target. With respect to these, shot 2 (using a 1 µm CH target) displays a reduced dose in the core thermistors. This is evident from the data outlined in Figure 11, which was taken from an analysis of the dose profile in the respective RCF layers.
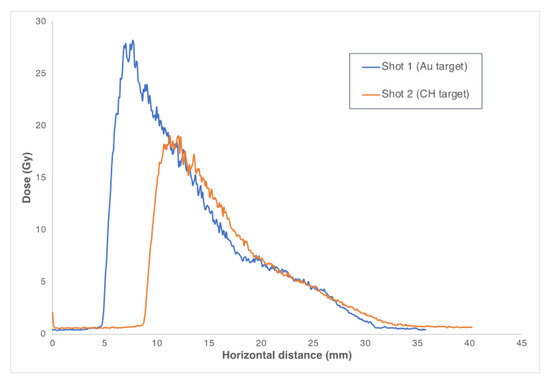
Figure 11.
Dose profiles for shots 1 and 2 employing gold (15 μm Au) and plastic (1 μm CH), respectively. The thinner nature and less-effective sheath acceleration in the CH likely lead to the reduced dose.
The differences in the dose profiles shown in Figure 11 are indicative of a less-efficient acceleration from the thinner CH target, giving a lower recorded measurement for the shot in which this target was used. Acceleration from this plastic target (shot 2 of Table 1) is less efficient than the others as the integrity of the rear surface of this thin target was not likely preserved, which has been shown to inhibit the effectiveness of acceleration for the TNSA regime [12,13]. This leads to a reduction in the dose measured between the surface RCF and the core thermistors that is more significant in this case, as outlined from the calculated data (Table 1).
4. Conclusions
The ultra-short duration of laser-driven beams, in addition to the harsh experimental environment resulting from the required intense laser–matter interactions, limits the application of conventional dosimetry techniques in the measurement of these modalities [10]. As a result, novel strategies must be explored to overcome the unique challenges presented by such a harsh environment and, above all, by the UHDRs. The first absorbed dose measurements of a laser-induced proton beam with a calorimeter have been presented based on the use of a small-body portable graphite calorimeter developed and maintained at the NPL, representing an approach to laser-driven dosimetry that had never been explored. The NPL SPGC was operated within a laser-driven proton beam using the VULCAN-PW laser system of the CLF at the RAL.
The absorbed dose was calculated for each of the irradiations performed through conversion of the radiation-induced temperature rises from each of the core thermistors. An additional measurement of the absorbed dose was carried out for each irradiation through the use of radiochromic film dosimetry, with film placed on the front surface of the SPGC. The decrease in the absorbed dose measured with the RCF compared with the dose measured with the SPGC indicated the amount of degradation of the beam after passing through the graphite jacket. The experimental setup was replicated for two of the shots in terms of the target used (i.e., shot 1 and shot 3), yielding the same degree of beam degradation. Radiochromic films have been used the most widely for the dosimetry of laser-driven beams. The outlined measurements conducted with both the SPGC and RCF indicate the ability of the calorimeter system to measure the absorbed dose from the radiation-induced temperature rise generated from the laser–target interactions, with the RCF acting as an additional measurement technique of the dose delivered. Furthermore, each of the shots, independent of the setup or target used, show good consistency in terms of the temperature rise measured by each of the thermistors. For dosimeters that are reliant on the use of electronics to some degree, the presence of a large EMP generated during the laser–target interaction may pose potential damaging effects to the equipment and/or signal. The excellent signal-to-noise ratio observed in the temperature curves indicated a lack of such distortion, with no evident effects of the EMP present in the calorimeter system.
Nevertheless, the induced temperature rises for each shot producing dose values on the Gy level, alongside the excellent signal–noise ratio and broad consistency with RCF measurements, demonstrate the ability of this device to operate within the environment of a high-power laser system. The limited number of irradiations performed, whilst being sufficient to demonstrate the proof-of-principle, should be expanded upon to improve the statistical variability, verify the accuracy and better assess the achievable level of uncertainty for calorimetry techniques in measuring the absorbed dose generated by laser-driven proton beams.
Author Contributions
For this article, the authors stated have contributed to the writing of this, in addition to the contained work in the following degree: methodology, S.M., F.R., A.S. and N.L.; software, N.L.; experiment preparation and data acquisition: S.M., N.L., G.M. and F.R.; formal analysis, S.M. and N.L.; writing—original draft preparation, S.M.; writing—review and editing, S.M., A.S., F.R., N.L., M.B., G.M. and A.M.; supervision, F.R., A.S. and M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This project, 18HLT04 UHDpulse, received funding from the EMPIR programme co-financed by the Participating States and from the European Union’s Horizon 2020 research and innovation programme. We also acknowledge funding from EPSRC (grant EP/K022415/1).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The work documented in this report is the result of a collaborative effort between Queen’s University and the National Physical Laboratory, with the measurements carried out at the Central Laser Facility, Rutherford Appleton Laboratory. This work would not have been possible without the efforts of all staff from each of the three institutions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- ECIS—European Cancer Information System. Available online: https://ecis.jrc.ec.europa.eu (accessed on 10 October 2020).
- Ferlay, J.; Steliarova-Foucher, E.; Lortet-Tieulent, J.; Rosso, S.; Coebergh, J.W.W.; Comber, H.; Forman, D.; Bray, F. Cancer incidence and mortality patterns in Europe: Estimates for 40 countries in 2012. Eur. J. Cancer 2013, 49, 1374–1403. [Google Scholar] [CrossRef] [PubMed]
- Jelonek, K.; Pietrowska, M.; Widlak, P. Systemic effects of ionizing radiation at the proteome and metabolome levels in the blood of cancer patients treated with radiotherapy: The influence of inflammation and radiation toxicity. Int. J. Radiat. Biol. 2017, 93, 683–696. [Google Scholar] [PubMed]
- Patriarca, A.; Fouillade, C.; Auger, M.; Martin, F.; Pouzoulet, F.; Nauraye, C.; Heinrich, S.; Favaudon, V.; Meyroneinc, S.; Dendale, R.; et al. Experimental set-up for FLASH proton irradiation of small animals using a clinical system. Int. J. Radiat. Oncol. 2018, 102, 619–626. [Google Scholar]
- Favaudon, V.; Caplier, L.; Monceau, V.; Pouzoulet, F.; Sayarath, M.; Fouillade, C.; Poupon, M.F.; Brito, I.; Hupé, P.; Bourhis, J.; et al. Ultrahigh dose-rate FLASH irradiation increases the differential response between normal and tumor tissue in mice. Sci. Transl. Med. 2014, 6, 245ra93. [Google Scholar]
- Loo, B.W.; Schuler, E.; Lartey, F.M.; Rafat, M.; King, G.J.; Trovati, S.; Koong, A.C.; Maxim, P.G. Delivery of ultra-rapid flash radiation therapy and demonstration of normal tissue sparing after abdominal irradiation of mice. Int. J. Radiat. Oncol. 2017, 98, E16. [Google Scholar] [CrossRef]
- Kraft, S.D.; Richter, C.; Zeil, K.; Baumann, M.; Beyreuther, E.; Bock, S.; Bussmann, M.; Cowan, T.E.; Dammene, Y.; Enghardt, W.; et al. Dose-dependent biological damage of tumour cells by laser-accelerated proton beams. New J. Phys. 2010, 12, 085003. [Google Scholar]
- Zeil, K.; Baumann, M.; Beyreuther, E.; Burris-Mog, T.; Cowan, T.E.; Enghardt, W.; Karsch, L.; Kraft, S.D.; Laschinsky, L.; Metzkes, J.; et al. Dose-controlled irradiation of cancer cells with laser-accelerated proton pulses. Appl. Phys. B 2013, 110, 437–444. [Google Scholar]
- Hanton, F.; Chaudhary, P.; Doria, D.; Gwynne, D.; Maiorino, C.; Scullion, C.; Ahmed, H.; Marshall, T.; Naughton, K.; Ro-magnani, L.; et al. DNA DSB repair dynamics following irradiation with laser-driven protons at ultra-high dose rates. Sci. Rep. 2019, 9, 4471. [Google Scholar] [PubMed]
- Ledingham, K.W.D.; Bolton, P.R.; Shikazono, N.; Ma, C.M.C. Towards laser driven hadron cancer radiotherapy: A review of progress. Appl. Sci. 2014, 4, 402–443. [Google Scholar]
- Macchi, A.; Borghesi, M.; Passoni, M. Ion acceleration by superintense laser-plasma interaction. Rev. Mod. Phys. 2013, 85, 751–793. [Google Scholar]
- Higginson, A.; Gray, R.J.; King, M.; Dance, R.J.; Williamson, S.D.R.; Butler, N.M.H.; Wilson, R.; Capdessus, R.; Armstrong, C.; Green, J.S.; et al. Near-100 MeV protons via a laser-driven transparency-enhanced hybrid acceleration scheme. Nat. Commun. 2018, 9, 724. [Google Scholar] [CrossRef] [PubMed]
- Consoli, F.; Tikhonchuk, V.T.; Bardon, M.; Bradford, P.; Carroll, D.C.; Cikhardt, J.; Cipriani, M.; Clarke, R.J.; Cowan, T.E.; Danson, C.N.; et al. Laser produced electromagnetic pulses: Generation, detection and mitigation. High Power Laser Sci. Eng. 2020, 8, E22. [Google Scholar] [CrossRef]
- Lee, E.; Lourenço, A.M.; Speth, J.; Lee, N.; Subiel, A.; Romano, F.; Thomas, R.; Amos, R.A.; Zhang, Y.; Xiao, Z.; et al. Ultrahigh dose rate pencil beam scanning proton dosimetry using ion chambers and a calorimeter in support of first in-human FLASH clinical trial. Med. Phys. 2022, 49, 6171–6182. [Google Scholar] [CrossRef] [PubMed]
- UHDPulse: Metrology for Advanced Radiotherapy Using Particle Beams with Ultra-High Pulse Dose Rates. Available online: http://uhdpulse-empir.eu (accessed on 30 July 2023).
- Subiel, A.; Moskvin, V.; Welsh, G.H.; Cipiccia, S.; Reboredo, D.; DesRosiers, C.; Jaroszynski, D.A. Challenges of dosimetry of ultra-short pulsed very high energy electron beams. Phys. Med. 2017, 42, 327–331. [Google Scholar] [CrossRef] [PubMed]
- McManus, M.; Romano, F.; Lee, N.D.; Farabolini, W.; Gilardi, A.; Royle, G.; Palmans, H.; Subiel, A. The challenge of ionisation chamber dosimetry in ultra-short pulsed high dose-rate Very High Energy Electron beams. Sci. Rep. 2020, 10, 9089. [Google Scholar] [CrossRef]
- Romano, F.; Subiel, A.; McManus, M.; Lee, N.D.; Palmans, H.; Thomas, R.; McCallum, S.; Milluzzo, G.; Borghesi, M.; McIlvenny, A.; et al. Challenges in dosimetry of particle beams with ultra-high pulse dose rates. J. Phys. Conf. Ser. 2020, 1662, 012028. [Google Scholar] [CrossRef]
- Scuderi, V.; Amato, A.; Amico, A.G.; Borghesi, M.; Cirrone, G.A.P.; Cuttone, G.; Fajstavr, A.; Giuffrida, L.; Grepl, F.; Korn, G.; et al. Diagnostics and Dosimetry Solutions for Multidisciplinary Applications at the ELIMAIA Beamline. Appl. Sci. 2018, 8, 1415. [Google Scholar] [CrossRef]
- Richter, C.; Karsch, L.; Dammene, Y.; Kraft, S.D.; Metzkes, J.; Schramm, U.; Schürer, M.; Sobiella, M.; Weber, A.; Zeil, K.; et al. A dosimetric system for quantitative cell irradiation experiments with laser-accelerated protons. Phys. Med. Biol. 2011, 56, 1529–1543. [Google Scholar] [CrossRef]
- Pommarel, L.; Vauzour, B.; Mégnin-Chanet, F.; Bayart, E.; Delmas, O.; Goudjil, F.; Nauraye, C.; Letellier, V.; Pouzoulet, F.; Schillaci, F.; et al. Spectral and spatial shaping of a laser-produced ion beam for radiation-biology experiments. Phys. Rev. Accel. Beams 2017, 20, 032801. [Google Scholar] [CrossRef]
- Fiorini, F.; Kirby, D.; Borghesi, M.; Doria, D.; Jeynes, J.C.G.; Kakolee, K.F.; Kar, S.; Litt, S.K.; Kirkby, K.J.; Merchant, M.J.; et al. Dosimetry and spectral analysis of a radiobiological experiment using laser-driven proton beams. Phys. Med. Biol. 2011, 56, 6969–6982. [Google Scholar] [CrossRef][Green Version]
- Bourgouin, A.; Cojocaru, C.; Ross, C.; McEwen, M. Determination of Wair in high-energy electron beams using graphite detectors. Med. Phys. 2019, 46, 5195–5208. [Google Scholar] [CrossRef] [PubMed]
- Renaud, J.; Marchington, D.; Seuntjens, J.; Sarfehnia, A. Development of a graphite probe calorimeter for absolute clinical dosimetry. Med. Phys. 2013, 40, 020701. [Google Scholar] [CrossRef] [PubMed]
- Renaud, J.; Sarfehnia, A.; Bancheri, J.; Seuntjens, J. Aerrow: A probe-format graphite calorimeter for absolute dosimetry of high-energy photon beams in the clinical environment. Med. Phys. 2018, 45, 414–428. [Google Scholar] [CrossRef] [PubMed]
- Bourgouin, A.; Keszti, F.; Schönfeld, A.A.; Hackel, T.; Kozelka, J.; Hildreth, J.; Simon, W.; Schüller, A.; Kapsch, R.P.; Renaud, J. The probe-format graphite calorimeter, Aerrow, for absolute dosimetry in ultrahigh pulse dose rate electron beams. Med. Phys. 2020, 49, 6635–6645. [Google Scholar] [CrossRef]
- Bass, G.A.; Shipley, D.R.; Flynn, S.F.; Thomas, R.A. A prototype low-cost secondary standard calorimeter for reference dosimetry with ultra-high pulse dose rates. Br. J. Radiol. 2023, 96, 20220638. [Google Scholar] [CrossRef]
- McEwen, M.R.; DuSautoy, A.R. Primary standards of absorbed dose for electron beams. Metrologica 2009, 46, S59–S79. [Google Scholar] [CrossRef]
- Seuntjens, J.; Duane, S. Photon absorbed dose standards. Metrologica 2009, 46, S39–S58. [Google Scholar] [CrossRef]
- Rossomme, S.; Palmans, H.; Thomas, R.; Lee, N.; Duane, S.; Bailey, M.; Shipley, D.; Bertrand, D.; Romano, F.; Cirrone, P.; et al. Reference dosimetry for light-ion beams based on graphite calorimetry. Radiat. Prot. Dosim. 2014, 161, 92–95. [Google Scholar] [CrossRef]
- Palmans, H.; Thomas, R.; Simon, M.; Duane, S.; Kacperek, A.; DuSautoy, A.; Verhaegen, F. A small-body portable graphite calorimeter for dosimetry in low-energy clinical proton beams. Phys. Med. Biol. 2004, 49, 3737–3749. [Google Scholar] [CrossRef]
- Sander, T.; Duane, S.; Lee, N.D.; Thomas, C.G.; Owen, P.J.; Bailey, M.; Palmans, H. NPL’s new absorbed dose standard for the calibration of HDR 192Ir brachytherapy sources. Metrologia 2012, 49, S184–S188. [Google Scholar] [CrossRef]
- Duane, S.; Aldehaybes, M.; Bailey, M.; Lee, N.D.; Thomas, C.G.; Palmans, H. An absorbed dose calorimeter for IMRT dosimetry. Metrologia 2012, 49, S168–S173. [Google Scholar] [CrossRef]
- Lourenço, A.; Lee, N.; Shipley, D.; Romano, F.; Kacperek, A.; Duane, S.; Cashmore, M.; Bass, G.; Palmans, H.; Thomas, R. Application of a portable primary standard level graphite calorimeter for absolute dosimetry in a clinical low-energy passively scattered proton beam. Phys. Med. Biol. 2022, 67, 225021. [Google Scholar] [CrossRef] [PubMed]
- Schüller, A.; Heinrich, S.; Fouillade, C.; Subiel, A.; De Marzi, L.; Romano, F.; Peier, P.; Trachsel, M.; Fleta, C.; Kranzer, R.; et al. The European Joint Research Project UHDpulse–Metrology for advanced radiotherapy using particle beams with ultra-high pulse dose rates. Phys. Medica 2020, 80, 134–150. [Google Scholar]
- McEwen, M.R.; Duane, S. A portable calorimeter for measuring absorbed dose in the radiotherapy clinic. Phys. Med. Biol. 2000, 45, 3675–3691. [Google Scholar] [CrossRef] [PubMed]
- Chaudhary, P.; Gwynne, D.C.; Odlozilik, B.; McMurray, A.; Milluzzo, G.; Maiorino, C.; Doria, D.; Ahmed, H.; Romagnani, L.; Alejo, A.; et al. Development of a portable hypoxia chamber for ultra-high dose rate laser-driven proton radiobiology applications. Radiat. Oncol. 2022, 17, 77. [Google Scholar]
- Available online: http://www.gafchromic.com/ (accessed on 15 July 2019).
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.J.N.I.; et al. Recent developments in Geant4. Nucl. Instrum. Methods A 2016, 835, 186–225. [Google Scholar]
- Allison, J.; Amako, K.; Apostolakis, J.E.A.; Araujo, H.A.A.H.; Dubois, P.A.; Asai, M.A.A.M.; Barrand, G.A.B.G.; Capra, R.A.C.R.; Chauvie, S.A.C.S.; Chytracek, R.A.C.R.; et al. Geant4 developments and applications. IEEE Trans. Nucl. Sci. 2006, 53, 270–278. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4—A Simulation Toolkit. Nucl. Instrum. Methods A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Available online: https://lise.nscl.msu.edu/lise.html (accessed on 15 July 2019).
- Borca, J.; Pasquino, M.; Russo, G.; Grosso, P.; Cante, D.; Sciacero, P.; Girelli, G.; La Porta, M.R.; Tofani, S. Dosimetric characterization and use of GAFCHROMIC EBT3 film for IMRT dose verification. J. Appl. Clin. Med. Phys. 2013, 14, 158–171. [Google Scholar] [CrossRef]
- Epson Electronics. Available online: https://www.epson.co.uk/en_GB (accessed on 10 October 2020).
- ImageJ: Image Processing and Analysis in Java. Available online: https://imagej.nih.gov/ij/download.html (accessed on 10 October 2020).
- Perl, J.; Shin, J.; Schümann, J.; Faddegon, B.; Paganetti, H. TOPAS: An innovative proton Monte Carlo platform for research and clinical applications. Med. Phys. 2012, 39, 6818–6837. [Google Scholar] [CrossRef]
- Faddegon, B.; Ramos-Méndez, J.; Schuemann, J.; McNamara, A.; Shin, J.; Perl, J.; Paganetti, H. The TOPAS tool for particle simulation, a Monte Carlo simulation tool for physics, biology and clinical research. Phys. Med. 2020, 72, 114–121. [Google Scholar] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).