Calibration of Sliding Friction Coefficient in DEM between Different Particles by Experiment
Abstract
1. Introduction
2. Experimental Methods
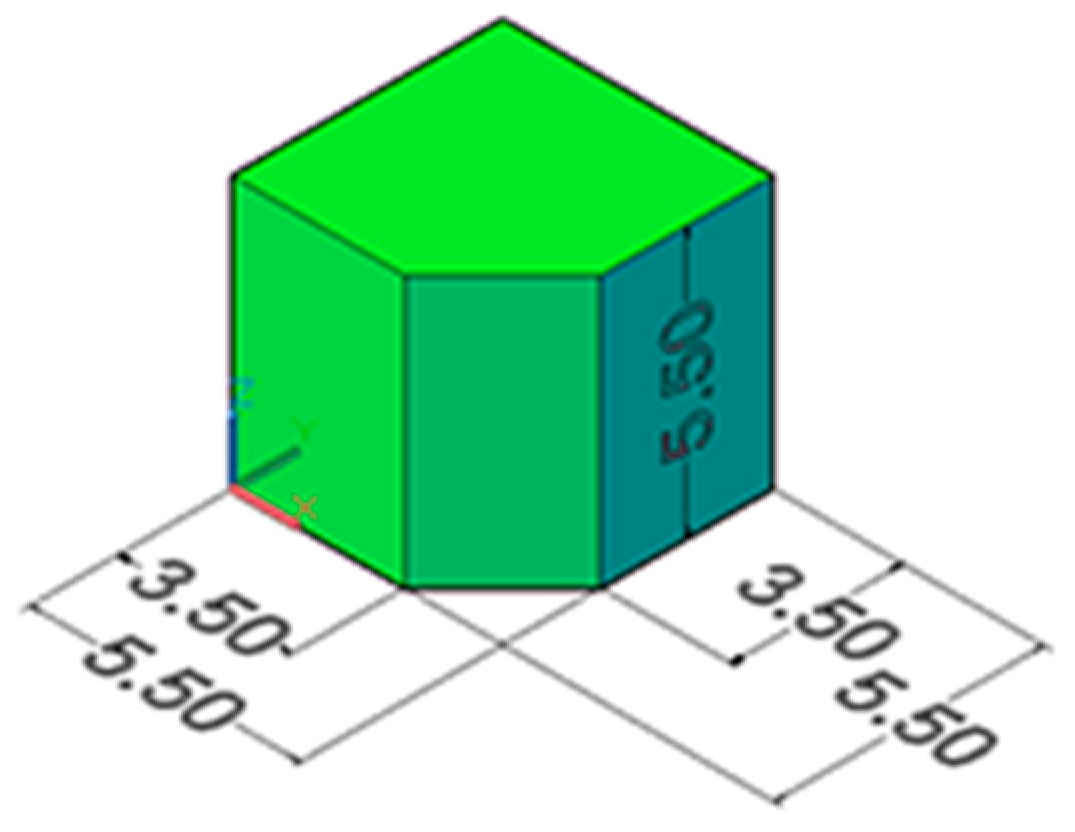
2.1. Particles and Pad Materials
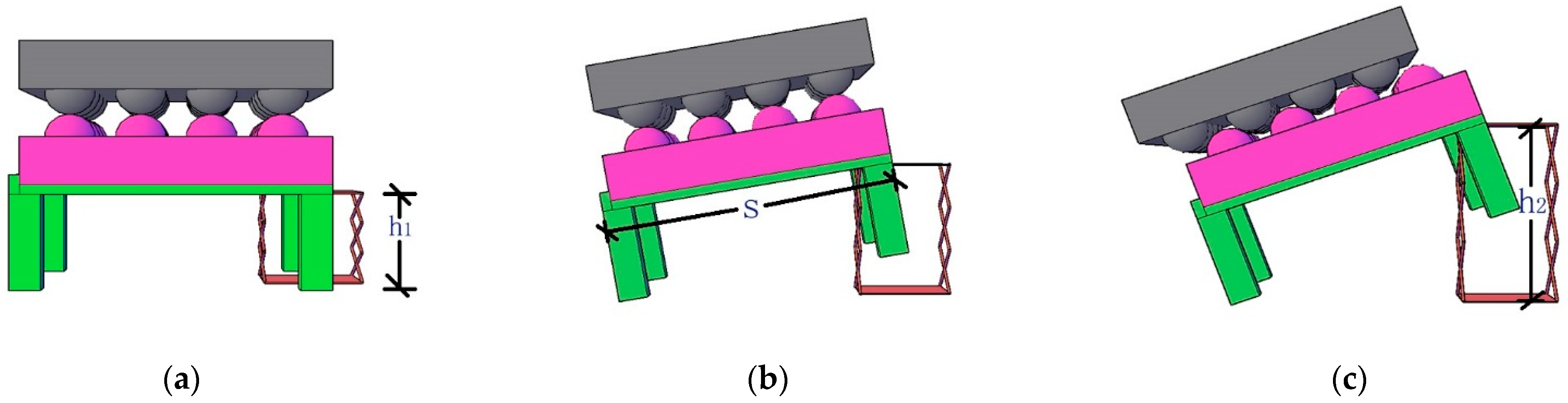
2.2. Determination of the Sliding Friction Coefficient
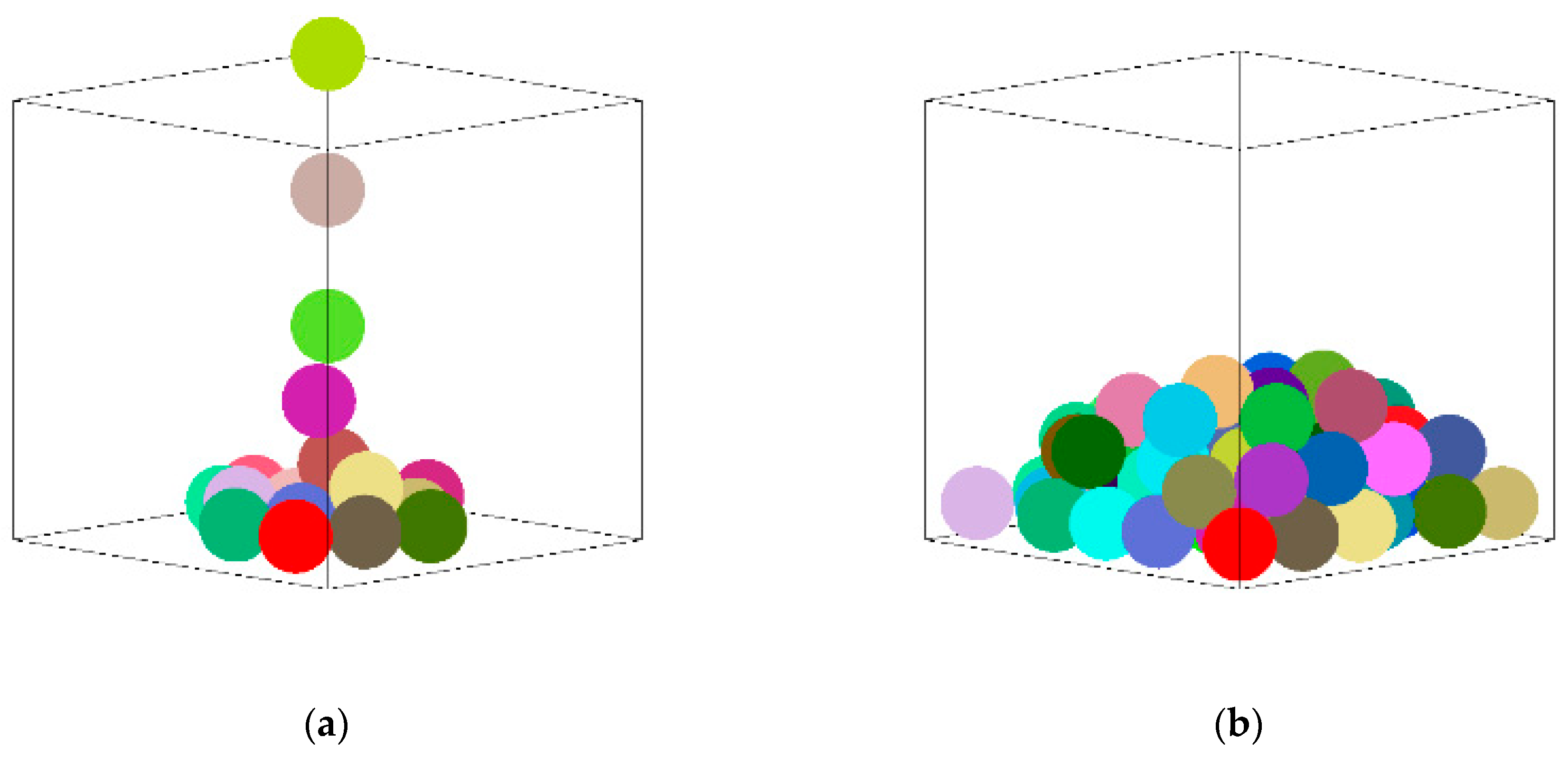
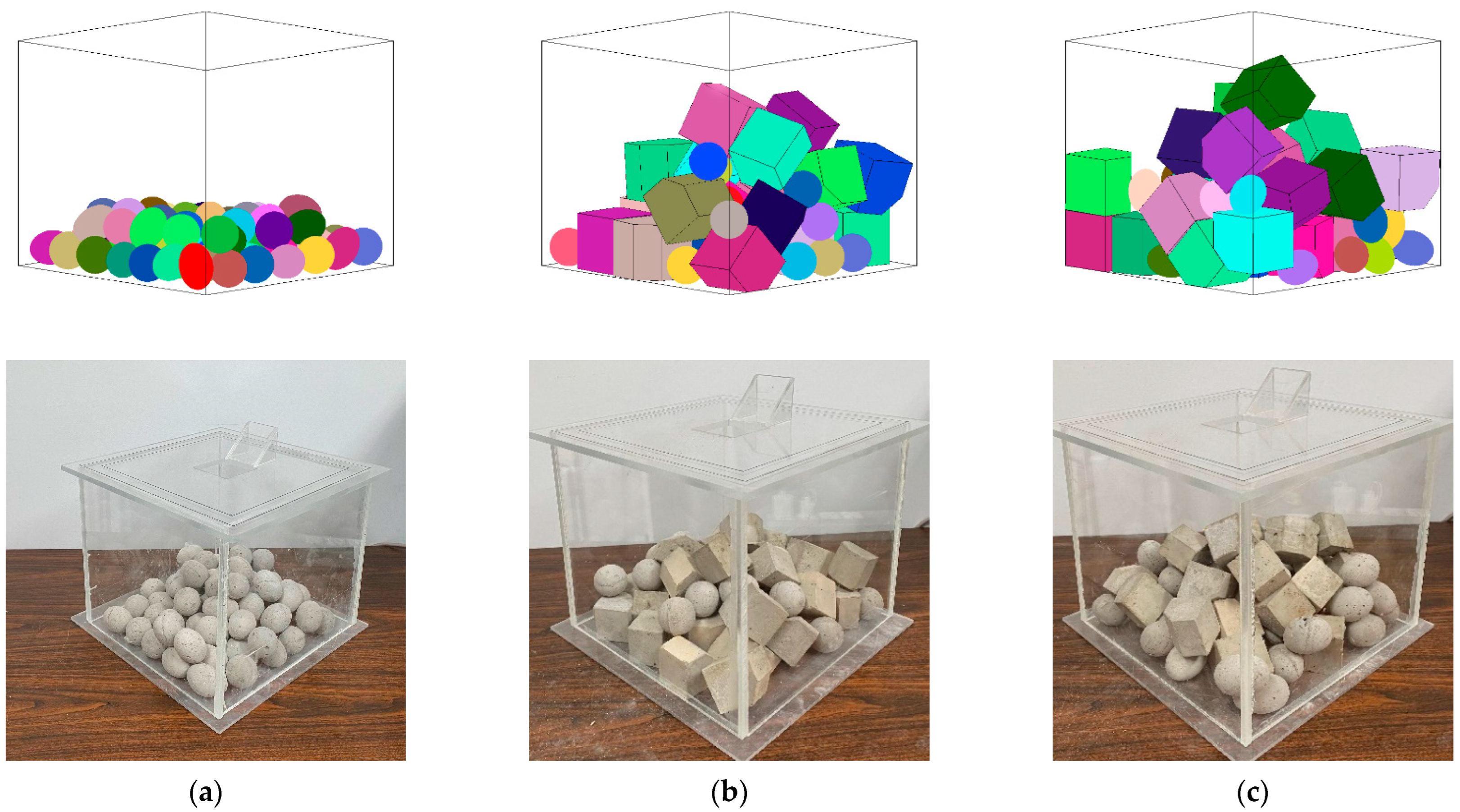
2.3. Method of Packing
| Particle Name | Average Size (cm) | Number of Particles |
|---|---|---|
| Sphere | D = 4.97 | 66 |
| Ellipsoid | 6.03 × 4.33 × 4.33 | 66 |
| Polyhedron | As is shown in Figure 4 | 29 |
| Group Name | Contain Particles | Amount |
|---|---|---|
| S–S | Sphere | 66 |
| E–E | Ellipsoid | 66 |
| P–P | Polyhedron | 29 |
| S–E | Sphere and ellipsoid | 33 for each |
| S–P | Sphere and polyhedron | 28 for each |
| E–P | Ellipsoid and polyhedron | 28 for each |
3. Simulated Method
4. Results and Discussion
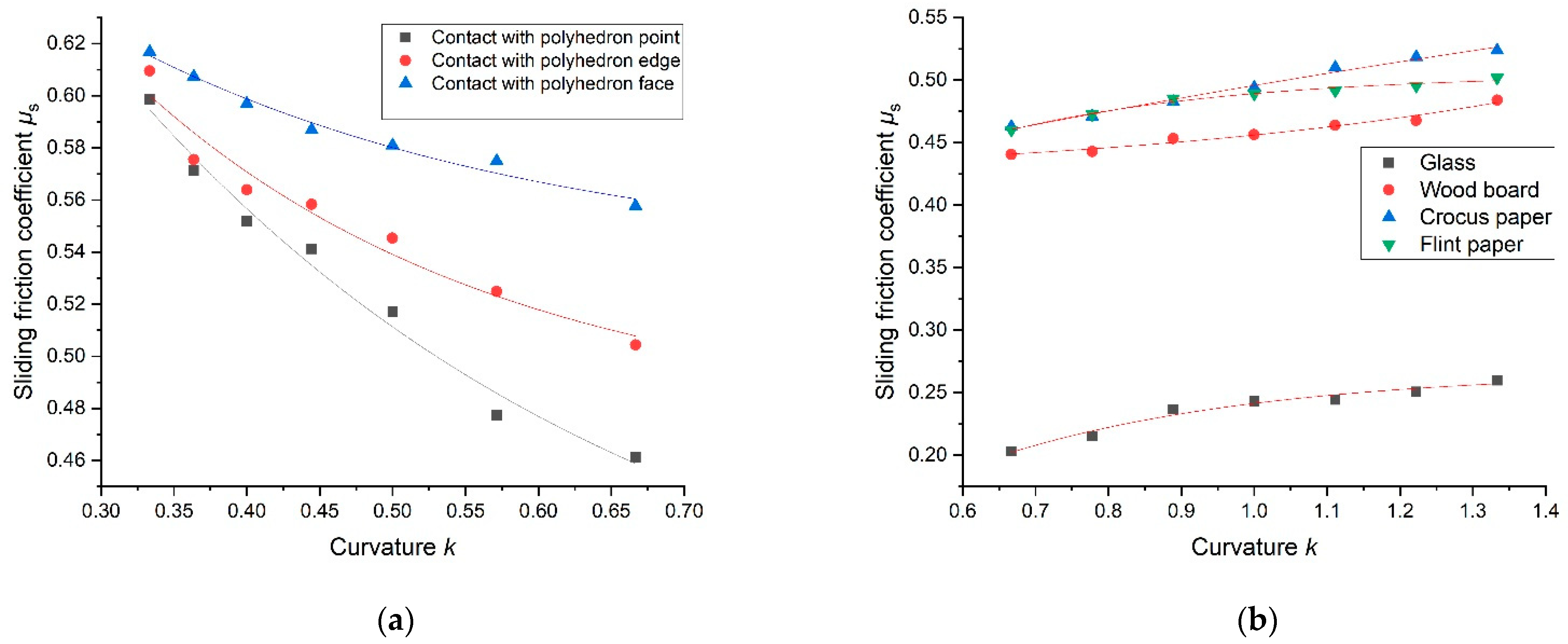
4.1. Analysis of Sliding Friction Coefficient
4.2. Analysis of Sandpile Formation
4.3. Sliding Friction Coefficient between Particles and Boundaries
5. Conclusions
- The sliding friction coefficient between two sphere particles varies with curvature and cannot be calculated based solely on the curvature of a single sphere. However, due to the variations in curvature at different points, this fitting result is not valid when the ellipsoid is involved in contact.
- Based on the sliding coefficient acquired using the suggested experiment approach, the packing experiment and the numerical simulation of the particles in the container are essentially the same. The experiment approach presented in this work can be used to efficiently determine the sliding friction coefficient between particles and between particles and boundaries in DEM.
- The sliding friction coefficient found by fitting the experimental data can be used to increase the accuracy of the numerical simulation of the DEM.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cundall, P.A. A computer model for simulating progressive, large-scale movement in blocky rock system. In Proceedings of the International Symposium on Rock Mechanics, Nancy, France, 4–6 October 1971; pp. 129–136. [Google Scholar]
- Cundall, P.; Strack, O. The Distinct Element Method as a Tool for Research in Granular Media; University of Minnesota: Minneapolis, MN, USA, 1978. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Mao, W.; Yang, Y.; Lin, W.; Aoyama, S.; Towhata, I. High frequency acoustic emissions observed during model pile penetration in sand and implications for particle breakage behavior. Int. J. Geomech. 2018, 18, 04018143. [Google Scholar] [CrossRef]
- Yu, F. Influence of particle breakage on behavior of coral sands in triaxial tests. Int. J. Geomech. 2019, 19, 04019131. [Google Scholar] [CrossRef]
- Li, M.; Li, A.; Zhang, J.; Huang, Y.; Li, J. Effects of particle sizes on compressive deformation and particle breakage of gangue used for coal mine goaf backfill. Powder Technol. 2020, 360, 493–502. [Google Scholar] [CrossRef]
- O’Sullivan, C. Particle-Based Discrete Element Modeling: Geomechanics Perspective. Int. J. Geomech. 2011, 11, 449–464. [Google Scholar] [CrossRef]
- Lehane, B.; Liu, Q. Measurement of shearing characteristics of granular materials at low stress levels in a shear box. Geotech. Geol. Eng. 2013, 31, 329–336. [Google Scholar] [CrossRef]
- Li, L.; Wu, W.; Liu, H.; Lehane, B. DEM analysis of the plugging effect of open-ended pile during the installation process. Ocean Eng. 2021, 220, 108375. [Google Scholar] [CrossRef]
- Mead, S.R.; Cleary, P.W. Validation of DEM prediction for granular avalanches on irregular terrain. J. Geophys. Res. Earth Surf. 2015, 120, 1724–1742. [Google Scholar] [CrossRef]
- Yin, Z.; Zhang, H.; Han, T. Simulation of particle flow on an elliptical vibrating screen using the discrete element method. Powder Technol. 2016, 302, 443–454. [Google Scholar] [CrossRef]
- Hadda, N.; Nicot, F.; Wan, R.; Darve, F. Microstructural self-organization in granular materials during failure. Comptes Rendus Mécanique 2015, 343, 143–154. [Google Scholar] [CrossRef]
- Guo, Y.G.; Morgan, J.K. Influence of normal stress and grain shape on granular friction: Results of discrete element simulations. J. Geophys. Res.-Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. Elastic-Plastic Contact Analysis of a Sphere and a Rigid Flat. J. Appl. Mech. 2002, 69, 657–662. [Google Scholar] [CrossRef]
- Mishra, B.K.; Murty, C.V.R. On the determination of contact parameters for realistic DEM simulations of ball mills. Powder Technol. 2001, 115, 290–297. [Google Scholar] [CrossRef]
- Natsui, S.; Ueda, S.; Oikawa, M.; Fan, Z.; Kano, J.; Inoue, R.; Ariyama, T. Optimization of Physical Parameters of Discrete Element Method for Blast Furnace and Its Application to the Analysis on Solid Motion around Raceway. Isij Int. 2009, 49, 1308–1315. [Google Scholar] [CrossRef][Green Version]
- Yoon, J. Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation. Int. J. Rock Mech. Min. Sci. 2007, 44, 871–889. [Google Scholar] [CrossRef]
- Starzec, P.; Andersson, J. Application of two-level factorial design to sensitivity analysis of keyblock statistics from fracture geometry. Int. J. Rock Mech. Min. Sci. 2002, 39, 243–255. [Google Scholar] [CrossRef]
- Ahuja, S.; Ferreira, G.; Moreira, A. Application of Plackett-Burman design and response surface methodology to achieve exponential growth for aggregated shipworm bacterium. Biotechnol. Bioeng. 2004, 85, 666–675. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Deresiewicz, H. Elastic spheres in contact under varying oblique forces. J. Appl. Mech. 1953, 20, 327–344. [Google Scholar] [CrossRef]
- Cundall, P. Computer simulations of dense sphere assemblies. In Studies in Applied Mechanics; Elsevier: Amsterdam, The Netherlands, 1988; Volume 20, pp. 113–123. [Google Scholar]
- Hunt, K.H.; Crossley, F.R.E. Coefficient of restitution interpreted as damping in vibroimpact. J. Appl. Mech. 1975, 42, 440–445. [Google Scholar] [CrossRef]
- Elata, D.; Berryman, J.G. Contact force-displacement laws and the mechanical behavior of random packs of identical spheres. Mech. Mater. 1996, 24, 229–240. [Google Scholar] [CrossRef]
- Nezamabadi, S.; Radjai, F.; Averseng, J.; Delenne, J.-Y. Implicit frictional-contact model for soft particle systems. J. Mech. Phys. Solids 2015, 83, 72–87. [Google Scholar] [CrossRef][Green Version]
- Ai, J.; Chen, J.F.; Rotter, J.M.; Ooi, J.Y. Assessment of rolling resistance models in discrete element simulations. Powder Technol. 2011, 206, 269–282. [Google Scholar] [CrossRef]
- Karkala, S.; Davis, N.; Wassgren, C.; Shi, Y.X.; Liu, X.; Riemann, C.; Yacobian, G.; Ramachandran, R. Calibration of Discrete-Element-Method Parameters for Cohesive Materials Using Dynamic-Yield-Strength and Shear-Cell Experiments. Processes 2019, 7, 278. [Google Scholar] [CrossRef]
- Angus, A.; Yahia, L.A.A.; Maione, R.; Khala, M.; Hare, C.; Ozel, A.; Ocone, R. Calibrating friction coefficients in discrete element method simulations with shear-cell experiments. Powder Technol. 2020, 372, 290–304. [Google Scholar] [CrossRef]
- Hartl, J.; Ooi, J.Y. Experiments and simulations of direct shear tests: Porosity, contact friction and bulk friction. Granul. Matter 2008, 10, 263–271. [Google Scholar] [CrossRef]
- Suhr, B.; Six, K. On the effect of stress dependent interparticle friction in direct shear tests. Powder Technol. 2016, 294, 211–220. [Google Scholar] [CrossRef]
- Coetzee, C.J.; Els, D.N.J. Calibration of granular material parameters for DEM modelling and numerical verification by blade-granular material interaction. J. Terramechanics 2009, 46, 15–26. [Google Scholar] [CrossRef]
- Roessler, T.; Katterfeld, A. DEM parameter calibration of cohesive bulk materials using a simple angle of repose test. Particuology 2019, 45, 105–115. [Google Scholar] [CrossRef]
- Elskamp, F.; Kruggel-Emden, H.; Hennig, M.; Teipel, U. A strategy to determine DEM parameters for spherical and non-spherical particles. Granul. Matter 2017, 19, 46. [Google Scholar] [CrossRef]
- Li, Y.J.; Xu, Y.; Thornton, C. A comparison of discrete element simulations and experiments for ‘sandpiles’ composed of spherical particles. Powder Technol. 2005, 160, 219–228. [Google Scholar] [CrossRef]
- Thao, D.; Indraratna, B.; Nguyen, T.T.; Rujikiatkamjorn, C. Interactive Role of Rolling Friction and Cohesion on the Angle of Repose through a Microscale Assessment. Int. J. Geomech. 2023, 23, 04022250. [Google Scholar] [CrossRef]
- Frankowski, P.; Morgeneyer, M. Calibration and Validation of DEM Rolling and Sliding Friction Coefficients in Angle of Repose and Shear Measurements. In Proceedings of the 7th International Conference on Micromechanics of Granular Media (Powders and Grains), Sydney, Australia, 8–12 July 2013; pp. 851–854. [Google Scholar]
- Zhou, Y.C.; Xu, B.H.; Yu, A.B.; Zulli, P. An experimental and numerical study of the angle of repose of coarse spheres. Powder Technol. 2002, 125, 45–54. [Google Scholar] [CrossRef]
- Barrios, G.K.P.; de Carvalho, R.M.; Kwade, A.; Tavares, L.M. Contact parameter estimation for DEM simulation of iron ore pellet handling. Powder Technol. 2013, 248, 84–93. [Google Scholar] [CrossRef]
- Jayasundara, C.T.; Yang, R.Y.; Yu, A.B.; Rubenstein, J. Effects of disc rotation speed and media loading on particle flow and grinding performance in a horizontal stirred mill. Int. J. Miner. Process. 2010, 96, 27–35. [Google Scholar] [CrossRef]
- Boikov, A.; Savelev, R.; Payor, V.; Potapov, A. Universal Approach for DEM Parameters Calibration of Bulk Materials. Symmetry 2021, 13, 1088. [Google Scholar] [CrossRef]
- Rosenkranz, S.; Breitung-Faes, S.; Kwade, A. Experimental investigations and modelling of the ball motion in planetary ball mills. Powder Technol. 2011, 212, 224–230. [Google Scholar] [CrossRef]
- Liu, J.; Yun, B.; Zhao, C.B. Identification and Validation of Rolling Friction Models by Dynamic Simulation of Sandpile Formation. Int. J. Geomech. 2012, 12, 484–493. [Google Scholar] [CrossRef]
- Zhou, Y.C.; Wright, B.D.; Yang, R.Y.; Xu, B.H.; Yu, A.B. Rolling friction in the dynamic simulation of sandpile formation. Phys. A—Stat. Mech. Its Appl. 1999, 269, 536–553. [Google Scholar] [CrossRef]
- Horabik, J.; Molenda, M. Parameters and contact models for DEM simulations of agricultural granular materials: A review. Biosyst. Eng. 2016, 147, 206–225. [Google Scholar] [CrossRef]
- Markauskas, D.; Kacianauskas, R.; Dziugys, A.; Navakas, R. Investigation of adequacy of multi-sphere approximation of elliptical particles for DEM simulations. Granul. Matter 2010, 12, 107–123. [Google Scholar] [CrossRef]
- Iwashita, K.; Oda, M. Micro-deformation mechanism of shear banding process based on modified distinct element method. Powder Technol. 2000, 109, 192–205. [Google Scholar] [CrossRef]
- Zarastvand, M.; Ghassabi, M.; Talebitooti, R. Prediction of acoustic wave transmission features of the multilayered plate constructions: A review. J. Sandw. Struct. Mater. 2022, 24, 218–293. [Google Scholar]
- Zarastvand, M.; Asadijafari, M.; Talebitooti, R. Acoustic wave transmission characteristics of stiffened composite shell systems with double curvature. Compos. Struct. 2022, 292, 115688. [Google Scholar]
- Procter, D.C.; Barton, R.R. Measurements of the angle of interparticle friction. Géotechnique 1974, 24, 581–604. [Google Scholar] [CrossRef]







| Group Label | Average Size (mm) | Number of Particles |
|---|---|---|
| S3 | 29.62 | 32 |
| S3.5 | 34.69 | 32 |
| S4 | 40.08 | 32 |
| S4.5 | 45.02 | 32 |
| S5 | 49.72 | 32 |
| S5.5 | 55.26 | 32 |
| S6 | 60.12 | 32 |
| Emaj | 60.30 × 43.32 × 43.32 | 32 |
| Emin | 60.30 × 43.32 × 43.32 | 32 |
| Pp | 40.24 | 32 |
| Pe | 40.24 | 32 |
| Pf | 40.24 | 32 |
| Group Name | S3 | S3.5 | S4 | S4.5 | S5 | S5.5 | S6 | Emaj | Emin | Pp | Pe | Pf |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S3 | 0.46 | 0.47 | 0.48 | 0.49 | 0.49 | 0.50 | 0.51 | \ | \ | \ | \ | \ |
| S3.5 | 0.47 | 0.48 | 0.48 | 0.49 | 0.50 | 0.50 | 0.52 | \ | \ | \ | \ | \ |
| S4 | 0.48 | 0.48 | 0.50 | 0.50 | 0.51 | 0.52 | 0.53 | \ | \ | \ | \ | \ |
| S4.5 | 0.49 | 0.49 | 0.50 | 0.50 | 0.52 | 0.52 | 0.53 | \ | \ | \ | \ | \ |
| S5 | 0.49 | 0.50 | 0.51 | 0.52 | 0.53 | 0.54 | 0.56 | \ | \ | \ | \ | \ |
| S5.5 | 0.50 | 0.50 | 0.52 | 0.52 | 0.54 | 0.57 | 0.58 | \ | \ | \ | \ | \ |
| S6 | 0.51 | 0.52 | 0.53 | 0.53 | 0.56 | 0.58 | 0.58 | \ | \ | \ | \ | \ |
| Emaj | 0.46 | 0.47 | 0.48 | 0.50 | 0.53 | 0.53 | 0.54 | 0.42 | \ | \ | \ | \ |
| Emin | 0.47 | 0.48 | 0.49 | 0.51 | 0.53 | 0.54 | 0.57 | 0.44 | 0.45 | \ | \ | \ |
| Pp | 0.46 | 0.48 | 0.52 | 0.54 | 0.55 | 0.57 | 0.60 | 0.51 | 0.59 | 0.35 | \ | \ |
| Pe | 0.50 | 0.52 | 0.55 | 0.56 | 0.56 | 0.58 | 0.61 | 0.56 | 0.60 | 0.54 | 0.55 | \ |
| Pf | 0.56 | 0.57 | 0.58 | 0.59 | 0.60 | 0.61 | 0.61 | 0.58 | 0.61 | 0.55 | 0.59 | 0.62 |
| Pad | Glass | Wood Board | Crocus Paper | Flint Paper | |
|---|---|---|---|---|---|
| Group Name | |||||
| S3 | 0.20 | 0.44 | 0.46 | 0.46 | |
| S3.5 | 0.22 | 0.44 | 0.47 | 0.47 | |
| S4 | 0.24 | 0.45 | 0.49 | 0.48 | |
| S4.5 | 0.24 | 0.46 | 0.49 | 0.49 | |
| S5 | 0.24 | 0.46 | 0.49 | 0.51 | |
| S5.5 | 0.25 | 0.47 | 0.50 | 0.52 | |
| S6 | 0.26 | 0.48 | 0.50 | 0.52 | |
| Variable | Symbol | Value |
|---|---|---|
| Particle density | ρ | 2500 (Kg/m3) |
| Young’s modulus | E | 35 (GPa) |
| Poisson ratio | n | 0.2 |
| Sliding friction coefficient | μs | Based on fitting of experiments |
| Group Name | Average Ordinate by Simulation | Average Ordinate by Experiment | Deviation |
|---|---|---|---|
| S–S | 3.93 cm | 3.89 cm | 1.03% |
| E–E | 4.20 cm | 4.25 cm | 1.18% |
| P–P | 13.89 cm | 14.12 cm | 1.63% |
| S–E | 4.13 cm | 4.35 cm | 5.06% |
| S–P | 10.53 cm | 10.66 cm | 1.22% |
| E–P | 10.50 cm | 10.42 cm | 0.77% |
| Group Name | Average Ordinate by Simulation | Average Ordinate by Experiment | Deviation |
|---|---|---|---|
| Glass | 4.07 cm | 4.13 cm | 1.21% |
| Wood board | 4.20 cm | 4.35 cm | 3.45% |
| Crocus paper | 5.66 cm | 5.72 cm | 1.05% |
| Flint paper | 5.75 cm | 5.81 cm | 1.03% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Liu, J.; Gao, S.; Wang, Y.; Zheng, H.; Zhen, M.; Zhao, F.; Liu, Z.; Ou, C.; Zhuang, R. Calibration of Sliding Friction Coefficient in DEM between Different Particles by Experiment. Appl. Sci. 2023, 13, 11883. https://doi.org/10.3390/app132111883
Liu P, Liu J, Gao S, Wang Y, Zheng H, Zhen M, Zhao F, Liu Z, Ou C, Zhuang R. Calibration of Sliding Friction Coefficient in DEM between Different Particles by Experiment. Applied Sciences. 2023; 13(21):11883. https://doi.org/10.3390/app132111883
Chicago/Turabian StyleLiu, Pengcheng, Jun Liu, Song Gao, Yue Wang, Haowen Zheng, Mengyang Zhen, Futian Zhao, Zheng Liu, Chen Ou, and Ruihong Zhuang. 2023. "Calibration of Sliding Friction Coefficient in DEM between Different Particles by Experiment" Applied Sciences 13, no. 21: 11883. https://doi.org/10.3390/app132111883
APA StyleLiu, P., Liu, J., Gao, S., Wang, Y., Zheng, H., Zhen, M., Zhao, F., Liu, Z., Ou, C., & Zhuang, R. (2023). Calibration of Sliding Friction Coefficient in DEM between Different Particles by Experiment. Applied Sciences, 13(21), 11883. https://doi.org/10.3390/app132111883







