Abstract
It is well established that the introduction of additive manufacturing in various domains has produced significant technological leaps due to the advantages over other manufacturing techniques. Furthermore, additive manufacturing allows the design of parts with complex internal structures (e.g., lattice, honeycomb) to achieve lightweight or other mechanical properties. This paper presents a computational model (integrated into a programable algorithm) designed to generate complex internal structures, using tree-like fractals, for components (mechanical parts) whose designs are achievable by additive manufacturing. The computational model is presented in detail, starting from the mathematical definition and the properties of the proposed tree-like fractals. The fractal data are computed and arranged unequivocally using table representations. Based on the fractal data, the structures are generated inside CAD parts (which are given as inputs in the algorithm). The proposed computational method is applied in different case studies to illustrate their functionality. The generated CAD components (with fractal internal structures) are intended for manufacturing (using selective laser melting) and laboratory (mechanical) testing and for finite element analysis, which in turn can validate the use of tree-like fractals as interior structures for mechanical components.
1. Introduction
Additive manufacturing (AM), also called 3D printing, is a revolutionary technology that enables the manufacturing of mechanical components with complex geometry (unfeasible using milling or molding). Many materials are available in AM, ranging from plastic (applied layer by layer) to ceramics or metal alloys [1,2] (e.g., selective laser melting). Furthermore, AM allows the for the design and manufacture (or even the repair [3]) of components with internal structures for which the aim is to achieve various specific mechanical properties. In [4], the authors detail different lattice structures achieved using AM, highlighting the mechanical properties of these structures. In a comprehensive review article [5], the authors studied the mechanical properties of gradient lattice structures available in the literature. One point, made in [5], is that many lattice structures are inspired by nature (biomimicry). A second point is that lattice structures have the potential to create lightweight and strong mechanical parts. Other authors have proposed modeling and optimization methods for lattice structures [6,7,8,9]. Another class of internal structures for AM studied in the literature contains fractal structures. Fractals (scale-invariant repetitive structures) are also structures inspired by nature. The scientific literature regarding the use of fractals in AM is significantly thinner than that regarding the use of lattices. However, the following are some reports regarding the use and study of fractal structures for AM. In [10], the authors describe a cross-based fractal designed for shock absorption, showing convincing results (for shock absorbing helmet). At the micro level, fractal structures have also been proposed for the generation of porous structures [11]. More recently, Hilbert curves have been proposed for internal structures in structured materials [12] with promising results in the material mechanical properties. It is worth noting that the authors in [9] also point out a lack in the use of fractals for internal structures in the current literature. Hilbert curve fractals are also studied in [13] for energy dissipation purposes. The authors conclude that the geometry of these structures influences the mechanical properties of the metamaterial. Tree-like fractal structures are also studied in the literature (though only briefly). In [14], the authors used tree-like fractal structures as support structures in AM, showing various application examples (and concluding that this approach impacts cost reduction and the environment).
The scientific literature points out that, although tree-like fractal structures can be considered for internal structures in AM parts, their study is in its infancy. Indeed, in [15], the authors point out the remaining potential and the challenges for the future development of AM technologies. More understanding (mechanical behavior, etc.) is required for AM parts with internal structures. In a nutshell, there is a blind spot with respect to the properties and applications of tree-like fractals (as internal structures) for AM, and this work aims to establish a model to generate such internal structures so as to open a window of opportunity to study them. Whether or not tree-like fractals have better mechanical properties (for a given domain of applications) remains the subject of further research. The hypothesis is that tree-like fractals perform better than lattice structures in non-homogenous meta-materials, e.g., 3D-printed bone or parts that must deform in a predictable manner under mechanical stress for safety reasons (e.g., helmets, vehicle components).
In [16], the authors present a mathematical model that generates tree-like fractal structures using the language of homogeneous transformation matrices (which have various technical applications, e.g., mechanism analysis [17,18]). To the authors’ best knowledge, there is no other such model in scientific literature. In [16], the authors present a technique to generate (logically and mathematically) a tree-like fractal structure without considering its intersection with other physical structures (inside the CAD part) or the physicality of the fractal structure. The fractal models in [16] were two dimensional (i.e., the fractals were defined by points and line segments), and the CAD parts were modeled manually (using Siemens NX) based on the fractal geometric parameters.
The mathematical model from [16] represents the basis for the computational model presented in this paper. A complete mathematical definition of the proposed tree-like fractal with all of the required properties is presented (as an extension of [16]). A tabular computational method to preserve the fractal structure geometrical data is proposed, which is highly compatible with vector programming languages (e.g., Matlab, Python numpy). Furthermore, this paper addresses the intersection of the fractal structures with other components given in CAD (which are defined as surface meshes). A generalization of the Möller and Trumbore [19] algorithm is used to intersect the fractal structure with a surface mesh. In addition, volume is applied to the fractal structures to provide a physical three-dimensional representation. Lastly, the paper presents methods to unite the fractal structures with the CAD component (the input shell that requires fractal fillings). Three case studies are presented to demonstrate the functionality of the computational model. The output of the proposed computational method, namely the CAD parts with internal fractal structures, will help to validate the use of such structures in two major ways. On the one hand, the CAD will be used to manufacture test samples for mechanical properties testing, and on the other hand, the CAD will be used in finite element analysis (FEA) tests to study the correlation between real laboratory experiments and computer simulations (to create numerical predictable models).
Following the introduction, the paper is structured as follows: Section 2 presents the general algorithm proposed to obtain the final CAD parts, where clear links are established between the inputs and the outputs of each step; Section 3 presents a complete, comprehensive, mathematical model for the tree-like fractal structures (all the necessary mathematical properties are derived); Section 4 presents the intersection of the tree-like fractals with relevant structures and the trimming (cutting the fractal where required) procedure; Section 5 presents the procedure of adding volume to the fractals and how to unite the fractals with the CAD component shell; Section 6 shows three cases studies; the conclusions are presented in Section 7.
2. Modelling Tree-like Fractal Structures into CAD Parts
The computational model aims to output CAD parts filled with tree-like fractal structures to manufacture lightweight parts (such as the lattice internal structures). The CAD model must be provided, which at this stage must include the cavities that require fractal fillings. We define the input CAD part with cavities as the shell. Furthermore, the fractal parameters (roots, branches, nodes, etc.), detailed in Section 3, must also be provided. With future development (i.e., testing the fractal structures’ mechanical properties and creating a predictable model for how the fractal geometry affects the final part properties), the shell and the fractal structures may be generated automatically (using AI or other intelligent modeling tools) leading to generative design; however, this is beyond the scope of this study. Note that the union between the shell and the fractals must be clean (without the branches of the fractals piercing the CAD model and leaving artifacts on the surface of the part). The final outputs of the algorithm are STL files that are ready for 3D printing. Samples can be manufactured and tested, which in turn will provide valuable information for the mechanical part properties. As stated before, these tests will be used to generate a predictable fractal model and automatically generate the shell and fractal structures. However, at this stage, the shell and fractals must be provided (in order to build and test components with fractal fillings).
The algorithm flow chart is presented (in a generalized manner) in Figure 1 and detailed as follows (in future sections, each step is explained in detail):
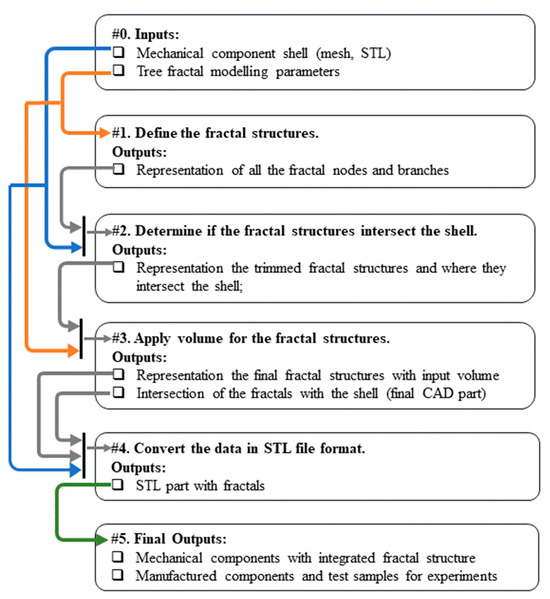
Figure 1.
Flowchart of the proposed computational model for CAD models with fractal filling.
- Step #0 defines the inputs for the algorithm. The first input is the CAD shell, expressed as a CAD model with internal cavities that require fractal filling. Figure 2 shows an example of a CAD shell formed by two hemispheres. Note that the shell is not necessarily a continuous solid as long as the discontinuous volume is filled with fractal structures, such as in instances where the fractals connect the multiple parts into a single rigid body. The algorithm’s second input is a fractal parameter list (roots, branches, angles, etc.) detailed in Section 3.
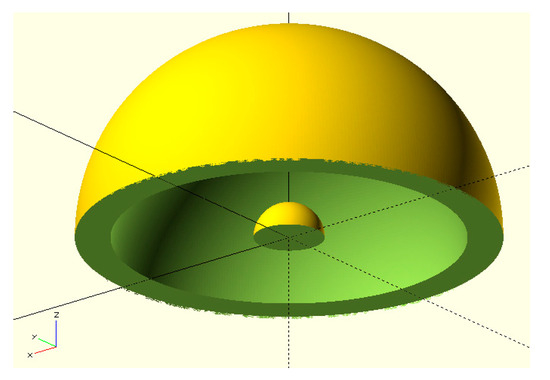 Figure 2. CAD part, with the shell defined by two hemispheres.
Figure 2. CAD part, with the shell defined by two hemispheres. - Step #1 computes a complete representation of the fractal structure based on the input parameters. This representation is one-dimensional, meaning that the fractal is defined only using points and line segments at this stage.
- Step #2 computes the intersection of each fractal structure (computed in Step#1) with the CAD shell. The goal is to connect the fractals with the shell without any artifacts remaining on the outer surface of the part. The output of this step is a fractal representation where branches that intersect the shell are trimmed. This representation is also one-dimensional.
- Step #3 applies volume to the one-dimensional fractal structures (the trimmed representation from Step#2). In this step, each fractal branch (represented by a line segment) is converted into a cylinder (radius provided in the inputs from Step#0), and all the cylinders form a union (the physical fractal structures). Furthermore, the physical fractal structures are united with the shell, resulting in the final CAD part.
- Step #4 converts the CAD part (fractal structures united with the shell) into an STL file format for manufacturing or FEA.
- Step #5 represents the final outputs of the algorithm. On the one hand, we can manufacture lightweight parts for various applications or testing samples. On the other hand, the CAD data are provided for FEA.
3. Mathematical Modeling of Tree-like Fractals
The structure of a tree-like fractal subject to this study is illustrated in Figure 3, and the following are defined:
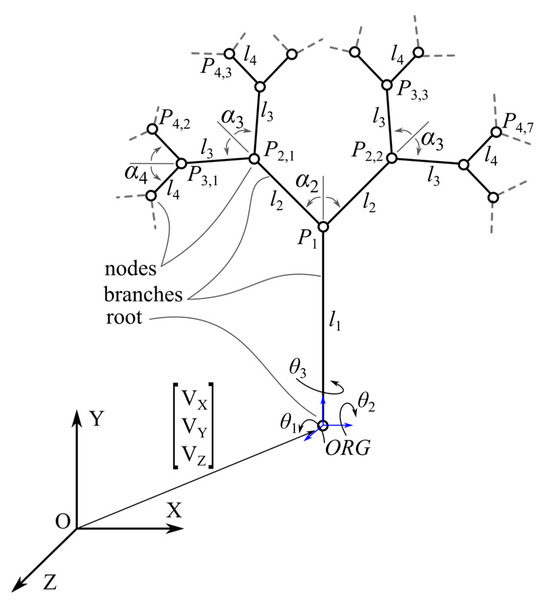
Figure 3.
Schematical representation of a tree-like fractal.
- The points Pi,j represent the nodes of the fractal.
- A branch is represented by a line segment of length li connecting two nodes.
- A node Pi, is a child node of Pk, if: (1) i > k; and (2) the branches of lengths lm that connect the two nodes always respect m > k. For example, P3,1 is a child of P2,1, whereas P3,3 is not (Figure 3).
- A node Pi is a parent node if it has at least one child node.
- A leaf is the final node.
- ORG represents the origin (root) of the fractal. The root is displaced (linearly) from a global coordinate system OXYZ by a vector [VX, VY, VZ]T. Furthermore, the orientation of the first branch is given by the angles θ1, θ2, θ3 (using a ZYX rotation convention).
- αi are angles between two connected branches.
Definition 1.
A tree-like fractal structure is a collection of points (root, nodes, leaves) connected through branches with the following properties:
Property 1.
Each node defined by a point P from the fractal structure can be uniquely defined using transformation matrices by [16]:
where various permutations of the αi signs produce different nodes. ORG represents the origin (root) of the fractal structure with respect to a chosen coordinate system OXYZ:
with:
RZi(±αi) represents rotation matrices about the Z axis, and TYi(li) represents translation matrices along the Y axis:
The Cartesian coordinates of the point P representation are extracted from the transformation matrix using the following relation:
Property 2.
If d is the depth of the fractal (d = 1 are nodes after the branch with length l1, d = 2 are nodes after the branch with length l2, and so on), then d = i (see Equation (1)), and the total number of nodes Nd at depth d is:
which means that if the depth d is given, all points Pi,j can be stored in a tabular (vector) representation with i being the number of rows and j = Nd the number of columns.
Property 3.
Each node is computed using a unique sequence of angles αi and lengths li. For example, the sequence {α1 = 0, α2, α3} together with {l1, l2, l3} computes the node P3,1, whereas the sequence {α1 = 0, −α2, α3} with {l1, l2, l3} computes the node P3,3.
Property 4.
Each parent node Pi,j i > 1, has a set of direct children (connected through a single branch) Cm,n given by:
To obtain the general set Cm,n that defines all children of a node Pi,j, the relations of m and n (Equation (7)) can be written recursively:
which has a recurring relationship:
where c is the difference in the nodes’ depths. The general set Cm,n of children nodes of a node Pi,j i > 1 is:
Finally, a range r at each depth i from the total depth d is defined. The range r does not have a physical meaning, but it is a useful measure.
Property 5.
A recursive model can be defined for the tree-like fractal:
P’i represents nodes in one distinct (without bifurcation) path. Figure 4 highlights an example of a distinct path (from ORG to P3,2). It is assumed that for any node in the fractal, Equation (12) can be recursively applied.
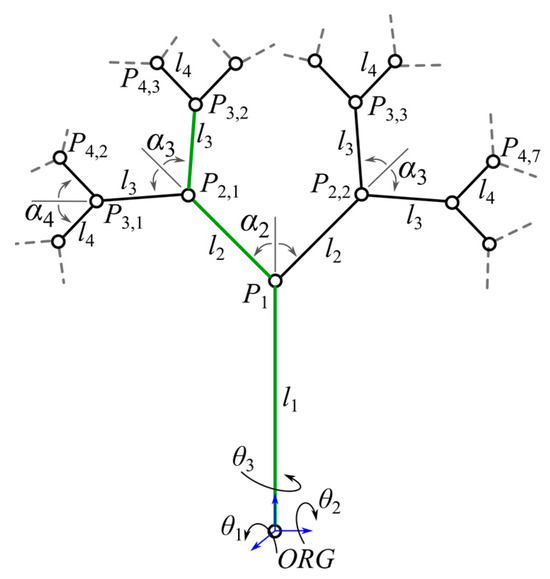
Figure 4.
Schematical representation of a tree-like fractal. Green highlighted path from origin to a point in a fractal tree.
Property 6.
Each branch of the fractal is defined by two points: Pi (the initial point of the branch) and Pf (the final point of the branch). A vector can be defined:
representing the direction of the branch, having the length:
Furthermore, as each node is an intersection of three branches (the root and the leaves are not considered), three vectors can be defined:
where V1 represents the vector of the parent branch and V2 and V3 represent the vectors of the children branches (V2 points out of the node whereas V3 points towards the node). Using Equation (15), three bisector vectors can be defined (it is assumed that any pair from V1, V2, V3 does not have the same orientation):
Property 7.
With respect to a global coordinate system OXYZ, two angles can be defined for every branch:
where Pi and Pf are the initial and final points of a branch, respectively.
Remark 1.
The mathematical model can be further generalized by not imposing symmetry. The rotation matrices may not necessarily be evaluated for ± αi but instead with values +w1αi, –w2αi, w1, w2 ∈ [0, 1] ⊂ ℝ. Furthermore, from a parent node Pi,j, the lengths li+1 may be different for the branching node. The model in Equation (1) is evaluated for new parameters, resulting in the node position. Various forms of fractals can be obtained using the generalized model and the recursion due to Property 5.
The presented properties will be further used in the computational model for fractal generation.
Considering a table that has dimensions exactly given by Property 2 for a given fractal depth d. This table is constructed such that each row contains values for αi and li for each node Pi,j. We use the number of solutions per row Nd Equation (6) and the range r Equation (11) and permute the values of ±αi and li until each row in the table is filled. Table 1 shows an example of a table for depth d = 4. Positive values are highlighted differently from negative ones to highlight the pattern.

Table 1.
Example of a table with fractal parameters.
Each column in Table 1 represents the fractal parameters required to compute each path (Figure 4). For example, column 1 contains the parameters to compute node P4,1. Furthermore, node P3,1 can be computed by ignoring the last row. The same parameters (for P3,1) are present in column 2 (overlooking the last row), showing the parent–child relations between nodes.
Table 1 shows how to compute each node from the fractal structure, assuming symmetry (branching angles are opposite and equal in magnitude, and the branches emerging from a node have the same length). The previous Remark 1 points out that the model can be generalized. Table 2 shows the general version of the fractal parameter table (for d = 4).

Table 2.
Table with generalized fractal parameters.
The proposed method to order the fractal parameters is used to compute every node from a tree-like fractal (symmetric or general). We can create another table by taking, e.g., Table 1 and in each table cell from column 1 onwards, the values (Equation (5)) of the Cartesian coordinates of each node. A general example for d = 4 is presented in Table 3.

Table 3.
Cartesian coordinates of each node.
Considering the following:
- Subtracting each (i − 1) from i rows i > 1,
- Removing the redundancies (multiple points repeating) in the table,
we obtain a table that contains information about each segment (nodes and branches) in the fractal. Table 4 shows an example for d = 4. The child–parent relationship of the nodes is also apparent; the subtrahend of the two points is the father node, and the minuend point represents the child node. Table 4 represents the final representation of the fractal. This representation is the output of Step#1 (Figure 1) of the whole algorithm.

Table 4.
Nodes and branch definition of each node.
In pseudocode, Step#1 can be defined as (Algorithm 1):
| Algorithm 1: Table representation for tree-like fractals. |
|
4. Computational Model for Surface-Fractal Intersections
So far, we have a tabular representation of the tree-like fractals, and the question is how to trim the fractal such that it does not pass through the CAD shell (defined or approximated by a surface in this model). The following inputs are defined:
- A surface mesh with a given set of points denoted PTS and triangulation denoted TR.
- A tabular fractal representation.
To determine if a given branch intersects the surface, we check if the branch intersects any triangle (given by PTS set as vertices and TR as triangle definition). First, the ray/triangle intersection algorithm (Möller and Trumbore) is used [19], which outputs the intersection point of a ray (infinite line defined by the two points of the branch) and a triangle (with vertices within PTS set). To evaluate whether the line segment is intersecting the triangle, we compare D1 with D2, where IP is the intersection point (with the triangle, and is an output for the ray/triangle intersection algorithm), OP is the origin of the ray (or branch), and FP is the final point in the branch:
If D1 ≥ D2, there is no intersection; otherwise, the intersection point (output for the ray/triangle intersection algorithm) is stored in Table 4 to overwrite the final value on the branch. Next, all the children of the final node of the intersecting branch are considered NaN. An example is given in Table 5. The yellow cell is the branch that intersects a triangle, and P2,2(x,y,z) was changed to the intersection IP2,2(x,y,z). The red cells are the children of P2,2(x,y,z). Table 5 is the final representation of the trimmed fractals (after they intersect a surface), and is the output of Step#2 (Figure 1).

Table 5.
Nodes and branch definition of each node (after trimming due to intersections).
It is important to note that the algorithm requires surface data (points and triangulation), which are assumed to form the input. If an STL file is provided, either a surface mesh is also provided for the intersection, or the trimming is performed via a CAD method (see Section 6).
In pseudocode, we can define Step#2 as follows (Algorithm 2):
| Algorithm 2: Table representation for trimmed tree-like fractals. |
compute intersection point IP if IP exists: break end for
|
5. Applying Volume to the Fractal Structures
In order to apply volume to the fractal, each tree branch (fully described in tables such as Table 5) is transformed into a cylinder (with the height being the branch itself and the radius provided as an input in Step#0). The union of all of the cylinders is a three-dimensional representation of a tree-like fractal structure. Furthermore, the fractals are united with the CAD shell to output the final part.
There are various ways in which volume may be applied to tree-like fractal structures. This work proposes two different methods to achieve this:
- Geometric computational method (suitable when the shell is defined by a surface shell but not for CAD format). In this approach, the cylinders are defined by 3D Cartesian points used to compute surface meshes. The surface meshes are stitched to obtain the final structure, which is stitched to the CAD shell.
- CAD method (suitable in both cases). If the shell is defined by a surface mesh with triangulations, the mesh is converted first in CAD format. The fractal cylinders are generated and united with the CAD shell using CAD software.
5.1. The Geometric Computational Method
Two objectives are defined for this method: (1) to compute a surface mesh (with triangulation) for all the fractal structures and (2) to stitch all the fractal meshes to the given (in Step#0) shell, which is also a surface mesh. After achieving these two objectives, the final part is converted into STL format for 3D printing. Real care must be taken when stitching the fractal branches or the fractal to the shell, as the final surface mesh must be the union of all of the involved geometries, i.e., the intersections of the geometries must be excluded from the final surface mesh. This is required to obtain the CAD part without errors. There are two techniques that are used to achieve the previously defined objectives:
- Stitch three branches at a node; to apply volume, branches are defined as cylinders with given height, orientation, and radii. The process of stitching branches at a node computes the union of three cylinders, and it is useful to generate fractal structures.
- Stitch one branch to a given surface mesh; the branches that do not intersect through nodes are stitched to the shell. This process enables the computation of the final surface mesh (the desired part).
The following steps are used to compute the union of three cylinders (with branches intersecting at a node):
- st1.1.
- Three cylinders are defined with heights constructed using Equation (14); CYL1 (defining the main/parent branch) with height defined by starting point Pi1 and endpoint Pf1; CYL2 (defining the first secondary/child branch) with starting point Pi2 and endpoint Pf2; and CYL3 (defining the second secondary/child branch) with starting point Pi3 and endpoint Pf3 (cells within tables such as, e.g., Table 5, contain information for all of the fractal branches).
- st1.2.
- All cylinders are created such that they contain a set of generators (straight lines on the surface of the cylinder), each generator with a known number of points; the set G1 is defined for CYL1 with g1i ∈ G1 (i = 1…n1), and each generator contains points p1ij ∈ g1i (j = 1…m1); furthermore, G2 is defined for CYL2 with g2i ∈ G2 (i = 1…m2), with the points p2ij ∈ g2i (j = 1…m2); finally G3 is defined for CYL3 with g3i ∈ G3 (i = 1…m3), and p3ij ∈ g3i (j = 1…m3). The n’s denote the number of generators of each cylinder, whereas the m’s denote the number of points of each generator. Figure 5 shows an example of three cylinders: (1) the first cylinder with Pi1 = [0 0 0] [mm], Pf1 = [0 0 15] [mm], radius R1 = 4 [mm], n1 = 80, m1 = 80; the second cylinder with Pi2 = [0 0 15] [mm], Pf2 = [0 5 25] [mm], radius R2 = 4 [mm], n2 = 80, m2 = 80; and the third cylinder with Pi3 = [0 0 15] [mm], Pf3 = [0 –5 25] [mm], radius R3 = 4 [mm], n3 = 80, m3 = 80. For each cylinder, the first three generators (g11, g12, and g13 from G1; g21, g22, and g23 from G2; and g31, g32, and g33 from G3) are colored differently to highlight the cylinder construction rules.
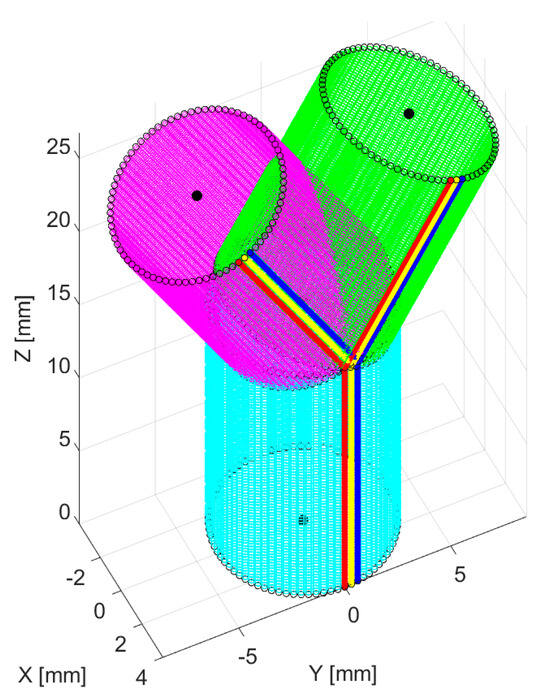 Figure 5. Example of three constructed cylinders; blue, red, and yellow dots represent three highlighted generators (first three generators of each cylinder); green, cyan, and magenta dots represent the rest of the three cylinders’ points; black empty dots represent the cylinders first and last circles; black filled points represent the initial (Pi) and final (Pf) points.
Figure 5. Example of three constructed cylinders; blue, red, and yellow dots represent three highlighted generators (first three generators of each cylinder); green, cyan, and magenta dots represent the rest of the three cylinders’ points; black empty dots represent the cylinders first and last circles; black filled points represent the initial (Pi) and final (Pf) points.
- st1.3.
- Three vectors are defined (using Equation (15)): V1 normal to the plane that contains the final circle face of the first cylinder (centered at Pf1); V2 normal to the plane that contains the first circle face (base) of the second cylinder (centered at Pi2); V3 normal to the plane that contains the first circle face (base) of the third cylinder (centered at Pi3). Three bisector vectors are defined using Equation (16).
- st1.4.
- Three cutoff planes (i.e., the planes that trim the cylinders such that the intersecting volumes are discarded) Δ1, Δ2, Δ3 are defined, with the normal vectors being the bisector vectors within Equation (16), and all three planes pass through Pf1:
- st1.5.
- To trim CYL1 with the Δ1 and Δ2 planes, the points p1ij of the generators g1i form the set G1 substituted in the x, y, z parameters of Equations (19a) and (19b) and must respect the inequalities Δ1 < 0, Δ2 < 0. To trim CYL2 with Δ1 and Δ3 planes, the points p2ij of the generators g2i form the set G3 (after substitution in Equations (19a) and (19b)) and must respect the inequalities Δ1 > 0, Δ3 > 0. Finally, to trim CYL3 with Δ2 and Δ3 planes, the points p3ij of the generators g3i form the set G3 (after substitution in Equations (19b) and (19c)) and must respect the inequalities Δ2 > 0, Δ3 > 0.
- st1.6.
- The last points (for all of the generators for all of the cylinders) that respect the inequalities defined in the previous step are projected in the cutoff planes to define the edge curves (denoted γ) of the cylinders’ intersection. The following sequential algorithm is used (presented in general form):
Each generator will produce a point for the intersection edge γ. In this work, the value for the admitted error was ε = 10−6. The edges of the corresponding cylinders are copied in the trimmed cylinders’ data points. Figure 6 shows the computed union of three cylinders (defined previously and illustrated in Figure 5).
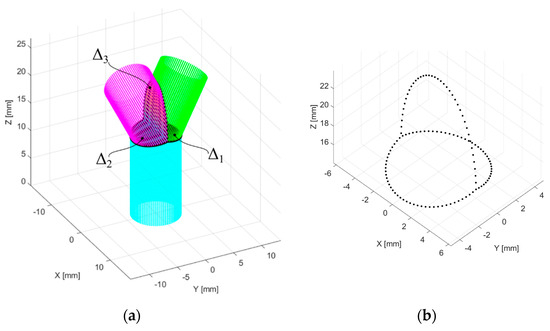
Figure 6.
Computed union of three cylinders (point cloud): (a) the trimmed cylinders and (b) the intersection edge curves γ.
- st1.7.
- An alpha shape is computed (in Matlab, the function is alphaShape [20]) for each of the three trimmed cylinders (with the added edges), and the boundary facets [21] are selected; this yields surface meshes with 3D points and their corresponding triangulation. For the union of the three cylinders, the 3D points of the three trimmed cylinders are concatenated. The triangulations are also concatenated after the necessary change in the indexing of the triangle vertices, e.g., if the first cylinder has 101 points, each triangle vertex of the second cylinder must add 101 and so on (to avoid overlapping triangulations). Moreover, the triangles containing only vertices from the intersection edge γ are discarded (to ensure correct surface stitching). Figure 7 shows the union of three cylinders (previously illustrated in Figure 5).
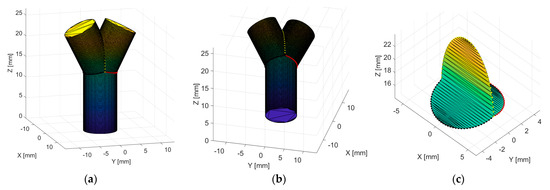 Figure 7. Computed union of three cylinders (surface mesh): (a) isometric view 1; (b) isometric view 2; and (c) excluded facets.
Figure 7. Computed union of three cylinders (surface mesh): (a) isometric view 1; (b) isometric view 2; and (c) excluded facets.
Using steps st1.1–st1.7 repeatedly, allows the stitching of a complete fractal structure. Each secondary/child branch becomes the main branch in the next stitching step up until the leaves are reached.
Next, the union of an arbitrary surface mesh with a cylinder is described (which allows the stitching of a branch with the shell):
- st2.1.
- A surface mesh α is given with a set of Cartesian points ki ∈ K (i = 1…n*) (n* being the total number of points) and a set of triangulations tj ∈ T (j = 1…m*) (m* being the number of triangles with vertices ∈ K). Furthermore, a cylinder CYL is defined with height by starting point Pi and endpoint Pf. The cylinder is constructed (again) using a set of generators, and each generator has a distinct set of points; the set G is defined for CYL with gi ∈ G (i = 1…n), and each generator contains points pij ∈ g1i (j = 1…m). The direction vector of the cylinders’ heights and generators is given by Equation (13).
- st2.2.
- All generators gi ∈ G are tested for intersection with the mesh α using the ray/triangle intersection algorithm (Möller and Trumbore) [19] for every triangle in T. To achieve this, a vector V is defined using the first and last points of the generator, and if the generator intersects a triangle tj ∈ T, the quantity norm(V) is compared with the distance D from the ray origin to the intersection point. If norm(V) ≥ D, the intersection point is considered a point on the intersection edge γ. Only geometric configurations that produce an intersection point for every gi ∈ G are allowed (the CAD method is used if this is not true).
- st2.3.
- The cylinder CYL is trimmed. The points pij ∈ gi up to the intersection point (on the edge γ) are kept, and the points of the edge γ are concatenated, resulting in a set G’1.
- st2.4.
- The shape α is trimmed. The points ki ∈ K that are inside the CYL (before trimming) are discarded, and the points of the edge γ are concatenated, resulting in a set k’i ∈ K’.
- st2.5.
- Two alpha shapes are computed, α1 for K’ and α2 for G’1. Then, boundary facets are computed for α1 containing the Cartesian points k’i ∈ K’ (i = 1…n’) and a new triangulation with t’j ∈ T’ (j = 1…m’), and for α2 containing the Cartesian points p’ij ∈ G’ (j = 1…n’’) and a triangulation t’’j ∈ T’’ (j = 1…m’’).
- st2.6.
- The triangles t’j ∈ T’ and t’’j ∈ T’’ that have all three vertices point from the intersection edge γ are discarded. Furthermore, the final surface mesh αfinal is defined with the Cartesian points kfinal,i ∈ K’ ∪ G’1 (i = 1… n’+ n’’) and the triangulation tfinal,j ∈ T’ ∪ T’’ (j = 1… m’+ m’’) where T’’ = T’’ + max(T’) (to account for the triangulation concatenation).
Figure 8 shows the stepwise process of stitching a given surface mesh (hemispherical shape) with a cylinder given in a point cloud (generated according to the definition from step 2.1). Figure 9a shows the end result for a hemispherical surface mesh stitched with a cylindrical shape. Figure 9b shows the end result for another example, where two cylinders are stitched using the steps (st2.1–st2.6) described previously.
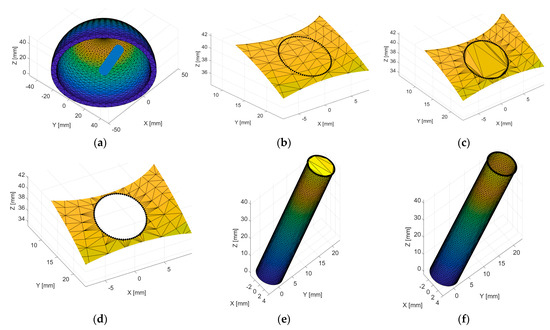
Figure 8.
Computational steps for a surface shell and a cylinder stitch: (a) input surface shell (hemispheric shape) and point cloud cylinder (step st2.1); (b) intersection edge on the input surface mesh (step st2.2); (c) intersection edge on the surface mesh (step st2.4. and step st2.5); (d) surface mesh cut around the intersection edge (step st2.6); (e) intersection edge on the cylindric surface mesh (step st2.4 and step st2.5); and (f) cylindrical surface mesh cut around the intersection edge (step st2.6).
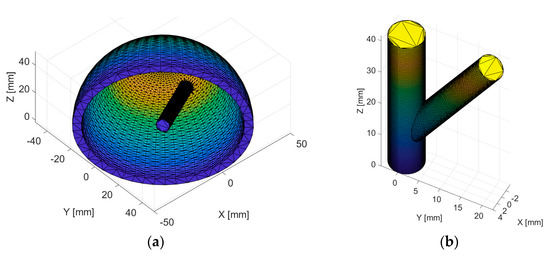
Figure 9.
Stitched surface meshes: (a) hemisphere–cylinder stitch and (b) cylinder–cylinder stitch.
The two techniques described at the beginning of the subsection (fractal stitching at nodes and shell-to-cylinder stitching) may be used to create surface meshes that can be further converted in an STL file format (e.g., using the function stlwrite [22] from Matlab). This achieves step#4 in the general algorithm.
In pseudocode, the two techniques are described below (Algorithm 3).
| Algorithm 3: CAD part with fractals (geometric method). |
end for
|
5.2. The CAD Method
Two objectives are defined for this method: (1) to generate the fractal structures using CAD techniques and (2) to unite the fractal structures with the CAD shell. The advantage over the geometric computational method is that the union of geometric components (to create fractals or to unite fractals to the shell) is computed automatically. Furthermore, trimming the fractals (when they intersect the shell) is not necessarily required in this approach as it is possible to create the fractals without surface intersection, unite them with the CAD shell, and then trim the unwanted parts (using a CAD component tool which is the negative of the CAD shell, as a trimming tool).
In this work, the OpenSCAD software is used [23] together with the Matlab library MatSCAD [24]. The following steps are used to achieve the fractal structures’ construction and their union with the CAD shell:
- st3.1.
- A SCAD structure is initialized as the workspace, and the CAD shell is imported.
- st3.2.
- The length Hi,j of each branch B of the fractal structure (data arranged in tables such as, e.g., Table 4 or Table 5) is computed using Equation (16). The initial point Pinit of each branch is also found in the fractal data. If a surface mesh is provided, the following must be considered:
- a.
- For thin shells (thickness in the order of the radii of the cylinders composing the fractals), even if the fractals are trimmed due to surface intersection, trimming with a CAD tool is recommended (see step st3.5).
- b.
- For thick shells (thickness in the order of at least two times the cylinder radii), no CAD tool trimming is required.
- st3.3.
- For each branch, a cylinder CYLi,j is created in CAD with height Hi,j, and radius R (given in Step#0).
- st3.4.
- Each cylinder CYLi,j is generated at the origin of the world coordinate system. Therefore, to position the branch correctly, each cylinder is rotated using the angles ψ and φ (Equation (17)) and then translated using Pinit. The cylinder is then united with the rest of the CAD structures (other cylinders within the fractals and the shell).
- st3.5.
- A CAD trimming tool, which is the negative of the shell, is used on every generated cylinder (assuming it is needed).
In Section 6.1, Section 6.2 and Section 6.3, there are case studies showing the results of applying the CAD method to generate internal fractal structures on predefined CAD shells. Following the steps st3.1–st3.5 finalizes step#4 in the general algorithm.
In pseudocode, the CAD method is described below (Algorithm 4).
| Algorithm 4: CAD part with fractals (CAD method). |
else if the CAD shell is thick, then goto 5 if the fractal structures are not trimmed (e.g., Table 4), then goto 4
end for
end for
|
Table 6 presents a broad comparison between the geometric and the CAD methods for tree-like fractal generation.

Table 6.
Broad comparison between the geometric and the CAD methods.
6. Case Studies
6.1. Creating Fractal Structures on a Surface Mesh Using the Geometric Method
For the first case study, the geometric computational method was used. The cad shell was defined using a surface mesh that had two components; the first component (the base of the shell) was defined by a planar structure (parallel to the XOZ plane) with 5 mm thickness and the second component (the top of the shell) was defined by a curved surface with thickness of 5 mm and the following equation:
which was scaled by a factor of 30 in the X and Z directions and by a factor of 25 in the Y direction. Furthermore, the surface was translated by 55 mm in the y direction. Four fractal structures were defined with different origins, branch angles, and branch lengths. The maximum allowed depth for each fractal in all four cases was d = 5, and the radii for all fractals were r = 1.5 mm.
For the fractal origins, the following parameters were used:
Furthermore, Table A1, Table A2, Table A3 and Table A4 in Appendix A show the input geometric data used to define the four tree-like fractals (the tables were constructed accruing to Table 1 and Table 2). As a reminder, each row in the tables represents the depth of the tree-like fractals, whereas each column represents the parameters needed to compute each node. The intersection of the fractals with the surface mesh was computed, resulting in a new set of data tables (Table A5, Table A6, Table A7 and Table A8 in Appendix A) for the trimmed tree-like fractals.
Figure 10 shows the computed fractals (after applying volume and uniting them with the shell according to the steps described in Section 5.1).
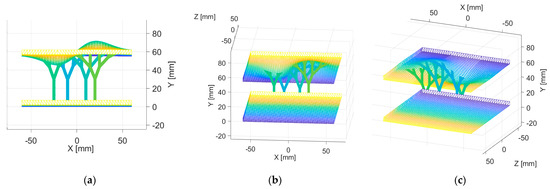
Figure 10.
Surface mesh for shell filled with tree-like fractal structures using the geometric computational method: (a) side view (XOY plane); (b) isometric view 1; and (c) isometric view 2.
To export the surface mesh into an STL file format, the function “stlwrite” [22] from Matlab was used, which takes as inputs the cartesian points of the surface and the triangulations (both being computed in the algorithm described in Section 5.1). At this point, step#4 is completed from the general algorithm (see Section 2), and the part is ready for 3D printing or further CAD tests such as FEA (thus achieving step#5).
6.2. Creating Fractal Structures on a Hemispherical Shell Using the CAD Method
For the second case study, a hemispherical CAD shell was chosen as an input. This has two components: the first component is a concave hemisphere (radius of 50 mm and thickness of 5 mm) and the second is a convex hemisphere (radius of 5 mm) with its center displaced by 5 mm (with respect to the concave hemisphere) on the z-axis. The maximum allowed depth of the fractals was d = 5, and the radii for all fractals were r = 1 mm.
Twenty-four fractal structures were generated using the following relation:
Furthermore, a hemispheric surface mesh was provided, defined for the inner surface of the CAD shell using the equation:
If the CAD shell is based on a well-defined surface, it is convenient to compute a surface mesh to compute the trimmed fractals.
Table A9 in Appendix B presents the input geometric data (branch angles and lengths) for the tree-like fractals used in this case study. Table A10 and Table A11 show two examples of tables computed for the trimmed fractals (not all fractal data are reported as they are lengthy and not relevant to the results presented in this subsection). Figure 11 shows the final CAD part (computed using MatSCAD) with the two hemispheres and the fractal structures uniting them.
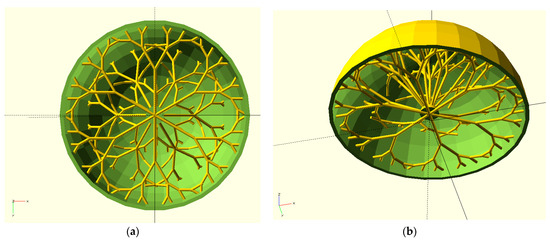
Figure 11.
Final CAD part with two hemispheres united by fractal structures: (a) bottom view (plane XOY) and (b) isometric view.
Exporting the CAD as an STL file format finalizes step#4 in the general algorithm (Section 2). In this case study, it was easy to provide the surface mesh to compute the fractal intersection (as the sphere has a well-defined surface equation). However, this surface is not required as a CAD cutting tool can be defined as the negative of the provided shell (which envelops the outer surface of the shell).
6.3. Creating Test Samples with Fractal Structures Using the CAD Method
For the third case study, two test samples were designed using the CAD method to study how the fractals behave under mechanical stress. The first sample was designed for a compression test, and the shell contains two planar parts (square shapes of 20 mm side and 1 mm thickness, displaced by 20 mm) that are united through six fractal structures. The origins of the fractals are defined by:
The radii of all fractal structure branches were 1 mm. Table A12 in Appendix C shows the input geometric data for the fractal structures, and Table A13 and Table A14 show the branch data for the fractals. Figure 12 shows the CAD model of the compression sample.
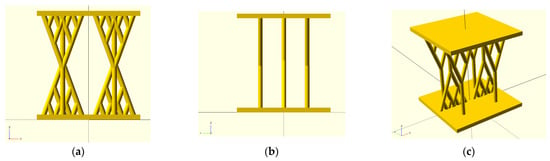
Figure 12.
CAD sample part for compression tests: (a) front view (plane XOZ); (b) side view (plane YOZ); and (c) isometric view.
The second test sample was designed for the bending tests. Again, the sample shell contains two planar components (rectangular shapes with sides 10 mm and 80 mm, respectively, with 1 mm thickness and displaced by 9.5 mm). The fractal structures were defined with the following origins:
The radii for all of the branches were set to 1 mm. Table A15 from Appendix D shows the geometric input data for the fractals, whereas Table A16 and Table A17 show the branch data for the fractals. Lastly, Figure 13 illustrates the test sample for bending in CAD. Exporting the test parts to an STL file format concludes step#4.

Figure 13.
CAD sample part for bending tests: (a) front view (plane XOZ); (b) side view (plane YOZ); and (c) isometric view.
7. Conclusions
Internal structures, such as lattice structures are of great interest for various domains of AM, and a lot of focus is given worldwide to understanding their properties. Tree-like fractals can also be used as internal structures in AM, but no significant progress has been reported in their modeling and implementation for AM.
This paper presented a computational model designed to generate tree-like fractals as internal structures in AM mechanical parts. The computational model brings several contributions with respect to the use of tree-like fractals in AM. Firstly, a comprehensive and detailed mathematical model is derived to construct various tree-like fractal structures. The fractals are viewed as mathematical structures with clearly defined properties. Secondly, a tabular arrangement is proposed for the fractal data, which is easily implemented using vectorized programming techniques (e.g., Matlab, Python with numpy). Lastly, two approaches were proposed to create three-dimensional fractal structures (with volume) and implement them in CAD components for AM.
It is reasonable to point out that the computational model ensures scalability on multiple fronts. On the computational level, the tabular representation and the recursive nature of the fractal structure computation should ensure scalability. On a practical level, one can achieve multi-scale fractal structures using the fractal properties and their proposed computation techniques. A CAD shell can be filled with several thick fractal structures and then iteratively with lower-thickness fractals.
Perhaps the most significant contribution of the proposed model is that it can provide some tools for the generation of parts with tree-like fractals as internal structures, which in turn can be studied to determine their feasibility in AM. Suppose predictable numerical models can be achieved (e.g., in regard to how the fractal geometry affects the part as a whole). In that case, the computational model becomes more valuable for generating components, metamaterials, etc., with predefined properties.
Further work is required to test the fractal structures in laboratory conditions (e.g., mechanical tests) and using final element analysis. This, again, will determine the feasibility of the tree-like fractals and possibly lead to numerical models for their mechanical behavior.
Author Contributions
Conceptualization, A.S.B. and N.B.; methodology, A.S.B.; software, A.S.B.; validation, N.B.; formal analysis, A.S.B.; investigation, A.S.B.; resources, N.B.; data curation, A.S.B.; writing—original draft preparation, A.S.B.; writing—review and editing, A.S.B. and N.B.; visualization, A.S.B. and N.B.; supervision, N.B.; project administration, N.B.; funding acquisition, N.B. All authors have read and agreed to the published version of the manuscript.
Funding
This paper was financially supported by the Project “Entrepreneurial competences and excellence research in doctoral and postdoctoral programs—ANTREDOC”, project co-funded by the European Social Fund financing agreement no. 56437/24.07.2019. This research was also supported by the HORIZON 2020—DiCoMI Project, “Directional Composites through Manufacturing Innovation”, GA Nr. 778068. Besides this, the infrastructure available from the European Development Fund and the Romanian Government through the Competitiveness Operational Programme 2014–2020, project ID P 34 466, MySMIS code 121349, contract no. 5/05.06.2018 is highly acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In Table A1, Table A2, Table A3 and Table A4, the dimensions of αi are radians, and the dimensions of li are mm.

Table A1.
First fractal parameters (root = ORG1).
Table A1.
First fractal parameters (root = ORG1).
| α1 = 0, l1 = 28 | α = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α =0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 |
| α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 |
| α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = −π/9, l3 = 14 | α3 = −π/9, l3 = 14 | α3 = −π/9, l3 = 14 | α3 = −π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = −π/9, l3 = 14 | α3 = −π/9, l3 = 14 | α3 = −π/9, l3 = 14 | α3 = −π/9, l3 = 14 |
| α4 = π/9, l4 = 14 | α4 = π/9, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = π/9, l4 = 14 | α4 = π/9, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = π/9, l4 = 14 | α4 = π/9, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = π/9, l4 = 14 | α4 = π/9, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = −π/9, l4 = 14 |
| α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 14 |
Blue represents the fractal origin; green represents positive angle values; and orange represents negative angle values.

Table A2.
Second fractal parameters (root = ORG2).
Table A2.
Second fractal parameters (root = ORG2).
| α1 = 0, l1 = 28 | α = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α =0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 |
| α2 = π/8, l2 = 14 | α2 = π/8, l2 = 14 | α2 = π/8, l2 = 14 | α2 = π/8, l2 = 14 | α2 = π/8, l2 = 14 | α2 = π/8, l2 = 14 | α2 = π/8, l2 = 14 | α2 = π/8, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 |
| α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = −π/8, l3 = 14 | α3 = −π/8, l3 = 14 | α3 = −π/8, l3 = 14 | α3 = −π/8, l3 = 14 | α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = −π/8, l3 = 14 | α3 = −π/8, l3 = 14 | α3 = −π/8, l3 = 14 | α3 = −π/8, l3 = 14 |
| α4 = π/8, l4 = 14 | α4 = π/8, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = π/8, l4 = 14 | α4 = π/8, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = π/8, l4 = 14 | α4 = π/8, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = π/8, l4 = 14 | α4 = π/8, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = −π/9, l4 = 14 |
| α5 = π/9, l5 = 14 | α5 = −π/8, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/8, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/8, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/8, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/8, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/8, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/8, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/8, l5 = 14 |
Blue represents the fractal origin; green represents positive angle values; and orange represents negative angle values.

Table A3.
Third fractal parameters (root = ORG3).
Table A3.
Third fractal parameters (root = ORG3).
| α1 = 0, l1 = 28 | α = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 |
| α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 | α2 = −π/9, l2 = 14 |
| α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = −π/9, l3 = 14 | α3 = −π/9, l3 = 14 | α3 = −π/9, l3 = 14 | α3 = −π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = −π/9, l3 = 14 | α3 = −π/9, l3 = 14 | α3 = −π/9, l3 = 14 | α3 = −π/9, l3 = 14 |
| α4 = π/9, l4 = 14 | α4 = π/9, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = π/9, l4 = 14 | α4 = π/9, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = π/9, l4 = 14 | α4 = π/9, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = π/9, l4 = 14 | α4 = π/9, l4 = 14 | α4 = −π/9, l4 = 14 | α4 = −π/9, l4 = 14 |
| α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 14 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 14 |
Blue represents the fractal origin; green represents positive angle values; and orange represents negative angle values.

Table A4.
Fourth fractal parameters (root = ORG4).
Table A4.
Fourth fractal parameters (root = ORG4).
| α1 = 0, l1 = 28 | α = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 | α1 = 0, l1 = 28 |
| α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = π/9, l2 = 14 | α2 = −π/8, l2 = 16 | α2 = −π/8, l2 = 16 | α2 = −π/8, l2 = 16 | α2 = −π/8, l2 = 16 | α2 = −π/8, l2 = 16 | α2 = −π/8, l2 = 16 | α2 = −π/8, l2 = 16 | α2 = −π/8, l2 = 16 |
| α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = −π/9, l3 = 16 | α3 = −π/9, l3 = 16 | α3 = −π/9, l3 = 16 | α3 = −π/9, l3 = 16 | α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = π/9, l3 = 14 | α3 = −π/9, l3 = 16 | α3 = −π/9, l3 = 16 | α3 = −π/9, l3 = 16 | α3 = −π/9, l3 = 16 |
| α4 = π/9, l4 = 14 | α4 = π/9, l4 = 14 | α4 = −π/8, l4 = 16 | α4 = −π/8, l4 = 16 | α4 = π/9, l4 = 14 | α4 = π/9, l4 = 14 | α4 = −π/8, l4 = 16 | α4 = −π/8, l4 = 16 | α4 = π/9, l4 = 14 | α4 = π/9, l4 = 14 | α4 = −π/8, l4 = 16 | α4 = −π/8, l4 = 16 | α4 = π/9, l4 = 14 | α4 = π/9, l4 = 14 | α4 = −π/8, l4 = 16 | α4 = −π/8, l4 = 16 |
| α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 16 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 16 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 16 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 16 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 16 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 16 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 16 | α5 = π/9, l5 = 14 | α5 = −π/9, l5 = 16 |
Blue represents the fractal origin; green represents positive angle values; and orange represents negative angle values.
In Table A5, Table A6, Table A7 and Table A8 each cell contains the initial and final points of a branch with X, Y, and Z Cartesian coordinates. The data in each cell are ordered as final point—initial point (where the final point is at the top of the cell and the initial point is at the bottom of the cell).

Table A5.
The first fractal data after trimming due to surface intersection.
Table A5.
The first fractal data after trimming due to surface intersection.
| [10, 1, 0] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [10, 29, 0] — [10, 1, 0] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [5.2, 42.2, 0] — [10, 29, 0] | [14.8, 42.2, 0] — [10, 29, 0] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−3.8, 52.9, 0] — [5.2, 42.2, 0] | [5.2, 56.2, 0] — [5.2, 42.2, 0] | [14.8, 56.2, 0] — [14.8, 42.2, 0] | [23.8, 52.9, 0] — [14.8, 42.2, 0] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−5.3, 53.7, 0] — [−3.8, 52.9, 0] | [−4.4, 54.4, 0] – [−3.8, 52.9, 0] | [3.5, 60.9, 0] — [5.2, 56.2, 0] | [8.2, 64.3, 0] — [5.2, 56.2, 0] | [11.2, 66.1, 0] — [14.8, 56.2, 0] | [19.3, 68.6, 0] — [14.8, 56.2, 0] | [28.6, 66, 0] — [23.8, 52.9, 0] | [35.9, 59.9, 0] — [23.8, 52.9, 0] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | [28.6, 67.6, 0] — [28.6, 66, 0] | [29.6, 67.3, 0] — [28.6, 66, 0] | [39.3, 63.9, 0] — [35.9, 59.9, 0] | [46, 61.7, 0] — [35.9, 59.9, 0] |

Table A6.
The second fractal data after trimming due to surface intersection.
Table A6.
The second fractal data after trimming due to surface intersection.
| [20, 1, 20] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [20, 29, 20] — [20, 1, 20] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [14.6, 41.9, 20] — [20, 29, 20] | [24.8, 42.2, 20] — [20, 29, 20] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [5.2, 52.3, 20] — [14.6, 41.9, 20] | [14.6, 55.9, 20] — [14.6, 41.9, 20] | [24.8, 56.2, 20] — [24.8, 42.1, 20] | [34.2, 52.5, 20] — [24.8, 42.1, 20] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−3.4, 56.2, 20] — [5.2, 52.3, 20] | [2.3, 59.2, 20] — [5.2, 52.3, 20] | [11.6, 63.3, 20] — [14.6, 55.9, 20] | [17.8, 64.7, 20] — [14.6, 55.9, 20] | [21.2, 64.8, 20] — [24.8, 56.2, 20] | [27.7, 64.3, 20] — [24.8, 56.2, 20] | [37.7, 62.1, 20] — [34.2, 52.5, 20] | [46.7, 58.9, 20] — [34.2, 52.5, 20] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | [47.7, 60, 20] — [46.7, 58.9, 20] | [51.9, 59.4, 20] — [46.7, 58.9, 20] |

Table A7.
The third fractal data after trimming due to surface intersection.
Table A7.
The third fractal data after trimming due to surface intersection.
| [−25, 1, 10] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [20, 29, 10] — [−25, 1, 10] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−29.8, 42.2, 10] — [−25, 29, 10] | [−20.2, 42.2, 10] — [−25, 29, 10] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−38.4, 52.5, 10] — [−29.8, 42.2, 10] | [−29.8, 49.7, 10] — [−29.8, 42.2, 10] | [−20.2, 48.5, 10] — [−20.2, 42.2, 10] | [−13.9, 49.7, 10] — [−20.2, 42.2, 10] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |

Table A8.
The fourth fractal data after trimming due to surface intersection.
Table A8.
The fourth fractal data after trimming due to surface intersection.
| [−10, 1, −10] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−10, 29, −10] — [−10, 1, −10] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−14.8, 42.2, −10] — [−10, 29, −10] | [−3.9, 43.8, −10] — [−10, 29, −10] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−20.1, 48.5, −10] — [−14.8, 42.2, −10] | [−14.8, 48.4, −10] — [−14.8, 42.2, −10] | [−3.4, 55.5, −10] — [−3.9, 43.8, −10] | [6.9, 55.6, −10] — [−3.9, 43.8, −10] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| NaN | NaN | NaN | NaN | NaN | NaN | [10.9, 65.1, −10] — [6.9, 55.6, −10] | [21.4, 62.3, −10] — [6.9, 55.6, −10] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | [26.2, 67.1, −10] — [21.4, 62.3, −10] | [37.4, 63.7, −10] — [21.4, 62.3, −10] |
Appendix B

Table A9.
Fractal parameters for a shell with two hemispheres (origins are given by Equation (23)).
Table A9.
Fractal parameters for a shell with two hemispheres (origins are given by Equation (23)).
| α1 = 0, l1 = 25 | α = 0, l1 = 25 | α1 = 0, l1 = 25 | α1 = 0, l1 = 25 | α1 = 0, l1 = 25 | α1 = 0, l1 = 25 | α1 = 0, l1 = 25 | α1 = 0, l1 = 25 | α1 = 0, l1 = 25 | α = 0, l1 = 25 | α1 = 0, l1 = 25 | α1 = 0, l1 = 25 | α1 = 0, l1 = 25 | α1 = 0, l1 = 25 | α1 = 0, l1 = 25 | α1 = 0, l1 = 25 |
| α2 = π/6, l2 = 13.9 | α2 = π/6, l2 = 13.9 | α2 = π/6, l2 = 13.9 | α2 = π/6, l2 = 13.9 | α2 = π/6, l2 = 13.9 | α2 = π/6, l2 = 13.9 | α2 = π/6, l2 = 13.9 | α2 = π/6, l2 = 13.9 | α2 = −π/6, l2 = 13.9 | α2 = −π/6, l2 = 13.9 | α2 = −π/6, l2 = 13.9 | α2 = −π/6, l2 = 13.9 | α2 = −π/6, l2 = 13.9 | α2 = −π/6, l2 = 13.9 | α2 = −π/6, l2 = 13.9 | α2 = −π/6, l2 = 13.9 |
| α3 = π/6, l3 = 6.9 | α3 = π/6, l3 = 6.9 | α3 = π/6, l3 = 6.9 | α3 = π/6, l3 = 6.9 | α3 = −π/6, l3 = 6.9 | α3 = −π/6, l3 = 6.9 | α3 = −π/6, l3 = 6.9 | α3 = −π/6, l3 = 6.9 | α3 = π/6, l3 = 6.9 | α3 = π/6, l3 = 6.9 | α3 = π/6, l3 = 6.9 | α3 = π/6, l3 = 6.9 | α3 = −π/6, l3 = 6.9 | α3 = −π/6, l3 = 6.9 | α3 = −π/6, l3 = 6.9 | α3 = −π/6, l3 = 6.9 |
| α4 = π/6, l4 = 6.9 | α4 = π/6, l4 = 6.9 | α4 = −π/6, l4 = 6.9 | α4 = −π/6, l4 = 6.9 | α4 = π/6, l4 = 6.9 | α4 = π/6, l4 = 6.9 | α4 = −π/6, l4 = 6.9 | α4 = −π/6, l4 = 6.9 | α4 = π/6, l4 = 6.9 | α4 = π/6, l4 = 6.9 | α4 = −π/6, l4 = 6.9 | α4 = −π/6, l4 = 6.9 | α4 = π/6, l4 = 6.9 | α4 = π/6, l4 = 6.9 | α4 = −π/6, l4 = 6.9 | α4 = −π/6, l4 = 6.9 |
| α5 = π/6, l5 = 6.9 | α5 = −π/6, l5 = 6.9 | α5 = π/6, l5 = 6.9 | α5 = −π/6, l5 = 6.9 | α5 = π/6, l5 = 6.9 | α5 = −π/6, l5 = 6.9 | α5 = π/6, l5 = 6.9 | α5 = −π/6, l5 = 6.9 | α5 = π/6, l5 = 6.9 | α5 = −π/6, l5 = 6.9 | α5 = π/6, l5 = 6.9 | α5 = −π/6, l5 = 6.9 | α5 = π/6, l5 = 6.9 | α5 = −π/6, l5 = 6.9 | α5 = π/6, l5 = 6.9 | α5 = −π/6, l5 = 6.9 |
Blue represents the fractal origin; green represents positive angle values; and orange represents negative angle values.
In Table A10 and Table A11 each cell contains the initial and final points of a branch with X, Y, and Z Cartesian coordinates. The data in each cell are ordered as final point—initial point (where the final point is at the top of the cell and the initial point is at the bottom of the cell).

Table A10.
Fractal data after trimming due to surface intersection (origin computed with θ1 = π/6, θ2 = 0, θ3 = π/6).
Table A10.
Fractal data after trimming due to surface intersection (origin computed with θ1 = π/6, θ2 = 0, θ3 = π/6).
| [0, 0, 5] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−10.8, 18.6, 17.5] — [0, 0, 5] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−22.1, 24.3, 23.5] — [−10.8, 18.6, 17.5] | [−10, 31.2, 23.5] — [−10.8, 18.6, 17.5] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−28.8, 23.9, 25.3] — [−22.1, 24.3, 23.5] | [−25.1, 29.5, 26.9] — [−22.1, 24.3, 23.5] | [−13, 36.5, 26.9] — [−10, 31.2, 23.5] | [−6.3, 36.9, 25.3] — [−10, 31.2, 23.5] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−34.8, 20.4, 25.2] — [−28.8, 23.9, 25.3] | [−32.7, 25.9, 27.4] — [−28.8, 23.9, 25.3] | [−27.4, 30.7, 28.2] — [−25.1, 29.5, 26.9] | [−24.9, 32.7, 28.5] — [−25.1, 29.5, 26.9] | [−15.8, 37.8, 28.5] — [−13, 36.5, 26.9] | [−12.9, 39.1, 28.3] — [−13, 36.5, 26.9] | [−6, 41.3, 27.4] — [−6.3, 36.9, 25.3] | [−0.3, 40.3, 25.2] — [−6.3, 36.9, 25.3] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−38.5, 14.8, 23.5] — [−34.8, 20.4, 25.2] | [−36.9, 20.3, 25.8] — [−34.8, 20.4, 25.2] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | [1.2, 42.6, 25.9] — [−0.3, 40.3, 25.2] | [6.4, 14.7, 23.5] — [−0.3, 40.3, 25.2] |

Table A11.
Fractal data after trimming due to surface intersection (origin computed with θ1 = π/2, θ2 = 0, θ3 = π/3).
Table A11.
Fractal data after trimming due to surface intersection (origin computed with θ1 = π/2, θ2 = 0, θ3 = π/3).
| [0, 0, 5] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−12.5, 0.8, 26.7] — [0, 0, 5] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−18.5, −6.9, 37.1] — [−12.5, 0.8, 26.7] | [−18.5, 6.9, 37.1] — [−12.5, 0.8, 26.7] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−20.3, −12.9, 40.1] — [−18.5, −6.9, 37.1] | [−21.9, −6.9, 43.1] — [−18.5, −6.9, 37.1] | [−21.9, 6.9, 43.1] — [−18.5, 6.9, 37.1] | [−20.3, 12.9, 40.1] — [−18.5, 6.9, 37.1] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−20.3, −19.9, 40.1] — [−20.3, −12.9, 40.1] | [−21.7, −14.6, 42.6] – [−20.3, −12.9, 40.1] | NaN | NaN | [−22.7, 6.2, 44.1] — [−21.9, −6.9, 43.1] | [−22.5, 7.5, 43.9] — [−21.9, −6.9, 43.1] | [−21.7, 14.6, 42.5] — [−21.9, 6.9, 43.1] | [−20.3, 19.9, 40.1] — [−20.3, 12.9, 40.1] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−18.5, −25.9, 37.1] — [−20.3, −19.9, 40.1] | [−20.5, −20.8, 40.5] — [−20.3, −19.9, 40.1] | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | [−20.5, 20.8, 40.5] — [−20.3, 19.9, 40.1] | [−18.5, 25.9, 37.1] — [−20.3, 19.9, 40.1] |
Appendix C

Table A12.
Fractal parameters for a compression sample (origins are given by Equation (25)).
Table A12.
Fractal parameters for a compression sample (origins are given by Equation (25)).
| α1 = 0, l1 = 10 | α = 0, l1 = 10 | α1 = 0, l1 = 10 | α1 = 0, l1 = 10 | α1 = 0, l1 = 10 | α1 = 0, l1 = 10 | α1 = 0, l1 = 10 | α1 = 0, l1 = 10 |
| α2 = π/9, l2 = 5 | α2 = π/9, l2 = 5 | α2 = π/9, l2 = 5 | α2 = π/9, l2 = 5 | α2 = −π/9, l2 = 5 | α2 = −π/9, l2 = 5 | α2 = −π/9, l2 = 5 | α2 = −π/9, l2 = 5 |
| α3 = 0, l3 = 2.5 | α3 = 0, l3 = 2.5 | α3 = −2π/9, l3 = 2.5 | α3 = −2π/9, l3 = 2.5 | α3 = 2π/9, l3 = 2.5 | α3 = 2π/9, l3 = 2.5 | α3 = 0, l3 = 2.5 | α3 = 0, l3 = 2.5 |
| α4 = 0, l4 = 2.5 | α4 = −2π/9, l4 = 2.5 | α4 = 2π/9, l4 = 2.5 | α4 = 0, l4 = 2.5 | α4 = 0, l4 = 2.5 | α4 = −2π/9, l4 = 2.5 | α4 = 2π/9, l4 = 2.5 | α4 = 0, l4 = 2.5 |
Blue represents the fractal origin; green represents positive angle values; and orange represents negative angle values.

Table A13.
Fractal data for the compression sample’s inner and outer layers.
Table A13.
Fractal data for the compression sample’s inner and outer layers.
| [−5 + i, ±5, 0] | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−5 + i, ±5, 10] — [−5 + i, ±5, 0] | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−6.7 + i, ±5, 14.7] — [−5 + i, ±5, 10] | [−3.3 + i, ±5, 14.7] — [−5 + i, ±5, 10] | NaN | NaN | NaN | NaN | NaN | NaN |
| [−7.9 + i, ±5, 17.8] — [−6.7 + i, ±5, 14.7] | [−5.6 + i, ±5, 17.8] — [−6.7 + i, ±5, 14.7] | [−4.4 + i, ±5, 17.8] — [−3.3 + i, ±5, 14.7] | [−2.1 + i, ±5, 17.8] — [−3.3 + i, ±5, 14.7] | NaN | NaN | NaN | NaN |
| [−8.7 + i, ±5, 20.2] — [−7.9 + i, ±5, 17.8] | [−6.9 + i, ±5, 20.2] – [−7.9 + i, ±5, 17.8] | [−6.4 + i, ±5, 20.2] — [−5.6 + i, ±5, 17.8] | [−4.7 + i, ±5, 20.2] — [−5.6 + i, ±5, 17.8] | [−5.3 + i, ±5, 20.2] — [−4.4 + i, ±5, 17.8] | [−3.6 + i, ±5, 20.2] — [−4.4 + i, ±5, 17.8] | [−3 + i, ±5, 20.2] — [−2.1 + i, ±5, 17.8] | [−1.3 + i, ±5, 20.2] — [−4.4 + i, ±5, 17.8] |
i = 0, 10.

Table A14.
Fractal data for the compression sample’s middle layer.
Table A14.
Fractal data for the compression sample’s middle layer.
| [−5 + i, 0, 21] | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−5 + i, 0, 11] — [−5 + i, 0, 21] | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−3.3 + i, 0, 14.7] — [−5 + i, 0, 11] | [−6.7 + i, 0, 14.7] — [−5 + i, 0, 11] | NaN | NaN | NaN | NaN | NaN | NaN |
| [−2.2 + i, 0, 3.2] — [−3.3 + i, 0, 14.7] | [−4.4 + i, 0, 3.2] — [−3.3 + i, 0, 14.7] | [−5.6 + i, 0, 3.2] — [−6.7 + i, 0, 14.7] | [−7.9 + i, 0, 3.2] — [−6.7 + i, 0, 14.7] | NaN | NaN | NaN | NaN |
| [−1.3 + i, 0, 0.8] — [−2.2 + i, 0, 3.2] | [−3 + i, 0, 0.8] — [−2.2 + i, 0, 3.2] | [−3.6 + i, 0, 0.8] — [−4.4 + i, 0, 3.2] | [−5.3 + i, 0, 0.8] — [−4.4 + i, 0, 3.2] | [−4.7 + i, 0, 0.8] — [−5.6 + i, 0, 3.2] | [−6.4 + i, 0, 0.8] — [−5.6 + i, 0, 3.2] | [−6.9 + i, 0, 0.8] — [−7.9 + i, 0, 3.2] | [−8.7 + i, 0, 0.8] — [−7.9 + i, 0, 3.2] |
i = 0, 10.
Appendix D

Table A15.
Fractal parameters for a bending sample (origins are given by Equation (26)).
Table A15.
Fractal parameters for a bending sample (origins are given by Equation (26)).
| α1 = 0, l1 = 5 | α = 0, l1 = 5 | α1 = 0, l1 = 5 | α1 = 0, l1 = 5 | α1 = 0, l1 = 5 | α1 = 0, l1 = 5 | α1 = 0, l1 = 5 | α1 = 0, l1 = 5 |
| α2 = π/6, l2 = 2.5 | α2 = π/6, l2 = 2.5 | α2 = π/6, l2 = 2.5 | α2 = π/6, l2 = 2.5 | α2 = −π/6, l2 = 2.5 | α2 = −π/6, l2 = 2.5 | α2 = −π/6, l2 = 2.5 | α2 = −π/6, l2 = 2.5 |
| α3 = 0, l3 = 1.25 | α3 = 0, l3 = 1.25 | α3 = −2π/6, l3 = 1.25 | α3 = −2π/6, l3 = 1.25 | α3 = 2π/6, l3 = 1.25 | α3 = 2π/6, l3 = 1.25 | α3 = 0, l3 = 1.25 | α3 = 0, l3 = 1.25 |
| α4 = 0, l4 = 1.25 | α4 = −2π/6, l4 = 1.25 | α4 = 2π/6, l4 = 1.25 | α4 = 0, l4 = 1.25 | α4 = 0, l4 = 1.25 | α4 = −2π/6, l4 = 1.25 | α4 = 2π/6, l4 = 1.25 | α4 = 0, l4 = 1.25 |
Blue represents the fractal origin; green represents positive angle values; and orange represents negative angle values.

Table A16.
Fractal data for the bending sample’s inner layer and outer layer.
Table A16.
Fractal data for the bending sample’s inner layer and outer layer.
| [−45 + i, ±4, 0]. | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−45 + i, ±4, 5] — [−45 + i, ±4, 0] | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−46.3 + i, ±4, 7.2] — [−45 + i, ±4, 5] | [−43.8 + i, ±4, 7.2] — [−45 + i, ±4, 5] | NaN | NaN | NaN | NaN | NaN | NaN |
| [−47.1 + i, ±4, 8.6] — [−46.3 + i, ±4, 7.2] | [−45.4 + i, ±4, 8.6] — [−46.3 + i, ±4, 7.2] | [−44.6 + i, ±4, 8.6] — [−43.8 + i, ±4, 7.2] | [−42.9 + i, ±4, 8.6] — [−43.8 + i, ±4, 7.2] | NaN | NaN | NaN | NaN |
| [−47.9 + i, ±4, 10.1] — [−47.1 + i, ±4, 8.6] | [−46.3 + i, ±4, 10.1] — [−47.1 + i, ±4, 8.6] | [−46.3 + i, ±4, 10.1] — [−45.4 + i, ±4, 8.6] | [−44.6 + i, ±4, 10.1] — [−45.4 + i, ±4, 8.6] | [−45.4 + i, ±4, 10.1] — [−44.6 + i, ±4, 8.6] | [−43.8 + i, ±4, 10.1] — [−44.6 + i, ±4, 8.6] | [−43.8 + i, ±4, 10.1] — [−42.9 + i, ±4, 8.6] | [−42.1 + i, ±4, 10.1] — [−42.9 + i, ±4, 8.6] |
i = 0, 5, 10, …, 100.

Table A17.
Fractal data for the bending sample’s middle layer.
Table A17.
Fractal data for the bending sample’s middle layer.
| [−45 + i, 0, 10.5] | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−45 + i, 0, 5.5] — [−45 + i, 0, 10.5] | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
| [−43.8 + i, 0, 3.3] — [−45 + i, 0, 5.5] | [−46.3 + i, 0, 3.3] — [−45 + i, 0, 5.5] | NaN | NaN | NaN | NaN | NaN | NaN |
| [−42.9 + i, 0, 1.9] — [−43.8 + i, 0, 3.3] | [−44.6 + i, 0, 1.9] — [−43.8 + i, 0, 3.3] | [−45.4 + i, 0, 1.9] — [−46.3 + i, 0, 3.3] | [−47.1 + i, 0, 1.9] — [−46.3 + i, 0, 3.3] | NaN | NaN | NaN | NaN |
| [−42.1 + i, 0, 0.4] — [−42.9 + i, 0, 1.9] | [−43.8 + i, 0, 0.4] — [−42.9 + i, 0, 1.9] | [−43.8 + i, 0, 0.4] — [−44.6 + i, 0, 1.9] | [−45.4 + i, 0, 0.4] — [−44.6 + i, 0, 1.9] | [−44.6 + i, 0, 0.4] — [−45.4 + i, 0, 1.9] | [−46.3 + i, 0, 0.4] — [−45.4 + i, 0, 1.9] | [−46.3 + i, 0, 0.4] — [−47.1 + i, 0, 1.9] | [−47.9 + i, 0, 0.4] — [−47.1 + i, 0, 1.9] |
i = 0, 5, 10, …, 100.
References
- Cosma, C.; Moldovan, C.; Campbell, I.; Cosma, A.; Nicolae, B. Theoretical Analysis And Practical Case Studies Of Powder-Based Additive Manufacturing. Acta Tech. Napoc. 2018, 61, 369–378. [Google Scholar]
- Cosma, C.; Drstvensek, I.; Berce, P.; Prunean, S.; Legutko, S.; Popa, C.; Balc, N. Physical–Mechanical Characteristics and Microstructure of Ti6Al7Nb Lattice Structures Manufactured by Selective Laser Melting. Materials 2020, 13, 4123. [Google Scholar] [CrossRef] [PubMed]
- Perini, M.; Bosetti, P.; Balc, N. Additive manufacturing for repairing: From damage identification and modeling to DLD. Rapid Prototyp. J. 2020, 26, 929–940. [Google Scholar] [CrossRef]
- Beyer, C.; Figueroa, D. Design and Analysis of Lattice Structures for Additive Manufacturing. J. Manuf. Sci. Eng. 2016, 138, 121014. [Google Scholar] [CrossRef]
- Seharing, A.; Azman, A.H.; Abdullah, S. A review on integration of lightweight gradient lattice structures in additive manufacturing parts. Adv. Mech. Eng. 2020, 12, 1687814020916951. [Google Scholar] [CrossRef]
- Savio, G.; Meneghello, R.; Concheri, G. Geometric modeling of lattice structures for additive manufacturing. Rapid Prototyp. J. 2018, 24, 351–360. [Google Scholar] [CrossRef]
- Savio, G.; Meneghello, R.; Concheri, G. Optimization of lattice structures for Additive Manufacturing Technologies. In Proceedings of the Advances on Mechanics, Design Engineering and Manufacturing: Proceedings of the International Joint Conference on Mechanics, Design Engineering & Advanced Manufacturing (JCM 2016), Catania, Italy, 14–16 September 2016; Springer International Publishing: Cham, Switzerland, 2016; pp. 213–222. [Google Scholar]
- Tao, W.; Leu, M.C. Design of lattice structure for additive manufacturing. In Proceedings of the 2016 International Symposium on Flexible Automation (ISFA), Cleveland, OH, USA, 1–3 August 2016; pp. 325–332. [Google Scholar]
- Nguyen, D.S.; Vignat, F. A method to generate lattice structure for Additive Manufacturing. In Proceedings of the 2016 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bali, Indonesia, 4–7 December 2016; pp. 966–970. [Google Scholar]
- Viccica, M.; Galati, M.; Calignano, F.; Iuliano, L. Design, additive manufacturing, and characterisation of a three-dimensional cross-based fractal structure for shock absorption. Thin-Walled Struct. 2022, 181, 110106. [Google Scholar] [CrossRef]
- Zhijia, X.; Qinghui, W.; Jingrong, L. Modeling porous structures with fractal rough topography based on triply periodic minimal surface for additive manufacturing. Rapid Prototyp. J. 2017, 23, 257–272. [Google Scholar]
- Martínez-Magallanes, M.; Cuan-Urquizo, E.; Crespo-Sánchez, S.E.; Valerga, A.P.; Roman-Flores, A.; Ramírez-Cedillo, E.; Treviño-Quintanilla, C.D. Hierarchical and fractal structured materials: Design, additive manufacturing and mechanical properties. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2023, 237, 650–666. [Google Scholar] [CrossRef]
- Zhang, Z.; Scarpa, F.; Bednarcyk, B.A.; Chen, Y. Harnessing fractal cuts to design robust lattice metamaterials for energy dissipation. Addit. Manuf. 2021, 46, 102126. [Google Scholar] [CrossRef]
- Lantada, A.D.; Romero, A.B.; Isasi, A.S.; Bellido, D.G. Design and Performance Assessment of Innovative Eco-Efficient Support Structures for Additive Manufacturing by Photopolymerization. J. Ind. Ecol. 2017, 21 (Suppl. S1), S179–S190. [Google Scholar] [CrossRef]
- Chen, L.Y.; Liang, S.X.; Liu, Y.; Zhang, L.C. Additive manufacturing of metallic lattice structures: Unconstrained design, accurate fabrication, fascinated performances, and challenges. Mater. Sci. Eng. 2021, 146, 100648. [Google Scholar] [CrossRef]
- Stanciu Birlescu, A.; Balc, N. Tree-like fractal structures modeling and their application in 3D printed bones. In Mechanisms and Machine Science; Springer Nature Switzerland: Cham, Switzerland, 2023; pp. 371–378. [Google Scholar]
- Pisla, D.; Tarnita, D.; Tucan, P.; Tohanean, N.; Vaida, C.; Geonea, I.D.; Bogdan, G.; Abrudan, C.; Carbone, G.; Plitea, N. A Parallel Robot with Torque Monitoring for Brachial Monoparesis Rehabilitation Tasks. Appl. Sci. 2021, 11, 9932. [Google Scholar] [CrossRef]
- Plitea, N.; Hesselbach, J.; Pisla, D.; Raatz, A.; Vaida, C.; Wrege, J.; Burisch, A. Innovative development of parallel robots and microrobots. Acta Teh. Napoc. Ser. Appl. Math. Mec. 2006, 49, 5–26. [Google Scholar]
- Möller, T.; Trumbore, B. Fast, Minimum Storage Ray-Triangle Intersection. J. Graph. Tools 1997, 2, 21–28. [Google Scholar] [CrossRef]
- MathWorks—AlphaShape. Available online: https://www.mathworks.com/help/matlab/ref/alphashape.html (accessed on 2 September 2023).
- MathWorks—BoundaryFacets. Available online: https://www.mathworks.com/help/matlab/ref/alphashape.boundaryfacets.html (accessed on 2 September 2023).
- MathWorks—Stlwrite. Available online: https://www.mathworks.com/help/matlab/ref/stlwrite.html (accessed on 2 September 2023).
- OpenSCAD. Available online: https://openscad.org/ (accessed on 2 September 2023).
- MathWorks—MatScad. Available online: https://www.mathworks.com/matlabcentral/fileexchange/99534-matscad (accessed on 2 September 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).