Abstract
Surface topography is an efficient tool for the understanding of physical phenomena, especially if multiscale roughness analysis is performed. However, the observable scale range in a topography measured with 3D optical profilometers is quite limited. Therefore, all scales linked to a physical phenomenon might not be measured, which impedes the correct analysis of the surface. Stitching of 3D topographies, a technique combining elementary topographic maps into a larger one, can be used to increase the scale range for an objective lens. A high resolution over a large field of measurement topography is then generated. A literature review of 3D topography stitching algorithm highlights the stitching procedure, and detailed explanations on in-plane registration algorithms are provided. However, some existing 3D topography stitching algorithms are not sufficiently accurate for the registration of surface, especially at smaller scales. This paper proposes a new reflectance-based multimap 3D stitching algorithm and three of its variants. These algorithm variants are compared to three existing 3D stitching algorithms (geometric, cross-correlation and global optimization of differences) on four test cases, containing measured elementary topographic maps obtained on four surfaces and with four 3D optical profilometers (two focus variation microscopes and two interferometers). Five qualitative and quantitative criteria and indicators are proposed for the comparison of 3D topography stitching algorithms: visual inspection, run time, memory usage, mean repositioning error and stitching error estimator. Lastly, two quantitative indicators and criteria are new indicators proposed in this article. Overall, the new 3D stitching algorithms based on reflectance and multimaps have a lower mean repositioning error and stitching error estimator compared to other existing algorithms. This highlights the relevance of multimap stitching algorithms in the case of 3D topographies. A new decision-helping tool, the stitching gain lift plot (SGL plot), is described for the selection of the best stitching algorithm for a given test case. The SGL plot especially highlights the higher performance of two of the variants of the novel algorithm compared to the three existing 3D stitching algorithms.
1. Introduction
Many physical phenomena are linked to surface roughness, either in manufacturing, such as friction and visual aspects, or in human daily life, such as object gripping and walking. Therefore, roughness study is an excellent analysis tool to better understand physical phenomena. This requires good quality data at the scale at which the physical phenomena occur. Scale can be defined as a segment of spatial wavelengths (or, alternatively, frequencies) [1]. Multiscale analysis is an advanced technique which isolates physical phenomena according to their scale of application. This facilitates the understanding phase of each phenomenon. The observable scale range depends on the profilometry technique used for the measurement of a given morphology, the measurement apparatus and its equipment (objective lens for optical system or probe for scanning probe microscopy, also known as SPM). Especially important, optical profilometers (focus variation microscope, confocal microscope and interferometer) can only measure a fixed field of view at given vertical and lateral resolutions. Their values are linked to the equipped objective lens. Therefore, the scale range is also fixed and often limited. Higher magnification objective lenses measure smaller details [2], but this comes at the price of a smaller field of measurement [3]. It is then crucial for metrologists to estimate, by making assumptions, the most relevant scale range which can capture the morphology linked to the studied physical phenomena, hoping that each phenomenon is included in the scale range. This arbitrary aspect is problematic and the scales of interest are often lacking from the topography or not completely measured.
Stitching tries to overcome this problem of limited scale range of topographic measures using 3D optical profilometers. This is an elementary map-merging technique which uses overlapping regions of two (or more) elementary maps to detect common structures and to perform data alignment, also called registration. Stitching increases the field of measurement while preserving the vertical and lateral resolutions. This then increases the scale range, which facilitates the detection of different physical phenomena during multiscale analysis, as more scales are explored [4,5].
As an example, tribology studies often rely on surface topography as contact is highly dependent on the morphology of first bodies and third body. Also, topography is useful for observation of surface wear, and is a complement to image for the determination of surface components and their respective wear. Lubrification has been widely studied, and surface morphology influences the distribution of lubricants. Tribology of surfaces is complex and the multiscale nature of the involved physical phenomena, interacting with each other’s, is difficult to study in the limited scale range of non-stitched topographies measured with optical profilometers. By increasing the scale range of the measured topography, stitching facilitates the simultaneous observation of physical phenomena involved in tribology, to which surface form, waviness and roughness all contribute. Using the same objective lens ensures that the same measurement gauge is used, which facilitates comparison of surfaces. Stitching also increases the number of pixels on each map (such as hundreds of millions or a few billions of pixels per map), which adds statistical stability to roughness parameters (ISO 25178-2 [6]). Therefore, stitching helps in the determination of the most relevant roughness parameters through statistical analysis [7], useful for the optimization of surface functionality (such as non-exhaustively: wettability, friction, or brightness).
While the principle of stitching is easy to understand, stitching algorithms are actually complex, as the difficulty is in registering overlapping data which are similar but not identical. More precisely, registering two identical overlapping regions is easy: only equality in overlapping regions is to be verified, and searching over multiple translations or rotations is just a question of run-time of the algorithm. Essentially, most algorithms perform perfect stitching of maps with identical overlapping regions. However, in the case of similar but not identical overlapping regions, the goal is to find the transformation to apply on one overlapping region, which results in the least different (or the most similar) regions. In practice, this is the case for every measured map, such as 3D topographies, as noise and uncertainties on the maps to stitch cannot be avoided. This implies that stitching algorithms are complex, as the problem of the registration of measured maps is challenging.
In the case of 3D topography stitching, uncertainties appear at two different levels. First, uncertainties exist at the level of the measurement of each elementary map, due to measurement environment, lighting conditions for optical system, the measurement technology, the noise of the metrological system and the nature of the surface to measure (brightness, slopes, materials). Due to uncertainties, it is then impossible to get two identical measures of a surface. At a second level, acquiring multiple elementary maps for stitching while moving between each elementary map position is also classified as an uncertainty due to XYZ positioning, thermal drifting, modification of lighting conditions or surface contamination during the acquisition process (such as dust deposition). Uncertainties of measurement and of the stitching acquisition process make the stitching procedure difficult and, in some more serious cases, impossible.
Marinello et al. [8] proposed a flowchart of the stitching procedure for 3D topographies. Based on this work, a more detailed and generalized version of this workflow is proposed by the authors of this article in Figure 1. The stitching procedure is composed of two main phases, i.e., the data measurement phase and the stitching algorithm phase, and contains five steps: the data acquisition, the elementary map preprocessing, the in-plane registration (i.e., elementary map alignment for X-translation and Y-translation and Z-rotation), the out-of-plane registration (for Z-translation, X-rotation and Y-rotation), and the blending (the merging step that aims at hiding visual defects, such as seams, in the resulting overlapping regions of the stitched map). Note that in-plane registration and out-of-plane registration can be performed either simultaneously or consecutively, but both are required for the stitching of 3D topographies.
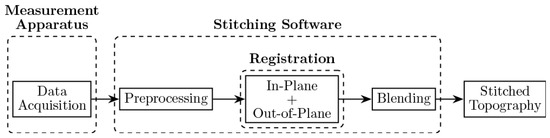
Figure 1.
Generalized stitching procedure flowchart.
Five categories exist for in-plane registration:
- Manual: this can be performed by the user, using either transparency, region pointing or colocalization of overlapping maps. Most manual techniques rely on a visual inspection of all elementary maps, which is a slow process, highly dependent on the user, and prone to registration error. On the other hand, automatic stitching algorithms were historically created for images before topography. Many techniques were first developed for image stitching, also called panorama, and then adapted for topography, with various success rates. Automatic stitching is much faster than manual stitching: Montgomery et al. [9] explained that the manual stitching of a pair of maps can reach 30 min, while the automatic stitching would only take a few seconds. Thus, larger stitching can be performed in a shorter period of time with automatic stitching.
- Geometric: this type of stitching uses metadata, such as absolute or relative positions of elementary maps, to perform the registration [10,11]. This technique is fast, but its precision depends on the accuracy and robustness of the profilometer. Geometric stitching is the most used in commercial profilometers. It can also be used for prepositioning before finer registration with a more accurate technique [12].
- Fiducialization: these algorithms consist in marking a surface to perform registration on the markers measured in profilometry [13,14]. Markers on the surface can either be all unique or form a unique pattern all over the surface, but a unique solution must be found by the registration step. Markers can be generated, such as with Focused Ion Beam (FIB) [15], or already on the surface, such as structures in microfluidics [16] and semi-conductors. This technique can be useful for stitching small-scale topographies by adding distinctive features on the surface. This comes at the cost of surface integrity, and a need for post-processing to remove markers before analyzing the original surface.
- Global optimization of differences: this is generally described as a minimization of differences between overlapping regions of elementary maps, in the least-square method meaning. Chen et al. compute the correct displacements along x, y and z axes to apply on elementary maps in order to perform in-plane registration [17]. Global optimization of differences is more accurate than geometric stitching, but is more noise-sensitive, such as in flat or small-scale surfaces. Global optimization algorithms can be used for registration. Simulated annealing has been explained by van Laarhoven and Aarts [18] using an analogy with the annealing process of solids. A faster version of the simulated annealing optimization algorithm was presented by Szu and Hartley [19]. Simulated annealing has been tested by Kirkpatrick et al. [20] on various combinatory problems. Lensch et al. [21] proposed a silhouette-based registration and stitching algorithm using simulation annealing optimization. On the other hand, a genetic algorithm can also be used. Genetic algorithms have been explained by Holland [22], Forest [23], Davis [24] and Gendreau and Potvin [25] as algorithms inspired by the natural selection of genes, using generation of an initial population of solutions to test, selection of best solutions at each iteration, and merging and mutation of parameters to find an optimal solution to a problem. Local search with genetic algorithms has been detailed by Mühlenbein [26]. The use of genetic algorithms for image registration and stitching appeared in the works of Xu and Sun [27], Yetis et al. [28], Wang and Xu [29] and Prejmerean [30]. Another global optimization algorithm, called particle swarm algorithm, is presented by Kennedy and Eberhart [31], Shi and Eberhart [32], Bratton and Kennedy [33] (in an attempt to define a standard for particle swarm algorithm). An overview of the particle swarm algorithm and its variants was written by Poli et al. [34]. Another variant, called the radius particle swarm optimization, was introduced by Anantathanavit and Munlin [35]. A 3D surface stitching algorithm based on particle swarm optimization was used by Zhu et al. [36] for the stitching of cylindrical surfaces. Combining prepositioning and global optimization of differences reduces errors during registration and reduces run-time of stitching as less solutions need to be explored before finding the optimal solution for the registration.
- Computer vision-based: this is historically linked to image processing before surface stitching. The goal of these algorithms is to find the maximum number of similarities between two elementary maps. This category is divided into two subsets: direct methods and feature detection methods [37]. Direct methods use all pixels of overlapping regions to perform in-plane registration. Cross-correlation-based registration is an example of a direct method [12]. When the maximum of cross-correlation is found when moving overlapping maps, the correct displacement to apply to each map is determined for the registration [8]. On the other hand, feature detection methods first extract points-of-interests on a map, before performing the in-plane registration on such points, also called features. Many descriptors (algorithms to find features) exist. The first major one, developed by Lowe [38], is the SIFT (Scale-Invariant Feature Transform) descriptor [39,40,41]. This descriptor was originally used for object recognition, but its usefulness for automatic image stitching came soon after [42]. Many other feature descriptors were developed with either increased precision or robustness, or shorter run time for the extraction, such as SURF [43,44], U-SURF [45], Harris Corner [46], BRISK [47], FAST [48], MSER [49,50], Min Eigen [51], ORB [52] or KAZE [53]. Table 1 provides more details about each descriptor. Tareen and Saleem [54] compare feature descriptors (SIFT, SURF, KAZE, AKAZE (a variant of KAZE), ORB and BRISK) and their performance for image registration, such as scale invariability, feature extraction run time and registration accuracy. A RANSAC (RANdom SAmple Consensus) algorithm [41,55] is used in feature detection to extract the most relevant features before performing the registration. Computer vision-based stitching algorithms can be very precise but also costly in time. While feature detection method aims at reducing run time by selecting a subset of interesting features for the registration, the use of these is viable with sufficiently large maps to observe a shorter run time compared to direct methods if features can be extracted, such as for surface defects or large structures. However, computer vision-based algorithms, and especially feature detection algorithms, cannot find features of high quality, i.e., of high gradient, or might find too many features of low quality, which behave in the same way as noise for the registration algorithm.
 Table 1. Description of feature descriptors.
Table 1. Description of feature descriptors.
The most common data classes are metadata and raw topographies, but a more promising data class is multimap data, i.e., a set of multiple layers with their own information about a surface sample (topography, image, quality map, etc.). A multimap stitching algorithm can then use multiple layers during the registration to improve the alignment precision and to reduce the vertical drift. This kind of stitching algorithm is notably used in the focus variation microscopes developed by Bruker AliconaTM (Raaba, Austria). Alicona’s stitching strategy is then used to compute in-plane registration with high quality images and to calculate the out-of-plane registration with topographies, as images do not contain out-of-plane information (Z-translation and XY-rotations).
A new stitching algorithm family, the rising sun stitching algorithm, is here proposed with three algorithm variants (naïve reflectance, exhaustive enumeration reflectance and two-step reflectance). The rising sun stitching algorithm and its variants are based on reflectance and multimap. Indeed, the new proposed algorithm uses the 2D reflectance maps generated on the elementary topographic maps to improve the 3D alignment of these elementary maps. These new algorithms are compared to in-plane stitching algorithms described above. As manual stitching is too user-dependent and fiducialization does not preserve surface integrity, only geometric, global optimization of differences and computer vision-based (cross-correlation) in-plane stitching algorithms will be used as references for the comparison of stitching algorithms.
2. Materials and Methods
2.1. Topographical Measurements
To evaluate the relevancy of the three variants of the new stitching algorithm, stitching tests are performed on four different surfaces. For each test, elementary maps are measured with a 3D optical profilometer, interferometer or focus variation microscope.
Table 2 details the measurement configuration for each stitching test. The four stitching tests are designed to test each stitching algorithm in various situations that can be encountered by surface metrologists and roughness researchers:

Table 2.
Measurement configurations for stitching test cases.
- A.
- Polymer rod abraded with FEPA grade 80 SiC abrasive paper: the aim is to verify that each tested algorithm can perform good quality stitching on a simple configuration. Succeeding in this test means that the test stitching algorithm has no major flaw, can handle non-measured points and can process elementary topographic maps with measurement uncertainties.
- B.
- Mirror-polished copper rod with indentations, dust and hair: a mirror-polished copper rod with indentations, dust and hair. As the surface is an Independent Multi-Physics (IMP) surface because of the presence of polishing, indentation, hair adhesion and dust adhesion, this is suitable to evaluate the flexibility of a stitching algorithm and its ability to perform a correct registration with various conditions within the same stitching. Moreover, two roughness scales (macroscopic and microscopic) are present and stitching algorithms should be able to register both at the same time.
- C.
- Arm skin replica: this test case evaluates the ability of a stitch algorithm to perform registration on macroscopic morphological structures. Moreover, as the polymer used for replication is more sensitive to thermal drift, this increases the difficulty of stitching as uncertainties might be amplified.
- D.
- Titanium alloy TA6V rod abraded with FEPA grade 80 SiC abrasive paper: as this surface contains a fractal pattern, the test evaluates the stitching algorithm ability to stitch a fractal pattern for many elementary maps, and to register microscopic morphological structures.
The tested stitching algorithms should be able to perform correctly with maps containing non-measured points and measurement uncertainties (i.e., overlapping regions are almost identical but not identical). These two points are what makes stitching difficult, though they are present in each measured topography.
2.2. New Reflectance-Based Stitching Algorithm
The stitching algorithms aim to detect a high gradient but they are statistically less present in topographies than in images. A data type fulfilling the high gradient condition is a reflectance map, which is used in the new developed stitching algorithm. In this new algorithm, reflectance maps are obtained by simulating the reflectance on the surface topographies measured by the profilometers. The reflectance simulation is based on Phong’s model [56]. Figure 2 shows a scheme representing the principle of reflectance: a light source, located at a (θ, ϕ) position, is directed towards a surface and a camera receives the light reflected by the surface.
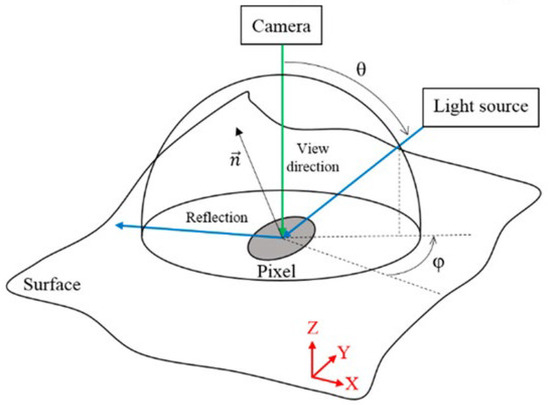
Figure 2.
Scheme of reflectance principle—extracted from [57].
The lighting and viewing angles influence the reflectance map. By lighting the surface at a high θ angle, i.e., at a grazing angle, each peak is half-lighted on a side and half shaded on the other. This creates a high gradient region in the interface between lighted and shaded sides of each peak, as seen in the reflectance map shown in Figure 3. Based on this observation, the reflectance-based stitching algorithm was named ‘rising sun stitching algorithm’, as most objects (for example, buildings) are lighted on only one side at sunrise. As topography is composed of multiple peaks of various scales, this light and dark interface pattern is always present when computing the reflectance map. Moreover, numerical gradient on reflectance maps has a lower sensitivity to discretization error compared to numerical gradient on topographic map [57], as most computer vision-based 3D topography stitching algorithms do during registration. Reflectance maps are then suited for computer vision-based registration algorithms.

Figure 3.
Example of blasted TA6V surface topography (a) and an associated reflectance map (b).
However, as reflectance maps do not contain the third spatial component (i.e., z-axis component), they are not sufficient for 3D topography stitching. Therefore, the idea is to use a multimap registration algorithm: reflectance maps, computed from the elementary topographies to stitch, are used for the in-plane registration (with cross-correlation on reflectance maps), while the original topographic datasets make the out-of-plane registration possible. Then, the question is the selection of the most suited lighting and viewing angles for optimizing the stitching.
2.2.1. Naive Reflectance Algorithm
The first approach of selection of lighting angles is a naive approach: lighting angles are arbitrary selected, e.g., ϕ = 40°. Reflectance maps are calculated for these lighting angles, but no optimization of the lighting angles occurs. This approach can reduce the quality of in-plane registration as the overlapping regions might not be lighted adequately, although computations are fast. A more interesting approach is an optimization process aiming at finding the best lighting and viewing angles so that the reflectance map contains as many details and contrast as possible.
2.2.2. Exhaustive Enumeration Reflectance Algorithm
To simplify and accelerate the optimization process, a hypothesis is made on Phong’s model. In this model, the best contrast is obtained if the θ angle between the viewing and the lighting positions is equal to 90°. Moreover, the best contrast is obtained if the lighting angle is at a grazing angle to the surface and this second hypothesis is assumed for the optimization process. Those simplifications are incorporated by setting the viewing angle at the surface normal to the surface (θ = 0°) and the lighting source at a grazing angle (θ = 90°).
Therefore, the contrast optimization of the reflectance map focuses on one variable considering the previous assumptions: the lighting in-plane angle (i.e., rotation around Z-axis). The optimization consists in maximizing the contrast of the reflectance map. The autocovariance can be used for this purpose and the contrast level is computed as the maximum value of the autocovariance matrix (Equation (1)). This represents the objective function in this optimization problem.
where A(θ, ϕ) is the reflectance map computed from a topography for given lighting angles θ and ϕ (the variables in the contrast optimization process) and A(θ, ϕ)T is the transposed matrix of A(θ, ϕ).
A simple approach is to compute the objective function for multiple angles, for example, the ϕ angles from 0° to 359°. Figure 4 sums up the optimization process of the reflectance in-plane lighting angle for an indented surface. The best lighting angle is determined when the value of the maximum of the autocovariance matrix is maximized, i.e., for a ϕ angle of 274°.
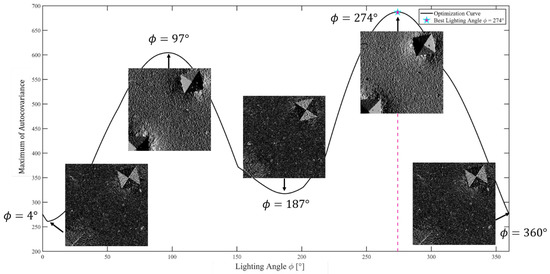
Figure 4.
Optimization curve of the reflectance lighting angle ϕ obtained with the exhaustive enumeration reflectance algorithm for an indented surface, with the resulting reflectance maps (θlight = 90°).
This variant of the rising sun algorithm is a simple method, but is lacking in speed. In the case of the lighting angle optimization, which contains only one variable, the exhaustive enumeration method is sufficient. Yet, it is possible to obtain a more efficient algorithm, which is necessary for a more intensive use, such as in the stitching procedure.
2.2.3. Two-Step Reflectance Algorithm
The study of the contrast optimization curve of the reflectance map in the optimization process, by plotting the maximum of the autocovariance matrix as a function of the light angle, highlights a pseudo-periodicity of 180°. In fact, this pseudo-periodicity is explained by the fact that a symmetry (or a pseudo-symmetry) is found for a given lighting angle, modulo 180°. The main source of pseudo-symmetry is the topography itself. Topographies with different spatial distribution of features, such as indentations, grooves and defects, produce different reflectance maps where the best lighting angles for maximization of contrast differ. On the other hand, the pseudo-symmetry partially results from the distance of large features of the surface, such as defects, from the lighting source. The shorter this distance, the more structures are in the shadow of these large features, especially for lighting at grazing angle.
Moreover, as measured surfaces are never perfectly symmetric (due to measurement errors), contrary to simulated surfaces, their pseudo-symmetry influences the value of maximum contrast for a given lighting angle ϕ, and creates a pseudo-periodicity in the contrast optimization curve of the reflectance map. Fortunately, this pseudo-periodicity makes the solution of the optimization process unique, i.e., a unique in-plane lighting angle provides the best contrast.
By considering this pseudo-periodicity, a smarter optimization algorithm can be used. The idea is to proceed in two steps. The first is a coarse step, which aims to find a rough estimate of the best lighting ϕ angle inside a range of 0° to 180° (half the range of the previous algorithm) by evaluating the solution at every 10°. Then, a more precise step evaluates solutions in the neighborhood of the coarse solution and at 180° of this coarse solution. The solution can be evaluated every 1° for more precision. Potentially, this process can be repeated for even more precision, such as every 0.1° or 0.01°, depending on the precision required by the user for a reasonable algorithm run time. Figure 5 presents the optimized reflectance map obtained after the two-step optimization algorithm (Figure 5a), along with the optimization curve for the determination of the best in-plane lighting angle (Figure 5b). Once again, an in-plane lighting angle of 274° provides the best contrast, which results in the same exact reflectance map as the exhaustive enumeration optimization.
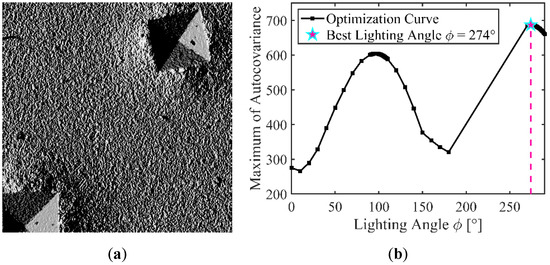
Figure 5.
Optimized reflectance map of an indented surface (a) and optimization curve (b), where each square is a tested lighting angle ϕ solution, obtained with the two-step reflectance optimization (θlight = 90°).
This strategy evaluates a lot fewer solutions compared to the exhaustive enumeration method, which results in a faster algorithm for an equivalent or greater precision. A speed comparison between the exhaustive enumeration optimization and the two-step optimization is provided in Table 3. Using the two-step optimization algorithm results in a significant gain of speed, roughly equal to six. A flowchart summing up the three variants of the rising sun 3D topography stitching algorithm based on reflectance and multimap is provided in Figure 6.

Table 3.
Run time comparison between exhaustive enumeration and two-step reflectance algorithms for two types of topography.
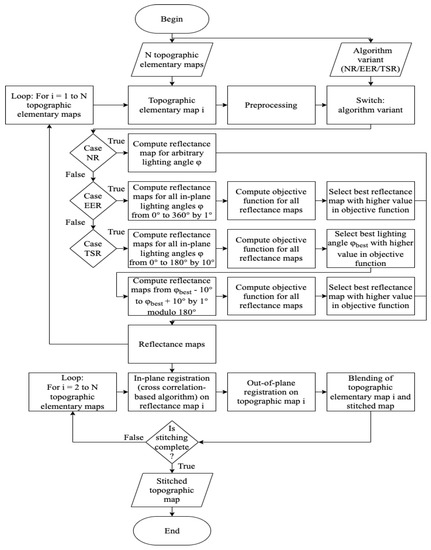
Figure 6.
Flowchart of the three variants of the rising sun 3D topography stitching algorithm: the naive reflectance (NR), the exhaustive enumeration reflectance (EER) and the two-step reflectance (TSR).
All reflectance-based stitching algorithms are contained in MorphoStitch, an in-house stitching software developed by one of the authors of this article, based on Matlab®. Furthermore, in MorphoStitch, elementary maps are processed in a domino fashion and the current elementary map is compared to the already placed and stitched elementary maps. Therefore, there is a dependency on the stitching order (which starts at the top-left of the stitching grid and ends at the bottom-right of the stitching grid, by processing elementary maps on the same line from left to right).
2.3. Description of the Evaluation Criteria for Stitching Algorithms
Five criteria are used to evaluate each stitching algorithm in the four stitching test cases: visual inspection (qualitative criterion), stitching algorithm run time, stitching algorithm memory usage, mean repositioning error and stitching quality estimator (quantitative criteria).
Only a few methods exist for evaluating stitching quality: mean height difference (or root mean square—RMS) between a known topography and a stitched version of this topography [17,58,59], or a size comparison along x and y axes between a stitched topography size and the true size of a known object [8,60]. However, these methods have two major drawbacks: they required a reference surface of known dimensions (that sometimes is not available in day-to-day usage of stitching) and they do not take into account measurement apparatus uncertainties, especially along x and y axes. Our method solves these two problems. It only uses the stitched dataset and registration information obtained during the stitching procedure, and takes into account measurement apparatus and its uncertainties. However, this method cannot determine the source of uncertainties, nor give a quantitative value for each uncertainty type.
2.3.1. Visual Inspection (Qualitative Criterion)
First, a visual inspection of the topography is performed to check if no major defects appear due to stitching, such as seams, holes, stitching chain reaction failure or major unexpected deformations of topographic maps. While this criterion is qualitative, this test is naturally performed by any stitching user, to determine if stitching has failed or not. However, a qualitative criterion is not enough for a correct assessment of stitching algorithms; therefore, four quantitative criteria are added.
2.3.2. Stitching Run Time and Memory Usage (Quantitative Criteria)
Two quantitative criteria are common for the assessment of any software: run time and RAM memory usage. These two pieces of information are important, especially for large stitching, as a high run time and memory usage would limit the stitching maximum size since these resources are limited. Next, stitching quality is evaluated through two other criteria: mean repositioning error and stitching quality estimator. These values are proposed by the authors of this paper. Their calculation is based on the hypothesis of the linearity of the accumulated repositioning errors in stitching.
2.3.3. Mean Repositioning Error (Quantitative Indicator)
For each local stitching, the displacements to apply to each elementary map are determined in the registration steps. Offsets can be calculated as the difference between these displacements (along x, y and z axes) and theoretical displacements on the stitching grid, which is defined by the measurement apparatus before the acquisition of elementary maps, depending on user inputs (such as overlap percentage, stitched topography desired dimensions, objective lens). For in-plane registration, offsets and can then be computed. Error for each local stitching can then be computed with Equation (2).
The hypothesis of linearity of cumulated errors in stitching is assumed, as statistically accumulated errors should be linear, given that measurement apparatuses have bounded uncertainties in displacement errors (also known as tolerance). In this hypothesis, it is then possible to assess stitching quality using a linear regression to compute how linear the error accumulation of each local stitching is. Sources of non-linearity are then mostly due to bad registration, sometimes resulting in stitching chain reaction failure, i.e., a bad local registration, which impedes the next local registration, makes the following ones increasingly difficult. Figure 7 shows the cumulative repositioning errors of the same set of elementary maps stitched with two different stitching algorithms: one that has failed (Figure 7a) and one that has successfully stitched the surface (Figure 7b). Linearity of the cumulative repositioning error is lower for the stitching algorithms that have failed registration of elementary maps. The numbers of the failed local stitching can be detected as the cumulated repositioning errors are locally higher, creating sharp edges on the cumulative repositioning error plot. The slope of the accumulated errors is then the mean repositioning error, which is used for the evaluation of the stitching quality in this paper.
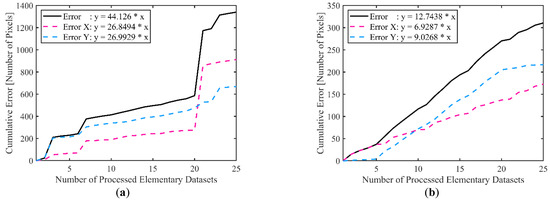
Figure 7.
Cumulative repositioning errors with two different stitching algorithms: one has failed (a) and the other has succeeded in stitching (b) the elementary maps.
2.3.4. Stitching Error Estimator (Quantitative Criterion)
The coefficient of determination R2 is an indicator of linearity, and the p-value indicates if linearity is obtained by chance or not. R2 would drop and p-value would rise if stitching performed badly or failed. As p-value is dependent on the number of elementary maps to stitch and is lower if the stitching quality is good, a derived indicator was created, the stitching error estimator SEE (Equation (3)).
where p is the p-value and N is the number of elementary maps to stitch. Dividing by N limits the dependence on the number of elementary maps in the calculation of the p-value of the linear regression. SEE is then lower when the stitching quality is higher and would increase if stitching has failed or has generated defects on the stitched surface. For correct result interpretation and comparison of 3D topography stitching algorithms, the mean repositioning error and the stitching error estimator SEE should be coupled. As the mean repositioning error increases (i.e., the slope of the cumulated repositioning error), the p-value (and by extension, the stitching error estimator SEE) should be higher for a given algorithm compared to other algorithms to bring relevance to the result. Note that computing the mean repositioning error and the stitching error estimator SEE is not applicable for geometric stitching algorithms, as only the theoretical displacements (linked to the stitching grid) are applied to elementary maps, and not a finer registration comparing overlapping regions of elementary topographic maps.
These five criteria and indicator (visual inspection, run time, memory usage, mean repositioning error and stitching error estimator SEE) can then be compared for each tested stitching algorithm to choose the best stitching algorithm to apply to a given test case.
3. Results
All test cases (A, B, C and D) were stitched using six stitching algorithms: geometric (GEO), cross-correlation (CC), global optimization of differences based on genetic algorithm (GOD), naive reflectance (NR), exhaustive enumeration reflectance (EER) and two-step reflectance (TSR). In the following figures, existing algorithms are presented in grey while new rising sun algorithm variants are presented in blue.
3.1. Test Case A—Polymer Abrasion
Stitching of four elementary topographic maps (test case A) was performed successfully with each algorithm and no stitching defects, such as holes or seams, can be observed through visual inspection (Figure 8). Height histograms are similar for all stitching algorithms.
Figure 8.
Three-dimensional view of the stitched topography in test case A. Stitching size: 2 × 2.
Figure 9 compares the six stitching algorithms based on the four quantitative criteria. Run time is higher for TSR algorithm, and even more for EER algorithm. Other stitching methods are close of each other’s. Memory usage is similar for GEO, CC and GOD algorithms, and higher for TSR, NR and EER, from lower to higher. GOD algorithm has an increased mean repositioning error and a lower stitching error estimator compared to CC, NR, EER and TSR algorithms.
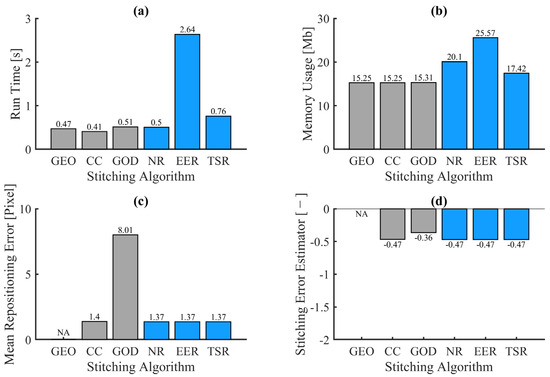
Figure 9.
Bar charts of the quantitative criteria for test case A: run time (a), memory usage (b), mean repositioning error (c) and stitching error estimator (d). NA = Non Applicable.
3.2. Test Case B—IMP Mirror-Polished Copper
The stitching result of each tested stitching algorithm is presented in Figure 10. A first-order form was removed to better observe small scale roughness in the stitching topographies. The CC stitching algorithm has failed, as a chain reaction occurred with local stitching. Other algorithms offer satisfactory results, but attenuated seams are slightly visible with the GEO and GOD algorithms, especially for the central elementary map. In addition, the indentation in one of the overlapping regions is deformed at the bottom edge. Best visual aspect, with no seams or deformed indentations, is obtained with the reflectance-based multimap stitching algorithm, the rising sun algorithm, proposed in this article (NR, EER and TSR).
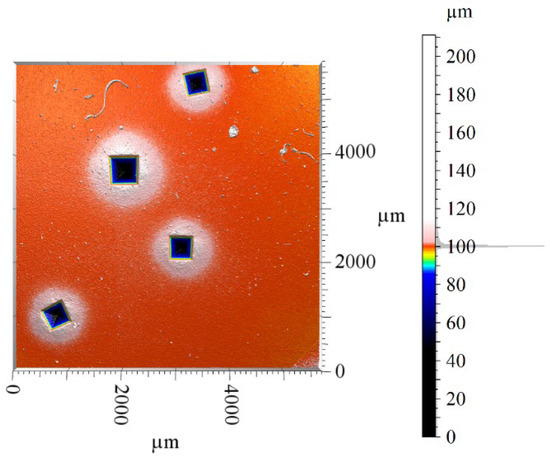
Figure 10.
Three-dimensional view of the stitched topography in test case B. Stitching size: 3 × 3.
Quantitative criteria for test case B are grouped in Figure 11. The GOD algorithm was the fastest, while the EER algorithm was the slowest. Other algorithms are in the same order of amplitude for run time. The CC algorithm uses more memory, followed by NR, and then by the four others, which are comparable. The chain reaction failure of CC algorithm is highlighted by a high mean repositioning error and a lowest stitching quality. Best quality is obtained using reflectance-based multimap stitching algorithms (NR, EER and TSR). GOD provides in-between mean repositioning error and stitching quality.
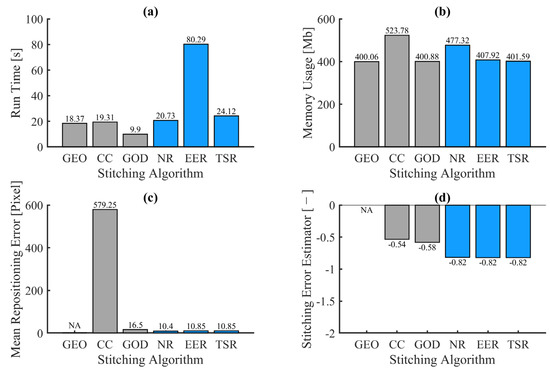
Figure 11.
Bar charts of the quantitative criteria for test case B: run time (a), memory usage (b), mean repositioning error (c) and stitching error estimator (d). NA = Not applicable.
3.3. Test Case C—Arm Skin Replica
The stitched topographic maps of test case C have been gathered in Figure 12, with inversed z-axis as a replica being measured. Once again, the CC algorithm has not succeeded in stitching the arm skin replica, a stitching chain reaction failure. Other algorithms provide a satisfactory visual aspect. Height amplitude is similar for all successfully stitched topographies.
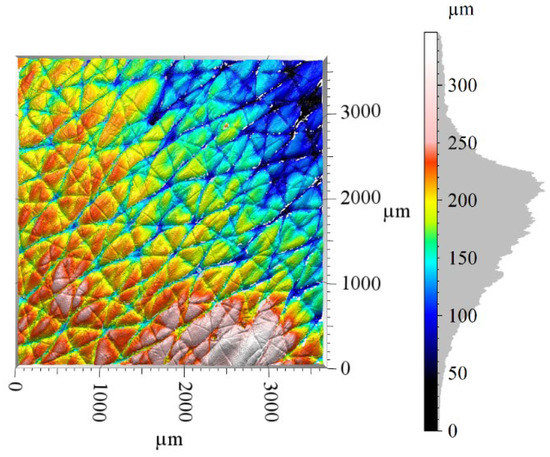
Figure 12.
Three-dimensional view of the stitched topography in test case C. Stitching size: 5 × 5.
Figure 13 shows the quantitative criteria of test case C. First, run time is lower for CC, despite a stitching chain reaction failure, followed in order by the GEO, GOD, NR, TSR and EER algorithms. Note that the latter algorithm is much slower than others. Memory usage is similar for all tested algorithms, although slightly higher for CC and NR. Regarding the quality of the stitching, the reflectance-based stitching algorithms (NR, EER and TSR) are better, with lower mean repositioning error and higher stitching error estimator, followed by the GOD and CC algorithms.
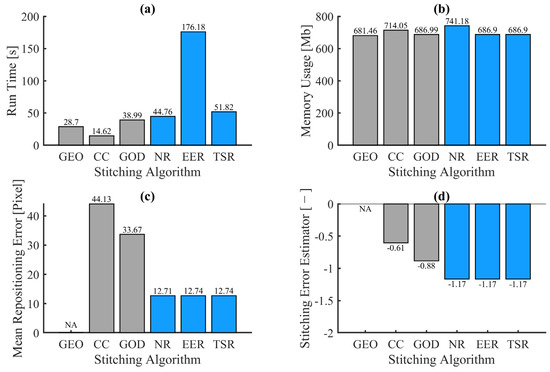
Figure 13.
Bar charts of the quantitative criteria for test case C: run time (a), memory usage (b), mean repositioning error (c) and stitching error estimator (d). NA = Not Applicable.
3.4. Test Case D—Titanium Alloy Abrasion
Figure 14 presents the topographic results for the test case D. A stitching chain reaction failure occurred with the CC stitching algorithm, while the right side of the topography stitched with GOD algorithm is notched, which is abnormal and a sign of local deformations within the surface, hidden by the blending step. All other tested stitching algorithms performed successfully.
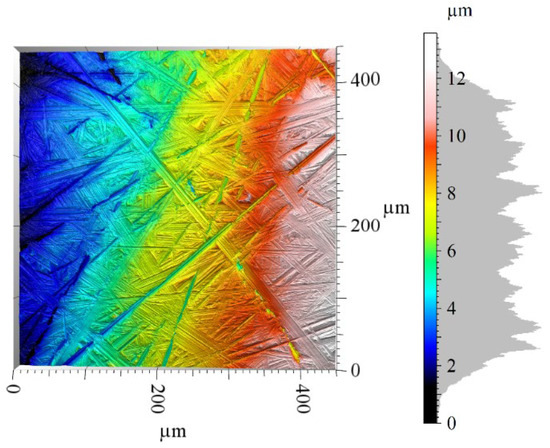
Figure 14.
Three-dimensional view of the stitched topography in test case D. Stitching size: 10 × 13.
Run time, memory usage, mean repositioning error and stitching error estimator for test case D are presented in Figure 15. The CC and GEO algorithms are the fastest, followed by a group composed of NR, GOD and TSR algorithms. Finally, EER can be found far behind. All algorithms have similar memory usage. However, differences can be observed for mean repositioning error, with the lowest values for observed with the reflectance-based multimap stitching algorithm. The CC algorithm has a higher value of mean repositioning error, which is coherent with the stitching chain reaction failure. Lastly, the GOD algorithm has the highest mean repositioning error from all the tested stitching algorithms on test case D. This is a sign of large displacements of elementary maps for registration, but this is hidden by blending when using visual inspection. The reflectance-based multimap algorithms (NR, EER and TSR) proposed in this paper show the best stitching quality, while the CC algorithm has a lower value, which is even lower for the GOD algorithm.
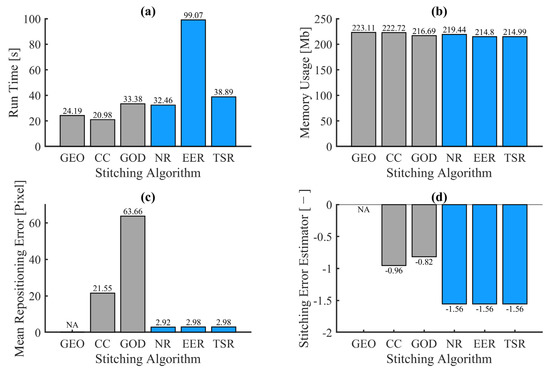
Figure 15.
Bar charts of the quantitative criteria for test case D: run time (a), memory usage (b), mean repositioning error (c) and stitching error estimator (d). NA = Not Applicable.
3.5. Comparison between Test Cases
For comparison of the stitching algorithms between each test case, a standardization using the Z-score method (Equation (4)) was applied on mean repositioning error and stitching error estimator SEE for each test case.
where z is the standardized value using Z-score method, x is the value to standardize, µ is the mean of the population and σ is the standard deviation of the population. This method brings all standardized data to a mean µ of 0 and to a standard deviation σ of 1. Figure 16 shows the standardized values of the mean repositioning error (Figure 16a) and stitching error estimator SEE (Figure 16b) for each test case.
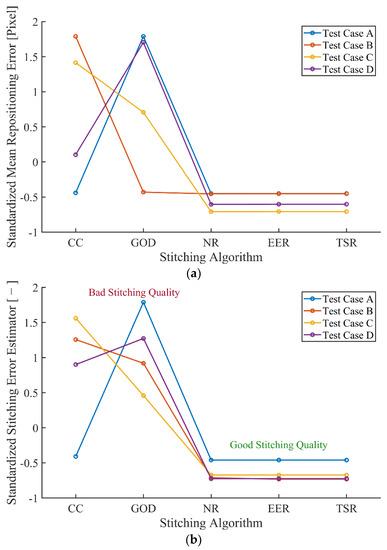
Figure 16.
Standardized mean repositioning error (a) and stitching error estimator (b) for each test case.
Successful stitching on each test case is then detectable with a low value of standardized mean repositioning error and low value of SEE. A better stitching quality is obtained with the novel 3D topography stitching algorithms (NR, EER and TSR), which highlights the relevance of multimap stitching based on reflectance maps, especially if the contrast of the reflectance map is optimized.
4. Discussion
The first test case (A) is important to verify that each stitching algorithm has no major flaws and can stitch simple cases, including non-measured points and height measurement uncertainties. All tested stitching algorithms succeeded in this test case. Other test cases (B, C and D) are increasingly difficult, either due to larger stitching size, various roughness scales, measurement conditions (measurement apparatus, technologies, objective lens, replication) or a combination of the previous points. In this regard, the CC stitching algorithm failed on test cases B, C and D. This is due to its high sensitivity for measurement height uncertainties and noise. In a test case with only simulated surface with no measurement height uncertainties and noise, it is likely that the CC algorithm would perform successfully, but this situation is never found in practice with genuine measurements.
The GOD stitching algorithm provides satisfactory stitched topographies in visual inspection. Only small defects can be observed, and roughness parameters from ISO standards 25178-2 [6] would not be significantly influenced by these defects. However, from a metrological point-of-view, surface fidelity is poor as local deformations, hidden by the blending step, are present with the GOD algorithm. This is confirmed by the mean repositioning error and the stitching error estimator, even though local deformations are difficult to observe by visual inspection.
Only GEO and the proposed reflectance-based multimap stitching algorithms performed the stitching of all test cases successfully. If only visual inspection, run time and memory usage are considered (other quantitative criteria cannot be calculated for geometric algorithm as explained in the Materials and Methods section), stitching users would a priori prefer geometric stitching algorithm. In fact, most 3D profilometers use geometric stitching algorithm as it can produce an acceptable stitching result in most cases, although it is not the optimal stitching result. However, geometric stitching is dependent on the accuracy, the precision and the robustness of the measurement apparatus, contrary to other stitching algorithms, which compare overlapping regions to perform a finer (and more optimal) registration. All topography measurements in this article were performed with high-end 3D profilometers, which are more accurate, precise and robust than most 3D profilometers. That is why geometric stitching performed so well in all test cases. However, it is likely that geometric stitching would fail for lower-end 3D profilometers. Choosing geometric stitching is then largely based on the quality of the 3D profilometers available to the user.
If overall qualitative and quantitative criteria are considered, reflectance-based multimap algorithms (NR, EER and TSR) should be selected. The mean repositioning error and stitching quality are similar for all the rising sun stitching algorithm variants. EER and TSR provide the same stitched topography, as the TSR algorithm should find the same lighting angle ϕ just as the EER algorithm would but faster, as per its design. TSR should then be preferred over EER. Finally, the question is whether to use the NR algorithm or the TSR algorithm. The TSR stitching algorithm optimizes the reflectance of the elementary map to stitch; however, in some cases, optimization cannot converge into a unique solution. These pathologic cases are either isotropic surfaces or periodic surfaces without measurement uncertainties. In these pathologic cases, which happen mostly with simulated surfaces, it is better to arbitrary select a lighting angle ϕ, such as in the NR algorithm. Otherwise, the TSR stitching algorithm should be preferred over the NR algorithm, as the optimization of the reflectance map, adapted to any elementary map, facilitates the in-plane registration, which in turn can be more precise, especially for the registration of the smaller roughness scales.
An optimization problem can be formulated to find the best algorithm for each test case. It is a multi-objective optimization problem, respecting the following sub-objectives:
- Minimization of run time;
- Minimization of memory usage;
- Minimization of mean repositioning error;
- Minimization of stitching error estimator.
A novel plot is proposed to compare stitching algorithms and to solve this multi-objective optimization problem graphically: the stitching gain lift plot or, shorter, the SGL plot. Memory usage is plotted as a function of the stitching run time. The size of each marker is inversely proportional to the mean repositioning error, so that a bigger marker indicates a lower mean repositioning error. The marker color depends on the value of the stitching error estimator: it is green if the stitching error estimator value is the best, red if the value is the lowest, and black if the stitching has failed. With the SGL plot, the best stitching algorithm to use for each test case would be closer to 0 in run time and memory usage, has a larger marker size and, preferably, a green color. The SGL plot is a simple tool allowing users to select the best stitching algorithm for a given elementary topographic dataset. In addition, all results from the five criteria for each test case are contained in this single plot, making it a good sum up plot for the comparison of 3D topography stitching. Figure 17 shows the SGL plot for each test case, and the stitching algorithm is indicated by the marker shape.
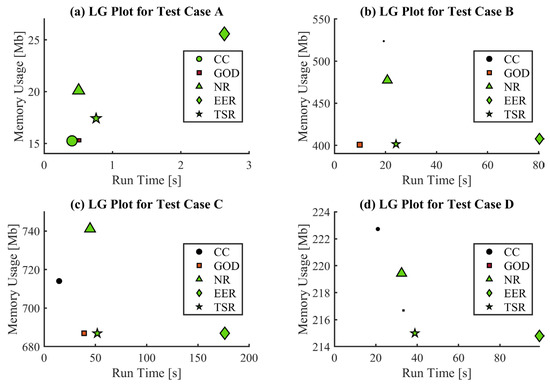
Figure 17.
SGL plots for each test case.
The qualitative and quantitative results show the interest in the use of the novel reflectance-based multimap algorithm, the rising sun algorithm, and its variants (NR, EER and TSR) for the stitching of 3D topography, for all scales and for any 3D optical profilometers, including large stitching. This could be especially useful for the stitching of microscopic or sub-microscopic elementary topographic maps, which are still a challenge for existing 3D topography stitching algorithms to this day.
5. Conclusions
Stitching makes the acquisition of high resolution over a large field of view 3D topography possible, which is helpful for multiscale analysis and to understand physical phenomena. However, stitching algorithms in 3D topography, especially of 3D optical profilometers, are either too sensitive to noise or too coarse. This paper proposes a novel reflectance-based multimap stitching algorithm, the rising sun stitching algorithm, in the form of three variants: the naïve reflectance, the exhaustive enumeration reflectance and the two-step reflectance stitching algorithms. These three variants were compared to three existing 3D topography stitching algorithms (geometric, cross-correlation-based and global optimization of differences) with the help of four test cases, composed of measured topographic elementary maps, acquired with four 3D profilometers (two focus variation microscopes from AliconaTM, an interferometer from BrukerTM and an interferometer from ZygoTM). Five criteria are used for comparison of stitching algorithms: visual inspection (qualitative criterion), run time, memory usage, mean repositioning error and stitching error estimator SEE (four quantitative criteria and indicator). Results show that the rising sun stitching algorithm and its variants provide the best result for all test cases, especially if stitching quality is important. A decision-helping tool, the stitching gain lift plot, was then proposed to select the best stitching algorithm for a given set of elementary topographic maps: this helps users to graphically solve this optimization problem and sums up all results from the five criteria for stitching comparison. Overall, the two-step reflectance (TSR) stitching algorithm should be preferred except in the case of pathologic morphology (perfectly isotropic surface, periodic surface without noise), in which case the naive reflectance (NR) stitching algorithm should be chosen.
Author Contributions
Conceptualization, J.L.; formal analysis, J.L. and M.B.; investigation, J.L.; methodology, J.L. and R.G.; software, R.G.; supervision, M.B.; validation, J.L., R.G. and M.B.; visualization, J.L. and R.G.; writing—original draft preparation, J.L. and R.G.; writing—review and editing, J.L., R.G. and M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the ELSAT2020 project, co-financed by the European Union with the European Regional Development Fund, the French state and the Hauts-de-France region.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank the MorphoMeca platform for the use of the measuring apparatus.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| GEO | GEOmetric stitching |
| CC | Cross-Correlation stitching |
| GOD | Global Optimization of Differences stitching |
| NR | Naive Reflectance stitching |
| EER | Exhaustive Enumeration Reflectance stitching |
| TSR | Two-Step Reflectance stitching |
| SEE | Stitching Error Estimator |
| SGL | Stitching Gain Lift plot |
References
- Brown, C.A.; Hansen, H.N.; Jiang, X.J.; Blateyron, F.; Berglund, J.; Senin, N.; Bartkowiak, T.; Dixon, B.; Le Goïc, G.; Quinsat, Y.; et al. Multiscale analyses and characterizations of surface topographies. CIRP Ann. 2018, 67, 839–862. [Google Scholar] [CrossRef]
- Wyant, J.C.; Schmit, J. Large field of view, high spatial resolution, surface measurements. Int. J. Mach. Tools Manuf. 1998, 38, 691–698. [Google Scholar] [CrossRef]
- Jansen, M.; Schellekens, P.; Haitjema, H. Development of a double sided stitching interferometer for wafer characterization. CIRP Ann. 2006, 55, 555–558. [Google Scholar] [CrossRef]
- Guibert, R.; Hanafi, S.; Deltombe, R.; Bigerelle, M.; Brown, C.A. Comparison of three multiscale methods for topographic analyses. Surf. Topogr. Metrol. Prop. 2020, 8, 024002. [Google Scholar] [CrossRef]
- Mironova, A.; Robache, F.; Deltombe, R.; Guibert, R.; Nys, L.; Bigerelle, M. Digital Cultural Heritage Preservation in Art Painting: A Surface Roughness Approach to the Brush Strokes. Sensors 2020, 20, 6269. [Google Scholar] [CrossRef]
- ISO 25178-2; Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 2: Terms, Definitions and Surface Texture Parameters. ISO: Geneva, Switzerland, 2021.
- Deltombe, R.; Kubiak, K.J.; Bigerelle, M. How to select the most relevant 3D roughness parameters of a surface: Relevance of 3D roughness parameters. Scanning 2014, 36, 150–160. [Google Scholar] [CrossRef]
- Marinello, F.; Bariani, P.; Chiffre, L.D.; Hansen, H.N. Development and analysis of a software tool for stitching three-dimensional surface topography data sets. Meas. Sci. Technol. 2007, 18, 1404–1412. [Google Scholar] [CrossRef]
- Montgomery, P.C.; Benatmane, A.; Fogarassy, E.; Ponpon, J.P. Large area, high resolution analysis of surface roughness of semiconductors using interference microscopy. Mater. Sci. Eng. B 2002, 91–92, 79–82. [Google Scholar] [CrossRef]
- Dong, B.; Xiao, W.; Pan, F.; Che, L. High-precision spherical subaperture stitching interferometry based on digital holography. Opt. Lasers Eng. 2018, 110, 132–140. [Google Scholar] [CrossRef]
- King, C.W.; Bibby, M. Development of a Metrology Workstation for Full-aperture and Sub-aperture Stitching Measurements. Procedia CIRP 2014, 13, 359–364. [Google Scholar] [CrossRef]
- Paul, P.; Knoll, A.W.; Holzner, F.; Duerig, U. Field stitching in thermal probe lithography by means of surface roughness correlation. Nanotechnology 2012, 23, 385307. [Google Scholar] [CrossRef] [PubMed]
- King, C. A New Approach to Stitching Optical Metrology Data; University of London: London, UK, 2008. [Google Scholar]
- Kammers, A.D.; Daly, S. Small-scale patterning methods for digital image correlation under scanning electron microscopy. Meas. Sci. Technol. 2011, 22, 125501. [Google Scholar] [CrossRef]
- Rust, M.A.; Todd, R.I. High Resolution Surface Studies of Superplastic Deformation. Mater. Sci. Forum 2007, 551–552, 615–620. [Google Scholar] [CrossRef]
- Xu, Z.; Li, S.; Burns, D.J.; Shilpiekandula, V.; Taylor, H.K.; Yoon, S.F.; Youcef-Toumi, K.; Reading, I.; Fang, Z.; Zhao, J.; et al. Three-dimensional profile stitching based on the fiducial markers for microfluidic devices. Opt. Commun. 2009, 282, 493–499. [Google Scholar] [CrossRef]
- Chen, S.; Xue, S.; Wang, G.; Tian, Y. Subaperture stitching algorithms: A comparison. Opt. Commun. 2017, 390, 61–71. [Google Scholar] [CrossRef]
- van Laarhoven, P.J.M.; Aarts, E.H.L. Simulated annealing. In Simulated Annealing: Theory and Applications: Mathematics and Its Applications, vol 37; Springer: Dordrecht, The Netherlands, 1987; pp. 7–15. [Google Scholar] [CrossRef]
- Szu, H.; Hartley, R. Fast simulated annealing. Phys. Lett. A 1987, 122, 157–162. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Lensch, H.P.A.; Heidrich, W.; Seidel, H.-P. A Silhouette-Based Algorithm for Texture Registration and Stitching. Graph. Model. 2001, 63, 245–262. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Forrest, S. Genetic Algorithms: Principles of Natural Selection Applied to Computation. Science 1993, 261, 872–878. [Google Scholar] [CrossRef]
- Davis, L. Handbook of Genetic Algorithms; Van Nostrand Reinhold: New York, NY, USA, 1991. [Google Scholar]
- Gendreau, M.; Potvin, J.-Y. (Eds.) Handbook of Metaheuristics. In International Series in Operations Research & Management Science, 2nd ed.; Springer: New York, NY, USA, 2010; ISBN 978-1-4419-1663-1. [Google Scholar]
- Mühlenbein, H. Genetic algorithms. In Local Search in Combinatorial Optimization; Aarts, E., Lenstra, J.K., Eds.; Princeton University Press: Princeton, NJ, USA, 2003; pp. 137–172. [Google Scholar]
- Xu, Y.; Sun, C. Image Stitching Method Based on Genetic Algorithm. Adv. Eng. 2017, 126, 7. [Google Scholar]
- Yetis, H.; Baygin, M.; Karakose, M. A New Micro Genetic Algorithm Based Image Stitching Approach for Camera Arrays at Production Lines. JOIG 2017, 5, 20–24. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, L. A Global Optimized Registration Algorithm for Image Stitching. In Proceedings of the 2008 Congress on Image and Signal Processing, Sanya, China, 27–30 May 2008; Volume 3, pp. 525–529. [Google Scholar]
- Prejmerean, V. The Stitching of Images. In Proceedings of the 2006 IEEE International Conference on Automation, Quality and Testing, Robotics, Cluj-Napoca, Romania, 25–28 May 2006; Volume 2, pp. 386–391. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 1945–1950. [Google Scholar]
- Bratton, D.; Kennedy, J. Defining a Standard for Particle Swarm Optimization. In Proceedings of the 2007 IEEE Swarm Intelligence Symposium, Honolulu, HI, USA, 1–5 April 2007; pp. 120–127. [Google Scholar]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization: An overview. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Anantathanavit, M.; Munlin, M. Radius Particle Swarm Optimization. In Proceedings of the 2013 International Computer Science and Engineering Conference (ICSEC), Nakhonpathom, Thailand, 4–6 September 2013; pp. 126–130. [Google Scholar]
- Zhu, F.; Guo, P.; Chen, X. A sub-aperture stitching algorithm for cylindrical surfaces. In Proceedings of the 9th International Symposium on Advanced Optical Manufacturing and Testing Technologies: Advanced Optical Manufacturing Technologies, Chengdu, China, 16 January 2019; Volume 10838, p. 1083805. [Google Scholar]
- Agier, R. Recalage de Groupes D’Images Médicales 3D Par Extraction de Points D’Intérêt. Ph.D. Thesis, Université de Lyon, Lyon, France, 2017. [Google Scholar]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; Volume 2, pp. 1150–1157. [Google Scholar]
- Brown, M.; Lowe, D. Invariant Features from Interest Point Groups. In Proceedings of the British Machine Vision Conference 2002, Cardiff, UK, 2–5 September 2002; pp. 23.1–23.10. [Google Scholar]
- Brown, M.; Lowe, D.G. Recognising panoramas. In Proceedings of the Ninth IEEE International Conference on Computer Vision, Nice, France, 13–16 October 2003; Volume 2, pp. 1218–1225. [Google Scholar]
- Moretti, M.; Gambucci, G.; Leach, R.K.; Senin, N. Assessment of surface topography modifications through feature-based registration of areal topography data. Surf. Topogr. Metrol. Prop. 2019, 7, 025003. [Google Scholar] [CrossRef]
- Brown, M.; Lowe, D.G. Automatic Panoramic Image Stitching using Invariant Features. Int. J. Comput. Vis. 2007, 74, 59–73. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van Gool, L. Surf: Speeded up robust features. In Proceedings of the European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 404–417. [Google Scholar]
- Li, L.; Liu, Q.; Huang, W. Robust subaperture stitching method based on three-dimensional surface data matching. OE 2019, 58, 034103. [Google Scholar] [CrossRef]
- Valgren, C.; Lilienthal, A. Sift, Surf and Seasons: Long-term Outdoor Localization Using Local Features. In Proceedings of the 3rd European Conference on Mobile Robots, ECMR’07, Freiburg, Germany, 19–21 September 2007. [Google Scholar]
- Harris, C.; Stephens, M. A combined corner and edge detector. In Proceedings of the Fourth Alvey Vision Conference, Manchester, UK, 31 August–2 September 1988; pp. 147–152. [Google Scholar]
- Leutenegger, S.; Chli, M.; Siegwart, R.Y. BRISK: Binary Robust invariant scalable keypoints. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2548–2555. [Google Scholar]
- Rosten, E.; Drummond, T. Fusing Points and Lines for High Performance Tracking. In Proceedings of the International Conference on Computer Vision, Beijing, China, 17–21 October 2005; pp. 1508–1515. [Google Scholar]
- Matas, J.; Chum, O.; Urban, M.; Pajdla, T. Robust wide-baseline stereo from maximally stable extremal regions. Image Vis. Comput. 2004, 22, 761–767. [Google Scholar] [CrossRef]
- Obdržálek, D.; Basovník, S.; Mach, L.; Mikulík, A. Detecting Scene Elements Using Maximally Stable Colour Regions. In Research and Education in Robotics-EUROBOT 2009; Communications in Computer and Information Science; Gottscheber, A., Obdržálek, D., Schmidt, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 82, pp. 107–115. ISBN 978-3-642-16369-2. [Google Scholar]
- Shi, J. Good features to track. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition CVPR-94, Seattle, WA, USA, 21–23 June 1994; pp. 593–600. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Alcantarilla, P.F.; Bartoli, A.; Davison, A.J. KAZE Features. In Proceedings of the Computer Vision–ECCV 2012; Fitzgibbon, A., Lazebnik, S., Perona, P., Sato, Y., Schmid, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 214–227. [Google Scholar]
- Tareen, S.A.K.; Saleem, Z. A comparative analysis of SIFT, SURF, KAZE, AKAZE, ORB, and BRISK. In Proceedings of the 2018 International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 3–4 March 2018; pp. 1–10. [Google Scholar]
- Juan, L.; Oubong, G. SURF applied in panorama image stitching. In Proceedings of the 2010 2nd International Conference on Image Processing Theory, Tools and Applications, Paris, France, 7–10 July 2010; pp. 495–499. [Google Scholar]
- Phong, B.T. Illumination for computer generated pictures. Commun. ACM 1975, 18, 311–317. [Google Scholar] [CrossRef]
- Lemesle, J.; Robache, F.; Le Goic, G.; Mansouri, A.; Brown, C.A.; Bigerelle, M. Surface Reflectance: An Optical Method for Multiscale Curvature Characterization of Wear on Ceramic—Metal Composites. Materials 2020, 13, 1024. [Google Scholar] [CrossRef]
- Yan, L.; Luo, W.; Yan, G.; Wang, X.; Zhang, H.; Chao, L.; Ma, D.; Tang, X. Subaperture stitching testing for fine flat mirrors with large apertures using an orthonormal polynomial fitting algorithm. Opt. Lasers Eng. 2019, 120, 49–58. [Google Scholar] [CrossRef]
- Gao, F.; Jiang, Z.; Zhao, Z.; Li, B. Measurement of aspheric surface combining point diffraction interferometry and annular subaperture stitching. Opt. Eng. 2015, 54, 014102. [Google Scholar] [CrossRef]
- Bariani, P. Dimensional Metrology for Microtechnology; Technical University of Denmark: Kongens Lyngby, Denmark, 2005. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).