A Systematic Approach for Energy-Efficient Design of Rolling Bearing Cages
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
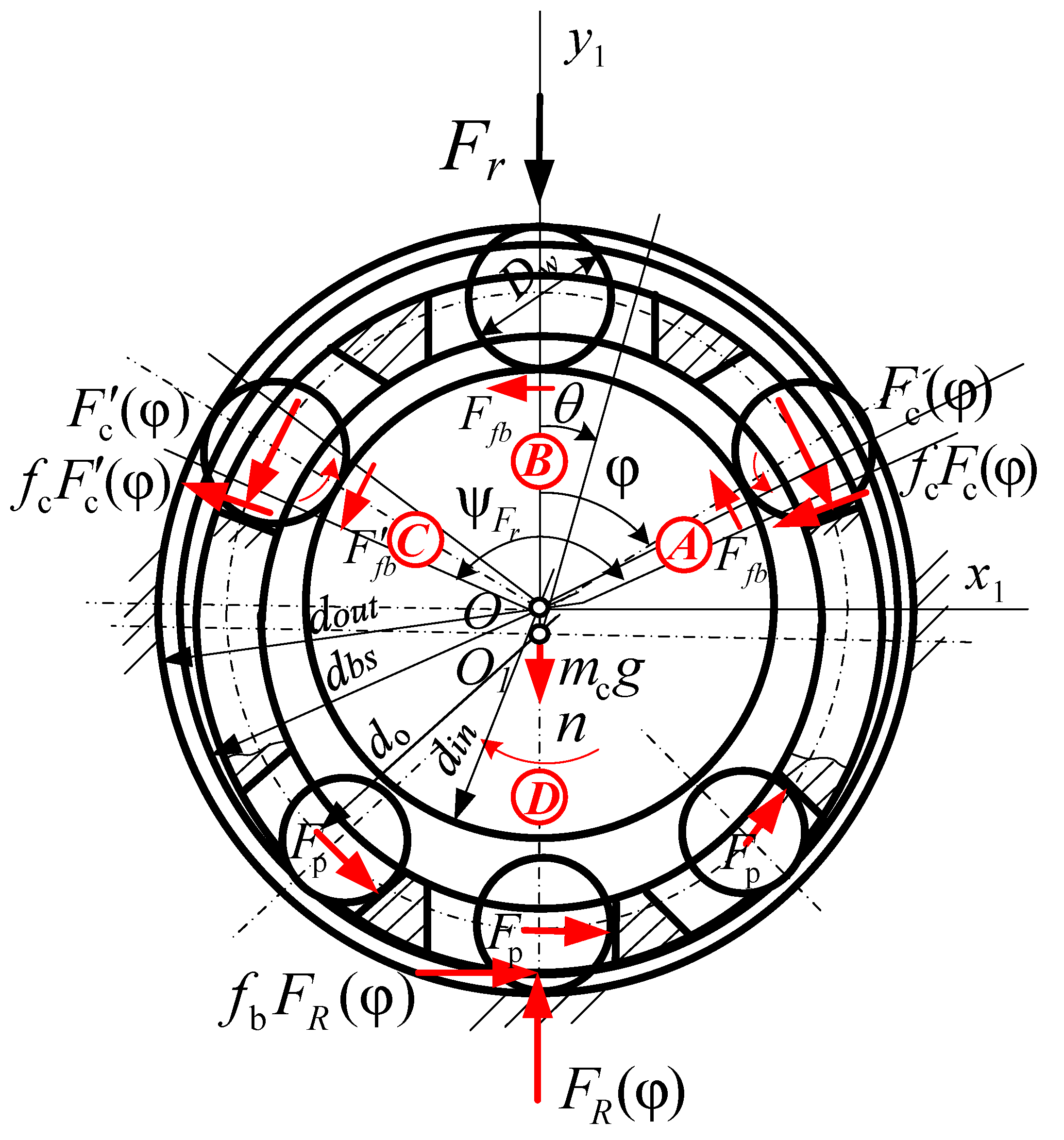
2.1. Heat Generation Model
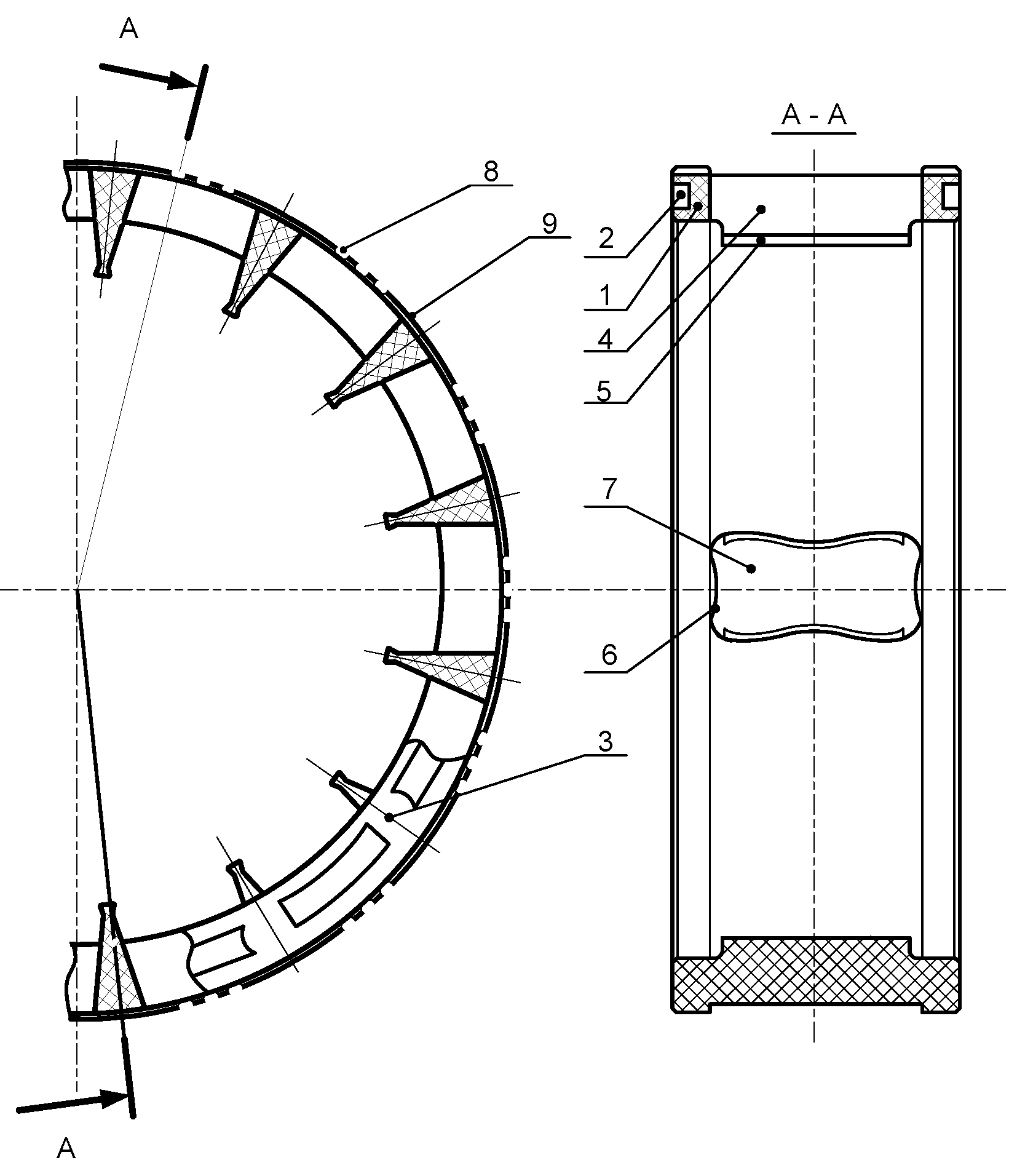
2.2. An Energy Efficient Cage Design
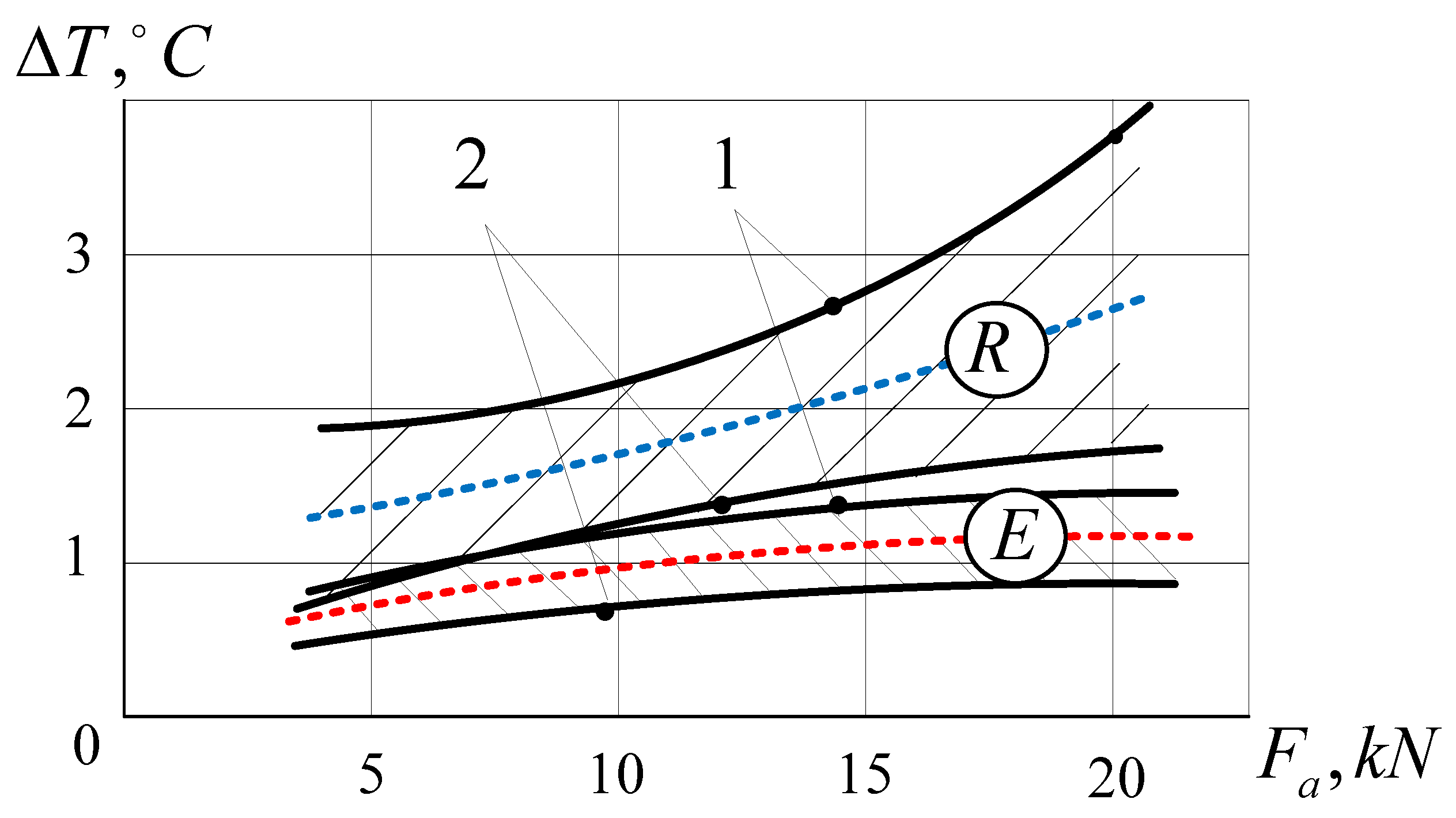
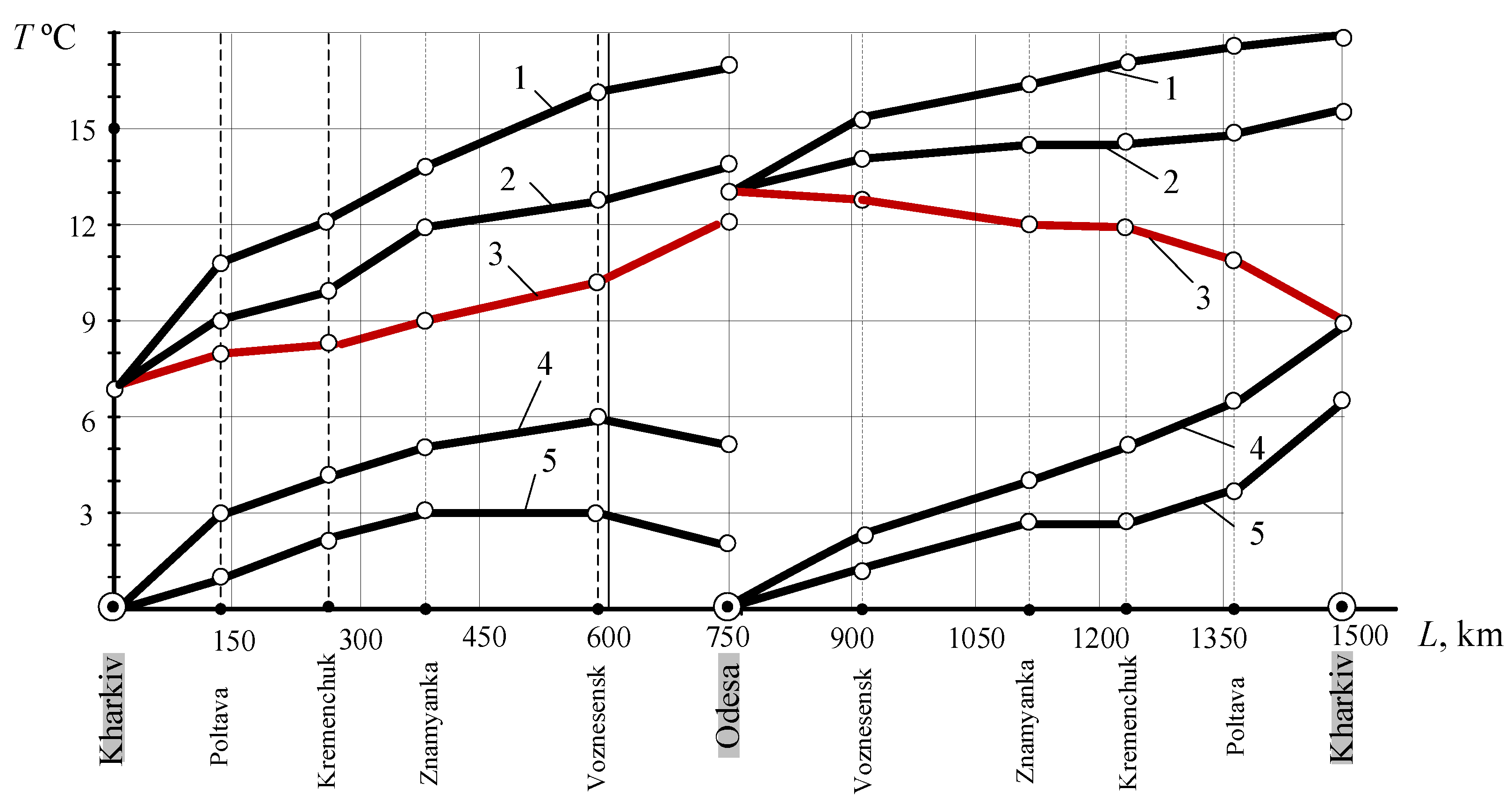
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Cooling factor | |
| Cage rotation frequency | |
| Cage weight | |
| Cage with the ring friction coefficient | |
| Cage with the rolling element friction coefficient | |
| Rolling element with the ring friction coefficient | |
| Rolling element diameter | |
| Rolling element center diameter | |
| Bearing ring groove radius | |
| Outer ring diameter | |
| Inner ring diameter | |
| Base ring edge diameter | |
| Ring thickness | |
| Rolling friction coefficient | |
| Bearing contact angle | |
| Force of the rolling element with ring interaction | |
| Radial force component from the inner ring | |
| Radial force component from the outer ring | |
| Second moment of inertia | |
| Cage eccentricity |
References
- Klitnoi, V.; Gaydamaka, A. On The Problem of Vibration Protection of Rotor Systems with Elastic Adaptive Elements of Quasi-Zero Stiffness. Diagnostyka 2020, 21, 69–75. [Google Scholar] [CrossRef]
- Gaydamaka, A.; Muzikin, Y.; Klitnoi, V.; Basova, Y.; Dobrotvorskiy, S. Selecting the Method for Pre-tightening Threaded Connections of Heavy Engineering. Int. Conf. Reliab. Syst. Eng. 2021, 305, 69–77. [Google Scholar] [CrossRef]
- Shevchenko, S.; Mukhovaty, A.; Krol, O. Geometric Aspects of Modifications of Tapered Roller Bearings. In Proceedings of the 2nd International Conference on Industrial Engineering, ICIE 2016, Chelyabinsk, Russia, 19–20 May 2016. [Google Scholar] [CrossRef]
- Gaydamaka, A.; Klitnoy, V.; Muzikin, Y.; Tat’kov, V.; Hrechka, I. Construction of a model for the distribution of radial load among the bearing’s rolling bodies. East.-Eur. J. Enterp. Technol. 2018, 6, 39–44. [Google Scholar] [CrossRef]
- Marchenko, A.; Grabovskiy, A.; Tkachuk, M.; Shut, O.; Tkachuk, M. Detuning of a supercharger rotor from critical rotational velocities. In Proceedings of the 4th International Conference on Design, Simulation, Manufacturing: The Innovation Exchange, DSMIE 2021, Lviv, Ukraine, 8–11 June 2021; pp. 137–145. [Google Scholar] [CrossRef]
- Prokopenko, D.; Shatskyi, I.; Vorobiov, M.; Ropyak, L. Cyclic deformation of separating tape in electromagnetic rolling pump. J. Phys. Conf. Ser. 2021, 1741, 012029. [Google Scholar] [CrossRef]
- Jones, A.B. A General Theory for Elastically Constrained Ball and Radial Roller Bearings. Trans. ASME Ser. D J. Basic Eng. 1960, 82, 309–320. [Google Scholar] [CrossRef]
- Yan, K.; Wang, Y.; Zhu, Y.; Hong, J.; Zhai, Q. Investigation on Heat Dissipation Characteristic of Ball Bearing Cage and Inside Cavity at Ultra High Rotation Speed. Tribol. Int. 2016, 93, 470–481. [Google Scholar] [CrossRef]
- Walters, C.T. The Dynamics of Ball Bearings. ASME J. Lubr. Tech. 1971, 93, 1–10. [Google Scholar] [CrossRef]
- Gupta, P.K. Dynamics of Rolling-Element Bearings—Part III: Ball Bearing Analysis. J. Lubr. Technol. 1979, 101, 312–318. [Google Scholar] [CrossRef]
- Gupta, P.K.; Burton, P. Advanced Dynamics of Rolling Elements; Pringer-Verlag Press: New York, NY, USA, 1984. [Google Scholar]
- Kim, S.J. Analytical Consideration of the Radial Clearance to Reduce Cage Slip of the Turbo Engine Roller. Bear. J. Mech. Sci. Technol. 2021, 35, 2827–2839. [Google Scholar] [CrossRef]
- Li, H.; Li, H.; Liu, Y.; Liu, H. Dynamic Characteristics of Ball Bearing with Flexible Cage Lintel and Wear. Eng. Fail. Anal. 2020, 117, 104956. [Google Scholar] [CrossRef]
- Dahiwal, R.; Bernd, S. Investigation of Cage Pocket Wear in Solid-Lubricated Rolling Bearings. Tribol. Online Jpn. Soc. Tribol. 2020, 15, 25–35. [Google Scholar] [CrossRef]
- Bizarre, L.; Nonato, F.; Cavalca, K.L. Formulation of Five Degrees of Freedom Ball Bearing Model Accounting for the Nonlinear Stiffness and Damping of Elastohydrodynamic Point Contacts. Mech. Mach. Theory 2018, 124, 179–196. [Google Scholar] [CrossRef]
- Kwak, W.; Lee, J.; Lee, Y.B. Theoretical and Experimental Approach to Ball Bearing Frictional Characteristics Compared with Cryogenic Friction Model and Dry Friction Model. Mech. Syst. Signal Process. 2019, 124, 424–438. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, W.; Qing, T.; Zhang, Y.; Liang, H.; Zhang, S. The Effect of Lubricant Temperature on Dynamic Behavior in Angular Contact Ball Bearings. Mech. Mach. Theory 2020, 149, 103832. [Google Scholar] [CrossRef]
- Kalinin, Y.; Olexander, S.; Volodymyr, R.; Koliesnik, I.; Kozhushko, A. Determining the Stresses in Beams Due to Short-Term Effect on Their Supports. In Proceedings of the International Conference on Business and Technology, ICBT 2020, Istanbul, Turkey, 14–15 November 2020; pp. 617–628. [Google Scholar] [CrossRef]
- Jiang, S.; Chen, X.; Gu, J.; Shen, X. Friction Moment Analysis of Space Gyroscope Bearing with Ribbon cage Under Ultra-Low Oscillatory Motion. Chin. J. Aeronaut. 2014, 27, 1301–1311. [Google Scholar] [CrossRef]
- Stammler, M.; Schwack, F.; Bader, N.; Reuter, A.; Poll, G. Friction Torque of Wind-Turbine Pitch Bearings–Comparison of Experimental Results with Available Models. Wind. Energy Sci. 2018, 5, 97–105. [Google Scholar] [CrossRef]
- Brecher, C.; Bäumler, S.; Rossaint, J. Calculation of Kinematics and Friction of a Spindle Bearing Using a Local EHL Friction Model. Tribol. Trans. 2013, 56, 245–254. [Google Scholar] [CrossRef]
- Cousseau, T.; Graça, B.; Campos, A.; Seabra, J. Friction Torque in Grease Lubricated Thrust Ball Bearings. Tribol. Int. 2011, 44, 523–531. [Google Scholar] [CrossRef]
- Geonea, I.; Dumitru, N.; Dumitru, I. Experimental and Theoretical Study of Friction Torque From Radial Ball Bearings. IOP Conf. Ser. Mater. Sci. Eng. 2017, 252, 012048. [Google Scholar] [CrossRef]
- Yuwei, L.; Xingyu, F.; Jia, W.; Xiayi, L. An Investigation for the Friction Torque of a Tapered Roller Bearing Considering the Geometric Homogeneity of Rollers. Lubricants 2022, 10, 154. [Google Scholar] [CrossRef]
- Gaydamaka, A. Models of Kinematics and Dynamics of Cylindrical Roller Bearings of Railway Transport. Sci. Transp. Prog. 2014, 3, 100–108. [Google Scholar] [CrossRef] [PubMed]
- Nosov, V.B. Bearing Units of Modern Machines and Devices: Handbook; Mashinostroenie: Moscow, Russia, 1997. [Google Scholar]
- The SKF Model for Calculating the Frictional Moment. 2017. Available online: http://www.skf.com/binary/110299767/The%20SKF%20model%20for%20calculating%20the%20frictional%20moment_tcm_12-299767.pdf (accessed on 6 November 2022).
- Abdan, S.; Stosic, N.; Kovacevic, C.; Smith, I.; Asati, N. Analysis of rolling bearing power loss models for twin screw oil injected compressor. IOP Conf. Ser.: Mater. Sci. Eng. 2019, 604, 012013. [Google Scholar] [CrossRef]
- Gaydamaka, A. Cylindrical Roller Bearing of the Maximum Load within the Specified Dimensions with a Polymer Separator of Onepiece Design. Ukraine Patent Number 91168, 25 June 2014. [Google Scholar]
- Baehr, H.D.; Stephan, K. Heat and Mass Transfer, 2nd ed.; Springer: New York, NY, USA, 2006; 688p. [Google Scholar] [CrossRef]

| 30 | 5 | 110/98 | 99/85 | 578/289 | 0.9/0.5 | 1.1/0.5 | 1.2/0.6 |
| 10 | 147/133 | 139/120 | 791/400 | 1.3/0.6 | 1.5/0.7 | 1.6/0.8 | |
| 15 | 182/167 | 175/156 | 987/510 | 1.6/0.8 | 1.8/0.9 | 1.9/1.0 | |
| 20 | 197/179 | 191/168 | 1073/548 | 1.7/0.9 | 2.0/1.0 | 2.2/1.1 | |
| 40 | 5 | 143/127 | 134/115 | 766/382 | 1.2/0.6 | 1.4/0.7 | 1.5/0.8 |
| 10 | 180/161 | 173/150 | 976/491 | 1.6/0.8 | 1.8/0.9 | 1.9/0.9 | |
| 15 | 215/196 | 210/186 | 1175/604 | 1.9/0.9 | 2.1/1.1 | 2.3/1.2 | |
| 20 | 230/210 | 226/200 | 1261/648 | 2.0/1.0 | 2.3/1.2 | 2.4/1.3 | |
| 50 | 5 | 177/155 | 170/143 | 959/471 | 1.5/0.8 | 1.8/0.9 | 1.9/0.9 |
| 10 | 213/191 | 208/181 | 1164/588 | 1.9/0.9 | 2.1/1.1 | 2.2/1.1 | |
| 15 | 248/224 | 245/214 | 1363/692 | 2.2/1.1 | 2.5/1.3 | 2.6/1.3 | |
| 20 | 263/239 | 261/230 | 1449/741 | 2.3/1.2 | 2.7/1.4 | 2.8/1.4 |
| Typical Bearing | Modernized Bearing | ||||
|---|---|---|---|---|---|
| Standard Deviation | Standard Deviation | ||||
| Poltava | 2.96 | 0.43 | 0.92 | 0.12 | 68.9 |
| Kremenchuk | 4.12 | 0.45 | 1.97 | 0.16 | 52.2 |
| Znamyanka | 4.94 | 0.89 | 3.08 | 0.36 | 37.6 |
| Voznesensk | 5.92 | 0.69 | 3.02 | 0.5 | 48.9 |
| Odesa | 4.98 | 0.45 | 1.81 | 0.14 | 63.6 |
| Voznesensk | 2.12 | 0.29 | 0.81 | 0.11 | 61.8 |
| Znamyanka | 3.57 | 0.6 | 2.8 | 0.52 | 21.5 |
| Kremenchuk | 5.07 | 0.93 | 2.78 | 0.4 | 45.1 |
| Poltava | 6.39 | 0.56 | 3.43 | 0.57 | 46.3 |
| Kharkiv | 8.87 | 1.5 | 6.32 | 1.08 | 28.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaydamaka, A.; Klitnoi, V.; Dobrotvorskiy, S.; Basova, Y.; Matos, D.; Machado, J. A Systematic Approach for Energy-Efficient Design of Rolling Bearing Cages. Appl. Sci. 2023, 13, 1144. https://doi.org/10.3390/app13021144
Gaydamaka A, Klitnoi V, Dobrotvorskiy S, Basova Y, Matos D, Machado J. A Systematic Approach for Energy-Efficient Design of Rolling Bearing Cages. Applied Sciences. 2023; 13(2):1144. https://doi.org/10.3390/app13021144
Chicago/Turabian StyleGaydamaka, Anatoliy, Volodymyr Klitnoi, Sergey Dobrotvorskiy, Yevheniia Basova, Demétrio Matos, and José Machado. 2023. "A Systematic Approach for Energy-Efficient Design of Rolling Bearing Cages" Applied Sciences 13, no. 2: 1144. https://doi.org/10.3390/app13021144
APA StyleGaydamaka, A., Klitnoi, V., Dobrotvorskiy, S., Basova, Y., Matos, D., & Machado, J. (2023). A Systematic Approach for Energy-Efficient Design of Rolling Bearing Cages. Applied Sciences, 13(2), 1144. https://doi.org/10.3390/app13021144









