Large-Scale Cluster Parallel Strategy for Regularized Lattice Boltzmann Method with Sub-Grid Scale Model in Large Eddy Simulation
Abstract
:1. Introduction
2. RLBM-LES and Boundary Condition
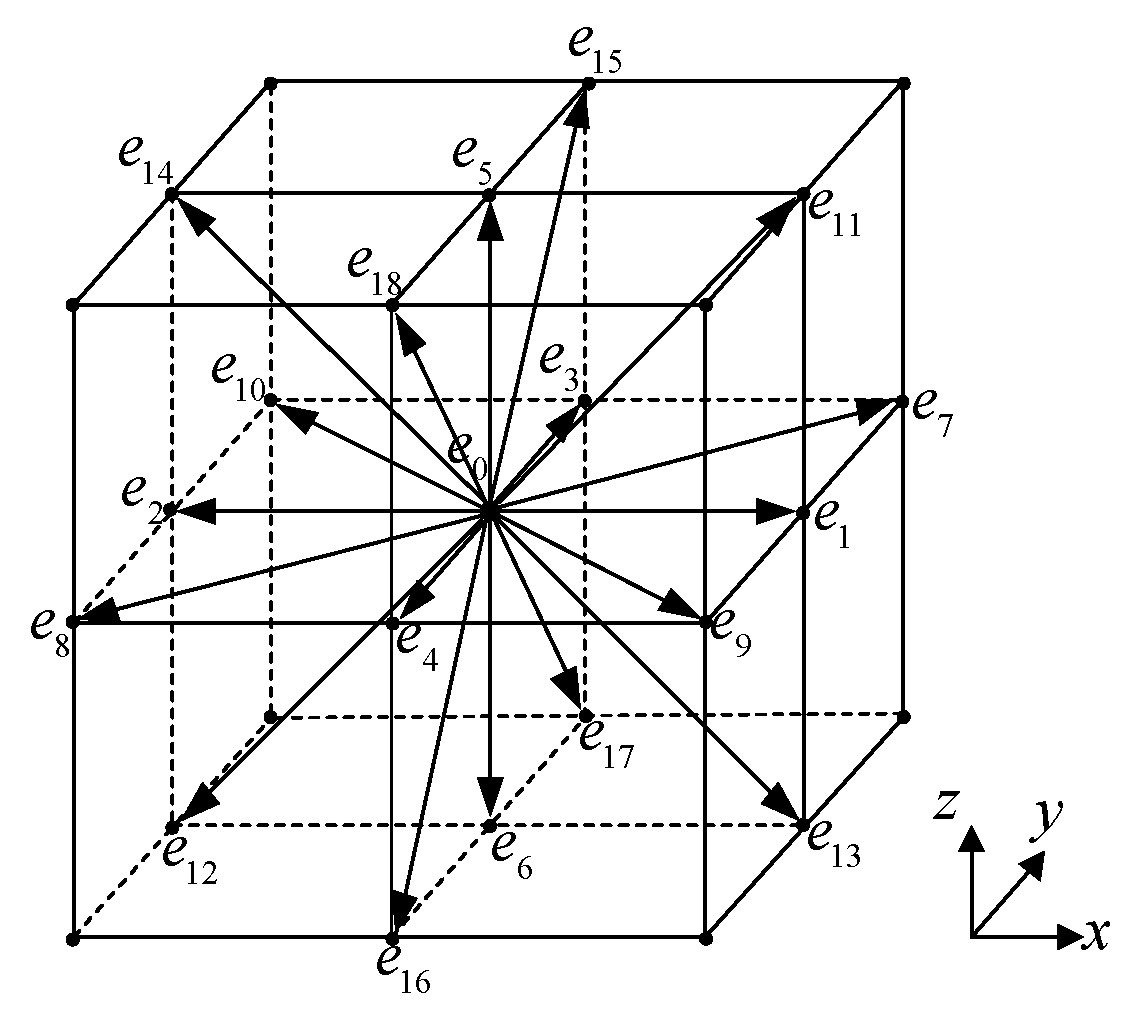
2.1. RLBM-LES
2.2. Boundary Condition
2.2.1. Grid-Aligned Botundary
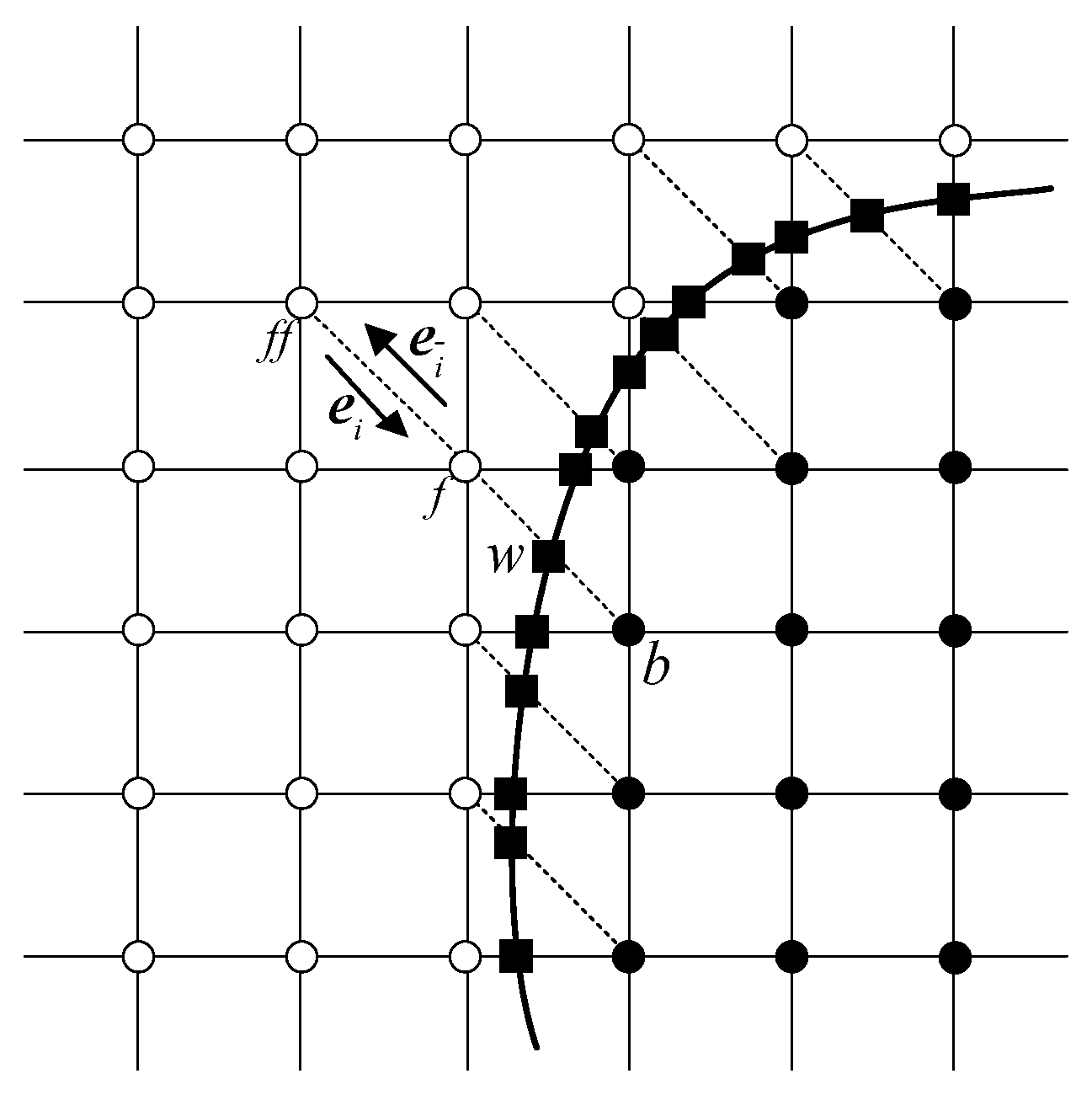
2.2.2. Curved Boundary
3. RLBM Parallel Strategy
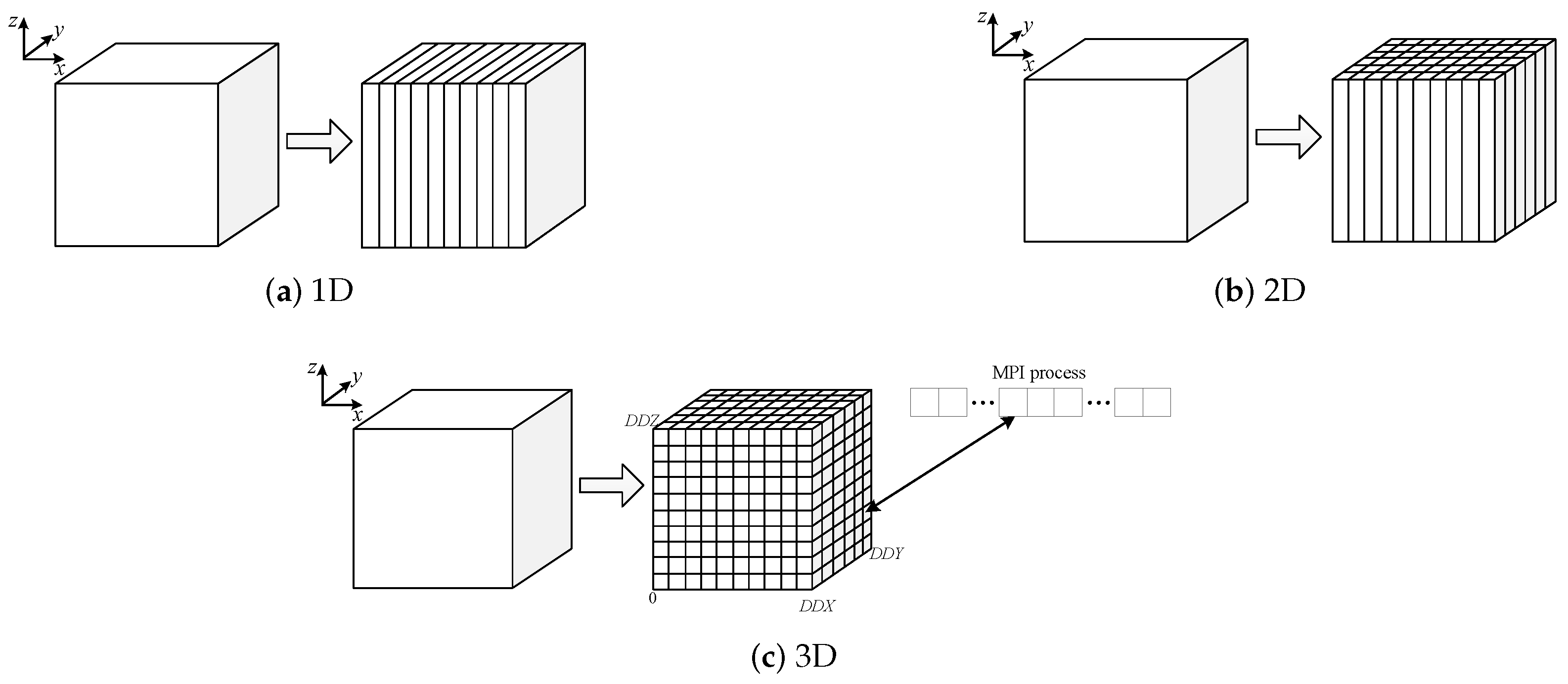
3.1. Domain Decomposition
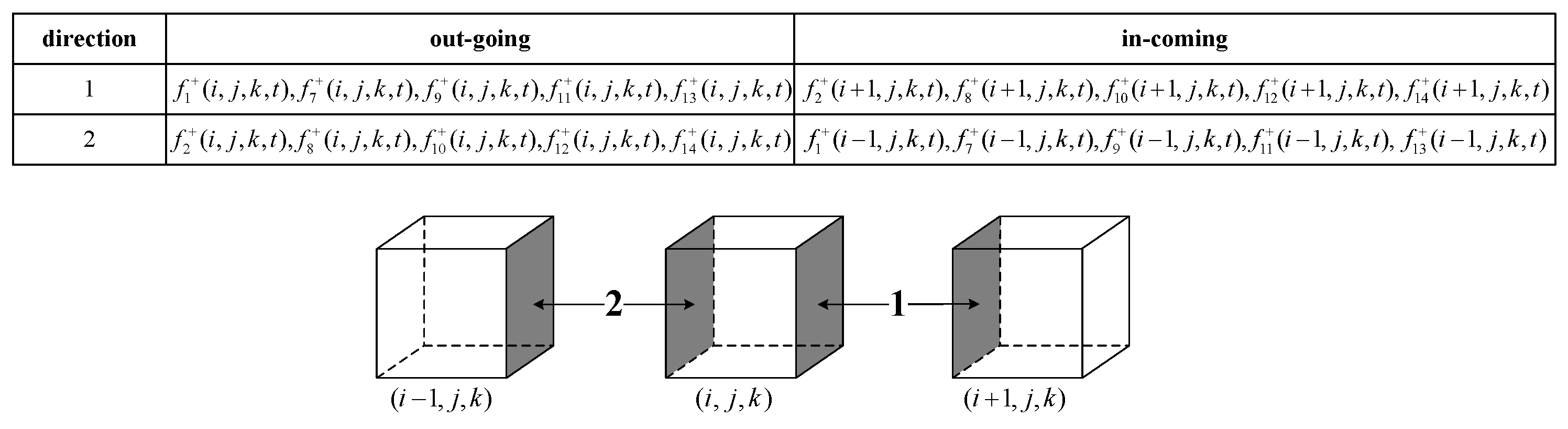
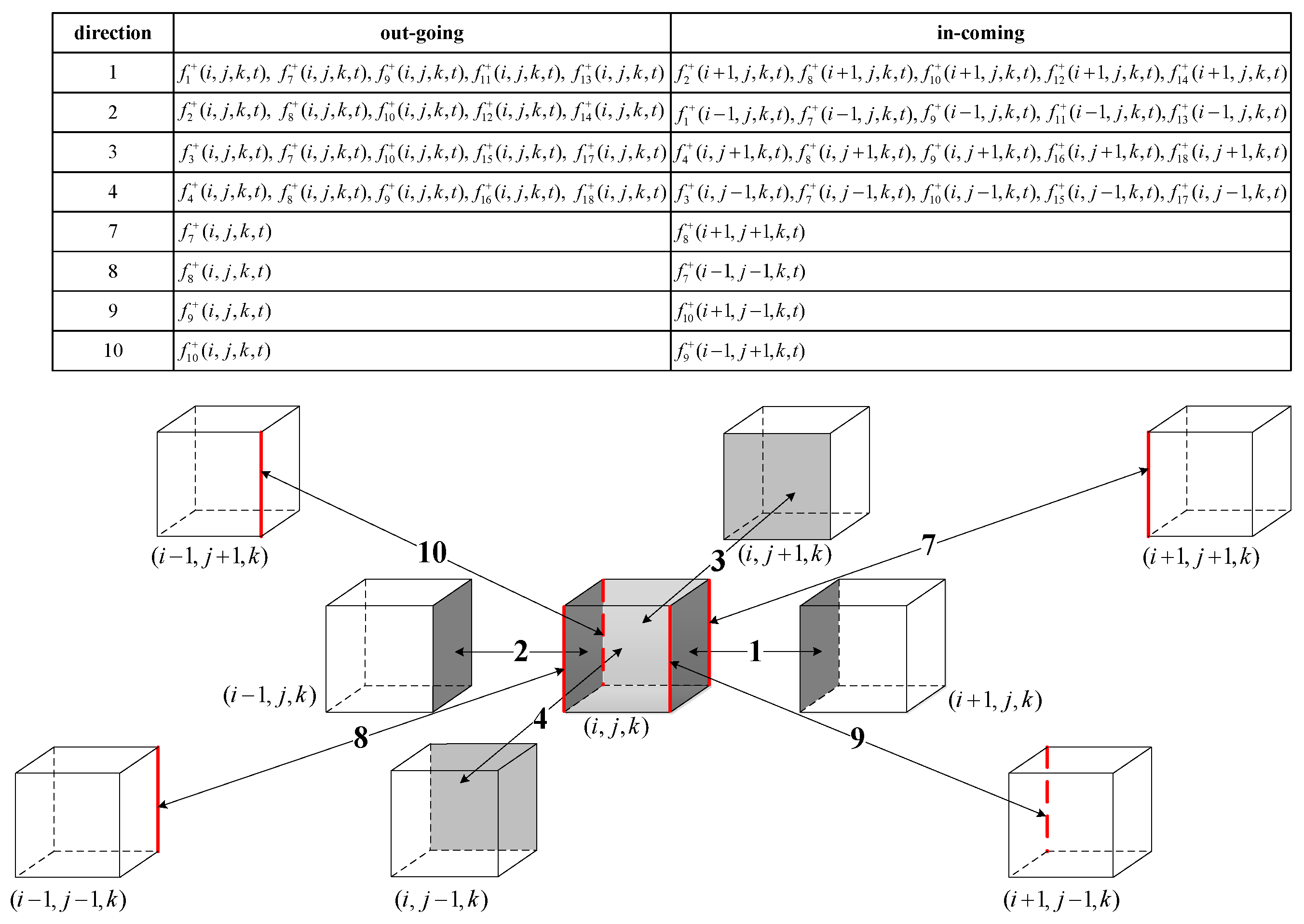
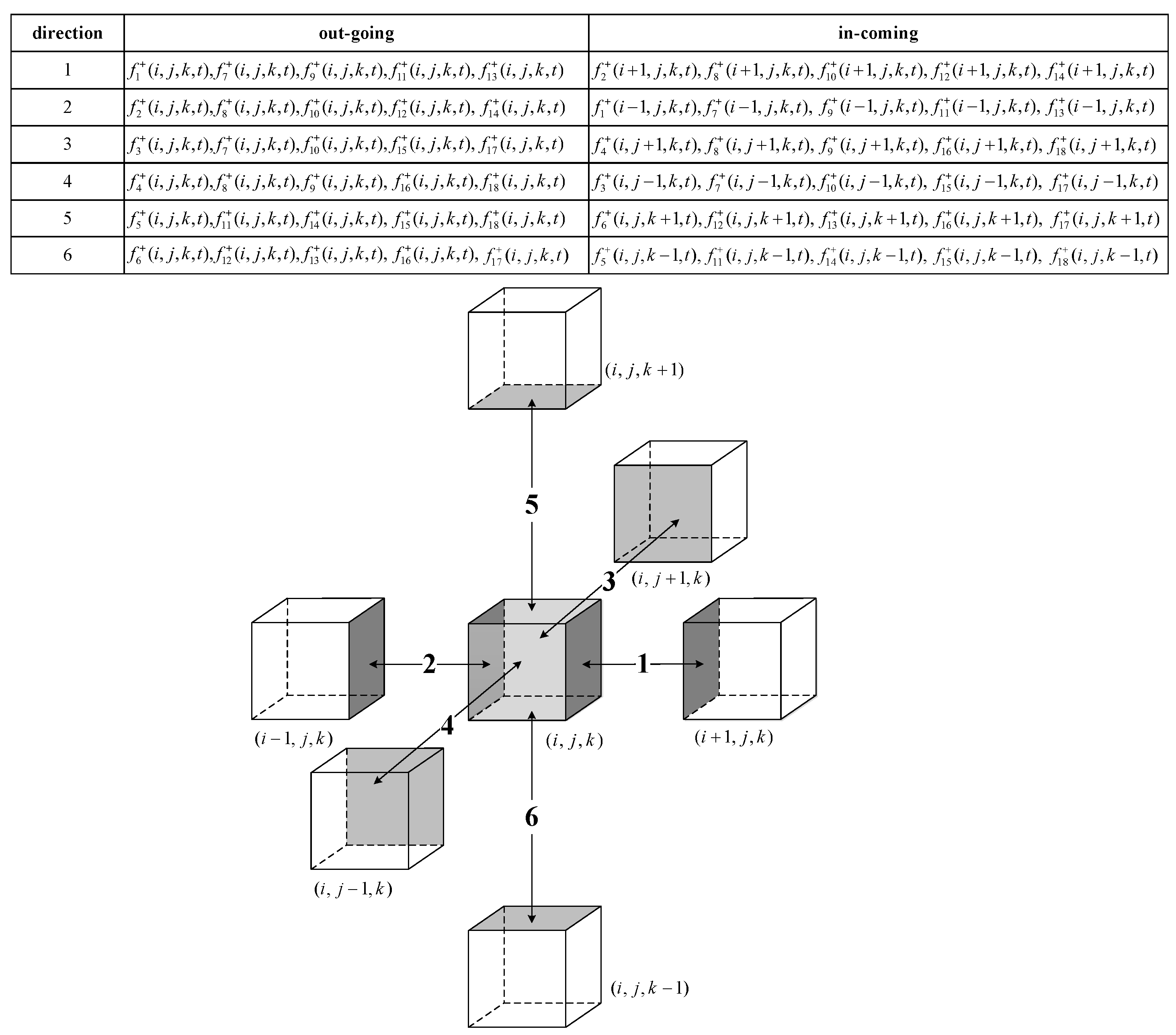
3.2. Data Exchange
3.3. Generate the Cartesian Grid
| Algorithm 1 Parallel algorithm of Cartesian grid generation. |
|
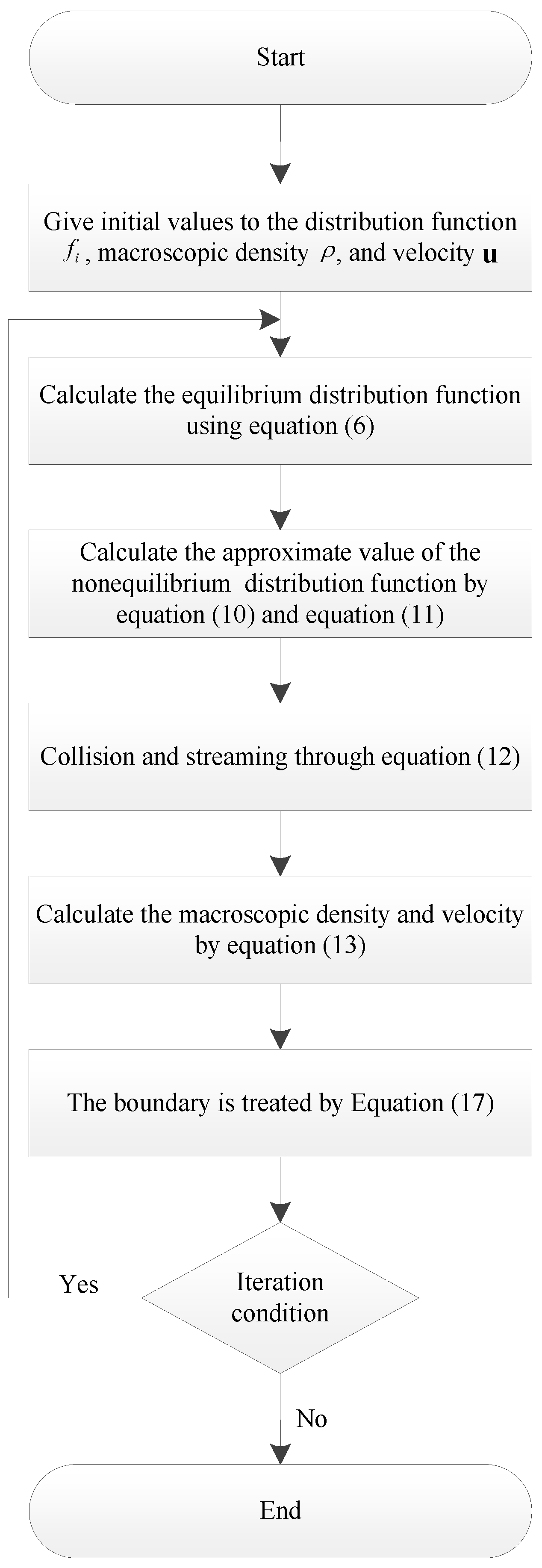
3.4. RLBM Parallel Algorithm
| Algorithm 2 RLBM Parallel Iterative Computation. |
|
4. Numerical Experiment
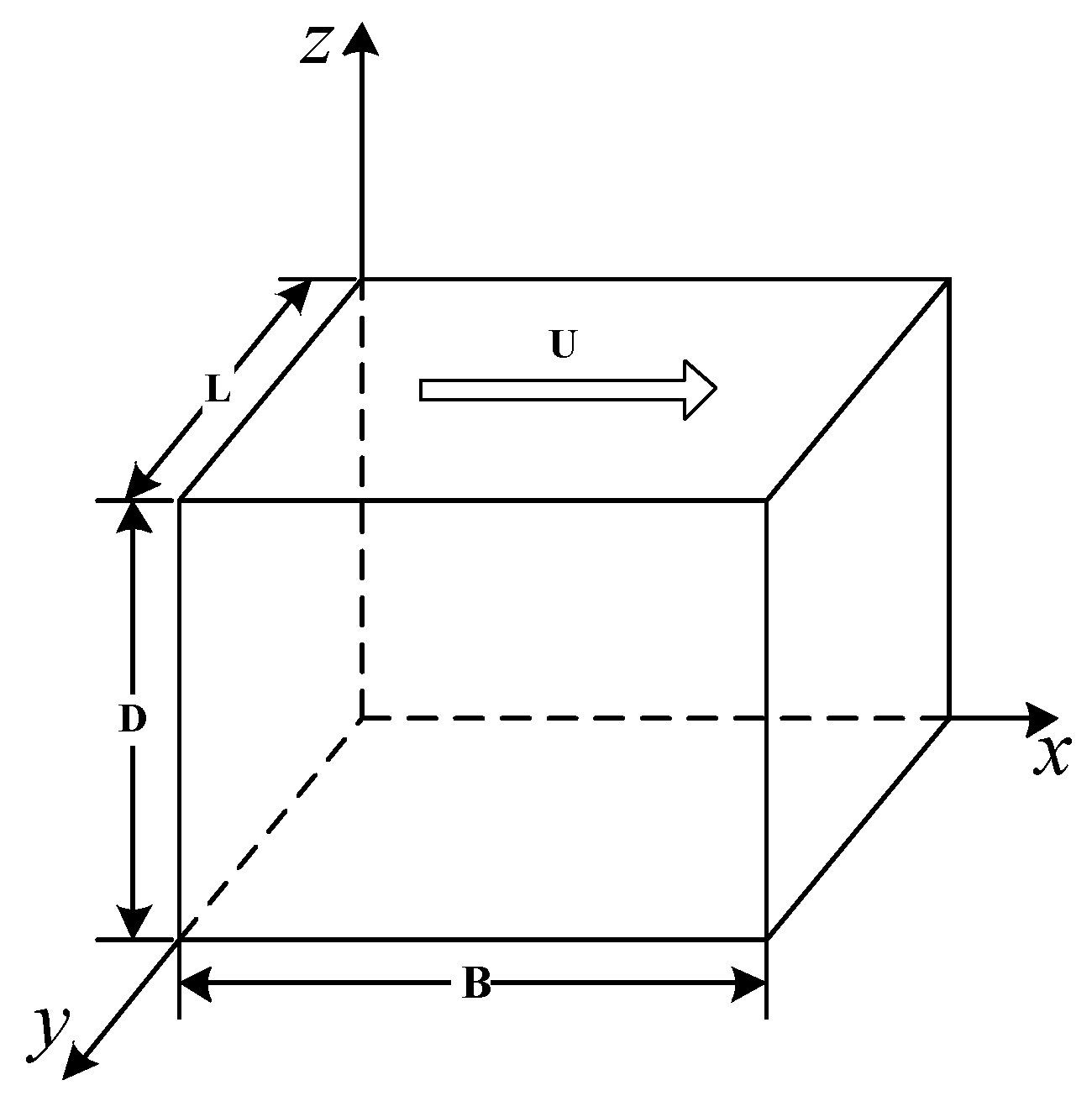
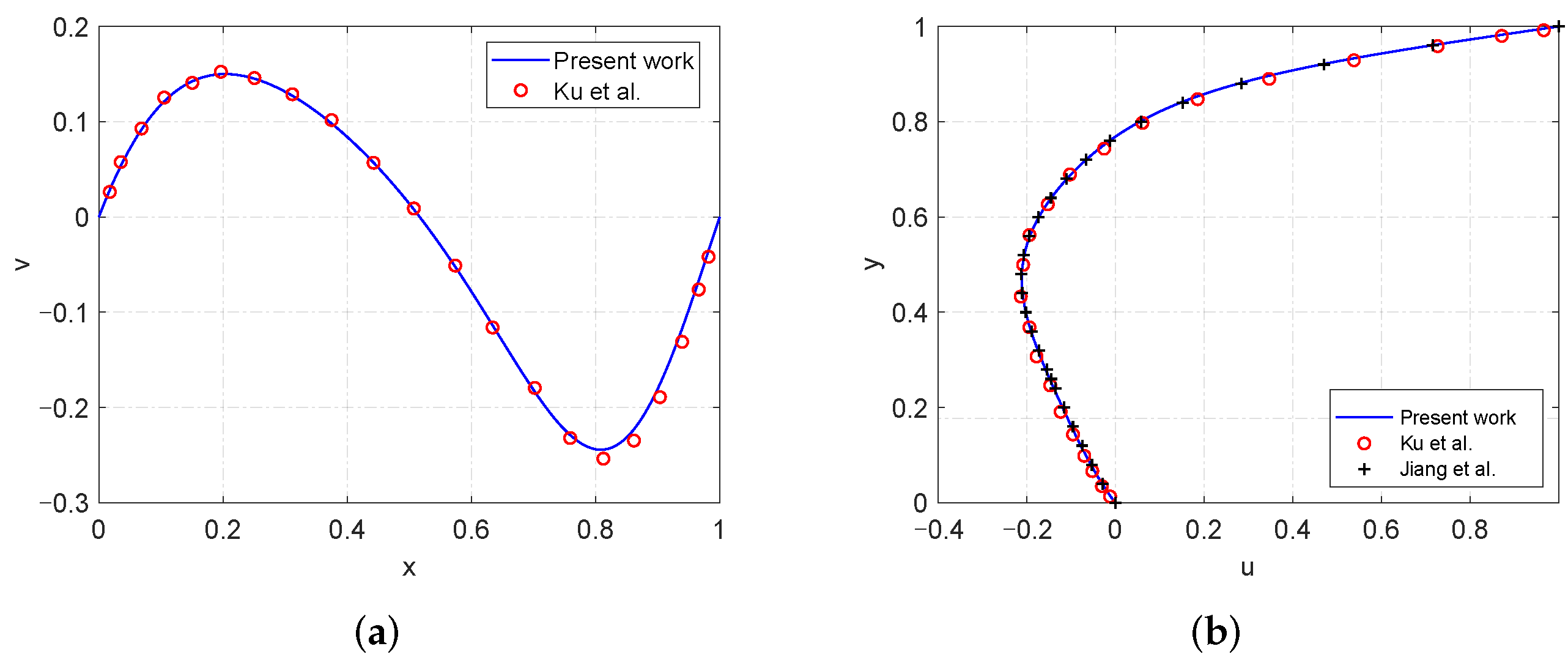
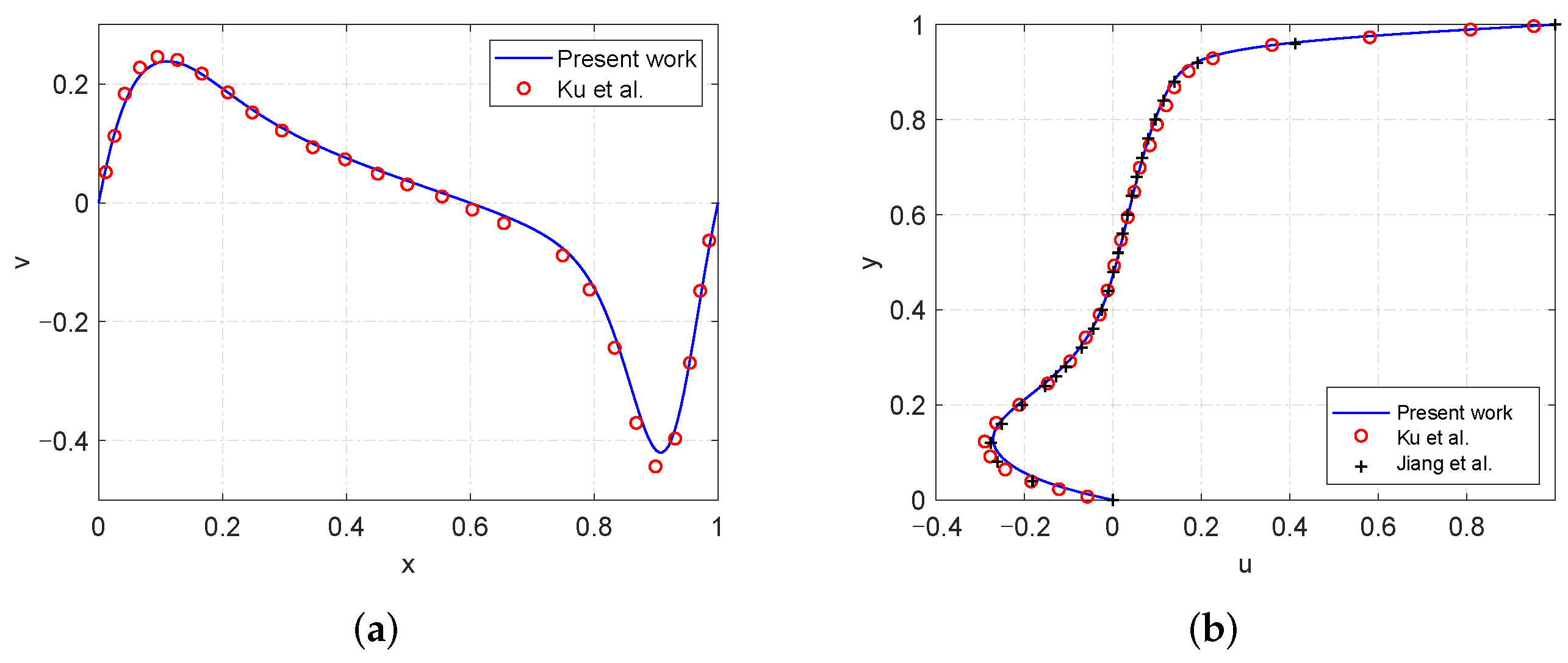
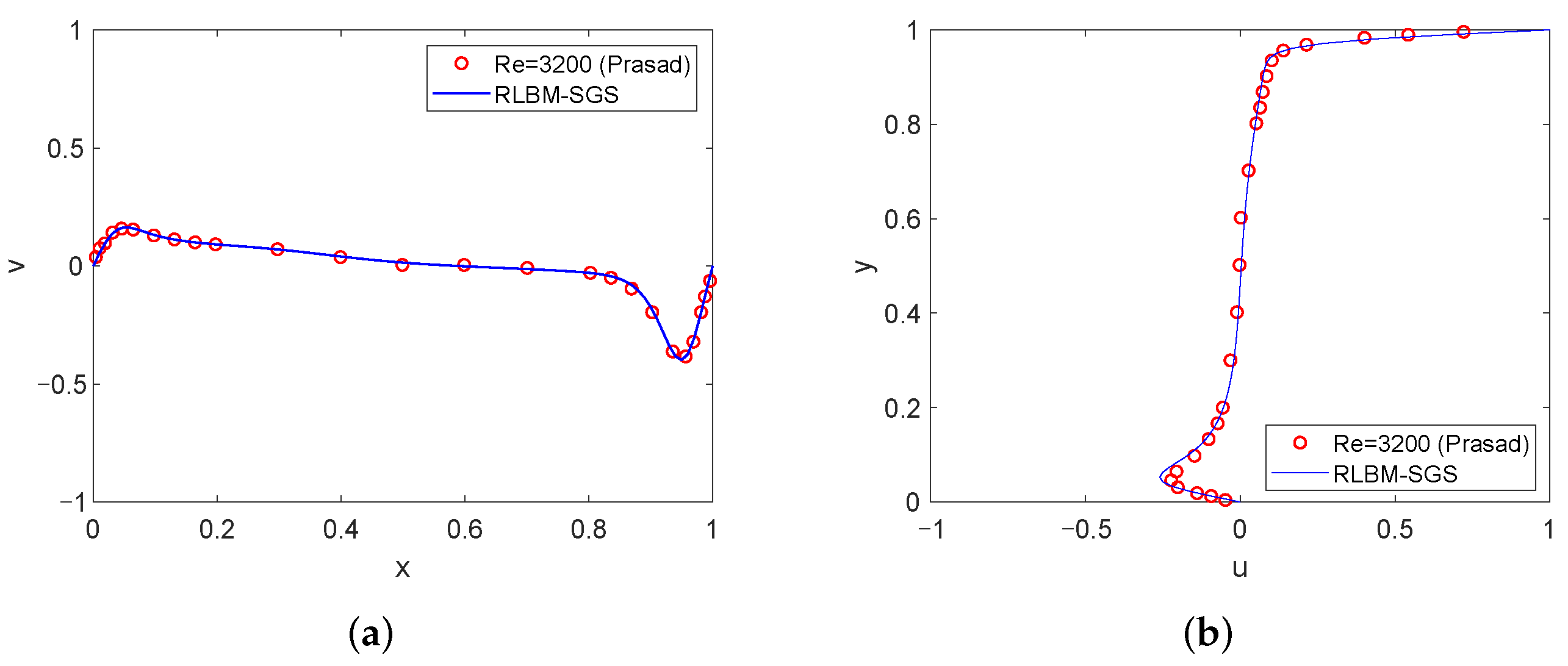
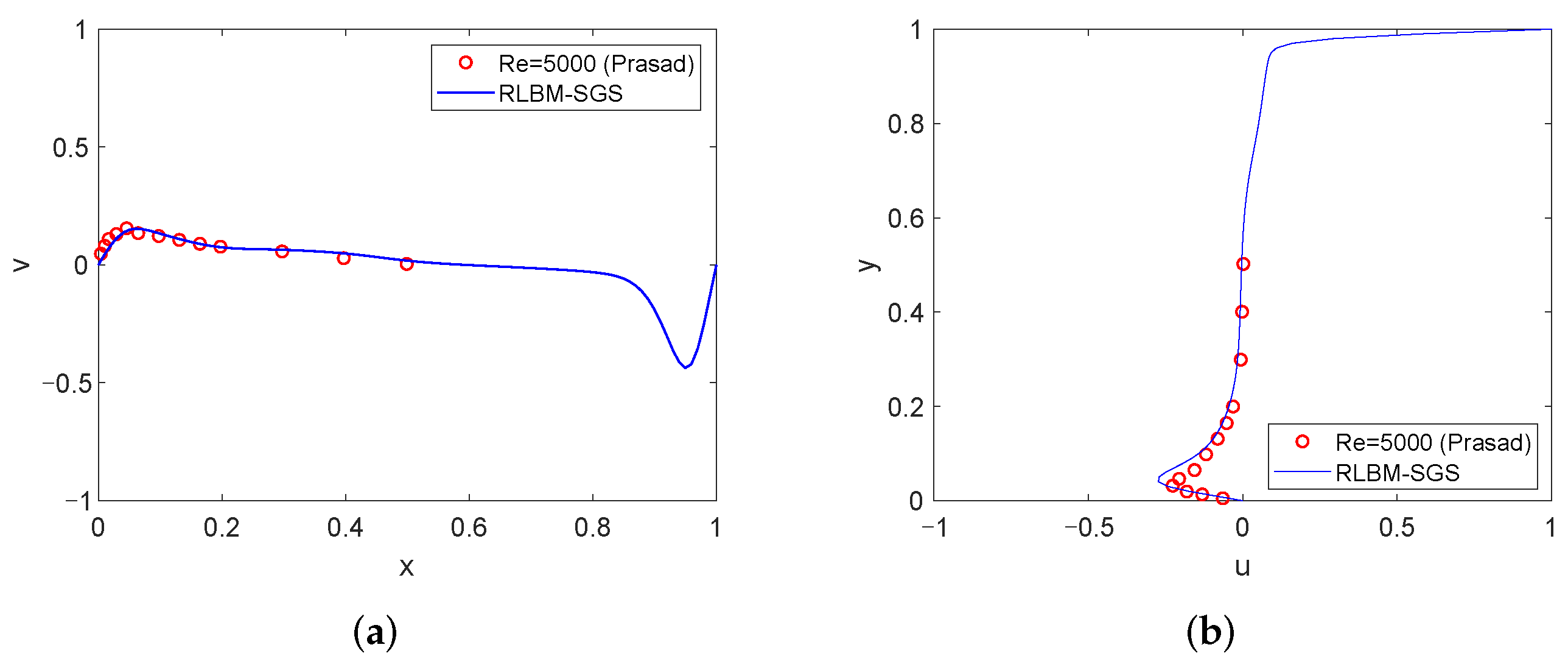
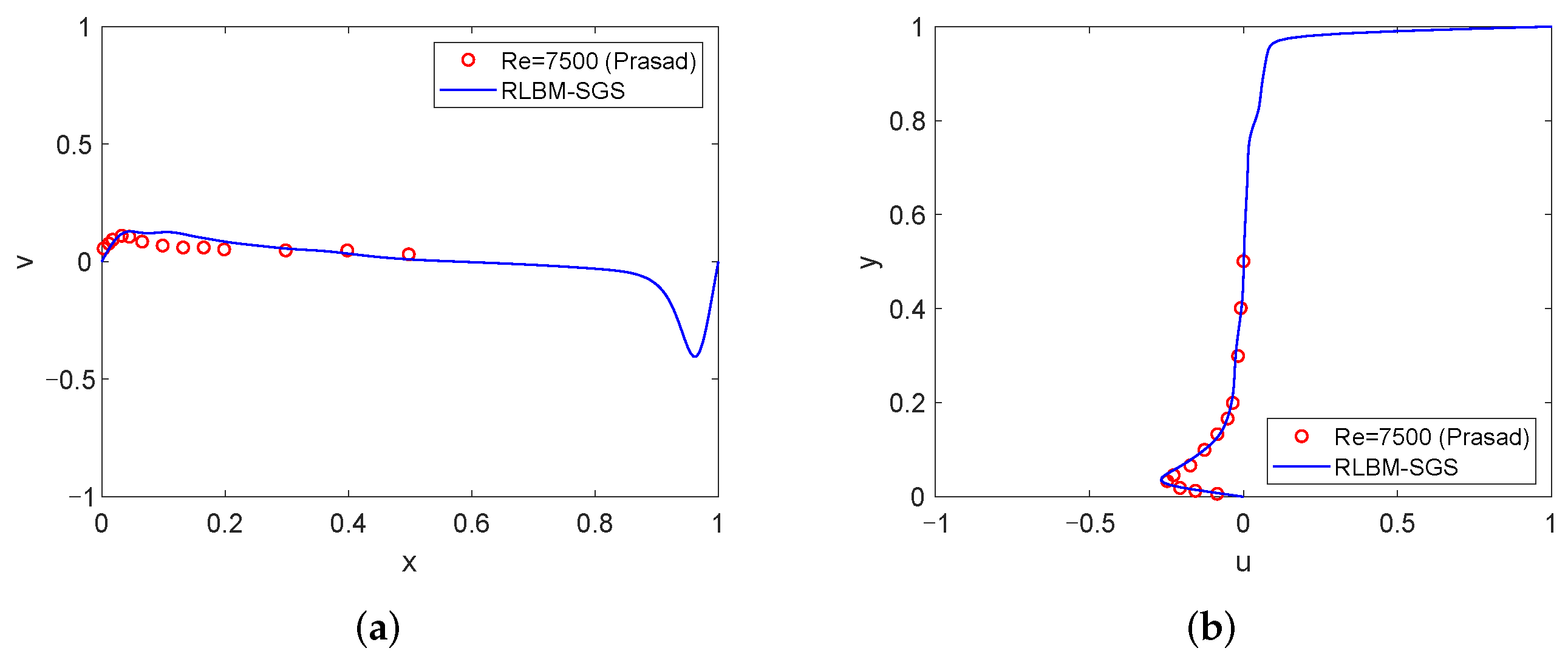
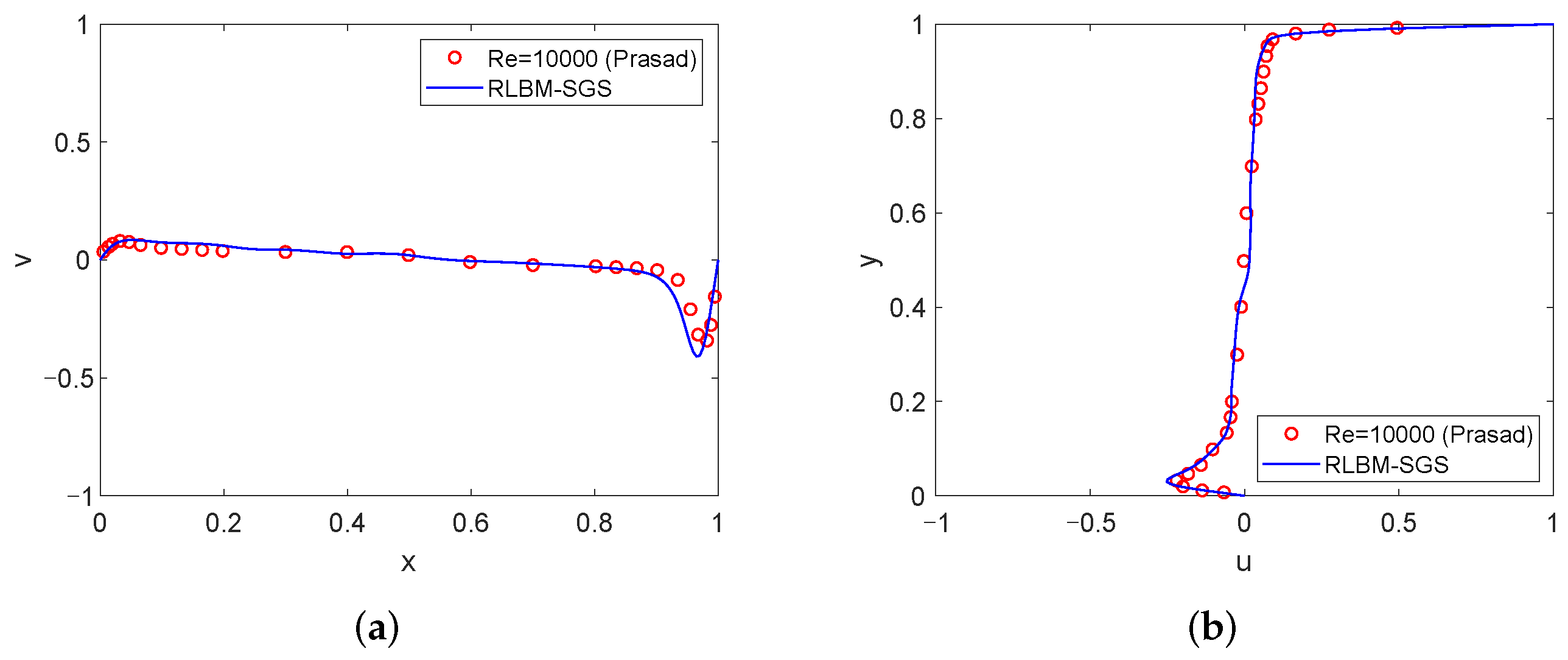
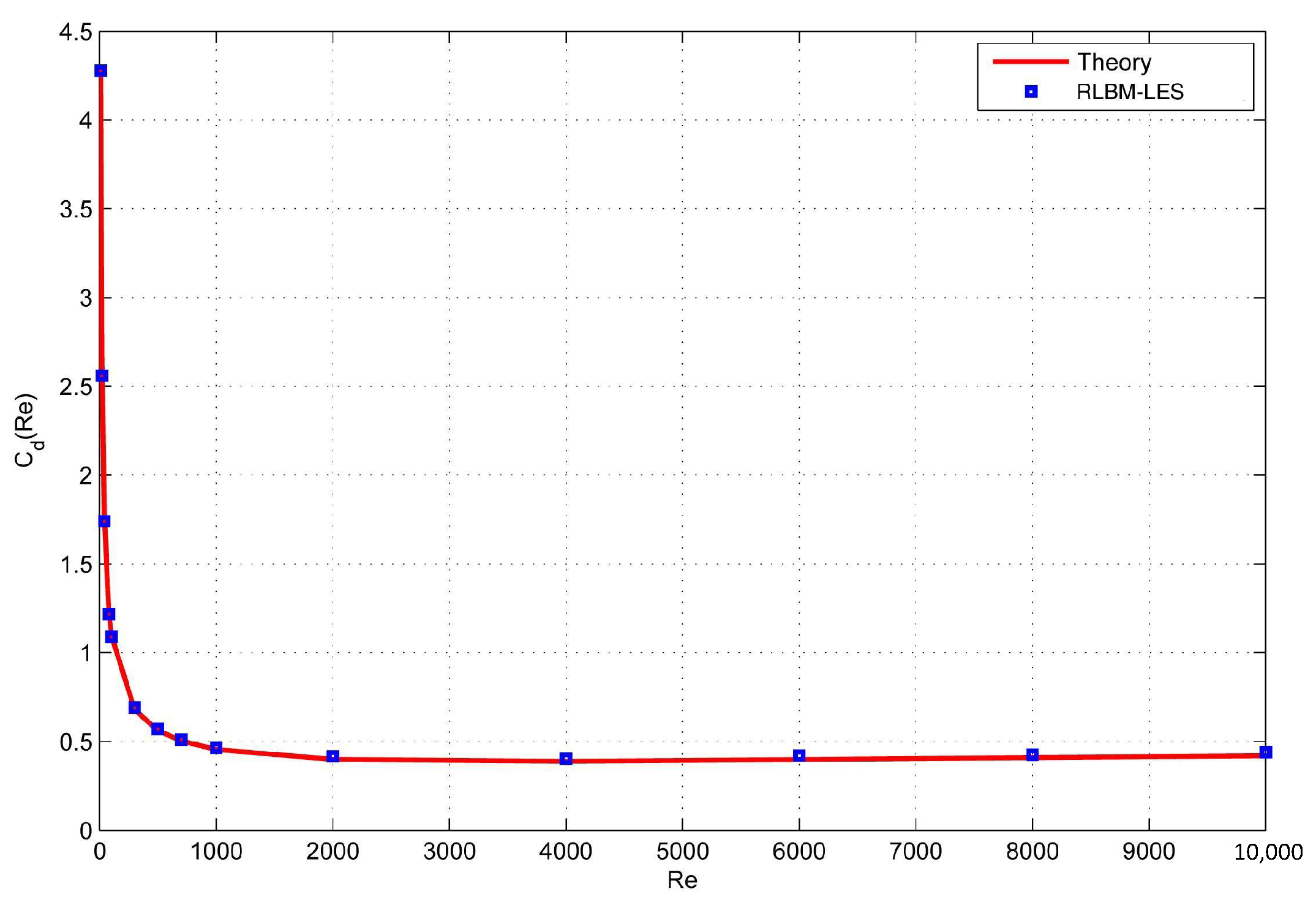
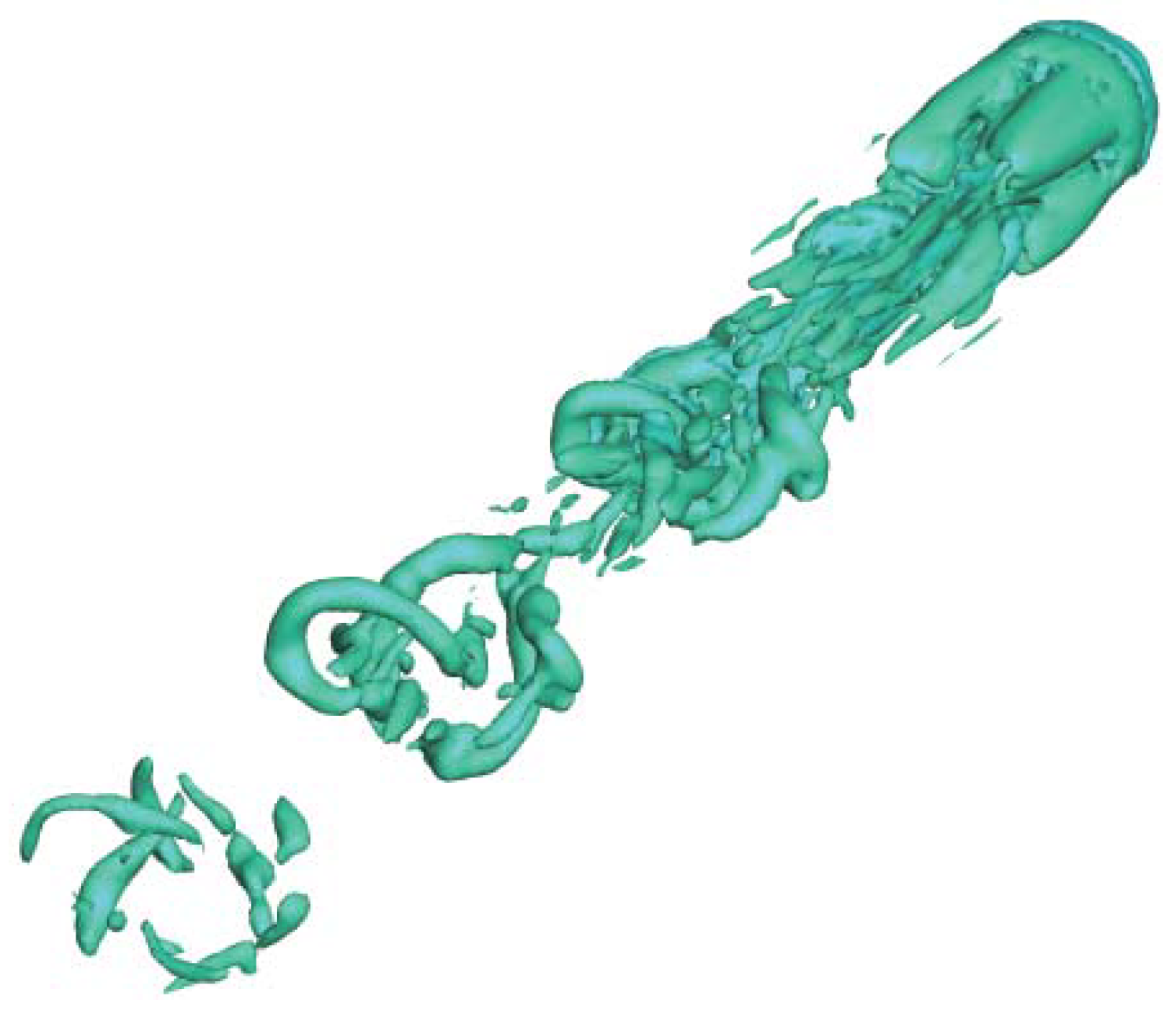
4.1. High Reynolds Number Simulation
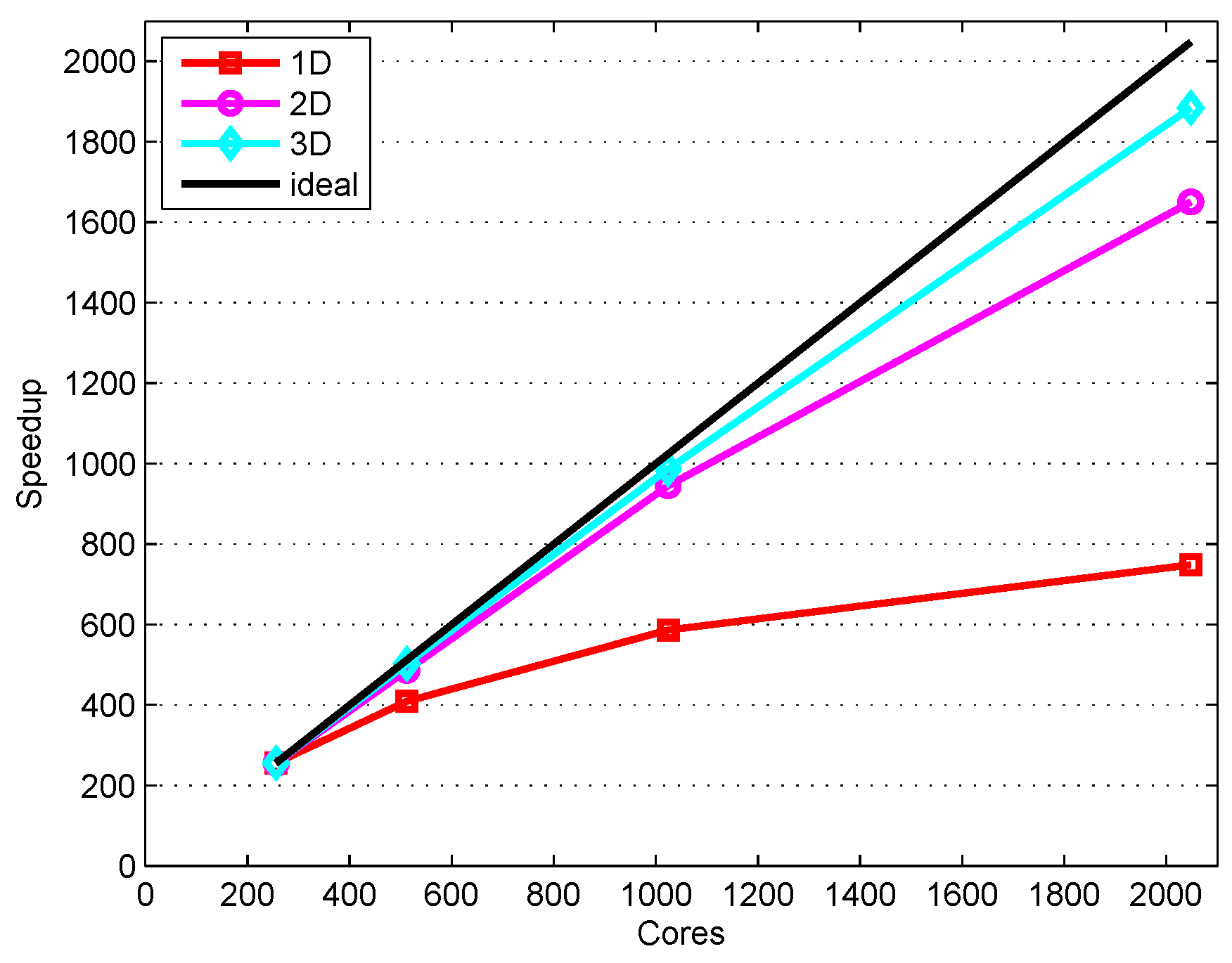
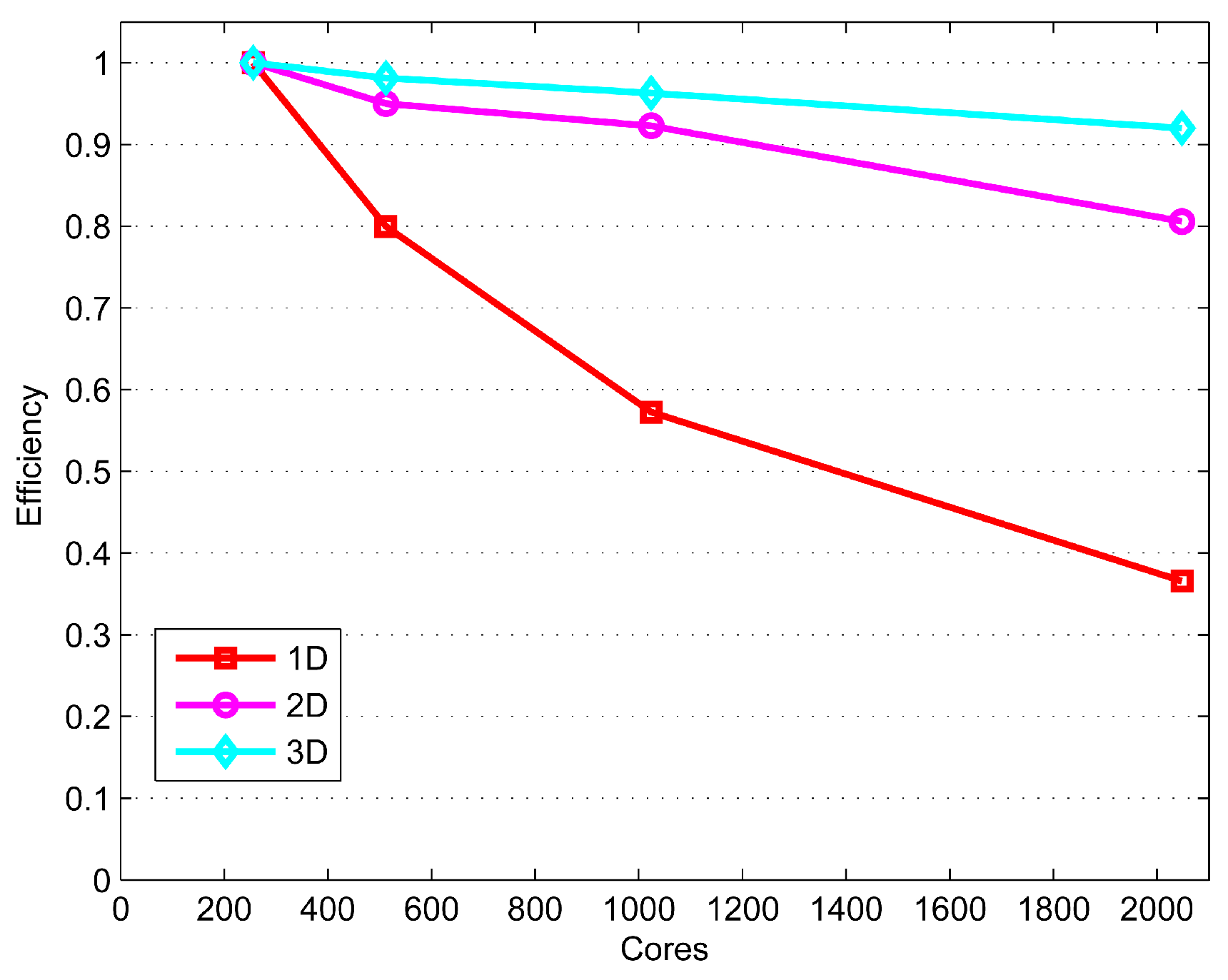
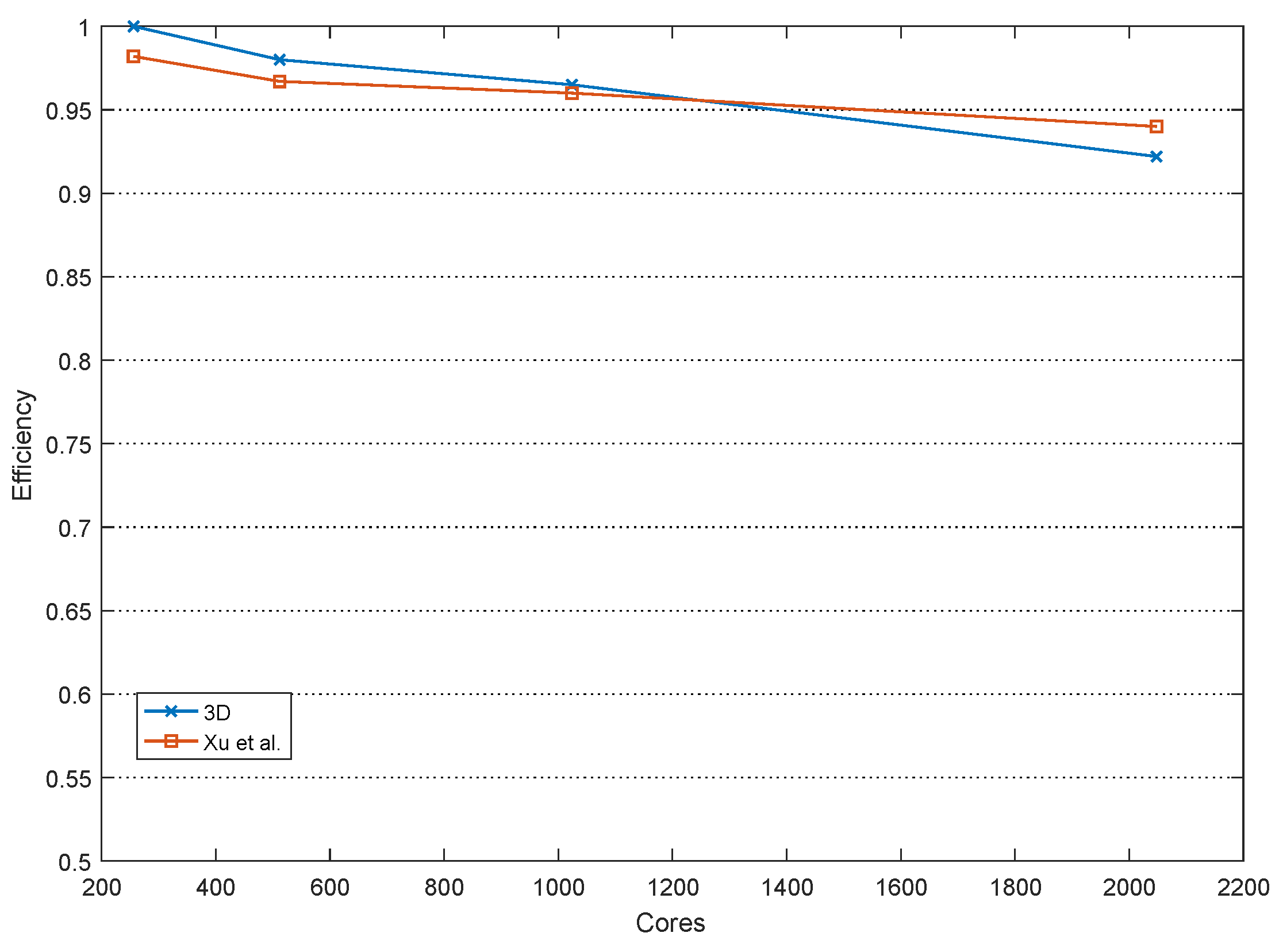
4.2. Comparison of Three Kinds of Domain Decomposition Methods
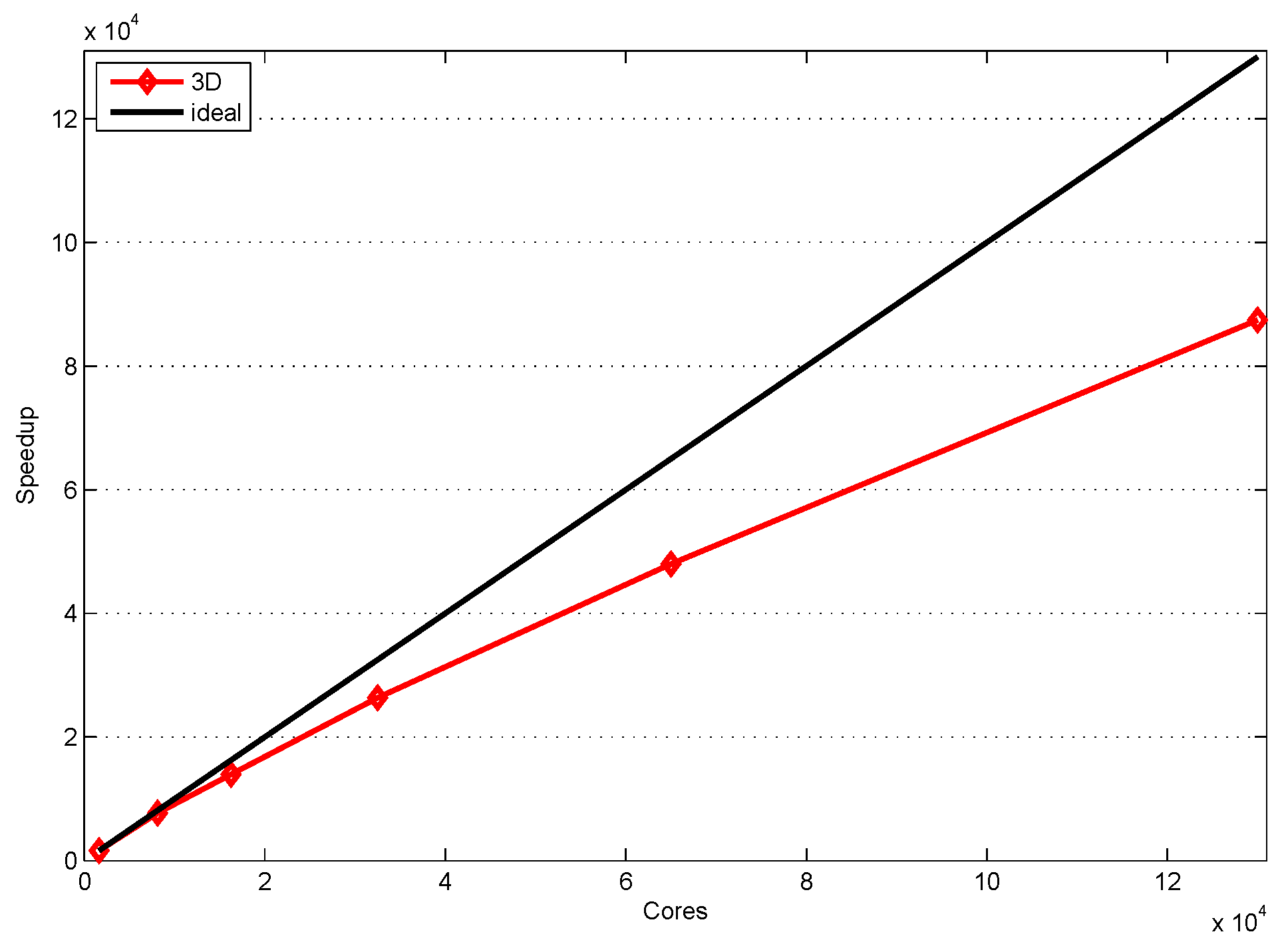
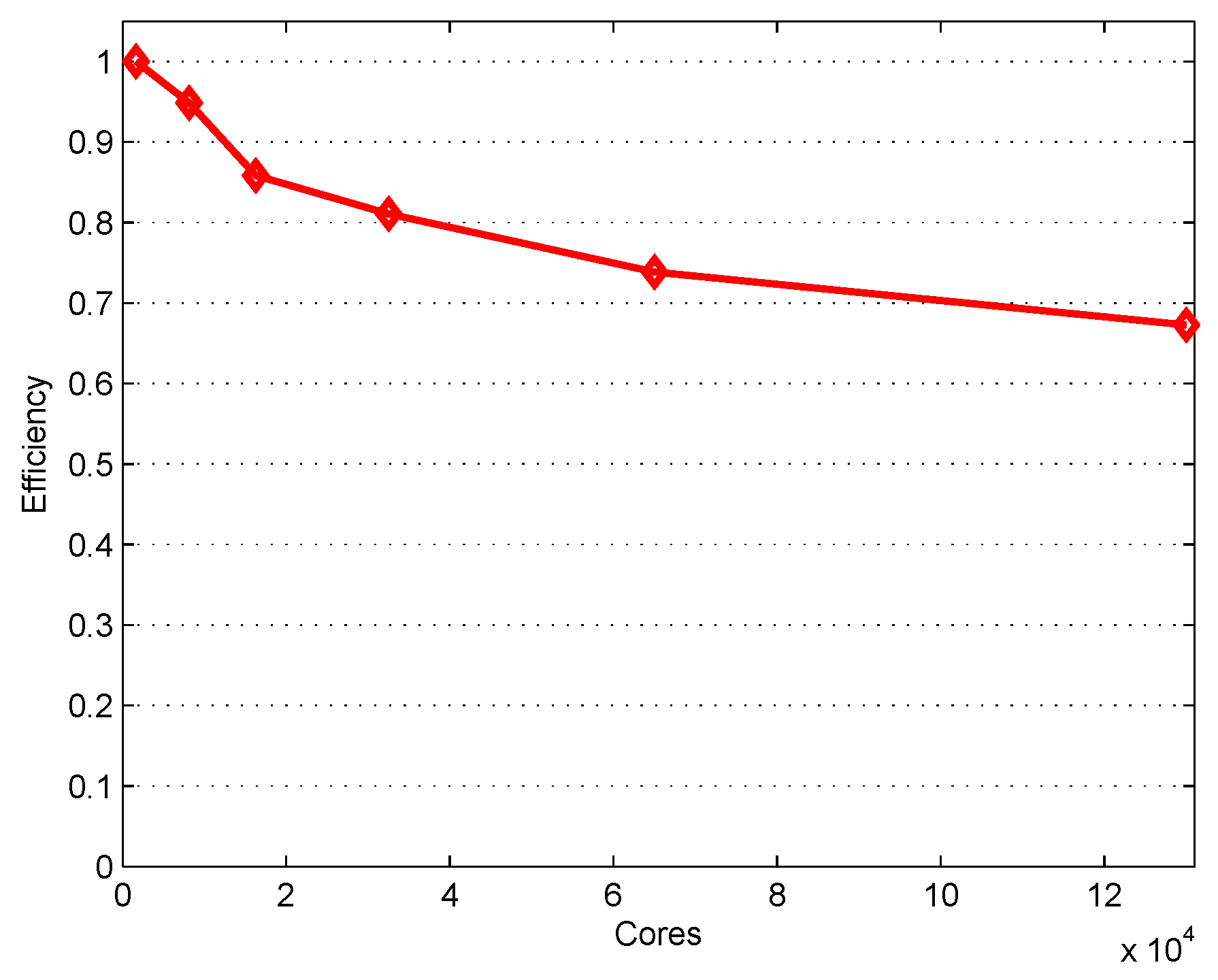
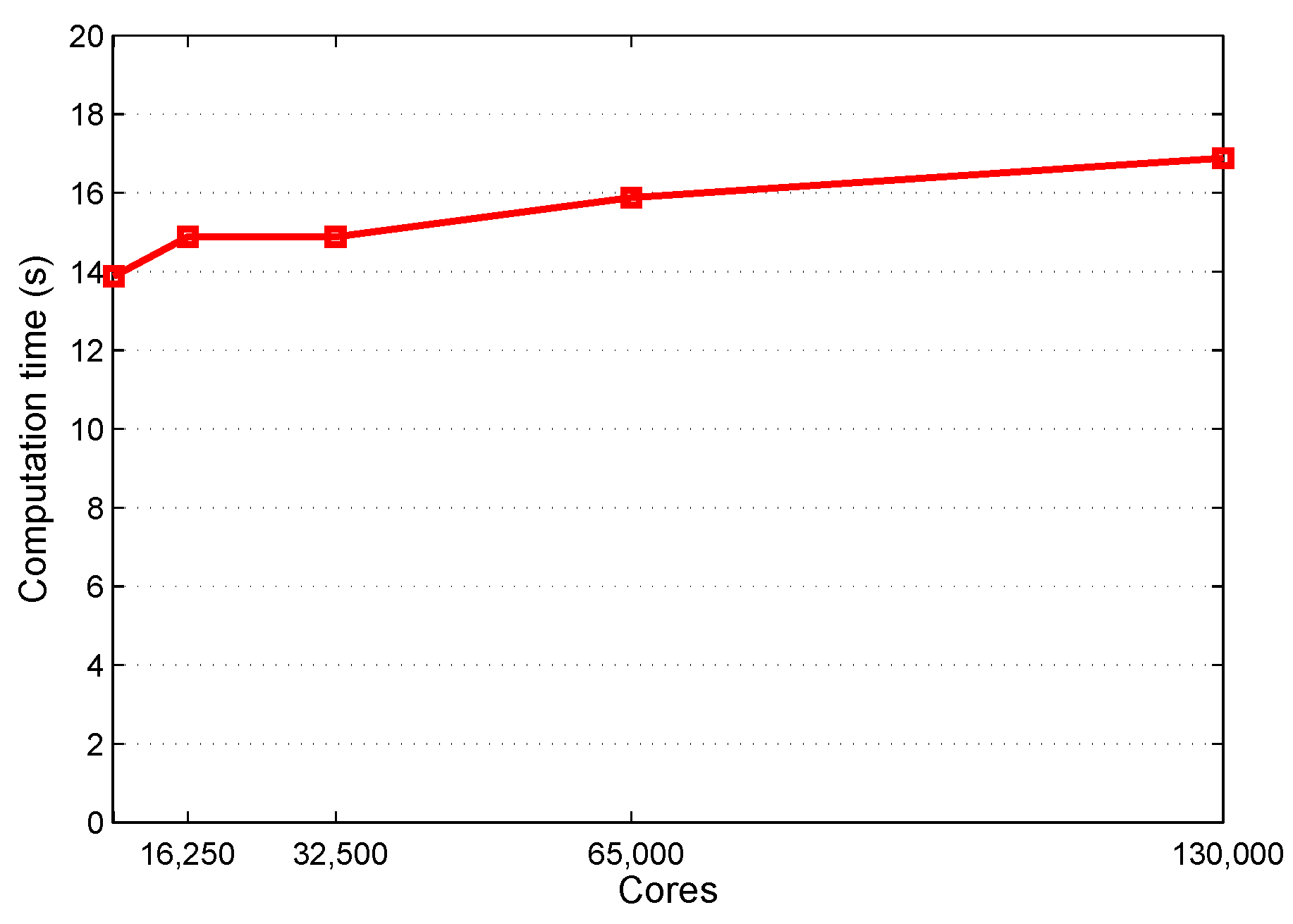
4.3. Performance of 3D Domain Decomposition on Hundreds of Thousands of Cores
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Godunov, S.K.; Bohachevsky, I. Finite difference method for numerical computation of discontinuous solutions of the equations of fluid dynamics. Mat. Sb. 1959, 47, 271–306. [Google Scholar]
- Eymard, R.; Gallouët, T.; Herbin, R. Finite volume methods. Handb. Numer. Anal. 2000, 7, 713–1018. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T. Spectral Methods: Evolution to Complex Geometries and Applications to Fluid Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Ullah, I. Activation energy with exothermic/endothermic reaction and Coriolis force effects on magnetized nanomaterials flow through Darcy–Forchheimer porous space with variable features. Waves Random Complex Media 2022, 1–14. [Google Scholar] [CrossRef]
- Ullah, I. Heat transfer enhancement in Marangoni convection and nonlinear radiative flow of gasoline oil conveying Boehmite alumina and aluminum alloy nanoparticles. Int. Commun. Heat Mass Transf. 2022, 132, 105920. [Google Scholar]
- Ullah, S.; Ullah, I.; Ali, A. Soret and Dufour effects on dissipative Jeffrey nanofluid flow over a curved surface with nonlinear slip, activation energy and entropy generation. Waves Random Complex Media 2023, 1–23. [Google Scholar] [CrossRef]
- Ullah, I.; Alam, M.M.; Shah, M.I.; Weera, W. Marangoni convection in dissipative flow of nanofluid through porous space. Sci. Rep. 2023, 13, 6287. [Google Scholar] [CrossRef] [PubMed]
- Ullah, I.; Shukat, S.; Albakri, A.; Khan, H.; Galal, A.M.; Jamshed, W. Thermal performance of aqueous alumina–titania hybrid nanomaterials dispersed in rotating channel. Int. J. Mod. Phys. B 2023, 37, 2350237. [Google Scholar] [CrossRef]
- Hollingsworth, S.A.; Dror, R.O. Molecular dynamics simulation for all. Neuron 2018, 99, 1129–1143. [Google Scholar]
- Wolfram, S. Cellular automata as models of complexity. Nature 1984, 311, 419–424. [Google Scholar] [CrossRef]
- Cheng, X.; Su, R.; Shen, X.; Deng, T.; Zhang, D.; Chang, D.; Zhang, B.; Qiu, S. Modeling of indoor airflow around thermal manikins by multiple-relaxation-time lattice Boltzmann method with LES approaches. Numer. Heat Transf. Part A Appl. 2020, 77, 215–231. [Google Scholar]
- Silva, G. Consistent lattice Boltzmann modeling of low-speed isothermal flows at finite Knudsen numbers in slip-flow regime. II. Application to curved boundaries. Phys. Rev. E 2018, 98, 023302. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Liu, H. A mesoscopic coupling scheme for solute transport in surface water using the lattice boltzmann method. J. Hydrol. 2020, 588, 125062. [Google Scholar] [CrossRef]
- Saboohi, Z.; Roofeh, S.; Salimi, M. Analysis of misalignment effects on hydrodynamic non-circular journal bearings using three-dimensional lattice boltzmann method. Iran. J. Sci. Technol. Trans. A Sci. 2020, 44, 1739–1751. [Google Scholar] [CrossRef]
- Wu, W.; Liu, X.; Dai, Y.; Li, Q. An in-depth quantitative analysis of wind turbine blade tip wake flow based on the lattice Boltzmann method. Environ. Sci. Pollut. Res. 2021, 28, 40103–40115. [Google Scholar] [CrossRef] [PubMed]
- Jiang, F.; Liu, H.; Chen, X.; Tsuji, T. A coupled LBM-DEM method for simulating the multiphase fluid-solid interaction problem. J. Comput. Phys. 2022, 454, 110963. [Google Scholar]
- Berra, E.M.; Faraji, M. Lattice Boltzmann Method Investigations of Natural Convection within a Cavity Equipped with a Heat Source: A Parametric Study. Heat Transf. Res. 2022, 53, 71–99. [Google Scholar] [CrossRef]
- Afra, B.; Karimnejad, S.; Delouei, A.A.; Tarokh, A. Flow control of two tandem cylinders by a highly flexible filament: Lattice spring IB-LBM. Ocean Eng. 2022, 250, 111025. [Google Scholar]
- Delouei, A.A.; Karimnejad, S.; He, F. Direct Numerical Simulation of pulsating flow effect on the distribution of non-circular particles with increased levels of complexity: IB-LBM. Comput. Math. Appl. 2022, 121, 115–130. [Google Scholar]
- Chen, S.; Chen, H.; Martnez, D.; Matthaeus, W. Lattice Boltzmann model for simulation of magnetohydrodynamics. Phys. Rev. Lett. 1991, 67, 3776. [Google Scholar] [CrossRef]
- Simonis, S.; Oberle, D.; Gaedtke, M.; Jenny, P.; Krause, M.J. Temporal large eddy simulation with lattice Boltzmann methods. J. Comput. Phys. 2022, 454, 110991. [Google Scholar] [CrossRef]
- Sun, H.; Jiang, L.; Xia, Y. LBM simulation of non-Newtonian fluid seepage based on fractional-derivative constitutive model. J. Pet. Sci. Eng. 2022, 213, 110378. [Google Scholar]
- Ezzatneshan, E. Comparative study of the lattice Boltzmann collision models for simulation of incompressible fluid flows. Math. Comput. Simul. 2019, 156, 158–177. [Google Scholar]
- Latt, J.; Chopard, B. Lattice Boltzmann method with regularized pre-collision distribution functions. Math. Comput. Simul. 2006, 72, 165–168. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Hou, S.; Sterling, J.; Chen, S.; Doolen, G. A lattice Boltzmann subgrid model for high Reynolds number flows. Pattern Form. Lattice Gas Autom. 1995, 151–166. [Google Scholar]
- Tiftikçi, A.; Kocar, C. Lattice Boltzmann simulation of flow across a staggered tube bundle array. Nucl. Eng. Des. 2016, 300, 135–148. [Google Scholar]
- Mekala, M.; Dhiman, G.; Srivastava, G.; Nain, Z.; Zhang, H.; Viriyasitavat, W.; Varma, G. A DRL-based service offloading approach using DAG for edge computational orchestration. IEEE Trans. Comput. Soc. Syst. 2022. Early Access. [Google Scholar]
- Shukla, S.K.; Gupta, V.K.; Joshi, K.; Gupta, A.; Singh, M.K. Self-aware execution environment model (SAE2) for the performance improvement of multicore systems. Int. J. Mod. Res. 2022, 2, 17–27. [Google Scholar]
- Vaishnav, P.K.; Sharma, S.; Sharma, P. Analytical review analysis for screening COVID-19 disease. Int. J. Mod. Res. 2021, 1, 22–29. [Google Scholar]
- Chatterjee, I. Artificial intelligence and patentability: Review and discussions. Int. J. Mod. Res. 2021, 1, 15–21. [Google Scholar]
- Gupta, V.K.; Shukla, S.K.; Rawat, R.S. Crime tracking system and people’s safety in India using machine learning approaches. Int. J. Mod. Res. 2022, 2, 1–7. [Google Scholar]
- Sharma, T.; Nair, R.; Gomathi, S. Breast cancer image classification using transfer learning and convolutional neural network. Int. J. Mod. Res. 2022, 2, 8–16. [Google Scholar]
- Alferaidi, A.; Yadav, K.; Alharbi, Y.; Razmjooy, N.; Viriyasitavat, W.; Gulati, K.; Kautish, S.; Dhiman, G. Distributed deep CNN-LSTM model for intrusion detection method in IoT-based vehicles. Math. Probl. Eng. 2022, 2022, 3424819. [Google Scholar] [CrossRef]
- Puri, T.; Soni, M.; Dhiman, G.; Ibrahim Khalaf, O.; Alazzam, M.; Raza Khan, I. Detection of emotion of speech for RAVDESS audio using hybrid convolution neural network. J. Healthc. Eng. 2022, 2022, 8472947. [Google Scholar] [CrossRef]
- Sharma, S.; Gupta, S.; Gupta, D.; Juneja, S.; Gupta, P.; Dhiman, G.; Kautish, S. Deep learning model for the automatic classification of white blood cells. Comput. Intell. Neurosci. 2022, 2022, 7384131. [Google Scholar] [CrossRef]
- Swain, S.; Bhushan, B.; Dhiman, G.; Viriyasitavat, W. Appositeness of optimized and reliable machine learning for healthcare: A survey. Arch. Comput. Methods Eng. 2022, 29, 3981–4003. [Google Scholar]
- Uppal, M.; Gupta, D.; Juneja, S.; Dhiman, G.; Kautish, S. Cloud-based fault prediction using IoT in office automation for improvisation of health of employees. J. Healthc. Eng. 2021, 2021, 8106467. [Google Scholar] [CrossRef]
- Kumar, R.; Dhiman, G. A comparative study of fuzzy optimization through fuzzy number. Int. J. Mod. Res. 2021, 1, 1–14. [Google Scholar]
- Xu, L.; Song, A.; Zhang, W. Scalable parallel algorithm of multiple-relaxation-time lattice Boltzmann method with large eddy simulation on multi-GPUs. Sci. Program. 2018, 2018, 1298313. [Google Scholar] [CrossRef]
- Abas, A.; Mokhtar, N.H.; Ishak, M.H.H.; Abdullah, M.Z.; Ho Tian, A. Lattice Boltzmann model of 3D multiphase flow in artery bifurcation aneurysm problem. Comput. Math. Methods Med. 2016, 2016, 6143126. [Google Scholar]
- Tan, J.; Sinno, T.R.; Diamond, S.L. A parallel fluid–solid coupling model using LAMMPS and Palabos based on the immersed boundary method. J. Comput. Sci. 2018, 25, 89–100. [Google Scholar]
- Závodszky, G.; Paál, G. Validation of a lattice Boltzmann method implementation for a 3D transient fluid flow in an intracranial aneurysm geometry. Int. J. Heat Fluid Flow 2013, 44, 276–283. [Google Scholar] [CrossRef]
- Basha, M.; Sidik, N.A.C. Numerical predictions of laminar and turbulent forced convection: Lattice Boltzmann simulations using parallel libraries. Int. J. Heat Mass Transf. 2018, 116, 715–724. [Google Scholar] [CrossRef]
- Safdari Shadloo, M. Numerical simulation of compressible flows by lattice Boltzmann method. Numer. Heat Transf. Part A Appl. 2019, 75, 167–182. [Google Scholar] [CrossRef]
- Jahidul Haque, M.; Mamun Molla, M.; Amirul Islam Khan, M.; Ahsan, K. Graphics process unit accelerated lattice Boltzmann simulation of indoor air flow: Effects of sub-grid scale model in large-eddy simulation. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 4024–4040. [Google Scholar] [CrossRef]
- Delbosc, N.; Summers, J.L.; Khan, A.; Kapur, N.; Noakes, C.J. Optimized implementation of the Lattice Boltzmann Method on a graphics processing unit towards real-time fluid simulation. Comput. Math. Appl. 2014, 67, 462–475. [Google Scholar] [CrossRef]
- Zhao-Li, G.; Chu-Guang, Z.; Bao-Chang, S. Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method. Chin. Phys. 2002, 11, 366. [Google Scholar] [CrossRef]
- Obrecht, C.; Kuznik, F.; Tourancheau, B.; Roux, J.J. Multi-GPU implementation of the lattice Boltzmann method. Comput. Math. Appl. 2013, 65, 252–261. [Google Scholar] [CrossRef]
- Lee, Y.H.; Huang, L.M.; Zou, Y.S.; Huang, S.C.; Lin, C.A. Simulations of turbulent duct flow with lattice Boltzmann method on GPU cluster. Comput. Fluids 2018, 168, 14–20. [Google Scholar] [CrossRef]
- Schneider, P.; Eberly, D.H. Geometric Tools for Computer Graphics (Morgan Kaufmann Series in Computer Graphics and Geometric Modeling); Morgan Kaufmann Publishers: Burlington, MA, USA, 2003. [Google Scholar]
- Ku, H.C.; Hirsh, R.S.; Taylor, T.D. A pseudospectral method for solution of the three-dimensional incompressible Navier-Stokes equations. J. Comput. Phys. 1987, 70, 439–462. [Google Scholar] [CrossRef]
- Jiang, B.N.; Lin, T.; Povinelli, L.A. Large-scale computation of incompressible viscous flow by least-squares finite element method. Comput. Methods Appl. Mech. Eng. 1994, 114, 213–231. [Google Scholar] [CrossRef]
- Prasad, A.K.; Koseff, J.R. Reynolds number and end-wall effects on a lid-driven cavity flow. Phys. Fluids A Fluid Dyn. 1989, 1, 208–218. [Google Scholar] [CrossRef]
- Mei, R.; Yu, D.; Shyy, W.; Luo, L.S. Force evaluation in the lattice Boltzmann method involving curved geometry. Phys. Rev. E 2002, 65, 041203. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, S.S.; Pal, E.; Bale, S.; Minocha, N.; Patwardhan, A.W.; Nandakumar, K.; Joshi, J.B. Flow past a single stationary sphere, 1. Experimental and numerical techniques. Powder Technol. 2020, 365, 115–148. [Google Scholar] [CrossRef]
- Turton, R.; Levenspiel, O. A short note on the drag correlation for spheres. Powder Technol. 1986, 47, 83–86. [Google Scholar] [CrossRef]
- Xu, C.; Wang, X.; Li, D.; Che, Y.; Wang, Z. OpenMP4. 5-enabled large-scale heterogeneous Lattice Boltzmann multiphase flow simulations. In Proceedings of the 2019 IEEE Intl Conf on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking (ISPA/BDCloud/SocialCom/SustainCom), Xiamen, China, 16–18 December 2019; pp. 1007–1016. [Google Scholar]
- Liu, Z.; Li, Y.; Song, W. Regularized lattice Boltzmann method parallel model on heterogeneous platforms. Concurr. Comput. Pract. Exp. 2022, 34, e6875. [Google Scholar] [CrossRef]




| DDM | nDDX | nDDY | nDDZ | Communication Amount | |||
|---|---|---|---|---|---|---|---|
| 1D | (0, ) | 1 | 1 | (0, ) | 512 | 512 | 5,242,880 |
| 2D | 256 | 8 | 1 | 2 | 64 | 512 | 679,936 |
| 128 | 16 | 1 | 4 | 32 | 512 | 372,736 | |
| 64 | 32 | 1 | 8 | 16 | 512 | 249,856 | |
| 3D | 256 | 4 | 2 | 2 | 128 | 256 | 673,808 |
| 128 | 8 | 2 | 4 | 64 | 256 | 355,872 | |
| 128 | 4 | 4 | 4 | 128 | 128 | 350,240 | |
| 64 | 16 | 2 | 8 | 32 | 256 | 212,288 | |
| 64 | 8 | 4 | 8 | 64 | 128 | 196,160 | |
| 32 | 32 | 2 | 16 | 16 | 256 | 171,264 | |
| 32 | 16 | 4 | 16 | 32 | 128 | 134,528 | |
| 32 | 8 | 8 | 16 | 64 | 64 | 124,032 | |
| 16 | 16 | 8 | 32 | 32 | 64 | 103,424 |
| DDM | nDDX | nDDY | nDDZ | Lattice Amount | |||
|---|---|---|---|---|---|---|---|
| 1D | 2048 | 1 | 1 | 1 | 512 | 512 | 786,432 |
| 2D | 256 | 8 | 1 | 8 | 64 | 512 | 337,920 |
| 128 | 16 | 1 | 16 | 32 | 512 | 313,344 | |
| 64 | 32 | 1 | 32 | 16 | 512 | 313,344 | |
| 3D | 256 | 4 | 2 | 8 | 128 | 256 | 335,400 |
| 128 | 8 | 2 | 16 | 64 | 256 | 306,504 | |
| 128 | 4 | 4 | 16 | 128 | 128 | 304,200 | |
| 64 | 16 | 2 | 32 | 32 | 256 | 298,248 | |
| 64 | 8 | 4 | 32 | 64 | 128 | 291,720 | |
| 32 | 32 | 2 | 64 | 16 | 256 | 306,504 | |
| 32 | 16 | 4 | 64 | 32 | 128 | 291,720 | |
| 32 | 8 | 8 | 64 | 64 | 64 | 287,496 | |
| 16 | 16 | 8 | 128 | 32 | 64 | 291,720 |
| nPX | nPY | nPZ | Iterative Time (s) | Communication Time (s) | Time to Generate Grid (s) | |
|---|---|---|---|---|---|---|
| 1D | 256 | 1 | 1 | 1410.78 | 53.2321 | 13.9915 |
| 512 | 1 | 1 | 882.0 | 54.5075 | 9.30438 | |
| 1024 | 1 | 1 | 616.1 | 53.7755 | 6.59018 | |
| 2048 | 1 | 1 | 482.4 | 54.7407 | 5.28579 | |
| 2D | 32 | 8 | 1 | 1172.85 | 12.9407 | 14.0736 |
| 64 | 8 | 1 | 624.2 | 10.3737 | 10.2649 | |
| 64 | 16 | 1 | 321.2 | 7.70774 | 6.99043 | |
| 128 | 16 | 1 | 183.9 | 6.26043 | 5.32507 | |
| 3D | 16 | 4 | 4 | 1152.59 | 10.3427 | 9.4711 |
| 32 | 4 | 4 | 592.6 | 7.17983 | 8.72643 | |
| 16 | 8 | 8 | 301.9 | 4.81678 | 5.17024 | |
| 64 | 8 | 4 | 157.9 | 3.48762 | 8.16628 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Chen, Y.; Xiao, W.; Song, W.; Li, Y. Large-Scale Cluster Parallel Strategy for Regularized Lattice Boltzmann Method with Sub-Grid Scale Model in Large Eddy Simulation. Appl. Sci. 2023, 13, 11078. https://doi.org/10.3390/app131911078
Liu Z, Chen Y, Xiao W, Song W, Li Y. Large-Scale Cluster Parallel Strategy for Regularized Lattice Boltzmann Method with Sub-Grid Scale Model in Large Eddy Simulation. Applied Sciences. 2023; 13(19):11078. https://doi.org/10.3390/app131911078
Chicago/Turabian StyleLiu, Zhixiang, Yuanji Chen, Wenjun Xiao, Wei Song, and Yu Li. 2023. "Large-Scale Cluster Parallel Strategy for Regularized Lattice Boltzmann Method with Sub-Grid Scale Model in Large Eddy Simulation" Applied Sciences 13, no. 19: 11078. https://doi.org/10.3390/app131911078
APA StyleLiu, Z., Chen, Y., Xiao, W., Song, W., & Li, Y. (2023). Large-Scale Cluster Parallel Strategy for Regularized Lattice Boltzmann Method with Sub-Grid Scale Model in Large Eddy Simulation. Applied Sciences, 13(19), 11078. https://doi.org/10.3390/app131911078







