Multi-Directional Displacement Threshold Energy and Crystal Irradiation Damage Model
Abstract
1. Introduction
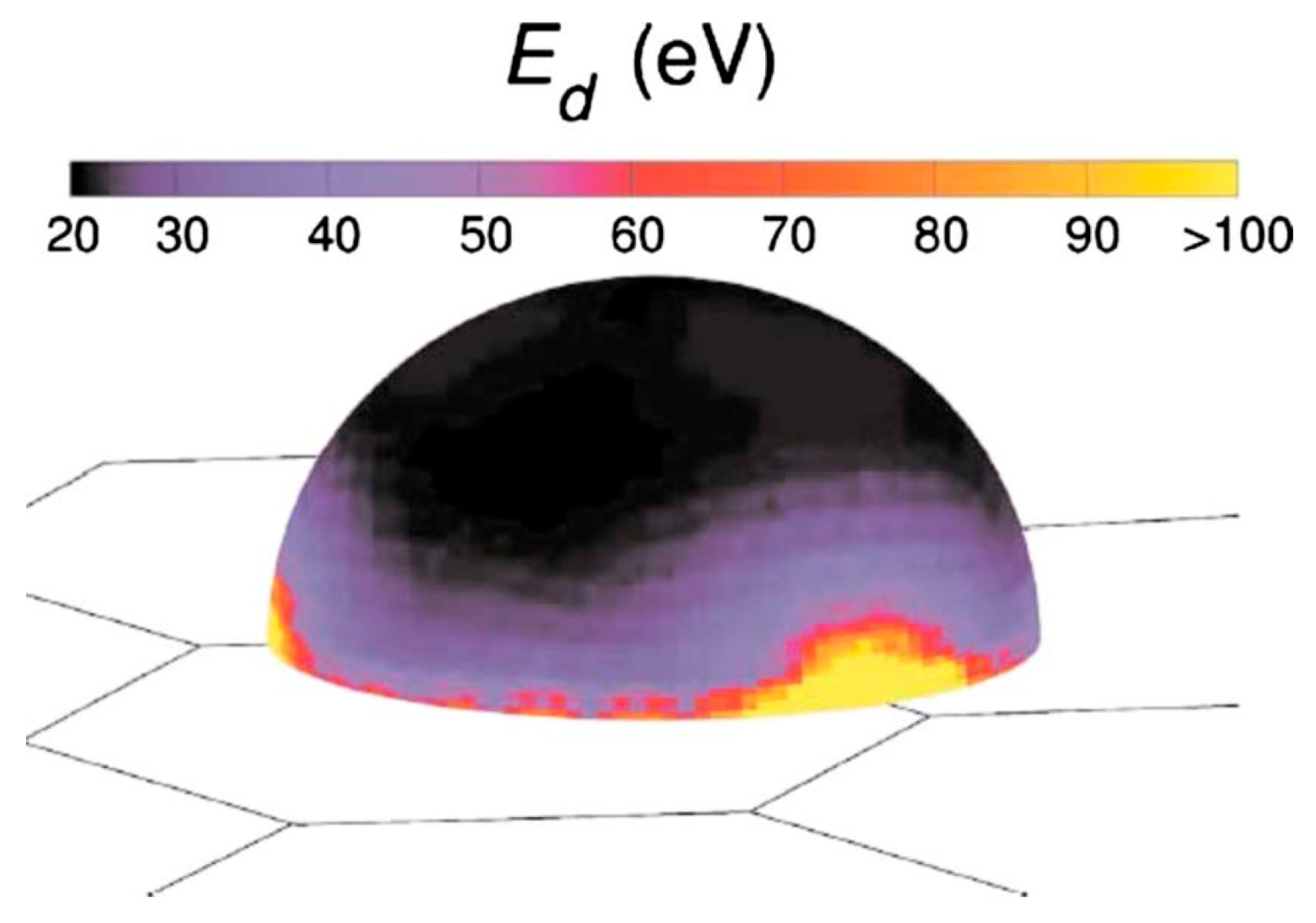
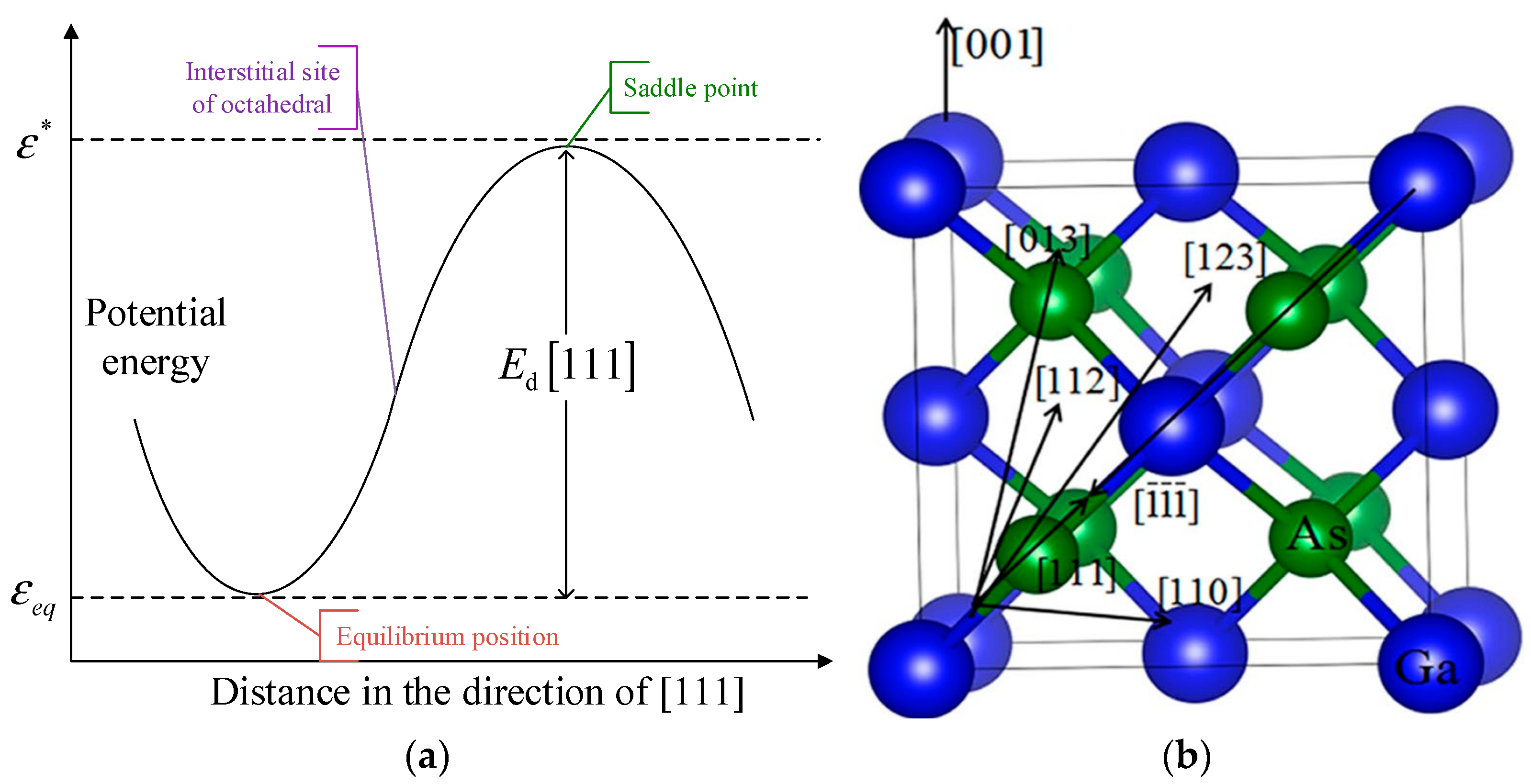
2. Displacement Threshold
3. Crystal Defect Types and Formation
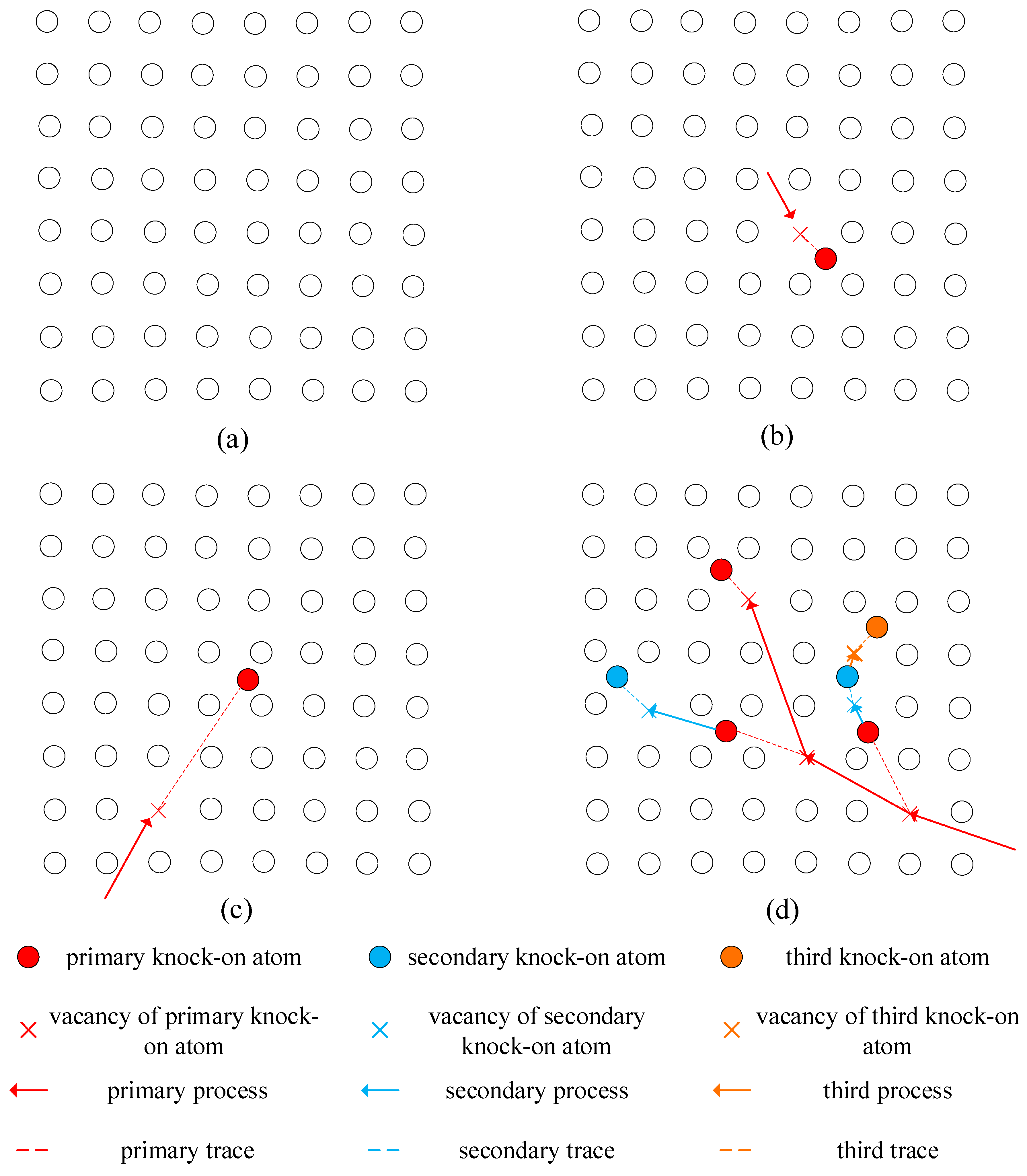
4. Atomic Displacement Model under Radiation
4.1. Development of Classical Models
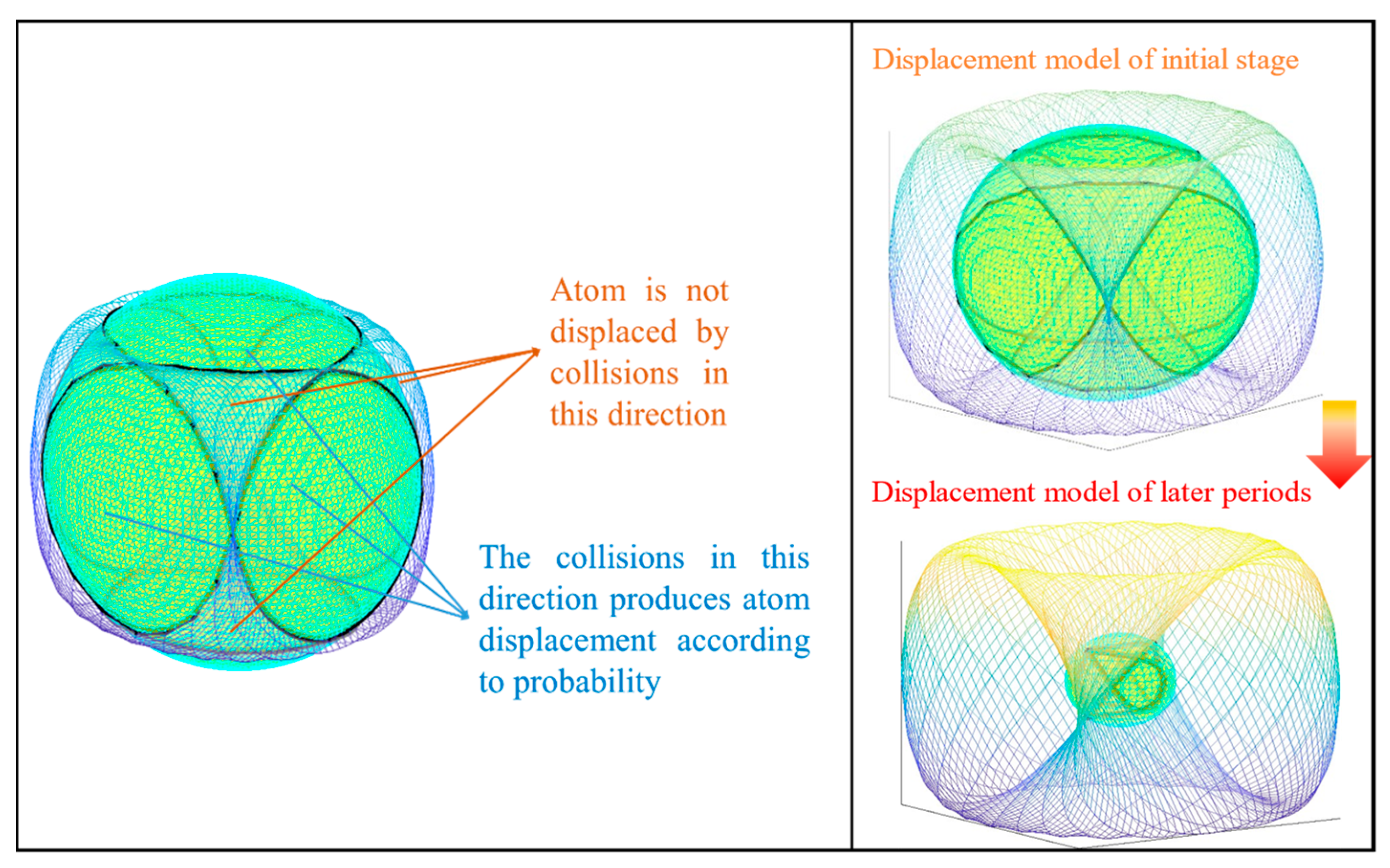
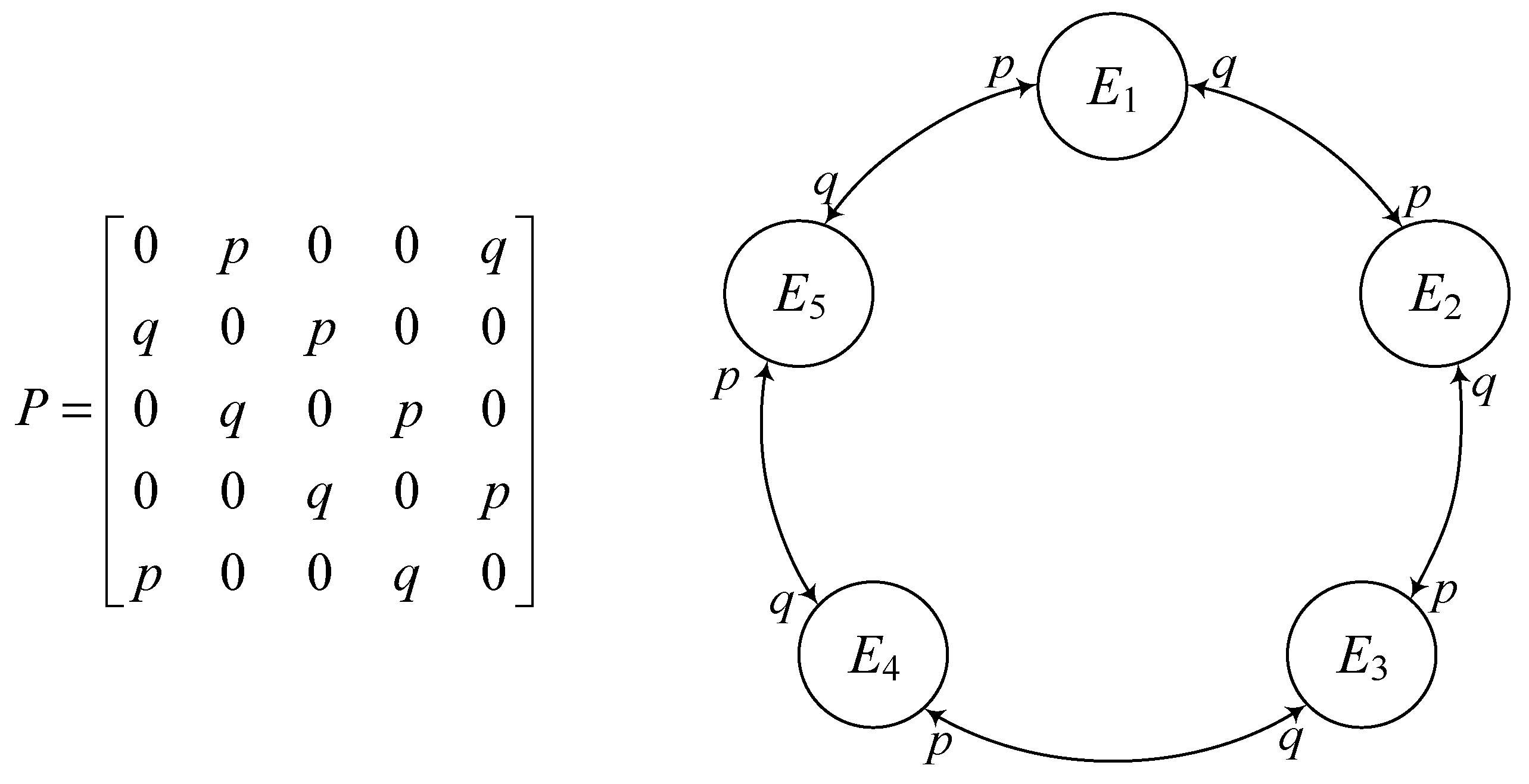
4.2. New Method for Displacement Probability
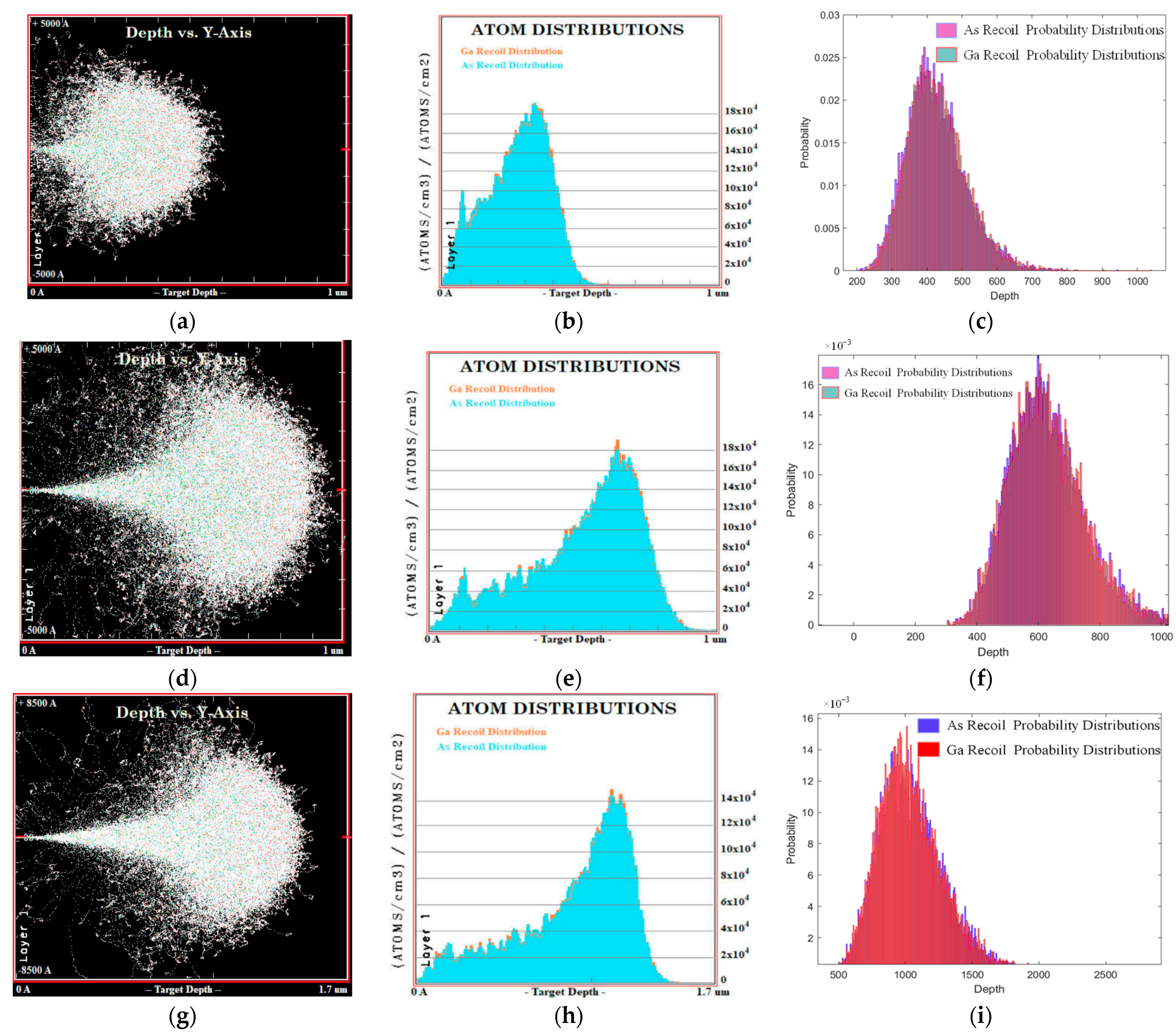
4.3. The Displacement Threshold Energy Transfer Probability of Different Crystal Types
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, D.H.; Lee, J.H.; Son, S.K. Band-structure simulations for overlap wave functions between electrons and holes for recombination in undoped GaAs/AlGaAs heterostructures. J. Korean Phys. Soc. 2022, 80, 161–166. [Google Scholar] [CrossRef]
- Kaczmarek, S.M. Recharging processes of active ions and radiation defects in some laser crystals doped with RE and TM ions under proton irradiation. Opt. Mater. 2007, 29, 1400–1407. [Google Scholar] [CrossRef]
- Kinchin, G.H.; Pease, R.S. The Displacement of atoms in solids by radiation. Rep. Prog. Phys. 1955, 18, 1329–1334. [Google Scholar] [CrossRef]
- Olander, D.R. Molecular Beam Sources Fabricated from Multichannel Arrays. III. The Exit Density Problem. J. Appl. Phys. 1970, 41, 2769–2776. [Google Scholar] [CrossRef]
- Robinson, M.T. Computer simulation studies of high-energy collision cascades. Nucl. Instr. Meth. Phys. Res. B 1992, 67, 396–400. [Google Scholar] [CrossRef]
- Nordlund, K. Historical review of computer simulation of radiation effects in materials. J. Nucl. Mater. 2019, 520, 273–295. [Google Scholar] [CrossRef]
- Norgett, M.J.; Robinson, M.T.; Torrens, I.M. A proposed method of calculating displacement dose rates. Nucl. Eng. Des. 1975, 33, 50–54. [Google Scholar] [CrossRef]
- Nordlund, K.H.; Sand, A.E.; Granberg, F.G.; Zinkle, S. Primary radiation damage in materials: Review of current understanding and proposed new standard displacement damage model to incorporate in cascade defect production efficiency and mixing effects. OECD Nucl. Energy Agency 2015, 9, 1–87. [Google Scholar]
- Robinson, M.T.; Torrens, I.M. Computer simulation of atomic-displacement cascades insolids in the binary-collision approximation. Phys. Rev. B 1974, 9, 5008. [Google Scholar] [CrossRef]
- Robinson, M.T.; Oen, O.S. On the use of thresholds in damage energy calculations. J. Nucl. Mater. 1982, 110, 147–149. [Google Scholar] [CrossRef]
- Biersack, J.P.; Haggmark, L.G. A Monte Carlo computer program for the transport of energetic ions in amorphous targets. Nucl. Instr. Meth. 1980, 174, 257–269. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM-The stopping and range of ions in matter. Nucl. Instr. Meth. Phys. Res. B 2010, 268, 1818–1823. [Google Scholar] [CrossRef]
- Posselt, M.; Biersack, J. Computer simulation of ion implantation into crystal inetargets. Nucl. Instr. Meth. Phys. Res. B 1992, 64, 706–710. [Google Scholar] [CrossRef]
- Posselt, M. Computer simulation of channeling implantation at high and mediumenergies. Nucl. Instr. Meth. Phys. Res. B 1993, 80, 28–32. [Google Scholar] [CrossRef]
- Djurabekova, F.G.; Pugacheva, T.S.; Umarov, F.F.; Yugay, S.V. Computer Simulation of Ion Implantation with Visual Observation of the Implantation Profiles. In Proceedings of the Conference on Ion Implantation Technology IEEE, Alpbach, Austria, 17–22 September 2000; pp. 228–231. [Google Scholar] [CrossRef]
- Schiettekatte, F. Fast Monte Carlo for ion beam analysis simulations. Nucl. Instr. Meth. Phys. Res. B 2008, 266, 1880–1885. [Google Scholar] [CrossRef]
- Wang, F.; Adolphsen, C.; Nantista, C. Performance limiting effects in X-band accelerators. Phys. Rev. Accel. Beams 2011, 14, 010401. [Google Scholar] [CrossRef]
- Available online: https://www-nds.iaea.org/CRPdpa/ (accessed on 15 May 2022).
- Wang, Z.; Muránsky, O.; Zhu, H. Impact of pre-existing crystal lattice defects on the accumulation of irradiation-induced damage in a C/C composite. J. Nucl. Mater. 2022, 546, 153684. [Google Scholar] [CrossRef]
- Karavaev, A.V.; Dremov, V.V.; Ionov, G.V. Equilibrium thermodynamics of radiation defect clusters in δ-phase Pu–Ga alloys. J. Nucl. Mater. 2016, 468, 46–55. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J. Monte Carlo simulation of pka distribution along nanowires under ion radiation. Nucl. Eng. Des. 2018, 340, 300–307. [Google Scholar] [CrossRef]
- Zobelli, A.; Gloter, A.; Ewels, C.P.; Seifert, G.; Colliex, C. Electron knock-on cross section of carbon and boron nitride nanotubes. Phys. Rev. B 2007, 75, 245402. [Google Scholar] [CrossRef]
- Sadigh, B.; Lenosky, T.J.; Theiss, S.K. Mechanism of Boron Diffusion in Silicon: An Ab Initio and Kinetic Monte Carlo Study. Phys. Rev. Lett. 1999, 83, 4341–4344. [Google Scholar] [CrossRef]
- Nordlund, K.; Averback, R.S. Role of Self-Interstitial Atoms on the High Temperature Properties of Metals. Phys. Rev. Lett. 1998, 80, 4201–4204. [Google Scholar] [CrossRef]
- Nelson, R.S. Ion implantation in semiconductors. AERE Rep. 1969, 20, 165. [Google Scholar] [CrossRef][Green Version]
- Jiang, M.; Xiao, H.Y.; Peng, S.M. A comparative study of low energy radiation response of AlAs, GaAs and GaAs/AlAs superlattice and the damage effects on their electronic structures. Sci. Rep. 2018, 8, 2012. [Google Scholar] [CrossRef] [PubMed]
- Sayed, M.; Jefferson, J.H.; Walker, A.B. Computer simulation of atomic displacements in Si, GaAs, and AlAs. Nucl. Instr. Meth. Phys. Res. B 1995, 102, 232–235. [Google Scholar] [CrossRef]
- Li, J.; Porter, L.; Yip, S. Atomistic modeling of finite-temperature properties of crystalline β-SiC: II. Thermal conductivity and effects of point defects. J. Nucl. Mater. 1998, 255, 139–152. [Google Scholar] [CrossRef]
- Zollo, G.; Tarus, J.; Nieminen, R.M. Reliability of analytical potentials for point-defect simulation in GaAs. J. Phys. Condens. Matter 2004, 16, 3923–3932. [Google Scholar] [CrossRef]
- Ihm, J.; Joannopoulos, J.D. Ground-state properties of GaAs and AlAs. Phys. Rev. B 1981, 24, 4191–4197. [Google Scholar] [CrossRef]
- Ahmed, R.; Hashemifar, S.; Akbarzadeh, H. Ab initio study of structural and electronic properties of III-arsenide binary compounds. Comput. Mater. Sci. 2007, 39, 580–586. [Google Scholar] [CrossRef]
- Nordlund, K.; Zinkle, S.J.; Sand, A.E.; Granberg, F. Primary radiation damage: A review of current understanding and models. J. Nucl. Mater. 2018, 512, 450–479. [Google Scholar] [CrossRef]
- Ji, H.; Yang, S. Stochastic Stability of Semi-Markov Jump Linear Systems: An LMI Approach. In Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 4668–4673. [Google Scholar] [CrossRef]
- Li, S.S.; Chiu, T.T.; Loo, R.Y. Effects of Low Temperature Periodic Annealing on the Deep-Level Defects in 200 KeV Proton Irradiated AlGaAs-GaAs Solar Cells. IEEE Trans. Nucl. Sci. 1981, 28, 4113–4118. [Google Scholar] [CrossRef]

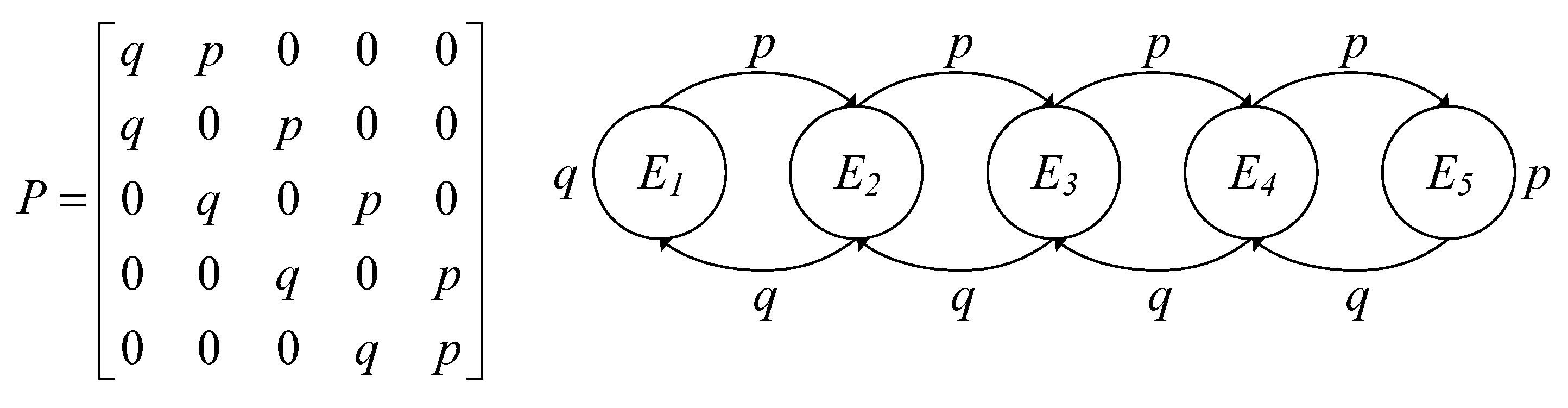

| Displacement Threshold in GaAs (eV) | ||
|---|---|---|
| Crystal Orientation | Ga | As |
| [001] | 14.5 [26], 14 [27] | 10 [26], 16 [27] |
| [110] | 12 [26], 16 [27] | 10 [26], 20 [27] |
| [111] | 12 [26], 16 [27] | 8.5 [26], 16 [27] |
| [013] | 17.5 [26] | 12 [26] |
| [112] | 22.5 [26] | 10 [26] |
| [123] | 30 [26] | 10 [26] |
| Lattice constant | 5.66 [28], 5.65 [29] | |
| Cohesive energy | 3.7 [30], 3.18 [31], 3.35 [29] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Zeng, Y.; Li, Y.-F.; Huang, H.-Z.; Gul Niazi, S. Multi-Directional Displacement Threshold Energy and Crystal Irradiation Damage Model. Appl. Sci. 2023, 13, 10701. https://doi.org/10.3390/app131910701
Zhang T, Zeng Y, Li Y-F, Huang H-Z, Gul Niazi S. Multi-Directional Displacement Threshold Energy and Crystal Irradiation Damage Model. Applied Sciences. 2023; 13(19):10701. https://doi.org/10.3390/app131910701
Chicago/Turabian StyleZhang, Tingyu, Ying Zeng, Yan-Feng Li, Hong-Zhong Huang, and Sajawal Gul Niazi. 2023. "Multi-Directional Displacement Threshold Energy and Crystal Irradiation Damage Model" Applied Sciences 13, no. 19: 10701. https://doi.org/10.3390/app131910701
APA StyleZhang, T., Zeng, Y., Li, Y.-F., Huang, H.-Z., & Gul Niazi, S. (2023). Multi-Directional Displacement Threshold Energy and Crystal Irradiation Damage Model. Applied Sciences, 13(19), 10701. https://doi.org/10.3390/app131910701









