Modeling of Pipe Whip Phenomenon Induced by Fast Transients Based on Fluid–Structure Interaction Method Using a Coupled 1D/3D Modeling Approach
Abstract
:1. Introduction
1.1. Background of Pipe Whip Tests
1.2. Pipe Whip Based on Water Hammer Effect
1.3. Applications of Numerical Codes for Pipe Whip Phenomenon
2. Experimental Setup
2.1. CEA Pipe Whip Tests
2.2. Previously Validated Research through Numerical Codes
3. Computational Modeling Method
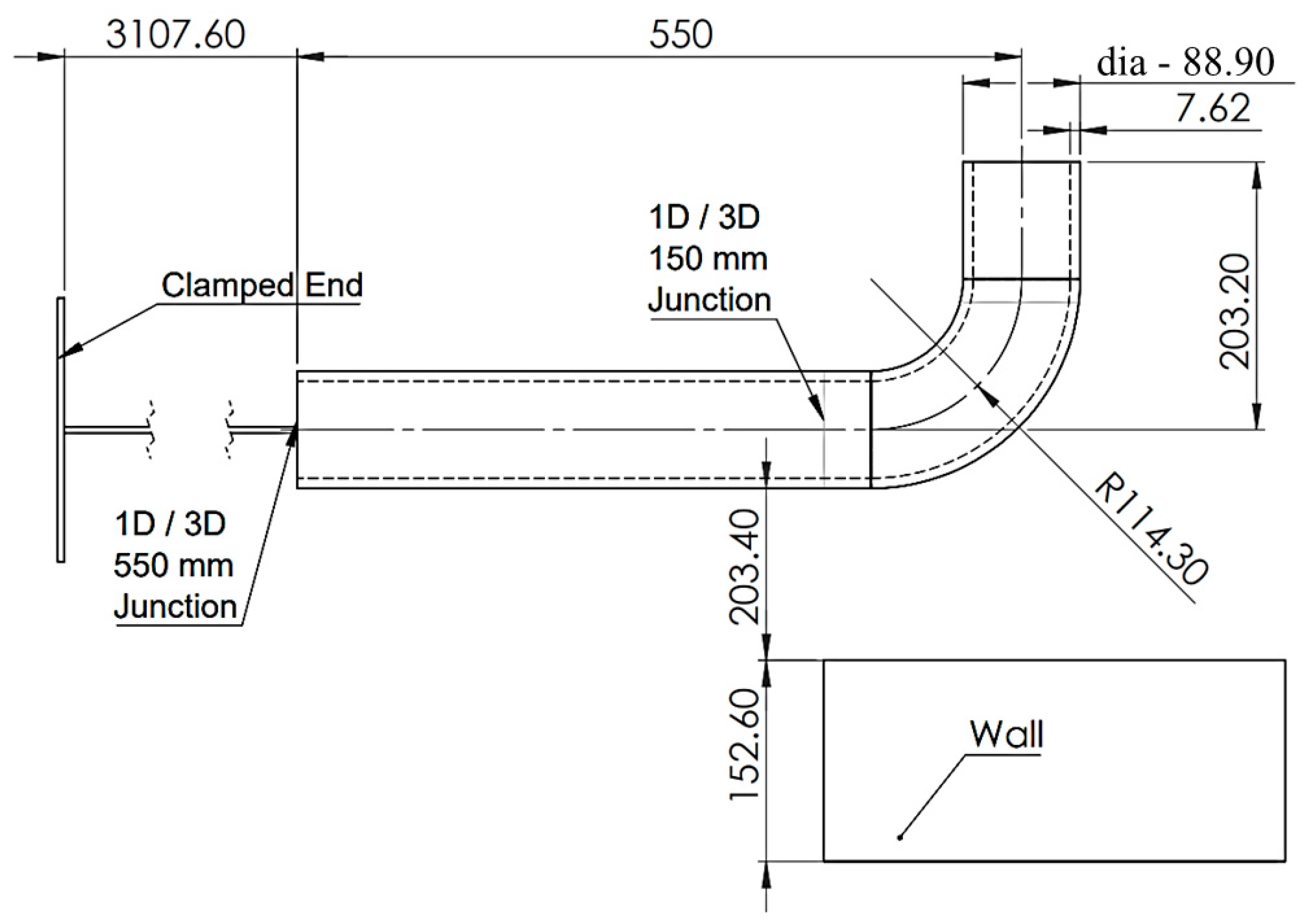
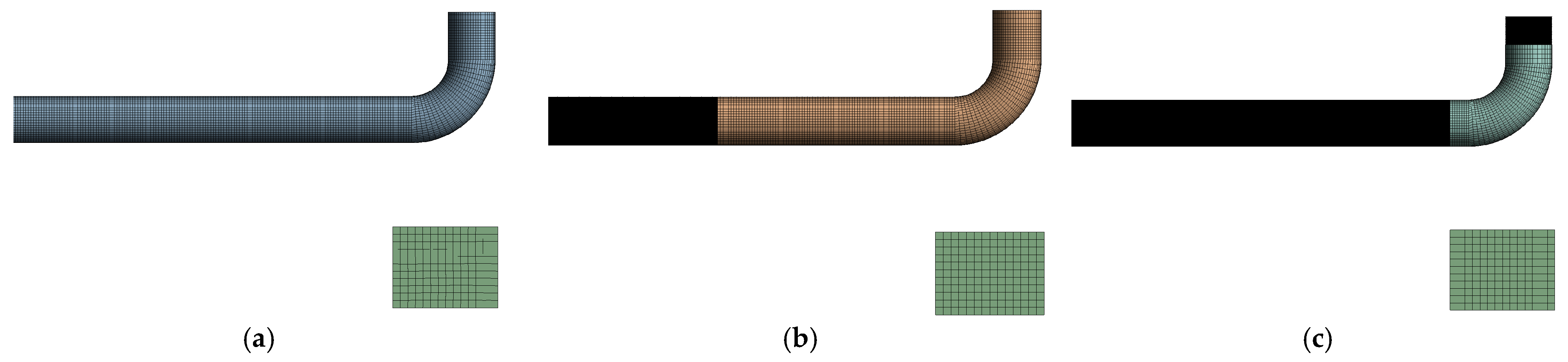
3.1. Pipe Whip Model
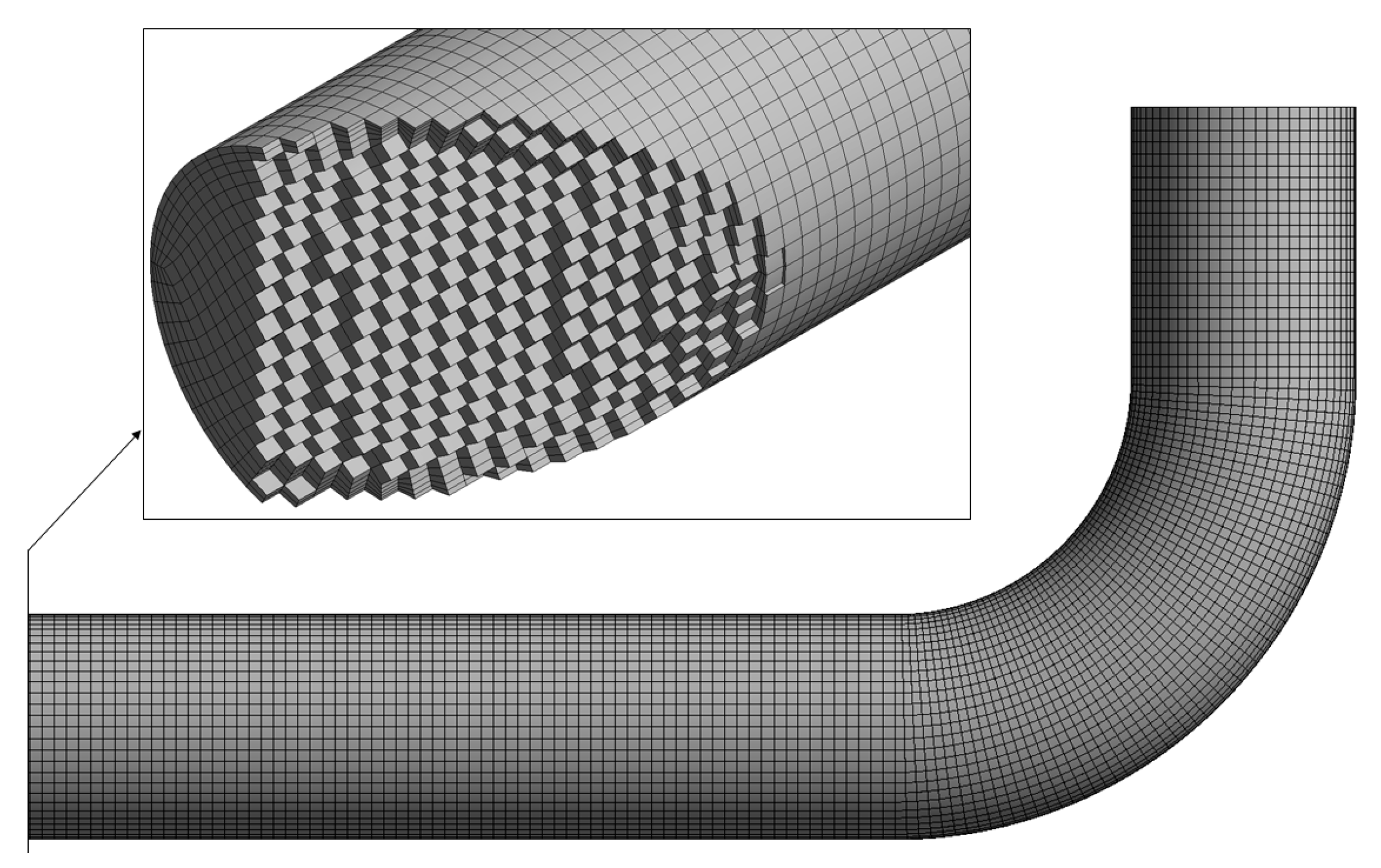
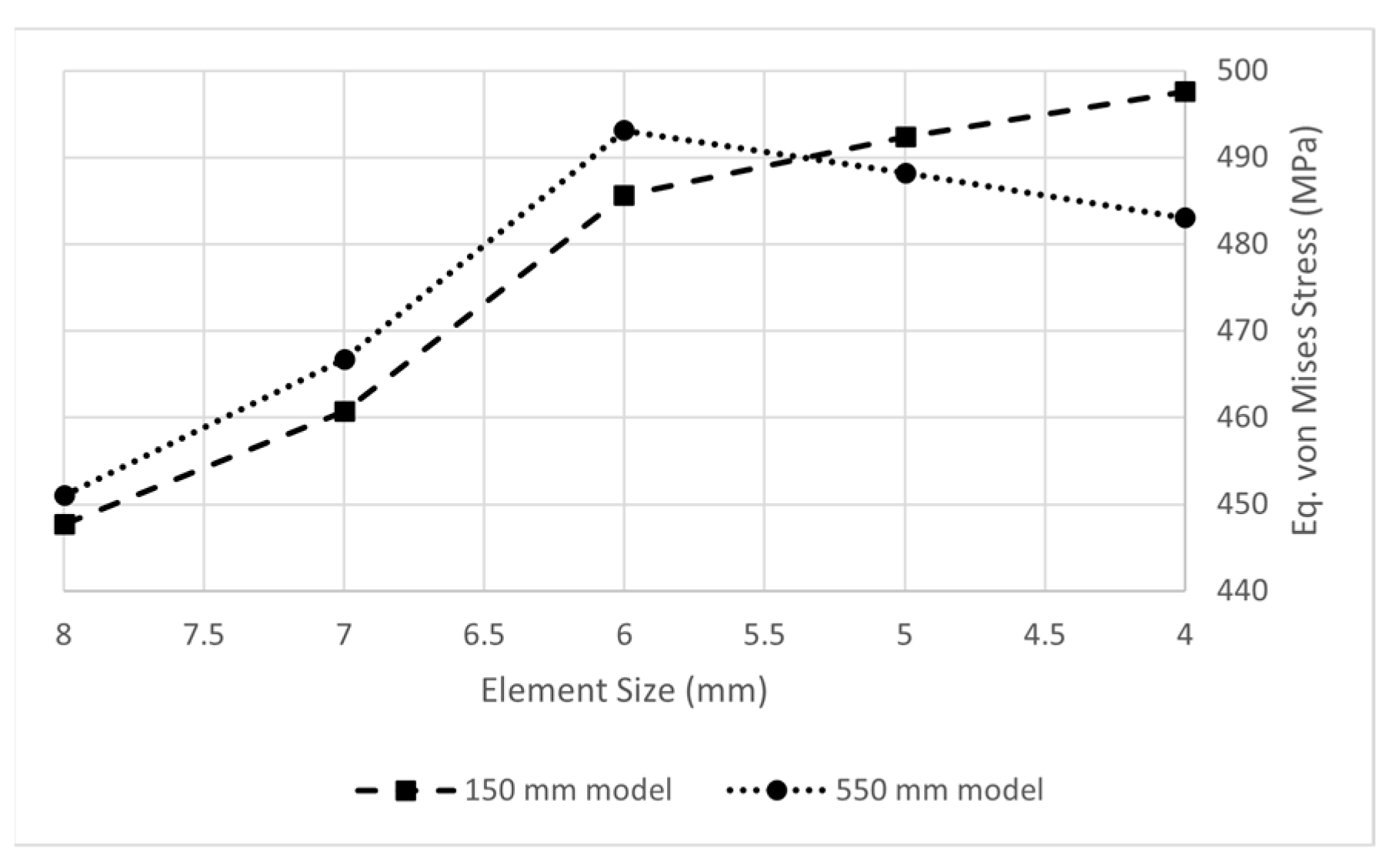
Grid Independence Study for the Fluid Domain
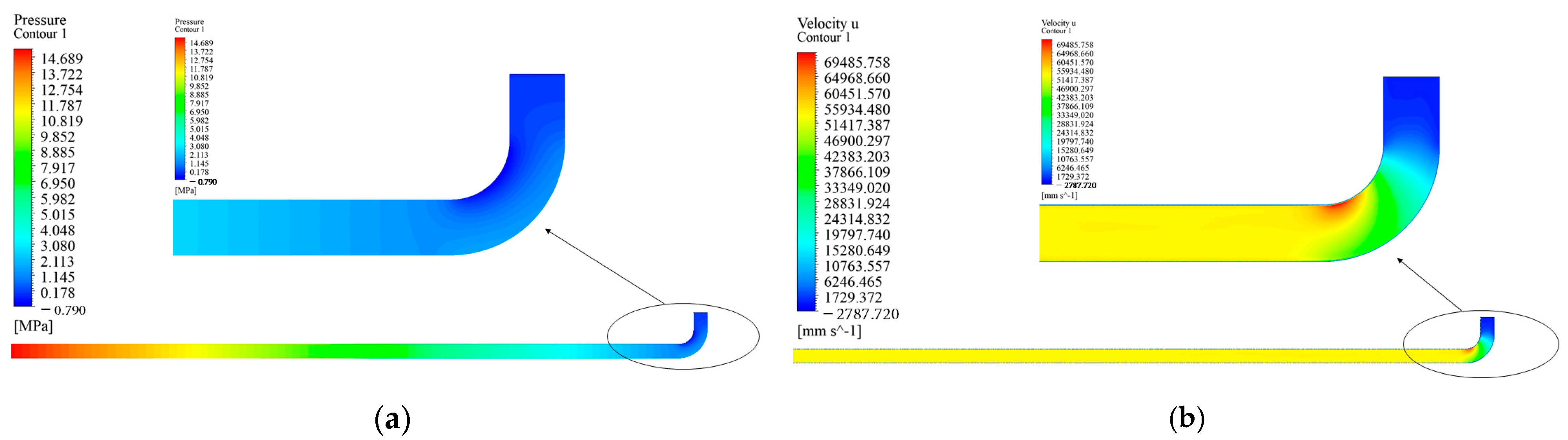
3.2. Fluid Flow Modeling
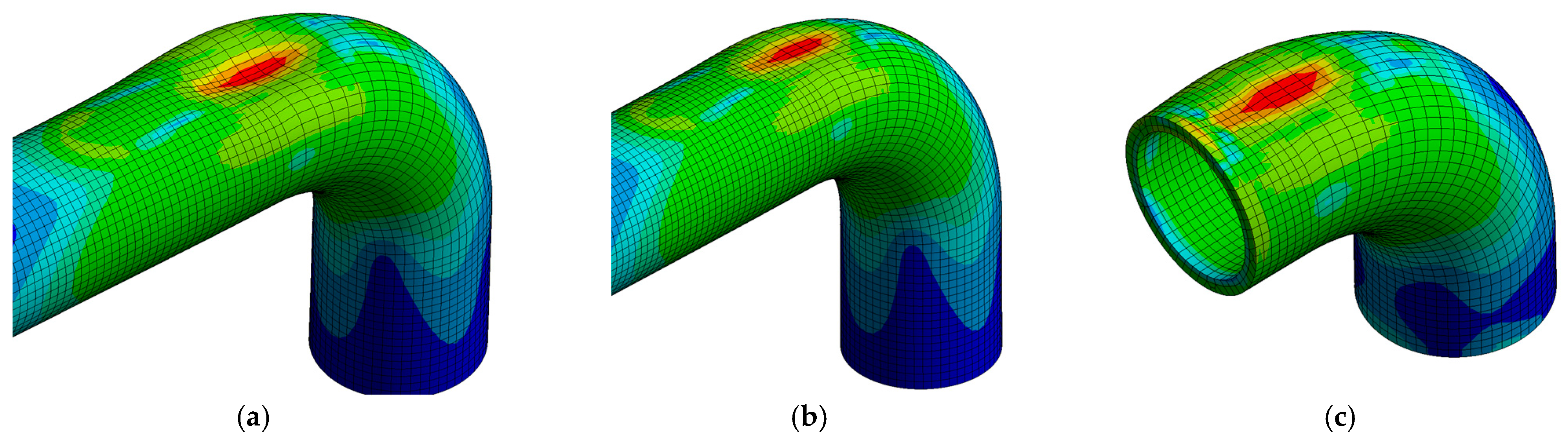
4. Fluid–Structure Interaction
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guilbaud, D.; Blay, N.; Broc, D.; Chaudat, T.; Feau, C.; Sollogoub, P.; Wang, F.; Baj, F.; Bung, H.; Combescure, D.; et al. An Overview of Studies in Structural Mechanics; CEA-R-6113; 2006; Available online: https://inis.iaea.org/search/search.aspx?orig_q=RN:38045517 (accessed on 21 September 2023).
- Garcia, J.L.; Chouard, P.; Sermet, E. Experimental Studies of Pipe Impact on Rigid Restraints and Concrete Slabs. Nucl. Eng. Des. 1984, 77, 357–368. [Google Scholar] [CrossRef]
- Kulak, R.F.; Narvydas, E. Verification of the NEPTUNE Computer Code for Pipe Whip Analysis. In Proceedings of the SMiRT 16—16th International Conference on Structural Mechanics in Reactor Technology, Washington, DC, USA, 12–17 August 2001. [Google Scholar]
- Hsu, L.C.; Kuo, A.Y.; Tang, H.T. Nonlinear Analysis of Pipe Whip. In Proceedings of the SMiRT 8, Brussels, Belgium, 19–23 August 1985. F1 4/6. [Google Scholar]
- Potapov, S.; Galon, P. Modelling of Aquitaine II Pipe Whipping Test with the EUROPLEXUS Fast Dynamics Code. Nucl. Eng. Des. 2005, 235, 2045–2054. [Google Scholar] [CrossRef]
- Daude, F.; Galon, P.; Douillet-Grellier, T. 1D/3D Finite-Volume Coupling in Conjunction with Beam/Shell Elements Coupling for Fast Transients in Pipelines with Fluid–Structure Interaction. J. Fluids Struct. 2021, 101, 103219. [Google Scholar] [CrossRef]
- Everstine, G.C. Dynamic Analysis of Fluid-Filled Piping Systems Using Finite Element Techniques. J. Press. Vessel. Technol. 1986, 108, 57–61. [Google Scholar] [CrossRef]
- Ezkurra, M.; Ander Esnaola, J.; Martinez Agirre, M. Analysis of One-Way and Two-Way FSI Approaches to Characterise the Flow Regime and the Mechanical Behaviour during Closing Manoeuvring Operation of a Butterfly Valve; ALUHYDRO View Project Green Hydrogen Technologies: H2 Generation, Storage and Transformation View Project; World Academy of Science, Engineering and Technology: Istanbul, Turkey, 2018. [Google Scholar]
- Dahmane, M.; Boutchicha, D.; Adjlout, L. One-Way Fluid Structure Interaction of Pipe under Flow with Different Boundary Conditions. Mechanics 2017, 22, 495–503. [Google Scholar] [CrossRef]
- Cai, S.; Li, Q.; Liu, C.; Zhou, Y. Evaporation of R32/R152a Mixtures on the Pt Surface: A Molecular Dynamics Study. Int. J. Refrig. 2020, 113, 156–163. [Google Scholar] [CrossRef]
- Lema, M.; López Peña, F.; Buchlin, J.-M.; Rambaud, P.; Steelant, J. Analysis of Fluid Hammer Occurrence with Phase Change and Column Separation Due to Fast Valve Opening by Means of Flow Visualization. Exp. Therm. Fluid Sci. 2016, 79, 143–153. [Google Scholar] [CrossRef]
- Bergant, A.; Simpson, A.R.; Tijsseling, A.S. Water Hammer with Column Separation: A Historical Review. J. Fluids Struct. 2006, 22, 135–171. [Google Scholar] [CrossRef]
- Uspuras, E.; Kaliatka, A.; Dundulis, G. Analysis of Potential Waterhammer at the Ignalina NPP Using Thermal-Hydraulic and Structural Analysis Codes. In Proceedings of the Transactions of the 15th International Conference on Structural Mechanics in Reactor Technology (SMiRT-15), Seoul, Republic of Korea, 15–20 August 1999. [Google Scholar]
- Martins, N.M.C.; Soares, A.K.; Ramos, H.M.; Covas, D.I.C. CFD Modeling of Transient Flow in Pressurized Pipes. Comput. Fluids 2016, 126, 129–140. [Google Scholar] [CrossRef]
- Jha, P.N.; Zhang, J.; Dalton, C. Numerical Simulation of Laminar Water Hammer Flow in a Pipe with Varying Cross-Section. J. Appl. Water Eng. Res. 2018, 6, 228–235. [Google Scholar] [CrossRef]
- Sun, Z.; Liu, D.; Yuan, H.; Sun, Z.; Pan, W.; Zhang, Z.; Ma, B.; Jiang, Z. The Water Hammer in the Long-Distance Steam Supply Pipeline: A Computational Fluid Dynamics Simulation. Cogent Eng. 2022, 9, 2127472. [Google Scholar] [CrossRef]
- Zhang, X.; Cheng, Y.; Xia, L.; Yang, J. CFD Simulation of Reverse Water-Hammer Induced by Collapse of Draft-Tube Cavity in a Model Pump-Turbine during Runaway Process. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 052017. [Google Scholar] [CrossRef]
- Geng, J.; Yuan, X.; Li, D.; Du, G. Simulation of Cavitation Induced by Water Hammer. J. Hydrodyn. 2017, 29, 972–978. [Google Scholar] [CrossRef]
- Huang, Q.; Liu, Z.; Wang, L.; Ravi, S.; Young, J.; Lai, J.C.S.; Tian, F.-B. Streamline Penetration, Velocity Error, and Consequences of the Feedback Immersed Boundary Method. Phys. Fluids 2022, 34, 097101. [Google Scholar] [CrossRef]
- Blair, S.R.; Kwon, Y.W. Modeling of Fluid–Structure Interaction Using Lattice Boltzmann and Finite Element Methods. J. Press. Vessel. Technol. 2015, 137, 021302. [Google Scholar] [CrossRef]
- Mei, R.; Shyy, W.; Yu, D.; Li, F.; Luo, L.-S. Lattice Boltzmann Method for 3-D Flows with Curved Boundary; NASA Langley Research Center: Hampton, VA, USA, 2002. [Google Scholar]
- Xu, L.; Tian, F.-B.; Young, J.; Lai, J.C.S. A Novel Geometry-Adaptive Cartesian Grid Based Immersed Boundary–Lattice Boltzmann Method for Fluid–Structure Interactions at Moderate and High Reynolds Numbers. J. Comput. Phys. 2018, 375, 22–56. [Google Scholar] [CrossRef]
- Feng, T.; Zhang, D.; Song, P.; Tian, W.; Li, W.; Su, G.H.; Qiu, S. Numerical Research on Water Hammer Phenomenon of Parallel Pump-Valve System by Coupling FLUENT with RELAP5. Ann. Nucl. Energy 2017, 109, 318–326. [Google Scholar] [CrossRef]
- Tijsseling, A.S.; Bergant, A.; Ljubljana, L.E. Meshless Computation of Water Hammer. Scientific Bulletin of the “Politehnica”. In Proceedings of the 2nd IAHR International Meeting of the Workgroup on Cavitation and Dynamic Problems in Hydraulic Machinery and Systems, Timisoara, Romania, 24–26 October 2007; Volume 52. [Google Scholar]
- Kumar Patel, A. Experimental Study of Water Hammer Pressure in a Commercial Pipe. IOSR J. Mech. Civ. Eng. Spec. Issue–AETM 2016, 16, 16–21. [Google Scholar] [CrossRef]
- Riedelmeier, S.; Becker, S.; Schlücker, E. Identification of the Strength of Junction Coupling Effects in Water Hammer. J. Fluids Struct. 2017, 68, 224–244. [Google Scholar] [CrossRef]
- Aliabadi, H.K.; Ahmadi, A.; Keramat, A. Frequency Response of Water Hammer with Fluid-Structure Interaction in a Viscoelastic Pipe. Mech. Syst. Signal Process 2020, 144, 106848. [Google Scholar] [CrossRef]
- Zhang, L.; Tijsseling, A.S.; Vardy, A.E. FSI Analysis of Liquid-Filled Pipes. J. Sound Vib. 1999, 224, 69–99. [Google Scholar] [CrossRef]
- Zhang, Y.; Vairavamoorthy, K. Analysis of Transient Flow in Pipelines with Fluid-Structure Interaction Using Method of Lines. Int. J. Numer. Methods Eng. 2005, 63, 1446–1460. [Google Scholar] [CrossRef]
- Daude, F.; Galon, P. A Finite-Volume Approach for Compressible Single- and Two-Phase Flows in Flexible Pipelines with Fluid-Structure Interaction. J. Comput. Phys. 2018, 362, 375–408. [Google Scholar] [CrossRef]
- Martins, N.M.C.; Carriço, N.J.G.; Covas, D.I.C.; Ramos, H.M. Velocity-Distribution in Pressurized Pipe Flow Using CFD: Mesh Independence Analysis; 2014; ISBN 9789899647923. Available online: https://www.researchgate.net/profile/Nuno-Martins-14/publication/266259133_Velocity-Distribution_in_Pressurized_Pipe_Flow_using_CFD_Mesh_Independence_Analysis/links/542aeac80cf29bbc126a7a27/Velocity-Distribution-in-Pressurized-Pipe-Flow-using-CFD-Mesh-Independence-Analysis.pdf (accessed on 21 September 2023). [CrossRef]
- Knotek, S.; Schmelter, S.; Olbrich, M. Assessment of Different Parameters Used in Mesh Independence Studies in Two-Phase Slug Flow Simulations. Meas. Sens. 2021, 18, 100317. [Google Scholar] [CrossRef]
- Förster, C.; Wall, W.A.; Ramm, E. Artificial Added Mass Instabilities in Sequential Staggered Coupling of Nonlinear Structures and Incompressible Viscous Flows. Comput. Methods Appl. Mech. Eng. 2007, 196, 1278–1293. [Google Scholar] [CrossRef]
- Meduri, S.; Cremonesi, M.; Perego, U.; Bettinotti, O.; Kurkchubasche, A.; Oancea, V. A Partitioned Fully Explicit Lagrangian Finite Element Method for Highly Nonlinear Fluid-Structure Interaction Problems. Int. J. Numer. Methods Eng. 2018, 113, 43–64. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, C.; Guo, Q.; Zhou, J.; Feng, Y.; Xu, K. Fluid-Structure Interaction in a Pipeline Embedded in Concrete During Water Hammer. Front. Energy Res. 2022, 10, 956209. [Google Scholar] [CrossRef]
- Gnedin, N.Y.; Semenov, V.A.; Kravtsov, A.V. Enforcing the Courant–Friedrichs–Lewy Condition in Explicitly Conservative Local Time Stepping Schemes. J. Comput. Phys. 2018, 359, 93–105. [Google Scholar] [CrossRef]
- Aune, V.; Valsamos, G.; Casadei, F.; Langseth, M.; Børvik, T. Fluid-Structure Interaction Effects during the Dynamic Response of Clamped Thin Steel Plates Exposed to Blast Loading. Int. J. Mech. Sci. 2021, 195, 106263. [Google Scholar] [CrossRef]
- Aune, V.; Valsamos, G.; Casadei, F.; Langseth, M.; Børvik, T. Influence of Fluid-Structure Interaction Effects on the Ductile Fracture of Blast-Loaded Steel Plates. EPJ Web Conf. 2021, 250, 02019. [Google Scholar] [CrossRef]
- Hu, J.; Wang, X.; Li, Y.; Wen, X.; Wu, Y.; Huang, Y. Investigation of Whipping Effect on High Energy Pipe Based on Fluid-Structure Interaction Method. Int. J. Impact Eng. 2023, 173, 104463. [Google Scholar] [CrossRef]
- Everstine, G.C. Transient Fluid-Structure Interaction Using Finite Elements. In Proceedings of the Fluid-Structure Interaction and Structural Mechanics—Joint ASME/JSME Pressure Vessels and Piping Conference, Honolulu, HI, USA, 23–27 July 1995; pp. 77–84. [Google Scholar]
- Andersson, C.; Ahl, D. Fluid Structure Interaction; Halmstad University: Halmstad, Sweden, 2011. [Google Scholar]
- Guo, Q.; Zhou, J.; Li, Y.; Guan, X.; Liu, D.; Zhang, J. Fluid-Structure Interaction Response of a Water Conveyance System with a Surge Chamber during Water Hammer. Water 2020, 12, 1025. [Google Scholar] [CrossRef]
- Sai, V.; Sudula, P. Bilinear Isotropic and Bilinear Kinematic Hardening of AZ31 Magnesium Alloy. Int. J. Adv. Res. Eng. Technol. 2020, 11, 518–531. [Google Scholar]








| General Material Properties of the Computational Model | ||
|---|---|---|
| Pipe (A106 Steel) | Wall (Concrete) | |
| Density (Kg/m3) | 7844 | 2400 |
| Young’s modulus (GPa) | 207 | 27 |
| Poisson’s ratio | 0.3 | 0.2 |
| Tensile stress (GPa) | 0.399 | 0.0015 |
| Pipe-to-Wall Impact Testing Method | ||
|---|---|---|
| Model Type | Time to Impact (ms) | Velocity at Impact (m/s) |
| CEA Experiment [2] | 13.2 | - |
| ANSI 58.2 Standard [4] | 10.1 | 13.42 |
| ABAQUS-EPGEN (V4.5) Code [4] (beam–shell formulation) | 7.1 | 13.51 |
| TEDEL (CEASEMT-V-1) Code [2] (beam formulation) | 8.4 | - |
| Fully 3D model (Ansys R2) | 18 | 16.26 |
| 550 mm Solid Pipe model (Extended) (beam–solid formulation) | 18 | 15.97 |
| 150 mm Solid Pipe model (Shortened) (beam–solid formulation) | 18 | 16.37 |
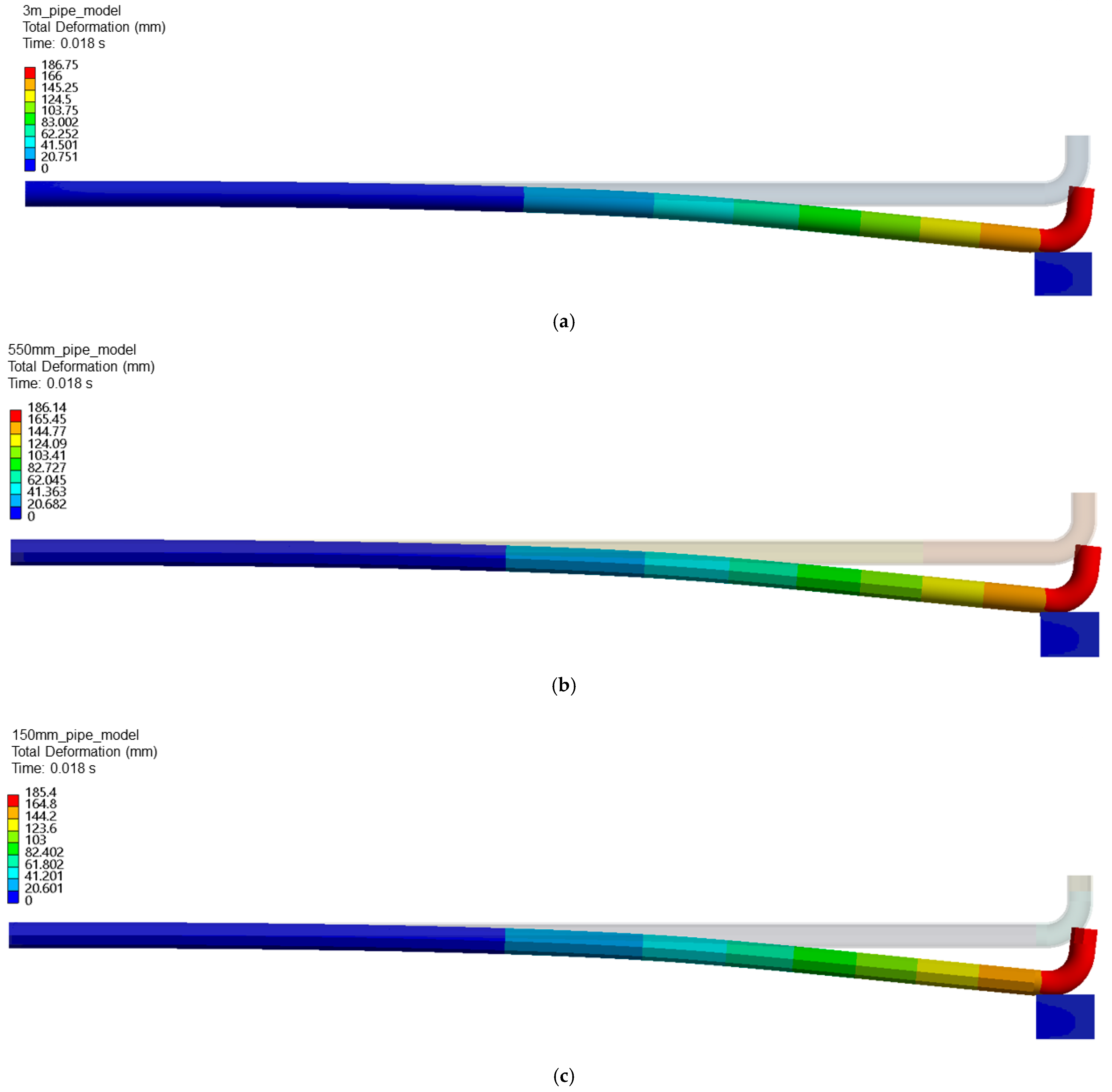
| Structural Pipe Models with 5 mm Element Size | ||||
|---|---|---|---|---|
| Fully 3D Model | 550 mm Pipe Model | 150 mm Pipe Model | ||
| Total displacement (mm) | 186.75 | 186.14 | 185.4 | |
| Eq. von Mises stress (MPa) | 487.49 | 488.19 | 492.32 | |
| Finite elements count | Total nodes | 448,244 | 87,021 | 35,184 |
| Total elements | 83,206 | 16,688 | 7149 | |
| Computational time (min) | 111.8 | 15.9 | 6.6 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solomon, I.; Dundulis, G. Modeling of Pipe Whip Phenomenon Induced by Fast Transients Based on Fluid–Structure Interaction Method Using a Coupled 1D/3D Modeling Approach. Appl. Sci. 2023, 13, 10653. https://doi.org/10.3390/app131910653
Solomon I, Dundulis G. Modeling of Pipe Whip Phenomenon Induced by Fast Transients Based on Fluid–Structure Interaction Method Using a Coupled 1D/3D Modeling Approach. Applied Sciences. 2023; 13(19):10653. https://doi.org/10.3390/app131910653
Chicago/Turabian StyleSolomon, Isaac, and Gintautas Dundulis. 2023. "Modeling of Pipe Whip Phenomenon Induced by Fast Transients Based on Fluid–Structure Interaction Method Using a Coupled 1D/3D Modeling Approach" Applied Sciences 13, no. 19: 10653. https://doi.org/10.3390/app131910653
APA StyleSolomon, I., & Dundulis, G. (2023). Modeling of Pipe Whip Phenomenon Induced by Fast Transients Based on Fluid–Structure Interaction Method Using a Coupled 1D/3D Modeling Approach. Applied Sciences, 13(19), 10653. https://doi.org/10.3390/app131910653






