Study of the Relationship between Mode I Fracture Toughness and Rock Brittleness Indices

Abstract

Mode I fracture toughness (K_IC) and rock brittleness are important properties that influence many rock engineering applications. Due to the difficulties in determining K_IC experimentally, previous studies have investigated the relationship between K_IC and rock brittleness indices. However, only rock brittleness indices (based on strength parameters) and K_IC obtained from Chevron Bend and Short Rod test methods were considered. In this paper, regression analysis was carried out to investigate the relationship between K_IC and rock brittleness using literature data collected from different rock types and core K_IC test methods under level I and static test conditions. Rock brittleness was assessed using ten indices based on strength and pre-peak elastic parameters. The results showed that elastic-based indices were not good predictors of K_IC, while strength-based indices correlated well with K_IC. A comparison with previous studies revealed that the correlations between K_IC and strength-based indices were significantly sensitive to the rock type, i.e., soft or hard, and the K_IC test method. However, a brittleness index, based on both strength and pre-peak elastic parameters, was found to be the best index to predict K_IC because of its lower sensitivity to the test method and rock type.

1. Introduction

Rock fracture toughness is an essential property in fracture mechanics [1]. It represents the rock’s resistance to fractures’ propagation. Following fracture mechanics principles, structures’ safety depends mainly on three factors: applied stresses, construction material’s fracture toughness and material flaws’ size [2]. In general, rocks are inhomogeneous, non-continuous and anisotropic, and they contain macro-scale and micro-scale flaws. Thus, studying rock fracture toughness is vital in many engineering applications, particularly where the role of natural discontinuities or generated fractures is significant. Rock fracture toughness was used to predict the power consumption of cone crushers for twelve rocks [3]. Moreover, rock fracture toughness plays an important role in the extraction of ornamental stone blocks, particularly hard stones such as granite, using Soundless Cracking Demolition Agents (SCDAs). The optimum hole spacing, in drilling patterns, was investigated in order to optimize the extraction process [4]. Compared to the empirical equations where spacing is determined in terms of hole diameter, it was concluded that additional rock properties such as Young’s modulus and fracture toughness must be considered. Moreover, the fracture growth between two holes filled with SCDAs was investigated in [5]. Considering Linear Elastic Fracture Mechanics (LEFM) principles, an algorithm was suggested to estimate the first fracture length due to the increasing expansive pressure, in terms of rock fracture toughness, in [5]. The effect of thermal cycling, up to 300 °C and 20 cycles, on the fracture characteristics of Suizhou granite (from China) located at a potential site for an Enhanced Geothermal System (EGS) was investigated in [6]. In the EGS, a fluid is injected into a fracture network artificially formed in a low-porosity and impermeable hot dry rock, such as granite. Hence, the rock is subjected to repeated heating–cooling thermal cycles. It was found that fracture toughness decreased with the number of thermal cycles and the temperature due to thermally induced micro-damages. Similarly, the variation in fracture toughness with temperature, up to 600 °C, was studied for three crystalline rocks collected from Deccan Volcanic Province, Western India where there was an interest in developing geothermal energy projects [7]. A negative effect of temperature on rock fracture toughness was reported due to the development of micro-cracks as a result of the differential stresses at the grain boundaries. As the treatment temperature increased, micro-crack density increased and pre-existing cracks became wider, resulting in irreversible thermal damages and leading to an extreme reduction in stiffness [7].

Propagation modes of fractures include mode I (opening or tension), mode II (in plane shear) and mixed mode or mode III (out of plane shear) [2]. It was believed that, in practical applications, fractures propagate under the mixed mode [8]. However, mode I fracture toughness (K_IC) was the most critical parameter because rocks were more vulnerable to tensile loads compared to shear loads [9].

Many K_IC test methods have been suggested in the scientific literature. They are classified into non-core and core test methods. Non-core methods include three-point and four-point bending tests. These methods, unlike core test methods, need relatively large rectangular samples that cannot be usually obtained within a usual rock testing program [10]. In this paper, only core test methods are considered, because their geometry is the easiest obtainable geometry particularly at great depths. The most commonly known core test methods are those suggested by the ISRM: Chevron Bend (CB) [11], Short Rod (SR) [11], Cracked Chevron Notched Brazilian Disc (CCNBD) [12]; and Semi-Circular Bend (SCB) [13]. For CB and SR methods, tests can be carried out while recording only maximum load, i.e., level I, or while recording the load and displacement, i.e., level II, to account for rock non-linearity [11]. Tests for K_IC determination are sometimes demanding because of the absence of suitable samples in terms of number and size, challenging sample preparation procedures as well as complicated, expensive and time-consuming testing procedures. Hence, K_IC prediction, in terms of rock properties, can substitute testing when needed [7,14,15]. Many researchers have suggested empirical formulas for the K_IC estimation, in terms of rock properties such as Tensile Strength (TS) [9,16], Uniaxial Compressive Strength (UCS) [14,17], point Load Strength [18], Young’s modulus [17,19], Poisson’s ratio [17], P-wave velocity [14,17,20], S-wave velocity, density [14,17,21], porosity [17] and permeability [6].

Moreover, researchers have investigated the correlation between K_IC and rock brittleness [22,23,24]. Rock brittleness can be defined as “Failure by fracture at or only slightly beyond the yield stress” [22] or “it is a property of materials that rupture or fracture with little or no plastic flow” [23]. Rock brittleness plays an important role in assessing the performance of several rock engineering applications. A rock brittleness index (i.e., the ratio of UCS to TS) was utilized at Sanshandao gold mine, in China, as an empirical indicator of rock burst possibility where a strong burst tendency was reported [25]. Moreover, this index was used to assess rock burst for 102 case studies from fourteen hard rock mines located in Italy, Russia and China [26]. However, it was recommended that this index cannot be solely used in rock burst tendency prediction, because it considered only the rock’s strength properties and it had low prediction accuracy [26,27]. The effect of ornamental stones’ brittleness on the production rate of circular sawing machines for seventeen different Iranian granitic and carbonate stones was investigated in [28]. The stones’ brittleness was assessed using three different strength-based indices in terms of UCS and TS. Although good correlations were found between the three indices and the production rate, it was concluded that the brittleness index (represented as 0.5*UCS*TS) was the best index to predict the production rate. Because, unlike the other indices, this brittleness index showed good correlation with the production rates of the combined data for granitic and carbonate ornamental stones, it can be used to predict the production rates for all types of Iranian ornamental stones [28]. The correlation between rock brittleness indices and the penetration rate of four different types of drilling operations, i.e., Tunnel Boring Machine (TBM), diamond, percussive and rotary, was investigated using literature data in [29]. Varying correlation significances were reported that depended on the used index and drilling methods. So, it was concluded that assessing the performance of rock excavation operations using a rock brittleness index depended on the practical application, e.g., brittleness index, that considered that impact strength parameters may be more suitable for the prediction of percussive drilling penetration rate [29]. Similarly, the effect of rock brittleness on the penetration rate for percussive, rotary and Down The Hole (DTM) drilling operations was investigated using literature data for different types of rocks having varying strength in [30]. Using multiple regression, three equations were proposed, one for each drilling type, to predict the penetration rate using three strength-based brittleness indices [30].

K_IC test methods assumed that rock fractures followed LEFM principles, which applied only to brittle fracturing that has a very small Fracture Process Zone (FPZ) at the fracture tip. Rocks generally exhibit quasi-brittle fracturing (a general type of brittle fractures), which has a significant FPZ [31,32]. FPZ size is controlled by several factors such as rock petrological properties, specimen geometries, test method and loading conditions. [31,33].

Accordingly, the obtained K_IC values from tests may not represent the true K_IC. For Mancos shale (from the USA), the LEFM assumption was invalid due to its inelastic behavior, so level II testing was carried out to estimate a fracture toughness correction factor. A significant inelasticity was reported such that the fracture toughness correction factor varied from 1.49 to 1.83 [34]. The Mode I failure mechanism of five rock types was investigated in [35]. It was concluded that K_IC measurement was more accurate for brittle rocks compared to soft rocks; therefore, two K_IC—tensile strength formulas were proposed corresponding to brittle and inelastic behaviors, because a significantly large FPZ, compared to the sample size, could result in failure due to loss of strength rather than fracture propagation [36,37]. A size effect law was suggested to quantitatively represent the FPZ effect on the failure mechanism of samples, in order to obtain the true size-dependent K_IC [38]. The size law effect was applied to different geo-materials in [36,39,40]. Moreover, the effect of samples’ size on the fracturing behavior of concrete was investigated in [41].

Rock brittleness can assess how brittle rock fractures would be and hence how applicable the LEFM assumption would be. Many researchers have suggested various brittleness indices for different rock engineering applications. Rock brittleness indices can be classified based on the parameters used in their estimation such as strength parameters, stress–strain curve parameters, elastic parameters, mineralogy and indentation characteristics [42,43]. Moreover, various formulas of a non-dimensional parameter called “brittleness number” were suggested in [36,37,44]. These formulas described the brittleness behavior of geo-materials quantitatively taking into account either the sample size or the FPZ size. The brittleness number suggested in [36] was independent of the sample geometrical shape unlike Carpinteri’s brittleness number proposed in [44] that was suggested for a notched beam sample under three-point bending (i.e., non-core test method) [36]. These brittleness numbers were not considered in this paper, because only core test methods were considered, and sample dimensions and peak loads were not available. Furthermore, there were not enough data available for each rock considering each test method to estimate the brittleness number suggested in [36].

In the literature, a few studies have focused on the relationship between K_IC and rock brittleness indices. The correlations between K_IC and two strength-based indices were investigated using two separate literature datasets [22]. In these datasets, K_IC results were obtained from two different test methods, i.e., CB and SR. Significant relationships between K_IC and a brittleness index represented as (0.5*UCS*TS) were reported [22]. The relationships between K_IC and three strength-based rock brittleness indices were studied in [23] using the same literature data used in [22]. There were good correlations between K_IC and only one brittleness index represented as (√ (0.5*UCS*TS)); however, more investigations were recommended to obtain a general relationship for other rock types. It should be noted that, in [22] and [23], the literature datasets were analyzed separately, and thus the effect of the K_IC test method on the K_IC-rock brittleness relationship was considered explicitly. Moreover, the correlations between K_IC and four strength-based indices were investigated in [24]. Three of these strength-based indices were the same as those investigated previously in [22] and [23]. Similar to [22] and [23], literature data were used to investigate the correlations, although this was a different dataset with most of the K_IC data obtained from the CB test [24]. Significant correlations with only two indices, represented as (0.5*UCS*TS) and ((UCS*TS)^0.72), were reported. Using a probabilistic approach, a new brittleness index was suggested, which provided a more accurate K_IC estimation [24]. The grain size effect on a strength-based rock brittleness index, i.e., (0.5*UCS*TS), was investigated for three granite types with small, medium and large grain sizes in [45]. A proportional trend between the brittleness index and the grain size was reported.

In these studies, only strength-based brittleness indices were considered in addition to the literature data used in [22,23], which were identical, and CB was the dominant K_IC test method in [22,23,24]. So, it would be interesting to investigate the correlation between K_IC and strength-based indices using an extended and updated dataset considering various K_IC test methods and rock types (i.e., different properties) in an attempt to generalize the K_IC—rock brittleness relationship as suggested in [23]. Furthermore, elastic-based brittleness indices, i.e., in terms of Young’s modulus and Poisson’s ratio, can provide a more accurate relationship when considering other, less brittle rock types, such as shale rocks [43].

This paper investigated the correlation between rock brittleness and the apparent K_IC, i.e., obtained from tests, using literature data in order to obtain a general relationship between rock brittleness and K_IC. Literature data were collected for different rock types and core test methods under level I and static testing conditions. Only core test methods were considered, because the core sample is the most obtainable sample geometry particularly at great depths. Rock brittleness was assessed using ten indices based on strength and pre-peak elastic parameters. The correlation between K_IC and elastic-based indices has not been considered before in the literature, to the best of the authors’ knowledge. We believe that investigating the relationship between K_IC and rock brittleness could be helpful in assessing the stability of rock structures and/or the performance of rock engineering operations. Furthermore, such a relationship can estimate K_IC with a good accuracy, using more common rock properties, where testing is not feasible.

2. Materials and Methods

The relationships between K_IC and rock brittleness indices were deduced based on regression analysis of literature data (

Table 1. Literature data used in this paper.

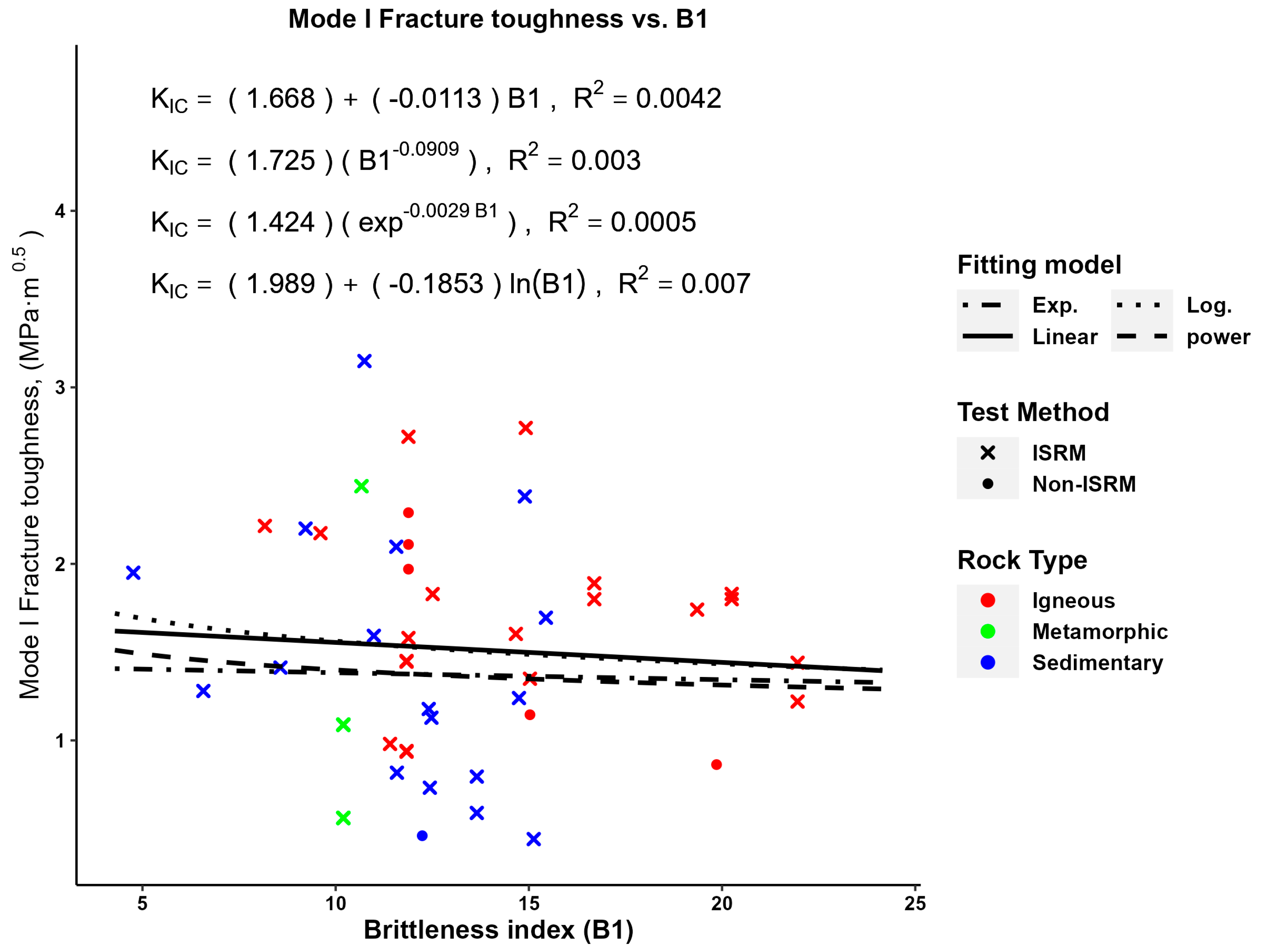
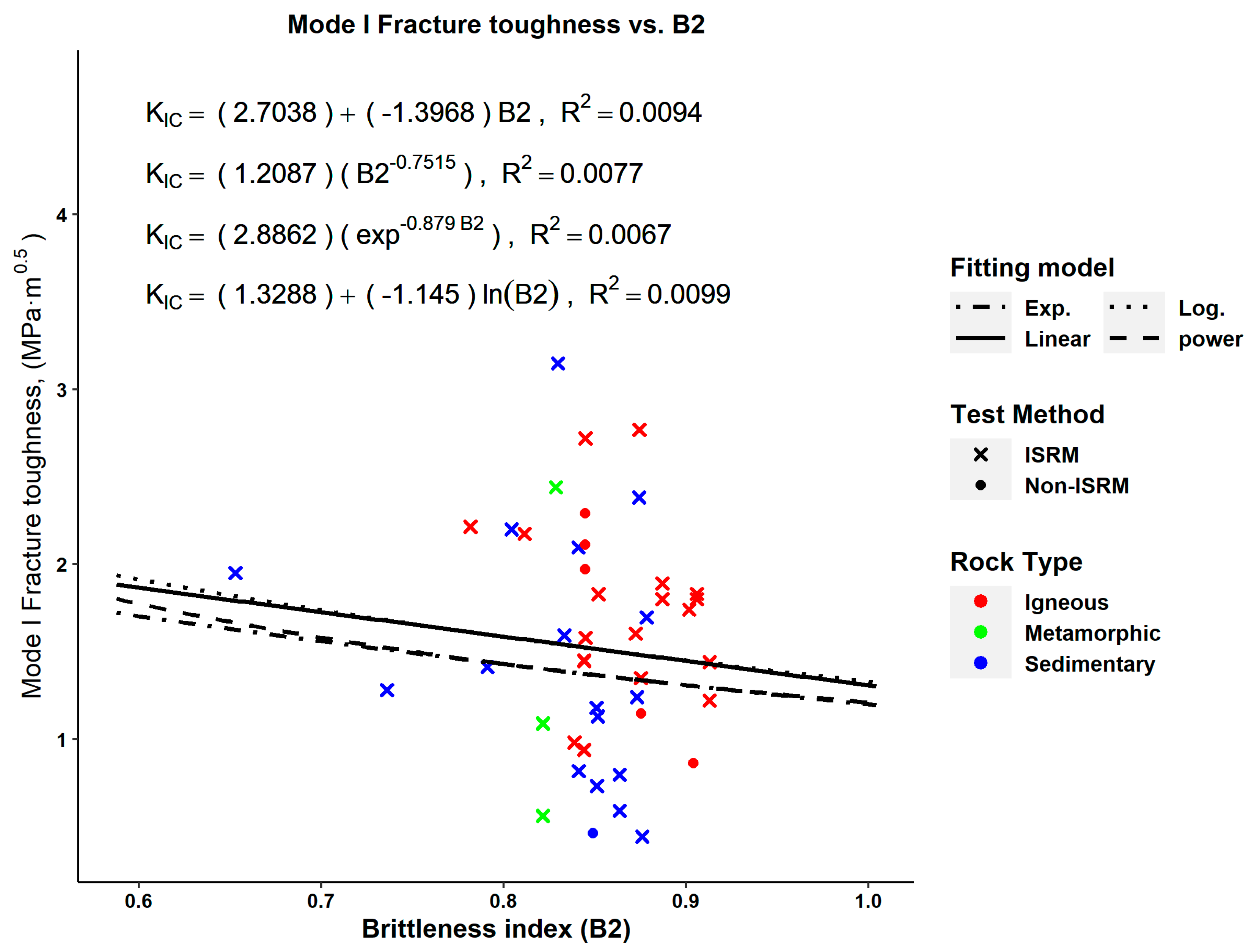
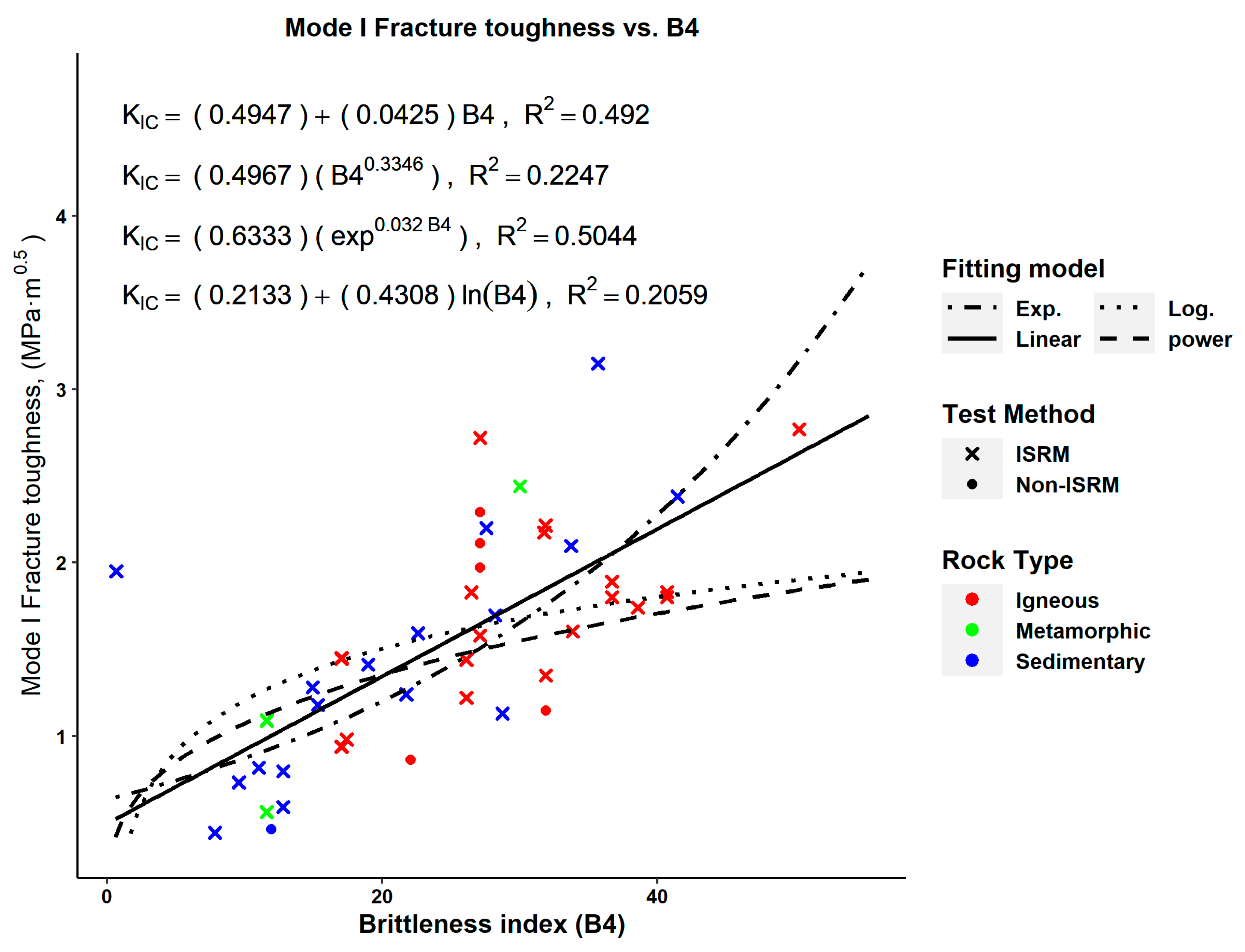
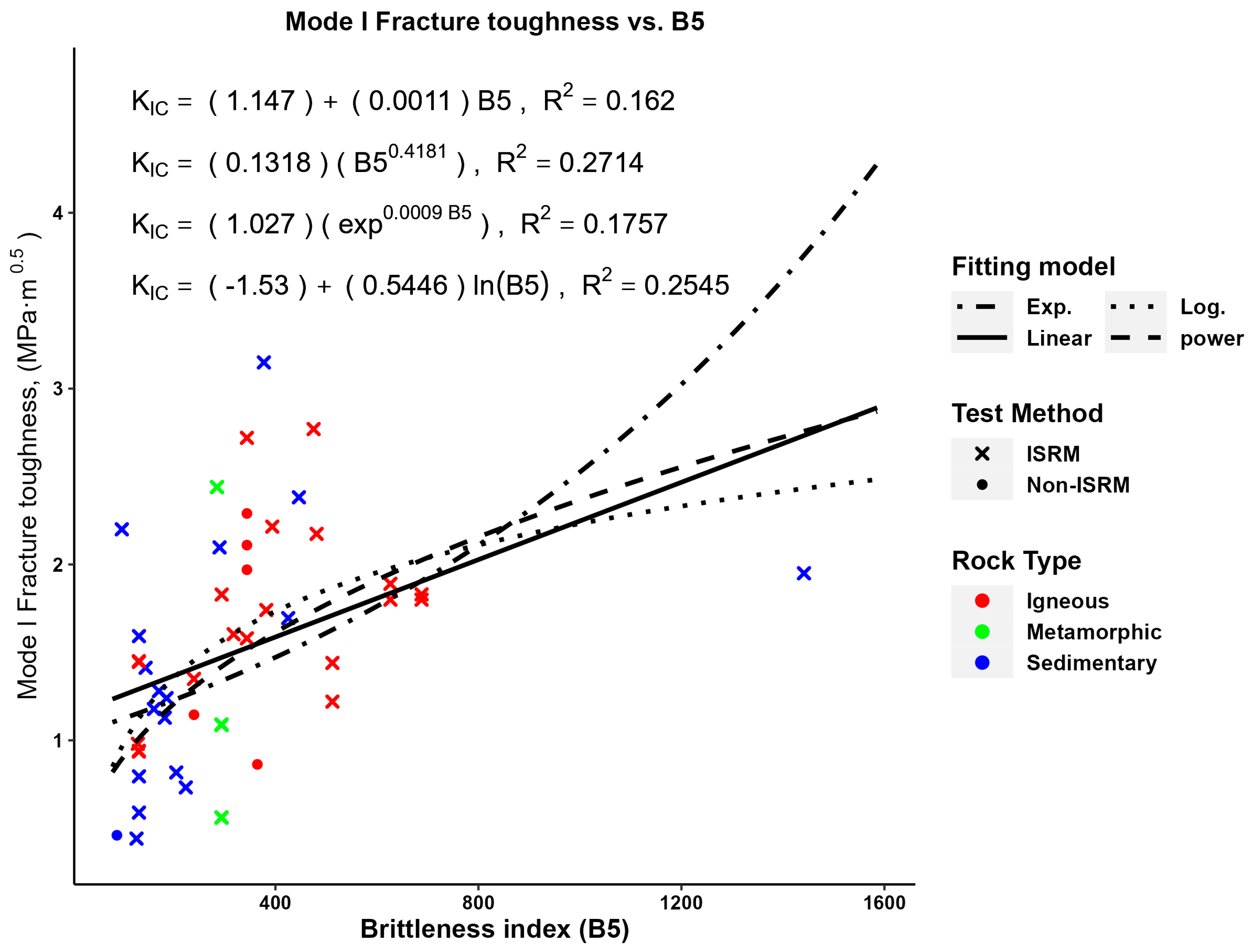
Reference	Rock Type	Test Method	${\mathbf{K}}_{\mathbf{I}\mathbf{C}}$ (MPa⋅m0.5)	${\mathsf{\sigma }}_{\mathbf{t}}$ (MPa)	${\mathsf{\sigma }}_{\mathbf{c}}$ (MPa)	$\mathbf{E}$ (GPa)	$\mathsf{\upsilon }$
[60]	Ankara andesite	SCB	0.936	7.000	82.840	12.334	0.150
	Ankara andesite	CCNBD	1.446	7.000	82.840	12.334	0.150
	white Afyon marble	SCB	0.561	5.130	52.320	34.294	0.120
	white Afyon marble	CCNBD	1.088	5.130	52.320	34.294	0.120
[61]	Pink Ankara andesite	SCB	0.980	7.290	83.160	12.330	0.160
[18]	Middleton limestone	CB	0.732	3.840	47.760	27.520	0.230
	Harrycroft limestone	CB	0.817	4.580	53.060	25.450	0.250
	Montclie sandstone	CB	1.178	6.150	76.310	15.920	0.130
	Wredon limestone	CB	1.695	10.150	156.730	57.170	0.280
	Penryn granite	CB	1.829	10.580	132.360	39.100	0.290
	Pennant sandstone	CB	2.097	14.020	162.190	39.070	0.310
	Whitwick andesite	CB	2.174	14.490	139.200	63.600	0.230
	Bolton hill diorite	CB	2.215	15.770	128.810	54.450	0.340
	Ingleton greywacke	CB	2.382	15.190	226.260	57.040	0.170
	Nuneaton quartzite	CB	2.440	12.990	138.580	36.400	0.240
	Clie hill diorite	CB	2.770	18.420	274.820	64.180	0.280
	Cornish greywacke	CB	3.149	15.390	165.360	49.620	0.250
[56]	Brisbane tuff	CCNBD	1.129	11.500	143.500	22.000	0.240
[6]	Suizhou Granite	SCB	1.741	12.400	240.000	50.000	0.240
[57]	Kimachi sandstone	SECRBB	0.460	4.820	59.000	8.230	0.220
[58]	Kimachi sandstone	SCB	0.589	4.900	66.900	13.200	0.180
	Kimachi sandstone	CB	0.795	4.900	66.900	13.200	0.180
[59]	Barre granite	CB	1.890	12.700	212.000	82.000	0.160
	Barre granite	CCNBD	1.800	12.700	212.000	82.000	0.160
	Laurentian granite	CB	1.800	12.790	259.000	92.000	0.210
	Laurentian granite	CCNBD	1.830	12.790	259.000	92.000	0.210
	Stanstead granite	CB	1.440	7.880	173.000	66.000	0.160
	Stanstead granite	CCNBD	1.220	7.880	173.000	66.000	0.160
[50]	Hunan Granite	CSTBD	0.863	7.000	139.000	48.100	0.260
[55]	Johnstone	SCB	1.950	0.420	2.000	200.000	0.300
[33]	Gabbro	SECRBB	2.290	11.120	132.150	42.980	0.180
	Gabbro	CB	2.720	11.120	132.150	42.980	0.180
	Gabbro	SCB	1.580	11.120	132.150	42.980	0.180
	Gabbro	SNSRB	1.970	11.120	132.150	42.980	0.180
	Gabbro	BDT	2.110	11.120	132.150	42.980	0.180
[19]	Shizhu Shale	CCNBD	1.240	8.010	118.100	24.957	0.328
	Shizhu Shale	CCNBD	1.280	8.243	54.200	20.687	0.251
	Shizhu Shale	CCNBD	1.413	9.170	78.600	17.977	0.285
	Shizhu Shale	CCNBD	1.593	9.638	105.900	16.803	0.309
	Shizhu Shale	CCNBD	2.200	12.840	118.400	13.827	0.371
[10]	Ankara andesite	SCB	0.940	7.000	82.840	12.334	0.150
	Ankara andesite	CCNBD	1.450	7.000	82.840	12.334	0.150
	Afyon marble	SCB	0.560	5.130	52.320	34.294	0.120
	Afyon marble	CCNBD	1.090	5.130	52.320	34.294	0.120
[51]	Fujian granite	SCB	1.603	12.500	183.300	40.710	0.230
[52]	Fujian granite	CSTBD	1.145	11.630	174.780	28.940	0.200
[53]	Fujian granite	SCB	1.349	11.630	174.780	28.940	0.200
[54]	Bayan Sandstone	SCB	0.441	2.850	43.110	12.240	0.170

${\mathrm{K}}_{\mathrm{I}\mathrm{C}}$: Mode I fracture toughness; ${\sigma }_t$: Brazilian tensile strength; ${\sigma }_c$: Uniaxial compressive strength; $E$: Young’s modulus; $\upsilon$: Poisson’s ratio; SECRBB: Single Edge Crack Round Bar Bending; CSTBD: Cracked Straight Through Brazilian Disc; SNSRB: Straight Notched Short Rod Bend; BDT: Brazilian Disk Test.

) using exponential, linear, logarithmic and power models. Regression analysis was carried out using R [46] and R packages [47,48,49]. Literature data were collected from various references such that different rock types, i.e., soft and hard, and core K_IC test methods can be represented. In the literature data, rocks from different countries were considered such as China [6,19,50,51,52,53,54], UK [18], Australia [55,56], Japan [57,58], USA [59], Canada [59] and Turkey [10,60,61]. Static and level I testing conditions were considered in this study because they are the most common and simplest conditions for K_IC testing. Where weak rocks or not enough samples (in number and size) were present, test methods that require large sample sizes such as CB and SECRBB may not be a feasible choice. So, it was vital to consider additional test methods such as CCNBD and SCB that require a significantly smaller sample size. Furthermore, considering different rock types would help generalize the K_IC—rock brittleness relationship.

Rock brittleness was assessed using ten indices (

Table 2. The brittleness indices used in this paper.

Brittleness Index Equation	No.	Reference
$B_1=\frac{{\sigma }_c}{{\sigma }_t}$	(1)	[42,43]
$B_2=\frac{{\sigma }_c-{\sigma }_t}{{\sigma }_c+{\sigma }_t}$	(2)	[42,43]
$B_3=\frac{{\sigma }_c\times {\sigma }_t}{2}$	(3)	[42,43]
$B_4=\sqrt{\frac{{\sigma }_c\times {\sigma }_t}{2}}$	(4)	[42,43]
$B_5=0.5\times 100\times [\left(\frac{E-1}{8-1}\right)+\left(\frac{\upsilon -0.4}{0.15-0.4}\right)]$	(5)	[42]
$B_6=\frac{3 K-5\lambda }{\lambda }=\frac{1}{\upsilon }-4$	(6)	[42,43]
$B_7=\frac{E}{\lambda }= \frac{1}{\upsilon }-1-2\upsilon$	(7)	[42,43]
$B_8=\frac{\lambda +2G}{\lambda }=\frac{1}{\upsilon }-1$	(8)	[42,43]
$B_9={({\sigma }_c\times {\sigma }_t)}^{0.72}$	(9)	[24]
$B_{10}=\frac{{{\sigma }_t}^{0.84} E^{0.51}}{{{\sigma }_c}^{0.21}}$	(10)	[24]

$K$: bulk modulus, defined as $K=\frac{E}{3(1-2\upsilon )}; \lambda$: Lame’s constant, defined as $\lambda =\frac{E \upsilon }{(1+\upsilon )(1-2\upsilon )}; G$: bulk modulus, defined as $G=\frac{E}{2(1+\upsilon )}$.

), which were either based on strength parameters, i.e., Equations (1)–(4) and (9), or pre-peak elastic parameters, i.e., Equations (5)–(8), or both, i.e., Equation (10).

In general, rock brittleness indices were chosen such that they can be estimated using rock properties common in most rock testing programs, i.e., UCS, TS, Young’s modulus and Poisson’s ratio. In this study, the considered brittleness indices (B1, B2, B3, B4, B9 and B10), in Table 2, were the same as those previously studied in [22,23,24]. In this way, the effect of considering additional K_IC test methods, i.e., other than CB or SR, on the K_IC—rock brittleness indices relationships could be investigated. Although strength-based indices B1, B2, B3 and B4 were used by many researchers due to their simplicity, they were criticized for not reflecting rock brittleness but rather the rock strength [42,43]. Nonetheless, they, particularly indices B3 and B4, were used to assess the performance of different rock operations such as ornamental stone production rate [28], rock burst tendency [25,26] and drilling operations [29,30,62]. Index B9 was proposed in [62] to assess the performance of drilling operations for thirty-two rocks from Turkey and Norway. It was concluded that B9 had good correlation with the drilling operation performance [62]. Moreover, Index B10 was proposed in [24] for K_IC perdition when rocks with significant pre-fracture plastic deformation were considered. However, it was argued that it has no physical meaning in [43].

Elastic-based indices (B5, B6, B7 and B8) defined rock brittleness in terms of only pre-peak elastic parameters, i.e., Young’s modulus and Poisson’s ratio. They were mainly utilized in quantifying the brittleness of reservoirs, e.g., shale formations, in the oil and gas exploitation operations. These indices assumed that rocks with high Young’s modulus and small Poisson’s ratio would be more brittle. However, they showed contradicting results for different shale formations so it was recommended that they may not represent the brittleness of all shale rocks with the same accuracy [43].

3. Results

Regression results between K_IC and brittleness indices B1 to B10 were shown in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10, respectively.

The results showed weak correlations, i.e., coefficient of correlation (R²) < 0.5, between K_IC and indices B1 (Figure 1), B2 (Figure 2), B3 (Figure 3), B5 (Figure 5), B6 (Figure 6), B7 (Figure 7) and B8 (Figure 8). Moreover, the correlations between K_IC and each of the indices B6 (Figure 6), B7 (Figure 7) and B8 (Figure 8) showed an inverse trend in contrast to the other indices. K_IC—index B6 relationships were investigated only for exponential and linear models since index B6 had negative values that were not valid mathematically for power and logarithmic models. On the other hand, the K_IC—index B4 relationship (Figure 4) was good, i.e., R² > 0.5, for the exponential model, while their correlation was weak for linear, logarithmic and power models. K_IC showed a good correlation with index B9 (Figure 9) for exponential and linear models and with index B10 (Figure 10) for all models. A summary of the relationships with R² > 0.5 is presented in

Table 3. Regression results of K_IC—rock brittleness index relationships with (R² > 0.5).

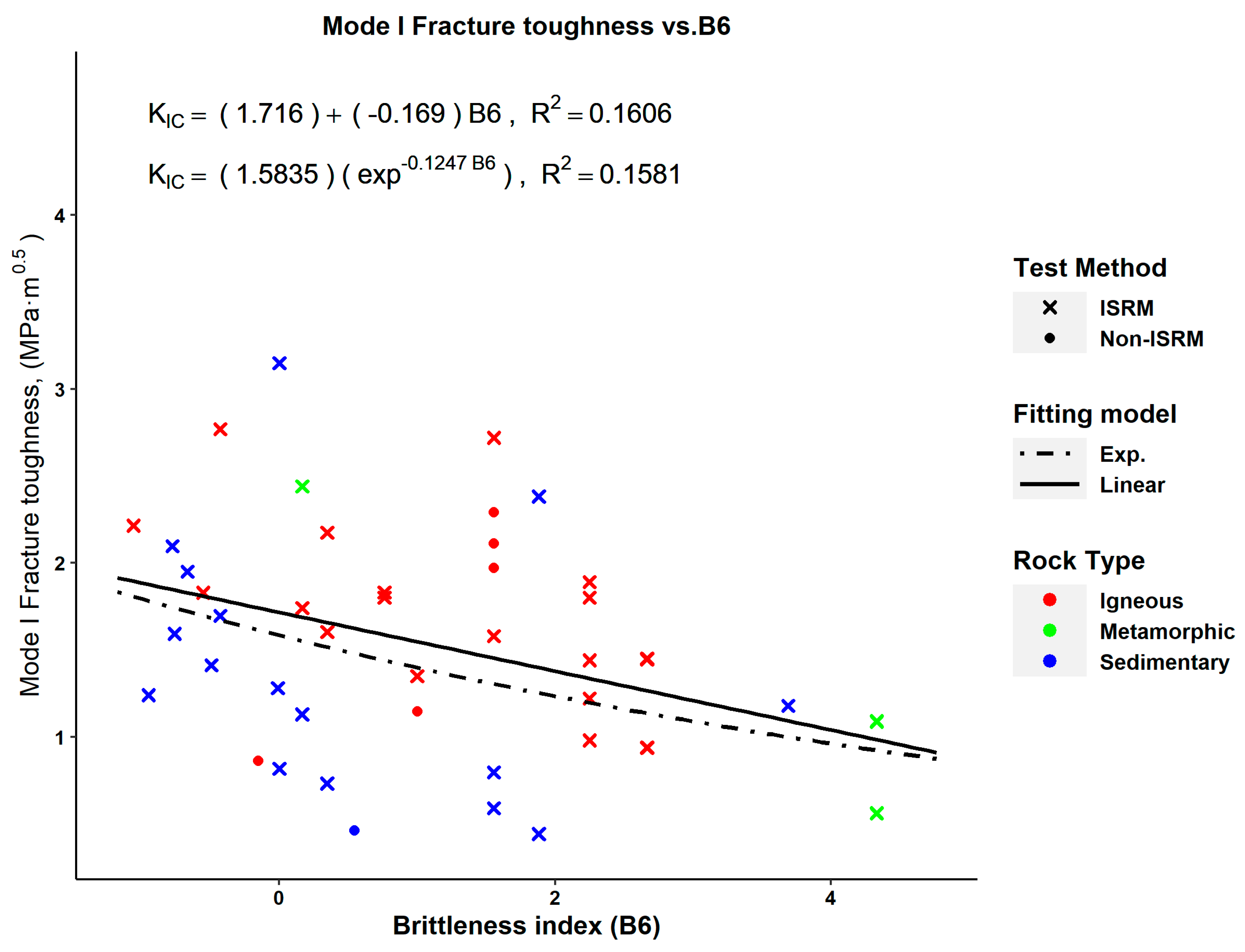
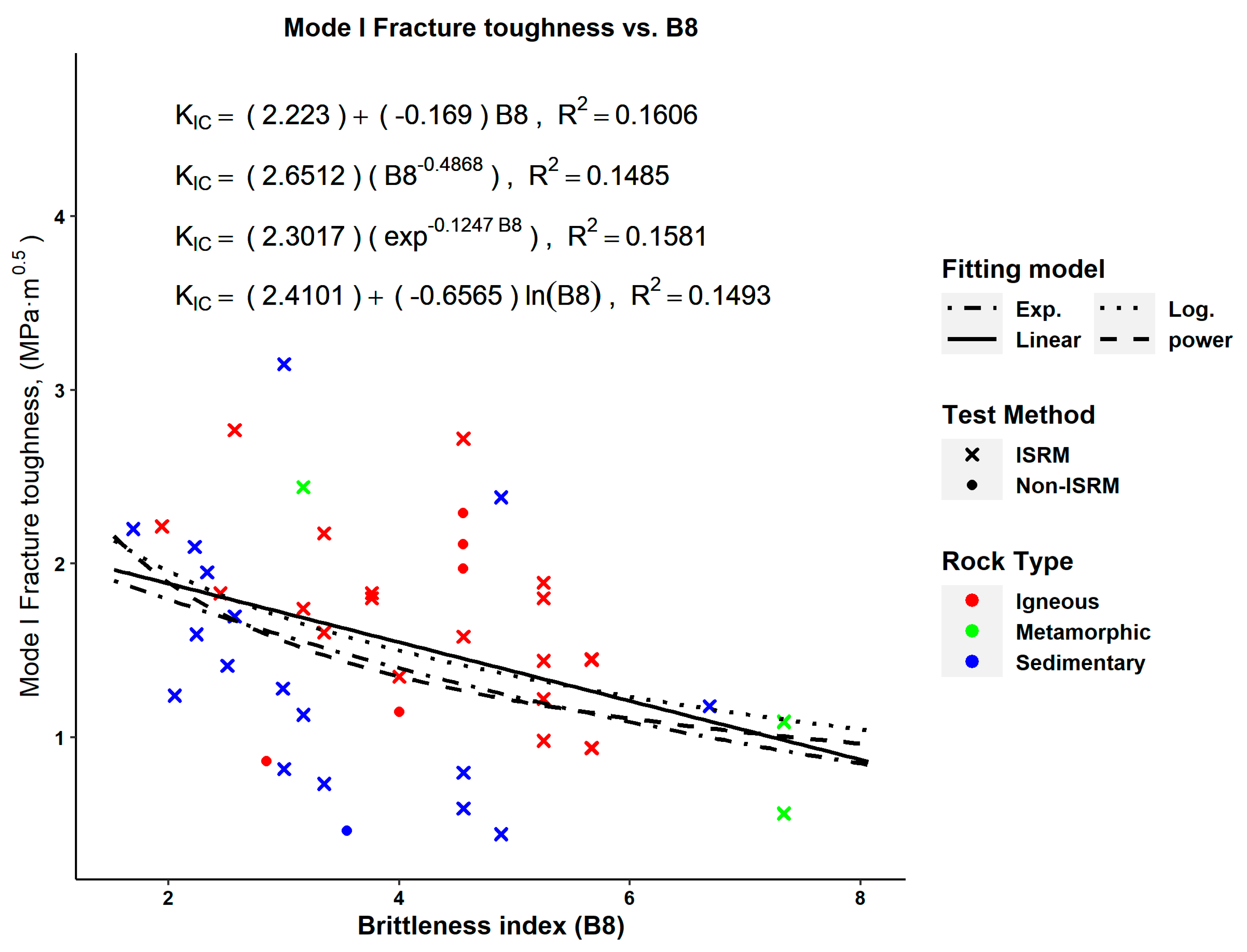
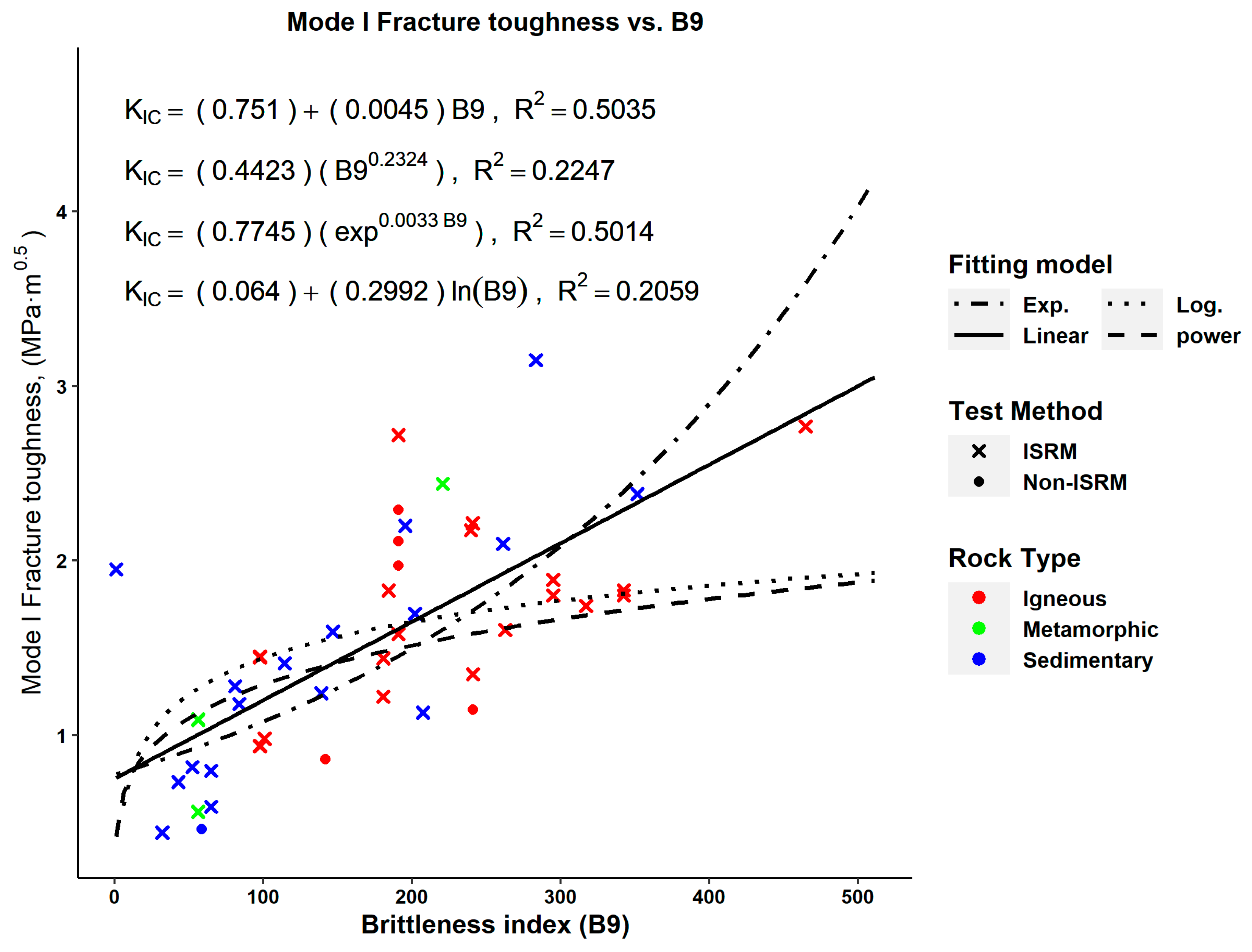
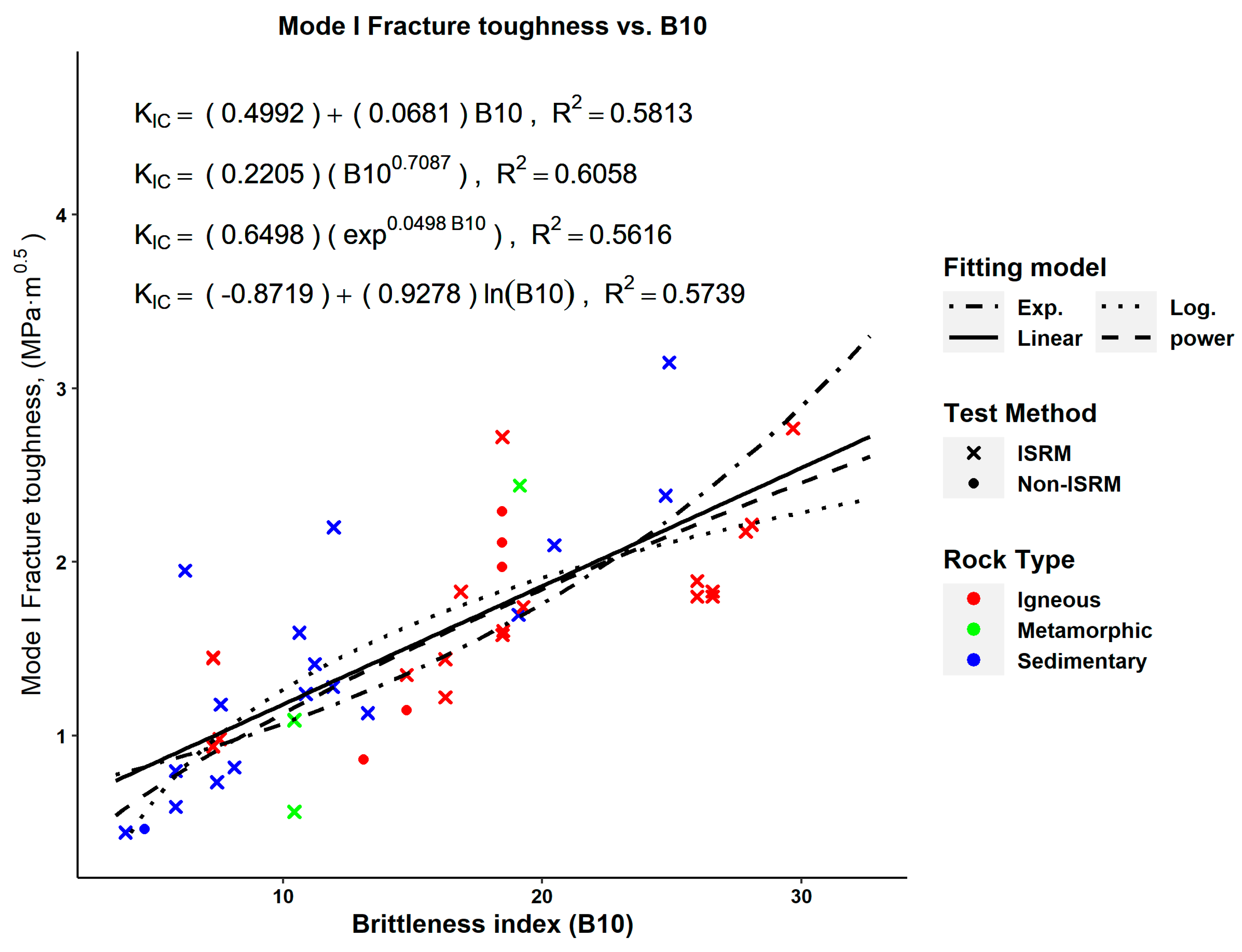
Equation	No.	Figure No.	RMSE	p-Value (Pearson)	p-Value (Spearman)
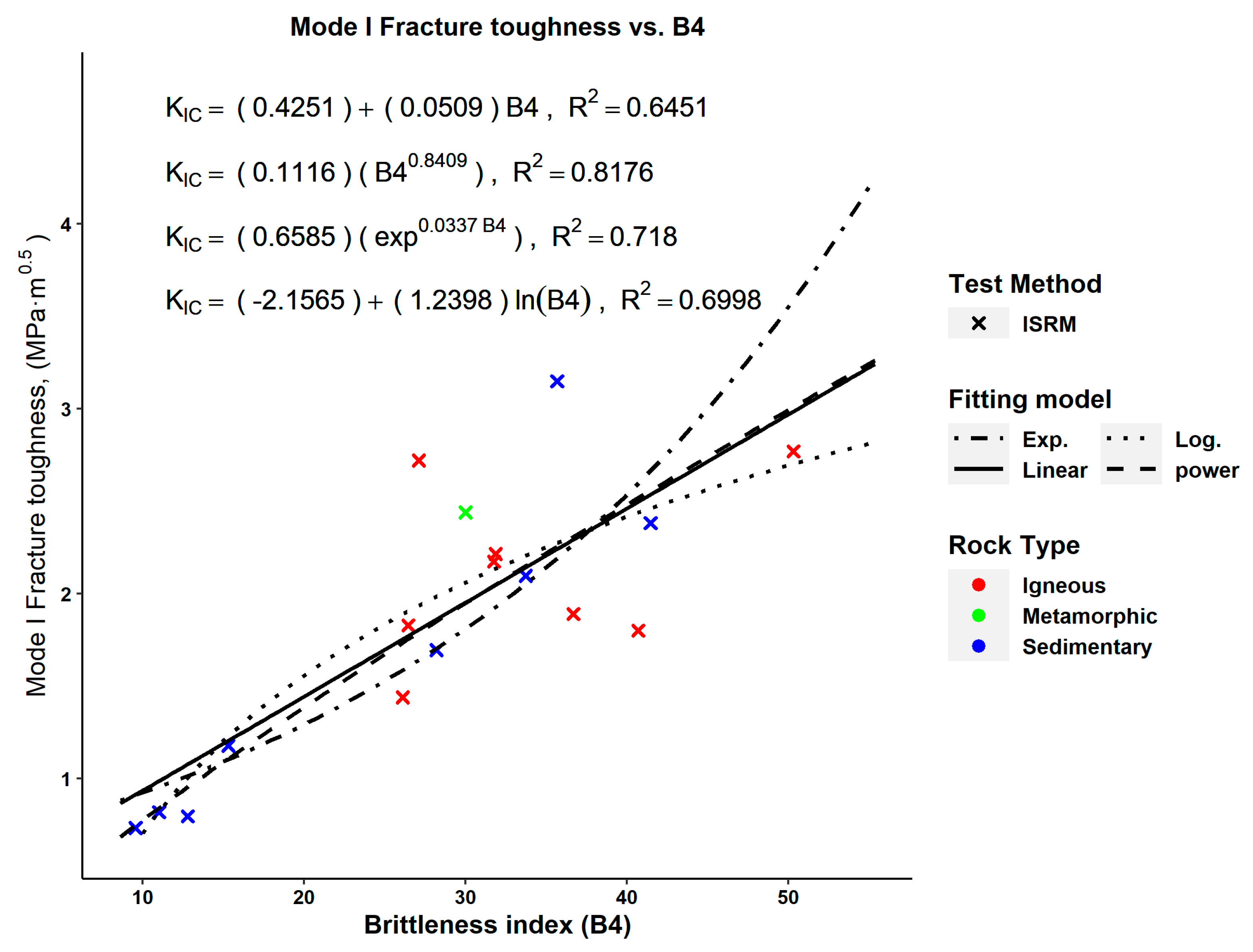
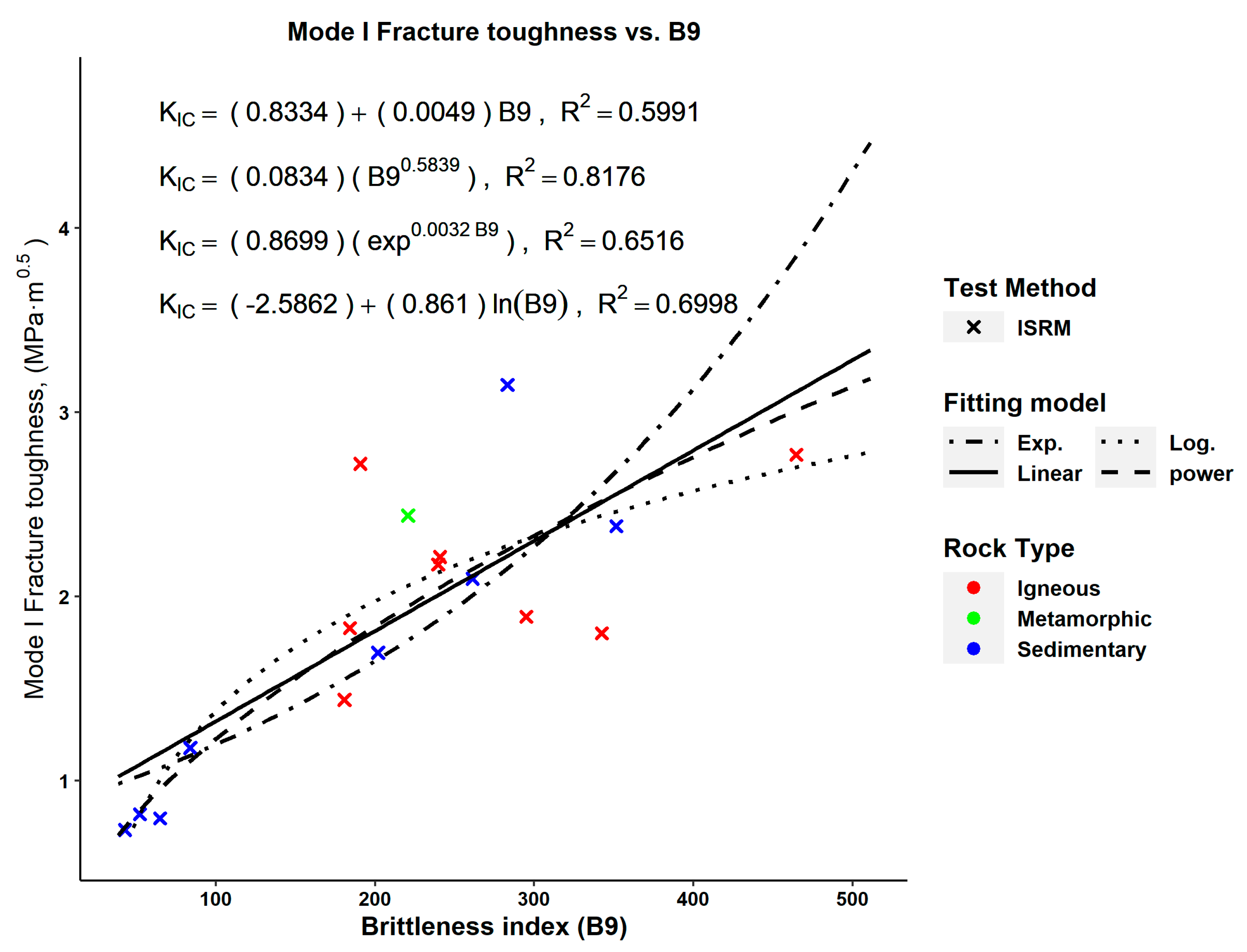
$K_{IC}=\left(0.6333\right) {exp}^{0.032 B4}, R^2=0.5044$	(11)	Figure 4	0.3375	1.57 × 10−8	N.A.
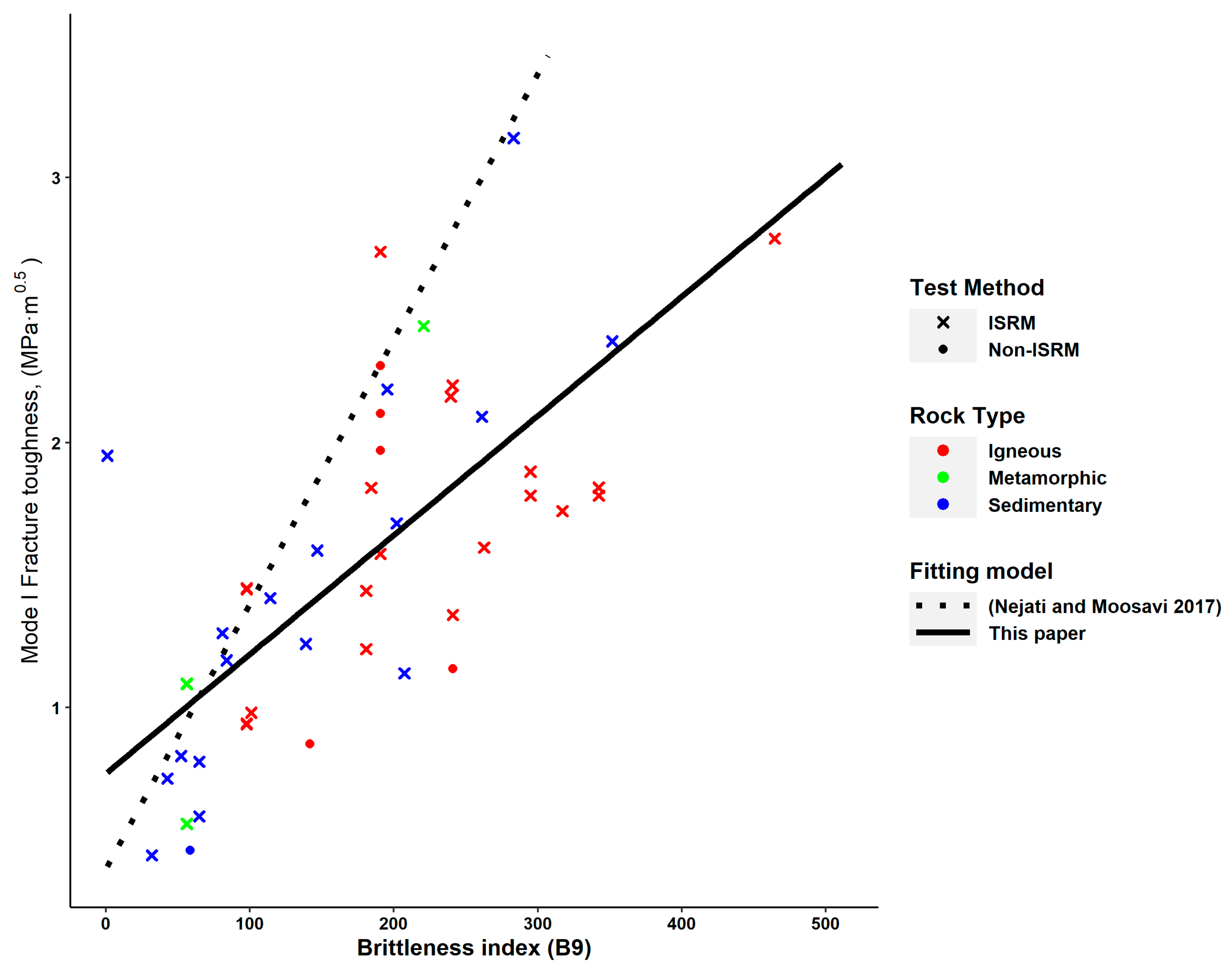
$K_{IC}=\left(0.7745\right) {exp}^{0.0033 B9}, R^2=0.5014$	(12)	Figure 9	0.3385	1.81 × 10−8	N.A.
$K_{IC}=\left(0.751\right)+\left(0.0045\right)B9, R^2=0.5035$	(13)		0.4543	1.64 × 10−8	N.A.
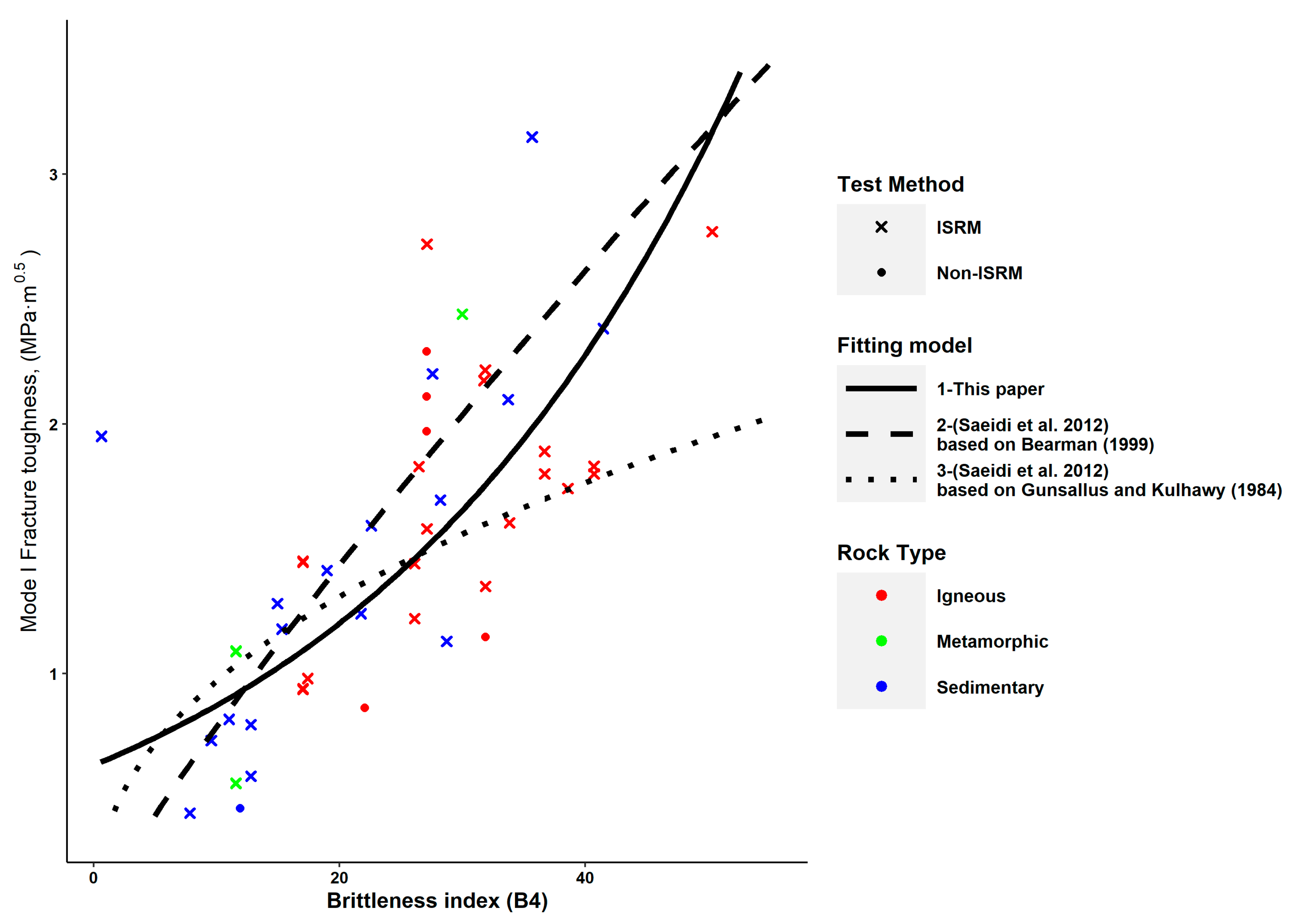
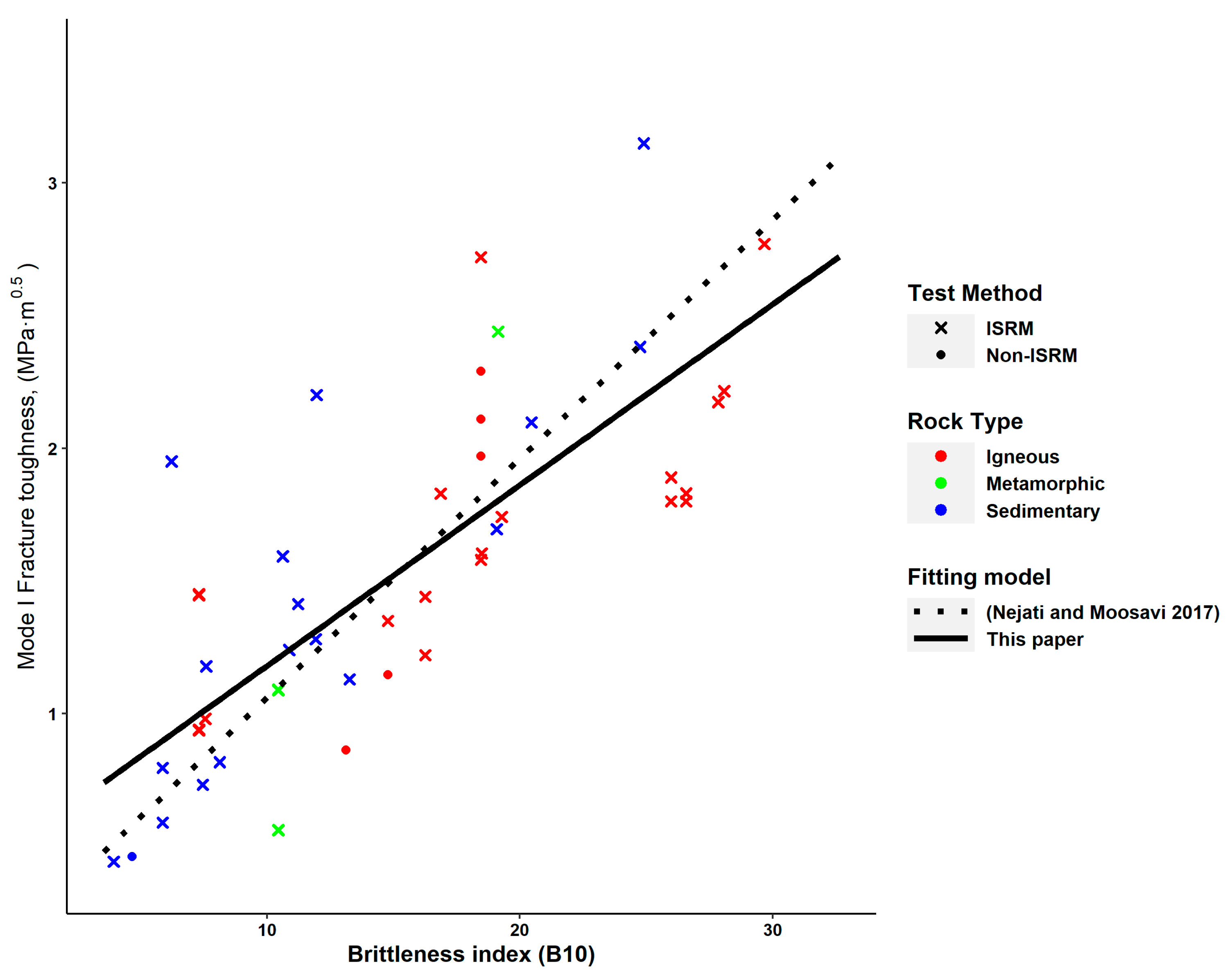
$K_{IC}=\left(0.6498\right){exp}^{0.0498 B10}, R^2=0.5616$	(14)	Figure 10	0.3174	N.A.	9.86 × 10−11
$K_{IC}=\left(-0.8719\right)+\left(0.9278\right) ln\left(B10\right), R^2=0.5739$	(15)		0.4209	N.A.	9.86 × 10−11
$K_{IC}=\left(0.4992\right)+\left(0.0681\right)B10, R^2=0.5813$	(16)		0.4173	N.A.	9.86 × 10−11
$K_{IC}=\left(0.2205\right) {B10}^{0.7087}, R^2=0.6058$	(17)		0.1307	N.A.	9.86 × 10−11

. Additionally, the Root-Mean-Square Error (RMSE) is presented in Table 3 for the relationships with (R² > 0.5). The RMSE was lowest for the K_IC—index B10 power model with a value of 0.1307, which is lower by more than 50% of the nearest RMSE values for the remaining relationships listed. In general, power and exponential models had the lowest RMSE compared to linear and logarithmic models.

The p-value can be used to determine the significance of the proposed relationships. When the variables have a normal distribution, then the p-value, obtained from Pearson’s correlation, can be used to judge the relationships’ significance; otherwise, the p-value obtained from Spearman’s correlation should be used [63,64,65]. The p-value (obtained using R) indicates the probability that the null hypothesis, i.e., the correlation is not significant, is true. For a 95% confidence level (i.e., α =0.05), a p-value lower than 0.05 indicates a significant correlation [64]. The Shapiro–Wilk test [66,67,68] was used to test the normality of brittleness indices (B4, B9 and B10) and K_IC datasets. The results of the Shapiro–Wilk test, obtained using R, are shown in

Table 4. Results of Shapiro–Wilk normality test.

	${\mathbf{K}}_{\mathbf{I}\mathbf{C}}$	${\mathsf{\sigma }}_{\mathbf{t}}$	${\mathsf{\sigma }}_{\mathbf{c}}$	$\mathbf{E}$	$\mathsf{\upsilon }$	B4	B9	B10
Statistic	0.9789	0.97599	0.9542	0.762	0.9497	0.9755	0.9544	0.9348
p-value	0.5351	0.4201	0.0589	1.98 × 10−7	0.0389	0.4071	0.06	0.0103

p-value > 0.05, the null hypothesis is accepted where there is no difference between the sample distribution and a normal distribution, i.e., there is not enough evidence of non-normality. Otherwise, the alternative hypothesis is accepted.

. The dataset of brittleness index (B10) showed evidence of non-normality; hence, the significance of K_IC -index B10 relationships was assessed using the p-value from Spearman’s correlation. A summary of the significant relationships proposed in this paper is presented in Table 3.

4. Discussion

Based on coefficient of correlation (R²) and p-value, the proposed relationships (Table 3) were significant. These relationships were compared with K_IC—rock brittleness relationships from the literature (

Table 5. K_IC—rock brittleness indices from the literature.

Equation	No.	Reference
$K_{IC}=\left(0.01\right) B9+\left(0.39\right) ,{ R}^2=0.61$	(18)	[24]
$K_{IC}=\left(0.09\right) B10+\left(0.16\right) , { R}^2=0.68$	(19)
$K_{IC}=\left(0.11\right) {B3}^{0.43} , R=0.96$	(20)	[22]
$K_{IC}=\left(0.107\right) {B4}^{0.8663} , { R}^2=0.9262$	(21)	[23]
$K_{IC}=\left(0.3952\right) {B4}^{0.4315} , { R}^2=0.5857$	(22)

).

In this paper, there were weak correlations between K_IC and each of the indices B1 and B2. Similar weak correlations were reported in [23,24] between K_IC and index B1 and in [22,23,24] between K_IC and index B2. This indicated that indices B1 and B2 may not be good predictors of K_IC.

For strength-based brittleness index B3, there was no significant correlation with K_IC in this study, despite the significant K_IC—index B3 relationship reported in [22], i.e., Equation (20) in Table 5.

The relationship between K_IC and index B4 proposed in this study, i.e., Equation (11) in Table 3, was significant but it had an R² lower than the relationships reported in [23], i.e., Equations (21) and (22) in Table 5, that were proposed using data from [18] and [69], respectively. A comparison between the K_IC—index B4 relationships is shown in Figure 11. There were significant differences between Equations (21) and (22), particularly at B4 values higher than 20, while Equation (11) showed an overall average trend between Equations (21) and (22).

The proposed K_IC—index B9 linear relationship, i.e., Equation (13) in Table 3, was compared to Equation (18) in Table 5. There were significant differences between the two relationships (Figure 12), particularly at B9 values higher than nearly 65.

These dissimilarities between the relationships proposed in this paper and the proposed ones in the literature, for indices B3, B4 and B9, may be owed to two main reasons.

The first reason may be the differences in the values of rock properties, namely ${\mathsf{\sigma }}_{\mathrm{t}}$ and ${\mathsf{\sigma }}_{\mathrm{c}}$. Indices B3 and B4 were criticized for reflecting rock strength rather than brittleness [42,43]. Based on the formula of indices B3, B4 and B9, they would be sensitive for variations in ${\mathsf{\sigma }}_{\mathrm{t}}$ and ${\mathsf{\sigma }}_{\mathrm{c}}$. So, considering other types of rocks (i.e., weaker or stronger rocks) would affect the value of these indices and in turn affect their correlation significance with K_IC.

A summary of descriptive statistics of the data used in this paper and [18,24,69] is shown in

Table 6. Descriptive statistics of the rock properties used in this paper.

Reference	Parameter	${\mathsf{\sigma }}_{\mathbf{t}}$ (MPa)	${\mathsf{\sigma }}_{\mathbf{c}}$ (MPa)	E (GPa)	$\mathsf{\upsilon }$
This paper	Mean	9.42	125.88	41.31	0.21
	Range	0.42 to 18.42	2 to 274.82	8.23 to 200.00	0.12 to 0.37
	Standard deviation	3.92	65.11	32.31	0.06
	Skewness	−0.0230	0.4782	2.7206	0.5499
[18]	Mean	11.8	141.79	44.13	0.25
	Range	3.84 to 18.42	47.76 to 274.82	15.92 to 64.18	0.13 to 0.34
	Standard deviation	4.76	65.58	15.91	0.06
	Skewness	−0.6026	0.452	−0.3654	−0.6731
[69]	Mean	12.82	150.83	-----	-----
	Range	5.9 to 17	57.2 to 264	-----	-----
	Standard deviation	3.61	58.84	-----	-----
	Skewness	−0.8834	0.3376	-----	-----
[24]	Mean	9.97	137.22	50.22	-----
	Range	2.3 to 17.6	32.3 to 224	9.9 to 78	-----
	Standard deviation	4.61	56.26	20.21	-----
	Skewness	−0.1017	−0.1939	−0.6577	-----

. The values of ${\mathsf{\sigma }}_{\mathrm{t}}$ and ${\mathsf{\sigma }}_{\mathrm{c}}$ were relatively close in general. However, the skewness (a measure of asymmetry) and the mean of ${\mathsf{\sigma }}_{\mathrm{t}}$ indicated that more rocks with lower tensile strength were considered in this paper (see Table 6). While the values of ${\mathsf{\sigma }}_{\mathrm{c}}$ were relatively close between the data in this paper and [18] and [69], rock types with higher ${\mathsf{\sigma }}_{\mathrm{c}}$ were considered in this paper compared to [24].

The second reason may be the K_IC test method effect. This paper used data collected from different references, where different K_IC test methods were used (Table 1). Meanwhile, Equations (18) and (20)–(22) in Table 5 were proposed using the data obtained, totally or mostly, using the CB test method, i.e., Equations (18), (20) and (21), or using the SR test method, i.e., Equation (22). In order to examine the effect of the K_IC test method more closely, the relationships between K_IC and each of the indices B3, B4 and B9 were examined using data in Table 1 considering only the data from the CB test. Most of these data, around 70%, were obtained from [18], i.e., the data used to obtain Equations (20) and (21). However, these data were completely different from those used to obtain Equations (18) and (22).

The results for B3, B4 and B9 are shown in Figure 13, Figure 14 and Figure 15, respectively. Considering only K_IC data from CB test produced significant correlations between K_IC and B3 in contrast to the weak correlations in Figure 3. Furthermore, the best correlations between K_IC and each of the B4 and B9 indices had a higher R² (0.8176 for power models) compared to R² = 0.5044 and 0.5035 for B4 (exponential model) and B9 (linear model), respectively (see Table 3). It should be noted that there were no changes in the correlation significance between K_IC and each of the B1 and B2 indices when only CB test data were considered. The increased correlation significance, particularly that between K_IC and B9, indicated that there was a significant effect of the K_IC test method on the correlation between K_IC and strength-based indices B3, B4 and B9. Furthermore, the test method’s insignificant effect on the correlation between K_IC and indices B1 and B2 confirmed that these indices were not good predictors for K_IC.

Much research has reported significant differences in K_IC results obtained from different test methods for the same rock. Six different K_IC test methods, CB, SECRBB, SCB, SNSRB, BDT and Flattened Brazilian Disk (FBD), were investigated in [33]. It was concluded that CB was the optimum K_IC test method due to its stable crack growth, which results in creating a sharp and narrow crack at the top of the notch, and the small FPZ, which satisfies the LEFM assumption. Furthermore, boundary conditions did not have any considerable effect on crack behavior [33]. Hence, CB was used, in many studies, as a reference in comparison with other test methods.

For Keochang Granite and Yeosan Marble, K_IC was determined using CCNBD, SCB, BDT and chevron-notched SCB test methods. Similar values were reported between CB and CCNBD; however, the SCB results were incomparable with the remaining methods and [17]. Moreover, lower K_IC values were obtained from CCNBD compared to those from CB and SR for the same rock type [31,59]. These differences may be caused by various factors such as specimen geometry and loading type [59].

The SCB test usually produced K_IC values lower than those using other test methods. The K_IC of Kimachi sandstone obtained from CB was 35% higher than that from SCB [58]. A 36.4% lower K_IC value from SCB was reported for Dazhou sandstone compared to that using CCNBD [70]. The main causes for the conservative results from SCB are the large FPZ size, compared to other methods [33,70], and the unstable crack propagation [33]. It is believed that the notch length, in SCB samples, did not represent the critical crack length associated with the maximum load because fractures, in SCB tests, propagated before FPZ fully develops, i.e., unstable crack propagation occurred [58]. The unstable crack propagation was also reported by [54].

Furthermore, BDT results were compared with those obtained from CB for six Australian rocks. It was concluded that the results were close except for basalt, which they could not explain [71]. Similarly, it was argued that BDT was a viable K_IC test method because its results were similar to CCNBD and it had simple sample preparations, i.e., no notch is needed, although a significant scatter in the BDT results was reported [17]. In contrast, BDT was found to be an improper test method in [33] due to the lack of a uniform load distribution in the sample, and the K_IC calculation was based on the infinite plate assumption and the significant boundary effect on the fracture initiation and propagation.

Furthermore, the K_IC obtained from the same test method and rock can vary with the sample geometry and dimensions due to their effect on the formed FPZ in samples during loading. A linear positive correlation between the FPZ size and diameter of concrete SCB samples was reported in [72]. Moreover, the notch-length-to-radius ratio was found to greatly affect K_IC for SCB, CSTBD and SECRBB test methods [57,73,74]. The variations in notch type between test methods affected the crack propagation and fracturing mechanics of samples. In general, sample geometries with straight notches are characterized by the unstable crack propagation, such as in SCB samples, unlike chevron-notched specimens [33]. This may be due to the larger FPZ associated with straight notches as reported in [75] for SCB and Cracked Chevron Notched Semi-Circular Bend test methods. In fact, sample size, particularly ligament length (i.e., area above the notch), should be large enough such that the FPZ size formed under loading has an insignificant effect on the fracturing mechanism and in turn on the obtained K_IC value [74,76]. Moreover, FPZ size varied between different rocks for the same test method, due to the variation in petrological properties, e.g., grain size heterogeneity and micro-crack-induced anisotropy [77,78].

Hence, we concluded that the inconsistencies in the values of rock strength properties and the different K_IC test methods could explain the weaker correlations between K_IC and strength-based rock brittleness indices B3, B4 and B9 reported in this paper compared to the relationships reported in the literature.

On the other hand, the K_IC—index B10 relationship (Equation (16) in Table 3) showed an overall closer trend to Equation (19) in Table 5. Equation (16) overestimated K_IC at values lower than nearly 15 at B10, compared to Equation (19), and underestimated K_IC at values above 15 (see Figure 16). These differences were lower than those observed in Figure 11 and Figure 12 for indices B4 and B9, respectively. It should be noted that Equations (16) and (19) were proposed using two distinct datasets. Equation (19) was proposed using K_IC data obtained mostly from the CB test [24], unlike this paper. This suggested that K_IC—index B10 relationships were not greatly influenced by the K_IC test method. However, K_IC—index B10 relationships, considering only CB data from Table 1, were more significant (see Figure 17).

Moreover, less stiff rocks, i.e., rocks having lower Young’s modulus values, were considered in this paper compared to those in [24] (see the skewness of Young’s modulus in Table 6). Nonetheless, a significant correlation between K_IC and index B10 was reported in this paper. For rocks that exhibit significant plastic deformation before fracturing (i.e., soft rocks), it was believed that both ultimate strength and elastic parameters must be considered in the rock brittleness index. In fact, the effect of Young’s modulus on the brittleness of such rocks was found to be more critical than ${\mathsf{\sigma }}_{\mathrm{c}}$ [24].

For the elastic-based indices, i.e., B5, B6, B7 and B8 in Table 2, there were weak correlations with K_IC in contrast to the strength-based indices. The reason may be that the elastic-based brittleness indices were proposed for softer rocks, such as shale [43]. Although this paper considered more soft rock types, stiff rocks were also considered (see the skewness of Young’s modulus in Table 6). Another possible reason may be the elastic parameters’ calculation technique. Strength parameters are determined experimentally, when samples fail. Typical stress strain curves have four regions before failure, i.e., macro-cracking; 1—crack closure, 2—elastic, 3—micro-cracks initiation and 4—unstable crack propagation that ends with failure [9,79]. Elastic parameters, of the whole rock material, are estimated using data collected in the second region [9], i.e., pre-peak region with no crack propagation. In fracture mechanics, macro-cracks, i.e., failures, occurred after micro-cracks’ formation around flaws, e.g., grain boundaries, when the stress intensity exceeded fracture toughness [2]. Since elastic parameters were estimated before micro-cracks’ formation, i.e., pre-peak softening, or the propagation of any existing cracks, it can be understood why the correlation between K_IC and elastic-parameter-based indices was insignificant. Compared to elastic-based indices, index B10 was proposed in terms of Young’s modulus, ${\mathsf{\sigma }}_{\mathrm{t}}$ and ${\mathsf{\sigma }}_{\mathrm{c}}$ such that the pre-fracture softening, i.e., beyond the elastic region, of rocks can be considered [24]. This may explain the significant correlation between K_IC and index B10 compared to elastic-based indices. Moreover, brittleness indices based on pre-peak and post-peak strain energies were found to be more accurate in evaluating geotechnical engineering applications such as drilling operations [80]. Regarding the effect of the K_IC test method, the correlations between K_IC and each of the indices B5, B6, B7 and B8 were not improved when only CB data were considered.

5. Conclusions

Rock fracture toughness and rock brittleness have profound impacts on the performance of many rock engineering operations. In this paper, a general K_IC—rock brittleness relationship was investigated considering different rock types and core test methods under level I and static test conditions. Rock brittleness was represented by ten indices, based on strength and pre-peak elastic parameters. It was concluded that brittleness indices based solely on pre-peak elastic parameters cannot be used for the prediction of K_IC. While strength-based brittleness indices (i.e., B4 and B9) can predict K_IC with reasonable accuracy, the prediction accuracy was sensitive to rock strength parameters (particularly tensile strength) and the K_IC test method. For different rock types and K_IC test methods, index B10 was the best brittleness index to predict K_IC, because it was less sensitive to the variation in the K_IC test method and rock types, in addition to considering the pre-fracture plastic deformation of weaker rock types. Taking into account that index B10 was suggested to consider pre-fracture softening and its significant correlation with K_IC, it may be concluded that the LEFM assumption may not be applied for the K_IC values cited in this paper and/or these values may not represent the true size-independent K_IC.

In future studies, it is recommended to (i) investigate the K_IC—rock brittleness relationship for each K_IC test method; (ii) consider the sample size effect; and (iii) consider additional brittleness indices based on pre- and post-peak elastic parameters such as strain energy and mineralogy-based brittleness indices.