Noise Reduction Based on a CEEMD-WPT Crack Acoustic Emission Dataset
Abstract
:1. Introduction
2. Basic Theory
2.1. CEEMD Noise Reduction
- (1)
- First, white noise is added in pairs to the original signal.
- (2)
- The xi(t) signal pair is decomposed using EMD.
- (3)
- The average value of the 2n group IMFs component is calculated, which is the result of CEEMD.
2.2. WPT Noise Reduction
- (1)
- A set of orthogonal wavelet bases is used to decompose the input signal into two parts: high frequency and low frequency, where the scale function α(t) and the wavelet function β(t) are calculated as follows:
- (2)
- The signal is decomposed by a wavelet packet.
- (3)
- The threshold method is used to process the wavelet packet coefficient and reconstruct the wavelet coefficient to obtain the signal after noise reduction.
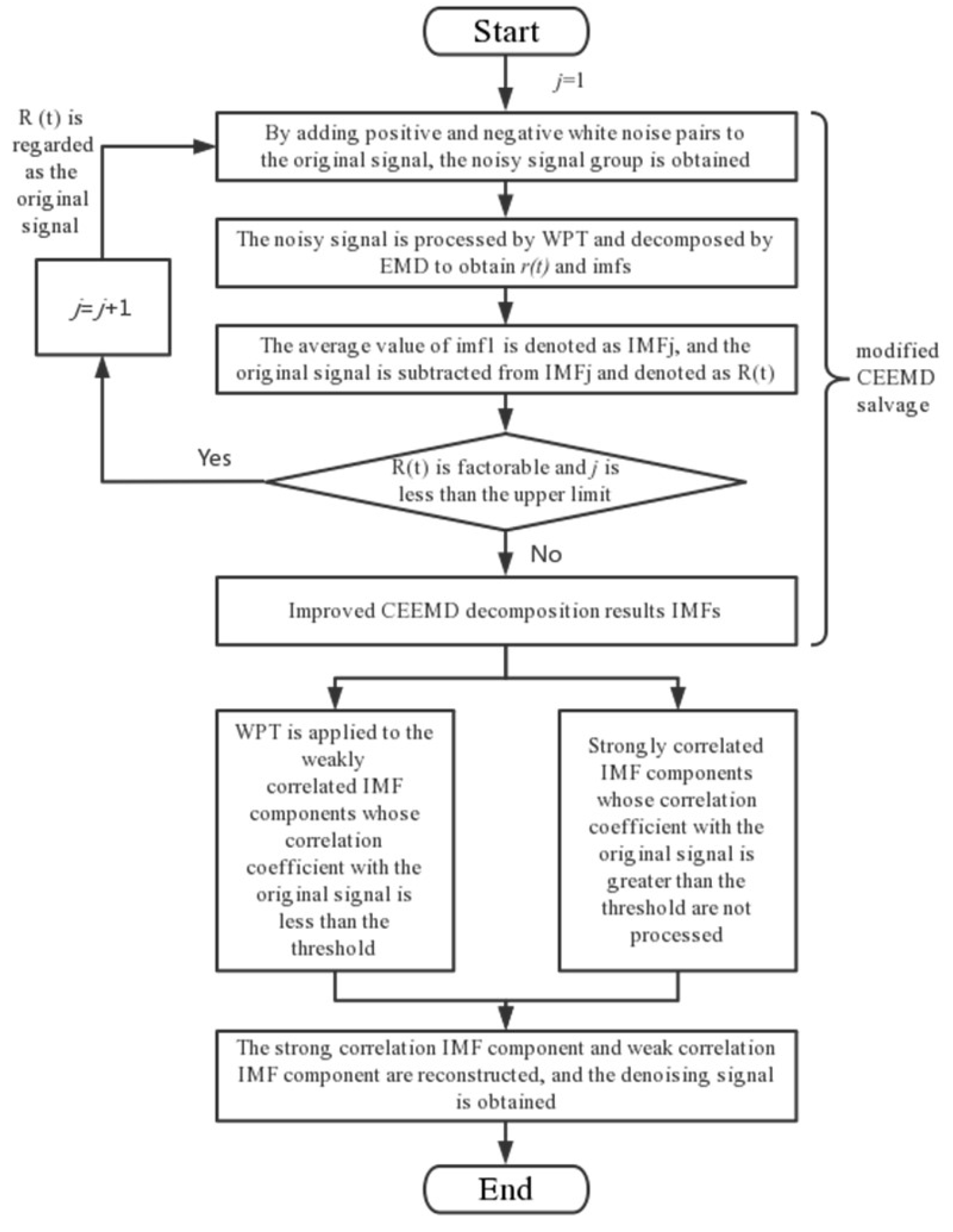
3. Improved CEEMD-WPT Noise Reduction Algorithm
3.1. Improved CEEMD-WPT Decomposition Method
3.2. Improved CEEMD-WPT Reconstruction Method
3.3. Improve the Algorithm Steps of CEEMD-WPT
- (1)
- Add n white noise to the collected signal x(t) to obtain a noisy signal group.
- (2)
- Process the noisy signal group with WPT first, and then with EMD to obtain the n imfs components and residual r(t).
- (3)
- Calculate the average value of imf1 as IMFj, and subtract IMFj from the original signal as R(t).
- (4)
- If R(t) can be decomposed or the number of decompositions is lower than the upper limit, then cycle steps (2–4).
- (5)
- Eliminate the residual r(t), and obtain the IMFs of improved CEEMD.
- (6)
- Calculate the correlation coefficient between each component in IMFs and the original signal, and distinguish the strong and weak correlation components according to the threshold value.
- (7)
- Conduct WPT noise reduction for weakly correlated components to remove noise components.
- (8)
- Reconstruct the weakly correlated component and the strongly correlated component with EMD, and finally obtain the signal x’(t) after noise reduction.
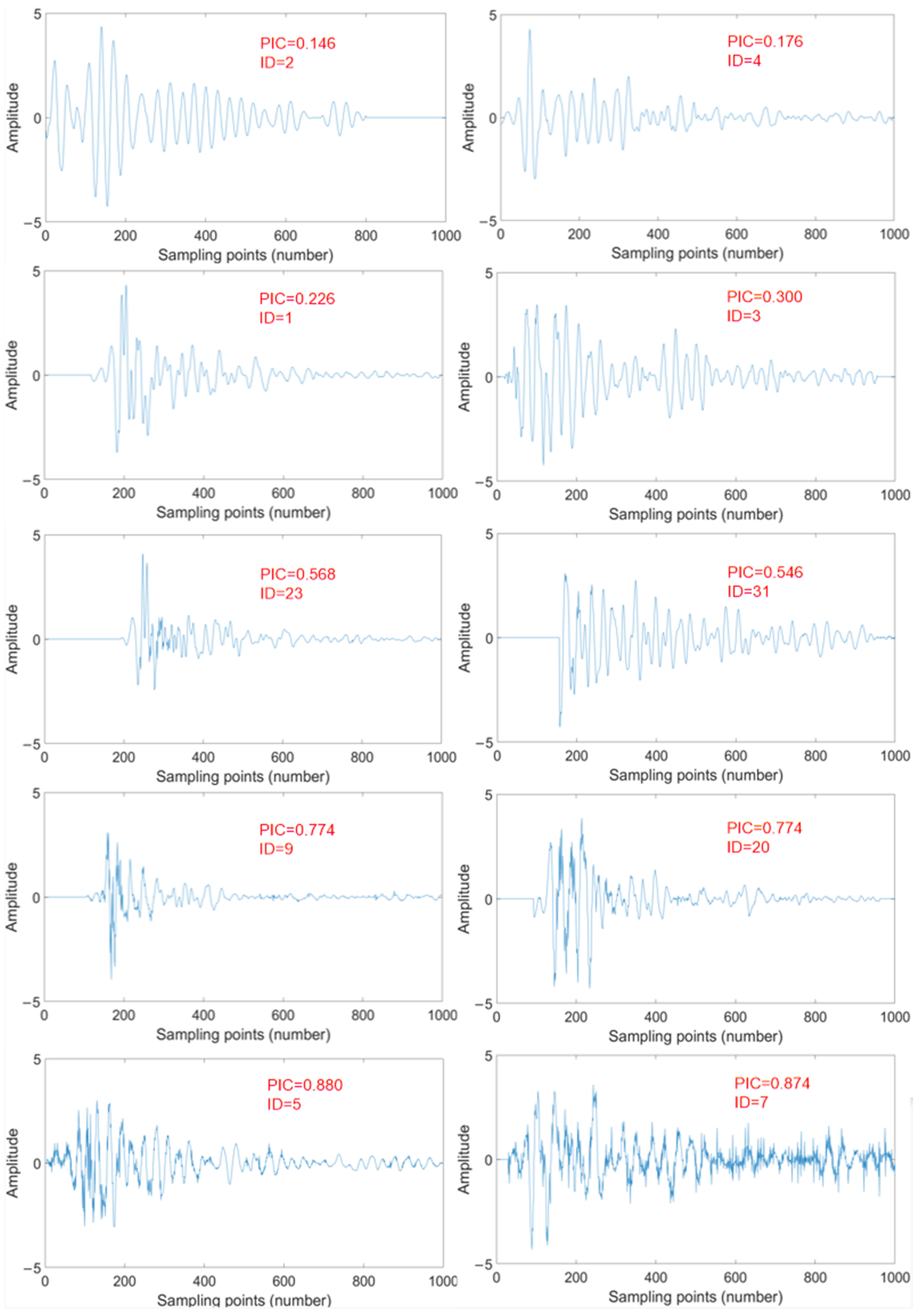
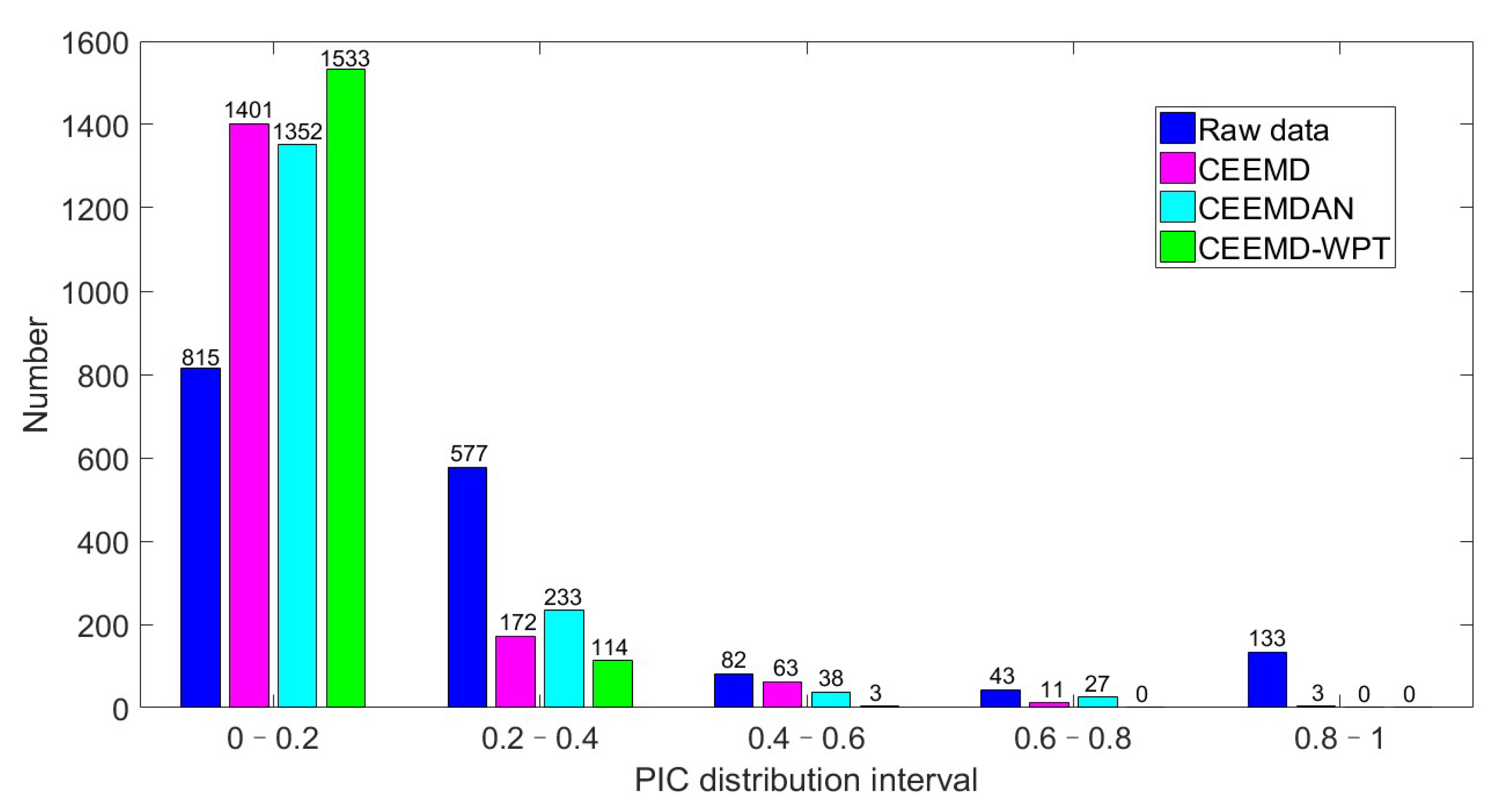
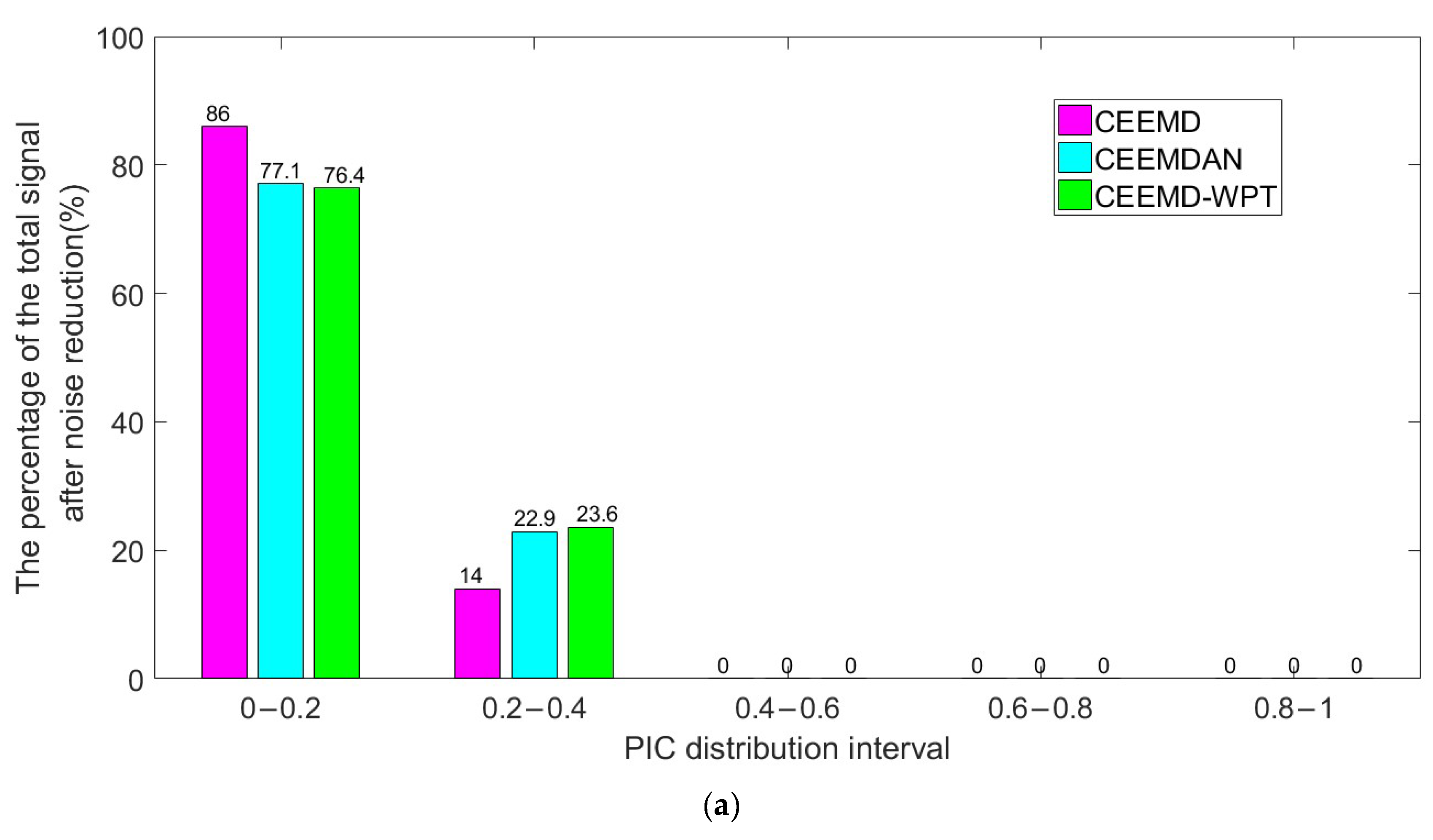
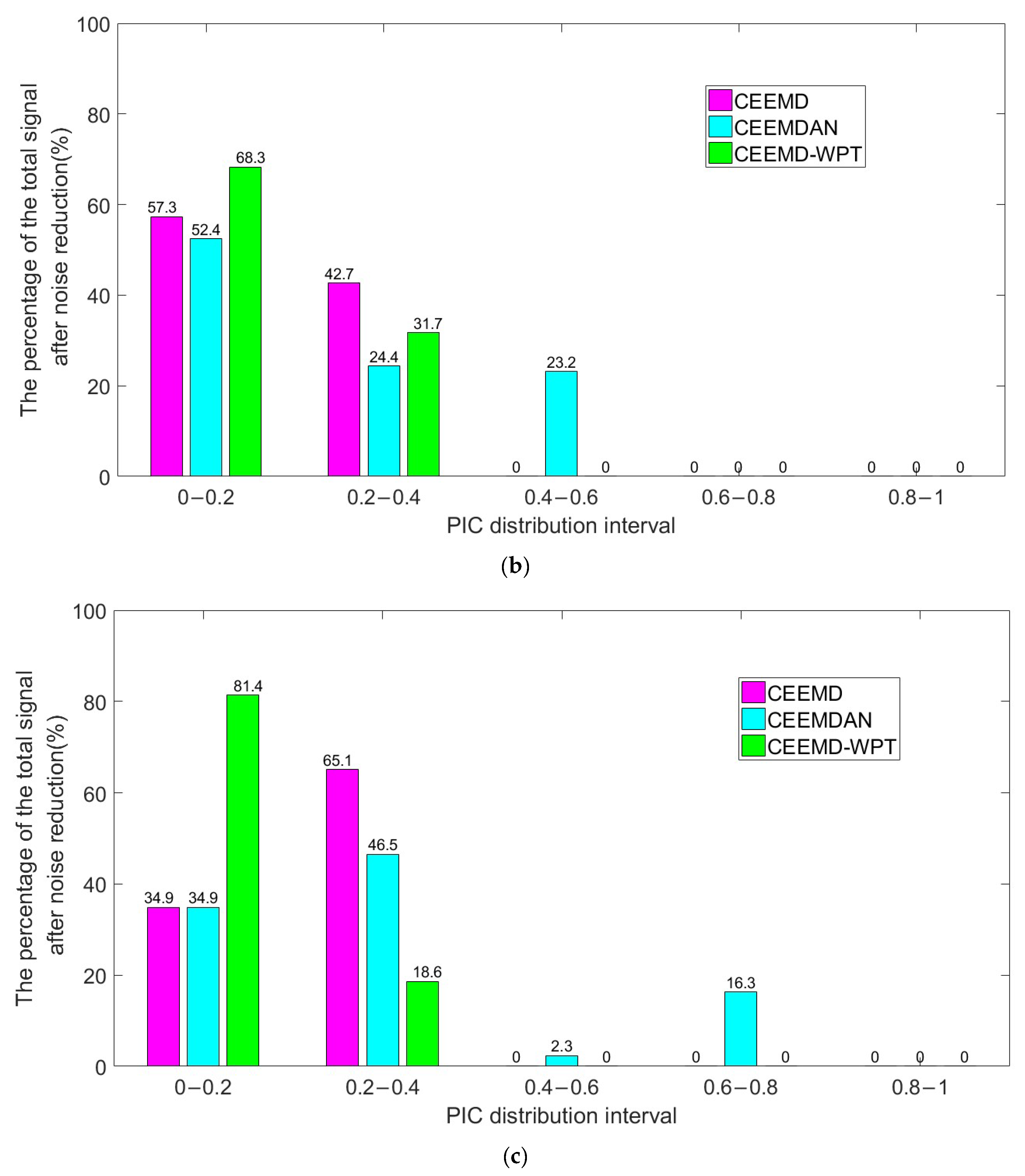
3.4. Principal Interval Coefficient
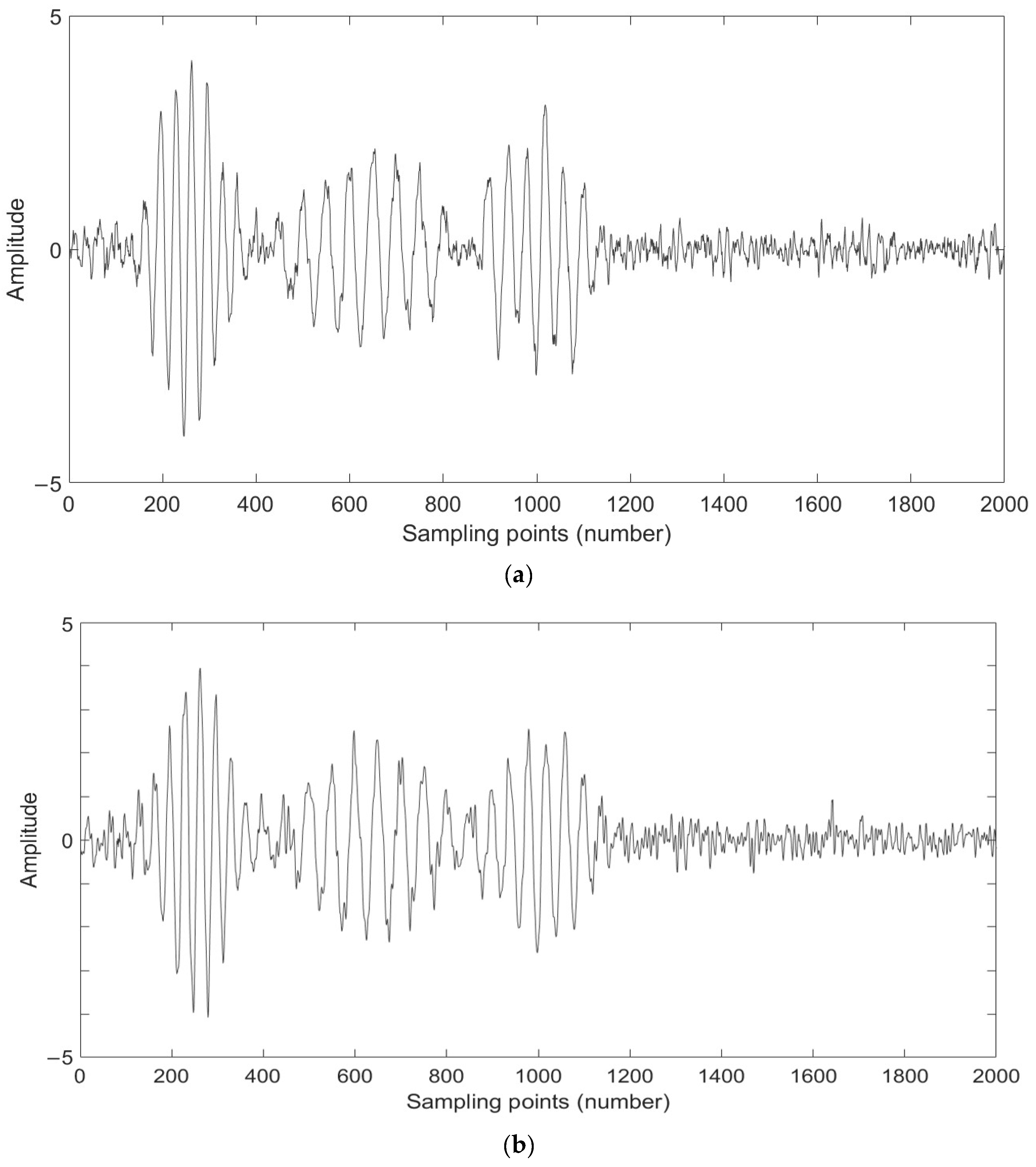
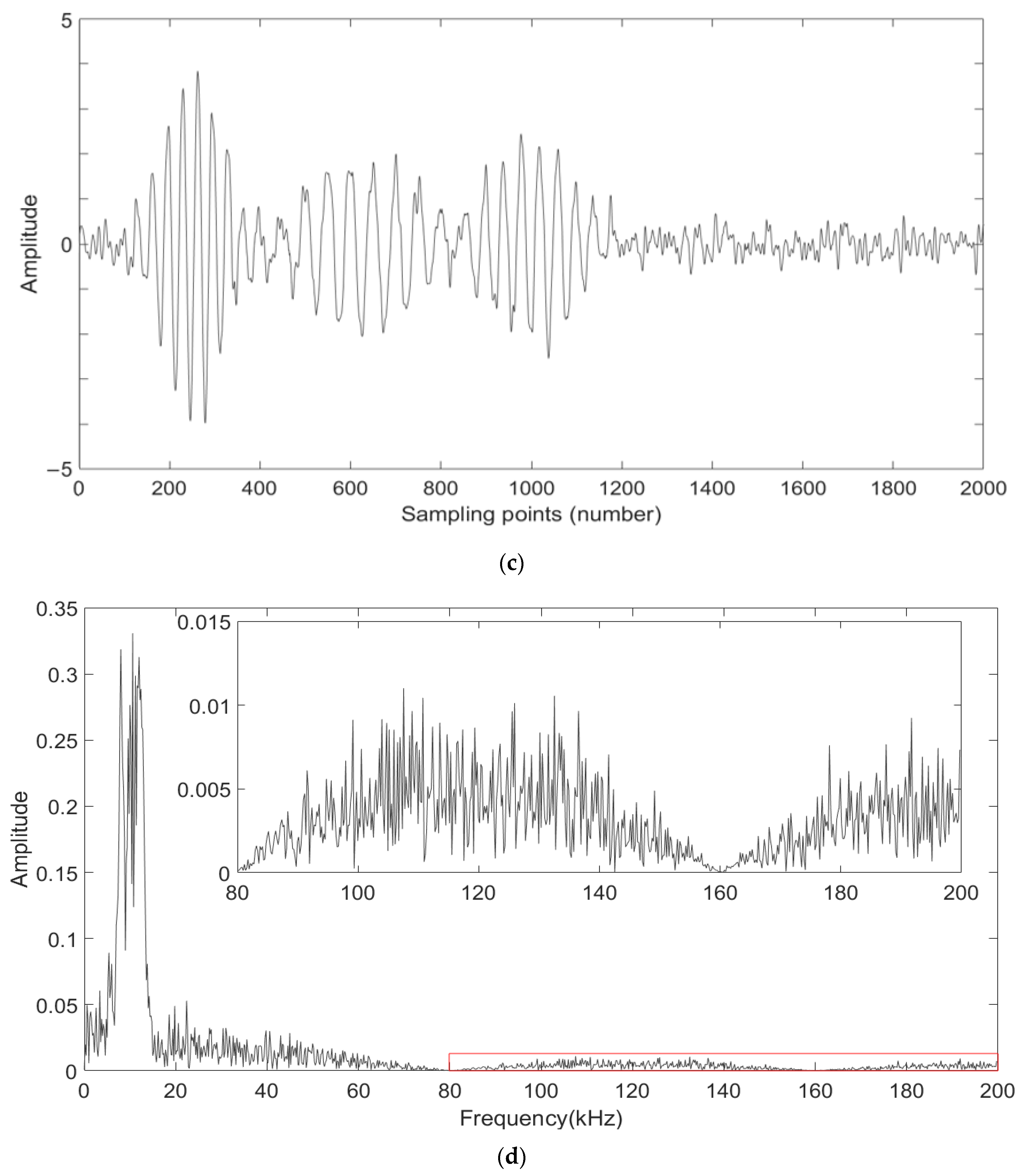
4. Simulation Analysis
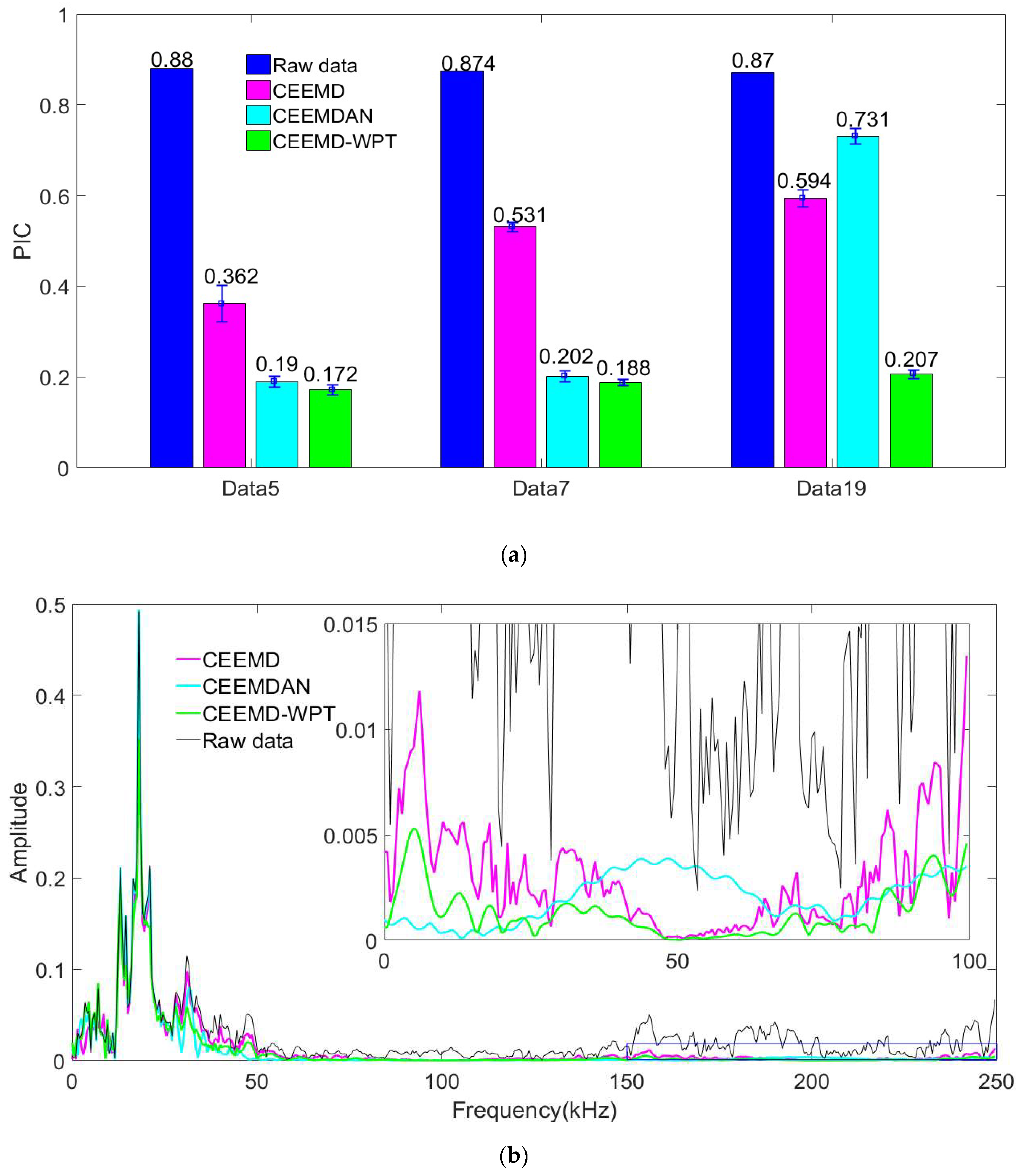
5. Experiment and Analysis
6. Conclusions
- (1)
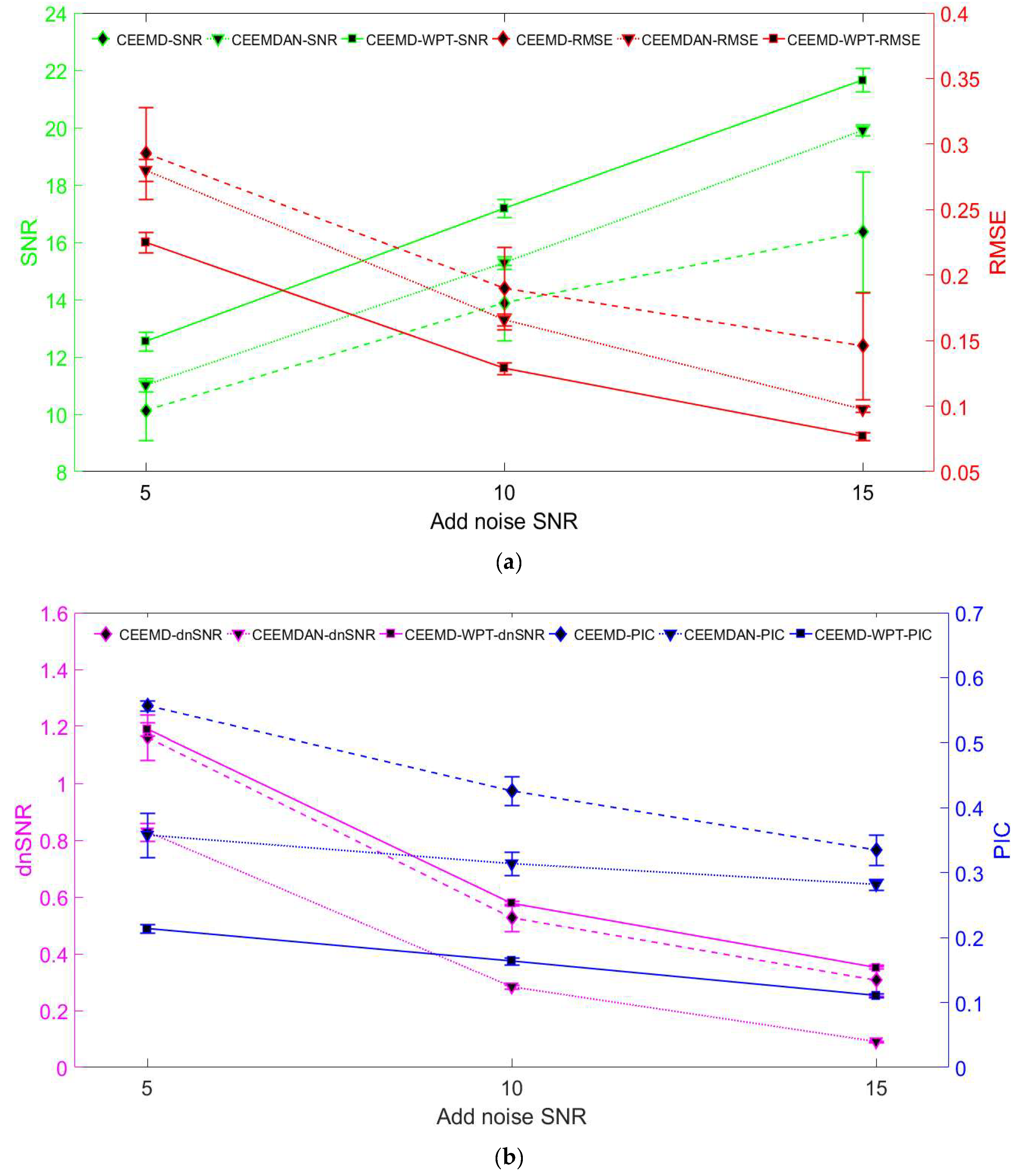
- In order to solve the problem of the poor noise reduction effect and the stability of the traditional CEEMD noise reduction algorithm, this paper designed the CEEMD-WPT noise reduction method, and verified the performance of the algorithm by using analog signals and an AE open dataset “Acoustic Event Dataset”. The results show that, compared with traditional CEEMD and CEEMDAN, CEEMD-WPT has the best noise reduction effect and the least noise residue. Moreover, the statistical variance in noise reduction of CEEMD-WPT is one order of magnitude smaller than that of traditional CEEMD, and it has greater stability.
- (2)
- In order to solve the problem of the noise reduction effect of real signals being difficult to quantify, the PIC index is designed according to the law of noise distribution. In the simulation signal test, it is proved that the PIC index has the same quantization reliability as the SNR and RMSE, and the quantization effect of the dnSNR is poor.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Variable and set | |
| Symbol | Significance |
| x(t) | original signal |
| ε(t) | noise |
| IMFij(t) | JTH component of the ith signal decomposition |
| α(t) | scale function |
| β(t) | wavelet function |
| l(n) | low-pass filters |
| h(n) | high-pass filters |
| dik(n) | NTH coefficient of the k node of the i layer of wavelet packet decomposition |
| Ci | number of correlations between the ith IMF component and the original signal |
| mean of the cross-relations | |
| T | threshold of the number of interrelationships |
| Y(t) | pure signal |
| y(t) | signal after noise reduction |
| PIC | main interval coefficient |
| Ai | amplitude corresponding to frequency i in the spectrum diagram |
| (x)* | frequency interval corresponding to x |
| H | total frequency interval |
| Qi | attenuation factor of the i signal |
| ti | delay time of the i signal |
| fi | frequency of the i signal |
References
- Jierula, A.; Oh, T.-M.; Wang, S.; Lee, J.-H.; Kim, H.; Lee, J.-W. Detection of damage locations and damage steps in pile foundations using acoustic emissions with deep learning technology. Front. Struct. Civ. Eng. 2021, 15, 318–332. [Google Scholar] [CrossRef]
- Ma, J.; Dong, L.; Zhao, G.; Li, X. Discrimination of seismic sources in an underground mine using full waveform inversion. Int. J. Rock Mech. Min. Sci. 2018, 106, 213–222. [Google Scholar] [CrossRef]
- Madarshahian, R.; Ziehl, P.; Caicedo, J.M. Acoustic emission Bayesian source location: Onset time challenge. Mech. Syst. Signal Process. 2019, 123, 483–495. [Google Scholar] [CrossRef]
- Schabowicz, K. Non-Destructive Testing of Materials in Civil Engineering. Materials 2019, 12, 3237. [Google Scholar] [CrossRef] [PubMed]
- Kek, T.; Potočnik, P.; Misson, M.; Bergant, Z.; Sorgente, M.; Govekar, E.; Šturm, R. Characterization of Biocomposites and Glass Fiber Epoxy Composites Based on Acoustic Emission Signals, Deep Feature Extraction, and Machine Learning. Sensors 2022, 22, 6886. [Google Scholar] [CrossRef] [PubMed]
- Supriyo, M.; Piyush, S.; Ramesh, B.N. A robust condition monitoring methodology for grinding wheel wear identification using Hilbert Huang transform. Precis. Eng. 2021, 70, 77–91. [Google Scholar]
- Ohtsu, M. Acoustic Emission (AE) and Related Non-Destructive Evaluation (NDE) Techniques in the Fracture Mechanics of Concrete; Elsevier Ltd.: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Xiao, P.; Hu, Q.; Tao, Q.; Dong, L.; Yang, Z.; Zhang, W. Acoustic Emission Location Method for Quasi-Cylindrical Structure With Complex Hole. IEEE Access 2020, 8, 35263–35275. [Google Scholar] [CrossRef]
- Ohtsu, M. Recommendation of RILEM TC 212-ACD: Acoustic emission and related NDE techniques for crack detection and damage evaluation in concrete: Test method for classification of active cracks in concrete structures by acoustic emission. Mater. Struct. 2010, 43, 1187–1189. [Google Scholar]
- Eline, V.; Menno, V.D.V.; Edwin, R.; Lombaert, G.; Verstrynge, E. Experimental study on acoustic emission sensing and vibration monitoring of corroding reinforced concrete beams. Eng. Struct. 2023, 293, 116553. [Google Scholar]
- Tayfur, S.; Alver, N.; Abdi, S.; Saatcı, S.; Ghiami, A. Characterization of concrete matrix/steel fiber de-bonding in an SFRC beam: Principal component analysis and k-mean algorithm for clustering AE data. Eng. Fract. Mech. 2018, 194, 73–85. [Google Scholar] [CrossRef]
- Kononenko, D.Y.; Nikonova, V.; Seleznev, M.; van den Brink, J.; Chernyavsky, D. An in situ crack detection approach in additive manufacturing based on acoustic emission and machine learning. Addit. Manuf. Lett. 2023, 5, 100130. [Google Scholar] [CrossRef]
- Chen, L.; Yao, X.; Tan, C.; He, W.; Su, J.; Weng, F.; Chew, Y.; Ng, N.P.H.; Moon, S.K. In-situ crack and keyhole pore detection in laser directed energy deposition through acoustic signal and deep learning. Addit. Manuf. 2023, 69, 103547. [Google Scholar] [CrossRef]
- González, D.; Alvarez, J.; Sánchez, J.A.; Godino, L.; Pombo, I. Deep Learning-Based Feature Extraction of Acoustic Emission Signals for Monitoring Wear of Grinding Wheels. Sensors 2022, 22, 6911. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhou, Y.; Zou, S.; Zhang, X. Research on noise reduction method of Hydraulic turbine cavitation acoustic emission signal with improved threshold wavelet. J. Hydroelectr. Power 2019, 45, 85–89+98. (In Chinese) [Google Scholar]
- Hassan, F.; Rahim, L.A.; Mahmood, A.K.; Abed, S.A. A Hybrid Particle Swarm Optimization-Based Wavelet Threshold Denoising Algorithm for Acoustic Emission Signals. Symmetry 2022, 14, 1253. [Google Scholar] [CrossRef]
- He, K.; Xia, Z.; Si, Y.; Lu, Q.; Peng, Y. Noise Reduction of Welding Crack AE Signal Based on EMD and Wavelet Packet. Sensors 2020, 20, 761. [Google Scholar] [CrossRef]
- Hu, L.; Gao, H.; Shi, D.; Lin, Z.; Li, K.; Zhao, L. Noise reduction method of mechanical seal acoustic emission signal based on CEEMD and improved wavelet threshold. Comput. Meas. Control 2019, 27, 157–161+166. (In Chinese) [Google Scholar]
- Sun, Y.; Wang, L.; Lei, Q.; Cao, Q. Research on Vibration Prediction of Hydropower Unit Based on CEEMDAN-IPSO-LSTM [J/OL]. The People of the Yellow River: 1-7 [2023-03-21]. Available online: http://kns.cnki.net/kcms/detail/41.1128.TV.20230309.1022.002.html (accessed on 17 April 2023). (In Chinese).
- Zhang, J.; Dong, L.; Xu, N. Noise Suppression of Microseismic Signals via Adaptive Variational Mode Decomposition and Akaike Information Criterion. Appl. Sci. 2020, 10, 3790. [Google Scholar] [CrossRef]
- Jing, G.; Zhao, Y.; Gao, Y.; Marin Montanari, P.; Lacidogna, G. Noise Reduction Based on Improved Variational Mode Decomposition for Acoustic Emission Signal of Coal Failure. Appl. Sci. 2023, 13, 9140. [Google Scholar] [CrossRef]
- Chen, N.; Sun, H.; Zhang, Q.; Li, S. A Short-Term Wind Speed Forecasting Model Based on EMD/CEEMD and ARIMA-SVM Algorithms. Appl. Sci. 2022, 12, 6085. [Google Scholar] [CrossRef]
- Yang, Z.; Lin, J.; Wang, K.; Cheng, X.; Liu, P. Research on noise reduction of concrete acoustic emission Signal based on CEEMDAN-Wavelet packet adaptive threshold. Vib. Shock. 2023, 3, 139–149. (In Chinese) [Google Scholar]
- Luan, X.; Li, Y.; Xu, S.; Sha, Y. Fault diagnosis method of rolling bearing based on wavelet packet transform and CEEMDAN [J/OL]. J. Air Power 2023, 3, 1–16. (In Chinese) [Google Scholar] [CrossRef]
- Yu, H.; Wen, H.; Liu, H.; Dong, J.; Lin, W. GNSS elevation time series denoising method based on CEEMDAN and wavelet packet multi-threshold. Geod. Geodyn. 2022, 10, 1005–1009. (In Chinese) [Google Scholar]
- Meng, J.; Han, Z.; Li, Y. Adaptive wavelet entropy threshold seismic random noise suppression algorithm based on improved complementary set empirical mode decomposition. Sci. Technol. Eng. 2019, 19, 52–61. (In Chinese) [Google Scholar]
- Yi, J.; An, H.; Xing, Y.; Li, J.; Zhang, G.; Bamisile, O.; Yamg, K.; Xu, Y. A cyber attack detection strategy for plug-in electric vehicles during charging based on CEEMDAN and Broad Learning System. Energy Rep. 2023, 9, 80–88. [Google Scholar] [CrossRef]
- Yu, J.; Zhao, S.; Wang, Q. Acoustic emission signal denoising based on empirical mode decomposition and wavelet transform. J. Harbin Inst. Technol. 2011, 43, 88–92. (In Chinese) [Google Scholar]
- Mitraković, D.; Grabec, I.; Sedmak, S. Simulation of AE signals and signal analysis systems. Ultrasonics 1985, 23, 227–232. [Google Scholar] [CrossRef]
- Siracusano, G. Acoustic Event Dataset; Harvard Dataverse: Cambridge, MA, USA, 2019. [Google Scholar] [CrossRef]
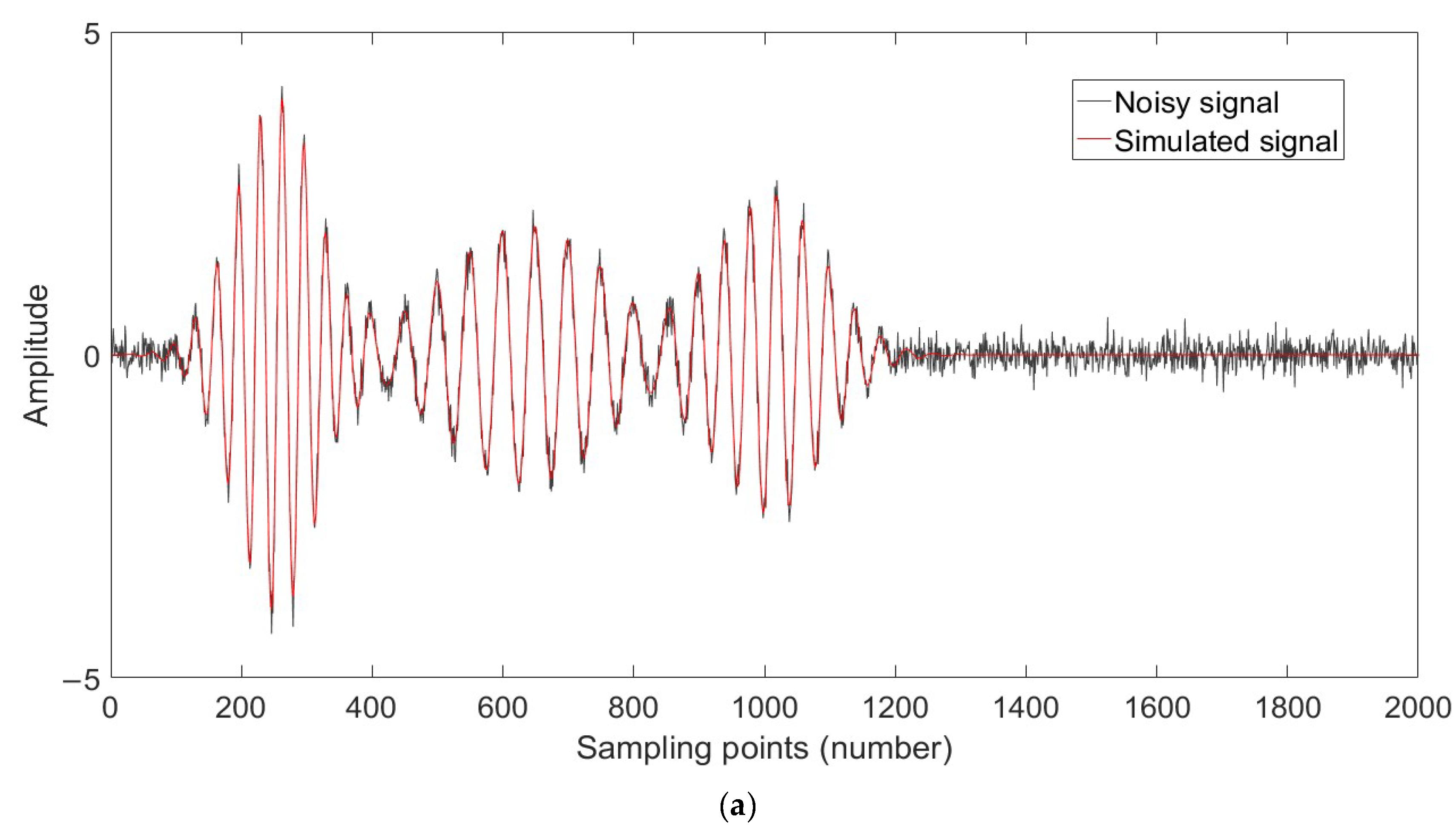
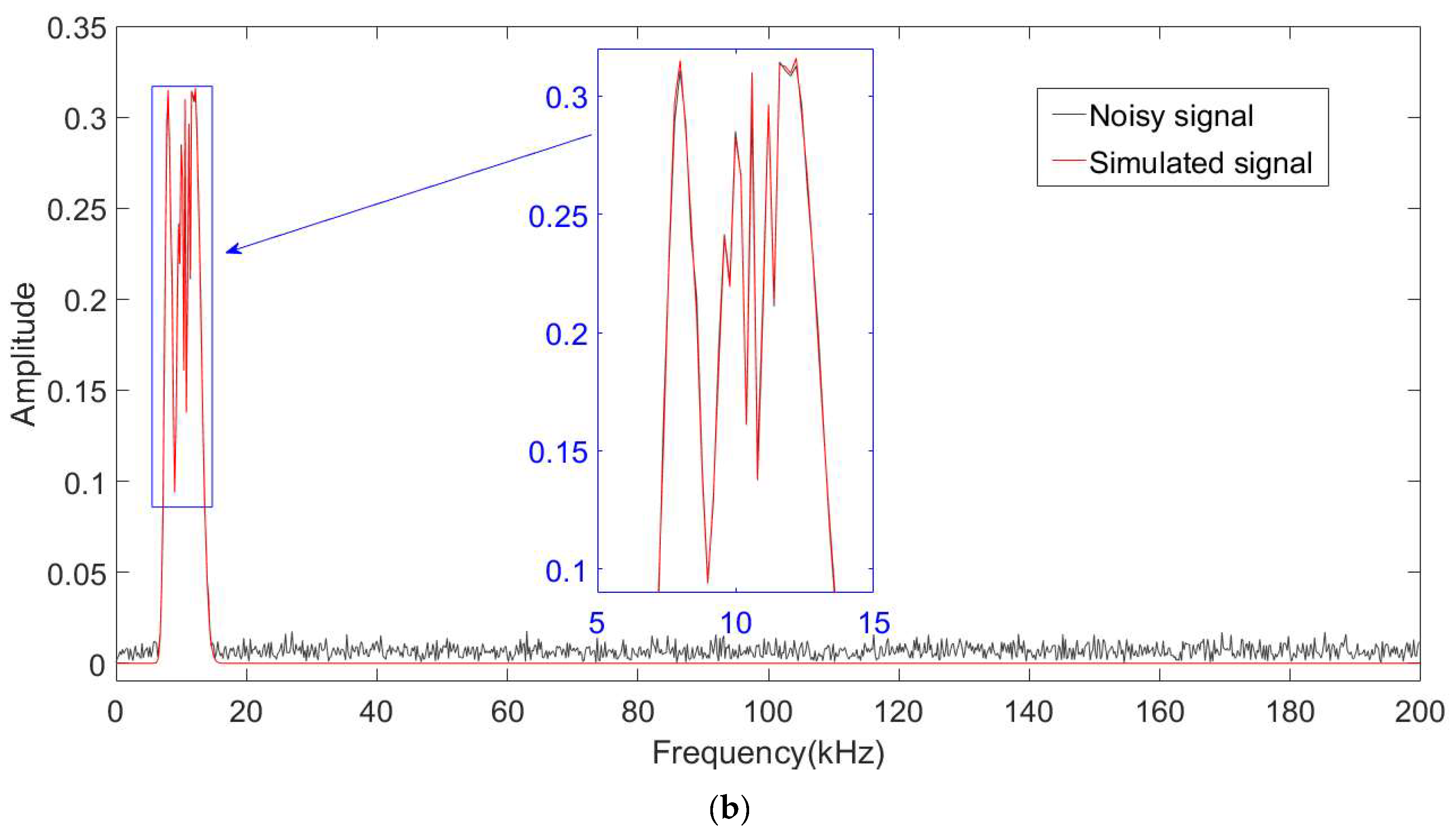
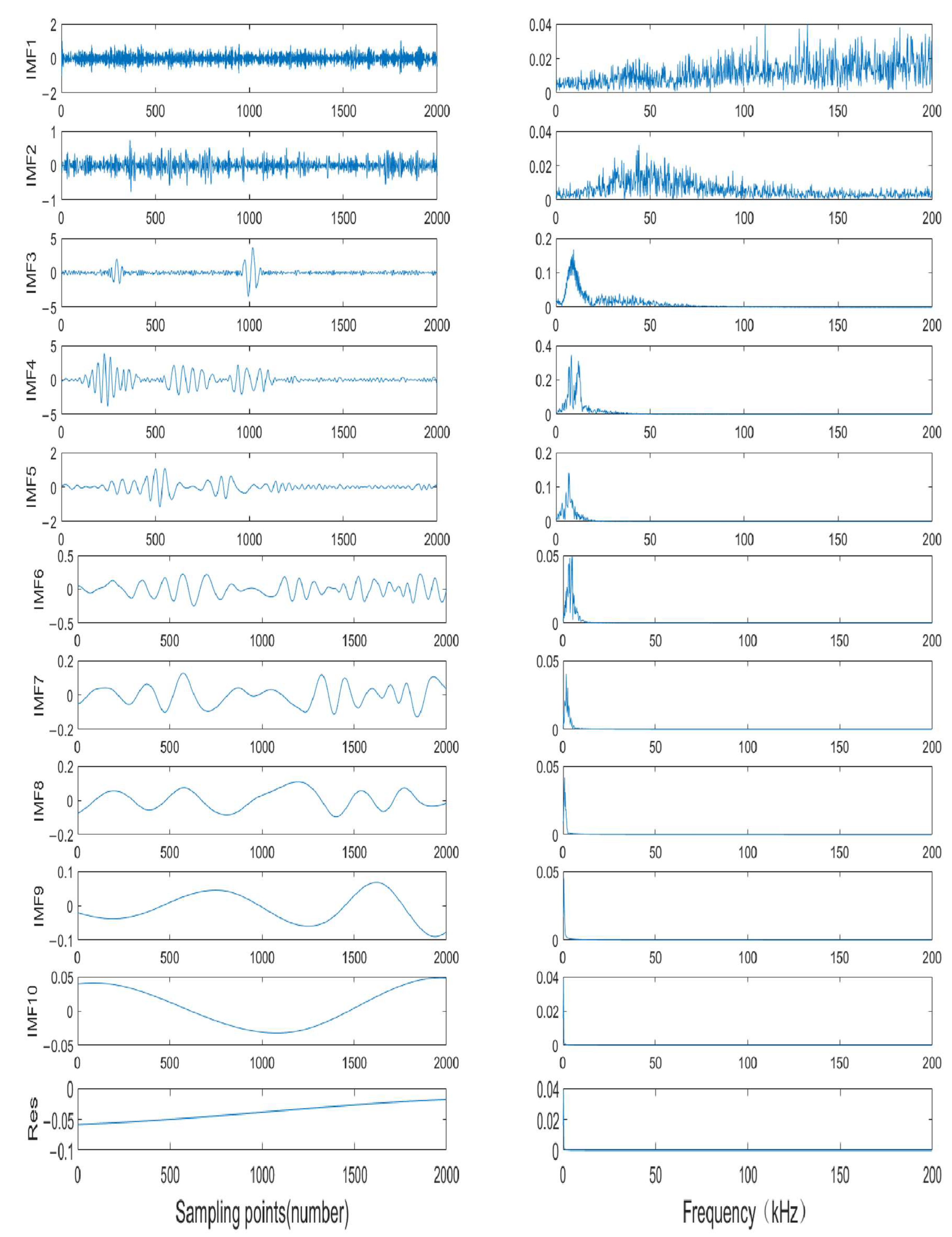




| Parameter | Ai | Qi | ti (ms) | fi (kHz) |
|---|---|---|---|---|
| i = 1 | 4 | 500 | 4 × 10−1.5 | 60 |
| i = 2 | 2 | 120 | 4 × 10−1.1 | 40 |
| i = 3 | 2.5 | 300 | 4 × 10−0.9 | 50 |
| Add Noise SNR | 5 db | 10 db | 15 db | ||||
|---|---|---|---|---|---|---|---|
| Mean | Variance (10−2) | Mean | Variance (10−2) | Mean | Variance (10−2) | ||
| SNR | Traditional CEEMD | 10.136 | 107.745 | 13.890 | 175.306 | 16.362 | 439.393 |
| CEEMDAN | 11.020 | 5.575 | 15.289 | 10.068 | 19.908 | 13.584 | |
| CEEMD-WPT | 12.548 | 9.992 | 17.186 | 9.765 | 21.663 | 16.517 | |
| RMSE | Noisy signal | 0.535 | 0.301 | 0.169 | |||
| Traditional CEEMD | 0.293 | 0.122 | 0.190 | 0.099 | 0.146 | 0.166 | |
| CEEMDAN | 0.280 | 0.007 | 0.166 | 0.002 | 0.098 | 0.004 | |
| CEEMD-WPT | 0.225 | 0.006 | 0.129 | 0.002 | 0.077 | 0.001 | |
| dnSNR | Traditional CEEMD | 1.162 | 0.638 | 0.527 | 0.231 | 0.307 | 0.297 |
| CEEMDAN | 0.830 | 0.099 | 0.284 | 0.005 | 0.091 | 0.0004 | |
| CEEMD-WPT | 1.191 | 0.054 | 0.578 | 0.005 | 0.352 | 0.0008 | |
| PIC | Primary signal | 0.065 | |||||
| Noisy signal | 0.869 | 0.842 | 0.792 | ||||
| Traditional CEEMD | 0.557 | 0.016 | 0.426 | 0.048 | 0.335 | 0.053 | |
| CEEMDAN | 0.338 | 0.118 | 0.314 | 0.032 | 0.282 | 0.007 | |
| CEEMD-WPT | 0.214 | 0.004 | 0.164 | 0.003 | 0.111 | 0.004 | |
| PIC Mean | ||||
|---|---|---|---|---|
| 0.2–0.4 | 0.4–0.6 | 0.6–0.8 | 0.8–1 | |
| Traditional CEEMD | 0.173 | 0.192 | 0.213 | 0.454 |
| CEEMDAN | 0.181 | 0.253 | 0.301 | 0.323 |
| CEEMD-WPT | 0.183 | 0.182 | 0.167 | 0.146 |
| Algorithm | PIC Mean | Variance (10−2) | |
|---|---|---|---|
| Test set for all data | Primary signal | 0.288 | |
| Traditional CEEMD | 0.169 | ||
| CEEMDAN | 0.159 | ||
| CEEMD-WPT | 0.156 | ||
| Data5 | Primary signal | 0.88 | |
| Traditional CEEMD | 0.362 | 0.158 | |
| CEEMDAN | 0.190 | 0.016 | |
| CEEMD-WPT | 0.172 | 0.013 | |
| Data7 | Primary signal | 0.874 | |
| Traditional CEEMD | 0.531 | 0.010 | |
| CEEMDAN | 0.202 | 0.016 | |
| CEEMD-WPT | 0.188 | 0.005 | |
| Data19 | Primary signal | 0.87 | |
| Traditional CEEMD | 0.594 | 0.034 | |
| CEEMDAN | 0.731 | 0.031 | |
| CEEMD-WPT | 0.207 | 0.009 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Ma, Y.; Du, J.; Wang, C.; Xia, D.; Xin, W.; Zhan, Z.; Zhang, R.; Chen, J. Noise Reduction Based on a CEEMD-WPT Crack Acoustic Emission Dataset. Appl. Sci. 2023, 13, 10274. https://doi.org/10.3390/app131810274
Zhao Y, Ma Y, Du J, Wang C, Xia D, Xin W, Zhan Z, Zhang R, Chen J. Noise Reduction Based on a CEEMD-WPT Crack Acoustic Emission Dataset. Applied Sciences. 2023; 13(18):10274. https://doi.org/10.3390/app131810274
Chicago/Turabian StyleZhao, Yongfeng, Yunrui Ma, Junli Du, Chaohua Wang, Dawei Xia, Weifeng Xin, Zhenyu Zhan, Runfeng Zhang, and Jiangyi Chen. 2023. "Noise Reduction Based on a CEEMD-WPT Crack Acoustic Emission Dataset" Applied Sciences 13, no. 18: 10274. https://doi.org/10.3390/app131810274
APA StyleZhao, Y., Ma, Y., Du, J., Wang, C., Xia, D., Xin, W., Zhan, Z., Zhang, R., & Chen, J. (2023). Noise Reduction Based on a CEEMD-WPT Crack Acoustic Emission Dataset. Applied Sciences, 13(18), 10274. https://doi.org/10.3390/app131810274






