An Accelerated Algorithm for 3D Inversion of Gravity Data Based on Improved Conjugate Gradient Method
Abstract
:1. Introduction
2. Theory
2.1. Smooth Inversion of Gravity Data Based on Conjugate Gradient Algorithm
2.2. An Accelerated 3D Fast Inversion Algorithm for Gravity Data
2.3. Software Overview
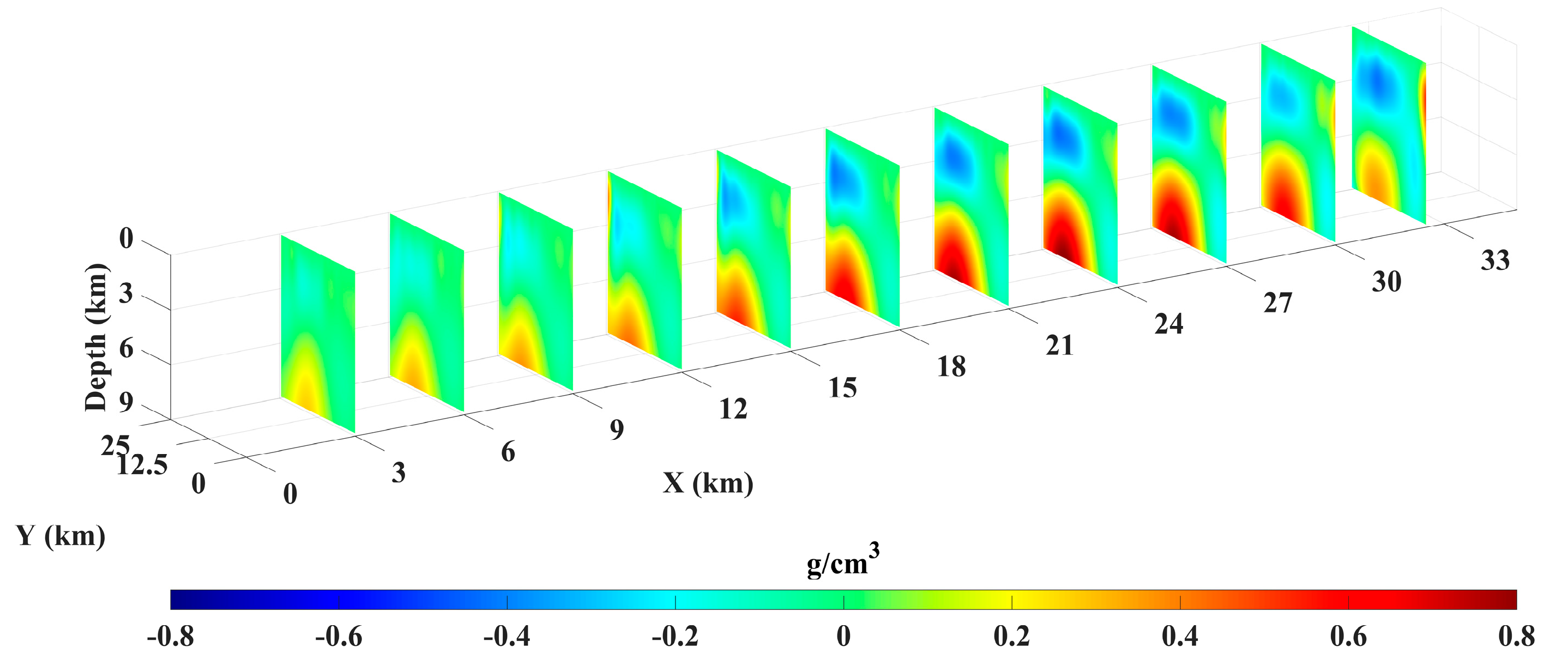
3. Data Testing
3.1. Synthetic Data Testing
| Algorithm 1 The workflow of traditional 3D inversion algorithm |
| (1) Input: S, d Set: k = 0, |
| (2) Calculate the weighted parameter matrix: |
| (3) Calculate the weighted parameter: |
| (4) Calculate intermediate variables: |
| (5) Calculate the initial search direction: , and calculate the initial search step size: |
| (6) Update the initial solution and calculate the error: |
| (7) Set the algorithm iteration condition: |
| : |
| (8) Upset parameter Q, and then update negative gradient : |
| (9) Calculate the intermediate parameter , and then update the search direction : |
| (10) Update the search step size: |
| (11) Update solution and return step (7) to determine whether it iterates: |
| Algorithm 2 The workflow of accelerated 3D fast inversion algorithm |
| (1) Input: S, d Set: k = 0, |
| (2) Calculate the weighted parameter matrix: |
| (3) Calculate the weighted parameter: |
| (4) Calculate intermediate variables: |
| (5) Calculate the initial search direction: , set , and calculate the initial search step size: |
| (6) Update the initial solution and calculate the error: |
| (7) Set the algorithm iteration condition: |
| : |
| (8) Upset parameter , and then update negative gradient : |
| (9) Calculate the intermediate parameter , and then update the search direction : |
| (10) Update the search step size: |
| (11) Update solution and return step (7) to determine whether it iterates: |
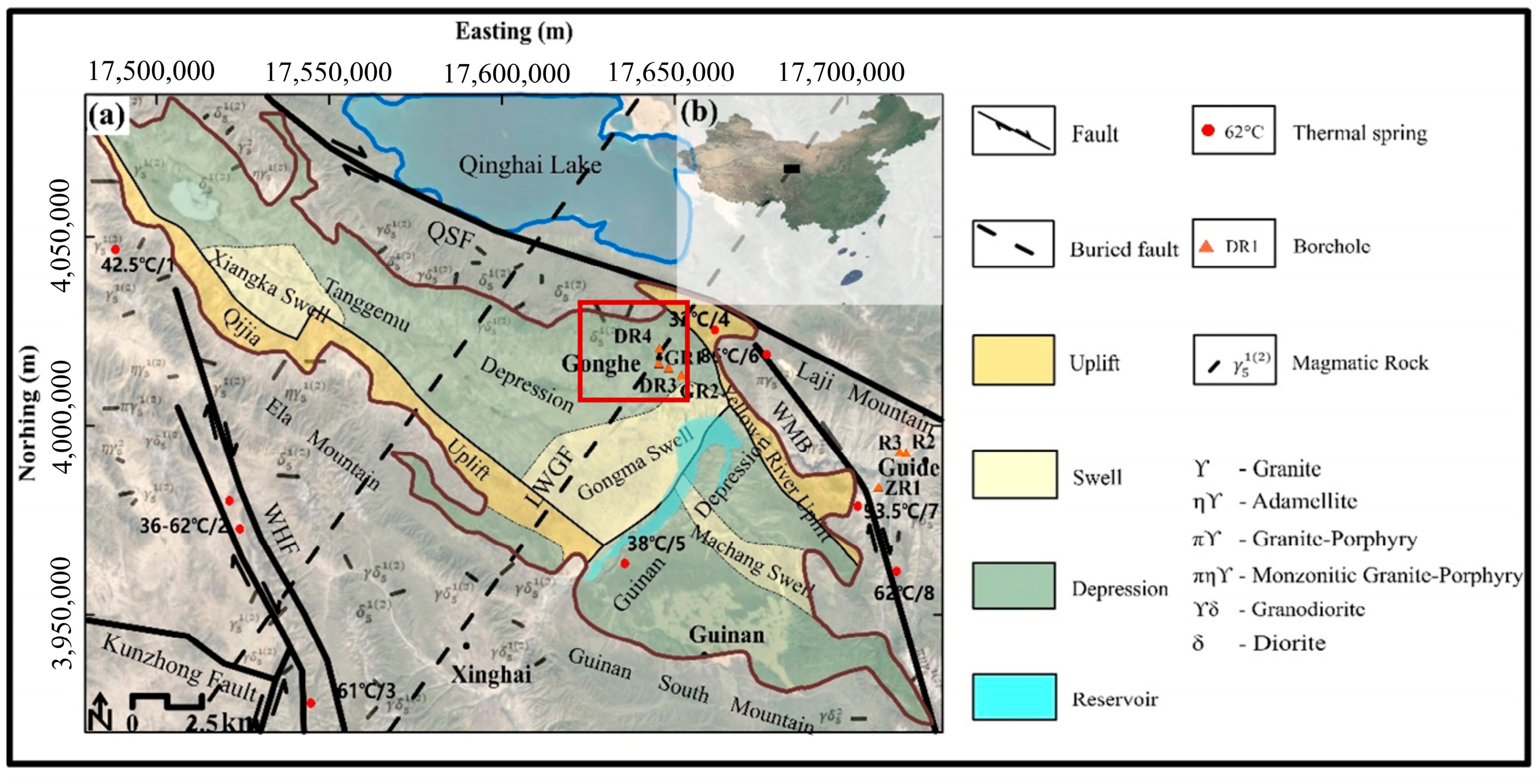
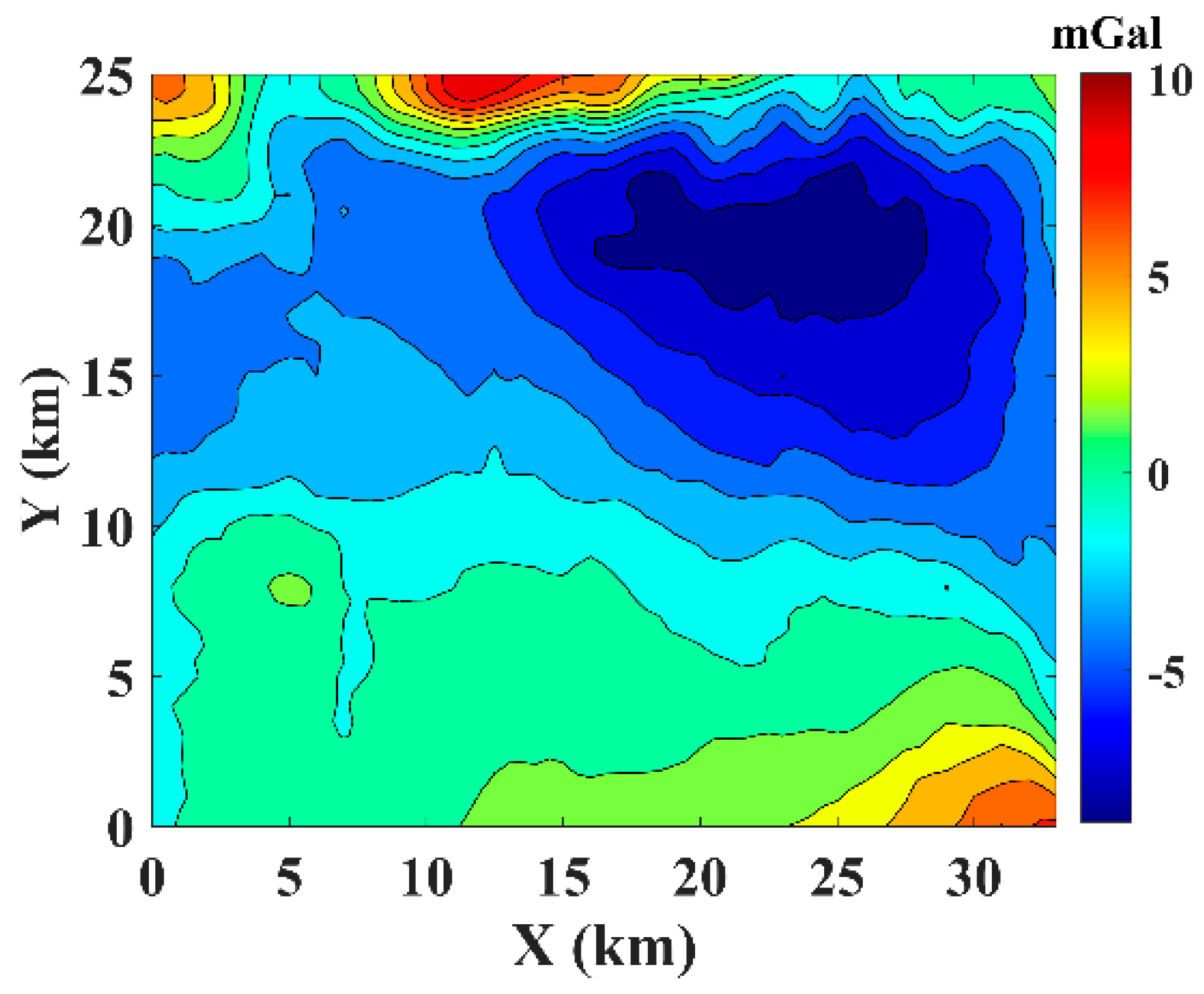
3.2. Real Data Testing
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Oldenburg, D.W. 3-D inversion of gravity data. Geophysics 1998, 63, 109–119. [Google Scholar] [CrossRef]
- Chasseriau, P.; Chouteau, M. 3D gravity inversion using a model of parameter covariance. J. Appl. Geophys. 2003, 52, 59–74. [Google Scholar] [CrossRef]
- Shamsipour, P.; Marcotte, D.; Chouteau, M.; Keating, P. 3D stochastic inversion of gravity data using cokriging and cosimulation. Geophysics 2010, 75, I1–I10. [Google Scholar] [CrossRef]
- Liu, G.; Yan, H.; Meng, X.; Chen, Z. An extension of gravity probability tomography imaging. Geophysics 2014, 102, 62–67. [Google Scholar] [CrossRef]
- Last, B.J.; Kubik, K. Compact gravity inversion. Geophysics 1983, 48, 713–721. [Google Scholar] [CrossRef]
- Portniaguine, O.; Zhdanov, M.S. Focusing geophysical inversion images. Geophysics 1999, 64, 874–887. [Google Scholar] [CrossRef]
- Portniaguine, O.; Zhdanov, M.S. 3-D magnetic inversion with data compression and image focusing. Geophysics 2002, 67, 1532–1541. [Google Scholar] [CrossRef]
- Zhdanov, M.S.; Ellis, R.; Mukherjee, S. Three-dimensional regularized focusing inversion of gravity gradient tensor component data. Geophysics 2004, 69, 925–937. [Google Scholar] [CrossRef]
- Zhdanov, M.S. Geophysical Inverse Theory and Regularization Problems; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Boulanger, O.; Chouteau, M. Constraints in 3D gravity inversion. Geophys. Prospect. 2001, 49, 265–280. [Google Scholar] [CrossRef]
- Pilkington, M. 3D magnetic data-space inversion with sparseness constraints. Geophysics 2009, 74, L7–L15. [Google Scholar] [CrossRef]
- Qin, P.B.; Huang, D.N.; Yuan, Y.; Geng, M.X.; Liu, J. Integrated gravity and gravity gradient 3D inversion using the non-linear conjugate gradient. J. Appl. Geophys. 2016, 126, 52–73. [Google Scholar] [CrossRef]
- Cuma, M.; Zhdanov, M.S. Large-scale 3D inversion of potential field data. Geophys. Prospect. 2012, 60, 1186–1199. [Google Scholar] [CrossRef]
- Meng, Z.H.; Xu, X.C.; Huang, D.N. Three-dimensional gravity inversion based on sparse recovery iteration using approximate zero norm. Appl. Geophys. 2019, 15, 524–535. [Google Scholar] [CrossRef]
- Martin, R.; Monteiller, V.; Komatitsch, D.; Perrouty, S.; Jessell, M.; Bonvalot, S.; Lindsay, M. Gravity inversion using wavelet-based compression on parallel hybrid CPU/GPU systems: Application to southwest Ghana. Geophys. J. Int. 2013, 195, 1594–1619. [Google Scholar] [CrossRef]
- Sun, S.Y.; Yin, C.C.; Gao, X.H.; Liu, Y.H.; Ren, X.Y. Gravity compressed sensing forward modeling and multiscale gravity inversion based on wavelet transform. Appl. Geophys. 2018, 15, 342–352. [Google Scholar] [CrossRef]
- Canning, F.X.; School, J.F. Diagonal preconditioners for the EFIE using a wavelet basis. IEEE Trans. Antennas Propag. 1996, 44, 1239–1246. [Google Scholar] [CrossRef]
- Pilkington, M. 3-D magnetic imaging using conjugate gradients. Geophysics 2012, 62, 1132–1142. [Google Scholar] [CrossRef]
- Chen, R.S.; Yung, E.K.; Chan, C.H.; Wang, D.X.; Fang, D.G. Application of the SSOR preconditioned CG algorithm to the vector fem for 3D full-wave analysis of electromagnetic-field boundary-value problems. IEEE Trans. Microw. Theory Tech. 2002, 50, 1165–1172. [Google Scholar] [CrossRef]
- Moorkamp, M.; Jegen, M.; Roberts, A.; Hobbs, R. Massively parallel forward modeling of scalar and tensor gravimetry data. Comput. Geosci. 2010, 36, 680–686. [Google Scholar] [CrossRef]
- Cuma, M.; Zhdanov, M.S. Massively parallel regularized 3D inversion of potential fields on CPUs and GPUs. Comput. Geosci. 2014, 62, 80–87. [Google Scholar] [CrossRef]
- Hou, Z.L.; Wei, X.H.; Huang, D.N.; Sun, X. Full tensor gravity gradiometry data inversion: Performance Geophysics analysis of parallel computing algorithms. Appl. Geophys. 2015, 12, 292–302. [Google Scholar] [CrossRef]
- Wang, T.H.; Huang, D.N.; Ma, G.Q.; Meng, Z.H.; Li, Y. Improved preconditioned conjugate gradient algorithm and application in 3D inversion of gravity-gradiometry data. Appl. Geophys. 2017, 14, 301–313. [Google Scholar] [CrossRef]
- Hou, Z.L.; Wei, J.K.; Mao, T.X.; Zheng, Y.J.; Ding, Y.C. 3D inversion of vertical gravity gradient with multiple graphics processing units based on matrix compression. Geophysics 2022, 87, 67–80. [Google Scholar] [CrossRef]
- Luo, Y. New expressions for gravitational attraction of a homogeneous rectangular prism and its deduction. Chin. J. Eng. Geophys. 2008, 5, 210–214. [Google Scholar]
- Gao, X.H.; Huang, D.N. Research on 3D focusing inversion of gravity gradient tensor data based on a conjugate gradient algorithm. Chin. J. Geophys. 2017, 60, 1571–1583. [Google Scholar]
- Wang, G.L.; Zhang, W.; Liang, J.Y.; Lin, W.J.; Liu, Z.M.; Wang, W.L. Evaluation of Geothermal Resources Potential in China. Acta Geosci. Sin. 2017, 39, 449–459. [Google Scholar]
- Mao, X.; Guo, D.B.; Luo, L.; Wang, T. Theglobal development process of hot dry rock (enhanced geothermal system) and its geological background. Geol. Rev. 2019, 65, 1462–1472. [Google Scholar]
- Xue, J.-Q.; Gan, B.; Li, B.; Wang, Z. Geological-geophysical charac teristics of enhanced geothermal systems (hot dry rocks) in gonghe-guide basin. Geophys. Geochem. Explor. 2013, 37, 35–41. [Google Scholar]
- Sun, Z.X.; Li, B.X.; Wang, Z.L. Exploration of the possibility of hot dry rock occurring in the qinghai gonghe basin. Hydrogeol. Eng. Geol. 2011, 38, 119–124. [Google Scholar]
- Zhang, H.; Huang, Q.; Zhao, G.; Guo, Z.; Chen, Y.J. Three dimensional conductivity model of crust and uppermost mantle at the northern trans north china orogen: Evidence for a mantle source of datong volcanoes. Earth Planet. Sci. Lett. 2016, 453, 182–192. [Google Scholar] [CrossRef]
- Zhang, S.; Yan, W.; Li, D.; Jia, X.; Zhang, S.; Li, S.; Fu, L.; Wu, H.; Zeng, Z.; Li, Z.; et al. Characteristics of geothermal geology of the qiabuqia hdr in gonghe basin, qinghai province. Geol. China 2018, 45, 1087–1102. [Google Scholar]
- Wang, Z.; Zeng, Z.; Liu, Z.; Zhao, X.; Li, J.; Bai, L.; Zhang, L. Heat flow distribution and thermal mechanism analysis of the Gonghe Basin based on gravity and magnetic methods. Acta Geol. Sin. Engl. Ed. 2021, 95, 1892–1901. [Google Scholar] [CrossRef]
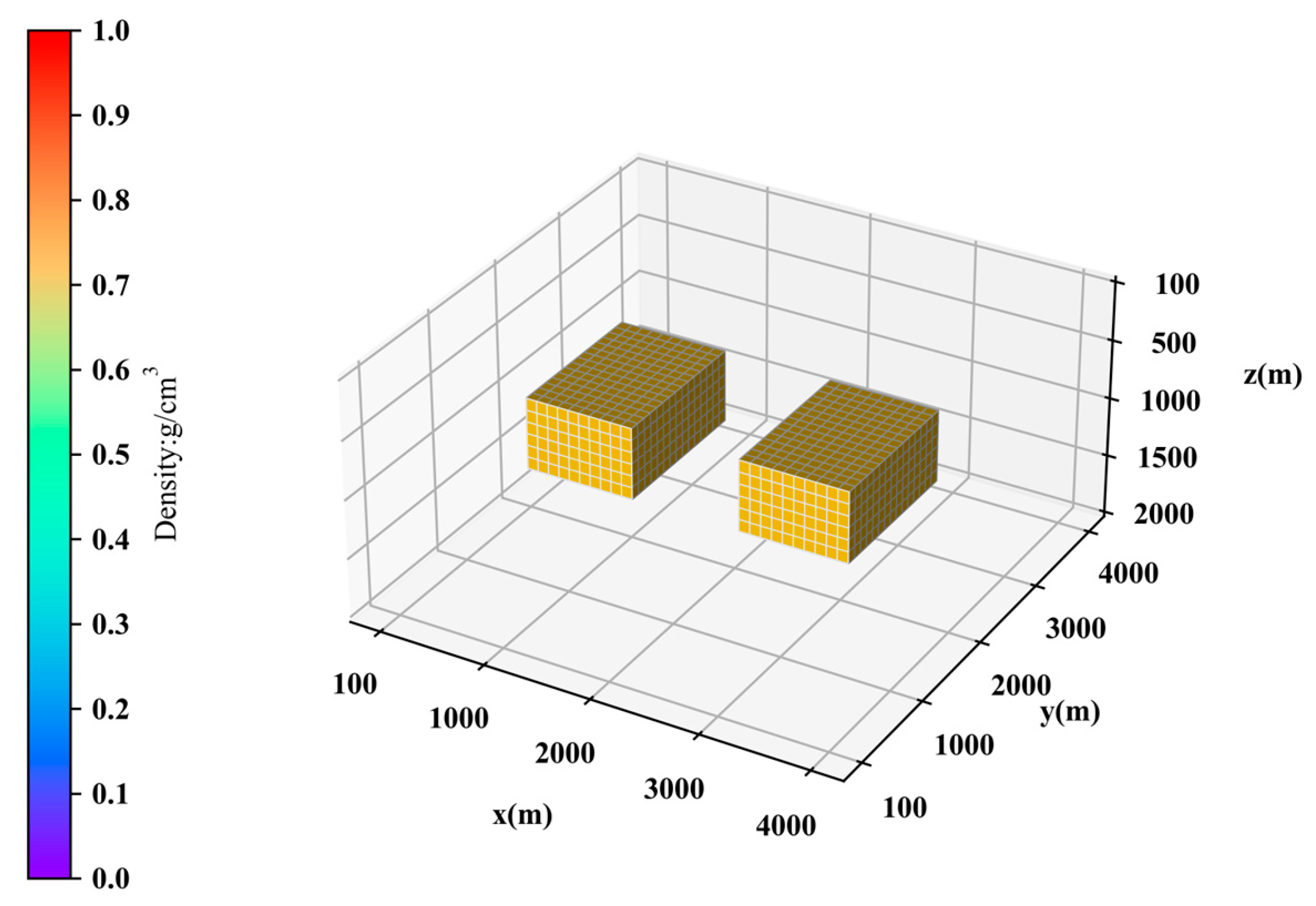
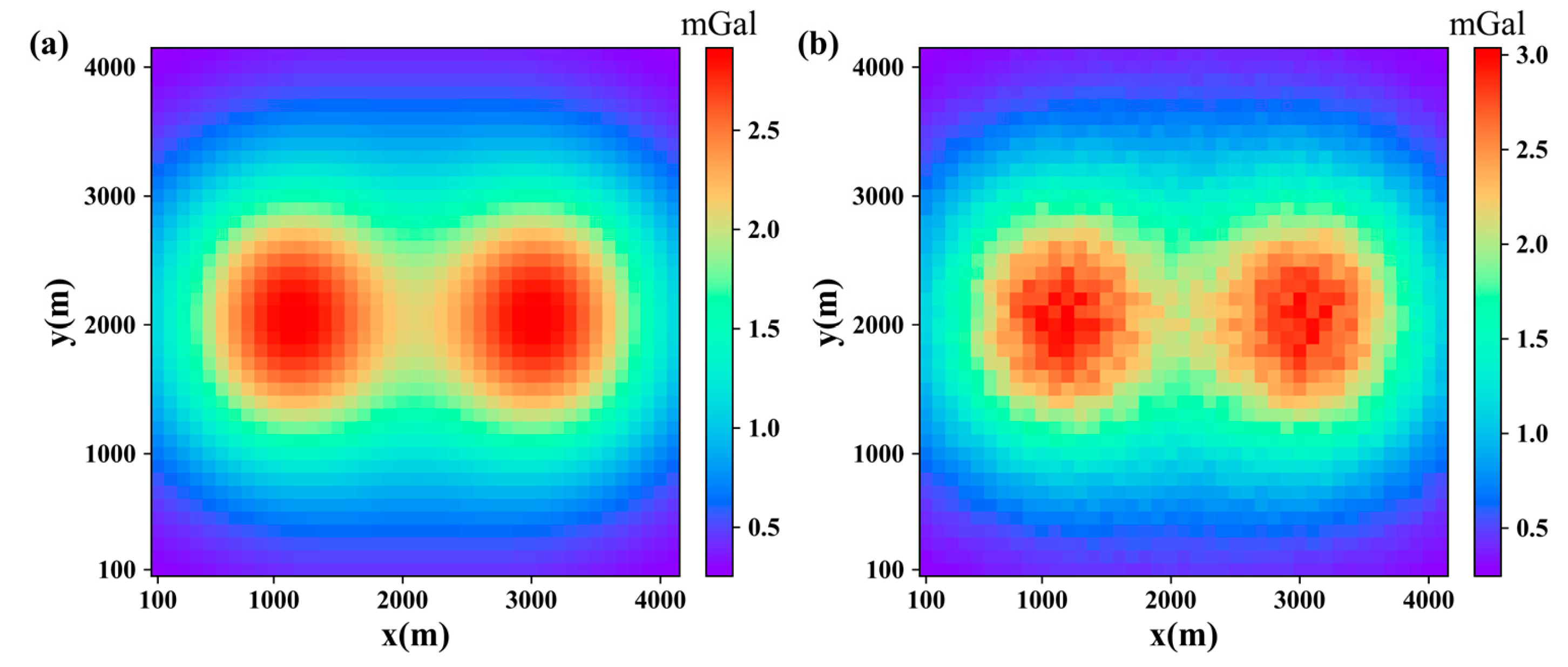
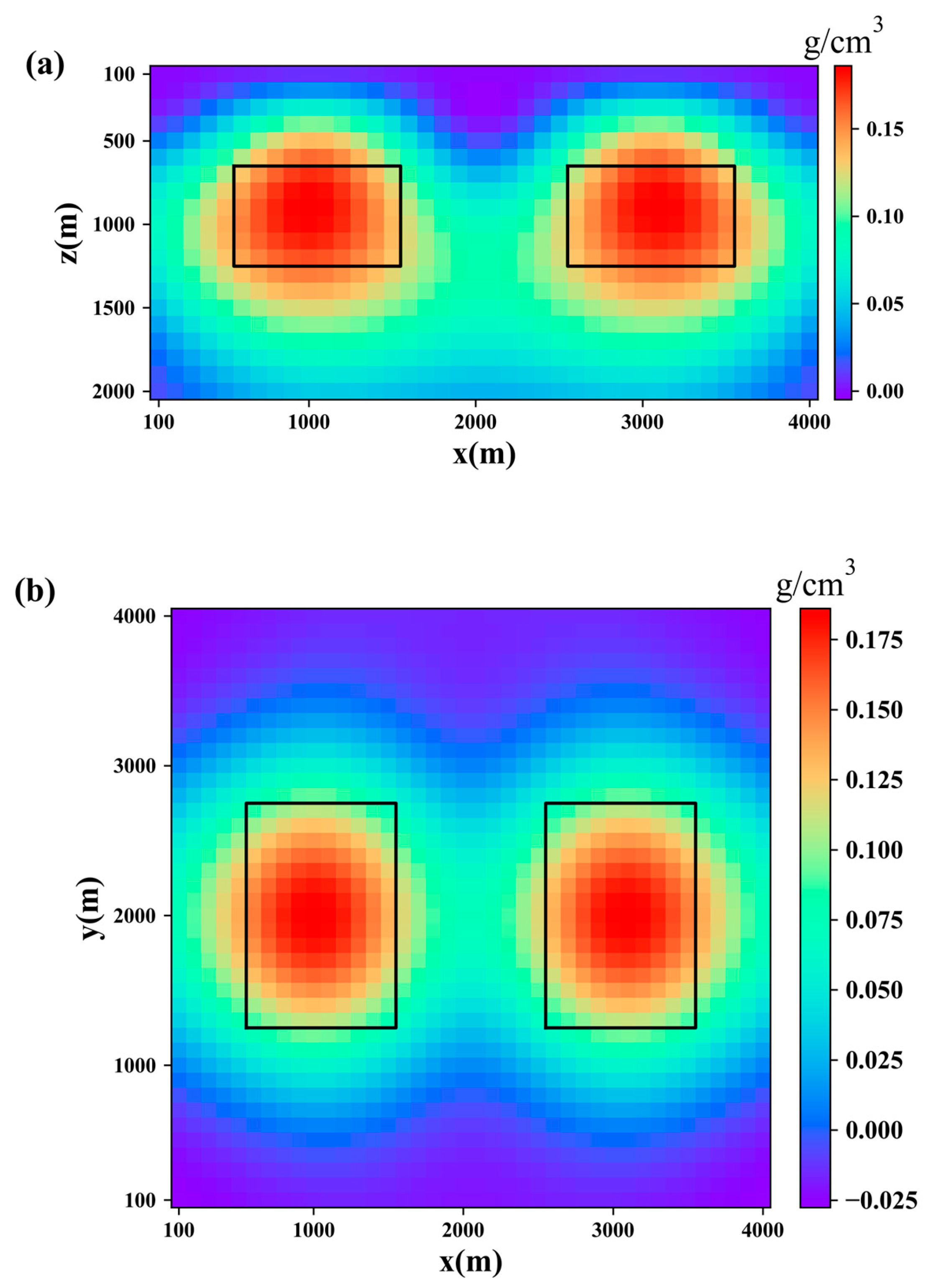
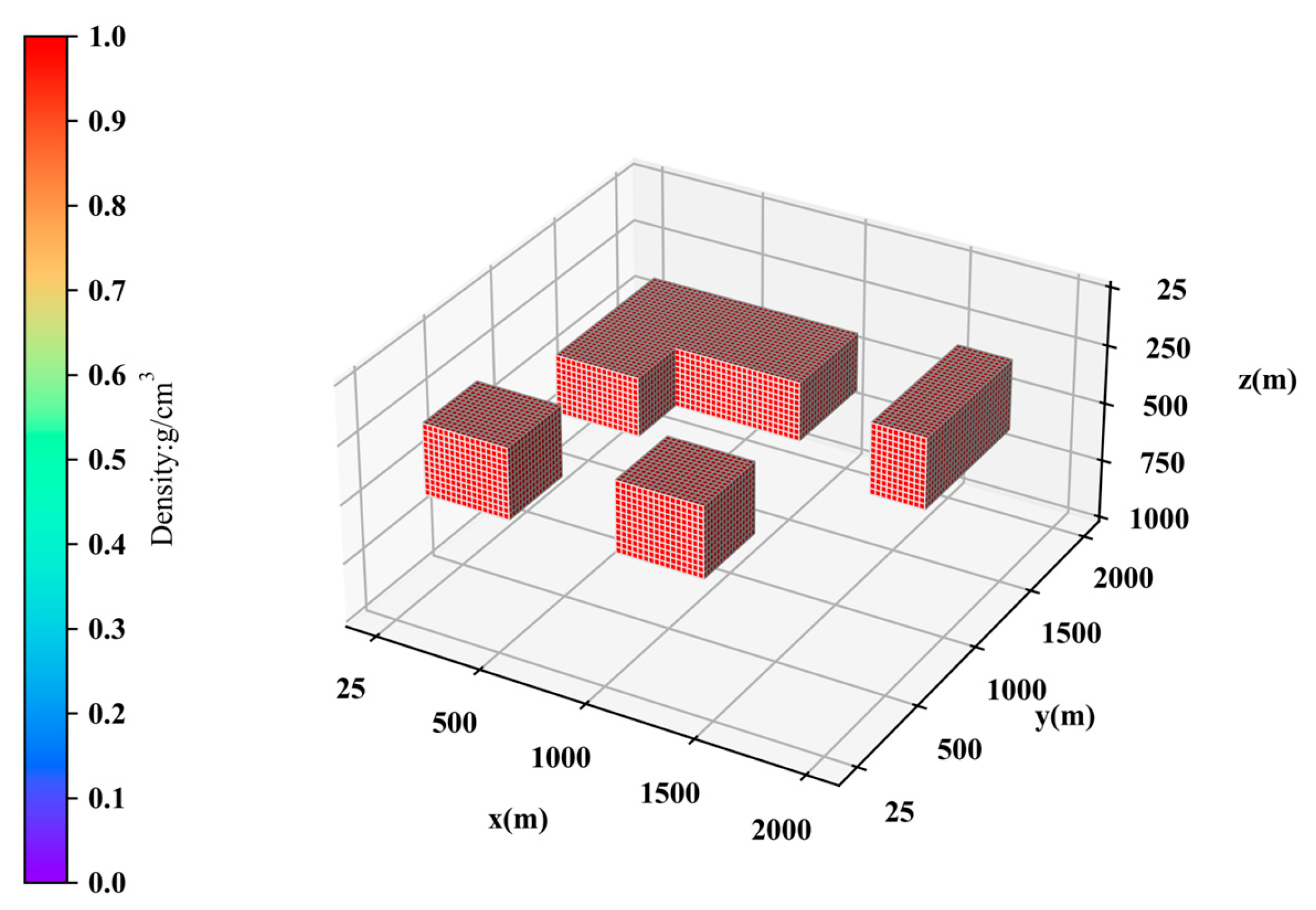
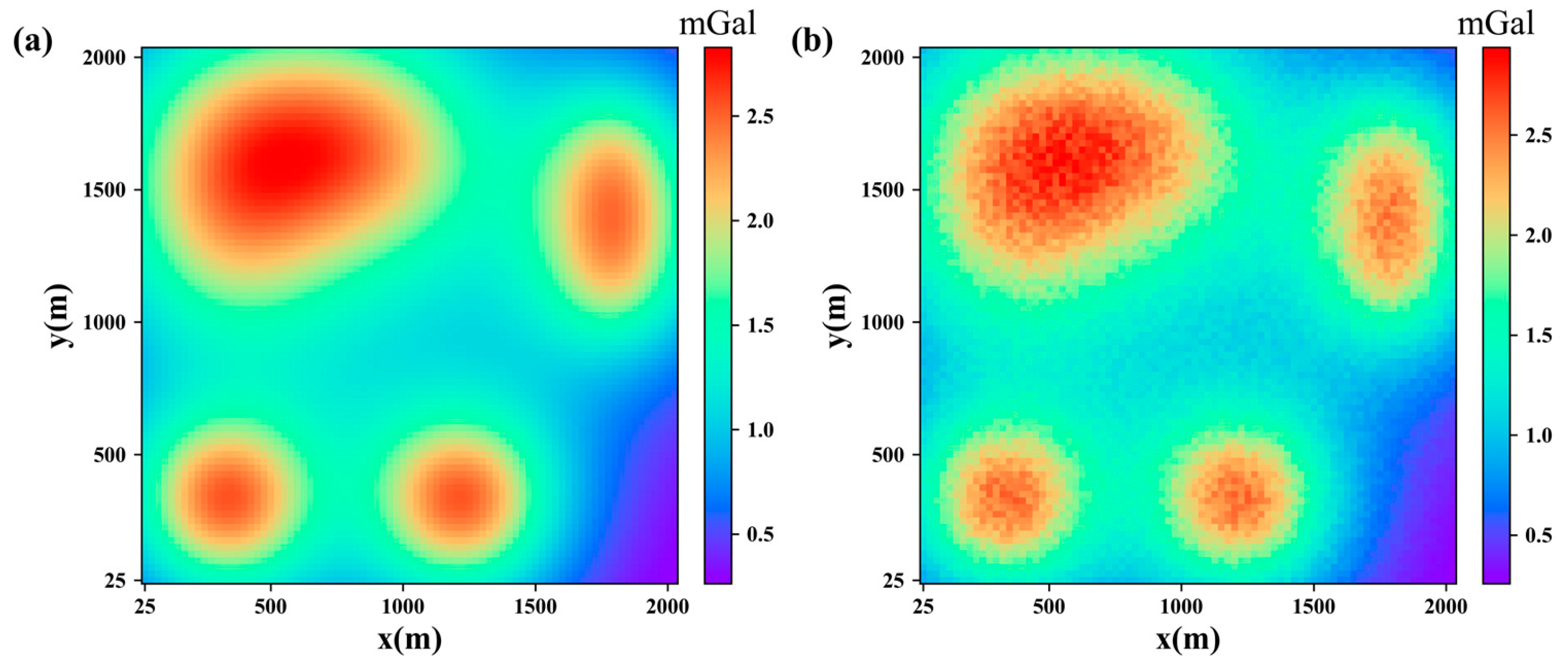
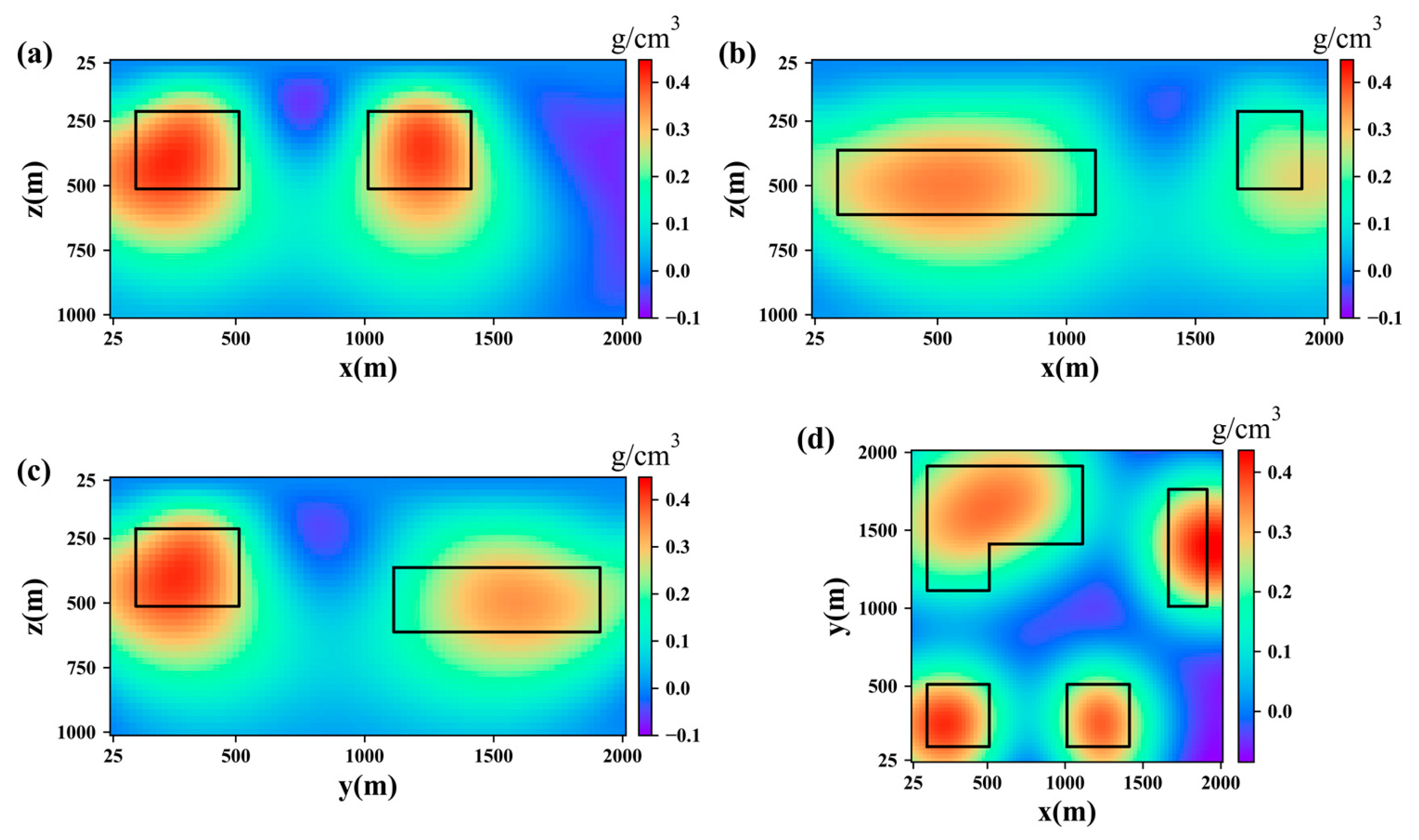
| Model I | Model II | |
|---|---|---|
| The number of prisms | 2 | 5 |
| Density () | 0.5 | 1.0 |
| Size (), Top depth (m) | ||
| Size (), Top depth (m) | ||
| Size (), Top depth (m) | ||
| Size (), Top depth (m) | ||
| Size (), Top depth (m) |
| Traditional algorithm | 107.54 | 282.98 | 4954.16 | - |
| Model I Acceleration algorithm | 8.75 | 20.39 | 167.59 | 350.71 |
| speedup | 12.55 | 13.88 | 29.56 | - |
| Traditional algorithm | 104.24 | 241.50 | 4483.66 | - |
| Model II Acceleration algorithm | 8.52 | 20.33 | 162.28 | 350.33 |
| speedup | 12.23 | 11.88 | 27.63 | - |
| Traditional algorithm | 19.90 | 34.83 | 641.34 | - |
| Model I Acceleration algorithm | 0.037 | 0.095 | 0.69 | 1.81 |
| speedup | 537.84 | 366.63 | 929.48 | - |
| Traditional algorithm | 19.25 | 33.60 | 728.13 | - |
| Model II Acceleration algorithm | 0.031 | 0.091 | 0.515 | 1.23 |
| speedup | 620.97 | 369.23 | 1413.84 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Jia, H.; Lin, T.; Zeng, Z.; Yu, P.; Jiao, J. An Accelerated Algorithm for 3D Inversion of Gravity Data Based on Improved Conjugate Gradient Method. Appl. Sci. 2023, 13, 10265. https://doi.org/10.3390/app131810265
Zhou S, Jia H, Lin T, Zeng Z, Yu P, Jiao J. An Accelerated Algorithm for 3D Inversion of Gravity Data Based on Improved Conjugate Gradient Method. Applied Sciences. 2023; 13(18):10265. https://doi.org/10.3390/app131810265
Chicago/Turabian StyleZhou, Shuai, Hongfa Jia, Tao Lin, Zhaofa Zeng, Ping Yu, and Jian Jiao. 2023. "An Accelerated Algorithm for 3D Inversion of Gravity Data Based on Improved Conjugate Gradient Method" Applied Sciences 13, no. 18: 10265. https://doi.org/10.3390/app131810265
APA StyleZhou, S., Jia, H., Lin, T., Zeng, Z., Yu, P., & Jiao, J. (2023). An Accelerated Algorithm for 3D Inversion of Gravity Data Based on Improved Conjugate Gradient Method. Applied Sciences, 13(18), 10265. https://doi.org/10.3390/app131810265








