Improved Learning-Automata-Based Clustering Method for Controlled Placement Problem in SDN
Abstract
:1. Introduction
2. Related Works
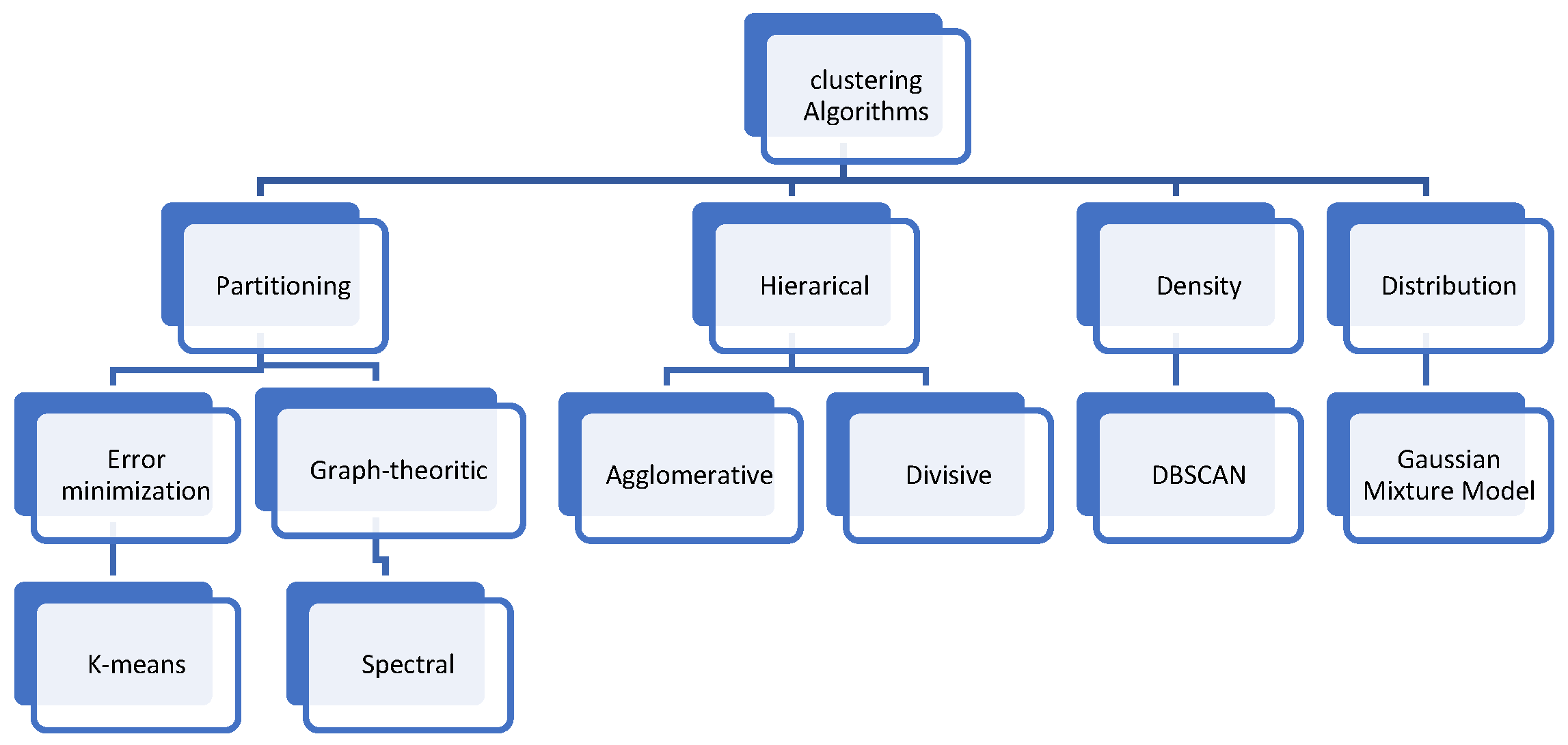
2.1. Types of Clustering Methods
2.2. Clustering APPLICATION in CPPs
3. Basic Concepts
3.1. K-Means Clustering
3.2. K-Harmonic Means
3.3. Learning Automata
- α = α1, α2, …, αr is the set of actions where r is the number of actions.
- β is the reinforcement signals where, in a P-model environment, β ∈ [0, 1}.
- P = {p1, p2, …, pr}} is the set of actions’ probability, P ∈{ 0, 1}.
- T is the learning algorithm where, in the nth step, p(n + 1) = T[p(n), α(n), β(n)] is linear, if p(n + 1) is a linear function of p(n), or nonlinear if p(n + 1) is a nonlinear function of p(n).
- If a = b, the learning algorithm will be of the linear reward penalty (LRP) type.
- If b = 0, the learning algorithm will be of the linear reward inaction (LRI) type.
- If a >> b (a is much larger than b), the learning algorithm will be of the reward epsilon penalty (LREP) type.
3.4. Learning-Automata-Based Clustering
- The input size: The input size is a function of the number of members and their attributes. It is necessary to mention that in the learning process of LA, the entirety of the given data are considered. It depends on the datasets.
- The cluster count: LA assign each datum to each cluster in during the learning process. The actions of the automata show the selection of a cluster for that particular member.
3.5. Software-Defined Networks and CPPs
4. LAC-KHM: The Proposed Algorithm
| Algorithm 1: LAC-KHM algorithm |
| This algorithm has three functions with input and output parameters, and operations that follow: Select Cluster: in fact, during rounds this function specifies to which cluster the data point belongs. It is noted that initially all actions in APV have the same probability. Input parameters: Membership_cluster, probability, num_cluster, num_data Output parameter: Membership_cluster Membership_cluster = Function Select_cluster (membership_cluster, probability, num_cluster, num_data) Update probability: This function updates the APV using learning rule LRP based on the received reinforcement signal. In fact, with each execution, the probability of the selected action is either decreased or increased based on the harmonic distance between data points and cluster centers. Input parameters: membership_cluster, probability, num_cluster, position _of_data, signal, alpha, beta Output parameter: Probability Probability = Function Update_probability (membership_cluster, probability, num_cluster, position _of_data, signal, alpha, beta) Calculate accuracy: This function evaluates the accuracy of the algorithm, demonstrating how closely it matches the expected results. Input parameters: obtained_result, expected_result, num_cluster Output parameter: Accuracy Accuracy = Function Calculate accuracy (obtained_result, expected_result, num_cluster) After initializing parameters, the algorithm keeps on running until output of KHM objective function changes significantly. Initialize parameters (x, y, until, n, k, d, numaction, probability, a, mask, signal, random centers) Membership_cluster = Function Select_cluster (membership_cluster, probability, num_cluster, num_data) while (KHM changes significantly), do for all data points, do Call select-action Function (action= actionselection((action, probability, numactions, n)) end for for all data points do Calculate Membership of data (m function in KHM) Calculate Weights of data (w function in KHM) Calculate new_centers according to their Membership and Weights end for Calculate KHM # Compute reinforcement signal for all data points do if actioni==clusteri : signali=0 else signali=1 for all data points do Membership_cluster = Function Select_cluster (membership_cluster, probability, num_cluster, num_data) Compute result (feedback of environment) end for # Update probability vector for all data points do Call Probability (probability = probabilityupdate(action, probability, numactions, n, signal, alpha, beta)) end for end while |
5. CLAC-KHM: Customized LAC-KHM for CCP
Problem Formulation
| Algorithm 2: CLAC-KHM algorithm |
| Initialize parameters (x, y, n, k, d, k, numaction, probability, a, mask, signal, random centers) while (KHM changes significantly) do for all switches do Call select-action Function end for for all switches do Calculate Membership of data (m function in KHM) Calculate Weights of data (w function in KHM) Calculate new_centers according to their Membership and Weights Calculate distance between controllers for all clusters: do Calculate objective function end for end for Calculate KHM for all of switches do Compute result (feedback of environment) end for for all of LAs do Call Probability end for end while |
6. Experimental Results
6.1. Performance Evaluation of LAC-KHM
6.2. Performance Evaluation of CLAC-KHM
7. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SDN | Software-defined network |
| CPP | Controller placement problem |
| LA | Learning automata |
| KHM | K-Harmonics mean |
| DBCP | Density-based controller placement |
References
- Anil, K.; Jain, A.K.; Dubes, R.C. Algorithms for Clustering Data; Prentice-Hall: Upper Saddle River, NJ, USA, 1988. [Google Scholar]
- Liu, Q.; Kang, B.; Hua, Q.; Wen, Z.; Li, H. Visual Attention and Motion Estimation-Based Video Retargeting for Medical Data Security. Secur. Commun. Netw. 2022, 2022, 1343766. [Google Scholar] [CrossRef]
- Arora, N.; Singh, A.; Al-Dabagh, M.Z.N.; Maitra, S.K. A Novel Architecture for Diabetes Patients’ Prediction Using K-Means Clustering and SVM. Math. Probl. Eng. 2022, 2022, 4815521. [Google Scholar] [CrossRef]
- Granda Morales, L.F.; Valdiviezo-Diaz, P.; Reátegui, R.; Barba-Guaman, L. Drug Recommendation System for Diabetes Using a Collaborative Filtering and Clustering Approach: Development and Performance Evaluation. J. Med. Internet Res. 2022, 24, e37233. [Google Scholar] [CrossRef] [PubMed]
- Septiarini, A.; Hamdani, H.; Sari, S.U.; Hatta, H.R.; Puspitasari, N.; Hadikurniawati, W. Image Processing Techniques for Tomato Segmentation Applying K-Means Clustering and Edge Detection Approach. In Proceedings of the 2021 International Seminar on Machine Learning, Optimization, and Data Science (ISMODE), Jakarta, Indonesia, 29–30 January 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 92–96. [Google Scholar]
- Avilov, M.; Shichkina, Y.; Kupriyanov, M. Using Clustering Methods of Anomalies and Neural Networks to Conduct Additional Diagnostics of a Computer Network. In Intelligent Distributed Computing XIV; Springer International Publishing: Cham, Switzerland, 2022; pp. 193–202. [Google Scholar]
- Yuan, L.; Chen, H.; Gong, J. Interactive Communication with Clustering Collaboration for Wireless Powered Communication Networks. Int. J. Distrib. Sens. Netw. 2022, 18, 15501477211069910. [Google Scholar] [CrossRef]
- Kumari, A.; Sairam, A.S. Controller Placement Problem in Software-Defined Networking: A Survey. Networks 2021, 78, 195–223. [Google Scholar] [CrossRef]
- Heller, B.; Sherwood, R.; McKeown, N. The Controller Placement Problem. ACM SIGCOMM Comput. Commun. Rev. 2012, 42, 473–478. [Google Scholar] [CrossRef]
- Ul Huque, M.T.I.; Si, W.; Jourjon, G.; Gramoli, V. Large-Scale Dynamic Controller Placement. IEEE Trans. Netw. Serv. Manag. 2017, 14, 63–76. [Google Scholar] [CrossRef]
- Narendra, K.S.; Thathachar, M.A. Learning Automata—A Survey. IEEE Trans. Syst. Man Cybern. 1974, 4, 323–334. [Google Scholar] [CrossRef]
- Hasanzadeh-Mofrad, M.; Rezvanian, A. Learning Automata Clustering. J. Comput. Sci. 2018, 24, 379–388. [Google Scholar] [CrossRef]
- Rokach, L.; Maimon, O. Clustering Methods. In Encyclopedia of Data Warehousing and Mining, 2nd ed.; Wang, J., Ed.; IGI Global: Hershey, PA, USA, 2009; pp. 254–258. [Google Scholar]
- Grover, N. A Study of Various Fuzzy Clustering Algorithms. Int. J. Eng. Res. 2014, 2, 177–181. [Google Scholar] [CrossRef]
- Bora, D.J.; Gupta, D.; Kumar, A. A Comparative Study between Fuzzy Clustering Algorithm and Hard Clustering Algorithm. arXiv 2014, arXiv:1404.6059. [Google Scholar]
- Reynolds, A.P.; Richards, G.; de la Iglesia, B.; Rayward-Smith, V.J. Clustering Rules: A Comparison of Partitioning and Hierarchical Clustering Algorithms. J. Math. Model. Algorithms 2006, 5, 475–504. [Google Scholar] [CrossRef]
- Huang, Z. Extensions to the k-Means Algorithm for Clustering Large Data Sets with Categorical Values. Data Min. Knowl. Discov. 1998, 2, 283–304. [Google Scholar] [CrossRef]
- Zhang, B.; Hsu, M.; Dayal, U. K-Harmonic Means-A Data Clustering Algorithm. Hewlett-Packard Labs Technical Report HPL-99-124. 1999. Available online: http://shiftleft.com/mirrors/www.hpl.hp.com/techreports/1999/HPL-1999-124.pdf (accessed on 20 June 2022).
- Kaufman, L.; Rousseeuw, P.J. Clustering by Means of Medoids. In Statistical Data Analysis Based on the L1-Norm and Related Methods; Dodge, Y., Ed.; North-Holland: Amsterdam, The Netherlands, 1987; pp. 405–416. [Google Scholar]
- Dussert, C.; Rasigni, G.; Rasigni, M.; Palmari, J.; Llebaria, A. Minimal Spanning Tree: A New Approach for Studying Order and Disorder. Phys. Rev. B 1986, 33, 3528–3531. [Google Scholar] [CrossRef] [PubMed]
- Urquhart, R. Graph Theoretical Clustering Based on Limited Neighbourhood Sets. Pattern Recognit. 1982, 15, 173–187. [Google Scholar] [CrossRef]
- Cheng, W.; Wang, W.; Batista, S. Grid-Based Clustering. Data 2018, 3, 25. [Google Scholar]
- Kriegel, H.P.; Kröger, P.; Sander, J.; Zimek, A. Density-Based Clustering. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 231–240. [Google Scholar] [CrossRef]
- McNicholas, P.D. Model-Based Clustering. J. Classif. 2016, 33, 331–373. [Google Scholar] [CrossRef]
- Honarpazhooh, S. Controller Placement in Software-Defined Networking Using Silhouette Analysis and Gap Statistic. Turk. J. Comput. Math. Educ. 2021, 13, 4848–4863. [Google Scholar]
- Liao, J.; Sun, H.; Wang, J.; Qi, Q.; Li, K.; Li, T. Density Cluster Based Approach for Controller Placement Problem in Large-Scale Software Defined Networkings. Comput. Netw. 2017, 112, 24–35. [Google Scholar] [CrossRef]
- Xiaolan, H.; Muqing, W.; Weiyao, X. A Controller Placement Algorithm Based on Density Clustering in SDN. In Proceedings of the 2018 IEEE/CIC International Conference on Communications in China (ICCC), Beijing, China, 16–18 August 2018; pp. 184–189. [Google Scholar]
- Yujie, R.; Muqing, W.; Yiming, C. An Effective Controller Placement Algorithm Based on Clustering in SDN. In Proceedings of the 2020 IEEE 6th International Conference on Computer and Communications (ICCC), Chengdu, China, 11 December 2020; pp. 2294–2299. [Google Scholar]
- Chen, J.; Xiong, Y.; He, D. A Density-based Controller Placement Algorithm for Software Defined Networks. In Proceedings of the 2022 IEEE International Conferences on Internet of Things (iThings) and IEEE Green Computing & Communications (GreenCom) and IEEE Cyber, Physical & Social Computing (CPSCom) and IEEE Smart Data (SmartData) and IEEE Congress on Cybermatics (Cybermatics), Espoo, Finland, 22–25 August 2022; pp. 287–291. [Google Scholar]
- Rodriguez, A.; Laio, A. Clustering by Fast Search and Find of Density Peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef]
- Xiao, P.; Qu, W.; Qi, H.; Li, Z.; Xu, Y. The SDN Controller Placement Problem for WAN. In Proceedings of the 2014 IEEE/CIC International Conference on Communications in China (ICCC), Shanghai, China, 13–15 October 2014; pp. 220–224. [Google Scholar]
- Xiao, P.; Li, Z.Y.; Guo, S.; Qi, H.; Qu, W.Y.; Yu, H.S. AK Self-Adaptive SDN Controller Placement for Wide Area Networks. Front. Inf. Technol. Electron. Eng. 2016, 17, 620–633. [Google Scholar] [CrossRef]
- Lu, J.; Zhen, Z.; Hu, T. Spectral Clustering Based Approach for Controller Placement Problem in Software Defined Networking. J. Phys. Conf. Ser. 2018, 1087, 042073. [Google Scholar] [CrossRef]
- Sahoo, K.S.; Sahoo, B.; Dash, R.; Tiwary, M. Solving Multi-Controller Placement Problem in Software Defined Network. In Proceedings of the 2016 International Conference on Information Technology (ICIT), Bhubaneswar, India, 21–24 December 2016; pp. 188–192. [Google Scholar]
- Zhao, Z.; Wu, B. Scalable SDN Architecture with Distributed Placement of Controllers for WAN. Concurr. Comput. Pract. Exp. 2017, 29, e4030. [Google Scholar] [CrossRef]
- Wang, G.; Zhao, Y.; Huang, J.; Duan, Q.; Li, J. A K-means-based network partition algorithm for controller placement in software defined network. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–6. [Google Scholar]
- Kuang, H.; Qiu, Y.; Li, R.; Liu, X. A Hierarchical K-Means Algorithm for Controller Placement in SDN-Based WAN Architecture. Proceedings 2018, 2, 78. [Google Scholar]
- Zhu, L.; Chai, R.; Chen, Q. Control Plane Delay Minimization Based SDN Controller Placement Scheme. Proceedings 2017, 1, 536. [Google Scholar]
- Bouzidi, E.H.; Outtagarts, A.; Langar, R.; Boutaba, R. Dynamic clustering of software defined network switches and controller placement using deep reinforcement learning. Comput. Netw. 2022, 207, 108852. [Google Scholar] [CrossRef]
- Narendra, K.S.; Thathachar, M.A. Learning Automata: An Introduction. Entropy 2012, 14, 1415–1463. [Google Scholar]
- Torkamani-Azar, S.; Jahanshahi, M. A New GSO Based Method for SDN Controller Placement. Comput. Commun. 2020, 163, 91–108. [Google Scholar] [CrossRef]
- The Internet Topology Zoo. Available online: http://www.topology-zoo.org/ (accessed on 1 April 2023).
- Sminesh, C.N.; Kanaga, E.G.M.; Sreejish, A.G. A Multi-Controller Placement Strategy in Software Defined Networks Using Affinity Propagation. Int. J. Internet Technol. Secur. Trans. 2020, 10, 229–253. [Google Scholar] [CrossRef]
| Dataset | Instances | Dimensions | Clusters | Membership_Cluster | LA Initial Prob |
|---|---|---|---|---|---|
| BCW | 683 | 10 | 2 | 2 | 1/2 |
| Sonar | 208 | 60 | 2 | 2 | 1/2 |
| CMC | 1473 | 9 | 3 | 3 | 1/3 |
| Hayes-Roth | 132 | 5 | 3 | 3 | 1/3 |
| Ionosphere | 531 | 34 | 2 | 2 | 1/2 |
| Sonar | 208 | 60 | 2 | 2 | 1/2 |
| Pima | 768 | 8 | 2 | 2 | 1/2 |
| Dataset | K-Means | K-Means++ | K-Medoid | LAC | LAC-KHM |
|---|---|---|---|---|---|
| BCW | 0.50 ± 0.00 | 0.54 ± 0.00 | 0.50 ± 0.00 | 0.45 ± 0.00 | 0.50 ± 0.01 |
| Sonar | 0.49 ± 0.06 | 0.49 ± 0.06 | 0.49 ± 0.06 | 0.51 ± 0.04 | 0.54 ± 0.01 |
| CMC | 0.33 ± 0.04 | 0.32± 0.00 | 0.32 ± 0.00 | 0.34 ± 0.02 | 0.35 ± 0.01 |
| Hayes-Roth | 0.36 ± 0.03 | 0.41 ± 0.02 | 0.41 ± 0.02 | 0.42 ± 0.02 | 0.42 ± 0.02 |
| Ionosphere | 0.46 ± 0.03 | 0.48 ± 0.00 | 0.48 ± 0.00 | 0.48 ± 0.00 | 0.48 ± 0.01 |
| Sonar | 0.58 ± 0.21 | 0.78 ± 0.16 | 0.78 ± 0.16 | 0.90 ± 0.01 | 0.92 ± 0.11 |
| Pima | 0.49 ± 0.00 | 0.51 ± 0.00 | 0.51 ± 0.00 | 0.50 ± 0.00 | 0.52 ± 0.01 |
| Parameter_Symbol | Explanation |
|---|---|
| α(LA) | Actions |
| β(LA) | Reinforcement signal |
| P | Action’s probability |
| T | The learning algorithm |
| a | Reward parameter |
| b | Penalty parameter |
| V | Set of switches |
| E | Set of links |
| L_B | Load-balancing coefficient |
| Delay between switches and controller | |
| Delay between controllers | |
| α(OF) | Coefficient of load balancing |
| β(OF) | Coefficient of delay between switches and their related controller |
| (OF) | Coefficient of delay between controllers |
| n | Number of the switches |
| k | Number of the controllers |
| Number of members in each cluster | |
| The average delay between each switch and its related controller | |
| The average delay between controllers | |
| Normalization of | |
| Normalization of |
| Number of Nodes | Number of Switches | Number of Edges | Geographical Area | Geographical Location |
|---|---|---|---|---|
| Dial telecom | 193 | 151 | country | Czech Republic |
| Aarnet | 19 | 24 | country | Australia |
| Intellifiber | 73 | 97 | country | USA |
| Iris | 51 | 64 | region | Tennessee, USA |
| Dial Telecom | Intellifiber | Iris | Aarnet | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NOC | S-C | C-C | OF | S-C | C-C | OF | S-C | C-C | OF | S-C | C-C | OF | |
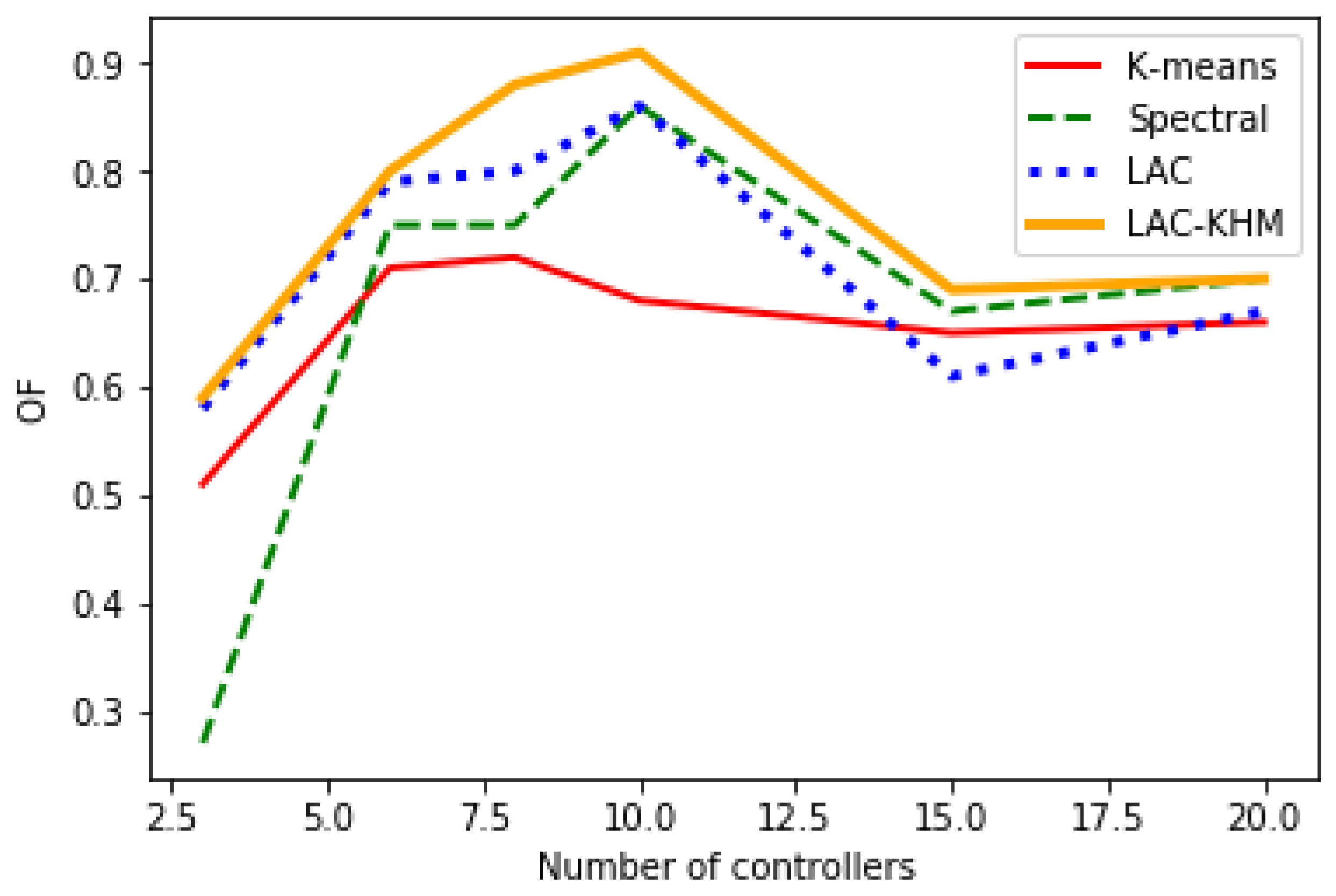
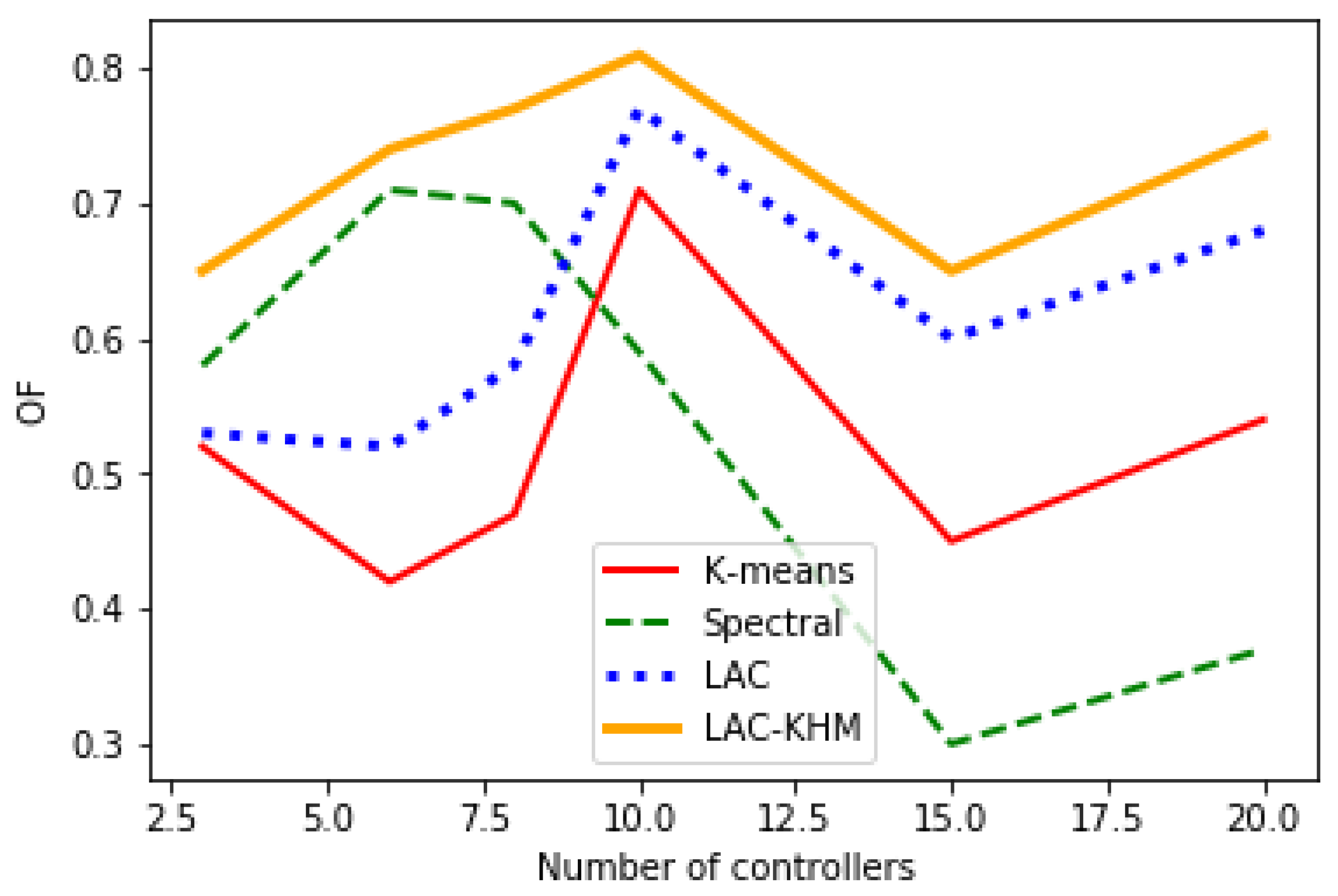
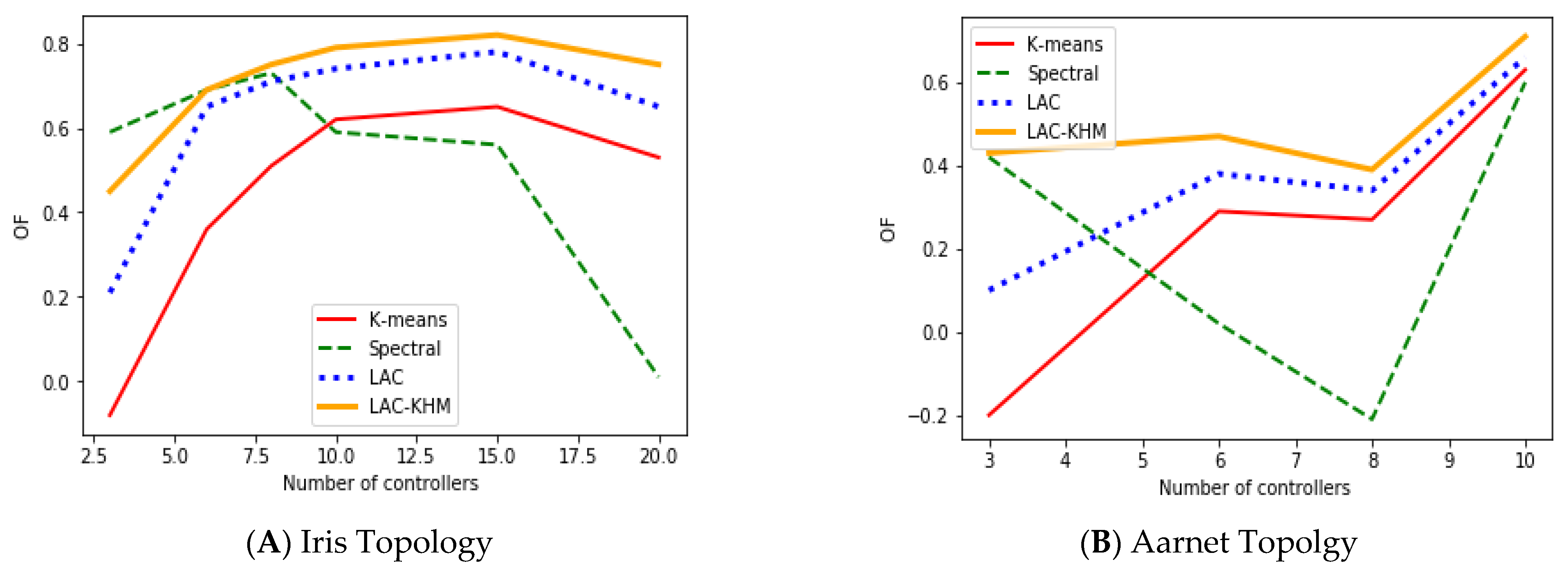
| K-means | 3 | 18.77 | 0.96 | 0.51 | 21.94 | 3.37 | 0.52 | 7.22 | 1.67 | -0.08 | 19.77 | 13.08 | -0.2 |
| 6 | 6.38 | 0.53 | 0.71 | 7.59 | 1.86 | 0.42 | 2.21 | 0.84 | 0.36 | 13.08 | 6.67 | 0.29 | |
| 8 | 3.9 | 0.45 | 0.72 | 4.78 | 1.64 | 0.47 | 1.35 | 0.67 | 0.51 | 1.65 | 5.48 | 0.27 | |
| 10 | 2.75 | 0.42 | 0.68 | 3.32 | 1.4 | 0.71 | 0.91 | 0.58 | 62 | 0.64 | 4.22 | 0.63 | |
| 15 | 1.48 | 0.32 | 0.65 | 1.65 | 1.18 | 0.45 | 0.41 | 0.44 | 0.65 | ||||
| 20 | 0.92 | 0.28 | 0.66 | 0.98 | 0.93 | 0.54 | 0.24 | 0.35 | 0.53 | ||||
| Spectral | 3 | 20.57 | 1.09 | 0.27 | 22.35 | 3.41 | 0.58 | 7.78 | 1.25 | 0.59 | 23.57 | 9.47 | 0.42 |
| 6 | 6.31 | 0.54 | 0.75 | 8.44 | 1.69 | 0.71 | 2.32 | 0.8 | 0.69 | 7.88 | 6.79 | 0.02 | |
| 8 | 3.95 | 0.46 | 0.75 | 5.28 | 1.41 | 0.7 | 1.4 | 0.61 | 0.73 | 3.76 | 3.59 | -0.21 | |
| 10 | 2.87 | 0.41 | 86 | 3.35 | 1.34 | 0.59 | 0.96 | 0.53 | 0.59 | 3.7 | 3.29 | 0.6 | |
| 15 | 1.87 | 0.29 | 0.67 | 2.11 | 1.03 | 0.3 | 0.65 | 0.37 | 0.56 | ||||
| 20 | 1 | 0.25 | 0.7 | 1.41 | 0.9 | 0.37 | 0.54 | 0.27 | 0.01 | ||||
| LAC | 3 | 17.78 | 0.95 | 0.58 | 20.14 | 3.01 | 0.53 | 6.72 | 1.37 | 0.21 | 17.77 | 12.08 | 0.1 |
| 6 | 6.03 | 0.43 | 0.79 | 6.12 | 1.44 | 0.52 | 1.08 | 0.75 | 0.65 | 9.14 | 5.43 | 0.38 | |
| 8 | 3.54 | 0.4 | 0.8 | 4.78 | 1.64 | 0.58 | 0.64 | 0.57 | 0.71 | 1.65 | 5.46 | 0.34 | |
| 10 | 2.21 | 0.31 | 0.86 | 2.76 | 1.22 | 0.77 | 0.77 | 0.52 | 0.74 | 0.61 | 3.22 | 0.66 | |
| 15 | 1.23 | 0.26 | 0.61 | 1.43 | 1.02 | 0.6 | 0.38 | 0.38 | 0.78 | ||||
| 20 | 0.92 | 0.28 | 0.67 | 0.87 | 0.75 | 0.68 | 0.21 | 0.22 | 0.65 | ||||
| LAC-KHM | 3 | 16.77 | 0.89 | 0.59 | 18.65 | 2.34 | 0.65 | 6.45 | 1.14 | 0.45 | 15.55 | 5.32 | 0.43 |
| 6 | 6.13 | 0.39 | 0.8 | 5.24 | 1.12 | 0.74 | 0.99 | 0.68 | 0.69 | 7.23 | 5.88 | 0.47 | |
| 8 | 3.32 | 0.36 | 0.88 | 4.12 | 1.34 | 0.77 | 0.61 | 0.52 | 0.75 | 1.04 | 4.43 | 0.39 | |
| 10 | 1.97 | 0.29 | 0.91 | 2.06 | 1.01 | 0.81 | 0.74 | 0.5 | 0.79 | 0.54 | 3.12 | 0.71 | |
| 15 | 1.12 | 0.26 | 0.69 | 1.06 | 0.78 | 0.65 | 0.32 | 0.35 | 0.82 | ||||
| 20 | 0.88 | 0.21 | 0.7 | 0.66 | 0.63 | 0.75 | 0.17 | 0.18 | 0.75 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amin, A.; Jahanshahi, M.; Meybodi, M.R. Improved Learning-Automata-Based Clustering Method for Controlled Placement Problem in SDN. Appl. Sci. 2023, 13, 10073. https://doi.org/10.3390/app131810073
Amin A, Jahanshahi M, Meybodi MR. Improved Learning-Automata-Based Clustering Method for Controlled Placement Problem in SDN. Applied Sciences. 2023; 13(18):10073. https://doi.org/10.3390/app131810073
Chicago/Turabian StyleAmin, Azam, Mohsen Jahanshahi, and Mohammad Reza Meybodi. 2023. "Improved Learning-Automata-Based Clustering Method for Controlled Placement Problem in SDN" Applied Sciences 13, no. 18: 10073. https://doi.org/10.3390/app131810073
APA StyleAmin, A., Jahanshahi, M., & Meybodi, M. R. (2023). Improved Learning-Automata-Based Clustering Method for Controlled Placement Problem in SDN. Applied Sciences, 13(18), 10073. https://doi.org/10.3390/app131810073





