Abstract
This paper presents the design and testing of an ultra-low-noise transimpedance amplifier (TIA) for low-frequency noise measurements on low-impedance (below 1 kΩ) devices, such as advanced IR photodetectors. When dealing with low-impedance devices, the main source of background noise in transimpedance amplifiers comes from the equivalent input voltage noise of the operational amplifier, which is used in a shunt–shunt configuration to obtain a transimpedance stage. In our design, we employ a hybrid operational amplifier in which an input front end based on ultra-low-noise discrete JFET devices is used to minimize this noise contribution. When using IF3602 JFETs for the input stage, the equivalent voltage noise of the hybrid operational amplifier can be as low as 4 nV/√Hz, 2 nV/√Hz, and 0.9 nV/√Hz at 1 Hz, 10 Hz, and 1 kHz, respectively. When testing the current noise of an ideal 1 kΩ resistor, these values correspond to a current noise contribution of the same order as or below that of the thermal noise of the resistor. Therefore, in cases in which the current flicker noise is dominant, i.e., much higher than the thermal noise, the noise contribution from the transimpedance amplifier can be neglected in most cases of interest. Test measurements on advanced low-impedance photodetectors are also reported to demonstrate the effectiveness of our proposed approach for directly measuring low-frequency current noise in biased low-impedance electronic devices.
1. Introduction
Noise measurements can be extremely useful in the characterization of electronic devices, since a proper interpretation of the measured noise spectra can provide information on their quality and reliability [1,2,3,4,5]. In the case of sensor devices such as photodetectors, reliable measurements of their current noise characteristics are needed to assess the value of fundamental parameters connected with their responsivity and noise [6,7]. Their values depend on their bias conditions, temperature, and frequency [8,9,10]. Noise models exist that might allow the estimation of such parameters, but they are generally quite inaccurate, because the low-frequency part of the noise spectrum is the most difficult to estimate and to correlate with the device structure [11]; therefore, actual noise measurements on each sample are required to obtain sensible results [12,13].
Low-frequency noise measurements on electronic devices can be performed in two configurations: voltage noise measurements through the Device Under Test (DUT) biased with a constant current IB; or measurements of the current noise through the DUT biased with a constant voltage VA [14]. The measurement of the Power Spectral Density (PSD) of the voltage noise SVD or the current noise SID provides the very same information, as long as the current–voltage characteristic IB (VB) of the DUT and its small signal impedance ZD at the selected bias point and vs. frequency are known, since [15,16]:
It may be worth mentioning that throughout this paper, whenever quantities representing the PSD of voltage or current fluctuations appear in an equation, it is intended that these values be expressed in the appropriate units, V2/Hz and A2/Hz. However, as is common practice in the field of noise measurements and instrumentation, when referring to specific values in the text, we will often express these quantities in terms of their square roots (i.e., V/√Hz and A/√Hz).
From an experimental point of view, it is easier to perform voltage noise measurements in the case of low-impedance DUTs, while current noise measurements are restricted to cases of high-impedance DUTs [17,18]. The advanced photodetectors we plan to investigate are characterized by impedances that can be on the order of or even below 1 kΩ, and thus belong to the class of devices for which voltage noise measurements are more easily performed. The problem, however, is that some interesting device parameters are more directly related to the current noise [19]. Using Equation (1) to obtain SID from SVD, however, requires detailed knowledge of the device impedance, which therefore needs to be accurately measured under exactly the same environmental and bias conditions as those under which the noise voltage spectrum was obtained. This procedure can become extremely time consuming and prone to error, since two different measurement steps and setups (for noise measurement and for impedance measurements) are involved.
For this reason, we decided to explore the feasibility of the realization of an ultra-low-noise transimpedance amplifier dedicated to the reliable measurement of low-frequency current noise in low-impedance devices. In Section 2, the proposed approach for the design of the TIA is presented; in Section 3, details on the circuit implementation are given; in Section 4, the results of measurements performed using photodetectors as DUTs are presented; and in Section 5, conclusions are drawn.
2. Proposed Approach
To better understand the challenges that must be faced when designing a transimpedance amplifier for performing current noise measurements on a low-impedance DUT, the simplified circuit presented in Figure 1 is considered.
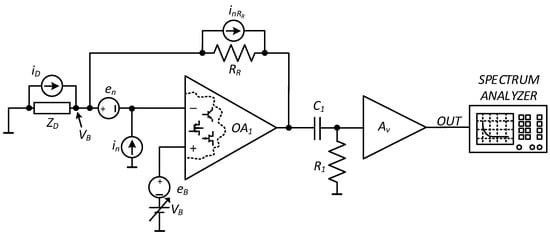
Figure 1.
Current noise measurement system.
In this system, the device under test (ZD) is biased at a constant voltage VB because of the virtual short circuit between the inputs of the operational amplifier OA1. The transimpedance gain between the DUT current source iD and the output voltage of OA1 is set by the resistor RR. In choosing the value of RR, the linearity range of OA1 must be taken into account, since the DC current flowing through the DUT also flows through the feedback resistance, causing a large DC component. Higher values of resistance RR will result in higher gain, but also in a reduced maximum bias current for the DUT. It will be assumed, however, that the gain of the first stage is sufficient to ensure a negligible influence of the noise contributions from the following stages to the overall noise of the system. The high-pass filter C1R1 rejects the DC component at the output of OA1 so that only the noise signal can be further amplified by the voltage amplifier. The value of Av ensures that the signal level at its output is compatible with the input range of the spectrum analyzer used for spectral estimation. The relevant noise sources that contribute to the background noise (BN) are also shown in Figure 1. For the amplifier to be effective, we need the noise contribution of these sources to be negligible with respect to the noise generated by the DUT. In the measurement bandwidth (determined by the corner frequency of the high-pass filter C1R1 and the bandwidth limit of the transresistance and the voltage amplifier stages), the Power Spectral Density (PSD) SOUT recorded by the spectrum analyzer is:
with
where Sin, Sen, and SeB are the PSDs of the noise sources in, en and eB, k is the Boltzmann constant, and T is the absolute temperature. To obtain the expression of the background noise SiBN, as shown in Equation (3), we assumed all noise sources to be uncorrelated.
When dealing with high DUT impedances, relatively high values of Sen and SeB can be tolerated, and this means that Junction Field-Effect Transistor (JFET) or Metal-Oxide-Semiconductor Field Effect Transistor (MOSFET) input operational amplifiers can be used to minimize the contribution from the current noise Sin. Indeed, in many cases of interest, the main contribution to the background noise comes from the feedback resistance RR, which must be chosen to be as large as possible, in a manner compatible with the limitations mentioned above as well as the desired bandwidth of the system [20,21]. However, for DUT impedances on the order of 1 kΩ or less, the contribution from Sen and SeB can become relevant and cannot be neglected any longer. To simplify this discussion, we limited our analyses to the low frequency range, in which the flicker noise component can be more easily detected. Moreover, at low frequencies, we assume the DUT impedance to behave as a resistance, that is ZD ≈ RD. For this reason, the DUT model does not contain any reactive component.
Flicker noise can only be measured when it is greater than the thermal noise of the DUT. Therefore, the thermal noise of the DUT represents a reference level with respect to which the background noise of the amplifier must be minimized. Minimizing the ratio between the DUT thermal noise SD and the background noise means minimizing the quantity Qn:
From Equation (4), we conclude that RD/RR << 1 is a necessary condition to obtain SiBN/SD << 1. If this condition is satisfied, we also have RD‖RR ≈ RD and Equation (4) can be rewritten as:
If we resort to either batteries or ultra-low-noise voltage sources for obtaining the required bias for the DUT, SeB can be made negligible [22]. From Equation (5), if SeB ≈ 0, the lowest value of Qn, for given values of Sin and Sen, is obtained when RD = RQmin
Note, however, that RQmin is frequency dependent, and that the value of RD is set by the DUT and cannot be easily modified.
To further simplify the discussion, we will assume a “typical” value of RD = 1 kΩ with a thermal voltage noise of 4kTRD ≈ 16.6 × 10−18 V2/Hz /√Hz) at room temperature. Let us first explore the possibility of using a monolithic low-noise operational amplifier with BJT (Bipolar Junction Transistor) or FET input stage technology. With BJT input stages, lower levels of input voltage noise can be achieved. On the other hand, the current noise obtained when using BJTs is typically six orders of magnitude higher than that obtained using MOSFET input amplifiers. As an example, the voltage noise of the MOSFET input TLC2201 operational amplifier at 1 Hz is 3.6 × 10−15 V2/Hz (60 nV/√Hz), with a specified current noise of less than 10−30 A2/Hz (1 fA/√Hz). With our assumed reference RD, the contribution of Sin to Qn is completely negligible (less than 10−8), but due to the value of Sen, Qn is about 225. For the low-noise BJT input OP27, the voltage noise is 100 times lower (36 × 10−18 V2/Hz) than that of the TLC2201, resulting in a contribution to Qn of about 2.25. On the other hand, the effect of the current noise is not negligible as before: at the same frequency (1 Hz), its value is about 22.4 × 10−24 A2/Hz (≈ 5 pA/√Hz), and this results in a further contribution of about 1.6 to Qn, for a total value of Qn close to 4. Note, moreover, that the reference value for our chosen resistance is close to the value that minimizes Qn at 1 Hz for the OP27 (RQmin = 1270 Ω). This means that for impedance values significantly below or above 1 kΩ, Qn becomes significantly greater than 4.
The results discussed above are quite typical and do not change significantly across the range of commercially available monolithic low-noise operational amplifiers. To obtain a value of Qn that is significantly below 1, we must therefore resort to a custom design for the operational amplifier OA1. In particular, we can take advantage of the noise characteristics of discrete component devices (BJTs or JFETs), allowing us to obtain significantly lower levels of equivalent voltage noise. The reduction in voltage noise, however, is accompanied by an increase in current noise. This means that unless we are dealing with very low impedances (well below 100 Ω), there is no advantage in using discrete BJTs as front-end devices. On the other hand, discrete low-noise JFET devices can make it possible to reach sufficiently low equivalent input voltage noise, with the contribution of the current noise to Qn remaining negligible.
On the basis of the above considerations, we resorted to very-low-noise discrete JFETs in order to obtain a super-operational amplifier characterized by equivalent input voltage and current noise levels that are sufficiently low as to allow the design of a TIA capable of enabling the reliable measurement of the low-frequency current noise in devices with equivalent impedances in the range of 1 kΩ or below.
3. Materials and Methods
The schematic of the proposed ultra-low-noise TIA amplifier is presented in Figure 2. The very-low-noise discrete JFET pair IF3602 is used to provide an ultra-low-noise input stage in front of the low-noise BJT input operational amplifier OPA227. The transistor Q1, together with the resistance RSS, behaves as a current source for biasing the JFET pair (J1 and J2). The collector current IC1 of Q1, with VDD = VSS = 12 V, is approximately:
where VBEON is the voltage drop between the base and the emitter of Q1 in the active region (in the range from about 0.6 to 0.7 V). At rest and under ideal conditions, the gate voltages VG1 and VG2 of J1 and J2 are at zero potential, so that the two JFETs operate with the same current: ID1 = ID2 = IC1/2 = 3.5 mA. The voltage drop across the drain resistances RD1 and RD2 is, therefore, 7 V, so that the drain-to-gate voltages VDG1 and VDG2 are maintained at about 5 V, ensuring operation in the active region (the typical pinch-off voltage for the IF3602 is −350 mV). The values of the bias currents for J1 and J2 are the result of a compromise between the need for low noise (equivalent input noise decreases when increasing bias) and the need to limit the power dissipated by the active devices in order to limit the convective motion of the air close to the JFET, which can induce large fluctuations at low frequencies.
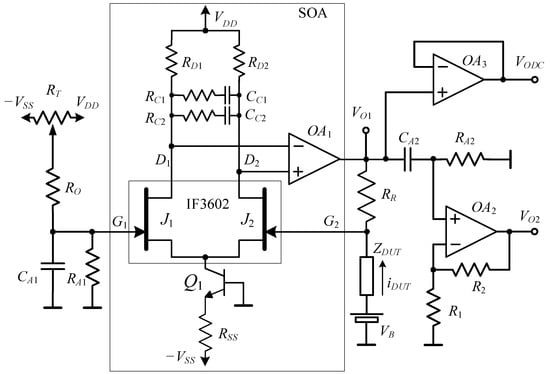
Figure 2.
Proposed TIA amplifier. The component types and their values are listed in Table 1.
With the selected bias, the total power dissipated by the IF3602 is 35 mW, which is a small fraction of the maximum allowed power dissipation for the device (300 mW). At the same time, the transimpedance gain gm of each JFET can be expected to be about 70 mA/V [14], and, because RD1 = RD2 = RD = 2 kΩ, the differential voltage gain AVDJ of the JFET differential stage at low frequencies can be estimated to be:
The cascade of the discrete JFET input stage with the OPA227 operational amplifier results in a Super Operational Amplifier (SOA in Figure 2), where the nodes G1 and G2 represent the non-inverting and inverting inputs, respectively. From Equation (8) and the fact that the DC gain of the OPA227 is about 160 dB, the DC gain of the SOA is above 200 dB, and therefore the internal compensation of the OPA227 is not sufficient to ensure stability for the entire amplifier. To address this issue, we resort to the compensation network made of RC1, RC2, CC1, and CC2 in Figure 2. The OPA227 introduces a pole at about 3 Hz as part of its frequency response. The compensation network introduces two poles and two zeroes, which reduce the open-loop gain to zero dB before the high-frequency poles of the OPA227 are able to introduce a further phase shift that would cause instability. Because of the 90° phase shift introduced by the dominant pole of the OPA227, the compensation network is designed in such a way that its phase contribution is less than 45° at any frequency. This can be achieved if the frequency of the zero is no larger than 10 times that of the pole. With this constraint, the gain amplitude reduction that is obtained with a single zero-pole compensation network is insufficient to reach the desired goal. For this reason, in our design, we introduce two RC networks between the drain of the JFETs. With the values for RC1CC1 and RC2CC2 listed in Table 1, the pole and zero frequencies are:

Table 1.
Component list for the circuit in Figure 2.
With these values, the SPICE simulations show that the open-loop gain reaches 0 dB with a phase margin of about 45°. This ensures that the shunt–shunt configuration possesses the stability required to produce a transimpedance amplifier for resistive DUTs of any value.
The super operational amplifier is used in a shunt–shunt configuration, as shown in Figure 1, in order to obtain a transimpedance stage with gain AR set by the feedback resistance RR, that is:
Assuming a negligible input offset for the SOA, Equation (10) holds for both the DC component and the fluctuations across the DUT. This means that the DC voltage at the output VO1 can be used to estimate the DC current through the DUT. It is for this reason that this voltage is carried by a buffer (OA3) to one of the outputs of the system (VODC).
The amplitude of the noise fluctuations at node VO1 is typically too low to be effectively detected using a spectrum analyzer, and therefore, a second stage is used to obtain high voltage gain (OA2) after rejecting the DC component using an AC coupling filter (CA2RA2).
Since this amplifier is intended for noise measurements on low-impedance DUTs, typical bias voltages VB across the DUT are often well below 1 V, and this means that the input offset of the SOA must be maintained low both for the voltage across the DUT to essentially coincide with the external bias voltage VB, and for the output VODC to provide the correct value for the DC current through the DUT. With a discrete JFET input stage for the SOA, the offset can be relevant. This offset is essentially due to the mismatch between the two JFETs in the IF3602 device. Offsets as large as ±50 mV can easily be experienced in the case of the IF3602 [14], and these values are quite relevant for bias voltages on the order of a few hundred mV. Therefore, the schematic diagram in Figure 2 includes a system for adding a DC voltage at the non-inverting input of the SOA, which is obtained by exploiting a trimmer (RT) together with a voltage divider (RO, RA1) and a capacitor CA1 in order to filter out, as much as possible, the thermal noise generated by the offset correction circuit itself.
With the approach shown in Figure 2, equivalent offsets below 5 mV were routinely obtained while testing the realized prototype.
The component list used to build the proposed amplifier is presented in Table 1.
The most important parameter for any amplifier designed for low-frequency noise measurements is the level of background noise, particularly at low frequencies, where the flicker noise of the active devices in the amplifier may mask the flicker noise generated by the DUT. Since we are mainly interested in the performances at low frequencies, and since it can be easily proven that the compensation network does not contribute significantly to the background noise at frequencies up to a few kHz, in discussing the noise performances of the system, we will neglect the presence of RC1, RC2, CC1 and CC2.
The equivalent circuit for noise calculation is shown in Figure 3. The ratio between useful noise (the noise coming from the DUT ZD) and background noise will be estimated with reference to the input of the last voltage amplifier in the noise measurement chain (vOB, corresponding to the non-inverting input of OA2 in Figure 2).
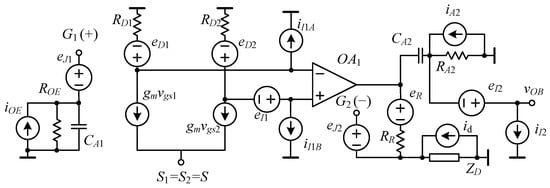
Figure 3.
Simplified equivalent circuit for noise calculation.
Besides omitting the compensation network, other simplifications are made: (a) the BJT-based current source is assumed to be characterized by very high equivalent impedance; (b) the current noise source representing the noise coming from the BJT-based circuit is omitted, since it is a common mode source whose effects are rejected by OA2; (c) the equivalent input current noise source at the input of OA3 is omitted, since it is shorted by the very low impedance at the output of OA2. Because of the high open-loop gain of the SOA and the fact that we are mainly interested in the noise at low frequencies, we can perform noise estimation under the assumption of a virtual short circuit between the inverting G2(−) and non-inverting G1(+) inputs of the SOA. We will also assume that we are working above the cut-off frequency of the AC coupling filter, with the minimum frequency of interest being 1 Hz. Note, however, that the capacitors CA1 and CA2 are not replaced with short circuits, because, due to the large amount of thermal noise introduced by the resistances ROE and RA2, their finite impedance may result in a non-negligible contribution to the BN of the system even above the cut-in frequency [23].
We will also take advantage of the reasonable assumption that all noise sources are uncorrelated, so that we can estimate the total noise at vOB by adding the noise contribution from each single source.
We can start by estimating the contribution SOB_iD to the PSD of the noise at vOB due to the DUT noise source iD with PSD SiD. We have:
It can be easily demonstrated that, assuming the PSD SJ1 of ej1 and Sj2 of ej2 to be the same, and equal to SJ, their total contribution SOB_J is given by:
As far as the contribution of the offset compensation network is concerned, with the component values in Table 1, the equivalent resistance ROE is essentially reduced to RO‖RA1, which, at the minimum frequency of interest (1 Hz), is much greater than the impedance XCA1 of the capacitor CA1. Therefore, the contribution SOB_OE due to the thermal noise iOE of the resistor ROE is reduced to:
where f is the frequency, k is the Boltzmann constant, and T is the absolute temperature.
With respect to the contribution from the thermal noise of the resistances RD1 and RD2 and the equivalent input voltage (eO1) and current noise sources (i1A and i1B), assuming a virtual short circuit at the inputs of the SOA, there is no contribution to the output noise. This result, however, is only an approximation, and depends on the magnitude of the loop gain and the magnitude of the PSD associated with the noise sources. Proper calculations show that these contributions can be neglected at low frequencies as long as the loop gain of the SOA in the shunt–shunt configuration in Figure 2 is high and gmRD >> 1.
In terms of the contribution SOB_RR of the thermal noise generated by the feedback resistance RR, it is given by:
Since we are assuming that we are operating well above the cut-in frequency of the AC filter RA2CA2, the reactance of the capacitor CA2 is much lower than the resistance RA2, and therefore, for the contributions SOB_A2 of the resistance RA2 and SOB_OI2 of the noise source iI2, we have:
where SII2 is the PSD of the current noise source iI2.
Finally, it is necessary to add the contribution SOB_EI2 due to the equivalent noise source eI2, that is:
where SeI2 is the PSD of the current noise source eI2.
In order to more easily understand the relative weight of the different noise contributions, we can proceed with the same simplifying assumption used in the previous section to obtain the equivalent input background noise, that is, the DUT impedance is assumed to be essentially a resistance with a value RD, and the condition RD/RR << 1 is satisfied.
Starting from the PSD SOB of the overall noise at the output vOB in the form:
we can calculate the parameter Qn as before. We have:
In Equation (18), Qn is expressed as the sum of two contributions to stress the fact that the contribution Qn2 can be made as small as desired by increasing the values of the coupling capacitors CA1 and CA2, at the cost, however, of increasing the time constants τA1 and τA2; the fact that these time constants increase means that the settling time of the circuit increases as well, and this, besides resulting in a waste of time when connecting a new DUT or setting a different bias voltage, can make offset correction a much more challenging task. When looking at the relative weight of the terms contributing to Qn2, we can start by evaluating the term that contains the PSD SII2. The ADA4625 is a JFET input operational amplifier. The PSD for the equivalent input current noise source reported in the datasheet is 4.5 fA/√Hz, and this means that the contribution of the fraction containing SII2 in Equation (18) is much lower than 1 for values of RA2 on the order of a MΩ or more (RA2 = 1 MΩ in our prototype). This, together with the fact that the two time constants τA1 and τA2 have similar values, and the fact that:
clearly indicates that Qn2 is essentially set by the first term in Equation (18), that is, by the thermal noise generated by the equivalent resistance ROE that is not completely filtered out by the capacitance CA1. At the minimum frequency of interest (1 Hz), assuming a typical value for RD of 1 kΩ, we have Qn2 ≈ 0.06. Note that, because of the proportionality to the inverse of the frequency squared, Qn2 rapidly decreases with increasing frequency.
In the case of Qn1, too, the highest value is obtained at the lowest frequency of interest because of the flicker noise component introduced by the JFETs and by the operational amplifier OA2. At the minimum frequency of interest (1 Hz), assuming a typical value of RD of 1 kΩ and a worst-case scenario in which RR is limited to 10 kΩ (RR/RD = 10), with SJ = 1 × 10−18 V2/Hz [14] and SeI2 = 1 × 10−16 V2/Hz, we obtain Qn2 ≈ 0.28. If the bias conditions are such that a feedback resistance of RR = 100 kΩ can be used, Qn2 is reduced to about 0.12, a value essentially set by the noise contribution coming from the JFETs. Overall, therefore, under the same conditions explored in the introduction (DUT resistance on the order of 1 kΩ), a value of Qn is obtained that is a small fraction of 1 (from 0.18 to 0.24, depending on the value of the feedback resistance). This is to be regarded as an excellent result in consideration of the fact that, when investigating the flicker noise, the thermal noise generated by the DUT can be regarded as part of the background noise of the system (i.e., the flicker noise must be much larger than the thermal noise for a reliable characterization). Therefore, obtaining a value of Qn that is a small fraction of 1 means that we are operating quite close to the ideal conditions under which no excess noise will be introduced by the amplifier.
The value of Qn obtained above is relative to the minimum frequency of interest (1 Hz). As the frequency increases, the background noise decreases because of the reduction of both the impedance of the coupling capacitances and the flicker noise contribution introduced by the active devices.
As can be deduced from Equation (18), if RD decreases significantly, Qn increases and the background noise of the system becomes relevant with respect to the thermal noise introduced by the DUT.
4. Results
We built the amplifier presented in Figure 1 to experimentally verify that sensible direct low-frequency current noise measurements on low-impedance devices are indeed possible. We tested the amplifier with two different values for the feedback resistance RR, i.e., 10 kΩ and 100 kΩ, as shown in Table 1. The test measurements were initially performed using known resistances as DUTs. In particular, we tested the system with both a 100 Ω resistor and a 1 kΩ resistor as the DUT. The 1 kΩ resistor was taken as representative of the typical impedance we expect with actual devices in noise measurements. The test using a 100 Ω resistor as a DUT was performed in order to more clearly evidence the noise contribution (background noise) introduced by the amplifier, since, as was shown in the previous section, its relative weight increases with decreasing DUT impedance.
As can be observed in Figure 4, when testing a 100 Ω resistance as a DUT, with RR = 10 kΩ, the background noise due to the amplifier had a noticeable effect on the measurement results, although it can be observed that even in this configuration, it should be possible to perform sensible flicker noise measurements within the frequency range in which the flicker noise is much greater than the thermal noise of the device. It can also be noticed that, as can be deduced from Equation (18), the background noise in this case is mostly due to the first term in Qn1, since RD/RR = 10−2. In other words, the background noise is set by the input JFETs, and increasing the value of the feedback resistance has a negligible effect on the background noise.
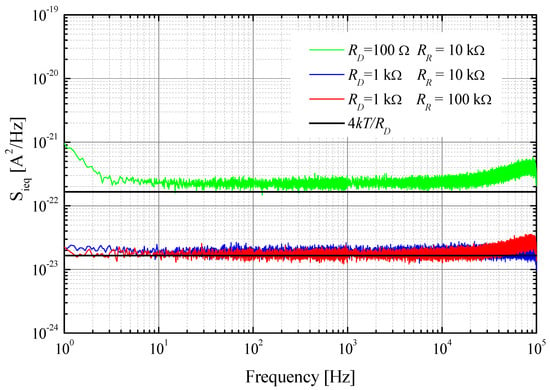
Figure 4.
Test results when using resistances at room temperature as DUTs. Tests were performed on 100 Ω and 1 kΩ resistances using two different values for the feedback resistance RR. The continuous black lines represent the expected noise, that is, the thermal current noise generated when using the resistances as DUTs.
When testing a 1 kΩ resistance as the DUT, from Figure 4 it can be observed that the measured value of the equivalent input current noise was very close to the noise generated by the DUT, except for at very low frequencies, where the deviation is, however, very small. A careful examination of the two curves relative to RR = 10 kΩ (blue curve) and RR = 100 kΩ (red curve) indicates, as should be expected, that employing a higher feedback resistance is beneficial as far as the BN is concerned. On the other hand, no significant difference can be expected when even a moderate level of flicker noise is present, and therefore, in general terms, and unless the DUT impedance is considerably below 1 kΩ, there is no significant advantage to employing feedback resistances above 10 kΩ, as this will result in a limitation of the bias level that can be applied to the DUT. It can be observed from Figure 4 that the measured noise increases above 10 kHz. This can be explained by the fact that, because of the compensation network, the gain in the first stage decreases as the frequency increases, and the equivalent input noise increases because the relative weights of the noise introduced by RD1, RD2, and OA1 increase [14].
Following the preliminary tests on resistances, we performed noise measurements on advanced photodetectors to demonstrate the ability of the new amplifier to directly perform current noise measurements on low-impedance DUTs.
The photodetector used in this investigation was an InAsSb (p+Bpun+)-based barrier backside illuminated device. It was grown on a GaAs substrate with GaAs and InAs Si-doped layers using molecular beam epitaxy. The architecture details of the investigated structure are shown in Figure 5. It consisted of four main layers, which were additionally supplemented by gradient layers. The absorber, which is the main layer on which the radiation is absorbed, was non-intentionally doped (n.i.d.) with n-type conductivity. The bandgap barrier for electrons was made using AlAsSb. The n+ contact placed at the bottom was made of a highly Si-doped InAs1-xSbx layer. To reduce tunneling currents and decrease the maximum electric field occurring on the junction the additional graded Si-doped InAs1−xSbx layer was sandwiched between the n+ contact and the absorber. A Be-doped (p-type) AlSb barrier was used to cap the absorber layer. The Be-doped (8 × 1018 cm−3 InAs1-xSbx contact layer was applied to the top of the structure. Thanks to this construction both dark current and noise were reduced. The ohmic contact to the structures was performed by etching followed by Au/Ti metallization. The overall structure with the contacts was closed inside a metal TO-8 package.
Typically, the resistance area product (R0A) of commercially available InAsxSb1−x diodes varies from about 4 to 60 Ω cm2 (with 0 ≤ x ≤ 0.36, T = 300 K) [24]. The tested detector was optimized for the 5 µm wavelength and mounted on a thermoelectric cooler to make it possible to improve its overall performance by operating at lower temperatures. In our experiments, we used a dedicated PID thermoelectric cooler controller to set up and precisely stabilize the temperature during measurements. Moreover, to dissipate heat from the “hot” side of the TEC, it was placed on a large-area aluminum radiator using thermoconductive paste. At zero bias voltage and A = 0.01 mm2, the R0A product of our sample at 300 K was about 7 mΩ·cm2. Further electro-optical details about the detector can be found in [25].
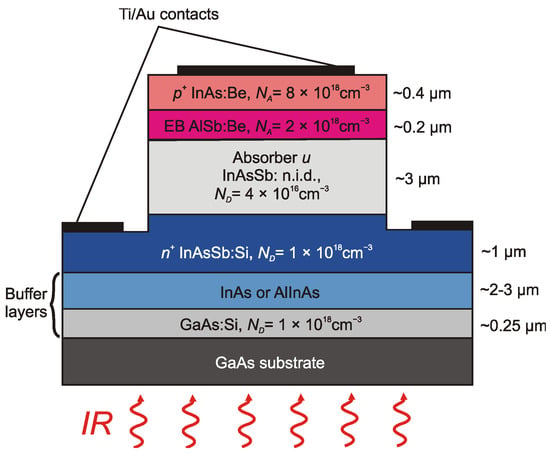
Figure 5.
The architecture of the investigated InAsSb-based barrier IR detector. Reprinted with permission from Ref. [25]. 2023, SPIE.
Figure 6 shows typical current–voltage characteristics of the investigated devices at different temperatures. These were measured using a precision SMU Keithley 236 using forcing voltage. While performing these measurements, the detector was covered to avoid any influence from background radiation coming from the environment. It was shown that for lower temperatures, the dependence of the current on reverse bias was much more visible than at higher ones. This confirms that the dynamic resistance of the investigated IR detector is a function of both the temperature and the bias.
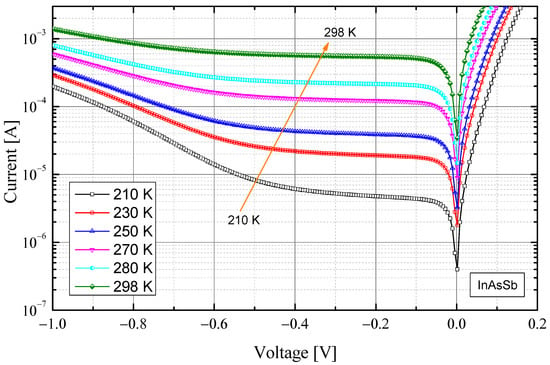
Figure 6.
Current–voltage (I-V) characteristics of the tested photodiode at different temperatures.
For this reason, all tests, including noise measurements, were performed while actively keeping the devices at a given temperature. To ensure proper temperature stabilization using TEC, the noise measurements reported in this paper were performed at 280 K, which is a temperature below, but not too far away from, ambient temperature. At this temperature, despite the cooling (which usually increases resistance), the detector is still characterized by relatively low resistance.
The impedance of the device vs. frequency was measured at different bias voltages and different operating temperatures, as well. In all cases, the impedance of the device is essentially coincident with the differential resistance at DC up to frequencies as high as a few tens of kHz. The differential resistance vs. bias for the tested photodiode at an operating temperature of 280 K is reported in Figure 7.
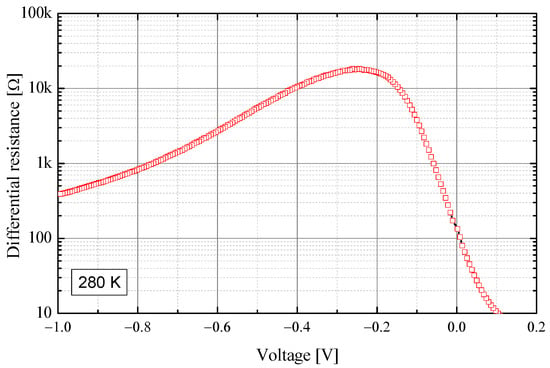
Figure 7.
The determined differential resistance of the photodiode at a temperature of 280 K.
The noise characterization of the photodetector is performed in reverse bias. As can be noticed from Figure 7, in the case of the device to be measured, its differential resistance ranges from a few hundred ohms (for a reverse bias of a few tens of mV) to a maximum of about 20 kΩ, at about −250 mV. It can also be noticed that, due to the peculiar shape of the I-V curve, the device resistance decreases at biases below −250 mV.
The results of the noise measurements performed on the photodiode at 280 K and different bias levels are reported in Figure 8. The thermal noise corresponding to the resistance of the unbiased photodiode is also shown.
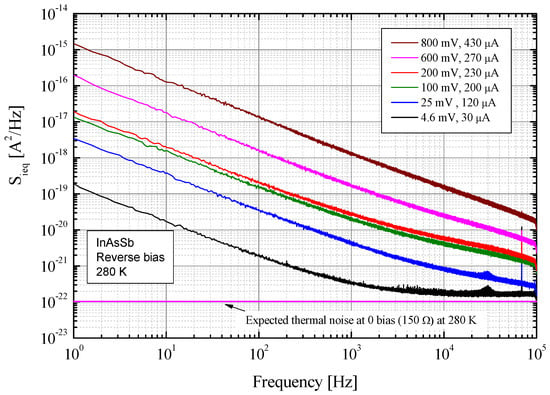
Figure 8.
Current noise measurement results at different bias levels.
From Figure 8, it is apparent that, except for the lowest biases at higher frequencies, the situation is one in which the flicker noise generated by the photodiode can be detected and estimated. Increasing the voltage causes a significant increase in flicker noise S(f) = 1/fα in situations in which it is dominant in the overall examined frequency range, where the α parameter has a value close to 1. The detailed behavior of the spectral noise in this type of photodetector has already been described in the literature [26], and it is outside the scope of this work.
It is, however, important to remark that the availability of effective instrumentation, such as that discussed in this paper, can be extremely useful. To show what can be obtained if effective and easy-to-use instrumentation is available, we can, for instance, discuss what can be inferred from the dependence of the current noise density at f = 10 Hz on the bias current, as reported in Figure 9.
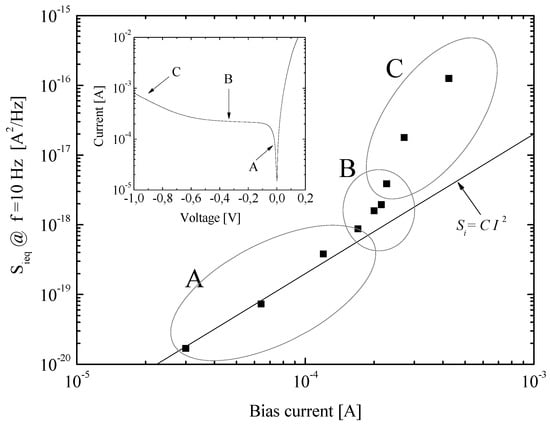
Figure 9.
Current noise at 10 Hz vs. bias current. The I-V characteristics of the device at 280 K from Figure 5 are reported in the inset.
The line in the plot represents the trend for the proportionality of the flicker noise to the bias current squared. From the results reported in Figure 9, it can be observed that the proportionality of the flicker noise vs. the bias current squared can be assumed for low bias voltages (region A in the I-V characteristics reported in the inset); with increasing voltage (in reverse bias), region B in the I-V characteristics is explored, and, when region C is reached, the dependence of the noise on the bias current is differs significantly from the behavior at low voltages/currents. The shape of this noise characteristic results from the properties of the tested photodiode. The results of studies described in the literature show that the total 1/f noise power spectral density is a complex function of a few noise currents. In [27], this function is presented by the model formula:
where Ish, Ig−r, Idiff and Itun are the shunt, generation-recombination, diffusion and tunneling dark current components, respectively, with the corresponding noise coefficients αsh, αg−r, αdiff and αtun. Depending on the photodiode construction and its operating point (temperature and bias voltage), each of the above noise sources will affect the total noise differently (i.e., the noise coefficients will take different values). Based on the results described in [26,27,28], the inset region in Figure 9 shows that the diffusion and g − r current components predominate in the detector’s dark current in the low- and mid-voltage ranges (A,B). Meanwhile, at high voltage bias (C), the tunneling current components predominates. However, there is no correlation between the total dark current and the measured 1/f noise PSD. This suggests that there are some current components other than diffusion that could have a higher influence on 1/f noise at different levels of bias voltage.
In the low-voltage range (A), the quadrature dependence is caused by the ohmic-like behavior of the tested device, and measured noise can be regarded as resistance fluctuation noise from detector shunt resistance.
Along with increasing the voltage (B), the 1/f noise components come from shunt, g − r, and tunneling currents. At the highest voltages (C), the overall noise is dominated by tunneling current.
5. Conclusions
This paper presented the analysis, construction, and verification of an ultra-low-noise transimpedance amplifier. It was dedicated to investigating low-frequency noise in photodetectors, which are characterized by relatively low resistance, on the order of or below 1 kΩ. As discussed in this paper, a low-impedance device connected to the input of a transimpedance amplifier results in a large amount of background noise due to the equivalent input voltage noise source represented by the operational amplifier used in typical shunt–shunt feedback configurations. This problem was addressed and solved by designing a transimpedance amplifier based on a discrete device input stage-based operational amplifier, characterized by very low input voltage noise, on the order of 4 nV/√Hz, 2 nV/√Hz, and 0.9 nV/√Hz at 1 Hz, 10 Hz, and 1 kHz, respectively. The results were obtained by resorting to a low-noise IF3602 differential pair n-channel JFET transistor as a discrete input stage for the operational amplifier, which was used in a shunt–shunt configuration, in order to obtain a transresistance stage. The resulting background noise was investigated and verified using known-value resistors as DUTs. After preliminary characterization, the amplifier was used to study the current noise in a low-resistance InAsSb barrier detector, demonstrating that direct and reliable measurement of the current noise in low-impedance devices is indeed possible with the instrumentation designed and tested here.
Author Contributions
Conceptualization, K.A., C.C. and G.S.; methodology, K.A. and G.S.; software, K.A.; validation, C.C., J.M., Z.B. and G.S.; formal analysis, J.M., Z.B., C.C. and G.S.; investigation, K.A.; data curation, K.A.; writing—original draft preparation, K.A.; writing—review and editing, G.S., J.M., C.C. and Z.B.; supervision, C.C. and Z.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by Military University of Technology grant no. UGB-22-871.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vandamme, L.K.J. Noise as a diagnostic tool for quality and reliability of electronic devices. IEEE Trans. Electron Devices 1994, 41, 2176–2187. [Google Scholar] [CrossRef]
- Tansel, T.; Kutluer, K.; Salihoglu, Ö.; Aydinli, A.; Aslan, B.; Arikan, B.; Kilinc, M.C.; Ergun, Y.; Serincan, U.; Turan, R. Effect of the passivation layer on the noise characteristics of mid-wave-infrared InAs/GaSb superlattice photodiodes. IEEE Photon. Technol. Lett. 2012, 24, 790–792. [Google Scholar] [CrossRef]
- Ciura, L.; Kolek, A.; Gomółka, E.; Murawski, K.; Kopytko, M.; Martyniuk, P.; Rogalski, A. Trap Parameters in the Infrared InAsSb Absorber Found by Capacitance and Noise Measurements. Semicond. Sci. Technol. 2019, 34, 105017. [Google Scholar] [CrossRef]
- Cowan, V.M.; Morath, C.P.; Myers, S.; Gautam, N.; Krishna, S. Low temperature noise measurement of an InAs/GaSb-based nBn MWIR detector. Infrared Technol. Appl. 2011, 8012, 801210. [Google Scholar]
- Gopal, V.; Gupta, S. Contribution of dislocations to 1/f noise in mercury cadmium telluride infrared photovoltaic detectors. Infrared Phys. Technol. 2006, 48, 59–66. [Google Scholar] [CrossRef]
- Bielecki, Z.; Achtenberg, K.; Kopytko, M.; Mikołajczyk, J.; Wojtas, J.; Rogalski, A. Review of photodetectors characterization methods. Bull. Pol. Acad. Sci. Tech. Sci. 2022, 70, e140534. [Google Scholar] [CrossRef]
- Rogalski, A.; Bielecki, Z. Detection of Optical Signals; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Abingdon, UK, 2022; ISBN 9781032059488. [Google Scholar]
- Kolek, A.; Ciura, L.; Jasik, A.; Kaniewski, J.B.; Sankowska, I.; Czuba, K.; Jurenczyk, J. Noise and Detectivity of InAs/GaSb T2SL 4.5 Um IR Detectors. SPIE Proc. 2017, 10404, 1040402. [Google Scholar] [CrossRef]
- Koçer, H.; Demir, M.; Saraydemir, Ş.; Durna, Y.; Torunoğlu, O. Numerical simulation of noise and detectivity of Infrared sensor for high performance thermal image processing applications. In Proceedings of the 2012 20th Signal Processing and Communications Applications Conference (SIU), Mugla, Turkey, 18–20 April 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Wu, Z.; Li, N.; Eedugurala, N.; Azoulay, J.D.; Leem, D.-S.; Ng, T.N. Noise and detectivity limits in organic shortwave infrared photodiodes with low disorder. NPJ Flex. Electron. 2020, 4, 6. [Google Scholar] [CrossRef]
- Ninness, B. Estimation of 1/f noise. IEEE Trans. Inf. Theory 1998, 44, 32–46. [Google Scholar] [CrossRef]
- Czuba, K.; Ciura, Ł.; Sankowska, I.; Papis-Polakowska, E.; Jasik, A. The Role of Noise in Specific Detectivity of InAs/GaSb Superlattice MWIR Bariodes. Sensors 2021, 21, 7005. [Google Scholar] [CrossRef]
- Ciura, Ł.; Kolek, A.; Jureńczyk, J.; Czuba, K.; Jasik, A.; Sankowska, I.; Kaniewski, J. 1/f Noise Modeling of InAs/GaSb Superlattice Mid-Wavelength Infrared Detectors. Opt. Quantum Electron. 2018, 50, 36. [Google Scholar] [CrossRef]
- Scandurra, G.; Ciofi, C.; Smulko, J.; Wen, H. A review of design approaches for the implementation of low-frequency noise measurement systems. Rev. Sci. Instrum. 2022, 93, 111101. [Google Scholar] [CrossRef] [PubMed]
- Ziel, A.V.D. Noise in Solid State Devices and Circuits; Wiley-Interscience: New York, NY, USA, 1986. [Google Scholar]
- Ziel, A.V.D. Noise in Measurements; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1976. [Google Scholar]
- Ferrari, G.; Sampietro, M. Wide bandwidth transimpedance amplifier for extremely sensitive continuous measurements. Rev. Sci. Instrum. 2007, 78, 094703. [Google Scholar] [CrossRef]
- Su, B.; Yang, X.; Cui, H.; Jones, D.R. How to maximize the bandwidth without increasing the noise in op-amp-based transimpedance amplifiers using positive feedback. Rev. Sci. Instrum. 2022, 93, 044702. [Google Scholar] [CrossRef] [PubMed]
- Michalczewski, K.; Martyniuk, P.; Kubiszyn, L.; Wu, C.-H.; Wu, Y.-R.; Jurenczyk, J.; Rogalski, A.; Piotrowski, J. Demonstration of the very long wavelength infrared type-II superlattice InAs/InAsSb GaAs immersed photodetector operating at thermoelectric cooling. IEEE Electron Device Lett. 2019, 40, 1396–1398. [Google Scholar] [CrossRef]
- Ferrari, G.; Gozzini, F.; Molari, A.; Sampietro, M. Transimpedance Amplifier for High Sensitivity Current Measurements on Nanodevices. IEEE J. Solid-State Circuits 2009, 44, 1609–1616. [Google Scholar] [CrossRef]
- Cretu, V.F.; Kehl, F.; Metz, B.C.; Willis, P.A. Open-Source Lab Hardware: Low Noise Adjustable Two-Stage Gain Transimpedance Amplifier with DC Offset for Low-Light Detection. HardwareX 2021, 10, e00233. [Google Scholar] [CrossRef] [PubMed]
- Scandurra, G.; Giusi, G.; Ciofi, C. A very low noise, high accuracy, programmable voltage source for low frequency noise measurements. Rev. Sci. Instrum. 2014, 85, 044702. [Google Scholar] [CrossRef]
- Scandurra, G.; Cannatà, G.; Giusi, G.; Ciofi, C. A new approach to DC removal in high gain, low noise voltage amplifiers. In Proceedings of the 2017 International Conference on Noise and Fluctuations (ICNF), Vilnius, Lithuania, 20–23 June 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Martyniuk, P.; Rogalski, A. Performance limits of the mid-wave InAsSb/AlAsSb nBn HOT infrared detector. Opt. Quant Electron. 2014, 46, 581–591. [Google Scholar] [CrossRef]
- Gomółka, E.; Kopytko, M.; Markowska, O.; Michalczewski, K.; Kubiszyn, Ł. Electrical and Optical Performance of Midwave Infrared InAsSb Heterostructure Detectors. Opt. Eng. 2018, 57, 1. [Google Scholar] [CrossRef]
- Ciura, Ł.; Kopytko, M.; Martyniuk, P. Low-Frequency Noise Limitations of InAsSb-, and HgCdTe-Based Infrared Detectors. Sens. Actuators A Phys. 2020, 305, 111908. [Google Scholar] [CrossRef]
- Ciura, Ł.; Kolek, A.; Jureńczyk, J.; Czuba, K.; Jasik, A.; Sankowska, I.; Papis-Polakowska, E.; Kaniewski, J. Noise-Current Correlations in InAs/GaSb Type-II Superlattice Midwavelength Infrared Detectors. IEEE Trans. Electron Devices 2016, 63, 4907–4912. [Google Scholar] [CrossRef]
- D’souza, A.I.; Stapelbroek, M.G.; Dolan, P.N.; Wijewarnasuriya, P.S.; DeWames, R.E.; Smith, D.S.; Ehlert, J.C. 1/f noise in large-area Hg1−xCdxTe photodiodes. J. Electron. Mater. 2003, 32, 633–638. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).