Decision Support Model for Allocating Maintenance Budgets for Bridges

Abstract

This paper introduces a newly developed decision support model for allocating a budget for bridge maintenance. The model is built based on capturing the experts’ knowledge for the prioritization of criteria for selecting a bridge maintenance plan. A literature review and interviews with a group of nine local experts were carried out to identify the criteria for bridge prioritization for maintenance. A questionnaire survey was then designed and administered, utilizing multi-criteria decision-making techniques through face-to-face meetings with local bridge maintenance managers to determine the weights of the identified criteria and develop the utility curves for each criterion. The developed model consists of four major modules: (1) bridge ranking module; (2) prioritization module of bridge structural elements; (3) optimization-based simulation module; and (4) the outputs module. The model was validated in a hypothetical network of four bridges. The validation reveals that the model can assist bridge maintenance managers in setting a bridge maintenance plan, with a high level of confidence using efficient frontier analysis technique. Utilizing frontier analysis enables comparisons of mean costs of different bridge maintenance plans against different levels of risk to enable decision-makers to make informed decisions. The result of this study indicated that bridge structural condition was the most important criterion amongst all the criteria influencing the decision of bridge prioritization for maintenance, followed by traffic and bridge location. Moreover, bridge deck and parapet, followed by bearing pads, were found to be the most important of the bridge’s structural elements.

1. Introduction

Bridges constitute a critical component in transportation networks. They connect intersections while reducing traffic congestion [1]. Due to the imposed traffic load and the presence of environmental criteria, which gradually contribute to bridge degradation, the structure of bridges deteriorates, resulting in worsened conditions [2]. Bridge managers need to carry out maintenance of those bridges periodically to keep their structures in an acceptable condition, and to operate at an acceptable level of service. Decision-makers usually face financial difficulties due to limited budgets to maintain operating existing bridges, along with other impediments to the decision-making process.

The distribution of the limited budget among bridges in the network under consideration is a challenging task for maintenance managers since there are several factors that must be taken into consideration other than the physical conditions, which will add to the objective nature of this process. In the presence of limited budget constraints, some bridges must wait until the next budget. The more severe the condition of the component of a bridge, the more it will be prioritized. It must be taken into consideration that the estimated cost for maintenance may vary during the maintenance works, which may result in deferring more less-prioritized bridges components until next year. The difficulty is attributed to determining which bridge should be maintained and which bridge can be undertaken according to one of the future maintenance plans. In the current practice, the main criterion in determining the bridge priority for maintenance and budgeting is the overall condition of the bridge [3]. Thus, condition assessment of bridges is a key task in aiding maintenance activities by providing a concise description of the current state of the bridge in terms of the internal and external damages, which might impact upon the safety and the performance of the structure [4]. In addition to condition assessment, other criteria should be considered in determining the bridge priority for maintenance and budgeting, such as taking into consideration the importance of the traffic of this bridge, the age of the bridge, and many other factors, which will be highlighted and discussed in the literature section. For example, a bridge may have an average condition assessment score but be located in a very important intersection and/or with high traffic volume that requires maintenance, and vice versa.

A number of maintenance managers at Saudi Arabia’s Ministry of Municipal, Rural Affairs, and Housing, Riyadh, Saudi Arabia were interviewed to examine the current practice of bridge maintenance and prioritization. The interviews concluded that the main limitations of the current practice are in an agreement with the findings of Rashidi and Gibson [5] and can be summarized as follows:

• Many bridge rating systems depend on subjective data, which reduce the accuracy of the condition assessment;
• Neglecting the actual deterioration of the bridges can significantly shorten their lifespan, hence increase their future repair costs.

Furthermore, the current bridges’ maintenance systems encounter uncertainties associated with the estimated maintenance cost, which results from the selected methodology of the estimation and the available information at the time of preparing the estimate, which makes the selection of bridge maintenance plan uncertain, unrealistic, and risky in terms of cost and schedule. Moreover, the condition assessment, which is mainly based on visual inspections, is greatly influenced by the experience of the bridge inspectors or engineers, accessibility to the structural elements, and the hidden existing defects covered by recent repairs [6].

This paper introduces a new model for bridges’ selection for maintenance, considering other criteria in addition to condition assessment. The introduced model aims to assist bridge owners in the selection process while considering the uncertainty associated with cost estimates and the risk of exceeding the limited budget in selecting the maintenance plan. The model also considers the local perspective and Saudi regulations on bridge maintenance to examine and develop picturization criteria suitable for Saudi practice.

The following sections present the content of the paper, and they are organized as follows. Applications of AHP and MAUT in construction, followed by a comprehensive literature review of previous studies, including the identification of bridge prioritization criteria at a network level. Research methodology is then presented, and the proposed model and its main components are then explained in detail. The paper ends with an example project for the purpose of validation.

2. Literature Review

Bridges constitute a critical component in the transportation networks that need to be maintained periodically to keep their structures in an acceptable condition, and to operate at an acceptable level of service. Maintenance managers of bridges encounter difficulties in determining which bridges to be maintained in light of the availability of limited maintenance budgets. These limited maintenance budgets would also be distributed to maintain the operations of existing bridges. In the traditional bridge management system (BMS), the required information regarding the condition assessment, maintenance activities, and inspection reports are stored in the BMS database. Such information is utilized to assist in the prioritization of bridge maintenance and selecting the optimal strategy plan [7]. The prioritization of bridges for maintenance also involves setting evaluation criteria to rate the bridges to obtain a total score for each bridge in the network under consideration. Traditionally, the bridge maintenance system depends on the condition assessment as the main criterion for bridge prioritization. It should be noted that adopting condition assessment as the main criterion for prioritization is inaccurate and other criteria should be considered. This includes the criteria that are related to the overall network, such as the location of the bridge, traffic volume, and the decision-maker’s assessment. The bridges with higher scores are more eligible for maintenance compared to other bridges [2]. Although such a method can provide acceptable results, the subjectivity and the uncertainties associated with the rating scale and maintenance costs make these methods impractical.

2.1. Applications of AHP and MAUT in Construction

The Analytic Hierarchy Process (AHP) is a quantitative approach which provides a rational model for decision-making through quantifying the criteria of the needed decision, as well as its alternative options. The decision maker would be comparing the importance of each criterion, two at a time, through conducting pair-wise comparisons [8]. The Multiple Attribute Utility Theory (MAUT) is utilized to guide the decision-making process when the selection is constrained to a few alternatives. The evaluation of each alternative is determined by adding all the weight values of the alternatives regarding each considered attribute [9].

The combination of two techniques, namely the AHP and the MAUT, is a method to overcome any shortcomings of any multi-criteria decision-making technique. AHP and MAUT have been used extensively in construction management applications (e.g., [10,11,12,13,14,15]). In bridge management systems, the goal of AHP is to determine the weights of the bridge prioritization criteria, while MAUT aims to evaluate different bridge maintenance plans to determine the utility scores of criteria for all alternatives (bridges).

Alshamrani et al. [12] proposed a model for lighting system selection in residential buildings, in Saudi Arabia, utilizing AHP and MAUT. The model utilizes the AHP technique for establishing weights for four selection criteria for lighting systems through the development and distribution of a questionnaire survey. The multi-attribute utility theory was then utilized to assess the performance of the lighting system alternatives against the selection criteria through the development of utility scores. The developed model was implemented and resulted in recommending the most optimal alternative for lighting systems in residential buildings.

Hamida and Alshibani [13] proposed a model for evaluating and selecting curtain wall systems in office buildings in Saudi Arabia. The study commenced with a literature review and experts’ interviews to identify the commonly utilized curtain wall systems in office building projects. A questionnaire was administered to determine the weight of the criteria using the AHP technique. The model was implemented based on integrating the weight of all assessed criteria and their utility scores.

El-Tourkey et al. [14] developed a computer-based system for mobile crane selection in Saudi Arabia. The developed system integrates the experts’ experience with AHP and MAUT in the selection procedure. The model comprised the utilization of AHP technique to assess the importance of mobile crane’s selection criteria, and the application of multi-attribute utility theory to determine the utility scores for the crane selection criteria, for all crane alternatives. Upon the implementation of the model, the study concluded that integration of the AHP and the MAUT techniques served to recommend the selection of the most technologically appropriate mobile crane alternative.

Abdullah and Alshibani [15] proposed a framework for the selection of a private partner in PPP project delivery systems for housing projects in Saudi Arabia. The framework integrates AHP and MAUT for measuring the importance of the selection criteria of private partners in Public Private Partnership.

2.2. Previous Studies

Bukhsh et al. [16] applied the MAUT for bridge maintenance planning in the Netherlands road network, through the case study. The considered performance indices are bridge condition index, cost to the owner, users’ experienced delay cost, and environmental cost. The study has established a single utility function for each of these indicators. Each of these indicators has a given weight out of 100. For each bridge these attributes are given a score, then the score is multiplied by the weight of the same indicator.

Rogulj et al. [17] utilized the AHP concept to compare between the criteria to evaluate the historical pedestrian bridges in Croatia. Following that, evidential reasoning was used to assess bridges against each criterion. After that, bridges were ordered using the TOPSIS technique. The criteria identified by them are bridge condition, the complexity of bridge rehabilitation, bridge load, last rehabilitation, rehabilitation cost, cost of waste material disposal, required time for rehabilitation, required time for document preparation, preservation of cultural heritage, tourist attraction, and historical importance.

Wakchaure and Jha [18] utilized the AHP to determine the weight of the structural components and subcomponents of bridges. The study utilized a five-point scale to assess the condition of each structural component of the bridge under consideration. The study then determined the overall bridge health index using the AHP weights and condition states for each component of the bridge. As the bridge health index approaches 100, it means that the bridge is in good health and requires no maintenance.

Rashid and Herabat [19] developed a prioritization model for the maintenance operations of road facilities. The MAUT was also used to assist in the decision-making process for the maintenance of road facilities. The prioritization attributes for bridges were identified along with other road elements such as roadside elements and traffic control devices. The prioritization attributes were then weighted with the help of local experts in Thailand. The bridge with a higher utility value is more prioritized. They identified six objectives and a total of fourteen performance indicators.

Chassiakos et al. [20] developed a knowledge-based system for bridge maintenance. The system has three functions—setting maintenance priority, evaluation of feasible treatment, and maintenance planning. The priority is determined by ranking several parameters, including type of defect, traffic load, environmental conditions, age of the bridge, types of foundation, and superstructure. Each of these factors has sub-factors and corresponding weights. From these weights the priority index is determined using model score equation. Following that, each possible treatment is evaluated by lifetime to cost ratio. Finally, the maintenance plan is evaluated by the cost and effectiveness of the selected treatment and the number of cases treated using model equations developed by the authors.

Rogulj et al. [21] developed a systematic methodology for condition assessment for historical road bridges based on the knowledge approach using fuzzy logic and sets of a-cuts. They divided each bridge into three components—substructure, superstructure, and equipment. These components were further divided into elements. After that, these elements were evaluated by experts and, using the fuzzy theory, each component condition rating was defined. AHP was used for the comparisons of components to find the relative importance of each component. The overall bridge condition rating is found by summing the multiplication of the components ratings by their relative importance defined from the AHP. The resulted value is called Historic Road Bridge Condition Assessment Index (HRBCAI).

Zhang and Wang [22] proposed a decision model that assists in determining maintenance prioritization for a set of bridges with constrained budget. The study utilized several techniques and indices to identify certain parameters to determine the performance of the network maintenance cost.

Abu Dabous [23] developed a decision support methodology for the rehabilitation management of bridge decks. In the context of the methodology, the author presented a means to rank bridges using MAUT. Abu Dabous and Alkass [24], in continuation of the previously developed model of Abu Dabous [23], developed a new model based on the owner ranks of the rehabilitation strategies. The model consists of a combination of strategies for each of the bridges creating a work program.

Rashidi et al. [25,26] developed a BMS known as Concrete Bridge Remediation Decision Support System (CBR-DSS). The developed BMS combines AHP and MAUT, and the developed system consists of two phases, namely ranking and remediation planning. Frangopol and Liu [27] developed a multi-objective maintenance optimization tool for bridges’ network, utilizing stochastic dynamic programming, which consists of two phases. The first phase is to find the optimal maintenance plan for an individual bridge, and the second phase is allocating the limited budget rationally to as many bridges as possible using MAUT and the reliability factor of each bridge.

2.3. Identification of Prioritization Criteria at Network Level

A comprehensive literature review was conducted for several studies in different geographic locations to investigate the bridges prioritization criteria for maintenance. In a comprehensive study, Amini et al. [28] gathered the most common criteria for bridges’ prioritization from several research projects conducted in different geographic locations such as the UK [2], Australia [29], USA [30], and Germany [31]. The authors categorized the criteria into five groups.

Table 1. The identified prioritization criteria extracted from the literature review.

References	Location	Factors Considered in the Study						Factors Not Considered in This Study
		Condition	Age	Location	Previous Maintenance	Scheduled Maintenance	Traffic Condition	Route	Material Vulnerability	Environmental	Inspection Quality	Load-Bearing Capacity	Vertical Clearance	Width	Bridge Barrier	Drainage	Socioeconomic	Political	Historical	Strategic Importance	Hydraulic Vulnerability	Seismic Risk	Remaining Service Life	Agency Cost	Vehicle Operating Cost	Travel Time Savings	Visibility Distance	Savings in Accident Costs	Danger Due to Bridge Collapse	Maintenance Division facilities	Budget for Maintenance Division	Bridge Structure	Bridge Aesthetics	Construction Quality	Passing Convenience	Weather Information	Disruption of Public Services	Deterioration Prediction	Other Factors *
[2]	UK	✔		✔				✔
[29]	Australia	✔	✔					✔	✔	✔	✔	✔	✔	✔	✔	✔	✔	✔	✔
[11]	Chile	✔																		✔	✔	✔
[19]	Thailand	✔					✔					✔		✔									✔	✔	✔	✔	✔	✔
[32]	Vietnam			✔			✔					✔
[31]	Belgium				✔							✔																	✔
[31]	France	✔						✔										✔												✔	✔
[31]	Slovenia	✔					✔	✔
[20]	Greece	✔	✔				✔	✔																								✔
[33]	Netherland						✔					✔																					✔	✔	✔
[31]	BRIME	✔	✔				✔												✔						✔								✔	✔				✔
[34]	Canada						✔	✔					✔																			✔					✔
[30]	USA						✔																									✔				✔
[35]	USA	✔	✔				✔
[36]	Iran				✔		✔	✔		✔		✔	✔			✔		✔				✔		✔						✔		✔	✔	✔					✔
Local Expert	KSA	✔	✔	✔	✔	✔	✔

* Other factors: Filling of expansion joints, oil and chemical material pouring from vehicles on the bridge, use sand or salt to prevent vehicles from sliding, bump creation because of pavement destruction, vibrations affect the bridge, fatigue, volume of traffic passing under the bridge and bridge design and construction code.

presents the identified criteria from the literature.

Since the identified criteria by the previous work may not be applied in every geographic location, interviews with local experts in the municipal bridges’ maintenance field were conducted to determine the criteria that affect the priority of bridges in the area of study. Interviews were conducted with nine local experts in bridge maintenance to review the identified criteria from the literature and to decide on its suitability to Saudi Arabia. Interviewing nine experts is satisfactory to obtain reliable feedback, and this is in agreement with previous research utilized sample sizes from four to nine for pairwise comparison-based questionnaire. Out of the nine experts were five owners’ representatives who worked as consultants, three project managers, and one bridge engineer, all with over 10 years of experience. The criteria proposed by these experts are the condition assessment, bridge age, bridge location, previous maintenance records, scheduled maintenance, and traffic volume.

Table 2. Final list of identified prioritization criteria selected by the experts.

SN	Criteria	References
1	Condition Factor	[2,19,20,29,31,35,37], Local Expert
2	Age Factor	[20,29,31,35], Local Expert
3	Location Factor	[2,32], Local Expert
4	Previous maintenance factor	[31,36], Local Expert
5	Scheduled maintenance factor	This factor is added by a Local Expert in case the scheduled maintenance is scheduled to be carried out very soon. In this case, the bridge will be more prioritized to be maintained
6	Traffic condition factor	[19,20,30,31,32,33,34,35,36], Local Expert

presents criteria recommended by experts and considered in this study.

2.4. Research Gaps

The shortcomings of the previous models, individually or collectively, can be summarized as follows:

• The available maintenance budget is allocated only to those bridges with the highest rank, even if all the structural elements of the selected bridges do not require maintenance, since the bridge is considered as one unit. Thus, very limited bridges will be maintained.
• The budget is allocated on the basis of the maintenance program/plan score, which is a combination of maintenance strategies considered for each bridge (e.g., [23,24,26]).
• Other important criteria such as the location of bridge are not considered. For example, a bridge located in a critical intersection could be selected for maintenance, while another bridge with a moderate condition assessment may not be selected.
• The review of previous reported models shows a lack of a relationship between the considerations of prioritizing the bridges in the network level and the main goal of the study which is allocating the budget for a set of bridges.
• The previously reported models require many iterative comparisons between the maintenance strategies as input data (e.g., [16,23,24,25]).
• Some models are simple and consider only one criterion, namely the condition assessment, as in the model reported by Wakchaure and Jha [18].
• Some approaches are not able to handle large networks.
• The uncertainty inherent in the maintenance cost and condition assessment is not considered, despite the fact that the condition assessment is one of the most common criteria, as it depends on the subjective evaluation of the bridge engineer.
• The outputs of the previously developed models are deterministic and do not consider the uncertainties associated with maintenance cost.
• The previously developed models do not provide either the optimal solution or the risk associated with the selected optimal solution.

This paper introduces a decision support model for bridge maintenance which aims to overcome the shortcomings of the previously reported models or systems. The developed model takes into consideration two main aspects: (1) uncertainties associated with the estimated maintenance cost and (2) optimization of the budget allocation while taking into account the risk using frontier analysis technique. This model also provides the most attritive solution in which the decision-maker will be more assured that the selected maintenance plan (a set of structural elements to be maintained) will be achieved with a certain level of confidence.

3. Methodology

The methodology followed in this research to accomplish the above-mentioned objectives can be summarized as follows:

Step 1: Involves two stages: (1) conducting a comprehensive literature review to identify the criteria of bridge prioritization for maintenance and (2) investigating the current practices of Bridge Management Systems (BMS) in Saudi Arabia to highlight its advantages and limitations.

Step 2: Reviewing the identified criteria with local experts in Saudi Arabia to short-list those criteria to suit the requirements in Saudi Arabia.

Step 3: Designing and developing AHP and MAUT questionnaire to be utilized to obtain feedback from the target professionals for ranking the bridge prioritization and developing utilities curves.

Step 4: Sharing the designed questionnaire with local experts through the pilot study to evaluate the questionnaire prior to obtaining their feedback.

Step 5: Collecting and analyzing the collected data for assessing the bridge prioritization and developing the criteria utilities curves.

Refer to Section 4.2.1, 4.2.2, and 4.3 in the proposed model section for the detailed steps of making the questionnaire and data collection and sample calculation of the results for both AHP and MAUT utilities curves. This covers steps 3–5.

Step 6: Developing the decision support model for allocating a maintenance budget for bridge maintenance. Refer to Section 4.4 Computation Process for detailed steps of the model and its workflow.

Step 7: Validating the developed model in one of the projects of Dammam municipality and share its outcome with local experts looking for their feedback or any additional information which might be helpful for improving the model. Refer to Section 5 example project for detailed calculations of an assumed hypothetical network of four bridges to test the model workflow and output.

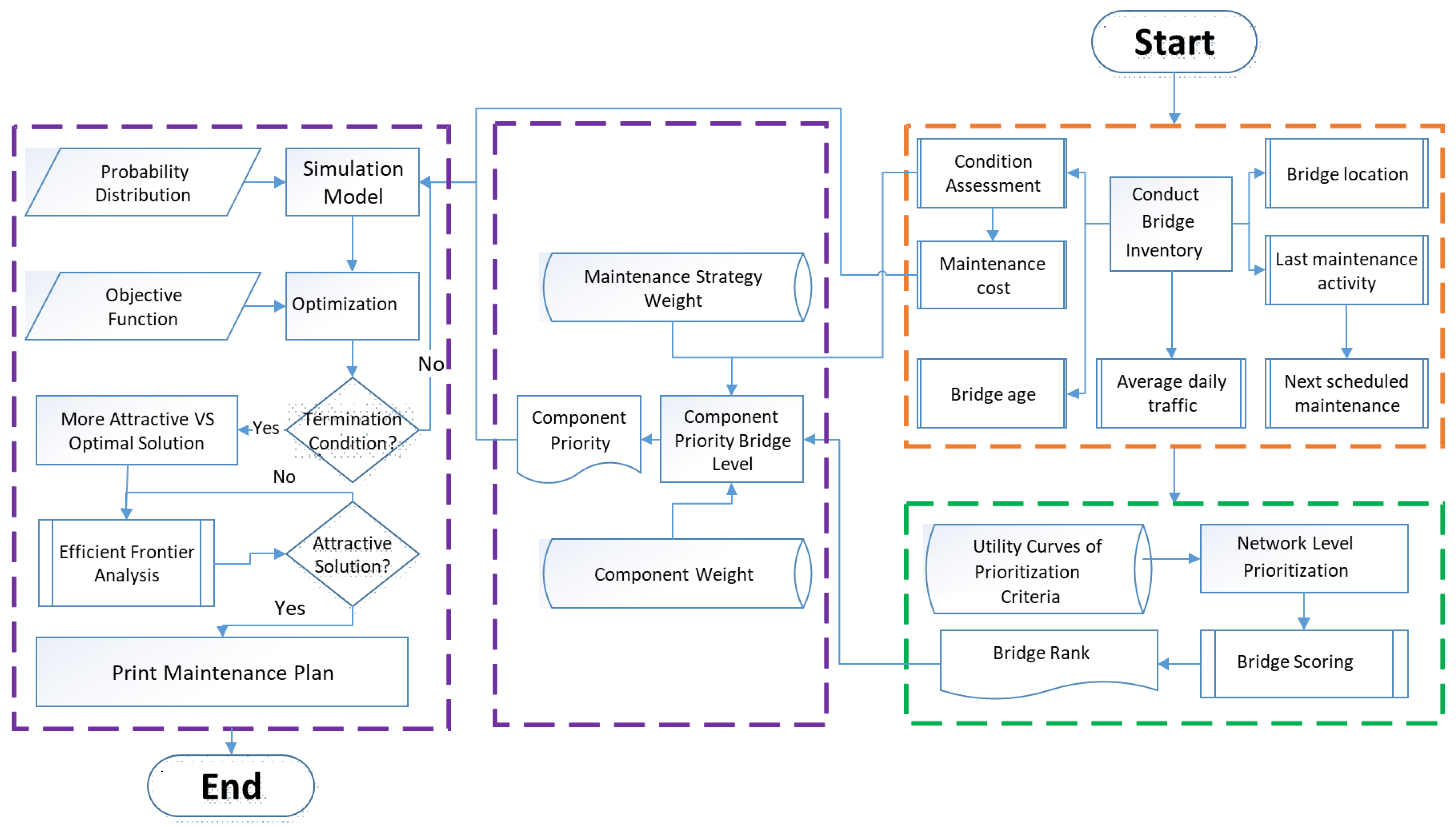
4. Proposed Model

4.1. Model Description

As illustrated in Figure 1, the developed decision support model consists of four major modules: (1) bridge ranking module to (a) identifying prioritization criteria and (b) weighting the identified prioritization criteria and utilities curves using pairwise comparison and MAUT; (2) module for prioritization of bridge structural elements at a bridge level with the assistance of existing BMS; (3) optimization-based simulation module in which the decision variables and objective function are defined to select the optimal maintenance strategy plan; and (4) the outputs module in which the most feasible maintenance plan is recommended.

The developed model incorporates the experience of local experts to produce an optimal work program (maintenance plan). The optimization-based simulation module aims to consider uncertainties associated with maintenance cost, maximizing the number of bridges to be maintained while minimizing the total maintenance cost. The output of the model consists of:

• Ranking each bridge in the target network by prioritizing the bridges at the network level through the prioritization of the identified criteria, along with the corresponding utility curves obtained from interviewing nine local experts and the bridge data from the BMS as indicated earlier.
• Identifying and obtaining the weights of the structural elements from the questionnaire using the concept of pairwise comparison of AHP.
• Providing the overall priority along with the estimated maintenance cost of each structural element of each bridge in the target network.

The output is then used as an input to risk analysis software in which the user:

• Defines the overall priority along with the estimated maintenance cost of each structural element.
• Recommends the near-optimum solution for the maintenance plan which is presented to the owner/engineer.

4.2. Pilot Study and Development of the Questionnaire Survey

The aim of the pilot study is to test the clarity of all questions. As mentioned earlier, the pilot study was conducted through face-to-face meetings with four local professionals to finalize the questionnaire survey before forwarding it to the targeted experts. It also includes reviewing the identified prioritization criteria from the literature by adding and removing some criteria. The final set of prioritization criteria after the pilot study are presented in Table 2.

The developed questionnaire adopted the use of multi-criteria decision-making techniques via face-to-face meetings with nine local experts. The developed questionnaire was structured to include three parts. The first part comprises the demographic information of participants (experts), such as the education level, years of professional experience, and organization size. The second part includes several matrices of pairwise comparison to facilitate the assessment of the criteria against each other to find weights of criteria through the AHP technique. Finally, the concluding part of the questionnaire enables the experts to determine the scores of each identified criterion to build the utility curves.

4.2.1. Weighting the Prioritization Criteria

The pairwise comparison has been applied to determine the weights of the identified prioritization criteria for bridge maintenance at the network level. The criteria matrix was established to express the importance of the criteria and to determine the priorities according to expert judgement. The scale introduced by Saaty [38] was adopted to conduct pairwise comparisons and establish the importance of the criteria at the network level, and at the bridge level. The value of 1 on the scale indicates the equity of importance of the compared criteria. The value of 9 means that the chosen criterion has the maximum importance level, upon comparison to another compared criterion [38]. Once the pairwise comparison matrix is established for the prioritization criteria, the local expert must answer two questions. The first question is which criterion is more important when prioritizing bridges for maintenance. The second question is what the intensity of that importance on a scale ranging from 1 to 9 (as explained above). Comparisons are made between every prioritization criterion on a scale ranging from 1 to 9, as follows:

• The numeric value of 1 is used when the importance of the two compared criteria is equal based on a local expert’s point of view and experience.
• The numeric value of 9 is used when the importance of the criteria in the row is extremely more important than the other criteria being compared with in the column.
• The numeric values of 3, 5, and 7 are used to describe the importance of the criteria, based on the expert’s perceived level of importance for the criterion under consideration.
• Reciprocation of the intensity is used when the criterion in the column is more important than the criteria in the row.

An Excel sheet was used to analyze the pairwise comparison data to calculate the relative weights (Eigen vector or weights of the criteria) and the consistency ratios (test of judgments of all pairwise comparisons) of all the considered matrices. Due to the limited number of words in this article, a detailed description of the consistency ratios calculation is not presented.

Table 3. Sample of pairwise comparison of R1 (expert 1).

R1		Condition Assessment	Bridge Age	Bridge Location	History of Maintenance	Scheduled Maintenance	Traffic Volume
Condition assessment		1.00	5.00	2.00	4.00	3.00	1.00
Bridge age		0.20	1.00	0.50	0.50	0.33	0.25
Bridge location		0.50	2.00	1.00	2.00	2.00	1.00
History of Maintenance		0.25	2.00	0.50	1.00	0.33	0.25
Scheduled Maintenance		0.33	3.00	0.50	3.00	1.00	0.50
Traffic volume		1.00	4.00	1.00	4.00	2.00	1.00
		3.28	17.00	5.50	14.50	8.67	4.00
Normalization
Condition assessment	Bridge age	Bridge location	History of Maintenance	Scheduled Maintenance	Traffic volume	Row Average	Consistency
0.305	0.294	0.364	0.276	0.346	0.250	0.306	6.243
0.061	0.059	0.091	0.034	0.038	0.063	0.058	6.117
0.152	0.118	0.182	0.138	0.231	0.250	0.178	6.259
0.076	0.118	0.091	0.069	0.038	0.063	0.076	6.120
0.102	0.176	0.091	0.207	0.115	0.125	0.136	6.254
0.305	0.235	0.182	0.276	0.231	0.250	0.246	6.236
1.000	1.000	1.000	1.000	1.000	1.000	1.000	37.228
# of Comparisons		Average Consistency	CI	RI	Consistency (CI/RI)	Consistent? Less than 0.1
6		6.204664	0.040933	1.24	0.03301	Yes

shows the pairwise comparisons conducted by response 1 (R1). The Eigen vector or weights of the criteria are calculated by normalizing the pairwise comparison matrix and averaging each row to find the weight of each prioritization criteria.

Table 4. Criteria weights.

	Condition Assessment	Bridge Age	Bridge Location	History of Maintenance	Scheduled Maintenance	Traffic Volume	Total
R1	0.3057	0.0577	0.1784	0.0758	0.136	0.2464	1
R2	0.1509	0.0831	0.272	0.1219	0.1951	0.1771	1
R3	0.1809	0.0672	0.2088	0.0997	0.1425	0.301	1
R4	0.2519	0.182	0.2243	0.0708	0.0935	0.1776	1
R5	0.1758	0.1074	0.2622	0.1993	0.0808	0.1744	1
R6	0.235	0.1738	0.0797	0.1729	0.1401	0.1985	1
R7	0.2813	0.102	0.151	0.0803	0.0973	0.2881	1
R8	0.3614	0.2217	0.0607	0.1229	0.0932	0.1401	1
R9	0.3896	0.1452	0.0929	0.068	0.0938	0.2105	1
Median	0.2519	0.1074	0.1784	0.0997	0.0973	0.1985	0.9331
Mean	0.2592	0.1267	0.17	0.1124	0.1192	0.2126	1
Mode	0.2519	0.1074	0.1784	0.0997	0.0973	0.1985	0.9331
SD	0.0833	0.0568	0.0789	0.047	0.037	0.0548	0.3579
VAR	0.0062	0.0029	0.0055	0.002	0.0012	0.0027	0.1281
∑VAR				0.0204
Cα				0.9456
Weight	25.9%	21.3%	17.0%	12.7%	11.9%	11.2%	100%

shows the criteria, along with the weights for each, based on the pairwise comparison data collected from nine experts. All nine responses showed a consistent comparison, and the consistency check was made according to the methodology developed by Saaty [38] to ensure that the pairwise comparisons are consistent. As presented in Table 4, the bridge condition criterion is the most important criterion in prioritizing bridges for maintenance, followed by traffic condition criterion.

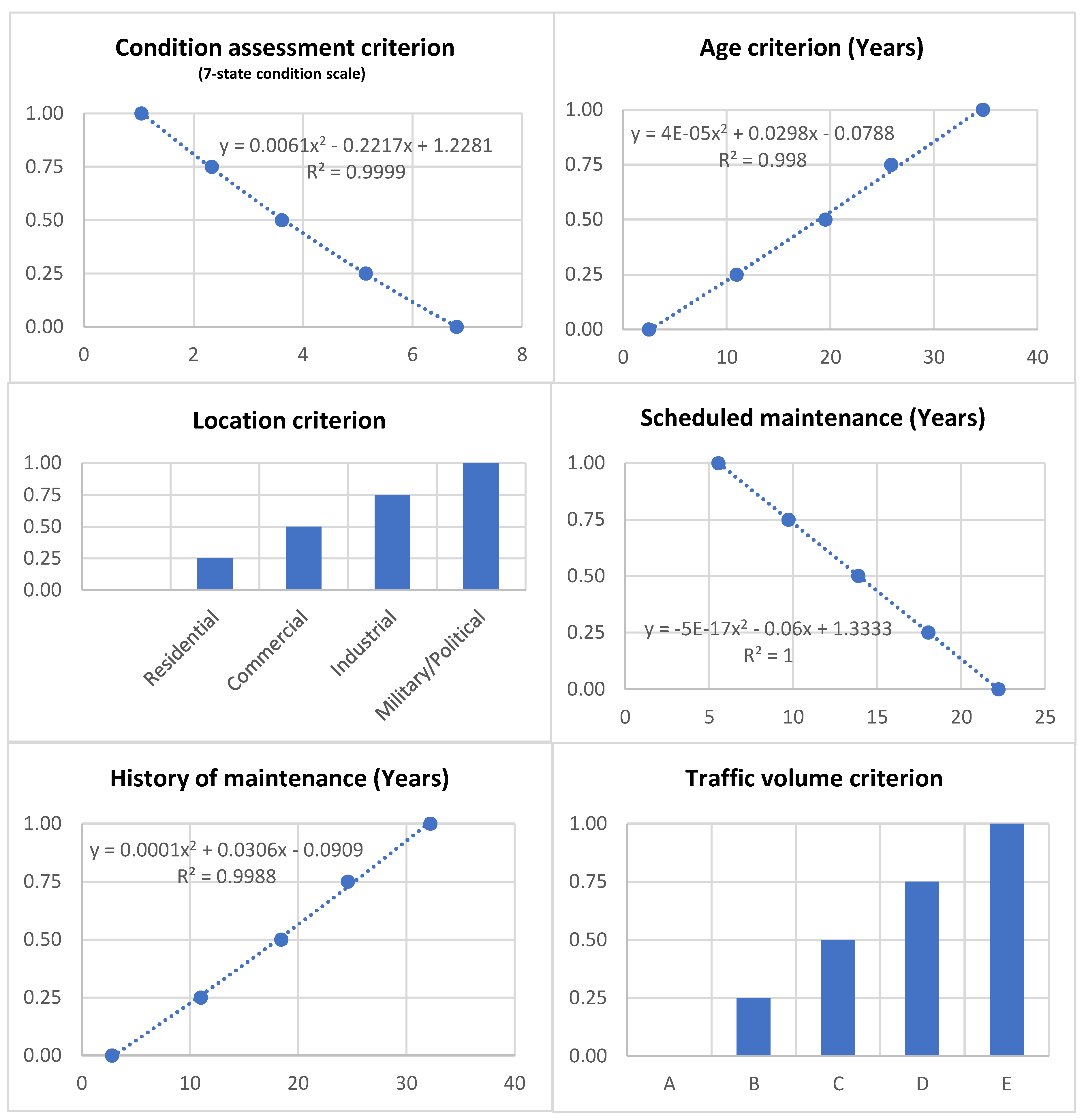
4.2.2. Establishing the MAUT Curves

As the weights of bridges prioritization criteria at network level and bridge structure elements were determined through the use of the AHP, the following step in the model was carried out to specify a range of scores for the identified criteria. The guidelines for establishing value attributes were considered as follows:

• The highest and lowest limit are desired to be determined before establishing the midpoints.
• The attributes scale can be either quantitative or qualitative according to the nature of the attributes.
• It is not necessary for qualitative criteria to have midpoints.

The utility scores were obtained from interviewing nine local experts. The experts were all in agreement for the overall limits, yet the curve trend from one expert to another can be different based on their experience. The final utility function is determined based on the average of all results as shown in Figure 2 and is discussed in the next sections.

Condition Assessment

According to the manual of the Saudi Arabia’s Ministry of Municipal, Rural Affairs, and Housing, Riyadh, Saudi Arabia [39], the bridge condition is assessed through a 7-state condition scale. The experts transformed the scale into a utility curve, as shown in Figure 2. Some of the experts recommended the linear relationship while others recommended a parabolic relationship. The average of the nine responses yielded a parabolic trend line with an R² value that equals the maximum among other degrees of trend lines, which means the most fit trend line. The average response suggests that when the condition is evaluated 1, potential danger is scored 1 (maximum priority), and when it is evaluated 7, a new case, it is scored 0 (least priority). If the bridge scored 0, very dangerous, then its score is 1, although it may be excluded from maintenance prioritization and may instead be prioritized for replacement.

Traffic Volume

The amount of traffic passing over a bridge is represented by the Annual Average Daily Traffic (AADT). The experts preferred to use differential prioritization for the AADT. This means that the AADT for all of the bridges being prioritized for maintenance are classified: the bridge with the highest AADT receives the full score and the bridge with the lowest AADT receives a zero score. The bridges in between receive a score proportional to their AADT. According to the experts there are ongoing projects for traffic counting. Based on the findings of this project, the AADT can be determined for each bridge. In the meantime, the municipality may depend on the Average Daily Traffic (ADT) or the peak hour volume.

Bridge Location

The location is categorized into four classes based on the traffic type and the load passing over the bridge in that location. The type of traffic in residential areas is lighter than any other location as traffic in that location is comprised of light vehicles, whereas trucks are prevented from entering these locations. Therefore, bridges located in a residential area have the least priority. The types of traffic passing over the bridges located in the commercial area are comparable to light trucks that are heavier than the first class. Thus, it receives a higher priority. The types of traffic using bridges in the industrial areas are heavier than the previous classes. Therefore, it receives a higher score. The types of traffic using bridges located in military/political areas are much heavier, which is also due to the importance of these locations to the government. The experts all agreed on this scale as they see it as representative of the bridge’s locations in the study area.

Bridge Age

Most experts have recognized the age of the bridges as being 50 years old. Some of them indicated 100 years. The experts suggest that a bridge has the highest priority for maintenance at the age of 35 years on average. Older bridges are excluded from maintenance and are prioritized for replacement. The experts recommended both a linear and a parabolic relation between the age and the score. The parabolic trend line is the most fit, since the value of R² for the second degree is the highest among the linear and the third degree.

Previous and Scheduled Maintenance

Recent maintenance activity on a bridge gives it a priority to be maintained next time based on the period since the last maintenance activity. The experts divided the period based on intervals. The average interval period is around seven years. This means that if a bridge was maintained 10 years ago its score would be around 0.25, but if it was maintained in the last 20 years its score would be 0.55. The experts proposed both a linear and a parabolic relation between the previous and the score. The second degree parabolic is the best fit, as the R² value was the highest.

4.3. Structural Element Weights from the AHP

As recognized by the experts, a bridge is comprised of structural elements: bridge deck and parapet, bearing pads, expansion joint abutment, walls, pier columns, and foundations. As in Section 4.2.1, the AHP analysis was performed to identify the weight of each structural element in terms of its importance in maintaining a safe bridge structure. Thus, the local experts were asked the following question: which structural element is more important for maintenance to keep the operation of the bridge and the flow of the traffic safe. Next, they were requested to indicate the intensity of the importance between the compared structural elements.

Table 5. Structural element weights.

Components	Bridge Deck and Parapet	Bearing Pads	Expansion Joint	Abutment Walls	Pier Columns	Foundations
Weights	17.3%	20.7%	16.9%	13.6%	16.4%	15.1%

shows the structural elements of concrete bridge and their relative weights. The results showed that the most influential structural element in maintaining the bridge structure is the bearing pad due to its shorter life expectancy compared to the other structural elements and its effects on the bridge and traffic movement in case of any sudden failure. The same applies to the expansion joint and deck slab. The other structural elements are designed to withstand the imposed load for a longer period. In case any of these structural elements have some major defects, the structural elements will be prioritized based on their condition state.

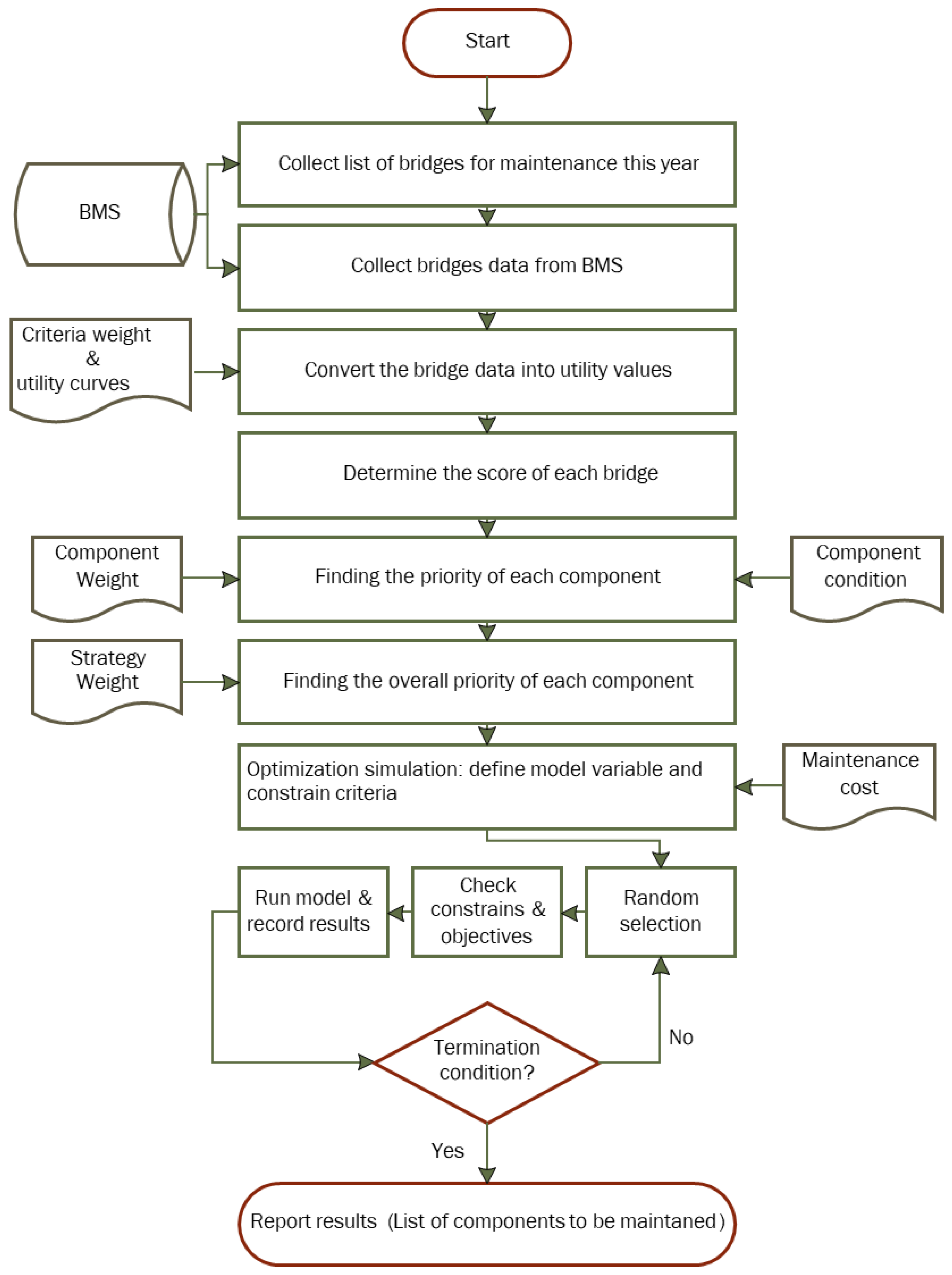
4.4. Computation Process Workflow

As shown in Figure 3, the model executes the following steps to find the optimal solution (maintenance plan) of bridges and how the limited budget can be distributed:

Step 1—Data entry

The following data were entered to start the model:

o

List of bridges to be maintained from the BMS;

o

Data related to the prioritization criteria of these bridges (e.g., age of the bridge, condition assessment of each structural element, etc.);

o

Pre-defined weight of each prioritization criterion and each structural element from the conducted AHP survey;

o

Pre-defined equations of each utility curve as presented in Figure 2;

o

The owner (Bridge Management Authority) enters score for each bridge criteria;

o

The estimated maintenance cost of each structural element in each bridge;

o

The available budget.

Step 2—Bridge prioritization at the network level

o

Starting from the Bridge Data, such as Bridge Age for the first bridge (which was taken from the BMS), the bridge age is then substituted in the equation of bridge age criteria to determine the corresponding utility value $U_{b,c}$. b is the bridge number and c is the criteria number;

o

The pre-defined Bridge Age criteria weight $W{C}_n$ is already entered in the first step;

o

The model starts by multiplying the utility value U_b,c of prioritization criterion C1 for bridge B_a by the weight of C1 which is $W{C}_n$;

o

The model does the same as previous points for all prioritization criterions for one bridge and records the sum of all products U_b,c × WC_n, which will be the bridge rank;

o

The model repeats the same previous points for all bridges to determine the rank of each bridge;

o

The mathematical expression of determining the bridge rank for certain number of prioritization criterion is shown in the following Equation (1):

$${\mathrm{Bridge} \mathrm{Rank} \mathrm{for} \mathrm{bridge} \mathrm{BR}}_b={\displaystyle \sum }_{c=1}^{c=6}(U_{b,c}\times W{C}_n)$$

(1)

where:

b is the number of bridges in the network that needs maintenance this year (b = 1, 2, …, n) and n is the last bridge;

c is the number of prioritization criteria considered in the model with six criteria;

$U_{b,c}$ is the utility score of bridge b for criteria c;

$W{C}_n$ is the weight of criteria (n).

The higher the rank is, the more the bridge is eligible for maintenance.

Step 3—Structural element prioritization at the bridge level

o

Upon determining the bridge rank, the model will have the following parameters: Bridge Rank BR_b, condition assessment of each structural element and the corresponding utility value U_b,se b is the bridge number, se is the structural element number (from BMS) and the pre-defined weight of each structural element W_se;

o

The model multiplies the Bridge Rank ${\mathrm{BR}}_b$ by the pre-defined weight of the structural element W_se (see Table 5) by the utility value of the condition assessment of the same structural element U_b,se to determine the bridge structure element rank;

o

The result obtained from the previous step is then multiplied by the maintenance strategy score to obtain the overall priority of that structural element (optional in case the owner wants to prioritize a certain maintenance strategy according to the condition assessment);

o

The higher the score value is, the more eligible the bridge’s structural element for maintenance becomes.

Step 4—Optimization-based simulation

o

The overall priority of the structural elements, maintenance costs, and the budget are then used as inputs to the optimization-based simulation in the risk analysis software;

o

The probability distribution is defined based on the uncertainty relevant to the two variables (priority and the structural element cost);

o

The objective function is set to be the maximum summation of the priorities of the selected structural elements, while the total maintenance cost for the same structural element must be equal to or less than the constraint budget;

o

The risk analysis software then randomly selects a set of structural elements between 1 and N (where N is the number of structural elements to be maintained), along with the estimated maintenance cost and its priority;

o

The total cost of the selected maintenance plan is compared with the budget;

o

If the selected maintenance plan satisfies the budget, the set of selected structural elements is recorded and prioritized;

o

The random selection methodology uses the concept of binary decisions. The structural element is either included or excluded from the maintenance plan. If it is to be included, then the decision given a value of 1, and is multiplied by the overall priority;

o

If the decision is not to include it, then the decision is given a value of 0. This is performed randomly and iteratively while the model is assigning a decision (1 or 0) for each structural element. The structural element which receives decision 1 means it is included in the maintenance plan and the zeros are excluded;

o

The output consists of list of structural elements to be included in the maintenance plan;

o

The model will record each list and its total cost and the sum of priority.

o

The lists having a total cost less than the budgeted cost will be compared with each other to figure out the list with the maximum sum of priorities;

o

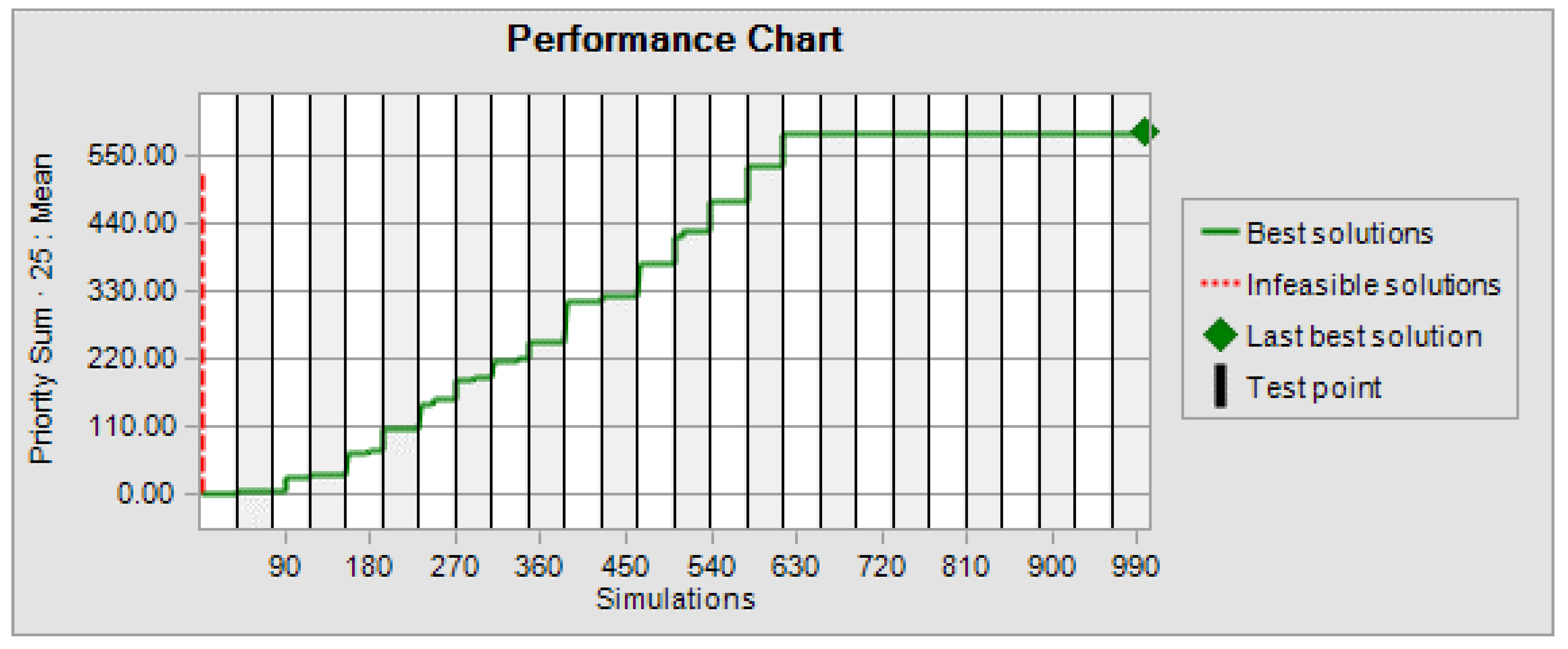
The near-optimum solution (maintenance plan) out of these solutions (maintenance plans) is the one with the highest priority and the least cost, which also satisfies the budget.

Step 5—Termination conditions

o

The termination condition in the optimization-based simulation is limited to the number of iterations.

o

The model reports the set of structural elements (maintenance plan) with the maximum sum of priority, while the sum of the maintenance cost is equal to or less than the budget. Figure 4 illustrates the model, including the major processes and data input.

4.4.1. Constraints

This limited maintenance budget, as the only constraint, is defined as the budget allocated for the maintenance of the network of bridges under consideration, as set by the maintenance managers. While the model searches for the near optimum solution, which is maximizing the number of bridges to be maintained, it accounts for the available budget. It can be expressed by Equation (2).

$${\displaystyle \sum }_{B=1}^{B=N}{\displaystyle \sum }_{C=1}^{C=6}\left(M{C}_{BC}\right) \le Budgeted Cost$$

(2)

where (B = 1, 2, …, N) is the number of bridges and (C = 1, 2, 3, 4, 5, 6) is the number of structural elements in each bridge. Also, MC_BC is the maintenance cost for Structural Element C in Bridge B.

On the other hand, the priority has a maximum limit of the summation of all the structural element priorities.

4.4.2. Model Objective Function

The objective function is set for maximizing the bridge priority to be maintained from a set of bridges defined by the maintenance managers. It can be mathematically expressed as Equation (3).

$$Max Priority={\displaystyle \sum }_{B=1}^{B=N}{\displaystyle \sum }_{C=1}^{C=6}\left(B{R}_B\times C{W}_C\times UC{A}_{BC}\times MS{W}_{BC}\right)$$

(3)

where:

B is the Bridge Number among the bridges prioritized this year for maintenance (1, 2, …, N), C is the Structural Element Number (6 Structural Elements defined in this study) (C = 1, 2, 3, 4, 5, 6), BR_B is the Bridge B Rank, CW_C is the Weight of Structural Element C, UCA_BC is Utility Value of Condition Assessment which corresponds to Structural Element C in Bridge B, and MSW_BC is the Maintenance Strategy Weight that corresponds to Structural Element C in Bridge B.

The model is searching for the greatest sum of priorities resulting from having more structural elements included in the maintenance plan for this year while taking into consideration the budget constraint. The model in each iteration records the sum of the priority of the structural elements and their maintenance cost. As the model starts with the first structural element it sums the priority and then takes the corresponding cost and sums it. The second iteration takes the first and second structural elements and sums their priorities and the corresponding costs, and so on. The model records all the iterations and finds the maximum sum of priority and compares the corresponding cost with the budget. If the budget is less, then the model looks for the next maximum sum and compares it with the budget. The process keeps going until it reaches a certain priority sum which corresponds to a total cost less than the budget. The priorities forming that sum are identified by the model as the structural elements requiring maintenance this year.

5. Example Project

A hypothetical network of four bridges is used as an example project to illustrate the methodology and the features of the proposed model.

Table 6. Bridge information.

	Bridge 1 (B1)	Bridge 2 (B2)	Bridge 3 (B3)	Bridge 4 (B4)
Condition assessment	4	6	3	5
Age (years)	15	9	23	26
Location	Industrial	Industrial	Commercial	Political
Previous maintenance (years)	10 year. ago	0	15	5
Scheduled maintenance (years)	5 year. later	6	0	10
Traffic volume (ADT)	78,563	89,487	54,127	104,369

,

Table 7. Details of bridge structural elements.

	Condition Assessment
		Bridge 1 (B1)	Bridge 2 (B2)	Bridge 3 (B3)	Bridge 4 (B4)
Bridge Deck and Parapet	M2	4	6	3	5
Bearing Pads	EA	3	5	4	5
Expansion Joint	LM	5	4	3	4
Abutment Walls	M3	4	6.5	2	3
Pier Columns	M3	4	6.5	2	6
Foundations	M3	4	7	4	6
	Quantity
		Bridge 1 (B1)	Bridge 2 (B2)	Bridge 3 (B3)	Bridge 4 (B4)
Bridge Deck and Parapet	M2	1314	2044	876	1752
Bearing Pads	EA	44	60	24	60
Expansion Joint	LM	53.8	68.4	39.2	68.4
Abutment Walls	M3	860	950	685	890
Pier Columns	M3	350	490	280	420
Foundations	M3	900	1125	675	810

and

Table 8. Maintenance cost for bridge structural elements.

		Bridge 1 (B1)	Bridge 2 (B2)	Bridge 3 (B3)	Bridge 4 (B4)
Bridge Deck and Parapet	SAR	394,200.00	613,200.00	262,800.00	525,600.00
Bearing Pads	SAR	660,000.00	900,000.00	360,000.00	900,000.00
Expansion Joint	SAR	134,500.00	171,000.00	98,000.00	171,000.00
Abutment Walls	SAR	645,000.00	712,500.00	513,750.00	667,500.00
Pier Columns	SAR	262,500.00	367,500.00	210,000.00	315,000.00
Foundations	SAR	675,000.00	843,750.00	506,250.00	607,500.00
Total	SAR	2,771,200.00	3,607,950.00	1,950,800.00	3,186,600.00
		11,516,550.00

1 $ = 3.76 SAR.

summarize the data for the example project.

Table 6 depicts the information provided by the bridge engineer, which is the input data to the BMS based on their evaluation of the bridges. These data include condition assessment, bridge age in years, bridge location, the last previous maintenance in years, scheduled maintenance in years, and traffic volume. This information is to be used to determine the score of each posterization criteria. Table 7 depicts the details of the bridge’s structural elements, namely bridge deck and parapet, bearing pads, expansion joint, abutment walls, pier columns, and foundations. In addition, the table depicts the quantity take-off for each structural element. Table 8 depicts the maintenance cost for bridge structural elements which can be carried out by the bridge engineer or through the quotation of the maintenance contractor. The bridges are of the same type, i.e., conventional reinforced concrete bridges.

Equation (4) below is a sample calculation to demonstrate the use of the utility curves to determine the equivalent utility values, and then the overall bridge rank. For example, the overall condition assessment of bridge 1 can be calculated as follows:

Overall score of condition assessment of bridge = 0.0061(X)² − 0.2217(X) + 1.2281

(4)

where X is the score of condition assessment of bridge under consideration as defined by the user in the seven state condition scale

Therefore,

Overall score of condition assessment of bridge 1 = 0.0061(4)² − 0.2217(4) + 1.2281 = 0.438

(5)

where the value of 4 corresponds to the condition assessment of bridge 1, as presented in Table 6. To find the overall score of each bridge, the equivalent utility value of each prioritization criteria for each bridge is multiplied by the weight of that prioritization criteria obtained in Section 4.2.1 and summarized in Table 4. Thus, the overall score can be calculated using Equation (1) as follows:

Overall bridge score = (0.438 × 25.9% + 0.377 × 12.7% + 0.750 × 17.0% + 0.225 × 11.2% + 1.000 × 11.9% + 0.500 × 21.3%) = 0.540

Discussion of the Results

The first step is to conduct the prioritization for the four bridges in the network level to determine the overall score (rank) for each bridge. The rank will then be used in the second step as a weight for each bridge. To do so, the bridge’s data shown in Table 6, along with the utility curves depicted in Figure 2, are used to convert the data into utility values from the curves. Alternatively, the trendline equation and the utility value of each criterion in each bridge is multiplied by the weight of the criterion and then the product is summed to find the overall score for each bridge.

Table 9. Overall score of each bridge.

Prioritization Factor	Weight	Bridge 1 (B1)	Bridge 2 (B2)	Bridge 3 (B3)	Bridge 4 (B4)
Condition assessment	25.9%	0.438	0.067	0.637	0.297
Age (Years)	12.7%	0.377	0.193	0.628	0.723
Location	17.0%	0.750	0.750	0.500	1.000
Previous of maintenance	11.2%	0.225	0.000	0.391	0.065
Scheduled maintenance	11.9%	1.000	0.973	1.000	0.733
Traffic volume (ADT)	21.3%	0.500	0.750	0.250	1.000
Overall score		0.540	0.445	0.546	0.646

summarizes the overall score/rank for each bridge.

The priority of structural element is computed by multiplying the utility value of condition assessment for that structural element by the weight/rank of the bridge and by the weight of the structural element. The values for the structural elements Priority in

Table 10. Structural element priority of each bridge.

Bridge		Bridge 1 (B1)	Bridge 2 (B2)	Bridge 3 (B3)	Bridge 4 (B4)
Components	Weight	0.540	0.445	0.546	0.646
Bridge Deck and Parapet	17.3%	0.439	0.118	0.618	0.272
Bearing Pads	20.7%	0.618	0.272	0.439	0.272
Expansion Joint	16.9%	0.272	0.439	0.618	0.439
Abutment Walls	13.6%	0.439	0.045	0.809	0.618
Pier Columns	16.4%	0.439	0.045	0.809	0.118
Foundations	15.1%	0.439	0.000	0.439	0.118
		Components Priority
		Bridge 1 (B1)	Bridge 2 (B2)	Bridge 3 (B3)	Bridge 4 (B4)
Bridge Deck and Parapet		40.9	9.0	58.2	30.3
Bearing Pads		69.1	25.1	49.6	36.4
Expansion Joint		24.8	33.0	57.1	48.0
Abutment Walls		32.3	2.7	60.2	54.4
Pier Columns		38.8	3.3	72.4	12.4
Foundations		35.7	0.0	36.1	11.4

are multiplied by 1000 for a better presentation. An example calculation for Bridge Deck and Parapet priority is as follows:

Priority of Bridge Deck and Parapet for Bridge 1 is = 0.439 × 0.540 × 17.3% × 1000 = 40.9

Where 0.439 is the priority of Bridge 1 Deck and Parapet Bridge as presented in Table 10; 0.540 is priority score as presented in Table 10; 17.3% is the weight of Bridge Deck and Parapet as presented in Table 5. The higher value means higher priority.

After that, the maintenance strategy weight was incorporated according to the condition state.

Table 11. Recommended maintenance strategies (plan).

Recommended Maintenances	Preventive	Remedial/Curative	Rehabilitation	Replacement
Score	0.5	0.75	1	0.25
Condition State	More than 5	5 to 4	4 to 3	Less than 3
Utility Value	0.272 or less	0.272–0.439	0.439–0.618	0.618 or more

lists the recommended maintenance strategy that corresponds to the condition state of each structural element. It should be noted that these weights are assigned by the owner depending on their preferences. These recommended maintenance strategies are proposed by the bridge maintenance manual of MOMRA (MOMRA, 2014). Following that, the result, which is a list of the structural elements to be maintained with its maintenance cost and priority, is further used as an input to the optimization-based simulation module to look for the near optimum solution or the most feasible solution which considers the uncertainty in the main two variables of the model.

Table 12. List of prioritized structural elements.

Condition	Code	Name	Structural Elements Priority	Maintenance Plan Priority	Overall Priority	Maintenance Cost
0.6179	B1C2	Bridge 1: Bearing Pads	69.075	1.00	69.075	660,000.00
0.6179	B3C1	Bridge 3: Bridge Deck and Parapet	58.212	1.00	58.212	262,800.00
0.6179	B3C3	Bridge 3: Expansion Joint	57.074	1.00	57.074	98,000.00
0.6179	B4C4	Bridge 4: Abutment Walls	54.370	1.00	54.370	667,500.00
0.4389	B3C2	Bridge 3: Bearing Pads	49.625	0.75	37.218	360,000.00
0.4389	B4C3	Bridge 4: Expansion Joint	47.967	0.75	35.975	171,000.00
0.4389	B1C1	Bridge 1: Bridge Deck and Parapet	40.882	0.75	30.661	394,200.00
0.4389	B1C5	Bridge 1: Pier Columns	38.837	0.75	29.128	262,500.00
0.2721	B4C2	Bridge 4: Bearing Pads	36.401	0.75	27.301	900,000.00
0.4389	B3C6	Bridge 3: Foundations	36.128	0.75	27.096	506,250.00
0.4389	B1C6	Bridge 1: Foundations	35.720	0.75	26.790	675,000.00
0.4389	B2C3	Bridge 2: Expansion Joint	33.021	0.75	24.766	171,000.00
0.4389	B1C4	Bridge 1: Abutment Walls	32.271	0.75	24.203	645,000.00
0.2721	B4C1	Bridge 4: Bridge Deck and Parapet	30.330	0.75	22.748	525,600.00
0.2721	B2C2	Bridge 2: Bearing Pads	25.059	0.75	18.794	900,000.00
0.2721	B1C3	Bridge 1: Expansion Joint	24.849	0.75	18.637	134,500.00
0.8091	B3C5	Bridge 3: Pier Columns	72.413	0.25	18.103	210,000.00
0.8091	B3C4	Bridge 3: Abutment Walls	60.171	0.25	15.042	513,750.00
0.1175	B4C5	Bridge 4: Pier Columns	12.442	0.5	6.221	315,000.00
0.1175	B4C6	Bridge 4: Foundations	11.444	0.5	5.722	607,500.00
0.1175	B2C1	Bridge 2: Bridge Deck and Parapet	9.016	0.5	4.508	613,200.00
0.044775	B2C5	Bridge 2: Pier Columns	3.264	0.5	1.632	367,500.00
0.044775	B2C4	Bridge 2: Abutment Walls	2.712	0.5	1.356	712,500.00
0	B2C6	Bridge 2: Foundations	0	0.5	0	843,750.00

summarizes the list of structural elements after incorporating the maintenance strategy. The uncertainty is examined in three different scenarios in which each case has different considerations. The results are compared to assess the effect of uncertainty on the model, along with the optimal solution and the final decision.

The first scenario is a deterministic case in which no uncertainty is considered, and the estimated cost is considered as a crisp number. The second scenario considers uncertainty in the two variables of priority and estimated maintenance cost. The third scenario considers uncertainty in one variable, which is the priority as the main variable.

Table 13. Parameter of the developed model.

Simulation Parameter	Data Source	Probability Distribution	Parameter Type
Component Priority	Component prioritization—Model	Constant	Assumption
Component Maintenance Cost	BMS	Constant	Assumption
Decision	Assumed Randomly	Discrete	Decision
Total Priority	Calculated	-	Forecast
Total Maintenance Cost	Calculated	-	Forecast

shows the model variables’ definitions for the first scenario (deterministic).

Table 14. Uncertainty scenario summary.

Case	Case Type	Priority Probability Distribution.it	Cost Probability Distribution.it	Optimal Solution
				Priority	Cost (SAR)
Scenario 1	Deterministic	NA	NA	586.38	7,858,350.00
Scenario 2	2—Variable Uncertainty	Triangular	Gamma	474.41	7,597,540.08
Scenario 3	1—Variable Uncertainty	Triangular	NA	572.4	7,770,300.00

summarizes the results of the three scenarios. It can be noticed that each scenario resulted in a different optimal solution. Owing to the characteristics of the variables, the probability distribution is assigned. The more suitable distribution requires gathering a considerable amount of data to create the proper probability distribution. The model after the simulation of uncertainty searches for the optimal solution considering the objective function which maximizes the priority sum, while total maintenance cost needs to be below or equal to the budget. The results show that considering the uncertainties results in yielding different solutions, with each solution constituting a maintenance plan. This means that the structural elements involved in each maintenance plan are different and thus the owner decision will involve an inherent risk in each solution. Therefore, the owner may wish to look for a more feasible solution than the optimal solution since the optimal solution has the most uncertainty and thus there is a risk at maximum compared with all solutions that satisfy the objective function and the constraint. The owner may look for a solution in which she/he can anticipate the final list of structural elements to be maintained with a certain level of confidence. In other words, the owner wants to select a maintenance plan by which she/he can maintain a maximum set of structural elements with the available budget without requiring an additional budget.

Efficient Frontier Analysis is used to assist the owner in judging the risk inherent in each solution (maintenance plan). The risk here is measured by the standard deviation of the sum of the priority for each solution in the maintenance plan. Efficient Frontier depicts the relation between the mean of the sum priority and the standard deviation for a set of optimal solutions (i.e., maintenance plans). Thus, each optimal maintenance plan has a sum of priority and a standard deviation which represents the level of risk inherent in that maintenance plan. Plans with higher standard deviation values means they are accompanied with higher potential of variation compared to the selected plan. In other words, the bridge management authority may end up maintaining different structural elements other than the selected structural elements in the originally selected plan.

Figure 5 shows the outputs of the Efficient Frontier Analysis for the example project, while Figure 6 shows the model steady state after 630 simulations.

Table 15. Maintenance plans output from efficient frontier analysis.

Rank	Cost ≤ 8,000,000	B1C1	B1C2	B1C3	B1C4	B1C5	B1C6	B2C1	B2C2	B2C3	B2C4	B2C5	B2C6	B3C1	B3C2	B3C3	B3C4	B3C5	B3C6	B4C1	B4C2	B4C3	B4C4	B4C5	B4C6
1	7,987,228.42	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.00	1.00	0.00	0.00	0.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.00
95	7,888,740.30	1.00	1.00	0.00	0.00	1.00	0.00	0.00	0.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.00	1.00	1.00	1.00	1.00	1.00	0.00	1.00
170	7,063,540.42	1.00	1.00	1.00	0.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.00	1.00	1.00	0.00	0.00	1.00	0.00	1.00	0.00	1.00	1.00	0.00	0.00
171	6,283,555.99	1.00	1.00	1.00	0.00	1.00	1.00	1.00	1.00	1.00	0.00	1.00	0.00	1.00	1.00	0.00	0.00	1.00	0.00	1.00	0.00	1.00	1.00	0.00	0.00
237	7,814,427.77	0.00	1.00	1.00	1.00	1.00	1.00	0.00	0.00	0.00	1.00	1.00	1.00	1.00	0.00	1.00	1.00	1.00	1.00	1.00	1.00	0.00	0.00	1.00	0.00
291	6,437,883.44	0.00	1.00	1.00	1.00	1.00	1.00	0.00	1.00	1.00	0.00	0.00	0.00	0.00	1.00	0.00	1.00	0.00	1.00	1.00	0.00	0.00	1.00	1.00	0.00
413	7,083,628.18	1.00	1.00	1.00	0.00	1.00	0.00	0.00	1.00	1.00	1.00	1.00	1.00	1.00	0.00	0.00	1.00	1.00	0.00	0.00	1.00	0.00	0.00	0.00	1.00
518	5,336,900.08	0.00	0.00	0.00	1.00	0.00	0.00	1.00	0.00	0.00	0.00	0.00	1.00	0.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	0.00	0.00	0.00
569	5,174,543.92	0.00	0.00	1.00	1.00	1.00	1.00	0.00	1.00	1.00	1.00	0.00	0.00	1.00	0.00	0.00	1.00	1.00	0.00	0.00	0.00	0.00	0.00	1.00	0.00
693	4,431,149.35	0.00	0.00	0.00	0.00	0.00	1.00	0.00	0.00	0.00	1.00	1.00	1.00	1.00	0.00	0.00	0.00	0.00	1.00	0.00	0.00	0.00	1.00	1.00	0.00
699	3,867,251.25	0.00	0.00	1.00	0.00	0.00	0.00	1.00	0.00	0.00	0.00	1.00	1.00	1.00	1.00	0.00	1.00	0.00	1.00	0.00	0.00	0.00	0.00	1.00	0.00
730	4,297,480.15	0.00	0.00	0.00	1.00	0.00	1.00	1.00	1.00	1.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	1.00	0.00	0.00	1.00	0.00	0.00	0.00	0.00
762	2,159,454.18	0.00	0.00	0.00	0.00	0.00	1.00	0.00	0.00	0.00	0.00	1.00	0.00	0.00	0.00	1.00	1.00	0.00	0.00	1.00	0.00	0.00	0.00	0.00	0.00
788	2,253,306.44	0.00	0.00	0.00	0.00	0.00	0.00	1.00	0.00	1.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	1.00	1.00	0.00	1.00	0.00	0.00	0.00	0.00
823	1,283,440.43	1.00	0.00	1.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	1.00	0.00	0.00	0.00	0.00	0.00	0.00	1.00
827	720,867.37	1.00	0.00	1.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	1.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
862	384,422.71	1.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
869	1,545,902.48	0.00	0.00	0.00	0.00	0.00	0.00	1.00	0.00	0.00	0.00	0.00	1.00	0.00	0.00	0.00	0.00	1.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
873	1,612,171.12	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	1.00	1.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	1.00	0.00
879	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00

shows the selected bridges and structural elements in each solution presented in Figure 5. The optimal solution, highlighted in the table, consists of selecting 19 different bridge structural elements from five different bridges with a total maintenance cost of 7,987,228.42 SAR, which is very close to the total available budget. The most feasible solution, which is ranked (291), consists of selecting 13 different bridge structural elements from only four different bridges with a total maintenance cost of 6,437,883.44 SAR. Although the two solutions satisfy the owner’s budget constraint, the second solution has a higher level of confidence and a lower level of risk that the maintenance plan will exceed the assigned budget.

Applying the Efficient Frontier Analysis allows the owner to look at each solution’s structural elements, along with the mean priority and the standard deviation. The solution with a higher deviation involves more risk as the mean is expected to vary within the same standard deviation. It can be concluded that the higher mean has a higher deviation; thus, the optimal solution is not always recommended, and another near optimum can be more feasible.

The experts were presented with the results and the report. They recommended the results and the shape of the report, as in practice the owner wants to know the total number and the cost of structural elements to be maintained, while the project manager wants to know what the prioritized structural elements are to start with. Moreover, the maintenance contracts are based on the unit rates of these structural elements. Consequently, the quantities are directly compensated to the contractor through the bill of quantities and hence there will be no further cost impact on the owner except for the additional quantities which are already considered in the risk and efficient frontier analysis.

6. Conclusions

This paper presents an optimization-based simulation model for assisting decision-makers in allocating a budget for bridge maintenance. The most common prioritization criteria for bridge maintenance were identified from the literature review and from meetings with experts. These criteria are bridge condition, age, location, traffic volume, and the previous and the following maintenance. The developed model aims to overcome the shortcomings of the previously reported models or systems. It has the following features:

• Considers uncertainties associated with the estimated maintenance cost.
• Provides an optimum maintenance plan while taking into account the risk using frontier analysis technique.
• Provides the most feasible solution in which the decision-maker will be more assured that the selected maintenance plan will be achieved with a certain level of confidence.
• Combines AHP and MAUT to obtain their individual benefits and overcome their limitations.
• Considers the rank of the bridge in the network level along with the condition of the structural elements to distribute the available budget.
• Capable of carrying out a risk analysis for the selected maintenance strategy plans by applying efficient frontier analysis. Eventually, the maintenance plan, the output of the model, is a list of prioritized structural elements with their budgeted cost equaling the budget or less.

This study revealed that bridge structural condition scored the highest important criterions of all criteria, influencing the decision of bridge prioritization for maintenance, followed by traffic and bridge location. Moreover, bridge deck and parapet, followed by bearing pads, were found to be the most important of the bridge’s structural elements.

The current study can be extended for future work by integrating digital technologies for monitoring purposes and to measure the condition of structure element in real time. Also, image analysis technique can be integrated in the developed model to inspect the conditions of the different bridge elements.