Enhanced Particle Swarm Optimization Algorithm for Sea Clutter Parameter Estimation in Generalized Pareto Distribution
Abstract
:1. Introduction
- In response to the non-closed expression phenomenon in different parameter estimation methods, this study investigates the construction of fitness functions for PSO algorithm and HPSO when solving target optimization problems.
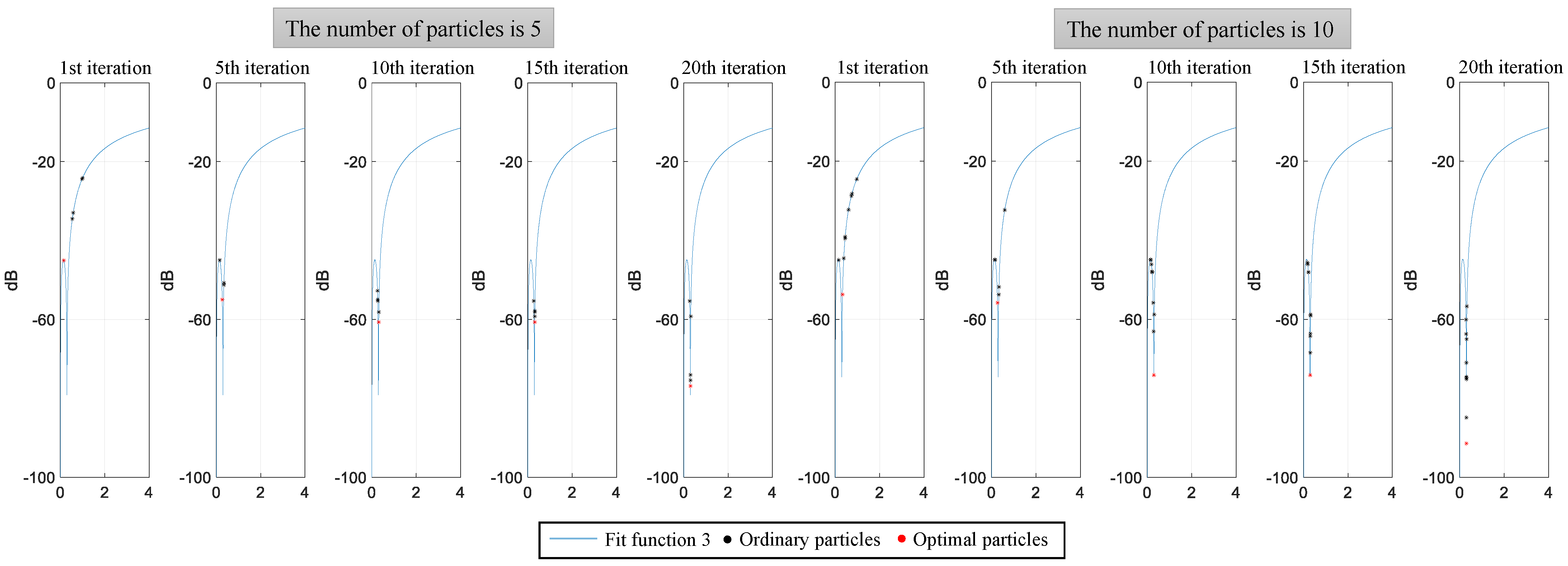
- By using simulated random data samples of the generalized Pareto distribution, the impact of parameters such as population size and iteration count in the PSO algorithm on its performance is examined, and the optimal parameter configuration for each targeted objective is determined.
- A goodness-of-fit test experiment is conducted on two sets of high-intensity ocean wave clutter measured data to compare the fitting performance of the generalized Pareto distribution models obtained through different parameter estimation methods.
- The performance of the HPSO algorithm and the PSO algorithm is compared using simulated data based on the parameter estimation fitness function constructed in this study.
2. Background
2.1. Generalized Pareto Distribution Model
2.2. Basic Parameter Estimation Methods for the Generalized Pareto Distribution
3. Method
3.1. Particle Swarm Optimization Algorithm
- (a)
- The positions X and velocities V of the particles are randomly initialized in the D-dimensional space of feasible solutions, where the i-th particle position and velocity can be expressed as
- (b)
- Based on the determined fitness function (particle population search object) and the corresponding position of each particle, the corresponding fitness value is calculated, and then the global optimum is evaluated, where the historical optimum of the particle and the global optimum of the population is assumed to be and , respectively, that is, we have
- (c)
- The particle population is continuously updated iteratively to search for the extreme value solution of the fitness function, and the velocity and position of each particle in the next iteration are updated by the individual historical optimal value and the current velocity Vi, and the k + 1th update of the particle is given bywhere w is the inertia weight, which gives the particle the inertia of motion trend; k is the number of current iterations; and are learning factors; and and are random numbers distributed in the interval of [0, 1]. To prevent the particles from searching blindly and falling into the risk of local optimum, the velocity and position of the particles are usually limited to a certain interval. The learning factor and inertia weight are particularly important parameters of the PSO algorithm, where the learning factor of the particle itself, also known as the cognitive parameter, is an important indicator of the particle’s search ability; the learning factor of the population is a social cognitive parameter that affects the search behavior of the whole particle population; and the size of the inertia weight is an expression of the movement ability of each particle.
- (d)
- Finally, the algorithm is terminated by setting the corresponding end conditions. There are generally two kinds of termination conditions: the first is to set the maximum number of iterations of the particle population, and the second criterion is to terminate when the optimal solution of the particle swarm has remained unchanged for five or more consecutive iterations.
3.2. Parameter Estimation Based on PSO Algorithm
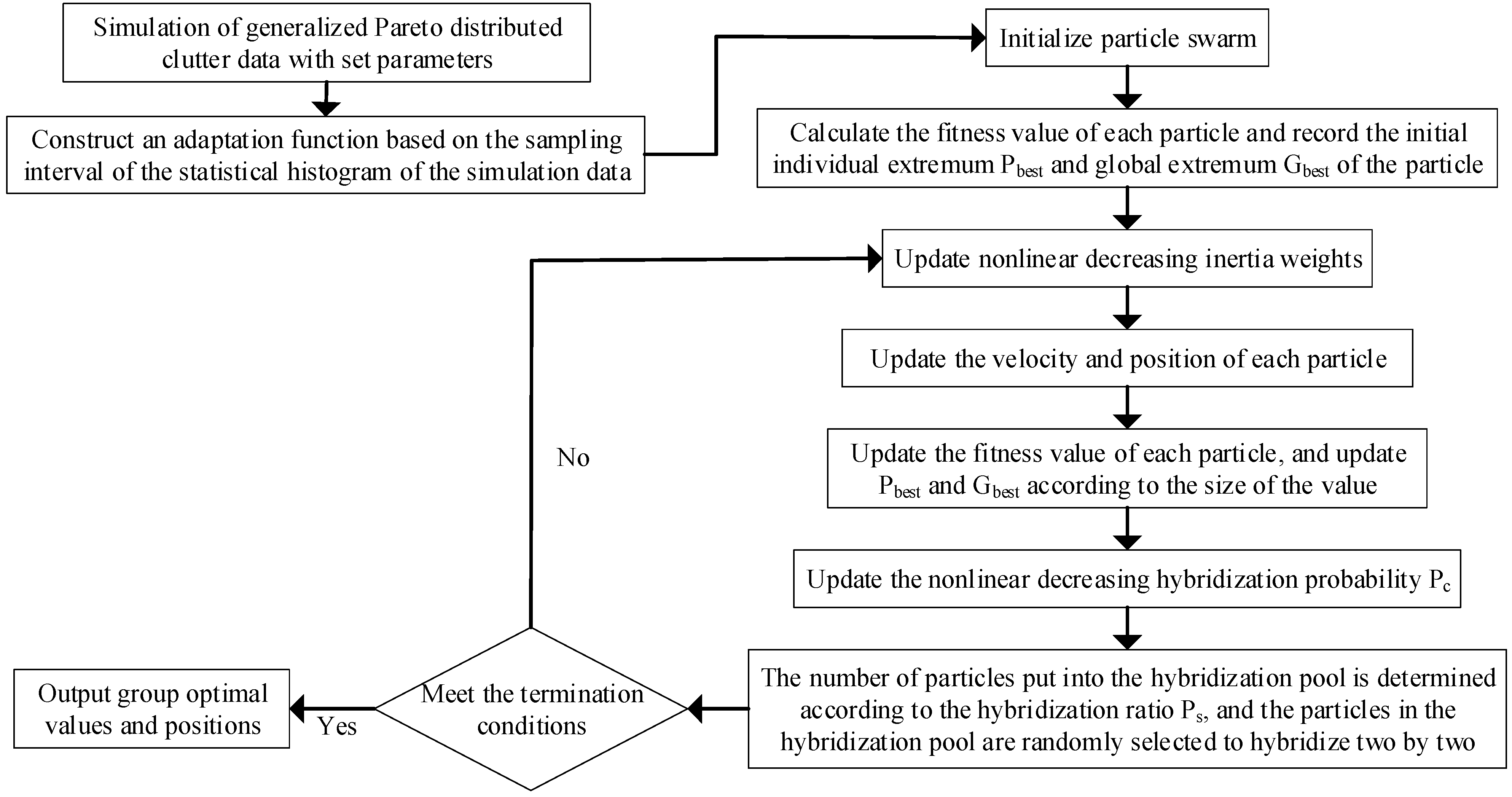
3.3. Improved Parameter Estimation for Particle Swarm Hybridization
4. Results and Discussion
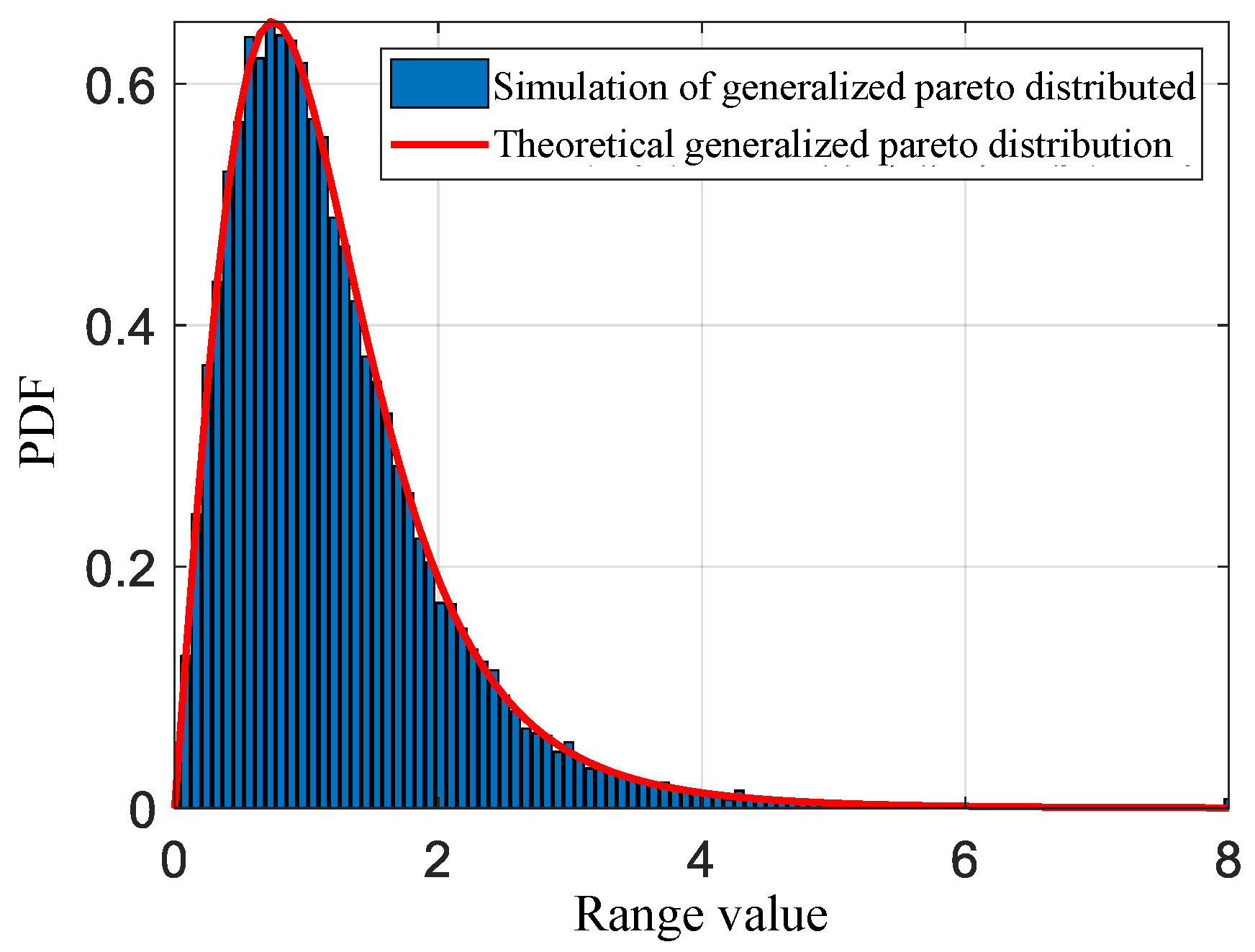
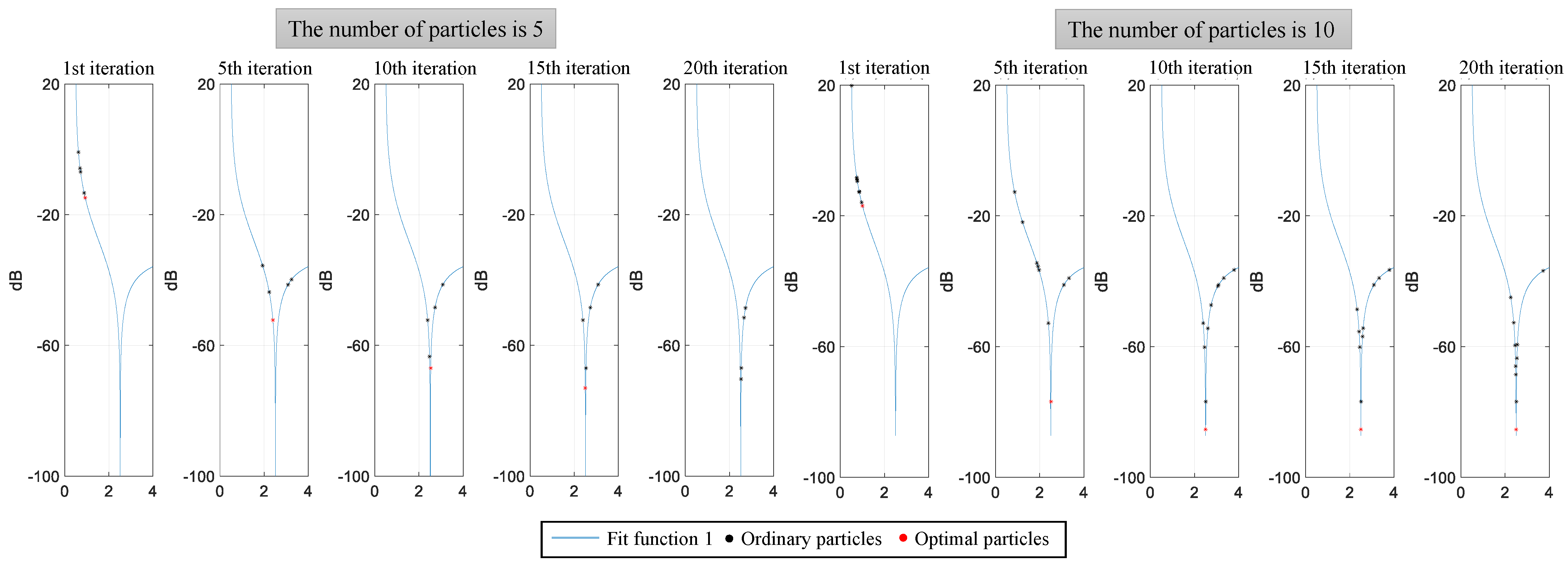
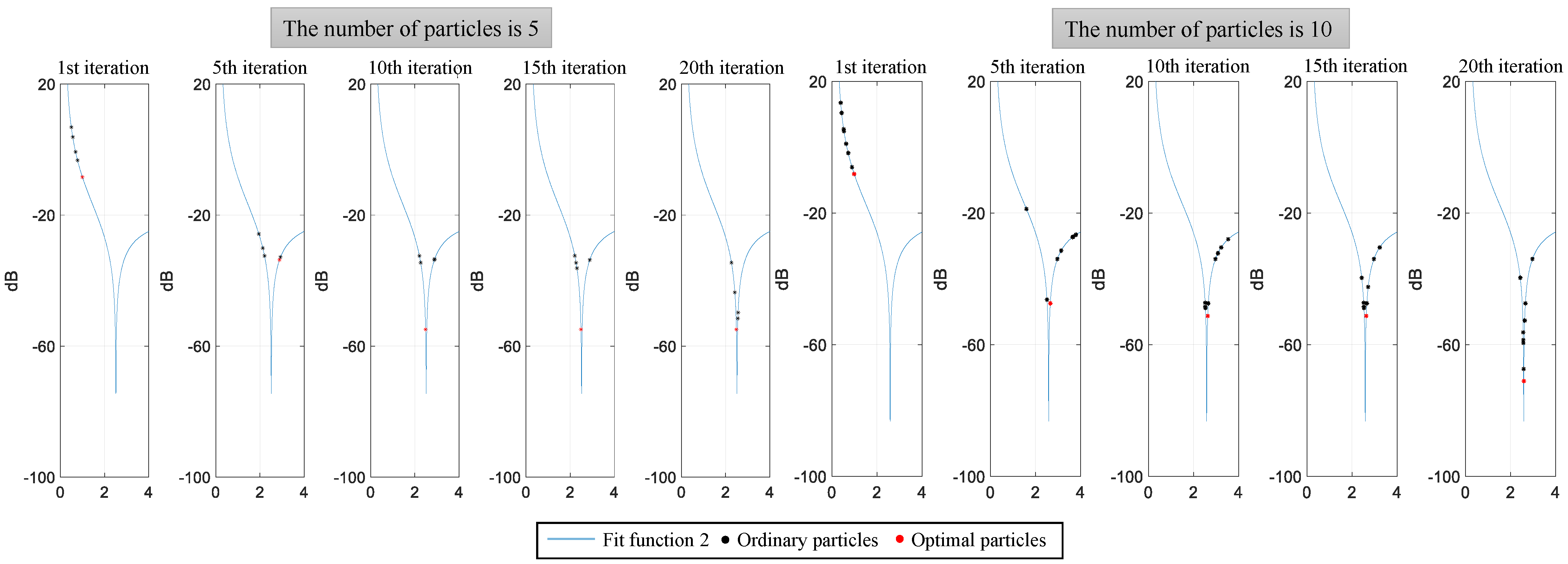
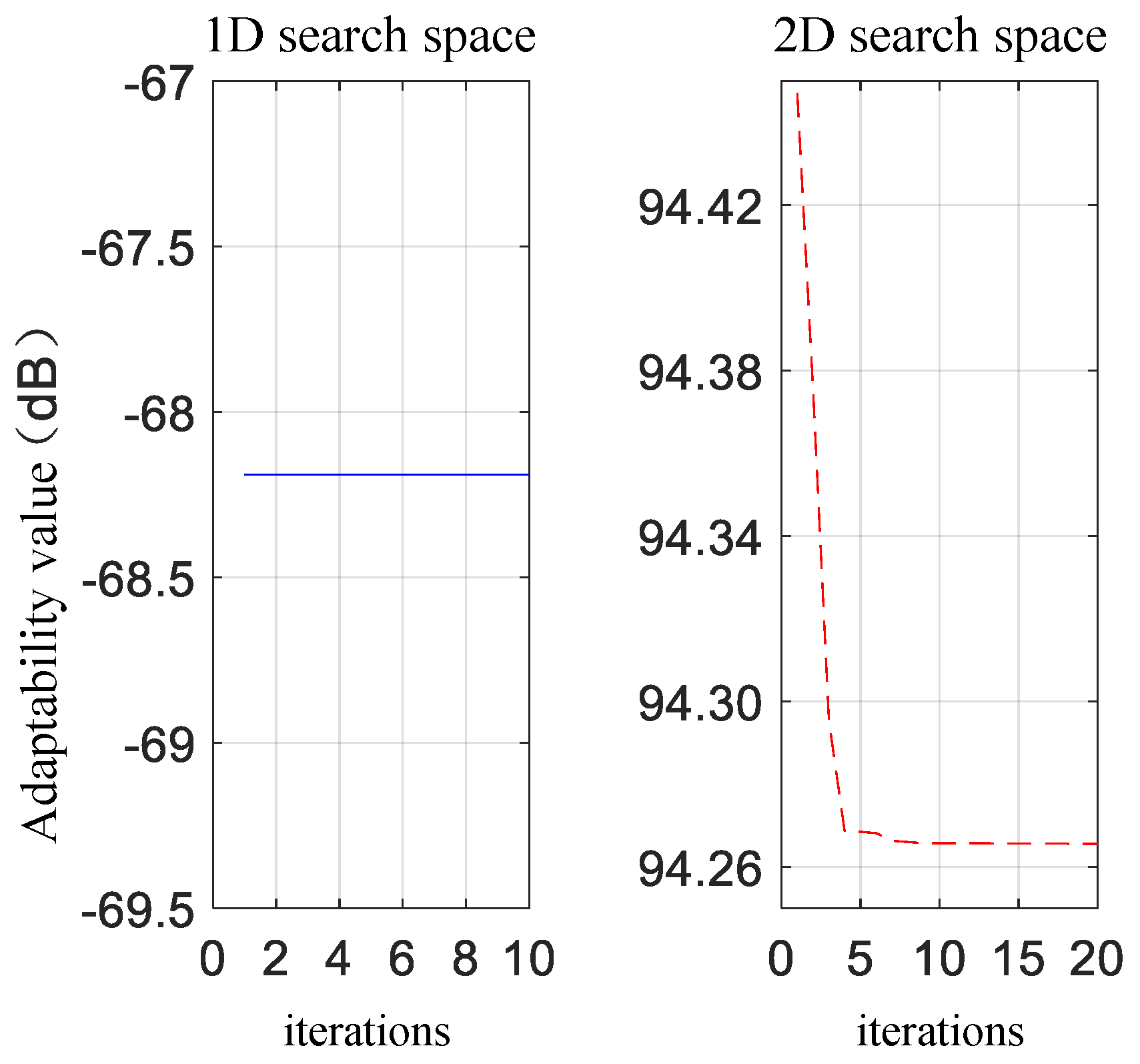
4.1. Simulation Experiment Analysis
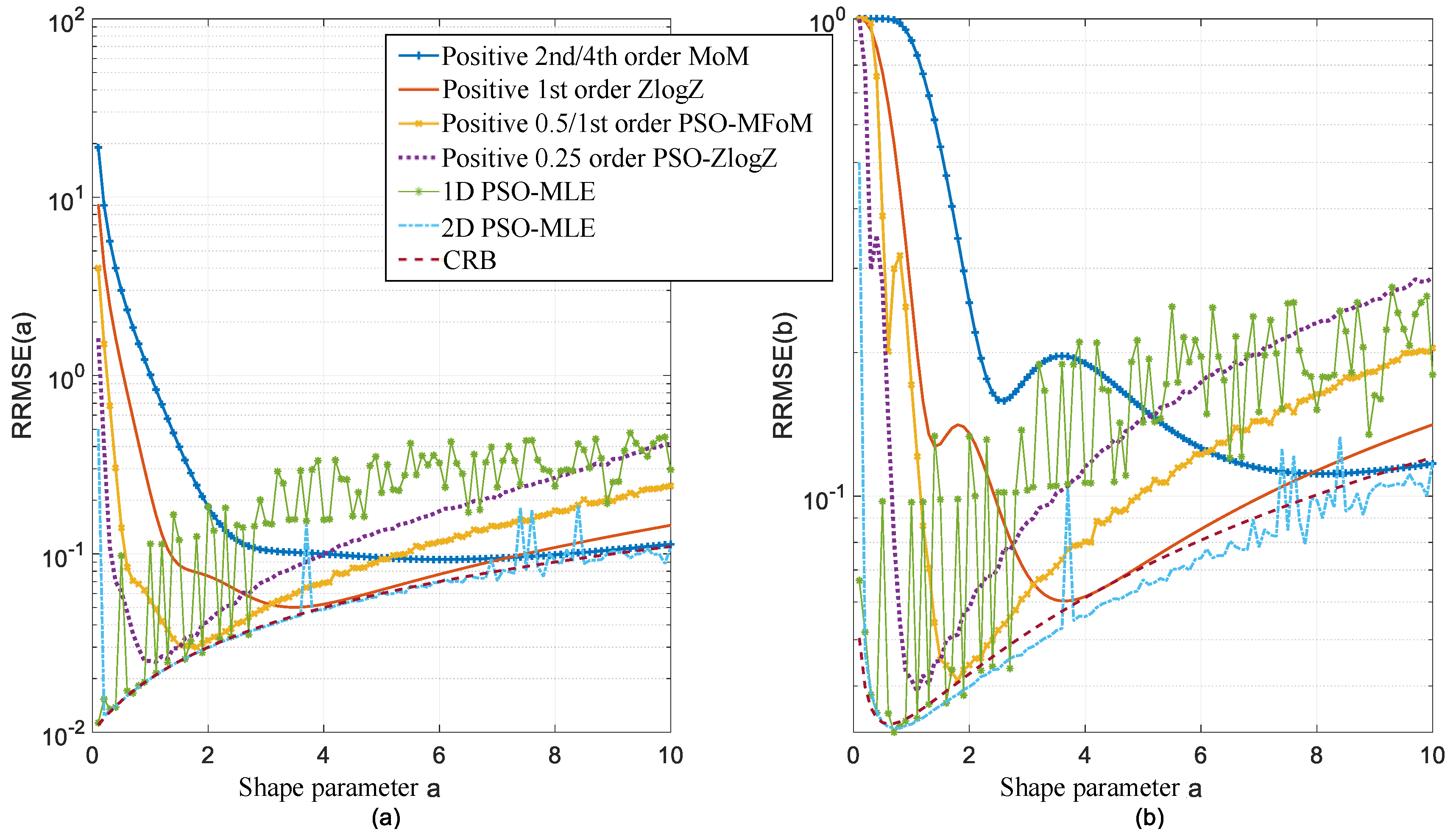
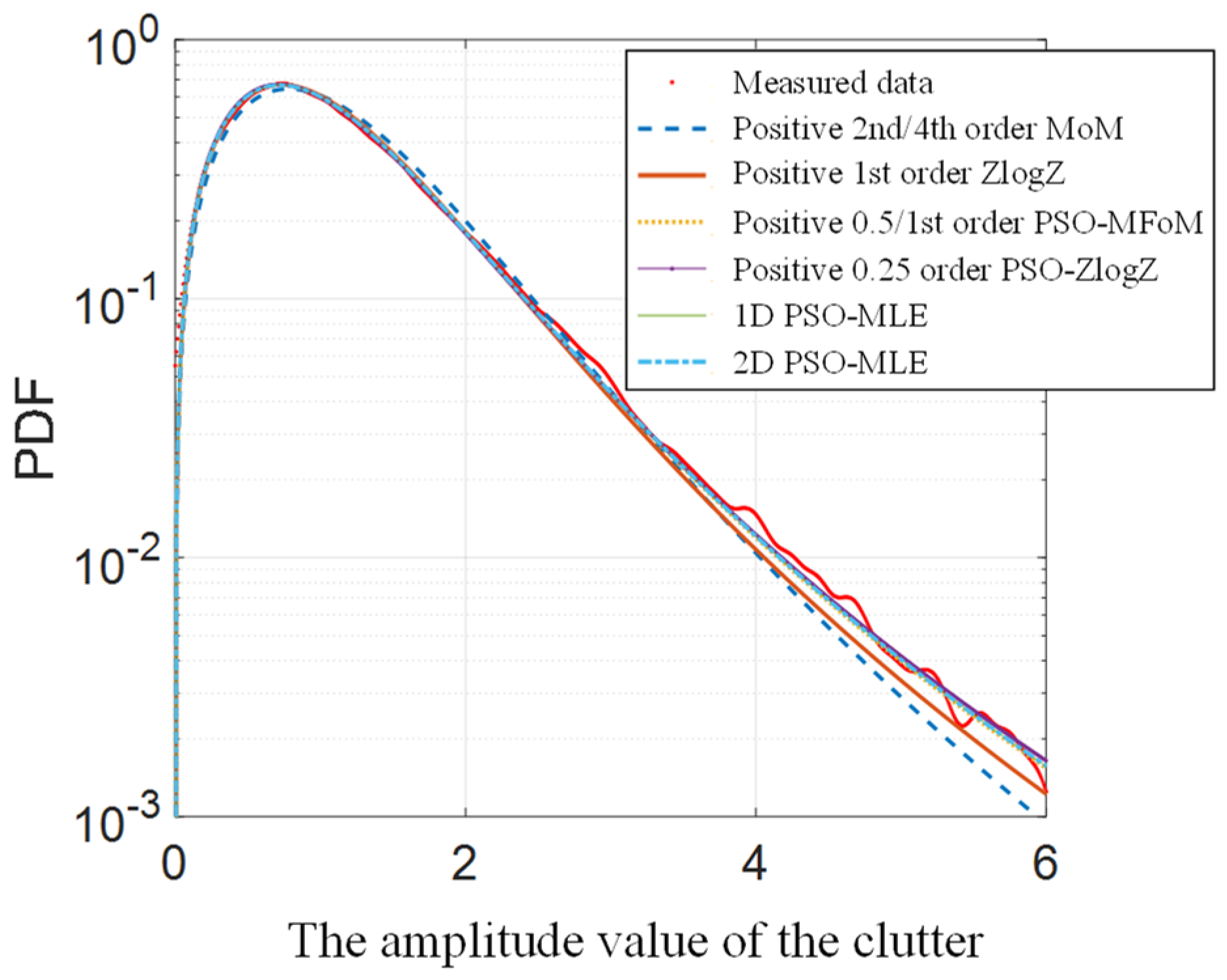
4.2. Analysis of the Fit of the Measured Data
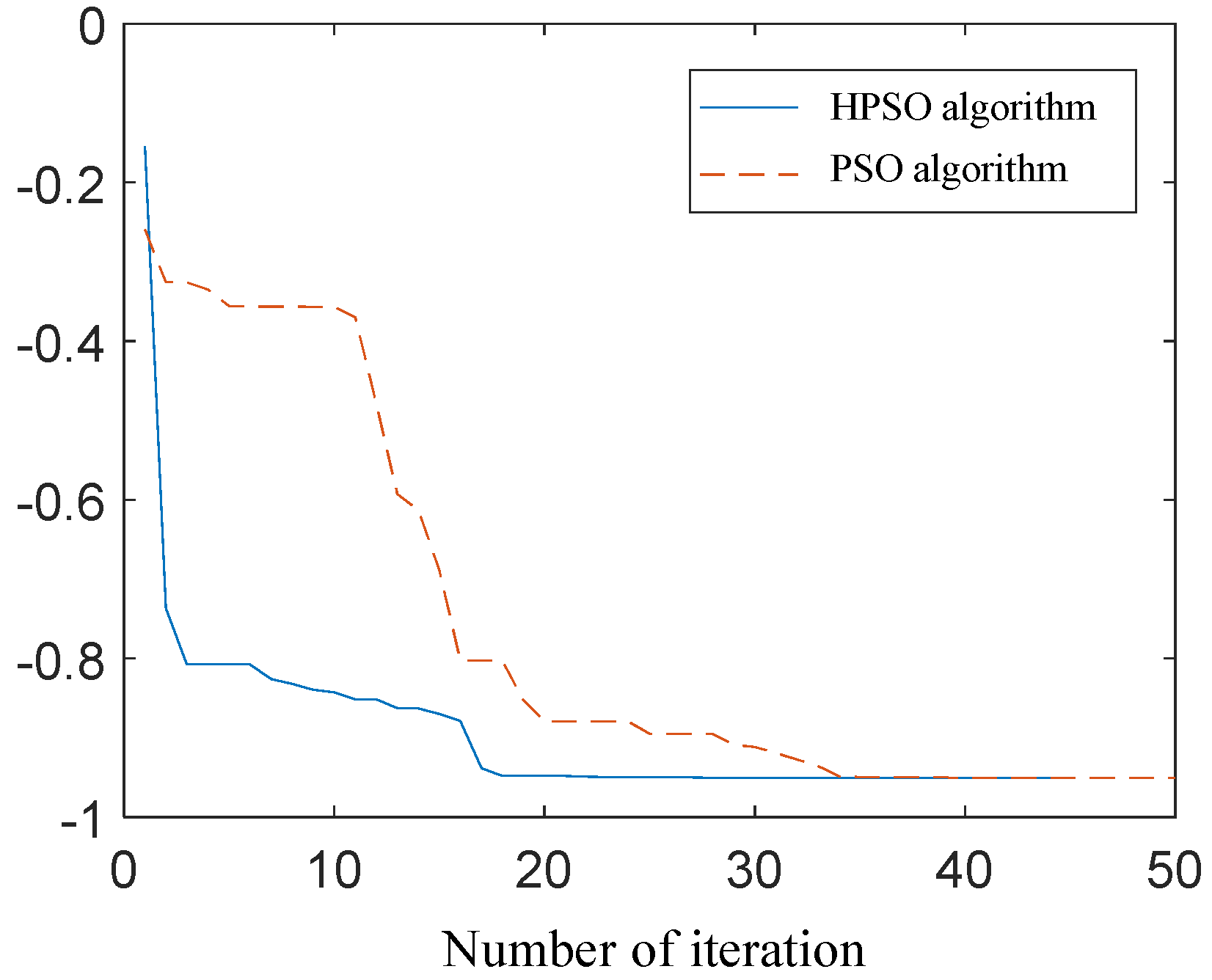
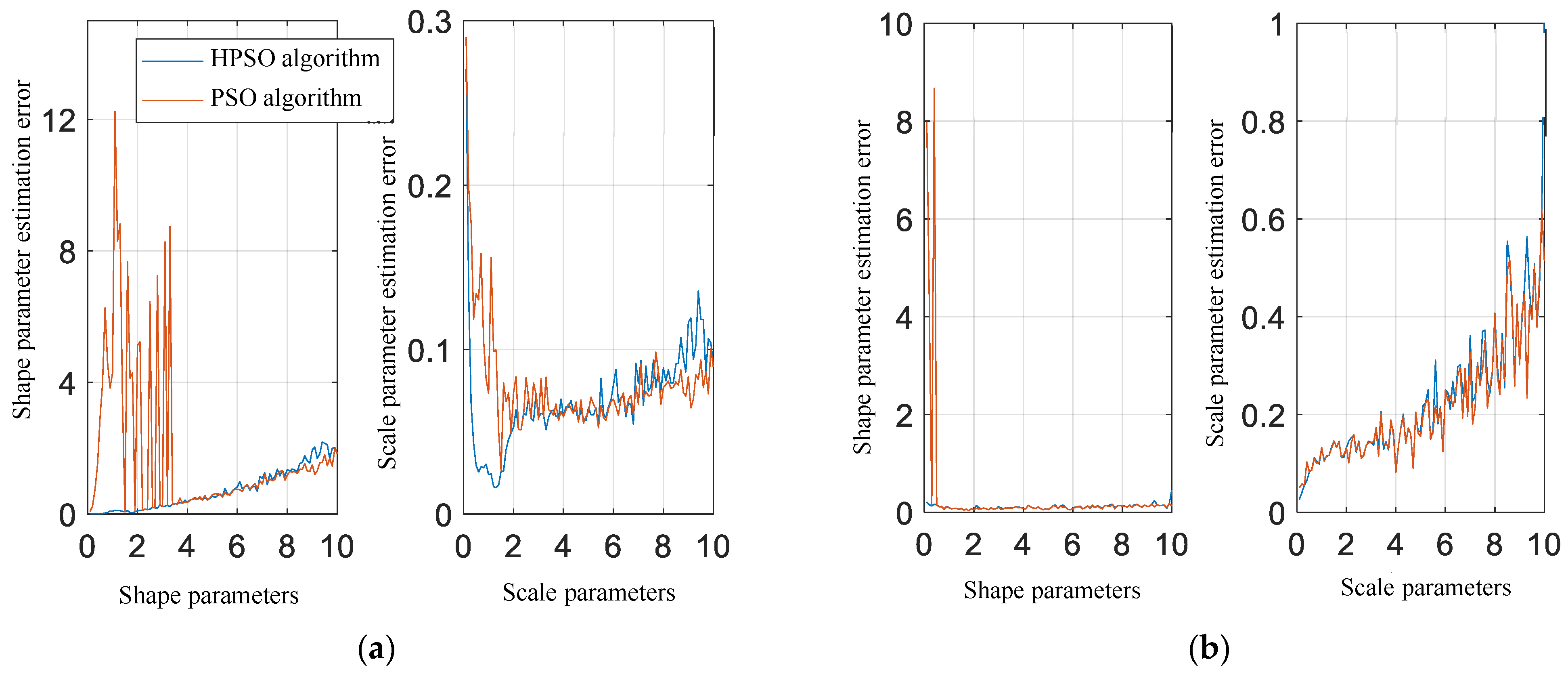
4.3. Performance Analysis of Parameter Estimation with HPSO Algorithm
5. Conclusions
- The HPSO algorithm overcame the premature convergence problem of the PSO algorithm and demonstrated better parameter estimation performance.
- The parameters of the HPSO algorithm were optimized, resulting in good performance.
- Through the analysis of parameter estimation variations, it was found that the parameter estimation results of the PSO algorithm were unstable.
- Compared to other methods, the generalized Pareto distribution estimated using the HPSO algorithm exhibited the most stable and optimal fitting results for real data, and it was not influenced by the range of shape parameter values.
- The HPSO algorithm achieved high-precision parameter estimation results while maintaining fast computational speed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, Z.-X.; Bai, X.-H.; Shui, P.-L.; Wang, L.; Su, J. Fast Dual Trifeature-Based Detection of Small Targets in Sea Clutter by Using Median Normalized Doppler Amplitude Spectra. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 4050–4063. [Google Scholar] [CrossRef]
- Huang, P.; Yang, H.; Zou, Z.; Xia, X.-G.; Liao, G.; Zhang, Y. Range-Ambiguous Sea Clutter Suppression for Multi-channel Spaceborne Radar Applications Via Alternating APC Processing. IEEE Trans. Aerosp. Electron. Syst. 2023, 1–18. [Google Scholar] [CrossRef]
- Yin, J.; Unal, C.; Schleiss, M.; Russchenberg, H. Radar Target and Moving Clutter Separation Based on the Low-Rank Matrix Optimization. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4765–4780. [Google Scholar] [CrossRef]
- Luo, F.; Feng, Y.; Liao, G.; Zhang, L. The Dynamic Sea Clutter Simulation of Shore-Based Radar Based on Stokes Waves. Remote Sens. 2022, 14, 3915. [Google Scholar] [CrossRef]
- Guidoum, N.; Soltani, F.; Mezache, A. Modeling of High-Resolution Radar Sea Clutter Using Two Approximations of the Weibull Plus Thermal Noise Distribution. Arab. J. Sci. Eng. 2022, 47, 14957–14967. [Google Scholar] [CrossRef]
- Watts, S.; Rosenberg, L. Challenges in radar sea clutter modelling. IET Radar Sonar Navig. 2022, 16, 1403–1414. [Google Scholar] [CrossRef]
- Zhao, J.; Jiang, R.; Li, R. Modeling of Non-homogeneous Sea Clutter with Texture Modulated Doppler Spectra. In Proceedings of the 2022 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xi’an, China, 25–27 October 2022; IEEE: New York, NY, USA, 2022. [Google Scholar]
- Wang, R.; Li, X.; Zhang, Z.; Ma, H.-G. Modeling and simulation methods of sea clutter based on measured data. Int. J. Model. Simul. Sci. Comput. 2020, 12, 2050068. [Google Scholar] [CrossRef]
- Amani, M.; Moghimi, A.; Mirmazloumi, S.M.; Ranjgar, B.; Ghorbanian, A.; Ojaghi, S.; Ebrahimy, H.; Naboureh, A.; Nazari, M.E.; Mahdavi, S.; et al. Ocean Remote Sensing Techniques and Applications: A Review (Part I). Water 2022, 14, 3400. [Google Scholar] [CrossRef]
- El Mashade, M.B. Heterogeneous Performance Assessment of New Approach for Partially-Correlated χ2-Targets Adaptive Detection. Radioelectron. Commun. Syst. 2021, 64, 633–648. [Google Scholar] [CrossRef]
- Rosenberg, L.; Bocquet, S. The Pareto distribution for high grazing angle sea-clutter. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; IEEE: New York, NY, USA, 2013. [Google Scholar]
- Mezache, A.; Bentoumi, A.; Sahed, M. Parameter estimation for compound-Gaussian clutter with inverse-Gaussian texture. IET Radar Sonar Navig. 2017, 11, 586–596. [Google Scholar] [CrossRef]
- Medeiros, D.S.; Garcia, F.D.A.; Machado, R.; Filho, J.C.S.S.; Saotome, O. CA-CFAR Performance in K-Distributed Sea Clutter With Fully Correlated Texture. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Mahgoun, H.; Taieb, A.; Azmedroub, B.; Souissi, B. Generalized Pareto distribution exploited for ship detection as a model for sea clutter in a Pol-SAR application. In Proceedings of the 2022 7th International Conference on Image and Signal Processing and their Applications (ISPA), Mostaganem, Algeria, 8–9 May 2022; IEEE: New York, NY, USA, 2022. [Google Scholar]
- Wang, J.; Wang, Z.; He, Z.; Li, J. GLRT-Based Polarimetric Detection in Compound-Gaussian Sea Clutter With Inverse-Gaussian Texture. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Cao, C.; Zhang, J.; Zhangs, X.; Gao, G.; Zhang, Y.; Meng, J.; Liu, G.; Zhang, Z.; Han, Q.; Jia, Y.; et al. Modeling and Parameter Representation of Sea Clutter Amplitude at Different Grazing Angles. IEEE J. Miniat. Air Space Syst. 2022, 3, 284–293. [Google Scholar] [CrossRef]
- Fan, Y.; Chen, D.; Tao, M.; Su, J.; Wang, L. Parameter Estimation for Sea Clutter Pareto Distribution Model Based on Variable Interval. Remote Sens. 2022, 14, 2326. [Google Scholar] [CrossRef]
- Zebiri, K.; Mezache, A. Triple-order statistics-based CFAR detection for heterogeneous Pareto type I background. Signal Image Video Process. 2023, 17, 1105–1111. [Google Scholar] [CrossRef]
- Hu, C.; Luo, F.; Zhang, L.; Fan, Y.; Chen, S. Widening valid estimation range of multilook Pareto shape parameter with closed-form estimators. Electron. Lett. 2016, 52, 1486–1488. [Google Scholar] [CrossRef]
- Shui, P.L.; Zou, P.J.; Feng, T. Outlier-robust truncated maximum likelihood parameter estimators of generalized Pareto distributions. Digit. Signal Process. 2022, 127, 103527. [Google Scholar] [CrossRef]
- Tian, C.; Shui, P.-L. Outlier-Robust Truncated Maximum Likelihood Parameter Estimation of Compound-Gaussian Clutter with Inverse Gaussian Texture. Remote Sens. 2022, 14, 4004. [Google Scholar] [CrossRef]
- Shui, P.L.; Tian, C.; Feng, T. Outlier-robust Tri-percentile Parameter Estimation Method of Compound-Gaussian Clutter with Inverse Gaussian Textures. J. Electron. Inf. Technol. 2023, 45, 542–549. [Google Scholar] [CrossRef]
- YU, H.; Shui, P.L.; Shi, S.N.; Yang, C.J. Combined Bipercentile Parameter Estimation of Generalized Pareto Distributed Sea Clutter Model. J. Electron. Inf. Technol. 2019, 41, 2836–2843. [Google Scholar] [CrossRef]
- Xue, J.; Xu, S.; Liu, J.; SHUI, P. Model for Non-Gaussian Sea Clutter Amplitudes Using Generalized Inverse Gaussian Texture. IEEE Geosci. Remote Sens. Lett. 2019, 16, 892–896. [Google Scholar] [CrossRef]
- Xia, X.-Y.; Shui, P.-L.; Zhang, Y.-S.; Li, X.; Xu, X.-Y. An Empirical Model of Shape Parameter of Sea Clutter Based on X-Band Island-Based Radar Database. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Liang, X.; Yu, H.; Zou, P.-J.; Shui, P.-L.; Su, H.-T. Multiscan Recursive Bayesian Parameter Estimation of Large-Scene Spatial-Temporally Varying Generalized Pareto Distribution Model of Sea Clutter. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Tang, J.; Liu, G.; Pan, Q. A Review on Representative Swarm Intelligence Algorithms for Solving Optimization Problems: Applications and Trends. IEEE/CAA J. Autom. Sin. 2021, 8, 1627–1643. [Google Scholar] [CrossRef]
- Wei, X.; Huang, H. A Survey on Several New Popular Swarm Intelligence Optimization Algorithms; Research Square Platform LLC: Durham, NC, USA, 2023. [Google Scholar]
- Hong, S.-H.; Kim, J.; Jung, H.-S. Special Issue on Selected Papers from “International Symposium on Remote Sensing 2021”. Remote Sens. 2023, 15, 2993. [Google Scholar] [CrossRef]
- Shui, P.-L.; Yu, H.; Shi, L.-X.; Yang, C.-J. Explicit bipercentile parameter estimation of compound-Gaussian clutter with inverse gamma distributed texture. IET Radar Sonar Navig. 2018, 12, 202–208. [Google Scholar] [CrossRef]
- Sergievskaya, I.A.; Ermakov, S.A.; Ermoshkin, A.V.; Kapustin, I.A.; Shomina, O.V.; Kupaev, A.V. The Role of Micro Breaking of Small-Scale Wind Waves in Radar Backscattering from Sea Surface. Remote Sens. 2020, 12, 4159. [Google Scholar] [CrossRef]
- Hu, C.; Luo, F.; Zhang, L.R.; Fan, Y.F.; Chen, S.L. Widening Efficacious Parameter Estimation Range of Multi-look Pareto Distribution. J. Electron. Inf. Technol. 2017, 39, 412–416. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: New York, NY, USA, 2002. [Google Scholar]
- Wu, J.; Hu, J.; Yang, Y. Optimized Design of Large-Body Structure of Pile Driver Based on Particle Swarm Optimization Improved BP Neural Network. Appl. Sci. 2023, 13, 7200. [Google Scholar] [CrossRef]
- Xu, Z.; Xia, D.; Yong, N.; Wang, J.; Lin, J.; Wang, F.; Xu, S.; Ge, D. Hybrid Particle Swarm Optimization for High-Dimensional Latin Hypercube Design Problem. Appl. Sci. 2023, 13, 7066. [Google Scholar] [CrossRef]
- Chandrashekar, C.; Krishnadoss, P.; Kedalu Poornachary, V.; Ananthakrishnan, B.; Rangasamy, K. HWACOA Scheduler: Hybrid Weighted Ant Colony Optimization Algorithm for Task Scheduling in Cloud Computing. Appl. Sci. 2023, 13, 3433. [Google Scholar] [CrossRef]
- Wang, D.; Meng, L. Performance Analysis and Parameter Selection of PSO Algorithms. Acta Autom. Sin. 2016, 42, 1552–1561. [Google Scholar]
- Xu, S.; Wang, L.; Shui, P.; Li, X.; Zhang, J. Iterative maximum likelihood and zFlogz estimation of parameters of compound-Gaussian clutter with inverse gamma texture. In Proceedings of the 2018 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Qingdao, China, 14–16 September 2018; IEEE: New York, NY, USA, 2018. [Google Scholar]
- Xu, S.; Ru, H.; Li, D.; Shui, P.; Xue, J. Marine Radar Small Target Classification Based on Block-Whitened Time–Frequency Spectrogram and Pre-Trained CNN. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–11. [Google Scholar] [CrossRef]
- Li, D.; Zhao, Z.; Zhao, Y. Analysis of Experimental Data of IPIX Radar. In Proceedings of the 2018 IEEE International Conference on Computational Electromagnetics (ICCEM), Chengdu, China, 26–28 March 2018; IEEE: New York, NY, USA, 2018. [Google Scholar]
- Ding, H.; Liu, N.B.; Dong, Y.L.; Chen, X.L.; Guan, J. Overview and Prospects of Radar Sea Clutter Measurement Experiments. J. Radars 2019, 8, 281–302. [Google Scholar] [CrossRef]
- Liu, N.B.; Ding, H.; Huang, Y.; Dong, Y.L.; Wang, G.Q.; Dong, K. Annual Progress of the Sea-detecting X-band Radar and Data Acquisition Program. J. Radars 2021, 10, 173–182. [Google Scholar] [CrossRef]
- Fan, Y.; Tao, M.; Su, J.; Wang, L. Analysis of goodness-of-fit method based on local property of statistical model for airborne sea clutter data. Digit. Signal Process. 2020, 99, 102653. [Google Scholar] [CrossRef]
- Huang, P.; Zou, Z.; Xia, X.-G.; Liu, X.; Liao, G. A Statistical Model Based on Modified Generalized-K Distribution for Sea Clutter. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]


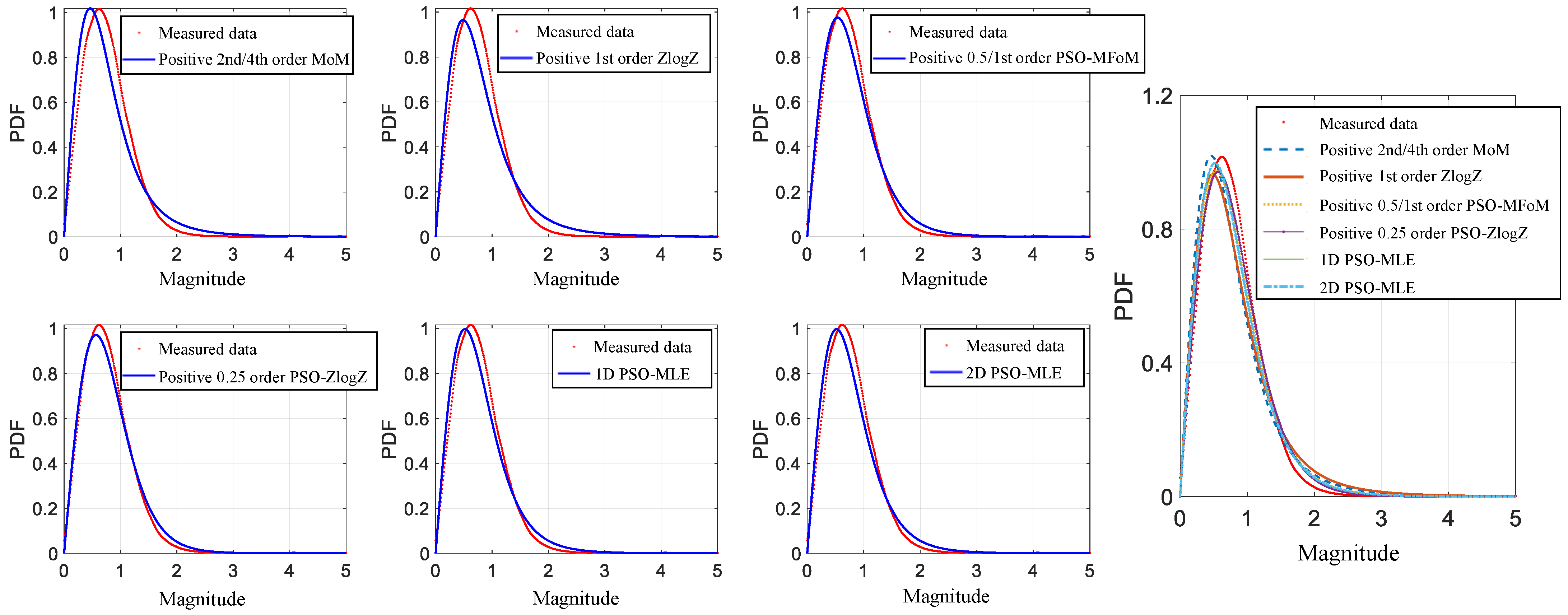
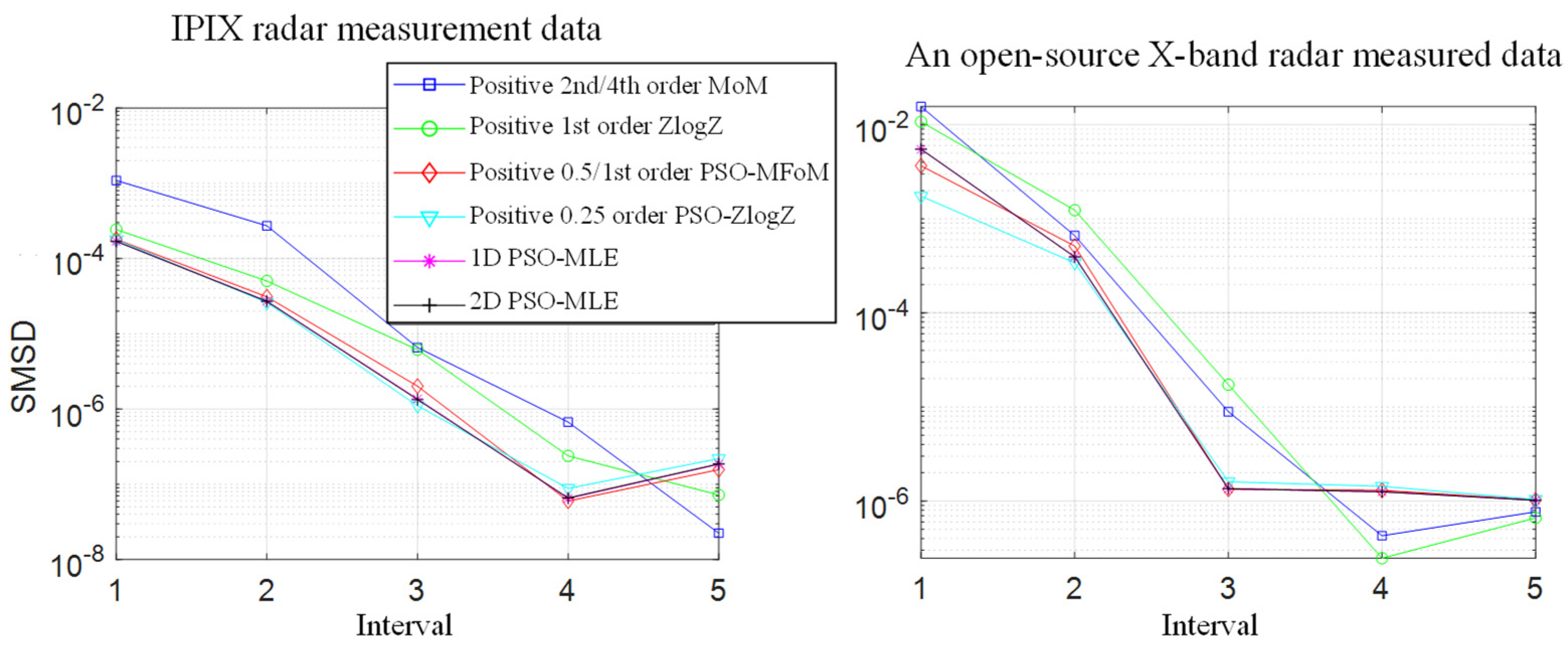

| Parameter Estimation Methods | Shape Parameter Estimated Range | Estimated Expressions |
|---|---|---|
| Positive 2nd/4th-order moment estimation (MoM) | (2, +∞) | Closure |
| Positive 0.5th/1st-order moment estimation (MfoM) | (0.5, +∞) | Non-closed |
| Positive 1st-order logarithmic moment estimation () | (1, +∞) | Closure |
| Positive 0.25th-order logarithmic moment estimation (Zlogz) | (0.25, +∞) | Non-closed |
| Maximum Likelihood Estimation (MLE) | (0, +∞) | Non-closed |
| Parameter Estimation Methods | MoM (2nd/4th-Order) | ZlogZ (1st-Order) | PSO-MFoM (0.5th/1st-Order) | PSO-ZlogZ (0.25th-Order) | PSO-MLE (1D) | PSO-MLE (2D) |
|---|---|---|---|---|---|---|
| Time/s | 2.43 × 10−2 | 8.94 × 10−3 | 3.02 × 10−2 | 3.66 × 10−2 | 8.51 × 10−2 | 9.37 × 10−1 |
| Estimation Method | IPIX Radar Measurement Data | An X-Band Radar Open-Source Measurement Data | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MoM (2/4) | ZlogZ (1) | MFoM (05/1) | ZlogZ (0.25) | MLE (1D) | MLE (2D) | MoM (2/4) | ZlogZ (1) | MFoM (0.5/1) | ZlogZ (0.25) | MLE (1D) | MLE (2D) | |
| Shape parameter | 3.125 | 2.636 | 2.419 | 2.351 | 2.415 | 2.410 | 2.165 | 2.096 | 3.933 | 6.022 | 3.599 | 3.603 |
| Scale Parameter | 0.225 | 0.298 | 0.330 | 0.343 | 0.329 | 0.330 | 0.876 | 0.817 | 0.392 | 0.240 | 0.454 | 0.453 |
| Assessment Metrics | MoM (2/4) | ZlogZ (1) | MFoM (05/1) | ZlogZ (0.25) | MLE (1D) | MLE (2D) |
|---|---|---|---|---|---|---|
| MSD | 2.73 × 10−4 | 5.98 × 10−5 | 4.26 × 10−5 | 4.10 × 10−5 | 3.96 × 10−5 | 3.94 × 10−5 |
| RMSD | 1.65 × 10−2 | 7.70 × 10−3 | 6.50 × 10−3 | 6.40 × 10−3 | 6.30 × 10−3 | 6.30 × 10−3 |
| K-S | 4.39 × 10−2 | 2.01 × 10−2 | 1.91 × 10−2 | 1.74 × 10−2 | 1.90 × 10−2 | 1.90 × 10−2 |
| Assessment Metrics | MoM (2/4) | ZlogZ (1) | MFoM (05/1) | ZlogZ (0.25) | MLE (1D) | MLE (2D) |
|---|---|---|---|---|---|---|
| MSD | 3.30 × 10−3 | 2.40 × 10−3 | 8.36 × 10−4 | 4.17 × 10−4 | 1.20 × 10−3 | 1.20 × 10−3 |
| RMSD | 5.70 × 10−2 | 4.90 × 10−2 | 2.89 × 10−2 | 2.04 × 10−2 | 3.43 × 10−2 | 3.44 × 10−2 |
| K-S | 5.84 × 10−2 | 6.09 × 10−2 | 3.37 × 10−2 | 2.84 × 10−2 | 3.00 × 10−2 | 3.01 × 10−2 |
| Parameter Estimation Methods | PSO | HPSO | 2nd/4th-MoM | 1st-Order ZlogZ | MLE |
|---|---|---|---|---|---|
| Running time (s) | 3.42 × 10−1 | 3.22 × 10−1 | 5.81 × 10−2 | 2.53 × 10−2 | 5.56 × 10−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Li, Q. Enhanced Particle Swarm Optimization Algorithm for Sea Clutter Parameter Estimation in Generalized Pareto Distribution. Appl. Sci. 2023, 13, 9115. https://doi.org/10.3390/app13169115
Yang B, Li Q. Enhanced Particle Swarm Optimization Algorithm for Sea Clutter Parameter Estimation in Generalized Pareto Distribution. Applied Sciences. 2023; 13(16):9115. https://doi.org/10.3390/app13169115
Chicago/Turabian StyleYang, Bin, and Qing Li. 2023. "Enhanced Particle Swarm Optimization Algorithm for Sea Clutter Parameter Estimation in Generalized Pareto Distribution" Applied Sciences 13, no. 16: 9115. https://doi.org/10.3390/app13169115
APA StyleYang, B., & Li, Q. (2023). Enhanced Particle Swarm Optimization Algorithm for Sea Clutter Parameter Estimation in Generalized Pareto Distribution. Applied Sciences, 13(16), 9115. https://doi.org/10.3390/app13169115






