Wave Diffraction from a Bicone Conjoined with an Open-Ended Conical Cavity

Abstract

The problem of axially symmetric TM-wave diffraction from a bicone conjoined with an open-ended conical cavity is analysed rigorously. The scatterer is formed by the perfectly conducting semi-infinite and truncated semi-infinite conical surfaces; the spherical termination of an internal area of the truncated cone creates the open-ended cavity. In this paper the certain physical aspects of diffraction which are known to cause mathematical difficulties are considered. It includes an accurate analysis of the wave-mode transformation phenomena at the open end of the cavity, as well as a study of wave radiation from the cavity into the biconical waveguide. The primary outcome of this paper is a precise treatment of the wave diffraction problem mentioned above using new techniques and establishing new properties of resonance modes’ penetration into the biconical waveguide region.

1. Introduction

The progress of wave diffraction simulation for determining the coupling between the radiating elements in radiophysics, optics, and acoustics often relies on the availability of solutions to canonical problems. This paper considers the bicone conjoined with an open-ended conical cavity formed by a perfectly conducting semi-infinite cone and a truncated one with an internal spherical termination. Variations in its geometric parameters make it possible to simulate wideband antennas, reference measurement probes, and verification antennas, which are the canonical area of applying the biconical surfaces [1,2,3,4]. Nowadays, an interest in bicones is associated with the design of nanoprobes and their application in nanotechnologies [5,6,7]. The main reason for their application is TEM wave excitation in the coaxial biconical region and the electromagnetic energy concentration near the conical vertices [6]. If, for example, the semi-infinite biconical shoulder degenerates into the plane, this structure becomes a model of the functional elements of an optic near-field microscope [6,7]. This structure includes the flat “preparation” desk illuminated by an open-ended conical waveguide and the remote sensing TEM wave “detector” created by the biconical area. When the truncated semi-infinite cone degenerates into the plane with a semi-spherical cavity, we arrive at the model of the cavity-like defect [8] detected by the conical probe [9]. This structure also has the potential to be applied for modeling of the absorbent properties of scattering surfaces [10,11,12].

Since the scatterer under consideration consists of fragments of canonical surfaces in a spherical coordinate system, this study aims to rigorously solve a corresponding wave diffraction problem. Such a solution correctly takes into account the wave interaction between the different scattering elements of a biconical structure and can be used to verify modern software packages and approximate approaches. For our study, we modified the well-known mode-matching technique; the modification involves transformations that allow the fields singularity at the edges to be explicitly taken into account.

The canonical results of wave diffraction from finite/truncated biconical scatterers have been obtained using field representations through the series of the normal waves of subdomains and application of traditional mode matching for seeking the unknown complex amplitudes of the scattered modes. In the literature, studies of wave diffraction from biconical structures are mainly focused on bicones formed by finite conical shoulders, or finite and semi-infinite ones. As a rule, they consider bicones formed by a hollow cone and closed by a spherical cap or partially filled by the dielectric. The general scheme of usage of the mode-matching method and its application for solving various problems of wave diffraction from bicones, as well as an analysis of the earlier works in this direction, was given in [13] and later in [14,15]. The solution of wave diffraction problems for particular cases of biconical scatterers is given via the Wiener–Hopf technique, which involves a Kontorovich–Lebedev integral transform [16]. Despite the simplicity of mode matching and its physical validity, the mode-matching series is the singular cause of the field singularity at the edges. Therefore, it needs to be taken into account. In our previous study, an explicit inversion of the mode-matching singularity was proposed for finite/truncated conical and biconical scatterers [17,18,19,20,21,22,23,24,25]; this technique is generally called an analytical regularization procedure. The main reason for such processing is to guarantee an accurate solution to the problem which satisfies all the necessary conditions, including the edge condition, for any geometrical and frequency parameters except the spectrum points. The basic principles of this powerful tool are presented in [26,27,28,29]. The application of this method for an accurate analysis of the spherical and simple sphere-conical cavities has been applied in [29,30,31]. It is worth noting that the well-known open-ended parallel-plate waveguide cavities have been studied rigorously using the Wiener–Hopf technique [32]. This technique has also been applied to analyse open-ended cylindrical and spherical cavities [33,34,35]. Various directions of analytical regularization methods are developed in [36,37,38,39], and references therein.

In this paper, we developed an analytical regularization technique to accurately study wave diffraction from a new geometry. Our study includes alternative techniques for deriving the constitutive equations, establishing the correlation between them, and proposing a new general method to seek the sets of regularizing operators that explicitly invert the singular part of the problem. We also derive an approximate solution for the small size of the cavity hole and an approximate expression to determine the perturbation of the cavity spectrum. Using numerical calculations, we study the near and far fields for the wideband parameters of our problem.

2. Statement of the Problem

Let us consider, in a spherical coordinate system $(r,\theta ,\phi )$, a perfectly conducting biconical scatterer conjoined with an open-ended conical cavity $Q=Q_1\bigcup Q_2$, where $Q_1$ is the semi-infinite cone and $Q_2$ is the truncated semi-infinite one with an internal spherical termination; the termination forms an open-ended conical cavity:

$$\begin{array}{c}{Q}_1:\left\{r\in (0,\infty );\theta ={\gamma }_1;\phi \in [0,2\pi )\right\},\hfill \\ \hfill \\ Q_2:\left\{(r,\theta ,\phi )|r\in \left\{\begin{array}{c}(a_1,\infty );\theta ={\gamma }_2-0\hfill \\ (a_1,c_1);\theta ={\gamma }_2+0\hfill \end{array}\right\},\theta ={\gamma }_2\right\}{\displaystyle \bigcup _{\phi \in [0,2\pi )}}\left\{(r,\theta ,\phi )|r=c_1;{\gamma }_2\le \theta \le \pi \right\}.\hfill \end{array}$$

(1)

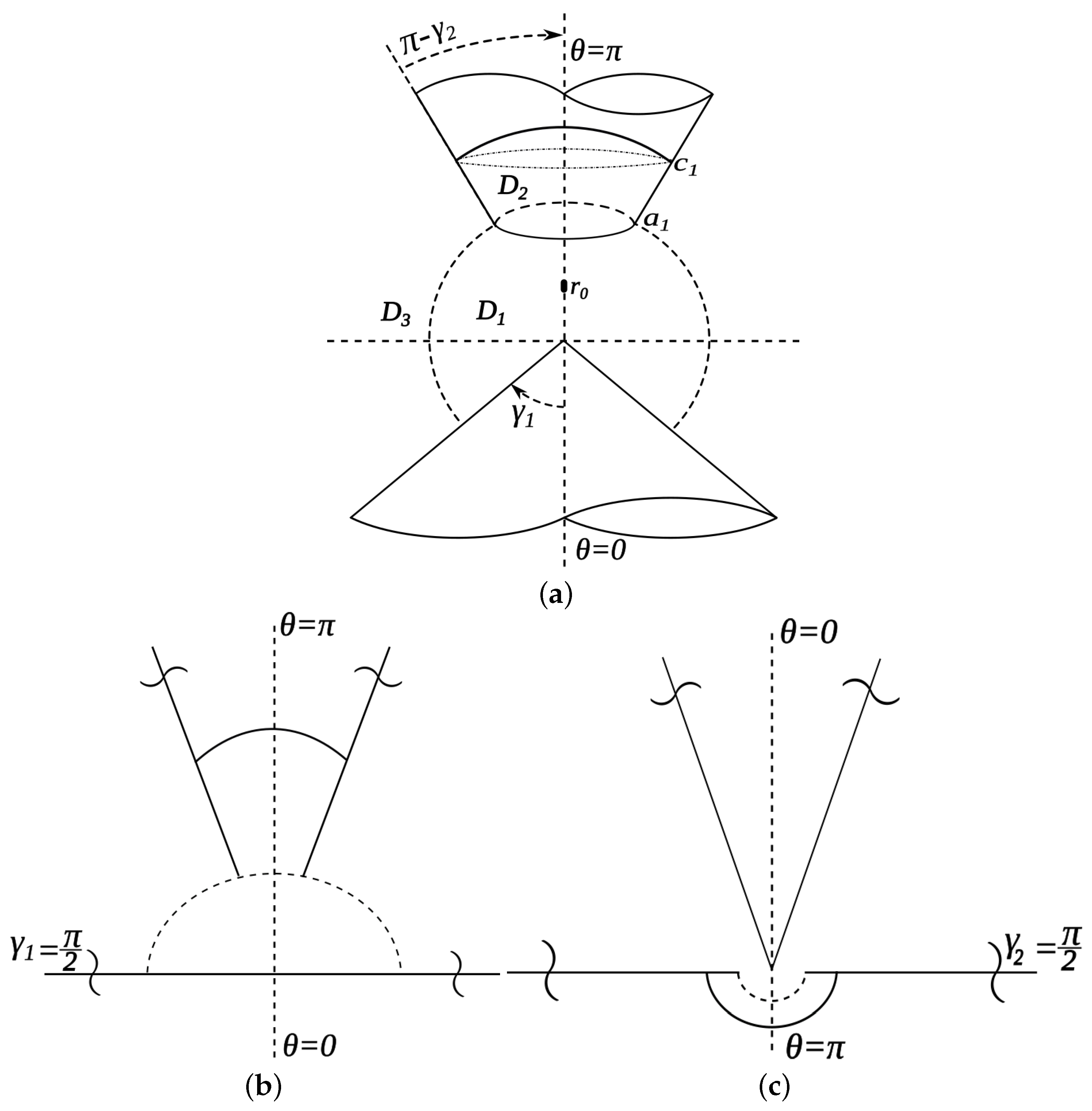
Here, ${\gamma }_1$ and ${\gamma }_2$ are the generating angles; $a_1$ and $c_1$ are the radial coordinates of the cavity aperture and the spherical termination, respectively, $c_1>a_1$; ${\gamma }_2>{\gamma }_1$ and ${\gamma }_{1\left(2\right)}\ne \pi /2$. The biconical scatterer and its particular cases are shown in Figure 1.

Let the bicone Q be excited axially symmetric by the TM-wave, produced by an electric dipole located on the symmetry axis. The time factor $e^{-i\omega t}$ is suppressed throughout this paper. Since the incident modes are independent of the azimuth angle $\phi$, then, as follows from Maxwell’s equations, only the three nonzero field components $E_r,E_{\theta }$, and $H_{\phi }(r,\theta )$ are excited [40]. The electric field components are expressed in terms of $H_{\phi }$ by

$$\begin{array}{c}{E}_r=-{(i\omega \epsilon rsin\theta )}^{-1}{\partial }_{\theta }(sin\theta H_{\phi }),E_{\theta }={\left(i\omega \epsilon r\right)}^{-1}{\partial }_r\left(r{H}_{\phi }\right)\hfill \end{array},$$

(2)

where $\epsilon$ is the dielectric permittivity of the medium.

Taking into account the axial symmetry of the initial problem, let us formulate the mixed boundary value problem to determine the $H_{\phi }$-field diffracted from Q as

$${\nabla }^2{H}_{\phi }-{(rsin\theta )}^{-2}{H}_{\phi }+k^2{H}_{\phi }=0,$$

(3)

$$\begin{array}{c}{(sin\theta )}^{-1}{\partial }_{\theta }\left[sin\theta (H_{\phi }+H_{\phi }^i)\right]=0\hfill \\ \hfill \\ \mathrm{if}r,\theta \in \{r\in (0,\infty ),\theta ={\gamma }_1\}\cup \{r\in (a_1,\infty ),\theta ={\gamma }_2-0\}\cup \{r\in (a_1,c_1),\theta ={\gamma }_2+0\}\hfill \end{array}$$

(4)

and

$$\begin{array}{c}{r}^{-1}{\partial }_r\left[r(H_{\phi }+H_{\phi }^i)\right]=0\hfill \\ \hfill \\ \mathrm{if}r,\theta \in \{r=c_1,\theta \in [{\gamma }_2,\pi ]\}.\hfill \end{array}$$

(5)

Here, $k=\omega \sqrt{\epsilon \mu }$ is the wave number; $\mu$ is the magnetic permeability; ${\nabla }^2$ is the axially symmetric Laplace operator in the spherical coordinate system;

$${\nabla }^2={\partial }_{rr}^2+2r^{-1}{\partial }_r+{(r^{2}sin\theta )}^{-1}{\partial }_{\theta }\left(sin\theta {\partial }_{\theta }\right);$$

$H_{\phi }^i$ is the known magnetic component of the incident field, and $H_{\phi }+H_{\phi }^i=H_{\phi }^t$ is the total field.

We search for the solution of the mixed boundary value problems (3)–(5) in the class of functions that satisfy the Silver–Muller radiation condition [41]

$$\underset{{\gamma }_1\le \theta \le {\gamma }_2}{\underset{r\to \infty }{lim}r\left[{\stackrel{\rightharpoonup }{e}}_r\times \overrightarrow{H}+Z^{-1}\overrightarrow{E}\right]}=0·{\overrightarrow{e}}_{\theta },$$

(6)

where $\overrightarrow{H}=(0,0,{\overrightarrow{e}}_{\phi }{H}_{\phi })$, $\overrightarrow{E}=(0,{\overrightarrow{e}}_{\theta }{E}_{\theta },0)$, $Z=\sqrt{\mu /\epsilon }$ is the medium wave resistance, and the energy limitation condition is [42]

$${\int }_V\left(\epsilon |\overrightarrow{E}{|}^2+\mu {\left|\overrightarrow{H}\right|}^2\right)dv<\infty .$$

(7)

Here, V is any finite volume of integration, $dv=r^{2}sin\theta drd\theta d\phi$. This condition, in our case, is reduced to the fulfilment of the Meixner condition at the edge of Q. In order to fulfil the radiation condition and prevent the arrival of waves from infinity, we assume that $k=k^{\prime }+i{k}^{\prime \prime }$, $k^{\prime }>0$, $k^{\prime \prime }\ge 0$. Due to these two additional conditions, the diffraction problems (3)–(5) are properly posed.

3. Fields Representation

Let us split the area surrounding the biconical scatterer Q into three canonical sub-regions as (see Figure 1a)

$$D_1:\left\{r\in (0,a_1),\theta \in ({\gamma }_1,\pi )\right\},D_2:\left\{r\in (a_1,c_1),\theta \in ({\gamma }_2,\pi ]\right\},D_3:\left\{r\in (a_1,\infty ),\theta \in [{\gamma }_1,{\gamma }_2)\right\}.$$

(8)

Here, for further convenience, the coordinate $\phi \in [0,2\pi )$ is omitted in the notation.

Since the unknown $H_{\phi }$ component satisfies Equation (3), we apply for the solution the method of separation variables and represent it using eigenfunctions in the appropriate domains $D_l(l=1,2,3)$, determined in (8) as $H_{\phi }^{\left(l\right)}=\sum {\left(H_{\phi }^{\left(l\right)}\right)}_n$, where ${\left(H_{\phi }^{\left(l\right)}\right)}_n$ is a normal magnetic TM-mode in a spherical coordinate system [43];

$${\left(H_{\phi }^{\left(l\right)}\right)}_n={\displaystyle \frac{i\omega \epsilon }{\sqrt{sr}}}\left[g_n^{\left(l\right)}{I}_{{\eta }_n}\left(sr\right)+t_n^{\left(l\right)}{K}_{{\eta }_n}\left(sr\right)\right]{\mathsf{\Phi }}_{{\eta }_n-1/2}^{\left(l\right)}(cos\theta ).$$

(9)

Here, $I_{{\eta }_n}\left(sr\right)$ and $K_{{\eta }_n}\left(sr\right)$ are modified Bessel and Macdonald functions; the indices ${\eta }_n$ and unknown coefficients $g_n^{\left(l\right)}$ and $t_n^{\left(l\right)}$ ($n=1,2,3,\dots$) are to be determined from the problem solution.

In order to satisfy the energy limitation and the radiation conditions, we accept that $t_n^{\left(l\right)}\equiv 0$ for $l=1$ and $g_n^{\left(l\right)}\equiv 0$ for $l=3$. The eigenfunctions ${\mathsf{\Phi }}_{{\eta }_n-1/2}^{\left(l\right)}(cos\theta )$ ($n=1,2,3,\dots$) are determined in the regions $D_l$ from the solution of Sturm–Liouville problems for the differential equation

$${\stackrel{⌢}{\Delta }}_{\theta }{\mathsf{\Phi }}_{{\eta }_n-1/2}^{\left(l\right)}(cos\theta )=-({\eta }_n^2-1/4){\mathsf{\Phi }}_{{\eta }_n-1/2}^{\left(l\right)}(cos\theta ),$$

(10)

where

$${\stackrel{⌢}{\Delta }}_{\theta }={(sin\theta )}^{-1}{\partial }_{\theta }\left(sin\theta {\partial }_{\theta }\right)-{(sin\theta )}^{-2}$$

is the Beltrami operator. We consider here the limited solution of Equation (10), which satisfies the boundary condition (4) that is taken in the form

$${(sin\gamma )}^{-1}{\partial }_{\theta }\left[sin\gamma {\mathsf{\Phi }}_{{\eta }_n-1/2}^{\left(l\right)}(cos\gamma )\right]=0$$

(11)

with $\gamma ={\gamma }_1$ if $l=1$, and $\gamma ={\gamma }_2$ if $l=2,3$.

Let us represent them as

$$\begin{array}{c}\underset{{\gamma }_1\le \theta \le \pi }{{\mathsf{\Phi }}_{z_n-1/2}^{\left(1\right)}(cos\theta )={\partial }_{\theta }{P}_{z_n-1/2}(-cos\theta )},\hfill \\ \underset{{\gamma }_2<\theta \le \pi }{{\mathsf{\Phi }}_{{\mu }_n-1/2}^{\left(2\right)}(cos\theta )={\partial }_{\theta }{P}_{{\mu }_n-1/2}(-cos\theta )},\hfill \\ \underset{{\gamma }_1\le \theta <{\gamma }_2}{{\mathsf{\Phi }}_{{\nu }_n-1/2}^{\left(3\right)}(cos\theta )={\mathsf{\Psi }}_{{\nu }_n-1/2}(cos\theta ).}\hfill \end{array}$$

(12)

Here, ${\eta }_n={\mu }_n({\nu }_n,z_n)$; $P_{\eta -1/2}(\pm cos\theta )$ and ${\partial }_{\theta }{P}_{\eta -1/2}(\pm cos\theta )=\pm P_{\eta -1/2}^1(\pm cos\theta )$ are the Legendre and the associated Legendre functions of the first order, respectively [44];

$${\mathsf{\Psi }}_{{\nu }_n-1/2}(cos\theta )=\left\{\begin{array}{c}{(sin\theta )}^{-1},n=1,\hfill \\ \hfill \\ {\partial }_{\theta }[R_{{\nu }_n-1/2}(cos\theta )],n>1,\hfill \end{array}\right.$$

(13)

where

$$\begin{array}{c}{R}_{{\nu }_n-1/2}(cos\theta )=P_{{\nu }_n-1/2}(cos\theta )P_{{\nu }_n-1/2}(-cos{\gamma }_1)-P_{{\nu }_n-1/2}(-cos\theta )P_{{\nu }_n-1/2}(cos{\gamma }_1)\hfill \end{array}.$$

(14)

Taking into account the relationship

$${(sin\theta )}^{-1}{\partial }_{\theta }\left[sin\theta {\partial }_{\theta }{P}_{\eta -1/2}(\pm cos\theta )\right]=-({\eta }^2-1/4)P_{\eta -1/2}(\pm cos\theta )$$

(15)

we find that the functions (12) satisfy the boundary condition (11) if their indices are determined from the solution of transcendental equations as

$$\begin{array}{c}{P}_{z_n-1/2}(-cos{\gamma }_1)=0,\hfill \\ \hfill \\ P_{{\mu }_n-1/2}(-cos{\gamma }_2)=0,\hfill \\ \hfill \\ R_{{\nu }_n-1/2}(cos{\gamma }_2)=0.\hfill \end{array}$$

(16)

The roots of these equations are real and in view that $P_{\eta -1/2}(\pm cos\theta )=P_{-\eta -1/2}(\pm cos\theta )$ are arranged symmetrically above zero on the number axis [45]. In order to satisfy the Meixner condition at the vertex of the cone, we consider the sets of the positive roots ${\left\{{\mu }_n\right\}}_{n=1}^{\infty }$, ${\left\{{\nu }_n\right\}}_{n=1}^{\infty }$, and ${\left\{z_n\right\}}_{n=1}^{\infty }$ that are arranged in growing sequences; the set of the positive roots of the transcendental equation $R_{{\nu }_n-1/2}(cos{\gamma }_2)=0$ starts from ${\nu }_1=1/2$ and ${\nu }_n\ne n-1/2$ for $n=2,3,4,\dots$.

Without loss of generality, the bicone Q is excited by the TM-modes produced by the vertical dipole that is located at the axis of symmetry $\{0\le r<\infty ;\theta =\pi \}$ in the conical region $D_1$. For further convenience, we represent the incident field in the form of the total field of the vertical dipole in the conical region limited by the semi-infinite conical surface $Q_1$ [22]:

$$H_{\phi }^{\left(i\right)}={\displaystyle \frac{i\omega \epsilon }{\sqrt{sr}}}\sum _{n=1}^{\infty }{A}_n{\partial }_{\theta }\left[P_{z_n-1/2}(-cos\theta )\right]\left\{\begin{array}{c}{I}_{z_n}\left(s{r}_0\right)K_{z_n}\left(sr\right),r>r_0,\hfill \\ K_{z_n}\left(s{r}_0\right)I_{z_n}\left(sr\right),r<r_0.\hfill \end{array}\right.$$

(17)

Here,

$$A_n={\displaystyle \frac{2A^{\left(0\right)}{z}_n{P}_{z_n-1/2}(cos{\gamma }_1)/\sqrt{s{r}_0}}{cos\left(\pi z_n\right){\partial }_z\left[P_{z_n-1/2}(-cos{\gamma }_1)\right]}},$$

$A^{\left(0\right)}=\pi I_r^{e}hZ/r_0$, $0<r_0<a_1$, $I_r^e$ is the electric current, and h is the length of the dipole.

Let us represent the total magnetic field in each of the sub-regions (8) as

$$H_{\phi }^t(r,\theta )={\displaystyle \frac{i\omega \epsilon }{\sqrt{sr}}}\left\{\begin{array}{c}{H}_{\phi }^{\left(i\right)}(r,\theta ){\displaystyle \frac{\sqrt{sr}}{i\omega \epsilon }}+{\displaystyle \sum _{n=1}^{\infty }}{x}_n^{\left(1\right)}{\partial }_{\theta }\left[P_{z_n-1/2}(-cos\theta )\right]{\displaystyle \frac{I_{z_n}\left(sr\right)}{I_{z_n}\left(s{a}_1\right)}},(r,\theta )\in D_1,\hfill \\ \hfill \\ {\displaystyle \sum _{n=1}^{\infty }}{\partial }_{\theta }\left[P_{{\mu }_n-1/2}(-cos\theta )\right]\left[x_n^{(2;1)}{\displaystyle \frac{K_{{\mu }_n}\left(sr\right)}{K_{{\mu }_n}\left(s{a}_1\right)}}+x_n^{(2;2)}{\displaystyle \frac{I_{{\mu }_n}\left(sr\right)}{I_{{\mu }_n}\left(s{a}_1\right)}}\right],(r,\theta )\in D_2,\hfill \\ \hfill \\ {\displaystyle \sum _{n=1}^{\infty }}{x}_n^{\left(3\right)}{\mathsf{\Psi }}_{{\nu }_n-1/2}(cos\theta ){\displaystyle \frac{K_{{\nu }_n}\left(sr\right)}{K_{{\nu }_n}\left(s{a}_1\right)}},(r,\theta )\in D_3.\hfill \end{array}\right.$$

(18)

Here, $x_n^{\left(1\right)}$, $x_n^{(2;1)}$, $x_n^{(2;2)}$, and $x_n^{\left(3\right)}$ are unknown expansion coefficients. It should be noted that according to the relations (11), (13), and (16), the representation (18) satisfies the boundary conditions (4) as well as the radiation and energy limitation conditions. In order to satisfy the Meixner condition at the aperture’s edge, we search the unknown expansion coefficients in the class of sequences $x_n^{\left(1\right)},x_n^{(2;1)}=O\left(n^{-2}\right)$, and $x_n^{\left(3\right)}=O\left(n^{-3/2}\right)$ for $n\to \infty$. The asymptotic behaviour of the unknowns $x_n^{(2;2)}$ is to be determined.

4. Mode-Matching Series Equations

Using the boundary condition (5) and representation (18), we arrive at the relation as

$$x_n^{(2;2)}=x_n^{(2;1)}{{\rm Y}}_{{\mu }_n}\left(\omega \right),$$

(19)

where

$${{\rm Y}}_{{\mu }_n}\left(\omega \right)=-{\displaystyle \frac{K_{{\mu }_n}\left(s{c}_1\right)I_{{\mu }_n}\left(s{a}_1\right)}{K_{{\mu }_n}\left(s{a}_1\right)I_{{\mu }_n}\left(s{c}_1\right)}}\left[{\displaystyle \frac{1+2s{c}_1{K}_{{\mu }_n}^{\prime }\left(s{c}_1\right)/K_{{\mu }_n}\left(s{c}_1\right)}{1+2s{c}_1{I}_{{\mu }_n}^{\prime }\left(s{c}_1\right)/I_{{\mu }_n}\left(s{c}_1\right)}}\right].$$

(20)

Considering the asymptotic properties of the modified Bessel and the Mcdonald functions and representation (20), we find that $x_n^{(2;2)}=O\left(n^{-2}{(a_1/c_1)}^{2n}\right)$ if $n\to \infty$.

In order to find the unknown expansion coefficients in (18), we use the mode matching of the tangential total fields $H_{\phi }^t$ and $E_{\theta }^t$ on the spherical surface $\stackrel{⌢}{S}:\{r=a_1,{\gamma }_1\le \theta \le \pi \}$, which covers the circular aperture of a truncated cone. This leads to the functional (series) equations that are defined on $\theta \in [{\gamma }_1,\pi ]$ with the associated Legendre functions kernel. Since the series representing the $E_{\theta }$ field is singular at the edge as $E_{\theta }(r,\theta )=O\left({\stackrel{⌢}{\rho }}^{-1/2}\right)$, where $\stackrel{⌢}{\rho }$ is the relative distance to the edge in the local coordinate system, the series are not absolutely convergent on $\stackrel{⌢}{S}$; their sums depend on the order of summation. Therefore, we depict the mode-matching series in the form of the limit transition as

$$\begin{array}{c}\underset{N\to \infty }{lim}\underset{(r,\theta )\in D_1}{{\displaystyle \sum _{n=1}^N}{P}_{z_{n-1/2}}^1(-cos\theta )\left[x_n^{\left(1\right)}+{\overline{A}}_n{\displaystyle \frac{K_{z_n}\left(s{a}_1\right)}{K_{z_n}\left(s{r}_0\right)}}\right]}\hfill \\ \hfill \\ =\left\{\begin{array}{c}\underset{P\to \infty }{lim}{\displaystyle \sum _{p=1}^P}{x}_n^{\left(2\right)}{P}_{{\mu }_{p-1/2}}^1(-cos\theta )\left[1+{{\rm Y}}_{{\mu }_p}\left(\omega \right)\right],(r,\theta )\in D_2,p=1,\dots P,\hfill \\ \hfill \\ -\underset{K\to \infty }{lim}{\displaystyle \sum _{k=1}^K}{x}_k^{\left(3\right)}{\mathsf{\Psi }}_{{\nu }_{k-1/2}}(cos\theta ),(r,\theta )\in D_3,k=1,\dots K;\hfill \end{array}\right.\hfill \end{array}$$

(21)

$$\begin{array}{c}\underset{N\to \infty }{lim}\underset{(r,\theta )\in D_1}{{\displaystyle \sum _{n=1}^N}{P}_{z_{n-1/2}}^1(-cos\theta )\left[x_n^{\left(1\right)}{\displaystyle \frac{I_{z_n}^{\prime }\left(s{a}_1\right)}{I_{z_n}\left(s{a}_1\right)}}+{\overline{A}}_n{\displaystyle \frac{K_{z_n}^{\prime }\left(s{a}_1\right)}{K_{z_n}\left(s{r}_0\right)}}\right]}\hfill \\ \hfill \\ =\left\{\begin{array}{c}\underset{P\to \infty }{lim}{\displaystyle \sum _{p=1}^P}{x}_p^{\left(2\right)}{P}_{{\mu }_{p-1/2}}^1(-cos\theta )\left[{\displaystyle \frac{K_{{\mu }_p}^{\prime }\left(s{a}_1\right)}{K_{{\mu }_p}\left(s{a}_1\right)}}+{{\rm Y}}_{{\mu }_p}\left(\omega \right){\displaystyle \frac{I_{{\mu }_p}^{\prime }\left(s{a}_1\right)}{I_{{\mu }_p}\left(s{a}_1\right)}}\right],(r,\theta )\in D_2,p=1,\dots P,\hfill \\ \hfill \\ -\underset{K\to \infty }{lim}{\displaystyle \sum _{k=1}^K}{x}_k^{\left(3\right)}{\mathsf{\Psi }}_{{\nu }_{k-1/2}}(cos\theta ){\displaystyle \frac{K_{{\nu }_k}^{\prime }\left(s{a}_1\right)}{K_{{\nu }_k}\left(s{a}_1\right)}};(r,\theta )\in D_3,k=1,\dots K.\hfill \end{array}\right.\hfill \end{array}$$

(22)

Here, $N=P+K$, the prime denotes a derivative with respect to the argument. For further convenience, we introduce the new notation as

$${\overline{A}}_n=A_n{I}_{z_n}\left(s{r}_0\right)K_{z_n}\left(s{r}_0\right)\mathrm{and}{x}_n^{\left(2\right)}=x_n^{(2;1)}.$$

Equations (21) and (22) are the desirable series equations of our problem. It is worth noting that the rules of the limit transition in (21) and (22) will be determined using the Meixner condition at the aperture’s edge.

It is well known that there are different ways to reduce the mode-matching equations to the infinite system of linear algebraic equations (ISLAE) using the orthogonality properties of the eigenfunctions. As a result, we arrive at different kinds of the ISLAE. In order to carry out the analytical regularization, we choose the ISLAE acceptable for the extraction of the singular part of their matrix operators.

5. The ISLAE of the First Kind

5.1. Equations with the Unknowns ${\left\{x_n^{\left(1\right)}\right\}}_{n=1}^{\infty }$

In order to reduce the series Equations (21) and (22) to the ISLAE, we use the orthogonality properties of the associated Legendre functions $P_{{\mu }_p-1/2}^1(-cos\theta )$ on the interval ${\gamma }_2<\theta \le \pi$ as well as the orthogonality of the biconical ones ${\mathsf{\Psi }}_{{\nu }_k-1/2}(cos\theta )$ for ${\gamma }_1\le \theta <{\gamma }_2$, and derive the representation of the associated Legendre function $P_{z_n-1/2}^1(-cos\theta )$ in the regions mentioned above as

$$P_{z_n-1/2}^1(-cos\theta )=q(z_n,{\gamma }_2)\left\{\begin{array}{c}\underset{P\to \infty }{lim}{\displaystyle \sum _{p=1}^P}{\displaystyle \frac{\overline{\alpha }({\mu }_p,{\gamma }_2)}{{\mu }_p^2-z_n^2}}{P}_{{\mu }_p-1/2}^1(-cos\theta ),{\gamma }_2<\theta \le \pi ,\hfill \\ \hfill \\ \underset{K\to \infty }{lim}{\displaystyle \sum _{k=1}^K}{\displaystyle \frac{\alpha ({\nu }_k;{\gamma }_1,{\gamma }_2)}{{\nu }_k^2-z_n^2}}{\mathsf{\Psi }}_{{\nu }_k-1/2}(cos\theta ),{\gamma }_1\le \theta <{\gamma }_2,\hfill \end{array}\right.$$

(23)

where

$$\begin{array}{c}q(z_n,{\gamma }_2)=(z_n^2-0.25)P_{z_n-1/2}(-cos{\gamma }_2),\hfill \\ \hfill \\ \overline{\alpha }({\mu }_p,{\gamma }_2)=-{\displaystyle \frac{2{\mu }_p}{({\mu }_p^2-1/4){\partial }_{\mu }{P}_{{\mu }_p-1/2}(-cos{\gamma }_2)}},\hfill \\ \hfill \\ \alpha ({\nu }_k;{\gamma }_1,{\gamma }_2)=\left\{\begin{array}{c}{\left\{ln\left[\mathrm{tg}({\gamma }_2/2)\mathrm{ctg}({\gamma }_1/2)\right]\right\}}^{-1},k=1,\hfill \\ \hfill \\ {\displaystyle \frac{2{\nu }_k}{({\nu }_k^2-1/4){\partial }_{\nu }{R}_{{\nu }_k-1/2}(cos{\gamma }_2)}},k>1.\hfill \end{array}\right.\hfill \end{array}$$

(24)

It is shown in [19] that series (23) are absolutely and uniformly convergent in the appropriate regions and tend to the function $P_{z_n-1/2}^1(-cos\theta )$ if $P,K\to \infty$.

Let us substitute the expression (23) into the left-hand side of Equations (21) and (22). Then, from each of them, we obtain a couple of series equations with $P_{{\mu }_p-1/2}^1(-cos\theta )$ and ${\mathsf{\Psi }}_{{\nu }_k-1/2}(cos\theta )$ kernels that are valid in the intervals ${\gamma }_2<\theta \le \pi$ and ${\gamma }_1\le \theta <{\gamma }_2$, respectively. As far as the series (22) are not absolutely convergent, we use the finite number of terms in the series, and, using the linear independence of any finite sets of kernel functions, we reduce the problem to a finite system of linear algebraic equations equating to zero the terms with the same eigenfunctions. As a result, we arrive at

$$\sum _{n=1}^N\left\{{\displaystyle \frac{x_n}{{\mu }_p^2-z_n^2}}+{\displaystyle \frac{{\overline{A}}_{n}q(z_n,{\gamma }_2)}{{\mu }_p^2-z_n^2}}{\displaystyle \frac{K_{z_n}\left(s{a}_1\right)}{K_{z_n}\left(s{r}_0\right)}}\right\}=x_p^{\left(2\right)}{\displaystyle \frac{1+{{\rm Y}}_{{\mu }_p}\left(\omega \right)}{\overline{\alpha }({\mu }_p,{\gamma }_2)}},p=1,\dots P,$$

(25)

$$\begin{array}{c}{\displaystyle \sum _{n=1}^N}\left\{{\displaystyle \frac{x_n}{{\mu }_p^2-z_n^2}}{\displaystyle \frac{I_{z_n}^{\prime }\left(s{a}_1\right)}{I_{z_n}\left(s{a}_1\right)}}+{\displaystyle \frac{{\overline{A}}_n{q}_{(}{z}_n,{\gamma }_2)}{{\mu }_p^2-z_n^2}}{\displaystyle \frac{K_{z_n}^{\prime }\left(s{a}_1\right)}{K_{z_n}\left(s{r}_0\right)}}\right\}\hfill \\ \hfill \\ ={\displaystyle \frac{x_p^{\left(2\right)}}{\overline{\alpha }({\mu }_p,{\gamma }_2)}}\left[{\displaystyle \frac{K_{{\mu }_p}^{\prime }\left(s{a}_1\right)}{K_{{\mu }_p}\left(s{a}_1\right)}}+{{\rm Y}}_{{\mu }_p}\left(\omega \right){\displaystyle \frac{I_{{\mu }_p}^{\prime }\left(s{a}_1\right)}{I_{{\mu }_p}\left(s{a}_1\right)}}\right],p=1,\dots P,\hfill \end{array}$$

(26)

$$\sum _{n=1}^N\left\{{\displaystyle \frac{x_n}{{\nu }_k^2-z_n^2}}+{\displaystyle \frac{{\overline{A}}_n{q}_{(}{z}_n,{\gamma }_2)}{{\nu }_k^2-z_n^2}}{\displaystyle \frac{K_{z_n}\left(s{a}_1\right)}{K_{z_n}\left(s{r}_0\right)}}\right\}=-{\displaystyle \frac{x_k^{\left(3\right)}}{\alpha ({\nu }_k;{\gamma }_1,{\gamma }_2)}},k=1,\dots K,$$

(27)

$$\sum _{n=1}^N\left\{{\displaystyle \frac{x_n}{{\nu }_k^2-z_n^2}}{\displaystyle \frac{I_{z_n}^{\prime }\left(s{a}_1\right)}{I_{z_n}\left(s{a}_1\right)}}+{\displaystyle \frac{{\overline{A}}_n{q}_{(}{z}_n,{\gamma }_2)}{{\nu }_k^2-z_n^2}}{\displaystyle \frac{K_{z_n}^{\prime }\left(s{a}_1\right)}{K_{z_n}\left(s{r}_0\right)}}\right\}=-{\displaystyle \frac{x_k^{\left(3\right)}}{\alpha ({\nu }_k;{\gamma }_1,{\gamma }_2)}}{\displaystyle \frac{K_{{\nu }_k}^{\prime }\left(s{a}_1\right)}{K_{{\nu }_k}\left(s{a}_1\right)}},k=1,\dots K.$$

(28)

Here, for further convenience, we introduce the new notation as

$$x_n=x_n^{\left(1\right)}q(z_n,{\gamma }_2).$$

(29)

Taking into account that $q(z_n,{\gamma }_2)=O\left(n^{3/2}\right)$ if $n\to \infty$, we find that $x_n=O\left(n^{-1/2}\right)$. Therefore, in order to obtain the solution of Equations (25)–(28) in the above mentioned class of sequences, we are going to find the rule for letting $N,P$, and K tend to infinity and represent the mathematical technique that guarantees obtaining this. For this purpose, let us exclude the unknowns $x_p^{\left(2\right)}$ and $x_k^{\left(3\right)}$ from the right-hand part of Equations (25)–(28) and reduce them to a finite system of linear algebraic equations in the form

$$\sum _{n=1}^N{\displaystyle \frac{x_n}{{\mu }_p^2-z_n^2}}\left\{{\displaystyle \frac{s{a}_{1}W{\left[K_{{\mu }_p}{I}_{z_n}\right]}_{s{a}_1}}{K_{{\mu }_p}\left(s{a}_1\right)I_{z_n}\left(s{a}_1\right)}}+{{\rm Y}}_{{\mu }_p}\left(\omega \right){\displaystyle \frac{s{a}_{1}W{\left[I_{{\mu }_p}{I}_{z_n}\right]}_{s{a}_1}}{I_{{\mu }_p}\left(s{a}_1\right)I_{z_n}\left(s{a}_1\right)}}\right\}=f_{{\mu }_p}^{\left(1\right)},p=1,\dots ,P.$$

(30)

$$\sum _{n=1}^N{\displaystyle \frac{x_n}{{\nu }_k^2-z_n^2}}{\displaystyle \frac{s{a}_{1}W{\left[K_{{\nu }_k}{I}_{z_n}\right]}_{s{a}_1}}{K_{{\nu }_k}\left(s{a}_1\right)I_{z_n}\left(s{a}_1\right)}}=f_{{\nu }_k}^{\left(2\right)},k=1,\dots ,K.$$

(31)

where

$$f_{{\mu }_p}^{\left(1\right)}=\sum _{n=1}^N{\displaystyle \frac{{\overline{A}}_{n}q(z_n,{\gamma }_2)}{{\mu }_p^2-z_n^2}}{\displaystyle \frac{K_{z_n}\left(s{a}_1\right)}{K_{z_n}\left(s{r}_0\right)}}\left[{\displaystyle \frac{s{a}_{1}W{\left[K_{z_n}{K}_{{\mu }_p}\right]}_{s{a}_1}}{K_{z_n}\left(s{a}_1\right)K_{{\mu }_p}\left(s{a}_1\right)}}+{{\rm Y}}_{{\mu }_p}\left(\omega \right){\displaystyle \frac{s{a}_{1}W{\left[K_{z_n}{I}_{{\mu }_p}\right]}_{s{a}_1}}{K_{z_n}\left(s{a}_1\right)I_{{\mu }_p}\left(s{a}_1\right)}}\right],$$

(32)

$$f_{{\nu }_k}^{\left(2\right)}=\sum _{n=1}^N{\displaystyle \frac{{\overline{A}}_{n}q(z_n,{\gamma }_2)}{{\nu }_k^2-z_n^2}}{\displaystyle \frac{K_{z_n}\left(s{a}_1\right)}{K_{z_n}\left(s{r}_0\right)}}{\displaystyle \frac{s{a}_{1}W{\left[K_{z_n}{K}_{{\nu }_k}\right]}_{s{a}_1}}{K_{z_n}\left(s{a}_1\right)K_{{\nu }_k}\left(s{a}_1\right)}},$$

(33)

$W{\left[f_{\nu }{\phi }_{\mu }\right]}_x=f_{\nu }\left(x\right){\phi }_{\mu }^{\prime }\left(x\right)-f_{\nu }^{\prime }\left(x\right){\phi }_{\mu }\left(x\right)$ is the Wronskian.

Let us introduce a growing sequence of the roots ${\left\{{\mu }_p\right\}}_{p=1}^{\infty }$ and ${\left\{{\nu }_k\right\}}_{k=1}^{\infty }$ for the second and third transcendental Equation (16) as

$${\left\{{\xi }_q\right\}}_{q=1}^{\infty }={\left\{{\nu }_k\right\}}_{k=1}^{\infty }\bigcup {\left\{{\mu }_p\right\}}_{p=1}^{\infty }.$$

(34)

Next, in Equations (30) and (31), we pass to the limit $N,P,K\to \infty (N=P+K)$ and arrange the ISLAE according to the sequence (34). Let us represent this equation in the matrix form as

$$({\mathbf{A}}_{\mathbf{11}}+{\mathbf{B}}_{\mathbf{11}})\mathbf{X}=\mathbf{F}.$$

(35)

Here, $\mathbf{X}:{\left\{x_n\right\}}_{n=1}^{\infty }$ is the unknown vector, ${\mathbf{A}}_{\mathbf{11}}:{\left\{a_{qn}^{(1,1)}\right\}}_{q,n=1}^{\infty }$ and ${\mathbf{B}}_{\mathbf{11}}:{\left\{b_{qn}^{(1,1)}\right\}}_{q,n=1}^{\infty }$ are infinite matrices with the elements

$$a_{qn}^{(1,1)}={\displaystyle \frac{s{a}_{1}W{\left[K_{{\xi }_q}{I}_{z_n}\right]}_{s{a}_1}}{({\xi }_q^2-z_n^2)K_{{\xi }_q}\left(s{a}_1\right)I_{z_n}\left(s{a}_1\right)}};$$

(36)

$$b_{qn}^{(1,1)}=\left\{\begin{array}{c}0,{\xi }_q\in {\left\{{\nu }_k\right\}}_{k=1}^{\infty },\hfill \\ \hfill \\ {\displaystyle \frac{s{a}_{1}W{\left[I_{{\xi }_q}{I}_{z_n}\right]}_{s{a}_1}{{\rm Y}}_{{\xi }_q}\left(\omega \right)}{({\xi }_q^2-z_n^2)I_{{\xi }_q}\left(s{a}_1\right)I_{z_n}\left(s{a}_1\right)}},{\xi }_q\in {\left\{{\mu }_p\right\}}_{p=1}^{\infty },\hfill \end{array}\right.$$

(37)

$\mathbf{F}:{\left\{f_q\right\}}_{q=1}^{\infty }$ is the known vector;

$${\left\{f_q\right\}}_{q=1}^{\infty }\equiv {\left\{f_{{\xi }_q}\right\}}_{q=1}^{\infty }={\left\{f_{{\mu }_p}^{\left(1\right)}\right\}}_{p=1}^{\infty }\bigcup {\left\{f_{{\nu }_k}^{\left(2\right)}\right\}}_{k=1}^{\infty }.$$

(38)

Note that Equation (35) is the desirable equation that we will investigate. An alternative way to solve our problem is to reduce it to linear algebraic equations with the unknowns ${\left\{x_n^{\left(2\right)}\right\}}_{n=1}^{\infty },{\left\{x_n^{\left(3\right)}\right\}}_{n=1}^{\infty }$. In order to determine the correlation between these two methods, let us derive the alternative ISLAE for our problem.

5.2. Equations with the Unknowns ${\left\{x_n^{\left(2\right)}\right\}}_{n=1}^{\infty }$ and ${\left\{x_n^{\left(3\right)}\right\}}_{n=1}^{\infty }$

Let us consider the representation of the associated Legendre functions of the form

$$\left.\begin{array}{c}{\mathsf{\Psi }}_{{\nu }_k-1/2}(cos\theta ),{\gamma }_1\le \theta <{\gamma }_2\hfill \\ \hfill \\ 0,{\gamma }_2<\theta \le \pi \hfill \end{array}\right\}={\tilde{q}}^{+}({\nu }_k,{\gamma }_2)\underset{N\to \infty }{lim}\sum _{n=1}^N{\displaystyle \frac{\tilde{\alpha }(z_n,{\gamma }_1,{\gamma }_2)}{{\nu }_k^2-z_n^2}}{P}_{z_n-1/2}^1(-cos\theta ),{\gamma }_1<\theta \le \pi ,$$

(39)

$$\left.\begin{array}{c}0,{\gamma }_1\le \theta <{\gamma }_2\hfill \\ \hfill \\ P_{{\mu }_p-1/2}^1(-cos\theta ),{\gamma }_2<\theta \le \pi \hfill \end{array}\right\}={\tilde{q}}^{-}({\mu }_p,{\gamma }_2)\underset{N\to \infty }{lim}\sum _{n=1}^N{\displaystyle \frac{\tilde{\alpha }(z_n,{\gamma }_1,{\gamma }_2)}{{\mu }_p^2-z_n^2}}{P}_{z_n-1/2}^1(-cos\theta ),{\gamma }_1\le \theta \le \pi ,$$

(40)

where $k,p=1,2,3,\dots$;

$$\begin{array}{c}{\tilde{q}}^{+}({\nu }_k,{\gamma }_2)=\pi sin{\gamma }_2{\mathsf{\Psi }}_{{\nu }_k-1/2}(cos{\gamma }_2),\hfill \\ \hfill \\ {\tilde{q}}^{-}({\mu }_p,{\gamma }_2)=\pi sin{\gamma }_2{P}_{{\mu }_p-1/2}^1(-cos{\gamma }_2),\hfill \\ \hfill \\ \tilde{\alpha }(z_n,{\gamma }_1,{\gamma }_2)={\displaystyle \frac{z_n{P}_{z_n-1/2}(cos{\gamma }_1)P_{z_n-1/2}(-cos{\gamma }_2)}{cos\left(\pi z_n\right){\partial }_t{\left[P_{t-1/2}(-cos{\gamma }_1)\right]}_{t=z_n}}}.\hfill \end{array}$$

(41)

Here, we use the orthogonality properties of the associated Legendre functions $P_{z_n-1/2}^1(-cos\theta )$ over the interval ${\gamma }_1\le \theta \le \pi$ to obtain these expressions [46]. It is worth noting that series (39) and (40) are formal because the asymptotic behaviour of the moduli of their terms decays as $n^{-1}$ if $n\to \infty$. Therefore, we substitute series (39) and (40) into the right-hand side of Equations (21) and (22), taking into account the finite numbers of their terms. Then, let us form the homogeneous series equations concerning kernel functions $P_{z_n-1/2}^1(-cos\theta )$ and equate the coefficients to zero. Therefore, we arrive at the finite linear algebraic system as

$$\sum _{k=1}^K{\displaystyle \frac{y_k^{\left(3\right)}}{{\nu }_k^2-z_n^2}}+\sum _{p=1}^P{\displaystyle \frac{y_p^{\left(2\right)}}{{\mu }_p^2-z_n^2}}\left[1+{{\rm Y}}_{{\mu }_p}\left(\omega \right)\right]={\displaystyle \frac{1}{\tilde{\alpha }(z_n,{\gamma }_1,{\gamma }_2)}}\left[x_n^{\left(1\right)}+{\overline{A}}_n{\displaystyle \frac{K_{z_n}\left(s{a}_1\right)}{K_{z_n}\left(s{r}_0\right)}}\right],$$

(42)

$$\begin{array}{c}{\displaystyle \sum _{k=1}^K}{\displaystyle \frac{y_k^{\left(3\right)}}{{\nu }_k^2-z_n^2}}{\displaystyle \frac{K_{{\nu }_k}^{\prime }\left(s{a}_1\right)}{K_{{\nu }_k}\left(s{a}_1\right)}}+\sum _{p=1}^P{\displaystyle \frac{y_p^{\left(2\right)}}{{\mu }_p^2-z_n^2}}\left[{\displaystyle \frac{K_{{\mu }_p}^{\prime }\left(s{a}_1\right)}{K_{{\mu }_p}\left(s{a}_1\right)}}+{{\rm Y}}_{{\mu }_p}\left(\omega \right){\displaystyle \frac{I_{{\mu }_p}^{\prime }\left(s{a}_1\right)}{I_{{\mu }_p}\left(s{a}_1\right)}}\right]\hfill \\ \hfill \\ ={\displaystyle \frac{1}{\tilde{\alpha }(z_n,{\gamma }_1,{\gamma }_2)}}\left[x_n^{\left(1\right)}{\displaystyle \frac{I_{z_n}^{\prime }\left(s{a}_1\right)}{I_{z_n}\left(s{a}_1\right)}}+{\overline{A}}_n{\displaystyle \frac{K_{z_n}^{\prime }\left(s{a}_1\right)}{K_{z_n}\left(s{r}_0\right)}}\right].\hfill \end{array}$$

(43)

Here, $n=1,2,3,\dots ,N$; $N=K+P$;

$$y_k^{\left(3\right)}=-x_k^{\left(3\right)}{\tilde{q}}^{+}({\nu }_k,{\gamma }_2),$$

(44)

$$y_p^{\left(2\right)}=x_p^{\left(2\right)}{\tilde{q}}^{-}({\mu }_p,{\gamma }_2).$$

(45)

Taking into account that ${\tilde{q}}^{+}({\nu }_k,{\gamma }_2)=O\left(1\right)$ and ${\tilde{q}}^{-}({\mu }_p,{\gamma }_2)=O\left(p^{1/2}\right)$ if $k,p\to \infty$, we find that $y_n^{\left(3\right)},y_n^{\left(2\right)}=O\left(n^{-3/2}\right)$. Let us exclude the unknowns $x_n^{\left(1\right)}$ from the right-hand part of Equations (42) and (43). Then, we pass to the limit $N,P,K\to \infty (N=P+K)$ and arrange the unknowns according to the sequence (34). This leads to the ISLAE

$$({\mathbf{C}}_{\mathbf{11}}+{\mathbf{D}}_{\mathbf{11}})\mathbf{Y}=\mathbf{\Phi }.$$

(46)

Here, $\mathbf{Y}:{\left\{y_q\right\}}_{q=1}^{\infty }$ is the unknown vector,

$$y_q=\left\{\begin{array}{c}{y}_k^{\left(3\right)},{\xi }_q\in {\left\{{\nu }_k\right\}}_{k=1}^{\infty },\hfill \\ \hfill \\ y_p^{\left(2\right)},{\xi }_q\in {\left\{{\mu }_p\right\}}_{p=1}^{\infty },\hfill \end{array}\right.$$

(47)

${\mathbf{C}}_{\mathbf{11}}:{\left\{c_{nq}^{(1,1)}\right\}}_{n,q=1}^{\infty }$, ${\mathbf{D}}_{\mathbf{11}}:{\left\{d_{nq}^{(1,1)}\right\}}_{n,q=1}^{\infty }$ are infinite matrices with the elements

$$c_{nq}^{(1,1)}={\displaystyle \frac{s{a}_{1}W{\left[K_{{\xi }_q}{I}_{z_n}\right]}_{s{a}_1}}{({\xi }_q^2-z_n^2)K_{{\xi }_q}\left(s{a}_1\right)I_{z_n}\left(s{a}_1\right)}};$$

(48)

$$d_{nq}^{(1,1)}=\left\{\begin{array}{c}0,{\xi }_q\in {\left\{{\nu }_k\right\}}_{k=1}^{\infty },\hfill \\ \hfill \\ {\displaystyle \frac{s{a}_{1}W{\left[I_{{\xi }_q}{I}_{z_n}\right]}_{s{a}_1}{{\rm Y}}_{{\xi }_q}\left(\omega \right)}{({\xi }_q^2-z_n^2)I_{{\xi }_q}\left(s{a}_1\right)I_{z_n}\left(s{a}_1\right)}},{\xi }_q\in {\left\{{\mu }_p\right\}}_{p=1}^{\infty },\hfill \end{array}\right.$$

(49)

$\mathsf{\Phi }:{\left\{{\phi }_n\right\}}_{n=1}^{\infty }$ is the known vector;

$${\phi }_n={\displaystyle \frac{A_n}{\tilde{\alpha }(z_n,{\gamma }_1,{\gamma }_2)}}{\displaystyle \frac{I_{z_n}\left(s{r}_0\right)}{I_{z_n}\left(s{a}_1\right)}}.$$

(50)

Here, $r_0<a_1$.

Note that correlation between Equations (35) and (46) directly follows from the expressions of the matrix elements (36), (37), (48), and (49), respectively:

$${\mathbf{C}}_{\mathbf{11}}={\mathbf{A}}_{11}^{\mathrm{T}},$$

(51)

$${\mathbf{D}}_{\mathbf{11}}={\mathbf{B}}_{11}^{\mathrm{T}},$$

(52)

where the upper mark “T” denotes the transposed matrix. The solution of Equations (35) and (46) allows us to determine all the necessary unknown coefficients for the expression (18). In order to obtain their solutions in the desirable class of sequences, we reduce them to the ISLAE of the second kind using the procedure of analytical regularization.

6. Analytical Regularization

In this section, we analyse the asymptotic properties of the matrix operators (36), (37), (48), and (49), derive the regularizing operators, and formulate an initial problem in terms of the ISLAE of the second kind. We introduce two types of regularization procedures, namely, right- and left-hand side ones.

6.1. Regularizing Operators

At the first stage in the regularization process, we estimate the asymptotic properties of the matrix operators ${\mathbf{A}}_{\mathbf{11}}:{\left\{a_{qn}^{(1,1)}\right\}}_{q,n=1}^{\infty }$ and ${\mathbf{B}}_{\mathbf{11}}:{\left\{b_{qn}^{(1,1)}\right\}}_{q,n=1}^{\infty }$. Due to the asymptotic behaviour of the modified Bessel and Macdonald functions as

$$I_{\eta }\left(z\right)\approx {\displaystyle \frac{1}{\mathsf{\Gamma }(\eta +1)}}{\left({\displaystyle \frac{z}{2}}\right)}^{\eta },K_{\eta }\left(z\right)\approx {\displaystyle \frac{\mathsf{\Gamma }\left(\eta \right)}{2}}{\left({\displaystyle \frac{z}{2}}\right)}^{-\eta }$$

if $\eta >>\left|z\right|$ and $K_{1/2}\left(z\right)=\sqrt{\pi /\left(2z\right)}{e}^{-z}$, where $\mathsf{\Gamma }\left(\eta \right)$ is the Gamma function, we find that

$$a_{qn}^{\left(11\right)}={\displaystyle \frac{1}{{\xi }_q-z_n}}+\left\{\begin{array}{c}O\left({\left\{{\xi }_q{z}_n({\xi }_q-z_n)\right\}}^{-1}\right),z_n,{\xi }_q>>\left|s{a}_1\right|,\hfill \\ \hfill \\ O\left({(s{a}_1/2)}^2\right),\left|s{a}_1\right|\to 0;q>1,n\ge 1\hfill \end{array}\right.$$

(53)

and, taking into account the definition of the function $K_{1/2}\left(z\right)$, we obtain

$$a_{1n}^{(1,1)}={\displaystyle \frac{1}{1/2-z_n}}+{\displaystyle \frac{s{a}_1}{1/4-z_n^2}}+O\left({(s{a}_1/2)}^2\right).$$

(54)

The asymptotic estimation of the matrix elements (37) if $q,n>>|s{a}_1|$ is as follows:

$$b_{qn}^{(1,1)}\approx \left\{\begin{array}{c}0,{\xi }_q\in {\left\{{\nu }_p\right\}}_{p=1}^{\infty },\hfill \\ \hfill \\ {\displaystyle \frac{1-2{\xi }_q}{1+2{\xi }_q}}{\displaystyle \frac{{\left(a_1/c_1\right)}^{2{\xi }_q}}{{\xi }_q+z_n}},{\xi }_q\in {\left\{{\mu }_p\right\}}_{p=1}^{\infty }.\hfill \end{array}\right.$$

(55)

Note that the asymptotic estimations of the matrix elements (48) and (49) directly follow from the expressions (53)–(55) based on the relations (51) and (52).

Let us introduce the operator formed by the main parts of the asymptotic (53) as

$${\mathbf{A}}_{\mathbf{1}}:{\left\{a_{qn}^{\left(1\right)}\equiv a^{\left(1\right)}({\xi }_q,z_n)={\left({\xi }_q-z_n\right)}^{-1}\right\}}_{q,n=1}^{\infty },$$

(56)

and the inverse operator that was introduced earlier in [17,19]

$${\mathbf{A}}_{\mathbf{1}}^{-\mathbf{1}}:{\left\{{\tau }_{kq}^{\left(1\right)}\equiv {\tau }^{\left(1\right)}(z_k,{\xi }_q)={〈{\left\{{\left[M_{-}\left({\xi }_q\right)\right]}^{-1}\right\}}^{{}^{\prime }}{M}_{-}^{\prime }\left(z_k\right)(z_k-{\xi }_q)〉}^{-1}\right\}}_{k,q=1}^{\infty }.$$

(57)

Here,

$${\mathbf{A}}_{\mathbf{1}}^{-\mathbf{1}}{\mathbf{A}}_{\mathbf{1}}=\mathbf{I},$$

(58)

$${\mathbf{A}}_{\mathbf{1}}{\mathbf{A}}_{\mathbf{1}}^{-\mathbf{1}}=\mathbf{I},$$

(59)

$\mathbf{I}$ is the identity matrix;

$$M_{-}^{\prime }\left(z_k\right)={\partial }_z\left[M_{-}\left(z_k\right)\right],{\left\{{\left[M_{-}\left({\xi }_q\right)\right]}^{-1}\right\}}^{\prime }={\partial }_{\xi }\left\{{\left[M_{-}\left({\xi }_q\right)\right]}^{-1}\right\},$$

where $M_{-}\left(\nu \right)$ is determined from the factorization of the even meromorphic function $M\left(\nu \right)$, which is regular in the strip $\prod :\left\{\right|\mathrm{Re}\left(\nu \right)|<1/2\}$ with simple zeroes and poles at $\nu =\pm z_k$ and $\nu =\pm {\xi }_j$ that are located at the real axis outside of the $\mathsf{\Pi }$;

$$M\left(\nu \right)=M_{+}\left(\nu \right)M_{-}\left(\nu \right)={\displaystyle \frac{P_{\nu -1/2}(-cos{\gamma }_1)cos\left(\pi \nu \right)}{({\nu }^2-1/4)P_{\nu -1/2}(-cos{\gamma }_2)R_{\nu -1/2}(cos{\gamma }_2)}},$$

(60)

$M_{+}\left(\nu \right)$ and $M_{-}\left(\nu \right)$ are split functions which are regular in the overlapping half-planes $\mathrm{Re}\left(\nu \right)>-1/2$ and $\mathrm{Re}\left(\nu \right)<1/2$, respectively; $M\left(\nu \right)=O\left({\nu }^{-1}\right)$ and $M_{+}\left(\nu \right)=M_{-}(-\nu )=O\left({\nu }^{-1/2}\right)$ if $\left|\nu \right|\to \infty$ in the regularity region;

$$M_{\pm }\left(\nu \right)={\displaystyle \frac{2A_0({\gamma }_1,{\gamma }_2)e^{\mp \nu \chi }{\displaystyle \prod _{k=1}^{\infty }}(1\pm \nu /z_k)e^{\mp \nu (\pi -{\gamma }_1)/\left(k\pi \right)}}{(1\pm \nu /(1/2)){\displaystyle \prod _{k=1}^{\infty }}(1\pm \nu /{\mu }_k)e^{\mp \nu (\pi -{\gamma }_2)/\left(k\pi \right)}{\displaystyle \prod _{k=1}^{\infty }}(1\pm \nu /{\nu }_{k+1})e^{\mp \nu ({\gamma }_2-{\gamma }_1)/\left(k\pi \right)}}},$$

(61)

where

$$\begin{array}{c}{A}_0({\gamma }_1,{\gamma }_2)=i{\left[{\displaystyle \frac{P_{-1/2}(-cos{\gamma }_1)}{P_{-1/2}(-cos{\gamma }_2)\left[P_{-1/2}(cos{\gamma }_2)P_{-1/2}(-cos{\gamma }_1)-P_{-1/2}(-cos{\gamma }_2)P_{-1/2}(cos{\gamma }_1)\right]}}\right]}^{1/2},\hfill \\ \hfill \\ \hfill \\ \chi ={\displaystyle \frac{\pi -{\gamma }_2}{\pi }}ln{\displaystyle \frac{\pi -{\gamma }_2}{\pi }}+{\displaystyle \frac{{\gamma }_2-{\gamma }_1}{\pi }}ln{\displaystyle \frac{{\gamma }_2-{\gamma }_1}{\pi }}-{\displaystyle \frac{\pi -{\gamma }_1}{\pi }}ln{\displaystyle \frac{\pi -{\gamma }_1}{\pi }}.\hfill \end{array}$$

(62)

The asymptotic estimates for matrix elements (57) are given by the formula

$${\tau }_{kq}^{\left(1\right)}\underset{k,q\to \infty }{=}O\left({\xi }_q^{-1/2}{z}_k^{1/2}{\{z_k-{\xi }_q\}}^{-1}\right).$$

(63)

Taking into account the expressions (51), (56), and (57), let us introduce the transposed matrices

$${\mathbf{C}}_{\mathbf{1}}={\mathbf{A}}_{\mathbf{1}}^{\mathbf{T}}\mathrm{and}{\mathbf{C}}_{\mathbf{1}}^{-\mathbf{1}}={\left({\mathbf{A}}_{\mathbf{1}}^{-\mathbf{1}}\right)}^{\mathbf{T}}\mathrm{as}$$

$${\mathbf{C}}_{\mathbf{1}}:{\left\{c_{nq}^{\left(1\right)}\equiv c^{\left(1\right)}(z_n,{\xi }_q)=a_{qn}^{\left(1\right)}={\left({\xi }_q-z_n\right)}^{-1}\right\}}_{q,n=1}^{\infty },$$

(64)

$${\mathbf{C}}_{\mathbf{1}}^{-\mathbf{1}}:{\left\{{\tau }_{kn}^{\left(2\right)}\equiv {\tau }^{\left(2\right)}({\xi }_k,z_n)={\tau }_{nk}^{\left(1\right)}={〈{\left\{{\left[M_{-}\left({\xi }_k\right)\right]}^{-1}\right\}}^{{}^{\prime }}{M}_{-}^{\prime }\left(z_n\right)(z_n-{\xi }_k)〉}^{-1}\right\}}_{k,n=1}^{\infty }.$$

(65)

Here,

$${\mathbf{C}}_{\mathbf{1}}^{-\mathbf{1}}{\mathbf{C}}_{\mathbf{1}}=\mathbf{I},$$

(66)

$${\mathbf{C}}_{\mathbf{1}}{\mathbf{C}}_{\mathbf{1}}^{-\mathbf{1}}=\mathbf{I}$$

(67)

and

$${\tau }_{kn}^{\left(2\right)}\underset{k,n\to \infty }{=}O\left({\xi }_k^{-1/2}{z}_n^{1/2}{\{z_n-{\xi }_k\}}^{-1}\right).$$

(68)

Note that in the case of finite matrices, the relations (66), (67) directly follow from (58), (59) and vice versa. For the infinite matrices, we prove the relations (66) and (67), similar to those we used in [17,19]. For this purpose, let us represent these equalities in the equivalent form

$$\sum _{n=1}^{\infty }{\tau }_{kn}^{\left(2\right)}{c}_{nq}^{\left(1\right)}={\delta }_k^q,$$

(69)

$$\sum _{n=1}^{\infty }{c}_{qn}^{\left(1\right)}{\tau }_{nk}^{\left(2\right)}={\delta }_q^k,$$

(70)

where ${\delta }_k^q$ is the Kronecker symbol.

Let us introduce the integral as follows:

$$J_{kq}={\displaystyle \frac{1}{2\pi i{\left\{{\left[M_{-}\left({\xi }_k\right)\right]}^{-1}\right\}}^{\prime }}}{\int }_{C_R}{\displaystyle \frac{dt}{M_{-}\left(t\right)(t-{\xi }_k)({\xi }_q-t)}}.$$

(71)

Here, $C_R$ is the circular integration path in the complex plane t, the point $t=0$ and R is the centre and the radius of the circle, respectively; $C_R$ is the outline that encompasses the simple poles of the integrand at $t=z_n$ ($n=1,2,3,\dots$) and $t={\xi }_k$ if $k=q$. For $\left|t\right|\to \infty$, the integrand as a function of t tends to zero not slower than $t^{-3/2}$, therefore, $J_{kq}\to 0$ if $R\to \infty$. Then, applying the residues theorem, we arrive at the representation (69).

Let us introduce the integral as follows

$$J_{qk}={\displaystyle \frac{1}{2\pi i{M}_{-}^{\prime }\left(z_k\right)}}{\int }_{C_R}{\displaystyle \frac{M_{-}\left(t\right)dt}{(t-z_q)(z_k-t)}}.$$

(72)

Here, $C_R$ is the outline that encompasses the simple poles of the integrand at $t={\xi }_n$ ($n=1,2,3,\dots$) and $t=z_k$ if $k=q$. For $\left|t\right|\to \infty$ the integrand as a function of t tends to zero not slower than $t^{-5/2}$, therefore, $J_{kn}\to 0$ if $R\to \infty$. Then, applying the residues theorem, we arrive at the representation (70).

6.2. Left-Hand Side Regularization

Next, using the ISLAE of the first kind (35) and (46) and taking into account the properties of the operators (58) and (66), we formulate the original diffraction problem via the ISLAE of the second kind as follows

$$\mathbf{X}={\mathbf{A}}_{\mathbf{1}}^{-\mathbf{1}}({\mathbf{A}}_{\mathbf{1}}-{\mathbf{A}}_{\mathbf{11}})\mathbf{X}-{\mathbf{A}}_{\mathbf{1}}^{-\mathbf{1}}{\mathbf{B}}_{\mathbf{11}}\mathbf{X}+{\mathbf{A}}_{\mathbf{1}}^{-\mathbf{1}}\mathbf{F}$$

(73)

to determine the unknown coefficients in the region $D_1$, and

$$\mathbf{Y}={\mathbf{C}}_{\mathbf{1}}^{-\mathbf{1}}({\mathbf{C}}_{\mathbf{1}}-{\mathbf{C}}_{\mathbf{11}})\mathbf{Y}-{\mathbf{C}}_{\mathbf{1}}^{-\mathbf{1}}{\mathbf{D}}_{\mathbf{11}}\mathbf{Y}+{\mathbf{C}}_{\mathbf{1}}^{-\mathbf{1}}\mathsf{\Phi }$$

(74)

to determine the unknowns in the regions $D_2$ and $D_3$.

Here, as follows from (53) and (63), Equations (73) and (74) admit the solution in the class of sequences

$$b\left({\sigma }_1\right):\left\{\right||\stackrel{⌢}{\mathbf{X}}\left|\right|=\underset{n}{sup}|{\stackrel{⌢}{x}}_n{n}^{\sigma }|,\underset{n\to \infty }{lim}|{\stackrel{⌢}{x}}_n{n}^{\sigma }|=0\},0\le \sigma <{\sigma }_1,$$

(75)

where $\stackrel{⌢}{\mathbf{X}}=\mathbf{X}\left(\mathbf{Y}\right)$; $\mathbf{X}\in b({\sigma }_1=1/2)$, $\mathbf{Y}\in b({\sigma }_1=3/2)$.

Taking into account the relations (25)–(29) and (42)–(45), it is found that each of the Equations (73) and (74) can be applied to the solution of our problem. As follows from their asymptotic estimation, $\mathbf{X}$ and $\mathbf{Y}$ belong to different classes of sequences. Nevertheless, the relation (29) as well as the relations (44) and (45) allow us to determine the unknown coefficients for field representation (18) in the desirable class of sequences, which provide the fulfilment of all the necessary conditions of the solution, including the Meixner condition on the edge. It is worth noting that the solution of Equation (74) can also be considered in $l_2$.

6.3. Right-Hand Side Regularization

Let us introduce the new unknowns $\stackrel{⃛}{\mathbf{X}}$, $\stackrel{⃛}{\mathbf{Y}}$ as

$$\mathbf{X}={\mathbf{A}}_{\mathbf{1}}^{-\mathbf{1}}\stackrel{⃛}{\mathbf{X}},$$

(76)

$$\mathbf{Y}={\mathbf{C}}_{\mathbf{1}}^{-\mathbf{1}}\stackrel{⃛}{\mathbf{Y}}.$$

(77)

Next, using the ISLAE of the first kind (35) and (46) and taking into account the properties of the operators (59) and (67), we formulate the original diffraction problem via the ISLAE of the second kind as follows

$$\stackrel{⃛}{\mathbf{X}}=({\mathbf{A}}_{\mathbf{1}}-{\mathbf{A}}_{\mathbf{11}}){\mathbf{A}}_{\mathbf{1}}^{-\mathbf{1}}\stackrel{⃛}{\mathbf{X}}-{\mathbf{B}}_{\mathbf{11}}{\mathbf{A}}_{\mathbf{1}}^{-\mathbf{1}}\stackrel{⃛}{\mathbf{X}}+\mathbf{F}$$

(78)

and

$$\stackrel{⃛}{\mathbf{Y}}=({\mathbf{C}}_{\mathbf{1}}-{\mathbf{C}}_{\mathbf{11}}){\mathbf{C}}_{\mathbf{1}}^{-\mathbf{1}}\stackrel{⃛}{\mathbf{Y}}-{\mathbf{D}}_{\mathbf{11}}{\mathbf{C}}_{\mathbf{1}}^{-\mathbf{1}}\stackrel{⃛}{\mathbf{Y}}+\mathsf{\Phi }.$$

(79)

This is an alternative couple of the ISLAE of the second kind for the solution of the problem.

7. Set of the Regularizing Operators

In this section, we generalize our theory and introduce a set of the regularizing operators that can simplify the regularization procedure.

Let there be a given set of even meromorphic functions

$$\Re :\{\stackrel{⌢}{M}\left(\nu \right)=\stackrel{⌢}{Q}\left(\nu \right)/\stackrel{⌢}{P}\left(\nu \right)\},$$

where $\stackrel{⌢}{Q}\left(\nu \right)$ and $\stackrel{⌢}{P}\left(\nu \right)$ are integers, even functions of the exponential type that are not equal to zero at $\nu =0$. We will denote the growing sequences of their positive simple non-coinciding roots ${\left\{{\stackrel{⌢}{z}}_n\right\}}_{n=1}^{\infty }$ and ${\left\{{\stackrel{⌢}{\xi }}_q\right\}}_{q=1}^{\infty }$. Let ${\stackrel{⌢}{z}}_n$ and ${\stackrel{⌢}{\xi }}_q$, as functions of indices, satisfy the following asymptotic estimations:

$$|z_n-{\stackrel{⌢}{z}}_n|=O(1/n),|{\xi }_q-{\stackrel{⌢}{\xi }}_q|=O(1/q),n,q\to \infty ,$$

(80)

where $z_n$ and ${\xi }_q$ are simple zeros and poles of function (60). Taking these into account, we form a set of couples of matrix operators ℑ${}_1$:{${\stackrel{⌢}{\mathbf{A}}}_{\mathbf{1}}$,${\stackrel{⌢}{\mathbf{A}}}_{\mathbf{1}}^{-\mathbf{1}}$} and ℑ${}_2$:{${\stackrel{⌢}{\mathbf{C}}}_{\mathbf{1}}$,${\stackrel{⌢}{\mathbf{C}}}_{\mathbf{1}}^{-\mathbf{1}}$} whose elements are written similarly to those represented by the couples (56), (57) and (64), (65), respectively using the functions $\stackrel{⌢}{M}\left(\nu \right)$ from ℜ. Further, using the matrix operators (56) and (64), we formally introduce two sets of equations

$${\mathbf{A}}_{\mathbf{1}}\mathbf{X}={\mathbf{F}}_{\mathbf{1}}$$

(81a)

and

$$\begin{array}{c}{\mathbf{C}}_{\mathbf{1}}\mathbf{Y}={\mathsf{\Phi }}_{\mathbf{1}},\end{array}$$

(81b)

where ${\mathbf{F}}_{\mathbf{1}}:{\left\{f_q^{\left(1\right)}\right\}}_{q=1}^{\infty }$, ${\mathsf{\Phi }}_{\mathbf{1}}:{\left\{{\phi }_q^{\left(1\right)}\right\}}_{q=1}^{\infty }$ are known vectors. Then, let us formulate the following statement:

Statement. An arbitrary couple of operators from ℑ${}_1$ and ℑ${}_2$ are the regularizing ones for the ISLAEs (35) and (46), respectively.

Proof 

(Proof of Statement). Let us apply the regularization procedure (73) to Equations (81a) and (81b)using the operators from ℑ${}_{1\left(2\right)}$. This leads to the ISLAE of the second kind, which we write as:

$$x_n+\sum _{p=1}^{\infty }{b}_{np}^{\left(1\right)}{x}_p={\eta }_n^{\left(1\right)}$$

(82a)

and

$$\begin{array}{c}{y}_n+\sum _{k=1}^{\infty }{b}_{nk}^{\left(2\right)}{y}_k={\eta }_n^{\left(2\right)}.\end{array}$$

(82b)

Here,

$$b_{np}^{\left(1\right)}=\sum _{k=1}^{\infty }{\stackrel{⌢}{\tau }}_{nk}^{\left(1\right)}{\displaystyle \frac{({\stackrel{⌢}{\xi }}_k-{\xi }_k)+(z_p-{\stackrel{⌢}{z}}_p)}{({\stackrel{⌢}{\xi }}_k-{\stackrel{⌢}{z}}_p)({\xi }_k-z_p)}},$$

$$b_{nk}^{\left(2\right)}=\sum _{p=1}^{\infty }{\stackrel{⌢}{\tau }}_{np}^{\left(2\right)}{\displaystyle \frac{({\stackrel{⌢}{\xi }}_k-{\xi }_k)+(z_p-{\stackrel{⌢}{z}}_p)}{({\stackrel{⌢}{\xi }}_k-{\stackrel{⌢}{z}}_p)({\xi }_k-z_p)}},$$

$${\eta }_n^{\left(1\right)}=\sum _{k=1}^{\infty }{\stackrel{⌢}{\tau }}_{nk}^{\left(1\right)}{f}_k^{\left(1\right)}<\infty ,{\eta }_n^{\left(2\right)}=\sum _{p=1}^{\infty }{\stackrel{⌢}{\tau }}_{np}^{\left(2\right)}{\phi }_p^{\left(2\right)}<\infty ,$$

${\stackrel{⌢}{\tau }}_{np}^{\left(1\right)}$ and ${\stackrel{⌢}{\tau }}_{np}^{\left(2\right)}$ are matrix elements of the operators ${\stackrel{⌢}{\mathbf{A}}}_{\mathbf{1}}^{-\mathbf{1}}$ and ${\stackrel{⌢}{\mathbf{C}}}_{\mathbf{1}}^{-\mathbf{1}}$, respectively.

Accounting to relations (63), (68), and (80), we establish by direct verification that $b_{np}^{\left(1\right)}=O\left(n^{-1/2}{p}^{-2}\right)$ and $b_{nk}^{\left(2\right)}=O\left(n^{-3/2}{k}^{-2}\right)$ if $n,p,k\to \infty$. Therefore, the solution of Equations (82a) and (82b) exist in $b({\sigma }_1=1/2)$ and in $b({\sigma }_1=3/2)$, respectively, and the couples operators ${\stackrel{⌢}{\mathbf{A}}}_{\mathbf{1}}$, ${\stackrel{⌢}{\mathbf{A}}}_{\mathbf{1}}^{-\mathbf{1}}$ and ${\stackrel{⌢}{\mathbf{C}}}_{\mathbf{1}}$, ${\stackrel{⌢}{\mathbf{C}}}_{\mathbf{1}}^{-\mathbf{1}}$ from $\Im {}_{\mathbf{1}}$ and ${\Im }_{\mathbf{2}}$ are regularizing ones for Equations (81a) and (81b). It follows directly from this that an arbitrary couple of operators from ${\Im }_{\mathbf{1}}$ and ${\Im }_{\mathbf{2}}$ are also regularizers for the ISLAEs (35) and (46). □

Therefore, left-hand side regularization of Equations (35) and (46) with use of the operators from ${\Im }_{\mathbf{1}}$ and ${\Im }_{\mathbf{2}}$ leads to the equations of the second kind, which can be written as

$$\mathbf{X}={\stackrel{⌢}{\mathbf{A}}}_{\mathbf{1}}^{-\mathbf{1}}({\stackrel{⌢}{\mathbf{A}}}_{\mathbf{1}}-{\mathbf{A}}_{\mathbf{11}})\mathbf{X}-{\stackrel{⌢}{\mathbf{A}}}_{\mathbf{1}}^{-\mathbf{1}}{\mathbf{B}}_{\mathbf{11}}\mathbf{X}+{\stackrel{⌢}{\mathbf{A}}}_{\mathbf{1}}^{-\mathbf{1}}\mathbf{F},$$

(83)

$$\mathbf{Y}={\stackrel{⌢}{\mathbf{C}}}_{\mathbf{1}}^{-\mathbf{1}}({\stackrel{⌢}{\mathbf{C}}}_{\mathbf{1}}-{\mathbf{C}}_{\mathbf{11}})\mathbf{Y}-{\stackrel{⌢}{\mathbf{C}}}_{\mathbf{1}}^{-\mathbf{1}}{\mathbf{D}}_{\mathbf{11}}\mathbf{Y}+{\stackrel{⌢}{\mathbf{C}}}_{\mathbf{1}}^{-\mathbf{1}}\mathsf{\Phi },$$

(84)

where $\mathbf{X}\in b({\sigma }_1=1/2)$, $\mathbf{Y}\in b({\sigma }_1=3/2)$.

Let us consider an example of the function $\stackrel{⌢}{M}\left(\nu \right)$ with the simple zeros ${\stackrel{⌢}{z}}_n$ and poles ${\stackrel{⌢}{\xi }}_q$ that coincide with the main parts of asymptotic indices $z_n$, ${\xi }_q$ if $n,q\to \infty$:

$$\begin{array}{c}{\stackrel{⌢}{z}}_n\in {\left\{[\pi /(\pi -{\gamma }_1)](n-1/4)\right\}}_{n=1}^{\infty },\end{array}$$

(85a)

$$\begin{array}{c}{\stackrel{⌢}{\xi }}_{q>1}\in {\left\{{\stackrel{⌢}{\nu }}_k\right\}}_{k=1}^{\infty }\bigcup {\left\{{\stackrel{⌢}{\mu }}_p\right\}}_{p=1}^{\infty },\end{array}$$

(85b)

where ${\stackrel{⌢}{\nu }}_k=\pi k/({\gamma }_2-{\gamma }_1)$, ${\stackrel{⌢}{\mu }}_p=\pi (p-1/4)/(\pi -{\gamma }_2)$, and ${\stackrel{⌢}{\xi }}_1={\xi }_1=1/2$. Then, $\stackrel{⌢}{M}\left(\nu \right)$ is expressed through the gamma functions as

$$\stackrel{⌢}{M}\left(\nu \right)={\displaystyle \frac{\mathsf{\Gamma }\left({\displaystyle \frac{3}{4}}+{\displaystyle \frac{\pi -{\gamma }_2}{\pi }}\nu \right)\mathsf{\Gamma }\left({\displaystyle \frac{3}{4}}-{\displaystyle \frac{\pi -{\gamma }_2}{\pi }}\nu \right)\mathsf{\Gamma }\left(1+{\displaystyle \frac{{\gamma }_2-{\gamma }_1}{\pi }}\nu \right)\mathsf{\Gamma }\left(1-{\displaystyle \frac{{\gamma }_2-{\gamma }_1}{\pi }}\nu \right)}{\left(\nu +{\displaystyle \frac{1}{2}}\right)\left(\nu -{\displaystyle \frac{1}{2}}\right)\mathsf{\Gamma }\left({\displaystyle \frac{3}{4}}+{\displaystyle \frac{\pi -{\gamma }_1}{\pi }}\nu \right)\mathsf{\Gamma }\left({\displaystyle \frac{3}{4}}-{\displaystyle \frac{\pi -{\gamma }_1}{\pi }}\nu \right)}}$$

(86)

Function (86) is even and regular in the strip ∏ and tends to zero as $\nu {}^{-1}$ if $\left|\nu \right|\to \infty$; simple zeros ${\stackrel{⌢}{z}}_n$ and poles ${\stackrel{⌢}{\xi }}_m$ are situated on the real axis beyond the strip ∏. This function is elementarily factorized and written as

$$\stackrel{⌢}{M}\left(\nu \right)={\stackrel{⌢}{M}}_{+}\left(\nu \right){\stackrel{⌢}{M}}_{-}\left(\nu \right),$$

where

$${\stackrel{⌢}{M}}_{\pm }\left(\nu \right)=iexp\{\mp \nu \chi \}{\displaystyle \frac{\mathsf{\Gamma }\left({\displaystyle \frac{3}{4}}\pm {\displaystyle \frac{\pi -{\gamma }_2}{\pi }}\nu \right)\mathsf{\Gamma }\left(1\pm {\displaystyle \frac{{\gamma }_2-{\gamma }_1}{\pi }}\nu \right)}{\left({\displaystyle \frac{1}{2}}\pm \nu \right)\mathsf{\Gamma }\left({\displaystyle \frac{3}{4}}\pm {\displaystyle \frac{\pi -{\gamma }_1}{\pi }}\nu \right)}}.$$

(87)

Here, ${\stackrel{⌢}{M}}_{+}\left(\nu \right)$ and ${\stackrel{⌢}{M}}_{-}\left(\nu \right)$ (${\stackrel{⌢}{M}}_{+}\left(\nu \right)={\stackrel{⌢}{M}}_{-}(-\nu )$) are regular functions in the semi-planes $\mathrm{Re}\left(\nu \right)>-1/2$ and $\mathrm{Re}\left(\nu \right)<1/2$ that decrease in infinity as ${\nu }^{-1/2}$ in the regularity regions.

Using the functions (86) and (87) instead of (60) and (61), we find the necessary couples of regularizing operators using the schemes represented in (56), (57) and in (64), (65).

It is worth noting that using the kernel functions (86) and (87) simplifies the formation of the regularizing operators ${\stackrel{⌢}{\mathbf{A}}}_{\mathbf{1}}$, ${\stackrel{⌢}{\mathbf{A}}}_{\mathbf{1}}^{-\mathbf{1}}$ and ${\stackrel{⌢}{\mathbf{C}}}_{\mathbf{1}}$, ${\stackrel{⌢}{\mathbf{C}}}_{\mathbf{1}}^{-\mathbf{1}}$. They allow for reducing the problem to the ISLAE of the second kind, to which solutions exist in the necessary class of sequences but their effectiveness is somewhat smaller than the initial couples of regularizing operators (56), (57) and (64), (65) because, as follows from our Statement, these new operators explicitly invert only the main part asymptotic of the operators (56) and (64).

8. Radiation through a Small-Sized Cavity Aperture

The solution of the problem of wave penetration through a small-sized hole allows the scattered field characteristics to be obtained in analytical form. The well-known results in this area are presented in [47,48]. The general theory for the solution to this problem is developed in [49]. It is worth noting that the main problem this study engages is correct accounting for the field singularity at the aperture edge. A technique for the solution of the problem of wave radiation from a small-sized hole of a sphere-conical cavity, which rigorously accounted for the field singularities at the edge, was considered in [31]. Here, we develop this technique for the solution of the problem of wave radiation from a cavity with a small-sized hole into a biconical region. For this purpose, we take into account the small dimension of the hole ($|s{a}_1/2|<<1$). Thus, we apply the asymptotic expressions for the modified Bessel and Macdonald functions [44] to estimate the known terms of the Equations (73) and (74) and, taking into account the resonant properties of the cavity, we derive the approximate equations as

$$x_k+\sum _{q=1}^{\infty }{\tau }_{kq}^{\left(1\right)}{\kappa }_{{\xi }_q}\left(s{c}_1\right){\tilde{x}}_q=\sum _{p=1}^{\infty }{\tau }_{kp}^{\left(1\right)}{f}_p,$$

(88)

$$y_k+\sum _{q=1}^{\infty }{\eta }_{kq}{\kappa }_{{\xi }_q}\left(s{c}_1\right)y_q=\sum _{n=1}^{\infty }{\tau }_{kn}^{\left(2\right)}{\overline{\phi }}_n.$$

(89)

Here,

$${\tilde{x}}_q=\sum _{n=1}^{\infty }{\displaystyle \frac{x_n}{{\xi }_q+z_n}},$$

(90)

$${\eta }_{kq}=\sum _{n=1}^{\infty }{\displaystyle \frac{{\tau }_{kn}^{\left(2\right)}}{{\xi }_q+z_n}}={\displaystyle \frac{1}{{\left\{{\left[M_{-}\left({\xi }_k\right)\right]}^{-1}\right\}}^{{}^{\prime }}{M}_{+}\left({\xi }_q\right)({\xi }_q+{\xi }_k)}},$$

(91)

$${\kappa }_{{\xi }_q}\left(s{c}_1\right)=\left\{\begin{array}{c}{\displaystyle \frac{2{(s{a}_1/2)}^{2{\xi }_q}}{\mathsf{\Gamma }\left({\xi }_q\right)\mathsf{\Gamma }({\xi }_q+1)}}\left[{\displaystyle \frac{K_{{\xi }_q}\left(s{c}_1\right)+2s{c}_1{K}_{{\xi }_q}^{\prime }\left(s{c}_1\right)}{I_{{\xi }_q}\left(s{c}_1\right)+2s{c}_1{I}_{{\xi }_q}^{\prime }\left(s{c}_1\right)}}\right],{\xi }_q\in {\left\{{\mu }_p\right\}}_{p=1}^{\infty },\hfill \\ \hfill \\ 0,{\xi }_q\in {\left\{{\nu }_k\right\}}_{k=1}^{\infty },\hfill \end{array}\right.$$

(92)

$$\begin{array}{c}{f}_p=-\sum _{n=1}^{\infty }{A}_{n}q(z_n,{\gamma }_2){\displaystyle \frac{{(r_0/a_1)}^{z_n}}{2z_n}}\left\{\begin{array}{c}{\displaystyle \frac{1}{{\xi }_p+z_n}}+{\displaystyle \frac{{\kappa }_{{\xi }_p}}{{\xi }_p-z_n}},{\xi }_p\in {\left\{{\mu }_p\right\}}_{p=1}^{\infty },\hfill \\ \hfill \\ {\displaystyle \frac{1}{{\xi }_p+z_n}},{\xi }_p\in {\left\{{\nu }_k\right\}}_{k=1}^{\infty },\hfill \end{array}\right.\end{array}$$

(93a)

$$\begin{array}{c}{\overline{\phi }}_n={\displaystyle \frac{A_n{(r_0/a_1)}^{z_n}}{\tilde{\alpha }(z_n,{\gamma }_1,{\gamma }_2)}}.\end{array}$$

(93b)

Let us consider the resonant excitation of a cavity with the small dimension of the hole. Taking into account the time factor $e^{-i\omega t}$, the real and imaginary parts of the complex resonance frequency of an open cavity ${\omega }_{res}=\mathrm{Re}\left({\omega }_{res}\right)+i\mathrm{Im}\left({\omega }_{res}\right)$ are determined as $\mathrm{Re}\left({\omega }_{res}\right)>0$ and $\mathrm{Im}\left({\omega }_{res}\right)\le 0$. Under these conditions, the resonance frequency has a physical sense: the wave moves from the scatterer to infinity, the corresponding vibration grows in volume and decreases with time. Let us introduce ${\overline{\rho }}_{pj}={\left(s{c}_1\right)}_{pj}=-i{\omega }_{{\mu }_{p}j}{c}_1\sqrt{\epsilon \mu }$ ($p,j=1,2,3,\dots$), where ${\omega }_{{\mu }_{p}j}$ is the real resonant frequency $(\mathrm{Re}\left({\omega }_{{\mu }_{p}j}\right)>0,\mathrm{Im}\left({\omega }_{{\mu }_{p}j}\right)=0$) of a closed sphere-conical resonator, which corresponds to the resonant $T{M}_{{\mu }_{p}0j}$ mode; ${\omega }_{{\mu }_{p}j}$ is determined from the solution of the transcendental equation as

$$I_{{\mu }_p}\left({\overline{\rho }}_{pj}\right)+2{\overline{\rho }}_{pj}{I}_{{\mu }_p}^{\prime }\left({\overline{\rho }}_{pj}\right)=0.$$

(94)

Let ${\rho }_{pj}={\overline{\rho }}_{pj}+\Delta {\rho }_{pj}$, ($\Delta {\rho }_{pj}\equiv -i\Delta {\omega }_{{\mu }_{p}j}{c}_1\sqrt{\epsilon \mu }$, $\Delta {\omega }_{{\mu }_{p}j}=\mathrm{Re}(\Delta {\omega }_{{\mu }_{p}j})+i\mathrm{Im}(\Delta {\omega }_{{\mu }_{p}j}))$, and $|\Delta {\rho }_{pj}|<<1$. Taking into account that $|{\rho }_{pj}|$ is very close to the $|{\overline{\rho }}_{pj}|$, we keep only the dominant term with the index ${\xi }_p={\mu }_p$ for the series of the ISLAE (88), (89) and rewrite them as

$$\begin{array}{c}{x}_k+{\tau }_{kp}^{\left(1\right)}{\kappa }_{{\xi }_p}\left({\rho }_{pj}\right){\tilde{x}}_p={\tau }_{kp}^{\left(1\right)}{f}_p,\end{array}$$

(95a)

$$\begin{array}{c}{y}_k+{\eta }_{kp}{\kappa }_{{\xi }_p}\left({\rho }_{pj}\right)y_p={\tilde{\phi }}_k.\end{array}$$

(95b)

Here, $k=1,2,3\dots ;$ index p corresponds to the ${\xi }_p$ resonance mode and is fixed;

$${\tilde{\phi }}_k=\sum _{n=1}^{\infty }{\tau }_{kn}^{\left(2\right)}{\overline{\phi }}_n.$$

The explicit solution of the ISLAE (95a) and (95b) is as follows [31]:

$$x_k={\displaystyle \frac{{\tau }_{kp}^{\left(1\right)}[a_{{\xi }_p}^{+}+a_{{\xi }_p}^{-}{\kappa }_{{\xi }_p}\left({\rho }_{pj}\right)]}{D_{{\xi }_p}\left({\rho }_{pj}\right)}},$$

(96a)

$$y_k={\displaystyle \frac{{\tilde{\phi }}_k{D}_{{\xi }_p}\left({\rho }_{pj}\right)-{\kappa }_{{\xi }_p}\left({\rho }_{pj}\right){\eta }_{kp}{\tilde{\phi }}_p}{D_{{\xi }_p}\left({\rho }_{pj}\right)}},$$

(96b)

where, k = 1, 2, 3, …;

$$\begin{array}{c}{D}_{{\xi }_p}\left({\rho }_{pj}\right)=1+{\displaystyle \frac{{\kappa }_{{\xi }_p}\left({\rho }_{pj}\right)}{2{\xi }_p{\left[M_{-}^{-1}\left({\xi }_p\right)\right]}^{{}^{\prime }}{M}_{+}\left({\xi }_p\right)}},\end{array}$$

(96c)

$$\begin{array}{c}{a}_{{\xi }_p}^{\pm }=-\sum _{n=1}^{\infty }{A}_{n}q(z_n,{\gamma }_2){\displaystyle \frac{{(r_0/a_1)}^{z_n}}{2z_n({\xi }_p\pm z_n)}}.\end{array}$$

(96d)

Equating the denominator (96c) to zero, we arrive at an expression for the determination of the perturbation $\Delta {\omega }_{{\mu }_{p}j}$ of the resonant frequency ${\omega }_{{\mu }_{p}j}$ as

$$\Delta {\omega }_{{\mu }_{p}j}={\left({\displaystyle \frac{k_{{\mu }_{p}j}{a}_1}{2}}\right)}^{2{\mu }_p}\mathsf{\Phi }\left({\mu }_p\right).$$

(97)

Here, $k_{{\mu }_{p}j}={\omega }_{{\mu }_{p}j}\sqrt{\epsilon \mu }$,

$$\mathsf{\Phi }\left({\mu }_p\right)={\displaystyle \frac{e^{-i\pi ({\mu }_p+1/2)}}{c_1\sqrt{\epsilon \mu }{M}_{+}\left({\mu }_p\right){\left[M_{-}^{-1}\left({\mu }_p\right)\right]}^{{}^{\prime }}{\mathsf{\Gamma }}^2({\mu }_p+1)}}\left[{\displaystyle \frac{K_{{\mu }_p}\left({\overline{\rho }}_{pj}\right)+2{\overline{\rho }}_{pj}{K}_{{\mu }_p}^{\prime }\left({\overline{\rho }}_{pj}\right)}{{\displaystyle \frac{d}{dx}}{[I_{{\mu }_p}\left(x\right)+2x{I}_{{\mu }_p}^{\prime }\left(x\right)]}_{x={\overline{\rho }}_{pj}}}}\right].$$

(98)

Taking into account that ${\omega }_{res}={\omega }_{{\mu }_{p}j}+\Delta {\omega }_{{\mu }_{p}j}$, the definition of ${\omega }_{res}$, the fact that ${\omega }_{{\mu }_{p}j}$ is real, and that ${\omega }_{{\mu }_{p}j}\gg |\Delta {\omega }_{{\mu }_{p}j}|$, we find that expression (97) correctly determines the frequency perturbation if $\mathrm{Im}(\Delta {\omega }_{{\mu }_{p}j})\le 0$; $\mathrm{Re}(\Delta {\omega }_{{\mu }_{p}j})$ can take an arbitrary sign. From the expressions (97), it follows that $\Delta {\omega }_{{\mu }_{p}j}$ depends on the truncated dimensionless radius $\left(k_{{\mu }_{p}j}{a}_1\right)$, the opening angles ${\gamma }_1$ and ${\gamma }_2$, and the resonant parameter of the closed sphere-conical resonator.

9. Numerical Analysis

All scattered field characteristics are calculated by reducing the ISLAE (73). We compared the solutions with those obtained from Equations (76) and (78) and found almost exact matching. This fact confirms the correctness of the solutions. The expressions (25)–(29) are applied for calculation of the expansion coefficients for the field representation (18). Based on this, we analyse the near- and far-field characteristics of our scatterer for different geometrical and frequency parameters. For the analysis of the radiated far field ($r\to \infty$), we apply the asymptotic representation of Formula (18) for the region $D_3$ as

$$H_{\phi }^t\left(\theta \right)\sim H\left(\theta \right){\displaystyle \frac{e^{ikr}}{r}},$$

(99)

where the far-field pattern $D\left(\theta \right)=\left|H\right(\theta \left)\right|$ is defined by

$$D\left(\theta \right)=Z^{-1}\sqrt{{\displaystyle \frac{\pi }{2}}}\left|\sum _{n=1}^{\infty }{\displaystyle \frac{x_n^{\left(3\right)}{\mathsf{\Psi }}_{{\nu }_n-1/2}(cos\theta )}{K_{{\nu }_n}\left(s{a}_1\right)}}\right|.$$

(100)

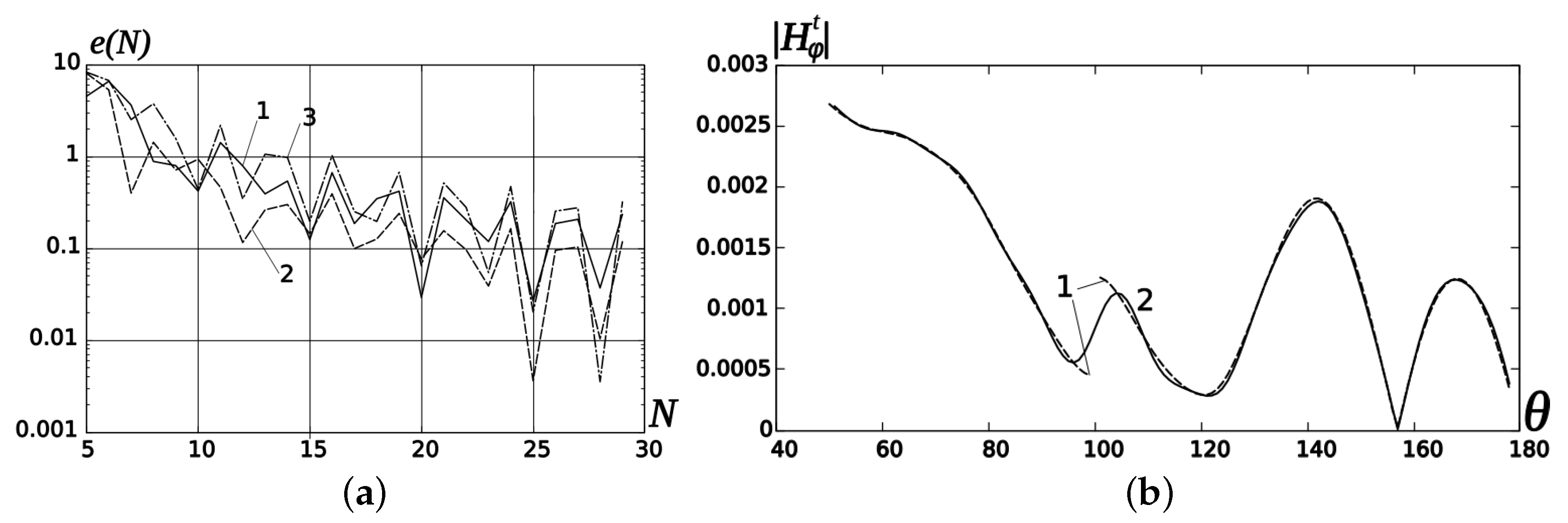
Let the bicone Q be placed in a hypothetical environment with single electrical and magnetic parameters and excited by the radial electric dipole of unit amplitude $A^{\left(0\right)}=1$. Let us consider the reduced ISLAE (73) and analyse the corresponding finite $N\times N$ set of linear algebraic equations, where N is the truncation order. In Figure 2a, we represent the dependencies of the relative error $e\left(N\right)$ of the near-$H_{\phi }(r,\theta )$-field calculation on the truncation parameter N for $kr=k{a}_1+1$ and for three points $\theta ={\gamma }_1,({\gamma }_1+{\gamma }_2)/2$ and ${\gamma }_2$,

$$e\left(N\right)=100\%\left|H_{\phi }^{(N+1)}-H_{\phi }^{\left(N\right)}\right|/\left|H_{\phi }^{\left(N\right)}\right|,$$

where $H_{\phi }^{\left(N\right)}=H_{\phi }^{\left(N\right)}(r,\theta )$ is the magnetic field, calculated using $N\times N$ set of linear algebraic equations.

We see from this figure that the truncation parameter must be greater than $k{a}_1$, and we chose it from the condition $N=\left[\right|s{a}_1\left|\right]+\left[q\right]$ with $4\le q\le 10$, where $[·]$ denotes the entire part. To verify the mode matching, we calculate $|H_{\phi }|$ on virtual spherical surfaces, the radii of which are somewhat greater and lower than $k{a}_1$, and find an excellent adjustment of the field behaviour on the above-mentioned virtual surfaces (see Figure 2b).

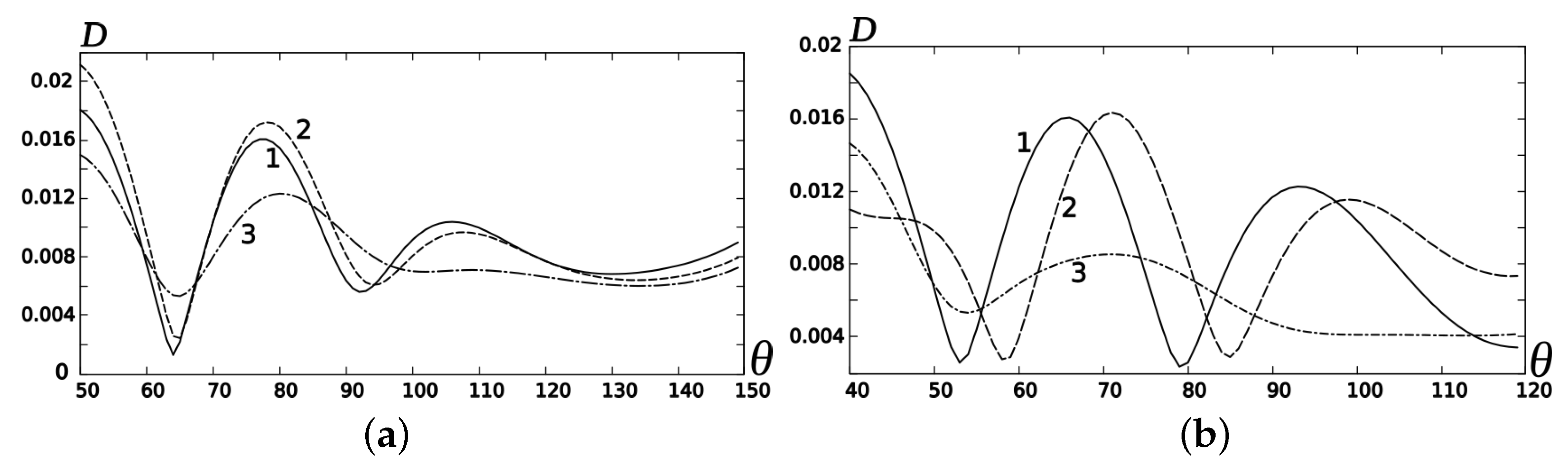
Figure 3a,b, shows the far field of the scatterers with a wide biconical region ${\gamma }_2-{\gamma }_1\ge {80}^{\circ }$. Curves 1 and 2 in this figure show the field distributions for different positions of the cavity termination. Curve 3 corresponds to the far field for the scatterer without an internal diaphragm. We observe in Figure 3 the effective far-field radiation along the semi-infinite conical surface $Q_1$. The field oscillations in this figure can be explained by the interference of the multiple waves scattered from the biconical waveguide surfaces, illuminated by the edge waves of the open cavity and the dipole.

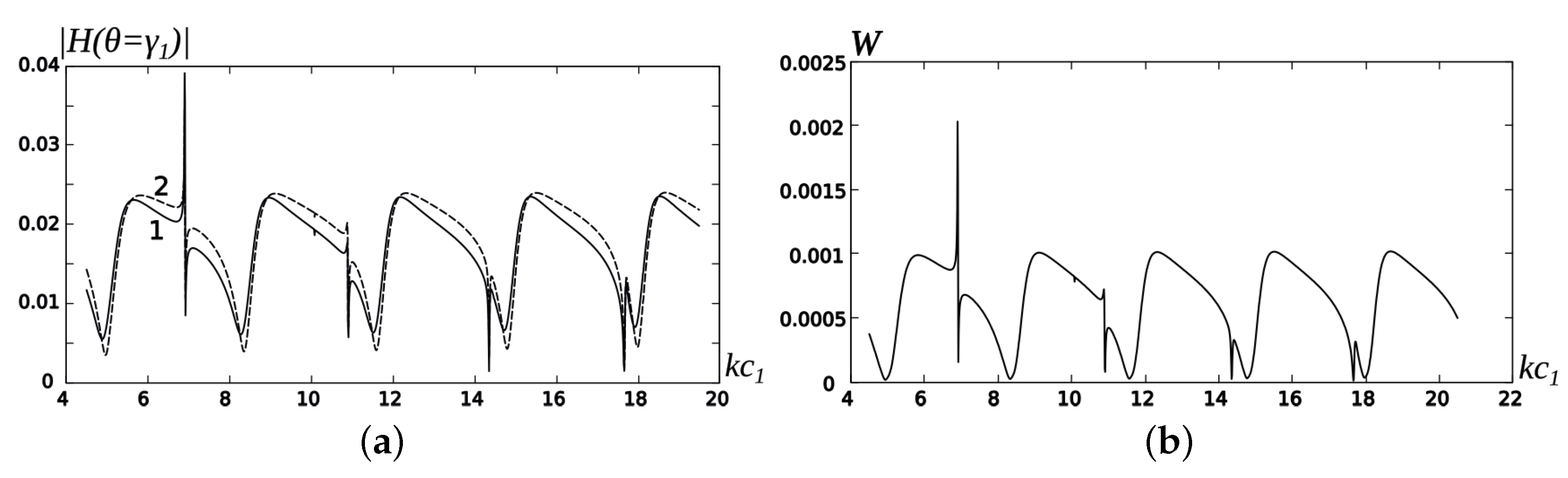
In order to study the resonance properties of our scatterer, we analyse the dependencies of the modulus of the magnetic far field at the conical surface $\theta ={\gamma }_1$ on $k{c}_1$. The value $\left|H\right(\theta ={\gamma }_1\left)\right|$ is proportional to the $j_r$ component of the far electric current density at the semi-infinite conical surface. Its analysis allows us to understand how the field radiated from the resonant volume penetrates the biconical area.

Let us consider a bicone with wide conical ($\pi -{\gamma }_2={60}^{\circ }$) and narrow biconical (${\gamma }_2-{\gamma }_1={31}^{\circ }$) regions formed by a cone $Q_1$ with ${\gamma }_1={89}^{\circ }$ and a truncated one with ${\gamma }_2={120}^{\circ }$ (see Figure 1b). This geometry can be considered as a simple model of a nano-probe with the resonance volume over the plane.

Curves 1 and 2 in Figure 4a show the dependencies of the magnetic field module $\left|H\right(\theta ={\gamma }_1\left)\right|$ for the total field and the module of the TEM mode on the parameter $k{c}_1$. Comparing these curves, we can conclude that the current density on the conical surface $\theta ={\gamma }_1$ is almost completely induced by the TEM mode. Figure 4b shows the behaviour of the radiating power W through the biconical area as a function of the parameter $k{c}_1$, where

$$W={\displaystyle \frac{{\pi }^2}{2Z}}{\displaystyle \frac{|x_1^{\left(3\right)}{|}^2}{|K_{{\nu }_1}\left(k{a}_1\right){|}^2}}ln\left(\mathrm{ctg}{\displaystyle \frac{{\gamma }_1}{2}}\mathrm{tg}{\displaystyle \frac{{\gamma }_2}{2}}\right)$$

$$+{\displaystyle \frac{{\pi }^2{sin}^2{\gamma }_2}{2Z}}\sum _{n=2}^{\infty }{\displaystyle \frac{|x_n^{\left(3\right)}{|}^2}{|K_{{\nu }_n}\left(k{a}_1\right){|}^2}}{\displaystyle \frac{{\nu }_n^2-1/4}{2{\nu }_n}}{\displaystyle \frac{\partial }{\partial {\nu }_n}}\left[R_{{\nu }_n-1/2}(cos{\gamma }_2)\right]{\mathsf{\Psi }}_{{\nu }_n-1/2}(cos{\gamma }_2).$$

We see that the shapes of the far field in Figure 4a and the radiated power of the oscillations in Figure 4b are similar, with the period approximately equal to $\lambda /2$ ($\lambda$ is the dimensionless wavelength). Therefore, we can suppose that the local maxima of the radiation that we observe from these curves are caused by the resonant excitation of an open cavity. We observe their sharp jumps if $k{c}_1$ is close to the dimensionless resonant radii $k_{{\mu }_{n}j}{c}_1$ for $T{M}_{{\mu }_{n}0j}$ modes of the closed sphere-conical resonator with the azimuthal index $n=2$ and the radial ones $j=1,\dots ,5$. Parameter $k_{{\mu }_{n}j}{c}_1$ is real and determined from the solution of Equation (94). Numerical examples of this parameter are given in

Table 1. Resonant radii of the axially symmetric $T{M}_{{\mu }_{n}0j}$ mode oscillation for the closed sphere-conical resonator with $\pi -{\gamma }_2={60}^{\circ }$.

${\mathit{\mu }}_{\mathit{n}}/{\mathit{k}}_{{\mathit{\mu }}_{\mathit{n}}\mathit{j}}{\mathit{c}}_1$	j = 1	j = 2	j = 3	j = 4	j = 5
${\mu }_1=2.27729$	3.6219	7.1526	10.4066	13.6051	16.7814
${\mu }_2=5.26278$	6.8853	10.9012	14.3663	17.6942	20.9595
${\mu }_3=8.25826$	10.0795	14.4705	18.128	21.5862	24.9479

.

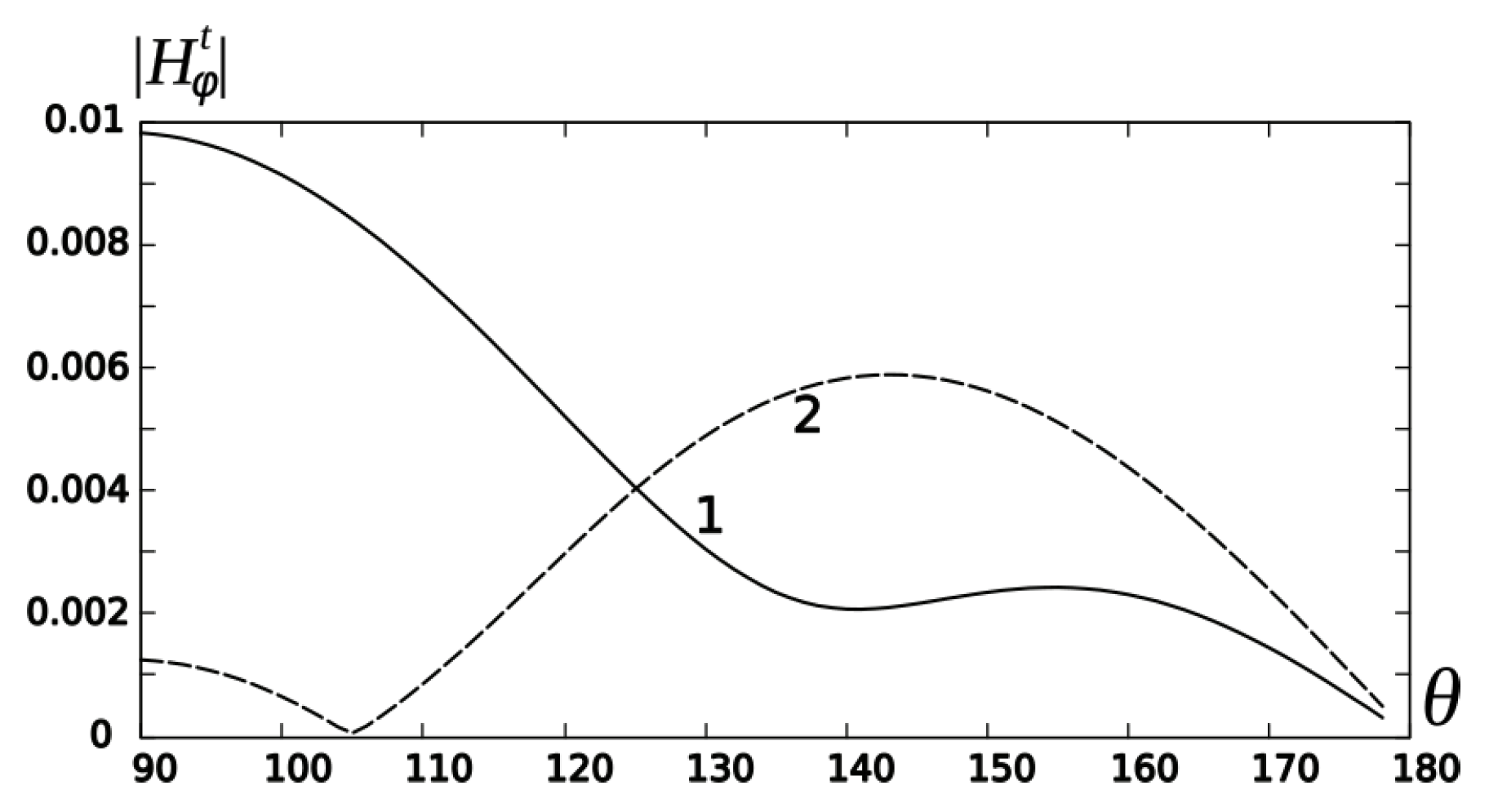
Figure 5 represents the near-total-field distribution at the virtual spherical surface $\{r<a_1,{\gamma }_1\le \theta \le \pi \}$ for the different positions of the cavity termination. Curves 1 and 2 in this figure are plotted if $k{c}_1$ corresponds to the maximum with $k{c}_1=5.66$ and minimum with $k{c}_1=8.28$ of curve 1 in Figure 4. Comparing these curves, we observe their essential difference in the angle sector ${\gamma }_1<\theta <{\gamma }_2$. As follows from the behaviour of curve 1 in Figure 5, the near field exceeds the maximum at the plane. Therefore, for this regime of excitation, we can amplify the far density current on the plane surface owing to the intensification of the TEM wave radiation and to the increase in the near field in the conical sector $(r<a_1,{\gamma }_1<\theta <{\gamma }_2)$ outside of the bicone area.

Let us consider a bicone with a semi-spherical cavity ($\pi -{\gamma }_2={91}^{\circ }$) and a narrow conical probe (${\gamma }_1={30}^{\circ })$, (see Figure 1c). This geometry can be considered as a model for detection of cavity-type defects under a plane surface using a semi-infinite conical probe.

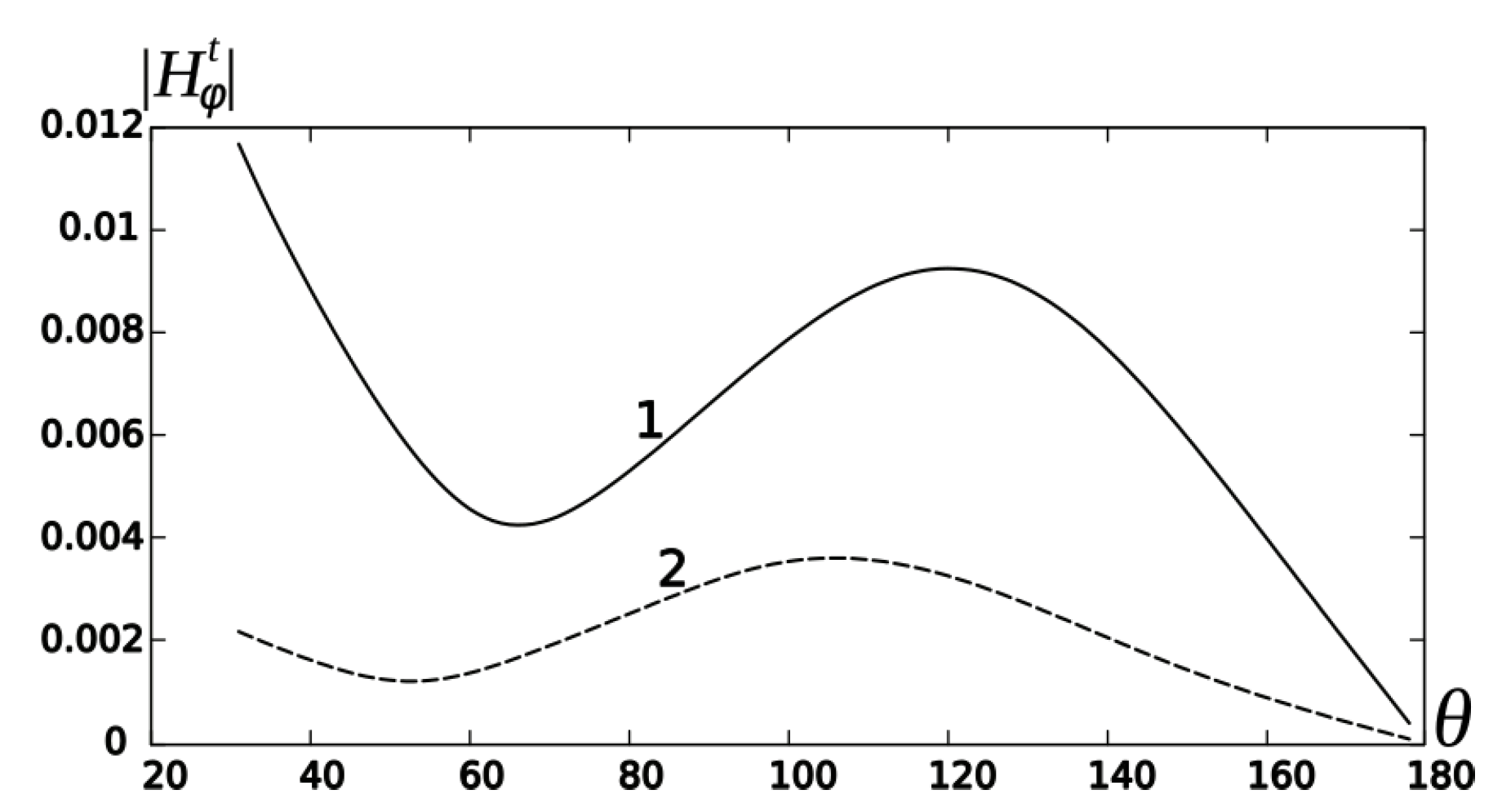
For this structure in Figure 6 and Figure 7, we represent the same scattering field characteristics as those we have studied in the previous case. In Figure 6, the sharp jumps are also observed if $k{c}_1$ is located close to $T{M}_{{\mu }_{n}0j}$ resonant oscillations of the corresponding closed cavity. Unlike in the previous case, we observe in this figure the excitation of the two types of the azimuthal resonant vibration with the indices $(n=2;j=2,\dots ,5)$ and $(n=3;j=1)$. The numerical examples of $k_{{\mu }_{n}j}{c}_1$ for the considered cavity are given in

Table 2. Resonant radii of the axially symmetric $T{M}_{{\mu }_{n}0j}$ mode oscillation for a closed sphere-conical resonator with $\pi -{\gamma }_2={91}^{\circ }$.

${\mathit{\mu }}_{\mathit{n}}/{\mathit{k}}_{{\mathit{\mu }}_{\mathit{n}}\mathit{j}}{\mathit{c}}_1$	j = 1	j = 2	j = 3	j = 4	j = 5
${\mu }_1=1.48274$	2.724	6.0934	9.2921	12.4608	15.6184
${\mu }_2=3.46116$	4.9309	8.6728	12.0119	15.2602	18.4697
${\mu }_3=5.43932$	7.0751	11.1155	14.5925	17.9283	21.1993

. Curves 1 and 2 in Figure 7 are calculated for the near field for $k{c}_1=6.68$ and $k{c}_1=7.68$ which correspond to the maximum and minimum of the curves in Figure 6. We can observe in these figures that the excitation of the cavity with $k{c}_1=6.68$ increases the magnetic field intensity at the surface of the conical probe. As follows from the dependencies represented in Figure 6a, we see the growth of the contribution of the higher TM-modes for the far field formation.

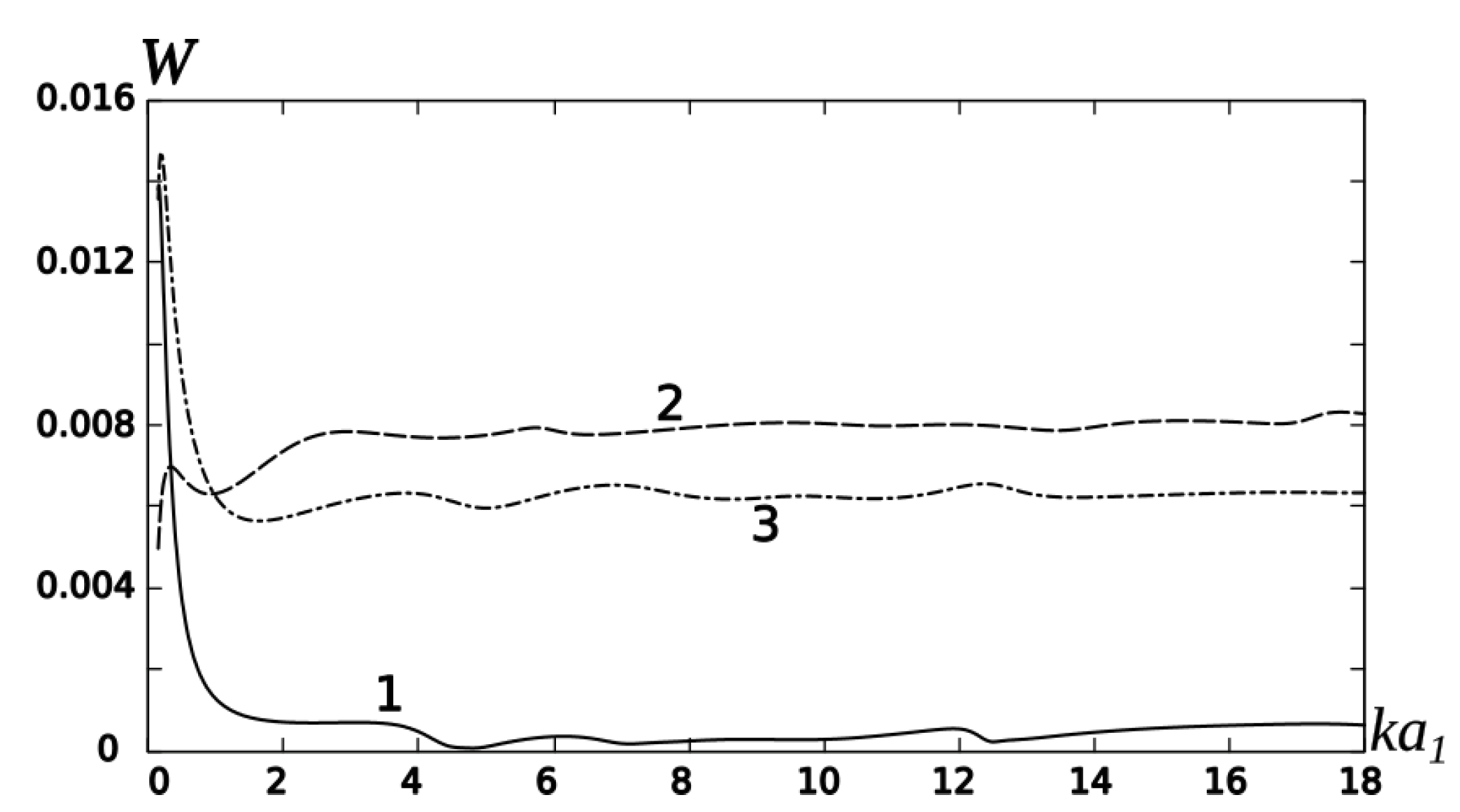
The curves in Figure 8 show the typical dependencies of the radiating power on the dimensionless truncation radius $k{a}_1$ for a large spherical radius of termination. In this figure, we observe the low frequency resonance if $k{a}_1<1$ for different geometrical parameters of the scatterer, and if $k{a}_1>4$ the radiated power depends weakly on the truncation parameter.

10. Conclusions

In this work, we have solved a new wave diffraction problem of an axially symmetric TM-wave diffraction from a bicone formed by a perfectly conducting semi-infinite cone and a truncated one with an internal termination. The problem is solved rigorously, using the analytical regularization technique. The field is expressed through the conical and biconical modes. Mode matching is applied for the derivation of the infinite system of linear algebraic Equations (35) and (46). These systems of equations are obtained for different groups of unknowns and represented as a special limit transition from the finite ones. The correlations (51) and (52) between them are established. It is shown that the matrix operators of the obtained equations allow for the selection of their singular parts, and the corresponding inverse operators in the analytical form are obtained. These operators are applied for the development of the analytical regularization technique and reduction of the problem to infinite systems of linear algebraic equations of the second kind. Equations (73), (74), (78), and (79) are the key ones. Two types of such regularizations are considered, namely, the left- and the right-hand side regularizations. The proposed techniques are generalized and we have shown a way to construct the set of regularizing operators for this problem. The resonance excitation of an open-ended sphere conical cavity is analysed analytically for a small-sized aperture of truncation. New approximate equations which allow for the explicit solutions for this case are obtained. It is found that the resonance excitation of the sphere-conical probe and the semi-spherical cavity can amplify the density of the surface current, owing to the intensification of the TEM wave radiation.