Plane-Wave Diffraction from Resistive-Filled Circular Hole in Infinite Resistive Plane: An Analytically Regularizing Approach
Abstract
:1. Introduction
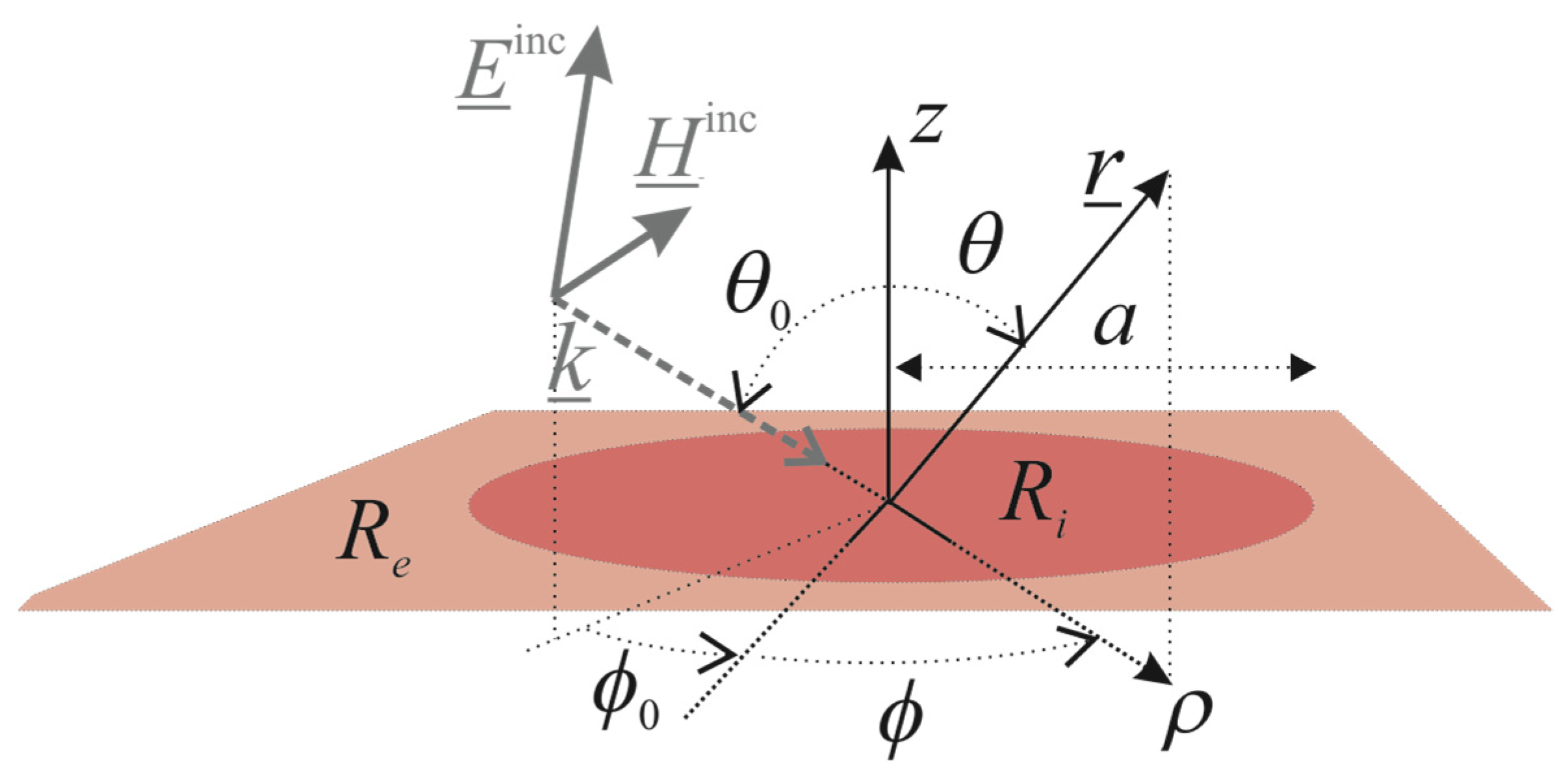
2. Formulation of the Problem
3. Proposed Solution
4. Near-Field and Far-Field Reconstruction
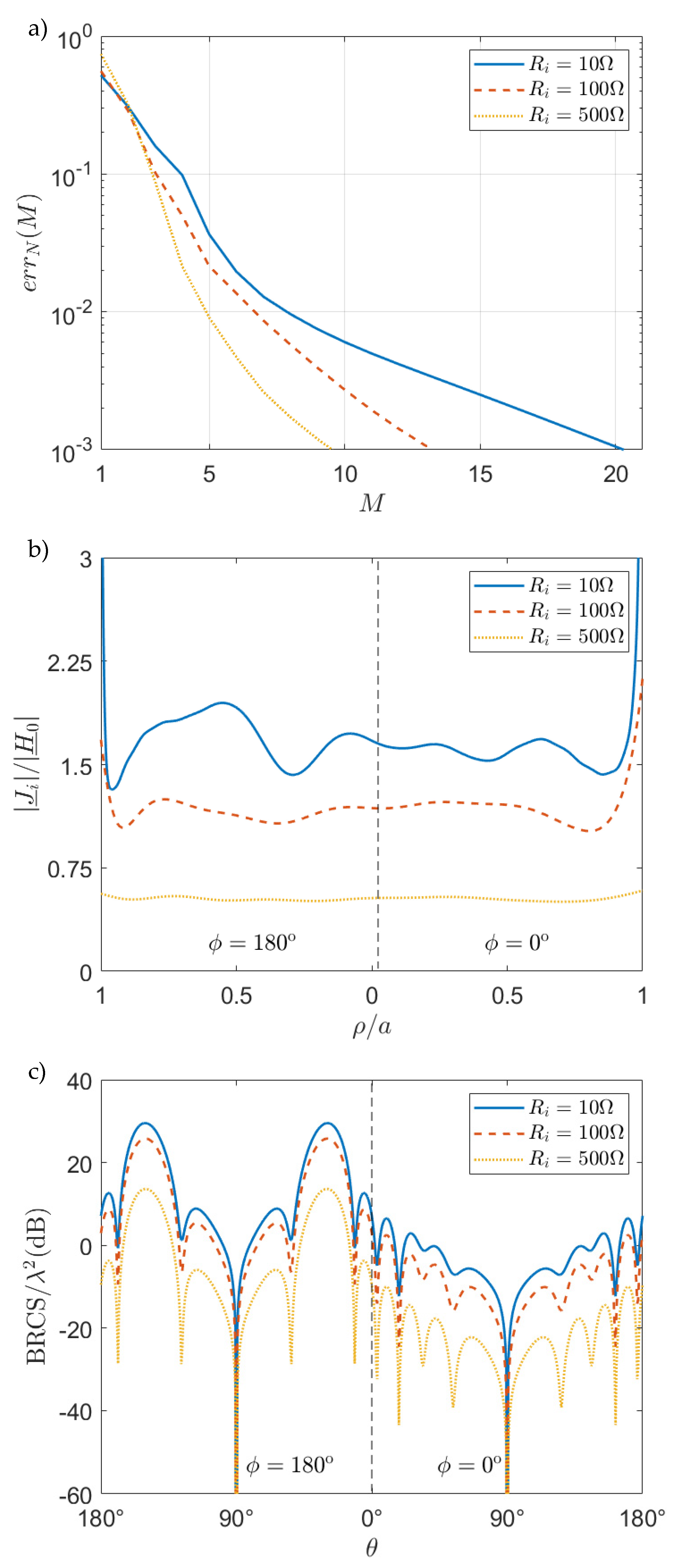
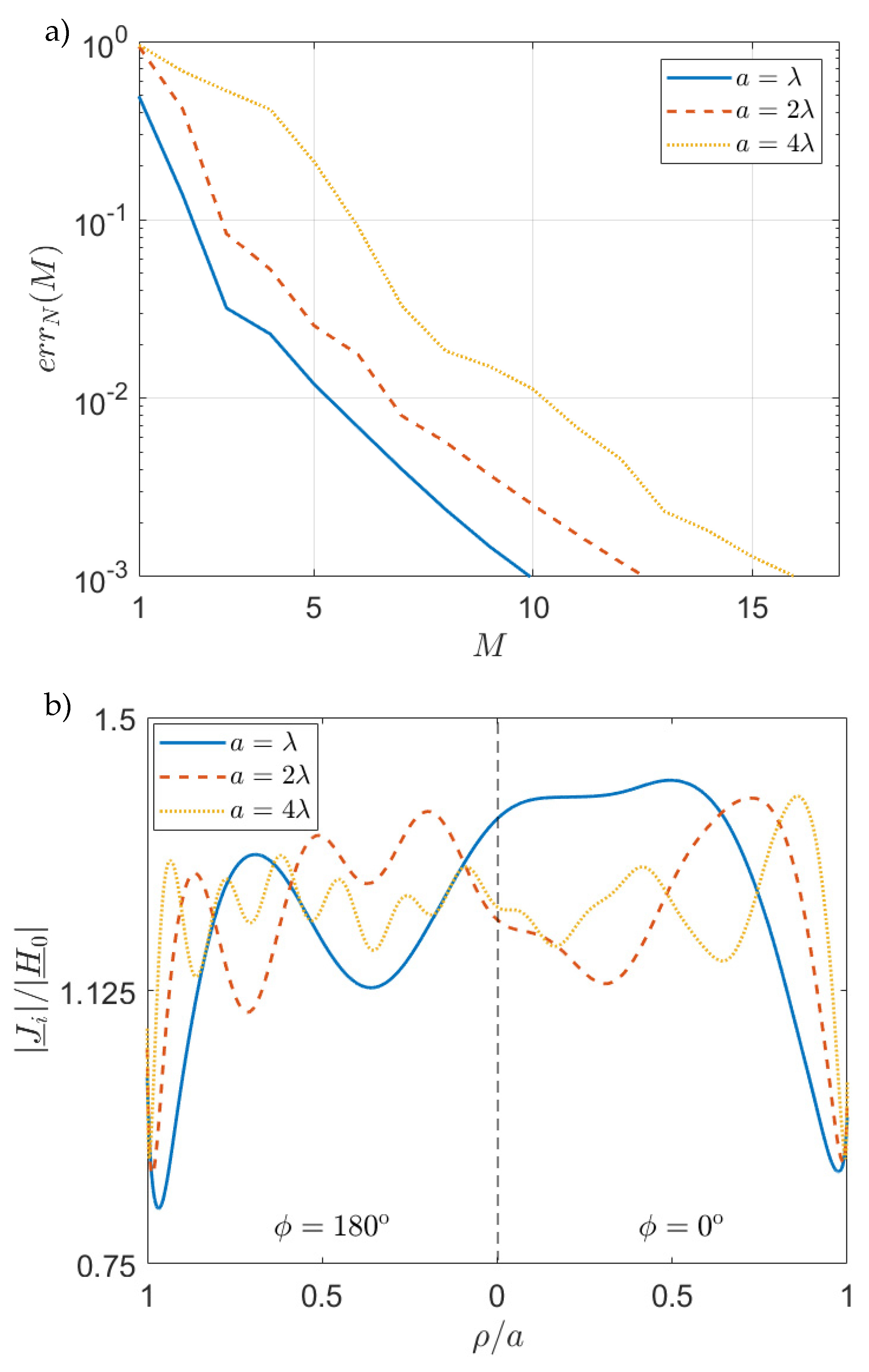
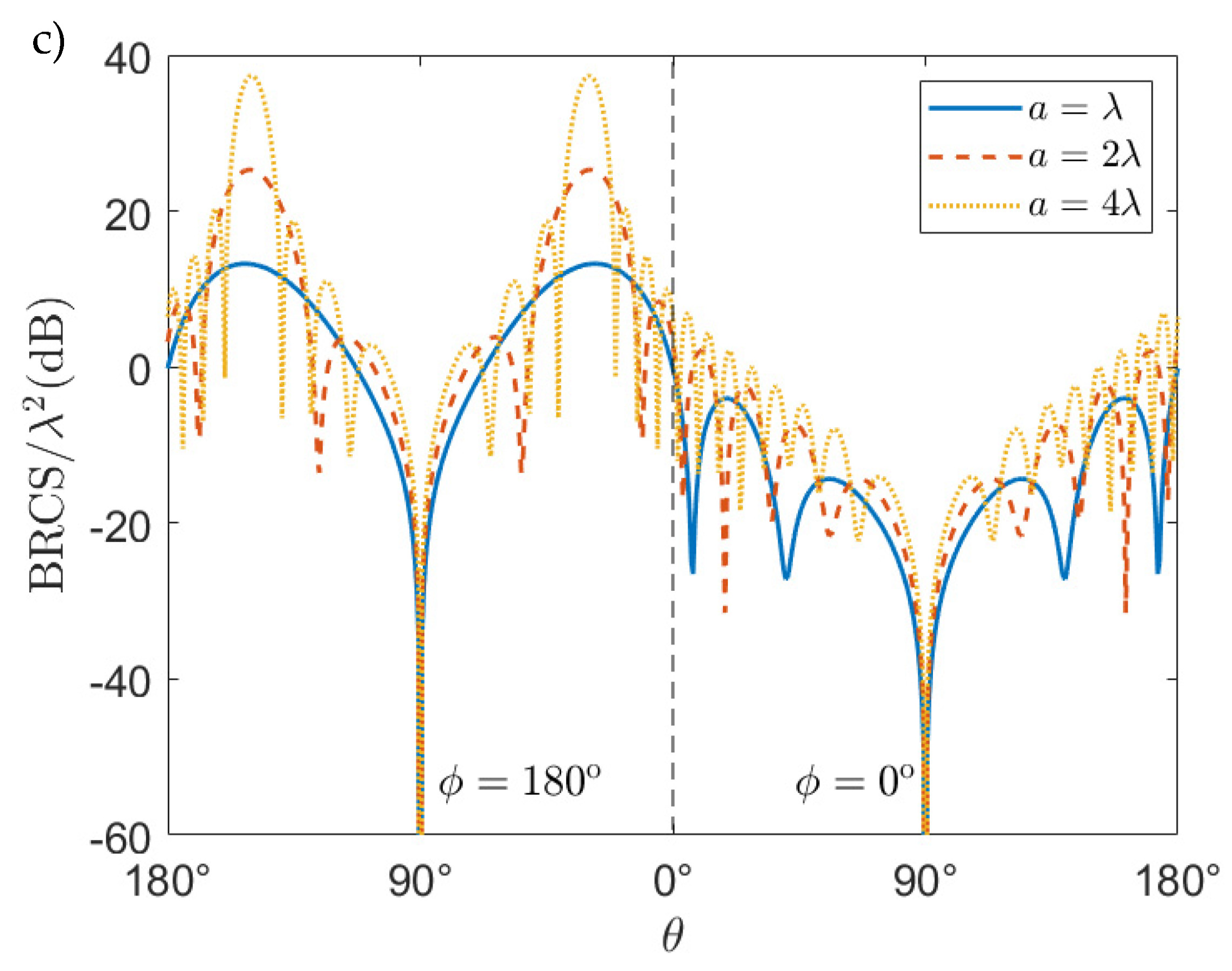
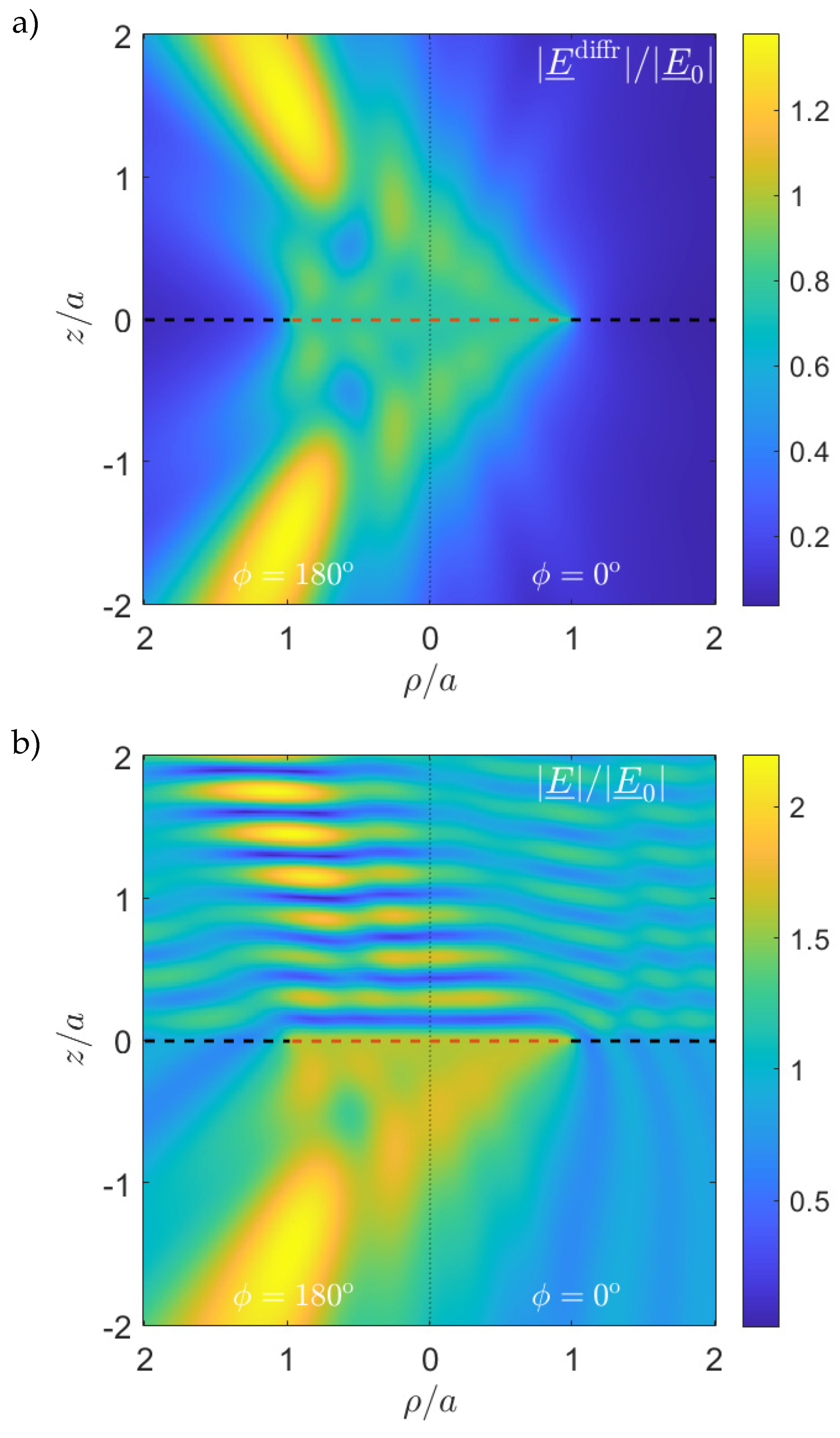
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Betzig, E.; Trautman, J.K. Near-field optics: Microscopy, spectroscopy, and surface modification beyond the diffraction limit. Science 1992, 257, 189–195. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lezec, H.J.; Degiron, A.; Devaux, E.; Linke, R.A.; Martin-Moreno, L.; Garcia-Vidal, F.J.; Ebbesen, T.W. Beaming light from a subwavelength aperture. Science 2002, 297, 820–822. [Google Scholar] [CrossRef] [PubMed]
- Levene, M.J.; Korlach, J.; Turner, S.W.; Foquet, M.; Craighead, H.G.; Webb, W.W. Zero-mode waveguides for single-molecule analysis at high concentrations. Science 2003, 299, 682–686. [Google Scholar] [CrossRef] [PubMed]
- Rigneault, H.; Capoulade, J.; Dintinger, J.; Wenger, J.; Bonod, N.; Popov, E.; Ebbesen, T.W.; Lenne, P.-F. Enhancement of single-molecule fluorescence detection in subwavelength apertures. Phys. Rev. Lett. 2005, 95, 117401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Juan, M.L.; Gordon, R.; Pang, Y.; Eftekhari, F.; Quidant, R. Self-induced back-action optical trapping of dielectric nanoparticles. Nat. Phys. 2009, 5, 915–919. [Google Scholar] [CrossRef]
- Kihm, H.W.; Koo, S.M.; Kim, Q.H.; Bao, K.; Kihm, J.E.; Bak, W.S.; Eah, S.H.; Lienau, C.; Kim, H.; Nordlander, P.; et al. Bethe-hole polarization analyser for the magnetic vector of light. Nat. Commun. 2011, 2, 451. [Google Scholar] [CrossRef] [Green Version]
- Yang, T.; Xu, C.; Ho, H.-P.; Zhu, Y.-Y.; Hong, X.-H.; Wang, Q.-J.; Chen, Y.-C.; Li, X.-A.; Zhou, X.-H.; Yi, M.-D.; et al. Miniature spectrometer based on diffraction in a dispersive hole array. Opt. Lett. 2015, 40, 3217–3220. [Google Scholar] [CrossRef]
- Rodrigo, S.G.; de León-Pérez, F.; Martín-Moreno, L. Extraordinary optical transmission: Fundamentals and applications. Proc. IEEE 2016, 104, 2288–2306. [Google Scholar] [CrossRef] [Green Version]
- Sajeev, V.; Jana, A.; Mallick, S.; Devi, K.M.; Chowdhury, D.R. Coulomb interaction mediated tuning of surface plasmon resonance in terahertz hole arrays. J. Phys. Photonics 2022, 4, 045001. [Google Scholar] [CrossRef]
- Ali, N.M.; Ali, T.A. Simple analytical model to use in CAD tools for designing FSS devices: Plasmonic transmission through hole arrays in thin films. Appl. Phys. B 2023, 129, 15. [Google Scholar] [CrossRef]
- Medina, F.; Mesa, F.; Marques, R. Extraordinary transmission through arrays of electrically small holes from a circuit theory perspective. IEEE Trans. Microw. Theory Tech. 2008, 56, 3108–3120. [Google Scholar] [CrossRef]
- Fiala, J.; Richter, I. Interaction of light with subwavelength apertures: A comparison of approximate and rigorous approaches. Opt. Quant. Electron. 2009, 41, 409–427. [Google Scholar] [CrossRef]
- Gunnarsson, R.; Bäckström, M. Transmission cross section for apertures and arrays calculated using time-domain simulations. In Proceedings of the 2014 International Symposium on Electromagnetic Compatibility, Gothenburg, Sweden, 4–8 August 2014. [Google Scholar]
- Pinchera, D.; Migliore, M.D.; Schettino, F. Optimizing antenna arrays for spatial multiplexing: Towards 6G systems. IEEE Access 2021, 9, 53276–53291. [Google Scholar] [CrossRef]
- Pinchera, D.; Migliore, M.D.; Panariello, G. Isophoric inflating deflating exploration algorithm (I-IDEA) for equal-amplitude aperiodic arrays. IEEE Trans. Antennas Propag. 2022, 70, 10405–10416. [Google Scholar] [CrossRef]
- Bouwkamp, C.J. Diffraction theory. Rep. Prog. Phys. 1954, 17, 35–100. [Google Scholar] [CrossRef]
- Bowman, J.J.; Senior, T.B.A.; Uslenghi, P.L.E. Electromagnetic and Acoustic Scattering by Simple Shapes; Wiley-Interscience: New York, NY, USA, 1969. [Google Scholar]
- Butler, C.M.; Rahmat-Samii, Y.; Mittra, R. Electromagnetic penetration through apertures in conducting surfaces. IEEE Trans. Antennas Propag. 1978, 26, 82–93. [Google Scholar] [CrossRef]
- Jull, E.V. Aperture Antennas and Diffraction Theory; Peter Peregrinus: London, UK, 1981. [Google Scholar]
- Hongo, K.; Naqvi, Q.A. Diffraction of electromagnetic wave by disk and circular hole in a perfectly conducting plane. Prog. Electromagn. Res. 2007, 68, 113–150. [Google Scholar] [CrossRef] [Green Version]
- Michalski, K.A.; Mosig, J.R. On the plane wave-excited subwavelength circular aperture in a thin perfectly conducting flat screen. IEEE Trans. Antennas Propag. 2014, 62, 2121–2129. [Google Scholar] [CrossRef]
- Lovat, G.; Burghignoli, P.; Araneo, R.; Celozzi, S. Magnetic-field penetration through a circular aperture in a perfectly-conducting plate excited by a coaxial loop. IET Microw. Antennas Propag. 2021, 15, 1147–1158. [Google Scholar] [CrossRef]
- Neugebauer, H. Diffraction of electromagnetic waves caused by apertures in absorbing plane screens. IRE Trans. Antennas Propag. 1956, 4, 115–119. [Google Scholar] [CrossRef]
- Ashour, A.A. Electromagnetic induction in finite thin sheets. Quart. J. Mech. Appl. Math. 1965, 18, 73–86. [Google Scholar] [CrossRef]
- Popov, E.; Nevière, M.; Sentenac, A.; Bonod, N.; Fehrembach, A.-L.; Wenger, J.; Lenne, P.-F.; Rigneault, H. Single-scattering theory of light diffraction by a circular subwavelength aperture in a finitely conducting screen. J. Opt. Soc. Am. A 2007, 24, 339–358. [Google Scholar] [CrossRef] [PubMed]
- Lovat, G.; Burghignoli, P.; Araneo, R.; Celozzi, S. Axially symmetric source field penetration through a circular aperture in a thin impedance plate. IEEE Trans. Antennas Propag. 2022, 70, 8348–8359. [Google Scholar] [CrossRef]
- Jin, J. The Finite Element Method in Electromagnetics; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Volakis, J.L.; Chatterjee, A.; Kempel, L.C. Finite Element Method for Electromagnetics; IEEE Press: Piscataway, NJ, USA, 1998. [Google Scholar]
- Lee, J.; Xiao, T.; Liu, Q.H. A 3-D spectral-element method using mixed-order curl conforming vector basis functions for electromagnetic fields. IEEE Trans. Microw. Theory Tech. 2006, 54, 437–444. [Google Scholar]
- Mahariq, I.; Kurt, H. On- and off-optical-resonance dynamics of dielectric microcylinders under plane wave illumination. J. Opt. Soc. Am. B 2015, 32, 1022–1030. [Google Scholar] [CrossRef]
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed.; Artech Hause: Norwood, MA, USA, 2005. [Google Scholar]
- Schild, S.; Chavannes, N.; Kuster, N. A robust method to accurately treat arbitrarily curved 3-D thin conductive sheets in FDTD. IEEE Trans. Antennas Propag. 2007, 55, 3587–3594. [Google Scholar] [CrossRef]
- Harrington, R.F. Field Computation by Moment Method; IEEE Press: New York, NY, USA, 1993. [Google Scholar]
- Pan, G.; Narayanan, R. Electromagnetic scattering from a dielectric sheet using the method of moments with approximate boundary condition. Electromagnetics 2004, 24, 369–384. [Google Scholar] [CrossRef]
- Lucido, M.; Schettino, F.; Panariello, G. Scattering from a thin resistive disk: A guaranteed fast convergence technique. IEEE Trans. Antennas Propag. 2021, 69, 387–396. [Google Scholar] [CrossRef]
- Lucido, M.; Balaban, M.V.; Dukhopelnykov, S.V.; Nosich, A.I. A fast-converging scheme for the electromagnetic scattering from a thin dielectric disk. Electronics 2020, 9, 1451. [Google Scholar] [CrossRef]
- Lucido, M. Natural mode resonances in the plane wave scattering from an infinite thin resistive plate with a circular hole. In Proceedings of the 2023 17th European Conference on Antennas and Propagation (EuCAP 2023), Florence, Italy, 26–31 March 2023. [Google Scholar]
- Lucido, M.; Kobayashi, K.; Medina, F.; Nosich, A.I.; Vinogradova, E.D. Guest editorial: Method of analytical regularisation for new frontiers of applied electromagnetics. IET Microw. Antennas Propag. 2021, 15, 1127–1132. [Google Scholar] [CrossRef]
- Lucido, M. Scattering by a tilted strip buried in a lossy half-space at oblique incidence. Prog. Electromagn. Res. M 2014, 37, 51–62. [Google Scholar] [CrossRef] [Green Version]
- Lucido, M.; Schettino, F.; Migliore, M.D.; Pinchera, D.; Di Murro, F.; Panariello, G. Electromagnetic scattering by a zero-thickness PEC annular ring: A new highly efficient MoM solution. J. Electromagn. Waves Appl. 2017, 31, 405–416. [Google Scholar] [CrossRef]
- Lucido, M.; Santomassimo, C.; Panariello, G. The method of analytical preconditioning in the analysis of the propagation in dielectric waveguides with wedges. J. Light. Technol. 2018, 36, 2925–2932. [Google Scholar] [CrossRef]
- Dukhopelnykov, S.V.; Lucido, M.; Sauleau, R.; Nosich, A.I. Circular dielectric rod with conformal strip of graphene as tunable terahertz antenna: Interplay of inverse electromagnetic jet, whispering gallery and plasmon effects. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 4600908. [Google Scholar] [CrossRef]
- Herasymova, D.O.; Dukhopelnykov, S.V.; Lucido, M.; Nosich, A.I. Optical sensing of electron-beam position with twin silver nanotube antenna tuned to hybrid surface plasmon resonance. IEEE J. Sel. Top. Quantum Electron. 2021, 27, 4601008. [Google Scholar] [CrossRef]
- Lucido, M.; Balaban, M.V.; Nosich, A.I. Plane wave scattering from thin dielectric disk in free space: Generalized boundary conditions, regularizing Galerkin technique and whispering gallery mode resonances. IET Microw. Antennas Propag. 2021, 15, 1159–1170. [Google Scholar] [CrossRef]
- Lucido, M.; Balaban, M.V.; Nosich, A.I. Terahertz-range plasmon and whispering gallery mode resonances in the plane wave scattering from thin microsize dielectric disk with graphene covers. Proc. Math. Phys. Eng. Sci. 2022, 478, 2262. [Google Scholar] [CrossRef]
- Herasymova, D.O.; Dukhopelnykov, S.V.; Natarov, D.M.; Zinenko, T.L.; Lucido, M.; Nosich, A.I. Threshold conditions for transversal modes of tunable plasmonic nanolasers shaped as single and twin graphene-covered circular quantum wires. Nanotechnology 2022, 33, 495001. [Google Scholar] [CrossRef]
- Bleszynski, E.; Bleszynski, M.; Jaroszewicz, T. Surface-integral equations for electrmagnetic scattering from impenetrable and penetrable sheets. IEEE Antennas Propag. Mag. 1993, 35, 14–24. [Google Scholar] [CrossRef]
- Chew, W.C.; Kong, J.A. Resonance of nonaxial symmetric modes in circular microstrip disk antenna. J. Math. Phys. 1980, 21, 2590–2598. [Google Scholar] [CrossRef]
- Braver, I.M.; Fridberg, P.S.; Garb, K.L.; Yakover, I.M. Edge conditions for the junction of two resistive half-planes with different surface impedances. In Proceedings of the 2014 IEEE 28th Convention of Electrical and Electronics Engineers in Israel, Eilat, Israel, 3–5 December 2014. [Google Scholar]
- Braver, I.M.; Fridberg, P.S.; Garb, K.L.; Yakover, I.M. The behavior of the electromagnetic field near the edge of a resistive half-plane. IEEE Trans. Antennas Propag. 1988, 36, 1760–1768. [Google Scholar] [CrossRef]
- Van Bladel, J. A discussion of Helmholtz’ theorem on a surface. AEÜ 1993, 47, 131–136. [Google Scholar]
- Lucido, M.; Di Murro, F.; Panariello, G. Electromagnetic scattering from a zero-thickness PEC disk: A note on the Helmholtz-Galerkin analytically regularizing procedure. Progr. Electromagn. Res. Lett. 2017, 71, 7–13. [Google Scholar] [CrossRef]
- Jones, D.S. The Theory of Electromagnetism; Pergamon Press: New York, NY, USA, 1964. [Google Scholar]
- Colton, D.; Kress, R. Integral Equation Methods in Scattering Theory; Wiley: New York, NY, USA, 1983. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Verlag Harri Deutsch: Frankfurt, The Netherlands, 1984. [Google Scholar]
- Wilkins, J.E. Neumann series of Bessel functions. Trans. Am. Math. Soc. 1948, 64, 359–385. [Google Scholar] [CrossRef]
- Gradstein, S.; Ryzhik, I.M. Tables of Integrals, Series and Products; Academic Press: New York, NY, USA, 2000. [Google Scholar]
- Geng, N.; Carin, L. Wide-band electromagnetic scattering from a dielectric BOR buried in a layered lossy dispersive medium. IEEE Trans. Antennas Propag. 1999, 47, 610–619. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lucido, M.; Chirico, G.; Migliore, M.D.; Pinchera, D.; Schettino, F. Plane-Wave Diffraction from Resistive-Filled Circular Hole in Infinite Resistive Plane: An Analytically Regularizing Approach. Appl. Sci. 2023, 13, 7465. https://doi.org/10.3390/app13137465
Lucido M, Chirico G, Migliore MD, Pinchera D, Schettino F. Plane-Wave Diffraction from Resistive-Filled Circular Hole in Infinite Resistive Plane: An Analytically Regularizing Approach. Applied Sciences. 2023; 13(13):7465. https://doi.org/10.3390/app13137465
Chicago/Turabian StyleLucido, Mario, Gaetano Chirico, Marco Donald Migliore, Daniele Pinchera, and Fulvio Schettino. 2023. "Plane-Wave Diffraction from Resistive-Filled Circular Hole in Infinite Resistive Plane: An Analytically Regularizing Approach" Applied Sciences 13, no. 13: 7465. https://doi.org/10.3390/app13137465
APA StyleLucido, M., Chirico, G., Migliore, M. D., Pinchera, D., & Schettino, F. (2023). Plane-Wave Diffraction from Resistive-Filled Circular Hole in Infinite Resistive Plane: An Analytically Regularizing Approach. Applied Sciences, 13(13), 7465. https://doi.org/10.3390/app13137465








