Predicting and Evaluating Decoring Behavior of Inorganically Bound Sand Cores, Using XGBoost and Artificial Neural Networks

Abstract

Complex casting parts rely on sand cores that are both high-strength and can be easily decored after casting. Previous works have shown the need to understand the influences on the decoring behavior of inorganically bound sand cores. This work uses black box and explainable machine learning methods to determine the significant influences on the decoring behavior of inorganically bound sand cores based on experimental data. The methods comprise artificial neural networks (ANN), extreme gradient boosting (XGBoost), and SHapley Additive exPlanations (SHAP). The work formulates five hypotheses, for which the available data were split and preprocessed accordingly. The hypotheses were evaluated by comparing the model scores of the various sub-datasets and the overall model performance. One sand-binder system was chosen as a validation system, which was not included in the training. Robust models were successfully trained to predict the decoring behavior for the given sand-binder systems of the test system but only partially for the validation system. Conclusions on which parameters are the main influences on the model behavior were drawn and compared to phenomenological–heuristical models of previous works.

1. Introduction

1.1. Motivation and Context

Complex cast parts require lost cores to form undercuts and cavities. Filigree cores need high strength to withstand the casting process and make them dimensionally stable. However, they have to be removable after casting. Inorganically bound sand cores have environmental advantages compared to organically bound sand cores [1]. However, unlike organically bound cores, inorganically bound cores cannot be completely rinsed out or burned out. They need to be broken up by a mechanical impulse on the surrounding cast part and thus are significantly harder to decore than organically bound sand cores [1]. Additionally, if the cores are too strong, the forces required to break them up deform the cast part. These issues can be addressed by changing the sand-binder systems’ chemical composition and manufacturing process. The acting influences on the decoring properties of inorganically bound sand cores must be understood to achieve these changes systematically. Ettemeyer [2] investigated these influences for the decoring behavior, collecting extensive experimental data. These data were used to capture cause–effect relations and to validate aspects of a formulated theory for the decoring behavior. This theory claims that the decoring behavior can be predicted by various key parameters of the sand-binder system of which the core consists and of the decoring process. Ettemeyer used heuristical and phenomenological methods for the prediction of decoring behavior. This work uses purely data-based machine learning models to predict the decoring behavior based on the same experimental data of the mentioned work. Additionally, the importance of various features for the machine learning model prediction of the decoring behavior is evaluated. This evaluation is achieved by varying the data composition for model training and using interpretable machine learning techniques. The importance of the features according to the machine learning models is then compared to the mentioned theory.

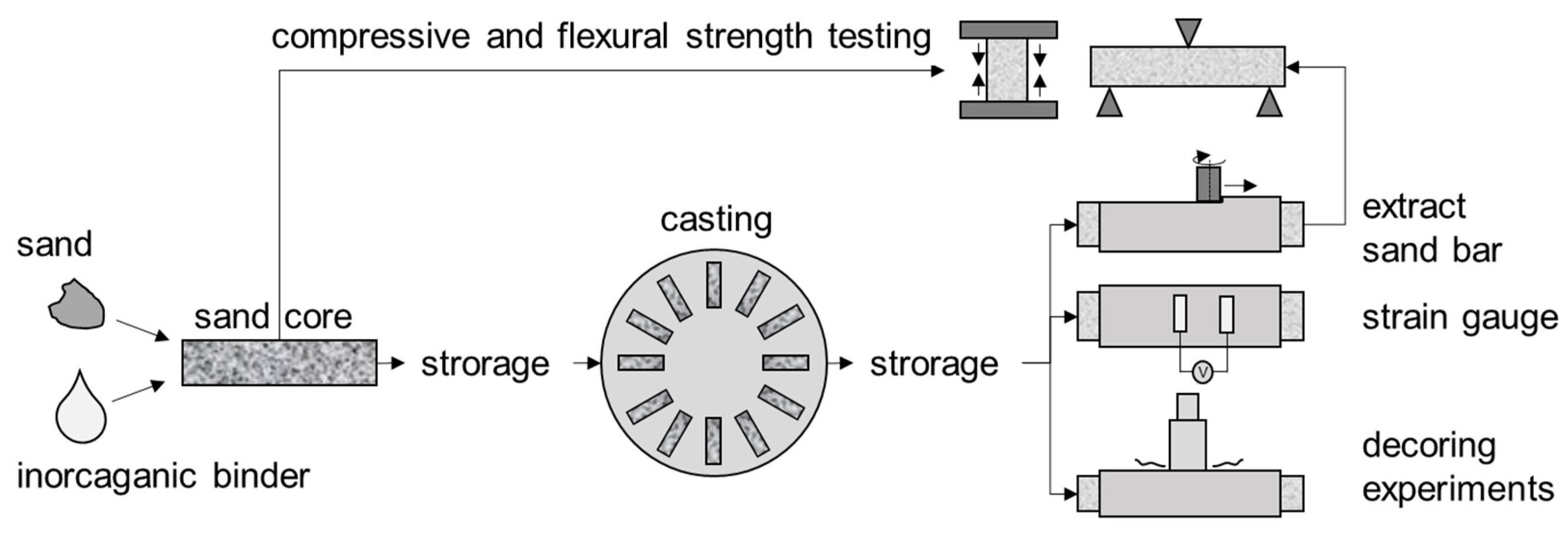
1.2. Decoring of Inorganically Bound Sandcores

Casting technology relies on sand cores to achieve complex, hollow structures with undercuts and cavities [3]. The cores are used individually or are assembled into sand-core packages. They are inserted into the mold. They must be held in position by core holders in the surrounding permanent or sand mold. The sand core stands out of these holding positions after casting and forms a connection to the cavity. This connection is used to extract the sand from the formed cast part, which is the decoring process step. The sand-binder system of the sand core determines which methods can be used to decore it. Sand cores are classified into organically and inorganically bound sand cores [1]. Organic sand-binder systems are based on hydrocarbons and can easily be burnt off. Most of the decoring process is achieved during the casting process due to the heat of the melt. It cracks the sand cores, burns parts of the binder, and allows shaking of the remaining sand out of the openings. The downsides are environmental considerations of the toxic waste and fumes produced during the burnup. Inorganic sand-binder systems use sodium-silicate to harden sand cores. It lacks hydrocarbons and, with it, the downsides of toxicity. However, it cannot be burnt off, and additionally, it hardens even more on the surface, which is in contact with the melt [1]. The decoring of inorganically bound sand cores is their main disadvantage. There are multiple approaches to change the properties, for example, adding additives or changing the ratio of binder to sand [4].

At the same time, research focuses on understanding the decoring behavior of inorganically bound sand cores [5]. Ettemeyer [2] describes the essential parameters to predict the decoring behavior of a sand-binder system and builds a matching theory. According to this theory, the flexural and compressive strength of the sand-binder mixture are the main parameters. Another factor for predicting the decoring behavior is the hydrostatic pressure on the sand core [6]. The cast part shrinks onto the sand core after casting, creating pressure on the sand core. This pressure influences the force needed to fracture the sand core. Starting from an initial fracture area, the decoring proceeds. The Drucker–Prager failure model describes this theory, as shown in Figure 1.

The failure straight is determined from a three-point bending test and a uniaxial compression test. The cohesion and the internal friction angle phi describe the experimentally calculated failure straight. If the von Mises equivalent stress for a prevailing hydrostatic pressure is above the failure straight, a fracture occurs in the sand core. The composition of sand and binder defines the parameters of cohesion and phi. If these parameters of a sand-binder system and the hydrostatic pressure state are known, the force needed to fracture can be predicted. The following bullet points summarize our findings:

• The assumption of a pressure-dependent material model to describe sand-binder systems is valid. It can be seen as essential for an accurate characterization of the mechanical behavior of decoring.
• The decoring behavior of inorganically bound sand-binder systems is significantly influenced by the molding material and the binder system used. The molding material dominates the influence on the decoring behavior.
• Larger binder quantities can lead to higher residual strengths and correspondingly poorer decoring behavior for the same molding material.
• Assuming constant decoring energy, the angle phi and the cohesion of the remaining residual strength after casting are the two main influencing variables for the decoring behavior.

1.3. Machine Learning Models

This work uses machine learning methods to model cause–effect relationships in the context of decoring inorganically bound sand cores. There are various examples of gaining insights from data in many technology areas, for example, material analysis [7], laser beam welding [8], or injection molding [9]. The basic idea is to train machine learning models using annotated data. The trained machine learning models are then evaluated using statistical approaches or explainable model architectures. This work follows the approach shown in [10,11] to use models such as extreme gradient boosting (XGB) with the evaluation and visualization tool SHapley Additive exPlanations (SHAP) to interpret datasets. Additionally, artificial neural networks (ANN), which are black box models, are trained and evaluated using their achieved model scores. These are evaluated based on their model scores. Both models—ANN and XGB—are trained for all datasets.

ANNs are well-suited for complex datasets. Due to their non-linear calculations, they can abstract non-linear links between input and label. With multiple layers of neurons, they can compute intermediate features from input data, performing a type of model-based feature engineering, an example of which can be found in [12]. Their broad abilities render them a standard tool in machine learning tasks. This advantage and their frequent use in machine learning publications are why they are used in this work as well, making it easier to compare the results to other works.

XGB models generate their predictions from ensembles of decision trees with low depth. Decision trees are transparent, as it is possible to read out each node and its decision. All decisions can be summarized and evaluated, for example, how often a feature is used in the model for a decision in all trees or how much the loss is reduced by these splits [13]. XGB has further advantages that make it a popular choice for machine learning tasks [14], for example, as it is an ensemble method that can be parallelized, thus speeding up calculations on multi-processer units, and can avoid overfitting by using different types of regularization [15].

SHAP allows generating even more information from machine learning models such as XGB. It uses game theory to calculate the average marginal contribution of each feature [16]. The general approach of SHAP is to leave one feature out of the model calculation and to determine the remaining model error, which is repeated for every feature in the dataset used by the investigated model. Lundberg and Lee developed the corresponding algorithm [17]. It allows the generation of various figures. This work uses its bee plot, which shows each feature vertically in descending order of its contribution to the model. All datapoints are depicted individually on a horizontal scale for each feature to illustrate the influence of each feature on each datapoint. This allows for a dense overview of feature importance, the identification of outliers, and an interpretation of the direction the features push at each datapoint.

1.4. Aim of This Work

Models can be categorized depending on the approach and the methods used. Figure 2 depicts a possible categorization of models [18]. Ettemeyer [2] used heuristical and phenomenological approaches to build his theory of important parameters for decoring behavior and predict new sand-binder systems’ decoring behavior. He collected an extensive amount of experimental data during the progress. This work aims to replicate these results with a purely statistical approach using machine learning methods and the collected experimental data. The new approach is evaluated by comparing which parameters are important to predict decoring behavior according to the machine learning models and according to Ettemeyer [2]. This results in three corresponding research questions:

• Is it possible to train robust machine learning models to predict the decoring behavior of sand-binder systems using the given data?
• Which features are important for the decoring behavior according to the machine learning models, and are those the same as described in the previous work?
• Is it possible to extract further, possibly new insights from the data using machine learning models?

All three questions are tested by a forwards–backward approach, as shown in Figure 3. Machine learning models are trained and optimized using the whole experimental data or subsets thereof. Depending on the resulting quality and behavior of the trained models, a conclusion is drawn whether the used subset of data includes the necessary parameters or not. A similar approach was used in [19], where insights into the main parameters of an industrial hydrocyclone were determined.

By optimizing the models, the likeliness increases that the differences in the model quality of the prediction for different feature sets result from the different feature sets and not from randomly better- or worse-fitting models. The second question formulates a general comparison. To be able to answer it, it is transformed into five testable specific hypotheses:

• Categorical features such as the name of the experimental series contain information beyond the collected data, for example, a different room temperature level during the decoring process or slight but systematical differences in the clamping of the specimen. Including these features in the model training will improve the model quality but reduce the interpretability due to the aggregation of information into a single variable.
• The acceleration data contain important information for predicting the decoring behavior. Including it in the model training will improve the model quality.
• Different processing methods of the acceleration data are differently suited for machine learning models.
• Including all features in the model training will reduce the model quality due to a high data complexity without more information than in a reduced dataset. Reducing the data complexity in multiple steps using a feature selection method will improve the model quality for each dataset. At a given threshold, the model quality will drop significantly and abruptly. All features included at that threshold can be considered significantly important for the decoring behavior.

1.5. Approach and Big Picture

The following approach is used to achieve the described aim and test the hypotheses. The basic idea is to use the behavior and quality of trained models to evaluate the feature sets used. The models will predict the decoring behavior with some degree of deviation. Varying the features selected from all the experimental data to train the model will result in varying deviations in the model prediction. This variation can be used to compare different feature sets for their information content. A feature set yielding a model with a comparatively low deviation can be seen as containing more relevant information than a feature set resulting in a higher error. By using a transparent machine learning model such as XGB, further indications of the importance of features can be generated. Hypotheses of which feature sets are more or less important to decoring behavior are formulated, and datasets are composed accordingly. In all cases, the model quality has to be ensured by optimizing the models and evaluating their robustness. Otherwise, an insufficiently trained or non-optimized model is just as likely as an insufficient feature set.

The specific approach is summarized in Figure 4. First, the target feature has to be defined. The possible alternatives are the measured decored mass after each interval and the measured difference in the decored distance from both open sides of the rectangular tube after each interval. Being easier to understand and easier to measure consistently, the decored mass is defined as the target feature for the model training. Thus, the trained models will predict the decored mass after each interval.

In step two, the ram-impact acceleration curves recorded with the laser vibrometer are converted into scalar features. Three approaches are used for this: Fast Fourier transforms (FFTs), mel frequency cepstral coefficients (mfcc), and a statistical evaluation of the signals in the time domain. All three are typical approaches to translating signal curves into features for machine learning methods. These characteristics are calculated individually for all ram impacts and summarized for the respective interval. Section 3.1 explains the exact calculations.

In step three, the division into datasets takes place. The original dataset with all features is split according to the previously described hypotheses. The main reason for this division of the data into feature sets is that the features in the data overlap in their information content. For example, the sand-binder system’s name indirectly contains the sand’s name, the binder’s name, the binder, the weight content of the binder in the mixture, and their specific properties. It makes evaluating specific features more complicated. The division into sub-datasets can reduce this effect but only negate it partially. The second reason is the number of datapoints. Using all features simultaneously results in a dataset with about as many or more features as datapoints. These kinds of sparse data can lead to more overfitting during training. It can also obstruct the model training if the input vector is overly large compared to the number of datapoints. The detailed data composition is explained in Section 3.2.

Step four is the first round of model calculations. As mentioned before, ANN and XGB models are used. The used programming libraries are listed in Used programming libraries of Appendix A. It is essential to try different model parameter sets and optimize the models for each dataset. Without this step, the achievable model quality may depend significantly on the chosen model parameters. Even with dataset-specific optimization, this is always the case to some degree and must be considered in the interpretation. The likelihood of overfitting is reduced by calculating each parameter set ten times with random initializations. The average of these ten calculations is used as the final model score for a given parameter set. The model quality metrics and their interpretation are explained in Section 2.2. The meta code and further details of the calculations can be found in Section 2.3.

In step five, a data complexity reduction is performed. As mentioned, the ratio of features to datapoints can be a crucial influence on model quality. Reducing the number of features can lead to better-performing models despite losing some of the information. There are multiple ways to reduce data complexity to achieve a high performance boost without losing too much information. One way is to keep all features but reduce the dimensionality by transforming the features into a new set of features, for example, using principle component analysis. Another way is to select features based on calculated metrics, for instance, feature importance values of a decision tree algorithm. This work uses feature selection based on the feature importance values of the XGB models. For each dataset, the XGB model with the lowest root mean square error (RMSE) is defined as the best-fitting XGB model. The feature importance values of this model are used to select the features. The percentage of features kept is called filter fraction (ff). A filter fraction of 100% is equal to all features used to train a model. Twelve filter fractions are used, with 10% steps between 100% and 10%. Smaller steps are used between 10% and 1%. The final number of features is rounded up to the next integer. Twelve datasets and twelve filter fractions result in 144 datasets used to train the models. Step six is to train and optimize ANN and XGB models for the reduced datasets in the same way as in step four.

It is essential to test whether the differences in the results of the datasets are significant. Other works used a two-sided Welch’s t-test to compare different models [20] and different datasets [21]. Therefore, this work applies a two-sided Welch’s t-test with a 0.5 significance level to test whether the results are significant. The test is performed for each dataset. The overall best dataset is used as a comparison set. This work focuses on obtaining insights by comparing model results for different datasets, which is why the Welch’s t-test is performed for the datasets and not explicitly between the ANN and XGBoost models.

Finally, the results of the two rounds of computation are visualized and discussed. The corresponding hypothesis is evaluated based on the model quality that can be achieved in each case. Plots of the model scores for varying filter fractions and selected parameters are discussed to assess the robustness of the models and the likelihood that the model score is a result of the feature selection and not of the model parameters.

2. Materials and Methods

2.1. Data Origin

The work of Ettemeyer [2] delivers the experimental basis of this work and the theory for the comparison. Ettemeyer investigated seventeen sand-binder systems. The sand, the binder, and the binder quantity varied for each system. A sequence of experiments was carried out for each system. Figure 5 depicts the tested specimen. It represents a rectangular bar of an inorganically bound sand core cast in a rectangular aluminum tube. It has two open sides, with some of the sand core extending out of the surrounding aluminum tube. The twelve specimens were carefully cut off from the casting system. The sand core was not damaged significantly, and the shape was preserved in most cases. This work focuses only on those kinds of specimens with undamaged or only slightly damaged specimens.

Figure 6 explains the experimental process. The selected sand was molded into a sand core with the selected binder amount and tempered. A varying share of the cores was tested in this raw state, determining their raw flexural strength and raw compressive strength. These tests were conducted at 25 °C, at 400 °C, at 600 °C, and at 750 °C. After a storage period, twelve sand cores were placed in one circular mold in each casting session, with the metal inflow located in the middle of the mold. The casting temperature of the aluminum melt was 750 °C. The number of casting sessions and, thus, the number of specimens varied for the various sand-binder systems. After an additional storage time, the specimens were cut off from the casting system and were tested. Three kinds of tests were conducted. The first test determined the sand cores’ residual flexural and compressive strength after casting. To make the test possible, some specimens were cut open in a very low-impact way to extract the undamaged sand core. These were destructively tested to measure the strengths after casting. The second test yielded the residual stress configuration of the aluminum tubes using strain gauges and cutting the cast part open near the strain gauges. These two tests were only conducted for some sand-binder systems and are referred to as extended features. The third test was the main decoring test. Figure 7 shows the decoring process. The decoring was achieved by a ram impacting the specimen. A laser vibrometer measured the velocity at a specific point of the specimen during each impact. The resulting velocity curve was translated into an acceleration curve. The ram impacted the specimen until it was fully decored. Figure 8 explains the division of the decoring process in intervals of ram impacts. After each interval, the mass and the decored distance on both open ends of the cast part were measured.

The cohesion and the internal friction angle phi were calculated for all experimentally determined compressive and flexural strengths and form part of the data input for the machine learning models.

In summary, the data collected represents a dataset with over 400 intervals measured and over 100 bars tested. The publication [2] describes the calculation of data, the quality of the collected data, and the considerations underlying its selection in greater detail.

2.2. Used Model Quality Criteria and Their Interpretation

Three different model scores describe the model quality in this work. The mean absolute error (MAE) is easily interpreted since it contains no non-linear transformation. It scores how well a model predicts the target feature on average. Being a linear calculation, it does not punish outliers in the prediction as the average levels them. Though always calculated with scaled values, the MAE is always shown rescaled in its corresponding unit in the Section 3. The root mean squared error (RMSE) is a double non-linear model score. Its unit is the same as the target feature, but the scale shifts due to the non-linear calculation. It loses interpretability, but generally, a low RMSE represents a more robust model than a low MAE since outliners are heavily punished. It is the main score for comparing models in the presented work. In this work, a lower RMSE means a better model. All models described as the best model of a series of calculations have the lowest RMSE for the test data of these models. The third model score is the coefficient of determination (R²). It measures how well a model fits the variation of the data. If the data are predicted perfectly, R² equals 1. If the resulting error of the prediction is the same as when using the mean of the data, R² equals 0. If the resulting error is worse than simply using the mean of the data, R² can become negative. Formulas 1 to 3 show the calculation of the scores, in which $y_i$ represents the true value of a datapoint, ${\widehat{y}}_i$ the corresponding predicted value, and $n$ the number of datapoints:

$$\mathrm{M}\mathrm{A}\mathrm{E}=\frac{{\sum }_i^n|y_i-{\widehat{y}}_i|}{n}$$

(1)

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{{\sum }_i^n{(y_i-{\widehat{y}}_i)}^2}{n}}$$

(2)

$${\mathrm{R}}^2=1-\frac{{\sum }_i^n{(y_i-{\widehat{y}}_i)}^2}{{\sum }_i^n{(y_i-\frac{1}{n}{\sum }_i^n{y}_i)}^2}$$

(3)

In the case of multiple randomly initialized calculation runs, the metrics are mean values over all runs. Therefore, mean MAE and mean RMSE refer to these metrics averaged over all runs. If a metric relates only to a single run, an additional marker is added, for example, best RMSE.

Although the MAE is calculated with scaled parameters, it can be rescaled to its original unit. Particularly meaningful is the relative MAE, which puts the MAE in relation to the mean target value, in this case, the decored mass. Its formal calculation is depicted in Formula 4. The results will show a mean, relative MAE, which is the MAE averaged over all ten randomized runs of the calculation relative to the mean target value:

$$\mathrm{r}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e} \mathrm{M}\mathrm{A}\mathrm{E}=\frac{\mathrm{M}\mathrm{A}\mathrm{E}}{\frac{1}{n}{\sum }_i^n{y}_i}$$

(4)

2.3. Model Training Sequence

Figure 9 shows the training procedure as a pseudo-code. For both types of models, hyperparameter optimization is performed for each dataset and filter fraction. Each parameter combination is computed with a different random seed ten times to avoid local overfitting. This random seed influences the generation of the train–test splits and the model initialization. The mean values of the ten calculations are used as comparison values to determine the best parameter combination. The results of the best model of each parameter combination are recorded as well.

Following the hold-out method, system D is kept from all model training and serves as a validation set. These validation data provide a second check to see whether overfitting has occurred. System D is chosen as a validation system because it represents a good tradeoff between having enough datapoints and a composition between the other sand-binder systems.

Scaling is always fitted to the training set and applied to all three datasets. Min–max scaling is chosen as the scaling method.

Table A4. Filter fractions and model parameters with values in the model calculations.

Filter Fractions in Percent:	100, 90, 80, 70, 60, 50, 40, 30, 20, 10, 7, 4, 1
XGB-parameter	value(s)
n_estimators	2000
early_stopping_rounds	50
eta	0.1
parallel tree	1, 3, 5, 7
max depth	2, 4, 6
min child weight	1
subsample	0.6
colsample_bytree	0.7
colsample_bylevel	0.7
colsample_bynode	0.7
alpha	0.0001
lambda	1
gamma	0
random seed	3
ANN-parameter	value(s)
max iter	2000
n iter no change	50
layers	(10, 10), (20, 20), (30, 30), (40, 40), (50, 50), (100, 100), (200, 200), (400, 400), (800, 800), (10, 5), (20, 10), (30, 15), (40, 20), (50, 25), (100, 50), (200, 100), (400, 200), (800, 400), (10, 10, 5), (20, 20, 10), (30, 30, 15), (40, 40, 20), (50, 50, 25), (100, 100, 50), (200, 200, 100), (400, 400, 200), (800, 800, 400)
alpha	0.0001
batch size	30
learning_rate_init	0.0001
tol	1 × 10−6
validation fraction	0.1
activation	relu
beta 1	0.9
beta 2	0.999
epsilon	1 × 10−8
max fun	15,000
learning rate	constant
shuffle	true
random state	3

in Appendix A shows the filter fractions and model parameters used. If multiple values are listed for a parameter, this parameter is varied over these values as part of the hyperparameter optimization. For the XGB models, the parameters eta, alpha, max depth, and parallel trees are varied. For the NN models, the number of layers, the number of neurons per layer, and alpha are varied. This approach is inspired by [22].

In the end, the results of 60,840 models were calculated for this work. This number does not include the number of models trained and evaluated to estimate the fixed hyperparameters.

3. Results

3.1. Generated Experimental Database and Time-Series Processing

In this sub-chapter, the exact features are shown and explained in as much detail as required for the scope of this work. For further details, the work of Ettemeyer [2] can be consulted. Following this work, the data are structured into sand-binder systems, specimen, and decoring intervals. System characteristics were determined for each sand-binder system. Each specimen was decored after a finite number of intervals. Each interval comprises between 10 and 80 ram impacts. It is fundamental for the discussion of the feature importance to understand the relation between the different kinds of features and the composition of the sand-binder systems.

This paper uses 8 of the 17 sand-binder systems investigated in work [2] for model training. Nine are discarded due to an insufficient number of datapoints.

Table 1. Sand-binder systems used in the presented work.

	Sand-Binder Systems
Feature	A	B	D	L	M	N	P	Q
binder name	R	R_low	R	R	R_low	R_low	R_low	R
binder content	1.9	1.5	2.25	1.9	1.9	1.9	1.9	2.25
sand name	H32	H32	F34	F34	H32	W65	F34	H32
number of specimens tested	17	12	2	16	12	6	5	5
total number of intervals conducted	64	17	23	48	54	8	36	53
extended features	yes	yes	yes	no	no	no	no	no

shows the sand-binder systems used for model training and their compositions. R refers to “reference binder”, and R_low to a binder with a lower modulus. The number of intervals and the number of specimens in each system are listed as well. In the last row, it is marked whether the previously mentioned extended features such as strain or temperature- depended strengths were recorded for this system.

Figure 10 summarizes the data used to train the models. Corresponding to the experimental design described in Section 2.1, the parameters are grouped into six sources.

Table A1. Features for each sand-binder system used for model training. “X” means these features are included in the dataset. _name_ refers to the individual name of binder, sand, or system.

System Feature Name	Unit	Composition Feature	Extended Feature	Abbreviated Name
binder name	-	X		binder_name_he
sand name	-	X		sand_name_he
binder content	%wt	X		binder_wt
sand-binder system name	-	X		system_name_he
sieving percentage	%			sieving_pct
mean grain diameter	µm		X	mean_grain_d_microm
flexural strength according to the manufacturer	MPa			flex_manuf
flexural strength at 25 °C	MPa			flex_raw
compressive strength at 25 °C	MPa			comp_raw
phi at 25 °C	°			phi_raw_grad
cohesion at 25 °C	-			cohesion_raw
flexural strength at 400 °C	MPa		X	flex_400_grC
compressive strength at 400 °C	MPa		X	comp_400_grC
phi at 400 °C	°		X	phi_400_grC_grad
cohesion at 400 °C	-		X	cohesion_400_grC
flexural strength after casting	MPa		X	flex_casted
compressive strength after casting	MPa		X	comp_casted
phi after casting	°		X	phi_casted_grad
cohesion after casting	-		X	cohesion_casted
tension in the middle, perpendicular	MPa		X	tension_pp_middle
tension in the middle, lengthwise	MPa		X	tension_lw_middle
tension near inflow, perpendicular	MPa		X	tension_pp_inflow
relative flexural strength after casting, according to the manufacturer	%		X	flex_residual_pct
flexural strength after casting, according to the manufacturer	MPa		X	flex_residual
relative drop of flexural strength after casting, according to the manufacturer	%		X	flex_residual_drop_pct

,

Table A2. Features available for each interval.

Interval Feature Name	Interval Phase	Unit	Abbreviated Name
decored mass target feature “DM”	end	g	06_i_m_progress
mass of specimen	start	g	00_i_s_m_total
already decored distance	start	cm	01_i_s_d_progress
sand mass of specimen	start	g	02_i_s_m_sand
already decored mass	start	g	03_i_s_m_progress
ratio of sand mass to metal mass	start	-	04_i_s_m_sand_r_metall
ratio of sand mass to total mass	start	-	05_i_s_m_sand_r_total
number of impacts during the interval			20_i_n_hammerblows

and

Table A3. Signal-processing methods and resulting features.

Preprocessing	No. of Features	Names
Fast Fourier Transformation 4800 bins of 4 Hz each	4800	fft_00004_Hz to fft_19200_hz
Mel Frequency Cepstral Coefficient Analysis mean, median, stdev, max, and min for five coefficients	25	mean_mfcc01…05 median_mfcc01…05 stdev_mfcc01…05 max_mfcc01…05 min_mfcc01…05
Time-Based Analysis a: absolute acceleration sum: sum over interval (i) or bar (b), max: maximum; pos: positive; neg: negative Example: 21_i_a_sum_max_posneg means “feature 21, absolute sum over all positive and negative maxima over all hammer blows of the examined interval”	7	21_i_a_sum_max_posneg 22_i_a_sum_max_pos 23_i_a_sum_max_neg 24_i_a_max_pos 25_i_a_max_pos 26_i_i_a_mean_max_pos 27_i_a_mean_max_neg

in Appendix A give a complete overview of all the parameters used in the training process. Additionally, they show their abbreviated names used in the SHAP plots. The target value predicted by the models is the decored mass in a single decoring interval, abbreviated as DM.

The original system features include 3 categorical, 73 scalar quantities, and 1 time series. The categorical quantities describe the name of the sand used, the name of the binder used, and the name of the sand-binder system in the experimental setup. Two different binders and three different sands were used in the data used for model training. By using different binder percentages, eleven systems were combined from these components. These four features describe the composition of a sand-binder system and are therefore aggregated features. They are referred to as “composition features” as the measured physical features directly result from this composition. Of the scalar features, 41 are not used because they represent the standard deviation or the number of measurements for a measurement such as flexural strength. Five scalar features are not used because they represent an evaluation of the target feature. They correlate linearly to the target feature. Six other variables have only been measured for individual sand-binder systems and are discarded. Twenty-one scalar features remain and are used to train the models, seven of which are available for all sand-binder systems that are summarized as “basic features” and another fourteen that are referred to as “extended features.”

This division leads to two basic datasets. The first dataset contains a maximum number of datapoints and thus does not use the extended features. The second dataset uses the maximum number of features with all extended features but not all datapoints. Using both extremes makes it possible to evaluate the extended features without leaving the large number of datapoints available for the basic features unused. Further parameters were measured at the beginning of the interval in terms of mass distribution and decoring progress. They describe the initial state of the decoring interval. The value range and variation of the target value are essential to put the resulting model scores into context. Figure 11 shows the evaluation of the target feature for the two base datasets.

The mentioned time series represents the acceleration at a defined point on the surface of a specimen. The acceleration of the specimen is influenced by deviations in the experimental setup, by variations of physical quantities such as rigidity, weight, shape, and Young’s modulus of the specimen. The signal curves thus describe the sequence of the decoring process in an aggregated manner. Three processing paths are carried out to provide the information content for the models as well as possible in scalar characteristics: Fast Fourier transforms (FFT), mel cepstral coefficient analysis (mfcc), and a time domain evaluation. The first two are standard methods of transforming audio or vibration data into scalar features. Analyzing the maxima and minima of the signal in the time domain results in additional, easily interpretable features.

A trigger signal was recorded for the acceleration process, as shown in Figure 7. This trigger signal is used to read out the number and duration of the impacts in the interval. With this information, the signal was split into individual impacts. The length of the impact signals was globally set to 200 ms by superpositioning all impacts. Figure 12 shows this superposition of 10,988 impact signals. With the selected signal length, the signal is cut off after the first post-oscillation. A constant signal duration and a constant sampling rate for all ram impacts allow the summarization of the calculated FFT and mfcc values over the impacts of an interval and to compare the resulting features between all intervals.

Table A3 in Appendix A summarizes the resulting features. The FFT calculated 4800 bins of 4 Hz width between 0 and 16,800 Hz. Each container is a feature used for model training. The mfcc analysis was performed for five coefficients. Each coefficient was summed over all time windows of the mfcc analysis to produce five quantities: Maximum, minimum, mean, median, and standard deviation. The signal processing in the time domains summarizes the maximum positive and negative accelerations of each hammer blow. The maximum positive and maximum negative acceleration in an entire interval, the sum and the mean value of the maximum positive acceleration of each hammer blow in an interval, the sum and the mean value of the maximum negative acceleration of each hammer blow in the interval, and the common absolute sum of all positive and negative maximum accelerations in the interval were stored as features.

3.2. Data Composition of the Twelve Datasets

As described above, using several datasets with different characteristics aims to improve the interpretability of the results and test the defined hypotheses. For this purpose, six subsets are formed for each of the two described base datasets. The first distinction concerns the composition features. The second distinction involves the processing of the signal data. The two base datasets contain all three processing methods. In addition, six other datasets combine one of the two base datasets and one of the processing methods each. These are intended to provide information about which of the signal-processing methods is most useful for model building. Two additional datasets are created using the base datasets with all signal features simultaneously.

Table 2. All datasets with their composition, feature, and data count. “X” means these features are included in the dataset.

Datasets	Base Features	Extended Features	Aggregated Composition Features	Signal Features	No. of Features	Number of Datapoints
DS 1	X			none	10	280
DS 2	X	X		none	24	81
DS 3	X		X	none	24	280
DS 4	X	X	X	none	32	81
DS 5	X			all	4842	280
DS 6	X	X		all	4856	81
DS 7	X			FFT	4810	280
DS 8	X	X		FFT	4824	81
DS 9	X			mfcc	35	280
DS 10	X	X		mfcc	49	81
DS 11	X			time-based	17	280
DS 12	X	X		time-based	31	81

lists all datasets and their composition.

3.3. Basic Model Scores for Unfiltered and Filtered Datasets

This chapter summarizes the model scores for all datasets, randomly initialized runs, and validation data. All shown ranks are calculated according to the mean RMSE over the ten random initializations of one parameter set. The values are calculated based on that dataset’s randomly selected 10% test data or the fixed-selected validation data. A filter fraction of less than 100% means that a reduced feature set achieved the lowest RMSE for that dataset. Due to the volume of results, the tabular overview can be found in Appendix A in

Table A6. Mean scores for all best models for all datasets.

Target Feature: Decored Mass in Interval (DM)
Test Dataset	Best XGBoost				Best ANN
	R2 (-)	RMSE (-)	MAE (g)	Rank	R2 (-)	RMSE (-)	MAE (g)	Rank
DS 1	0.75	0.099	5.79	1/2	0.73	0.105	6.30	1
DS 2	0.56	0.145	10.2	8	0.57	0.148	9.98	6
DS 3	0.75	0.099	5.85	1/2	0.71	0.108	6.38	2
DS 4	0.53	0.149	10.4	9	0.55	0.146	9.60	5
DS 5	0.61	0.127	7.85	5/6	0.27	0.172	10.9	9
DS 6	0.32	0.179	11.3	12	−0.25	0.248	16.1	12
DS 7	0.61	0.127	7.91	5/6	0.27	0.173	10.9	10
DS 8	0.35	0.174	11.3	11	−0.12	0.229	14.6	11
DS 9	0.73	0.105	6.74	3	0.66	0.118	7.51	4
DS 10	0.52	0.151	10.0	10	0.48	0.160	10.6	8
DS 11	0.70	0.110	6.60	4	0.68	0.113	6.85	3
DS 12	0.62	0.138	9.29	7	0.54	0.149	9.81	7
Val Dataset	Same XGB Model as Above				Same ANN Model as Above
	R2 (-)	RMSE (-)	MAE (g)	Rank	R2 (-)	RMSE (-)	MAE (g)	Rank
DS 1	−1.47	0.261	25.0	4	−2.47	0.31	28.8	5
DS 2	−2.54	0.330	33.4	7	−1380	6.12	100,409	12
DS 3	−1.54	0.266	25.4	5	−2.83	0.33	30.4	6
DS 4	−3.50	0.371	36.8	9	−894	4.16	100,239	11
DS 5	−0.90	0.230	22.3	1/2	−1.52	0.26	25.1	3
DS 6	−4.54	0.411	40.0	12	−7.54	0.47	44.5	7
DS 7	−0.90	0.230	22.3	1/2	−1.19	0.25	23.7	2
DS 8	−4.17	0.397	38.8	10	−29.7	0.82	71.2	8
DS 9	−1.21	0.247	23.8	3	−0.64	0.21	20.9	1
DS 10	−4.34	0.403	39.4	11	−1188	5.33	427	9
DS 11	−1.59	0.269	25.6	6	−1.80	0.28	26.2	4
DS 12	−2.66	0.335	33.8	8	−2803	7.51	400,179	10

and

Table A7. Using filtered data, mean scores for all best models for all datasets.

Target Feature: Decored Mass
Test Dataset	Best XGBoost					Best ANN
	R2 (-)	RMSE (-)	MAE (g)	Filter Fraction (%)	Rank	R2 (-)	RMSE (-)	MAE (g)	Filter Fraction (%)	Rank
DS 1	0.76	0.098	5.83	90	2/3	0.73	0.105	6.30	100	3/4
DS 2	0.56	0.145	10.2	100	9	0.59	0.142	9.59	30	9
DS 3	0.75	0.099	5.85	100	4	0.73	0.104	6.05	60	2
DS 4	0.55	0.146	10.2	90	10	0.61	0.138	9.23	30	5
DS 5	0.67	0.117	7.44	4	6	0.54	0.137	8.78	4	6
DS 6	0.47	0.153	10.1	1	12	0.42	0.157	10.4	4	11
DS 7	0.68	0.114	7.26	7	5	0.51	0.141	9.03	4	8
DS 8	0.50	0.147	9.25	4	11	0.43	0.161	10.7	4	12
DS 9	0.78	0.093	5.78	40	1	0.75	0.100	6.19	20	1
DS 10	0.64	0.133	9.07	30	8	0.56	0.143	9.47	30	10
DS 11	0.76	0.098	5.83	50	2/3	0.73	0.105	6.37	50	3/4
DS 12	0.67	0.127	8.41	30	7	0.62	0.139	9.19	70	7
Val. Dataset	Same XGB Model as Above					Same ANN Model as Above
	R2 (-)	RMSE (-)	MAE (g)	Filter Fraction (%)	Rank	R2 (-)	RMSE (-)	MAE (g)	Filter Fraction (%)	Rank
DS 1	−1.51	0.264	25.2	90	4/5	−2.5	0.308	28.8	100	6
DS 2	−2.54	0.330	33.4	100	8	−3.8	0.382	37.5	30	7
DS 3	−1.54	0.266	25.4	100	6	−2.0	0.288	27.2	60	5
DS 4	−3.33	0.364	36.2	90	10	−54	0.932	79.1	30	10
DS 5	−1.00	0.236	22.9	4	1	−0.6	0.213	20.9	4	3
DS 6	−5.01	0.428	41.3	1	12	−5.1	0.429	41.4	4	9
DS 7	−1.12	0.243	23.4	7	2	−1.0	0.236	22.9	4	4
DS 8	−3.94	0.388	38.1	4	11	−4.4	0.404	39.4	4	8
DS 9	−1.15	0.245	23.6	40	3	−0.3	0.190	19.0	20	1
DS 10	−2.66	0.335	33.8	30	9	−44	1.002	87.0	30	11
DS 11	−1.51	0.264	25.2	50	4/5	−0.5	0.205	20.3	50	2
DS 12	−2.40	0.322	32.8	30	7	−1260	5309	2.00 × 105	70	12

.

As a point graph, Figure 13 shows the results for the three core metrics, mean RMSE, mean MAE rescaled, and relative mean MAE. A linear connection line was added to indicate the trend and connection of the points. The datasets are sorted by the achieved mean RMSE of their best model in ascending order meaning the overall best model is on the very left and the overall worst model on the very right. The integrated table depicts the composition of each dataset. It also includes the filter fraction and model type of the best model for each dataset.

The range of the mean MAE is between 5.9 g and 10 g, corresponding to a relative mean MAE of 19% to 33%. The difference between the mean MAE and the best-achieved MAE of the model depicts the variation and range of the MAE for the ten runs of a parameter set. For the best-ranking models, this variation diminishes, which can be interpreted as a parameter set resulting in a robust model.

The figure also includes the best run value for all three core metrics. The best run out of the ten randomly initialized runs is defined as the one with the lowest RMSE. Furthermore, for each dataset, the lowest achieved RMSE overall runs of all models was added to illustrate the absolute minimum achieved for all datasets. An evident diminishing variation for the best-ranking models can be seen. Additionally, it depicts the less robust behavior of models for datasets with fewer datapoints, DS 2, 4, 6, 8, 10, and 12. Therefore, some models achieved lower RMSE with the extended features of these datasets than the best-ranking models according to the mean RMSE. However, the high difference to the mean value indicates a high variation in the randomly initialized model runs and, therefore, a less robust model. All four datasets that include FFT features yield the worst scores for both kinds of datasets. All datasets except DS 3 profited from the reduction in data complexity. No significant difference can be seen in the use of composition features for both kinds of datasets.

Two more values extend the view of the model performance. The first one is the mean MAE divided by the standard deviation of DM in the corresponding dataset, which allows comparing the model performance to the variation of the target value. The standard deviation and statistical evaluation of DM are depicted in Figure 11. The second one is the coefficient of determination R², which estimates the models’ level of abstraction regarding the cause–effect correlations toward the target value. Figure 14 summarizes these metrics for all twelve models shown in Figure 13 and adds the highest achieved R²-value by any model for each dataset. DS 9 reaches the best R²-score for the models that performed best on average, which is also the closest to its highest-performing model. This low deviation between the best model on average and the best model overall indicates a robust parameter set. DS 11, which uses time-based features, achieves the overall highest R²-score. However, the difference between its mean best and overall best models is far higher than for DS 9. The highest achieved R²-score for any model is above 0.75, contrary to the diminishing scores shown in Figure 13. The increasing difference can be interpreted as less robust models. The mean MAE of the models depicted in Figure 13 divided by the target value’s standard deviation ranges between 0.34 and 0.57. All model prediction errors variate far less than the target value in the datasets.

Figure 15 illustrates the results for the validation data. Two sets of models are included. The yellow, full line datapoints represent the same models as in Figure 13. The green, separated line datapoints depict the model that achieved the lowest mean RMSE for each dataset for the validation data. These are different models than those in Figure 13. The best achieved RMSE of the ten random initialized runs is also included for both sets of models. An extreme variation in the results can be seen for DS 4, where the difference between the mean and best value is significant compared to the other datapoints. The same datasets achieve the lowest mean RMSE as for the test data, only with slight differences. However, all models perform far worse for the validation data than for the test data. They still show that the same models performing best for the training data also achieved the best values for the validation data. This fact indicates that these robust models can predict some of the outcomes of the validation dataset. However, it can be suspected that they are missing relevant information unique about sand-binder system D in the training process. On the other hand, other models resulted in better predictions for the validation data. These models were less accurate for the test data than the previously discussed models but have generalized more information that allows for better prediction values of the validation data. However, even these models are still significantly worse than the mean model scores for the train data. In summary, the trained models are partially suited for the validation data. Still, not all relevant influences on system D were included in the other systems used to train the models.

Table 3. Statistical evaluation of the twelve parameter sets. The p-value of a two-tailed Welch’s t-test with a 0.05 significance level was calculated between each dataset and DS 9, which yielded the overall best RMSE. The first three columns represent the evaluation of the mean RMSE of all 507 parameter sets of each dataset. The last three columns show the evaluation of the mean RMSE of the best 20 parameter sets, which scored the best mean RMSE for each dataset.

	All 507 Parameter Sets			20 Best Parameter Sets of Each Dataset (According to Mean RMSE)
Datasets	Average	Standard Deviation	p-Value	Average	Standard Deviation	p-Value
DS 9	0.128	6.07 × 10−4	-	0.096	1.24 × 10−6	-
DS 1	0.138	6.12 × 10−4	3.08 × 10−10	0.100	2.76 × 10−7	1.97 × 10−14
DS 11	0.138	9.57 × 10−4	1.82 × 10−8	0.101	4.98 × 10−7	4.31 × 10−18
DS 3	0.134	8.85 × 10−4	6.63 × 10−4	0.100	1.49 × 10−7	2.15 × 10−14
DS 7	0.161	5.84 × 10−4	2.43 × 10−86	0.117	1.68 × 10−6	1.43 × 10−37
DS 5	0.161	5.50 × 10−4	1.67 × 10−84	0.119	1.23 × 10−6	7.83 × 10−41
DS 12	0.174	8.28 × 10−4	9.63 × 10−123	0.132	8.68 × 10−6	3.11 × 10−26
DS 10	0.179	6.70 × 10−4	2.97 × 10−157	0.137	5.05 × 10−6	8.84 × 10−34
DS 4	0.176	6.40 × 10−4	4.81 × 10−147	0.147	6.46 × 10−6	5.84 × 10−33
DS 2	0.177	5.92 × 10−4	3.43 × 10−152	0.148	3.77 × 10−6	2.65 × 10−40
DS 8	0.218	1.73 × 10−3	2.57 × 10−206	0.152	1.20 × 10−5	3.85 × 10−28
DS 6	0.220	1.56 × 10−3	1.61 × 10−222	0.156	3.29 × 10−6	6.30 × 10−45

evaluates the results statistically, as described in the approach chapter. It lists the average, the standard deviation, and the p-value obtained by the two-sided Welch’s t-test for each dataset. DS 9 was used to evaluate the other datasets since it yielded the best mean RMSE. The first test on the left of Table 3 was performed for the mean RMSE calculated over the ten randomly initialized runs of all 507 parameter sets of each dataset. A second Welch’s t-test was applied to gather more insight into the model behavior for the optimized parameter sets by using only the mean RMSE of each dataset’s best 20 parameter sets. The resulting averages show a similar ranking as Figure 13 with only slight changes, like for DS 3 and 11. All obtained p-values are far smaller than the threshold of 5%, with the highest p-value of 6.63 × 10⁻⁴ for DS 3. Thus, the different results of the datasets are statistically significant.

3.4. Feature Importance Values

Figure 16 shows SHAP plots of the best XGB model for six datasets. The meaning of the shortened feature names can be found in Table A1, Table A2 and Table A3 in Appendix A. DS 1 in Figure 16a contains only the base features. DS 3 Figure 16b contains the aggregated features describing the composition of the sand-binder system. DS 7 in Figure 16c comprises the base data and FFT features. DS 9 in Figure 16d uses the mfcc features, and DS 11 in Figure 16e uses only the time-based signal features.

Interestingly, the XGB model for DS 11 achieving the lowest mean RMSE filters all signal features and equals DS 1, which explains the same model scores for both datasets a shown in Figure 13. The sieving percentage of the used sand is the most important feature in all four plots. The sand mass, absolute and relative at the beginning of the interval, is also an important factor. The flexural strength, cohesion, phi, and compressive strength are also influential for all four models. The dataset using the mfcc features scores the lowest mean RMSE. Accordingly, 5 of the 25 mfcc features are listed in the most important feature plot. Figure 16b includes the sand-binder system names. In most cases, these aggregated composition features influence only its corresponding datapoints. For example, feature “system_N” has nearly no effect except on the datapoints belonging to system N, colored red in the plot.

A further aspect is whether the most important features change with varying the filter fraction, which is investigated by comparing DS 1, DS 3, and DS 9. The best model of DS 3 in Figure 16b has a filter fraction of 100%, meaning no filtering occurred. It is identical to DS 1 in Figure 16a except for including the composition features. DS 1 has a filter fraction of 90%, meaning that nearly no feature reduction was performed. DS 9 in Figure 16e has the overall best model score and a much lower filtering fraction of 40%. It contains the same features as DS 1 and the mfcc signal features. For all three datasets, the resulting feature importance is very similar. Even more so, the results for the models of DS 1 and DS 9 are identical. The complexity reduction does not affect the resulting feature importance. DS 7 in Figure 16c seems to contradict this statement. However, aside from the many FFT features, five of the same features as before are listed in the top influences. As DS 7 performed significantly worse than the other three datasets, it can be assumed that even at 4% filter fraction, the multitude of remaining FFT features led to a high content of noise in its dataset, and the main information came from the same features as before.

3.5. Model Scores for Varying ANN Complexity

The number of neurons in total and the number of layers in an ANN influence its ability to interpret complex data. The downside is that a larger ANN requires more datapoints; otherwise, overfitting becomes more likely. The RMSEs in Figure 17, Figure 18, Figure 19 and Figure 20 are the mean over all ten random runs for the best parameter set. Twenty-seven different ANN structures were calculated for each parameter set. The layer sets can be grouped into three groups. The first group consists of two layers, where both layers have the same number of neurons. The second group also has two layers, with the second layer having half as many neurons. The third group has three layers; the first two have the same number of neurons, and the third has half as many. Figure 17 shows the absolute number of neurons in the ANNs, which varied between values of 15 and 2000. Depending on the datasets, the RMSE of the ANN models decreases with an increasing number of neurons until a threshold between 40 and 90 total neurons. After this threshold, the model quality variates too much to identify whether the model quality is decreasing slightly or varying along a plateau. Figure 18, Figure 19 and Figure 20 depict the same behavior as Figure 17 showing a threshold after which the RMSE does not decrease significantly. All models trained with DS 5 and DS 7, which contain the FFT features, systematically have a higher mean RMSE. The high number of features introduces disturbance or noise than information. The points of the graphs resemble the best model, using unfiltered and filtered data. Therefore, filtering did not reduce the noise enough to achieve a benefit, even for more complex ANNs.

3.6. Comparing ANN and XGB over Varying Filter Fractions

As mentioned in the explanation of the approach to this work, two different models are used to predict the decored mass. Figure 13 already gives a first hint about their corresponding performance. The XGB models achieved the lowest RMSE and generated the best models for all except two datasets. Figure 21 and Figure 22 allow a second perspective as they show the mean RMSE plotted over the filter fractions for both kinds of models. The values at 100% filter fraction can be used to compare the results of both models. The XGB models demonstrate less variation in the model scores than the ANN models. Furthermore, they indicate a clear preference for the light-colored datasets without extended features. The ANN models achieve the best performance with the datasets without the extended features but show less preference. ANN models demonstrate exceptionally high RMSE for all datasets containing FFT features, especially compared to the XGB models. These score worse values for the FFT features as well but less strongly than the ANN. With increasing feature reduction, the ANN score improves more than the XGB scores. With increasing feature reduction, the ANN score improves more than the XGB scores.

In summary, the best models of each type perform similarly. Nevertheless, the ANN models have more difficulty handling the data and profit more from the complexity reduction. DS 6 and DS 8 profit the most from the data complexity reduction. Both datasets contain a high number of FFT features. Interestingly, DS 5 and DS 7 do not show this behavior to such a high degree. The explanation is the ratio of features to datapoints. DS 6 and 8 are extended-feature datasets with significantly fewer datapoints than DS 5 and DS 7. Reducing the complexity allowed for a similar mean RMSE for all four datasets, despite the difference in the number of datapoints. All models show a stagnating or decreasing RMSE for reducing data complexity up to a given threshold. Going below this filter fraction leads to a significantly higher mean RMSE. The features of the given dataset at this filter threshold are important for predicting the decoring behavior. Dropping them from the dataset reduces the model quality. Figure 16 shows the features in descending order of importance. The features on top are, thus, the last to be dropped when reducing the filter fraction further. The number of features is always an integer and is rounded up as appropriate. Especially for the datasets with few features, only a single feature remains below single-digit filter fractions.

4. Discussion

4.1. Global Model Results

Figure 13 describes the datasets in descending order of their global rank. First, using the rank and the ratio of the mean MAE to the mean target feature value, the five hypotheses described in Section 1.4 are evaluated.

The first hypothesis claims that aggregated features improve the model quality due to their hidden information about the conduction of experiments. DS 1 and DS 2 versus DS 3 and DS 4 differ in the use of the aggregated composition features. DS 1 scores a lower mean RMSE than DS 3, but DS 4 scores better than DS 2. Looking at the exact values, the use of the extended features is far more significant than the use of the aggregated features. They have no significant effect on the model quality, refuting the hypothesis.

The second hypothesis claims that using the acceleration data improve the model quality. The best dataset (DS 9) uses the mfcc features calculated from the acceleration data. The relative difference in mean RMSE is 5.1% to the base dataset (DS 1), which scores rank 2. As seen in Figure 16e, DS 11 scores best when the time-based signals are dropped. DS 5, 6, 7, and 8 contain the FFT features and are reliably the worst for both base datasets. The high number of features was too complex for the number of datapoints, even after complexity reduction. Figure 16e shows the SHAP plot for the best model using FFT features at a 4% filter fraction, which still results in 193 remaining features. It contains the flexural and compressive strengths and the relative masses at the start of the interval. The other listed features are FFT bins without a recognizable pattern. For the datasets containing the extended features, DS 12 scores best using the time-based signal data. Figure 16f shows its most important features, which comprise the base features and two evaluation features of the maximum negative acceleration. In summary, the signal data contain, in the best case, some information and, in the worst case, mostly noise. Once again, this can be explained with constant experimental processes during data collection. Without significant variation, those features contain mostly noise. The 5.1% improvement for DS 9 is too low to be sure whether the improvement comes from more information or model training.

The third hypothesis claims varying model qualities for different signal-processing approaches. As just explained, the differences between the mfcc and time-based features are small. The FFT features yield worse models due to their high count and complexity.

The fourth hypothesis states that including all features will reduce the model quality despite the use of complexity reduction. This statement is true. DS 5 and DS 6 yield for both base datasets the worst model quality. More features without more information merely introduce noise to the data.

The fifth hypothesis states that lower data complexity results in a better model score. This hypothesis can be confirmed. Only DS 3 achieved its lowest mean RMSE with a 100% filter fraction. All other datasets used filter fractions between 1 and 90%. The results and filter fractions in Figure 13 show that all datasets containing extended features profited from a lower filter fraction than those only containing the base features. The remaining most important features for the extended datasets are only the base features. Only the strengths at 400 °C are used in three out of six datasets, but these are in the lower third of important features in all cases. The datasets using the FFT features profited significantly from the data complexity reduction, as seen in Figure 21. The datasets containing the extended features yielded worse models than the less complex datasets. However, the number of datapoints in this last comparison is not constant.

The number of datapoints in the datasets with the extended features was too small to achieve a low mean RMSE. The best model using extended features is DS 12, with 30% filter fraction, and achieves a mean RMSE of 0.127 and a mean MAE of 8.41 g. This is a 37% higher RMSE than the best dataset not using the extended features.

4.2. Comparison to Decoring Theory

The best models achieved a mean MAE of 16 to 20% of the dataset’s mean decored mass. With only a handful of datapoints for each sand-binder system, this can be adjudged a very good fit. The containing features in the data are suited to predict the target feature. The remaining important features after complexity reduction shown in Figure 16 are the flexural strength, compressive strength, phi, and cohesion, all at room temperature, combined with the absolute and relative mass at the start of the decoring process. This collection supports the claim of the previous work that these features describe the decoring behavior of sand-binder systems.

The signal data have no major influence, as discussed above. The theory of decoring explained in [2] suggests that the way of impact is a significant influence. Therefore, the signal data should have a beneficial effect on model scores. This effect cannot be seen, which leads to the explanations already given in the context of the second hypothesis, or that the signal data were processed in a way that is not suitable for extracting the relevant information. Another explanation is that the unintentional variations during the decoring experiments were insignificant for the decoring behavior, which indicates a robust experimental setup of the previous work.

According to the decoring theory described in [2], cohesion and phi are calculated using the measured flexural and compressive strengths. The best models use all four features and deem them equally important. If both sets contain the same information, at least one of the four should be filtered during the complexity reduction. All four are still deemed valuable for the modeling, which leads to two possible explanations. First, the models divided the information equally between the two sets, and they are still the most important compared to other features. Second, the sets are related, but each contains information not transported by the other.

The extended features, such as the strengths of the sand core after casting, were deemed insignificant by the models. A low effect of the extended features contradicts the conclusions of the previous work. These strengths are a major indication of the decoring behavior in the latter. None of the best models used these features. Instead, some of the models used the strengths at 400 °C. Two explanations are possible. First, the strengths at 400 °C already describe the behavior of inorganically bound sand cores for higher temperatures and during casting in a more direct way than the strengths after casting. Second, the low number of datapoints for the extended features did not allow the models to learn the additional information contained in the extended features.

4.3. Discussion of the Model Training and Model Behavior

Each parameter set was calculated with ten different random initializations. The scores are the mean of these ten calculations. The best runs of each parameter set yield 36% lower RMSE on average than the corresponding mean over all ten runs. All models are far less suited for the validation sand-binder system D. Interestingly, models that do not achieve the best RMSE for the test data have better scores for the validation data. This difference suggests that despite the ten randomly initialized runs, there was some overfitting toward the test data. Figure 15 summarizes this behavior. Despite the lower prediction quality, this graph shows a clear learning process by the models. The best models score a mean RMSE for the validation data of 0.166. This is 78% higher than the best model score for the test data. Nevertheless, they score a similar mean RMSE for both test (0.148) and validation data (0.167), suggesting that these models are less suited for the test data but are similar and partially valid for other sand-binder systems.

The models abstracted some information suitable to predict the validation system D. However, they lacked relevant parameters during the training phase to gain similar prediction values as they gained for the test data. Figure 17, Figure 18, Figure 19, Figure 20, Figure 21 and Figure 22 show robust behavior for the test data without significant outliners. The models can be summarized as robust and usable, but only for sand-binder systems known through the training data. New sand-binder systems can contain variations in the features not modeled during the training, which might change by including more sand-binder systems in future works.

Figure 14 summarizes R² for the models shown in Figure 13. The R²-scores support the previously derived model behavior. DS 9 shows the most reliable scores of all datasets with a low difference between the highest achieved score and the best mean model. All datasets were able to score R² values above 0.75, indicating that models could learn a significant part of the cause–effect correlations between the input data and the target value DM. Furthermore, it shows the mean MAE achieved by the models in Figure 13 divided by the standard deviation of the target value. The mean MAE is 34% to 57% of the standard deviation of DM. Thus, the prediction is below the datasets’ variations, indicating functioning models.

Interestingly, the XGB models yielded better scores than the ANN in most cases, which can be explained by the features contained in the dataset. These can be used directly for predicting the target features. No complex model building or meta-feature calculations are needed, which is confirmed by Figure 17, Figure 18, Figure 19 and Figure 20. Only the very low number of neurons have slightly worse scores than the more complex ones. Starting with 20 neurons in each layer, the mean RMSE does not improve significantly with more neurons.

5. Conclusions

In summary, experimental data were used to predict the decoring behavior of various sand-binder systems. Robust models were achieved, yielding a mean MAE between 16% and 37% of the mean of the predicted feature and a mean MAE to standard deviation of 34% to 57%. The chosen forward–backward approach using machine learning models to learn about experimental data and physical relations was successful. Varying the data composition demonstrated the relative importance of various feature sets in predicting the decoring behavior. The acceleration data of the decoring process, which was suspected of having a significant influence, was not used significantly by the models for the prediction. The authors conclude that a constant experimental setup led to the reduced importance of the acceleration signal. The same explanation is used for the low importance of the aggregated composition features. One sand-binder system was used as a validation system to test whether the models could describe the decoring behavior for unknown sand-binder systems. The prediction scores are significantly worse for the validation system. However, the models indicate that some generalized correlations were learned that are also valid for the validation system. The authors suspect that the validation system variates in some parameters in ways unique to it. It is suspected that some overfitting occurred in the models that achieved the lowest mean RMSE for the test data, despite averaging over ten runs of randomized initializations. The best models for the validation system scored similar values for the test data and indicated no overfitting. This work focuses on a specific case of decoring for one sample geometry. The machine learning models calculated in this do not claim to predict the decoring behavior for other geometries. However, the behavior of the models and the identified relevant parameters can be interpreted in a generalized way. Determining which features in this dataset are particularly relevant for ML model training is, therefore, a first step towards a more generally valid ML model. This work provided helpful indications as to which data should be ascribed higher priority in future decoring experiments.