Interaction of Segmental Tunnel Linings and Dip-Slip Faults—Tabriz Subway Tunnels
Abstract
:1. Introduction
2. Literature Review
3. Materials and Methods
3.1. Reference Case
3.2. Three-Dimensional Numerical Simulation
3.3. Model Validation
Validation Results
3.4. Bedrock Fault Intersection with Segmental Lining: Numerical Simulation
4. Results and Discussion
4.1. Displacement Outputs
4.1.1. Soil Displacements
4.1.2. Lining Displacements
4.2. Internal Structural Forces
4.3. Limitations and Future Recommendation
- There is no elastoplastic constitutive model for the tunnel lining, and cracks cannot be considered.
- There is no modeling of the rebars within the concrete lining.
- Full dynamic loadings of fault movements.
- Use of solid elements and evaluation of the rebar presence in segmental tunnel linings the intersection of the faults.
- Investigation of combined fault interaction with segmental tunnels.
- Investigation of methods to reduce the damage on tunnel linings, such as an over-excavation and the use of compressible materials behind the segmental tunnel linings.
5. Conclusions
- Normal faults intersecting with segmental linings have tensile rupture mechanisms, and segmental lining joints undergo greater deformations and openings than reverse faults. It has been observed that as the tunnel depth increases, the degree of separation of segmental rings, the opening of longitudinal joints, and the severity of failures increase, while the range affected by the fault in segmental lining declines, and the breakage and opening of joints approach the fault line, as a result. Vertical displacement and tunnel rupture rates increase dramatically as the slope angle of the fault increases, and the rupture path tends to follow the footwall as the fault slope increases.
- The function of the segmental tunnel in the reverse fault was compressive. Thus, unlike normal faults, it will not suffer extensive damage. As a result of reverse faulting, the segmental lining experiences smoother displacement along the entire tunnel length, and only undergoes limited deformation and opening of longitudinal and transverse joints. Furthermore, segmental linings with oblique joints perform better than straight joints. In comparison to straight joint linings, they have less displacement and their internal force, including bending moments, extends to a smaller area. The maximum ground displacement value increases gradually with increasing tunnel overburden in a normal fault. The vertical displacement of the ground also increases with an elevation of the fault angle. This is due to an increase in the vertical component of the fault force. Through a decrease in the fault slope angle, the fault area is further developed towards the footwall, and further affects the surface.
- Comparing the performance of segmental and continuous lining at the intersection with the reverse fault, it can be concluded that, unlike segmental lining, continuous tunnel lining in interaction with the fault suffers sudden failure at the fault line. The displacements were concentrated at the fault line location due to the rigidity of the continuous tunnel lining. Consequently, the probability of rupture and failure of the continuous tunnel lining at the intersection with the fault is high. In addition, the majority of the fault force is transmitted to the tunnel lining in the hanging wall. In a continuous lining, the bending moment is about twice as great as in a segmented lining, and the normal force is ten times as great.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chang, Y.Y.; Lee, C.J.; Huang, W.C.; Hung, W.Y.; Huang, W.J.; Lin, M.L.; Chen, Y.H. Evolution of the Surface Deformation Profile and Subsurface Distortion Zone during Reverse Faulting through Overburden Sand. Eng. Geol. 2015, 184, 52–70. [Google Scholar] [CrossRef]
- Kiani, M.; Akhlaghi, T.; Ghalandarzadeh, A. Experimental Modeling of Segmental Shallow Tunnels in Alluvial Affected by Normal Faults. Tunn. Undergr. Space Technol. 2016, 51, 108–119. [Google Scholar] [CrossRef]
- Ahmadi, M.; Moosavi, M.; Jafari, M.K. Experimental Investigation of Reverse Fault Rupture Propagation through Cohesive Granular Soils. Geomech. Energy Environ. 2018, 14, 61–65. [Google Scholar] [CrossRef]
- Azizkandi, A.S.; Ghavami, S.; Baziar, M.H.; Hasanaklou, S.H. Assessment of Damages in Fault Rupture–Shallow Foundation Interaction Due to the Existence of Underground Structures. Tunn. Undergr. Space Technol. 2019, 89, 222–237. [Google Scholar] [CrossRef]
- Cai, Q.P.; Peng, J.M.; Ng, C.W.W.; Shi, J.W.; Chen, X.X. Centrifuge and Numerical Modelling of Tunnel Intersected by Normal Fault Rupture in Sand. Comput. Geotech. 2019, 111, 137–146. [Google Scholar] [CrossRef]
- Baziar, M.H.; Nabizadeh, A.; Khalafian, N.; Lee, C.J.; Hung, W.Y. Evaluation of Reverse Faulting Effects on the Mechanical Response of Tunnel Lining Using Centrifuge Tests and Numerical Analysis. Géotechnique 2020, 70, 490–502. [Google Scholar] [CrossRef]
- Wang, W.L.; Wang, T.T.; Su, J.J.; Lin, C.H.; Seng, C.R.; Huang, T.H. Assessment of Damage in Mountain Tunnels Due to the Taiwan Chi-Chi Earthquake. Tunn. Undergr. Space Technol. 2001, 16, 133–150. [Google Scholar] [CrossRef]
- Rashiddel, A.; Koopialipoor, M.; Hadei, M.R.; Rahmannejad, R. Numerical Investigation of Closed-Form Solutions for Seismic Design of a Circular Tunnel Lining (by Quasi-Static Method). Civ. Eng. J. 2018, 4, 239. [Google Scholar] [CrossRef]
- Yang, Z.; Lan, H.; Zhang, Y.; Gao, X.; Li, L. Nonlinear Dynamic Failure Process of Tunnel-Fault System in Response to Strong Seismic Event. J. Asian Earth Sci. 2013, 64, 125–135. [Google Scholar] [CrossRef]
- Yeats, R.S.; Sieh, K.; Allen, C.R. The Geology of Earthquakes; Oxford University Press: Oxford, UK, 1997; Volume 68. [Google Scholar]
- Machette, M.N. Active, Capable, and Potentially Active Faults—A Paleoseismic Perspective. J. Geodyn. 2000, 29, 387–392. [Google Scholar] [CrossRef]
- Kiani, M. Effects of Surface Fault Rupture on Shallow Segmental Soil Tunnels-Centrifuge Modeling. Ph.D. Thesis, University of Tabriz, Tabriz, Iran, 2016. (In Persian). [Google Scholar]
- Kelson, K.I. Representative Styles of Deformation along the Chelungpu Fault from the 1999 Chi-Chi (Taiwan) Earthquake: Geomorphic Characteristics and Responses of Man-Made Structures. Bull. Seismol. Soc. Am. 2004, 91, 930–952. [Google Scholar] [CrossRef]
- Zhang, H.J.; Wang, Z.Z.; Lu, F.; Xu, G.Y.; Qiu, W.G. Analysis of the Displacement Increment Induced by Removing Temporary Linings and Corresponding Countermeasures. Tunn. Undergr. Space Technol. 2018, 73, 236–243. [Google Scholar] [CrossRef]
- Lin, M.-L.; Chung, C.-F.; Jeng, F.-S.; Yao, T.-C. The Deformation of Overburden Soil Induced by Thrust Faulting and Its Impact on Underground Tunnels. Eng. Geol. 2007, 92, 110–132. [Google Scholar] [CrossRef]
- Anastasopoulos, I.; Gerolymos, N.; Drosos, V.; Georgarakos, T.; Kourkoulis, R.; Gazetas, G. Behaviour of Deep Immersed Tunnel under Combined Normal Fault Rupture Deformation and Subsequent Seismic Shaking. Bull. Earthq. Eng. 2008, 6, 213–239. [Google Scholar] [CrossRef]
- Zhao, K.; Janutolo, M.; Barla, G.; Chen, G. 3D Simulation of TBM Excavation in Brittle Rock Associated with Fault Zones: The Brenner Exploratory Tunnel Case. Eng. Geol. 2014, 181, 93–111. [Google Scholar] [CrossRef]
- Zhao, K.; Chen, W.; Yang, D.; Zhao, W.; Wang, S.; Song, W. Mechanical Tests and Engineering Applicability of Fibre Plastic Concrete Used in Tunnel Design in Active Fault Zones. Tunn. Undergr. Space Technol. 2019, 88, 200–208. [Google Scholar] [CrossRef]
- Wang, X.; Xiong, Q.; Zhou, H.; Chen, J.; Xiao, M. Three-Dimensional (3D) Dynamic Finite Element Modeling of the Effects of a Geological Fault on the Seismic Response of Underground Caverns. Tunn. Undergr. Space Technol. 2020, 96, 103210. [Google Scholar] [CrossRef]
- Baziar, M.H.; Nabizadeh, A.; Jung Lee, C.; Hung, W.Y. Centrifuge Modeling of Interaction between Reverse Faulting and Tunnel. Soil Dyn. Earthq. Eng. 2014, 65, 151–164. [Google Scholar] [CrossRef]
- Shen, Y.S.; Wang, Z.Z.; Yu, J.; Zhang, X.; Gao, B. Shaking Table Test on Flexible Joints of Mountain Tunnels Passing through Normal Fault. Tunn. Undergr. Space Technol. 2020, 98, 103299. [Google Scholar] [CrossRef]
- Sabagh, M.; Ghalandarzadeh, A. Numerical Modelings of Continuous Shallow Tunnels Subject to Reverse Faulting and Its Verification through a Centrifuge. Comput. Geotech. 2020, 128, 103813. [Google Scholar] [CrossRef]
- Gregor, T.; Garrod, B.; Young, D. Analyses of Underground Structures Crossing an Active Fault in Coronado, California. In Proceedings of the World Tunnel Congress; Taylor & Francis: London, UK, 2007; Volume 3, pp. 445–450. [Google Scholar]
- Baziar, M.H.; Nabizadeh, A.; Mehrabi, R.; Lee, C.J.; Hung, W.Y. Evaluation of Underground Tunnel Response to Reverse Fault Rupture Using Numerical Approach. Soil Dyn. Earthq. Eng. 2016, 83, 1–17. [Google Scholar] [CrossRef]
- Nemati, M.; Derakhshani, R. Short-Term Seismicity Patterns along the Most Active Faults in Iran. J. Iber. Geol. 2021, 47, 441–459. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, F.; Li, N.; He, M. Influence of Fault on the Surrounding Rock Stability for a Mining Tunnel: Distance and Tectonic Stress. Adv. Civ. Eng. 2019, 2019, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Sheng, Q.; Zhang, G.; Cui, Z. A 3D Discrete-Continuum Coupling Approach for Investigating the Deformation and Failure Mechanism of Tunnels across an Active Fault: A Case Study of Xianglushan Tunnel. Appl. Sci. 2019, 9, 2318. [Google Scholar] [CrossRef] [Green Version]
- Esmatkhah Irani, A.; Azadi, A.; Nikbakht, M.; Azarafza, M.; Hajialilue Bonab, M.; Behrooz Sarand, F. GIS-Based Settlement Risk Assessment and Its Effect on Surface Structures: A Case Study for the Tabriz Metro—Line 1. Geotech. Geol. Eng. 2022, 40, 5081–5102. [Google Scholar] [CrossRef]
- Yan, G.; Gao, B.; Shen, Y.; Zheng, Q.; Fan, K.; Huang, H. Shaking Table Test on Seismic Performances of Newly Designed Joints for Mountain Tunnels Crossing Faults. Adv. Struct. Eng. 2020, 23, 248–262. [Google Scholar] [CrossRef]
- Zhou, H.; He, C.; Wang, S.; Peng, F.; Zhu, S.; Yuan, D. Dynamic Stress Concentration Factors and Damage Mode of Horseshoe Tunnels Crossing Fault Fracture Zone. Geotech. Geol. Eng. 2020, 38, 5127–5141. [Google Scholar] [CrossRef]
- Aygar, E.B.; Gokceoglu, C. A Special Support Design for a Large-Span Tunnel Crossing an Active Fault (T9 Tunnel, Ankara–Sivas High-Speed Railway Project, Turkey). Environ. Earth Sci. 2021, 80, 37. [Google Scholar] [CrossRef]
- Wen, Y.M.; Xin, C.L.; Shen, Y.S.; Huang, Z.M.; Gao, B. The Seismic Response Mechanisms of Segmental Lining Structures Applied in Fault-Crossing Mountain Tunnel: The Numerical Investigation and Experimental Validation. Soil Dyn. Earthq. Eng. 2021, 151, 107001. [Google Scholar] [CrossRef]
- An, S.; Tao, L.J.; Han, X.C.; Zhang, Y. Application of Two-Level Design Method on Subway Tunnel Crossing Active Fault: A Case Study on Urumqi Subway Tunnel Intersected by Reverse Fault Dislocation. Bull. Eng. Geol. Environ. 2021, 80, 3871–3884. [Google Scholar] [CrossRef]
- Somerville, P.G. Implications of the Northridge and Kobe Earthquakes for the National Earthquake Hazard Reduction Program. Seismol. Res. Lett. 1997, 68, 711–713. [Google Scholar] [CrossRef]
- Hosseini, M.; Rahimi, H. Probabilistic Fault Displacement Hazard Analysis for the North Tabriz Fault. Nat. Hazards Earth Syst. Sci. 2022, 22, 3571–3583. [Google Scholar] [CrossRef]
- RAHAB. Consulting Engineers Geotechnical Studies Report of the Route and Eastern Parking; RAHAB: Tabriz, Iran, 2018. [Google Scholar]
- Wells, D.L.; Coppersmith, K.J. New Empirical Relationships among Magnitude, Rupture Length, Rupture Width, Rupture Area, and Surface Displacement. Bull. Seismol. Soc. Am. 1994, 84, 974–1002. [Google Scholar]
- TURO. Structural Analysis and Design of Segmental Tunnel Lining of the Line 2 Metro of Tabriz; Section l.: Tabriz, Iran, 2012. (In Persian) [Google Scholar]
- Lambrughi, A.; Medina Rodríguez, L.; Castellanza, R. Development and Validation of a 3D Numerical Model for TBM–EPB Mechanised Excavations. Comput. Geotech. 2012, 40, 97–113. [Google Scholar] [CrossRef]
- Ramesh, A.; Hajihassani, M.; Rashiddel, A. Ground Movements Prediction in Shield-Driven Tunnels Using Gene Expression Programming. Open Constr. Build. Technol. J. 2020, 14, 286–297. [Google Scholar] [CrossRef]
- Hejazi, Y.; Dias, D.; Kastner, R. Impact of Constitutive Models on the Numerical Analysis of Underground Constructions. Acta Geotech. 2008, 3, 251–258. [Google Scholar] [CrossRef]
- Rashiddel, A.; Kharghani, M.; Dias, D.; Hajihassani, M. Numerical Study of the Segmental Tunnel Lining Behavior under a Surface Explosion—Impact of the Longitudinal Joints Shape. Comput. Geotech. 2020, 128, 103822. [Google Scholar] [CrossRef]
- Rashiddel, A.; Hajihassani, M.; Kharghani, M.; Valizadeh, H.; Rahmannejad, R.; Dias, D. Numerical Analysis of Segmental Tunnel Linings-Use of the Beam-Spring and Solid-Interface Methods. Geomech. Eng. 2022, 29, 471–486. [Google Scholar]
- Itasca Consulting Group, Inc. FLAC3D—Fast Lagrangian Analysis of Continua in Three-Dimensions, Ver. 7.0; Itasca: Minneapolis, MN, USA, 2019. [Google Scholar]
- Do, N.-A.; Dias, D.; Oreste, P.; Djeran-Maigre, I. Three-Dimensional Numerical Simulation of a Mechanized Twin Tunnels in Soft Ground. Tunn. Undergr. Space Technol. 2014, 42, 40–51. [Google Scholar] [CrossRef]
- Leonhardt, F.; Reimann, H. Betongelenke. Der Bauing. 1966, 41, 49–56. [Google Scholar]
- Janssen, P. Tragverhalten von Tunnelausbauten Mit Gelenktübbings; Report-No. 83-41; Institute for Structural Analysis, Department of Civil Engineering, University of Braunschweig: Braunschweig, Germany, 1983. [Google Scholar]
- Do, N.A. Numerical Analyses of Segmental Tunnel Lining under Static and Dynamic Loads. Ph.D. Thesis, Civil Engineering, INSA de Lyon, Lyon, France, 2014. (In English). [Google Scholar]
- Do, N.-A.; Dias, D.; Oreste, P.; Djeran-Maigre, I. 2D Numerical Investigation of Segmental Tunnel Lining Behavior. Tunn. Undergr. Space Technol. 2013, 37, 115–127. [Google Scholar] [CrossRef]
- Do, N.-A.; Dias, D.; Oreste, P.; Djeran-Maigre, I. Three-Dimensional Numerical Simulation for Mechanized Tunnelling in Soft Ground: The Influence of the Joint Pattern. Acta Geotech. 2014, 9, 673–694. [Google Scholar] [CrossRef]
- Ramesh, A. Numerical Investigation of Fault Interaction with Segmental Lining in Tabriz Metro Tunnels. Master’s Thesis, Urmia University, Urmia, Iran, 2022. (In English). [Google Scholar]
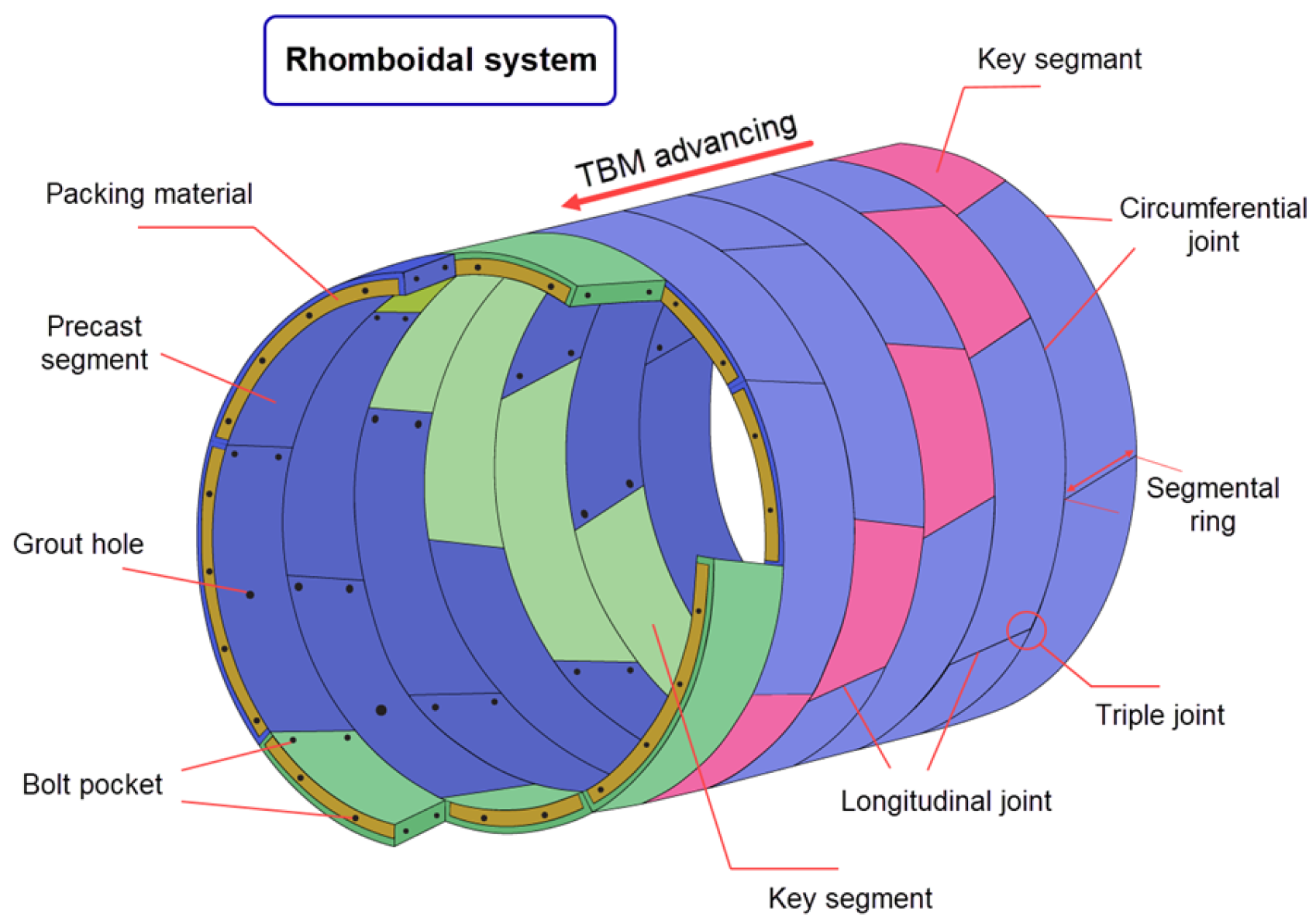

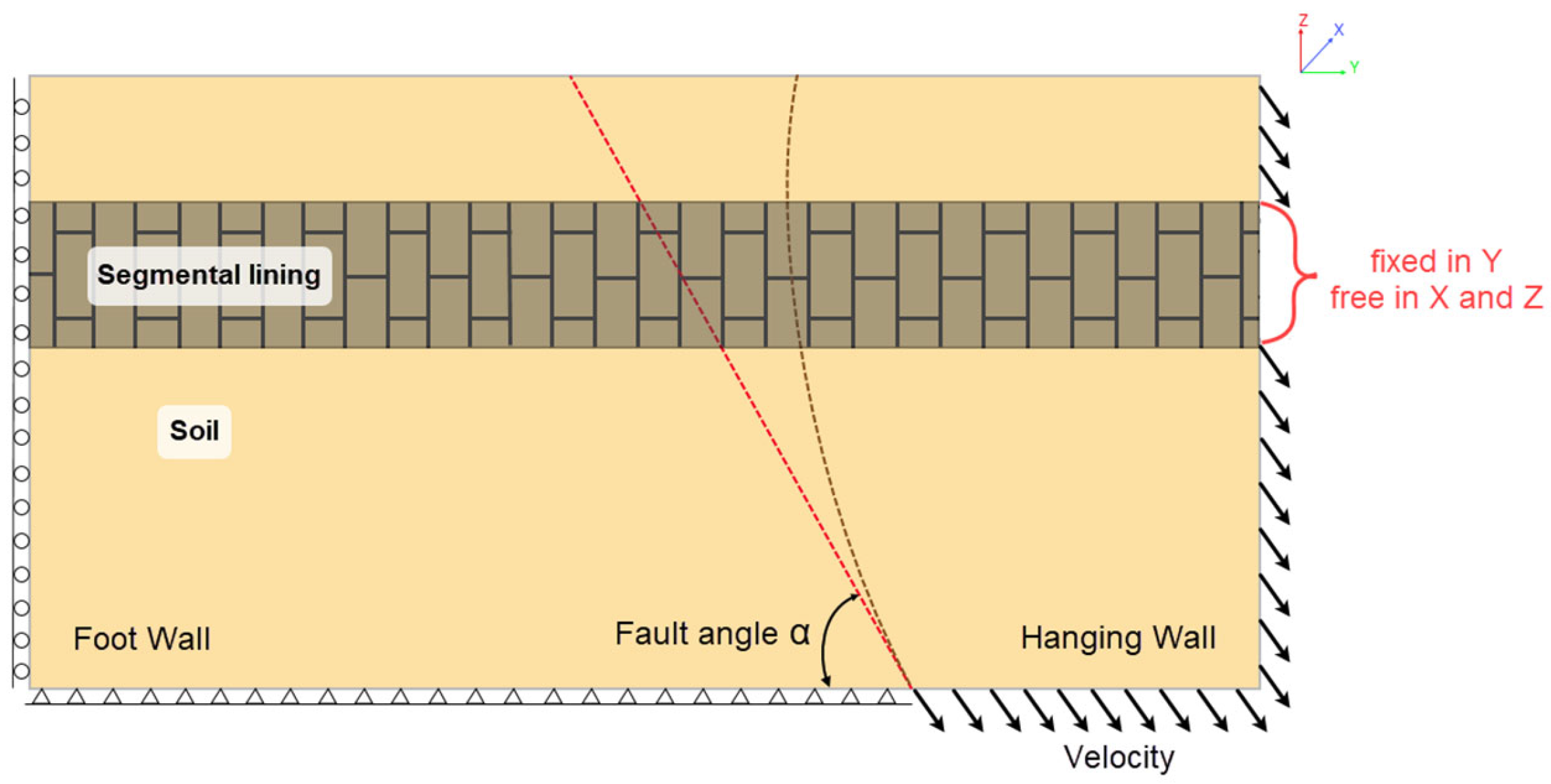










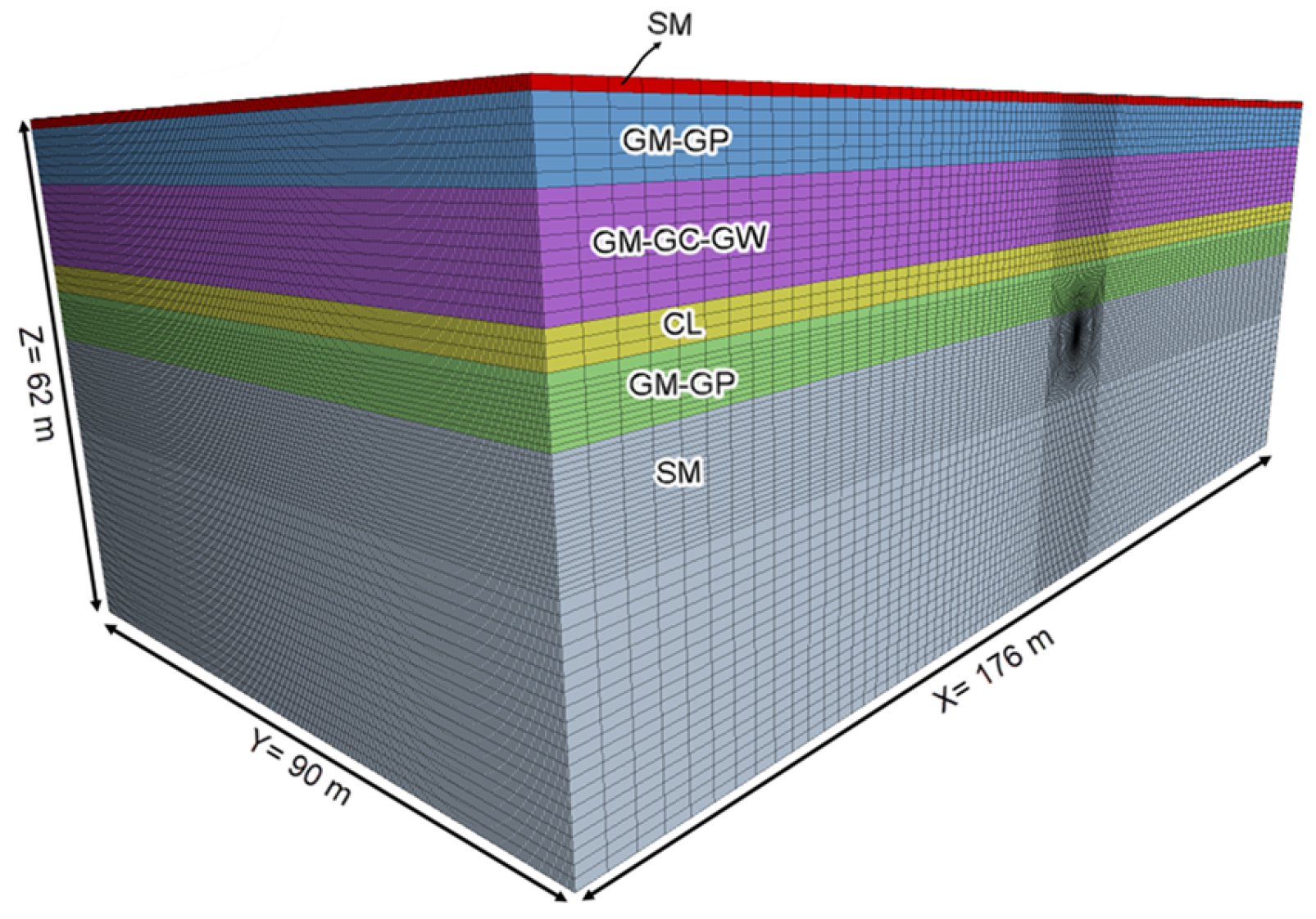








| Parameters | Symbol | Unit | Value | Value | Value | Value | Value | Value |
|---|---|---|---|---|---|---|---|---|
| Soil type | L | - | Filling material (SM) | CL–ML | GM–GC–GW | CL | GM–GP | SM |
| Depth | D | m | 0–1.5 | 1.5–7 | 7–17 | 17–20 | 20–26 | 26–35 |
| Dry density | g/cm3 | 1.65 | 1.775 | 1.775 | 1.775 | 1.850 | 1.825 | |
| Cohesion | C | kPa | 0 | 11 | 6 | 25 | 5 | 5 |
| Angle of internal friction | φ | Degree | 27 | 24 | 32 | 23 | 33 | 32 |
| Triaxial loading secant Young’s modulus | MPa | 10 | 25 | 47.5 | 35 | 65 | 55 | |
| Unloading–reloading Young’s modulus | MPa | 30 | 75 | 150 | 105 | 195 | 165 | |
| Oedometric loading Young’s modulus | MPa | 12 | 30 | 60 | 42 | 78 | 66 | |
| Coefficient of earth lateral pressure | K0 | - | 0.54 | 0.593 | 0.47 | 0.6 | 0.455 | 0.47 |
| Poisson’s ratio | - | 0.33 | 0.39 | 0.32 | 0.39 | 0.33 | 0.32 | |
| Failure ratio | Rf | - | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 | 0.9 |
| Janbu-type parameter | m | - | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| Reference mean pressure | Pref | kPa | 100 | 100 | 100 | 100 | 100 | 100 |
| Parameters | Symbol | Unit | Value |
|---|---|---|---|
| Properties of the segmental liner | |||
| Young’s modulus | E | GPa | 30 |
| Density | kg/m3 | 2500 | |
| External diameter | D | m | 9.5 |
| Thickness | t | cm | 35 |
| Poisson’s ratio | - | 0.2 | |
| Width of the segment ring | W | m | 1.5 |
| Properties of the grouting layer (28-day) | |||
| Young’s modulus | E | MPa | 160 |
| Poisson’s ratio | - | 0.22 | |
| Density | kg/m3 | 2000 | |
| Grouting layer thickness | t | cm | 15.5 |
| Parameters | Symbol | Unit | Value |
|---|---|---|---|
| Properties of the soil | |||
| Soil type | L | - | Firoozkuh # 161 sand |
| Density | kg/m3 | 1700 | |
| Cohesion | C | kPa | 1 |
| The angle of internal friction | φ | Degree | 37 |
| Dilation angle | ψ | Degree | 10 |
| Triaxial loading secant Young’s modulus | MPa | 20 | |
| Unloading–reloading Young’s modulus | MPa | 60 | |
| Oedometric loading Young’s modulus | MPa | 16 | |
| Coefficient of earth lateral pressure | K0 | - | 0.38 |
| Poisson’s ratio | - | 0.28 | |
| Failure ratio | Rf | - | 0.9 |
| Janbu-type parameter | m | - | 0.5 |
| Reference mean pressure | Pref | kPa | 100 |
| Properties of the liner [2,12] | |||
| Young’s modulus | E | GPa | 34 |
| Density | kg/m3 | 2600 | |
| Diameter | D | m | 5.9 |
| Thickness | t | m | 0.35 |
| Poisson’s ratio | - | 0.2 | |
| Width of the segmental ring | w | m | 1.15 |
| Segmental Joints | Value | Ring Joints | Value |
|---|---|---|---|
| Radial stiffness KR (MN/m) | 216 | Radial stiffness KRR (MN/m) | 216 |
| Axial stiffness KA (MN/m) | 4434 | Axial stiffness KAR (MN/m) | 4434 |
| Rotational stiffness Kθ (MN×m/rad/m) | 62.046 | Rotational stiffness KθR (MN×m/rad/m) | 62.046 |
| The maximum bending moment at segmental joint Myield (kN×m/m) | 121 | The maximum bending moment at ring joint MRyield (kN×m/m) | 121 |
| Segmental Joints | Value | Ring Joints | Value |
|---|---|---|---|
| Radial stiffness KR (MN/m) | 1050 | Radial stiffness KRR (MN/m) | 1050 |
| Axial stiffness KA (MN/m) | 500 | Axial stiffness KAR (MN/m) | 500 |
| Rotational stiffness Kθ (MN×m/rad/m) | 100 | Rotational stiffness KθR (MN×m/rad/m) | 100 |
| The maximum bending moment at segmental joint Myield (kN×m/m) | 150 | The maximum bending moment at ring joint MRyield (kN×m/m) | 150 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramesh, A.; Rashiddel, A.; Hajihassani, M.; Dias, D.; Kiani, M. Interaction of Segmental Tunnel Linings and Dip-Slip Faults—Tabriz Subway Tunnels. Appl. Sci. 2023, 13, 7866. https://doi.org/10.3390/app13137866
Ramesh A, Rashiddel A, Hajihassani M, Dias D, Kiani M. Interaction of Segmental Tunnel Linings and Dip-Slip Faults—Tabriz Subway Tunnels. Applied Sciences. 2023; 13(13):7866. https://doi.org/10.3390/app13137866
Chicago/Turabian StyleRamesh, Asma, Alireza Rashiddel, Mohsen Hajihassani, Daniel Dias, and Majid Kiani. 2023. "Interaction of Segmental Tunnel Linings and Dip-Slip Faults—Tabriz Subway Tunnels" Applied Sciences 13, no. 13: 7866. https://doi.org/10.3390/app13137866
APA StyleRamesh, A., Rashiddel, A., Hajihassani, M., Dias, D., & Kiani, M. (2023). Interaction of Segmental Tunnel Linings and Dip-Slip Faults—Tabriz Subway Tunnels. Applied Sciences, 13(13), 7866. https://doi.org/10.3390/app13137866








