Modular Bus Unit Scheduling for an Autonomous Transit System under Range and Charging Constraints
Abstract
:1. Introduction
- The optimization model for determining the optimal formation and trip sequences of MB units is developed. In particular, given that the vehicles are electrically powered, battery range limits and charging plans are considered in the system scheduling process.
- A column generation-based heuristic algorithm is designed to efficiently solve this model. The constraints of trip demand and charging station capacity are included in the main problem, and the problem of the mileage of modular units under a limited range is solved by subproblems.
- Taking real data from transit operations for numerical examples, the proposed model performs well in terms of both algorithmic performance and practical applications, enabling strategic support for the promotion of modular bus technology in transit systems.
2. Modular Bus Scheduling Model
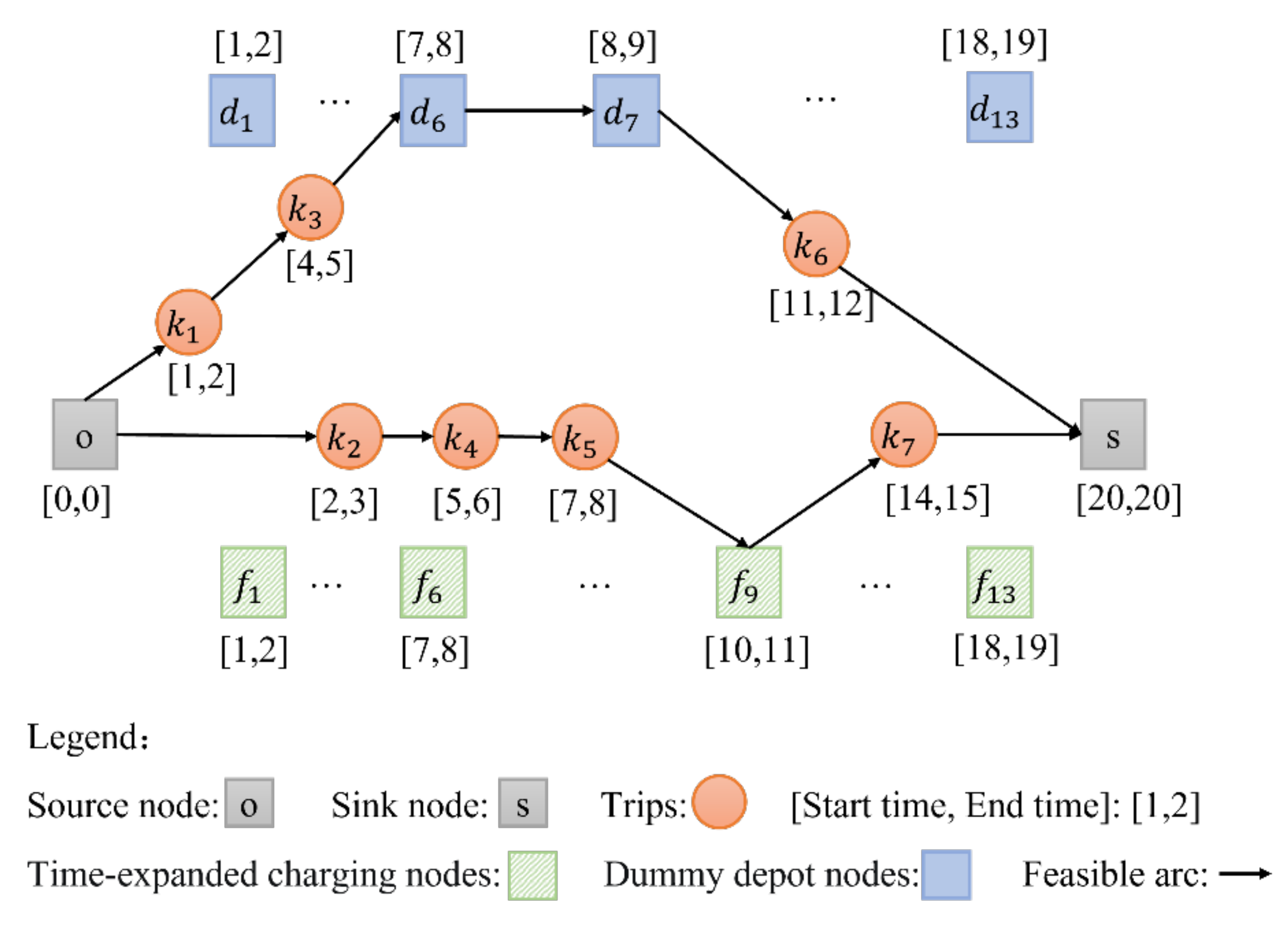
2.1. Preliminaries
2.2. Mathematical Formulation
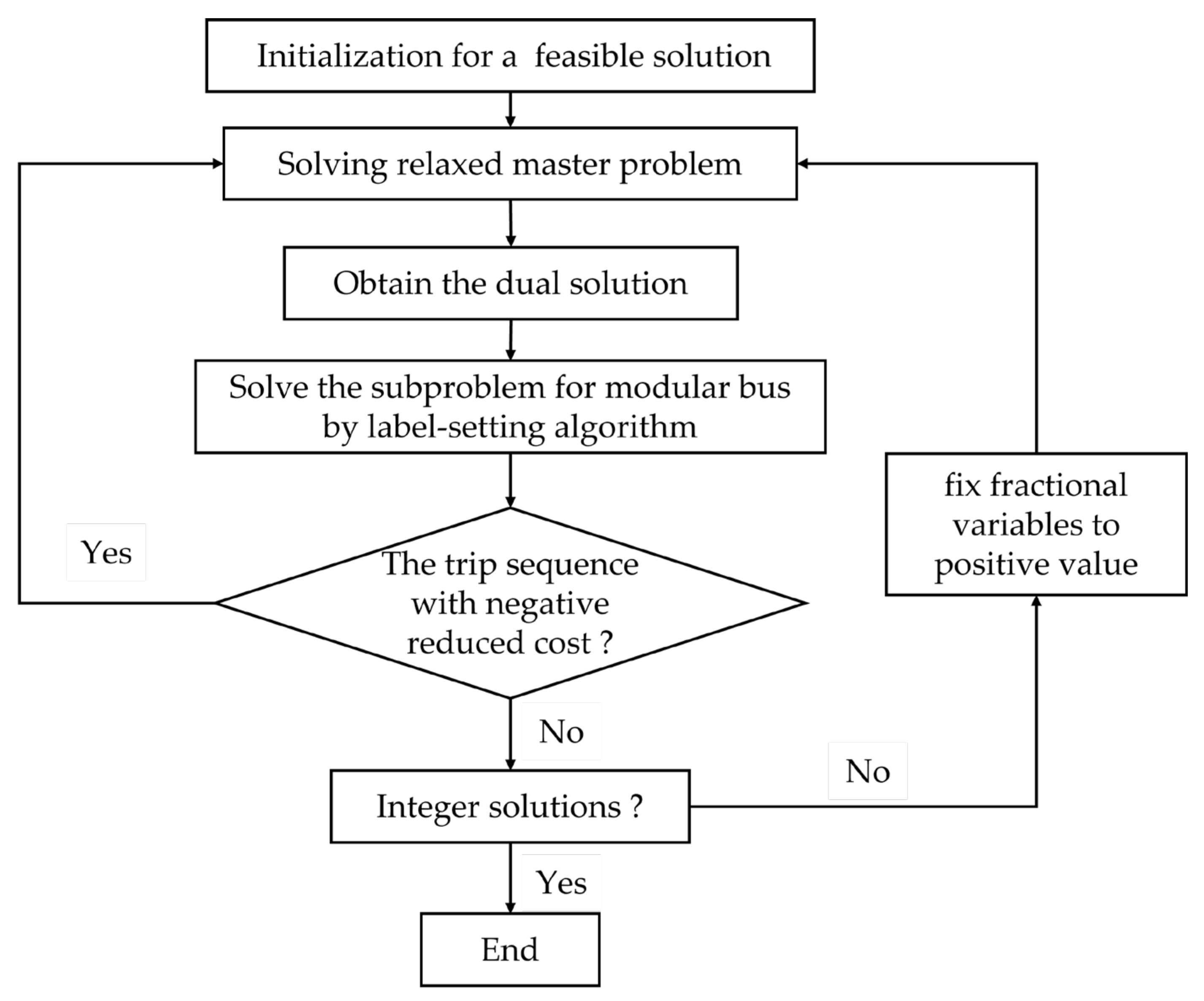
3. Solution Algorithm
3.1. Master Problem
3.2. Pricing Subproblems
3.3. Solution Procedure
4. Computational Results
4.1. Case Setup
4.2. Algorithm Efficiency
4.3. Results and Analyses
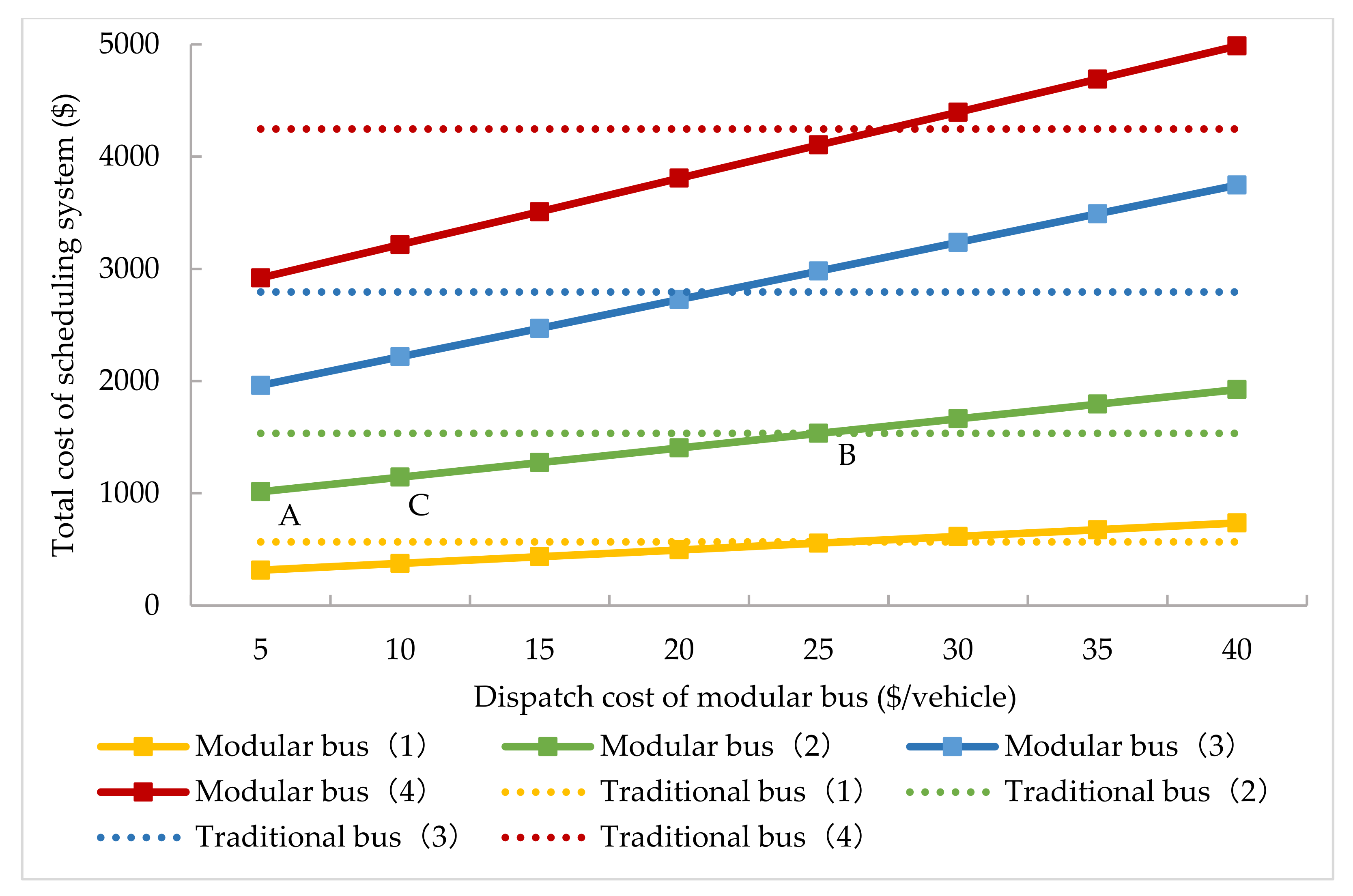
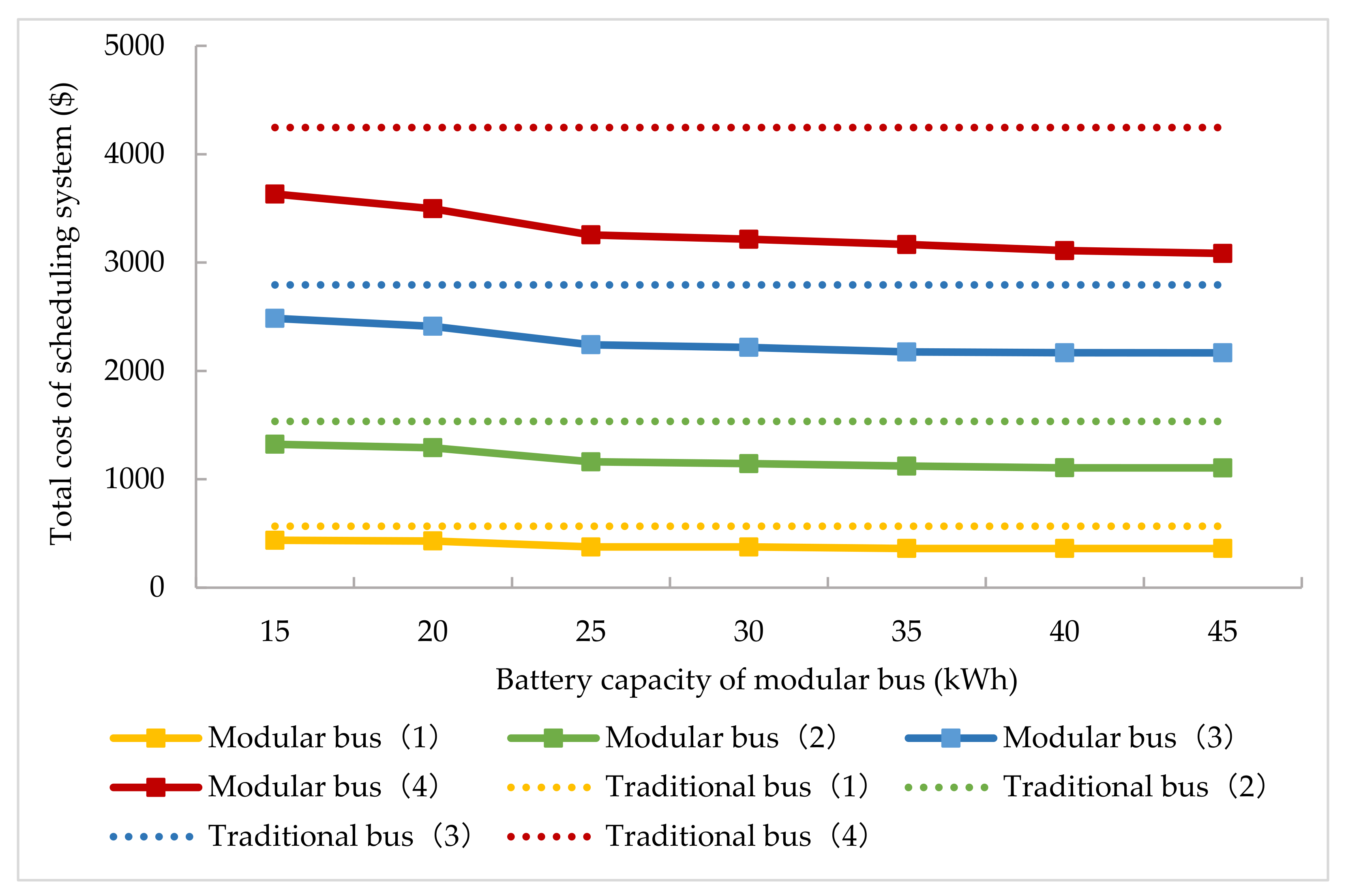
4.4. Effects of the Dispatch Cost and Battery Capacity
5. Concluding Remarks
- The proposed column generation-based heuristic algorithm, which decomposes the original problem into a master problem and subproblems, outperforms widely used solvers in terms of time and computation speed. Even in a network of 214 nodes, the scheduling strategy can be obtained in about 10 min with a gap of less than 0.3%.
- The optimal modular bus scheduling scheme can reduce the overall system cost from $1534.31 to $1144.26, a reduction of approximately 25%, while accommodating uneven trip demand and embracing battery and charging station capacity constraints.
- Sensitivity analysis highlights the impact of dispatch cost and battery capacity of modular buses on system total costs. Compared to the traditional bus, operators are recommended to consider applying modular units in scenarios with low or volatile demand; there may still be scope for profitability even if the dispatching cost is high. Additionally, procuring modular buses with 25 kWh–35 kWh capacity can avoid frequent charging.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Sets | |
| : | The set of nodes, index by or |
| : | The set of arcs, index by |
| : | The set of trips, index by or |
| : | The set of dummy nodes providing temporary stay for modular vehicles, index by or |
| : | The set of time-expanded charging stations, index by or |
| : | The set of nodes succeeding node on the directed graph, G, that is , index by or |
| : | The set of nodes preceding node on the directed graph , that is , index by or |
| : | The set of modular bus platoons, index by |
| : | The set of trip sequence, index by |
| Parameters | |
| : | The source node (depot departure) |
| : | The sink node (depot arrival) |
| : | Start time of node |
| : | End time of node |
| : | Passenger demand of node |
| : | Distance of node |
| : | Energy consumption of node |
| : | Energy consumption of arc |
| : | Idle time between node and node |
| : | Constant threshold to ensure the smooth coupling/decoupling action between the modular bus units. |
| : | Constant threshold introduced to prevent the nodes from being visited prematurely |
| : | Cost of a modular bus passing through arc |
| : | Dispatch cost of one modular unit |
| : | Charging cost of the modular bus |
| : | Idling cost per unit time of the modular bus |
| : | Operating cost per unit time of the modular bus |
| : | Waiting cost per unit time of the modular bus |
| : | The number of module units carried by module bus platoon . , where is the maximum number of module units allowed to be carried |
| : | Capacity of single modular bus |
| : | Charging station capacity |
| : | Battery capacity of single modular bus |
| : | Battery loss rate |
| : | Time interval between adjacent time-expanded charging nodes |
| : | The -th node ahead of charging node , where , |
| : | Cost of the trip sequence |
| : | if node is covered by the trip sequence provided by the subproblem and 0 otherwise |
| : | Values of the dual variables associated with constraints (11) |
| : | Values of the dual variables associated with constraints (12) |
| Variables | |
| : | Binary decision variable that equals 1 if module bus platoon traverses arc , and 0 otherwise |
| : | Intermediate variables, denoting the cumulative energy consumption of the module bus platoon at node |
| : | Integer variable, reveals the number of modular bus units assigned to the sequence |
| : | Binary decision variable that equals 1 if the modular bus traverses arc and 0 otherwise |
| : | Intermediate variables, denoting the cumulative energy consumption of the module bus at node |
References
- Badia, H.; Jenelius, E. Design and Operation of Feeder Systems in the Era of Automated and Electric Buses. Transp. Res. Part A Policy Pract. 2021, 152, 146–172. [Google Scholar] [CrossRef]
- Perumal, S.S.G.; Lusby, R.M.; Larsen, J. Electric Bus Planning & Scheduling: A Review of Related Problems and Methodologies. Eur. J. Oper. Res. 2022, 301, 395–413. [Google Scholar] [CrossRef]
- Häll, C.H.; Ceder, A.; Ekström, J.; Quttineh, N.-H. Adjustments of Public Transit Operations Planning Process for the Use of Electric Buses. J. Intell. Transp. Syst. 2019, 23, 216–230. [Google Scholar] [CrossRef]
- Zhou, G.-J.; Xie, D.-F.; Zhao, X.-M.; Lu, C. Collaborative Optimization of Vehicle and Charging Scheduling for a Bus Fleet Mixed With Electric and Traditional Buses. IEEE Access 2020, 8, 8056–8072. [Google Scholar] [CrossRef]
- Fu, L. Planning and Design of Flex-Route Transit Services. Transp. Res. Rec. 2002, 1791, 59–66. [Google Scholar] [CrossRef] [Green Version]
- Quadrifoglio, L.; Dessouky, M.M.; Ordóñez, F. Mobility Allowance Shuttle Transit (MAST) Services: MIP Formulation and Strengthening with Logic Constraints. Eur. J. Oper. Res. 2008, 185, 481–494. [Google Scholar] [CrossRef]
- NextFutureTransport. Available online: https://www.next-future-mobility.com/ (accessed on 5 February 2023).
- Guo, Q.W.; Chow, J.Y.J.; Schonfeld, P. Stochastic Dynamic Switching in Fixed and Flexible Transit Services as Market Entry-Exit Real Options. Transp. Res. Part C Emerg. Technol. 2018, 94, 288–306. [Google Scholar] [CrossRef]
- Gao, H.; Li, A.; Wang, J.; Liu, K.; Zhang, L. Design of an Intelligent Platoon Transit System towards Transportation Electrification. World Electr. Veh. J. 2022, 13, 153. [Google Scholar] [CrossRef]
- Rau, A.; Tian, L.; Jain, M.; Xie, M.; Liu, T.; Zhou, Y. Dynamic Autonomous Road Transit (DART) for Use-Case Capacity More Than Bus. Transp. Res. Procedia 2019, 41, 812–823. [Google Scholar] [CrossRef]
- Bold Business Editorial Team. Pods, The Self Driving Car Technology Can Be The Cure to Traffic Jams. 2017. Available online: https://www.boldbusiness.com/transportation/driverless-car-funding-grows/ (accessed on 28 April 2023).
- Nehra, W. Berlin’s Little Yellow Driverless Bus is Back! 2020. Available online: https://www.iamexpat.de/expat-info/german-expat-news/berlins-little-yellow-bus-back (accessed on 28 April 2023).
- Caros, N.S.; Chow, J.Y.J. Day-to-Day Market Evaluation of Modular Autonomous Vehicle Fleet Operations with En-Route Transfers. Transp. B 2021, 9, 109–133. [Google Scholar] [CrossRef]
- Wu, J.M.; Kulcsar, B.; Selpi; Qu, X.B. A Modular, Adaptive, and Autonomous Transit System (MAATS): An in-Motion Transfer Strategy and Performance Evaluation in Urban Grid Transit Networks. Transp. Res. Part A Policy Pract. 2021, 151, 81–98. [Google Scholar] [CrossRef]
- Tian, Q.; Lin, Y.H.; Wang, D.Z.W.; Liu, Y. Planning for Modular-Vehicle Transit Service System: Model Formulation and Solution Methods. Transp. Res. Part C Emerg. Technol. 2022, 138, 103627. [Google Scholar] [CrossRef]
- Li, Q.; Li, X. Trajectory Planning for Autonomous Modular Vehicle Docking and Autonomous Vehicle Platooning Operations. Transp. Res. Part E Logist. Transp. Rev. 2022, 166, 102886. [Google Scholar] [CrossRef]
- Khan, Z.S.; He, W.; Menéndez, M. Application of Modular Vehicle Technology to Mitigate Bus Bunching. Transp. Res. Part C Emerg. Technol. 2023, 146, 103953. [Google Scholar] [CrossRef]
- Chen, Z.; Li, X.; Zhou, X. Operational Design for Shuttle Systems with Modular Vehicles under Oversaturated Traffic: Discrete Modeling Method. Transp. Res. Part B Methodol. 2019, 122, 1–19. [Google Scholar] [CrossRef]
- Chen, Z.; Li, X.; Zhou, X. Operational Design for Shuttle Systems with Modular Vehicles under Oversaturated Traffic: Continuous Modeling Method. Transp. Res. Part B Methodol. 2020, 132, 76–100. [Google Scholar] [CrossRef]
- Dai, Z.; Liu, X.C.; Chen, X.; Ma, X. Joint Optimization of Scheduling and Capacity for Mixed Traffic with Autonomous and Human-Driven Buses: A Dynamic Programming Approach. Transp. Res. Part C Emerg. Technol. 2020, 114, 598–619. [Google Scholar] [CrossRef]
- Ji, Y.; Liu, B.; Shen, Y.; Du, Y. Scheduling Strategy for Transit Routes with Modular Autonomous Vehicles. Int. J. Transp. Sci. Technol. 2021, 10, 121–135. [Google Scholar] [CrossRef]
- Liu, X.; Qu, X.; Ma, X. Improving Flex-Route Transit Services with Modular Autonomous Vehicles. Transp. Res. Part E Logist. Transp. Rev. 2021, 149, 102331. [Google Scholar] [CrossRef]
- Pei, M.; Lin, P.; Du, J.; Li, X.; Chen, Z. Vehicle Dispatching in Modular Transit Networks: A Mixed-Integer Nonlinear Programming Model. Transp. Res. Part E Logist. Transp. Rev. 2021, 147, 102240. [Google Scholar] [CrossRef]
- Dakic, I.; Yang, K.; Menendez, M.; Chow, J.Y.J. On the Design of an Optimal Flexible Bus Dispatching System with Modular Bus Units: Using the Three-Dimensional Macroscopic Fundamental Diagram. Transp. Res. Part B Methodol. 2021, 148, 38–59. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Pei, M.; Li, X. Variable-Capacity Operations with Modular Transits for Shared-Use Corridors. Transp. Res. Rec. 2020, 2674, 230–244. [Google Scholar] [CrossRef]
- Shi, X.; Li, X. Operations Design of Modular Vehicles on an Oversaturated Corridor with First-in, First-out Passenger Queueing. Transp. Sci. 2021, 55, 1187–1205. [Google Scholar] [CrossRef]
- Zhang, Z.; Tafreshian, A.; Masoud, N. Modular Transit: Using Autonomy and Modularity to Improve Performance in Public Transportation. Transp. Res. Part E Logist. Transp. Rev. 2020, 141, 102033. [Google Scholar] [CrossRef]
- Liu, K.; Gao, H.; Liang, Z.; Zhao, M.; Li, C. Optimal Charging Strategy for Large-Scale Electric Buses Considering Resource Constraints. Transp. Res. Part D Transp. Environ. 2021, 99, 103009. [Google Scholar] [CrossRef]
- Liu, K.; Gao, H.; Wang, Y.; Feng, T.; Li, C. Robust Charging Strategies for Electric Bus Fleets under Energy Consumption Uncertainty. Transp. Res. Part D Transp. Environ. 2022, 104, 103215. [Google Scholar] [CrossRef]
- Dougier, N.; Celik, B.; Chabi-Sika, S.-K.; Sechilariu, M.; Locment, F.; Emery, J. Modelling of Electric Bus Operation and Charging Process: Potential Contribution of Local Photovoltaic Production. Appl. Sci. 2023, 13, 4372. [Google Scholar] [CrossRef]
- Zoltowska, I.; Lin, J. Optimal Charging Schedule Planning for Electric Buses Using Aggregated Day-Ahead Auction Bids. Energies 2021, 14, 4727. [Google Scholar] [CrossRef]
- Li, J.Q. Transit Bus Scheduling with Limited Energy. Transp. Sci. 2014, 48, 521–539. [Google Scholar] [CrossRef]
- Tang, X.; Lin, X.; He, F. Robust Scheduling Strategies of Electric Buses under Stochastic Traffic Conditions. Transp. Res. Part C Emerg. Technol. 2019, 105, 163–182. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, E.; Liu, S. Energy Consumption Optimization Model of Multi-Type Bus Operating Organization Based on Time-Space Network. Appl. Sci. 2019, 9, 3352. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Lo, H.K.; Xiao, F. Mixed Bus Fleet Scheduling under Range and Refueling Constraints. Transp. Res. Part C Emerg. Technol. 2019, 104, 443–462. [Google Scholar] [CrossRef]
- Olsen, N.; Kliewer, N. Location Planning of Charging Stations for Electric Buses in Public Transport Considering Vehicle Scheduling: A Variable Neighborhood Search Based Approach. Appl. Sci. 2022, 12, 3855. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, E.; Lu, M.; Yuan, L. Regional Electric Bus Driving Plan Optimization Algorithm Considering Charging Time Window. Math. Probl. Eng. 2019, 2019, 7863290. [Google Scholar] [CrossRef] [Green Version]
- Rinaldi, M.; Picarelli, E.; D’Ariano, A.; Viti, F. Mixed-Fleet Single-Terminal Bus Scheduling Problem: Modelling, Solution Scheme and Potential Applications. Omega 2020, 96, 102070. [Google Scholar] [CrossRef]
- Rinaldi, M.; Parisi, F.; Laskaris, G.; D’Ariano, A.; Viti, F. Optimal Dispatching of Electric and Hybrid Buses Subject to Scheduling and Charging Constraints. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 41–46. [Google Scholar]
- Irnich, S.; Desaulniers, G. Shortest Path Problems with Resource Constraints BT—Column Generation; Desaulniers, G., Desrosiers, J., Solomon, M.M., Eds.; Springer: Boston, MA, USA, 2005; pp. 33–65. ISBN 978-0-387-25486-9. [Google Scholar]
- Barnhart, C.; Johnson, E.L.; Nemhauser, G.L.; Savelsbergh, M.W.P.; Vance, P.H. Branch-and-Price: Column Generation for Solving Huge Integer Programs. Oper. Res. 1998, 46, 316–329. [Google Scholar] [CrossRef] [Green Version]


| × | × | × | × | |||
| × | × | |||||
| × | ||||||
| × | × | |||||
| × | × | × | × | × | ||
| Instance | GUROBI | CGBH | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Number | Trip | Node | LB ($) | Obj ($) | Time (s) | Gap (%) | LB ($) | Obj ($) | Time (s) | Gap (%) |
| (1) | 10 | 52 | 375.45 | 375.45 | 43.13 | 0.00 | 375.45 | 375.45 | 0.89 | 0.00 |
| (2) | 30 | 92 | 1106.22 | 1147.16 | >7200 | 3.57 | 1144.26 | 1144.26 | 18.93 | 0.00 |
| (3) | 60 | 184 | 2166.27 | 2438.63 | >7200 | 11.17 | 2213.68 | 2217.35 | 464.87 | 0.17 |
| (4) | 90 | 214 | 3094.25 | 4113.42 | >7200 | 24.78 | 3207.08 | 3215.24 | 824.40 | 0.25 |
| Number | Trip Sequence | Number of Units Equipped with MB Platoon | Cumulative Energy Consumption (kWh) | Cost ($) |
|---|---|---|---|---|
| 1 | -1-7-14-84-21-27- | 3 | 45.37 | 155.23 |
| 2 | -3-9-80-18-26-30- | 1 | 15.76 | 53.25 |
| 3 | -2-7-48-51-54-88-25-29- | 1 | 15.01 | 48.18 |
| 4 | -4-70-10-17-59-26-30- | 1 | 18.13 | 50.89 |
| 5 | -6-11-18-24- | 1 | 18.34 | 39.57 |
| 6 | -3-41-13-19- | 1 | 17.37 | 34.6 |
| 7 | -3-70-10-17-23-28- | 3 | 52.26 | 152.08 |
| 8 | -5-11-52-55-22- | 1 | 15.87 | 32.79 |
| 9 | -6-12-54-22- | 2 | 33.6 | 67.38 |
| 10 | -5-11-18- | 1 | 15.76 | 32.91 |
| 11 | -15-20-26-30- | 3 | 57.16 | 116.52 |
| 12 | -9-16-22- | 1 | 16.46 | 32.02 |
| 13 | -2-8-14-84-57-25-29- | 1 | 15.01 | 53.34 |
| 14 | -5-11-18-24- | 1 | 19.05 | 40.02 |
| 15 | -6-12-54-57-60-26-30- | 1 | 19.05 | 41.27 |
| 16 | -2-8-77-17-23-28- | 1 | 15.16 | 50.17 |
| 17 | -1-68-9-16-22- | 1 | 16.46 | 43.25 |
| 18 | -4-41-13-19- | 3 | 52.13 | 100.79 |
| Total | Satisfying the demands of 30 trips | 27 | Not exceeding the battery capacity | 1144.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Liu, K.; Wang, J.; Guo, F. Modular Bus Unit Scheduling for an Autonomous Transit System under Range and Charging Constraints. Appl. Sci. 2023, 13, 7661. https://doi.org/10.3390/app13137661
Gao H, Liu K, Wang J, Guo F. Modular Bus Unit Scheduling for an Autonomous Transit System under Range and Charging Constraints. Applied Sciences. 2023; 13(13):7661. https://doi.org/10.3390/app13137661
Chicago/Turabian StyleGao, Hong, Kai Liu, Jiangbo Wang, and Fangce Guo. 2023. "Modular Bus Unit Scheduling for an Autonomous Transit System under Range and Charging Constraints" Applied Sciences 13, no. 13: 7661. https://doi.org/10.3390/app13137661
APA StyleGao, H., Liu, K., Wang, J., & Guo, F. (2023). Modular Bus Unit Scheduling for an Autonomous Transit System under Range and Charging Constraints. Applied Sciences, 13(13), 7661. https://doi.org/10.3390/app13137661










