Model-Based Control and Model-Free Control Techniques for Autonomous Vehicles: A Technical Survey
Abstract
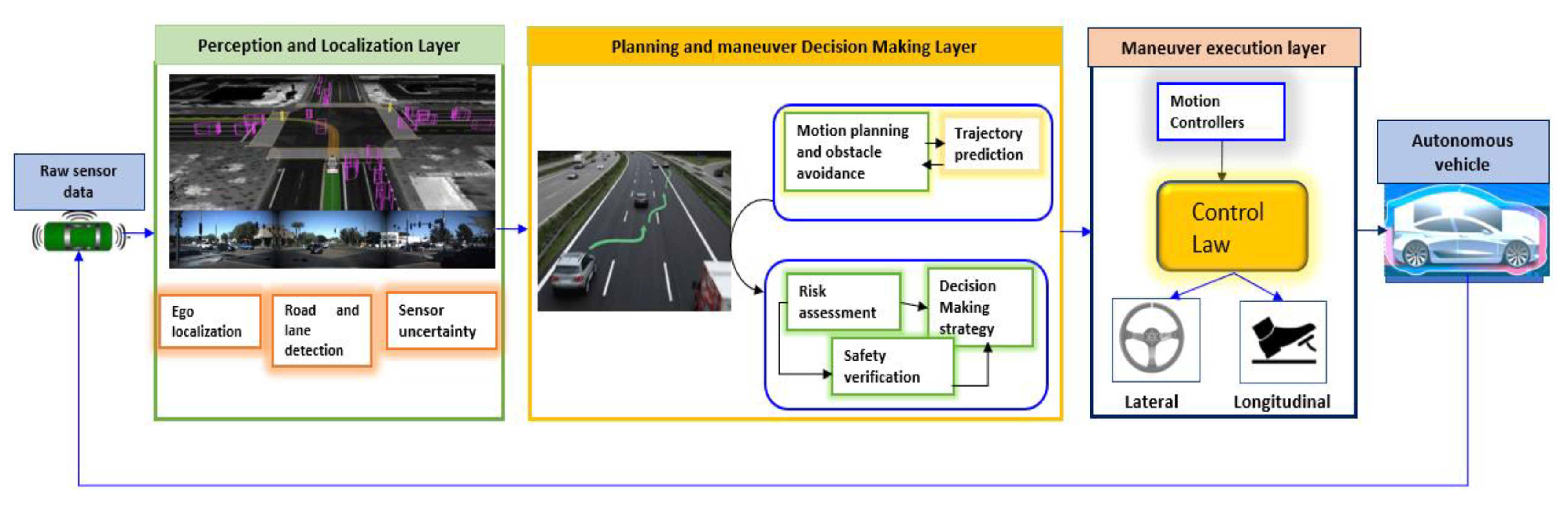
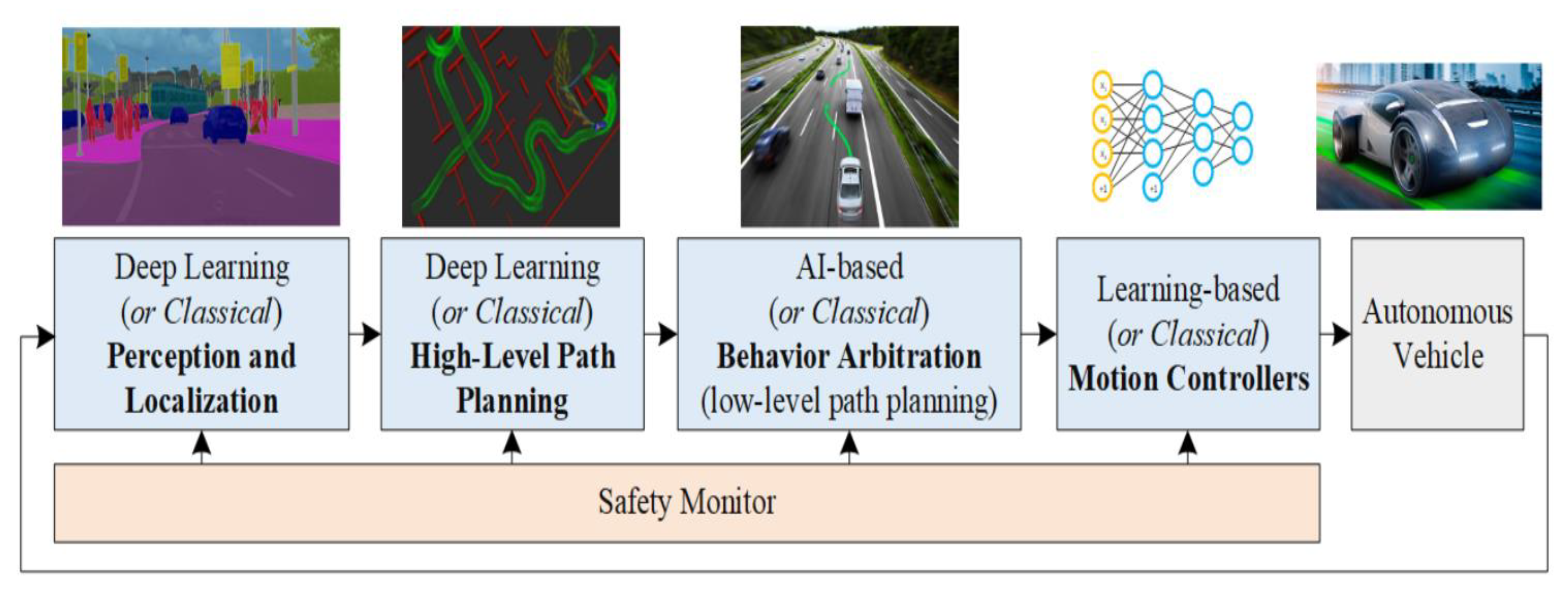
1. Introduction
2. Control of Autonomous Vehicle
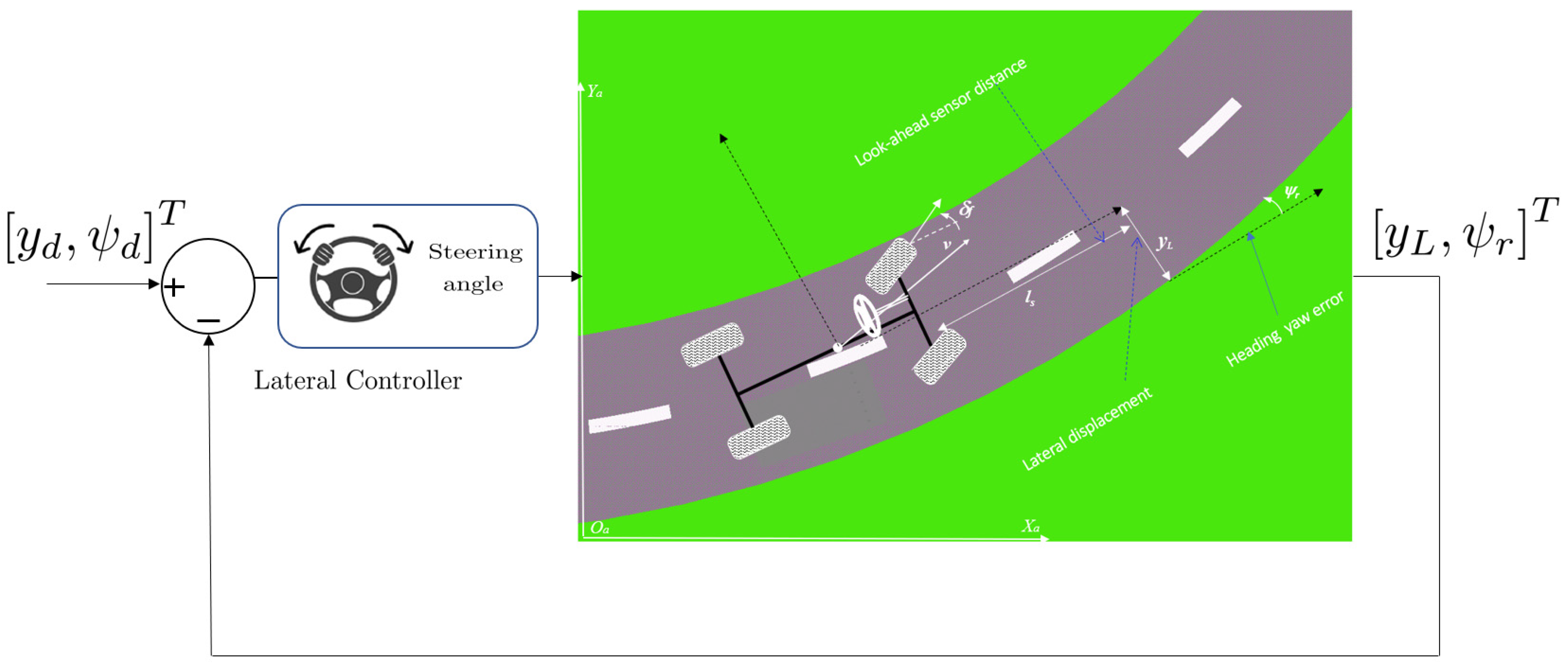
2.1. Lateral Control of Autonomous Vehicles
2.1.1. Lateral Model-Based Control Techniques
2.1.2. Lateral Model-Free Control techniques
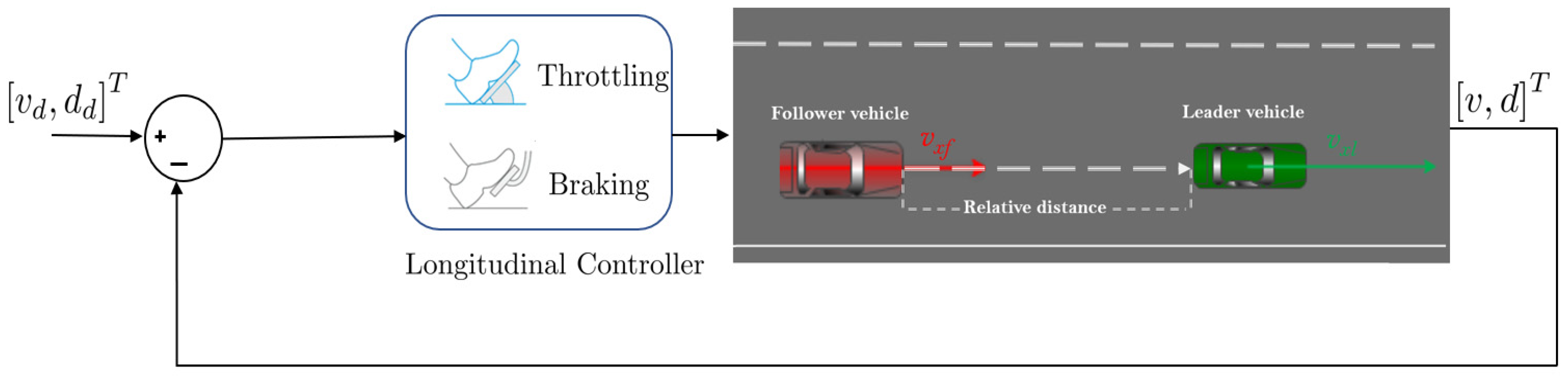
2.2. Longitudinal Control of Autonomous Vehicles
2.2.1. Longitudinal Model-Based Control Techniques
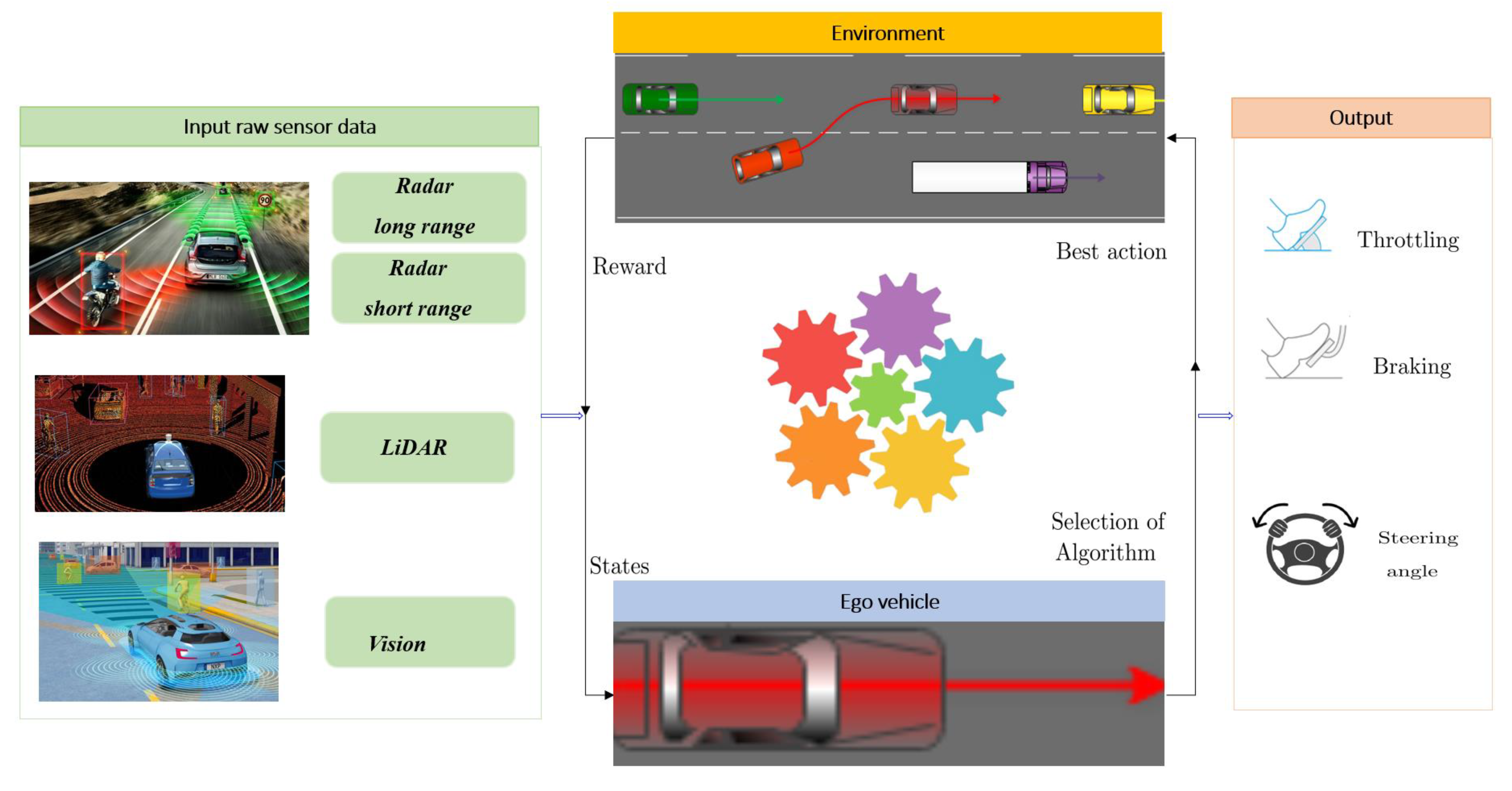
2.2.2. Longitudinal Model-Free Control Techniques
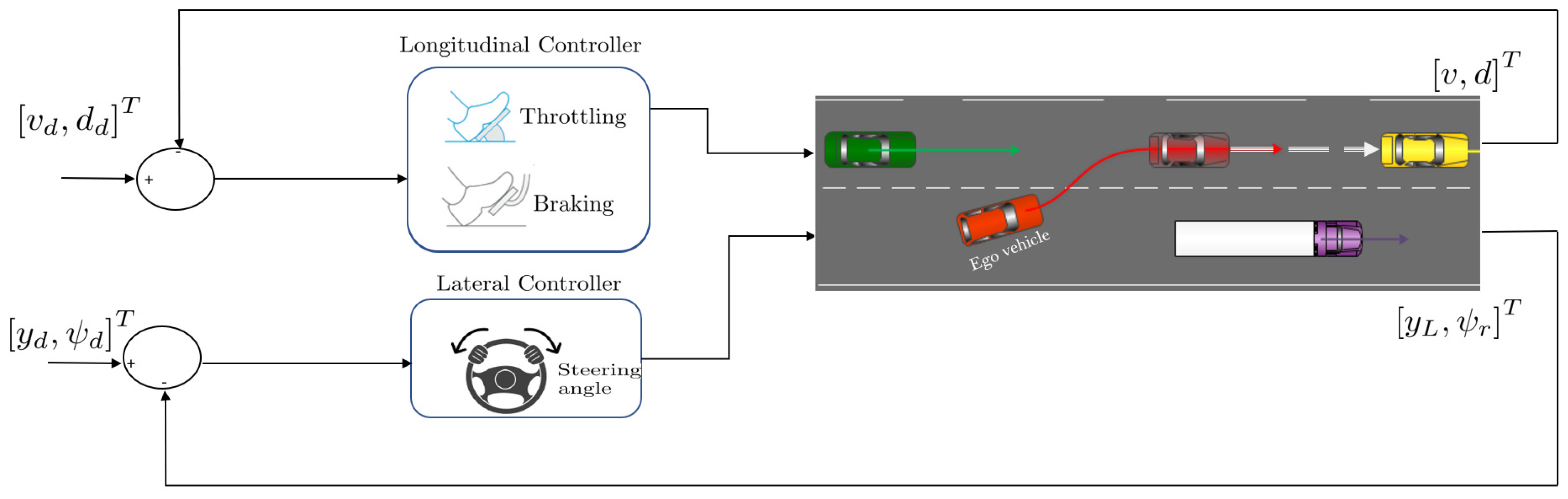
2.3. Integrated Lateral and Longitudinal Control of Autonomous Vehicles
2.3.1. Integrated Lateral and Longitudinal Model-Based Control Techniques
2.3.2. Integrated Lateral and Longitudinal Model-Free Control Techniques
3. Discussion
- −
- Require a mathematical model of the system being controlled;
- −
- Use the model to predict the behavior of the system and optimize control inputs;
- −
- Are often more efficient and accurate than model-free techniques when the model is accurate;
- −
- May be limited by the accuracy and completeness of the model;
- −
- Are typically designed by control engineers who have expertise in modeling and system identification.
- −
- Model-free control techniques are as follows:
- −
- Do not require an explicit model of the system being controlled;
- −
- Learn control policies from data through trial and error;
- −
- Can be used when the system is highly complex, poorly understood, or changing rapidly;
- −
- Are often more robust to model uncertainties than model-based techniques;
- −
- May require a large amount of data and time to learn a control policy;
- −
- Are typically designed by machine learning experts who have expertise in reinforcement learning or other model-free techniques.
4. Concluding Remarks and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Parekh, D.; Poddar, N.; Rajpurkar, A.; Chahal, M.; Kumar, N.; Joshi, G.P.; Cho, W. A review on autonomous vehicles: Progress, methods and challenges. Electronics 2022, 11, 2162. [Google Scholar] [CrossRef]
- Chan, C.-Y. Advancements, prospects, and impacts of automated driving systems. Int. J. Transp. Sci. Technol. 2017, 6, 208–216. [Google Scholar] [CrossRef]
- Martínez-Díaz, M.; Soriguera, F.; Pérez, I. Autonomous driving: A bird’s eye view. IET Intell. Transp. Syst. 2019, 13, 563–579. [Google Scholar] [CrossRef]
- World Health Organization. World Health Organization Road Traffic Injuries. 2018. Available online: https://www.who.int/newsroom/fact-sheets/detail/road-traffic-injuries (accessed on 14 July 2019).
- Brown, V.; Barr, A.; Scheurer, J.; Magnus, A.; Zapata-Diomedi, B.; Bentley, R. Better transport accessibility, better health: A health economic impact assessment study for Melbourne, Australia. Int. J. Behav. Nutr. Phys. Act. 2019, 16, 89. [Google Scholar] [CrossRef]
- Cohen, T.; Stilgoe, J.; Stares, S.; Akyelken, N.; Cavoli, C.; Day, J.; Dickinson, J.; Fors, V.; Hopkins, D.; Lyons, G.; et al. A constructive role for social science in the development of automated vehicles. Transp. Res. Interdiscip. Perspect. 2020, 6, 100133. [Google Scholar] [CrossRef]
- Shadrin, S.S.; Ivanova, A.A. Analytical review of standard Sae J3016 «taxonomy and definitions for terms related to driving automation systems for on-road motor vehicles» with latest updates. Avtomob. Doroga. Infrastrukt. 2019, 3, 10. [Google Scholar]
- Iberraken, D. Safe Trajectories and Sequential Bayesian Decision-Making Architecture for Reliable Autonomous Vehicle Navigation. Ph.D. Thesis, Clermont Auvergne University, Clermont-Ferrand, France, 2020. [Google Scholar]
- Kesting, A.; Treiber, M.; Helbing, D. General lane-changing model MOBIL for car-following models. Transp. Res. Rec. 2007, 1999, 86–94. [Google Scholar] [CrossRef]
- Arifin, B.; Suprapto, B.Y.; Sri Prasetyowati, A.D.; Nawawi, Z. The lateral control of autonomous vehicles: A review. In Proceedings of the 2019 International Conference on Electrical Engineering and Computer Science (ICECOS), Batam, Indonesia, 2–3 October 2019; pp. 277–282. [Google Scholar]
- Rajamani, R. Vehicle Dynamics and Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Marino, R.; Scalzi, S.; Netto, M. Nested PID steering control for lane keeping in autonomous vehicles. Control Eng. Pract. 2011, 19, 1459–1467. [Google Scholar] [CrossRef]
- Kang, C.M.; Kim, W.; Chung, C.C. Observer-based backstepping control method using reduced lateral dynamics for autonomous lane-keeping system. ISA Trans. 2018, 83, 214–226. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Gao, S.; Li, L.; Cheng, S.; Zhao, L. Automatic steering control strategy for unmanned vehicles based on robust backstepping sliding mode control theory. IEEE Access 2019, 7, 64984–64992. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, Y.; Liu, C.; Chen, B.; Zhang, W.; Li, L.; Ji, X. Hierarchical lateral control scheme for autonomous vehicle with uneven time delays induced by vision sensors. Sensors 2018, 18, 2544. [Google Scholar] [CrossRef] [PubMed]
- Liaw, D.-C.; Chung, W.C. A feedback linearization design for the control of vehicle’s lateral dynamics. Nonlinear Dyn. 2008, 52, 313–329. [Google Scholar] [CrossRef]
- Norouzi, A.; Masoumi, M.; Barari, A.; Sani, S.F. Lateral control of an autonomous vehicle using integrated backstepping and sliding mode controller. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2019, 233, 141–151. [Google Scholar] [CrossRef]
- Tagne, G.; Talj, R.; Charara, A. Higher-order sliding mode control for lateral dynamics of autonomous vehicles, with experimental validation. In Proceedings of the 2013 IEEE Intelligent Vehicles Symposium (IV), Gold Coast, QLD, Australia, 23–26 June 2013; pp. 678–683. [Google Scholar]
- Zhang, W. A robust lateral tracking control strategy for autonomous driving vehicles. Mech. Syst. Signal Process. 2021, 150, 107238. [Google Scholar] [CrossRef]
- Wang, X.; Fu, M.; Ma, H.; Yang, Y. Lateral control of autonomous vehicles based on fuzzy logic. Control Eng. Pract. 2015, 34, 1–17. [Google Scholar] [CrossRef]
- Hu, C.; Chen, Y.; Wang, J. Fuzzy observer-based transitional path-tracking control for autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 22, 3078–3088. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, R.; Zhao, L.; Wang, H.; Wei, Z. Control of chaos in vehicle lateral motion using the sliding mode variable structure control. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 776–789. [Google Scholar] [CrossRef]
- Akermi, K.; Chouraqui, S.; Boudaa, B. Novel SMC control design for path following of autonomous vehicles with uncertainties and mismatched disturbances. Int. J. Dyn. Control 2020, 8, 254–268. [Google Scholar] [CrossRef]
- Kebbati, Y.; Ait-Oufroukh, N.; Ichalal, D.; Vigneron, V. Lateral control for autonomous wheeled vehicles: A technical review. Asian J. Control, 2022; in print. [Google Scholar] [CrossRef]
- Rokonuzzaman, M.; Mohajer, N.; Nahavandi, S.; Mohamed, S. Review and performance evaluation of path tracking controllers of autonomous vehicles. IET Intell. Transp. Syst. 2021, 15, 646–670. [Google Scholar] [CrossRef]
- Ahmadian, N.; Khosravi, A.; Sarhadi, P. Managing driving disturbances in lateral vehicle dynamics via adaptive integrated chassis control. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2021, 235, 122–133. [Google Scholar]
- Qin, W. Unit sliding mode control for disturbed crowd dynamics system based on integral barrier Lyapunov function. IEEE Access 2020, 8, 91257–91264. [Google Scholar] [CrossRef]
- Han, S.I.; Cheong, J.Y.; Lee, J.M. Barrier Lyapunov function-based sliding mode control for guaranteed tracking performance of robot manipulator. Math. Probl. Eng. 2013, 2013, 978241. [Google Scholar] [CrossRef]
- Khan, R.; Malik, F.M.; Mazhar, N.; Raza, A.; Azim, R.A.; Ullah, H. Robust control framework for lateral dynamics of autonomous vehicle using barrier Lyapunov function. IEEE Access 2021, 9, 50513–50522. [Google Scholar] [CrossRef]
- Cortez, W.S.; Tan, X.; Dimarogonas, D.V. A robust, multiple control barrier function framework for input constrained systems. IEEE Control Syst. Lett. 2021, 6, 1742–1747. [Google Scholar] [CrossRef]
- He, S.; Zeng, J.; Zhang, B.; Sreenath, K. Rule-based safety-critical control design using control barrier functions with application to autonomous lane change. In Proceedings of the 2021 American Control Conference (ACC), New Orleans, LA, USA, 25–28 May 2021; pp. 178–185. [Google Scholar]
- Dong, X.; Pei, H.; Gan, M. Autonomous Vehicle Lateral Control Based on Fractional-order PID. In Proceedings of the 2021 IEEE 5th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Xi’an, China, 15–17 October 2021; pp. 830–835. [Google Scholar] [CrossRef]
- Choi, W.Y.; Kim, D.J.; Kang, C.M.; Lee, S.-H.; Chung, C.C. Autonomous Vehicle Lateral Maneuvering by Approximate Explicit Predictive Control. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 4739–4744. [Google Scholar] [CrossRef]
- Li, Y.; Chai, S.; Chai, R.; Liu, X. An Improved Model Predictive Control Method for Vehicle Lateral Control. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 5505–5510. [Google Scholar] [CrossRef]
- Lee, Y.; You, B. Comparison and Evaluation of Various Lateral Controller for Autonomous Vehicle. In Proceedings of the 2020 International Conference on Electronics, Information, Communication (ICEIC), Barcelona, Spain, 19–22 January 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Jiang, J.; Astolfi, A. Lateral control of an autonomous vehicle. IEEE Trans. Intell. Veh. 2018, 3, 228–237. [Google Scholar] [CrossRef]
- Kianfar, R.; Falcone, P.; Fredriksson, J. A distributed model predictive control approach to active steering control of string stable cooperative vehicle platoon. IFAC Proc. 2013, 46, 750–755. [Google Scholar] [CrossRef]
- Elallid, B.B.; Benamar, N.; Hafid, A.S.; Rachidi, T.; Mrani, N. A comprehensive survey on the application of deep and reinforcement learning approaches in autonomous driving. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 7366–7390. [Google Scholar] [CrossRef]
- Rausch, V.; Hansen, A.; Solowjow, E.; Liu, C.; Kreuzer, E.; Hedrick, J.K. Learning a deep neural net policy for end-to-end control of autonomous vehicles. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 4914–4919. [Google Scholar]
- Sharma, S.; Tewolde, G.; Kwon, J. Behavioral cloning for lateral motion control of autonomous vehicles using deep learning. In Proceedings of the 2018 IEEE International Conference on Electro/Information Technology (EIT), Rochester, MI, USA, 3–5 May 2018; pp. 0228–0233. [Google Scholar]
- Lee, M.-J.; Ha, Y.-G. Autonomous driving control using end-to-end deep learning. In Proceedings of the 2020 IEEE International Conference on Big Data and Smart Computing (BigComp), Busan, Republic of Korea, 19–22 February 2020; pp. 470–473. [Google Scholar]
- Maqueda, A.I.; Loquercio, A.; Gallego, G.; García, N.; Scaramuzza, D. Event-based vision meets deep learning on steering prediction for self-driving cars. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5419–5427. [Google Scholar]
- Chen, Y.; Praveen, P.; Priyantha, M.; Muelling, K.; Dolan, J. Learning on-road visual control for self-driving vehicles with auxiliary tasks. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa Village, HI, USA, 7–11 January 2019; pp. 331–338. [Google Scholar]
- Mújica-Vargas, D.; Luna-Álvarez, A.; de Jesús Rubio, J.; Carvajal-Gámez, B. Noise gradient strategy for an enhanced hybrid convolutional-recurrent deep network to control a self-driving vehicle. Appl. Soft Comput. 2020, 92, 106258. [Google Scholar] [CrossRef]
- Kebria, P.M.; Khosravi, A.; Salaken, S.M.; Nahavandi, S. Deep imitation learning for autonomous vehicles based on convolutional neural networks. IEEE/CAA J. Autom. Sin. 2019, 7, 82–95. [Google Scholar] [CrossRef]
- Li, D.; Zhao, D.; Zhang, Q.; Chen, Y. Reinforcement learning and deep learning based lateral control for autonomous driving [application notes]. IEEE Comput. Intell. Mag. 2019, 14, 83–98. [Google Scholar] [CrossRef]
- Amini, A.; Gilitschenski, I.; Phillips, J.; Moseyko, J.; Banerjee, R.; Karaman, S.; Rus, D. Learning robust control policies for end-to-end autonomous driving from data-driven simulation. IEEE Robot. Autom. Lett. 2020, 5, 1143–1150. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, C.; Luo, J.; Xie, J.; Wan, Y. Driving maneuvers prediction based autonomous driving control by deep monte carlo tree search. IEEE Trans. Veh. Technol. 2020, 69, 7146–7158. [Google Scholar] [CrossRef]
- Wang, P.; Chan, C.-Y.; de La Fortelle, A. A reinforcement learning based approach for automated lane change maneuvers. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Suzhou, China, 26–30 June 2018; pp. 1379–1384. [Google Scholar]
- Liu, S.; Hou, Z.; Tian, T.; Deng, Z.; Li, Z. A Novel Dual Successive Projection-Based Model-Free Adaptive Control Method and Application to an Autonomous Car. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3444–3457. [Google Scholar] [CrossRef] [PubMed]
- Swain, S.K.; Rath, J.J.; Veluvolu, K.C. Neural network based robust lateral control for an autonomous vehicle. Electronics 2021, 10, 510. [Google Scholar] [CrossRef]
- Moreno-Gonzalez, M.; Artuñedo, A.; Villagra, J.; Join, C.; Fliess, M. Speed-adaptive model-free lateral control for automated cars. IFAC-PapersOnLine 2022, 55, 84–89. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, X.; Wang, J. Extremum-Seeking-Based Adaptive Model-Free Control and Its Application to Automated Vehicle Path Tracking. IEEE/ASME Trans. Mechatron. 2022, 27, 3874–3884. [Google Scholar] [CrossRef]
- Zhu, L. Analyze the Advantages and Disadvantages of Different Sensors for Autonomous Vehicles. In Proceedings of the 2022 7th International Conference on Social Sciences and Economic Development (ICSSED 2022), Wuhan, China, 25–27 March 2022; Atlantis Press: Paris, France, 2022; pp. 1020–1024. [Google Scholar]
- Reschka, A.; Böhmer, J.R.; Saust, F.; Lichte, B.; Maurer, M. Safe, dynamic and comfortable longitudinal control for an autonomous vehicle. In Proceedings of the 2012 IEEE Intelligent Vehicles Symposium, Alcala de Henares, Spain, 3–7 June 2012; pp. 346–351. [Google Scholar]
- Milanés, V.; Villagrá, J.; Pérez, J.; González, C. Low-speed longitudinal controllers for mass-produced cars: A comparative study. IEEE Trans. Ind. Electron. 2011, 59, 620–628. [Google Scholar] [CrossRef]
- Ando, T.; Zhou, Y.; Momiyama, F.; Aoki, K.; Yang, B.; Nakano, K. Design of longitudinal controller for automated driving bus. Int. J. Intell. Transp. Syst. Res. 2020, 18, 436–450. [Google Scholar] [CrossRef]
- Dias, J.E.A.; Pereira, G.A.S.; Martinez Palhares, R. Longitudinal model identification and velocity control of an autonomous car. IEEE Trans. Intell. Transp. Syst. 2014, 16, 776–786. [Google Scholar] [CrossRef]
- Németh, B.; Gáspár, P.; Orjuela, R.; Basset, M. Robust H∞ design of an automotive cruise control system. IFAC-PapersOnLine 2015, 48, 341–346. [Google Scholar] [CrossRef]
- Abdullahi, A.; Akkaya, S. Adaptive cruise control: A model reference adaptive control approach. In Proceedings of the 2020 24th International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 8–10 October 2020; pp. 904–908. [Google Scholar]
- Raffin, A.; Taragna, M.; Giorelli, M. Adaptive longitudinal control of an autonomous vehicle with an approximate knowledge of its parameters. In Proceedings of the 2017 11th International Workshop on Robot Motion and Control (RoMoCo), Wąsowo Palace, Poland, 3–5 July 2017; pp. 1–6. [Google Scholar]
- Azızıaghdam, E.T.; Alankuş, O.B. Longitudinal control of autonomous vehicles consisting power-train with non-linear characteristics. IEEE Trans. Intell. Veh. 2021, 7, 133–142. [Google Scholar] [CrossRef]
- Gao, H.B.; Zhang, X.Y.; Li, D.Y.; Liu, Y.C. Longitudinal control for mengshi autonomous vehicle via cloud model. IOP Conf. Ser. Mater. Sci. Eng. 2018, 320, 012018. [Google Scholar] [CrossRef]
- Dunbar, W.B.; Caveney, D.S. Distributed receding horizon control of vehicle platoons: Stability and string stability. IEEE Trans. Autom. Control 2011, 57, 620–633. [Google Scholar] [CrossRef]
- Li, S.; Li, K.; Rajamani, R.; Wang, J. Model predictive multi-objective vehicular adaptive cruise control. IEEE Trans. Control Syst. Technol. 2010, 19, 556–566. [Google Scholar] [CrossRef]
- Szilassy, P.; Németh, B.; Gáspár, P. Design and robustness analysis of autonomous vehicles in intersections. IFAC-PapersOnLine 2019, 52, 321–326. [Google Scholar] [CrossRef]
- Al-Sharman, M.; Murdoch, D.; Cao, D.; Lv, C.; Zweiri, Y.; Rayside, D.; Melek, W. A sensorless state estimation for a safety-oriented cyber-physical system in urban driving: Deep learning approach. IEEE/CAA J. Autom. Sin. 2020, 8, 169–178. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, Y.; Pu, Z.; Hu, J.; Wang, X.; Ke, R. Safe, efficient, and comfortable velocity control based on reinforcement learning for autonomous driving. Transp. Res. Part C Emerg. Technol. 2020, 117, 102662. [Google Scholar] [CrossRef]
- Lin, Y.; McPhee, J.; Azad, N.L. Comparison of deep reinforcement learning and model predictive control for adaptive cruise control. IEEE Trans. Intell. Veh. 2020, 6, 221–231. [Google Scholar] [CrossRef]
- Peake, A.; McCalmon, J.; Raiford, B.; Liu, T.; Alqahtani, S. Multi-agent reinforcement learning for cooperative adaptive cruise control. In Proceedings of the 2020 IEEE 32nd International Conference on Tools with Artificial Intelligence (ICTAI), Baltimore, MD, USA, 9–11 November 2020; pp. 15–22. [Google Scholar]
- Yoon, Y.; Yi, K. Trajectory Prediction Using Graph-Based Deep Learning for Longitudinal Control of Autonomous Vehicles: A Proactive Approach for Autonomous Driving in Urban Dynamic Traffic Environments. IEEE Veh. Technol. Mag. 2022, 17, 18–27. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, H.; Tang, J.; Meng, X.; Hu, L. Velocity control in car-following behavior with autonomous vehicles using reinforcement learning. Accid. Anal. Prev. 2022, 174, 106729. [Google Scholar] [CrossRef] [PubMed]
- Kianfar, R.; Augusto, B.; Ebadighajari, A.; Hakeem, U.; Nilsson, J.; Raza, A.; Tabar, R.S.; Irukulapati, N.V.; Englund, C.; Falcone, P.; et al. Design and experimental validation of a cooperative driving system in the grand cooperative driving challenge. IEEE Trans. Intell. Transp. Syst. 2012, 13, 994–1007. [Google Scholar] [CrossRef]
- Maschuw, J.P.; Keßler, G.C.; Abel, D. LMI-based control of vehicle platoons for robust longitudinal guidance. IFAC Proc. 2008, 41, 12111–12116. [Google Scholar] [CrossRef]
- Naus, G.J.L.; Vugts, R.P.A.; Ploeg, J.; van de Molengraft, M.J.G.; Steinbuch, M. String-stable CACC design and experimental validation: A frequency-domain approach. IEEE Trans. Veh. Technol. 2010, 59, 4268–4279. [Google Scholar] [CrossRef]
- Kritayakirana, K.; Gerdes, J.C. Controlling an autonomous racing vehicle: Using feedforward and feedback to control steering and speed. In Proceedings of the Dynamic Systems and Control Conference, Los Angeles, CA, USA, 12–14 October 2009; Volume 48920, pp. 173–180. [Google Scholar]
- Attia, R.; Orjuela, R.; Basset, M. Nonlinear cascade strategy for longitudinal control in automated vehicle guidance. Control Eng. Pract. 2014, 29, 225–234. [Google Scholar] [CrossRef]
- Kianfar, R.; Ali, M.; Falcone, P.; Fredriksson, J. Combined longitudinal and lateral control design for string stable vehicle platooning within a designated lane. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 1003–1008. [Google Scholar]
- Attia, R.; Orjuela, R.; Basset, M. Combined longitudinal and lateral control for automated vehicle guidance. Veh. Syst. Dyn. 2014, 52, 261–279. [Google Scholar] [CrossRef]
- Chebly, A.; Talj, R.; Charara, A. Coupled longitudinal/lateral controllers for autonomous vehicles navigation, with experimental validation. Control Eng. Pract. 2019, 88, 79–96. [Google Scholar] [CrossRef]
- Kebbati, Y.; Ait-Oufroukh, N.; Vigneron, V.; Ichalal, D. Coordinated PSO-PID based longitudinal control with LPV-MPC based lateral control for autonomous vehicles. In Proceedings of the 2022 European Control Conference (ECC), London, UK, 11–14 July 2022; pp. 518–523. [Google Scholar]
- Qin, Z.; Chen, L.; Hu, M.; Chen, X. A Lateral and Longitudinal Dynamics Control Framework of Autonomous Vehicles Based on Multi-Parameter Joint Estimation. IEEE Trans. Veh. Technol. 2022, 71, 5837–5852. [Google Scholar] [CrossRef]
- Latrech, C.; Chaibet, A.; Boukhnifer, M.; Glaser, S. Integrated Longitudinal and Lateral Networked Control System Design for Vehicle Platooning. Sensors 2018, 18, 3085. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, Y.; Yu, J.; Cai, J.; Luo, J. End-to-end multi-modal multi-task vehicle control for self-driving cars with visual perceptions. In Proceedings of the 2018 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 2289–2294. [Google Scholar]
- Guo, J.; Cheng, S.; Liu, Y. Merging and diverging impact on mixed traffic of regular and autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 22, 1639–1649. [Google Scholar] [CrossRef]
- Toromanoff, M.; Wirbel, E.; Moutarde, F. End-to-end model-free reinforcement learning for urban driving using implicit affordances. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 7153–7162. [Google Scholar]
- Mohseni, F.; Voronov, S.; Frisk, E. Deep learning model predictive control for autonomous driving in unknown environments. IFAC-PapersOnLine 2018, 51, 447–452. [Google Scholar] [CrossRef]
- Grigorescu, S.; Trasnea, B.; Cocias, T.; Macesanu, G. A survey of deep learning techniques for autonomous driving. J. Field Robot. 2020, 37, 362–386. [Google Scholar] [CrossRef]
- Tork, N.; Amirkhani, A.; Shokouhi, S.B. An adaptive modified neural lateral-longitudinal control system for path following of autonomous vehicles. Eng. Sci. Technol. Int. J. 2021, 24, 126–137. [Google Scholar] [CrossRef]
- Sharma, S.; Tewolde, G.; Kwon, J. Lateral and longitudinal motion control of autonomous vehicles using deep learning. In Proceedings of the 2019 IEEE International Conference on Electro Information Technology (EIT), Brookings, SD, USA, 16–18 May 2019; pp. 1–5. [Google Scholar]
- Chen, C.; Seff, A.; Kornhauser, A.; Xiao, J. Deepdriving: Learning affordance for direct perception in autonomous driving. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 2722–2730. [Google Scholar]
- Devineau, G.; Polack, P.; Altché, F.; Moutarde, F. Coupled longitudinal and lateral control of a vehicle using deep learning. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 642–649. [Google Scholar]
- Li, X.; Sun, Z.; Cao, D.; Liu, D.; He, H. Development of a new integrated local trajectory planning and tracking control framework for autonomous ground vehicles. Mech. Syst. Signal Process. 2017, 87, 118–137. [Google Scholar] [CrossRef]
- Liang, X.; Wang, T.; Yang, L.; Xing, E. Cirl: Controllable imitative reinforcement learning for vision-based self-driving. In Proceedings of the 2018 European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 584–599. [Google Scholar]
- Wu, Y.; Tan, H.; Qin, L.; Ran, B. Differential variable speed limits control for freeway recurrent bottlenecks via deep actor-critic algorithm. Transp. Res. Part C 2020, 117, 102649. [Google Scholar] [CrossRef]
- Baheri, A.; Kolmanovsky, I.; Girard, A.; Tseng, H.E.; Filev, D. Vision-based autonomous driving: A model learning approach. arXiv 2020, arXiv:2003.08300. [Google Scholar]
- Bouton, M.; Nakhaei, A.; Isele, D.; Fujimura, K.; Kochenderfer, M.J. Reinforcement learning with iterative reasoning for merging in dense traffic. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; pp. 1–6. [Google Scholar]
- Ye, F.; Cheng, X.; Wang, P.; Chan, C.-Y.; Zhang, J. Automated lane change strategy using proximal policy optimization-based deep reinforcement learning. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 9 October–13 November 2020; pp. 1746–1752. [Google Scholar]
| Acronyms | Definition |
|---|---|
| AVs | Autonomous vehicles |
| RNNs | Recurrent neural networks |
| DN | Deep network |
| EN | Evolutionary network |
| MPC | Model predictive control |
| ML | Machine learning |
| RL | Reinforcement learning |
| WHO | World Health Organization |
| RADAR | Radio detection and ranging |
| DNN | Deep neural networks |
| DDPG | Deep deterministic policy gradient |
| MCTS | Monte Carlo tree search |
| DQN | Deep Q network |
| TORCS | The open racing car simulator |
| CNNs | Convolutional neural network |
| LSTM | Long short-term memory |
| AI | Artificial intelligence |
| DL | Deep learning |
| LIDAR | Light detection and ranging |
| MFCN | Motion-aid feature calibration network |
| NN | Neural networks |
| MDP | Markov decision process |
| DVSL | Differential variable speed limit |
| DoF | Degrees of freedom |
| GAN | Generative adversarial network |
| PID | Proportional integral derivative |
| OEM | Original equipment manufacturer |
| PPC | Pure pursuit controller |
| Papers | Publication Year | Control Technique | Vehicle Model/Vehicle Type Modeling | Output/Primary Objective | Validation | Advantages | Disadvantages |
|---|---|---|---|---|---|---|---|
| [12] | 2011 | Nested PID | Simplified single track vehicle model | Steering control and lane keeping | Simulation and real |
| Does not consider the interactions between the proposed controller and the driver both in normal driving and during emergency conditions. |
| [13,14] | 2018, 2019 | Backstepping | Reduced second-order model of lateral vehicle motion and a vehicle–road system model | Lane keeping and steering control | Simulation and real |
| There is no guarantee of the boundedness of the lateral offset in transient response. |
| [15] | 2018 | Hierarchical vision-based lateral control | The vehicle lateral model | Steering angle control | Simulation |
| |
| [17,18] | 2019, 2013 | Backstepping controller and sliding mode control (SMC) | Two-degree-of-freedom vehicle bicycle model and dynamic bicycle model | Steering control/angle and trajectory tracking | Simulation |
|
|
| [19] | 2021 | Gain scheduling | Two-degree-of-freedom (2-DOF) lateral vehicle model | Tracking references of lateral position and heading angle | Simulation |
| |
| [20,21] | 2015, 2020 | Fuzzy logic | Lateral kinematic model of an autonomous vehicle and Takagi-Sugeno (T-S) vehicle lateral dynamic model | Steering control and path-tracking control | Simulation |
| |
| [22] | 2019 | Sliding mode variable structure | Three-degree-of-freedom (DOF) nonlinear model | Improved a vehicle’s lateral stability under extreme operating conditions | Simulation |
| |
| [23] | 2020 | SMC in conjunction with disturbance observer and gain scheduling | The model of the vehicle lateral dynamics, including the modeling of the external disturbances | Path-following control | Simulation |
|
|
| [25] | 2021 | Feedback linearization (FL); two most common robust controllers: H∞ controller and sliding mode controller (SMC), the Lyapunov’s direct method (LDM); two geometry-based controllers: Stanley controller and pure pursuit controller (PPC); neural network (NN) controller; and two optimization-based controllers: model predictive control (MPC) and linear quadratic regulator (LQR) | Kinematic and dynamic vehicle model | Path-following task of autonomous ground vehicles (AGVs) | Simulation | (FL)
(LDM)
(Stanley)
(PPC)
(Adaptive)
(MPC)
(LQR)
| (FL)
(LDM)
(Stanley)
(PPC)
(Adaptive)
(MPC)
(LQR)
|
| [26] | 2021 | Multi-input multi-output (MIMO) model reference adaptive control (MRAC) strategy | Single-track (ST) 2-degree-of-freedom (DOF) vehicle model | Yaw rate tracking and handling of sideslip limitation | Simulation | Improves the handling and yaw stability of the lateral dynamics of the vehicle. | |
| [29] | 2021 | A sliding mode control (SMC) with barrier Lyapunov function | Nonlinear second-order system—following the model reduction approach in the literature, the slow and fast system dynamics are separately controlled | Tracking the system’s desired outputs while restricting the output in certain bounds | Simulation |
| |
| [30] | 2021 | Type-II ZCBF | Nonlinear affine system | Ensuring forward invariance and robustness of a constraint set. | Simulation |
|
|
| [31] | 2021 | CBF-CLF | Kinematic bicycle mode | Guaranteeing a vehicle’s safety during lane-change maneuvers in a complex traffic environment. | Simulation |
|
|
| [36] | 2018 | Hierarchical controllers | Two-DOF bicycle model/ SIMO system | Guaranteeing the stability and robustness under various environments | Simulation |
|
|
| [37] | 2013 | A distributed model predictive control approach | Model of lateral inter-vehicle dynamics between two adjacent vehicles | Steering control | Simulation | The proposed approach can deal with the actuator, comfort, and safety constraints. |
| Papers | Publication Year | Control Technique | Vehicle Model/Vehicle Type Modeling | Output/Primary Objective | Validation | Advantages | Disadvantages |
|---|---|---|---|---|---|---|---|
| [57] | 2020 | Adaptive cruise control | A linear longitudinal model | Reducing the acceleration of the vehicle | Simulation | Improved ride comfort in urban areas. | The maximum delay from reference and the maximum overshooting rate are especially large in rural areas, which affects the ride comfort. |
| [58] | 2014 | Model identification and velocity control | Model of longitudinal dynamics of a commercial car | Velocity control | Simulation and real |
| |
| [59] | 2015 | control | Simplified longitudinal model deals with = structured uncertainties such as mass variations and road slope | Precise velocity tracking at varying vehicle mass and road inclinations | Simulation |
| |
| [61] | 2017 | Model reference adaptive control (MRAC) | Longitudinal vehicle model with approximately known parameters | Tracking the speed profile with comfort acceleration | Simulation |
| The initial condition of the adaptive parameters has to be properly chosen to guarantee an effective implementation. |
| [62] | 2021 | This control methodology combines an inner controller and an outer controller | Reverse plant model of the vehicle | Controlling an autonomous vehicle with nonlinear power-train dynamics | Simulation and real |
| The control design is limited to the parameters known to OEMs (original equipment manufacturer). |
| [63] | 2018 | Longitudinal control based on cloud model | Cloud model for Mengshi AV | Ensuring the dynamic stability and tracking performance of Mengshi AV | Simulation | Guarantees the tracking performance and dynamic stability of Mengshi autonomous vehicle. | The speed and acceleration of the cloud model are classified according to experience without certification. |
| [64] | 2011 | Distributed receding horizon control | Platoon of vehicles with nonlinear dynamics | Ensuring asymptotic stability, leader–follower string stability, and predecessor–follower string stability, following a step speed change in the platoon | Simulation |
| The platoon size depends on the individual choices and the behavior of the constituent vehicles. |
| [65] | 2010 | Vehicular adaptive cruise control (ACC) (a hierarchical control architecture composed of a lower controller used to compensate for nonlinear vehicle dynamics and to track the desired acceleration and upper controller designed in the framework of MPC) | Model of nonlinear vehicle dynamics | Compensating for nonlinear vehicle dynamics and tracking the desired acceleration | Simulation |
|
| Papers | Publication Year | Control Technique | Vehicle model/Vehicle Type Modeling | Output/Primary Objective | Validation | Advantages | Disadvantages |
|---|---|---|---|---|---|---|---|
| [79] | 2014 | Nonlinear model predictive control (NLMPC) for lateral control and Lyapunov theory for longitudinal control | Nonlinear bicycle model and Longitudinal synthesis model | Path tracking at variable speeds and correctly tracking longitudinal speed reference | Simulation and real |
| Does not consider the road slope in the trajectory generation to ameliorate the reference generation. |
| [80] | 2019 | The first controller used Lyapunov control techniques, and the second controller used invariance and immersion with sliding mode control technique | Four-wheel vehicle model | Trajectory tracking and robust speed tracking | Simulation and real | Guarantees a robust tracking of the desired speed and the reference trajectory. |
|
| [81] | 2022 | PSO-PID for longitudinal control and LPV-MPC for lateral control | A vehicle consists of several subsystems for longitudinal dynamics and an LPV version of the standard bicycle model for lateral dynamics | Lateral and longitudinal tracking with robustness against wind disturbances | Simulation |
| Does not handle both lateral and longitudinal control simultaneously. |
| [82] | 2022 | Lateral and longitudinal control of AVs based on multi-parameter joint estimation | Longitudinal model for longitudinal dynamics and 3-DOF vehicle model for lateral dynamics | Improving the trajectory-tracking accuracy and vehicle lateral stability | Simulation and real | Provides excellent performance and enhances the lateral stability and tracking accuracy. | The parameters need to be estimated, and the control structure is not simple. |
| Papers | Publication Year | Sensor Input | Dataset | Output | Neural Network Architecture | DL Framework | Hardware | Validation | Advantages | Disadvantages |
|---|---|---|---|---|---|---|---|---|---|---|
| [84] | 2018 | Cameras | Udacity and SAIC | Steering angle and speed command | CNNs and LSTM | Not reported | GPUs | Real |
| |
| [90] | 2019 | Camera | TORCS data | Steering angle and vehicle speed | CNNs | Not reported | NVIDIA GeForce GTX | Simulation and real |
| The system performs well only on the two testing tracks due to the limited training data. |
| [91] | 2015 | Camera LIDAR | KITTI | Steering and acceleration and brake | CNNs | Caffe | NVIDIA | Simulation and real |
| |
| [92] | 2018 | - | Nine-DoF data | Steering angle | CNNs | Not reported | Not reported | Simulation |
| The proposed controller is a black-box and cannot be used in standalone. |
| Papers | Publication Year | Contributions | Output | RL Technique | Scenarios | Validation |
|---|---|---|---|---|---|---|
| [93] | 2017 | Modeling of driver and vehicle interactions using game theoretic and RL | Decelerate and hard decelerate and maintain | MDP | Multi-lane highways | Simulation |
| [94] | 2018 | Controllable imitative reinforcement learning to achieve higher success | Steering and brake and acceleration | DDPG | Urban traffic | Simulation |
| [95] | 2020 | RL model for differential variable speed limit control | Speed limits | DDPG | Freeway with five-lane | Simulation |
| [96] | 2020 | Model-based RL of the complex driving environment methodology | Steering and acceleration and brake | RNNs and EN and DN | Urban driving | Simulation |
| [97] | 2020 | Combination of RL and game theory to learn merging behaviors | Steering and velocity | DQN | Urban traffic | Simulation |
| [98] | 2020 | Automated lane-change strategy using proximal policy optimization-based RL | Lane change and acceleration | NN | Highways | Simulation and real |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rizk, H.; Chaibet, A.; Kribèche, A. Model-Based Control and Model-Free Control Techniques for Autonomous Vehicles: A Technical Survey. Appl. Sci. 2023, 13, 6700. https://doi.org/10.3390/app13116700
Rizk H, Chaibet A, Kribèche A. Model-Based Control and Model-Free Control Techniques for Autonomous Vehicles: A Technical Survey. Applied Sciences. 2023; 13(11):6700. https://doi.org/10.3390/app13116700
Chicago/Turabian StyleRizk, Hanan, Ahmed Chaibet, and Ali Kribèche. 2023. "Model-Based Control and Model-Free Control Techniques for Autonomous Vehicles: A Technical Survey" Applied Sciences 13, no. 11: 6700. https://doi.org/10.3390/app13116700
APA StyleRizk, H., Chaibet, A., & Kribèche, A. (2023). Model-Based Control and Model-Free Control Techniques for Autonomous Vehicles: A Technical Survey. Applied Sciences, 13(11), 6700. https://doi.org/10.3390/app13116700






