Optimizing Efficiency of Machine Learning Based Hard Disk Failure Prediction by Two-Layer Classification-Based Feature Selection
Abstract
1. Introduction
- From the perspective of the data in ML/AI-based hard disk failure prediction, this paper discusses and analyzes improving the prediction accuracy and timeliness of modeling by effectively selecting crucial attributes;
- An attribute filtering scheme is designed to remove unimportant attributes based on the idea of classification tree models, where entropy and the Gini index are the kernel techniques of these models; thus, both entropy and the Gini index are considered and employed to determine the importance of attributes;
- An attribute reduction scheme is proposed, to reduce the number of attributes in deep learning.First, this classifies features into different groups by mining their mutual correlation, where Pearson’s correlation coefficient and Spearman’s correlation coefficient are considered to mine the correlation between attributes. Then, it selects the most critical attribute from each group for modeling;
- We employ real disk health data to evaluate our scheme. The experimental results show that the proposed scheme can improve the prediction accuracy of ML/AI-based prediction models, and it can reduce the training and prediction latency by up to 75% and 83%, respectively, compared with the baseline methods. Our proposed scheme based on the Gini index and Pearson’s correlation coefficient performs best when using RF and LSTM.
2. Background and Related Work
2.1. ML/AI Based HDD Failure Prediction
2.2. Related Works
3. Motivation
4. Design
4.1. Problem Description and Data Processing
4.2. Attribute Filtering Based on Feature Importance
4.3. Attributes Reduction Based on Correlation Classification
| Algorithm 1 Two-layer Classification-Based Feature Selection |
| Input: , X, Y, , . Output:A set of selected attributes R.
|
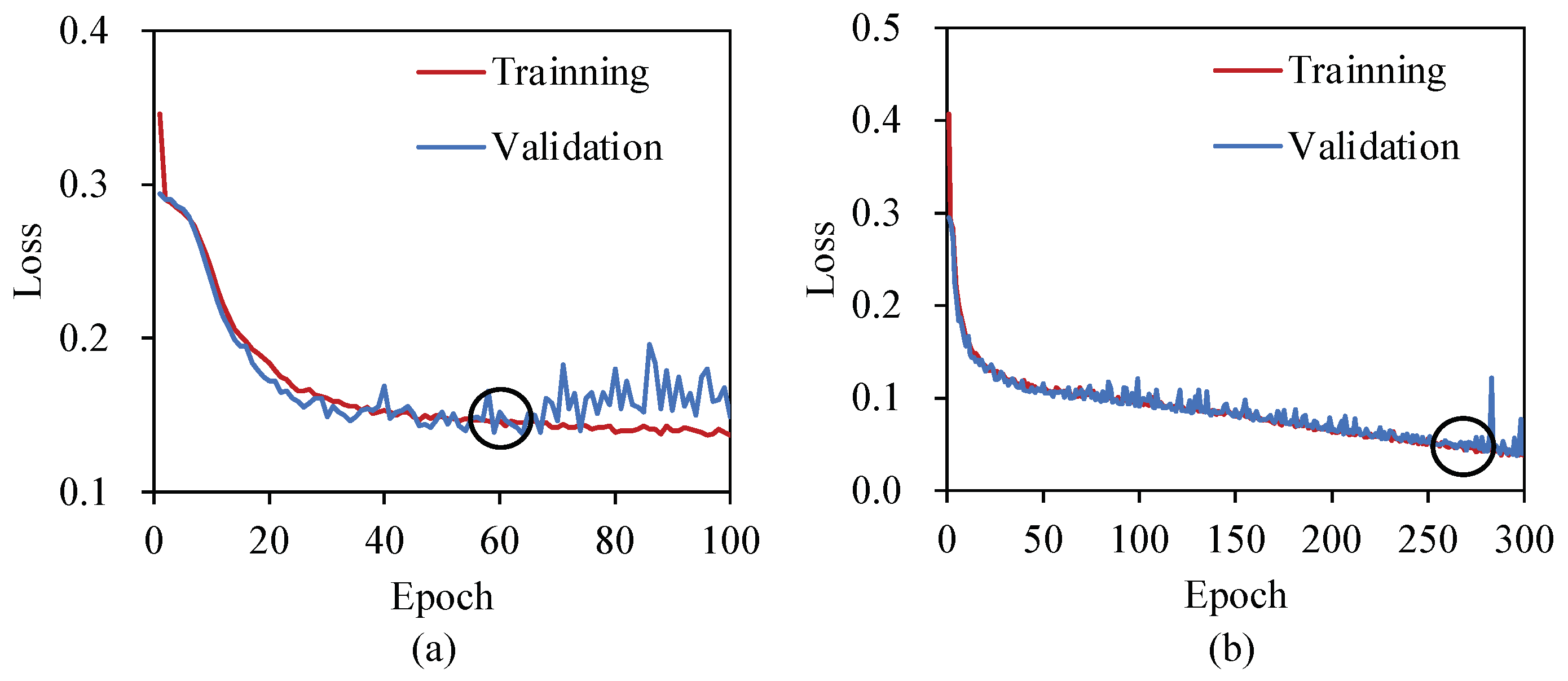
4.4. Modeling and Prediction
5. Results and Analysis
5.1. Experimental Setup
- Original is the baseline, which uses all attributes for modeling;
- Pearson is the scheme that selects features based on Pearson’s correlation coefficient, as used in [9];
- Spearman is the scheme that selects features based on Spearman’s correlation coefficient.
- J-Index is a feature selection method based on J-index, as used in [8];
- Entropy is the proposed scheme that uses entropy to select features without further attribute reduction;
- Gini is the proposed scheme without further attributes reduction, which selects features based on the Gini index.
5.2. Results
5.2.1. Results after Feature Selection
5.2.2. Prediction Quality
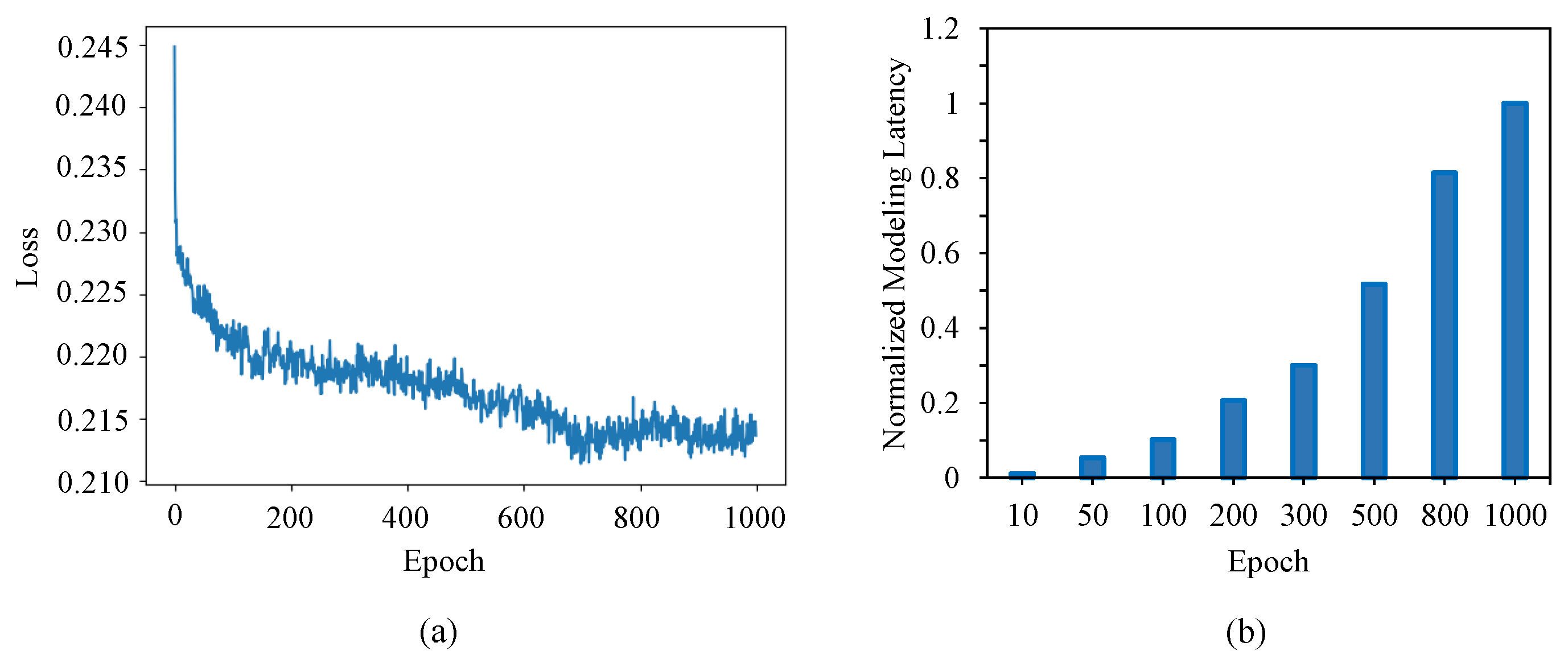
5.2.3. Modeling Latency
5.2.4. Computation Latency
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, G.; Zhang, L.; Xu, W. What can we learn from four years of data center hardware failures? In Proceedings of the DSN, Denver, CO, USA, 26–29 June 2017; pp. 25–36. [Google Scholar]
- Ghemawat, S.; Gobioff, H.; Leung, S.T. The Google file system. In Proceedings of the SOSP, New York, NY, USA, 19–22 October 2003; pp. 29–43. [Google Scholar]
- Huang, C.; Simitci, H.; Xu, Y.; Ogus, A.; Calder, B.; Gopalan, P.; Li, J.; Yekhanin, S. Erasure coding in windows azure storage. In Proceedings of the ATC, Boston, MA, USA, 13–15 June 2012; pp. 15–26. [Google Scholar]
- Patterson, D.A.; Gibson, G.; Katz, R.H. A case for redundant arrays of inexpensive disks (RAID). In Proceedings of the SIGMOD, Chicago, IL, USA, 1–3 June 1988; pp. 109–116. [Google Scholar]
- Li, J.; Stones, R.J.; Wang, G.; Li, Z.; Liu, X.; Xiao, K. Being accurate is not enough: New metrics for disk failure prediction. In Proceedings of the SRDS, Budapest, Hungary, 26–29 September 2016; pp. 71–80. [Google Scholar]
- Allen, B. Monitoring hard disks with SMART. Linux J. 2004, 74–77. [Google Scholar]
- Shen, J.; Wan, J.; Lim, S.J.; Yu, L. Random-forest-based failure prediction for hard disk drives. Int. J. Distrib. Sens. Netw. 2018, 14, 1550147718806480. [Google Scholar] [CrossRef]
- Lu, S.; Luo, B.; Patel, T.; Yao, Y.; Tiwari, D.; Shi, W. Making disk failure predictions smarter! In Proceedings of the FAST, Santa Clara, CA, USA, 24–27 February 2020; pp. 151–167. [Google Scholar]
- Zhang, J.; Huang, P.; Zhou, K.; Xie, M.; Schelter, S. HDDse: Enabling High-Dimensional Disk State Embedding for Generic Failure Detection System of Heterogeneous Disks in Large Data Centers. In Proceedings of the ATC, Nha Trang, Vietnam, 8–10 October 2020; pp. 111–126. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Murray, J.F.; Hughes, G.F.; Kreutz-Delgado, K.; Schuurmans, D. Machine Learning Methods for Predicting Failures in Hard Drives: A Multiple-Instance Application. J. Mach. Learn. Res. 2005, 6, 783–816. [Google Scholar]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Mahdisoltani, F.; Stefanovici, I.; Schroeder, B. Improving storage system reliability with proactive error prediction. In Proceedings of the ATC, Santa Clara, CA, USA, 12–14 July 2017; pp. 391–402. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Xu, C.; Wang, G.; Liu, X.; Guo, D.; Liu, T.Y. Health status assessment and failure prediction for hard drives with recurrent neural networks. IEEE Trans. Comput. 2016, 65, 3502–3508. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Han, S.; Lee, P.P.; Shen, Z.; He, C.; Liu, Y.; Huang, T. Toward adaptive disk failure prediction via stream mining. In Proceedings of the 2020 IEEE 40th International Conference on Distributed Computing Systems (ICDCS), Singapore, 29 November–1 December 2020; pp. 628–638. [Google Scholar]
- Fluss, R.; Faraggi, D.; Reiser, B. Estimation of the Youden Index and its associated cutoff point. Biom. J. J. Math. Methods Biosci. 2005, 47, 458–472. [Google Scholar] [CrossRef] [PubMed]
- Jiang, T.; Zeng, J.; Zhou, K.; Huang, P.; Yang, T. Lifelong disk failure prediction via GAN-based anomaly detection. In Proceedings of the 2019 IEEE 37th International Conference on Computer Design (ICCD), Abu Dhabi, United Arab Emirates, 17–20 November 2019; pp. 199–207. [Google Scholar]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J.; Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Chaves, I.C.; de Paula, M.R.P.; Leite, L.G.; Queiroz, L.P.; Gomes, J.P.P.; Machado, J.C. Banhfap: A bayesian network based failure prediction approach for hard disk drives. In Proceedings of the 2016 5th Brazilian Conference on Intelligent Systems (BRACIS), Recife, Brazil, 9–12 October 2016; pp. 427–432. [Google Scholar]
- Anantharaman, P.; Qiao, M.; Jadav, D. Large scale predictive analytics for hard disk remaining useful life estimation. In Proceedings of the 2018 IEEE International Congress on Big Data (BigData Congress), San Francisco, CA, USA, 2–7 July 2018; pp. 251–254. [Google Scholar]
- Botezatu, M.M.; Giurgiu, I.; Bogojeska, J.; Wiesmann, D. Predicting disk replacement towards reliable data centers. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 39–48. [Google Scholar]
- Zhang, J.; Zhou, K.; Huang, P.; He, X.; Xiao, Z.; Cheng, B.; Ji, Y.; Wang, Y. Transfer learning based failure prediction for minority disks in large data centers of heterogeneous disk systems. In Proceedings of the 48th International Conference on Parallel Processing, Kyoto, Japan, 5–8 August 2019; pp. 1–10. [Google Scholar]
- Myers, L.; Sirois, M.J. Spearman correlation coefficients, differences between. In Encyclopedia of Statistical Sciences; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation coefficients: Appropriate use and interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef] [PubMed]
- Rish, I. An empirical study of the naive Bayes classifier. In Proceedings of the IJCAI 2001 Workshop on Empirical Methods in Artificial Intelligence, Seattle, WA, USA, 4–10 August 2001; Volume 3, pp. 41–46. [Google Scholar]
- Noble, W.S. What is a support vector machine? Nat. Biotechnol. 2006, 24, 1565–1567. [Google Scholar] [CrossRef] [PubMed]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef] [PubMed]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the OSDI, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Gulli, A.; Pal, S. Deep learning with Keras; Packt Publishing Ltd.: Birmingham, UK, 2017. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Backblaze. Hard Drive Data and Stats. 2021. Available online: https://www.backblaze.com/b2/hard-drive-test-data.html (accessed on 2 February 2023).


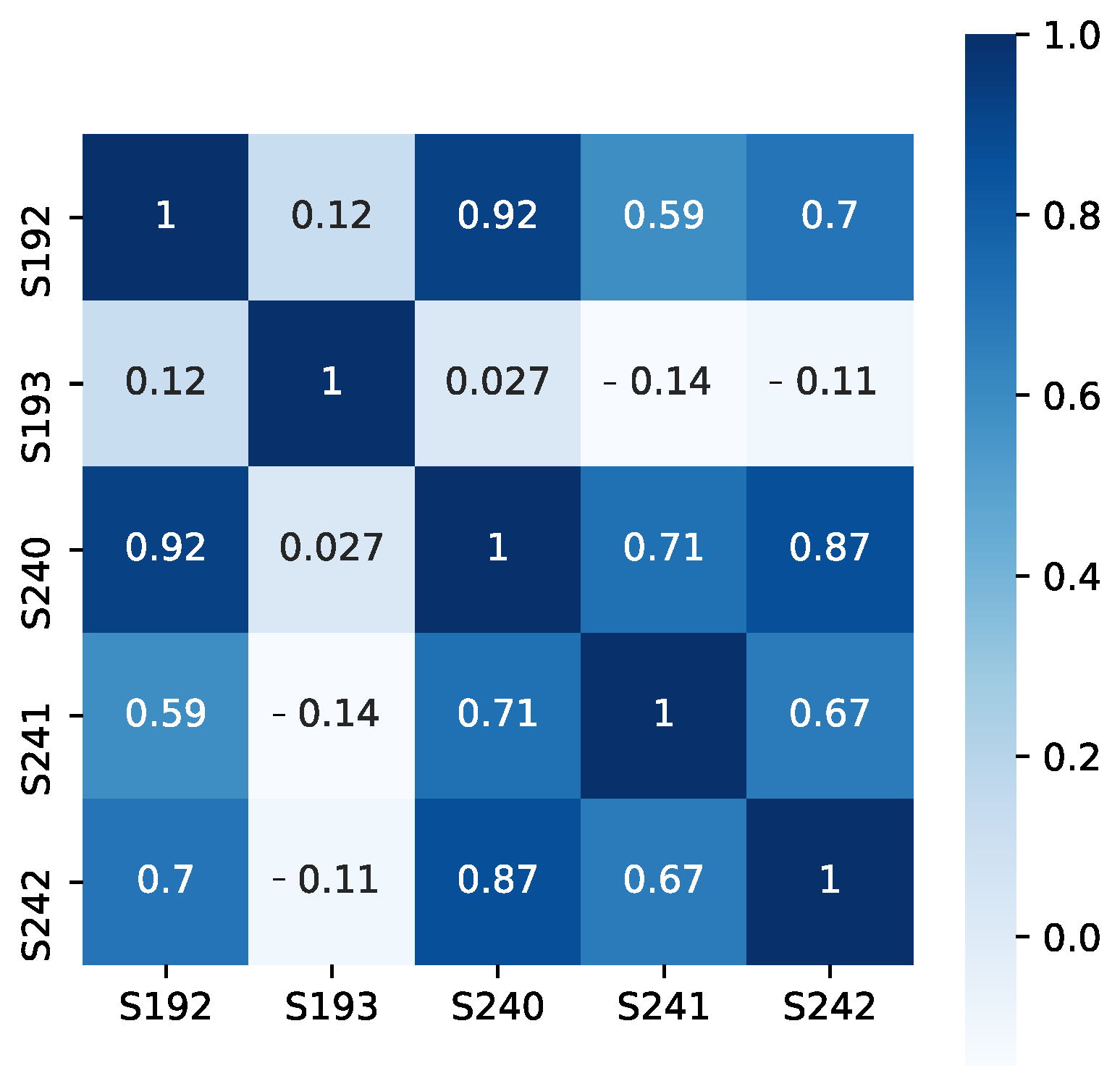


| ID | S.M.A.R.T Attribute Name |
|---|---|
| 192 | Power-Off Retract Cycles |
| 193 | Load/Unload Cycles |
| 240 | Head Flying Hours |
| 241 | Total LBAs Written |
| 242 | Total LBAs Read |
| Model | Duration | Total | Healthy | Failed | Healthy Sample | Failure Sample | Attr. |
|---|---|---|---|---|---|---|---|
| ST4000DM000 | 12 months | 19,241 | 18,972 | 269 | 24,800 | 2344 | 36 |
| ST12000NM0007 | 12 months | 37,255 | 36,916 | 339 | 27,300 | 2413 | 33 |
| DM000 | NM0007 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Original | Pearson | Spearman | J-Index | Entropy | Gini | Original | Pearson | Spearman | J-Index | Entropy | Gini |
| 36 | 13 | 13 | 13 | 13 | 13 | 33 | 12 | 12 | 12 | 16 | 12 |
| Org_Prs | Prs_Prs | Sprm_Prs | Jidx_Prs | Ent_Prs | Gini_Prs | Org_Prs | Prs_Prs | Sprm_Prs | Jidx_Prs | Ent_Prs | Gini_Prs |
| 21 | 7 | 7 | 7 | 10 | 10 | 19 | 8 | 9 | 9 | 9 | 8 |
| Org_Sprm | Prs_Sprm | Sprm_Sprm | Jidx_Sprm | Ent_Sprm | Gini_Sprm | Org_Sprm | Prs_Sprm | Sprm_Sprm | Jidx_Sprm | Ent_Sprm | Gini_Sprm |
| 21 | 8 | 8 | 8 | 10 | 10 | 19 | 8 | 10 | 10 | 9 | 8 |
| DM000 | NM0007 | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Group1 | Group2_Prs | Group2_Sprm | Group1 | Group2_Prs | Group2_Sprm | ||||||||||||||
| Pre | Re | F1 | Pre | Re | F1 | Pre | Re | F1 | Pre | Re | F1 | Pre | Re | F1 | Pre | Re | F1 | ||
| Original | NB | 0.69 | 0.38 | 0.49 | 0.7 | 0.37 | 0.49 | 0.72 | 0.37 | 0.48 | 0.79 | 0.31 | 0.45 | 0.81 | 0.27 | 0.41 | 0.8 | 0.3 | 0.43 |
| RF | 0.99 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 1 | 0.98 | 0.99 | 1 | 0.97 | 0.98 | 0.99 | 0.94 | 0.97 | 1 | 0.95 | 0.97 | |
| SVM | 0.91 | 0.54 | 0.68 | 0.89 | 0.09 | 0.17 | 0.94 | 0.46 | 0.62 | 0.84 | 0.31 | 0.45 | 0.83 | 0.29 | 0.43 | 0.77 | 0.24 | 0.36 | |
| GBDT | 0.97 | 0.79 | 0.87 | 0.95 | 0.76 | 0.85 | 0.97 | 0.77 | 0.86 | 0.93 | 0.71 | 0.81 | 0.92 | 0.61 | 0.73 | 0.91 | 0.68 | 0.78 | |
| CNN | 0.9 | 0.62 | 0.74 | 0.8 | 0.54 | 0.65 | 0.77 | 0.54 | 0.64 | 0.82 | 0.35 | 0.49 | 0.86 | 0.36 | 0.51 | 0.74 | 0.33 | 0.46 | |
| LSTM | 0.98 | 0.9 | 0.94 | 0.96 | 0.95 | 0.96 | 0.99 | 0.91 | 0.95 | 0.91 | 0.92 | 0.92 | 0.94 | 0.92 | 0.93 | 0.96 | 0.81 | 0.91 | |
| Pearson | NB | 0.78 | 0.36 | 0.49 | 0.78 | 0.35 | 0.48 | 0.78 | 0.35 | 0.48 | 0.78 | 0.3 | 0.43 | 0.81 | 0.26 | 0.4 | 0.79 | 0.29 | 0.42 |
| RF | 0.95 | 0.46 | 0.62 | 0.95 | 0.46 | 0.62 | 0.95 | 0.47 | 0.63 | 0.95 | 0.72 | 0.82 | 0.89 | 0.57 | 0.69 | 0.94 | 0.72 | 0.82 | |
| SVM | 0.78 | 0.24 | 0.36 | 0.75 | 0.12 | 0.21 | 0.77 | 0.12 | 0.21 | 0.77 | 0.32 | 0.46 | 0.82 | 0.31 | 0.45 | 0.73 | 0.25 | 0.37 | |
| GBDT | 0.92 | 0.43 | 0.59 | 0.9 | 0.42 | 0.57 | 0.92 | 0.43 | 0.59 | 0.9 | 0.62 | 0.74 | 0.87 | 0.54 | 0.67 | 0.9 | 0.62 | 0.74 | |
| CNN | 0.72 | 0.34 | 0.47 | 0.77 | 0.24 | 0.36 | 0.8 | 0.2 | 0.32 | 0.72 | 0.4 | 0.51 | 0.77 | 0.36 | 0.49 | 0.68 | 0.37 | 0.48 | |
| LSTM | 0.94 | 0.36 | 0.52 | 0.87 | 0.37 | 0.52 | 0.87 | 0.37 | 0.52 | 0.95 | 0.48 | 0.64 | 0.88 | 0.46 | 0.6 | 0.88 | 0.46 | 0.6 | |
| Spearman | NB | 0.73 | 0.35 | 0.47 | 0.74 | 0.34 | 0.47 | 0.74 | 0.34 | 0.47 | 0.78 | 0.3 | 0.43 | 0.81 | 0.26 | 0.4 | 0.79 | 0.29 | 0.42 |
| RF | 0.99 | 0.49 | 0.66 | 0.98 | 0.48 | 0.64 | 0.96 | 0.5 | 0.65 | 0.96 | 0.71 | 0.81 | 0.91 | 0.56 | 0.7 | 0.95 | 0.72 | 0.82 | |
| SVM | 0.78 | 0.23 | 0.36 | 0.74 | 0.12 | 0.2 | 0.76 | 0.11 | 0.2 | 0.77 | 0.32 | 0.46 | 0.82 | 0.31 | 0.45 | 0.73 | 0.25 | 0.37 | |
| GBDT | 0.95 | 0.42 | 0.59 | 0.93 | 0.41 | 0.57 | 0.95 | 0.42 | 0.59 | 0.89 | 0.62 | 0.73 | 0.87 | 0.54 | 0.67 | 0.9 | 0.62 | 0.74 | |
| CNN | 0.71 | 0.35 | 0.47 | 0.77 | 0.29 | 0.42 | 0.77 | 0.24 | 0.36 | 0.77 | 0.33 | 0.46 | 0.73 | 0.38 | 0.5 | 0.7 | 0.33 | 0.45 | |
| LSTM | 0.95 | 0.23 | 0.37 | 0.68 | 0.29 | 0.41 | 0.78 | 0.29 | 0.42 | 0.87 | 0.51 | 0.65 | 0.91 | 0.45 | 0.61 | 0.85 | 0.54 | 0.66 | |
| J-Index | NB | 0.62 | 0.36 | 0.46 | 0.63 | 0.35 | 0.45 | 0.71 | 0.3 | 0.43 | 0.77 | 0.32 | 0.45 | 0.77 | 0.32 | 0.46 | 0.75 | 0.3 | 0.43 |
| RF | 0.98 | 0.93 | 0.96 | 0.98 | 0.91 | 0.95 | 0.97 | 0.89 | 0.93 | 0.98 | 0.88 | 0.93 | 0.97 | 0.84 | 0.9 | 0.98 | 0.84 | 0.91 | |
| SVM | 0.81 | 0.3 | 0.44 | 0.77 | 0.15 | 0.25 | 0.79 | 0.15 | 0.25 | 0.88 | 0.34 | 0.49 | 0.88 | 0.35 | 0.5 | 0.8 | 0.22 | 0.35 | |
| GBDT | 0.88 | 0.68 | 0.76 | 0.87 | 0.68 | 0.76 | 0.87 | 0.68 | 0.76 | 0.89 | 0.69 | 0.78 | 0.87 | 0.69 | 0.77 | 0.9 | 0.68 | 0.78 | |
| CNN | 0.79 | 0.47 | 0.59 | 0.54 | 0.65 | 0.59 | 0.57 | 0.62 | 0.59 | 0.66 | 0.54 | 0.6 | 0.71 | 0.44 | 0.54 | 0.54 | 0.5 | 0.52 | |
| LSTM | 0.94 | 0.83 | 0.88 | 0.94 | 0.81 | 0.87 | 0.88 | 0.75 | 0.81 | 0.83 | 0.73 | 0.78 | 0.88 | 0.73 | 0.8 | 0.85 | 0.67 | 0.75 | |
| Entropy | NB | 0.63 | 0.37 | 0.47 | 0.7 | 0.37 | 0.49 | 0.71 | 0.36 | 0.47 | 0.72 | 0.43 | 0.54 | 0.78 | 0.31 | 0.45 | 0.75 | 0.32 | 0.44 |
| RF | 1 | 0.98 | 0.99 | 0.99 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 1 | 0.97 | 0.98 | 1 | 0.97 | 0.98 | 1 | 0.97 | 0.98 | |
| SVM | 0.94 | 0.54 | 0.69 | 0.82 | 0.21 | 0.33 | 0.93 | 0.54 | 0.68 | 0.91 | 0.42 | 0.57 | 0.85 | 0.33 | 0.47 | 0.8 | 0.26 | 0.4 | |
| GBDT | 0.96 | 0.78 | 0.86 | 0.95 | 0.75 | 0.84 | 0.96 | 0.77 | 0.85 | 0.93 | 0.72 | 0.81 | 0.91 | 0.6 | 0.72 | 0.92 | 0.65 | 0.76 | |
| CNN | 0.78 | 0.76 | 0.77 | 0.86 | 0.7 | 0.77 | 0.86 | 0.69 | 0.76 | 0.85 | 0.39 | 0.54 | 0.36 | 0.56 | 0.44 | 0.63 | 0.44 | 0.52 | |
| LSTM | 0.99 | 0.98 | 0.99 | 0.99 | 0.96 | 0.97 | 0.96 | 0.85 | 0.9 | 0.9 | 0.92 | 0.91 | 0.95 | 0.88 | 0.91 | 0.99 | 0.94 | 0.96 | |
| Gini | NB | 0.7 | 0.37 | 0.49 | 0.76 | 0.35 | 0.48 | 0.77 | 0.35 | 0.48 | 0.75 | 0.4 | 0.52 | 0.78 | 0.31 | 0.44 | 0.75 | 0.32 | 0.44 |
| RF | 0.99 | 0.99 | 0.99 | 1 | 0.99 | 0.99 | 0.99 | 0.97 | 0.98 | 1 | 0.97 | 0.98 | 1 | 0.95 | 0.97 | 1 | 0.96 | 0.98 | |
| SVM | 0.94 | 0.51 | 0.66 | 0.92 | 0.52 | 0.67 | 0.92 | 0.51 | 0.66 | 0.89 | 0.41 | 0.56 | 0.84 | 0.31 | 0.45 | 0.78 | 0.24 | 0.37 | |
| GBDT | 0.96 | 0.78 | 0.86 | 0.96 | 0.77 | 0.85 | 0.97 | 0.96 | 0.85 | 0.91 | 0.71 | 0.8 | 0.92 | 0.6 | 0.73 | 0.92 | 0.68 | 0.78 | |
| CNN | 0.81 | 0.71 | 0.76 | 0.87 | 0.73 | 0.79 | 0.83 | 0.78 | 0.8 | 0.36 | 0.72 | 0.48 | 0.77 | 0.42 | 0.54 | 0.76 | 0.36 | 0.49 | |
| LSTM | 1 | 0.97 | 0.98 | 0.99 | 0.98 | 0.98 | 1 | 0.96 | 0.98 | 1 | 0.98 | 0.99 | 1 | 0.99 | 0.99 | 0.98 | 0.92 | 0.95 | |
| DM000 | NM0007 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Original | Pearson | Spearman | J-Index | Entropy | Gini | Original | Pearson | Spearman | J-Index | Entropy | Gini |
| ∖ | 2.4 s | 7.4 s | 5.3 s | 1.6 s | 2.8 s | ∖ | 1.6 s | 5.5 s | 4.2 s | 2.2 s | 3.8 s |
| Org_Prs | Prs_Prs | Sprm_Prs | Jidx_Prs | Ent_Prs | Gini_Prs | Org_Prs | Prs_Prs | Sprm_Prs | Jidx_Prs | Ent_Prs | Gini_Prs |
| 2.2 s | 5.4 s | 10.5 s | 8.5 s | 5.6 s | 6.4 s | 1.6 s | 4.1 s | 8.3 s | 7.1 s | 6.7 s | 6.3 s |
| Org_Sprm | Prs_Sprm | Sprm_Sprm | Jidx_Sprm | Ent_Sprm | Gini_Sprm | Org_Sprm | Prs_Sprm | Sprm_Sprm | Jidx_Sprm | Ent_Sprm | Gini_Sprm |
| 7.3 s | 13.1 s | 12.6 s | 10.6 s | 14.1 s | 14.4 s | 5.2 s | 10.8 s | 11.3 s | 13.1 s | 16.2 s | 12.6 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhuge, Q.; Sha, E.H.-M.; Xu, R.; Song, Y. Optimizing Efficiency of Machine Learning Based Hard Disk Failure Prediction by Two-Layer Classification-Based Feature Selection. Appl. Sci. 2023, 13, 7544. https://doi.org/10.3390/app13137544
Wang H, Zhuge Q, Sha EH-M, Xu R, Song Y. Optimizing Efficiency of Machine Learning Based Hard Disk Failure Prediction by Two-Layer Classification-Based Feature Selection. Applied Sciences. 2023; 13(13):7544. https://doi.org/10.3390/app13137544
Chicago/Turabian StyleWang, Han, Qingfeng Zhuge, Edwin Hsing-Mean Sha, Rui Xu, and Yuhong Song. 2023. "Optimizing Efficiency of Machine Learning Based Hard Disk Failure Prediction by Two-Layer Classification-Based Feature Selection" Applied Sciences 13, no. 13: 7544. https://doi.org/10.3390/app13137544
APA StyleWang, H., Zhuge, Q., Sha, E. H.-M., Xu, R., & Song, Y. (2023). Optimizing Efficiency of Machine Learning Based Hard Disk Failure Prediction by Two-Layer Classification-Based Feature Selection. Applied Sciences, 13(13), 7544. https://doi.org/10.3390/app13137544






