A Double Interpolation and Mutation Interval Reconstruction LMD and Its Application in Fault Diagnosis of Reciprocating Compressor
Abstract
1. Introduction
2. Methods
2.1. Double Interpolation of Optimization Local Mean Decomposition (LMD)
2.1.1. Review of Local Mean Decomposition (LMD)
- (1)
- Find out all the extreme points of the signal , and the mean value and the envelope value are calculated for every two adjacent extreme points ( and ):
- (2)
- Obtain the resulting signal by separating the local mean function from the original signal , and then divide by the envelope estimation function to obtain :
- (3)
- Repeat step (1) to solve the envelope estimation function corresponding to ; if , illustrate that is a pure FM signal, and terminate this iteration; if , then repeat step (1) and step (2) n times until :
- (4)
- Multiply all envelope estimation functions generated by the above process to obtain the envelope signal of the PF component:
- (5)
- The envelope estimation function is multiplied by the pure FM signal to obtain the first PF component:
- (6)
- Subtract from the original signal to obtain the first residual component , and repeat steps (1) to (5) with as the original signal until the residual component is monotonous:
2.1.2. The Interpolation-Based Local Mean Decomposition
2.1.3. Limitations of Single Interpolation-Based LMD
2.1.4. Optimal Criteria for PF Components
2.1.5. Double Interpolation PF Optimization Scheme
2.2. Mutation Interval Reconstruction Envelope
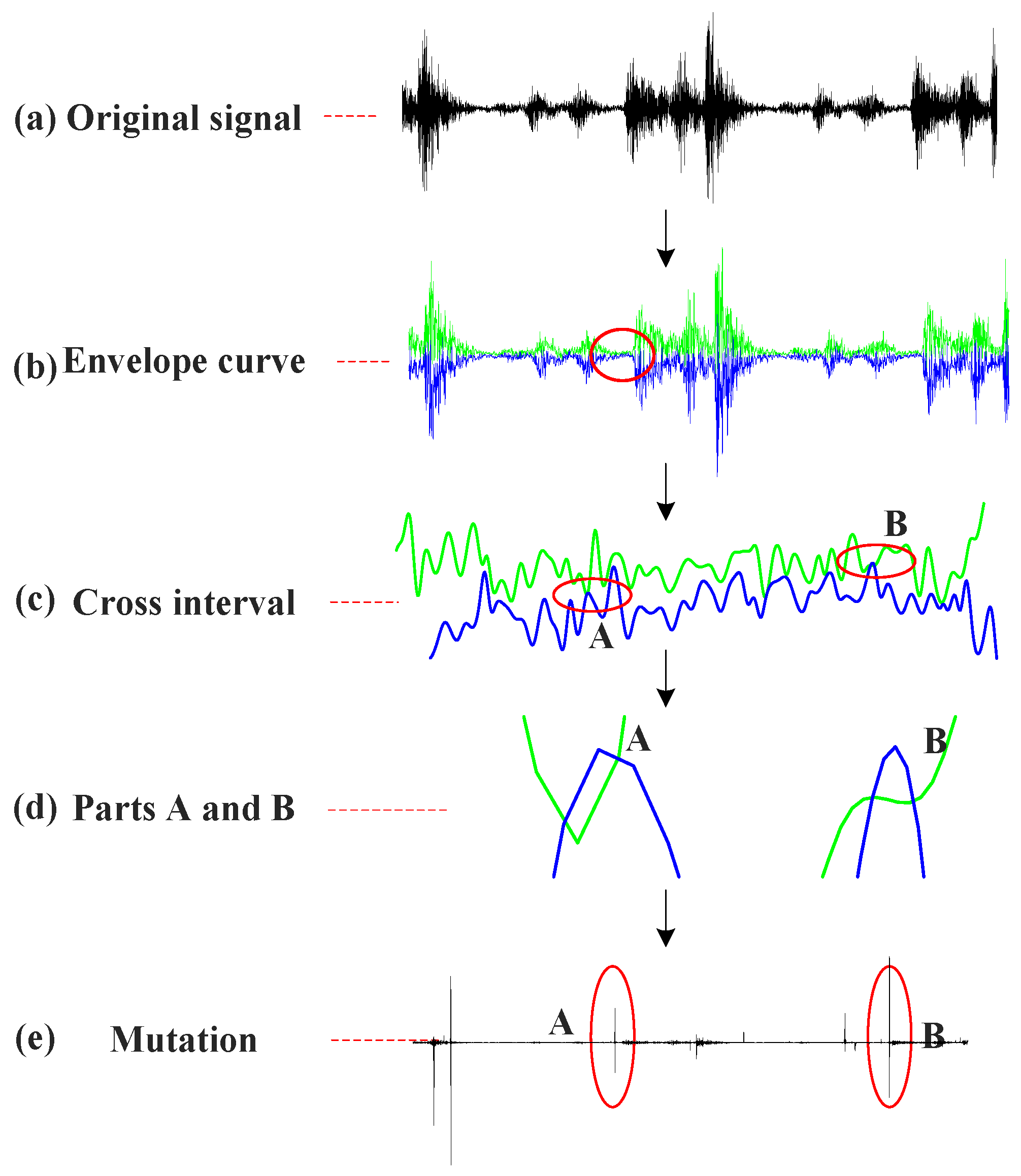
2.2.1. Demodulation Mutation Phenomenon
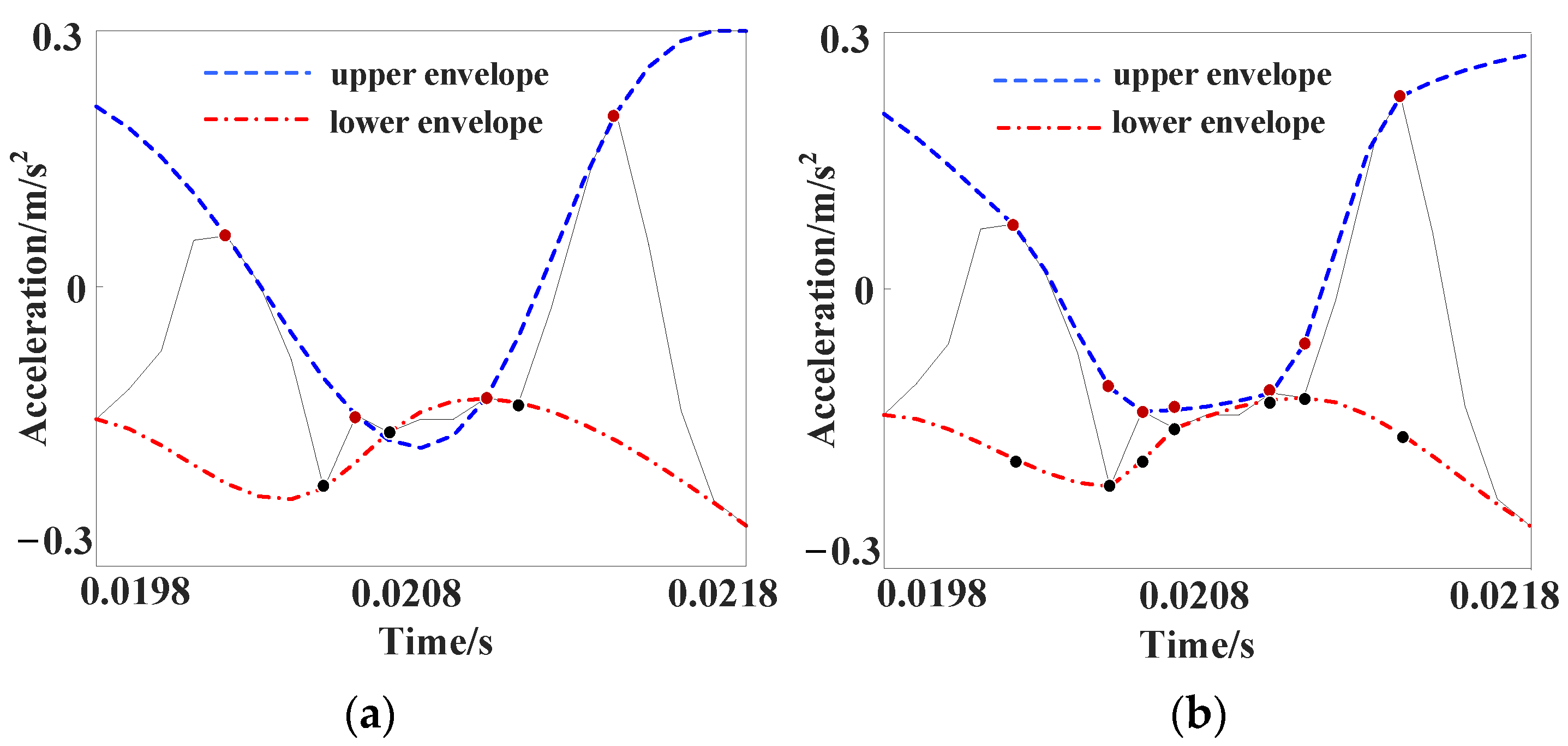
2.2.2. Mutation Interval Reconstruction
- (1)
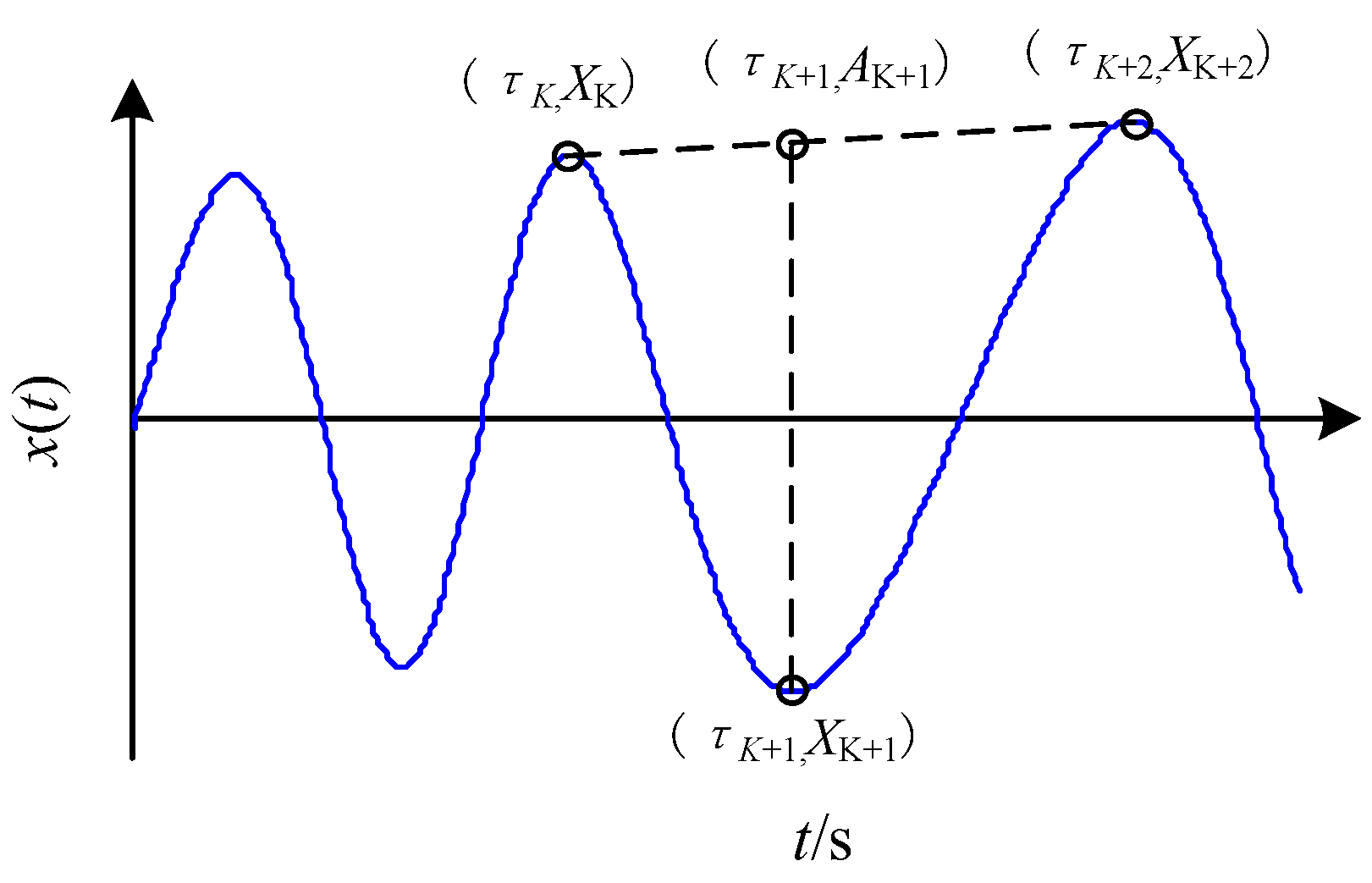
- Calculate the local extreme point sequence of the signal ( represents the local maximum point sequence or local minimum point sequence ), using cubic spline interpolation (or cubic Hermite interpolation) to construct the upper and lower envelope of the signal, and record the first derivative value of the envelope.
- (2)
- Take the difference between the upper and lower envelope lines to find the local maximum point interval [ and local minimum point interval [ ] (or [ ]) of the original signal where the intersection point is located.
- (3)
- Formula (12) is applied to calculate the extremum augmentation point between the two maxima ; calculate the extreme augmentation point between the two minimum points (or ).
- (4)
- According to and the first derivative value here, cubic Hermite is used to reconstruct the local interval interpolation of the upper envelope; the lower envelope local interval interpolation is reconstructed according to (or ).
- (5)
- Repeat step (3) and step (4) to reconstruct all the singular intervals in the construction process of the envelope. Finally, connect the reconstructed singular intervals and normal intervals to obtain the processed upper and lower envelope lines.
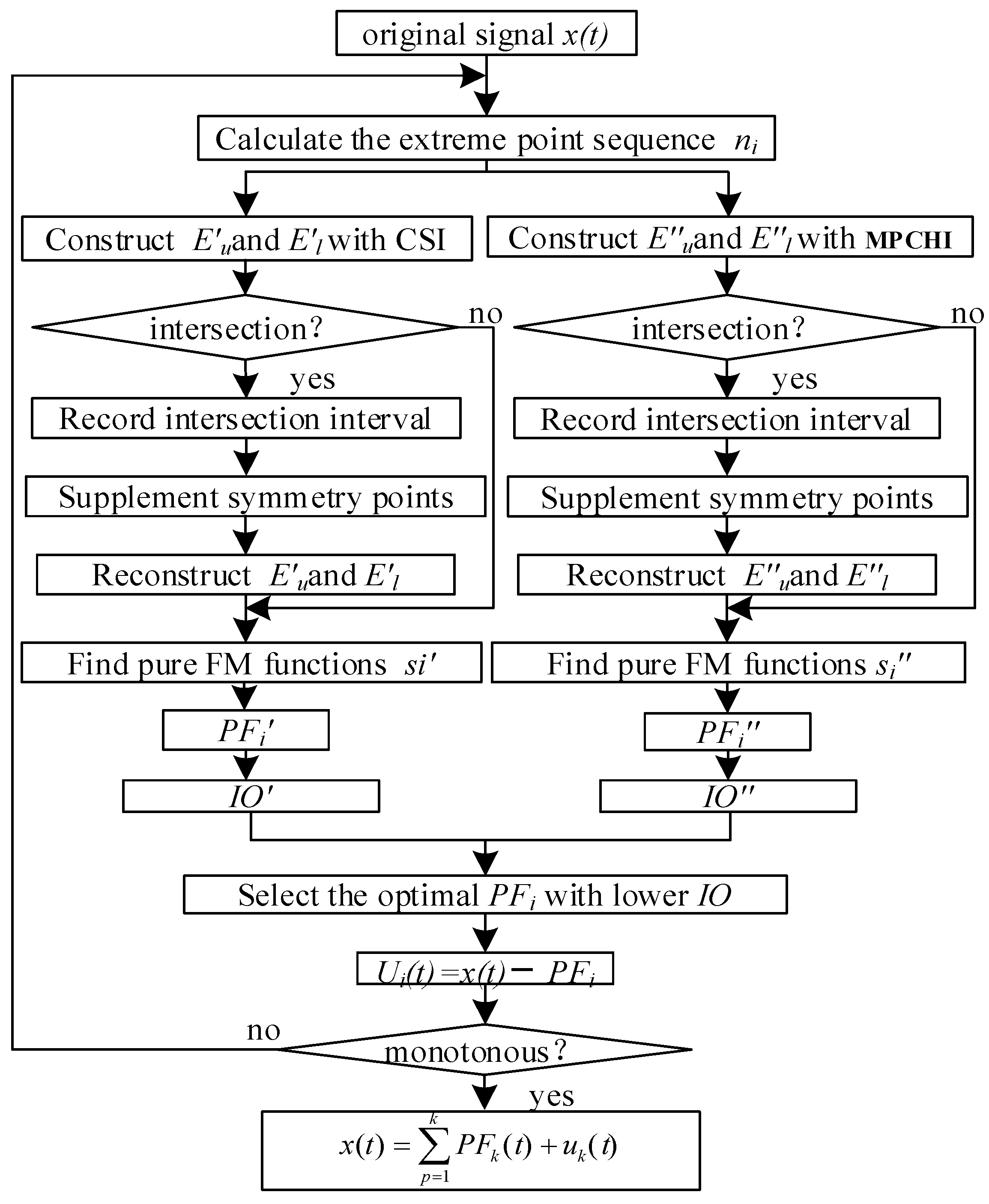
2.3. Double Interpolation and Mutation Interval Reconstruction Local Mean Decomposition (DIMIRLMD)
2.3.1. DIMIRLMD Scheme
2.3.2. DIMIRLMD Algorithm
- (1)
- Calculate the local extreme point sequence of the signal x(t).
- (2)
- Apply the CSI method to construct the upper envelope and lower envelope using the extreme point sequence.
- (3)
- The mutation intervals where the upper and lower envelopes overlap should be determined; add the extreme symmetry points to the original extreme point sequence in the mutation interval to form a new extreme point sequence.
- (4)
- Reconstruct new envelopes and with the refreshed extreme point sequence; if the reconstructed envelopes still exhibit mutation intervals, return to step (3) until the exclusion of mutation intervals.
- (5)
- Calculate the continuous local mean function m11(t) and the envelope function using the reconstructed upper envelope and the lower envelope :
- (6)
- Subtract from the original signal x(t) to obtain , and then the resulting signal is divided by .
- (7)
- Instead of the CSI method, employ the MPCHI method and repeat steps (1) to (6) to obtain the first MPCHI-based product function of the original signal.
- (8)
- Calculate the of and of , and then select the PF component with lower IO as the first optimal PF1(t) component.
- (9)
- Subtract PF1(t) from the original signal x(t) and obtain a new signal u1(t); the above procedure is repeated k times until uk becomes a monotonic function, and then we obtain a series of optimal PF components.
3. Results
3.1. Simulated Signal Analysis
3.2. Application for Reciprocating Compressor Fault Diagnosis
4. Conclusions
- (1)
- The main reason for the demodulation mutation phenomenon is found to be the intersection of upper and lower envelopes, and the extreme symmetry points are employed to reconstruct the envelopes. The mutation interval reconstruction algorithm effectively suppressed the demodulation mutation phenomenon.
- (2)
- Two typical interpolation envelope methods, CSI and MPCHI, are used to obtain PF components, and then the optimal PF component is selected based on the index of orthogonality (IO). Double interpolation PF optimization achieves a better hierarchical property for each order PF component. The orthogonality of decomposition results is improved, and the accuracy of the PF component is guaranteed.
- (3)
- A numerical simulation experiment indicated that DIMIRLMD outperforms the other three LMD methods in MSE and sifting iterations of PF components. The fault characteristics of the strong nonstationary vibration signal of the reciprocating compressor are more accurately quantified.
- (4)
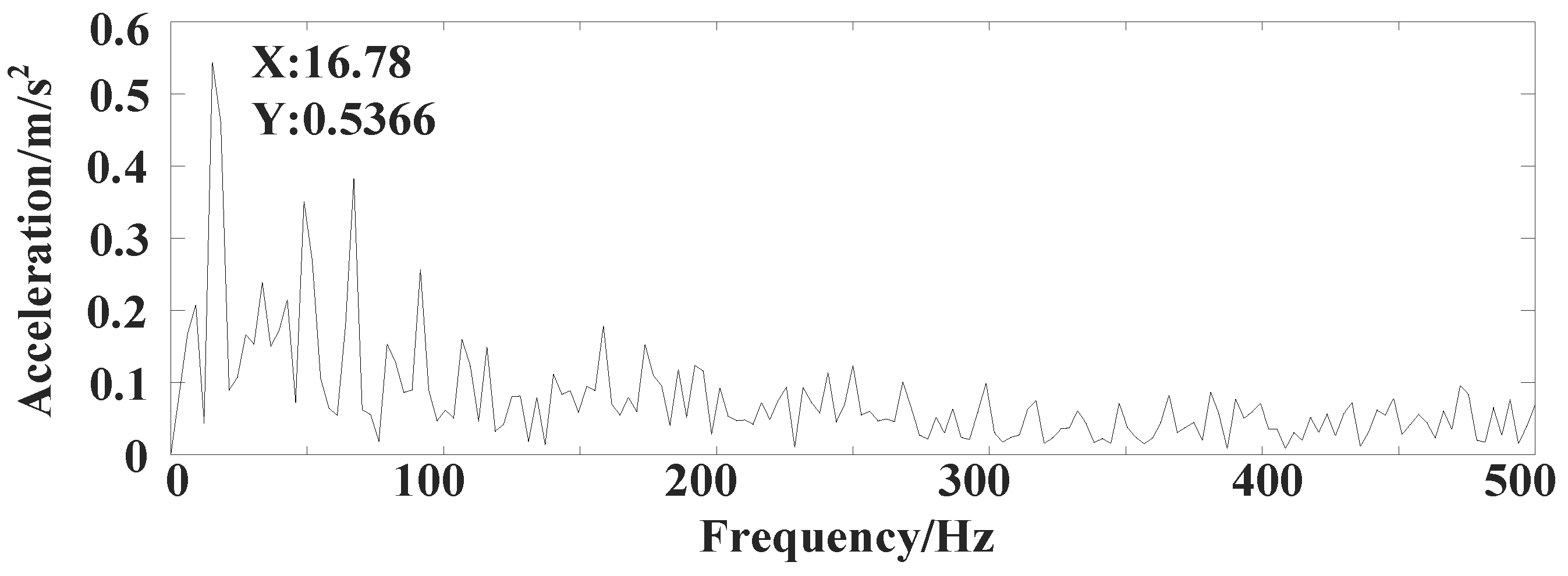
- DIMIRLMD was applicated in feature extraction from the vibration signals of the reciprocating compressor in an oversized bearing clearance fault state; results show it is superior in the sifting iterations, IO, and IEC compared to the other three LMD methods. Furthermore, the significant peak index of the PF component envelope frequency spectrum verified the superiority of DIMIRLMD in increased reciprocating pressure compressor fault identification accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, X.; Wang, S.; Qiao, B.; Chen, Q. Basic research on machinery fault diagnostics: Past, present, and future trends. Front. Mech. Eng. 2018, 13, 264–291. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, J.; Lee, J.; Li, Y. A compound interpolation envelope local mean decomposition and its application for fault diagnosis of reciprocating compressors. Mech. Syst. Signal Process. 2018, 110, 273–295. [Google Scholar]
- Feng, Z.; Liang, M.; Chu, F. Recent advances in time–frequency analysis methods for machinery fault diagnosis: A review with application examples. Mech. Syst. Signal Process. 2013, 38, 165–205. [Google Scholar] [CrossRef]
- Rachna, V.; Saurabh, D.U.D.; Tripathi, S.M. Machine learning applications in power system fault diagnosis: Research advancements and perspectives. Eng. Appl. Artif. Intell. 2021, 106, 104504. [Google Scholar]
- Zhao, N.; Zhang, J.; Mao, Z.; Jiang, Z. Variational time–frequency adaptive decomposition of machine multi-impact vibration signals. Mech. Syst. Signal Process. 2023, 189, 110084. [Google Scholar] [CrossRef]
- Sharma, V.; Parey, A. Performance evaluation of decomposition methods to diagnose leakage in a reciprocating compressor under limited speed variation. Mech. Syst. Signal Process. 2019, 125, 275–287. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, G.; Zhang, D.; Wang, T. Investigation on recognition method of acoustic emission signal of the compressor valve based on the deep learning method. Energy Rep. 2021, 7, 62–71. [Google Scholar] [CrossRef]
- Zhang, Y.; Ji, J.; Ma, B. Fault diagnosis of reciprocating compressor using a novel ensemble empirical mode decomposition-convolutional deep belief network. Measurement 2020, 156, 107619. [Google Scholar] [CrossRef]
- Cabrera, D.; Guamán, A.; Zhang, S.; Cerrada, M.; Sánchez, R.-V.; Cevallos, J.; Long, J.; Li, C. Bayesian approach and time series dimensionality reduction to LSTM-based model-building for fault diagnosis of a reciprocating compressor. Neurocomputing 2020, 380, 51–66. [Google Scholar] [CrossRef]
- Lv, Q.; Cai, L.; Yu, X.; Ma, H.; Li, Y.; Shu, Y. An Automatic Fault Diagnosis Method for the Reciprocating Compressor Based on HMT and ANN. Appl. Sci. 2022, 12, 5182. [Google Scholar] [CrossRef]
- Li, Y.; Pan, Y.; Ba, P.; Wu, S.; Chen, J. Fault Feature Extraction Method of Reciprocating Compressor Valve Based on SPA-MF. IEEE Access 2022, 10, 127182–127191. [Google Scholar] [CrossRef]
- Norden, E. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. A Mathmatical Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar]
- Jonathan, S. The Local Mean Decomposition and Its Application to EEG Perception Data. J. R. Soc. Interface 2022, 2, 443–454. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Rohit, M.; Bhagat, S. Stability analysis in milling process using spline based local mean decomposition (SBLMD) technique and statistical indicators. Measurement 2021, 174, 108999. [Google Scholar]
- Ezzat, D.; Hassanien, A.; Darwish, A.; Yahia, M.; Ahmed, A.; Abdelghafar, S. Multi-Objective Hybrid Artificial Intelligence Approach for Fault Diagnosis of Aerospace Systems. IEEE Access 2021, 9, 41717–41730. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Wang, H.; Jiaqiang, E. Research on gearbox composite fault diagnosis based on improved local mean decomposition. Int. J. Dyn. Control. 2021, 9, 1411–1422. [Google Scholar] [CrossRef]
- Liu, Z.; Zuo, M.J.; Jin, Y.; Pan, D.; Qin, Y. Improved local mean decomposition for modulation information mining and its application to machinery fault diagnosis. J. Sound Vib. 2017, 397, 266–281. [Google Scholar] [CrossRef]
- Guo, W.; Huang, L.; Chen, C.; Zou, H.; Liu, Z. Elimination of End Effects in Local Mean Decomposition Using Spectral Coherence and Applications for Rotating Machinery. Digit. Signal Process. 2016, 55, 52–63. [Google Scholar] [CrossRef]
- Li, Y.; Liang, X.; Yang, Y.; Xu, M.; Huang, W. Early Fault Diagnosis of Rotating Machinery by Combining Differential Rational Spline-Based LMD and K–L Divergence. IEEE Trans. Instrum. Meas. 2017, 66, 3077–3099. [Google Scholar] [CrossRef]
- Yang, Y.; Cheng, J.; Zhang, K. An ensemble local means decomposition method and its application to local rub-impact fault diagnosis of the rotor systems. Measurement 2012, 45, 561–570. [Google Scholar] [CrossRef]
- Li, Y.; Si, S.; Liu, Z.; Liang, X. Review of local mean decomposition and its application in fault diagnosis of rotating machinery. J. Syst. Eng. Electron. 2019, 30, 799–814. [Google Scholar]
- Yang, S.; Hu, J.; Mao, Z.; Wu, S. Empirical Mode Decomposition Based on Higher Order Spline interpolation. Zhejiang Univ. 2004, 3, 12–15. [Google Scholar]
- Liao, M.; Liu, C.; Wang, C.; Yang, J. Research on a Rolling Bearing Fault Detection Method With Wavelet Convolution Deep Transfer Learning. IEEE Access 2021, 9, 45175–45188. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Zhang, A.; Li, C.; Qiu, L. A Novel Bearing Fault Diagnosis Method Based on Few-Shot Transfer Learning across Different Datasets. Entropy 2022, 24, 1295. [Google Scholar] [CrossRef] [PubMed]
- Cheng, G.; Li, H.; Hu, X.; Chen, X.; Liu, H. Fault diagnosis of gearbox based on local mean decomposition and discrete hidden Markov models. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 231, 2706–2717. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, K.; Yang, Y. An order tracking technique for the gear fault diagnosis using local mean decomposition method. Mech. Mach. Theory 2012, 55, 67–76. [Google Scholar] [CrossRef]
- Liu, Z.-H.; Lu, B.-L.; Wei, H.-L.; Chen, L.; Li, X.-H.; Wang, C.-T. A Stacked Auto-Encoder Based Partial Adversarial Domain Adaptation Model for Intelligent Fault Diagnosis of Rotating Machines. IEEE Trans. Ind. Informatics 2021, 17, 6798–6809. [Google Scholar] [CrossRef]
- Ye, X.; Wang, P.; Yang, Z. Time Sequential Phase Partition and Modeling Method for Fault Detection of Batch Processes. IEEE Access 2018, 6, 1249–1260. [Google Scholar] [CrossRef]
- Qin, Y.; Zou, J.; Cao, F. Adaptively Detecting the Transient Feature of Faulty Wind Turbine Planetary Gearboxes by the Improved Kurtosis and Iterative Thresholding Algorithm. IEEE Access 2018, 6, 14602–14612. [Google Scholar] [CrossRef]
- Pu, X.; Li, C. Online Semi-Supervised Broad Learning System for Industrial Fault Diagnosis. IEEE Trans. Ind. Inform. 2021, 17, 6644–6654. [Google Scholar] [CrossRef]
- Mezni, Z.; Delpha, C.; Diallo, D.; Braham, A. Performance of Bearing Ball Defect Classification Based on the Fusion of Selected Statistical Features. Entropy 2022, 24, 1251. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Guo, A.; Chen, H. Feature Extraction Based on EWT With Scale Space Threshold and Improved MCKD for Fault Diagnosis. IEEE Access 2021, 9, 45407–45417. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L. Intelligent fault detection of reciprocating compressor using a novel discrete state space. Mech. Syst. Signal Process. 2022, 169, 108583. [Google Scholar] [CrossRef]
- Sim, H.Y.; Ramli, R.; Saifizul, A.; Soong, M.F. Detection and estimation of valve leakage losses in reciprocating compressor using acoustic emission technique. Measurement 2020, 152, 107315. [Google Scholar] [CrossRef]
- Song, M.; Wang, J.; Zhao, H.; Li, Y. Bearing failure of reciprocating compressor sub-health recognition based on CAGOA-VMD and GRCMDE. Adv. Mech. Eng. 2022, 14, 168781322210829. [Google Scholar] [CrossRef]
- Song, Y.; Wang, W. A Fault Feature Extraction Method for Rolling Bearings Based on Refined Composite Multi-Scale Amplitude-Aware Permutation Entropy. IEEE Access 2021, 9, 71979–71993. [Google Scholar] [CrossRef]
- Ma, J.; Zhuo, S.; Li, C.; Zhan, L.; Zhang, G. An Enhanced Intrinsic Time-Scale Decomposition Method Based on Adaptive Lévy Noise and Its Application in Bearing Fault Diagnosis. Symmetry 2021, 13, 617. [Google Scholar] [CrossRef]



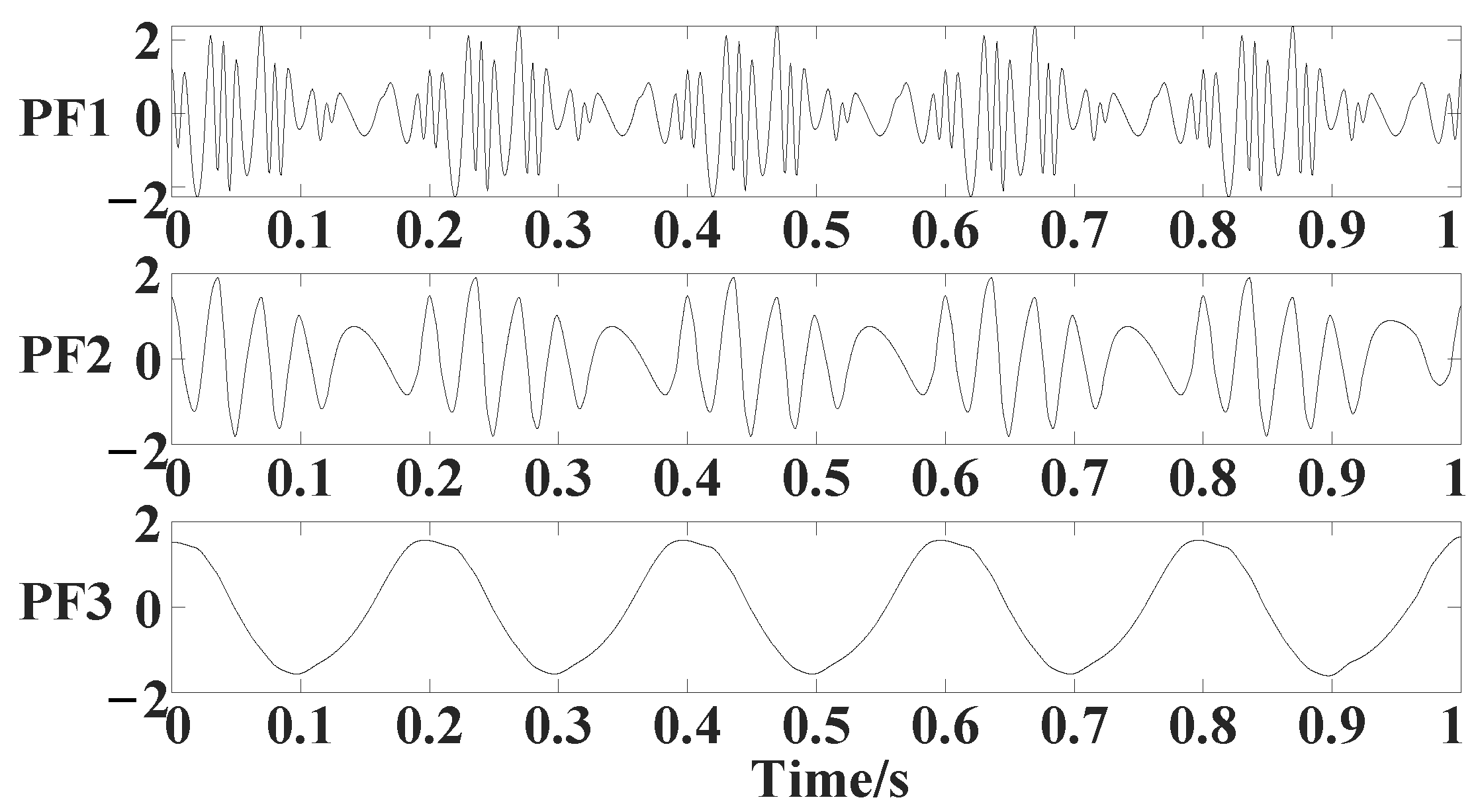

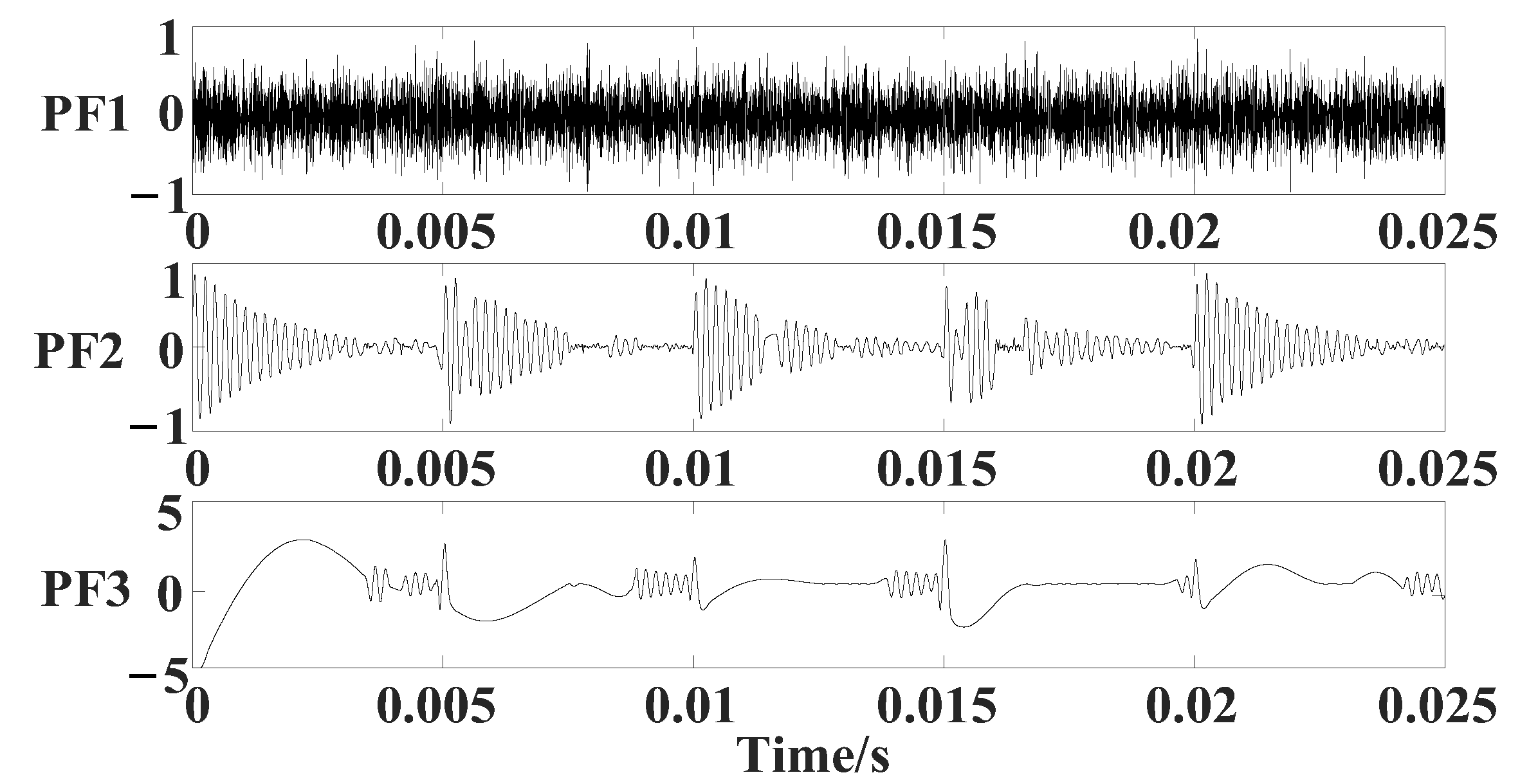
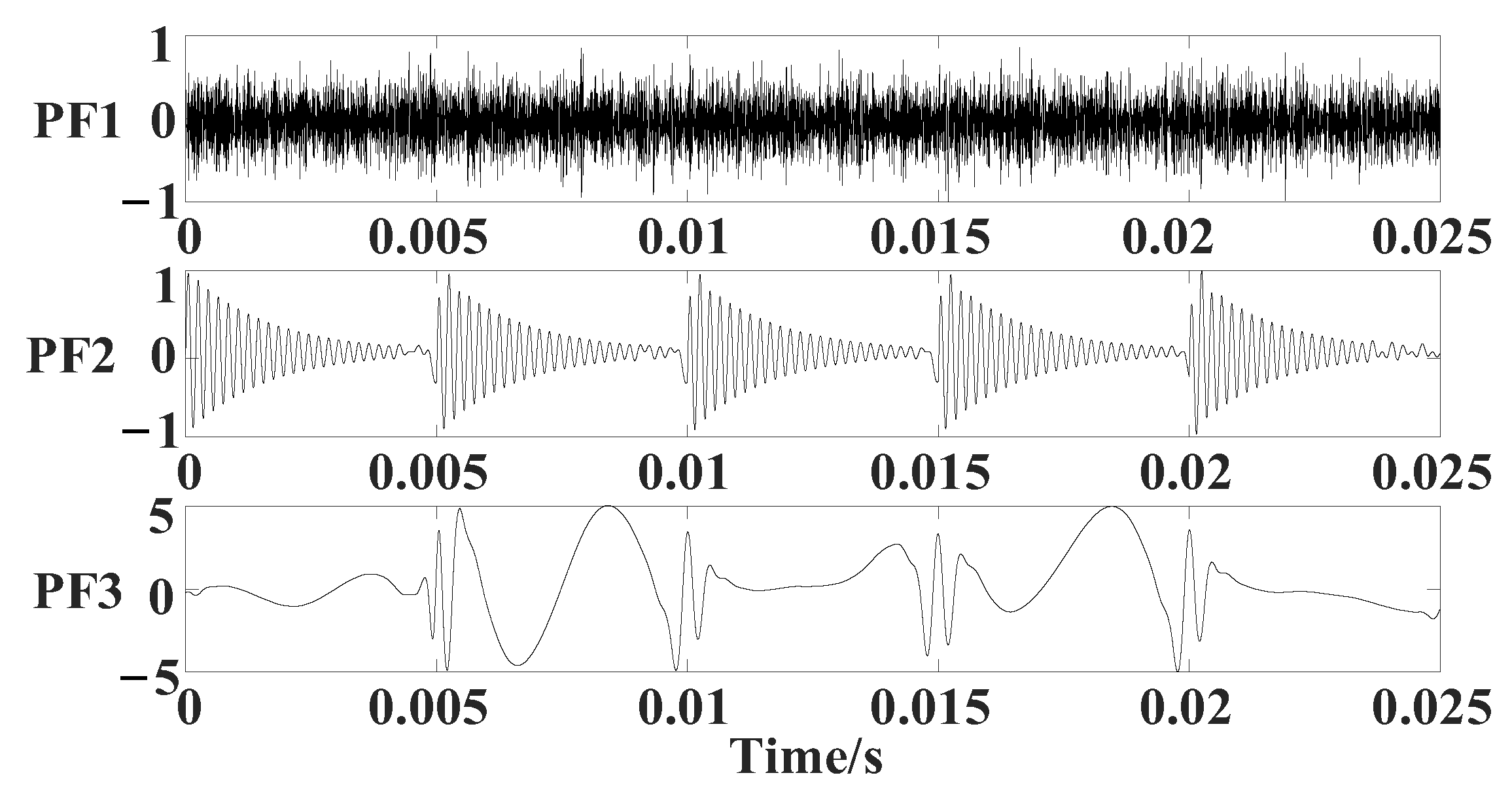
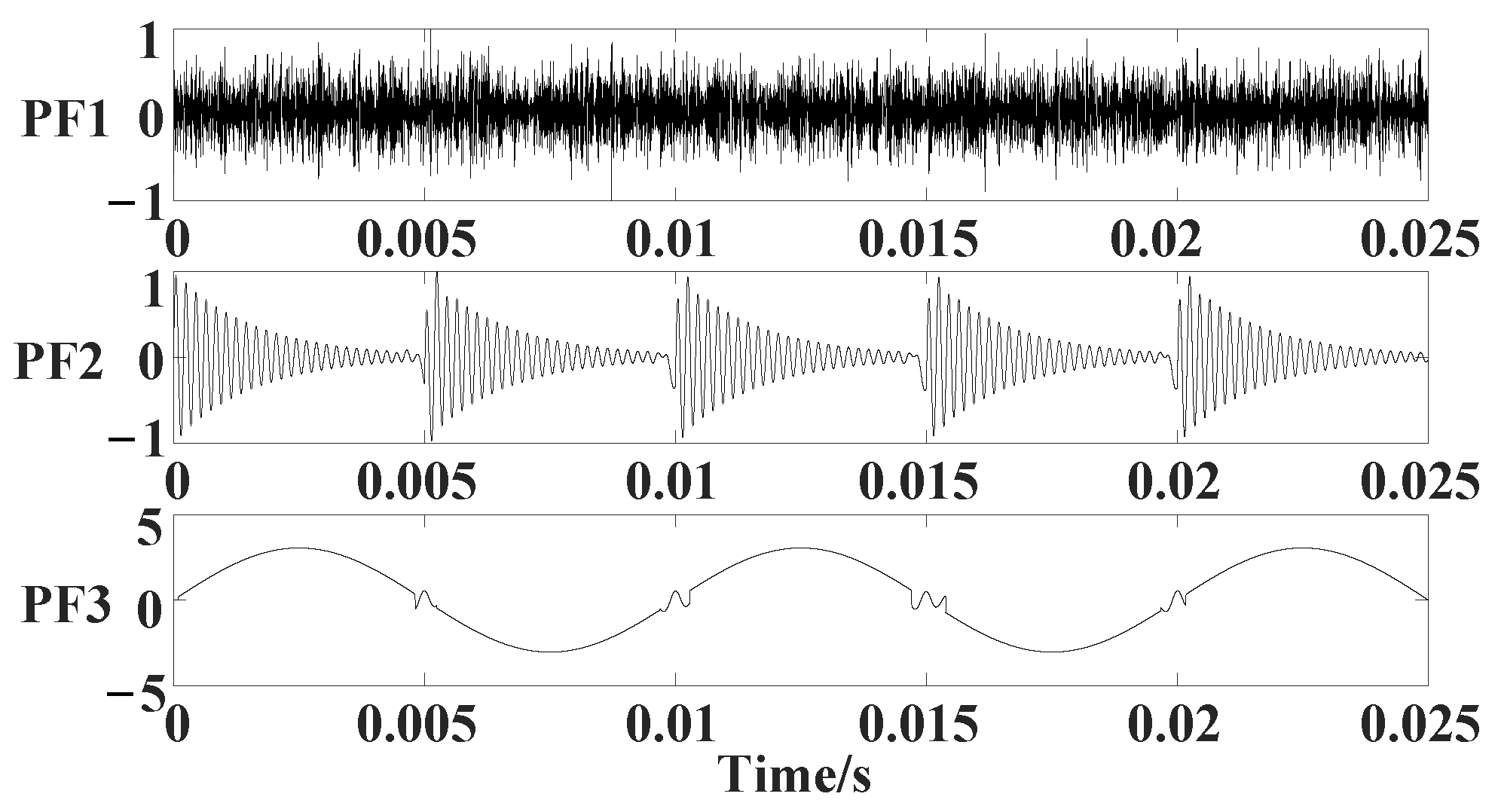
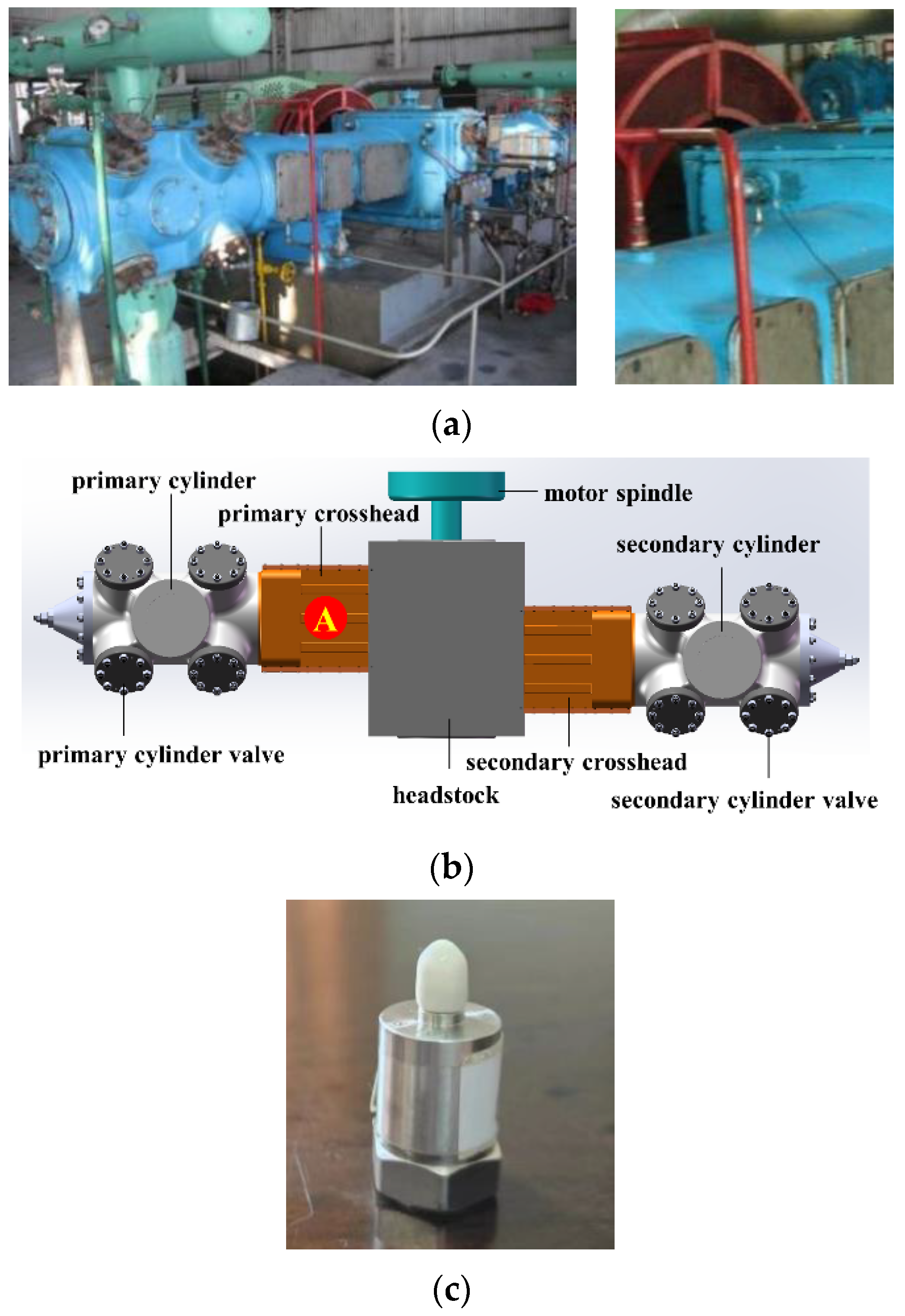

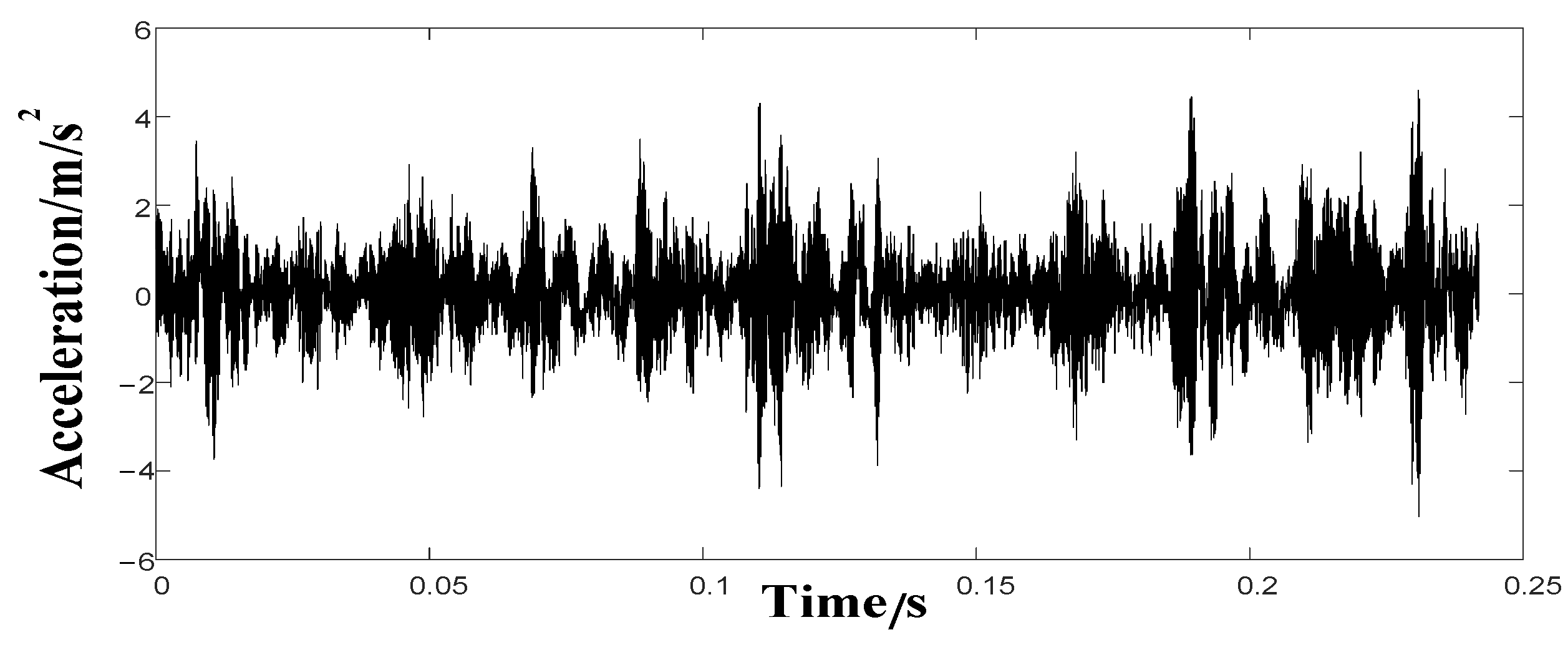
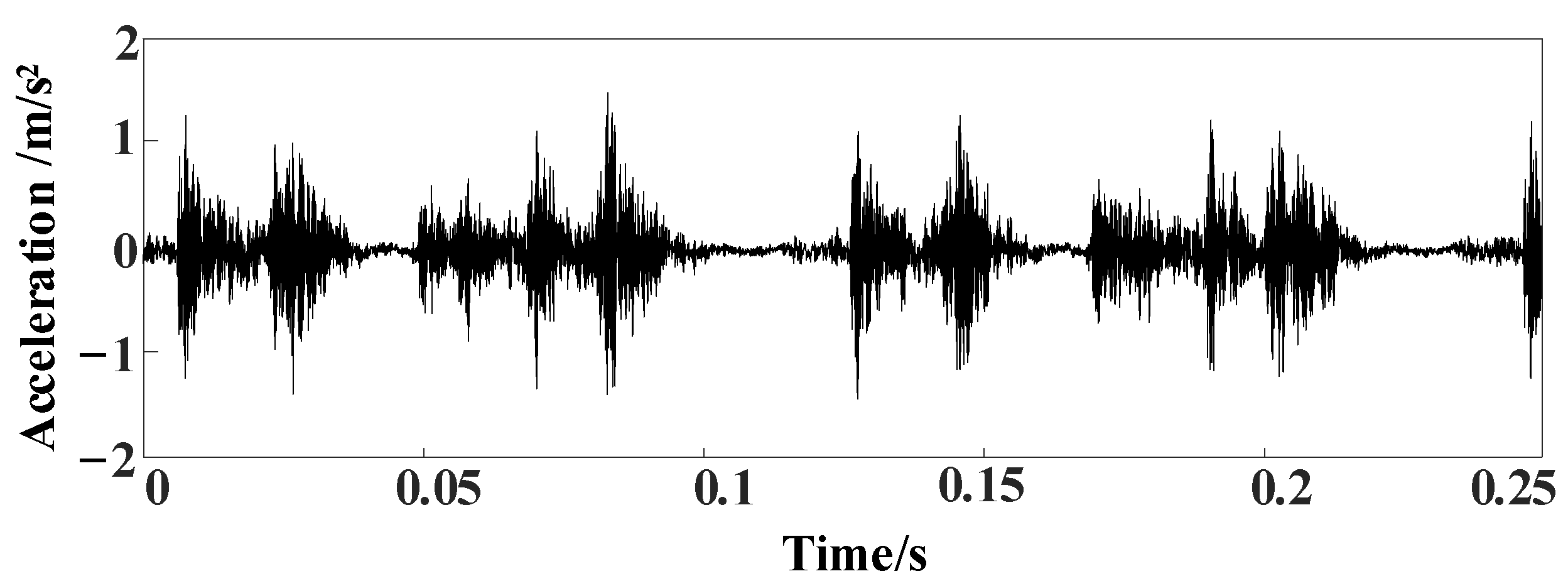
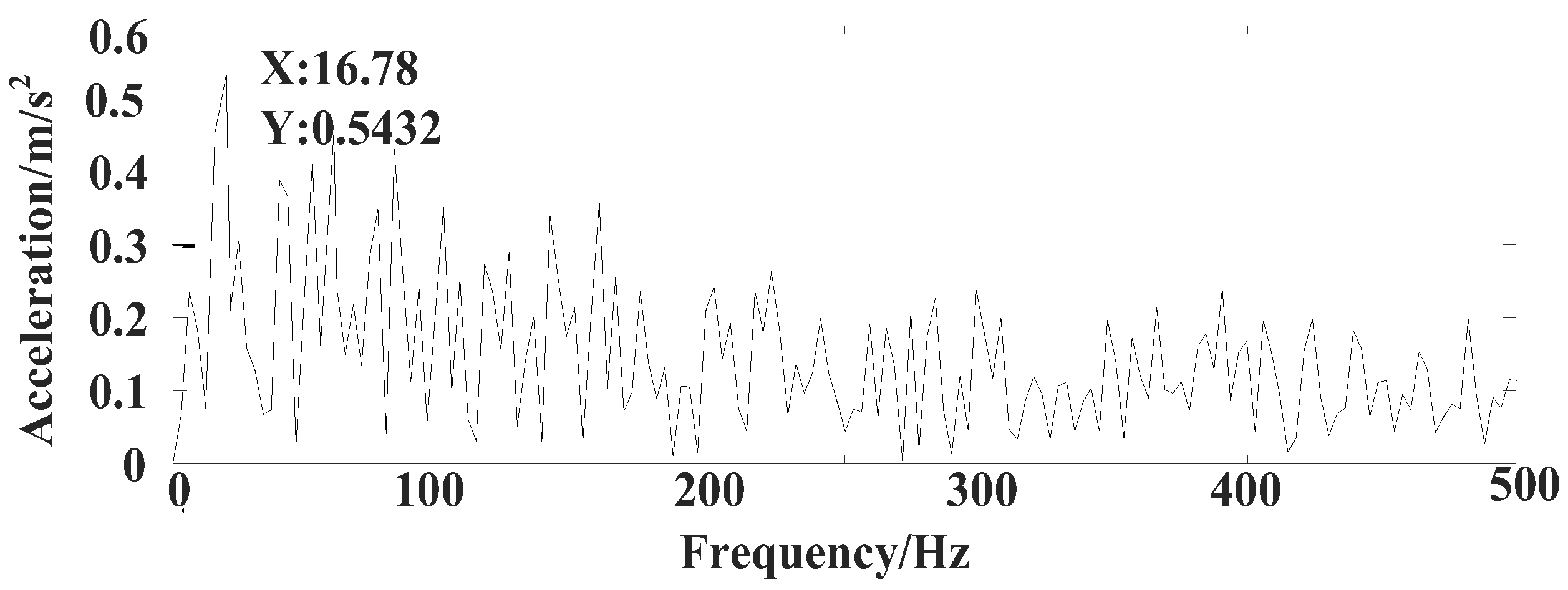
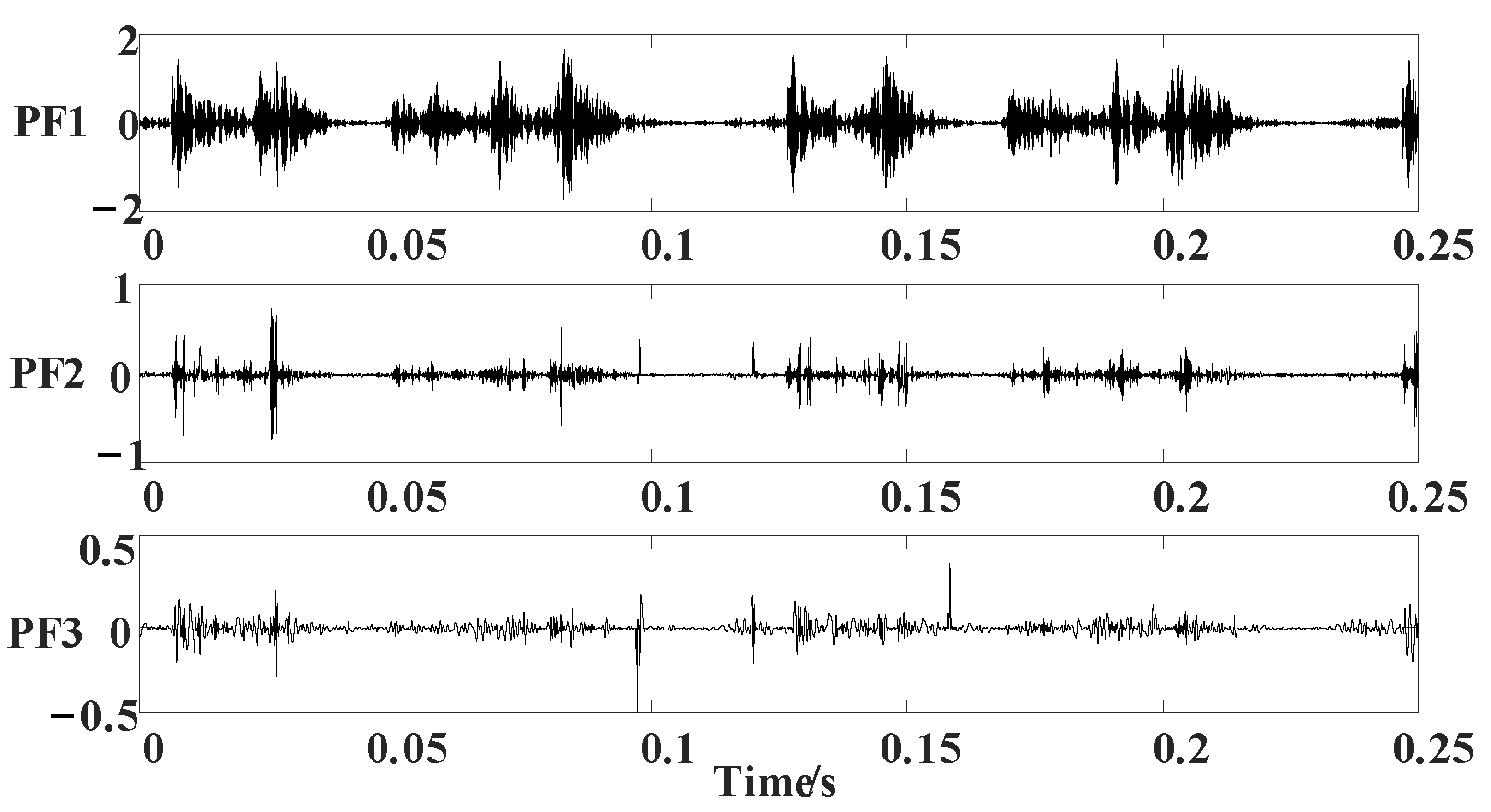


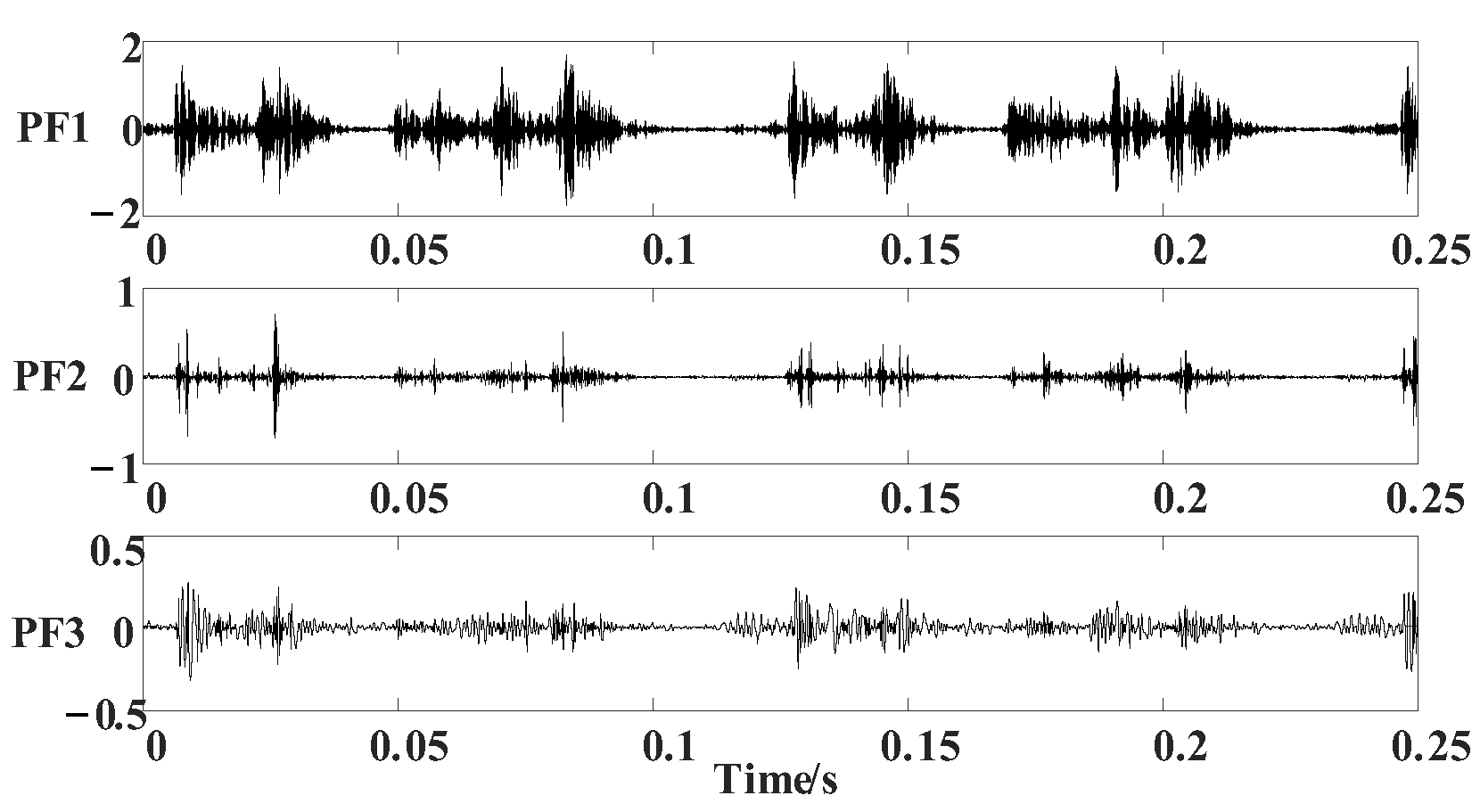

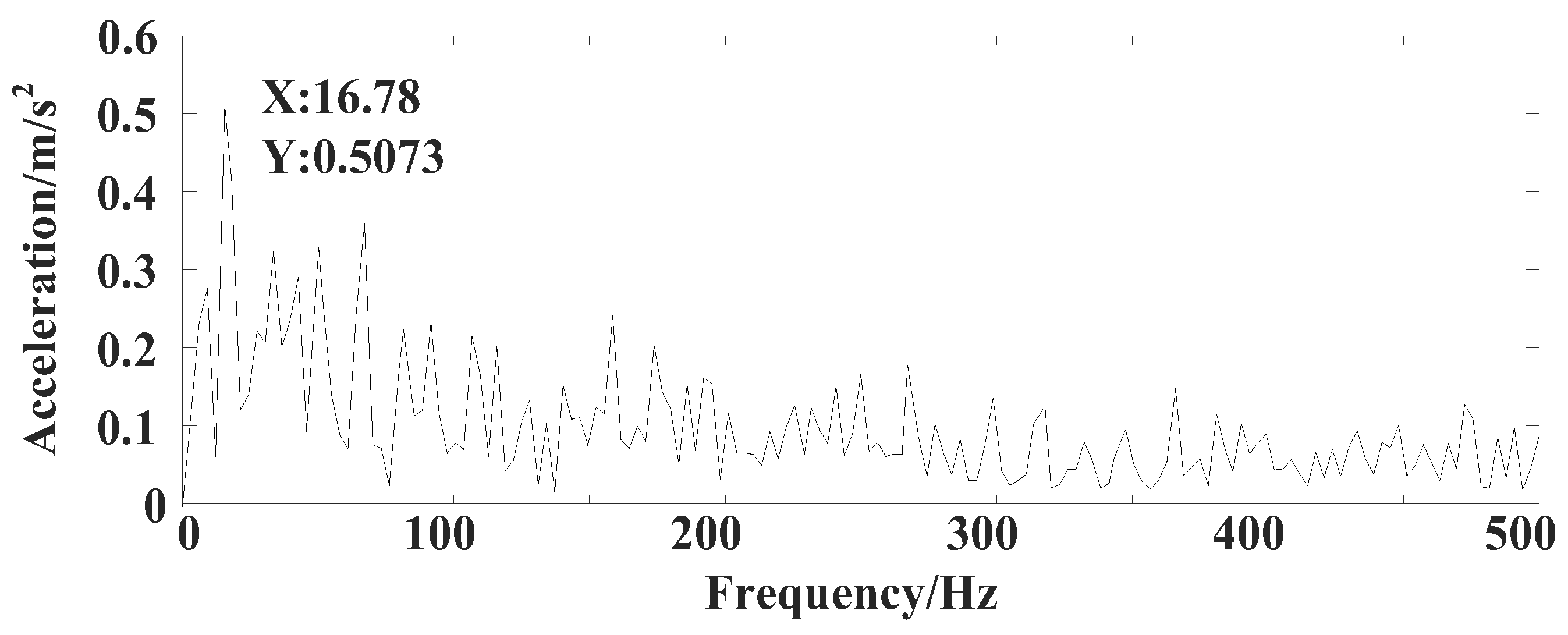
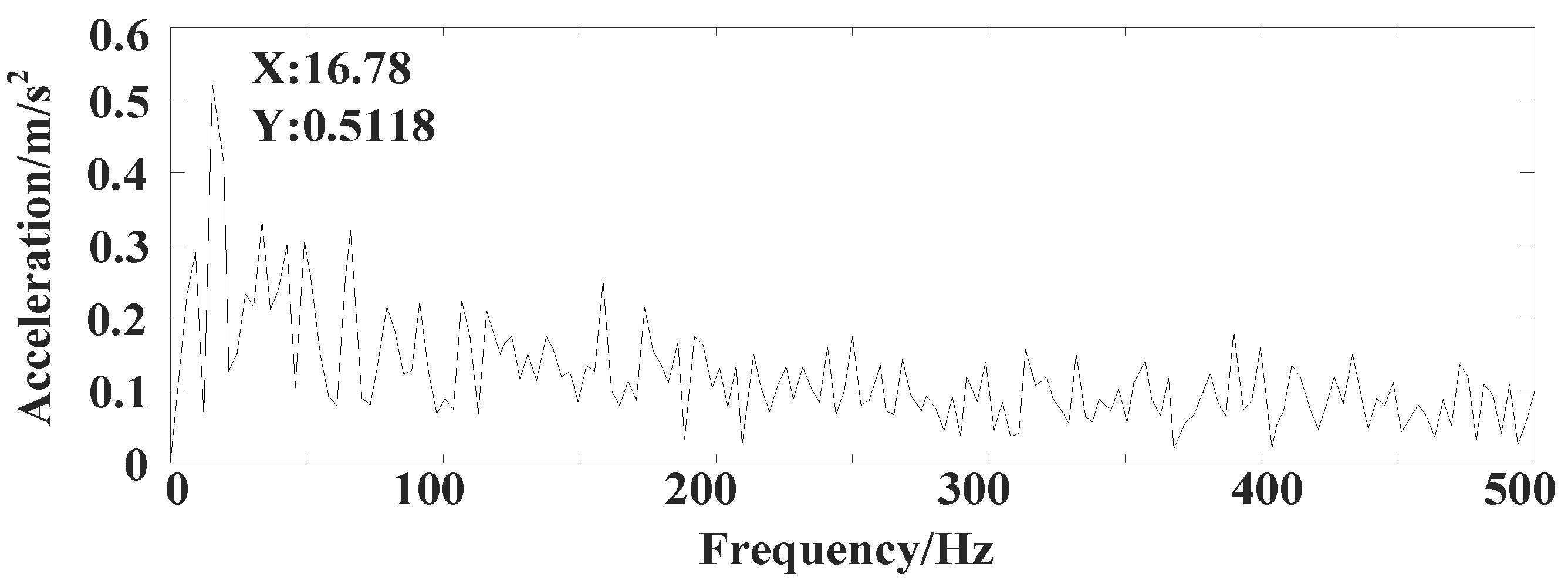
| Method | MSE | ||
|---|---|---|---|
| PF1 | PF2 | PF3 | |
| CSILMD | 0.0266 | 0.0322 | 0.0291 |
| MPCHILMD | 0.0281 | 0.0185 | 0.0355 |
| Method | PF2 | PF3 | Time (s) | ||
|---|---|---|---|---|---|
| MSE | Iterations | MSE | Iterations | ||
| LMD | 65.482 | 12 | 98.994 | 14 | 0.871 |
| CSI LMD | 25.281 | 9 | 14.584 | 8 | 0.701 |
| MPCHI LMD | 16.203 | 8 | 20.420 | 7 | 0.677 |
| DIMIR LMD | 7.130 | 5 | 6.051 | 5 | 0.733 |
| Parameter Type | Parameter Value |
|---|---|
| Shaft power (kW) | 500 |
| Air displacement (m3/min) | 70 |
| Primary exhaust pressure (MPa) | 0.2746~0.2942 |
| Secondary exhaust pressure (MPa) | 1.2749 |
| Piston stroke (mm) | 240 |
| Crank speed (rpm) | 496 |
| Parameter Type | Parameter Value |
|---|---|
| Sensitivity (mV/ms−2) | 10.04 |
| Maximum lateral sensitivity ratio (%) | <5 |
| Maximum allowable acceleration (ms−2) | 5×102 |
| Electrical property | + |
| Operating temperature (℃) | −40~120 |
| Working current (mA) | 2~10 |
| Index Value | Method | ||||
|---|---|---|---|---|---|
| Original | LMD | CSI LMD | MPCHI LMD | DIMIRLMD | |
| Peak Value | 0.5432 | 0.5121 | 0.5073 | 0.5118 | 0.5336 |
| RMS Value | 0.1521 | 0.0824 | 0.0728 | 0.0695 | 0.0652 |
| Peak Index | 3.5713 | 6.2148 | 6.9684 | 7.3640 | 8.1840 |
| Method | Iteration | IO | |
|---|---|---|---|
| PF1 PF2 PF3 | PF1 PF2 PF3 | ||
| LMD | 7.121 6.487 5.846 ±1.311 ±1.552 ±1.648 | 0.315 0.346 0.415 ±0.052 ±0.081 ±0.074 | 0.811 ±0.098 |
| CSI LMD | 5.943 10.434 9.567 ±1.225 ±1.965 ±1.841 | 0.253 0.537 0.695 ±0.053 ±0.086 ±0.093 | 0.874 ±0.086 |
| MPCHI LMD | 5.454 4.454 5.524 ±0.891 ±1.078 ±1.447 | 0.185 0.243 0.286 ±0.049 ±0.054 ±0.065 | 0.887 ±0.072 |
| DIMIR LMD | 4.665 3.823 3.735 ±0.628 ±0.752 ±0.848 | 0.177 0.232 0.273 ±0.046 ±0.051 ±0.058 | 0.905 ±0.048 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Li, X.; Liu, Z.; Wen, H.; He, J. A Double Interpolation and Mutation Interval Reconstruction LMD and Its Application in Fault Diagnosis of Reciprocating Compressor. Appl. Sci. 2023, 13, 7543. https://doi.org/10.3390/app13137543
Zhao H, Li X, Liu Z, Wen H, He J. A Double Interpolation and Mutation Interval Reconstruction LMD and Its Application in Fault Diagnosis of Reciprocating Compressor. Applied Sciences. 2023; 13(13):7543. https://doi.org/10.3390/app13137543
Chicago/Turabian StyleZhao, Haiyang, Xue Li, Zujian Liu, Haodong Wen, and Jinyi He. 2023. "A Double Interpolation and Mutation Interval Reconstruction LMD and Its Application in Fault Diagnosis of Reciprocating Compressor" Applied Sciences 13, no. 13: 7543. https://doi.org/10.3390/app13137543
APA StyleZhao, H., Li, X., Liu, Z., Wen, H., & He, J. (2023). A Double Interpolation and Mutation Interval Reconstruction LMD and Its Application in Fault Diagnosis of Reciprocating Compressor. Applied Sciences, 13(13), 7543. https://doi.org/10.3390/app13137543






