Multiple-Criteria Decision-Making for Medical Rescue Operations during Mass Casualty Incidents

Abstract

Mass casualty incident (MCI) is an unpredictable situation where a great number of people have been injured after an accident or sudden disease. Survival of the injured in the MCI depends on the efficiency of the directed emergency system (DES). The organization and management of medical assistance is of paramount importance. The shortest possible time to provide medical services to injured persons is crucial. The medical service in the case of the MCI primarily requires decisions on the priority of the order of treatment of the injured, the choice of medical transport and the location of specialized emergency treatment. As part of this paper, the effectiveness of the DES has been analyzed, and criteria used to improve rescue operations have been formulated. A formalized mathematical description of the medical rescue operations in MCIs has been proposed, and the optimization problem as the mixed integer linear programming (MILP) task was formulated. Optimization of an example case of rescue operations in MCIs has been presented. A computer simulator for optimal decision-making in medical rescue operations (CSMRO) has been developed for this purpose. The CSMRO implements various multi-criteria optimization methods to solve the formulated problem of rescue operations optimization. The results of computations made with the developed CSMRO simulator significantly shorten the time of decision-making in mass casualty incident handling.

1. Introduction

A mass casualty incident (MCI) is the situation where a great number of people have been injured after an accident or sudden disease. Most often MCIs are traffic accidents, construction building accidents, fires, floods, etc. or epidemics of infectious diseases or mass poisoning [1] and chemical incidents [2]. The reason for the MCI can also be certain people’s behavior, e.g., a panic during mass events or terrorist attacks [3]. The main feature of MCIs is the randomness of their location and time.

Initially, consideration was given to how to prevent mass casualty incidents, but due to the randomness of the time and place of their occurrence, attention was focused on the response phase, i.e., on improving rescue operations. In mass casualty incidents, the organization and management of medical assistance are of paramount importance, and rescue procedures differ from those applicable to ordinary or multiple incidents.

The Provincial Emergency System (PES), in whose area of responsibility the incident occurred due to limited resources, is usually unable to meet the service needs of injured persons. They cannot be provided with medical care to the desired extent as in the case of single or multiple incidents. Once the MCI has occurred, forces and resources are separated from the PES to immediately deal with the consequences, forming a Directed Emergency System (DES). If the number and/or quality of resources of the PES specific to the incident prove insufficient, then it is necessary to support with forces and resources from another, usually neighboring province. Survival and avoiding extensive disability of the injured in the MCI depend on the efficiency and quality of the DES.

In emergency medicine, many approaches have been developed over the years to organize rescue operations to deal with the consequences of MCIs [4]. One of the most widely used is the Anglo-American model, which is also used in Poland. Its characteristic feature is the approach to medical handling of persons injured in the MCI and minimizing the time needed to initiate emergency treatment of victims in Hospital Emergency Departments (EDs).

At the scene of an incident, the initial segregation of victims (triage) is carried out upon arrival of the emergency services. Many triage systems for rescue operations have been developed [5]. In Poland, the START (simple triage and rapid treatment—meaning “simple segregation and rapid treatment”) segregation system is used. All pre-segregation systems have a common denominator—as a result of their implementation, victims of the MCI are assigned to one of the available clinical-transport priority groups, marked with a specific color.

Prehospital emergency [6] measures are based on the principle of the so-called survival chain. According to this standard, emergency medical activities should be introduced after approximately 8–10 min. The injured should be transported to the Emergency Department (ED) no later than 30 min after the incident is reported. In emergency medicine, the golden hour rule applies, after which the probability of survival of the injured persons is usually negligible. When selecting an ED for a given casualty, consideration should be given to those that the selected ED has the necessary medical resources at the time of delivery.

The assessment of the health status of victims should be repeated periodically as a part of the so-called secondary medical segregation. It is performed by the most competent personnel in emergency medicine (paramedics and medics). The examination is then carried out in more detail based on a selected injury severity scale. In Poland, the Triage Revised Trauma Score (TRTS) system is used in medical segregation, whereby the severity of Trauma of the victim is determined by assessing the state of consciousness, systolic blood pressure and respiratory rate. In current practice, the recording of the injured person’s condition at the scene is done using paper segregation sheets [7].

In summary, in practice to date in the mass casualty incident, three basic issues of medical rescue management stand out:

• Medical segregation (primary and secondary) of the injured [8,9].
• Selection of Hospital Emergency Departments where emergency treatment should be implemented and preparation for specialist treatment in the hospital setting, enabling the most effective medical handling of the incident [10].
• Allocation of medical transport means (Medical Rescue Teams—MRTs) transport those injured in the incident to their assigned ED. A distinction is made between basic and specialized modes of transport. The latter also includes HEMS (Helicopter Emergency Medical Service) air units.

The current method of dispatching forces and resources to a medical rescue undertaking in an MCI is inefficient. In this study, a mathematical description of a mass casualty incident is proposed. The proposed simulator was developed in close cooperation with Polish emergency services and was tested during field trials, and the feedback from these services was very good.

The remainder of this paper is organized as follows: In Section 2, related works are described. In Section 3, a mathematical model of the medical operations in mass casualty incidents is presented, and the effectiveness of the directed emergency system (DES) is analyzed. In Section 4, an optimization problem of medical rescue operations in the MCI is formulated as a MILP (mixed integer linear programming) problem [11,12]. In Section 5, a developed computer simulator for optimal decision-making in medical rescue operations (CSMRO) is presented. The results and discussion on the obtained results of computations processed by the CSMRO are shown in Section 6. In Section 7, final conclusions are drawn.

2. Literature Review

The work on improving the organization and management of emergency medical services in the case of mass incidents is mainly concerned with the problem of optimal dislocation of emergency system units to handle mass incidents, as well as research related to the quality of prioritization of the handling of casualties in a mass casualty incident.

Cotta, in his article [13], makes a comparison of metaheuristic methods, especially hyperheuristic methods (a combination of basic heuristic methods) and a pilot method for the problem of efficient prioritization of medical service. Statistical tests are conducted on the two most urgent medical service priority groups to which casualties are allocated based on the START system. The test variables are the number of operating rooms, the number of injured persons and the probability of survival of these persons based on a Weibull distribution, which is often used when the probability of survival varies over time. The test results represent the percentages of all injured persons who received adequate medical attention. According to the author, the four-class START system used in practice needs to be improved, and the results of the study confirm the validity of the hyper-heuristic method in conjunction with the pilot method. Guttinger et al., in their article [14], formulate the problem of optimizing the allocation of emergency medical services forces and resources in mass casualty incident and then compare three methods for solving this problem. They use the D’Hondt method, the greedy algorithm and the simulated annealing algorithm. Parameters such as the individual’s waiting times at the scene and the waiting times in the ED for rescue treatment are characteristic of this model. In addition, the injured persons in the worst condition are considered first. In addition, the authors of the model develop functions mapping the severity of selected injury types to the passage of time.

In [15], a model is developed to optimize the allocation of injured people to hospitals, taking into account the optimal number of patients that can be efficiently served within a given time limit. The model is implemented within a system called ISCRAM (Information Systems for Crisis Response and Management). In [4], authors develop a discrete-event simulation policy model by evaluating realistic scenarios. The model performs scheduling and outcomes at operative and online levels. Based on a variety of such situations, the authors derive general policy implications at both the macro (e.g., strategic rescue policy) and micro (e.g., operative and online scheduling strategies at the emergency site) levels. Mills et al., in their paper [16], address the problem of prioritizing the medical handling of casualties in a mass casualty incident. The aim is to investigate the impact of not taking into account the current state of availability of forces and resources of the local emergency medical system in the process of determining medical service priority groups. The authors develop a model based on a modification of the START system, which takes into account only two classes of clinical-transport priority: immediate and delayed. This is because they find that, in practice, these two groups, in particular, are crucial in analyzing the problem of medical transport and service. The model takes into account the time-varying probability of survival of casualties depending on the priority group to which they belong. The availability of transport means at a given time, and the total number of casualties are also taken into account. In the model, the arrival times of the means of transport at the scene of the incident are determined using Poisson distribution. The survival times of people due to their belonging to one of the two priority groups are described by a logistic function.

In [17], Wilson et al. develop a model based on the Fixed Job Scheduling Problem (FJSP) algorithm, a modified job scheduling problem—a general sequencing problem with parallel machines. The model defines jobs as affected persons, operations as tasks and machines as emergency response units. Five objective functions are considered, such as (1) the expected value of the number of deaths among injured persons, (2) the total projected time required to transport individuals to hospitals, (3) the quality of medical service offered by the assigned hospital to individuals, (4) the total time between a specific action taken by rescuers and (5) the current total time taken by rescuers to perform actions. The model takes into account factors such as the projected average time of the assigned medical task and the change in the probability of survival of casualties with time. A characteristic feature of the model is the stochastic approach to the change in the probability of survival of casualties in the danger zone at the scene before the time of the start of medical rescue operations. Approximate methods—the Variable Neighborhood Search (VNS) metaheuristics and its deterministic variant Variable Neighborhood Descent (VND)—are used to solve the problem. A resource-constrained triage model called SAVE (Severity-Adjusted Victim Evacuation) is proposed by Dean and Nair in [11]. The model takes into account the state of the injured in the process of assigning transport means and hospital places after an MCI. The objective of the optimization problem considered is to maximize the number of people still alive while not overwhelming any single hospital. This problem is formulated as a mixed-integer program. Kilic et al. [18] present a numerical solution which uses the deterministic optimal control theory for determination by Pontryagin’s minimum principle of the optimal service rate according to the priority classes. This queueing system aims to minimize the expected value of the square differences between the number of servers and the number of patients and the cost of serving these patients over a determined time period.

The optimization of the allocation of forces and resources (rescue teams) to earthquake hazard zones is presented in [19]. The objective function is to maximize the number of living persons. The affected persons are assigned to two categories of people. The first is people who urgently need medical assistance, and the second is people whose assistance can be deferred. The danger zones are divided into three types, i.e., the most endangered zone, the vulnerable zone and the less endangered zone. Based on the danger zones, the expected probability of survival is assumed. The utility principle of achieving the maximum number of survivors is applied. Integer non-linear programming is used to solve the optimization problem. In [20], Markov Chain is used for establishing a function from treated time to probability of death. A flexible job shop scheduling model and a genetic algorithm are designed. In [21], a multi-criteria optimization problem is solved in which three objective functions are defined, expressed as: (1) effectiveness—the rate of survival or well-being of those affected by a mass casualty event, (2) efficiency—expressed in terms of the rate of human suffering caused by the delay of humanitarian assistance and (3) the efficiency of providing humanitarian assistance. The optimization problem is solved by the weighted sum method of the criteria.

In [22], the integer (mixed) linear programming is proposed for optimal dislocation and redislocation of ambulances. Lagrangian Dual Decomposition (LDD) is used to partition the set of ambulance allocations.

Debacker et al., in [23], design the SIMEDIS (Simulation for the Assessment and Optimization of Medical Disaster Management) simulation model, which consists of 3 interacting components: the victim creation model, the victim monitoring model and the medical response model. SIMEDIS, characterized by the interaction between the two models, is provided by a time trigger or medical intervention. At each service point, triage is carried out with a decision on the disposition of casualties for treatment based on the priority code assigned to them and the availability of resources at the service point. In [24], the authors develop a model for the optimal allocation of hospital places due to the predicted occupancy time of each place and the weights of the distinguished priority classes of medical service. Dynamic programming is used to extract data on hospital arrivals of casualties and data on their treatment.

Mills in [25] uses the survival look ahead decision support rule that can handle survival probability functions and an arbitrary number of patient classifications, which prioritizes patients who will deteriorate the most over a predefined period of time. Repoussis [26] presents a response model for the combined ambulance dispatching, assignment of casualties to hospitals and treatment ordering problem. Heuristic solution methods based on a mixed integer programming (MIP) formulation are proposed. The objectives are to minimize the overall response time and the total flow time required to treat all patients, including a hierarchical treatment. Sung et al. [27] propose a solution to the problem of optimal transport by available medical means of people injured in a mass casualty incident to designated hospitals. The authors used the set partitioning problem and the linear programming method, the column generation algorithm, within the developed model. Given solutions derived by the algorithm outperform fixed-priority resource allocations. In [28], Wilson et al. extend a multi-objective combinatorial optimization model for the MCI response to use in real-time, with continuous communication between the optimization model and the problem environment. The authors define two objective functions, the first concerns the prediction of the probability of death of the injured persons when they are likely to reach hospitals, and the second concerns the degree of alleviation of suffering of the injured persons. A lexicographic optimization method is proposed prioritizing the relevance of the death criterion over suffering. In [29], Kamali et al. propose a mathematical model in which they optimize the process of assigning treatment and transport priorities to casualties at the scene of a mass casualty incident. The aim here is to maximize the expected value of the number of survivors. The model considers (1) the number of injured persons in a specific medical service demand group, (2) the handling times of injured persons and (3) the number of available emergency medical teams. The integer linear programming approach is used. This mathematical model includes prioritization of casualties, categorized by criticality and care requirements, which must be transported to hospitals in the region using a fleet of available ambulances. In [30], an approach of simulation combined with optimization of rescue operations in MCIs is proposed. In terms of simulation, the process of reallocation of emergency services is automated, and in terms of optimization, two objective functions are used: (1) the expected value of the total rescue time and (2) the expected value of the total number of deaths among the victims. The assumed expected values are minimized. Three optimization methods are used: (1) the gradient method (local optimization method), (2) the global optimization method - the OptQuest meta-heuristic and (3) the response surface methodology (RSM). Authors of [31] formulated the decision problem as a decentralized-partially observable Markov decision process (dec-POMDP) model with multi-agent reinforcement learning (MARL) using as a solution technique. They proposed a MARL algorithm augmented by pretraining, especially using behavioral cloning (BC) as a means to pre-train a neural network.

The hybrid method of Malmquist and DEA is used in [32]. For the other assessment, a framework based on muli-criteria decision making (MCDM) is provided that integrates spherical fuzzy Analytical Hierarchical Process (SF-AHP) and grey Complex Proportional Assessment (G-COPRAS), in which spherical fuzzy sets and grey numbers are used to express the ambiguous linguistic evaluation statements of experts as presented in [33].

In [34], Baghaian et al. develop a scenario-based stochastic optimization model to choose optimal policies for the integrated deployment of local urban relief teams in the MCIs. Factors such as the deployment of local relief teams in an urban area with several affected sites, allocation of casualties to treatment centers and assignment of medical teams to casualty treatment centers and triage groups are simultaneously determined. Olivia et al., in [35], integrate the Gravitational Search-based Back Propagation Neural Network prediction model along with a qSOFA medical score to generate an accurate prediction of casualty’s health condition deteriorated and thus enable the classification of casualties into risk profiles. DuBois and Albert [36] consider optimally dislocated ambulances to prioritize patients during MCIs as a Markov decision process model with two classes of ambulances. In [37], Chang et al. designed casualty collection point (CCP) locations and the efficient allocation of limited emergency medical service (EMS) resources to transport casualties quickly to appropriate hospitals and increase the survival rate of casualties. A hybridsimulation–optimization approach to optimize the CCP location and the EMS resource allocation problem over mixed binary and integer feasible domains for the minimization of the expected complete delivery time of all casualties from the disaster region to hospitals is presented. A novel two-stage sequential algorithm, namely a combination of optimal computing budget allocation-based rapid-screening algorithm and an adaptive particle global and hyper box local search (ORSA-APGHLS), is developed.

Chen et al. presented in [38], combining particle swarm optimization and the genetic algorithm in solving distributed scheduling problems and applied them to problems such as multi-agent task planning.

After a literature review on the subject, the most important factors influencing the number of deaths and permanent disability of people injured in the MCI are:

• A number of casualties who will survive, in emergency medicine, i.e., the so-called “avoidable deaths” [11,13].
• Post-accident status of the injured is described by the following values [13,39]: respiratory rate, pulse, state of consciousness and systolic arterial pressure. The post-accident condition can be supplemented [40] by introducing age, sex and the characteristics of capillary recurrence.
• The expected value of survival of the injured in the MCI depends on the post-accident status of the injured person [13,17,41]. In [16], the author conducted research on the change in the probability of survival of the injured over time due to the group of medical segregation to which these persons were assigned. In [16], the author described the survival time of people due to belonging to a segregating group with an appropriate logistic function. In [11], the author took into account the expected value of the casualty’s survival due to the post-accident condition.
• Availability and quality of transport for injured persons are characterized respectively by the total number and types of means of transport [11]. An important factor is the information on the availability of means of transport at a given moment [12,16].
• Availability of hospital emergency department (HED) resources and the effectiveness of treatment of individual post-traumatic conditions. In [42,43], an analysis was made of the appointment of specific personnel to treat a specific medical case—the post-accident state of the injured. In [13], the number of operating rooms was taken into account when determining the target HED. In [12], the availability of vacant places of treatment centers, both existing and created temporarily after the MCI, was analyzed.
• The time elapses from the occurrence of the MCI to the moment of medical rescue operations at the scene. In [12], an analysis of the problem of minimizing the total transport time and the waiting of injured persons for medical service during the search and rescue operation was carried out.
• The time that elapses from the moment of the event to the commencement of emergency treatment in the HED. The presented literature analysis shows that the effectiveness of rescue actions in a mass incident is largely determined by the time after which emergency treatment is undertaken [12] in the HED. The quality of the access routes has a great influence on the time of reaching the means of emergency medical transport both to the place of the accident and to the HED. In [44], among others, the number and distribution of event sites and hospitals, as well as the degree of disruption to individual sections of the route, were considered.

Guided by the considerations of saving human life and health, the most important criteria used in improving the effectiveness of emergency medical services should be:

• the expected value of the death and
• the expected value of the disability.

In order to determine the most reliable and comprehensive assessment, economic aspects should also be taken into account:

• the expected value of the cost of a rescue operation and
• the expected value of the cost of long-term treatment and rehabilitation.

The problems of object dislocation, unit allocation and resource allocation are among the logistical issues where the linear programming approach and transport issues are usually used.

The activities of emergency services in Poland are not supported by decision support systems, biocybernetics tools, etc. Artificial intelligence is practically unused, and information and decision-making processes are carried out directly with the use of voice communication (telephone and radio). The currently used method of disposing of forces and resources to implement a medical rescue undertaking in the MCI is not effective, and even less is not optimal in any sense. The proposed mathematical description of a mass casualty incident and the way it is solved is original, developed on the basis of many years of experience with medical rescue teams in Poland. The proposed simulator was developed in close cooperation with Polish Emergency Services and was tested during field trials, and the feedback from these services was very good. Therefore, it is planned to implement this simulator in mass casualty incident management teams in Poland.

3. Mathematical Description of the Medical Rescue Operations after Mass Casualty Incident

3.1. Characteristics of the Directed Emergency System

In order to formalize the problem of optimizing emergency medical services in mass casualty incidents, the following quantities describing the RERS are introduced and explained below.

A set of HEDs located in the area of the DES is defined as

$$S=\{\hspace{0.17em}s:s=\overline{1,S}\hspace{0.17em}\},$$

(1)

where $s$ is the number of a given HED, $S$ is the total number of HEDs in the region.

The current possibilities of providing medical emergency services by the given HED are characterized by the following triple:

$$h_s=<h_{s,1},h_{s,2},h_{s,3}>\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}s\in S,$$

(2)

where: $h_{s,1}$ is the location of the $s$-th HED, $h_{s,2}$ is the number of injured people that can be handled by the $s$-th HED, where $h_{s,2}\ge 0$, $h_{s,3}$ is a set of types of post-accident injuries handled by the $s$-th HED:

$$h_{s,3}=\left\{u:d_s(u)=1,\hspace{0.17em}u\in U\right\},$$

(3)

wherein,

$$d_s(u)=\left\{\begin{array}{l}1,\hspace{0.17em}\hspace{0.33em}\hspace{0.33em}\mathrm{if} \mathrm{the}\hspace{0.17em}s\text{-}\mathrm{th}\hspace{0.17em}\mathrm{HED}\hspace{0.17em}\mathrm{accepts} \mathrm{an} \mathrm{injured} \mathrm{with} \mathrm{an} \mathrm{injury}\hspace{0.17em}u\in U,\\ 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{otherwise}.\end{array}\right.$$

(4)

The forces and means of emergency medical transport are characterized by a set of medical rescue transport bases (MRTB) in a given RERS:

$$B=\left\{b:b=\overline{1,B}\right\},$$

(5)

where $b$ is the number of a given MRTB and $B$ is the total number of MRTBs in a given RERS.

A set of different modes of medical rescue transport (MRT) is defined as:

$$R=\left\{r:r=\overline{1,R}\right\},$$

(6)

where $R$ is the total number of different modes of MRT.

The current possibilities of providing medical emergency services by the MRTB $b\in B$ are characterized by the following couple:

$$a_b=<a_{b,1},a_{b,2}>,$$

(7)

where $a_{b,1}$ is the location of the $b$-th MRTB, and $a_{b,2}$ is the characteristics of the modes of MRT of the $b$-th MRTB:

$$a_{b,2}=<a_{b,2,1},\dots ,a_{b,2,r},\dots ,a_{b,2,R}>,$$

(8)

where $a_{b,2,r}$ is the number of the $r$-th type of MRT modes stationed in the $b$-th MRTB where $a_{b,2,r}\ge 0$.

3.2. Characteristics of the Mass Casualty Incident

A mass casualty incident is described by the following triple:

$$z=<z_1,z_2,z_3>,$$

(9)

where $z_1$ is the location of the incident; $z_2=t^z$ is the time elapsed from the moment of the incident to the moment of notifying the DES about the incident; $z_3$ is characteristic of the health condition of people injured in the incident:

$$z_3=(z_{3,1},\dots ,z_{3,l},\dots ,z_{3,L}),$$

(10)

where $z_{3,l}$ is the condition of the $l$-th injured person, and $L$ is the total number of people injured in the incident.

3.3. Characteristics of the Health Condition of People Injured in a Mass Casualty Incident

Based on the analysis of literature [45,46] and interviews with experts, it was assumed that the condition of the $l$-th person injured in the MCI would be characterized by the following sextuple [47]:

$$z_{3,L}=c_l=〈c_{l,1},c_{l,2},c_{l,3},c_{l,4},c_{l,5},c_{l,6}〉,l\in L,$$

(11)

where $c_{l,1}$ is the severity of the traumatic state; $c_{l,2}$ is the degree of the state of consciousness, $c_{l,3}$ is the degree of basic life dysfunctions, $c_{l,4}$ is gender; $c_{l,5}$ is existence of pregnancy, $c_{l,6}$ is age and $L=\{l:l=\overline{1,L}\}$ is a set of people injured in a mass casualty incident.

3.3.1. Severity of the Traumatic State

The severity $c_{l,1}$ of the traumatic state is determined as follows. Define a set of different degrees of severity of the traumatic state:

$$N=\{\hspace{0.17em}n:n=\overline{1,N}\hspace{0.17em}\},$$

(12)

where $N$ is the number of different degrees of severity of the traumatic state of post-incident injuries. Define a set of types of injuries with the $n$-th degree of severity:

$$U_n=\{\hspace{0.17em}u: d_n(u)=1,\hspace{0.17em}u\in U\hspace{0.17em}\},n\in N,$$

(13)

where:

$$d_n(u)=\left\{\begin{array}{l}1, \mathrm{if} \mathrm{the} \mathrm{injury} u\in U \mathrm{is} \mathrm{of} \mathrm{the} n\text{-}\mathrm{th} \mathrm{degree} \mathrm{of} \mathrm{severity},\\ 0, \mathrm{otherwise}.\end{array}\right.$$

(14)

where $U$ is a set of distinguished types of post-incident injuries; $\underset{m,n\in N}{\forall }:m\ne n\Rightarrow U_m\cap U_n=\varnothing$; $\underset{n\in N}{\forall }:U_n\ne \varnothing$.

As a result of the incident, the injured person may be injured several times. Thus, the traumatic state of the $l$-th injured person is defined by the set:

$$U_l^{inc}=\{u:d^l(u)=1,\hspace{0.17em}\hspace{0.17em}u\in U\},$$

(15)

wherein

$$d^l(u)=\left\{\begin{array}{l}1, \mathrm{if} \mathrm{the} l\text{-}\mathrm{th} \mathrm{person} \mathrm{was} \mathrm{injured} \mathrm{with} \mathrm{a} \mathrm{given} \mathrm{injury},\\ 0, \mathrm{otherwise}.\end{array}\right.$$

(16)

The set of injuries of the $n$-th degree of severity from which the $l$-th injured suffered is defined as:

$$U_{l,n}^{inc}=U_n\cap U_l^{inc}\hspace{0.17em}\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}l\in L,\hspace{0.17em}\hspace{0.17em}n\in N.$$

(17)

It is assumed that the higher the value $n$, the higher the severity of the traumatic state of the $l$-th injured person:

$$c_{l,1}=\underset{n\in N}{\max n:U_{l,n}^{inc}\ne \varnothing }.$$

(18)

3.3.2. State of Consciousness

The state of consciousness of the $l$-th injured person is determined on the Glasgow Coma Scale (GCS) [45,48] and is characterized by the following triple:

$$c_{l,2}=<c_{l,2,1},c_{l,2,2},c_{l,2,3}>,$$

(19)

where $c_{l,2,1}$ is a quantity determining the degree of eye-opening efficiency of the $l$-th injured person:

$$c_{l,2,1}=\left\{\begin{array}{l}4, \mathrm{if} \mathrm{opens} \mathrm{his}/\mathrm{her} \mathrm{eyes} \mathrm{simply},\\ 3, \mathrm{if} \mathrm{opens} \mathrm{his}/\mathrm{her} \mathrm{eyes} \mathrm{only} \mathrm{on} \mathrm{command},\\ 2, \mathrm{if} \mathrm{opens} \mathrm{his}/\mathrm{her} \mathrm{eyes} \mathrm{to} \mathrm{the} \mathrm{pain} \mathrm{stimulus},\\ 1, \mathrm{if} \mathrm{doesn}’\mathrm{t} \mathrm{open} \mathrm{his}/\mathrm{her} \mathrm{eyes}.\end{array}\right.$$

(20)

Quantity $c_{l,2,2}$ determines the level of verbal communication efficiency of the $l$-th injured person. The definition $c_{l,2,2}$ depends on the age of the injured person. If the injured person is at least four years old, then:

$$c_{l,2,2}=\left\{\begin{array}{l}5, \mathrm{if} \mathrm{can} \mathrm{speak} \mathrm{and} \mathrm{is} \mathrm{not} \mathrm{confused}, \\ 4, \mathrm{if} \mathrm{is} \mathrm{confused},\\ 3, \mathrm{if} \mathrm{speaks} \mathrm{illogically},\\ 2, \mathrm{if} \mathrm{makes} \mathrm{incomprehensible} \mathrm{sounds} \mathrm{or} \mathrm{moans},\\ 1, \mathrm{if} \mathrm{doesn}’\mathrm{t} \mathrm{react}.\end{array}\right.$$

(21)

If the injured person is not four years old, then:

$$c_{l,2,2}=\left\{\begin{array}{l}5, \mathrm{if} \mathrm{can} \mathrm{speak} \mathrm{ordinary} \mathrm{childish} \mathrm{speech}, \\ 4, \mathrm{if} \mathrm{makes} \mathrm{an} \mathrm{irritating} \mathrm{scream},\\ 3, \mathrm{if} \mathrm{screams} \mathrm{only} \mathrm{after} \mathrm{a} \mathrm{pain} \mathrm{stimulus},\\ 2, \mathrm{if} \mathrm{grunts} \mathrm{only} \mathrm{after} \mathrm{a} \mathrm{pain} \mathrm{stimulus},\\ 1, \mathrm{if} \mathrm{doesn}’\mathrm{t} \mathrm{react}.\end{array}\right.$$

(22)

Quantity $c_{l,2,3}$ determines the degree of mobility of the $l$-th injured person:

$$c_{l,2,3}=\left\{\begin{array}{l}6, \mathrm{if} \mathrm{responds} \mathrm{apropriately} \mathrm{to} \mathrm{commands}, \\ 5, \mathrm{if} \mathrm{responds} \mathrm{intentionally} \mathrm{to} \mathrm{a} \mathrm{pain} \mathrm{stimulus},\\ 4, \mathrm{if} \mathrm{responds} \mathrm{by} \mathrm{fleeing} \mathrm{the} \mathrm{pain},\\ 3, \mathrm{if} \mathrm{responds} \mathrm{to} \mathrm{pain} \mathrm{or} \mathrm{spontaneously} \mathrm{withdrawal}\text{-}\mathrm{reflex},\\ 2, \mathrm{if} \mathrm{responds} \mathrm{to} \mathrm{pain} \mathrm{or} \mathrm{spontaneously} \mathrm{extension}\text{-}\mathrm{reflex},\\ 1, \mathrm{if} \mathrm{doesn}’\mathrm{t} \mathrm{react}.\end{array}\right.$$

(23)

The resultant state of consciousness of the injured is determined on the basis of the GCS scale according to the following dependence:

$$c_{l,2}={\displaystyle \sum _{i=1}^3{c}_{l,2,i}},$$

(24)

whereby the higher the value of the resultant score $c_{l,2}$, the higher the degree of consciousness of the $l$-th casualty. The minimum value of the index determined by Equation (24) is $c_{l,2}=3$, which means the death of the casualty. The maximum value of this index is $c_{l,2}=15$, which means full awareness of the casualty. The resultant score $c_{l,2}=8$ means that the casualty is unconscious [48].

3.3.3. Degree of Basic Life Dysfunctions

The degree $c_{l,3}$ of basic life dysfunctions of the $l$-th injured person is determined in accordance with the Triage Revised Trauma Score (TRTS) used during mass casualty incidents and given in [46]. The assessment of basic life dysfunctions is characterized by the following couple:

$$c_{l,3}=<c_{l,3,1},c_{l,3,2}>,$$

(25)

where $c_{l,3,1}$ is the value representing the respiratory rate per minute and $c_{l,3,2}$ is the value determining the systolic blood pressure of the $l$-th injured person:

$$c_{l,3,1}=\left\{\begin{array}{l}4, \mathrm{if} \mathrm{respiratory} \mathrm{rate} \mathrm{is} 10–29 \mathrm{per} \mathrm{minute},\\ 3, \mathrm{if} \mathrm{respiratory} \mathrm{rate} \mathrm{is} \mathrm{larger} \mathrm{than} 29 \mathrm{per} \mathrm{minute},\\ 2, \mathrm{if} \mathrm{respiratory} \mathrm{rate} \mathrm{is} 6–9 \mathrm{per} \mathrm{minute},\\ 1, \mathrm{if} \mathrm{respiratory} \mathrm{rate} \mathrm{is} 1–5 \mathrm{per} \mathrm{minute},\\ 0, \mathrm{if} \mathrm{doesn}’\mathrm{t} \mathrm{breathe}.\end{array}\right.$$

(26)

$$c_{l,3,2}=\left\{\begin{array}{l}4, \mathrm{if} \mathrm{systolic} \mathrm{blood} \mathrm{pressure} \mathrm{is} \mathrm{larger} \mathrm{than} 89 \mathrm{mm} \mathrm{Hg},\\ 3, \mathrm{if} \mathrm{systolic} \mathrm{blood} \mathrm{pressure} \mathrm{is} 76–89 \mathrm{mm} \mathrm{Hg},\\ 2, \mathrm{if} \mathrm{systolic} \mathrm{blood} \mathrm{pressure} \mathrm{is} 50–75 \mathrm{mm} \mathrm{Hg},\\ 1, \mathrm{if} \mathrm{systolic} \mathrm{blood} \mathrm{pressure} \mathrm{is} 1–49 \mathrm{mm} \mathrm{Hg},\\ 0, \mathrm{if} \mathrm{systolic} \mathrm{blood} \mathrm{pressure} \mathrm{is} 0 \mathrm{mm} \mathrm{Hg}.\end{array}\right.$$

(27)

When determining the degree of basic life dysfunctions $c_{l,3}$ of the $l$-th injured person according to the TRTS, the level of his/her state of consciousness should be additionally taken into account [46]. For this purpose, quantity $e_l$ is introduced, defined as:

$$e_l=\left\{\begin{array}{l}4, \mathrm{if} 13\le c_{l,2}\le 15,\\ 3, \mathrm{if} 9\le c_{l,2}\le 12,\\ 2, \mathrm{if} 6\le c_{l,2}\le 8,\\ 1, \mathrm{if} 4\le c_{l,2}\le 5,\\ 0{, \mathrm{if} \mathrm{c}}_{l,2}=3.\end{array}\right.$$

(28)

After determining the value of $e_l$, the resultant assessment of the degree of basic life dysfunctions of the $l$-th injured person can be determined as [46]:

$$c_{l,3}=e_l+c_{l,3,1}+c_{l,3,2},$$

(29)

whereby the lower the value of the resultant score $c_{l,3}$, the higher the degree of basic life functions dysfunctions of the $l$-th casualty.

3.4. Rules for Qualifying Injured to Medical Priority Groups

According to START [13,29,40,41] (Simple Triage and Rapid Treatment), there are four medical priority injured groups in the MCI. During medical rescue operations, these people are marked with colors or numbers. Each color corresponds to the priority of the victim’s medical care [4]. Based on the assessment of the health condition of the injured person, qualification to the appropriate group is made.

Let $g$ characterizes the priority of the victim’s medical care:

$$g=\overline{1,4},$$

(30)

where:

• $g= 1$ means immediate medical operations upon arrival of emergency services.
• $g= 2$ means urgent medical operations with a possible delay.
• $g= 3$ means medical operations with a delay of up to several hours.
• $g= 4$ means resignation from medical care. This is the priority group of injured people who are not expected to survive the next 24 h.

$L_g$ is a set of numbers of people injured in a mass casualty incident classified to the g-th group of medical treatment priority:

$$L_g=\{l:d_g^{group}(l)=1, l\in L\},g=\overline{1,4}\hspace{0.17em},$$

(31)

where

$$d_g^{group}(l)=\left\{\begin{array}{l}1, \mathrm{if} \mathrm{the} l\text{-}\mathrm{th} \mathrm{injured} \mathrm{person} \mathrm{is} \mathrm{qualified} \mathrm{to} \mathrm{the} g\text{-}\mathrm{th} \mathrm{group},\\ 0, \mathrm{otherwise}.\end{array}\right.$$

(32)

where $\underset{g,h\in G}{\forall }:g\ne h\Rightarrow L_g\cap L_h=\varnothing$.

The detailed conditions for assigning casualties to priority groups are omitted due to the lack of article space.

3.5. Quantities Characterizing Medical Rescue Operations of DES during MCI

A random variable $W_{1,g}$ is assumed to be the probability of death of the $l$-th injured person, which was qualified to the g-th medical treatment priority group. $W_{1,g}$ takes values from the interval $\left[0;1\right]$, where value one means the death of the injured person, zero—otherwise.

The travel time of the r-th mode of transportation between the current place y and the place of the event $z_1$ is described by the following formula:

$$t^{travel}(y,z_1,r)=\frac{d_{z_1}(r,y)}{V_r}\hspace{0.17em},\hspace{0.17em}$$

(33)

where $d_{z_1}(r,y)$ is the distance which the r-th mode of MRT has to travel from place y to the MCI scene $z_1$ according to Equation (9). Here y means the actual location of the s-th HED, i.e., $h_{s,1}$ according to Equation (2) or the location of the $b$-th MRTB, i.e., $a_{b,1}$ according to (6),$V_r$ is the average speed of the r-th mode of MRT.

The time measured from the moment the incident occurred to the moment of arrival of the r-the mode of MRT from the b-th MRTB to the s-th HED is described by the following equation:

$$\tau (b,s,r)=t^z+t^{travel}(a_{b,1},z_1,r)+t^{travel}(h_{s,1},z_1,r),$$

(34)

where $t^z$ is the time elapsed from the moment of the incident to the moment of notifying the DES about the incident according to Equation (9) and $t^{travel}$ is the travel time of the MRT, according to Equation (33).

The expected value of the death in the MCI depends on the severity of the traumatic state and, in most cases, may be characterized by the logistic function [16]. Let $E(W_{1,g}/\tau )$ be the expected value of random variable $W_{1,g}$ after time $\tau$ has elapsed:

$$E(W_{1,g}/\tau )=\frac{1}{1+e^{-k_g\left(\tau -{\upsilon }_g\right)}},$$

(35)

where $k_g$${\upsilon }_g$ are the parameters of the logistic function depending on the g-th medical treatment priority group, where the $k_g$ value is responsible for the exponential growth of the function vertically, and expression $\left(\tau -{\upsilon }_g\right)$ specifies the horizontal translation of the function plot.

The logistic function of the form of the Equation (35) takes values from zero (for which the expected value of the death is minimal) to one (for which the expected value is maximal and means a certain death).

Injuries with a state of severity over three ($n\ge 3$) are a direct threat to life.

Survival of people injured in the MCI additionally depends on the capabilities of HEDs, which will take care of these people.

Let $S_l^{trauma}$ be a set of HEDs, which can effectively treat the l-th injured person because of his/her worst injuries ($n\ge 3$):

$$S_l^{trauma}=\left\{s:U_{l,n}^{inc}\subset h_{s,3}\hspace{0.17em}\hspace{0.17em}\mathrm{for}\hspace{0.17em}\hspace{0.17em}n\ge 3 \mathrm{and} \mathrm{s}\in \mathrm{S}\right\}, l\in L.$$

(36)

In regard to the above, the expected value of the l-th injured person’s death depending on the moment of arrival of the r-th mode of MRT from the b-th MRTB to the s-th HED is yielded as:

$$f^{death}\left(l,b,s,r\right)=\left\{\begin{array}{cc}E\left(W_{1,g}/\tau (b,s,r)\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}l\in L_g,g\in G& \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{if}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}s\in \hspace{0.17em}{S}_l^{trauma}\hspace{0.17em},\\ 1,& \mathrm{otherwise},\end{array}\right.$$

(37)

where $f^{death}\left(l,b,s,r\right)=1$ means that the l-th injured person will not survive if he/she will be transported by the r-th mode of MRT from the b-th MRTB to the s-th HED.

Description of other expected values (e.g., the expected value of disabilities or the expected value of the cost of emergency medical care), which determine the effectiveness of the DES during the rescue undertaking of the MCI, is neglected because they are similar to the expected value of death.

4. Formulation of the Optimization Problem

The solution to the problem of optimizing medical rescue operations after the MCI consists in assigning each injured person:

• The MRTB from which the MRT should be allocated.
• the HED to which the injured person should be taken.
• the mode of MRT which should be chosen.

To achieve minimization of the MCI consequences, i.e., the minimum expected value of the death, the minimum expected value of the disability, the minimum expected value of the cost of the rescue operation and the minimum expected value of the cost of long-term treatment and rehabilitation of the injured person.

In the formulated optimization problem, a binary decision variable is introduced using the following function:

$$x=x\left(l,b,s,r\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if} \mathrm{the} l\text{-}\mathrm{th} \mathrm{injured} \mathrm{person} \mathrm{is} \mathrm{taken} \hfill \\ & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{from} \mathrm{the}\hspace{0.17em}b\text{-}\mathrm{th} \mathrm{MRTB} \hfill \\ & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{to} \mathrm{the} s\text{-}\mathrm{th} \mathrm{HED}\hfill \\ & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{by} \mathrm{the} r\text{-}\mathrm{th} \mathrm{mode} \mathrm{of} \mathrm{MRT},\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.,$$

(38)

The vector of decision variables, is denoted as:

$$\overrightarrow{x}=\left(x_i\right)=\left(l_i,b_i,s_i,r_i\right)\in L\times B\times S\times R,$$

(39)

where $x_i$ is the $i$-th unique assignment variant $\left(l_i,b_i,s_i,r_i\right)$ where $i=\overline{1,L\times B\times S\times R}$.

It should be noted that decisions can take one of two values: zero or one. The value one in the described problem means a certain allocation of the $r$-th MRT and the $s$-th HED to treat the indicated person. The zero value means there is no exact allocation. Taking into account this limitation, the optimization problem becomes a special case of MILP, namely the binary integer programming (BIP) problem.

The consequences of the MCI are described by many criteria (multi-criteria optimization). Let the objective function vector be:

$$f=<f_1,f_2,f_3,f_4>,$$

(40)

where:

• $f_k\left(\overrightarrow{x}\right)$—objective function due to the $k$-th criterion for evaluating the effectiveness of DES activities for decision variables vector $\overrightarrow{x}$. There are four objective functions of DES effectiveness:
• $f_1$—the expected value of death,
• $f_2$—the expected value of disability,
• $f_3$—the expected value of the cost of carrying out the rescue operation and
• $f_4$—the expected value of long-term treatment and rehabilitation costs.

The optimization problem of DES activities in the case of the MCI, i.e., the problem of minimization of consequences of the MCI, can be presented as follows:

$$\underset{l,b,s,r}{\min }\left\{f\left[\overrightarrow{x}\left(l,b,s,r\right)\right]\right\}$$

(41)

Subject to:

$$\left\{\begin{array}{c}\underset{l}{\forall }{\displaystyle \sum x\left(l,b,s,r\right)}=1\\ \underset{b}{\forall }\underset{r}{\forall }{\displaystyle \sum x\left(l,b,s,r\right)}\le f_{MRTB}^{limit}(b,r)\\ \underset{s}{\forall }{\displaystyle \sum x\left(l,b,s,r\right)}\le f_{HED}^{limit}(s)\\ \begin{array}{c}x\left(l,b,s,r\right)\in \left\{0;1\right\}\\ l\in L,b\in B,s\in S,r\in R\end{array}\end{array}\right.$$

In this optimization task, the following constraints must be met:

• for each injured person, exactly one mode of MRT is taken, and exactly one HED is assigned to treat this person:

$$\underset{l}{\forall }{\displaystyle \sum x\left(l,b,s,r\right)}=1,$$

(42)

• The number of MRTs already assigned to transport service cannot exceed the number of still available MRTs:

$$\underset{b}{\forall }\underset{r}{\forall }{\displaystyle \sum x\left(l,b,s,r\right)}\le f_{MRTB}^{limit}(b,r),$$

(43)

where $f_{MRTB}^{limit}(b,r)$ is a function which describes the number of still available r-th modes of MRT in the b-th MRTB,

• The number of HED beds assigned for injured persons cannot exceed a limit of vacant beds in a certain HED:

$$\underset{s}{\forall }{\displaystyle \sum x\left(l,b,s,r\right)}\le f_{HED}^{limit}(s),$$

(44)

where $f_{HED}^{limit}(s)$ is a function which describes the number of still available beds for injured persons in the $s$-th HED.

• The assignment of the HED and the MRT mode to each person can take exactly one of two values zero or one (binary variable constraint), i.e.,

$$x\in \left\{0;1\right\}.$$

(45)

5. Computer Simulator for Optimal Decision-Making in Medical Rescue Operations

In order to conduct simulation studies of the effectiveness of making optimal decisions about rescue operations after the MCI has occurred, a computer simulator for optimal decision-making in medical rescue operations (CSMRO) has been developed.

The CSMRO was implemented in the Microsoft Visual Studio .NET C#. The main role of the created simulator CSMRO is to assess the effectiveness of the intelligent medical rescue operations management system (IMROMS) after the MCI has occurred, taking into account the following factors:

• different multi-criteria optimization methods and their parameters,
• different computing environments (optimization software modules),
• different boundary conditions that describe the MCI and
• scale (size) of the MCI.

The CSMRO simulator is also used to compare and assess the usefulness of the tested computing environments and optimization methods in terms of the time of results generation and accuracy of the MCI consequences problem solution.

The methods of the multi-criteria optimization, which are applied in the CSMRO are [49,50]:

• the weighted sum method,
• the weighted global criterion method,
• the hierarchical optimization method and
• the e-constraint method (bounded objective function method).

The multi-criteria optimization problem of DES activity effectiveness after the MCI has occurred is transformed to the one-criteria mixed integer linear programming, and the method that is implemented in the CSMRO for this purpose is the branch-and-cut (B and C) method [51]. For each computational environment, there are certain optimal solution methods which are listed in

Table 1. Computational multi-objective optimization environments used branch-and-cut (B and C) algorithms to determine the optimal solution.

Symbol of the Computational Environment	Name of the Computational Environment	Optimal Solution Method Applied in the Computational Environment
S1	LINDO API [52]	int lindo.LSsolveMIP(IntPtr pModel, ref int pnMIPSolStatus)
S2	CPLEX [53]	bool Cplex.Solve()
S3	MATLAB [54]	intlinprog(objective, intcon, A_ineq, b_ineq, A_eq, b_eq, lb, ub, options)
S4	MOSEK [55]	mosek.rescode mosek.Task.optimize()

.

6. Results and Discussion

In this chapter, an example of the step-by-step optimal allocation of DES forces within medical rescue operations after the MCI has occurred is presented in accordance with the following assumptions:

• eight people are injured, L = 8,
• injuries encountered are specified in

  Table 2. A set of types of injuries with the degree of severity (Equation (13)) is featured in the example.

  u-th Trauma	Trauma	n-th Degree of Severity
  1	flesh wound	1
  2	burns up to 10% below 3rd degree	1
  3	forearm fracture	1
  4	feet fracture	1
  5	hand fracture	1
  6	spine injury	2
  7	hip injury	2
  8	shoulder injury	2
  9	isolated fracture of the lower leg bones	3
  10	traumatic limb amputation	3
  11	hypothermia	3
  12	head injury	3
  13	unstable chest	3
  14	shock	3
  15	severe skull injury	4
  16	brain tissue damage	4
  17	extensive crushing	4

  ,
• health condition of injured people is summarized in

  Table 3. The severity of the traumatic state (Equations (11) and (16)).

  Injured Number l	${\mathit{U}}_{\mathit{l}}^{\mathit{i}\mathit{n}\mathit{c}}$	The Severity of the Traumatic State
  		${\mathit{c}}_{\mathit{l},1}$	${\mathit{c}}_{\mathit{l},2}$	${\mathit{c}}_{\mathit{l},3}$	${\mathit{c}}_{\mathit{l},4}$	${\mathit{c}}_{\mathit{l},5}$	${\mathit{c}}_{\mathit{l},6}$
  1	1, 6	2	15	11	1	0	30
  2	15	4	3	1	1	0	34
  3	8, 14	3	9	8	1	0	22
  4	8	2	15	10	0	0	24
  5	11	3	14	10	1	0	46
  6	1, 5	1	15	12	0	1	27
  7	7	2	15	10	0	0	50
  8	11, 12	3	11	8	1	0	57

  ,
• the time that elapsed from the moment of occurrence of the incident to the moment of notifying the DES about this incident is $z_2=0.2$ (0.2 h = 12 min),
• HEDs and MRTBs settings and their distances to MCI’s scene are described accordingly in

  Table 4. Current possibilities of HEDs (as defined in Equation (2)).

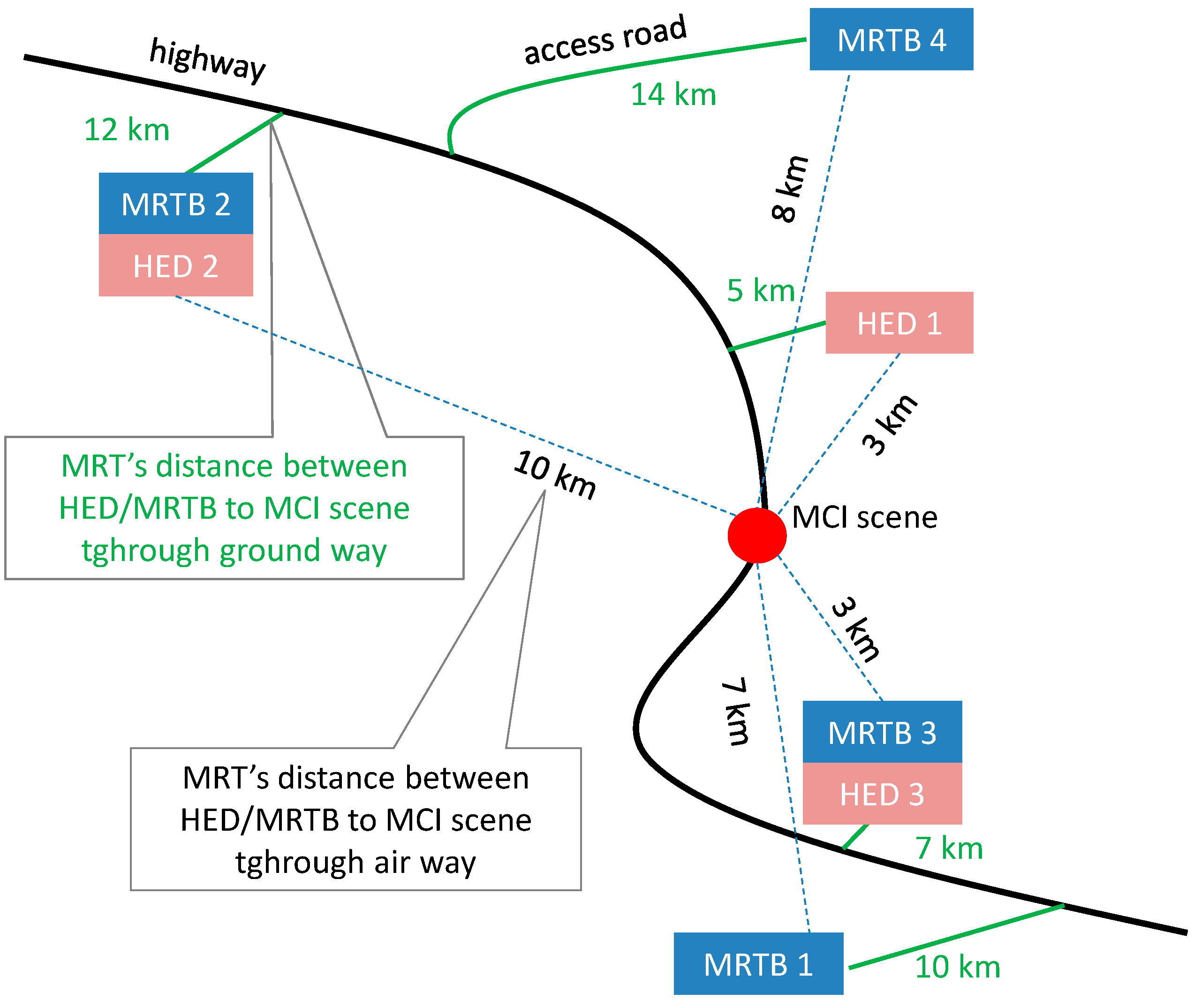
  HED’s Number s	Distance from the HED ${\mathit{h}}_{\mathit{s},1}$ to the Scene of the MCI ${\mathit{z}}_1$ in Kilometers		Number of Injured People That Can Be Handled by the s-th HED ${\mathit{h}}_{\mathit{s},2}$	A Set of Types of Post-Accident Injuries Handled by the s-th HED ${\mathit{h}}_{\mathit{s},3}$
  	for the Ground Type of the MRT ($\mathit{r} = 1$)	for the Air Type of the MRT ($\mathit{r} = 2$)
  1	5	3	10	1, 7, 8, 9, 10, 11, 12
  2	12	10	10	3, 4, 5, 6, 7, 14
  3	7	3	10	1, 2, 3, 4, 5, 6, 7, 8, 9, 13, 15

  and

  Table 5. MRTB characteristics (as defined in Equation (7)).

  Number of the MRTB b	Distance from the MRTB ${\mathit{a}}_{\mathit{b},1}$ to the Scene of the MCI ${\mathit{z}}_1$ in Kilometers		Number of the r-th Mean of the MRT from the b-th MRTB ab,2,r
  	for the Ground Type of the MRT ($\mathit{r} = 1$)	for the Air Type of the MRT ($\mathit{r} = 2$)
  1	10	7	<10,10>
  2	12	10	<10,10>
  3	7	3	<10,10>
  4	14	8	<10,10>

  ; the average speed of different MRT modes are given in

  Table 6. The average speed of the MRT mode (as defined in Equation (33)).

  Number of the Transport Mode r	Transport Mode	Average Speed Vr of the r-th Transport Mode in Kilometers per Hour
  1	air	60
  2	ground	250

  , and sufficient limits of medical service within MRTBs and HEDs are taken for all those injured in the MCI,
• the optimization problem is solved with the method of the sum of weighted criteria, and the following weight values describing the effectiveness of DES activities are taken: $\alpha =\left({\alpha }_1;{\alpha }_2;{\alpha }_3;{\alpha }_4\right)=\left(0.4;0.3;0.2;0.1\right)$; it is also noted that the human’s life is the most important factor. Therefore it is assumed that ${\alpha }_1=0.4$,
• the logistic function describing the probability of an injured person’s death according to their treatment priority group defined by Equation (35) is set in

  Table 7. Parameters of the logistic function describing the expected value of death according to the priority group of medical treatment (as defined in Equation (35)).

  Priority Group’s Number g	Logistic Function Parameter ${\mathit{k}}_{\mathit{g}}$	Logistic Function Parameter ${\mathit{\upsilon }}_{\mathit{g}}$
  1	30	0.25
  2	30	0.58(3)
  3	12	1.16(6)
  4	30	0.08(3)

  . Parameters of the other criteria are intentionally skipped,
• the optimal solution is solved using the LINDO API math software module and
• a more detailed dataset from this example created and used in the CSMRO is available in the open-access repository at the link [56].

Taking into account the above assumptions, the situation shown in Figure 1 is obtained.

The victims in the mass casualty incident are assigned to groups based on their identified health status using the quantities given in Section 3.5. This assignment is summarized in

Table 8. Assignment of persons injured in the MCI to medical treatment priority groups.

Injured Person Number l	Priority Group Number g of the l-th Injured Person $\mathit{g}:\mathit{l}\in {\mathit{L}}_{\mathit{g}}$
1	2
2	4
3	1
4	2
5	1
6	3
7	2
8	1

.

The presented problem of optimizing the allocation of forces and resources to injured persons was programmed in the LINDO API using the B and C algorithms to search for local minimum values of the objective function. The number of binary decision variables is equal to the power of the feasible solutions: $L\times B\times S\times R=8\times 4\times 3\times 2=192$, while the number of non-zero decision variables, which is the optimal solution, is equal to the number of injured persons ($L=8$). The example was solved using the weighted sum method in the LINDO API.

Under this method, the auxiliary objective function is defined:

$$Z(\overrightarrow{x})={\displaystyle \sum _j\widehat{f_j}(\overrightarrow{x})\cdot {\alpha }_j},$$

(46)

where $\alpha =\left({\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4\right)$ is the vector of weights of individual performance evaluation criteria of DES and ${\alpha }_1+{\alpha }_2+{\alpha }_3+{\alpha }_4=1$ and $\widehat{f_j}(\overrightarrow{x})$ is the j-th normalized quality index of the vector of decision variables $\overrightarrow{x}$, where:

$$\widehat{f_j}(x_i)=\frac{f_j(x_i)-\underset{i}{\min }{f}_j(x_i)}{\underset{i}{\max }{f}_j(x_i)-\underset{i}{\min }{f}_j(x_i)},$$

(47)

and $x_i$ stands for the $i$-th decision variable and $f_j$ stands for the j-th component objective function $f_j$.

It should be noted that the component objective functions usually have different units and ranges of variation, and therefore their prior normalization is carried out according to Equation (47).

Then, the multi-criteria optimization problem in the form of Equation (41) reduces to the following one criteria Mixed Integer Linear Programming problem:

$$\underset{l,b,s,r}{\min }\left\{Z\left[\overrightarrow{x}\left(l,b,s,r\right)\right]\right\},$$

(48)

with the constraints defined in Equations (42)–(45).

In the weighted sum method of criteria, the optimal solution is one $\overrightarrow{x}\in \mathit{X}$ for which the surrogate objective function $Z$ takes the minimum value. The main advantage of this method is that it is intuitive and gives the meaning of the criteria by specifying their weights.

The solution time of the presented example problem was 0.465 s, and the value of the auxiliary function, according to Equation (46) (for the values of the criteria function previously normalized according to Equation (47)), was $Z(\overrightarrow{x})=1.38039$. The optimal solution in the form of the allocation of forces and resources to all injured in the MCI is summarized in

Table 9. Optimal solution with values of the auxiliary function $Z$ computed by CSMRO for non-zero decision variables ($x=1$) in the example set.

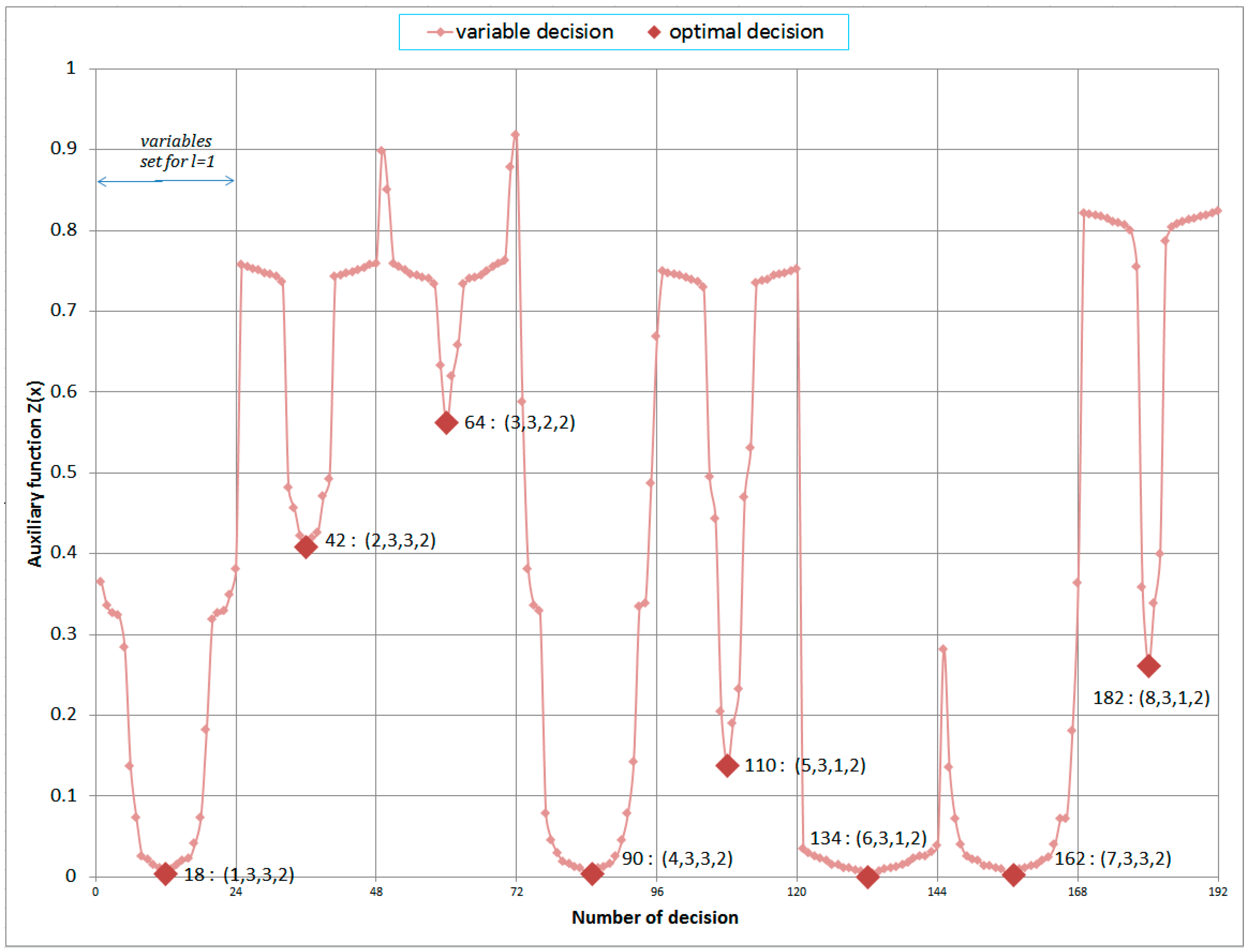
Number of Non-Zero Decision Variables $(\mathit{x}\ne 0)$	Number of the Injured Persons $\mathit{l}$	Number of the MRTB $\mathit{b}$	Number of the HED $\mathit{s}$	Number of the MRT Type $\mathit{r}$	$\mathit{Z}(\mathit{x})={\displaystyle \sum _{\mathit{j}=1}^4\widehat{{\mathit{f}}_{\mathit{j}}}(\mathit{x})\cdot {\mathit{\alpha }}_{\mathit{j}}}$ as Defined in Equation (46)	$\mathit{\tau }(\mathit{b},\mathit{s},\mathit{r})$ as Defined in Equation (34)
18	1	3	3	2	0.00315323	0.224 (13 min 44 s)
42	2	3	3	2	0.40871449	0.224 (13 min 44 s)
64	3	3	2	2	0.56225483	0.252 (15 min 12 s)
90	4	3	3	2	0.00425728	0.224 (13 min 44 s)
110	5	3	1	2	0.13780012	0.224 (13 min 44 s)
134	6	3	1	2	0.00012702	0.224 (13 min 44 s)
162	7	3	3	2	0.00280106	0.224 (13 min 44 s)
182	8	3	1	2	0.26127769	0.224 (13 min 44 s)

.

According to Table 9, the solution for the (non-zero) decision variable number 18 is as follows: the first injured person ($l=1$) will be transported by the second mode of MRT ($r=2$) from the third MRTB ($b=3$) to the second HED ($s=3$).

The form of the optimal solution is shown in Figure 2. Non-zero variables indicating allocation $(l,b,s,r)$ with their corresponding numbers are marked in dark gray. Number of solutions are ordered by auxiliary function values, from the lowest to the highest, in the context of solutions for each person in the MCI.

In Figure 2, variables creating optimal solutions at the local minima can be seen. The obtained results prove the correctness of the solution for the given values of the auxiliary function $Z$ as defined in Equation (46).

Based on the data collected in Table 9, it can be seen that optimal solutions are correlated with the moment when each injured person is treated in the HED exactly $\tau (b,s,r)$ (as defined by Equation (34)). The maximum $\tau$ takes the value of 0.633 (37 min), and the minimum $\tau$ takes the value of 0.224 (13.4 min).

The set of decision variables forming the optimal solution of the studied problem by the weighted sum of criteria method was determined identically by all modules of the CSMRO simulator using B and C algorithm: LINDO API, CPLEX, MATLAB and MOSEK (S1–S4 methods in Table 1).

During simulation tests, different resource allocation tasks of varying complexity have been analyzed using the developed CSMRO. For all computing environments (see Table 1), the same solution for a certain task was always obtained, which confirms that all implemented environments generate the same optimal solution. Large-scale MCI tasks were also analyzed with the CSMRO to find the optimal solution. No problems were encountered with the number of injured persons equal to 100, assuming 10 available MRTs of two different types and 10 HEDs (resulting in an optimization problem of 20,000 variables). The CSMRO was able to handle such a large amount of data without any problems and generated a tabular solution (similar to the one presented in Table 9) with a calculation time of less than 1 s. Even if, for the vast number of people affected, the calculation time is 1 min, this will still be very short for the DES personnel to make appropriate decisions based on the calculation results obtained from the CSMRO. It is worth emphasizing that in this short solution time, the CSMRO generates a ready-made solution for direct handling the mass casualty incident.

Thus, the CSMRO can be used to:

• detailed statistical analysis of actual mass incidents to identify the relationship between the various post-accident conditions of the injured and the expected values of death, disability and long-term medical costs;
• dynamic analysis of the current situation at the scene of a mass casualty incident by taking into account the time factor and
• analysis of very large-scale tasks.

In summary, the proposed model for medical rescue operations in MCIs is briefly compared with the models described in the literature (

Table 10. Comparison of the proposed model with selected models found in the literature.

Literature Reference	Optimization Method	Is Multi-Criteria	New Method of Triage or Currently in Practice START	Injured Persons Health Modelling	Complete Service (Injured Assigned to the Certain MRT and ED)
Rauner et al. [4]	Discrete-event simulation	no	START	no	yes
Cotta [13]	Hyperheuristic	no	START	no	no
Güttinger et al. [14]	D’Hondt, greedy strategy simulated annealing	no	START	no	yes
Wilson et al. [17]	Fixed Job Scheduling Problem Variable Neighborhood Search (VNS) metaheuristics and its deterministic variant Variable Neighborhood Descent (VND)	yes	START	no	yes
Dean and Nair [11]	MIP	no	START	no	yes
Kilic et al. [18]	Pontryagin’s minimum principle	no	START	no	yes
Chu et al. [20]	MIP Flexible job shop scheduling model and a genetic algorithm	no	START	no	yes
Repoussis et al. [26]	MIP	no	START	no	yes
Sung and Lee [27]	LP, column generation	no	START	no	yes
Chang et al. [37]	Rapid-screening algorithm and an adaptive particle global and hyperbox local search	no	START	no	yes
The proposed model	MIP	yes	new	yes	yes

).

From Table 10, it can be seen that many approaches are based on a linear programming approach. Almost none of them include a multi-criteria formulation of MCI problems. They are all primarily based on the START algorithm. This means that the casualties are assigned to priority groups, but are not examined individually, i.e., the exact details of the condition of the injured are not used. In the proposed model, a novel method of assigning each casualty to a specific emergency department and to a specific mode of transport is introduced. The current health status of the injured is classified and included in the considered optimization problem. The allocation of emergency medical services forces and resources in the MCI is formulated as the multi-criteria optimization problem.

7. Conclusions

Organizational decisions after MCI’s occurrence are made on the basis of intuition and experience of rescue DES functionaries; the flow of information between individual rescue functionaries is still largely limited to voice transmission via radio communication. The DES continues to prepare for the MCI using traditional methods such as color-coded triage paper cards.

The results of simulation studies conducted with the developed CSMRO indicate that DES decision-making processes in MCIs can be significantly improved. The CSMRO can be used for the optimal allocation of available DES forces and resources to those injured in the MCI. This translates strictly into a maximum reduction in time for the injured to reach designated HEDs. The time for the CSMRO to work out a decision on how to handle a mass event has been significantly reduced to less than a second (depending strictly on the computing power of the computer). As a result, the execution time of the actions taken in various stages of the rescue operation will also be shorter.

Computations made in the developed CSMRO simulator clearly indicate that the implementation of the developed Intelligent Medical Rescue Operations Management System will:

• significantly shorten the time of decision-making in mass casualty incident handling,
• improve the accuracy of decisions regarding medical care of the injured,
• reduce the stress factor in DES physicians by supporting the decisions made,
• maximize the use of DES forces and resources available at a given moment and
• eliminate information chaos and minimize the risk of making a mistake.

The proposed simulator was developed in close cooperation with the Polish Emergency Services. It presents the specifics of mass casualty incidents management in Poland, is adapted to local realities, and is already planned for implementation in mass casualty incidents management teams in the near future.

The main limitation of the CSMRO approach is shifting from typical telecommunications to a data exchange system. The communication infrastructure needed to ensure communication of the IMROMS system modules needs to be established. Another issue is to equip the DES with hardware infrastructure, servers, mobile devices, etc. In addition, the DES personnel should be trained and prepared to work with the IMROMS. In the initial stage of IMROMS implementation and commissioning, it is recommended to employ assistants to do parallel data entry with the rescuers at the MCI scene. The DES operational personnel should be supported by technicians—knowledge engineers. The DES decision-maker personnel should be supported by instant propositions of optimal solutions provided by those technicians and obtained from the CSMRO.

Future extension of the CSMRO will include the ability to conduct analysis of several mass casualty incidents at one time and to include the use of biosensors for rapid acquisition of data to assess the condition of the injured.