A New Windage Loss Model for S-CO2 Turbomachinery Design
Abstract
:1. Introduction
2. Description of S-CO2 Windage Loss Experiment
2.1. Experimental Design of S-CO2 Windage Loss Measurement
2.2. Uncertainty of Measured Windage Loss
3. Comparison of Data to Existing Windage Loss Models
| Author | Empirical Equation | Note | |
|---|---|---|---|
| Mack [12,13] | is obtained with assuming continuous change of at Air test | ||
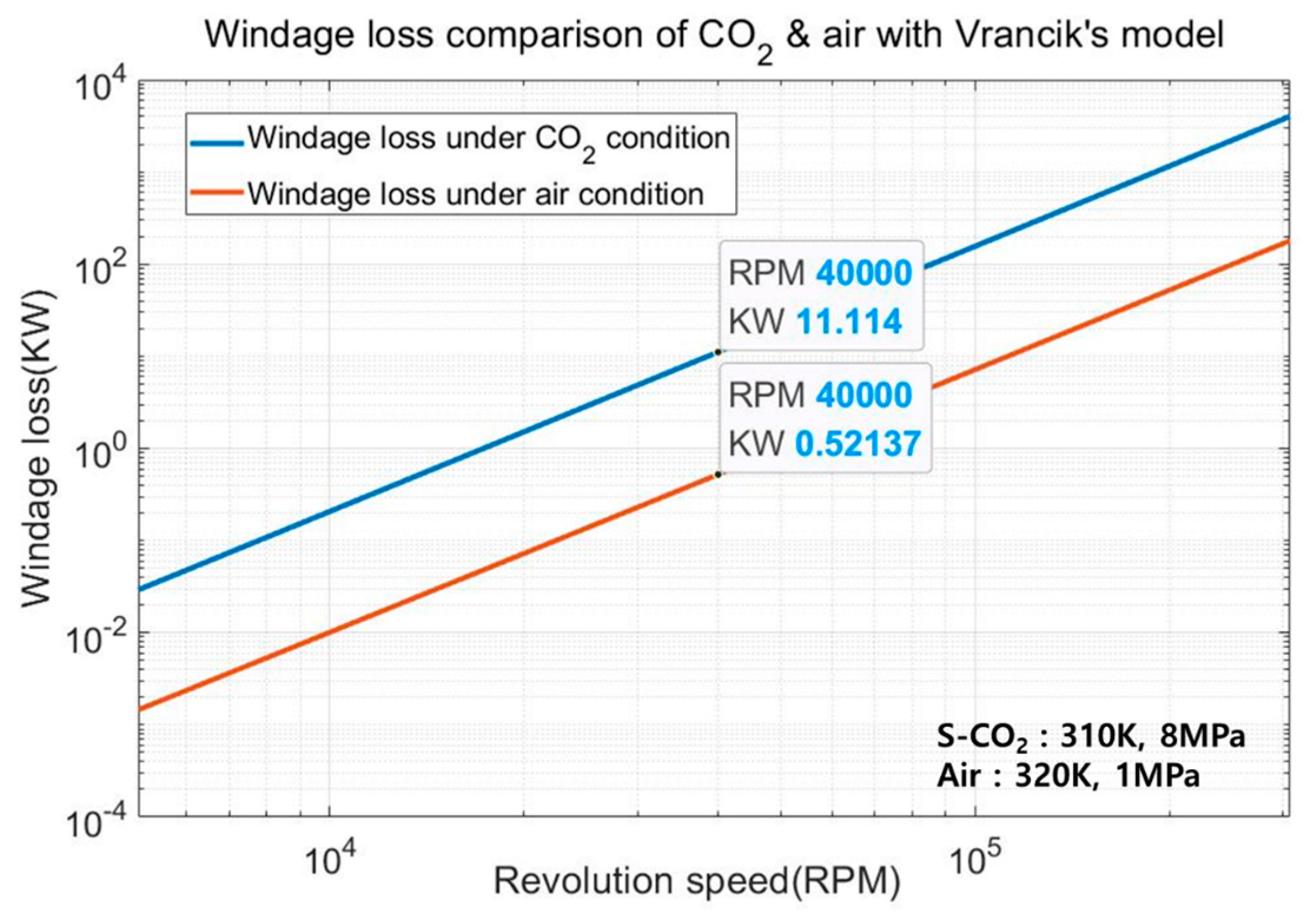
| Vrancik [14] | Couette velocity profile in laminar and air test for in turbulence regime Air test for | ||
| Wendt [15,16] | Pure water, water-glycerin mixture Gap size: 0.95~4.7 cm | ||
| Yamada [15,17] | Spindle oil test | ||
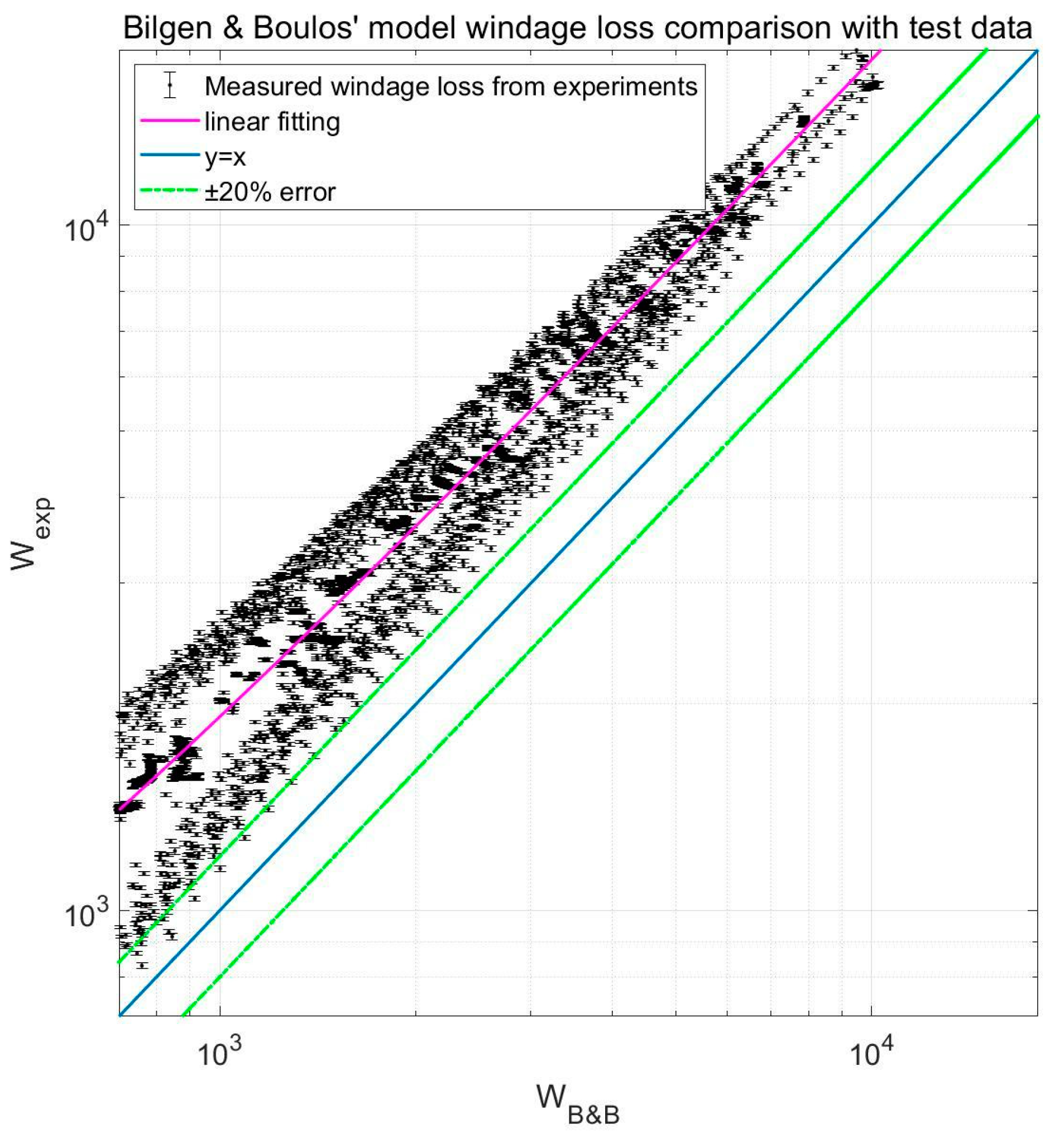
| Bilgen and Boulos [15,18] | Pure water, water-glycerin mixture Gap size: 0.32~4.45 cm | ||
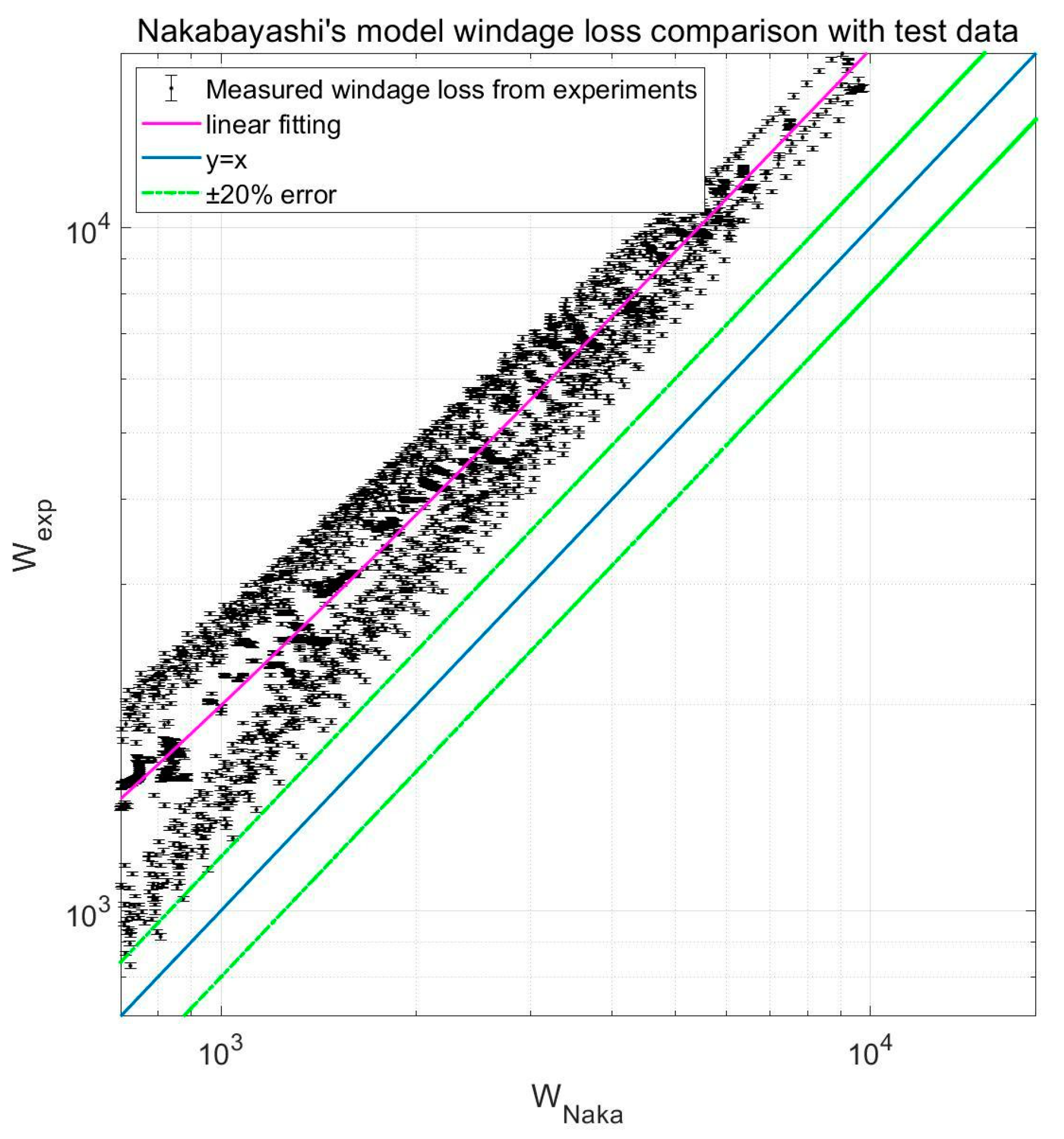
| Nakabayashi [15,19] | Freezer oil, pure water, water-glycerin mixture Roughness test | ||
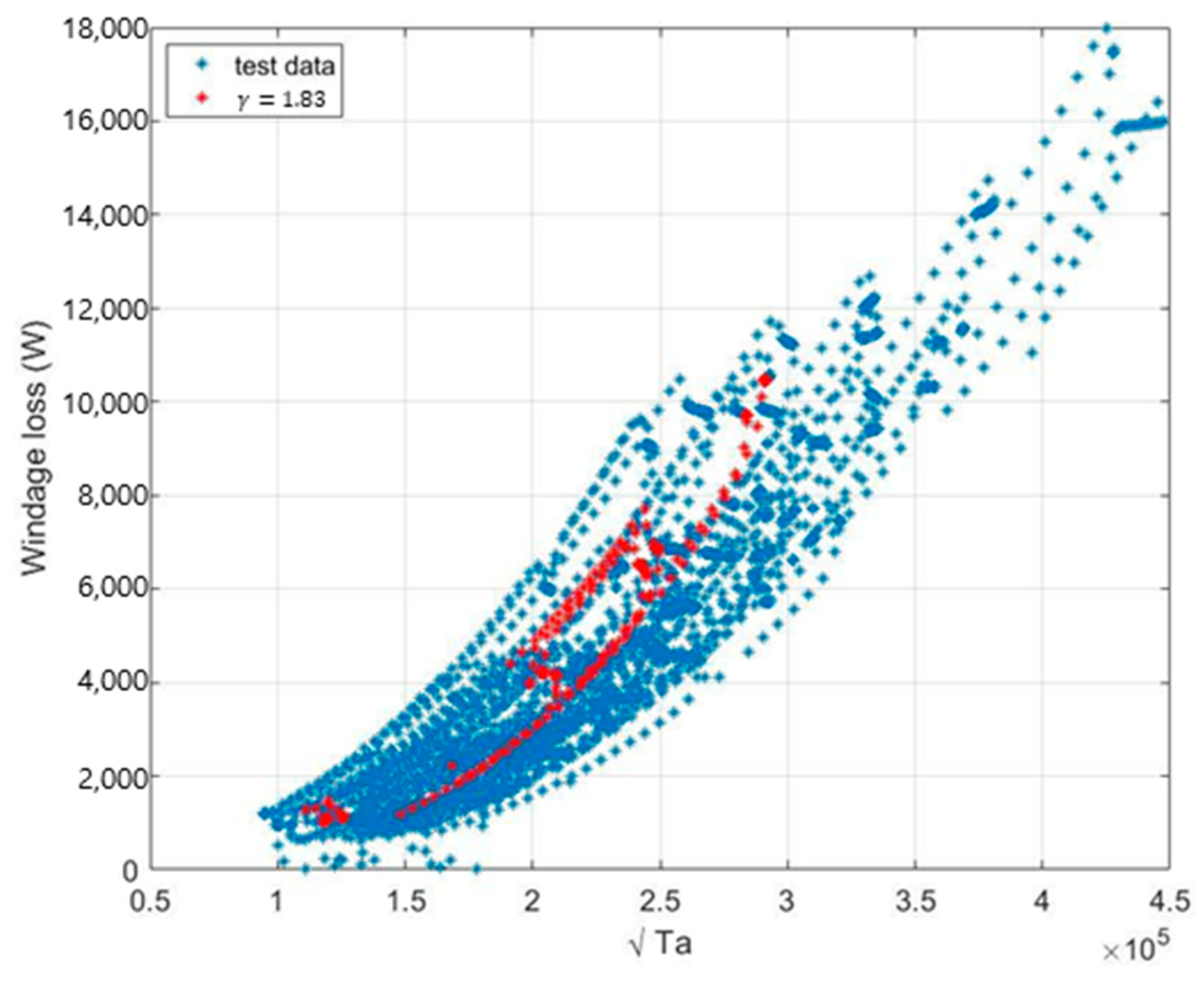
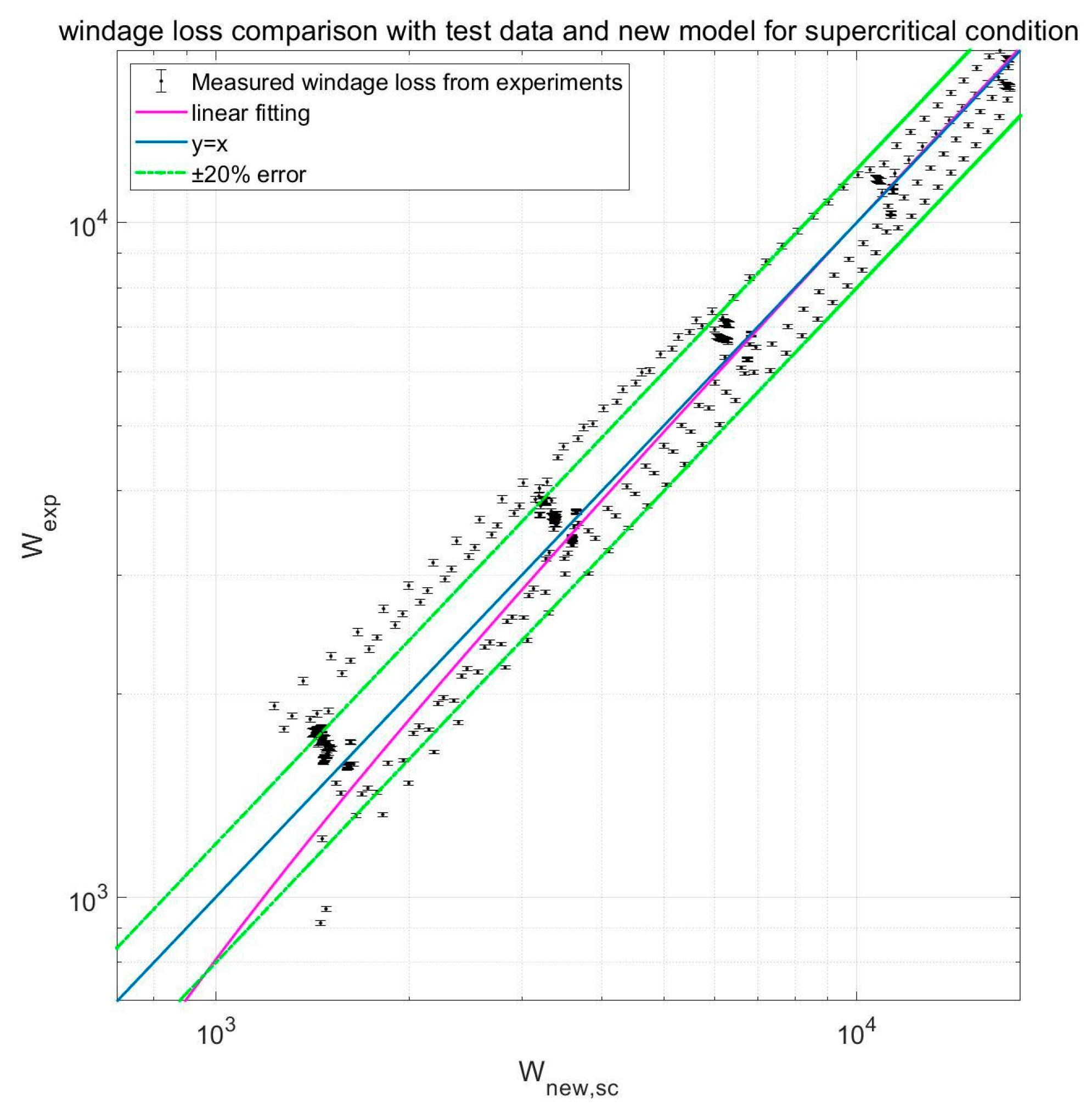
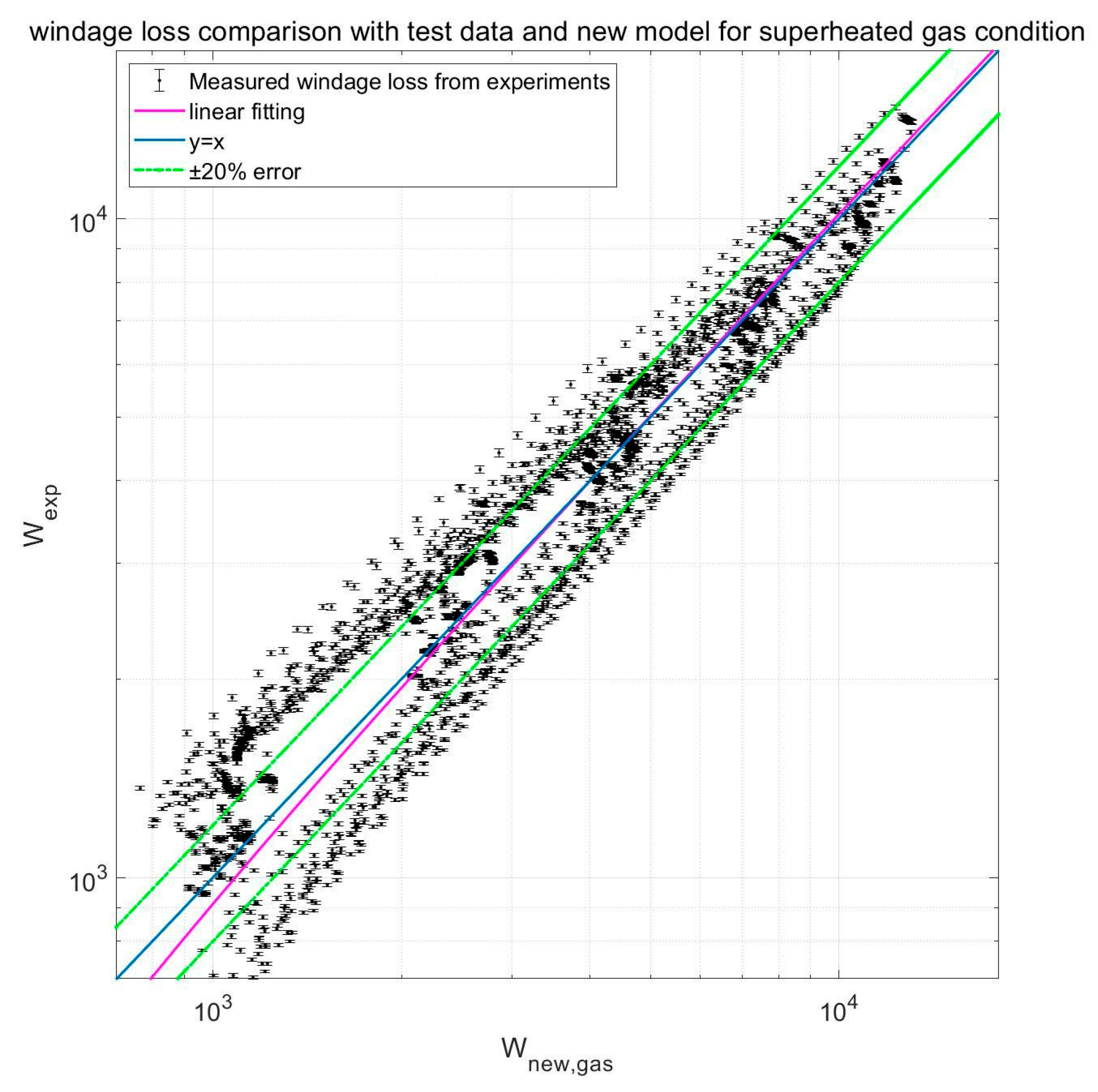
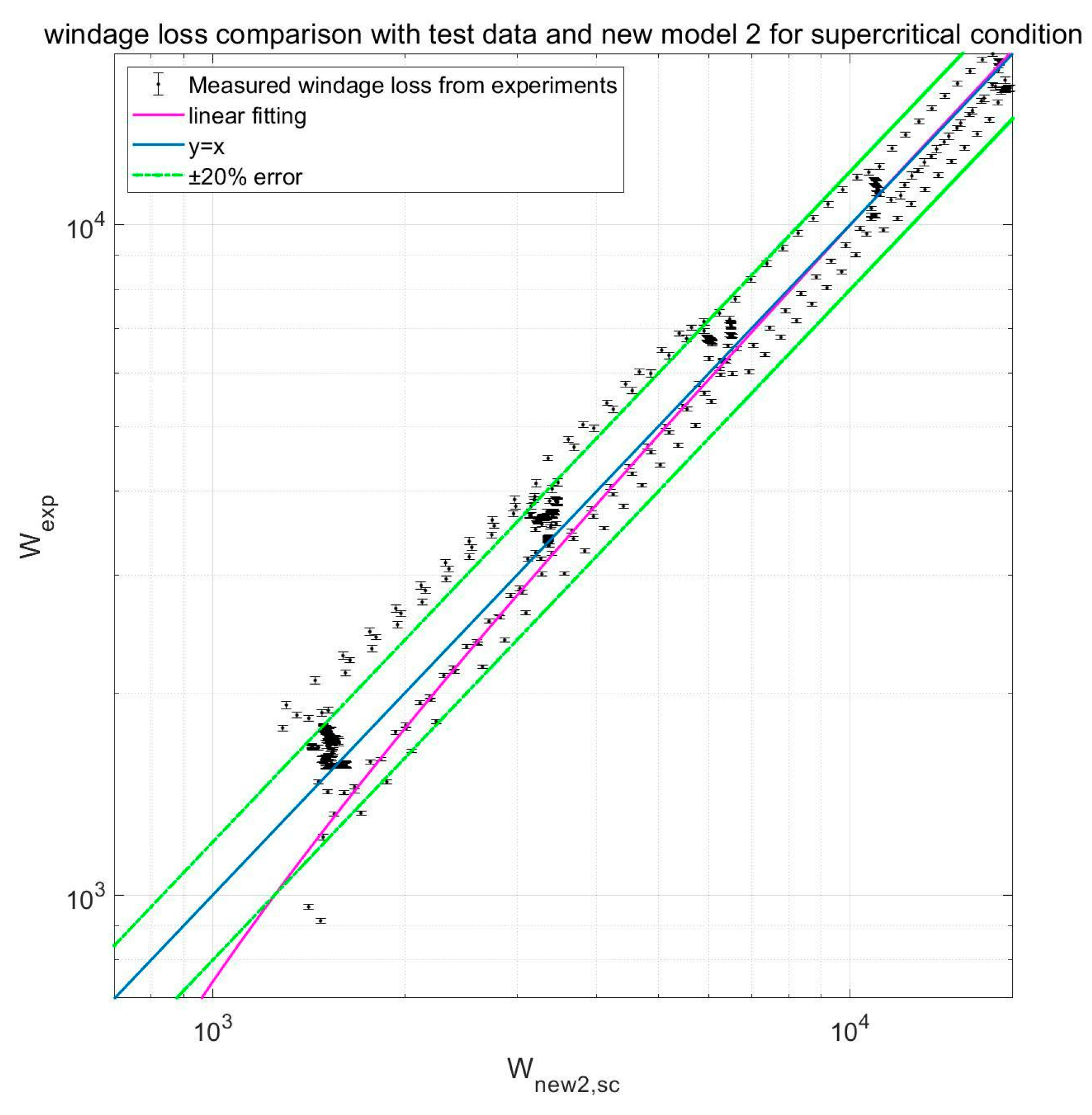
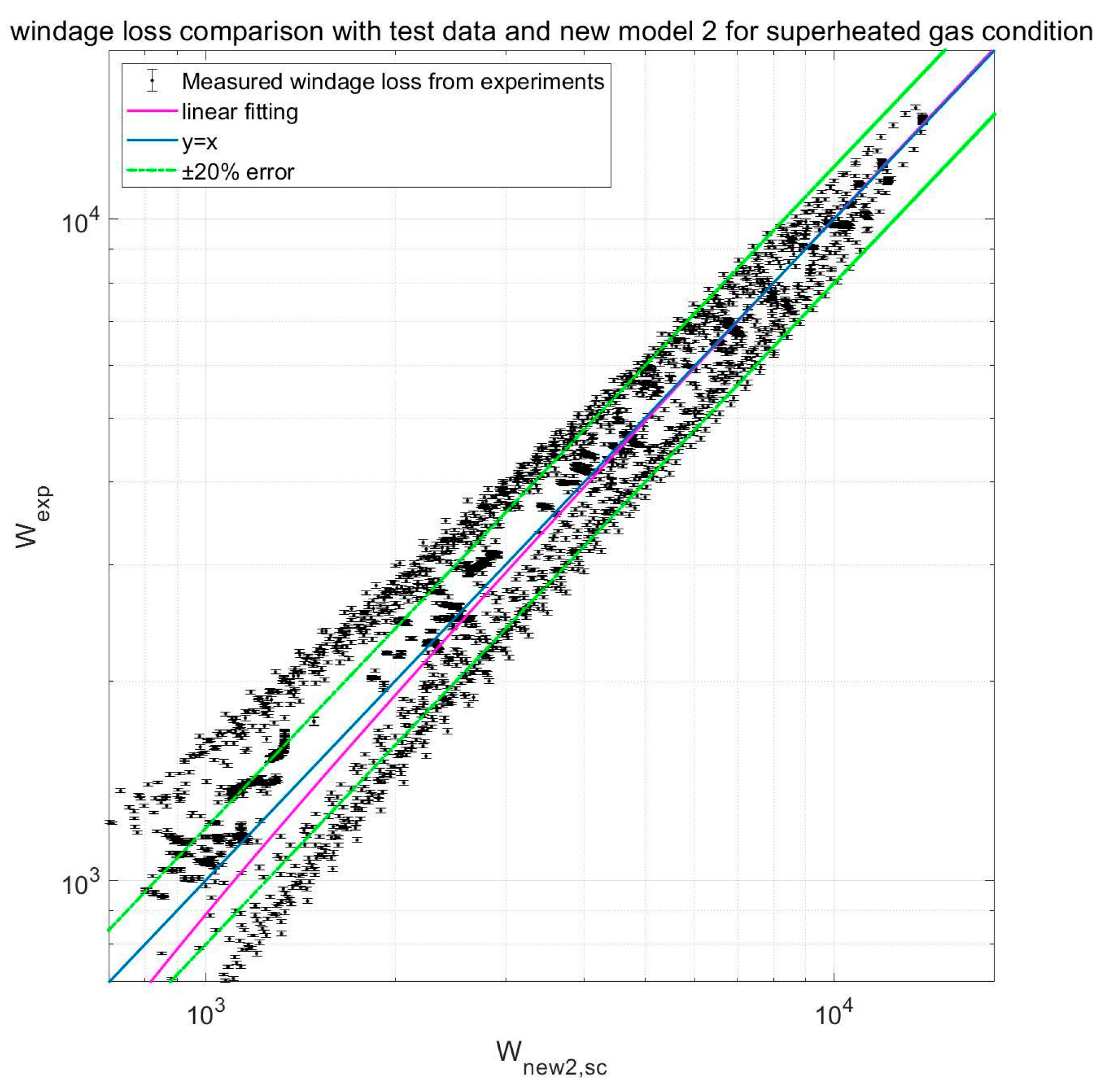
4. New S-CO2 Windage Loss Model Development
5. Summary Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | |
| Shaft length | |
| Shaft radius | |
| Clearance | |
| Clearance ratio, c/r | |
| Shaft rotation speed | |
| Axial flow velocity | |
| Pressure | |
| Temperature | |
| Enthalpy | |
| Density | |
| Kinematic viscosity | |
| Skin friction coefficient | |
| External loss | |
| Motor power input from power analyzer | |
| Disk loss | |
| Bearing loss | |
| , Reynolds number with shaft end | |
| , Reynolds number with clearance | |
| , Reynolds number with axial direction | |
| Hydraulic diameter, 2 times of clearance | |
| Uncertainty | |
| Subscript | |
| i | The values with ith control volume |
| inlet | Inlet condition |
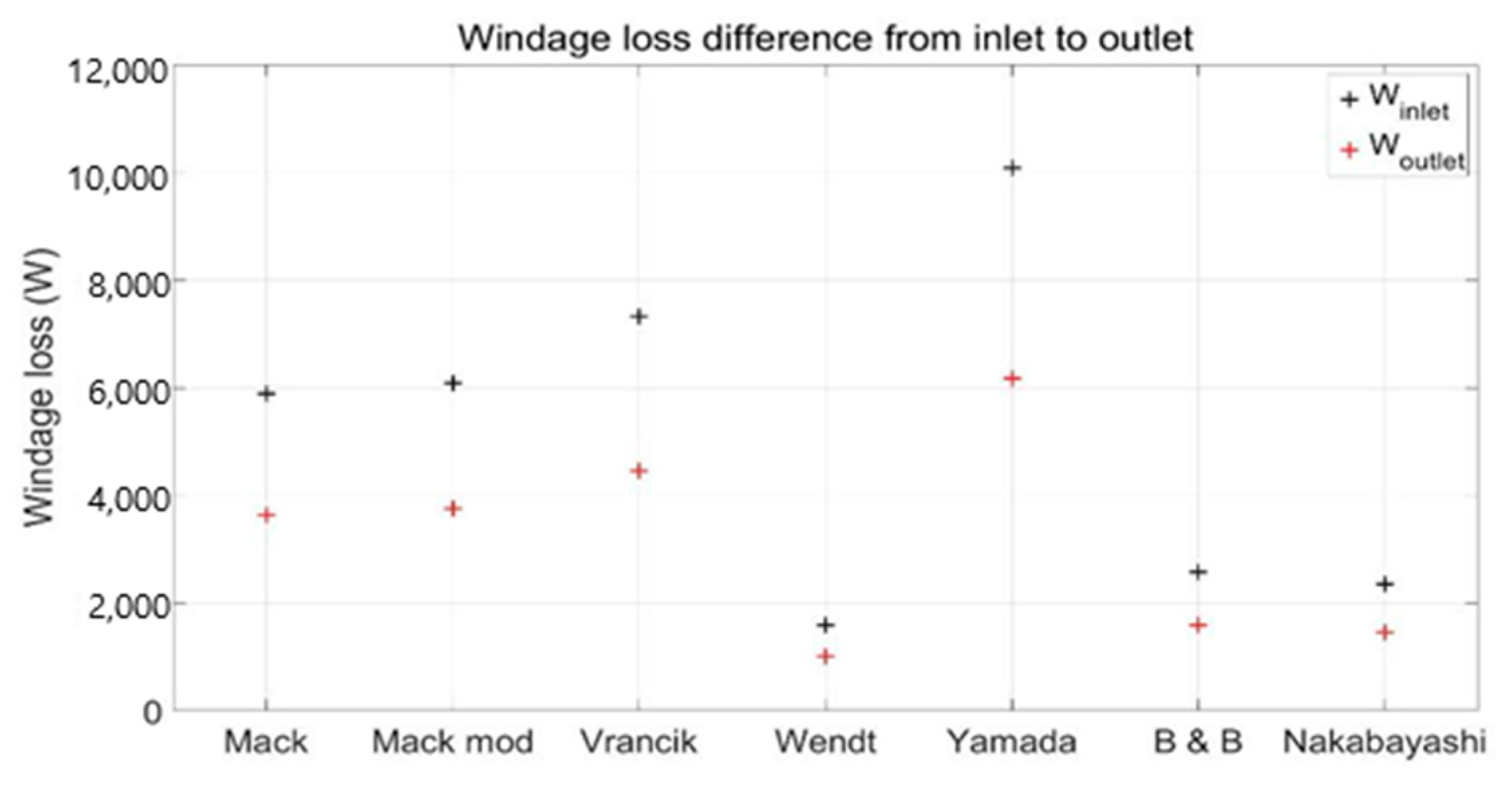
| axial | The difference through axial direction is considered |
| uniform | The condition through axial direction is uniform |
| ext | External |
| corr | Corrected model |
| T | Temperature transmitter |
| P | Pressure transmitter |
| s | Supercritical phase |
| g | Superheated gas phase |
References
- Dostal, V.; Driscoll, M.J.; Hejzlar, P. A Supercritical Carbon Dioxide Cycle for Next Generation Nuclear Reactors; Design MIT-ANP-TR-100, Advanced Nuclear Power Technology Program; MIT: Cambridge, MA, USA, 2004. [Google Scholar]
- Cho, S.K.; Bae, S.J.; Jeong, Y.; Lee, J.; Lee, J.I. Direction for high-performance supercritical CO2 centrifugal compressor design for dry cooled supercritical CO2 Brayton cycle. Appl. Sci. 2019, 9, 4057. [Google Scholar] [CrossRef] [Green Version]
- Moroz, L.; Burlaka, M.; Rudenko, O. Study of a supercritical CO2 power cycle application in a cogeneration power plant. In Proceedings of the 4th International Symposium-Supercritical CO2 Power Cycles, Pittsburgh, PA, USA, 9–10 September 2014. [Google Scholar]
- Uusitalo, A.; Turunen-Saaresti, T.; Grönman, A. Design and loss analysis of radial turbines for supercritical CO2 Brayton cycles. Energy 2021, 230, 120878. [Google Scholar] [CrossRef]
- Cho, J.; Choi, M.; Baik, Y.J.; Lee, G.; Ra, H.S.; Kim, B.; Kim, M. Development of the turbomachinery for the supercritical carbon dioxide power cycle. Int. J. Energy Res. 2016, 40, 587–599. [Google Scholar] [CrossRef]
- Persky, R.; Sauret, E. Loss models for on and off-design performance of radial inflow turbomachinery. Appl. Therm. Eng. 2019, 150, 1066–1077. [Google Scholar] [CrossRef]
- Pasch, J.J.; Conboy, T.M.; Fleming, D.D.; Rochau, G.E. Supercritical CO2 Recompression Brayton Cycle: Completed Assembly Description; No. SAND2012-9546; Sandia National Laboratories (SNL): Albuquerque, NM, USA; Livermore, CA, USA, 2012. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.K. Study of Magnetic Bearing Instability for KAIST Micro Modular Reactor Application. Master’s Thesis, KAIST, Daejeon, Republic of Korea, 2019. Available online: https://koasas.kaist.ac.kr/handle/10203/266559 (accessed on 22 June 2023).
- Kim, S.G. A Design Study of a Supercritical S-CO2 Radial Compressor by Analyzing Three-Dimensional Flow Field. Ph. Dissertation, KAIST, Daejeon, Republic of Korea, 2018. Available online: https://koasas.kaist.ac.kr/handle/10203/265052 (accessed on 22 June 2023).
- Daily, J.W.; Nece, R.E. Chamber dimension effects on induced flow and frictional resistance of enclosed rotating disks. Trans. ASME J. Basic Eng. 1960, 82, 217–232. [Google Scholar] [CrossRef]
- Kim, S.G.; Yu, H.; Moon, J.; Baik, S.; Kim, Y.; Jeong, Y.H.; Lee, J.I. A concept design of supercritical CO2 cooled SMR operating at isolated microgrid region. Int. J. Energy Res. 2017, 41, 512–525. [Google Scholar] [CrossRef]
- Rosset, K.; Schiffmann, J. Extended windage loss models for gas bearing supported spindles operated in dense gases. J. Eng. Gas Turbines Power 2020, 142, 061010. [Google Scholar] [CrossRef]
- Mack, M. Luftreibungsverluste Bei Elektrischen Maschinen Kleiner Baugrösse. Ph.D. Thesis, Universität Stuttgart, Stuttgart, Germany, 1967. [Google Scholar]
- Vrancik, J.E. Prediction of Windage Power Loss in Alternators; NASA Technical Note TN D-4849; NASA: Washington, DC, USA, 1968. [Google Scholar]
- Nachouane, A.B.; Abdelli, A.; Friedrich, G.; Vivier, S. Estimation of windage losses inside very narrow air gaps of high speed electrical machines without an internal ventilation using CFD methods. In Proceedings of the 2016 XXII International Conference on Electrical Machines (ICEM), Lausanne, Switzerland, 4–7 September 2016; pp. 2704–2710. [Google Scholar] [CrossRef]
- Wendt, F. Turbulente Strmungen zwischen zwei rotierenden konaxialen Zylinderen. Ing. Arch. 1933, 9, 577–595. [Google Scholar] [CrossRef]
- Yamada, Y. Torque Resistance of a Flow between Rotating Co-Axial Cylinders Having Axial Flow. Jpn. Soc. Mech. Eng. 1962, 5, 634–642. [Google Scholar] [CrossRef] [Green Version]
- Bilgen, E.; Boulos, R. Functional dependence of torque coefficient of coaxial cylinders on gap width and Reynolds numbers. J. Fluid Eng. 1973, 95, 122–126. [Google Scholar] [CrossRef]
- Nakabayashi, K.; Yamada, Y.; Kishimoto, T. Viscous frictional torque in the flow between two concentric rotating rough cylinders. J. Fluid Mech. 1982, 119, 409–422. [Google Scholar] [CrossRef]






| Measurement Devices | |
|---|---|
| Pressure transmitter (Rosemount 3051 s), | : 0.025% |
| Temperature transmitter (RTD, A class), | : 0.2% 0.015 K |
| Power analyzer (Yokogawa WT 3000), | : 0.02% |
| Shaft length tolerance, | : 0.03 mm |
| Shaft radius tolerance, | : 0.02 mm |
| Empirical Models | R2 Value |
|---|---|
| Mack | 0.8604 |
| Vrancik | 0.7133 |
| Wendt | −6.2276 |
| Yamada | −31.8137 |
| Bilgen and Boulos | −0.4311 |
| Nakabayashi | −0.7444 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.; Jeong, Y.; Son, I.W.; Lee, J.I. A New Windage Loss Model for S-CO2 Turbomachinery Design. Appl. Sci. 2023, 13, 7463. https://doi.org/10.3390/app13137463
Kim D, Jeong Y, Son IW, Lee JI. A New Windage Loss Model for S-CO2 Turbomachinery Design. Applied Sciences. 2023; 13(13):7463. https://doi.org/10.3390/app13137463
Chicago/Turabian StyleKim, Dokyu, Yongju Jeong, In Woo Son, and Jeong Ik Lee. 2023. "A New Windage Loss Model for S-CO2 Turbomachinery Design" Applied Sciences 13, no. 13: 7463. https://doi.org/10.3390/app13137463
APA StyleKim, D., Jeong, Y., Son, I. W., & Lee, J. I. (2023). A New Windage Loss Model for S-CO2 Turbomachinery Design. Applied Sciences, 13(13), 7463. https://doi.org/10.3390/app13137463





