Temperature-Controlled Hyperthermia with Non-Invasive Temperature Monitoring through Speed of Sound Imaging
Abstract
1. Introduction
2. Mathematical Model and Theory
2.1. Acoustic Heating
2.2. Speed of Sound Imaging
3. Experiment and Analysis
3.1. Simulation Tools
3.2. Simulation Setup
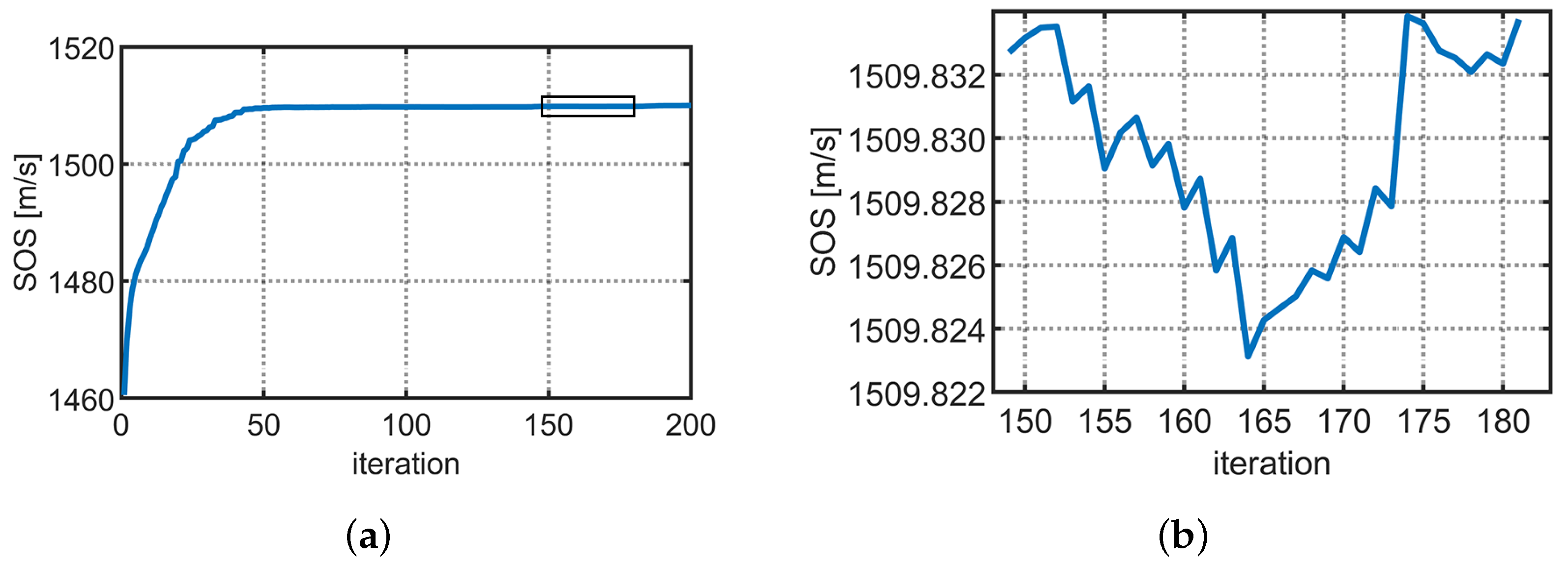
3.3. Imaging
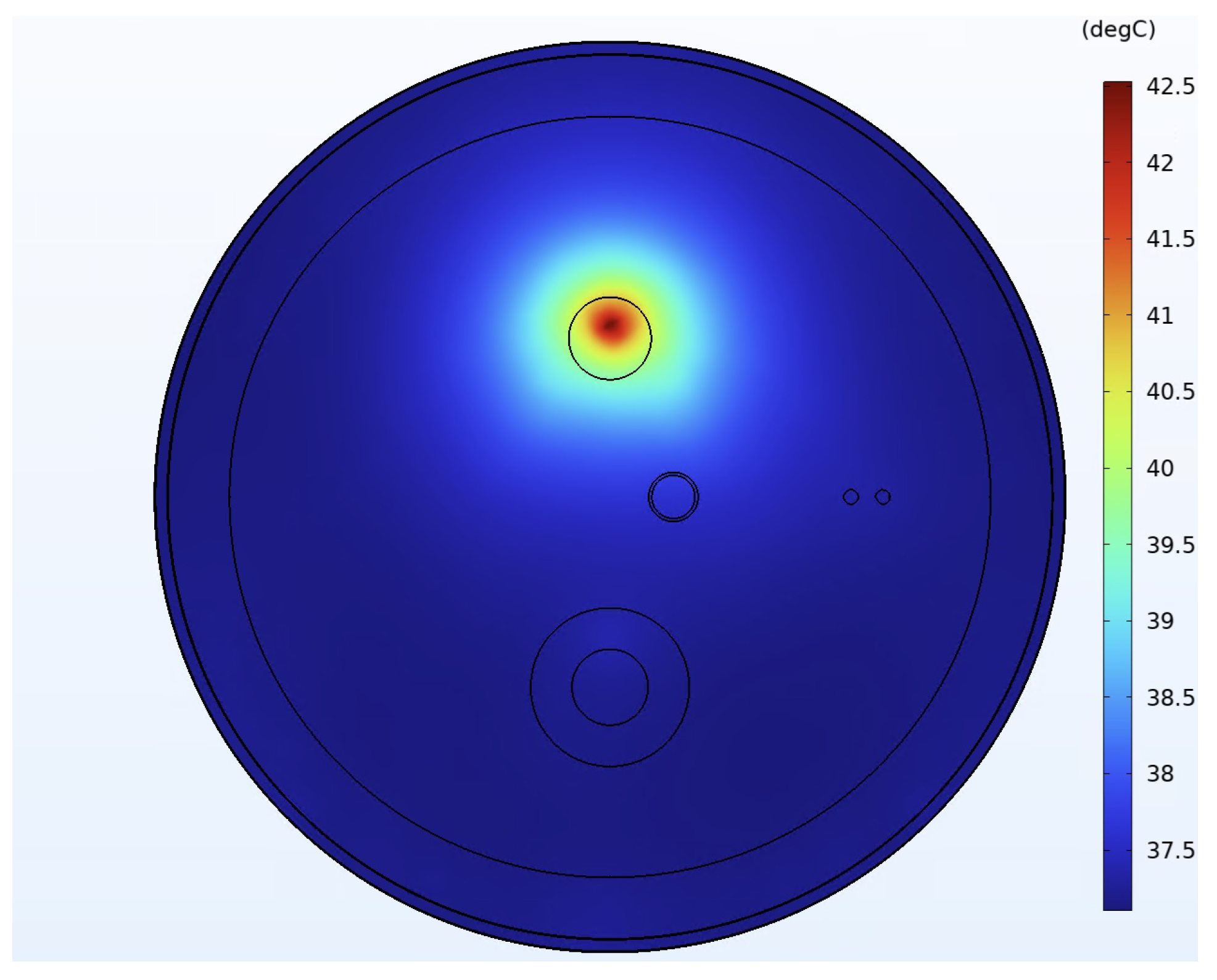
3.4. Temperature-Controlled Hyperthermia
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mallory, M.; Gogineni, E.; Jones, G.C.; Greer, L. Therapeutic hyperthermia: The old, the new, and the upcoming. Crit. Rev. Oncol. 2016, 97, 56–64. [Google Scholar] [CrossRef] [PubMed]
- Al-Bataineh, O.; Jenne, J.; Huber, P. Clinical and future applications of high intensity focused ultrasound in cancer. Cancer Treat. Rev. 2012, 38, 346–353. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.-F. High intensity focused ultrasound in clinical tumor ablation. World J. Clin. Oncol. 2011, 2, 8. [Google Scholar] [CrossRef] [PubMed]
- Group, I.C.H.; Vernon, C.C.; Hand, J.W.; Field, S.B.; Machin, D.; Whaley, J.B.; van der Zee, J.; van Putten, W.L.; van Rhoon, G.C.; van Dijk, J.D.; et al. Radiotherapy with or without hyperthermia in the treatment of superficial localized breast cancer: Results from five randomized controlled trials. Int. J. Radiat. Oncol. Biol. Phys. 1996, 35, 731–744. [Google Scholar]
- Longo, T.A.; Gopalakrishna, A.; Tsivian, M.; Van Noord, M.; Rasch, C.R.; Inman, B.A.; Geijsen, E.D. A systematic review of regional hyperthermia therapy in bladder cancer. Int. J. Radiat. Oncol. Biol. Phys. 2016, 32, 381–389. [Google Scholar] [CrossRef]
- der Zee, T.J.V. Heating the patient: A promising approach? Ann. Oncol. 2002, 13, 1173–1184. [Google Scholar] [CrossRef]
- Habash, R.; Krewski, D.; Bansal, R.; Alhafid, H.T. Principles, applications, risks and benefits of therapeutic hyperthermia. Front. Biosci. Elite Ed. 2011, 3, 1169–1181. [Google Scholar] [CrossRef]
- Zhu, L.; Altman, M.B.; Laszlo, A.; Straube, W.; Zoberi, I.; Hallahan, D.E.; Chen, H. Ultrasound hyperthermia technology for radiosensitization. Ultrasound Med. Biol. 2019, 45, 1025–1043. [Google Scholar] [CrossRef]
- Eranki, A.; Srinivasan, P.; Ries, M.; Kim, A.; Lazarski, C.A.; Rossi, C.T.; Khokhlova, T.D.; Wilson, E.; Knoblach, S.M.; Sharma, K.V.; et al. High-Intensity focused ultrasound (HIFU) triggers immune sensitization of refractory murine neuroblastoma to checkpoint inhibitor therapy. Clin. Cancer Res. 2020, 26, 1152–1161. [Google Scholar] [CrossRef]
- Ebbini, E.S.; Haar, G.T. Ultrasound-guided therapeutic focused ultrasound: Current status and future directions. Int. J. Hyperth. 2015, 31, 77–89. [Google Scholar] [CrossRef]
- Botros, Y.Y.; Volakis, J.L.; VanBaren, P.; Ebbini, E.S. A hybrid computational model for ultrasound phased-array heating in presence of strongly scattering obstacles. IEEE Trans. Biomed. Eng. 1997, 44, 1039–1050. [Google Scholar] [CrossRef]
- Kennedy, J.E.; Haar, G.T.; Cranston, D. High intensity focused ultrasound: Surgery of the future? Br. J. Radiol. 2003, 76, 590–599. [Google Scholar] [CrossRef]
- Hindley, J.; Gedroyc, W.M.; Regan, L.; Regan, L.; Stewart, E.; Tempany, C.; Hynnen, K.; Macdanold, N.; Inbar, Y.; Itzchak, Y.; et al. MRI guidance of focused ultrasound therapy of uterine fibroids: Early results. Am. J. Roentgenol. 2004, 183, 1713–1719. [Google Scholar] [CrossRef]
- Huber, P.E.; Jenne, J.W.; Rastert, R.; Simiantonakis, I.; Sinn, H.P.; Strittmatter, H.J.; von Fournier, D.; Wannenmacher, M.F.; Debus, J. A new noninvasive approach in breast cancer therapy using magnetic resonance imaging-guided focused ultrasound surgery. Cancer Res. 2001, 61, 8441–8447. [Google Scholar]
- Martin, E.; Jeanmonod, D.; Morel, A.; Zadicario, E.; Werner, B. High-intensity focused ultrasound for noninvasive functional neurosurgery. Ann. Neurol. Off. J. Am. Neurol. Assoc. Child Neurol. Soc. 2009, 66, 858–861. [Google Scholar] [CrossRef]
- Wright, N.; Humphrey, J. Denaturation of collagen via heating: An irreversible rate process. Annu. Rev. Biomed. Eng. 2002, 4, 109–128. [Google Scholar] [CrossRef]
- Hildebr, T.B.; Wust, P.; Ahlers, O.; Dieing, A.; Sreenivasa, G.; Kerner, T.; Felix, R.; Riess, H. The cellular and molecular basis of hyperthermia. Crit. Rev. Oncol. 2002, 43, 33–56. [Google Scholar] [CrossRef]
- Mazumder, D.; Vasu, R.M.; Roy, D.; Kanhirodan, R. A remote temperature sensor for an ultrasound hyperthermia system using the acoustic signal derived from the heating signals. Int. J. Hyperth. 2018, 34, 122–131. [Google Scholar] [CrossRef]
- Solovchuk, M.A.; Hwang, S.C.; Chang, H.; Thiriet, M.; Sheu, T.W. Temperature elevation by HIFU in ex vivo porcine muscle: MRI measurement and simulation study. Med. Phys. 2014, 41, 052903. [Google Scholar] [CrossRef]
- Poorter, J.D.; Wagter, C.D.; Deene, Y.D.; Thomsen, C.; Ståhlberg, F.; Achten, E. Noninvasive MRI thermometry with the proton resonance frequency (PRF) method: In vivo results in human muscle. Magn. Reson. Med. 1995, 33, 74–81. [Google Scholar] [CrossRef]
- Crezee, J.; Van Leeuwen, C.M.; Oei, A.L.; van Heerden, L.E.; Bel, A.; Stalpers, L.J.A.; Ghadjar, P.; Franken, N.A.P.; Kok, H.P. Biological modelling of the radiation dose escalation effect of regional hyperthermia in cervical cancer. Radiat. Oncol. 2016, 11, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Datta, N.R.; Rogers, S.; Ordóñez, S.G.; Puric, E.; Bodis, S. Hyperthermia and radiotherapy in the management of head and neck cancers: A systematic review and meta-analysis. Int. J. Hyperth. 2016, 32, 31–40. [Google Scholar] [CrossRef] [PubMed]
- Hurwitz, M.D.; Ghanouni, P.; Kanaev, S.V.; Iozeffi, D.; Gianfelice, D.; Fennessy, F.M.; Kuten, A.; Meyer, J.E.; LeBlang, S.D.; Roberts, A.; et al. Magnetic resonance–guided focused ultrasound for patients with painful bone metastases: Phase III trial results. JNCI J. Natl. Cancer Inst. 2014, 106, dju082. [Google Scholar] [CrossRef]
- Ellis, S.; Rieke, V.; Kohi, M.; Westphalen, A.C. Clinical applications for magnetic resonance guided high intensity focused ultrasound (MRgHIFU): Present and future. J. Med. Imaging Radiat. Oncol. 2013, 57, 391–399. [Google Scholar] [CrossRef] [PubMed]
- Celicanin, Z.; Manasseh, G.; Petrusca, L.; Scheffler, K.; Auboiroux, V.; Crowe, L.A.; Hyacinthe, J.N.; Natsuaki, Y.; Santini, F.; Becker, C.D.; et al. Hybrid ultrasound-MR guided HIFU treatment method with 3 D motion compensation. Magn. Reson. Med. 2018, 79, 2511–2523. [Google Scholar] [CrossRef] [PubMed]
- Ries, M.; de Senneville, B.D.; Regard, Y.; Moonen, C. Combined magnetic resonance imaging and ultrasound echography guidance for motion compensated HIFU interventions. AIP Conf. Proc. 2012, 1503, 202–206. [Google Scholar]
- Maloney, E.; Hwang, J.H. Emerging HIFU applications in cancer therapy. Int. J. Hyperth. 2015, 31, 302–309. [Google Scholar] [CrossRef]
- Vaezy, S.; Shi, X.; Martin, R.W.; Chi, E.; Nelson, P.I.; Bailey, M.R.; Crum, L.A. Real-time visualization of high-intensity focused ultrasound treatment using ultrasound imaging. Ltrasound Med. Biol. 2001, 27, 33–42. [Google Scholar] [CrossRef]
- Yagawa, Y.; Tanigawa, K.; Kobayashi, Y.; Yamamoto, M. Cancer immunity and therapy using hyperthermia with immunotherapy, radiotherapy, chemotherapy, and surgery. J. Cancer Metastasis Treat. 2017, 3, 218–230. [Google Scholar] [CrossRef]
- Bakker, A.; Holman, R.; Rodrigues, D.B.; Dobsicek Trefna, H.; Stauffer, P.R.; van Tienhoven, G.; Rasch, C.R.; Crezee, H. Analysis of clinical data to determine the minimum number of sensors required for adequate skin temperature monitoring of superficial hyperthermia treatments. Int. J. Hyperth. 2018, 34, 910–917. [Google Scholar] [CrossRef]
- Pierce, A.D. Acoustics: An Introduction to Its Physical Principles and Applications; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Waters, K.R.; Mobley, J.; Miller, J.G. Causality-imposed (Kramers-Kronig) relationships between attenuation and dispersion. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 822–823. [Google Scholar] [CrossRef]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef]
- Pérez-Liva, M.; Herraiz, J.; Udías, J.; Miller, E.; Cox, B.; Treeby, B. Time domain reconstruction of sound speed and attenuation in ultrasound computed tomography using full wave inversion. J. Acoust. Soc. Am. 2017, 141, 1595–1604. [Google Scholar] [CrossRef]
- Shishitani, T.; Yoshizawa, S.; Umemura, S.-I. 2P-46 Study on Change in Sound Speed by HIFU-Exposure in Chicken Breast Muscle. In Proceedings of the Symposium on Ultrasonic Electronics, Tokyo, Japan, 6–8 December 2010; Institute for Ultrasonic Elecronics: Hong Kong, China; Volume 31, pp. 381–382. [Google Scholar]
- Zhu, Y.H.; Yuan, J.; Pinter, S.Z.; Kripfgans, O.D.; Cheng, Q.; Wang, X.D.; Tao, C.; Liu, X.J.; Xu, G.; Carson, P.L. Adaptive optimization on ultrasonic transmission tomography-based temperature image for biomedical treatment. Chin. Phys. B 2017, 26, 064301. [Google Scholar] [CrossRef]
- Anam, C.; Haryanto, F.; Widita, R.; Arif, I.; Dougherty, G. An investigation of spatial resolution and noise in reconstructed CT images using iterative reconstruction (IR) and filtered back-projection (FBP). Ournal Phys. Conf. Ser. 2019, 1127, 012016. [Google Scholar] [CrossRef]
- Yuan, Y.; Shen, Y.; Zhao, Y.; Xiao, Y.; Jin, J.; Feng, N. A Modified Ray Tracing Method for Ultrasound Computed Tomography in Breast Imaging. In Proceedings of the 2020 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Dubrovnik, Croatia, 25–28 May 2020; pp. 1–6. [Google Scholar]
- Ozmen, N.; Dapp, R.; Zapf, M.; Gemmeke, H.; Ruiter, N.V.; van Dongen, K.W. Comparing different ultrasound imaging methods for breast cancer detection. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 637–646. [Google Scholar] [CrossRef]
- Hormati, A.; Jovanović, I.; Roy, O.; Vetterli, M. Robust ultrasound travel-time tomography using the bent ray model. In Medical Imaging 2010: Ultrasonic Imaging, Tomography, and Therapy; International Society for Optics and Photonics: Bellingham, WA, USA, 2010; Volume 7629, p. 76290I. [Google Scholar]
- Zhang, Z.; Huang, L.; Lin, Y. Efficient implementation of ultrasound waveform tomography using source encoding. In Medical Imaging 2012: Ultrasonic Imaging, Tomography, and Therapy; International Society for Optics and Photonics: Bellingham, WA, USA, 2012; p. 832003. [Google Scholar]
- Roy, O.; Jovanović, I.; Hormati, A.; Parhizkar, R.; Vetterli, M. Sound speed estimation using wave-based ultrasound tomography: Theory and GPU implementation. In Medical Imaging 2010: Ultrasonic Imaging, Tomography, and Therapy; International Society for Optics and Photonics: Bellingham, WA, USA, 2010; p. 76290J. [Google Scholar]
- Wiskin, J.; Borup, D.; Johnson, S.; Berggren, M. Non-linear inverse scattering: High resolution quantitative breast tissue tomography. J. Acoust. Soc. Am. 2012, 131, 3802–3813. [Google Scholar] [CrossRef]
- Wang, K.; Matthews, T.; Anis, F.; Li, C.; Duric, N.; Anastasio, M.A. Waveform inversion with source encoding for breast sound speed reconstruction in ultrasound computed tomography. IEEE Trans. Ultrason. Ferroelectr. 2015, 62, 475–493. [Google Scholar] [CrossRef]
- Li, Y.; Shi, Q.; Li, Y.; Song, X.; Liu, C.; Ta, D.; Wang, W. High-resolution bone microstructure imaging based on ultrasonic frequency-domain full-waveform inversion. Chin. Phys. B 2021, 30, 014302. [Google Scholar] [CrossRef]
- Treeby, B.E.; Cox, B.T. K-Wave: MATLAB toolbox for the simulation and reconstruction of photoacoustic wave fields. J. Biomed. Opt. 2010, 15, 021314. [Google Scholar] [CrossRef]
- Treeby, B.E.; Jaros, J.; Rendell, A.P.; Cox, B. Modeling nonlinear ultrasound propagation in heterogeneous media with power law absorption using ak-space pseudospectral method. J. Acoust. Soc. Am. 2012, 131, 4324–4336. [Google Scholar] [CrossRef] [PubMed]
- Treeby, B.E.; Cox, B.T. Modeling power law absorption and dispersion for acoustic propagation using the fractional Laplacian. J. Acoust. Soc. Am. 2010, 127, 2741–2748. [Google Scholar] [CrossRef] [PubMed]
- Folkman, J. Tumor angiogenesis: Therapeutic implications. N. Engl. J. Med. 1971, 285, 1182–1186. [Google Scholar] [PubMed]
- Eyckeshymer, A.C.; Schoemaker, D.M. A Cross-Sectional Anatomy; Meridith Corp: New York, NY, USA, 1970; p. 137. [Google Scholar]
- Duck, F.A. Physical Properties of Tissues: A Comprehensive Reference Book; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Klemm, M.; Craddock, I.J.; Leendertz, J.A.; Preece, A.; Benjamin, R. Improved delay-and-sum beamforming algorithm for breast cancer detection. Int. J. Antennas Propag. 2008, 2008, 761402. [Google Scholar] [CrossRef]
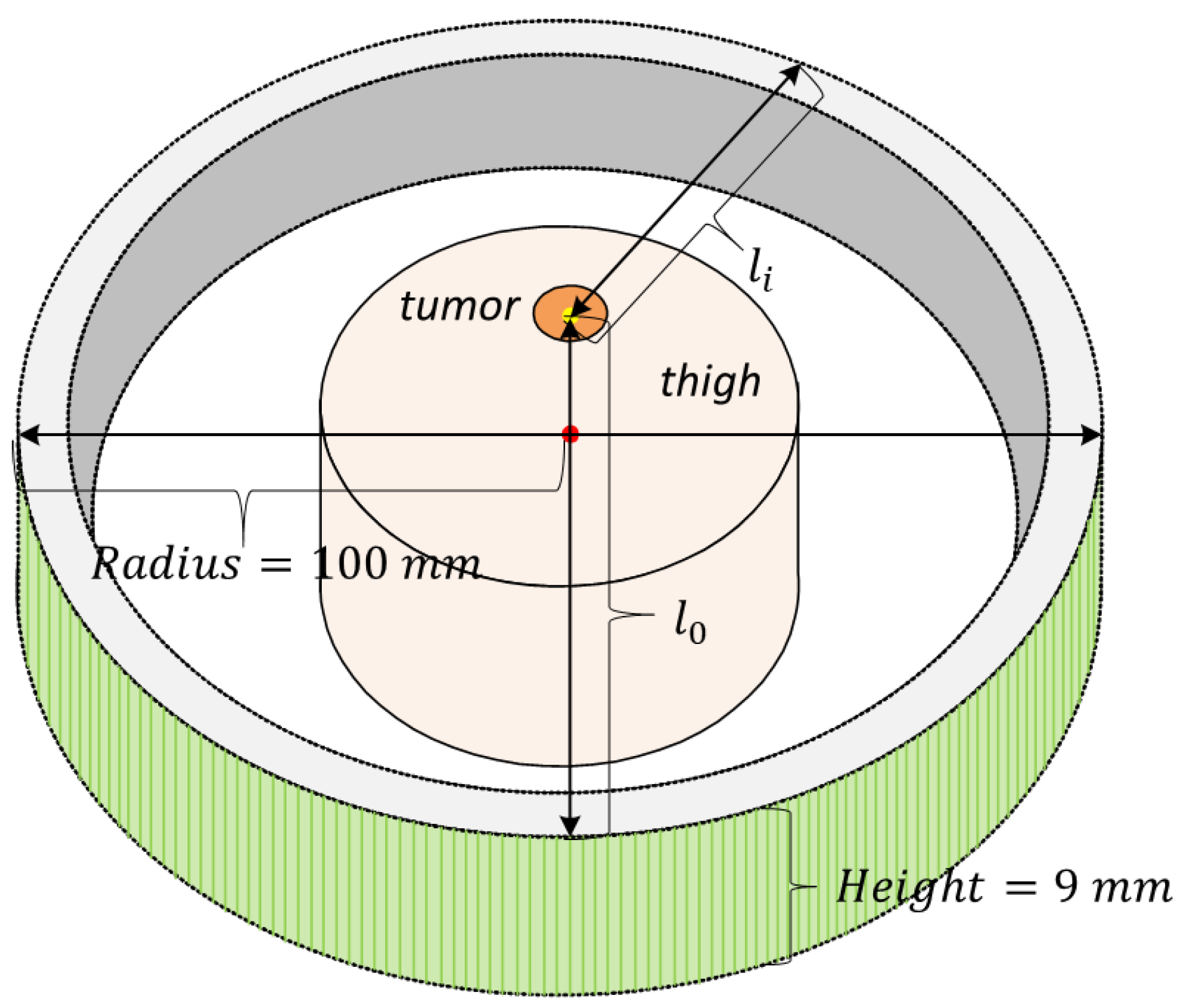
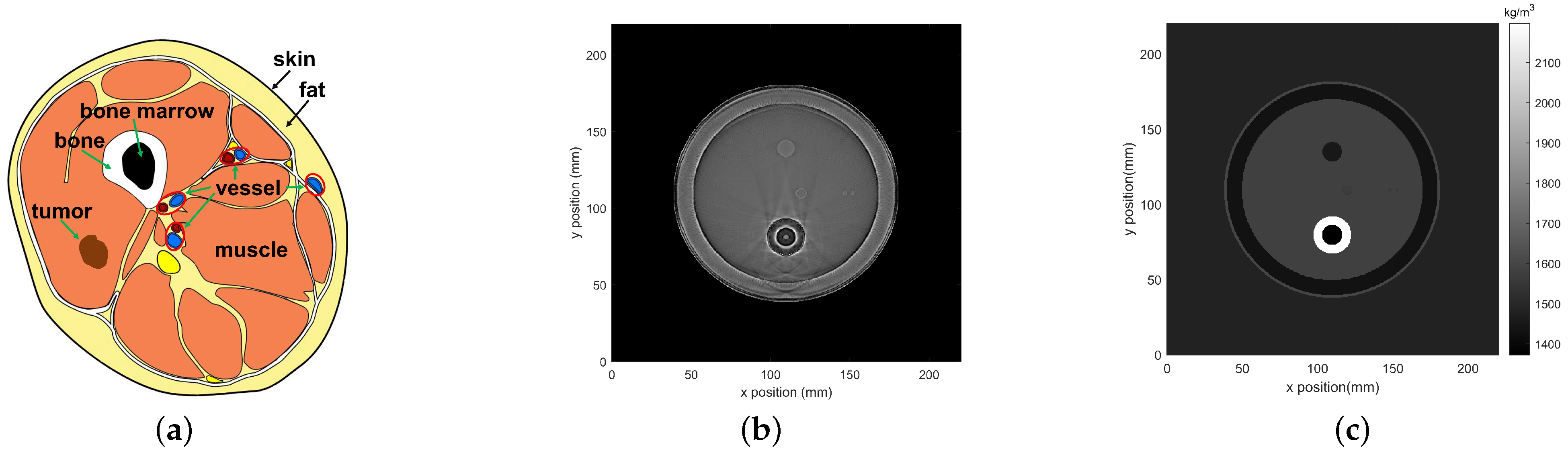
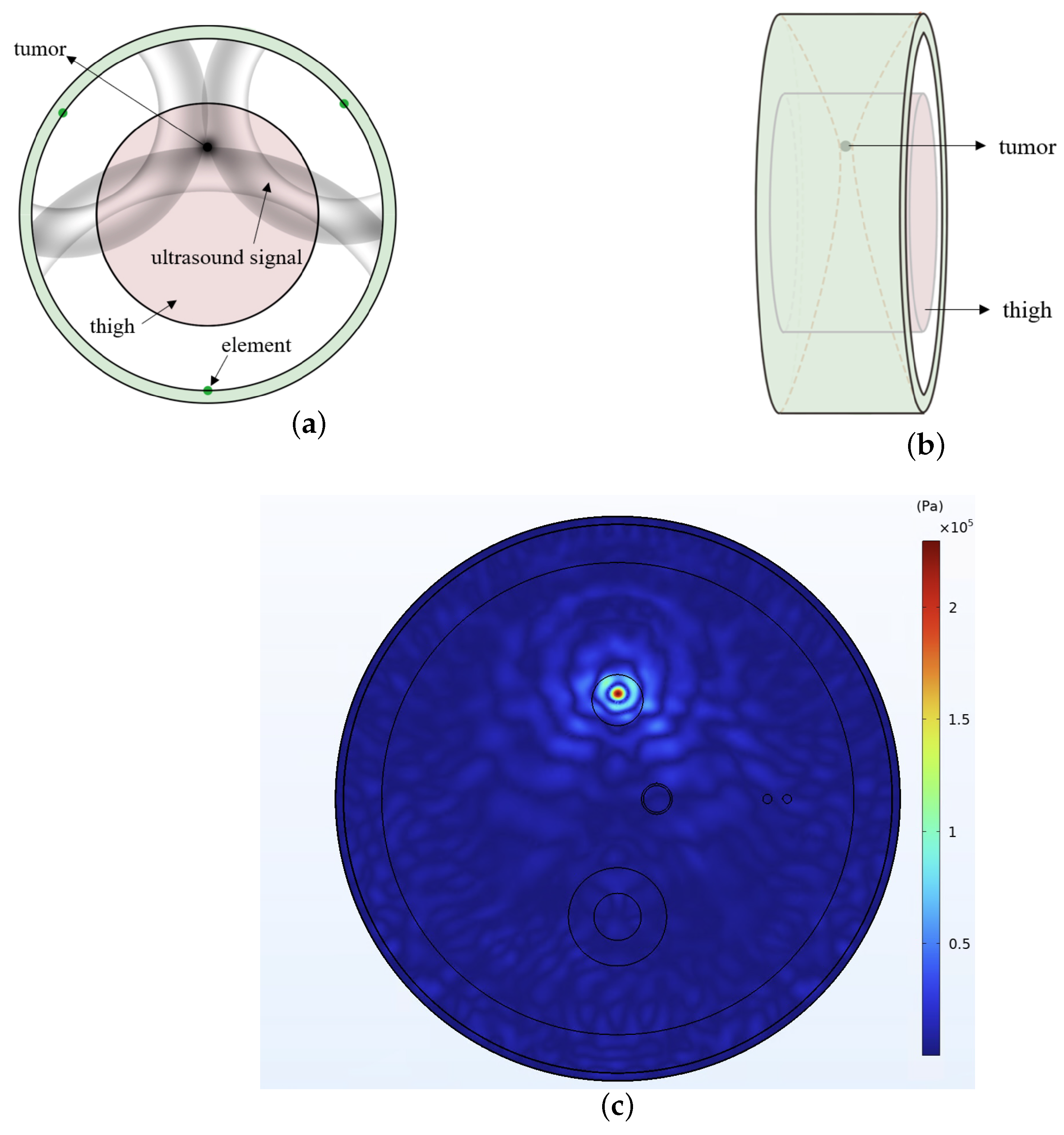
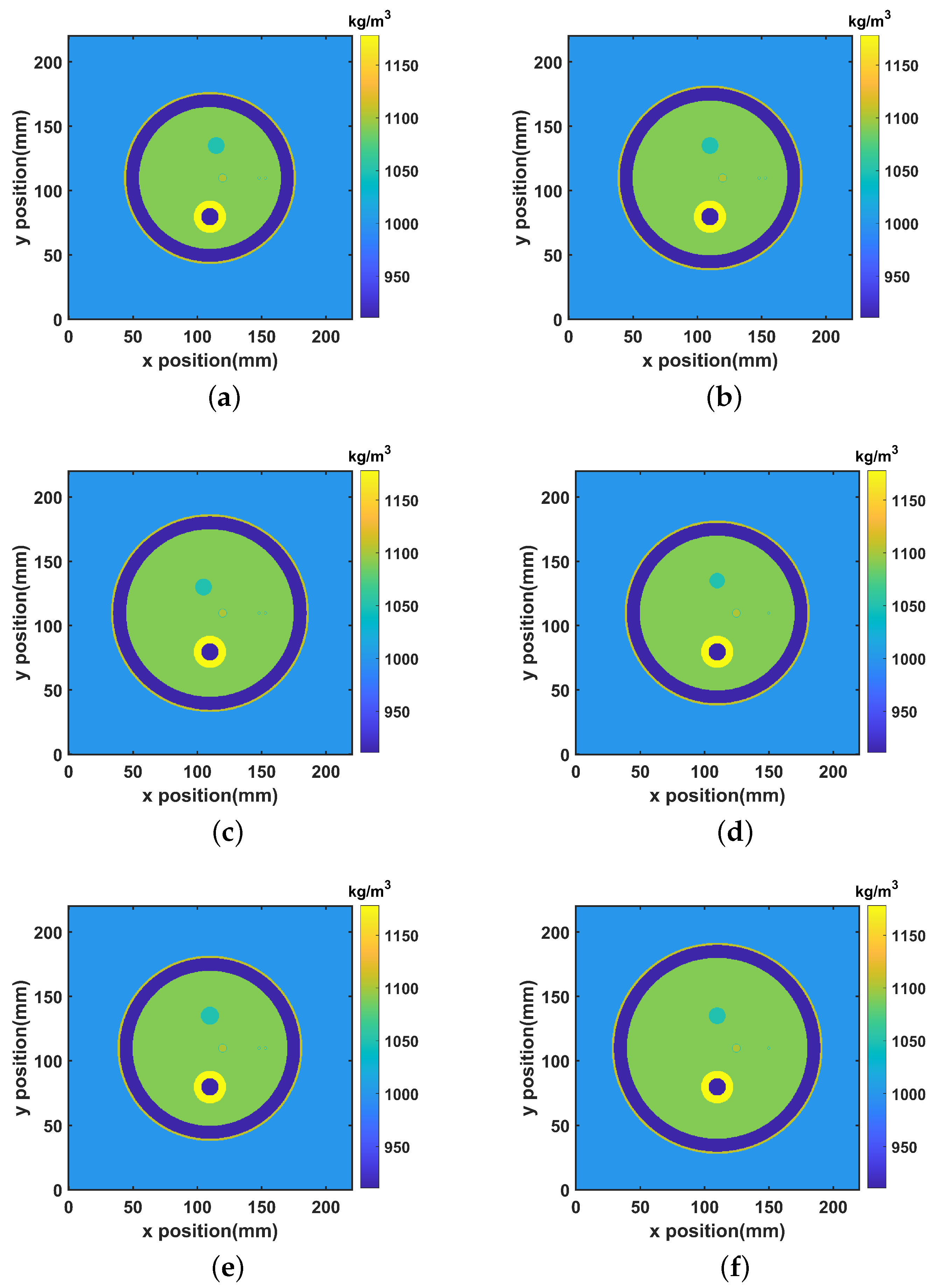

| Medium | Size (mm) | SOS (m/s) | Density (kg/m) | Attenuation Coefficient (NP/Mhz·m) | Thermal Conductivity (W/m · °C) | Specific Heat Capacity (J/kg · °C) |
|---|---|---|---|---|---|---|
| Water | 220 × 220 × 18 | 1482 | 1000 | 0.025 | 0.60 | 4178 |
| Skin | 1.70 (Thickness) | 1595 | 1109 | 21.158 | 0.37 | 3391 |
| Fat | 10.00 (Radius) | 1430 | 911 | 4.358 | 0.21 | 2348 |
| Muscle | 60.00 (Radius) | 1580 | 1090 | 7.109 | 0.49 | 3421 |
| Bone | 5.80 (Radius) | 2198 | 1178 | 47.000 | 0.32 | 1313 |
| Bone Marrow | 6.70 (Radius) | 1372 | 980 | 4.358 | 0.20 | 2065 |
| Tumor | 6.50 (Radius) | 1450 | 1050 | 5.650 | 0.51 | 3540 |
| Blood Vessel Wall | 0.50 (Thickness) | 1570 | 1100 | 7.020 | 0.46 | 3306 |
| Big Vessel (Blood) | 2.90 (Radius) | 1550 | 1060 | 2.368 | 0.52 | 3617 |
| small Vessel (Blood) | 0.65 (Radius) | 1550 | 1060 | 2.368 | 0.52 | 3617 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Sun, Y.; Wang, Y.; Chen, Y.; Ge, Y.; Yuan, J.; Carson, P. Temperature-Controlled Hyperthermia with Non-Invasive Temperature Monitoring through Speed of Sound Imaging. Appl. Sci. 2023, 13, 7317. https://doi.org/10.3390/app13127317
Wang H, Sun Y, Wang Y, Chen Y, Ge Y, Yuan J, Carson P. Temperature-Controlled Hyperthermia with Non-Invasive Temperature Monitoring through Speed of Sound Imaging. Applied Sciences. 2023; 13(12):7317. https://doi.org/10.3390/app13127317
Chicago/Turabian StyleWang, Haoyang, Yuchen Sun, Yuxin Wang, Ying Chen, Yun Ge, Jie Yuan, and Paul Carson. 2023. "Temperature-Controlled Hyperthermia with Non-Invasive Temperature Monitoring through Speed of Sound Imaging" Applied Sciences 13, no. 12: 7317. https://doi.org/10.3390/app13127317
APA StyleWang, H., Sun, Y., Wang, Y., Chen, Y., Ge, Y., Yuan, J., & Carson, P. (2023). Temperature-Controlled Hyperthermia with Non-Invasive Temperature Monitoring through Speed of Sound Imaging. Applied Sciences, 13(12), 7317. https://doi.org/10.3390/app13127317






