Interactive Guiding Sparse Auto-Encoder with Wasserstein Regularization for Efficient Classification
Abstract
1. Introduction
Main Contributions
- We reduce overfitting of the autoencoder to propose a new structure that can utilize both label information and reconstruction information, similar to semi-supervised learning by proposing a guiding layer before and after the reconstruction layer of the autoencoder.
- We design an architecture that consists of two different autoencoders and show outstanding classification performance compared to six representative feature extraction methods.
2. Background and Related Works
2.1. Sparse Autoencoder (SAE)
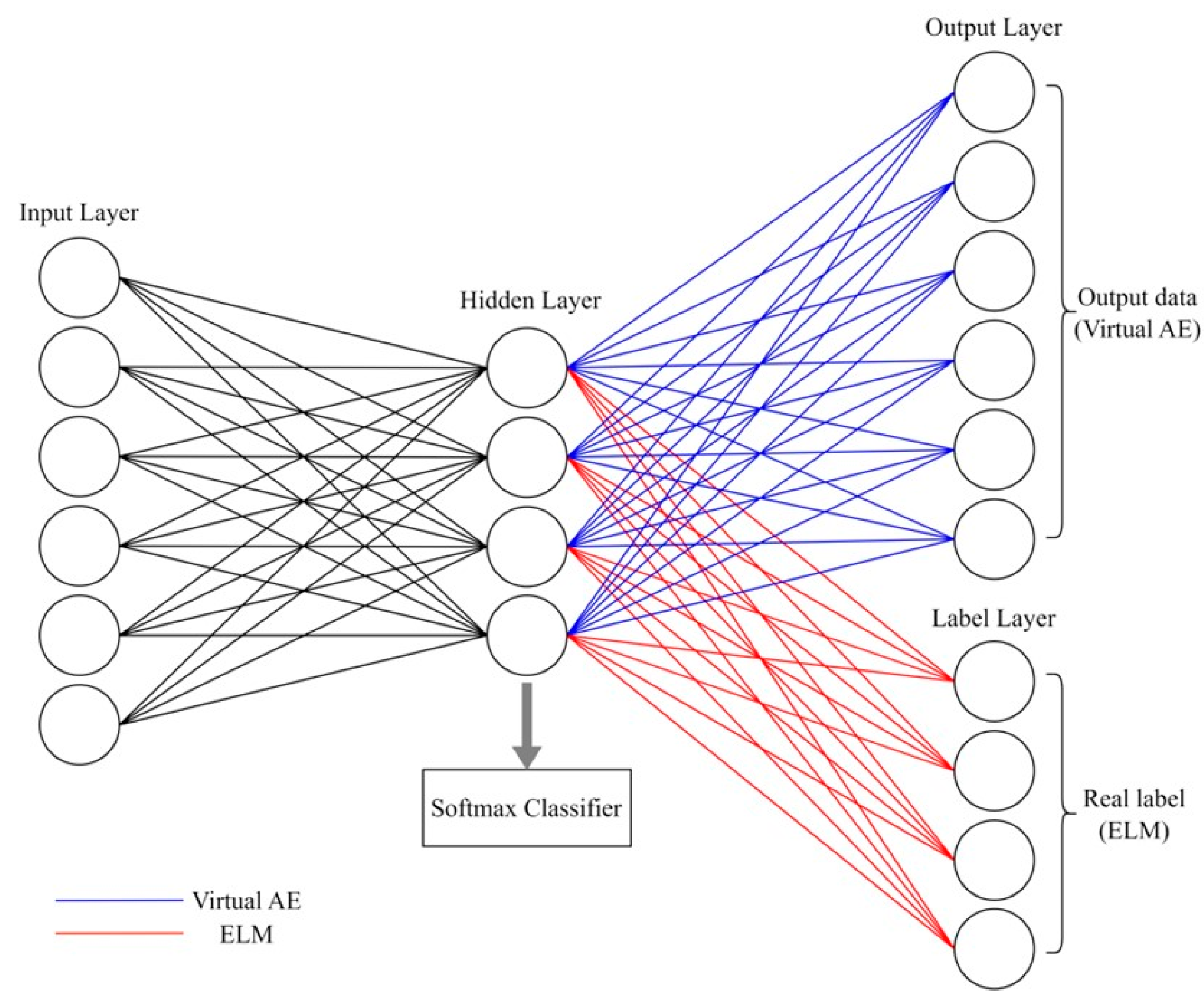
2.2. Label and Sparse Regularization Autoencoder (LSRAE)
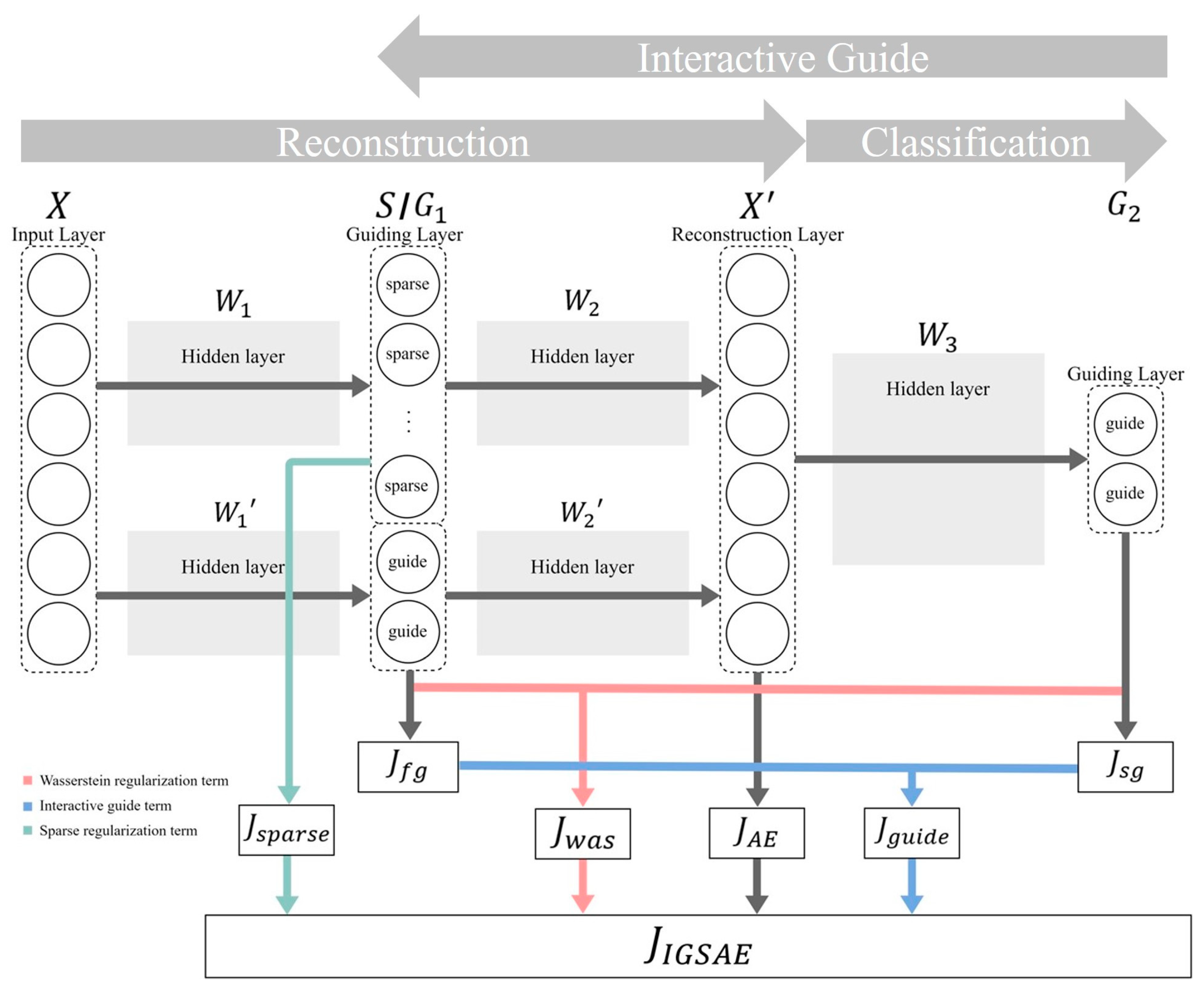
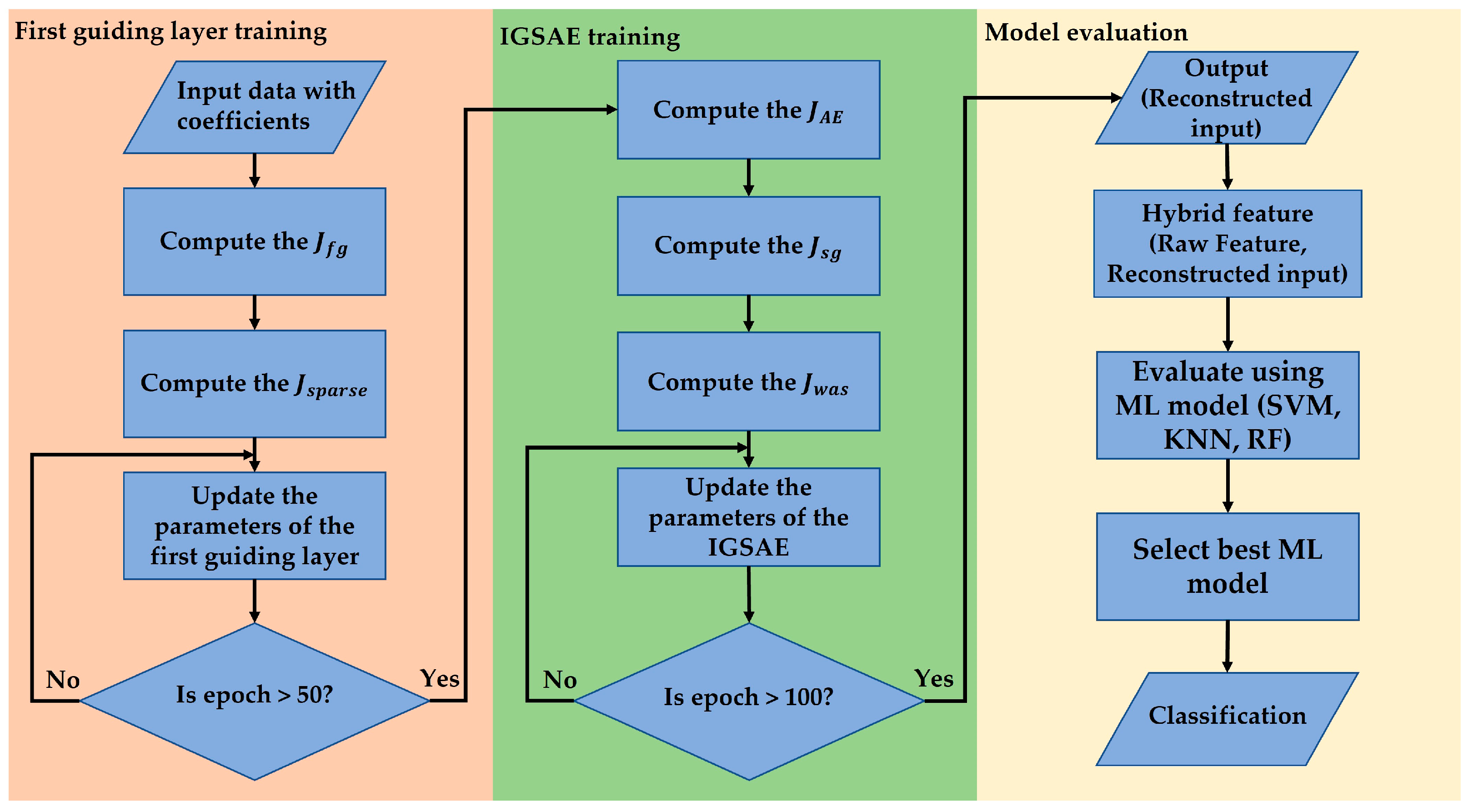
3. Interactive Guiding Sparse Autoencoder
| Algorithm 1: IGSAE |
| Input: Guided feature (input data), Guiding feature 1: Setting hyper parameters: . Number of hidden layers and units. 2: Pretraining about of the first guiding layer using Equation (10) 3: Training start 4: Compute and of the first guiding layer and the and terms. 5: Compute of the reconstruction layer and term. 6: Compute of the second guiding layer and the and terms. 7: Compute partial derivative , and to compute the gradients by Equations (22)–(25) 8: Update the weights using gradient descent. 9: Repeat until iterations. Output: Reconstructed guided feature |
4. Experimental Result of IGSAE
4.1. Datasets and Experimental Setups
4.2. Authentication of Main Innovation
4.3. Comparison of the Benchmark Datasets
4.4. Prevention of Transforming Irrelevant Data Such as Training Data
4.5. Effect of the Coefficients and Classifiers
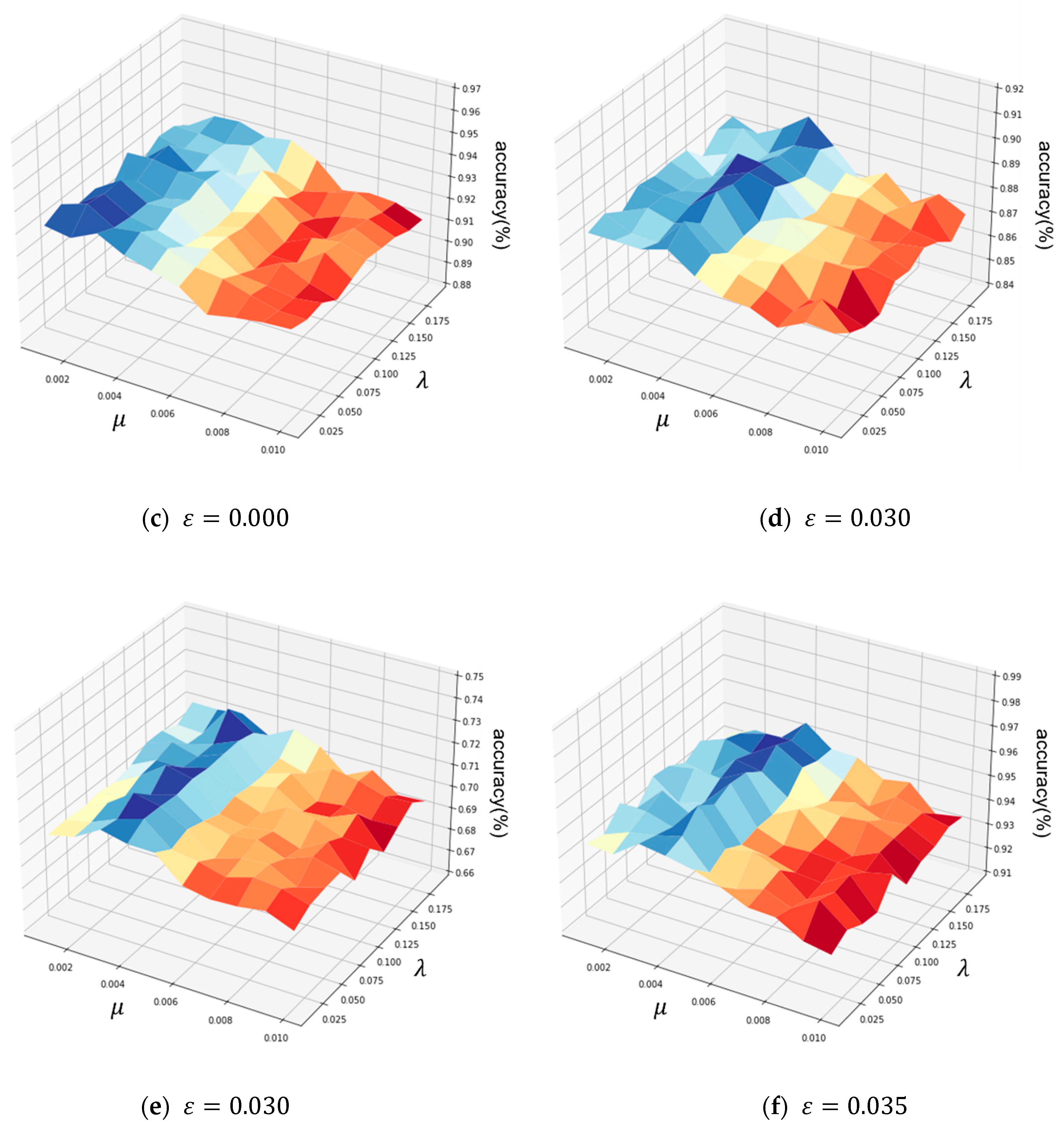
4.5.1. Coefficients Optimization on the Six Datasets
4.5.2. Effects of Classifier
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Storcheus, D.; Rostamizadeh, A.; Kumar, S. A survey of modern questions and challenges in feature extraction. In Proceedings of the 1st International Workshop on Feature Extraction: Modern Questions and Challenges at NIPS 2015, PMLR2015, Montreal, QC, Canada, 11 December 2015; pp. 1–18. [Google Scholar]
- Zhou, F.; Fan, H.; Liu, Y.; Zhang, H.; Ji, R. Hybrid Model of Machine Learning Method and Empirical Method for Rate of Penetration Prediction Based on Data Similarity. Appl. Sci. 2023, 13, 5870. [Google Scholar] [CrossRef]
- Janiesch, C.; Zschech, P.; Heinrich, K. Machine learning and deep learning. Electron Mark. 2021, 31, 685–695. [Google Scholar] [CrossRef]
- Chen, X.; Ding, M.; Wang, X.; Xin, Y.; Mo, S.; Wang, Y.; Han, S.; Luo, P.; Zeng, G.; Wang, J. Context autoencoder for self-supervised representation learning. arXiv 2022, arXiv:2202.03026. [Google Scholar]
- Aguilar, D.L.; Medina-Pérez, M.A.; Loyola-Gonzalez, O.; Choo KK, R.; Bucheli-Susarrey, E. Towards an interpretable autoencoder: A decision-tree-based autoencoder and its application in anomaly detection. IEEE Trans. Dependable Secur. Comput. 2022, 20, 1048–1059. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, H.; Zhao, S. Auto-encoder based dimensionality reduction. Neurocomputing 2016, 184, 232–242. [Google Scholar] [CrossRef]
- Liou, C.-Y.; Cheng, W.-C.; Liou, J.-W.; Liou, D.-R. Autoencoder for words. Neurocomputing 2014, 139, 84–96. [Google Scholar] [CrossRef]
- Li, J.; Luong, M.-T.; Jurafsky, D. A hierarchical neural autoencoder for paragraphs and documents. arXiv 2015, arXiv:1506.01057. [Google Scholar]
- Tschannen, M.; Bachem, O.; Lucic, M. Recent advances in autoencoder-based representation learning. arXiv 2018, arXiv:1812.05069. [Google Scholar]
- Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Trevino, R.P.; Tang, J.; Liu, H. Feature selection: A data perspective. ACM Comput. Surv. (CSUR) 2017, 50, 1–45. [Google Scholar] [CrossRef]
- Jović, A.; Brkić, K.; Bogunović, N. A review of feature selection methods with applications. In Proceedings of the 2015 38th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 25–29 May 2015; pp. 1200–1205. [Google Scholar]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Osia, S.A.; Taheri, A.; Shamsabadi, A.S.; Katevas, K.; Haddadi, H.; Rabiee, H.R. Deep private-feature extraction. IEEE Trans. Knowl. Data Eng. 2018, 32, 54–66. [Google Scholar] [CrossRef]
- Ghojogh, B.; Samad, M.N.; Mashhadi, S.A.; Kapoor, T.; Ali, W.; Karray, F.; Crowley, M. Feature selection and feature extraction in pattern analysis: A literature review. arXiv 2019, arXiv:1905.02845. [Google Scholar]
- Schmidt, M.; Fung, G.; Rosales, R. Fast optimization methods for L1 regularization: A comparative study and two new approaches. In Proceedings of the 18th European Conference on Machine Learning, Warsaw, Poland, 17–21 September 2007; pp. 286–297. [Google Scholar]
- Van Laarhoven, T. L2 regularization versus batch and weight normalization. arXiv 2017, arXiv:1706.05350. [Google Scholar]
- Azhagusundari, B.; Thanamani, A.S. Feature selection based on information gain. Int. J. Innov. Technol. Explor. Eng. 2013, 2, 18–21. [Google Scholar]
- Bryant, F.B.; Satorra, A. Principles and practice of scaled difference chi-square testing. Struct. Equ. Model. A Multidiscip. J. 2012, 19, 372–398. [Google Scholar] [CrossRef]
- Mika, S.; Schölkopf, B.; Smola, A.J.; Müller, K.-R.; Scholz, M.; Rätsch, G. Kernel PCA and De-noising in feature spaces. Adv. Neural Inf. Process. Syst. 1998, 11, 536–542. [Google Scholar]
- Ding, C.; Zhou, D.; He, X.; Zha, H. R 1-pca: Rotational invariant l 1-norm principal component analysis for robust subspace factorization. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 281–288. [Google Scholar]
- Andrew, G.; Arora, R.; Bilmes, J. Livescu, Deep canonical correlation analysis. In Proceedings of the International Conference on Machine Learning, PMLR2013, Atlanta, GA, USA,, 17–19 June 2013; pp. 1247–1255. [Google Scholar]
- Yu, H.; Yang, J. A direct LDA algorithm for high-dimensional data—With application to face recognition. Pattern Recognit. 2001, 34, 2067–2070. [Google Scholar] [CrossRef]
- Martinez, A.M.; Kak, A.C. Pca versus lda. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 228–233. [Google Scholar] [CrossRef]
- Zhou, P.; Han, J.; Cheng, G.; Zhang, B. Learning compact and discriminative stacked autoencoder for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4823–4833. [Google Scholar] [CrossRef]
- Sun, M.; Wang, H.; Liu, P.; Huang, S.; Fan, P. A sparse stacked denoising autoencoder with optimized transfer learning applied to the fault diagnosis of rolling bearings. Measurement 2019, 146, 305–314. [Google Scholar] [CrossRef]
- Coutinho, M.G.; Torquato, M.F.; Fernandes, M.A. Deep neural network hardware implementation based on stacked sparse autoencoder. IEEE Access 2019, 7, 40674–40694. [Google Scholar] [CrossRef]
- Shi, Y.; Lei, J.; Yin, Y.; Cao, K.; Li, Y.; Chang, C.-I. Discriminative feature learning with distance constrained stacked sparse autoencoder for hyperspectral target detection. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1462–1466. [Google Scholar] [CrossRef]
- Xiao, Y.; Wu, J.; Lin, Z.; Zhao, X. A semi-supervised deep learning method based on stacked sparse auto-encoder for cancer prediction using RNA-seq data. Comput. Methods Programs Biomed. 2018, 166, 99–105. [Google Scholar] [CrossRef] [PubMed]
- Sankaran, A.; Vatsa, M.; Singh, R.; Majumdar, A. Group sparse autoencoder. Image Vis. Comput. 2017, 60, 64–74. [Google Scholar] [CrossRef]
- Chai, Z.; Song, W.; Wang, H.; Liu, F. A semi-supervised auto-encoder using label and sparse regularizations for classification. Appl. Soft Comput. 2019, 77, 205–217. [Google Scholar] [CrossRef]
- Xu, H.; Luo, D.; Henao, R.; Shah, S.; Carin, L. Learning autoencoders with relational regularization. In Proceedings of the International Conference on Machine Learning, PMLR2020, Virtual Event, 13–18 July 2020; pp. 10576–10586. [Google Scholar]
- Vayer, T.; Chapel, L.; Flamary, R.; Tavenard, R.; Courty, N. Fused Gromov-Wasserstein distance for structured objects. Algorithms 2020, 13, 212. [Google Scholar] [CrossRef]
- Liang, J.; Liu, R. Stacked denoising autoencoder and dropout together to prevent overfitting in deep neural network. In Proceedings of the 2015 8th International Congress on Image and Signal Processing (CISP), Shenyang, China, 14–16 October 2015; pp. 697–701. [Google Scholar]
- Goldberger, J.; Gordon, S.; Greenspan, H. An Efficient Image Similarity Measure Based on Approximations of KL-Divergence Between Two Gaussian Mixtures. In Proceedings of the Ninth IEEE International Conference on Computer Vision, ICCV2003, Nice, France, 13–16 October 2003; pp. 487–493. [Google Scholar]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No. 04CH37541), Budapest, Hungary, 25–29 July 2004; pp. 985–990. [Google Scholar]
- Yang, Z.; Xu, B.; Luo, W.; Chen, F. Autoencoder-based representation learning and its application in intelligent fault diagnosis: A review. Measurement 2022, 189, 110460. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhao, P.; Zhang, D.; Wang, H. MR-DCAE: Manifold regularization-based deep convolutional autoencoder for unauthorized broadcasting identification. Int. J. Intell. Syst. 2021, 36, 7204–7238. [Google Scholar] [CrossRef]
- Li, Y.; Lei, Y.; Wang, P.; Jiang, M.; Liu, Y. Embedded stacked group sparse autoencoder ensemble with L1 regularization and manifold reduction. Appl. Soft Comput. 2021, 101, 107003. [Google Scholar] [CrossRef]
- Steck, H. Autoencoders that don′t overfit towards the Identity. Adv. Neural Inf. Process. Syst. 2020, 33, 19598–19608. [Google Scholar]
- Probst, M.; Rothlauf, F. Harmless Overfitting: Using Denoising Autoencoders in Estimation of Distribution Algorithms. J. Mach. Learn. Res. 2020, 21, 2992–3022. [Google Scholar]
- Kunin, D.; Bloom, J.; Goeva, A.; Seed, C. Loss landscapes of regularized linear autoencoders. In Proceedings of the International Conference on Machine Learning, PMLR2019, Long Beach, CA, USA, 9–15 June 2019; pp. 3560–3569. [Google Scholar]
- Pretorius, A.; Kroon, S.; Kamper, H. Learning dynamics of linear denoising autoencoders. In Proceedings of the International Conference on Machine Learning, PMLR2018, Stockholm, Sweden, 10–15 July 2018; pp. 4141–4150. [Google Scholar]
- Bunte, K.; Haase, S.; Biehl, M.; Villmann, T. Stochastic neighbor embedding (SNE) for dimension reduction and visualization using arbitrary divergences. Neurocomputing 2012, 90, 23–45. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Melville, J. Umap: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
- Becht, E.; McInnes, L.; Healy, J.; Dutertre, C.A.; Kwok, I.W.; Ng, L.G.; Newell, E.W. Dimensionality reduction for visualizing single-cell data using UMAP. Nat. Biotechnol. 2018, 37, 38–44. [Google Scholar] [CrossRef]
- Wang, H.; van Stein, B.; Emmerich, M.; Back, T. A new acquisition function for Bayesian optimization based on the moment-generating function. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; pp. 507–512. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. Adv. Neural Inf. Process. Syst. 2012, 25, 1–9. [Google Scholar]
- Audet, C.; Denni, J.; Moore, D.; Booker, A.; Frank, P. A surrogate-model-based method for constrained optimization. In Proceedings of the 8th Symposium on Multidisciplinary Analysis and Optimization, Long Beach, CA, USA, 6–8 September 2000; p. 4891. [Google Scholar]
- Lin, W.; Wu, Z.; Lin, L.; Wen, A.; Li, J. An ensemble random forest algorithm for insurance big data analysis. IEEE Access 2017, 5, 16568–16575. [Google Scholar] [CrossRef]
- Nikoloulopoulou, N.; Perikos, I.; Daramouskas, I.; Makris, C.; Treigys, P.; Hatzilygeroudis, I. A Convolutional Autoencoder Approach for Boosting the Specificity of Retinal Blood Vessels Segmentation. Appl. Sci. 2023, 13, 3255. [Google Scholar] [CrossRef]


| Dataset | Classes | Features | Training | Testing | Dimensionality after Feature Extraction | |
|---|---|---|---|---|---|---|
| Low-dimension | Heart | 2 | 13 | 240 | 63 | 9 |
| Wine | 2 | 12 | 4873 | 1624 | 8 | |
| Medium-dimension | USPS | 10 | 256 | 7291 | 2007 | 180 |
| Fashion-MNIST | 10 | 784 | 60,000 | 10,000 | 549 | |
| High-dimension | Yale | 15 | 1024 | 130 | 35 | 717 |
| COIL-100 | 100 | 1024 | 1080 | 360 | 717 | |
| Dataset | Guiding Units of IGSAE | |||
|---|---|---|---|---|
| Heart | 64 – 32 – 64 | 0.040 | 0.119 | 0.004 |
| Wine | 64 – 32 – 64 | 0.035 | 0.166 | 0.003 |
| USPS | 256 – 128 – 256 | 0 | 0.025 | 0.001 |
| Fashion-MNIST | 256 – 128 – 256 | 0.030 | 0.115 | 0.003 |
| Yale | 512 – 256 – 512 | 0.030 | 0.171 | 0.002 |
| COIL-100 | 512 – 256 – 512 | 0.035 | 0.172 | 0.003 |
| Dataset | RF (%) | DF (%) | DF & WR (%) | DF & WR & SR (%) |
|---|---|---|---|---|
| Heart | 82.47 2.1 | 81.24 1.3 | 82.44 1.8 | 82.64 2.0 |
| Wine | 96.84 0.5 | 94.62 2.0 | 96.12 0.6 | 96.25 1.1 |
| USPS | 94.92 3.4 | 93.15 1.6 | 93.50 2.4 | 93.24 2.3 |
| Fashion-MNIST | 90.60 0.4 | 86.76 2.3 | 88.46 2.1 | 88.87 1.8 |
| Yale | 74.56 2.1 | 70.51 5.7 | 71.08 4.2 | 71.35 5.5 |
| COIL-100 | 96.19 0.2 | 93.87 1.1 | 94.56 1.2 | 95.33 0.5 |
| Dataset | RF (%) | Kernel PCA (%) | LDA (%) | SAE (%) | SSAE (%) | UMAP (%) | t-SNE (%) | IGSAE (%) | Hybrid IGSAE (%) |
|---|---|---|---|---|---|---|---|---|---|
| Heart | 82.47 ± 2.1 | 81.82 ± 1.1 | 76.86 ± 4.5 | 82.23 ± 2.8 | 81.82 ± 2.7 | 74.38 ± 5.2 | 60.33 ± 9.2 | 82.64 ± 2.0 | 83.22 ± 1.7 |
| Wine | 96.84 ± 0.5 | 96.00 ± 1.2 | 93.15 ± 1.4 | 95.98 ± 1.5 | 96.87 ± 1.1 | 95.54 ± 2.2 | 95.52 ± 2.9 | 96.25 ± 1.1 | 97.93 ± 0.8 |
| USPS | 94.92 ± 3.4 | 91.46 ± 5.6 | 92.78 ± 5.7 | 93.47 ± 3.9 | 93.23 ± 4.5 | 89.23 ± 9.9 | 86.36 ± 8.4 | 93.50 ± 2.4 | 95.37 ± 3.1 |
| Fashion-MNIST | 90.60 ± 0.4 | 87.07 ± 3.5 | 87.27 ± 3.2 | 87.98 ± 2.7 | 88.65 ± 1.8 | 81.28 ± 6.4 | 81.38 ± 4.7 | 88.87 ± 1.8 | 91.08 ± 1.0 |
| Yale | 74.56 ± 2.1 | 71.48 ± 6.8 | 68.26 ± 3.6 | 67.44 ± 7.4 | 70.78 ± 4.1 | 69.33 ± 5.5 | 61.45 ± 8.5 | 71.35 ± 5.5 | 76.58 ± 4.2 |
| COIL-100 | 96.19 ± 0.2 | 94.55 ± 1.3 | 92.95 ± 1.5 | 95.01 ± 0.9 | 95.12 ± 1.1 | 90.03 ± 4.6 | 89.85 ± 4.2 | 95.33 ± 0.5 | 96.76 ± 0.8 |
| Dataset | Basic AE (%) | SAE (%) | SSAE (%) | IGSAE (%) |
|---|---|---|---|---|
| Heart | 0.3521 | 0.3213 | 0.3494 | 0.3132 |
| Wine | 0.4560 | 0.4651 | 0.4476 | 0.4242 |
| USPS | 0.1757 | 0.1634 | 0.1654 | 0.1537 |
| Fashion-MNIST | 0.2463 | 0.2578 | 0.2563 | 0.2487 |
| Yale | 0.8754 | 0.8743 | 0.8864 | 0.8435 |
| COIL-100 | 0.4749 | 0.4836 | 0.4798 | 0.4803 |
| Heart | Wine | USPS | Fashion-MNIST | Yale | COIL-100 | |
|---|---|---|---|---|---|---|
| SVM (%) | 82.64 ± 2.0 | 96.25 ± 1.1 | 93.50 ± 2.4 | 88.87 ± 1.8 | 71.35 ± 5.5 | 95.33 ± 0.5 |
| KNN (%) | 77.48 ± 6.3 | 92.78 ± 3.2 | 89.75 ± 4.7 | 83.79 ± 2.9 | 69.95 ± 4.1 | 86.46 ± 4.6 |
| Random Forest (%) | 81.72 ± 1.8 | 94.55 ± 2.1 | 90.56 ± 2.2 | 86.78 ± 2.7 | 72.17 ± 4.8 | 94.8 ± 11.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Hur, C.; Ibrokhimov, B.; Kang, S. Interactive Guiding Sparse Auto-Encoder with Wasserstein Regularization for Efficient Classification. Appl. Sci. 2023, 13, 7055. https://doi.org/10.3390/app13127055
Lee H, Hur C, Ibrokhimov B, Kang S. Interactive Guiding Sparse Auto-Encoder with Wasserstein Regularization for Efficient Classification. Applied Sciences. 2023; 13(12):7055. https://doi.org/10.3390/app13127055
Chicago/Turabian StyleLee, Haneum, Cheonghwan Hur, Bunyodbek Ibrokhimov, and Sanggil Kang. 2023. "Interactive Guiding Sparse Auto-Encoder with Wasserstein Regularization for Efficient Classification" Applied Sciences 13, no. 12: 7055. https://doi.org/10.3390/app13127055
APA StyleLee, H., Hur, C., Ibrokhimov, B., & Kang, S. (2023). Interactive Guiding Sparse Auto-Encoder with Wasserstein Regularization for Efficient Classification. Applied Sciences, 13(12), 7055. https://doi.org/10.3390/app13127055





