Probabilistic Seismic Sensitivity Analyses of High-Speed Railway Extradosed Cable-Stayed Bridges
Abstract
Featured Application
Abstract
1. Introduction
2. Analysis of Structural Uncertainty Based on Probability Reliability
2.1. Latin Hypercube Sampling
2.2. Nataf Transformation of Model Parameter Correlation
3. Numerical Analysis
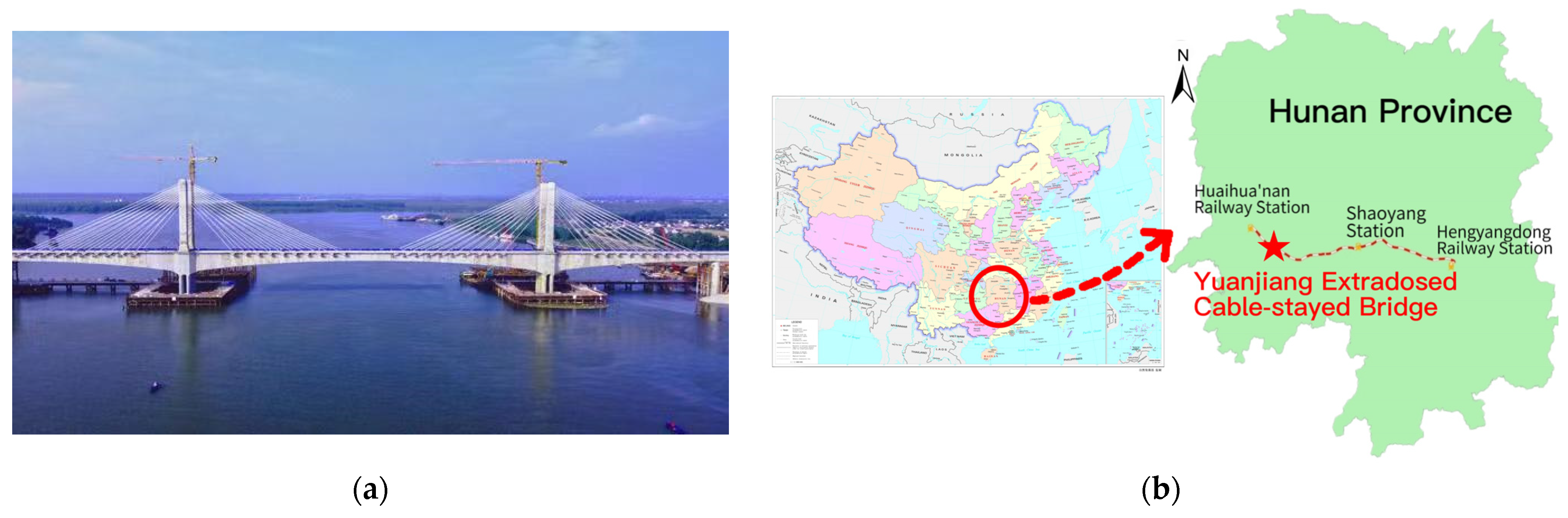
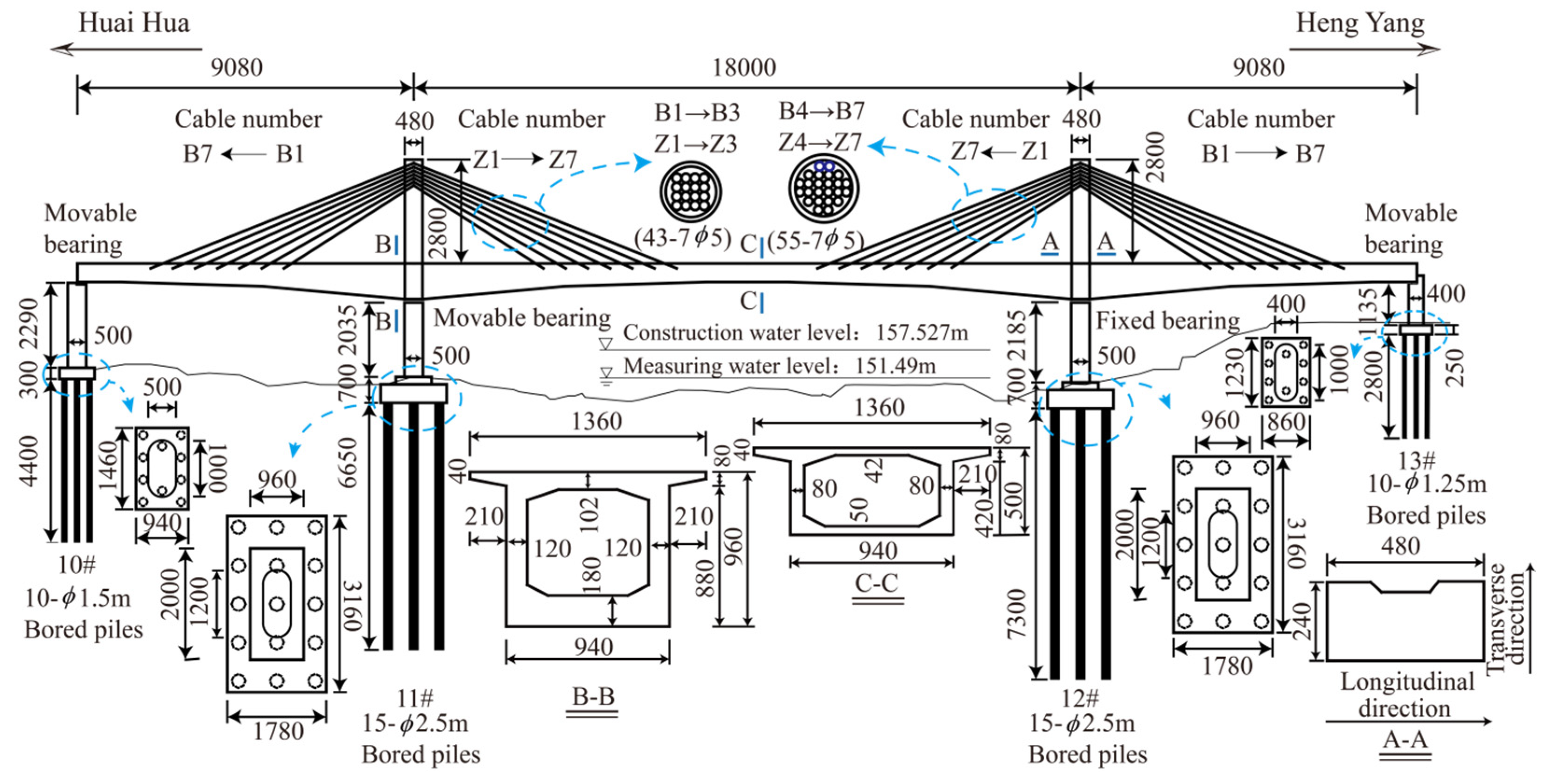
3.1. Background of the Bridge
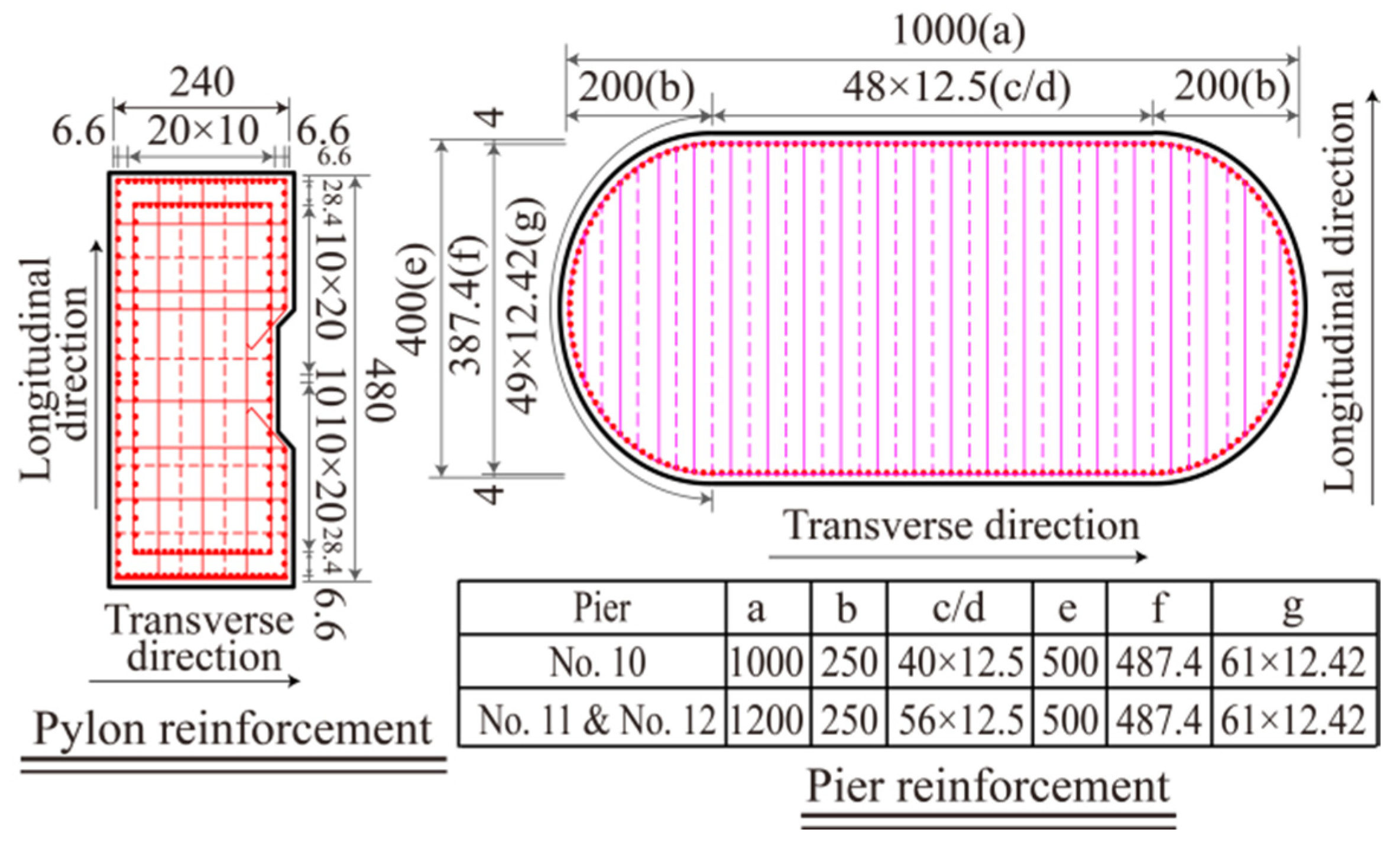
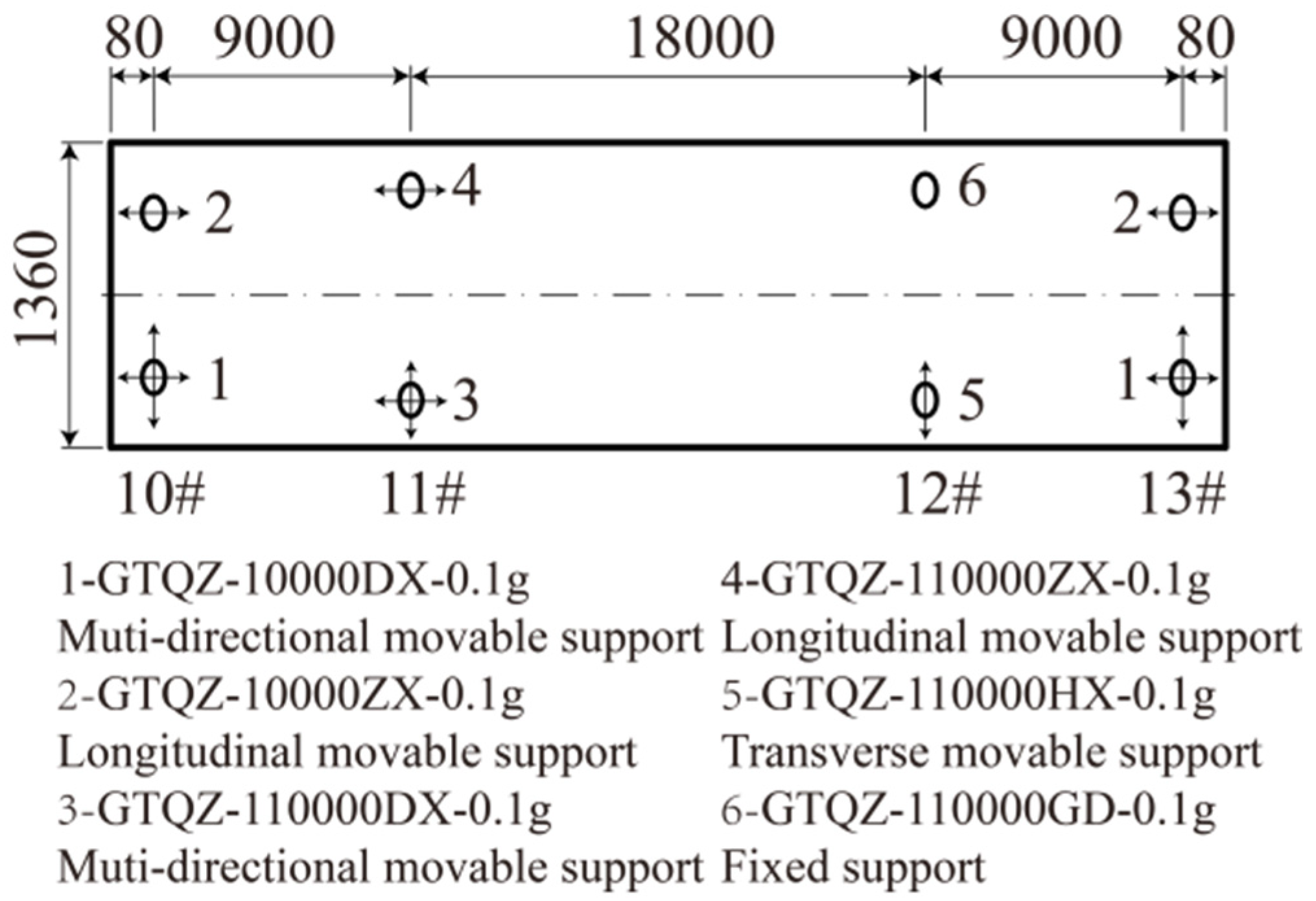
3.2. Nonlinear Finite Element Model
3.3. Seismic Ground Motions
4. Analysis of Structural Uncertainty
4.1. Random Parameter Selection and Distribution of the Bridge
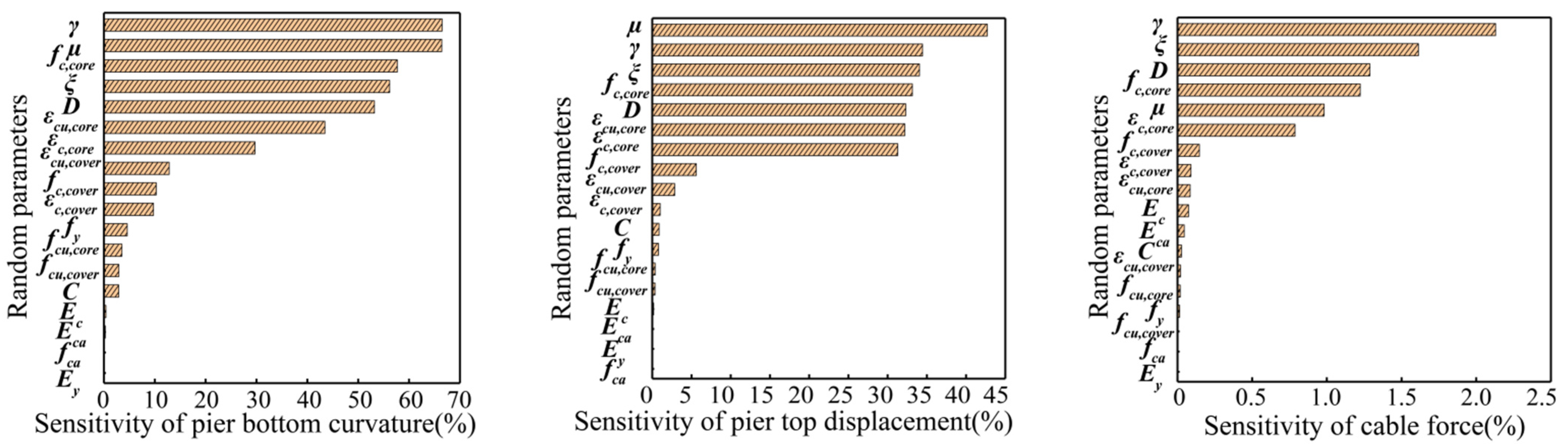
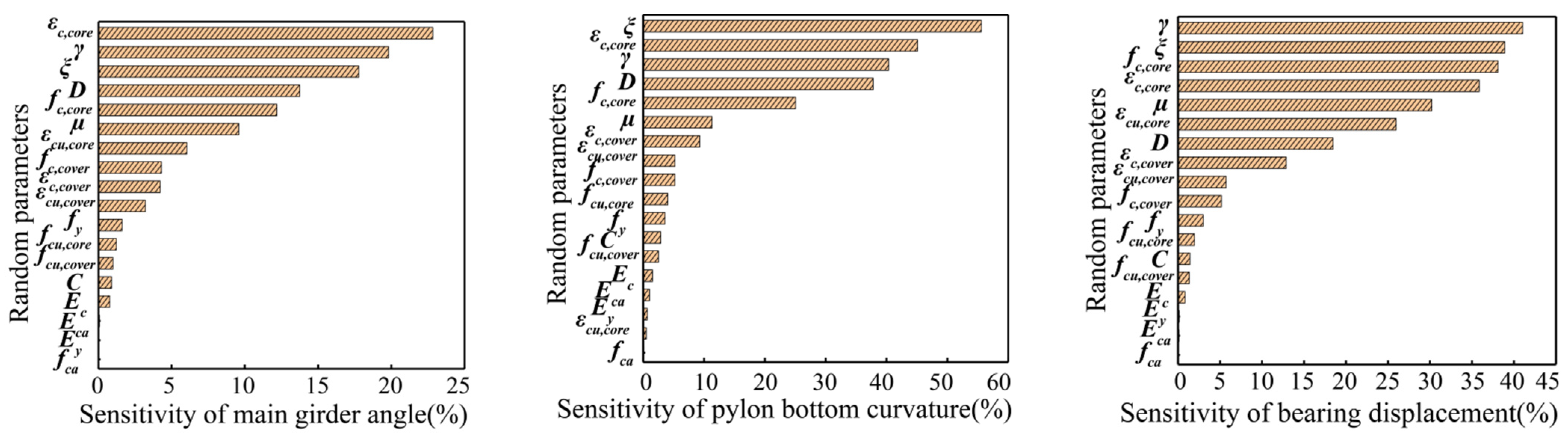
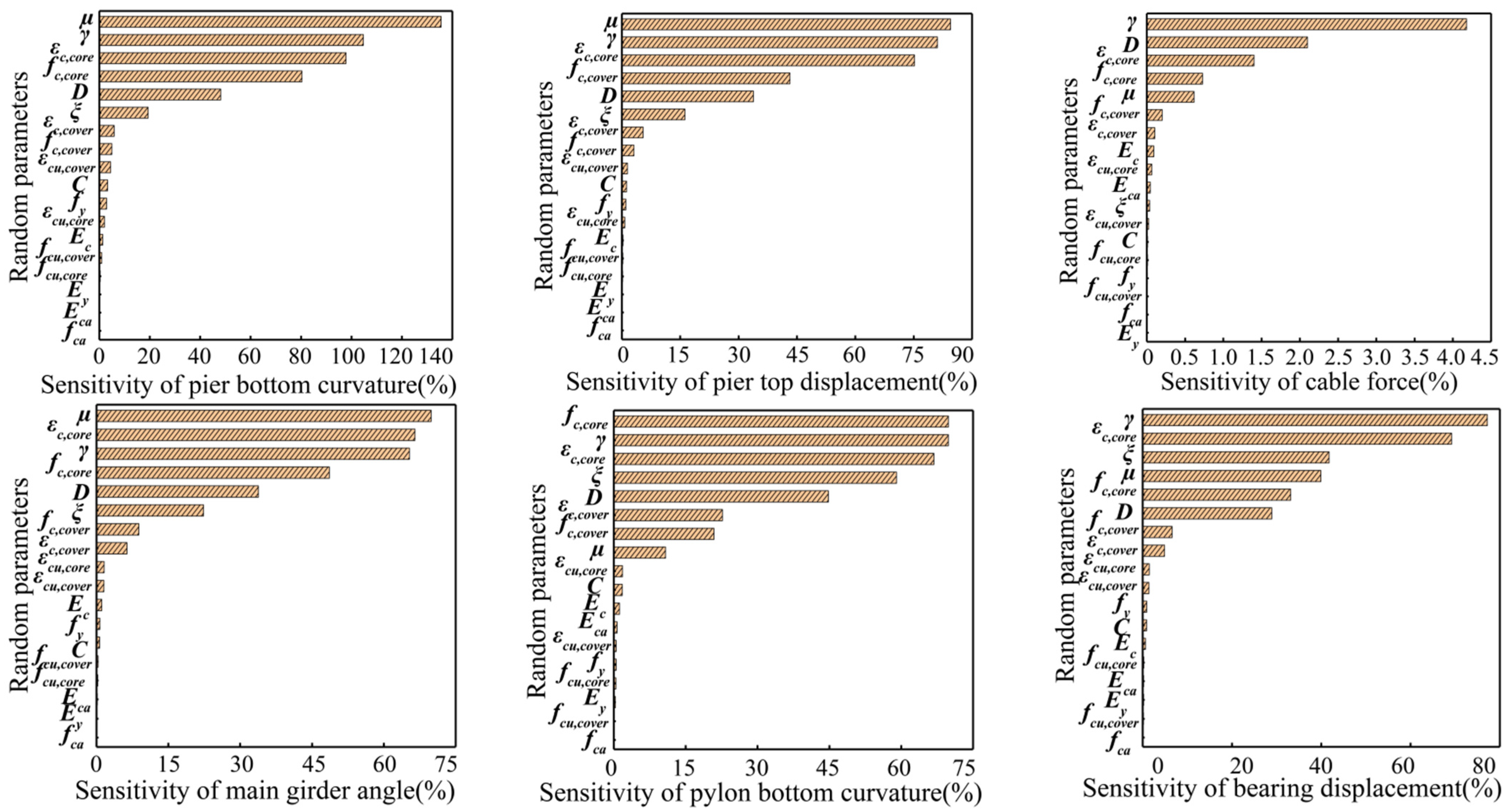
4.2. Sensitivity Analysis of Tornado Diagram
- (1)
- For high-speed railway bridge damage, the SFDP of an extradosed cable-stayed bridge are selected, such as angles of girder, support displacement, pier displacement, pier curvature, tower curvature and cable force;
- (2)
- According to the probability distribution characteristics of each random parameter in Table 4 and considering the correlation, the upper limit and lower limit values can be determined using Latin hypercube sampling. Then, the single random variable x is changed, and its upper limit and lower limit values are brought into the dynamic analysis model, while the other parameters remain unchanged. Subsequently, the difference between the upper limit and lower limit value of the SFDP can be calculated. Finally, the difference is divided by the maximum value of the SFDP of a benchmark model, and its ratio is defined as the sensitivity of the SFDP;
- (3)
- The sensitivity of the demand parameters to random variables can be analyzed after repeating step (2), and then the sensitivity as a “horizontal graph” of the random variable X can be drawn in the graph;
- (4)
- Finally, a “horizontal graph” of each parameter can be obtained by repeating step (3); these can be arranged in descending order to analyze the parameter sensitivity of dynamic damage of the extradosed cable-stayed bridge.
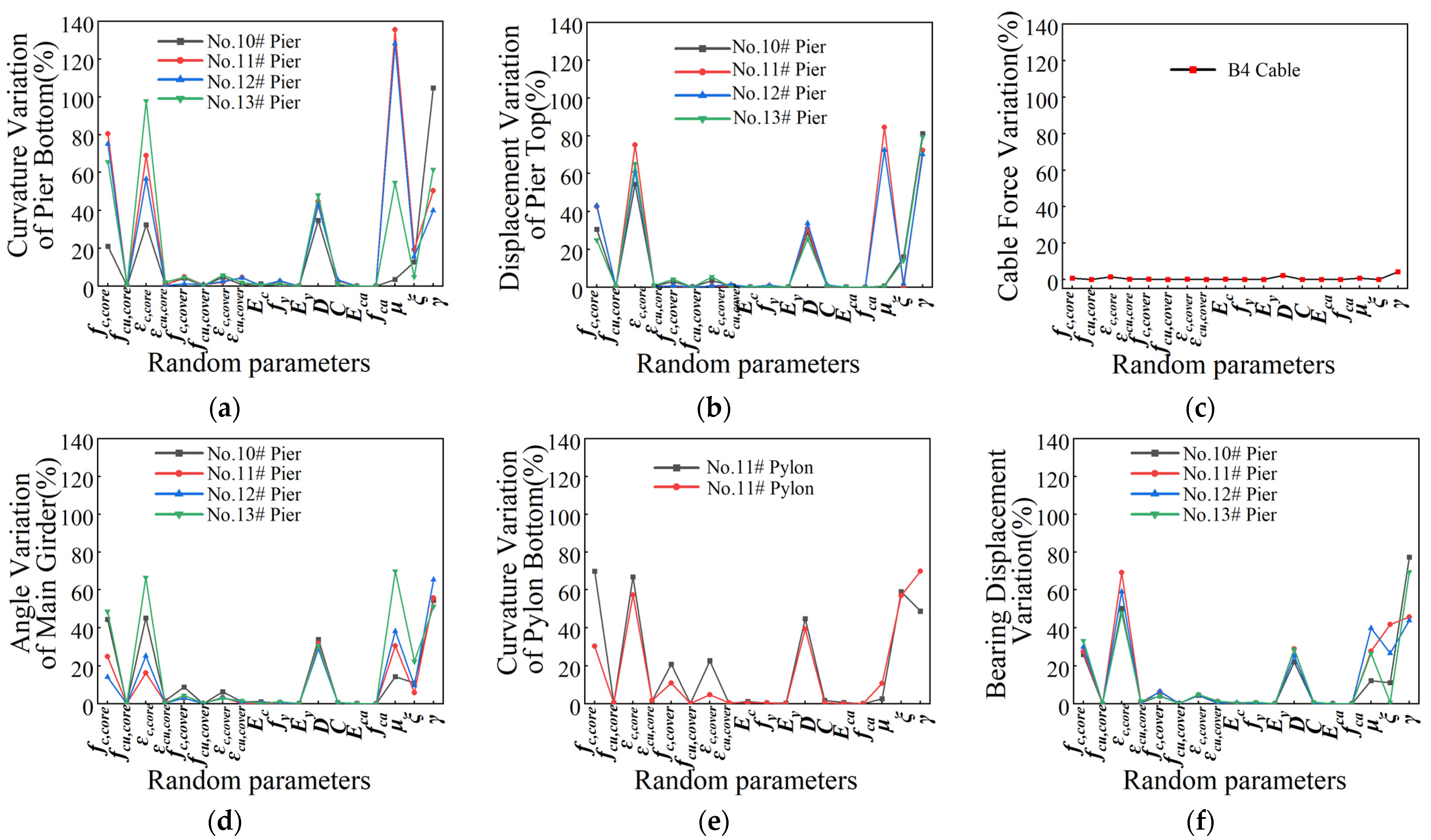
4.3. Analysis of Structural Uncertainty
5. Conclusions
- (1)
- SFDP are greatly affected by structural uncertainty. The sensitive parameters with the greatest influence on dynamic response are the friction coefficient of bearing, concrete bulk density, damping ratio, peak compressive strength of confined concrete, component size and peak strain of confined concrete. The secondary parameters are the strength and strain of unconfined concrete, the impact of which on the bridge cannot be ignored. The other parameters are insensitive to responses of high-speed railway extradosed cable-stayed bridges;
- (2)
- The effects of material properties and cross-section should be fully considered for nonlinear dynamic time-history analysis. Therefore, accurate calculation of material parameter characteristics and accurate simulation of structural characteristics are the prerequisites for ensuring accurate and reliable calculation results. In addition, the variation ratio of cable force is less sensitive than other SFDP, and it is difficult to quantify the seismic function damage;
- (3)
- Structural uncertainty has a great impact on the dynamic response of high-speed railway extradosed cable-stayed bridges, and it is quite different from traditional static parameter sensitivity analysis. Therefore, it is necessary to clarify the influence of random parameters on the bridge dynamic responses, and to explore the relationship between seismic demand and structural random parameters.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lozano-Galant, J.A.; Paya-Zaforteza, I. Analysis of Eduardo Torroja’s Tempul Aqueduct an important precursor of modern cable-stayed bridges, extradosed bridges and prestressed concrete. Eng. Struct. 2017, 150, 955–968. [Google Scholar] [CrossRef]
- Meng, X.B.; Zhang, C.H. Extradosed and intradosed cable-stayed bridges with continuous cables: Conceptual consideration. J. Bridge Eng. 2014, 19, 5–14. [Google Scholar] [CrossRef]
- He, X.H.; Wu, T.; Zou, Y.F.; Chen, Y.F.; Guo, H.; Yu, Z.W. Recent developments of high-speed railway bridges in China. Struct. Infrastruct. Eng. 2017, 13, 1584–1595. [Google Scholar] [CrossRef]
- Qin, S.Q.; Gao, Z.Y. Developments and prospects of long-span high-speed railway bridge technologies in China. Engineering 2017, 3, 787–794. [Google Scholar] [CrossRef]
- Yang, S.L.; Pu, Q.H.; Shi, Z.; Hong, Y. Mechanical behavior of steel-concrete composite joints in railway hybrid cable-stayed bridges. J. Construct. Steel Res. 2020, 173, 106242. [Google Scholar] [CrossRef]
- Pu, Q.H.; Yang, S.L.; Shi, Z.; Hong, Y. Fatigue performance of an innovative steel-concrete joint in long-span railway hybrid box girder cable-stayed bridges. J. Bridge Eng. 2021, 26, 04020129. [Google Scholar] [CrossRef]
- Feng, D.M.; Li, A.Q.; Guo, T. Seismic control of a single-tower extradosed railway bridge using the E-Shaped steel damping bearing. Soil Dyn. Earthq. Eng. 2020, 136, 106249. [Google Scholar] [CrossRef]
- Li, S.; Dezfuli, F.H.; Wang, J.Q.; Alam, M.S. Longitudinal seismic response control of long-span cable-stayed bridges using shape memory alloy wire-based lead rubber bearings under near-fault records. J. Intell. Mater. Syst. Struct. 2018, 29, 703–728. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, W.; Zheng, K.F.; Li, H.G. Seismic design of a long-span cable-stayed bridge with fluid viscous dampers. Pract. Period. Struct. Des. Constr. 2016, 21, 04015006. [Google Scholar] [CrossRef]
- Yang, M.G.; Cai, C.S. Longitudinal vibration control for a suspension bridge subjected to vehicle braking forces and earthquake excitations based on magnetorheological dampers. J. Vib. Contr. 2016, 22, 3659–3678. [Google Scholar] [CrossRef]
- Xu, X.L.; Li, Z.J.; Liu, W.Q.; Feng, D.M.; Li, X.H. Investigation of the wind-resistant performance of seismic viscous dampers on a cable-stayed bridge. Eng. Struct. 2017, 145, 283–292. [Google Scholar] [CrossRef]
- Zhang, X.J.; Zhao, C.Y.; Guo, J. Investigation of seismic performance of super long-span cable-stayed bridges. Earthq. Struct. 2018, 14, 493–503. [Google Scholar] [CrossRef]
- Wei, B.; Hu, Z.L.; He, X.H.; Jiang, L.Z. Evaluation of optimal ground motion intensity measures and seismic fragility analysis of a multi-pylon cable-stayed bridge with super-high piers in Mountainous Areas. Soil Dyn. Earthq. Eng. 2020, 129, 105945. [Google Scholar] [CrossRef]
- Chang, L.; Peng, F.; Ouyang, Y.F.; Elnashai, A.S.; Spencer, B.F. Bridge seismic retrofit program planning to maximize postearthquake transportation network capacity. J. Infrastruct. Syst. 2012, 18, 75–88. [Google Scholar] [CrossRef]
- Gou, H.Y.; Leng, D.; Yang, L.C.; Jia, H.Y. Modeling the cumulative residual deformation of high-speed railway bridge pier subjected to multiple earthquakes. Earthq. Struct. 2019, 17, 317–327. [Google Scholar] [CrossRef]
- Guan, Z.G.; Zhang, J.H.; Li, J.Z. Multilevel performance classifications of tall RC bridge columns toward postearthquake rehabilitation requirements. J. Bridge Eng. 2017, 22, 04017080. [Google Scholar] [CrossRef]
- Zhong, J.; Jeon, J.S.; Yuan, W.C.; DesRoches, R. Impact of spatial variability parameters on seismic fragilities of a cable-stayed bridge subjected to differential support motions. J. Bridge Eng. 2017, 22, 04017013. [Google Scholar] [CrossRef]
- Pang, Y.T.; Wu, X.; Shen, G.Y.; Yuan, W.C. Seismic fragility analysis of cable-stayed bridges considering different sources of uncertainties. J. Bridge Eng. 2014, 19, 04013015. [Google Scholar] [CrossRef]
- Ho, L.V.; Khatir, S.; Roeck, G.D.; Bui-Tien, T.; Wahab, M.A. Finite element model updating of a cable-stayed bridge using metaheuristic algorithms combined with Morris method for sensitivity analysis. Smart Struct. Syst. 2020, 26, 451–468. [Google Scholar] [CrossRef]
- Deco, A.; Bocchini, P.; Frangopol, D.M. A probabilistic approach for the prediction of seismic resilience of bridges. Earthq. Eng. Struct. Dyn. 2013, 42, 1469–1487. [Google Scholar] [CrossRef]
- Wang, P.; Lu, Z.Z.; Tang, Z.C. An application of the Kriging method in global sensitivity analysis with parameter uncertainty. Appl. Math. Model. 2013, 37, 6543–6555. [Google Scholar] [CrossRef]
- Wan, H.P.; Ren, W.X. Parameter selection in finite-element-model updating by global sensitivity analysis using Gaussian process metamodel. J. Struct. Eng. 2015, 141, 04014164. [Google Scholar] [CrossRef]
- Wan, H.P.; Ren, W.X. A residual-based Gaussian process model framework for finite element model updating. Comput. Struct. 2015, 156, 149–159. [Google Scholar] [CrossRef]
- Luedtke, N.; Panzeri, S.; Brown, M.; Broomhead, D.S.; Knowles, J.; Montemurro, M.A.; Kell, D.B. Information-theoretic sensitivity analysis: A general method for credit assignment in complex networks. J. R. Soc. Interface 2008, 5, 223–235. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.X.; Ran, Z.H. Sensitivity analysis of creep effect parameters based on 175 m-span extradosed cable-stayed bridge. In Proceedings of the 4th International Conference on Applied Materials and Manufacturing Technology 2018, Nanchang, China, 25–27 May 2018. [Google Scholar] [CrossRef]
- Shi, J.X.; Ran, Z.H. Calculation of creep effect of extradosed cable-stayed bridge based on Midas Civil. In Proceedings of the 4th International Conference on Applied Materials and Manufacturing Technology, Nanchang, China, 25–27 May 2018. [Google Scholar] [CrossRef]
- Xie, M.Z.; Yang, Y.Q.; Bu, Y.Z.; Wang, X.W.; Wei, R. Influence of error of unstressed cable length on mechanical behavior of thousand-meter-scale hybrid girder cable-stayed bridge. J. Highw. Tran. Res. Devel. 2014, 8, 30–36. [Google Scholar] [CrossRef]
- Yi, L.X.; Mei, D.P.; Zhou, C. Design of a rail-road asymmetrical low-pylon cable-stayed bridge with a main span of 588 m. Proc. Inst. Civ. Eng. Bridge Eng. 2020, 173, 190–197. [Google Scholar] [CrossRef]
- Nariman, N.A. Aerodynamic stability parameters optimization and global sensitivity analysis for a cable stayed bridge. KSCE J. Civil Eng. 2017, 21, 1866–1881. [Google Scholar] [CrossRef]
- Wu, F.W.; Xu, C.; Zhao, L. Analysis on sensitivity of stochastic seismic response parameters of super-long-span cable-stayed bridges. Tiedao Xuebao J. China Railw. Soc. 2014, 36, 107–114. [Google Scholar] [CrossRef]
- Jia, H.Y.; Zhang, D.Y.; Zheng, S.X.; Xie, W.C.; Pandey, M.D. Local site effects on a high-pier railway bridge under tridirectional spatial excitations: Nonstationary stochastic analysis. Soil Dyn. Earthq. Eng. 2013, 52, 55–69. [Google Scholar] [CrossRef]
- Jia, H.Y.; Lan, X.L.; Zheng, S.X.; Li, L.P.; Liu, C.Q. Assessment on required separation length between adjacent bridge segments to avoid pounding. Soil Dyn. Earthq. Eng. 2019, 120, 398–407. [Google Scholar] [CrossRef]
- Jia, H.Y.; Yue, W.Q.; Zheng, S.X.; Gou, H.Y.; Zhao, C.H.; You, G. Time-dependent pounding probability analysis between adjacent decks of bridges under non-stationary stochastic seismic excitations. Structure 2020, 28, 2355–2366. [Google Scholar] [CrossRef]
- Jahangiri, V.; Yazdani, M. Seismic reliability and limit state risk evaluation of plain concrete arch bridge. Struct. Infrastruct. Eng. 2021, 17, 170–190. [Google Scholar] [CrossRef]
- Homaei, F.; Yazdani, M. The probabilistic seismic assessment of aged concrete arch bridges: The role of soil-structure interaction. Structures 2020, 28, 894–904. [Google Scholar] [CrossRef]
- Helton, J.C.; Davis, F.J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliability Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef]
- Olsson, A.; Sandberg, G.; Dahlblom, O. On Latin hypercube sampling for structural reliability analysis. Struct. Saf. 2003, 25, 47–68. [Google Scholar] [CrossRef]
- Au, S.K.; Beck, J.L. A new adaptive importance sampling scheme for reliability calculations. Struct. Saf. 1999, 21, 135–158. [Google Scholar] [CrossRef]
- Liu, P.L.; Der, K.A. Multivariate distribution models with prescribed marginals and covariances. Probab. Eng. Mech. 1986, 1, 105–112. [Google Scholar] [CrossRef]
- Yuan, B.; Chen, M.; Chen, W.; Luo, Q.; Li, H. Effect of Pile-Soil Relative Stiffness on Deformation Characteristics of the Laterally Loaded Pile. Adv. Mater. Sci. Eng. 2022, 2022, 4913887. [Google Scholar] [CrossRef]
- Barbato, M.; Gu, Q.; Conte, J.P. Probabilistic Push-Over analysis of structural and soil-structure systems. J. Struct. Eng. 2010, 136, 1330–1341. [Google Scholar] [CrossRef]
- Thomos, G.C.; Trezos, C.G. Examination of the probabilistic response of reinforced concrete structures under static non-linear analysis. Eng. Struct. 2006, 28, 120–133. [Google Scholar] [CrossRef]
- Porter, K.A.; Beck, J.L.; Shaikhutdinov, R.V. Sensitivity of building loss estimates to major uncertain variables. Earthq. Spectra 2002, 18, 719–743. [Google Scholar] [CrossRef]

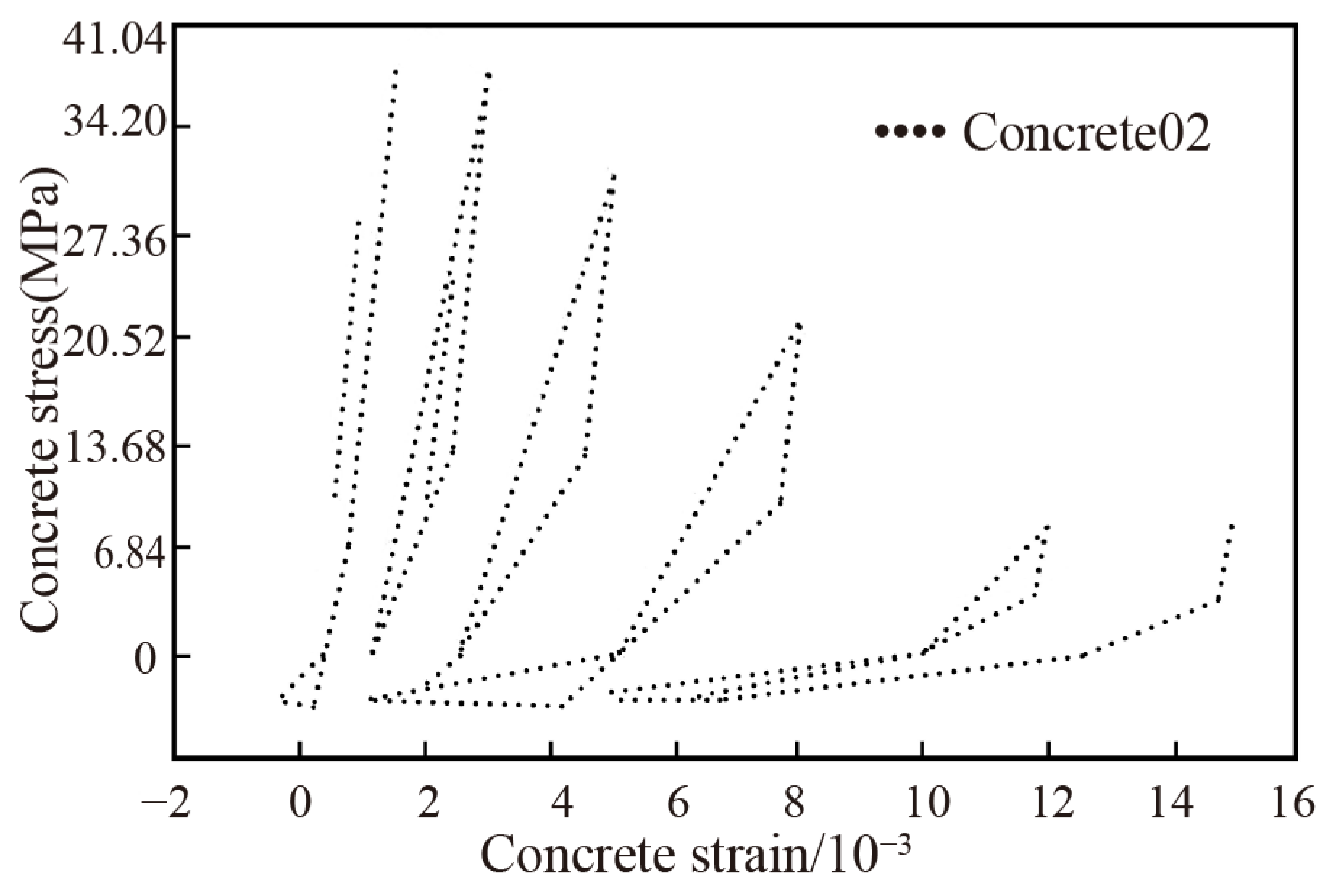
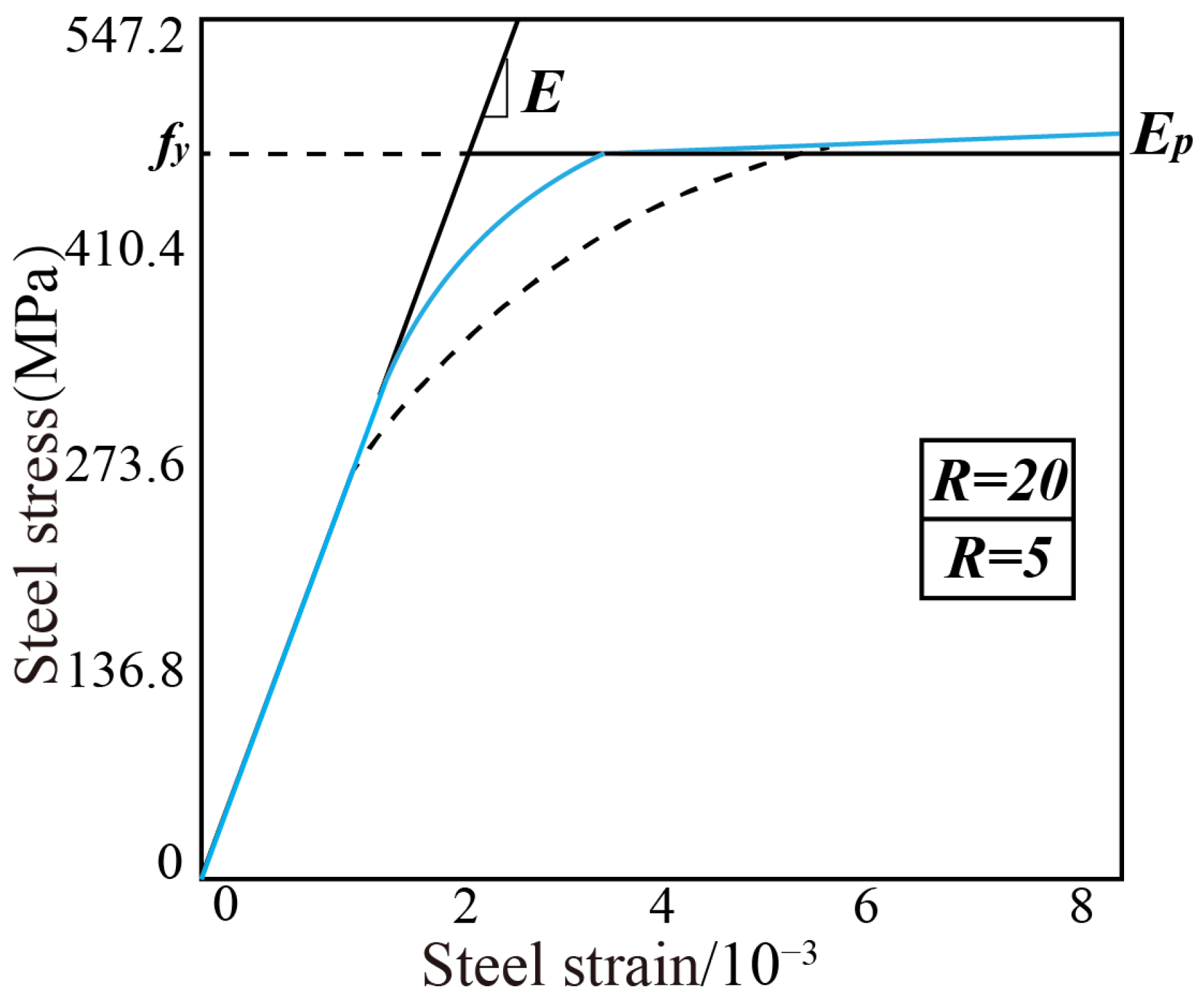

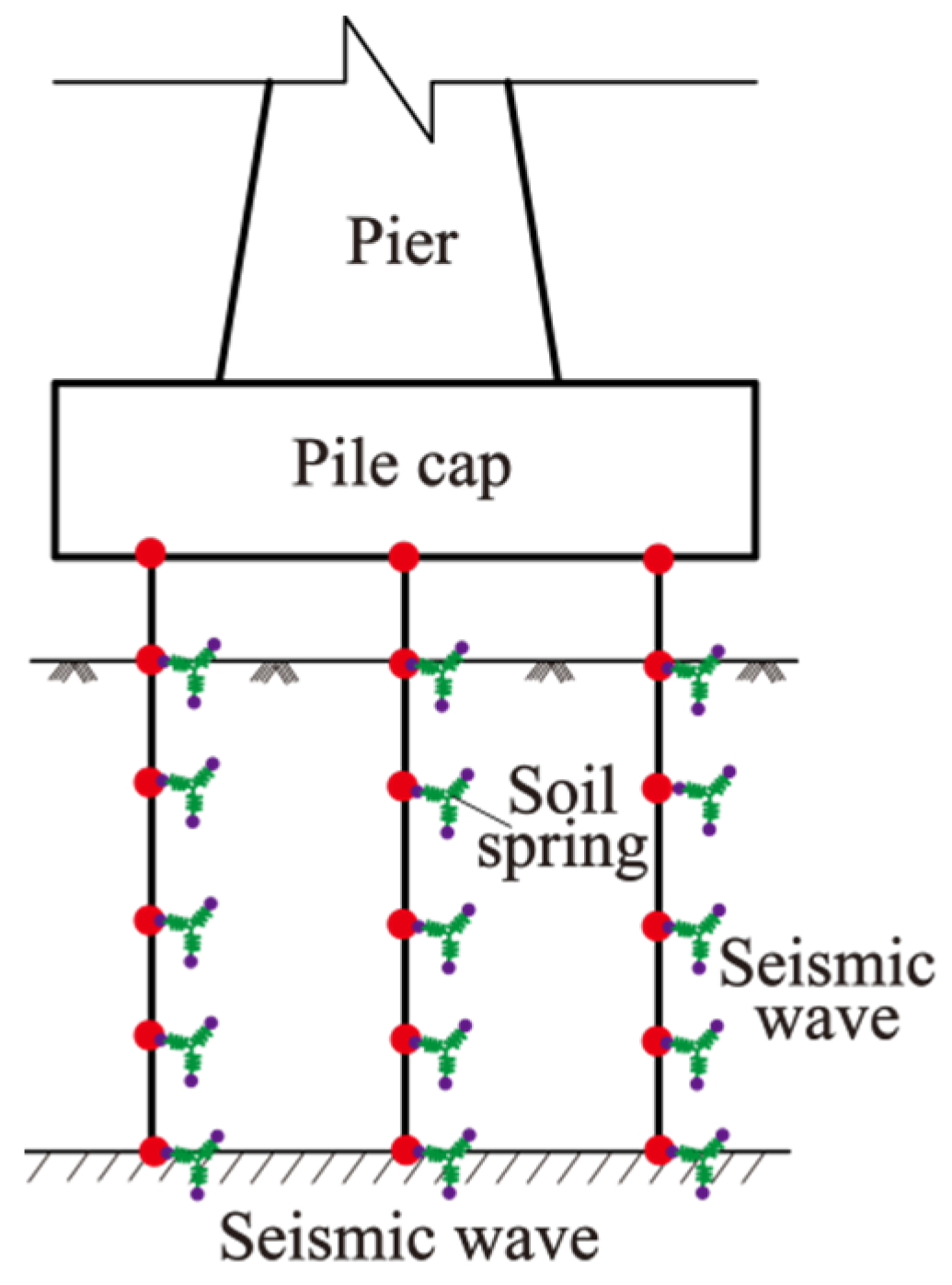
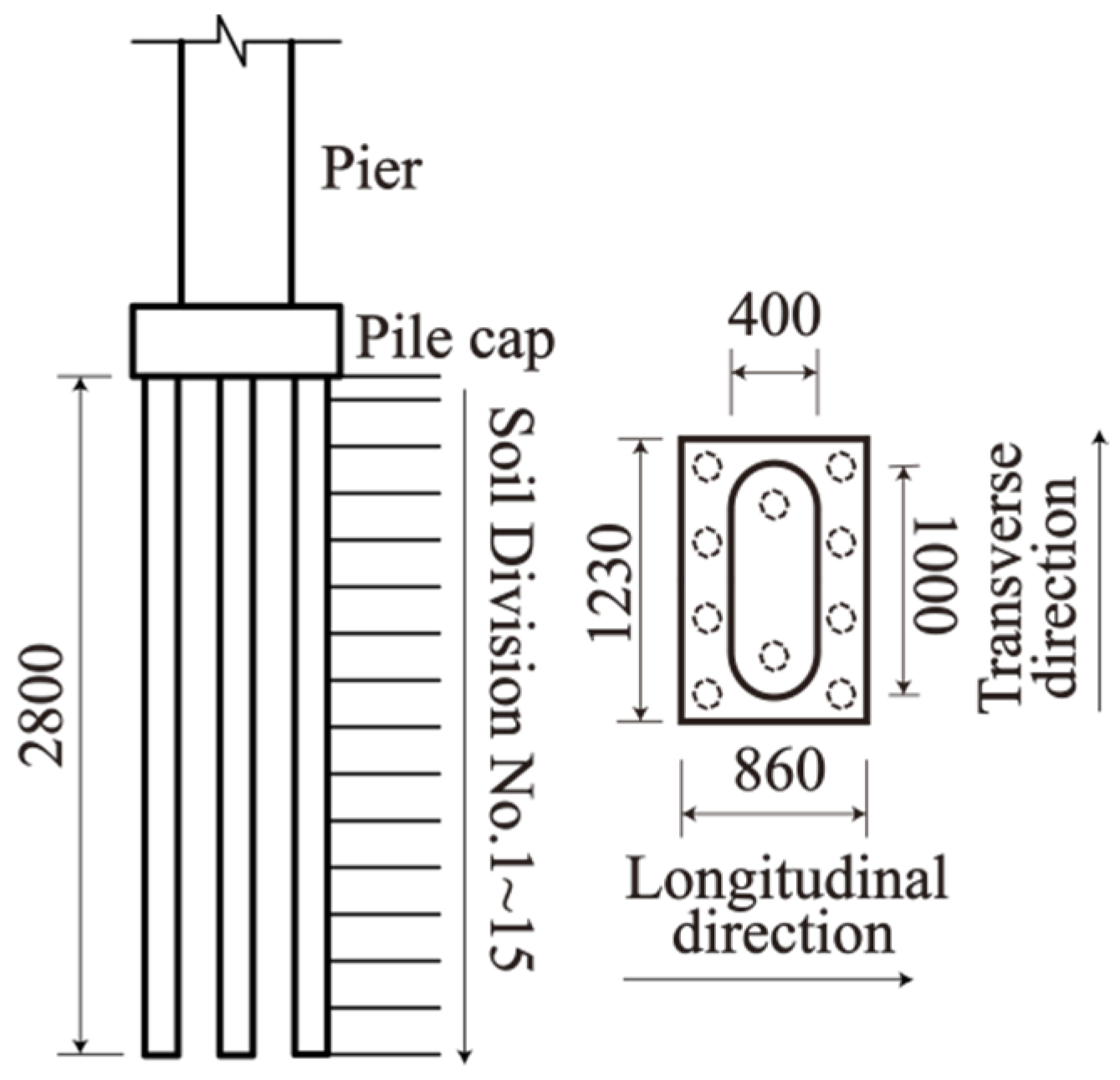
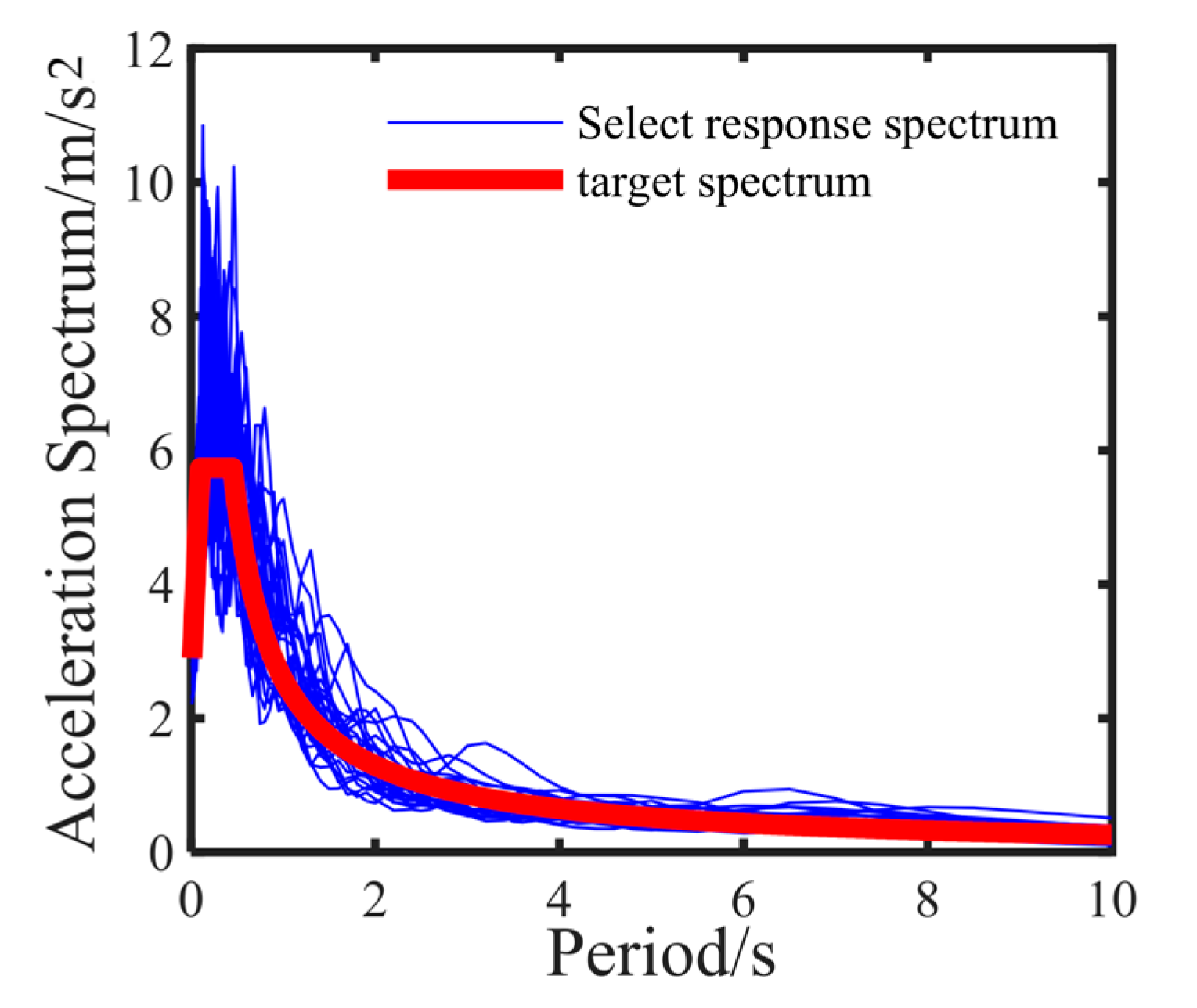


| Component | Element Type | Material |
|---|---|---|
| Cable | Truss Element | Steel02 Material |
| Pylon | Nonlinear Beam-Column Element | Concrete02 Material |
| Steel02 Material | ||
| Main girder | Elastic Beam-Column Element | Elastic Material |
| Bearing | ZeroLength Element | Elastic-Perfectly Plastic Material |
| Pier | Nonlinear Beam-Column Element | Concrete02 Material |
| Steel02 Material | ||
| Pile | Nonlinear Beam-Column Element | Concrete02 Material |
| Steel02 Material | ||
| Soil spring | ZeroLength Element | Elastic Material |
| Connecting rigid arm | Elastic Beam-Column Element | Elastic Material |
| No. | Model Parameter | Pylon/Pier/Pile | Unit | No. | Model Parameter | Pylon/Pier/Pile | Unit |
|---|---|---|---|---|---|---|---|
| 1 | Peak compressive strength of confined concrete | 48.1/30.55/30.55 | MPa | 7 | Peak strain of unconfined concrete | 0.002/0.002/0.002 | |
| 2 | Ultimate compressive strength of confined concrete | 9.62/6.11/6.11 | MPa | 8 | Ultimate strain of unconfined concrete | 0.004/0.004/0.004 | |
| 3 | Peak strain of confined concrete | 0.0045/0.0045/0.0045 | 9 | Elastic modulus of concrete | 36000/33000/33000 | MPa | |
| 4 | Ultimate strain of confined concrete | 0.009/0.009/0.009 | 10 | Yielding strength of steel | 400/400/400 | MPa | |
| 5 | Peak compressive strength of unconfined concrete | 37/23.5/23.5 | MPa | 11 | Elastic modulus of steel | 200000/200000/200000 | MPa |
| 6 | Ultimate compressive strength of unconfined concrete | 7.4/4.7/4.7 | MPa | 12 | Thickness of cover layer | 0.035/0.04/0.06 | m |
| 13 | Elastic modulus of main girder | 36,000 | MPa | 16 | Friction coefficient of bearing | 0.02 | |
| 14 | Elastic modulus of cable | 195,000 | MPa | 17 | Damping ratio | 0.05 | |
| 15 | Yielding strength of cable | 1860 | MPa | 18 | Concrete bulk density | 26.5 | kN/m3 |
| Calculation Parameters | Longitudinal Direction Soil Spring Stiffness | Transverse Direction Soil Spring Stiffness | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Soil Division | a | b1 | m | z | k | a | b1 | m | z | k |
| (m) | (m) | (kN/m4) | (m) | (kN/m) | (m) | (m) | (kN/m4) | (m) | (kN/m) | |
| 1.0 | 2.0 | 1.6 | 21,425.1 | 1.0 | 69,631.6 | 2.0 | 1.4 | 21,425.1 | 1.0 | 60,847.3 |
| 2.0 | 2.0 | 1.6 | 21,425.1 | 3.0 | 208,894.8 | 2.0 | 1.4 | 21,425.1 | 3.0 | 182,541.9 |
| 3.0 | 2.0 | 1.6 | 21,425.1 | 5.0 | 348,158.0 | 2.0 | 1.4 | 21,425.1 | 5.0 | 304,236.5 |
| 4.0 | 2.0 | 1.6 | 21,425.1 | 7.0 | 487,421.1 | 2.0 | 1.4 | 21,425.1 | 7.0 | 425,931.1 |
| 5.0 | 2.0 | 1.6 | 21,425.1 | 9.0 | 626,684.3 | 2.0 | 1.4 | 21,425.1 | 9.0 | 547,625.7 |
| 6.0 | 2.0 | 1.6 | 21,425.1 | 11.0 | 765,947.5 | 2.0 | 1.4 | 21,425.1 | 11.0 | 669,320.3 |
| 7.0 | 2.0 | 1.6 | 21,425.1 | 13.0 | 905,210.7 | 2.0 | 1.4 | 21,425.1 | 13.0 | 791,014.9 |
| 8.0 | 2.0 | 1.6 | 21,425.1 | 15.0 | 1,044,473.9 | 2.0 | 1.4 | 21,425.1 | 15.0 | 912,709.5 |
| 9.0 | 2.0 | 1.6 | 21,425.1 | 17.0 | 1,183,737.1 | 2.0 | 1.4 | 21,425.1 | 17.0 | 1,034,404.1 |
| 10.0 | 2.0 | 1.6 | 21,425.1 | 19.0 | 1,323,000.3 | 2.0 | 1.4 | 21,425.1 | 19.0 | 1,156,098.7 |
| 11.0 | 2.0 | 1.6 | 21,425.1 | 21.0 | 1,462,263.4 | 2.0 | 1.4 | 21,425.1 | 21.0 | 1,277,793.3 |
| 12.0 | 2.0 | 1.6 | 21,425.1 | 23.0 | 1,601,526.6 | 2.0 | 1.4 | 21,425.1 | 23.0 | 1,399,487.9 |
| 13.0 | 2.0 | 1.6 | 21,425.1 | 25.0 | 1,740,789.8 | 2.0 | 1.4 | 21,425.1 | 25.0 | 1,521,182.5 |
| 14.0 | 2.0 | 1.6 | 21,425.1 | 27.0 | 1,880,053.0 | 2.0 | 1.4 | 21,425.1 | 27.0 | 1,642,877.1 |
| 15.0 | 2.0 | 1.6 | 21,425.1 | 28.0 | 1,9496,84.6 | 2.0 | 1.4 | 21,425.1 | 28.0 | 1,703,724.4 |
| No. | Uncertainty Parameter | Radom Variables | Variables Distribution Type | Standard Deviation | Coefficient of Variation | Unit |
|---|---|---|---|---|---|---|
| 1 | Peak compressive strength of confined concrete | fc,core | Normal distribution | 4.076/2.5889/2.5889 | 0.14 | MPa |
| 2 | Ultimate compressive strength of confined concrete | fcu,core | Normal distribution | 0.8217/0.5218/0.5218 | 0.14 | MPa |
| 3 | Peak strain of confined concrete | ec,core | Normal distribution | 0.0008/0.0008/0.0008 | 0.15 | |
| 4 | Ultimate strain of confined concrete | ecu,core | Normal distribution | 0.002/0.002/0.0019 | 0.15 | |
| 5 | Peak compressive strength of unconfined concrete | fc,cover | Normal distribution | 3.351/2.1283/2.1283 | 0.14 | MPa |
| 6 | Ultimate compressive strength of unconfined concrete | fcu,cover | Normal distribution | 0.71/0.4509/0.4509 | 0.14 | MPa |
| 7 | Peak strain of unconfined concrete | ec,cover | Normal distribution | 0.0003/0.0003/0.0003 | 0.15 | |
| 8 | Ultimate strain of unconfined concrete | ecu,cover | Normal distribution | 0.0006/0.0006/0.0006 | 0.15 | |
| 9 | Elastic modulus of concrete | Ec | Normal distribution | 2880/2640/2640 | 0.08 | MPa |
| 10 | Yielding strength of steel | fy | Normal distribution | 16/16/16 | 0.045 | MPa |
| 11 | Elastic modulus of steel | Ey | Normal distribution | 6600/6600/6600 | 0.10 | MPa |
| 12 | Component size | D | Log-normal distribution | / | 0.2 | m |
| 13 | Thickness of cover layer | C | Normal distribution | 0.0017/0.0019/0.0029 | 0.2 | m |
| 14 | Elastic modulus of main girder | Eg | Normal distribution | 2880 | 0.08 | MPa |
| 15 | Elastic modulus of cable | Eca | Normal distribution | 19,500 | 0.1 | MPa |
| 16 | Yielding strength of cable | fca | Normal distribution | 74.4 | 0.04 | MPa |
| 17 | Friction coefficient of bearing | m | Normal distribution | 0.002 | 0.5 | |
| 18 | Damping ratio | x | Normal distribution | 0.005 | 0.2 | |
| 19 | Concrete bulk density | g | Normal distribution | 1.75 | 0.1 | kN/m3 |
| Correlation Coefficient | fc,core | fcu,core | ec,core | ecu,core | fc,cover | fcu,cover | ec,cover | ecu,cover |
|---|---|---|---|---|---|---|---|---|
| fc,core | 1 | 0.8 | 0.8 | 0.64 | ||||
| fcu,core | 0.8 | 1 | 0.64 | 0.8 | ||||
| ec,core | 1 | 0.8 | 0.8 | 0.64 | ||||
| ecu,core | 0.8 | 1 | 0.64 | 0.8 | ||||
| fc,cover | 0.8 | 0.64 | 1 | 0.8 | ||||
| fcu,cover | 0.64 | 0.8 | 0.8 | 1 | ||||
| ec,cover | 0.8 | 0.64 | 1 | 0.8 | ||||
| ecu,cover | 0.64 | 0.8 | 0.8 | 1 |
| Seismic Response in Longitudinal Direction | Seismic Response in Transverse Direction | |||||||
|---|---|---|---|---|---|---|---|---|
| 10# Pier | 11# Pier | 12# Pier | 13# Pier | 10# Pier | 11# Pier | 12# Pier | 13# Pier | |
| Displacement of pier Top (units: m) | 0.38 | 0.33 | 0.363 | 0.338 | 0.059 | 0.123 | 0.149 | 0.043 |
| Main girder angle (units: ×10−3 rad) | 2.40 | 3.10 | 2.90 | 1.70 | 1.90 | 3.40 | 3.10 | 2.20 |
| Curvature of pier bottom(/×10−3) | 3.80 | 4.70 | 3.30 | 7.60 | 0.12 | 1.10 | 1.30 | 0.11 |
| Bearing displacement (units: m) | 0.015 | 0.048 | 0.043 | 0.025 | 0.016 | 0.123 | 0.13 | 0.016 |
| 11# Pylon | 12# Pylon | 11# Pylon | 12# Pylon | |||||
| Curvature of pylon Bottom (/×10−5) | 4.10 | −2.40 | 110 | 140 | ||||
| Cable force (units: KN) | 5905.6 | 6055.2 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, M.; Yuan, J.; Jia, H.; Yang, Y.; Huang, S.; Sun, B. Probabilistic Seismic Sensitivity Analyses of High-Speed Railway Extradosed Cable-Stayed Bridges. Appl. Sci. 2023, 13, 7036. https://doi.org/10.3390/app13127036
Xie M, Yuan J, Jia H, Yang Y, Huang S, Sun B. Probabilistic Seismic Sensitivity Analyses of High-Speed Railway Extradosed Cable-Stayed Bridges. Applied Sciences. 2023; 13(12):7036. https://doi.org/10.3390/app13127036
Chicago/Turabian StyleXie, Mingzhi, Jinglian Yuan, Hongyu Jia, Yongqing Yang, Shengqian Huang, and Baolin Sun. 2023. "Probabilistic Seismic Sensitivity Analyses of High-Speed Railway Extradosed Cable-Stayed Bridges" Applied Sciences 13, no. 12: 7036. https://doi.org/10.3390/app13127036
APA StyleXie, M., Yuan, J., Jia, H., Yang, Y., Huang, S., & Sun, B. (2023). Probabilistic Seismic Sensitivity Analyses of High-Speed Railway Extradosed Cable-Stayed Bridges. Applied Sciences, 13(12), 7036. https://doi.org/10.3390/app13127036







