Proposals for Flexural Capacity Prediction of Precast Segmental Concrete Beam Prestressed with Internal Un-Bonded CFRP Tendons
Abstract
1. Introduction
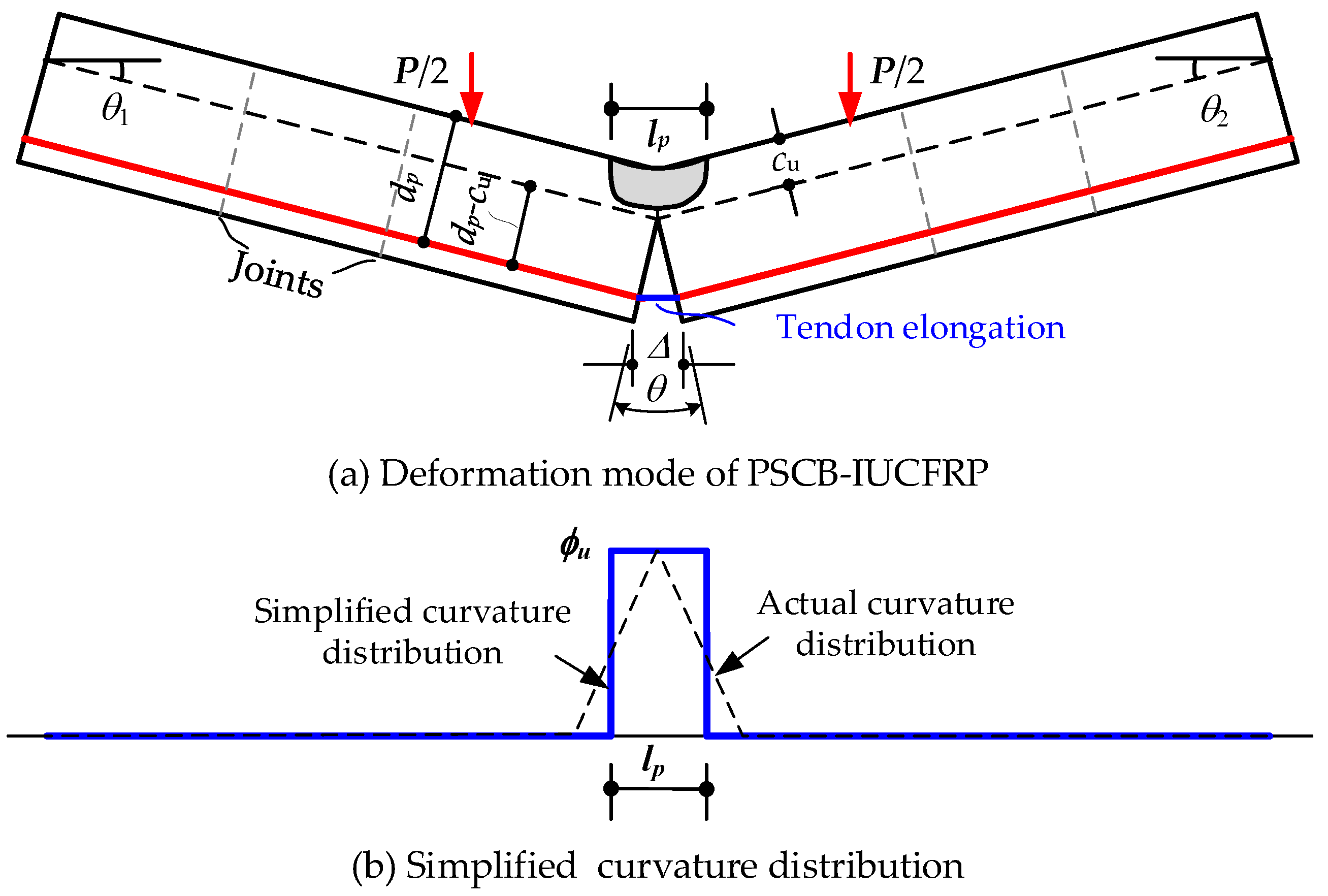
2. Flexural Behaviors of Precast Segmental Concrete Beam Prestressed with Internal Un-Bonded CFRP Tendons
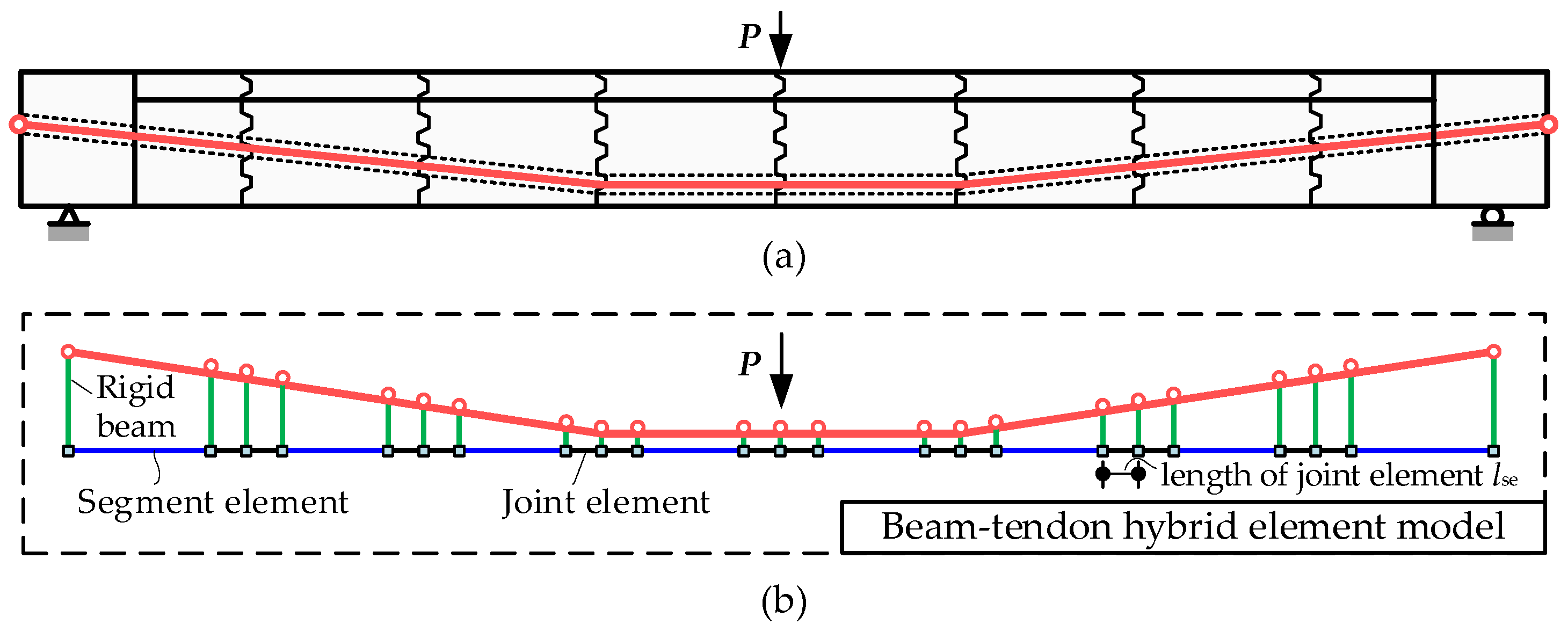
2.1. Nonlinear Numerical Model
- The model included four kinds of elements: free-slip tendon elements, segment elements, joint elements, and rigid beam connection elements.
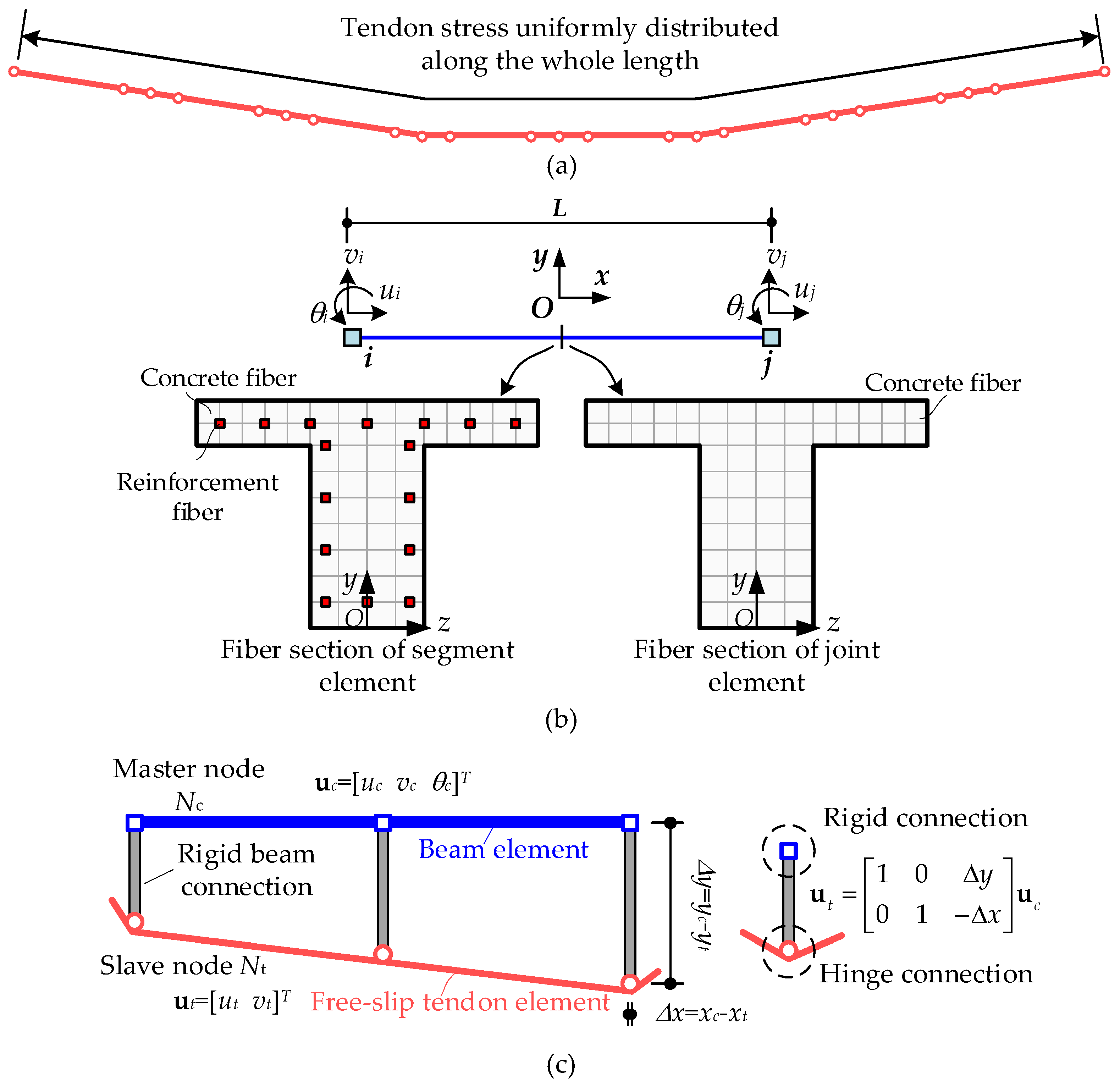
- The free-slip tendon element was a newly developed element type for un-bonded tendons. Considering the un-bonded phenomenon, the tendon stress was uniformly distributed along the whole tendon length, as shown in Figure 3a.
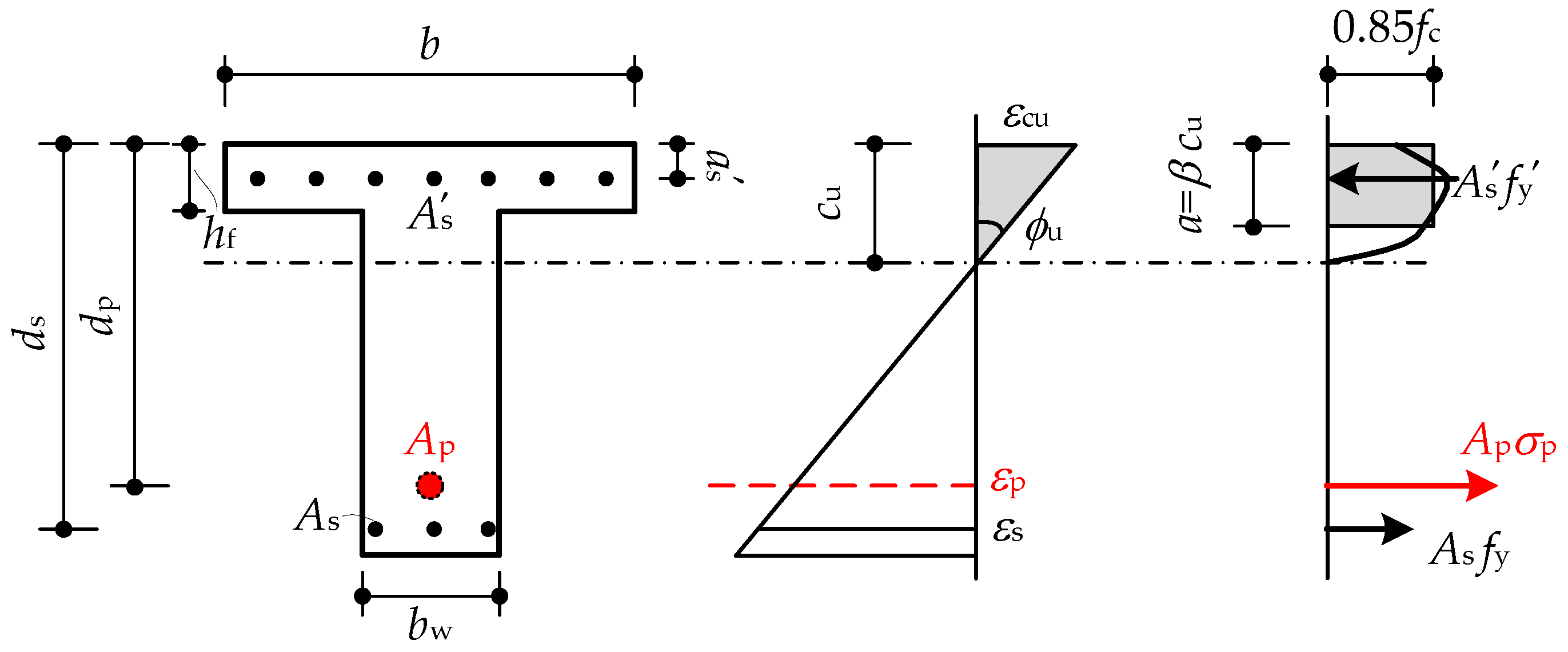
- The segment and joint element were all modeled by the displacement-based fiber beam element, as shown in Figure 3b. For the joint element, considering the joint discontinuity, the fiber section contained no reinforcement fiber, and the tensile strength of the concrete fiber was also ignored.
- The rigid beam connection element was employed to model the interaction between the beam and free-slip tendon elements.
- All elements were one-dimensional element types, reducing the number of degrees of freedom and significantly improving the computational efficiency. We considered all critical mechanical behaviors in the model, such as material nonlinearity, geometric nonlinearity, open joint discontinuity, and tendon free-slip effects. Details on the finite element formulas, constitutive model, and developed procedure can be seen in the previous studies [25,36].
2.2. Numerical Model Validation and Flexural Performances Comparisons
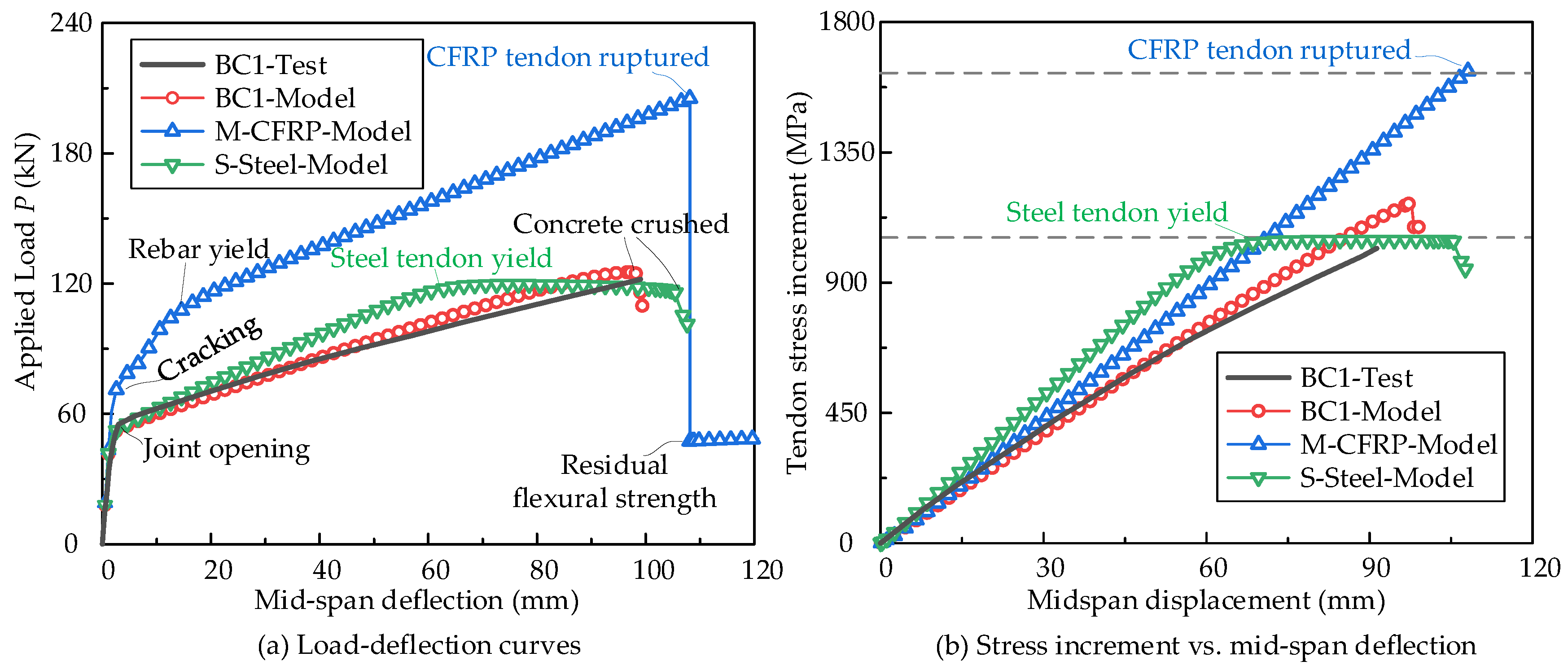
- Failure in BC1 is caused by concrete crushing. The CFRP tendon is still elastic, consistent with the experimental observations. The calculated values for structural deformation, capacity, and tendon stress all agreed well with the experimental results, verifying the effectiveness of the numerical model.
- Without the segmental joints, the M-CFRP beam shows a larger flexural capacity than beam BC1. Under the same mid-span deflection, the tendon stress increment of the monolithic beam M-CFRP is larger than that of the segmental beam BC1. The failure mode is changed to CFRP tendon rupture. These differences demonstrate the effects of segmental joints on flexural performance, which should be considered in capacity prediction.
- For the S-Steel beam, structural failure is caused by the steel tendon yielding and then concrete crushing, which is different from the BC1 beam. The effects of the tendon type are non-negligible when predicting flexural capacity.
- Figure 5b shows that the relationship between tendon stress increment and mid-span deflection is almost linear before tendon failure. The slope of the linear relationship is affected by the tendon type and segmental joints. The stress increments of steel tendons in the beam S-Steel are more significant than the CFRP tendon in the beam BC1 due to the steel tendon’s higher elastic modulus than the CFRP tendon. The comparisons between the M-CFRP and BC1 beams show that the tendon stress increments in the segmental beam are lower than the monolithic one.
- The sectional curvature distribution and deflection curves along the beam length are extracted from the analysis results to address the effects of segmental joints on the tendon stress increment, as shown in Figure 6. We find that the plastic deformations only occur at the mid-span joint section, and the other regions are almost elastic. However, the plastic deformations are distributed within the flexural span for the monolithic beam M-CFRP. The un-bonded tendon elongation is associated with the whole beam deformation, causing the differences in tendon stress increments between the monolithic and segmental beams.
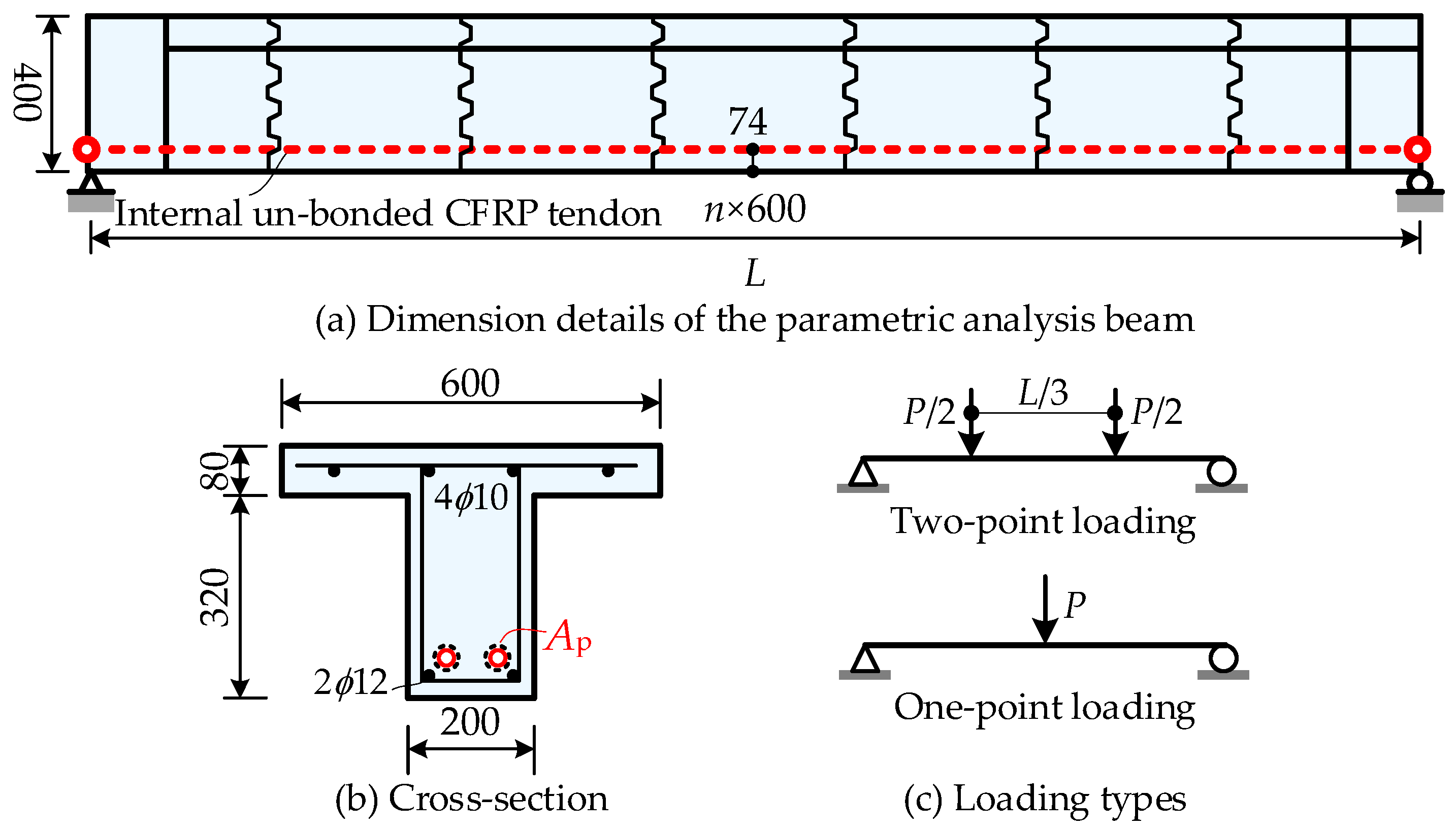
2.3. Parametric Analysis Study
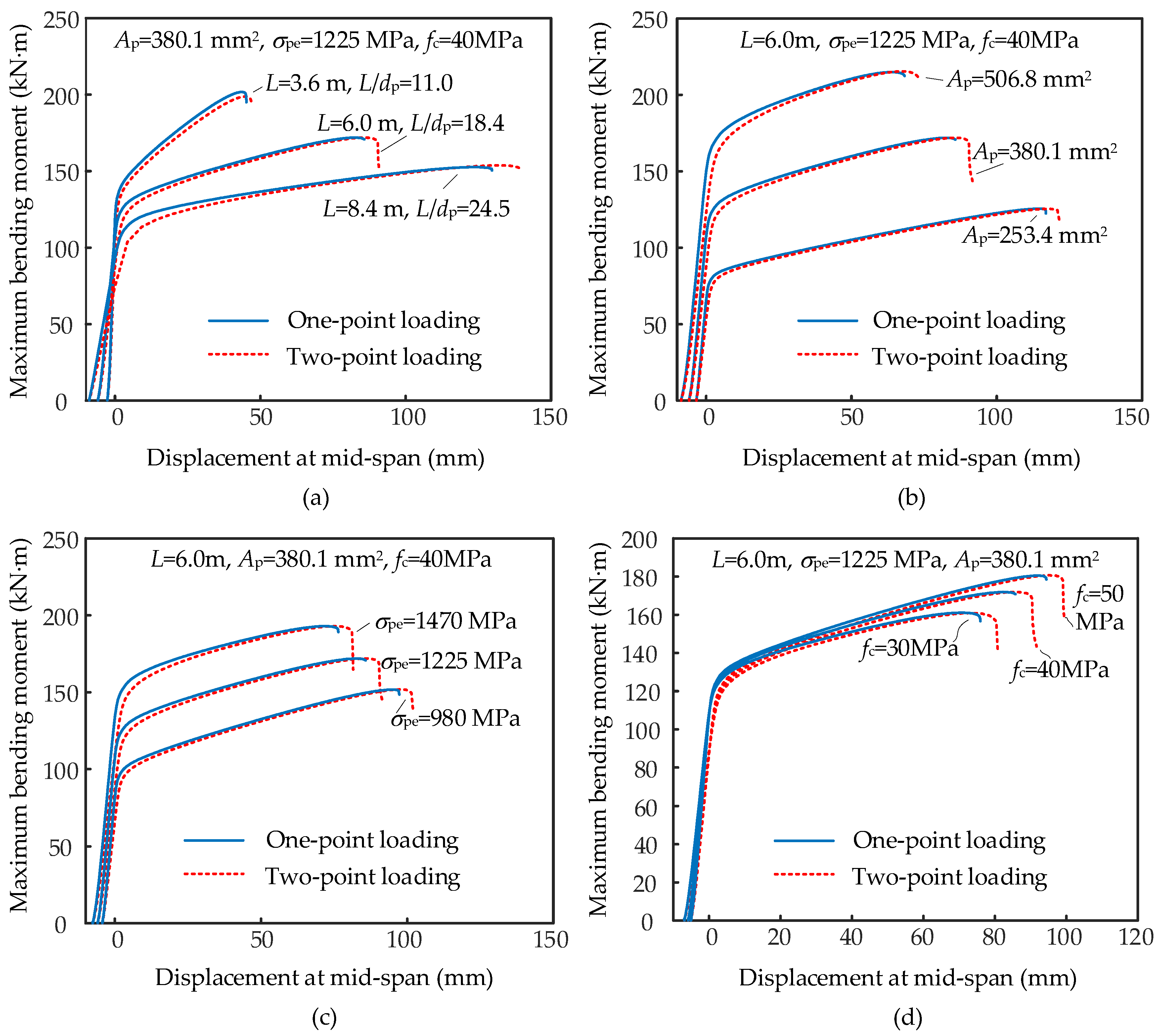
- Figure 8 shows the load-deflections curves of numerical beams under different loading patterns. The mid-span moment by the applied loads is set as the vertical coordinates in Figure 8 to make comparisons. As the loading patterns shown in Figure 7c, the vertical coordinate in Figure 8 is PL/6 for the two-point loading cases and PL/4 for the one-point loading cases. The loading types have a minor influence on the tendon stress increment and flexural capacity of PSCB-IUCFRP. This phenomenon differs from observations made in the experimental tests on monolithic beams [38,39]. The reason for this is that the plastic region of the segmental beam is concentrated at the failure joint cross-section, regardless of the loading type. In contrast, they are distributed across a monolithic beam. The different deformation modes between segmental and monolithic beams caused the difference.
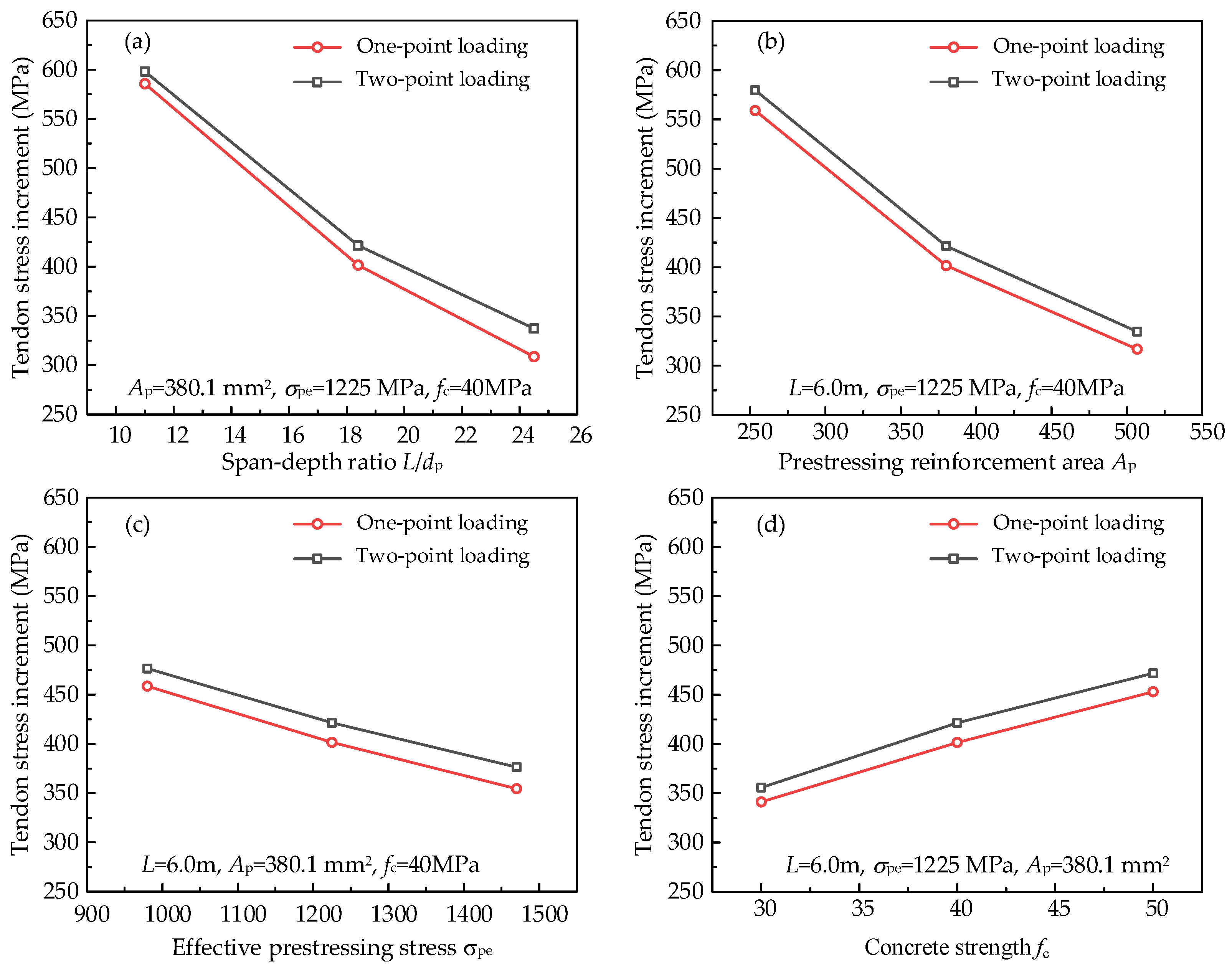
- Figure 9 shows the effects of parameters on the tendon stress increment. With the increase in the parameters L/dp, Ap, and σpe, the tendon stress increments decrease. The effects of fc on the tendon stress increments are positive. The sensitivity of tendon stress increments to L/dp and Ap is more prominent than the other parameters.
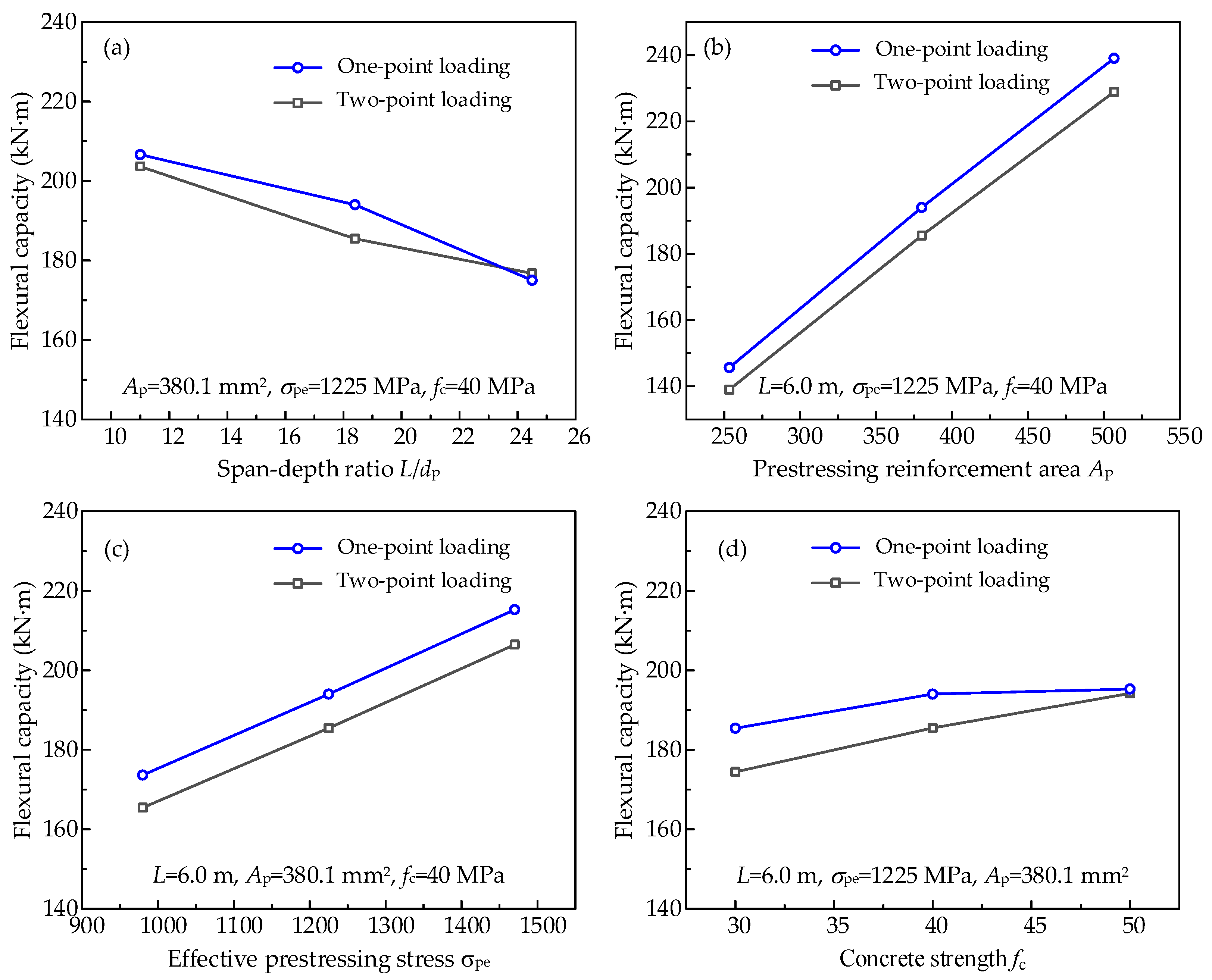
- Figure 10 shows the effects of parameters on the flexural capacity. The parameter L/dp has a negative correlation with flexural capacity. In comparison, the flexural capacity increases with increasing parameters Ap, σpe, and fc.
3. Flexural Capacity Prediction Methods and Applicability Analysis
3.1. Widely Used Methods for Predicting Flexural Capacity
3.1.1. Statistical-Based Method
3.1.2. Bond-Reduction Method
3.1.3. Deformation-Based Method
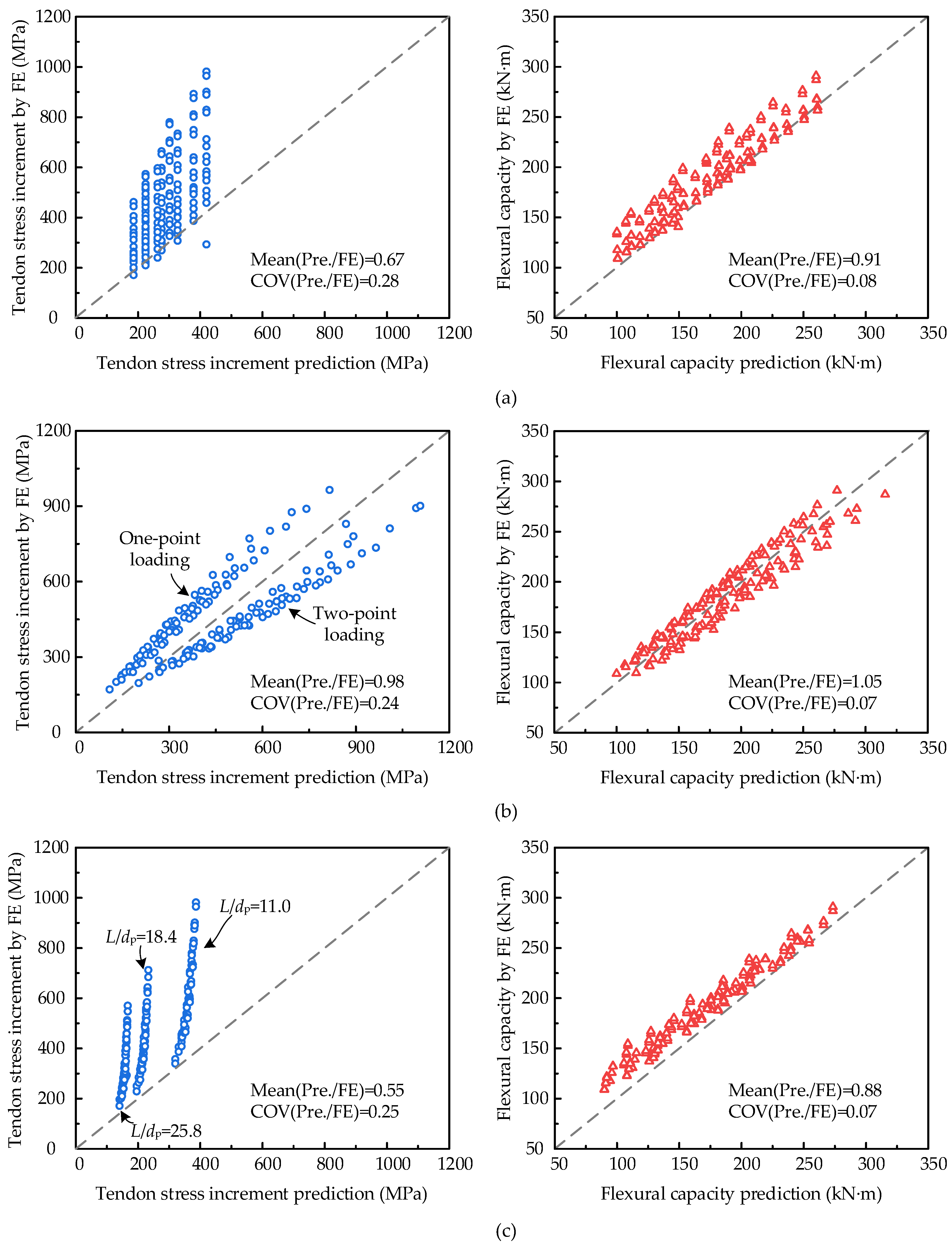
3.2. Applicability Evaluation of the Widely Used Prediction Equations
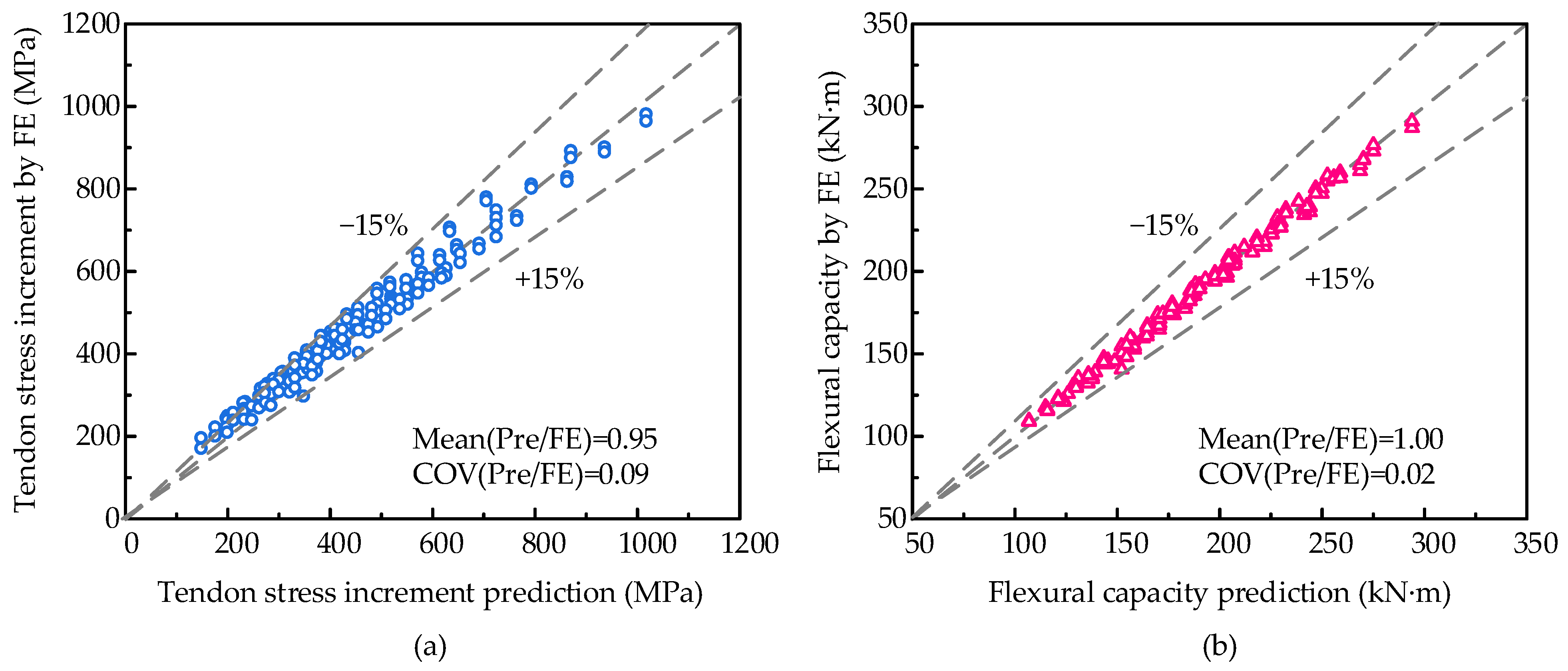
3.3. Proposals for the Flexural Capacity Prediction Equation
4. Discussion
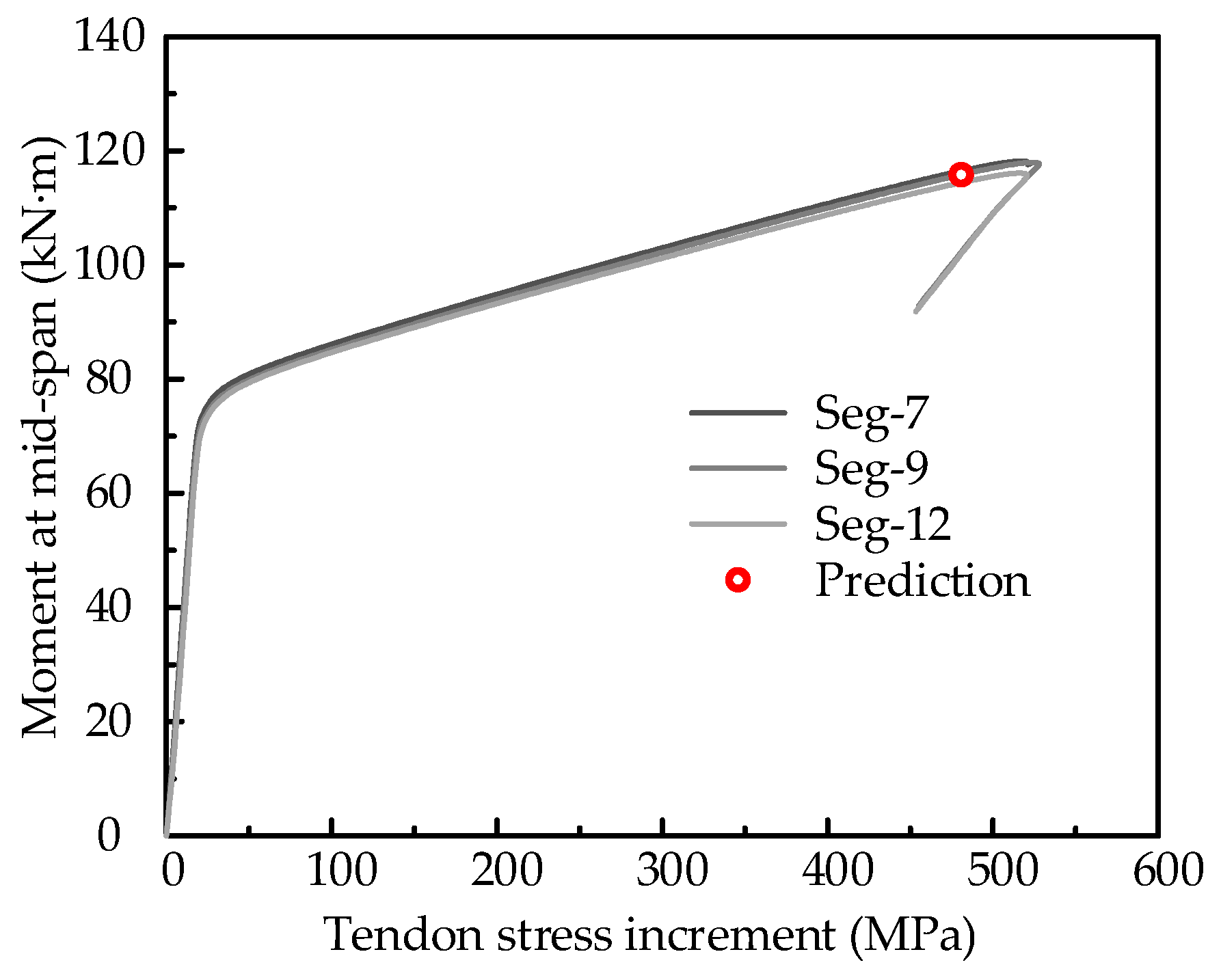
4.1. Effects of Segment Size and Joint Positions
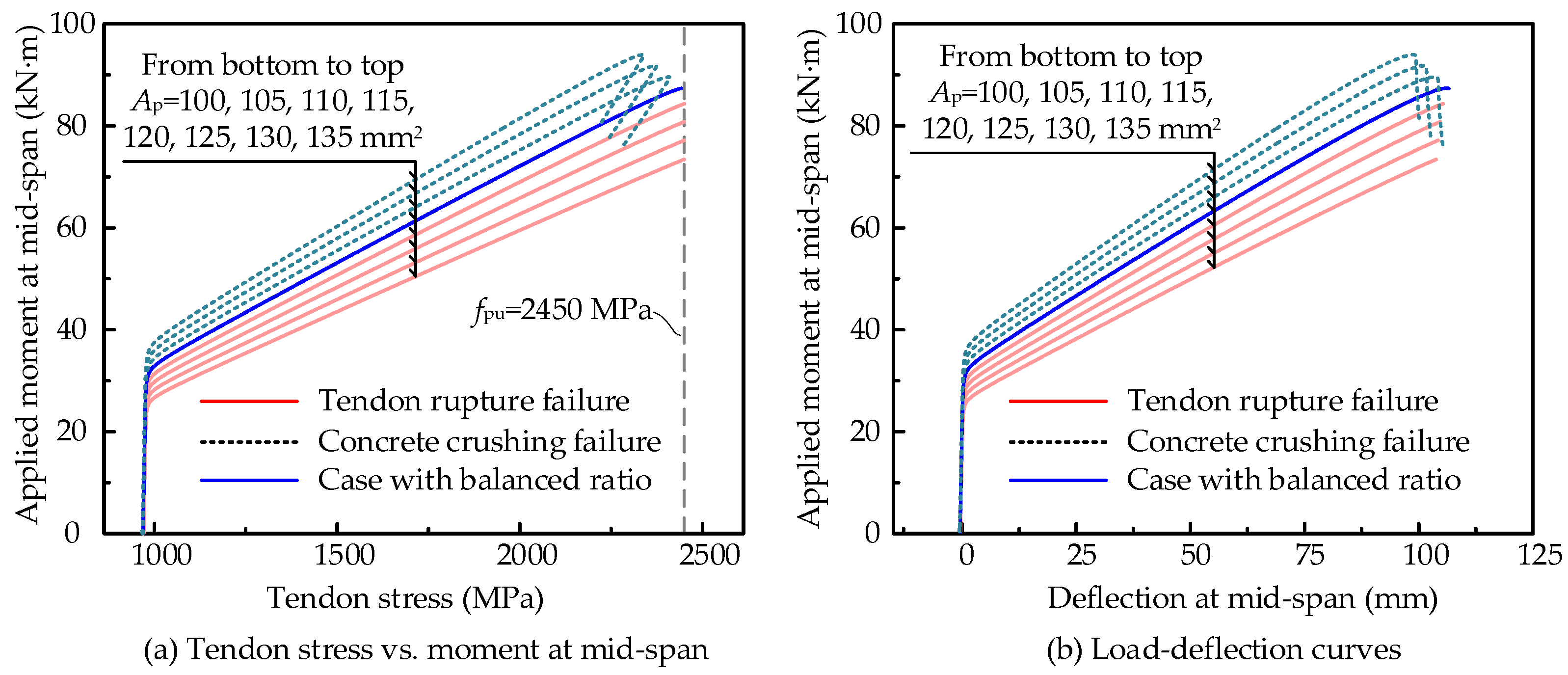
4.2. Balanced Prestressing Reinforcement Ratio for PSCB-IUCFRP
5. Conclusions
- The comparisons between segmental and monolithic beams show that plastic deformation in the segmental beam is concentrated at the failure joint cross-section, which differs from the monolithic beam’s distributed modes. With the same conditions, the monolithic beam’s stress increment, flexural capacity, and ultimate deflection are more significant than those of the segmental beam.
- The parametric study shows that the loading types have a minor influence on the tendon stress increment and flexural capacity of PSCB-IUCFRP. The factors L/dp, Ap, and σpe are negatively correlated with tendon stress increment. However, the factor fc has the opposite effect. The flexural capacity decreases with an increase in L/dp, and an increase in Ap, σpe, and fc improves the flexural capacity.
- The equations of the ACI 440.4R model, based on the bond-reduction method, show the best prediction accuracy for tendon stress increment with a mean index value of 0.98 and COV index value of 0.24. It underestimates the results of cases under one-point loading but overestimates those under two-point loading. The predictions of the ACI 318-14 model and the AASHTO LRFD model are all conservative.
- The predictions of the proposed equation, derived according to the failure mechanism and deformation analysis, show good agreement with the numerical model results for both tendon stress increment and flexural capacity. The simplified plastic hinge length for PSCB-IUCFRP is recommended to be 2.1 dp. The balanced prestressing reinforcement ratio of PSCB-IUCFRP is smaller than that of the bonded prestressed members, and the suggested equations are put forward.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| ID | L (m) | Ap (mm2) | σpe (MPa) | fc (MPa) | Two-Point Loading | One-Point Loading | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| ∆σp (MPa) | umax (mm) | Mu (kN·m) | ∆σp (MPa) | umax (mm) | Mu (kN·m) | |||||
| 1 | 3.6 | 253.4 | 980 | 30 | 780.3 | 58.8 | 133.5 | 771.3 | 58.2 | 135.5 |
| 2 | 3.6 | 253.4 | 980 | 40 | 892.5 | 66.0 | 144.1 | 876.0 | 64.6 | 146.1 |
| 3 | 3.6 | 253.4 | 980 | 50 | 981.6 | 71.5 | 152.8 | 964.7 | 70.1 | 154.7 |
| 4 | 3.6 | 253.4 | 1225 | 30 | 706.8 | 53.3 | 145.3 | 697.4 | 52.7 | 147.6 |
| 5 | 3.6 | 253.4 | 1225 | 40 | 811.6 | 59.9 | 156.1 | 801.9 | 59.3 | 158.4 |
| 6 | 3.6 | 253.4 | 1225 | 50 | 901.3 | 65.7 | 164.8 | 889.6 | 64.9 | 167.1 |
| 7 | 3.6 | 253.4 | 1470 | 30 | 644.1 | 48.6 | 157.7 | 625.9 | 47.1 | 160.2 |
| 8 | 3.6 | 253.4 | 1470 | 40 | 749.0 | 55.5 | 168.6 | 730.7 | 54.0 | 171.3 |
| 9 | 3.6 | 253.4 | 1470 | 50 | 829.4 | 60.5 | 177.5 | 818.6 | 59.8 | 180.1 |
| 10 | 3.6 | 380.1 | 980 | 30 | 573.7 | 44.0 | 171.5 | 563.0 | 43.3 | 174.1 |
| 11 | 3.6 | 380.1 | 980 | 40 | 664.5 | 49.9 | 185.4 | 652.7 | 49.1 | 188.0 |
| 12 | 3.6 | 380.1 | 980 | 50 | 734.7 | 54.3 | 196.4 | 723.9 | 53.6 | 199.2 |
| 13 | 3.6 | 380.1 | 1225 | 30 | 512.5 | 39.1 | 189.5 | 494.7 | 37.7 | 192.4 |
| 14 | 3.6 | 380.1 | 1225 | 40 | 598.1 | 44.8 | 203.6 | 585.7 | 44.0 | 206.6 |
| 15 | 3.6 | 380.1 | 1225 | 50 | 668.1 | 49.3 | 215.0 | 654.8 | 48.4 | 218.1 |
| 16 | 3.6 | 380.1 | 1470 | 30 | 454.8 | 34.1 | 208.2 | 441.8 | 33.3 | 211.5 |
| 17 | 3.6 | 380.1 | 1470 | 40 | 539.6 | 40.1 | 222.8 | 525.8 | 39.2 | 226.2 |
| 18 | 3.6 | 380.1 | 1470 | 50 | 608.3 | 44.8 | 234.3 | 589.8 | 43.4 | 237.9 |
| 19 | 3.6 | 506.8 | 980 | 30 | 461.8 | 35.7 | 205.8 | 444.9 | 34.4 | 208.7 |
| 20 | 3.6 | 506.8 | 980 | 40 | 533.7 | 40.3 | 222.6 | 521.1 | 39.5 | 225.6 |
| 21 | 3.6 | 506.8 | 980 | 50 | 596.8 | 44.5 | 236.0 | 584.2 | 43.7 | 239.2 |
| 22 | 3.6 | 506.8 | 1225 | 30 | 405.8 | 30.6 | 229.7 | 386.8 | 29.2 | 232.9 |
| 23 | 3.6 | 506.8 | 1225 | 40 | 477.4 | 35.7 | 247.1 | 462.2 | 34.7 | 250.5 |
| 24 | 3.6 | 506.8 | 1225 | 50 | 534.6 | 39.5 | 260.9 | 520.5 | 38.6 | 264.5 |
| 25 | 3.6 | 506.8 | 1470 | 30 | 357.3 | 25.8 | 254.8 | 339.8 | 24.7 | 258.2 |
| 26 | 3.6 | 506.8 | 1470 | 40 | 425.5 | 31.0 | 272.9 | 408.4 | 29.9 | 276.6 |
| 27 | 3.6 | 506.8 | 1470 | 50 | 482.3 | 35.2 | 287.1 | 465.5 | 34.1 | 291.1 |
| 28 | 6.0 | 253.4 | 980 | 30 | 558.7 | 115.8 | 117.7 | 546.8 | 113.9 | 125.9 |
| 29 | 6.0 | 253.4 | 980 | 40 | 640.3 | 130.3 | 125.9 | 627.2 | 128.3 | 132.2 |
| 30 | 6.0 | 253.4 | 980 | 50 | 712.3 | 143.7 | 132.5 | 684.0 | 137.6 | 130.9 |
| 31 | 6.0 | 253.4 | 1225 | 30 | 496.5 | 102.7 | 130.7 | 485.3 | 101.1 | 139.1 |
| 32 | 6.0 | 253.4 | 1225 | 40 | 579.8 | 118.2 | 139.0 | 559.0 | 114.1 | 145.6 |
| 33 | 6.0 | 253.4 | 1225 | 50 | 643.7 | 129.7 | 145.7 | 621.4 | 125.3 | 144.6 |
| 34 | 6.0 | 253.4 | 1470 | 30 | 444.4 | 91.5 | 144.2 | 428.1 | 88.5 | 152.9 |
| 35 | 6.0 | 253.4 | 1470 | 40 | 521.4 | 105.8 | 152.7 | 503.9 | 102.8 | 159.5 |
| 36 | 6.0 | 253.4 | 1470 | 50 | 584.2 | 117.4 | 159.4 | 566.2 | 114.4 | 154.8 |
| 37 | 6.0 | 380.1 | 980 | 30 | 409.3 | 85.6 | 154.7 | 394.9 | 83.1 | 165.2 |
| 38 | 6.0 | 380.1 | 980 | 40 | 476.6 | 98.1 | 165.4 | 458.6 | 94.9 | 173.7 |
| 39 | 6.0 | 380.1 | 980 | 50 | 532.2 | 108.4 | 174.0 | 509.5 | 103.9 | 174.6 |
| 40 | 6.0 | 380.1 | 1225 | 30 | 355.7 | 73.1 | 174.4 | 341.2 | 70.7 | 185.4 |
| 41 | 6.0 | 380.1 | 1225 | 40 | 421.4 | 85.9 | 185.5 | 401.6 | 82.3 | 194.0 |
| 42 | 6.0 | 380.1 | 1225 | 50 | 471.7 | 95.2 | 194.2 | 453.1 | 92.1 | 195.3 |
| 43 | 6.0 | 380.1 | 1470 | 30 | 316.5 | 63.6 | 195.0 | 297.4 | 60.1 | 206.5 |
| 44 | 6.0 | 380.1 | 1470 | 40 | 376.4 | 75.6 | 206.5 | 354.5 | 71.6 | 215.3 |
| 45 | 6.0 | 380.1 | 1470 | 50 | 425.6 | 85.1 | 215.4 | 405.0 | 81.6 | 188.5 |
| 46 | 6.0 | 506.8 | 980 | 30 | 328.0 | 68.2 | 188.7 | 311.5 | 65.2 | 201.4 |
| 47 | 6.0 | 506.8 | 980 | 40 | 383.7 | 78.8 | 201.9 | 364.5 | 75.3 | 211.6 |
| 48 | 6.0 | 506.8 | 980 | 50 | 428.8 | 87.2 | 212.4 | 408.7 | 83.7 | 214.9 |
| 49 | 6.0 | 506.8 | 1225 | 30 | 284.2 | 56.7 | 215.1 | 263.7 | 52.8 | 228.4 |
| 50 | 6.0 | 506.8 | 1225 | 40 | 334.6 | 66.9 | 228.9 | 316.8 | 64.0 | 239.0 |
| 51 | 6.0 | 506.8 | 1225 | 50 | 379.3 | 75.8 | 239.7 | 358.2 | 72.2 | 242.3 |
| 52 | 6.0 | 506.8 | 1470 | 30 | 250.4 | 46.8 | 242.6 | 229.0 | 43.0 | 256.5 |
| 53 | 6.0 | 506.8 | 1470 | 40 | 300.1 | 58.1 | 257.1 | 275.2 | 53.5 | 267.6 |
| 54 | 6.0 | 506.8 | 1470 | 50 | 340.2 | 66.5 | 268.3 | 315.6 | 62.1 | 254.1 |
| 55 | 8.4 | 253.4 | 980 | 30 | 444.8 | 180.9 | 109.6 | 430.2 | 176.1 | 108.9 |
| 56 | 8.4 | 253.4 | 980 | 40 | 512.4 | 204.5 | 116.5 | 493.0 | 197.8 | 115.6 |
| 57 | 8.4 | 253.4 | 980 | 50 | 570.4 | 225.5 | 122.0 | 547.6 | 217.1 | 121.0 |
| 58 | 8.4 | 253.4 | 1225 | 30 | 390.2 | 157.7 | 123.5 | 372.5 | 151.8 | 122.7 |
| 59 | 8.4 | 253.4 | 1225 | 40 | 459.6 | 183.6 | 130.3 | 435.4 | 174.5 | 129.4 |
| 60 | 8.4 | 253.4 | 1225 | 50 | 507.2 | 199.1 | 136.1 | 485.3 | 192.1 | 134.8 |
| 61 | 8.4 | 253.4 | 1470 | 30 | 339.9 | 135.7 | 137.8 | 326.9 | 132.3 | 137.1 |
| 62 | 8.4 | 253.4 | 1470 | 40 | 408.3 | 161.8 | 144.9 | 386.8 | 154.4 | 143.9 |
| 63 | 8.4 | 253.4 | 1470 | 50 | 459.0 | 180.1 | 150.5 | 293.2 | 112.0 | 140.7 |
| 64 | 8.4 | 380.1 | 980 | 30 | 321.8 | 130.9 | 146.4 | 306.1 | 125.9 | 145.1 |
| 65 | 8.4 | 380.1 | 980 | 40 | 377.1 | 151.0 | 155.5 | 285.7 | 111.9 | 148.2 |
| 66 | 8.4 | 380.1 | 980 | 50 | 426.4 | 169.9 | 162.6 | 400.5 | 160.2 | 160.8 |
| 67 | 8.4 | 380.1 | 1225 | 30 | 282.0 | 112.7 | 167.5 | 261.1 | 105.2 | 166.0 |
| 68 | 8.4 | 380.1 | 1225 | 40 | 337.3 | 134.2 | 176.8 | 308.7 | 123.3 | 175.0 |
| 69 | 8.4 | 380.1 | 1225 | 50 | 370.6 | 145.1 | 184.2 | 349.1 | 138.4 | 182.1 |
| 70 | 8.4 | 380.1 | 1470 | 30 | 244.9 | 94.3 | 189.4 | 222.1 | 86.3 | 187.8 |
| 71 | 8.4 | 380.1 | 1470 | 40 | 298.9 | 116.4 | 199.1 | 269.3 | 105.4 | 197.1 |
| 72 | 8.4 | 380.1 | 1470 | 50 | 334.3 | 129.4 | 206.6 | 307.8 | 120.5 | 204.4 |
| 73 | 8.4 | 506.8 | 980 | 30 | 258.1 | 103.3 | 180.7 | 239.1 | 96.9 | 178.7 |
| 74 | 8.4 | 506.8 | 980 | 40 | 306.1 | 122.0 | 191.9 | 282.3 | 113.5 | 189.4 |
| 75 | 8.4 | 506.8 | 980 | 50 | 342.5 | 135.2 | 200.8 | 318.7 | 127.3 | 197.9 |
| 76 | 8.4 | 506.8 | 1225 | 30 | 222.5 | 84.6 | 208.8 | 200.9 | 77.2 | 206.6 |
| 77 | 8.4 | 506.8 | 1225 | 40 | 267.3 | 103.1 | 220.6 | 241.7 | 94.1 | 217.9 |
| 78 | 8.4 | 506.8 | 1225 | 50 | 302.4 | 116.9 | 229.8 | 275.0 | 107.5 | 226.7 |
| 79 | 8.4 | 506.8 | 1470 | 30 | 196.6 | 69.2 | 237.9 | 171.3 | 60.2 | 235.4 |
| 80 | 8.4 | 506.8 | 1470 | 40 | 240.1 | 88.8 | 250.5 | 209.8 | 77.8 | 247.4 |
| 81 | 8.4 | 506.8 | 1470 | 50 | 274.3 | 103.3 | 260.1 | 240.2 | 90.9 | 256.6 |
References
- Tran, D.T.; Pham, T.M.; Hao, H.; Do, T.V.; Tran, T.T. Blast Behaviour of Precast Segmental vs. Monolithic Concrete Beams Prestressed with Unbonded Tendons: A Numerical Investigation. Int. J. Impact Eng. 2023, 173, 104434. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z.; Hu, F.; Du, X.; Lu, Y.; Zhu, J. Full-Scale Experimental Study on Shear Behavior of Multiple-Keyed Epoxy Joints in Precast Concrete Segmental Bridges. Structures 2022, 45, 437–447. [Google Scholar] [CrossRef]
- Behrmann, T.; Frohlich, M.; Wenger, P.; Hierl, M. Technical Challenges in the Design of Prestressed Concrete Precast Beams with Dry and Smooth Joints in Bridge Construction. Bautechnik 2022, 99, 288–295. [Google Scholar] [CrossRef]
- Elsamak, G.; Salama, M.I.; Hamoda, A. Behavior of Precast Segmental Beams Made of High-Strength Concrete and Ultra-High Performance Fiber Concrete Connected by Shear Keys Technique. Arab. J. Sci. Eng. 2022, 48, 4907–4923. [Google Scholar] [CrossRef]
- Ahmed, G.H.; Aziz, O.Q. Shear Strength of Joints in Precast Posttensioned Segmental Bridges During 1959–2019, Review and Analysis. Structures 2019, 20, 527–542. [Google Scholar] [CrossRef]
- Yuen, T.Y.P.; Halder, R.; Chen, W.-W.; Zhou, X.; Deb, T.; Liu, Y.; Tseng, Y.; Wen, T.-H. DFEM of a Post-Tensioned Precast Concrete Segmental Bridge with Unbonded External Tendons Subjected to Prestress Changes. Structures 2020, 28, 1322–1337. [Google Scholar] [CrossRef]
- Jiang, H.; Hu, Z.; Cao, Z.; Gao, X.; Tian, Y.; Sun, X. Experimental and Numerical Study on Shear Performance of Externally Prestressed Precast UHPC Segmental Beams without Stirrups. Structures 2022, 46, 1134–1153. [Google Scholar] [CrossRef]
- Jiang, H.; Cao, Q.; Liu, A.; Wang, T.; Qiu, Y. Flexural Behavior of Precast Concrete Segmental Beams with Hybrid Tendons and Dry Joints. Constr. Build. Mater. 2016, 110, 1–7. [Google Scholar] [CrossRef]
- Jiang, H.; Li, Y.; Liu, A.; Chen, L.; Chen, Y.; Xiao, J. Experimental Study on Shear Behavior of Precast Concrete Segmental Beams with Hybrid Tendons and Dry Joints. KSCE J. Civ. Eng. 2019, 23, 4354–4367. [Google Scholar] [CrossRef]
- Anania, L.; Badalà, A.; D’Agata, G. Damage and Collapse Mode of Existing Post Tensioned Precast Concrete Bridge: The Case of Petrulla Viaduct. Eng. Struct. 2018, 162, 226–244. [Google Scholar] [CrossRef]
- Wouters, J.P.; Kesner, K.; Poston, R.W. Tendon Corrosion in Precast Segmental Bridges. J. Transp. Res. Board 1999, 1654, 128–132. [Google Scholar] [CrossRef]
- Woodward, R.; Williams, F. Collapse of Yns-Y-Gwas Bridge, Glamorgan. Proc. Inst. Civ. Eng. 1988, 84, 635–669. [Google Scholar] [CrossRef]
- Halder, R.; Yuen, T.Y.P.; Chen, W.-W.; Zhou, X.; Deb, T.; Zhang, H.; Wen, T.-H. Tendon Stress Evaluation of Unbonded Post-Tensioned Concrete Segmental Bridges with Two-Variable Response Surfaces. Eng. Struct. 2021, 245, 112984. [Google Scholar] [CrossRef]
- Jia, L.; Fang, Z.; Huang, Z.; Pilakoutas, K.; Wang, Q.; Tan, X. Flexural Behavior of UHPC Beams Prestressed with External CFRP Tendons. Appl. Sci. 2021, 11, 9189. [Google Scholar] [CrossRef]
- Rogowski, J.; Kotynia, R. Comparison of Prestressing Methods with CFRP and SMA Materials in Flexurally Strengthened RC Members. Materials 2022, 15, 1231. [Google Scholar] [CrossRef]
- Lou, T.; Lopes, S.M.R.; Lopes, A.V. External CFRP Tendon Members: Secondary Reactions and Moment Redistribution. Compos. Part B 2014, 57, 250–261. [Google Scholar] [CrossRef]
- Lou, T.; Lopes, S.M.R.; Lopes, A.V. Factors Affecting Moment Redistribution at Ultimate in Continuous Beams Prestressed with External CFRP Tendons. Compos. Part B 2014, 66, 136–146. [Google Scholar] [CrossRef]
- Lou, T.; Lopes, S.M.R.; Lopes, A.V. A Comparative Study of Continuous Beams Prestressed with Bonded FRP and Steel Tendons. Compos. Struct. 2015, 124, 100–110. [Google Scholar] [CrossRef]
- Lou, T.; Liu, M.; Lopes, S.M.R.; Lopes, A.V. Effect of Bond on Flexure of Concrete Beams Prestressed with FRP Tendons. Compos. Struct. 2017, 173, 168–176. [Google Scholar] [CrossRef]
- Lou, T.; Karavasilis, T.L. Time-Dependent Assessment and Deflection Prediction of Prestressed Concrete Beams with Unbonded CFRP Tendons. Compos. Struct. 2018, 194, 365–376. [Google Scholar] [CrossRef]
- Le, T.D.; Pham, T.M.; Hao, H.; Haoc, Y. Flexural Behaviour of Precast Segmental Concrete Beams Internally Prestressed with Unbonded CFRP Tendons under Four-Point Loading. Eng. Struct. 2018, 168, 371–383. [Google Scholar] [CrossRef]
- Le, T.D.; Pham, T.M.; Hao, H.; Yuan, C. Performance of Precast Segmental Concrete Beams Posttensioned with Carbon Fiber-Reinforced Polymer (CFRP) Tendons. Compos. Struct. 2019, 208, 56–69. [Google Scholar] [CrossRef]
- Le, T.D.; Pham, T.M.; Hao, H.; Li, H. Behavior of Precast Segmental Concrete Beams Prestressed with External Steel and CFRP Tendons. J. Compos. Constr. 2020, 24, 04020053. [Google Scholar] [CrossRef]
- Tran, D.T.; Pham, T.M.; Hao, H.; Chen, W. Numerical Investigation of Flexural Behaviours of Precast Segmental Concrete Beams Internally Post-Tensioned with Unbonded FRP Tendons under Monotonic Loading. Eng. Struct. 2021, 249, 113341. [Google Scholar] [CrossRef]
- Yan, W.; Chen, L.; Han, B.; Xie, H.; Sun, Y. Numerical Model for Flexural Analysis of Precast Segmental Concrete Beam with Internal Unbonded CFRP Tendons. Materials 2022, 15, 4105. [Google Scholar] [CrossRef] [PubMed]
- Ghallab, A. Calculating Ultimate Tendon Stress in Externally Prestressed Continuous Concrete Beams Using Simplified Formulas. Eng. Struct. 2013, 46, 417–430. [Google Scholar] [CrossRef]
- Maguire, M.; Chang, M.; Collins, W.N.; Sun, Y. Stress Increase of Unbonded Tendons in Continuous Posttensioned Members. J. Bridge Eng. 2017, 22, 04016115. [Google Scholar] [CrossRef]
- Alqam, M.; Alkhairi, F.; Naaman, A. An Improved Methodology for the Prediction of the Stress at Ultimate in Unbonded Internal and External Steel Tendons. Arab. J. Sci. Eng. 2020, 45, 7915–7954. [Google Scholar] [CrossRef]
- Yan, W.-T.; Chen, L.-J.; Han, B.; Wei, F.; Xie, H.-B.; Yu, J.-P. Proposals for Flexural Capacity Prediction Method of Externally Prestressed Concrete Beam. Struct. Eng. Mech. 2022, 83, 363–375. [Google Scholar]
- Lee, C.; Shin, S.; Lee, H. Balanced Ratio of Concrete Beams Internally Prestressed with Unbonded CFRP Tendons. Int. J. Concr. Struct. Mater. 2017, 11, 1–16. [Google Scholar] [CrossRef]
- Sun, Y.; Wu, T.; Liu, X. Design of Concrete Beams Reinforced and Unbonded Prestressed with FRP Bars Based on Serviceability Requirements. Compos. Struct. 2022, 300, 116133. [Google Scholar] [CrossRef]
- Sun, Y.; Wu, T.; Liu, X.; Zhang, B. Failure Mode and Flexural Capacity of Concrete Beams Prestressed with Unbonded FRP Tendons. Compos. Struct. 2022, 283, 114956. [Google Scholar] [CrossRef]
- Fu, C.; Zhu, Y.; Wang, Y. Stiffness Assessment of Cracked Post-Tensioned Concrete Beams with Unbonded Tendons Based on the Cracking Pattern. Eng. Struct. 2020, 214, 110599. [Google Scholar] [CrossRef]
- Zhou, W.; Xie, X. Flexural Response of Continuous Unbonded Post-Tensioned Beams Strengthened with CFRP Laminates. Compos. Struct. 2019, 211, 455–468. [Google Scholar] [CrossRef]
- Peng, F.; Xue, W. Calculating Method for Ultimate Tendon Stress in Internally Unbonded Prestressed Concrete Members. ACI Struct. J. 2019, 116, 225–234. [Google Scholar] [CrossRef]
- Yan, W.-T.; Han, B.; Xie, H.-B.; Li, P.-F.; Zhu, L. Research on Numerical Model for Flexural Behaviors Analysis of Precast Concrete Segmental Box Girders. Eng. Struct. 2020, 219, 110733. [Google Scholar] [CrossRef]
- Mckenna, F.; Fenves, G. Opensees 2.5.0, Computer Software; UC Berkeley: Berkeley, CA, USA, 2015; Available online: http://opensees.berkeley.edu (accessed on 1 March 2023).
- Naaman, A.E.; Alkhairi, F.M. Stress at Ultimate in Unbonded Post-Tensioning Tendons. Part 1-Evaluation of the State-of-the-Art. ACI Struct. J. 1991, 88, 641–651. [Google Scholar]
- Naaman, A.E.; Alkhairi, F.M. Stress at Ultimate in Unbonded Post-Tensioning Tendons: Part 2-Proposed Methodology. ACI Struct. J. 1991, 88, 683–692. [Google Scholar]
- ACI 318-14; Building Code Requirements for Reinforced Concrete (ACI 318-14). American Concrete Institute: Detroit, MI, USA, 2014.
- Chee-Khoon, N. Tendon Stress and Flexural Strength of Externally Prestressed Beams. ACI Struct. J. 2003, 100, 644–653. [Google Scholar]
- He, Z.Q.; Liu, Z. Stresses in External and Internal Unbonded Tendons: Unified Methodology and Design Equations. J. Struct. Eng. 2010, 136, 1055–1065. [Google Scholar] [CrossRef]
- Roberts-Wollmann, C.L.; Kreger, M.E.; Rogowsky, D.M.; Breen, J.E. Stresses in External Tendons at Ultimate. ACI Struct. J. 2005, 102, 206–213. [Google Scholar]
- Lee, S.-H.; Shin, K.-J.; Thomas, H.K.K. Non-Iterative Moment Capacity Equation for Reinforced Concrete Beams with External Post-Tensioning. ACI Struct. J. 2014, 111, 1111–1122. [Google Scholar] [CrossRef]
- Peng, F.; Xue, W.; Tan, Y. Design Approach for Flexural Capacity of Prestressed Concrete Beams with External Tendons. J. Struct. Eng. 2018, 144, 04018215. [Google Scholar] [CrossRef]
- Alan, H.; Mattock, J.Y.; Basil, T.K. Comparative Study of Prestressed Concrete Beams, with and without Bond. J. Proc. 1971, 68, 116–125. [Google Scholar]
- Mojtahedi, S.; Gamble, W.L. Ultimate Steel Stresses in Unbonded Prestressed Concrete. J. Struct. Div. 1978, 104, 1159–1165. [Google Scholar] [CrossRef]
- ACI 440.4R; Prestressing Concrete Structures with FRP Tendons. American Concrete Institute: Farmington Hills, MI, USA, 2004.
- Tam, A.; Pannell, F.N. Ultimate Moment Resistance of Unbonded Partially Prestressed Reinforced Concrete Beams. Mag. Concr. Res. 1976, 28, 203–208. [Google Scholar] [CrossRef]
- AASHTO. AASHTO LRFD Bridge Design Specifications; AASHTO: Washington, DC, USA, 2017. [Google Scholar]
- AASHTO. Bridge Design Specification; AASHTO: Washington, DC, USA, 1994. [Google Scholar]
- Au, F.T.K.; Du, J. Prediction of Ultimate Stress in Unbonded Prestressed Tendons. Mag. Concr. Res. 2004, 56, 1–11. [Google Scholar] [CrossRef]




| Name | Structural Type | Tendon Type | Effective Tendon Stress (MPa) |
|---|---|---|---|
| BC1 [21] | Segmental | CFRP | 818 |
| M-CFRP | Monolithic | CFRP | 818 |
| S-Steel | Segmental | Steel | 818 |
| Parameter Name | Values |
|---|---|
| L (mm) | 3600, 6000, 8400 |
| Ap (mm2) | 253.4, 380.1, 506.8 |
| Effective prestressing stress σpe (MPa) | 980, 1225, 1470 |
| Concrete strength fc (MPa) | 30, 40, 50 |
| Loading types | Two-point loading, One-point loading |
| α | Tendon Stress Increment | Flexural Capacity | ||
|---|---|---|---|---|
| Mean (Pre./FE) | COV (Pre./FE) | Mean (Pre./FE) | COV (Pre./FE) | |
| 1.5 | 0.733 | 0.101 | 0.942 | 0.019 |
| 1.6 | 0.772 | 0.100 | 0.953 | 0.017 |
| 1.7 | 0.810 | 0.098 | 0.963 | 0.016 |
| 1.8 | 0.847 | 0.096 | 0.973 | 0.015 |
| 1.9 | 0.884 | 0.095 | 0.983 | 0.015 |
| 2.0 | 0.920 | 0.093 | 0.992 | 0.016 |
| 2.1 | 0.955 | 0.092 | 1.001 | 0.017 |
| 2.2 | 0.989 | 0.091 | 1.011 | 0.018 |
| 2.3 | 1.023 | 0.090 | 1.019 | 0.020 |
| 2.4 | 1.056 | 0.089 | 1.028 | 0.020 |
| 2.5 | 1.088 | 0.088 | 1.037 | 0.022 |
| 2.6 | 1.120 | 0.088 | 1.045 | 0.024 |
| 2.7 | 1.152 | 0.088 | 1.054 | 0.026 |
| 2.8 | 1.183 | 0.087 | 1.061 | 0.027 |
| 2.9 | 1.213 | 0.087 | 1.069 | 0.028 |
| 3.0 | 1.242 | 0.088 | 1.077 | 0.030 |
| Beams | Experimental Results | ACI 318-14 [40] | ACI 440.4R [48] | AASHTO LRFD [50] | Proposed Equation | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| ∆σp, exp (MPa) | Mexp (kN·m) | ∆σp, pre/∆σp, exp | Mpre/Mexp | ∆σp, pre/∆σp, exp | Mpre/Mexp | ∆σp, pre/∆σp, exp | Mpre/Mexp | ∆σp, pre/∆σp, exp | Mpre/Mexp | |
| BC1 | 956 | 135.6 | 0.429 | 0.732 | 1.277 | 1.198 | 0.404 | 0.72 | 1.025 | 1.061 |
| BC2 | 1026 | 147.6 | 0.399 | 0.588 | 1.252 | 1.052 | 0.379 | 0.577 | 1.014 | 0.924 |
| mean | - | - | 0.414 | 0.660 | 1.265 | 1.125 | 0.392 | 0.649 | 1.020 | 0.993 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, W.; Jiang, F.; Chen, L.; Sun, Y. Proposals for Flexural Capacity Prediction of Precast Segmental Concrete Beam Prestressed with Internal Un-Bonded CFRP Tendons. Appl. Sci. 2023, 13, 6652. https://doi.org/10.3390/app13116652
Yan W, Jiang F, Chen L, Sun Y. Proposals for Flexural Capacity Prediction of Precast Segmental Concrete Beam Prestressed with Internal Un-Bonded CFRP Tendons. Applied Sciences. 2023; 13(11):6652. https://doi.org/10.3390/app13116652
Chicago/Turabian StyleYan, Wutong, Fangxin Jiang, Liangjiang Chen, and Yue Sun. 2023. "Proposals for Flexural Capacity Prediction of Precast Segmental Concrete Beam Prestressed with Internal Un-Bonded CFRP Tendons" Applied Sciences 13, no. 11: 6652. https://doi.org/10.3390/app13116652
APA StyleYan, W., Jiang, F., Chen, L., & Sun, Y. (2023). Proposals for Flexural Capacity Prediction of Precast Segmental Concrete Beam Prestressed with Internal Un-Bonded CFRP Tendons. Applied Sciences, 13(11), 6652. https://doi.org/10.3390/app13116652





