Stress Analysis and Spalling Failure Simulation on Surrounding Rock of Deep Arch Tunnel

Abstract

To study the stress distribution characteristics of surrounding rock and the spalling mechanism of deep hard rock tunnels with different arch heights, the complex variable function and angle-preserving transformation method in elasticity theory were applied to the analytic solution of tangential stress distribution of arch tunnels during stress adjustment. In addition, true triaxial tests were conducted on granite cube specimens (100 mm × 100 mm × 100 mm) containing holes with three arch heights (including the 25 mm semi-circular arch, 16.7 mm three-centered arch, 12.5 mm three-centered arch) to simulate the spalling process under different initial ground stresses. The stress distribution solution and experimental results show that the initial failure stress of arch holes is 0.39–0.48 times the uniaxial compressive strength (UCS) of the rock. The initial failure location occurs at the arch foot, where tangential stress maximizes. When the lateral pressure coefficient is in the range of 0.38–0.50, the tangential stress is 3.2–3.5 times the UCS. The rock debris of the hole wall are in thin flake shapes. Symmetrical V-shaped or curved failure zones occurred on hole sidewalls. The stress distribution resolution of the surrounding rock of tunnels with different arch heights shows that with the increasing burial depth, the bearing performance of the semi-circular arch tunnel is optimal. In addition, the maximum tangential stress increases as the height of the arch decreases or the lateral stress increases, making it easier for the initial failure to occur at the foot of the arch.

1. Introduction

Underground mining of metal resources requires the construction of a series of excavated passages close to the ore body, including shafts and tunnels. The most common tunnel section adopted in metal mines is the arch section. After excavation of a deeply buried tunnel, the sidewalls are prone to stress failure, resulting in rock slabs that are approximately parallel to the tunnel surface, i.e., spalling [1,2]. Spalling is the precursor to rockburst, as the burial depth increases, the failure mode of the surrounding rock changes from surface spalling to strong rockburst [3]. Under high stress conditions, spalling or rockburst failure of surrounding tunnel rock has a detrimental effect on the support structure and poses a great threat to the underground construction and equipment safety [4,5], as shown in Figure 1. Under extreme stress conditions or harsh environments, such as damage to the surrounding rock caused by cyclic mining [6,7], the spalling process can lead to a complete collapse of tunnels (Figure 1b), seriously compromising the long-term stability of the tunnels [8]. Accurate prediction of spalling or rockburst is difficult [9,10,11]. Scholars have studied the energy storage and release performance of rock under the influences of temperature, joint, lithology, fracture, and age, and provided the basis for the prevention and control of spalling and rockburst from the perspective of energy [12,13,14,15,16,17,18,19]. It has been reported that spalling failure mostly occurs in the direction parallel to the maximum principal stress [20,21,22], by analyzing the surrounding rock stress when the tunnel spalling or rockburst occurs, these underground disasters can be further guided and controlled.

Stress analysis of the surrounding rock of tunnels containing holes has been systematically studied by scholars [24,25,26,27,28,29,30]. For example, in terms of arch tunnels, Wu et al. [31] analyzed the shape and size effect caused by the variation of geometric parameters of straight-walled three-centered arch tunnels on the surrounding rock stresses based on the analytical solutions obtained from the conformal mapping. Wu et al. [32,33] revealed the crack evolution mechanism of the inverted “U-shaped” cavity under uniaxial stress and investigated the mechanical response behavior of horseshoe openings in a cylindrical rock model under biaxial compression through stress distribution analysis. Tan et al. [34] used the complex variable theory to study the stress distribution in rock bodies containing complex-shaped holes and found that the hole shape affects the stability of rock containing holes mainly by influencing the degree of stress concentration around the hole. In addition, a large number of indoor simulation experiments have been carried out on specimens containing prefabricated circular, elliptical, and rectangular holes [35,36,37,38,39,40,41,42,43,44,45]. For rocks containing arched holes under uniaxial compression, Zhang et al. [46] performed rockburst tests on straight-walled semi-circular arch tunnels and observed that the specimens showed an obvious splitting rockburst phenomena as a whole. They also obtained the range of stress-intensity ratios for splitting rockburst. As the stress-intensity ratios increased, the main failure developed into a shear failure. For the biaxial compression test, Zhu et al. [47] conducted a physical model test to investigate the deep hard rock spalling in horseshoe tunnels and observed that micro-cracks and swelling first appeared on the surface of sidewalls. Then, cracks continued to expand and combine to produce thin rock sheets and spalling in a laminar fashion from shallow to deep. They also noted that the degree of spalling failure was positively correlated with the initial boundary stress. For the true triaxial test, cubic red sandstone and granite specimens containing straight-walled arch holes were commonly used to simulate the spalling failure after stress adjustment following deep tunnel excavation [48]. Luo et al. [49] used red sandstone specimens to simulate the spalling process and failure characteristics of “D-shaped” tunnel sidewalls. They found that tunnels in a “D” shape effectively reduced the failure severity of surrounding rock compared to circular tunnels. Si et al. [50] carried out a true triaxial test on cubic granite specimens with penetrating D-shaped tunnel and observed four stages of the spalling failure on tunnel sidewalls, i.e., the calm phase, the fine particle ejection phase, the crack generation and expansion phase, and the rock slab progressive flexural spalling phase. The spalling failure exhibited tensile characteristics. Under higher vertical stress and constant horizontal axial stress, increasing the lateral stress can reduce the severity of spalling failure and the depth of the V-shaped notch. In most underground hydraulic and hydroelectric projects, tunnels are lined with concrete to improve the self-supporting capacity of the surrounding rock, or modified materials are added to improve the strength of the backfill [51,52]. Some scholars have combined the analytical solution of non-circular tunnels with numerical simulation software to construct a three-dimensional analysis model for analyzing the stability of the tunnel face of shallow-buried shield tunnels and deep-buried tunnel projects [53,54,55,56,57,58]. Their research may provide relevant construction experience and suggestions for similar projects.

The above investigations have greatly enriched the understanding of the stress evolution mechanism and spalling failure of surrounding rock for deeply buried hard rock straight-walled arch tunnels, and are of great guidance in revealing the formation mechanism of tunnel failure or rock instability. However, the existing research mainly focused on the stress analysis of the surrounding rock of a single hole or on indoor simulation experiments of straight-walled arch hole specimens with a single rise-span ratio f/B (the ratio of arch height to the hole width). There are few studies on the stress analysis of the surrounding rock of hole walls considering the structural parameters of the arch structure or section shape, further revealing the spalling failure. Therefore, this paper first analyses the stresses of surrounding rock of holes with arch heights of 25 mm, f/B = 1/2, 16.7 mm, f/B = 1/3, 12.5 mm, f/B = 1/4, straight wall heights of 25 mm and widths of 50 mm). Then, the stress analysis results were validated in combination with indoor true-triaxial compression tests. The results help further deepen the understanding of spalling failure in deep hard rock tunnels with different arch heights.

2. Stress Analysis of Surrounding Rock

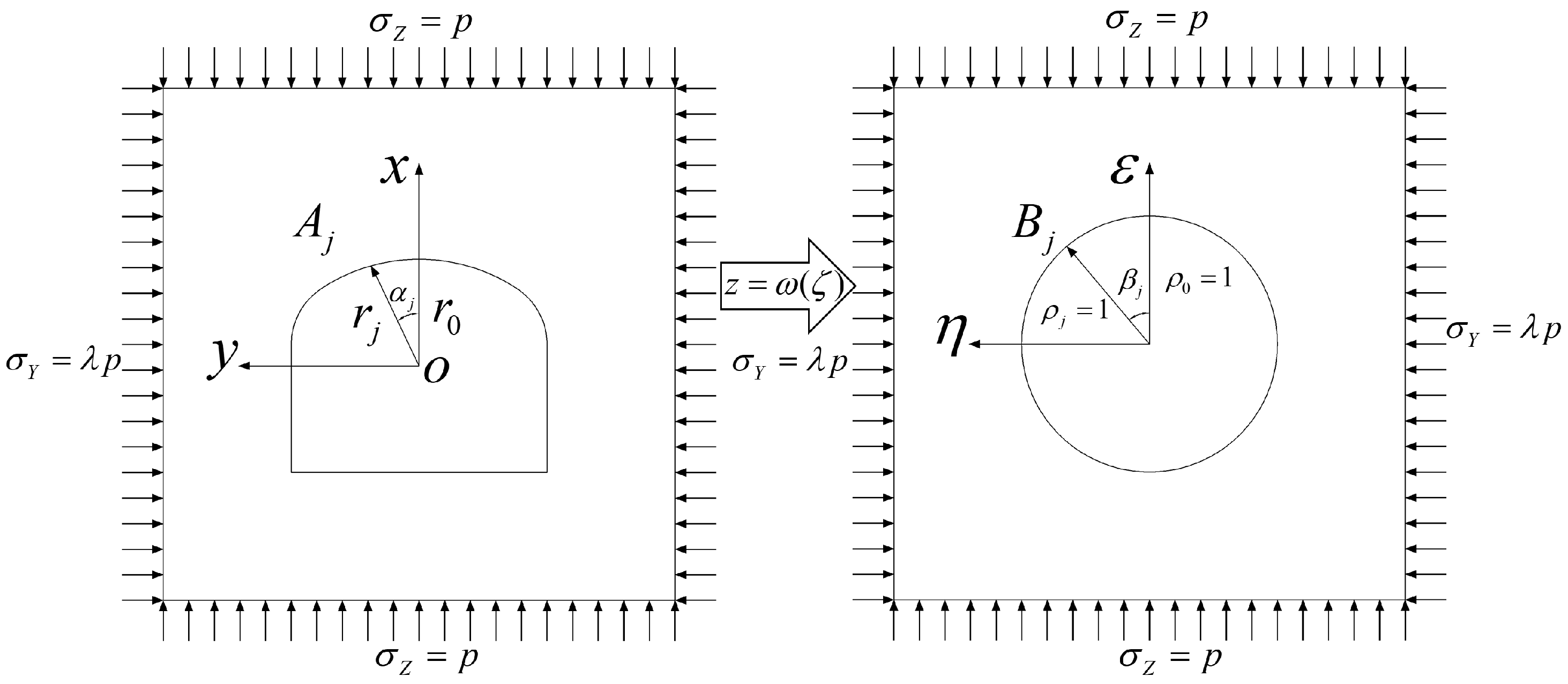
2.1. Complex Functions for Stress Distribution

For simplicity, the deep subsurface rock mass is assumed as a homogeneous, isotropic, and linearly elastic material. For the burial depths much greater than the cross-sectional dimensions of openings, rock mass can be considered as an infinite plane containing holes (z-plane) under plane strain conditions. According to Muskhelishvili’s theory [59], the stress component on the z-plane (${\sigma }_z,{\sigma }_y,{\tau }_{zy}$) in the right-angle coordinate system can be expressed as follows:

$$\left\{\begin{array}{c}{\sigma }_z+{\sigma }_y=4\mathrm{Re}[{\phi }_1^{\prime }(z)]\\ {\sigma }_z-{\sigma }_y+2i{\tau }_{zy}=2[\overline{z}{\phi }_1^{″}(z)+{\psi }_1^{\prime }(z)]\end{array}\right.$$

(1)

where ${\phi }_1(z)$ and ${\psi }_1(z)$ are two complex stress functions of the complex variable z.

The stress component (${\sigma }_{\rho },\hspace{0.33em}{\sigma }_{\theta },\hspace{0.33em}{\tau }_{r\theta }$) in polar coordinates can be obtained by [25]

$$\left\{\begin{array}{c}{\sigma }_{\rho }+{\sigma }_{\theta }={\sigma }_z+{\sigma }_y\\ {\sigma }_{\rho }-{\sigma }_{\theta }+2i{\tau }_{r\theta }=({\sigma }_z-{\sigma }_y+2i{\tau }_{zy})e^{2i\theta }\end{array}\right.$$

(2)

where ${\sigma }_{\theta }$,${\sigma }_{\rho }$, and ${\tau }_{\rho \theta }$ are the tangential stress, radial stress, and shear stress of surrounding rock, respectively.

According to the Riemann mapping theorem, any single connected domain with multiple boundary points in the z-plane can usually be mapped to a unit circle on the complex plane via a mapping function. Substituting Equation (2) into Equation (1), the stress component can be expressed as follows:

$$\left\{\begin{array}{c}{\sigma }_{\rho }+{\sigma }_{\theta }=4\mathrm{Re}[\Phi (\zeta )]\\ {\sigma }_{\theta }-{\sigma }_{\rho }+2i{\tau }_{r\theta }=\frac{2{\zeta }^2}{{\rho }^2{\omega }^{\prime }(\zeta )}[\overline{\omega }(\zeta ){\Phi }^{\prime }(\zeta )+{\omega }^{\prime }(\zeta )\Psi (\zeta )]\end{array}\right.$$

(3)

where $\zeta$ is the coordinate of a given point on the boundary of the complex plane mapping, Re is the real part of the complex number, i is the imaginary unit, $\omega (\zeta )$ is the mapping function, and $\Phi (\zeta )$, and $\Psi (\zeta )$ are two complex potential functions, which can be expressed by the following:

$$\Phi (\zeta )={\phi }_1^{\prime }(z)=\frac{{\phi }^{\prime }(\zeta )}{{\omega }^{\prime }(\zeta )},\hspace{1em}\Psi (\zeta )={\psi }_1^{\prime }(z)=\frac{{\psi }^{\prime }(\zeta )}{{\omega }^{\prime }(\zeta )}$$

(4)

The two complex stress functions $\phi (\zeta )$ and $\psi (\zeta )$ in the ζ-plane can be expressed as [60]

$$\left\{\begin{array}{l}\phi (\zeta )=B\omega (\zeta )+{\phi }_0(\zeta )\\ \psi (\zeta )=(B^{\prime }+i{C}^{\prime })\omega (\zeta )+{\psi }_0(\zeta )\end{array}\right.$$

(5)

The constants $B$, $B^{\prime }$, $C^{\prime }$ reflect the stress conditions of far-field surrounding rock and can be derived using the following equation:

$$B=\frac{{\sigma }_y^{\infty }+{\sigma }_z^{\infty }}{4},\hspace{1em}{B}^{\prime }=\frac{{\sigma }_z^{\infty }-{\sigma }_y^{\infty }}{2},\hspace{1em}{C}^{\prime }={\tau }_{zy}^{\infty }$$

(6)

Let ${\sigma }_z^{\infty }=p$, the coefficient of lateral pressure $\lambda =\frac{{\sigma }_y^{\infty }}{{\sigma }_z^{\infty }}$, ${\tau }_{zy}^{\infty }=0$. Then Equation (6) can be expressed as follows:

$$B=\frac{1+\lambda }{4}p,\hspace{1em}{B}^{\prime }=\frac{1-\lambda }{2}p,\hspace{1em}{C}^{\prime }=0$$

(7)

The unknown functions ${\phi }_0(\zeta )$ and ${\psi }_0(\zeta )$ can be expressed in terms of the Laurent series as follows:

$${\phi }_0(\zeta )={\displaystyle \sum _{n=1}^{\infty }{a}_n}{\zeta }^{-n},\hspace{1em}{\psi }_0(\zeta )={\displaystyle \sum _{n=1}^{\infty }{b}_n}{\zeta }^{-n}\hspace{0.33em}$$

(8)

The boundary conditions $f(\sigma )$ at the hole boundary are the following:

$$f(\sigma )=\phi (\sigma )+\frac{\omega (\sigma )}{\overline{{\omega }^{\prime }(\sigma )}}\overline{{\phi }^{\prime }(\sigma )}+\overline{\psi (\sigma )}$$

(9)

Substituting Equation (5) into Equation (9), the equilibrium equation for the boundary stress is obtained given that $\zeta =\sigma$ as follows [25]:

$${\phi }_0(\sigma )+\frac{\omega (\sigma )}{\overline{{\omega }^{\prime }(\sigma )}}\overline{{{\phi }^{\prime }}_0(\sigma )}+\overline{{\psi }_0(\sigma )}=-2B\omega (\sigma )-(B^{\prime }-i{C}^{\prime })\overline{\omega (\sigma )}$$

(10)

The analytical solutions of $\phi (\zeta )$ and $\psi (\zeta )$ are generally solved using the Cauchy integration method or the power series method [61].

2.2. Determination of the Mapping Function

According to the principle of angle-preserving transformation, the boundary outer domain of the arched hole on the z-plane can be converted to the unit circle boundary outer domain on the ζ-plane by the mapping function Z, as shown in Figure 2. The mapping function is as follows:

$$Z=\omega (\zeta )=R(\zeta +{\displaystyle \sum _{k=0}^{\infty }{C}_k{\zeta }^{-k})}$$

(11)

where R is a real number and is related to the hole size on the z-plane, and C_k is generally a series of complex constants. However, it represents the real constants when the hole is symmetric on the x-axis [62].

A given point on the boundary of the z-plane surface hole is marked by $A_j$, and polar coordinates $(r_j,\hspace{0.33em}{\alpha }_j)$. Assuming that its polar coordinates correspond to a point mapped on the ζ-plane as $(1,\hspace{0.33em}{\theta }_j)$, the relationship between the two points can be determined according to Equation (11):

$$r_j{e}^{i{\alpha }_j}=R(e^{i{\theta }_j}+{\displaystyle \sum _{k=0}^{\infty }{C}_k{e}^{-ik{\theta }_j})}$$

(12)

Equation (12) can be modified as follows:

$$r_j=R(e^{i({\theta }_j-{\alpha }_j)}+{\displaystyle \sum _{k=0}^{\infty }{C}_k{e}^{-i(k{\theta }_j+{\alpha }_j)})}$$

(13)

According to Euler’s formula, the real and imaginary parts of Equation (13) give the following:

$$\sin ({\alpha }_j-{\theta }_j)+{\displaystyle \sum _{k=0}^{\infty }{C}_k\sin ({\alpha }_j+k{\theta }_j)=0}$$

(14)

$$r_j=R[\cos ({\alpha }_j-{\theta }_j)+{\displaystyle \sum _{k=0}^{\infty }{C}_k(\cos {\alpha }_j+k{\theta }_j)]}$$

(15)

Assuming that the polar position $(1,\hspace{0.33em}0)$ on the boundary of the unit circle hole on the ζ-plane corresponds to the mapping point $(r_0,\hspace{0.33em}0)$ on the z-plane, we have the following:

$$R=\frac{r_0}{1+{\displaystyle \sum _{k=1}^{\infty }{C}_k}}$$

(16)

Substituting the m sampling points of the boundary attachment of the z-plane surface hole into Equation (15), the objective function h can be defined according to the least squares principle as follows:

$$h={{\displaystyle \sum _{j=1}^m\left\{r_j-R[\cos ({\alpha }_j-{\theta }_j)+{\displaystyle \sum _{k=0}^{n+1}{C}_k(\cos {\alpha }_j+k{\theta }_j)]}\right\}}}^2$$

(17)

In Equation (17), $C_k$ and ${\theta }_j$ should satisfy the following conditions:

$$\sin ({\alpha }_j-{\theta }_j)+{\displaystyle \sum _{k=0}^{n+1}{C}_k\sin ({\alpha }_j+k{\theta }_j)=0\hspace{1em}j=1\hspace{0.33em},\hspace{0.33em}2,\hspace{0.33em}3,\hspace{0.33em}\dots ,\hspace{0.33em}m}$$

(18)

In the above equations, $C_k$ can generally be solved by optimization methods [63].

2.3. Stress Solution of the Surrounding Rock

The determination of the analytical solution for the surrounding rock stress of a tunnel with an arch cross-section shape is more complex. It requires the use of complex functions and angle-preserving transformations in the elasticity theory. Replacing the corner points in the tunnel cross-section with circular angle approximations and the approximate elastic solutions for the stress distribution in the surrounding rock were obtained through mapping transformations.

Given the stress at any point on the boundary of the unit circle on a complex plane [31], the stress around the tunnel on the physical plane is determined by the following:

$$\left\{\begin{array}{l}{\sigma }_{\rho }=\frac{1}{2}\left\{4\mathrm{Re}(\Phi (\zeta ))-\mathrm{Re}\left[\frac{2{\zeta }^2}{\overline{{\omega }^{\prime }(\zeta )}}[\overline{\omega (\zeta )}{\Phi }^{\prime }(\zeta )+{\omega }^{\prime }(\zeta )\Psi (\zeta )]\right]\right\}\\ {\sigma }_{\theta }=\frac{1}{2}\left\{4\mathrm{Re}(\Phi (\zeta ))+\mathrm{Re}\left[\frac{2{\zeta }^2}{\overline{{\omega }^{\prime }(\zeta )}}[\overline{\omega (\zeta )}{\Phi }^{\prime }(\zeta )+{\omega }^{\prime }(\zeta )\Psi (\zeta )]\right]\right\}\\ {\tau }_{\rho \theta }=\frac{1}{2i}\mathrm{Im}\left\{\frac{2{\zeta }^2}{\overline{{\omega }^{\prime }(\zeta )}}[\overline{\omega (\zeta )}{\Phi }^{\prime }(\zeta )+{\omega }^{\prime }(\zeta )\Psi (\zeta )]\right\}\end{array}\right.$$

(19)

For a semi-circular arch with a rise-span ratio of f/B = 1/2 and aspect ratio of B/H = 1, the surrounding rock stresses of a three-centered arch with a rise-span ratio of f/B = 1/3 and f/B = 1/4, and aspect ratios of B/H = 1.20 and B/H = 1.33, the constant coefficients of the mapping function for different tunnels were obtained using the BOX composite shape method from the literature [32] based on the geometrical parameters of the aforementioned tunnels, as shown in

Table 1. The results of C_k obtained by the optimization method.

k	h Value	C0	C1	C2	C3	C4	C5	C6
6	0.6193	−0.1089	−0.0067	0.0845	−0.0796	0.0333	0.0075	−0.0083
	0.6419	−0.0915	−0.0947	0.0749	−0.0963	0.0285	0.0135	−0.0109
	0.4767	−0.0717	−0.1468	0.0543	−0.1043	0.0265	0.0192	−0.0088

.

Substituting the results in Table 1 into Equations (11) and (16) yields the following mapping function for each tunnel:

$$\left\{\begin{array}{l}{\omega }_1(\zeta )=27.12\zeta -2.95-0.18{\zeta }^{-1}+2.29{\zeta }^{-2}-2.16{\zeta }^{-3}+0.90{\zeta }^{-4}+0.20{\zeta }^{-5}-0.23{\zeta }^{-6}\\ {\omega }_2(\zeta )=25.30\zeta -2.31-2.40{\zeta }^{-1}+1.89{\zeta }^{-2}-2.44{\zeta }^{-3}+0.72{\zeta }^{-4}+0.34{\zeta }^{-5}-0.28{\zeta }^{-6}\\ {\omega }_3(\zeta )=24.40\zeta -1.75-3.58{\zeta }^{-1}+1.32{\zeta }^{-2}-2.55{\zeta }^{-3}+0.65{\zeta }^{-4}+0.47{\zeta }^{-5}-0.21{\zeta }^{-6}\end{array}\right.$$

(20)

According to Equation (20), the contours of the mapping function for the arched hole are shown in Figure 3 (the bottom boundary line shifts to the same level). The standard arch hole boundary and the hole profile boundary determined through the mapping function are extremely close and can be approximated to reflect the arch hole boundaries.

Based on the mapping function derived from Equation (20), the following equation can be directly derived (for a semi-circular arch with a rise-span ratio f/B = 1/2 and an aspect ratio B/H = 1):

$$\left\{\begin{array}{l}{\omega }_1(\sigma )=27.12\sigma -2.95-0.18{\sigma }^{-1}+2.29{\sigma }^{-2}-2.16{\sigma }^{-3}+0.90{\sigma }^{-4}+0.20{\sigma }^{-5}-0.23{\sigma }^{-6}\\ {{\omega }^{\prime }}_1(\sigma )=27.12+0.18{\sigma }^{-2}-4.58{\sigma }^{-3}+6.48{\sigma }^{-4}-3.60{\sigma }^{-5}-1.00{\sigma }^{-6}+1.38{\sigma }^{-7}\\ \overline{{\omega }_1(\sigma )}=27.12{\sigma }^{-1}-2.95-0.18\sigma +2.29{\sigma }^2-2.16{\sigma }^3+0.90{\sigma }^4+0.20{\sigma }^5-0.23{\sigma }^6\\ \overline{{\omega }_1^{\prime }(\sigma )}=27.12+0.18{\sigma }^2-4.58{\sigma }^3+6.48{\sigma }^4-3.60{\sigma }^5-1.00{\sigma }^6+1.38{\sigma }^7\end{array}\right.$$

(21)

$$\frac{\omega (\sigma )}{\overline{{\omega }^{\prime }(\sigma )}}=D_6{\sigma }^{-6}+D_5{\sigma }^{-5}+D_4{\sigma }^{-4}+D_3{\sigma }^{-3}+D_2{\sigma }^{-2}+D_1{\sigma }^{-1}+D_0+{\displaystyle \sum _{k=1}^{\infty }{d}_k}{\sigma }^k$$

(22)

In the above equation, $\omega (\sigma )/\overline{{\omega }^{\prime }(\sigma )}$ can be expressed in the form of a Laurent series. The real constant coefficients D₆, D₅, D₄, D₃, D₂, D₁, D₀, and d_k (k = 1, 2, 3, ⋯, ∞) in Equation (22) can be obtained by multiplying the denominator on the left side of the equation by the term on the right side of the equation, given that the coefficients of the same power on both sides of the equation are equal. The results are as following: D₆ = −0.00848, D₅ = 0.00737, D₄ = 0.03324, D₃ = −0.08113, D₂ = 0.08749, D₁ = −0.00337, D₀ = −0.13033, d₁ = 1.0393, d₂ = −0.03053, ⋯, d₁₀₀ = −3.74 × 10⁻⁸. In this paper, the maximum value of k is set to 100, which has little effect on the stress solutions. This is because when k is sufficiently large, the value of d_k is approximately zero.

Substituting Equations (4) and (5) into Equation (10), comparing the same power coefficients on both sides of the equation to be equal gives the values of a_n and b_n in conjunction with Equation (21). The a_n and b_n in Equation (8) are calculated as follows: a₆ = 0.115p(λ + 1), a₅ = −0.10p(λ + 1), a₄ = (−0.344λ + 0.557)p, a₃ = (1.105λ + 1.186)p, a₂ = −(1.611λ + 0.767)p, a₁ = (−12.527λ + 12.620)p, a₇ = a₈ = ⋯=a_n = 0, b₁ = −(14.012λ + 14.199)p, b₂ = (0.865λ − 0.014)p, b₃ = (−11.586λ + 12.093)p, ⋯, b₉₉ = −(6.176 × 10⁻⁷λ + 9.919 × 10⁻⁷)p, b₁₀₀ = (9.743 × 10⁻⁷λ + 5.615 × 10⁻⁸)p. Note that the number of terms in a_n is 6, while the number of terms in b_n is infinite. However, we find that the b_n is approximately zero when n is sufficiently large. Therefore, n in b_n is also set to 100 in this study.

Substituting a_n and b_n into Equation (5) yields the following two analytic functions:

$$\left\{\begin{array}{l}{\phi }_1(\zeta )=p[6.78p(\lambda +1)\zeta -0.738p(\lambda +1)+\frac{p(-12.572\lambda +12.575)}{\zeta }-\frac{p(1.039\lambda +0.194)}{{\zeta }^2}+\\ \hspace{0.33em}\frac{p(0.475\lambda +0.646)}{{\zeta }^3}-\frac{p(0.119\lambda +0.332)}{{\zeta }^4}-\frac{0.05p(\lambda +1)}{{\zeta }^5}+\frac{0.0575p(\lambda +1)}{{\zeta }^6}]\\ {\psi }_1(\zeta )=p[13.56p(\lambda -1)\zeta -1.475p(\lambda -1)-\frac{p(14.102\lambda +14.109)}{\zeta }+\frac{p(2.010\lambda -1.159)}{{\zeta }^2}+\\ \frac{p(-12.666\lambda +13.173)}{{\zeta }^2}+\dots -\frac{p(6.176\times {10}^{-7}\lambda +9.919\times {10}^{-7})}{{\zeta }^{99}}+\frac{p(9.743\times {10}^{-7}\lambda +5.615\times {10}^{-8})}{{\zeta }^{100}}]\end{array}\right.$$

(23)

Similarly, for a three-centered arch with a rise-span ratio of f/B = 1/3 and an aspect ratio of B/H = 1.20, D₆, D₅, D₄, D₃, D₂, D₁, D₀ and d_k (k = 1, 2, 3, ⋯, ∞) can be calculated as follows: D₆ = −0.01107, D₅ = 0.01344, D₄ = 0.02951, D₃ = −0.09937, D₂ = 0.07711, D₁ = −0.08617, D₀ = −0.12121, d₁ = 1.05344, d₂ = −0.03391, ⋯, d₁₀₀ = −3.119 × 10⁻⁷. In addition, the a_n, b_n are calculated as follows: a₆ = 0.14p(λ + 1), a₅ = −0.17p(λ + 1), a₄ = −(0.245λ + 0.50)p, a₃ = (1.109λ + 1.404)p, a₂ = −(1.325λ + 0.636)p, a₁ = (−10.436λ + 12.636)p, a₇ = a₈ = ⋯= a_n = 0, b₁ = −(11.135λ + 15.535)p, b₂ = (0.888λ + 0.033)p, b₃ = (−9.705λ + 11.837)p, ⋯, b₉₉ = (1.608 × 10⁻⁵λ−3.649 × 10⁻⁶)p, b₁₀₀ = (−7.402 × 10⁻⁶λ + 1.510 × 10⁻⁵)p.

$$\left\{\begin{array}{l}{\phi }_2(\zeta )=p[6.325p(\lambda +1)\zeta -0.578p(\lambda +1)+\frac{p(-11.036\lambda +12.036)}{\zeta }-\frac{p(0.853\lambda +0.163)}{{\zeta }^2}+\\ \frac{p(0.499\lambda +0.794)}{{\zeta }^3}-\frac{p(0.065\lambda +0.320)}{{\zeta }^4}-\frac{0.085p(\lambda +1)}{{\zeta }^5}+\frac{0.07p(\lambda +1)}{{\zeta }^6}]\\ {\psi }_2(\zeta )=p[12.65p(\lambda -1)\zeta -1.155p(\lambda -1)-\frac{p(12.335\lambda +14.335)}{\zeta }+\frac{p(1.833\lambda -0.912)}{{\zeta }^2}+\\ \frac{p(-10.925\lambda +10.617)}{{\zeta }^2}+\dots +\frac{p(1.608\times {10}^{-5}\lambda -3.649\times {10}^{-6})}{{\zeta }^{99}}+\frac{p(-7.402\times {10}^{-6}\lambda +1.510\times {10}^{-5})}{{\zeta }^{100}}]\end{array}\right.$$

(24)

The results for a three-centered arch with a rise-span ratio of f/B = 1/4 and an aspect ratio of B/H = 1.33, D₆, D₅, D₄, D₃, D₂, D₁, D₀ and d_k (k = 1, 2, 3, ⋯, ∞) are as follows: D₆ = −0.00861, D₅ = 0.01926, D₄ = 0.0279, D₃ = −0.10827, D₂ = 0.05479, D₁ = −0.13477, D₀ = −0.099, d₁ = 1.0649, d₂ = −0.02708,..., d₁₀₀ = −4.935 × 10⁻⁷. The a_n and b_n are calculated as follows: a₆ = 0.105p(λ + 1), a₅ = −0.235p(λ + 1), a₄ = -(0.244λ + 0.434)p, a₃ = (1.111λ + 1.526)p, a₂ = −(0.988λ + 0.359)p, a₁ = (−9.377λ + 12.698)p, a₇ = a₈ = ⋯= a_n = 0, b₁ = −(9.671λ + 16.313)p, b₂ = (0.803λ − 0.082)p, b₃ = (−8.873λ + 11.751)p,⋯, b₉₉ = −(4.332 × 10⁻⁶λ + 1.319 × 10⁻⁵)p, b₁₀₀ = (9.556 × 10⁻⁶λ + 2.997 × 10⁻⁶)p.

$$\left\{\begin{array}{l}{\phi }_3(\zeta )=p[6.10p(\lambda +1)\zeta -0.438p(\lambda +1)+\frac{p(-10.272\lambda +11.803)}{\zeta }-\frac{p(0.658\lambda +0.029)}{{\zeta }^2}+\\ \frac{p(0.474\lambda +0.888)}{{\zeta }^3}-\frac{p(0.082\lambda -0.272)}{{\zeta }^4}-\frac{0.1175p(\lambda +1)}{{\zeta }^5}+\frac{0.0525p(\lambda +1)}{{\zeta }^6}]\\ {\psi }_3(\zeta )=p[12.20p(\lambda -1)\zeta -0.875p(\lambda -1)-\frac{p(11.461\lambda +14.523)}{\zeta }+\frac{p(1.463\lambda -0.742)}{{\zeta }^2}+\\ \frac{p(-10.148\lambda +10.476)}{{\zeta }^2}+\dots +\frac{p(-4.332\times {10}^{-6}\lambda +1.319\times {10}^{-5})}{{\zeta }^{99}}+\frac{p(9.556\times {10}^{-6}\lambda +2.997\times {10}^{-6})}{{\zeta }^{100}}]\end{array}\right.$$

(25)

3. Simulation of Spalling Failure

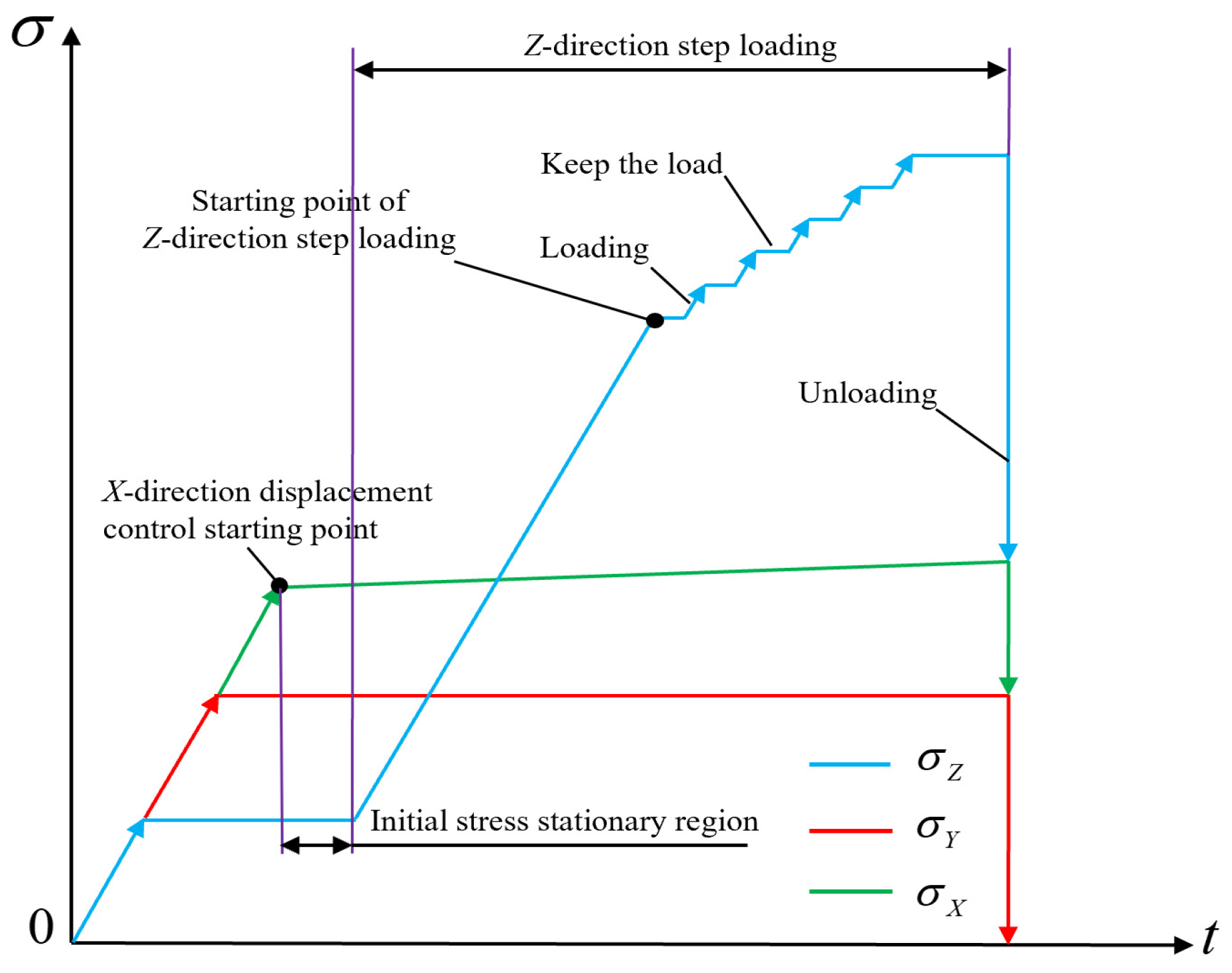
3.1. Test Materials and Methods

The Miluo granite was used for the experimental simulations and was machined into cubic (100 mm × 100 mm × 100 mm) specimens containing arched holes (arches are 25 mm high, f/B = 1/2, and 16.7 mm, f/B = 1/3, 12.5 mm, f/B = 1/4; straight walls are 25 mm high and 50 mm wide). The UCS of the granite is 144.77 MPa, and the modulus of elasticity is 42.67 GPa. These specimens were machined to an accuracy in accordance with ISRM standards, i.e., a recommended standard tolerance of 0.0175 mm and a vertical tolerance of 0.025 mm on each side as a datum. The prepared specimens were tested on a true triaxial test system with a loading rate of 2000 N/s. The stress path of the test process is shown in Figure 4. Firstly, the stresses in X, Y, and Z directions were increased with 2000 N/s to the set initial stress level and maintained for 120 s after reaching the initial stress level. The stress in the Y direction was kept constant, and in the X direction (axial direction of the hole), the loading method was changed from force to displacement-controlled loading to keep the axial displacement constant (plane strain problem) [64]. Subsequently, the stress in the Z direction was continuously increased with 2000 N/s. To ensure that only partial failure occurs on the hole sidewall, the loading rate was kept unchanged, and step loading was exerted. The loading was stopped when the failure area of the hole walls basically occurred along the X direction, and the stress in the Z direction was kept unchanged. When the hole wall reached stability, the stresses in the X, Y, and Z directions were released to 0 MPa at a rate of 20 mm/min.

According to Brown, Hoek [65], and Stephansson et al. [66], estimated ground stresses at burial depths of 500 m, 650 m, and 800 m were used to simulate the spalling failure characteristics of tunnel walls. The vertical stresses of surrounding rock at burial depths of 500 m, 650 m, and 800 m are calculated according to the following empirical formula:

$${\sigma }_v=0.027H$$

(26)

The horizontal stress is calculated by the following:

$${\sigma }_{h\max }=6.7+0.0444H$$

(27)

$${\sigma }_{h\min }=0.8+0.0329H$$

(28)

where ${\sigma }_v$ is the vertical stress, ${\sigma }_{h\max }$ and ${\sigma }_{h\min }$ are the maximum and minimum horizontal stresses, H is the burial depth, respectively. The initial ground stresses at burial depths of 500 m, 650 m, and 800 m are listed in

Table 2. The initial crustal stresses at different burial depths.

Depth (m)	σhmax (MPa)	σhmin (MPa)	σv (MPa)
500	28.90	17.25	13.50
650	35.56	22.19	17.55
800	42.22	27.12	21.60

. The three initial horizontal stresses of rock specimens in the true triaxial test are shown in Figure 5. The σ_X, σ_Y, and σ_Z represent the stresses in the X, Y, and Z directions, respectively.

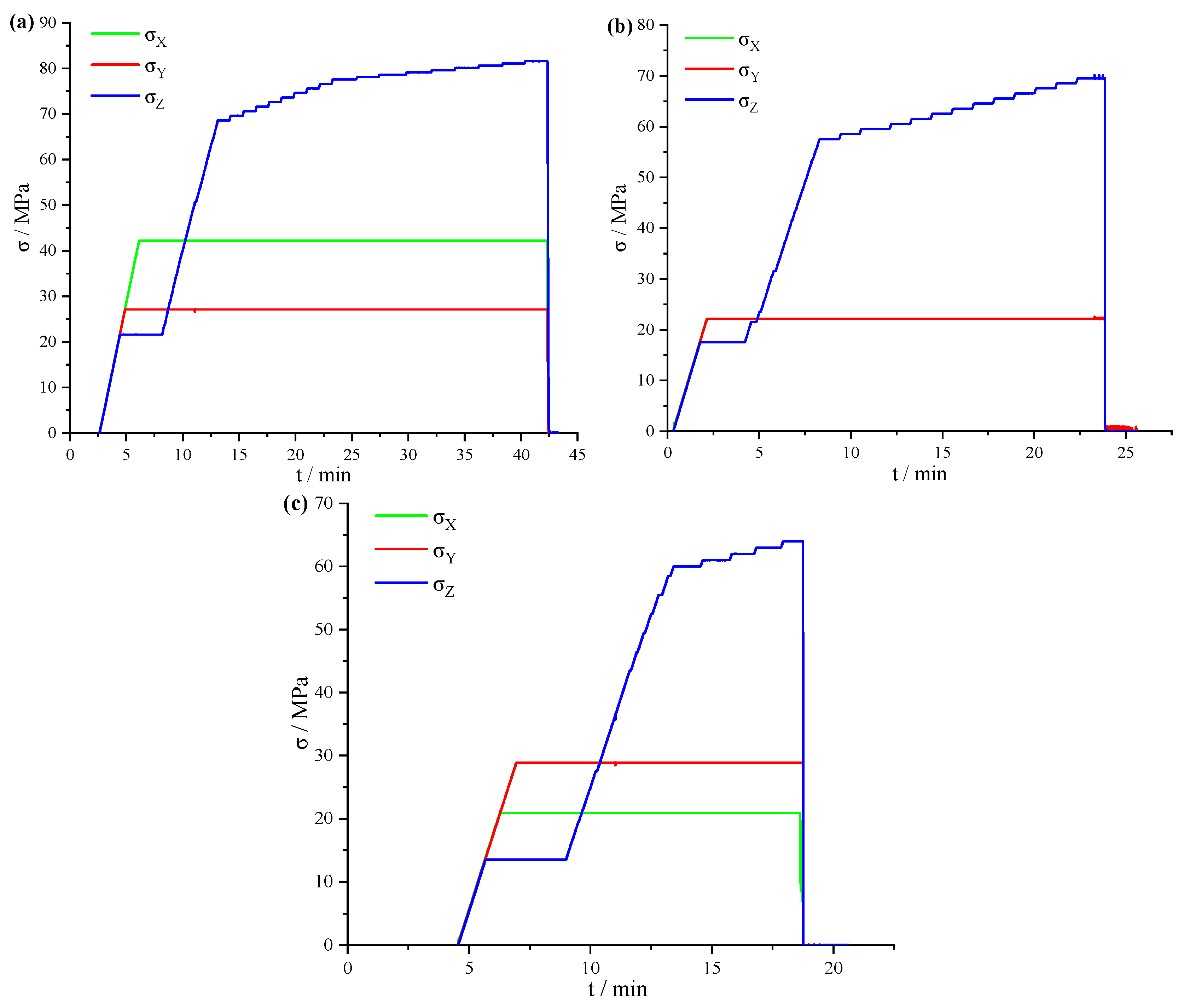
3.2. Test Results

In this test, the Z-directional stress of specimen A12-42.2-27.1 was increased to 81.6 MPa after 18 steps starting at 68.6 MPa; the Z-directional stress of specimen A13-22.2-22.2 was increased to 64.0 MPa after 13 steps starting at 58.5 MPa; the Z-directional stress of specimen A14-17.3-28.9 was increased to 69.5 MPa after 5 steps starting at 59.5 MPa, as shown in Figure 6. Under the “high stress + stress adjustment” conditions, the complete failure process of the arched hole sidewall was monitored in real-time using a miniature camera. The failure states of the sidewall at different moments were obtained in combination with the video monitoring. The failure process of the hole sidewall is shown in Figure 7, Figure 8 and Figure 9.

The complete failure process of the arched hole sidewall of specimen A12-42.2-27.1 is shown in Figure 7. At 788 s, the vertical stress σ_Z was increased to 68.6 MPa. The test was in the load-holding phase of the loading process at this moment, resulting in a small particle ejection from the right wall, as shown in Figure 7a. The vertical stress σ_Z was increased to 70.6 MPa at 951 s, and cracks appeared at the arch foot and extended from the middle towards the wall foot. Rock flakes spalled from the arch shoulder of the left sidewall and the corner of the right wall, as shown in Figure 7b. Subsequently, σ_Z was increased to 73.6 MPa after 215 s. The middle arch foot of the right wall buckled and opened towards the arch shoulder. With further increasing vertical stress, the buckling and opening intensified, and the sidewall bulged, as shown in Figure 7c. Then, the vertical stress continued to be increased in steps of 1.0 MPa. During the load-holding stage, rock flaking occurred successively at both sidewalls, with flaking on the right side first, followed by flaking on the left side, as shown in Figure 7d,e. At 1714 s, a large spalling occurred at the middle of the right sidewall and developed from the middle to 1/2 length of the sidewall under a high vertical stress σ_Z of 78.6 MPa (Figure 7f). When the sidewall failure is no longer extended, the vertical stress σ_Z and horizontal stresses σ_X and σ_Y are released to 0 MPa.

The complete failure process of the arched hole sidewall of specimen A13-22.2-22.2 is shown in Figure 8. From Figure 8a, it can be seen that the vertical stress at the initial sidewall failure was 55.9 MPa and occurred at 489 s. A small particle ejection was observed at the bottom of the left sidewall close to the loading block. For a longer period, no obvious failure was noted. At 1080 s, σ_Z = 64.6 MPa, and small particles were ejected from the middle bottom of the right sidewall. This indicates that the energy accumulated due to stress concentration was released at this location. After 43 s, the vertical stress was increased to 65.6 MPa. As shown in Figure 8b, at this moment, the rock specimen is in the load-retaining phase, and the previously flexed rock fragments spalled from the middle of the left wall. At 1183 s, σ_Z = 66.6 MPa (Figure 8c), the rock specimen was undergoing the stepped loading stage of vertical stress. Particle ejection occurred again at the original failure location on the left and right sidewalls. As shown in Figure 8d, the failure pit at the middle-left sidewall extended deeper, producing more pronounced extensional cracks and flexural bulging of rock fragments. At the moment, between 1313 s and 1377 s, through cracks can be found at the bottom of the sidewalls. When the vertical stress was continuously increased to 69.6 MPa, a large bulge of rock fragments was produced between the cracks running through the bottom and middle of the straight sidewall. Figure 8f shows a rock piece from the left sidewall, with the bottom of the straight sidewall buckling upwards. In view of this, the vertical stress σ_Z and horizontal stresses σ_X and σ_Y were rapidly released to 0 MPa.

The spalling failure process on the sidewalls of specimen A14-17.3-28.9 is shown in Figure 9. At 793 s, σ_Z = 58.5 MPa, and a small particle ejection occurred at the middle of the arch foot on the left sidewall. After 39 s, a bulge occurred near the location of particle ejection. The bulge subsequently extended to both sides, and the particle ejection occurred again within a short time (Figure 9a,b). Figure 9c shows that at 872 s, the σ_Z reached 60.1 MPa. The vertical stress was kept constant, and spalling occurred frequently on the left sidewall at this phase. The vertical stress was increased to 62.0 MPa at 961 s, as shown in Figure 9d. A small particle ejection also occurred at the bottom of the right sidewall in the middle of the hole, indicating that the energy accumulated in the right arch foot was released. As Figure 9e shows, with an increase of 1.0 MPa in the vertical stress, a flake with topple tendency is produced at a location symmetrical to that of the left bulging and spalling. Subsequently, a sharp spalling occurred on the sidewall during loading, accompanied by a large spalling area. This indicates that through cracks are produced from the free surface of the hole to the outside. Finally, an instability or sinking of the specimen occurred, and no longer displacement was produced.

Figure 10 shows the actual failure of deep engineering structures. Combined with Figure 7, Figure 8 and Figure 9, it can be seen that the reproduced failure is similar to the surrounding rock spalling at in-situ deep engineering, indicating that the simulation test is reasonable and valid.

3.3. Characteristics of Sidewall Fragments

Figure 11 shows the characteristics of the rock flakes from the specimens tested. Most rock flakes are in thin shapes. Some rock flakes are also in the form of thick in the middle and thin on both sides. Fine powders were observed on the rock flakes, which were mainly produced by the tension-shear failure between rock particles during spalling. This phenomenon is similar to that observed in actual engineering. The mass of individual rock flakes from specimen A12-42.22-27.12 is in the range of 0.17–2.75 g. A spalling of small flakes first occurred in the central part of the hole sidewalls. Then a spalling of a large piece of thin wedge-shaped rock flake occurred. As the spalling developed along the axial direction of the hole, the mass of spalling rock flakes from both sidewalls decreased. There are still flexural rock pieces hanging on the sidewalls after testing. The mass of individual rock flakes from specimen A13-22.2-22.2 varies from 0.38 to 8.04 g. The mass of a single rock flake from specimen A14-17.3-28.9 varies from 0.45 to 5.12 g, with the morphology varying from flake to thin wedge shape. It was reported that after the excavation of branch tunnels, the main failure modes of the surrounding rock included the spalling failure, the thin slab failure, and the wedge-shaped slab failure. The thickness of rock flakes ranged from 2 mm to 2 cm. The thickness of rock flakes was relatively uniform, and the shape was irregular. These flakes were broken into several pieces after falling from the sidewalls, and the surface of the rock flakes was rough, as shown in Figure 12a. In addition, the wedge-shaped rock slabs are like a “stone knife”, which are thick in the middle and thin at the edges, with a maximum thickness ranging from 3 cm to 0.1 m, as shown in Figure 12c. It was also revealed that both the first and third failure modes considered the splitting and stretching as the main mechanism of rock flakes. In the first mode, the surrounding rock failed with a lesser depth, whereas the third failure mode resulted in a greater spalling depth. The main failure mode of specimen A13-22.2-22.2 is flake failure, the specimen A12-42.22-27.12 underwent a wedge-shaped slab failure, and the failure of specimen A13-22.2-22.2 is a combination of them. The flake failure mechanism was influenced by the horizontal stress conditions of the surrounding rock. It can be seen from Figure 11 that the shape of the rock fragments produced in our simulated tests is comparable to that of rock fragments in actual rock engineering.

4. Discussion

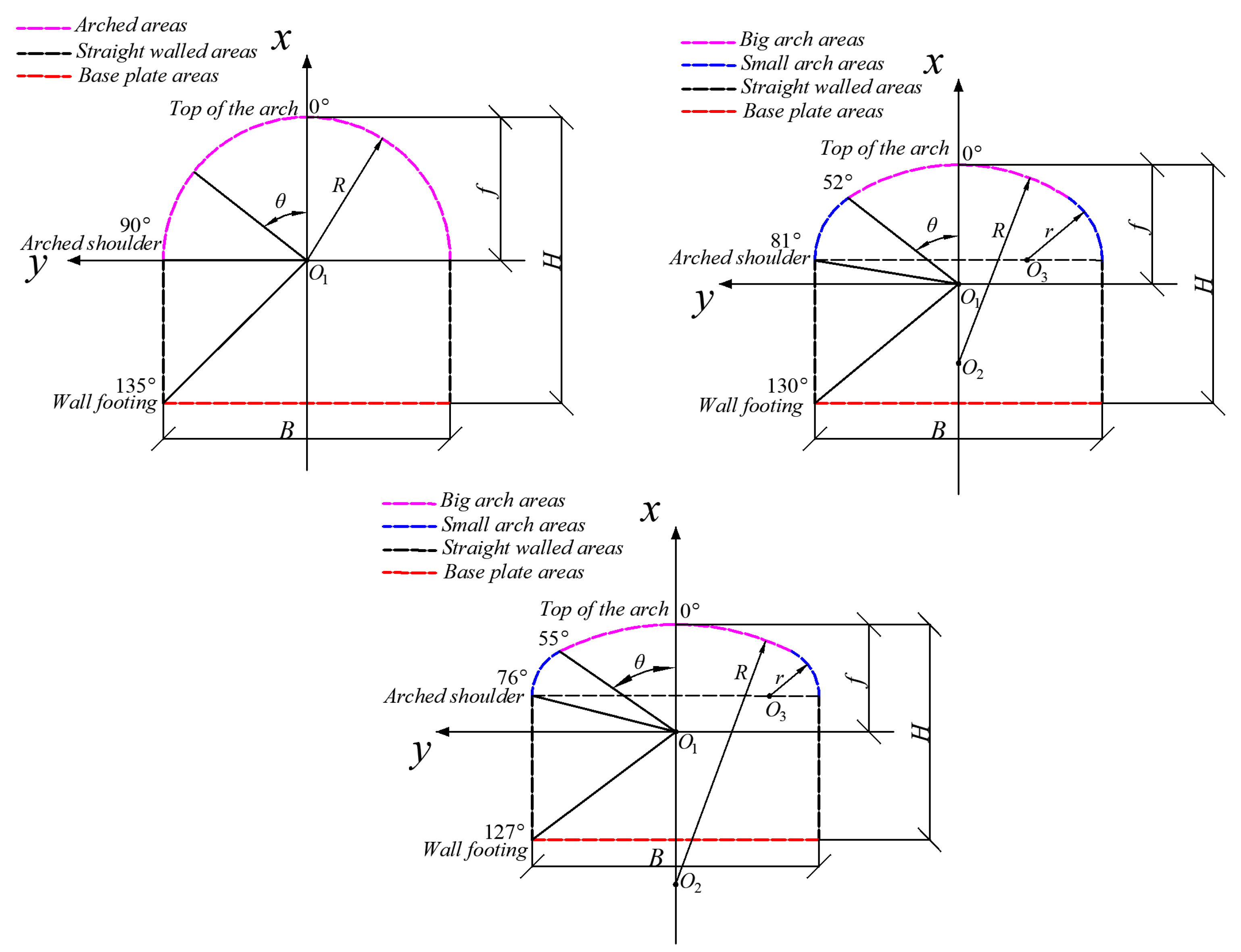
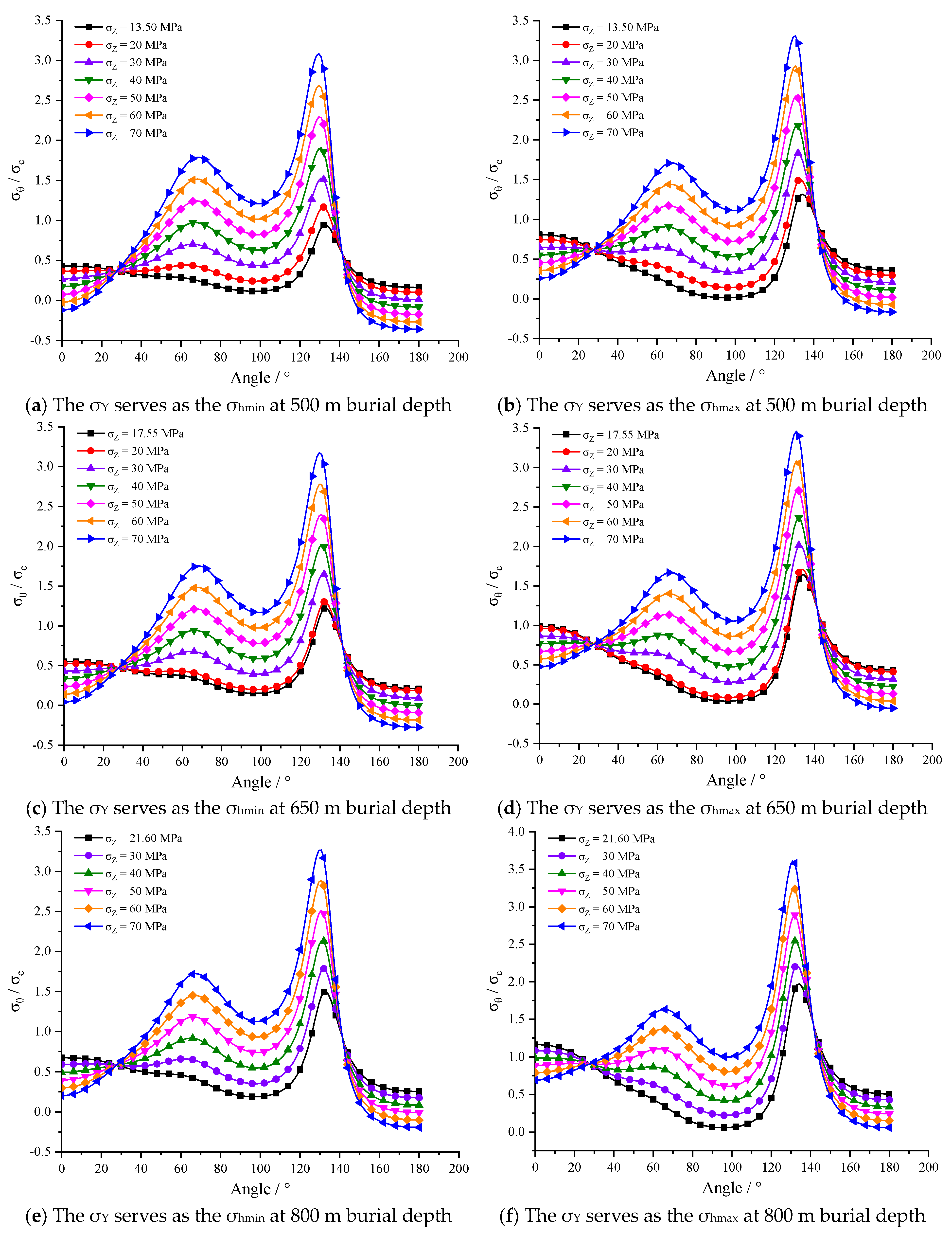
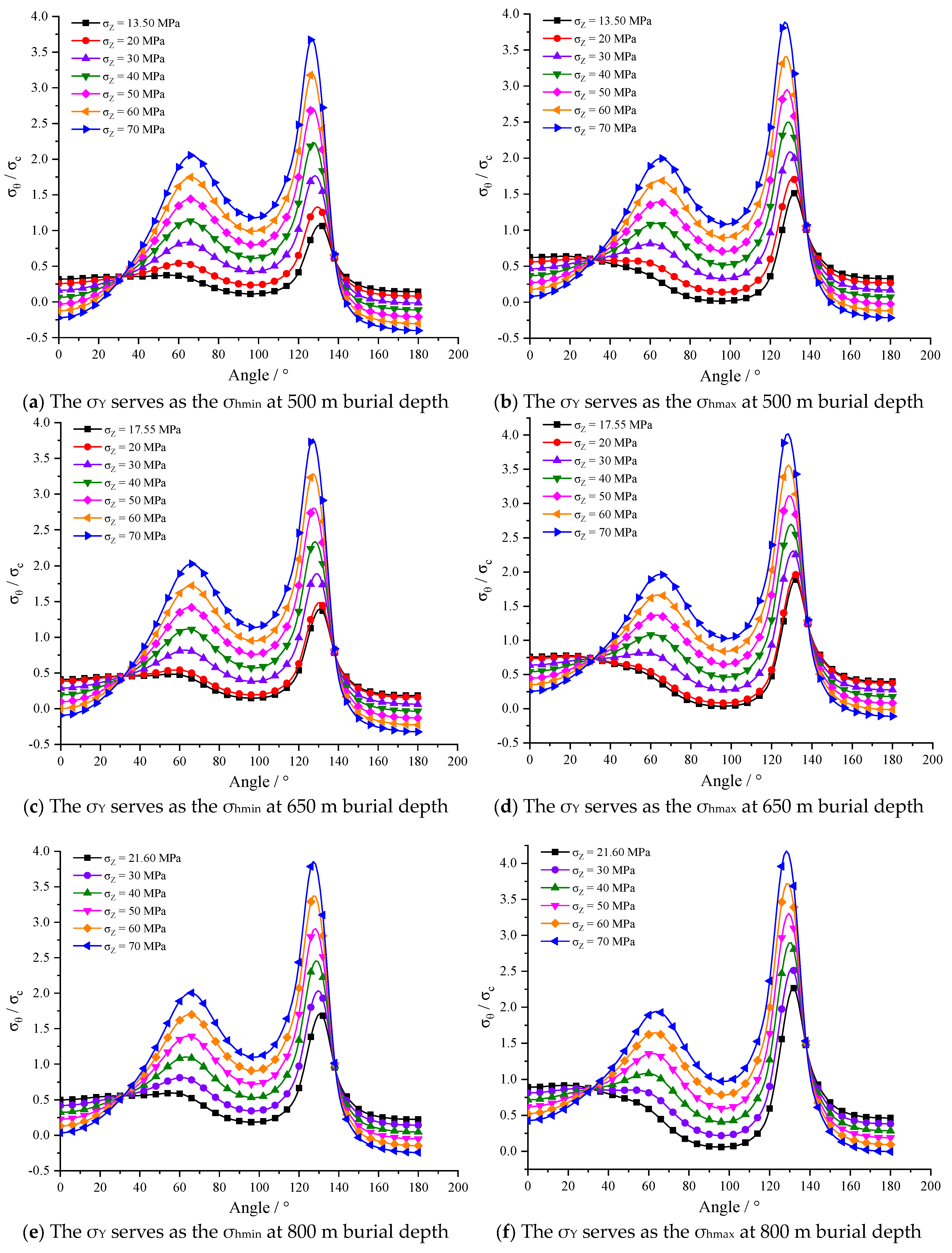
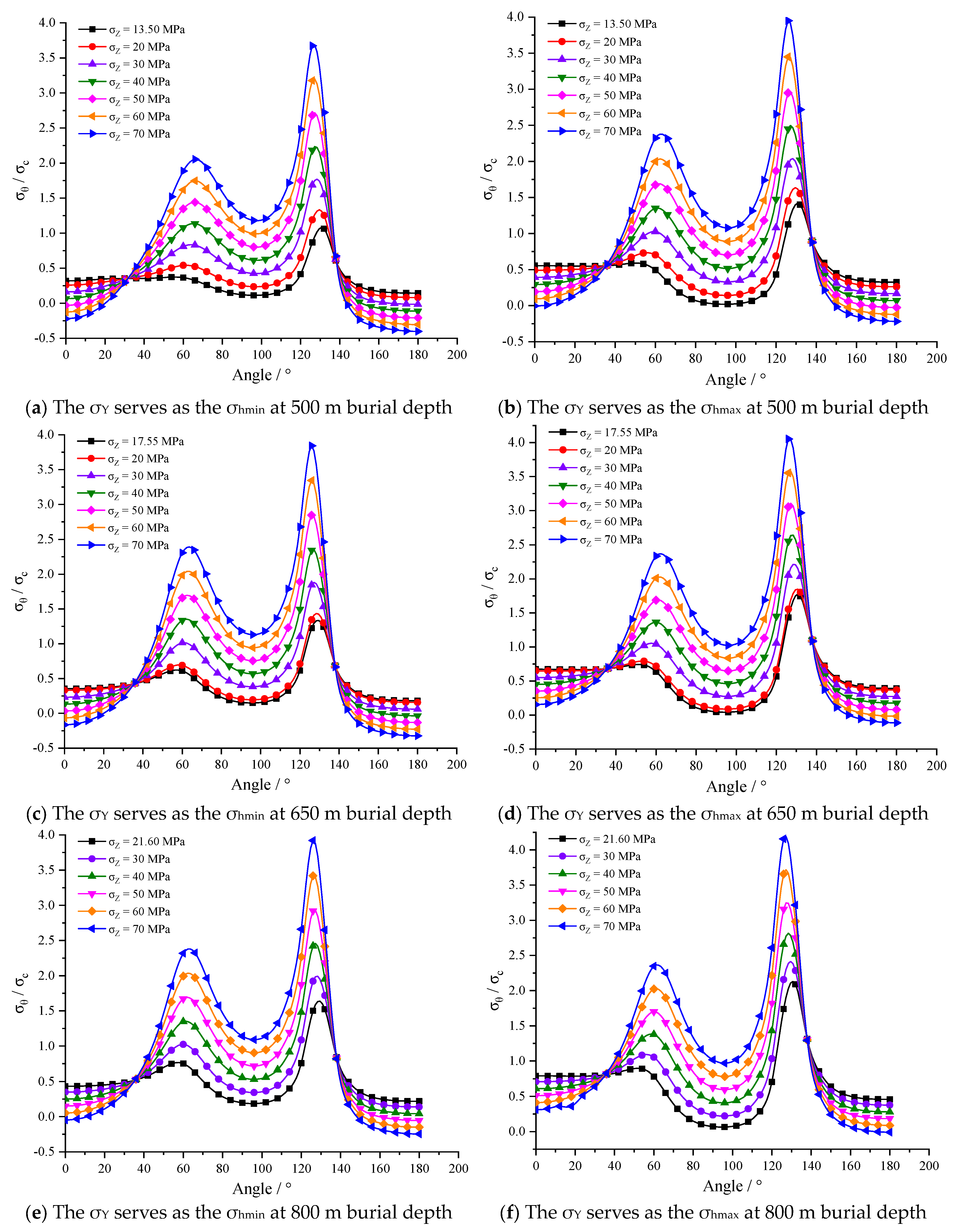
4.1. Stress Distribution Analysis of Surrounding Rock under Different Working Conditions

The literature [69] adopted the method of opening the hole first and loading it afterward to simulate rockburst, mainly focusing on the rockburst caused by static stress adjustment. In this section, the stress distribution of the surrounding rock of tunnels with different arch heights at each stage under static stress adjustment is based on this loading path. The correlation between the boundary points and the polar angle of the tunnel is schematically drawn for subsequent convenience in describing the variation characteristics of the stress curve around the tunnel, as shown in Figure 13. Taking the origin of the coordinate system O₁ and the x-positive half-axis as the starting edge, the polar angle θ is obtained. The arch section was divided into four regions and five points, and named regions 1~4 (which are polar angles 0°~60°, 60°~96°, 96°~130°, and 130°~180°) and points 1~5 (which are polar angles 0°, 54°~66°, 96°, 126°~132°, and 180°).

Figure 14, Figure 15 and Figure 16 show the tangential stress distributions around the hole during the simulated stress adjustment. The stress distribution of the surrounding rock of the tunnel with three arch heights is consistent. When σ_Z > 40 MPa, in the vast majority of cases, the lowest tangential stress occurs at points 1 and 5. The tangential stress at point 4 is the largest, followed by that at point 2. With the adjustment of vertical stress, the tangential stress at points 1 and 5 gradually decreases, which transfers from compressive stress to tensile stress. For a semi-circular arch with a rise-span ratio of f/B = 1/2, the σ_Z should be loaded to more than 40 MPa at point 5, and a three-centered arch with a rise-span ratio of f/B = 1/3 and f/B = 1/4 σ_Z should be loaded to more than 30 MPa at point 5. However, tensile stress appears at point 1 after σ_Z rises about 20 MPa. As σ_Y doubles, the σ_Z value of tensile stress at the arch top and the floor middle increases by 20 MPa correspondingly. The tangential stress in region 2, region 3, and region 4 gradually increases with stress adjustment and is manifested as the compressive stress. With the increase in σ_Z or σ_Y, the same maximum tangential stress is first reached at point 3, where precedence order is the rise-span ratio of f/B = 1/4 arch tunnel, f/B = 1/3 arch tunnel, f/B = 1/2 arch tunnel.

Under the initial burial depth stresses, the magnitudes of the tangential stresses at points 4 and point 2 are as follows: f/B = 1/3 three-centered arch > f/B = 1/4 three-centered arch > f/B = 1/2 semi-circular arch. With an increase in vertical stress (σ_Z = 40 MPa), the magnitude of the tangential stress at point 2 follow f/B = 1/4 three-centered arch > f/B = 1/3 three-centered arch. The magnitude of tangential stress at point 4 is as follows: f/B = 1/4 three-centered arch ≈ f/B = 1/3 three-centered arch. The tangential stress of the semi-circular arch with f/B = 1/2 is the lowest in this part. When the vertical stress increased to 70 MPa, the magnitude of the tangential stresses at point 2 and point 4 satisfied a sequence of f/B = 1/4 three-centered arch > f/B = 1/3 three-centered arch > f/B = 1/2 semi-circular arch. The tangential stress of the tunnels with three f/B ratios increased with burial depth. Under the low vertical stresses of the initial burial depth state, f/B = 1/2 semi-circular arch tangential stresses in region 1 show a decreasing trend, while the f/B = 1/3 three-centered arch and the f/B = 1/4 three-centered arch show an increasing trend, the growth rate of the tangential stress is as follows: f/B = 1/4 three-centered arch > f/B = 1/3 three-centered arch. The tangential stresses in the arch section for the three rise-span ratios show a decreasing trend in the region 2 and region 4, but an increasing trend in the region 3, the growth rate of the tangential stresses all show the following: f/B = 1/4 three-centered arch > f/B = 1/3 three-centered arch > f/B = 1/2 semi-circular arch. With the adjustment of the vertical stresses, the tangential stresses where the f/B = 1/2 semi-circular arch in the region 1 change from a negative growth rate to a positive growth rate, while the growth rates of the tangential stresses in the f/B = 1/3 three-centered arch and the f/B = 1/4 three-centered arch at this point increase continuously, the growth rate of the tangential stress values as follows: f/B = 1/4 three-centered arch > f/B = 1/3 three-centered arch, the trend of which is the same as under the initial burial depth stress, with the difference that the larger the vertical stress value, the faster the growth rate; The growth rates for the three rise-span ratios of arch sections at high vertical stresses are similar in the region 2 and region 3, while the growth rates in region 2, region 3, and region 4 show the following: f/B = 1/4 three-centered arch > f/B = 1/3 three-centered arch > f/B = 1/2 semi-circular arch.

The effects of horizontal stress arrangement on the tangential stress of the arch tunnels with the three rise-span ratios are as follows: Under the initial stress conditions, when the minimum horizontal stress was transformed into the maximum horizontal stress, the tangential stress at point 2 and point 3 decreased. The maximum tangential stress at point 4 and the tangential stress at point 1 and point 5 increased. With the adjustment of vertical stress, when the minimum horizontal stress was laid on the hole sides, the growth rate of the tangential stress in region 1 and region 2 is greater than that of the maximum horizontal stress laid on the hole side. However, the growth rate of tangential stress in region 3 and region 4 under the minimum horizontal stress is less than that under the maximum horizontal stress.

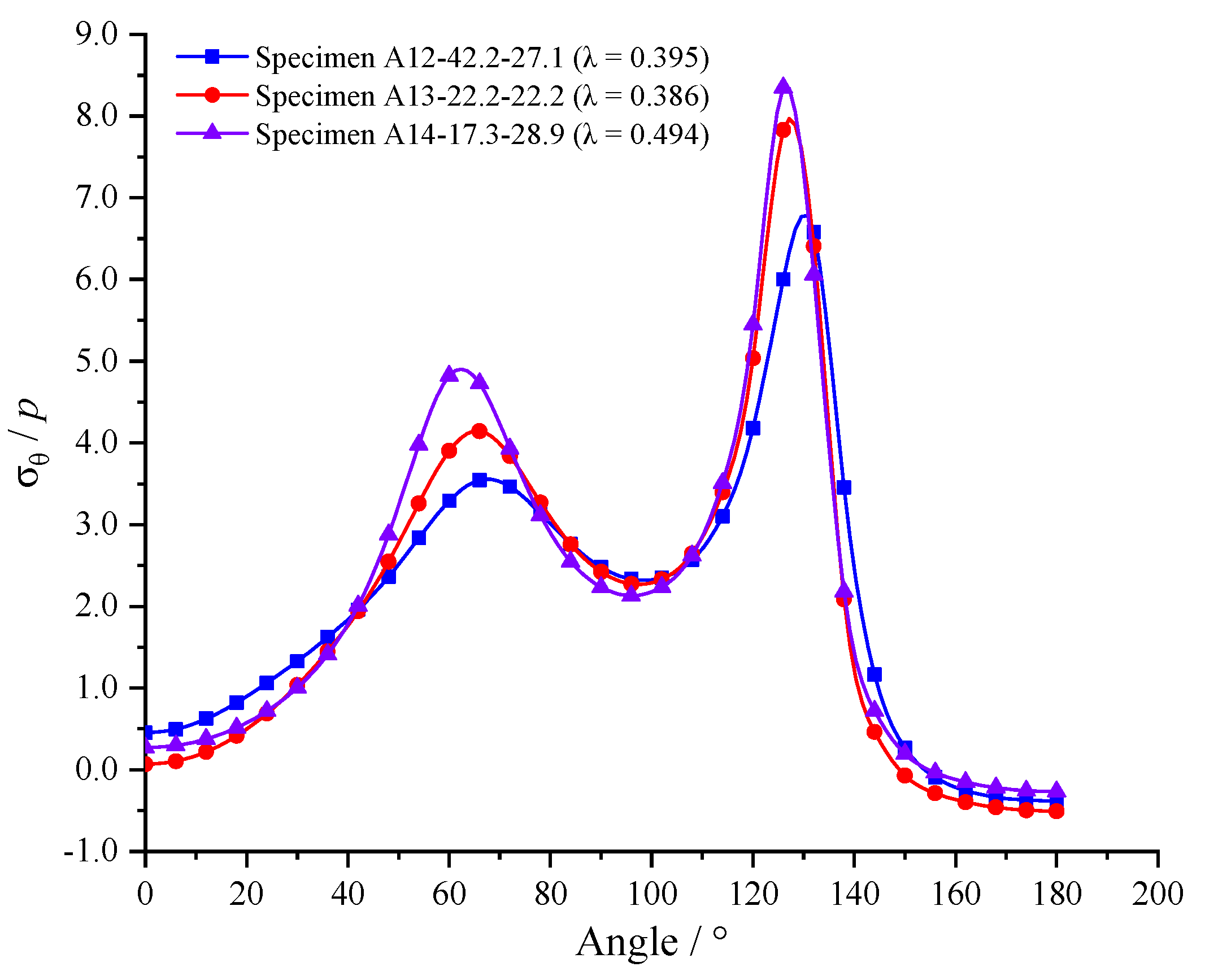
4.2. Characteristics of Initial Failure Stress of Tunnel Sidewall

The calculations of the initial failure stress of sidewalls are shown in

Table 3. The initial failure stresses of tunnel walls.

Specimen	σX/(MPa)	σY/(MPa)	σZ/(MPa)	σZi/(MPa)	σZj/(MPa)
A12-42.2-27.1	42.2	27.1	21.6	68.6	68.6
A13-22.2-22.2	22.2	22.2	17.6	57.5	65.6
A14-17.3-28.9	17.3	28.9	13.5	58.5	60.0

, where σ_Zi is the stress at the onset of particle ejection from the hole sidewalls, and σ_Zj is the stress at the onset of rock chips spalling from the hole sidewalls (rock chips fall onto the floor). The initial vertical stress at which particle ejection occurred follows a sequence of f/B = 1/2 semi-circular arch > f/B = 1/4 three-centered arch > f/B = 1/3 three-centered arch. The initial vertical stress at which spalling occurred is as follows: f/B = 1/2 semi-circular arch > f/B = 1/3 three-centered arch > f/B = 1/4 three-centered arch. The initial stresses of the specimens were determined according to Brown, Hoek [65], and Stephansson et al. [66]. The tunnel stresses induced by different excavation directions were simulated. The following preliminary conclusions can be drawn: The initial stress for particle ejection and rock flake initiation of f/B = 1/2 semi-circular arch tunnel is the highest, which is in line with the fact that a semi-circular arch tunnel has a stronger pressure-bearing capacity. The pressure-bearing capacity of f/B = 1/3 and f/B = 1/4 three-centered arch tunnels is similar. The spalling becomes more violent as the arch height of the three-centered arch tunnels decreases.

The lateral pressure coefficient (λ) was calculated according to the initial failure stresses (see Table 3), which is 0.395, 0.386, and 0.494 for specimens A12-42.2-27.1, A13-22.2-22.2, and A14-17.3-28.9, respectively. Substituting the analytical functions in Equations (23), (25) and (27) into Equation (4), the stress at different hole boundary locations of the three specimens was obtained, as shown in Figure 17. The visual stress distribution in the hole boundary is shown in Figure 18. It can be seen from Figure 17 that the stress at the arch foot is the highest, followed by that at the arch shoulder. The highest stress concentration coefficients at the foot of sidewalls of reached 6.85 p, 8.24 p, and 8.53 p. At this moment, the tangential stresses at the foot sidewalls are 471.9 MPa, 473.4 MPa, and 499.5 MPa, which are 3.26, 3.27, and 3.45 times the UCS respectively. A slight buckling occurred at the arch foot, as shown in Figure 7, Figure 8 and Figure 9. When the lateral pressure coefficient is in the range of 0.38–0.50, tensile stress acted on the floor, and the tensile stress was transferred to compressive stress on the roof. However, the floor always showed a higher stress than the roof. Although tensile stress was present on the roof, there was less room for tensile deformation to occur on the roof, and thus tensile failure did not occur. The comparative tangential stress occurred at both corners, which acts as the compressive stresses and decreases to the minimum at the sidewalls. The experimental results showed that the spalling of rock flakes occurred on both sidewalls, and the particle ejection occurred at the four corners. The particle ejection is caused by the stress concentration, while the spalling of rock flakes is caused by the axial micro-cracks generated at the four corners, which is a spalling course towards the free face under tangential stress.

Comparing the initial failure stress σ_Zi and the maximum tangential stress σ_θmax of specimens A12-42.2-27.1 and A13-22.2-22.2, with similar lateral pressure coefficient, it was found that the excavation in the direction of the maximum horizontal principal stress can improve the stability of the tunnel, i.e., σ_X > σ_Y. The σ_θmax of holes can be reduced in this manner. Comparing the stress states of specimens A12-42.2-27.1 and A14-17.3-28.9, it can be seen that the initial failure stress σ_Zi of the semi-circular arch with f/B = 1/2 is greater than that of the three-centered arch with f/B = 1/4 under constant σ_Y. This indicates that the pressure-bearing capacity of the semi-circular arch tunnel is greater than that of the three-centered arch tunnel. Figure 17 shows that when the polar angle is in the range of 0–90° (corresponding to the arc segment of the arch hole), the growth rate of the tangential stress follows the semi-circular arch hole < three-centered arch hole combined with the tangential stress distribution of the arc segment in Figure 17. The growth rate of the tangential stress accelerates with the increase in arch height. Comparing the σ_Zi of specimens A13-22.2-22.2 and A14-17.3-28.9 shows that, although the arch height decreases by 4.17 mm, the initial failure stress of the three-centered arch holes is similar. If the lateral pressure coefficients of the two specimens are equal and the effect of σ_X is out of consideration, the maximum tangential stress under the conditions of f/B = 1/3 is smaller than that under the conditions of f/B = 1/4. This indicates that the maximum tangential stress can be increased by reducing the arch height of the three-centered arch hole.

From the above analysis, it can be concluded that the initial failure stresses of the arch-shaped holes are 0.39–0.48 times the related UCS. The hole contained in specimen A12-42.2-27.1 tested here is consistent with that in the literature [50], which is also a D-shaped hole. The stress precondition for the initial spalling failure of the D-shaped hole is that σ_Zi/σ_c ≈ 0.35–0.44 under different stress states at the same burial depth. This is consistent with our results. It has also been stated that the σ_Zi/σ_c ≈ 0.175–0.22 (half of the above test results) can be used for a rough evaluation of tunnel spalling failure. Ortlepp et al. [70] evaluated the stability of brittle rock tunnels in South African gold mines using the ratio of the maximum far-field stress (σ₁) to UCS (σ_c). This also pointed out that spalling occurred when σ₁/σ_c > 0.2. In our study, the σ_Zi/σ_c at the initial failure of tunnels with different arch heights is in the range of 0.195–0.24, with further confirms the findings of Ortlepp et al. In addition, the initial failure in this work all occurred at the arch foot, where the tangential stress was the maximum. When the lateral pressure coefficient is in the range of 0.38–0.50, which is 3.2–3.5 times the UCS. It has been reported that the ratio of the maximum tangential stress to UCS was 1.27 when the sidewall of a 50 mm diameter circular hole started to fail and that the tangential stress of the hole surrounding rock reached UCS when the failure occurred [71]. Our test results (σ_θmax/σ_c ≈ 3.2–3.5) and the published data indicate that σ_θmax/σ_c > 1. The reason for this is that there is a significant difference in the distribution of tangential stress between circular and arch holes. That is, the maximum tangential stress of a circular hole on both sidewalls is smaller than that of an arch hole at the arch foot. In addition, this may also be attributed to the strength size effect and structural effect of rocks [4].

4.3. Spalling Process

By comparison, it was found that the failure process of the sidewalls of the three specimens was similar. Under the initial loading, there is a calm period. This means the period during which the pores within the specimens were compacted and internal microcracks initiated, as shown in Figure 19a. Then, particle ejection occurred at the foot or shoulder of sidewalls, accompanied by a further expansion of internal microcracks (Figure 19b). This is consistent with the stress analysis in Section 4.2. In other words, the maximum tangential stress of the three specimens reached the maximum at the foot of the arch, followed by that at the shoulder. This results in the stress concentration and the release of the accumulated energy, as shown in Figure 7a, Figure 8 and Figure 9a. As the vertical stress increased, macro fractures were created on the straight wall under the action of internal microfractures. Rock fragments were created due to the penetration of macro fractures. As shown in Figure 19c, under the tangential stress, the surrounding rock bent and opened until toppled onto the floor the test results corresponding to this period are shown in Figure 7c–f, Figure 8b–e and Figure 9b–e. The rock fragments produced on the sidewall kept bulging and breaking from the middle straight wall towards the axial ends of the hole, gradually flexing and opening towards the free surface. Spalling occurred after the rock fragments opened to a certain extent. With the development of the sidewall failure, a wide range of spalling areas was produced on both sidewalls and eventually the V-shaped or curved grooves were produced on the sidewalls, as shown in Figure 19d.

Overall, the failure process hole sidewalls can be divided into the following four periods: the calm period of internal crack expansion, the ejection period of fine particles at the foot or shoulder of the arch, the macroscopic crack penetration and spalling period, and the V- or arc-shaped groove formation period. The spalling process of specimen A12-42.22-27.12 is consistent with the results in the literature [48,49,50] (specimens containing D-shaped holes of the same size were tested), the spalling finally results in a V-shaped groove. Unlike the semi-circular tunnel, for specimens A13-22.2-22.2 and A14-17.3-28.9, finally, arc-shaped grooves were produced due to the changes in arch height and arch structure in the three-centered arch holes. The results of the true triaxial compression test on specimens containing 40 mm rectangular holes also suggested that the spalling zone gradually developed horizontally towards the deeper hole walls and finally produced a symmetrical arc-shaped groove along the axial direction of the hole [72]. The maximum tangential stress of the rectangular hole was reached at the four corners of the hole. The final distribution of tangential stress tended to be similar to that of the rectangular hole as the semi-circular arch hole changed to the three-centered arch hole with lower arch heights.

5. Conclusions

In this paper, stress analysis of surrounding rock and the true triaxial simulation tests were carried out on hard rock tunnels with different arch heights (or rise-span ratios). The following conclusions are obtained:

• The stress distributions of the surrounding rock of the tunnel with three arch heights are consistent. With the adjustment of vertical stress, when σ_Z > 30 MPa, the tensile stress appears on rise-span ratios of f/B = 1/4, f/B = 1/3, f/B = 1/2 arch tunnel in order at the floor middle, while tensile stress appears at the arch top after σ_Z rises about 20 MPa. As σ_Y doubles, the σ_Z value of tensile stress at the arch top and the floor middle increases by 20 MPa correspondingly. With the increase in σ_Z or σ_Y, the same maximum tangential stress value is first reached at the foot of the straight wall, which is f/B = 1/4 first, f/B = 1/3 second, f/B = 1/2 last, and all of them are compressive stress;
• Indoor tests were performed to simulate the spalling process of deep hard rock tunnels with different arch heights using a true triaxial test machine. The initial failure stress of the holes with different arch heights is 0.39–0.48 times the UCS of the rock. The initial failure occurs at the arch foot, where the tangential stress is the maximum. When the lateral pressure coefficient is in the range of 0.38–0.50, the tangential stress is 3.2–3.5 times the UCS. By comparison, it was found that the semi-circular arch tunnel has a better pressure-bearing capacity than the three-centered arch tunnel. The maximum tangential stress increases as the arch height decreases or the burial depth increases;
• The four spalling periods of surrounding rock of hard rock tunnels with different arch heights were clarified. In the calm period of internal crack expansion, the internal pores were compressed, and microfractures were initiated in the rock sample. The ejection period of fine particles at the foot or shoulder of the arch represents a stage of crack expansion along the arch foot and sidewalls after an initial failure of the arch or shoulder. In the macrocrack penetration and spalling stage, macrocracks expanded after the internal microfractures. In the V- or arc-shaped groove formation period, macrocracks developed deeper in rock spalling parallel to the sidewalls continuously occurred.

In this study, only the tentative experiments of three kinds of arch height specimens are considered, and the stress distribution function is solved by using the theory of elastic mechanics combined with the complex variable function. The influence of axial stress (σ_X in this paper) on the experimental results is not considered. In future work, the biaxial and true triaxial control experiments will be further carried out to make the results more universal.