High-Precision Isogeometric Static Bending Analysis of Functionally Graded Plates Using a New Quasi-3D Spectral Displacement Formulation
Abstract
Featured Application
Abstract
1. Introduction
2. Fundamental Assumptions and Formulations
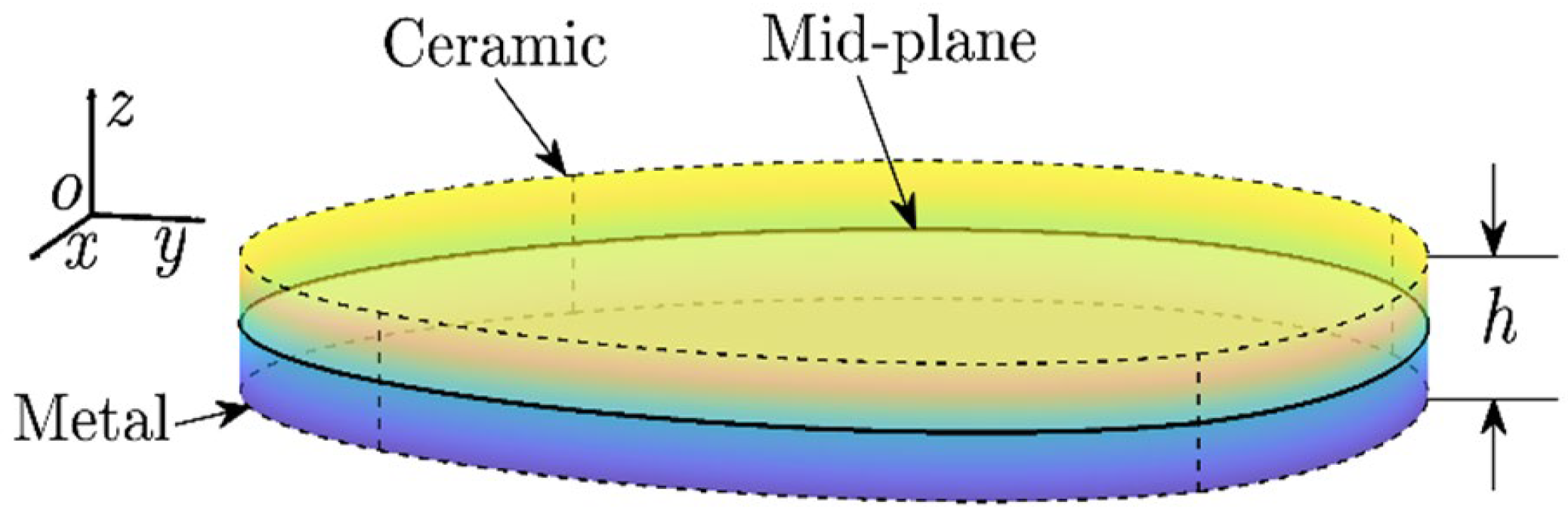
2.1. Functionally Graded Material Plate
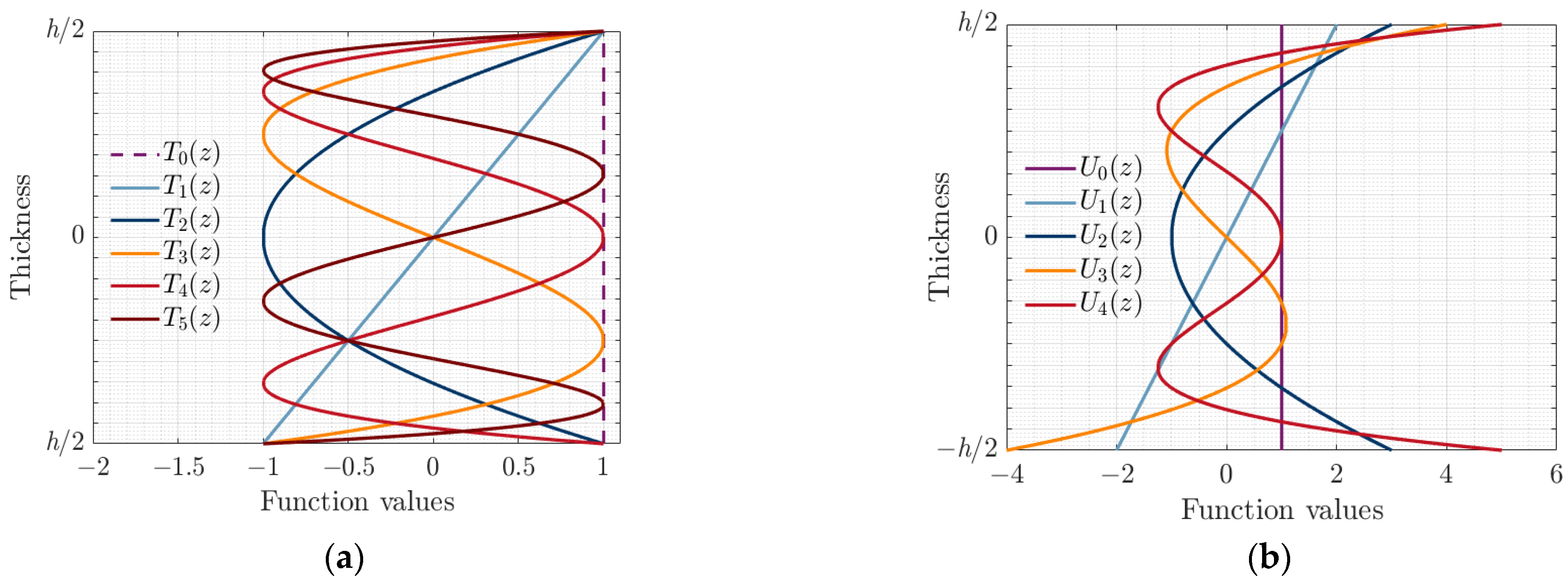
2.2. Spectral Displacement Formulation
2.3. Integral Governing Equations
3. NURBS-Based Isogeometric Analysis
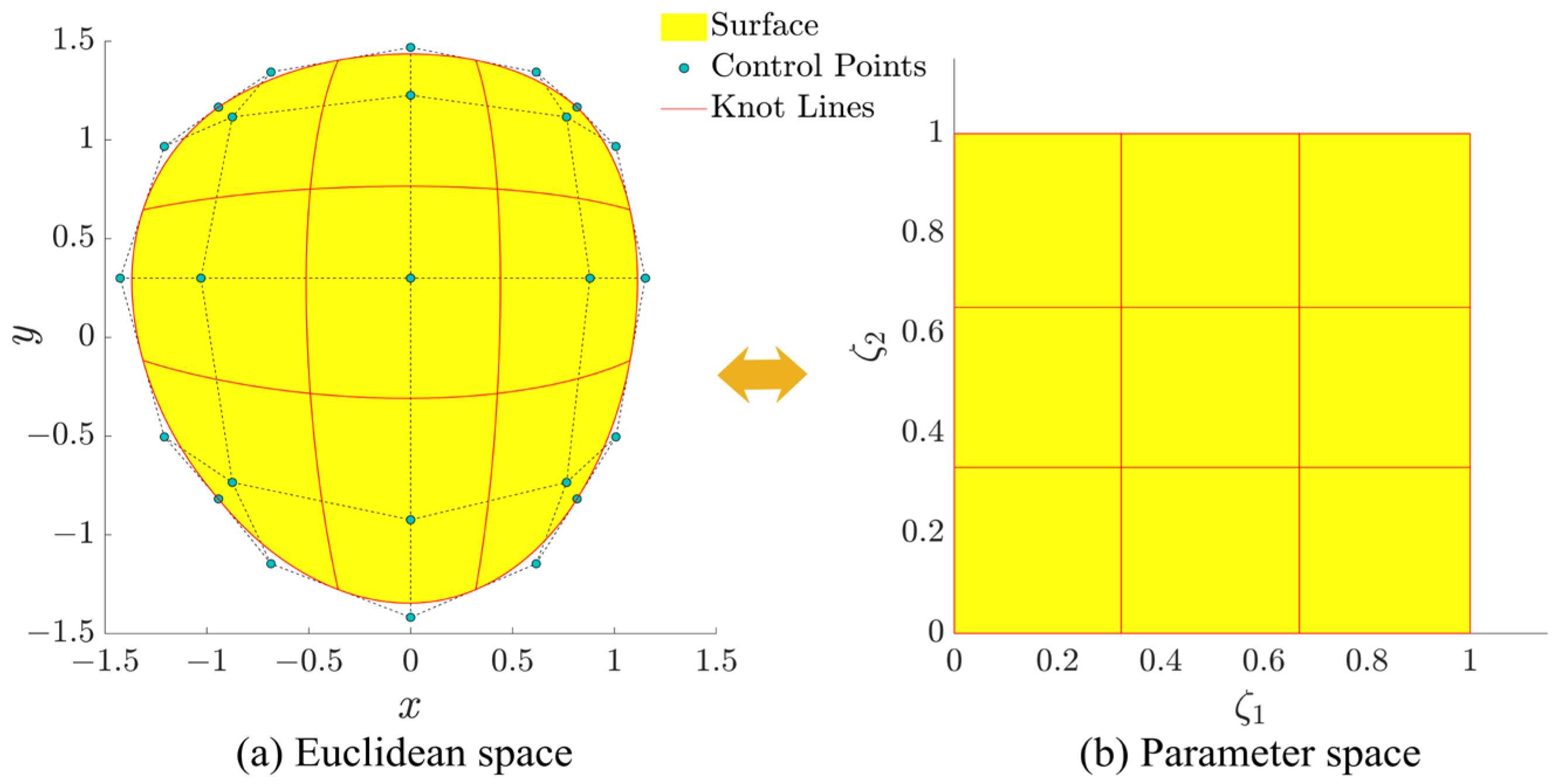
3.1. A Brief on NURBS
3.2. Discrete Governing Equations
4. Numerical Examples
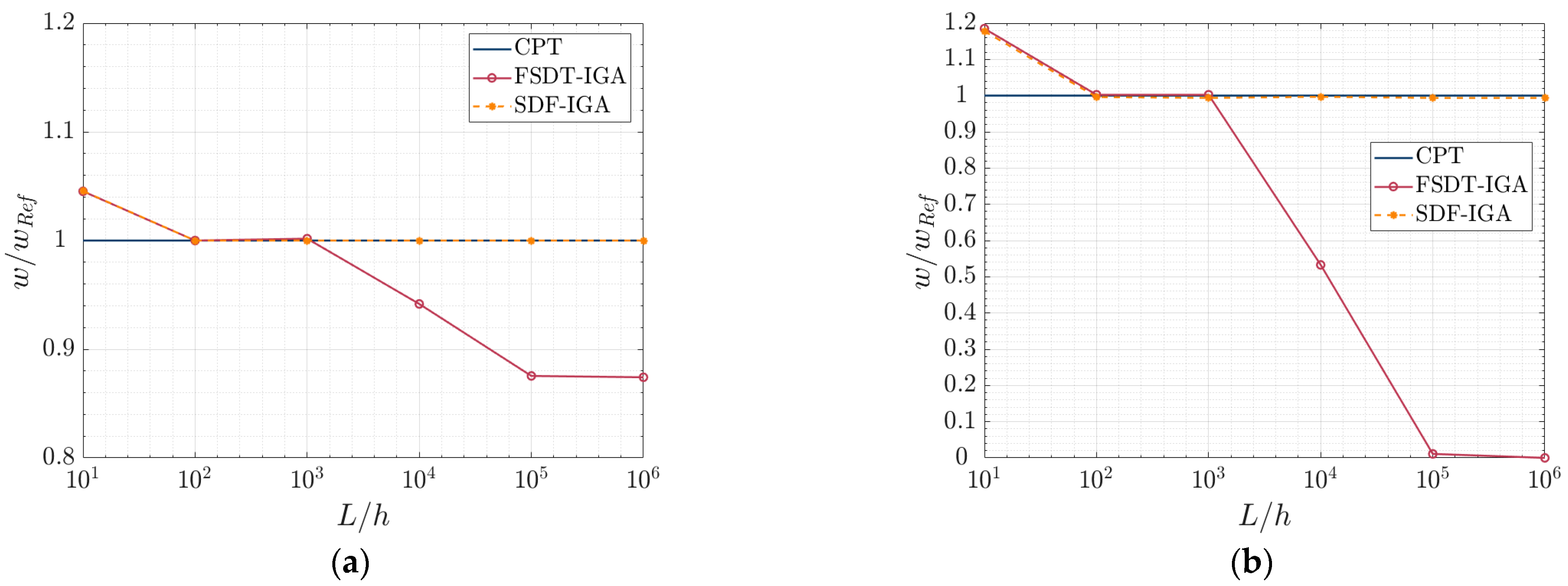
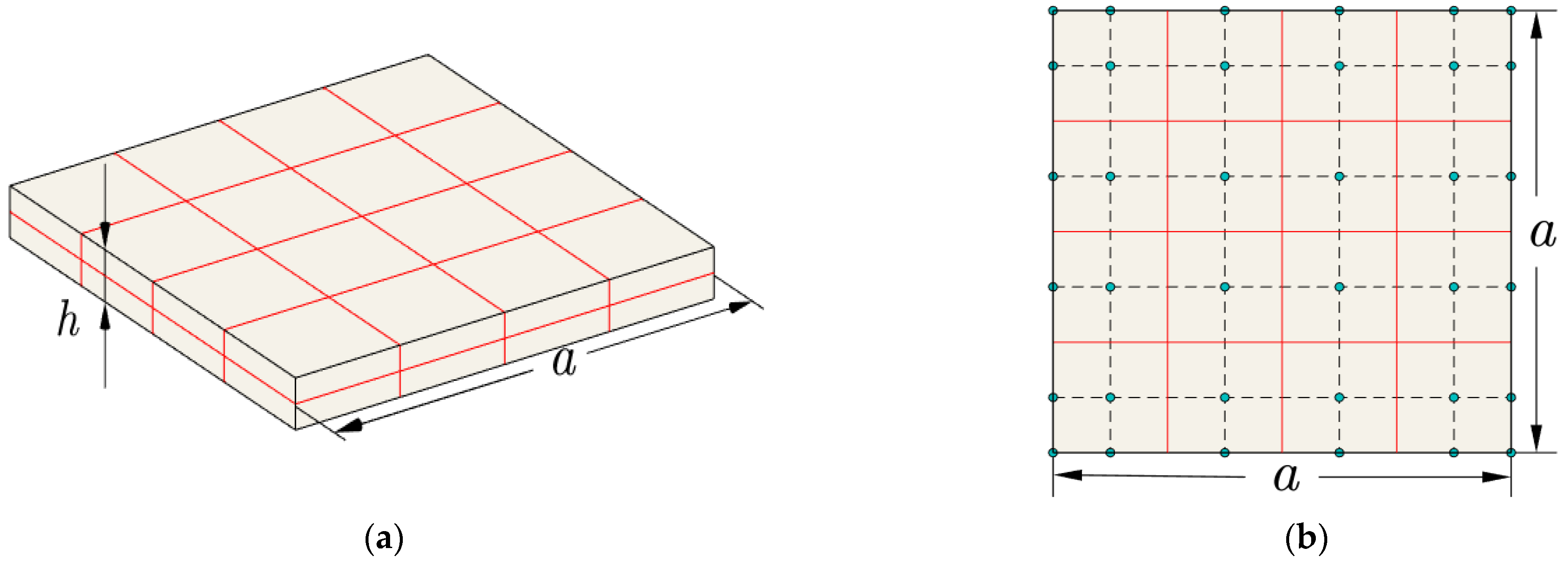
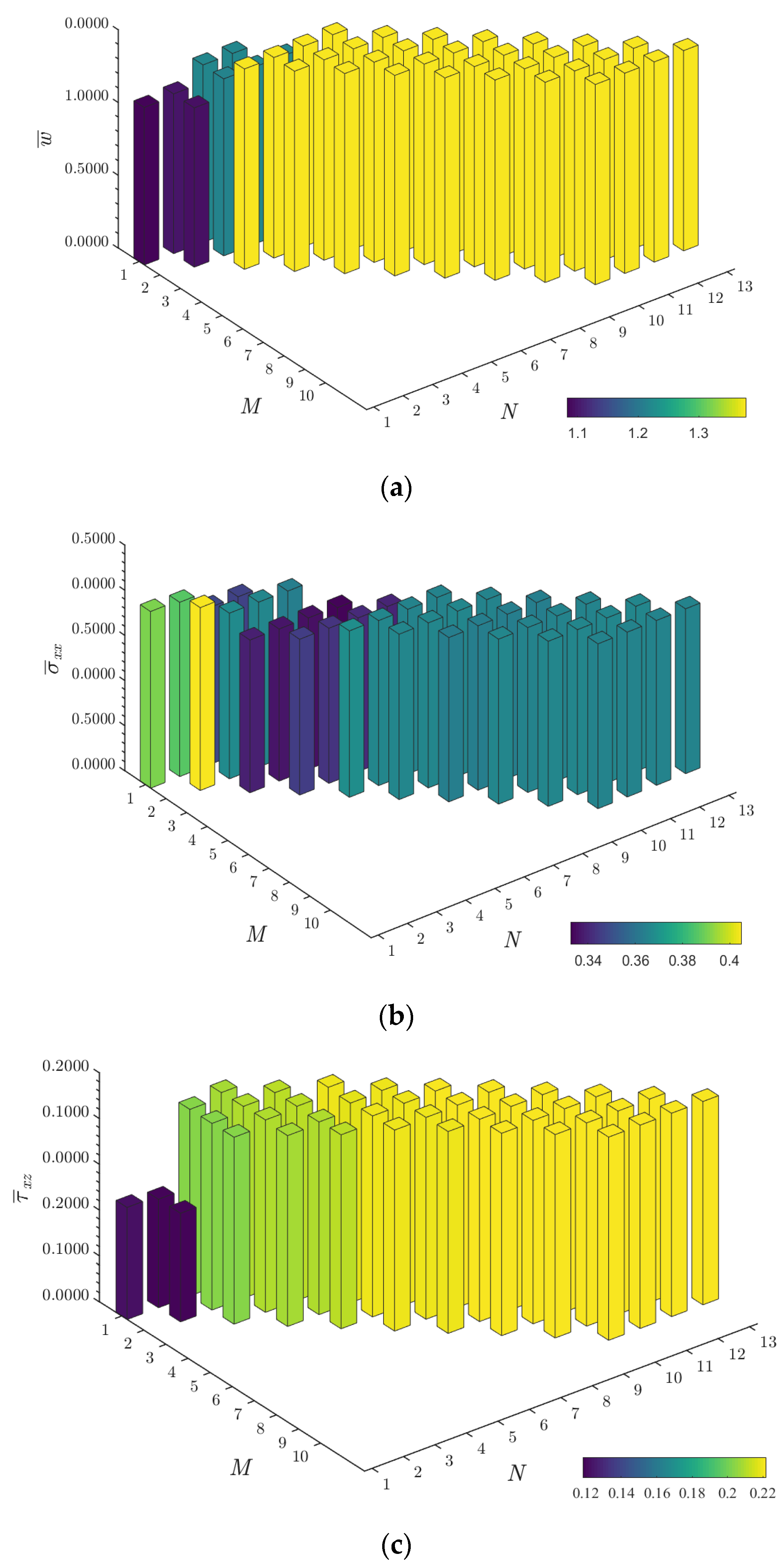
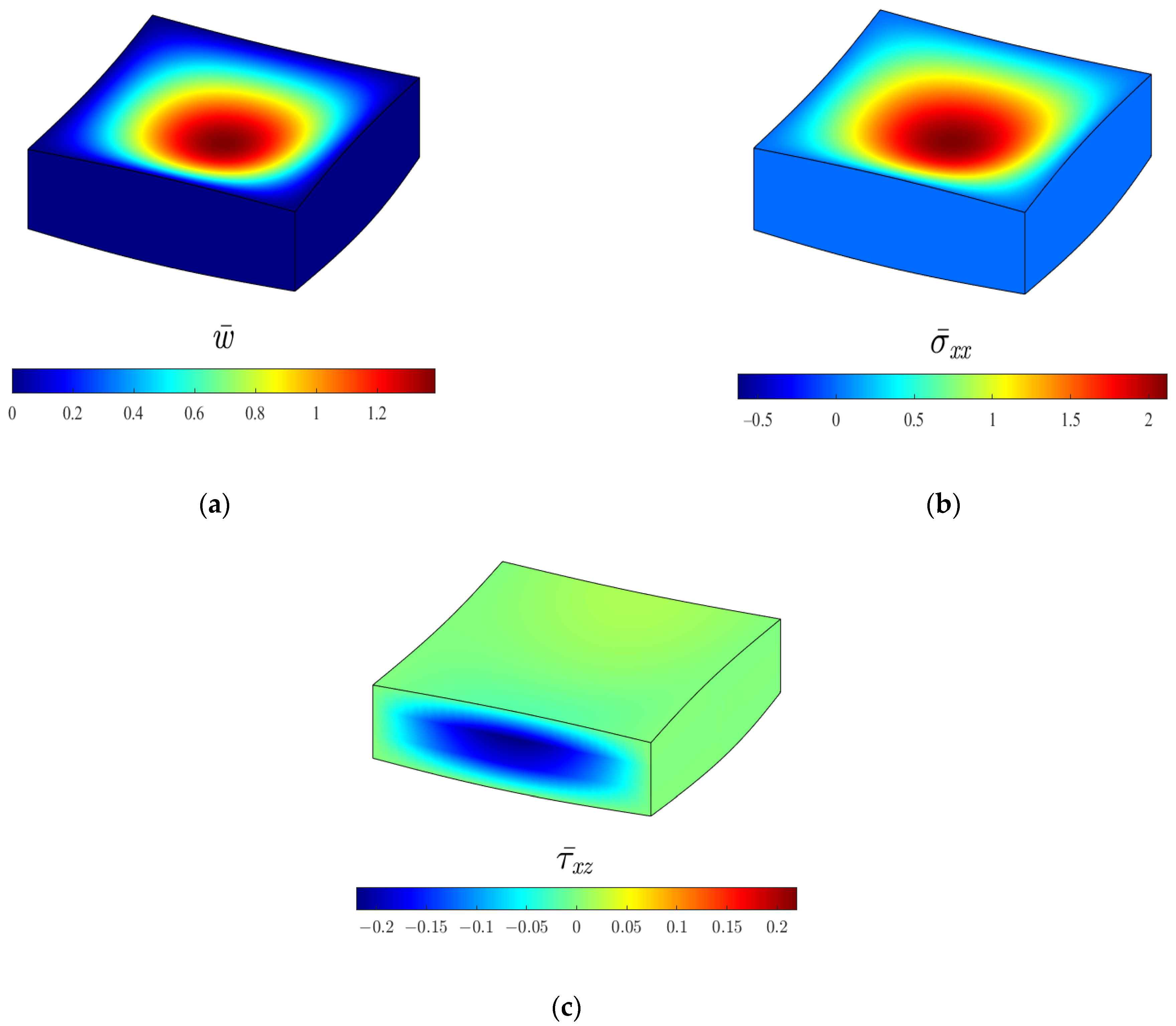
4.1. Square Al2O3 Plate
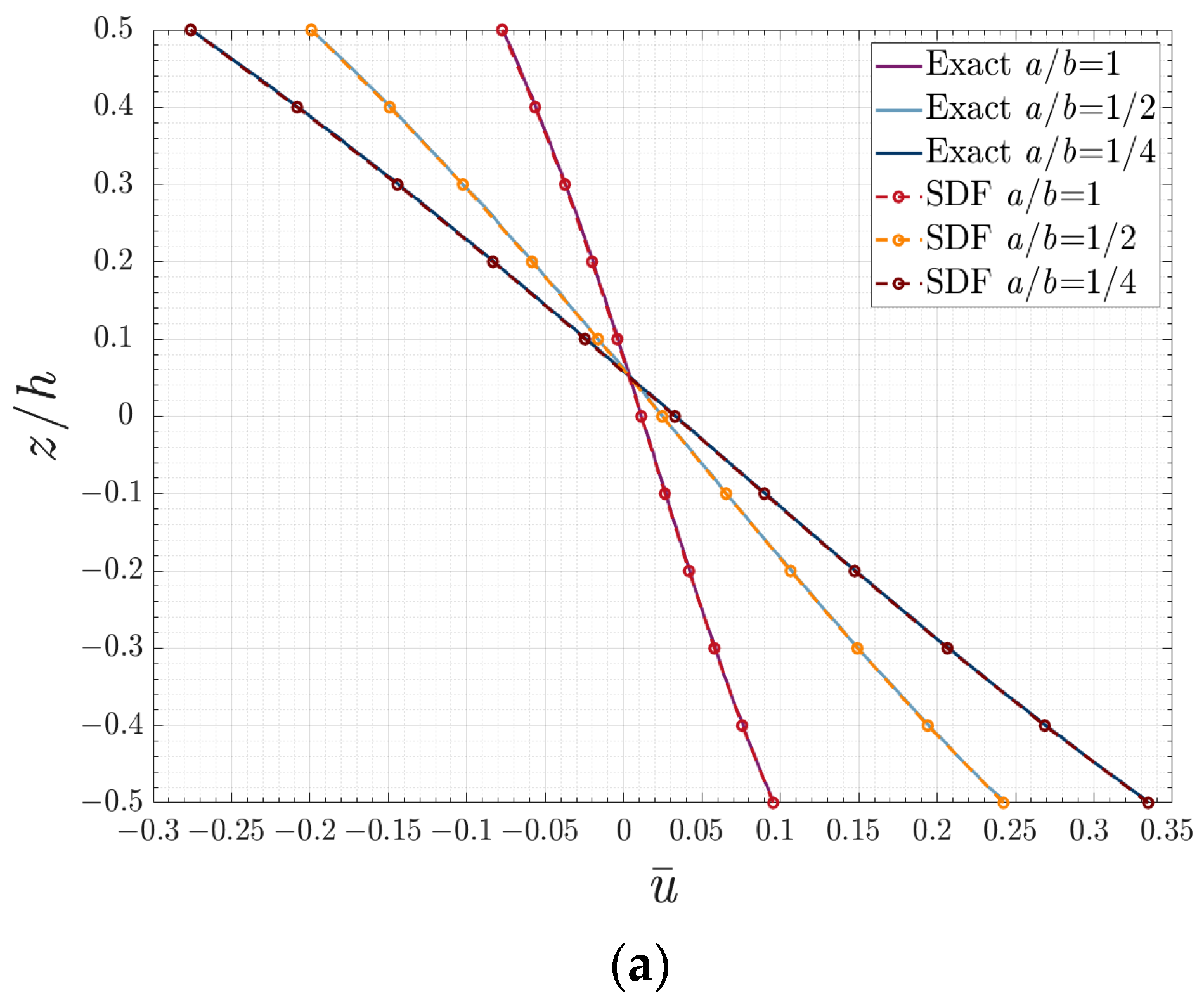
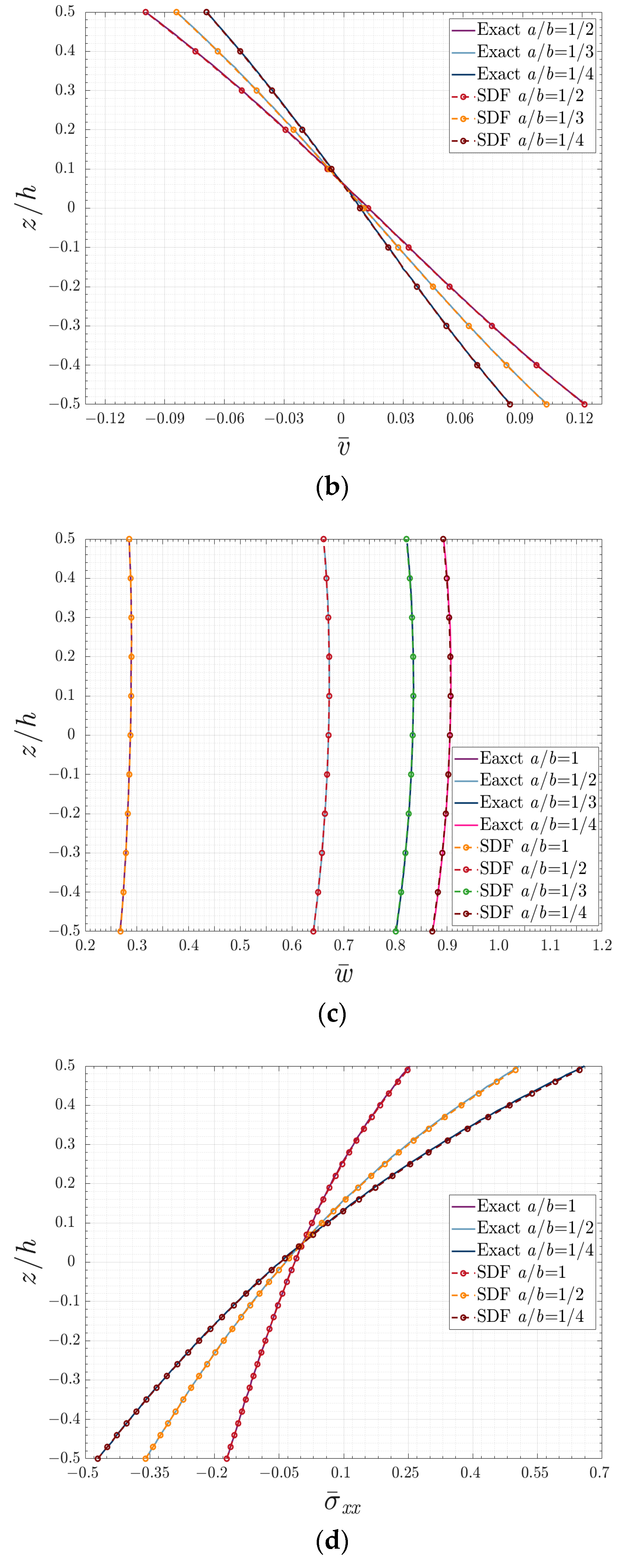
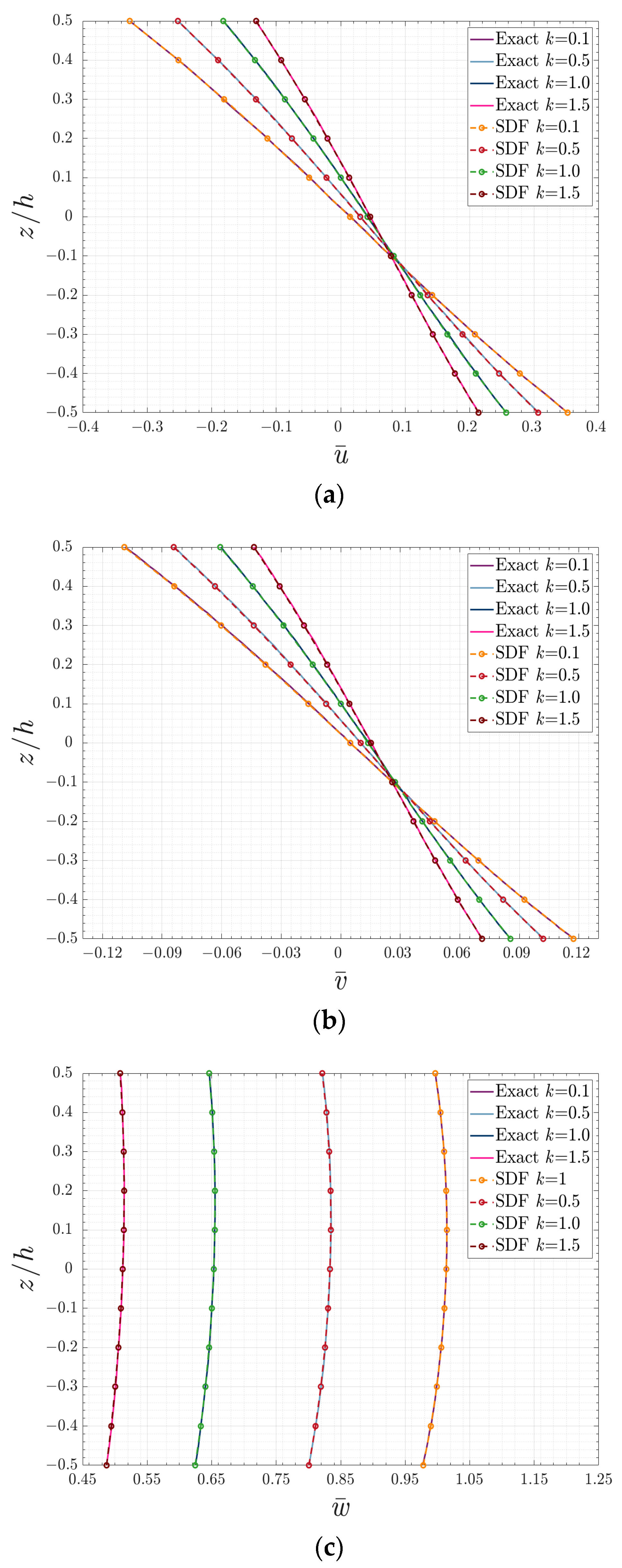
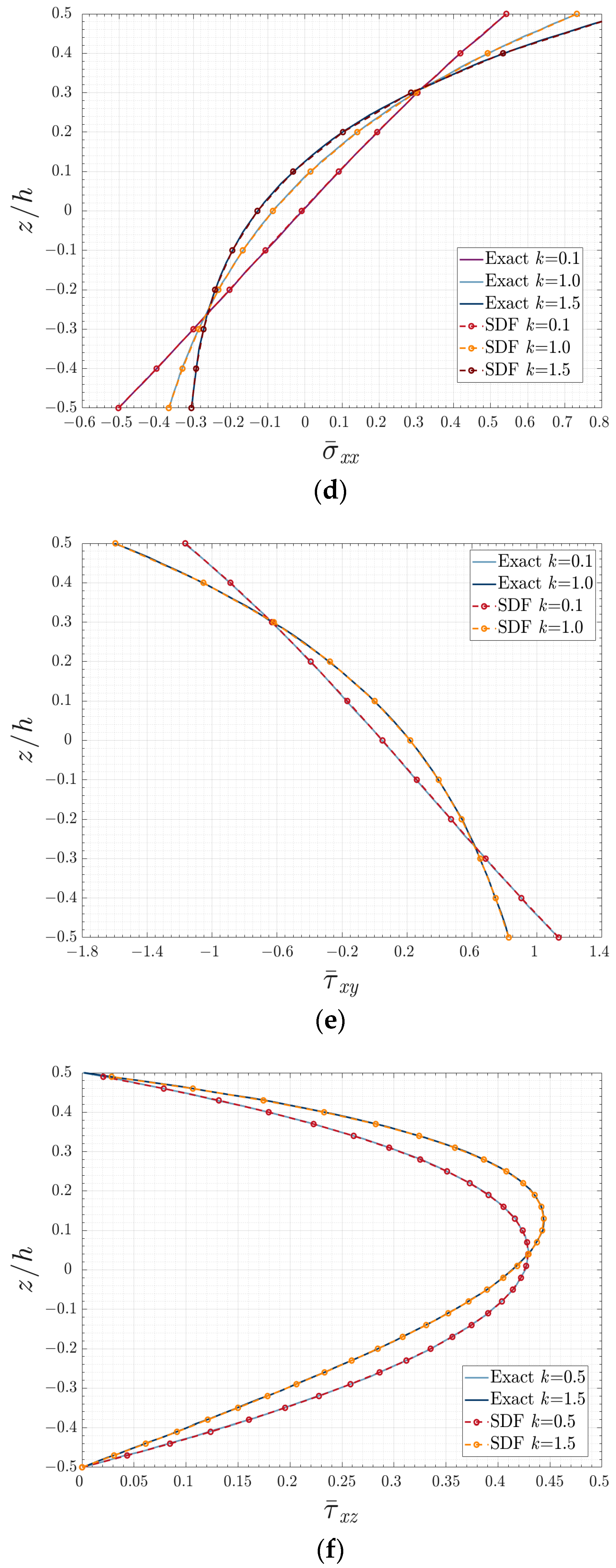
4.2. Rectangular E-FGM Plate
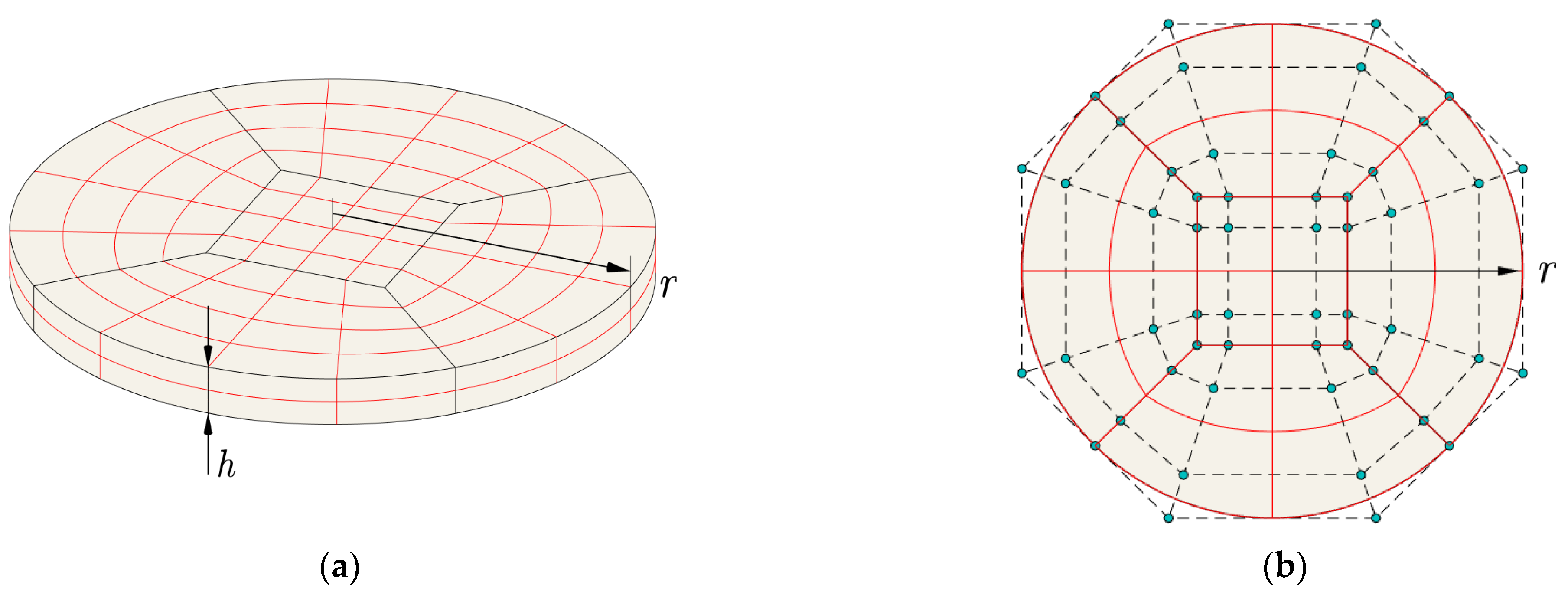
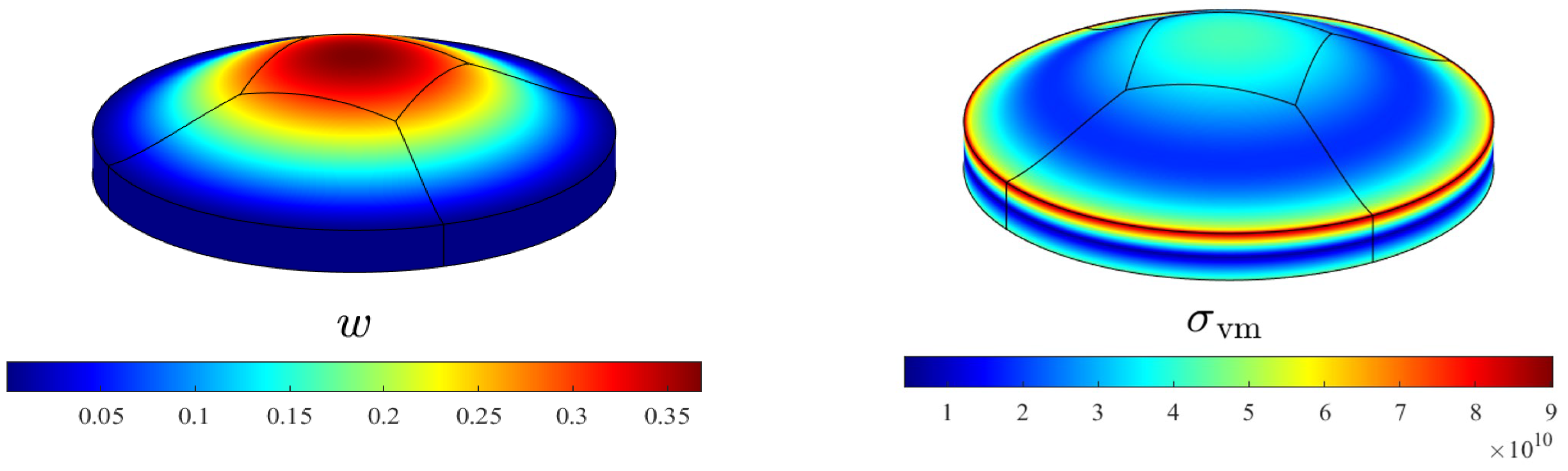
4.3. Circular Ti/ZrO2 Plate
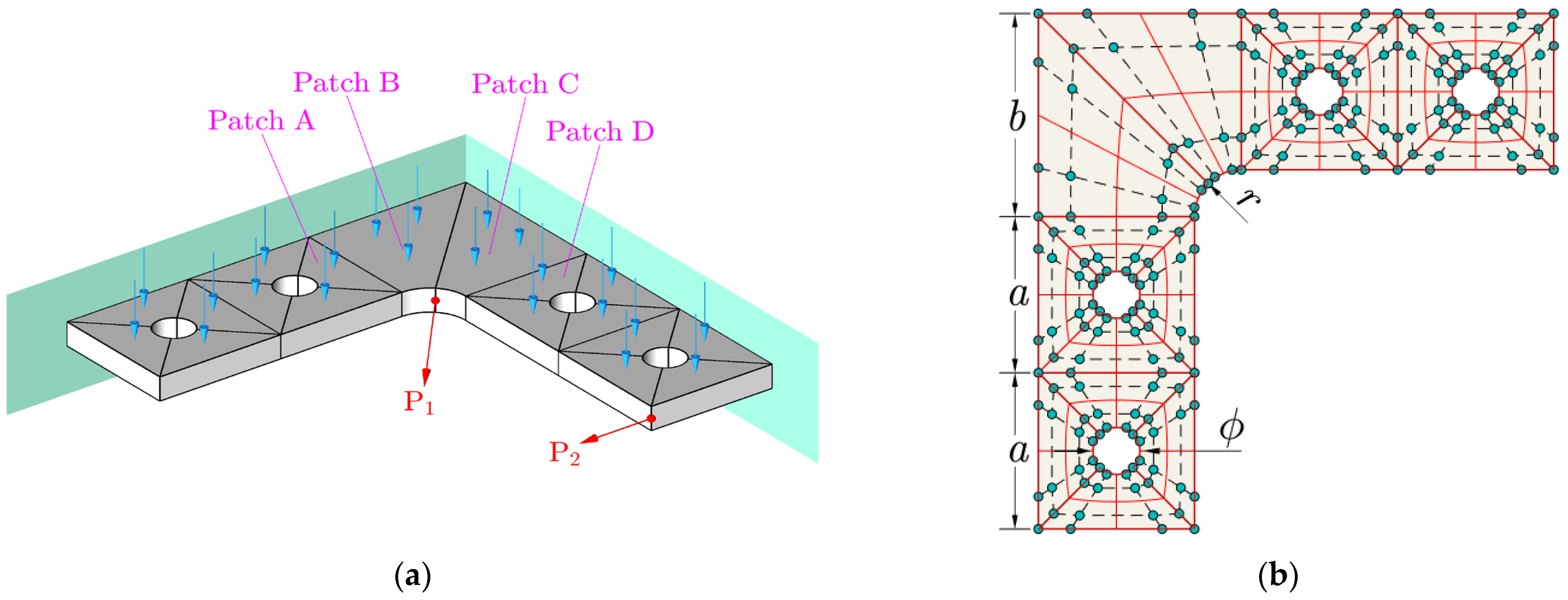
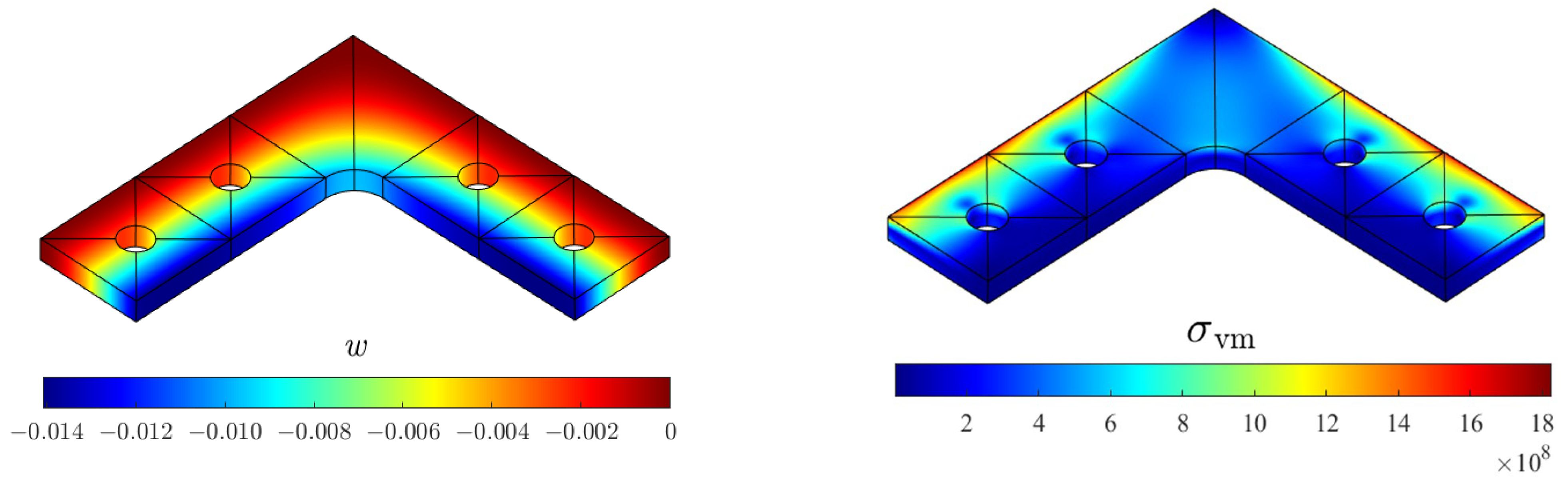
4.4. L-Shaped Al/SiC Plate
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, F.; Zhang, X.; Zhang, H. A review on functionally graded structures and materials for energy absorption. Eng. Struct. 2018, 171, 309–325. [Google Scholar] [CrossRef]
- Saleh, B.; Jiang, J.; Fathi, R.; Al-hababi, T.; Xu, Q.; Wang, L.; Song, D.; Ma, A. 30 Years of functionally graded materials: An overview of manufacturing methods, applications and future challenges. Compos. Part B Eng. 2020, 201, 108376. [Google Scholar] [CrossRef]
- Jha, D.K.; Kant, T.; Singh, R.K. A critical review of recent research on functionally graded plates. Compos. Struct. 2013, 96, 833–849. [Google Scholar] [CrossRef]
- Thai, H.T.; Kim, S.E. A review of theories for the modeling and analysis of functionally graded plates and shells. Compos. Struct. 2015, 128, 70–86. [Google Scholar] [CrossRef]
- Swaminathan, K.; Naveenkumar, D.T.; Zenkour, A.M.; Carrera, E. Stress, vibration and buckling analyses of FGM plates—A state-of-the-art review. Compos. Struct. 2015, 120, 10–31. [Google Scholar] [CrossRef]
- Reddy, J.N. A simple higher-order theory for laminated composite plates. J. Appl. Mech. 1984, 51, 745–752. [Google Scholar] [CrossRef]
- Fan, F.; Safaei, B.; Sahmani, . Buckling and postbuckling response of nonlocal strain gradient porous functionally graded micro/nano-plates via NURBS-based isogeometric analysis. Thin Walled Struct. 2021, 159, 107231. [Google Scholar] [CrossRef]
- Nguyen-Xuan, H.; Thai, C.H.; Nguyen-Thoi, T. Isogeometric finite element analysis of composite sandwich plates using a higher order shear deformation theory. Compos. Part B Eng. 2013, 55, 558–574. [Google Scholar] [CrossRef]
- Xiang, S.; Jin, Y.; Bi, Z.; Jiang, S.; Yang, M. A n-order shear deformation theory for free vibration of functionally graded and composite sandwich plates. Compos. Struct. 2011, 93, 2826–2832. [Google Scholar] [CrossRef]
- Touratier, M. An efficient standard plate theory. Int. J. Eng. Sci. 1991, 29, 901–916. [Google Scholar] [CrossRef]
- Soldatos, K.P. A transverse shear deformation theory for homogeneous monoclinic plates. Acta Mech. 1992, 94, 195–220. [Google Scholar] [CrossRef]
- Karama, M.; Afaq, K.S.; Mistou, S. Mechanical behaviour of laminated composite beam by the new multi-layered laminated composite structures model with transverse shear stress continuity. Int. J. Solids Struct. 2003, 40, 1525–1546. [Google Scholar] [CrossRef]
- Mantari, J.L.; Oktem, A.S.; Soares, C.G. A new trigonometric shear deformation theory for isotropic, laminated composite and sandwich plates. Int. J. Solids Struct. 2012, 49, 43–53. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Cottrell, J.A.; Bazilevs, Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef]
- Carrera, E.; Brischetto, S.; Cinefra, M.; Soave, M. Effects of thickness stretching in functionally graded plates and shells. Compos. Part B Eng. 2011, 42, 123–133. [Google Scholar] [CrossRef]
- Zenkour, A.M. Benchmark trigonometric and 3-D elasticity solutions for an exponentially graded thick rectangular plate. Arch. Appl. Mech. 2007, 77, 197–214. [Google Scholar] [CrossRef]
- Matsunaga, H. Free vibration and stability of functionally graded plates according to a 2-D higher-order deformation theory. Compos. Struct. 2008, 82, 499–512. [Google Scholar] [CrossRef]
- Matsunaga, H. Free vibration and stability of functionally graded shallow shells according to a 2D higher-order deformation theory. Compos. Struct. 2008, 84, 132–146. [Google Scholar] [CrossRef]
- Talha, M.; Singh, B.N. Static response and free vibration analysis of FGM plates using higher order shear deformation theory. Appl. Math. Model. 2010, 34, 3991–4011. [Google Scholar] [CrossRef]
- Mantari, J.L.; Soares, C.G. Generalized hybrid quasi-3D shear deformation theory for the static analysis of advanced composite plates. Compos. Struct. 2012, 94, 2561–2575. [Google Scholar] [CrossRef]
- Mantari, J.L.; Soares, C.G. Optimized sinusoidal higher order shear deformation theory for the analysis of functionally graded plates and shells. Compos. Part B Eng. 2014, 56, 126–136. [Google Scholar] [CrossRef]
- Mantari, J.L.; Soares, C.G. A quasi-3D tangential shear deformation theory with four unknowns for functionally graded plates. Acta. Mech. 2015, 226, 625–642. [Google Scholar] [CrossRef]
- Thai, H.T.; Kim, S.E. A simple quasi-3D sinusoidal shear deformation theory for functionally graded plates. Compos. Struct. 2013, 99, 172–180. [Google Scholar] [CrossRef]
- Thai, H.T.; Vo, T.P.; Bui, T.Q.; Nguyen, T.K. A quasi-3D hyperbolic shear deformation theory for functionally graded plates. Acta. Mech. 2014, 225, 951–964. [Google Scholar] [CrossRef]
- Hebali, H.; Tounsi, A.; Houari, M.S.A.; Bessaim, A.; Bedia, E.A.A. New quasi-3D hyperbolic shear deformation theory for the static and free vibration analysis of functionally graded plates. J. Eng. Mech. 2014, 140, 374–383. [Google Scholar] [CrossRef]
- Bessaim, A.; Houari, M.S.A.; Tounsi, A.; Mahmoud, S.R.; Bedia, E.A.A. A new higher-order shear and normal deformation theory for the static and free vibration analysis of sandwich plates with functionally graded isotropic face sheets. J. Sandw. Struct. Mater. 2013, 15, 671–703. [Google Scholar] [CrossRef]
- Bennoun, M.; Houari, M.S.A.; Tounsi, A. A novel five-variable refined plate theory for vibration analysis of functionally graded sandwich plates. Mech. Adv. Mater. Struct. 2016, 23, 423–431. [Google Scholar] [CrossRef]
- Belabed, Z.; Houari, M.S.A.; Tounsi, A.; Mahmoud, S.R.; Bég, O.A. An efficient and simple higher order shear and normal deformation theory for functionally graded material (FGM) plates. Compos. Part B Eng. 2014, 60, 274–283. [Google Scholar] [CrossRef]
- Mantari, J.L.; Granados, E.V. Thermoelastic analysis of advanced sandwich plates based on a new quasi-3D hybrid type HSDT with 5 unknowns. Compos. Part B Eng. 2015, 69, 317–334. [Google Scholar] [CrossRef]
- Mantari, J.L.; Granados, E.V.; Hinostroza, M.A.; Soares, C.G. Modelling advanced composite plates resting on elastic foundation by using a quasi-3D hybrid type HSDT. Compos. Struct. 2014, 118, 455–471. [Google Scholar] [CrossRef]
- Neves, A.M.A.; Ferreira, A.J.M.; Carrera, E.; Cinefra, M.; Roque, C.M.C.; Jorge, R.M.N.; Soares, C.M.M. A quasi-3D hyperbolic shear deformation theory for the static and free vibration analysis of functionally graded plates. Compos. Struct. 2012, 94, 1814–1825. [Google Scholar] [CrossRef]
- Neves, A.M.A.; Ferreira, A.J.M.; Carrera, E.; Cinefra, M.; Jorge, R.M.N.; Soares, C.M.M. Buckling analysis of sandwich plates with functionally graded skins using a new quasi-3D hyperbolic sine shear deformation theory and collocation with radial basis functions. ZAMM J. Appl. Math. Mech. 2012, 92, 749–766. [Google Scholar] [CrossRef]
- Mantari, J.L.; Oktem, A.S.; Soares, C.G. A new higher order shear deformation theory for sandwich and composite laminated plates. Compos. Part B Eng. 2012, 43, 1489–1499. [Google Scholar] [CrossRef]
- Farzam-Rad, S.A.; Hassani, S.A.B.; Karamodin, A. Isogeometric analysis of functionally graded plates using a new quasi-3D shear deformation theory based on physical neutral surface. Compos. Part B Eng. 2017, 108, 74–189. [Google Scholar] [CrossRef]
- Sun, X.; Gao, R.; Zhang, Y. Spectral stochastic isogeometric analysis of bending and free vibration of porous functionally graded plates. Appl. Math. Model. 2023, 116, 711–734. [Google Scholar] [CrossRef]
- Neves, A.M.A.; Ferreira, A.J.M.; Carrera, E.; Cinefra, M.; Roque, C.M.C.; Jorge, R.M.N.; Soares, C.M.M. Static, Free vibration and buckling analysis of isotropic and sandwich functionally graded plates using a quasi-3D higher-order shear deformation theory and a meshless technique. Compos. Part B Eng. 2013, 44, 657–674. [Google Scholar] [CrossRef]
- Montassir, S.; Moustabchir, H.; Elkhalfi, A. Application of NURBS in the Fracture Mechanics Framework to Study the Stress Intensity Factor. Stat. Optim. Inf. Comput. 2023, 11, 106–115. [Google Scholar]
- Yakoubi, K.; Montassir, S.; Moustabchir, H.; Elkhalfi, A.; Scutaru, M.L.; Vlase, S. T-Stress Evaluation Based Cracking of Pipes Using an Extended Isogeometric Analysis (X-IGA). Symmetry 2022, 14, 1065. [Google Scholar] [CrossRef]
- Bao, G.; Wang, L. Multiple cracking in functionally graded ceramic/metal coatings. Int. J. Solids Struct. 1995, 32, 2853–2871. [Google Scholar] [CrossRef]
- Szilard, R. Theories and applications of plate analysis: Classical, numerical and engineering methods. Appl. Mech. Rev. 2004, 57, B32–B33. [Google Scholar] [CrossRef]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods; Courier Corporation: Chelmsford, MA, USA, 2001; pp. 101–105. [Google Scholar]
- Thai, C.H.; Kulasegaram, S.; Tran, L.V.; Nguyen-Xuan, H. Generalized shear deformation theory for functionally graded isotropic and sandwich plates based on isogeometric approach. Comput. Struct. 2014, 141, 94–112. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Thai, C.H.; Nguyen-Xuan, H.; Lee, J. Geometrically nonlinear analysis of functionally graded material plates using an improved moving Kriging meshfree method based on a refined plate theory. Compos. Struct. 2018, 193, 268–280. [Google Scholar] [CrossRef]
- Cottrell, J.A.; Hughes, T.J.R.; Bazilevs, Y. Isogeometric Analysis: Toward Integration of CAD and FEA; John Wiley and Sons: Hoboken, NJ, USA, 2009; pp. 154–176. [Google Scholar]
- Piegl, L.; Tiller, W. The NURBS Book; Springer Science and Business Media: Berlin, Germany, 2012; pp. 1–254. [Google Scholar]
- Farin, G. Curves and Surfaces for Computer-Aided Geometric Design: A Practical Guide; Elsevier: Cham, Switzerland, 2014; pp. 154–296. [Google Scholar]
- Brannon, R.M. Curvilinear Analysis in a Euclidian Space; University of New Mexico: Albuquerque, NM, USA, 2004; pp. 78–97. [Google Scholar]
- Adam, C.; Hughes, T.J.R.; Bouabdallah, S.; Zarroug, M.; Maitournam, H. Selective and reduced numerical integrations for NURBS-based isogeometric analysis. Comput. Methods Appl. Mech. Eng. 2015, 284, 732–761. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Xu, Z.; Zeng, L.F.; Samuelsson, A.; Wiberg, N.E. Linked interpolation for Reissner-Mindlin plate elements: Part I—A simple quadrilateral. Int. J. Numer. Methods Eng. 1993, 36, 3043–3056. [Google Scholar] [CrossRef]
- Nguyen, N.D.; Nguyen, T.K.; Nguyen, T.N.; Thai, H.T. New Ritz-solution shape functions for analysis of thermo-mechanical buckling and vibration of laminated composite beams. Compos. Struct. 2018, 184, 452–460. [Google Scholar] [CrossRef]
- Reddy, J.N.; Wang, C.M.; Kitipornchai, S. Axisymmetric bending of functionally graded circular and annular plates. Eur. J. Mech. A/Solids 1999, 18, 185–199. [Google Scholar] [CrossRef]
- Yin, S.; Hale, J.S.; Yu, T.; Bui, T.Q.; Bordas, S.P. Isogeometric locking-free plate element: A simple first order shear deformation theory for functionally graded plates. Compos. Struct. 2014, 118, 121–138. [Google Scholar] [CrossRef]
- Tran, L.V.; Ferreira, A.J.M.; Nguyen, X.H. Isogeometric analysis of functionally graded plates using higher-order shear deformation theory. Compos. Part B Eng. 2013, 51, 368–383. [Google Scholar] [CrossRef]


| Young’s Modulus (GPa) | Poisson’s Ratio | Density (kg/m3) | |
|---|---|---|---|
| Al | 70 | 0.3 | 2707 |
| Ti | 110.25 | 0.288 | - |
| Al2O3 | 380 | 0.3 | 3800 |
| ZrO2 | 278.41 | 0.288 | - |
| SiC | 427 | 0.17 | 3210 |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| 1 | Quasi-3D [15] | 0.7171 | 0.5875 | 0.5625 | 0.6221 | 1.5064 | 14.9690 |
| TSDT-IGA [42] | 0.7284 | 0.5889 | 0.5625 | 0.5783 | 1.4816 | 14.8890 | |
| FSDT [15] | 0.7291 | 0.5889 | 0.5625 | 0.8060 | 2.0150 | 20.1500 | |
| Present | 0.7172 | 0.5875 | 0.5625 | 0.6219 | 1.5064 | 14.9692 | |
| 4 | Quasi-3D [15] | 1.1585 | 0.8821 | 0.8286 | 0.4877 | 1.1971 | 11.9230 |
| TSDT-IGA [42] | 1.1598 | 0.8815 | 0.8287 | 0.4406 | 1.1711 | 11.8436 | |
| FSDT [15] | 1.1125 | 0.8736 | 0.8286 | 0.6420 | 1.6049 | 16.0490 | |
| Present | 1.1589 | 0.8823 | 0.8287 | 0.4884 | 1.1974 | 11.9198 | |
| 10 | Quasi-3D [15] | 1.3745 | 1.0072 | 0.9361 | 0.3695 | 0.8965 | 8.9077 |
| TSDT-IGA [42] | 1.3908 | 1.0087 | 0.9362 | 0.3230 | 0.8733 | 8.8582 | |
| FSDT [15] | 1.3178 | 0.9966 | 0.9360 | 0.4796 | 1.1990 | 11.9900 | |
| Present | 1.3757 | 1.0074 | 0.9362 | 0.3657 | 0.8947 | 8.9076 | |
| Method | |||||||
|---|---|---|---|---|---|---|---|
| 0.2 | FSDT [51] | 1.6130 | 1.4730 | 1.3620 | 1.3330 | 1.2160 | 1.1990 |
| sFSDT–IGA [52] | 1.6051 | 1.4659 | 1.3548 | 1.3260 | 1.2097 | 1.1918 | |
| HSDT–IGA [53] | 1.5958 | 1.4557 | 1.3467 | 1.3187 | 1.2060 | 1.1884 | |
| Present | 1.5962 | 1.4556 | 1.3468 | 1.3189 | 1.2065 | 1.1891 | |
| 0.1 | FSDT [51] | 1.4440 | 1.3200 | 1.2170 | 1.1900 | 1.0800 | 1.0630 |
| sFSDT–IGA [52] | 1.4428 | 1.3186 | 1.2159 | 1.1889 | 1.0785 | 1.0615 | |
| HSDT–IGA [53] | 1.4386 | 1.3143 | 1.2123 | 1.1855 | 1.0762 | 1.0592 | |
| Present | 1.4378 | 1.3131 | 1.2112 | 1.1845 | 1.0754 | 1.0620 | |
| 0.05 | FSDT [51] | 1.4020 | 1.2820 | 1.1810 | 1.1550 | 1.0460 | 1.0290 |
| sFSDT–IGA [52] | 1.4023 | 1.2817 | 1.1812 | 1.1546 | 1.0458 | 1.0289 | |
| HSDT–IGA [53] | 1.3990 | 1.2786 | 1.1785 | 1.1520 | 1.0435 | 1.0267 | |
| Present | 1.3990 | 1.2785 | 1.1783 | 1.1518 | 1.0435 | 1.0266 |
| Point | Method | |||||||
|---|---|---|---|---|---|---|---|---|
| 0.2 | Ansys | 3.089 × 10−3 | 8.246 × 10−3 | 9.745 × 10−3 | 1.037 × 10−2 | 1.083 × 10−2 | 1.121 × 10−2 | |
| Present | 3.088 × 10−3 | 8.215 × 10−3 | 9.714 × 10−3 | 1.034 × 10−2 | 1.078 × 10−2 | 1.117 × 10−2 | ||
| Ansys | 4.480 × 10−3 | 1.188 × 10−2 | 1.400 × 10−2 | 1.488 × 10−2 | 1.551 × 10−2 | 1.606 × 10−2 | ||
| Present | 4.485 × 10−3 | 1.183 × 10−2 | 1.394 × 10−2 | 1.481 × 10−2 | 1.544 × 10−2 | 1.599 × 10−2 | ||
| 0.1 | Ansys | 2.376 × 10−2 | 6.357 × 10−2 | 7.431 × 10−2 | 7.852 × 10−2 | 8.163 × 10−2 | 8.442 × 10−2 | |
| Present | 2.464 × 10−2 | 6.330 × 10−2 | 7.396 × 10−2 | 7.813 × 10−2 | 8.122 × 10−2 | 8.400 × 10−2 | ||
| Ansys | 3.448 × 10−2 | 9.166 × 10−2 | 1.071 × 10−1 | 1.131 × 10−1 | 1.176 × 10−1 | 1.216 × 10−1 | ||
| Present | 3.324 × 10−2 | 9.136 × 10−2 | 1.067 × 10−1 | 1.127 × 10−1 | 1.171 × 10−1 | 1.212 × 10−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Sun, X.; Cai, Z.; Peng, H.; Zhang, Y. High-Precision Isogeometric Static Bending Analysis of Functionally Graded Plates Using a New Quasi-3D Spectral Displacement Formulation. Appl. Sci. 2023, 13, 6412. https://doi.org/10.3390/app13116412
Yang S, Sun X, Cai Z, Peng H, Zhang Y. High-Precision Isogeometric Static Bending Analysis of Functionally Graded Plates Using a New Quasi-3D Spectral Displacement Formulation. Applied Sciences. 2023; 13(11):6412. https://doi.org/10.3390/app13116412
Chicago/Turabian StyleYang, Shaowei, Xianbo Sun, Zhiqin Cai, Haijun Peng, and Yahui Zhang. 2023. "High-Precision Isogeometric Static Bending Analysis of Functionally Graded Plates Using a New Quasi-3D Spectral Displacement Formulation" Applied Sciences 13, no. 11: 6412. https://doi.org/10.3390/app13116412
APA StyleYang, S., Sun, X., Cai, Z., Peng, H., & Zhang, Y. (2023). High-Precision Isogeometric Static Bending Analysis of Functionally Graded Plates Using a New Quasi-3D Spectral Displacement Formulation. Applied Sciences, 13(11), 6412. https://doi.org/10.3390/app13116412






