Magnetic Properties of Gd-Doped Fe₃O₄ Nanoparticles

Abstract

The magnetic properties of pure and rare earth ion-doped Fe${}_3$O${}_4$ nanoparticles are investigated using a microscopic model and the Green’s function theory. The magnetization $M_s$ and Curie temperature $T_C$ are calculated depending on size, temperature and Gd doping concentration. $M_s$ and $T_C$ decrease with decreasing nanoparticle size and with increasing the doping concentration. The band gap energy increases with decreasing size and Gd dopants. The obtained results are in good agreement with the experimental data.

1. Introduction

Nanoparticles (NPs) have received a lot of attention in the last decade due to their unique properties and wide range of applications. The magnetic behavior of magnetic NPs greatly depends on their size, shape, purity and crystal structure. Magnetite Fe${}_3$O${}_4$ is one of the most widely used nanomaterials for biomedical applications. Masrour et al. [1] performed self-consistent ab initio calculations and investigated the magnetic properties of bulk Fe${}_3$O${}_4$. The magnetic behavior of spherical and cubic magnetite NPs are studied by Goya et al. [2], Abbad et al. [3], Sahadevan et al. [4], Wang et al. [5], Zhao et al. [6]. With decreasing particle size, the magnetic properties begin to change. Specifically, the lattice parameters are slightly enhanced [7]. Decreasing NP size leads to reduced ferrimagnetic behavior [8]. The saturation magnetization and the Curie temperature $T_C$ of Fe${}_3$O${}_4$ NPs are lower than that of the bulk one [7,9]. High-saturation magnetization in small Fe${}_3$O${}_4$ NPs is observed by Correa et al. [10] and Nagesha et al. [11].

The magnetic properties of magnetite Fe${}_3$O${}_4$ can be achieved by ion doping. From a theoretical point of view, doping is a method by which the structural parameters of the crystal lattice can be drastically changed, causing shrinkage and stretching processes and changes in the nature of magnetic arrangement. Doping can significantly renormalize the magnetic phase transition temperature, magnetization, magnetic anisotropy and coercivity. The influence of rare earth (RE) doping on the magnetic properties of Fe${}_3$O${}_4$ NPs is investigated by Kershi et al. [12]. They observed a reduction of the magnetization and increase of the band gap. The influence of Gd doping on structural and magnetic properties of Fe${}_3$O${}_4$ NPs is studied by Hazarika et al. [13]. Zhang et al. [14] also considered the magnetic properties of Gd-doped magnetite NPs.

The aim of the present paper is to investigate theoretically for the first time the magnetic and optical properties of Fe${}_3$O${}_4$ NPs using a microscopic model and the Green’s function theory.

It should be noted that the most theoretical papers consider the magnetic properties of bulk Fe${}_3$O${}_4$ using the density functional theory (DFT) [1,15]. The DFT is a very powerful tool in investigation of many body problems. However, DFT is mostly concerned with ground-state properties at zero temperature. In our approach, we are able to cover the whole temperature regime. It is a finite temperature analysis including the entire excitation spectrum. In particular, the method allows us to study the total phase diagram, which is based on the different excitation energies realized in the system. The disadvantage of our approach consists of the consideration of collective properties from the beginning. Our basic quantities are not the “naked” electrons, but the effective spins of the underlying quasi-particles. Whereas, within DFT, all of the parameters of the system can be—at least in principle—calculated, we are forced to use additional models to find out those parameters. We are convinced that both approaches, DFT and Green’s function method, are appropriate and, to a certain extent, are an alternative in describing many body systems.

2. Model and Green’s Functions

Magnetite Fe${}_3$O${}_4$ is a ferrimagnetic mineral with a Curie temperature of $T_C$ = 850 K [7]. Compounds with the structural formula Fe${}_3$O${}_4$ can crystallize in an inverse spinel crystal structure where the tetrahedral A sites are occupied by Fe${}^{3+}$-ions, and the octahedral B sites by an equal amount of Fe${}^{2+}$- and Fe${}^{3+}$-ions. The magnetic ions in the A and B sites interact through super-exchange interactions through an intermediate oxygen ion A-O-A, A-O-B and B-O-B, with the following relation of the exchange interaction constants: $\mid J_{A-B}\mid >\mid J_{B-B}\mid >>\mid J_{A-A}\mid$. The antiferromagnetic A-O-B interaction is the most important for the cooperative behaviour of the magnetic moments in ferrites and is of greatest intensity [16,17]. In the A and B sublattices, the exchange interactions are ferromagnetic.

By doping with RE ions, whose radius is larger than that of the iron ions (for example Gd${}^{3+}$), they can only substitute ions at the octahedral sites. The exchange interaction between the spins of the RE and the Fe ion is mediated by a nonmagnetic oxygen ion and preserves the interaction character between the tetrahedral and octahedral sites, i.e., antiferromagnetic collinear.

The Hamiltonian, which describes the behavior of the spin subsystem of pure and Gd${}^{+3}$-doped Fe${}_3$O${}_4$, is the modified Heisenberg one:

$$\begin{array}{ccc}\hfill H_s& =& -(1-x)\sum _{ij}{J}_{ij}^{FeA-FeB}{\mathbf{S}}_i^{FeA}·{\mathbf{S}}_j^{FeB}-(1-x)\sum _{ij}{J}_{ij}^{FeB-FeB}{\mathbf{S}}_i^{FeB}·{\mathbf{S}}_j^{FeB}\hfill \\ & -& x\sum _{ij}{J}_{ij}^{FeA-GdB}{\mathbf{S}}_i^{FeA}·{\mathbf{S}}_j^{GdB}-x\sum _{ij}{J}_{ij}^{FeB-GdB}{\mathbf{S}}_i^{FeB}·{\mathbf{S}}_j^{GdB}\hfill \\ & -& \sum _i{D}_i^{FeA}{\left(S_i^{FeAz}\right)}^2-(1-x)\sum _i{D}_i^{FeB}{\left(S_i^{FeBz}\right)}^2-x\sum _i{D}_i^{GdB}{\left(S_i^{FeAz}\right)}^2\hfill \\ & -& g{\mu }_B\mathbf{h}·\sum _i{\mathbf{S}}_i^{FeA}-(1-x)g{\mu }_B\mathbf{h}·\sum _i{\mathbf{S}}_i^{FeB}-xg{\mu }_B\mathbf{h}·\sum _i{\mathbf{S}}_i^{GdB}\hfill \end{array}$$

(1)

where ${\mathbf{S}}_i^{X\alpha }$ ($\alpha$ = A-, B-sublattices and X = Fe, Gd) is the Heisenberg spin operator at i-site. $J_{ij}^{FeA-FeB}$, $J_{ij}^{FeB-FeB}$, $J_{ij}^{FeA-GdB}$, $J_{ij}^{FeB-GdB}$ are the exchange interaction constants between the A-B and B-B magnetic ions at the i and j sites. $D_i^{X\alpha }$ are the constants of the single-ion anisotropy, $\mathbf{h}$ is a magnetic field along the z-axis, which is also the axis of the easy magnetization, x is the Gd doping concentration.

The Hamiltonian of the magnetic system is built under the following assumptions:

• The Gd${}^{3+}$-ions substitute only the Fe${}^{2+}$-ions at the octahedral sites (B-sublattice). The tetrahedral sites have a volume smaller than the octahedral ones and the radius of the Gd${}^{3+}$-ions (1.07 $\dot{A}$) is larger than that of the Fe${}^{2+}$-ions (0.70 $\dot{A}$). Thus, the structural formula of the doped magnetite with Gd ions is as follows: [Fe${}_A^{3+}$][Fe${}_{1-x}^{2+}$Gd${}_x^{3+}$Fe${}^{3+}{]}_B$O${}_4$. This is valid for Gd concentrations up to x = 0.5. This is the concentration range in which the magnetic phase transition temperature in doped magnetite is biocompatible in the sense for medical applications. Above these concentrations, the Gd${}^{3+}$ ions replace the Fe${}^{3+}$ ions in the tetrahedral sites [13].
• The magnetic interaction between the magnetic ions in the tetrahedral sites (A-O-A) is neglected because it is shown experimentally to be 10 times smaller compared to the other interactions B-O-B and A-O-B [16].
• The substitution of the Fe-ion by the RE Gd${}^{3+}$-ion (B-sublattice) does not lead to a change in the interaction character of the Fe-ions between the A- and B-sublattices. This assumption is related to the fact that the antiferromagnetic nature of the interaction between octahedral and tetrahedral sites is preserved and makes possible the use of the Neel model for antiferromagnetism.

For the magnetite, a strong-spin phonon interaction has been demonstrated [18], which, from the microscopic point of view, renormalizes the magnetic exchange interactions. This is taken into account with the following Hamiltonian:

$$H_{sp}=-\frac{1}{2}\sum _{i,j,k}F(i,j,k)Q_i{S}_j^{X\alpha z}{S}_k^{X\alpha z}-\frac{1}{4}\sum _{i,j,k,l}R(i,j,k,l)Q_i{Q}_j{S}_k^{X\alpha z}{S}_l^{X\alpha z}+h.c.$$

(2)

where $F_{ijk}$ and $R_{ijkl}$ are the spin-dependent lattice vibration constants, which are the first and second derivatives of the exchange interaction constants in relation to the phonon displacements, respectively. $Q_i$ is the normal coordinate of the lattice mode.

The spontaneous magnetization $M_s$ of the Gd-doped Fe${}_3$O${}_4$ is

$$M_s=\mid M_A-M_B\mid .$$

(3)

$M_A$ and $M_B$ are the magnetizations of the two sublattices:

$$M_A=M^{FeA};M_B=(1-x)M^{FeB}+x{M}^{GdB},$$

(4)

where $M^{X\alpha }=(1/N){\sum }_i\langle {\left(S_i^{X\alpha }\right)}^z\rangle$ with X = Fe, Gd and $\alpha$ = A, B.

$\langle {\left(S_i^{X\alpha }\right)}^z\rangle$ is determined from the following expression:

$$\langle {\left(S_i^{X\alpha }\right)}^z\rangle =\left[(S^{X\alpha }+0.5)coth\left[(S^{X\alpha }+0.5)\beta E_i^{X\alpha }\right]-0.5coth\left(0.5\beta E_i^{X\alpha }\right)\right],$$

(5)

where $\beta =\frac{1}{k_{B}T}$ and $E_i^{X\alpha }=(1/N^{\alpha }){\sum }_j{E}_{ij}^{X\alpha }$. $E_{ij}$ is the excitation energy observed from the poles of the following Green’s functions:

$$\langle \langle S_i^{FeA+};S_j^{FeB-}\rangle \rangle ;\langle \langle S_i^{FeB+};S_j^{FeA-}\rangle \rangle ;\langle \langle S_i^{GdB+};S_j^{FeA-}\rangle \rangle ;\langle \langle S_i^{FeA+};S_j^{GdB-}\rangle \rangle ;$$

$$\langle \langle S_i^{FeB+};S_j^{GdB-}\rangle \rangle ;\langle \langle S_i^{GdB+};S_j^{FeB-}\rangle \rangle ;\langle \langle S_i^{FeA+};S_j^{FeA-}\rangle \rangle ;\langle \langle S_i^{FeB+};S_j^{FeB-}\rangle \rangle ,$$

where the operators $S_i^{X{\alpha }_{\pm }}$ are determined from the following expression: ${\left(S_i^{X\alpha }\right)}^{\pm }={\left(S_i^{X\alpha }\right)}^x\pm i{\left(S_i^{X\alpha }\right)}^y$.

The spin-phonon interaction is observed within the mean field approximation. This leads to a renormalization of the exchange interactions in the system making them temperature dependent $J_{eff}=J+2F^2/({\omega }_0-R{M}_s)$ where ${\omega }_0$ is the harmonic frequency of the polar lattice mode and J is a formal denotation for all exchange interaction constants.

As mentioned in the Introduction, by doping the magnetite with RE ions, the band gap width increases. The band gap width in Fe${}_3$O${}_4$ defines the latter as a semiconductor, which makes these oxide NPs suitable for optical sensors. The changes in the magnetic characteristics caused by the Gd doping will cause changes in the band structure and the width of the band gap. We will account for this influence by including in the Hamiltonian of the system the interaction I between the localized spins and conduction ones at the i site, i.e., the s-d model:

$$H_{s-d}=\sum _{i}I{\mathbf{S}}_i^{X\alpha }·{\mathbf{s}}_i,$$

(6)

where ${\mathbf{s}}_i$ are the spin operators of the conduction electrons.

Then, we can define the band gap energy $E_g$ as the difference between the valence and conduction bands:

$$E_g={\xi }^{+}(\mathbf{k}=0)-{\xi }^{-}(\mathbf{k}={\mathbf{k}}_{\sigma })$$

(7)

with the electronic energies

$${\xi }^{\pm }\left(k\right)={ϵ}_k-0.5\sigma I{M}_s$$

(8)

which are observed from the Green’s functions [19] $g\left(\mathbf{k}\sigma \right)=\ll c_{k\sigma };c_{k\sigma }^{+}\gg$, $\sigma =\pm 1$ where $c_{i\sigma }^{+}$ and $c_{i\sigma }$ are Fermi-creation and -annihilation operators.

3. Results and Discussion

In the numerical calculations, we will use a model of a spherical, cubooctahedral, structurally heterogeneous NP composed of core and surface shell. A nanoparticle is defined by fixing the origin at a certain Fe spin in the center of the particle and including all spins within the particle into shells numbered by $n=1,$...$,N$, where $n=1$ is the central spin and $n=N$—the surface shell. In our case, the the NPs offer an icosahedral symmetry, i.e., there are 12 spherical particles in the first shell, 42 in the second shell, 92 ones in the third shell, etc.

The exchange interaction $J_{ij}\equiv J(r_i-r_j)$ depends inversely on the lattice parameters. The surface effects are included by the exchange interaction constant on the surface layer $J_s$, which is different from the bulk one $J_b$. The indices s and b are used for all model parameters.

The calculations are made for non-interacting NPs with a diameter below 80 nm. The reason is that the dipole-dipole interaction between magnetic NPs is important. It modifies their magnetic anisotropy, which will affect the magnetic characteristics of the latter. The dipole-dipole interaction itself depends on the geometrical arrangement of particles. The inclusion of this effect, in our opinion, would lead to further complication from a theoretical point of view without significantly modifying the qualitative picture of the described processes.

Since the magnetite is an inverse spinel, the super-exchange interaction between the magnetic A- and B-sublattices is antiferromagnetic. This is the most intense interaction compared to the others, so that it practically determines the magnetic structure of Fe${}_3$O${}_4$. The interaction in the sublattices is ferromagnetic. As we mentioned in the introduction, the interaction between the magnetic moments in the tetrahedral sites is weakest and will be neglected. For the exchange interaction constants, we will use the following values: $J^{FeB-FeB}$ = 7.31 K, $J^{FeA-FeB}$ = −33.9 K, $J^{FeA-FeA}$ = 0 [20]. By doping, the Gd${}^{3+}$ ions substitute the Fe${}^{2+}$ ions from the octahedral sites. If we assume that the interaction between the spins of the Gd${}^{3+}$ ions with the Fe${}^{3+}$ ions in the octahedral sites is ferromagnetic and taking into account the inequality S(Gd${}^{3+}$) = 7/2$>$S(Fe${}^{2+}$) = 2, then the saturation magnetization should increase with increasing the doping concentration. However, experimental results show that for $0<x<0.5$ the saturation magnetization decreases [13]. This is only possible if $J^{FeB-GdB}$ is antiferromagnetic, i.e., $J^{FeB-GdB}<0$. Such an antiferromagnetic interaction has also been reported in Gd-Fe alloys [21] and, following the method of determining the exchange interaction between Gd and Fe ions in the same paper, we obtain $J^{FeB-GdB}$ = −2.28 K. For the interaction between the spins of the Gd ions at the octahedral sites and the spins of the iron ions at the tetrahedral sites, we will assume that it is also antiferromagnetic, but weaker than $J^{FeA-FeB}$ because as the ion doping increases, the magnetic phase transition temperature strongly decreases. This could be due to the weaker overlap of the 4f orbitals and the p ones of the oxygen anion acting as a mediator in the double-exchange interaction. Based on these results for the numerical value of $J^{FeA-GdB}$, we get the following: $J^{FeA-GdB}$ = −10.5 K. Let us emphasize that we investigate small doping concentrations so we can neglect the interaction between the Gd ions in the octahedral sites, i.e., $J^{GdB-GdB}$ = 0 K. From experimental data [18] for the spin-phonon interaction constants, we get the following: F = 27.3 K and R = −23.5 K. For the single ion anisotropy constant D, we use for the bulk compound $D^{Fe}$ (bulk) = −0.87 K [22]; whereas for single domain NPs for the surface anisotropy, we use $D^{Fe}$ (surface) = −0.28 K [23]. RE ions have a large value of single-ion magnetic anisotropy; therefore, we will assume a value of one order of magnitude larger compared to that of the iron ions $D^{Gd}$ = 8.7 K. By the numerical calculations of the NPs we will consider a core with microscopic parameters such as bulk material. The shell has changed parameters due to the interrupted translational invariance, uncompensated bonds and oxidation. With the index “s”, we will denote the interactions on the surface while with “b” in the volume. As for the decrease of the NP size in the pure magnetite, a reduction of the phase transition temperature is observed. We believe that the following relation between the surface and bulk exchange interaction constants hold true for all exchange interactions: $J_s<J_b$.

The NP is composed of shells, with each subsequent shell containing an increasing number of atoms. The model is constructed from cubooctahedra or truncated octahedra with a tightly packed cubic crystal structure [24]. The first built shell is composed of equilateral triangles. In the subsequent shells, cubooctahedrons appear, which are surrounded by triangular and square walls. The NP is defined fixing the origin in an arbitrary spin at the centre of the particle and arranging all the remaining spins in the particle on shells [25]. The shells are denoted by n = 0.1, …, N, where n = 0 denotes the central spin and $n=N$ represents the surface shell of the NP.

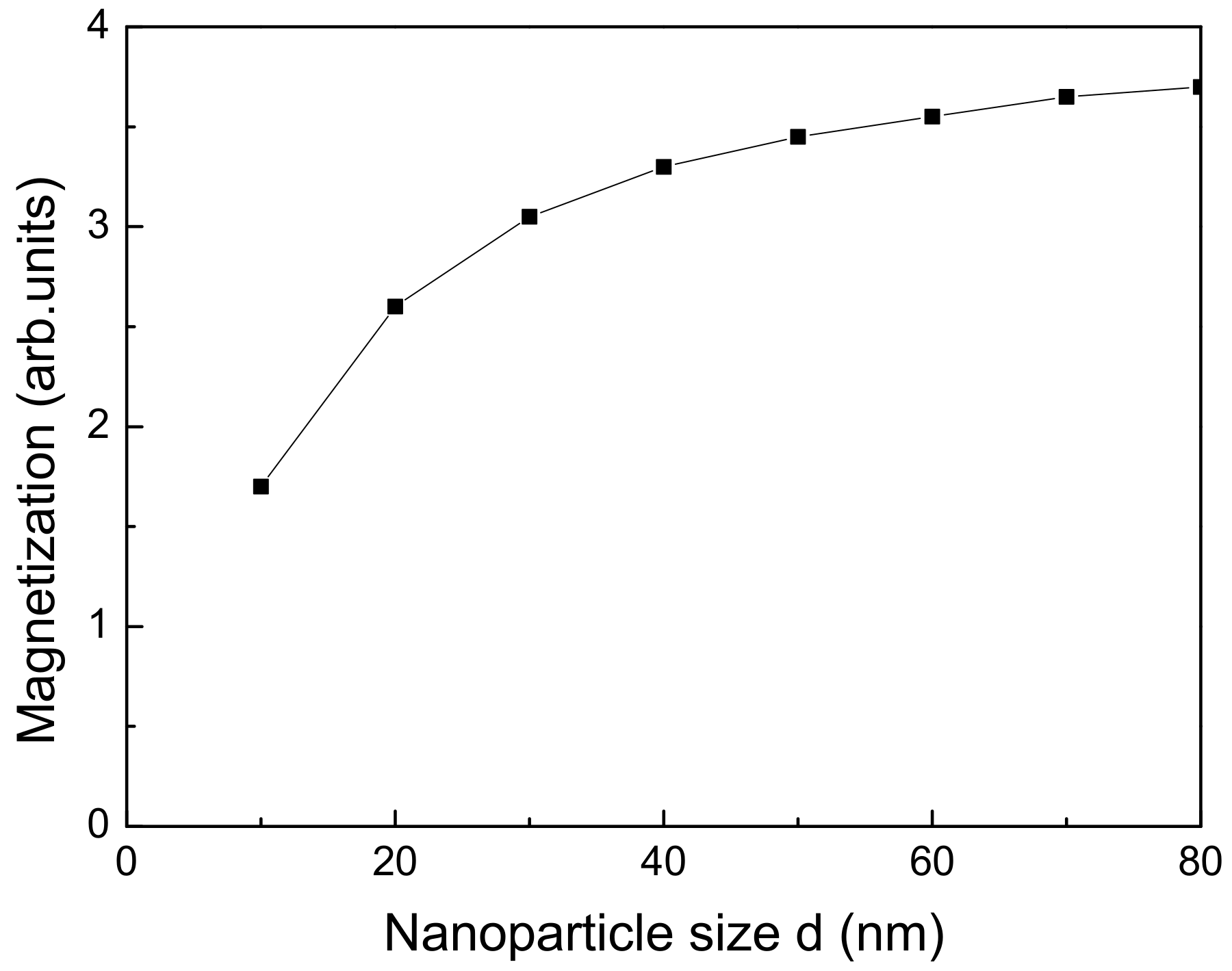
3.1. Size Dependence of the Magnetization and Curie Temperature

At first, we will present numerical calculations of the dependence of the spontaneous magnetization $M_s$ and the magnetic phase transition temperature $T_C$ on the size of Fe${}_3$O${}_4$ NPs. Let us emphasize that the lattice parameters of the NPs increases slightly compared to the bulk value [26].

The results are presented in Figure 1 and Figure 2. With a decrease of the size of the NP, $M_s$ and $T_C$ decrease. A similar decrease of $M_s$ in Fe${}_3$O${}_4$ NPs is observed experimentally by Mohapatra et al. [27]. Let us emphasize that $M_s$ decreases with increasing temperature and vanishes at $T_C$. Moreover, $M_s$ and $T_C$ depend on the spin value S and the exchange interaction constants $J_s$ and $J_b$. A similar effect, a decrease with decreasing d, is observed also for the Curie temperature $T_C$ (see Figure 2). We obtain $T_C$ ≈ 690 K for d = 20 nm and $T_C$ ≈ 600 K for d = 10 nm. The decrease is due to size and surface effects becoming predominant as the ratio surface to core volume increases. Below d = 10 nm, we have a superparamagnetism. It must be mentioned that Mohapatra et al. [27] obtained a $T_C$ value of 665 K for d = 10 nm for Fe${}_3$O${}_4$ NPs, whereas Manohar et al. [28] reported $T_C$ = 713 K for d = 12 nm. Using Monte Carlo simulation, Maazouzi et al. [20] calculated for thin magnetite films a $T_C$ increase with increasing film thickness.

Qualitatively, these results can be explained as follows: with decreasing the NP size, the surface area/volume ratio increases, i.e., the influence of the surface on the structural and magnetic characteristics increases. The oxidation, broken bonds at the surface, unpaired electron orbitals, and increased surface anharmonism lead to reduction of the net magnetic moment. Therefore, as the influence of the surface grows (i.e., the diameter of the magnetic NP decreases), the total magnetization become smaller. The decrease of the phase transition temperature with size reduction of the NP can be qualitatively explained by the fact that, with decreasing the size, the volume of the elementary cell increases, which leads to an increase in the distance between the spins. To the extent that the exchange interaction is highly sensitive to the distance between the interacting magnetic ions, this will lead to a decrease of the exchange interaction in the shell and at the surface of the magnetic NP and to a reduction of $T_C$. The observed qualitative coincidence with the experimental results is evidence that the presented microscopic model of magnetic NPs adequately represents and explains the main magnetic characteristics of Fe${}_3$O${}_4$ NP and their dependence on surface and size effects.

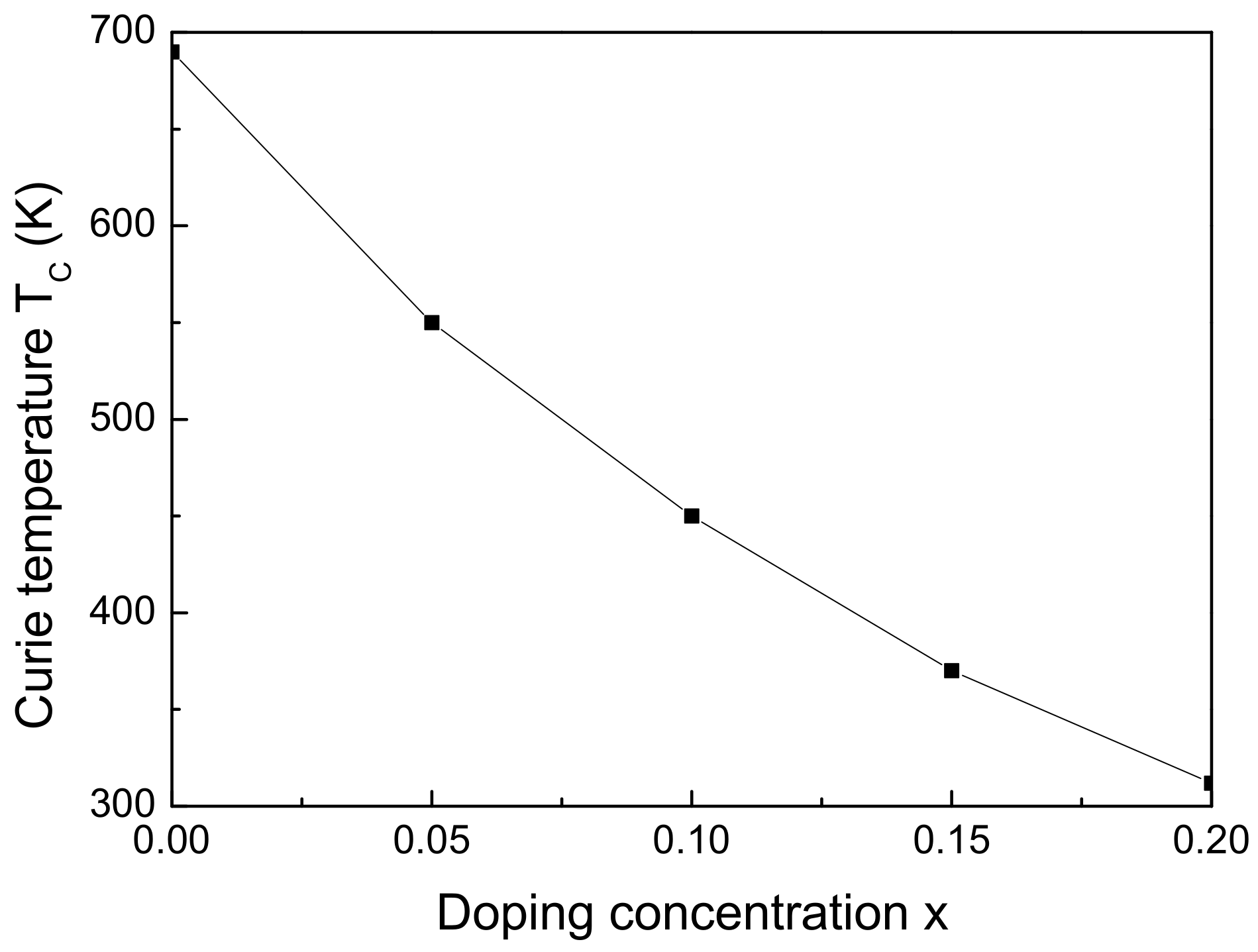
3.2. Gd Doping Dependence of the Magnetization and Curie Temperature

Next, we will study the influence of RE ion doping on the spontaneous magnetization $M_s$ and the Curie temperature $T_C$. It must be mentioned that the Gd ions substitute the Fe ions in the whole NP, in the surface shell and in the bulk, in the core. Moreover, due to the different ionic radii of the Gd and the Fe ions, there appear a strain which changes the interaction constants at the doped state noted as $J_d$ compared to the undoped one $J_b$. The results for Gd doping for $0\le x\le 0.2$ on the spontaneous magnetization $M_s$ and the Curie temperature $T_C$ are shown in Figure 3 and Figure 4, respectively. It is clearly seen that the Gd ion doping leads to decrease of $M_s$ and $T_C$. Zhang et al. [14] reported also a slightly decreased magnetization at 260 K in Gd-doped Fe${}_3$O${}_4$ NPs in contrast to the undoped ones. A similar decrease of $M_s$ is observed also in Ce [29] or Dy, Nd, La doped Fe${}_3$O${}_4$ NPs [12]. We observe for Gd-doped Fe${}_3$O${}_4$ NPs a $T_C$ value of 312 K for x = 0.2. Thorat et al. [30] and Sun et al. [31] have obtained also a decrease of the critical temperature $T_C$ of Gd-doped Fe${}_3$O${}_4$ NPs. Moreover, a decrease of the magnetic coercive field, the remanent magnetization and the Curie temperature with decreasing the thickness of a Fe${}_3$O${}_4$ thin film is reported recently by Maazouzi et al. [20].

The decrease of the magnetization and magnetic phase transition temperature with doping qualitatively is explained as follows: The larger ionic radius of Gd${}^{3+}$ compared to the Fe${}^{2+}$ radius leads to an increase in the volume of the elementary cell. As a consequence, the distance between the interacting magnetic moments increases, which leads to a decrease in the exchange interaction constants and to a decrease of $T_C$. Although the net magnetic moment of the Gd ion (7${\mu }_B$) is larger compared with that of the Fe${}^{2+}$ ion (5${\mu }_B$), $M_s$ and the saturation magnetization decrease. This is a consequence of the antiferromagnetic arrangement of the Gd and Fe spins at the octahedral sites. The interaction between the magnetic moments of the RE and the Fe${}^{3+}$ ions in the tetrahedral sites is antiferromagnetic, which means that, in the A sublattice, antiparallel iron spins will appear, leading to an additional reduction of $M_s$ and the saturation magnetization. Speculation suggests that competing magnetic interactions arise due to Gd doping, leading to magnetic system frustration and the potential emergence of non-collinear structures. However, there is a lack of experimental results either confirming or refuting this hypothesis.

Let us emphasize that Daoush [9] have studied Co-doped Fe${}_3$O${}_4$ NPs with d ≈ 30 nm and reported a decrease of $M_s$ and $T_C$. This result can be confirmed from our model. The ionic radius of Co is larger compared to that of the Fe ion, i.e., the tensile strain that appears leads to a decrease of the magnetization and the Curie temperature. The transition metal ion-doped Fe${}_3$O${}_4$ NPs will be investigated in a future paper.

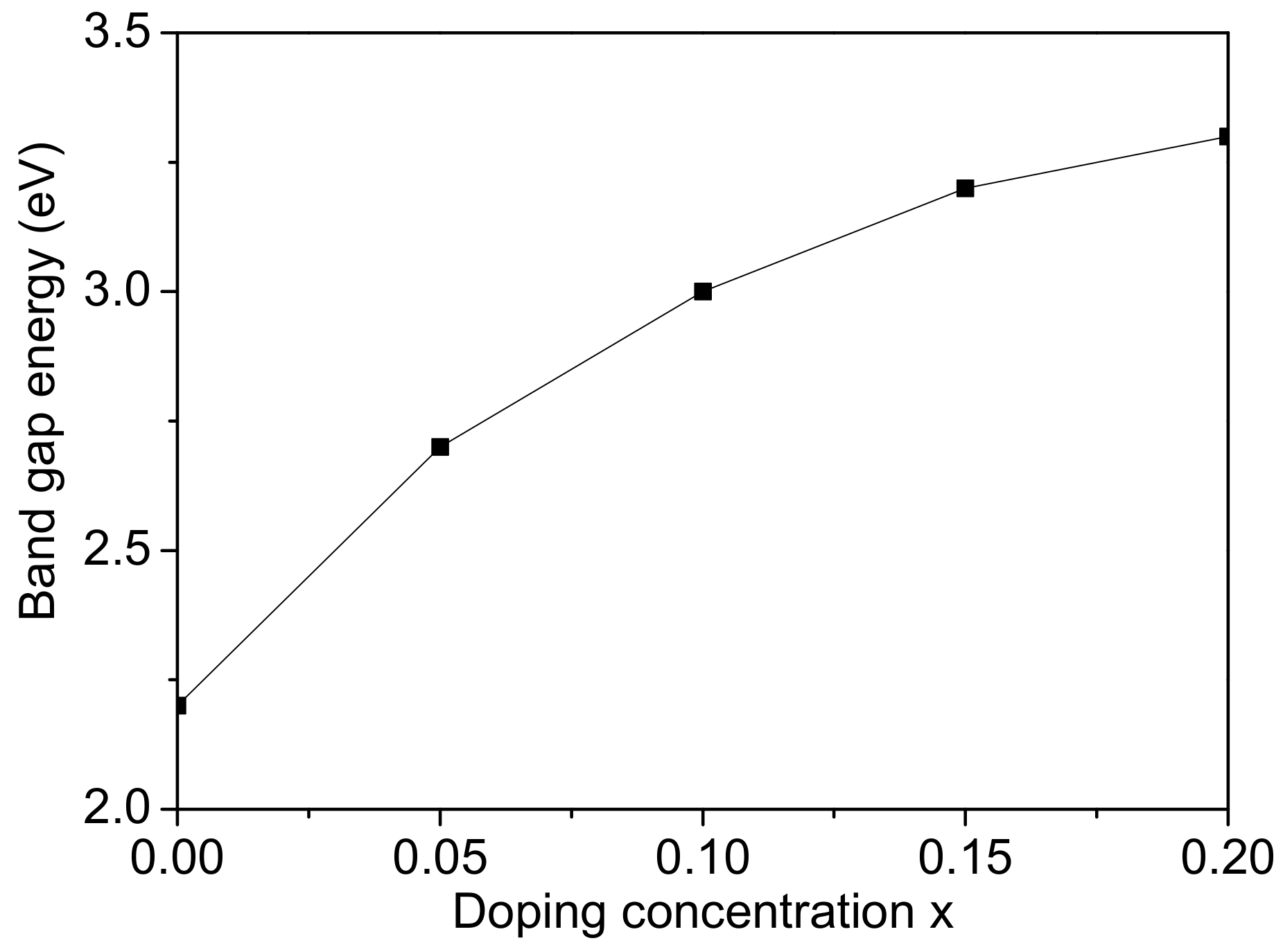
3.3. Size and Gd Doping Effects on the Band Gap

Finally, we studied the band gap energy $E_g$ of Fe${}_3$O${}_4$ NPs as a function of size and ion doping. Radon et al. [32] reported that, with decrease in the crystallite size, the optical band gap energy $E_g$ increases. The result for the band gap width $E_g$ of Gd-doped Fe${}_3$O${}_4$ NPs is presented in Figure 5. We find a blue shift for $E_g$ with increasing the doping with RE ions. The direct optical band gap $E_g$ of pure Fe${}_3$O${}_4$ NPs is around 2.2 eV [12], which may vary with particle size, composition and structure. We observe that $E_g$ for a pure Fe${}_3$O${}_4$ NP is slightly larger than that of a bulk one (2.0 eV [12]), which is related to surface effects (not shown here).

The band gap energy $E_g$ is enhanced with increasing Gd dopants due to the tensile strain which appears by the ion doping. As we discussed in Section 3.1, the growth of the crystal lattice volume and the appearance of an antiferromagnetic ordering between the spins of Gd and Fe in the octahedral sites reduces the spontaneous magnetization $M_s$ for small doping concentration x (see Figure 3). Then, it is clear from Equation (8) that, with increasing x, the band width $E_g$ increases.

Our model could explain also the enhanced band gap energy by doping with other RE ions, as experimentally found by Kershi et al. [12] for Dy, Nd, La doped Fe${}_3$O${}_4$ NPs. The RE ions have, similar to that of the Gd ion, an ionic radius larger than that of the Fe ion, but they have no biological role.

4. Conclusions

Based on a microscopic model and the method of the Green’s functions, this article presents analytical and numerical calculations of the magnetic and optical properties of a pure and Gd${}^{3+}$-doped magnetite NP with the chemical formula Fe${}_3$O${}_4$. The investigations were carried out under the assumptions that the sample of [Fe${}_A^{3+}$][Fe${}_{1-x}^{2+}$Gd${}_x^{3+}$Fe${}^{3+}{]}_B$O${}_4$ NP is monodisperse and there is not interaction between the NPs.

The magnetization $M_s$ and the Curie temperature $T_C$ are calculated depending on size, temperature, and Gd doping concentration. In qualitative agreement with the experimental data, we observe that $M_s$ and $T_C$ decrease with decreasing NP size and with increasing Gd doping concentration. The band gap energy $E_g$ increases with decreasing NP size and Gd dopants.