A General Analytical Solution for Two-Dimensional Columnar Crystal Growth during Laser Beam Welding of Thin Steel Sheets

Abstract

A technique for calculating the main solidification parameters for a two-dimensional columnar crystal growth during complete penetration laser beam welding of thin steel sheets was developed. Given that the weld pool interface is described by Lamé curves (superellipses) within the horizontal plane of growth, general analytical solutions were derived for the geometry of the crystal axis and the corresponding growth rate and cross-sectional area of the crystal. A dimensionless analysis was performed to provide insights on the dependence of the solidification parameters on the shape and dimensions of the rear part of the weld pool boundary. The derived solutions were applied for the case of complete penetration laser beam keyhole welding of 2 mm thick 316L austenitic chromium-nickel steel sheets. It was shown that the reconstruction of the weld pool boundary with Lamé curves provides higher accuracy and flexibility compared to results obtained with elliptical functions. The validity of the proposed technique and the derived analytical solutions was backed up by a comparison of the obtained solutions to known analytical solutions and experimentally determined shapes and sizes of the crystals on the top surface of the sheet. The dimensions of the calculated crystal axis correlated well with the experimentally obtained results.

1. Introduction

The solidification morphology of the liquid metal in the weld pool can be adequately described by three parameters: the crystal axis, the growth rate, and the cross-sectional area of the crystal. These three parameters determine some of the most important properties of the weld metal, such as its primary microstructure and strength. For example, the orientation of the crystal axis near the weld centerline influences the susceptibility to hot cracking to a large extent. On the other hand, the rate of crystallization and the temperature gradient determine the crystallization mode [1,2,3].

The solidification process in welding is extremely complicated as it depends on many factors such as the weld pool shape, the local temperature field and chemical composition (impurity concentration), the crystallographic orientation of the crystals, etc. [1,2,4,5,6,7]. Despite the fact that mathematical methods have been used to model and analyze the crystallization of the weld metal for more than 50 years, see, e.g., [4,7,8,9,10,11], the dependence of the crystallization parameters on the complex weld pool shape has not been studied sufficiently and no general solution has been obtained so far [4,8,9]. Thereby, two of the main difficulties are the determination of the weld pool boundary, especially when more complex weld pool shapes are formed, see, e.g., [12,13], and its precise mathematical description [9,14,15]. Furthermore, to provide a generalized analysis of the trajectory of the crystal axis and the corresponding growth rate and cross-sectional area, the solution should be obtained in the form of analytical expressions [4,8,9], which remains a non-trivial task to this day. To the best of the authors’ knowledge, most of the available literature deals with numerical algorithms, see, e.g., [10,11], and only a few analytical solutions have been obtained [4,9]. Nonetheless, these solutions are limited to a specific group of weld pool shapes and thus do not represent a general solution of the solidification problem, allowing consideration of any dimensions and shape of the weld pool boundary.

In recent years, however, a new algorithm providing a time and calibration efficient way to reconstruct the weld pool boundary by local Lamé curves, well known as superellipses, was developed [15]. By making use of this algorithm, an analytical equation can be constructed that can describe any weld pool shape, thus allowing further attempts at a generalized analysis of the solidification process.

The present work aims to obtain a general solution for the most important parameters of the crystallization process, namely the crystal axis, the growth rate, and the cross-sectional area of the crystal, in the case of two-dimensional columnar crystal growth during complete penetration laser beam keyhole welding of thin steel sheets. In addition, the dependence of the solidification parameters on the shape and dimensions of the rear part of the weld pool boundary is studied by dimensionless analysis. Thereby, the weld pool boundary is assumed to be known, either obtained from experiments or as the solution of the corresponding thermo-fluid dynamics problem and described by analytical expressions. The validity of the proposed technique and the derived analytical solutions is demonstrated in examples of laser beam welding of 2 mm thick 316L austenitic chromium-nickel steel sheets considering complete penetration laser beam keyhole welding. The derived analytical solutions are compared to known analytical solutions and experimentally determined the shape and size of the crystals on the top surface of the steel sheet.

2. Materials and Methods

Given the complex nature of the solidification process, it is inevitable to simplify its mathematical description to the most influential effects. Therefore, the derivation of the analytical expressions and all corresponding calculations are based on the following assumptions, simplifications, and methods:

• The dimensions of the weld pool boundary change only to a minor extent along the thickness, which is the case when welding thin plates in complete penetration keyhole mode. Thus, the crystallization problem becomes two-dimensional, i.e., the crystals do not grow in the thickness direction.
• The crystallization process reaches a steady state, i.e., the shape and size of the weld pool boundary do not vary with time.
• The weld pool boundary is not affected by the increasing impurity concentration ahead of the solid–liquid interface. Furthermore, the boundary is defined by the isosurface of the liquidus temperature, $T_{\mathrm{liq}}$.
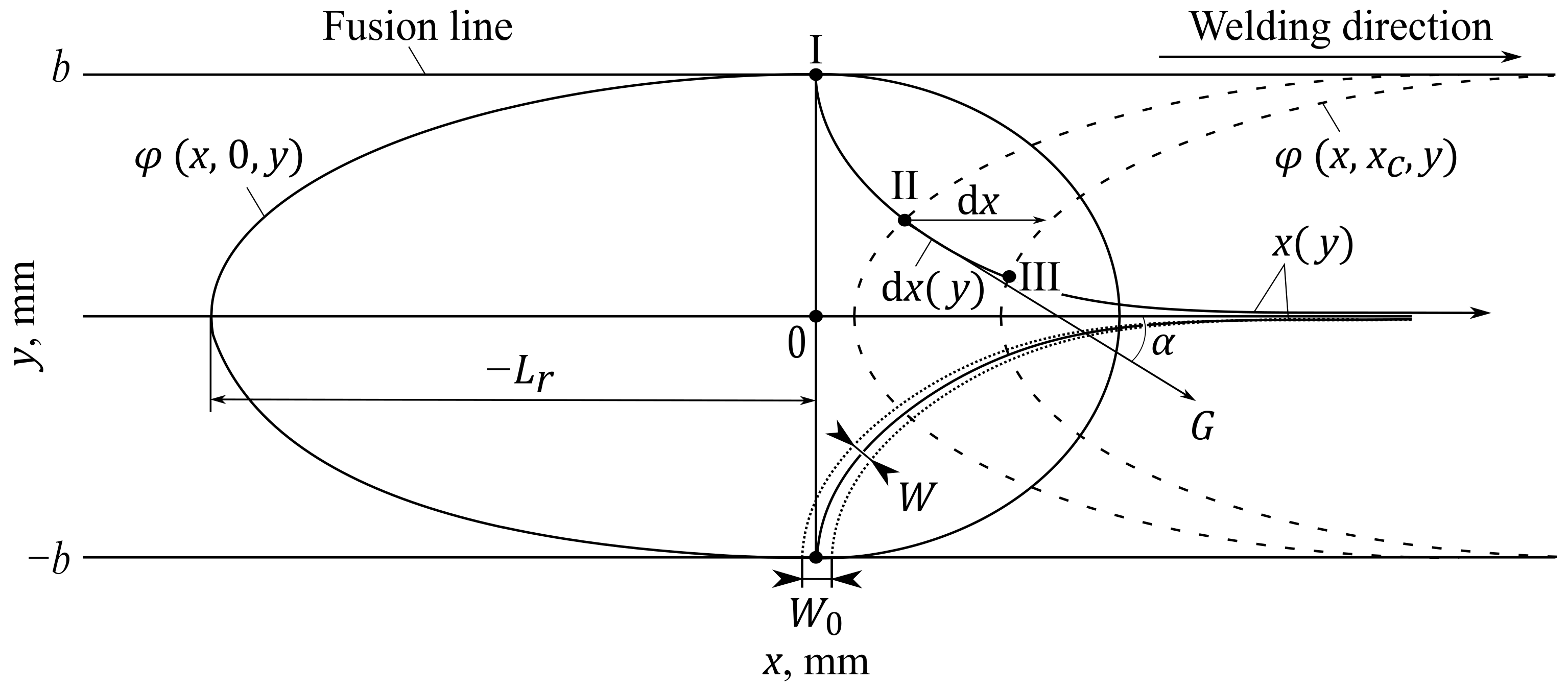
• The weld pool boundary, obtained experimentally or from a thermo-fluid dynamics simulation, is mathematically reconstructed with Lamé curves according to [15].
• The formation of substructures, e.g., planar, cellular, or dendritic, inside the crystals is not taken into account as it has a rather insignificant effect on the macroscopic crystal structure in polycrystalline materials [2].
• The crystallographic orientation and competitive growth are neglected as their consideration would significantly complicate the task [7,16]. As a consequence, the crystal is assumed to grow along the temperature gradient which coincides with the inward normal direction to the crystallization front [4,7,8,9].

The technique proposed in this paper refers to previously developed concepts for the analysis of the crystallization process; however, these concepts were based on elliptical functions and thus limited the analysis to weld pool boundaries of certain shapes, see, e.g., [4,5,6,8].

The crystal axis, $x\left(y\right)$, crystal growth rate, R, and crystal cross-sectional area (or width in the two-dimensional case), W, are uniquely determined by the shape of the rear part of the weld pool boundary, see Figure 1. According to the reconstruction technique of the weld pool boundary presented in [15] and the metallographic analysis from [4,17], the movement of the solidification front, i.e., the rear part of the weld pool boundary, can be precisely described by a set of shifted Lamé curves, as follows:

$$\phi \left(x,x_c,y\right)={\left(\frac{x-x_c}{L_r}\right)}^m+{\left(\frac{y}{b}\right)}^n-1=0,\mathrm{for}y\ge 0,x\le x_c,m>1,n>1.$$

(1)

Here $\phi$ represents the set of shifted Lamé curves in a coordinate system with origin at point 0, see Figure 1. x and y are the Cartesian coordinates; $x_c$ is the coordinate of the center of the shifted Lamé curve. Note that the shifting distance between the curves is denoted as $\mathrm{d}x$, and should not be confused with the function of the crystal axis, $x\left(y\right)$, derived below. $L_r$, b, m, and n are parameters of the Lamé curve, describing the rear part of the weld pool boundary. Thereby, $L_r$ and b are used to define the semi-major axes of the superellipses, i.e., the length and the half-width of the rear part of the weld pool; m and n determine the shape of the boundary and the corresponding condition in Equation (1) is required to ensure smoothness of the continuous functions reconstructing the complete weld pool boundary (front and rear part). Note, however, that since only solidification and not melting is considered in the present paper, there is no need to reconstruct the front part of the weld pool boundary. As seen in Figure 1, the crystal axis starts growing from point I, located on the weld pool boundary described by the curve $\phi \left(x,0,y\right)$. The crystal grows normally to the crystallization front, e.g., at point II, $\phi \left(x,x_c,y\right)$, the crystal grows along the inward normal of the boundary, i.e., along with the temperature gradient, G, at an angle $\alpha$ to the x-axis, as shown in Figure 1. To find the crystal axis equation as a function, $x\left(y\right)$, the theory of orthogonal trajectories can be applied, see [18]. Since the trajectory of the shifted Lamé curves and the trajectory of the crystal axis are orthogonal, the crystal axis equation can be found by solving the following partial differential equation:

$$\frac{\partial \phi }{\partial y}\mathrm{d}x=\frac{\partial \phi }{\partial x}\mathrm{d}y.$$

(2)

Finding the partial derivatives of Equation (1), substituting these into Equation (2), and rearranging the terms results in:

$$\mathrm{d}x=\frac{mb}{n{L}_r}{\left(1-{\left(\frac{y}{b}\right)}^n\right)}^{\frac{m-1}{m}}{\left(\frac{y}{b}\right)}^{1-n}\mathrm{d}y.$$

(3)

Taking the indefinite integrals on both sides of Equation (3) gives:

$$x\left(y\right)=\frac{m{b}^{\frac{n}{m}}}{n{L}_{\mathrm{r}}}\int {\left(b^n-y^n\right)}^{\frac{m-1}{m}}{y}^{1-n}\mathrm{d}y+const.$$

(4)

The constant in Equation (4) can be found by using the condition $x\left(y=b\right)=0$ and equals zero in the case of ellipse-shaped weld pool boundaries, i.e., using $m=n=2$ for the reconstruction procedure. Nonetheless, in the general case the constant is not zero. Using the condition given above the general columnar crystal axis equation is found:

$$x\left(y\right)=\frac{m{b}^n}{n\left(n-2\right)L_{\mathrm{r}}}\left({y^{2-n}}_2{F}_1\left(\frac{1}{m}-1,\frac{2}{n}-1;\frac{2}{n};{\left(\frac{y}{b}\right)}^n\right)\right.\left.{-b^{2-n}}_2{F}_1\left(\frac{1}{m}-1,\frac{2}{n}-1;\frac{2}{n};1\right)\right)$$

(5)

for $n\ne 2$; ${}_2{F}_1$ is the hypergeometric function [19].

To check the validity of the general solution for the columnar crystal axis, derived above, the known solution for weld pool boundaries with ellipse-shaped rear part, i.e., $m=n=2$, is compared to the solution obtained with Equation (5) for different m and n values. The solution for ellipse-shaped weld pool boundaries is derived in [9] and given as:

$$x\left(y\right)=\frac{b^2}{L_r}\left(\sqrt{1-{\left(\frac{y}{b}\right)}^2}-ln\left|\frac{{1+\left(1-{\left(\frac{y}{b}\right)}^2\right)}^{\frac{1}{2}}}{\frac{y}{b}}\right|\right).$$

(6)

The comparison of the results is shown in Figure 2. Because Equation (5) has a singularity at $n=2$, the results obtained with Equation (6) for $m=n=2$ are compared with the results obtained with Lamé curves for $m=2$ and $n=1.99$. As seen in Figure 2, the calculated crystal axes are nearly identical, at least from a practical point of view.

Furthermore, the shape parameters were slightly varied to demonstrate one of the biggest advantages of the proposed algorithm, namely its flexibility to account for weld pool boundaries of almost any shape, thus significantly improving the accuracy of subsequently calculated crystallization parameters such as the solidification rate. By making use of the solutions presented in Equations (5) and (6) the remaining crystallization parameters, the growth rate, $R\left(x\left(y\right)\right)$, and the cross-sectional area, W, of the columnar crystal, can be calculated as well. Thereby, the growth rate represents the change in the crystal length during an infinitesimal time interval $\mathrm{d}t$. Since $\mathrm{d}t$ can be determined by the shifting distance, $\mathrm{d}x$, see Figure 1, and the welding speed, $v_w$, $R\left(x\left(y\right)\right)$ can be defined using the following relationships:

$$R\left(x\left(y\right)\right)=\frac{\mathrm{d}x\left(y\right)}{\mathrm{d}t}=\frac{\mathrm{d}x\left(y\right)}{\frac{\mathrm{d}x}{\left|v_w\right|}}=\left|v_w\right|cos\alpha .$$

(7)

The value of $cos\alpha$ can be as well obtained using the crystal axis equations, Equation (5), giving:

$$cos\alpha ={\left(1+\left(\frac{\mathrm{d}x\left(y\right)}{\mathrm{d}y}\right)\right)}^{-1/2},$$

(8)

and thus, the final equation for the growth rate is expressed as:

$$R\left(x\left(y\right)\right)=\frac{\left|v_w\right|}{\sqrt{1+{\left(\frac{n{L}_r}{mb}\right)}^2{\left(1-{\left(\frac{y}{b}\right)}^n\right)}^{\frac{2-2m}{m}}{\left(\frac{y}{b}\right)}^{2n-2}}}.$$

(9)

The cross-sectional area of the crystal (or width in the two-dimensional case), W, is determined by using trigonometric relationships as well derived from Equation (5). Thereby, the cross-sectional area of the columnar crystal is uniquely defined by the shape of the crystal axis. As seen in Figure 1, it reduces as the crystal grows, at least for the particular example shown; the cross-sectional area can, however, also decrease during crystal growth, as it depends on the local curvature of the crystal axis. The cross-sectional area of the columnar crystal is defined as:

$$W=W_{0}sin\alpha =W_0\sqrt{1-{cos}^2\alpha },$$

(10)

where $W_0$ is the initial cross-sectional area at the beginning of the solidification process, located at the fusion line. This can be obtained experimentally from metallographic samples.

3. Results

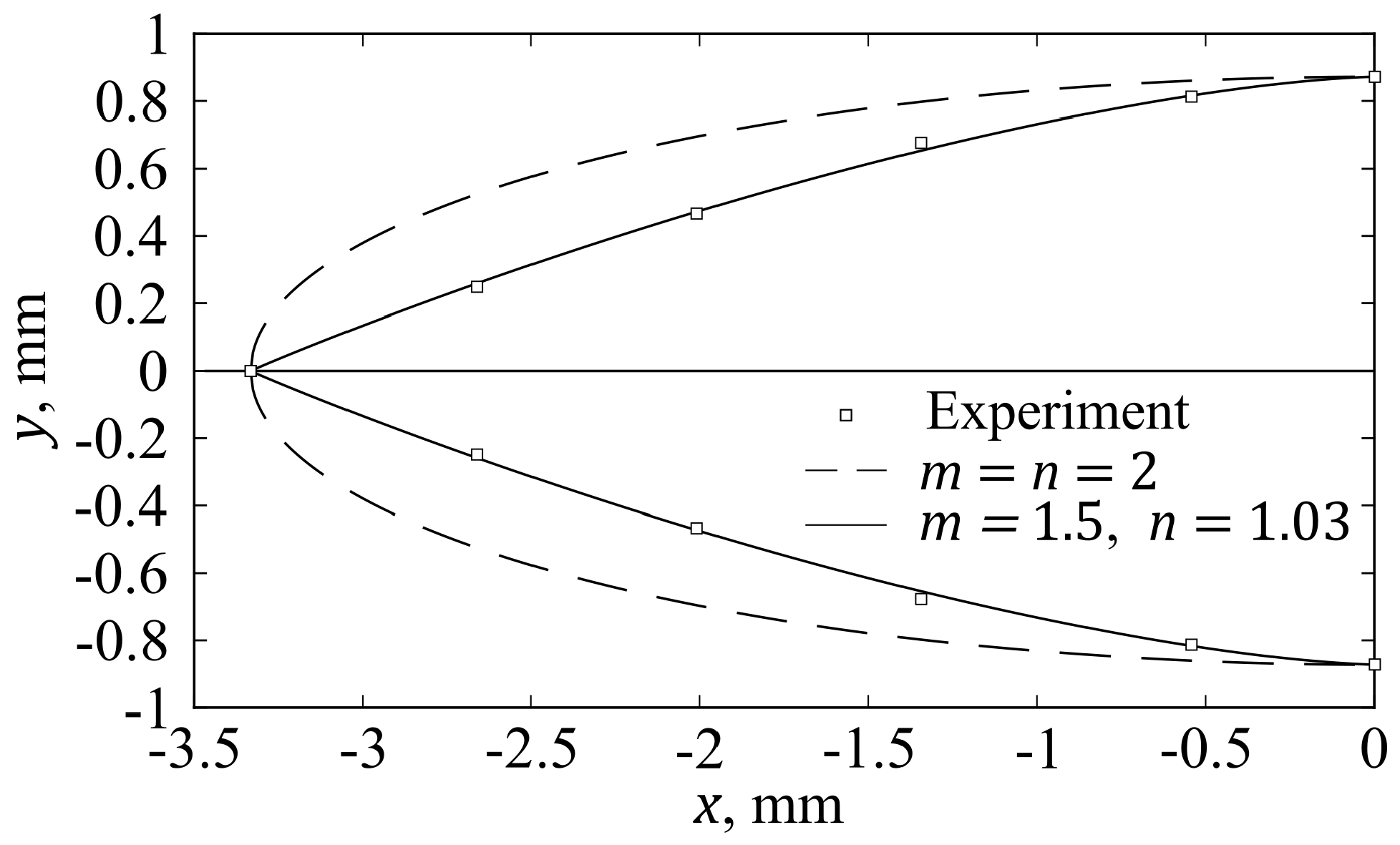
3.1. Experimental Validation

For the validation experiments, 2 mm thick 316L austenitic chromium-nickel steel sheets were used. The chemical composition of the material used was measured with spark optical emission spectroscopy and is given together with the corresponding standard DIN EN10088-3 [20] in

Table 1. Measured and standardized chemical composition of the austenitic 316L steel in wt.%.

	C	Cr	Ni	Fe
DIN EN 10088-3	≤0.03	16.5−18.5	10.0−13.0	bal.
Measured	0.03	16.95	10.57	bal.

. The steel sheet was bead-on-plate welded in complete penetration keyhole mode. The laser beam welding experiments were performed with a Trumpf 16002 laser system, using a laser power of 2.3 kW, a welding speed of 1.2 m/min, a focal diameter of $420 \mathsf{\mu }\mathrm{m}$, a focal position of 5 mm above the top surface of the steel sheet, and an Argon shielding gas with a flow rate of 50 L/min and a nozzle angle of 35°. Note that all measured data utilized to validate the derived equations for the three main crystallization parameters were performed according to the ISO/TS 18166:2016 standard providing a workflow for the execution, validation, verification, and documentation of a numerical welding simulation within the field of computational welding mechanics [21].

First, the assumption of a two-dimensional crystallization problem is verified by the weld seam width in the metallographic cross-section shown in Figure 3 (left). To obtain the metallographic samples, the specimen was first polished to obtain an even surface. The corresponding microstructure was then visualized in the cross-section and the horizontal section by using color etching according to Bloech and Wedl. As seen, the weld seam width is practically constant along the thickness of the steel sheet, i.e., parallel seam flanks, and differs only slightly with an averaged deviation of below 3%. For more details, see [22] as well. Hence, the solidification problem can be considered two-dimensional, and the derived equations, Equations (5)–(10), can be utilized for the analysis of the crystallization problem. Congruously, for the validation of the theoretical results, only experimental data obtained from the top surface of the sheet are needed. In Figure 3 (right), an exemplary metallographic horizontal section from the top surface of the welded sheets is shown. This was obtained by polishing and subsequent color etching according to [23]. As observed in the figure, there are several solidification lines, directly underneath the top surface, often referred to as ripples, highlighting the local weld pool boundary at the time of solidification. Using these ripples, the length and width of the rear part of the weld pool boundary can be estimated and thus reconstructed by elliptical functions or Lamé curves. Note as well that the weld pool shape on the top surface could be experimentally obtained using a high-speed camera during the process, see, e.g., [13], or by theoretical correction of the weld end crater dimensions [22,24]. For the sake of completeness, the rear part of the weld pool boundary is reconstructed using both methods. Thereby, the length and half-width of the weld pool rear part were kept constant with $L_{\mathrm{r}}=3.33$ mm and $b=0.87$ mm, respectively, but the values for m and n were varied to find an optimal parameter combination. The comparison of the obtained results is shown in Figure 4. It can be easily seen that the results obtained using ellipses, $m=n=2$, lead to a distorted weld pool boundary with quite a different radius of the curvature. This deviation in the weld pool shape will directly influence the calculation of the crystal axis, and thus, as explained above, the subsequently calculated growth rate and cross-sectional area of the columnar crystal. It becomes clear from the comparison of the reconstructed rear part of the weld pool boundary that the Lamé curves provide more flexibility and significantly improve the accuracy of the predicted crystallization parameters, thus allowing for a sufficient reconstruction of the weld pool boundary. This is confirmed by the comparison of the experimentally visualized crystals on the top surface of the 316L steel sheets and the calculated crystal axis, $x\left(y\right)$, highlighted in white color in Figure 3 (right).

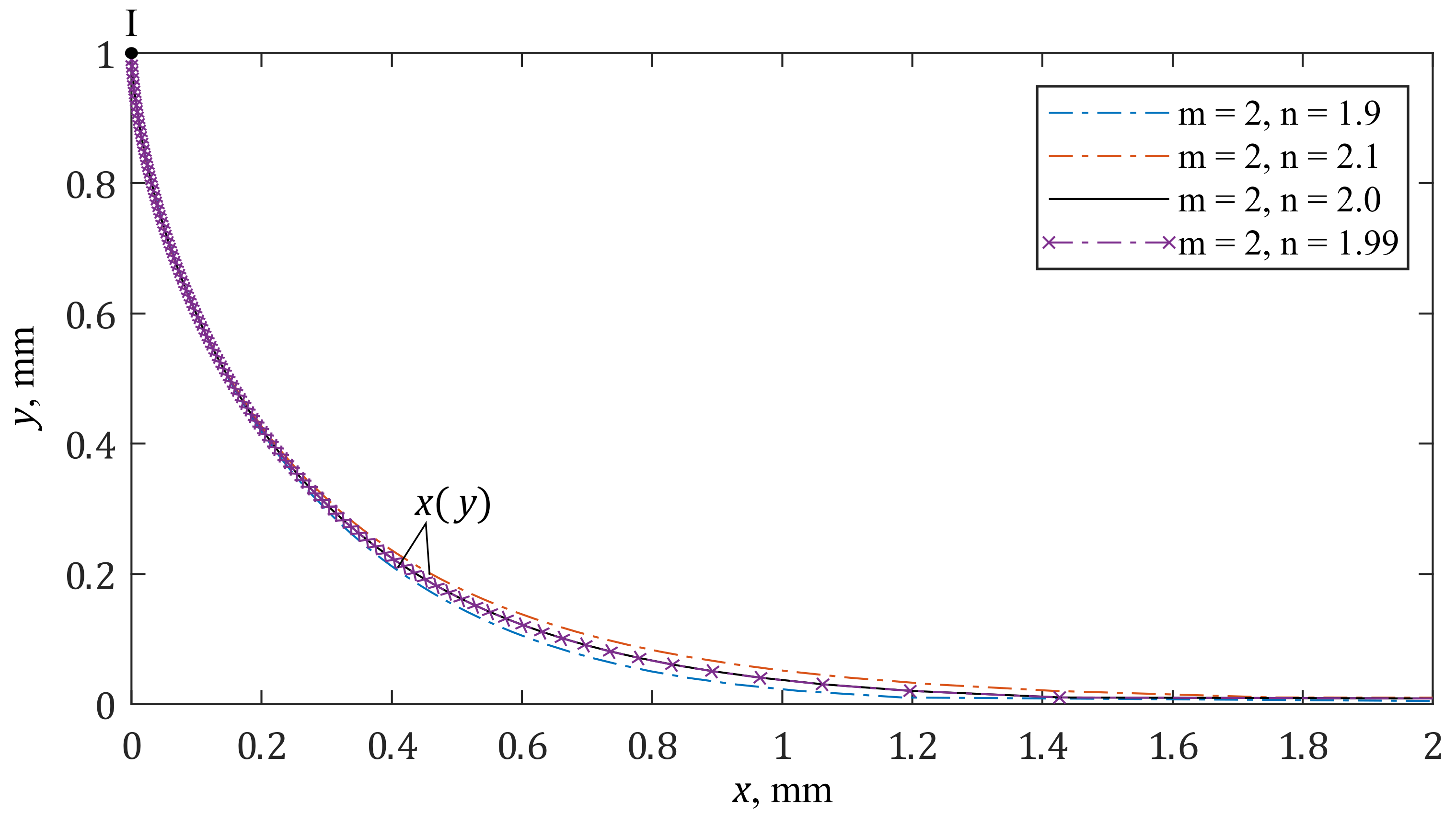
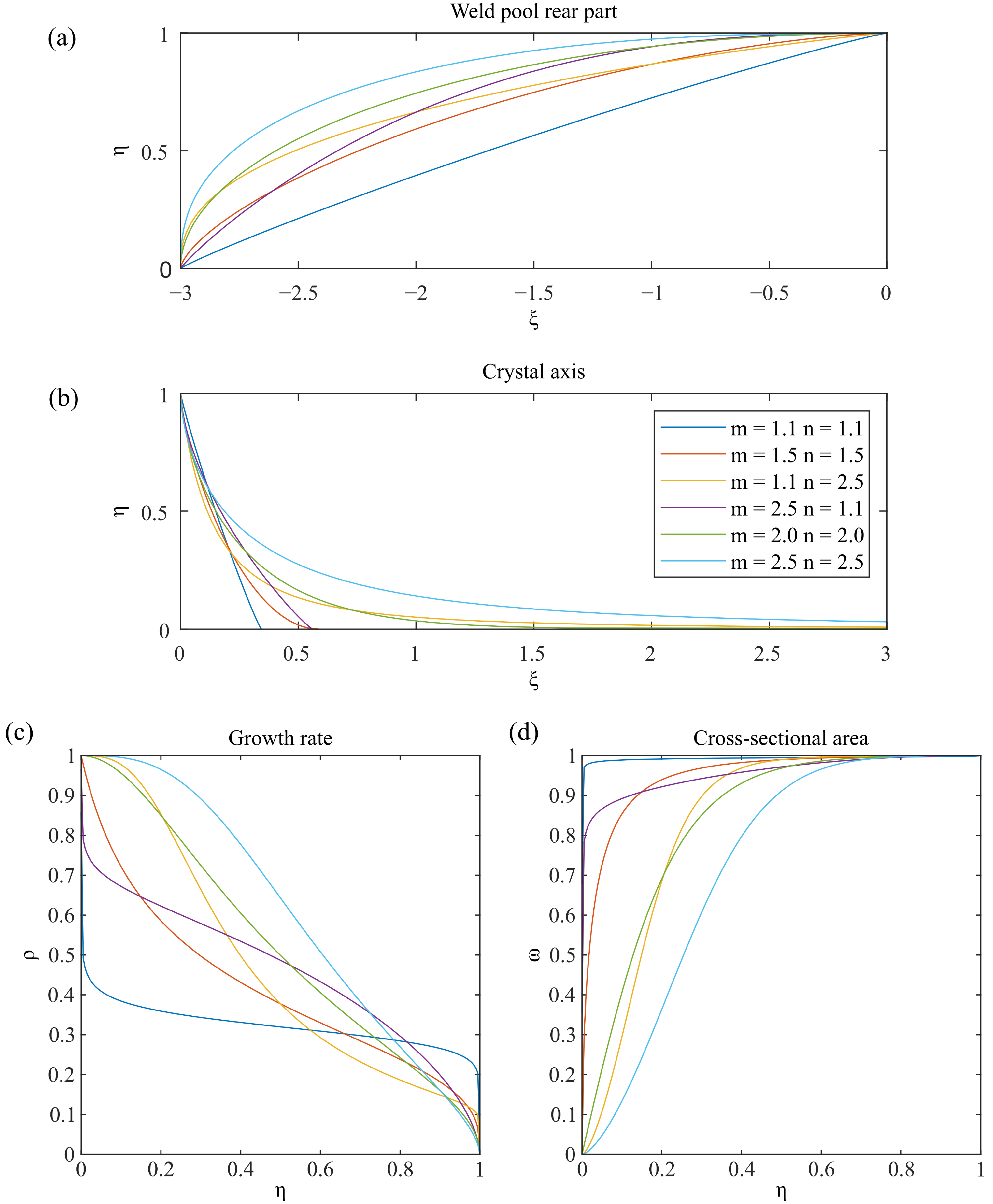
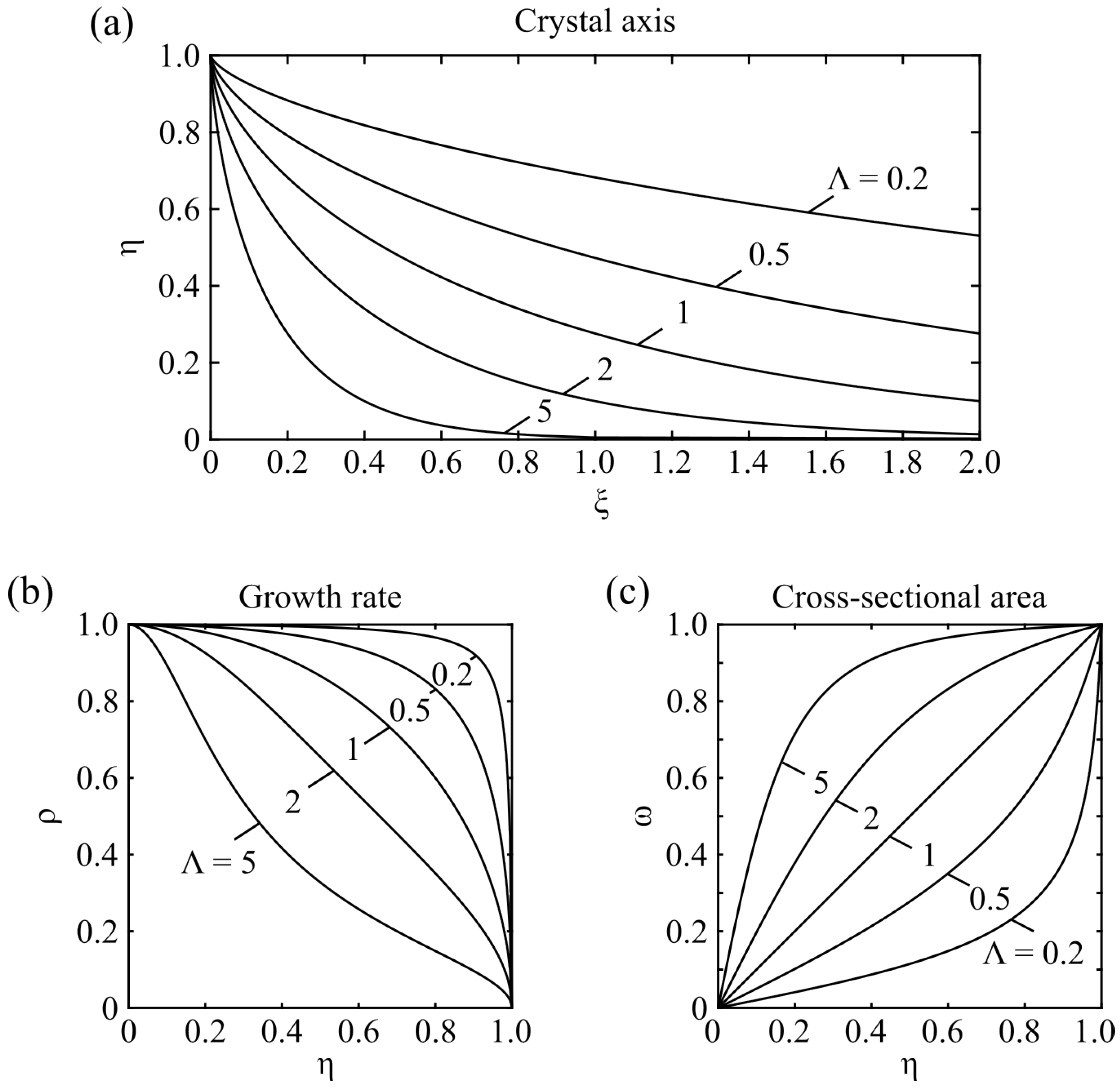
3.2. Dimensionless Analysis

Based on the comparison shown in Figure 4, naturally the question arises: how do the crystallization parameters depend on the shape of the rear part of the weld pool? To answer this question, and for convenience of the further analysis, the following dimensionless parameters are defined:

$$\xi =\frac{x-x_c}{L_r},\eta =\frac{y}{b},\mathsf{\Lambda }=\frac{L_r}{b},\rho =\frac{R}{v_w},\omega =\frac{W}{W_0}.$$

(11)

Figure 5a shows the contours of the upper rear part of the weld pool boundary when its length, $L_r$ is three times its half-width, b, i.e., $\mathsf{\Lambda }=3$, in the practical range of shape parameters, $1.1\le m,n\le 2.5$. As seen in Figure 5a, all curves merge seamlessly into the lower and upper part of the weld pool. It can be seen that for lower values of the shape parameters, $n\le 1.5$, the rear part of the weld pool boundary is sharpened (the curvature of the boundary is very large near the weld centerline), which is typically the case when welding alloys with a large amount of latent heat of solidification or when welding at high speed [9,24].

An elliptical shape of the weld pool, i.e., $m=n=2$, however, corresponds to a smoother curvature with a relatively large radius. The shape parameter, m, affects the shape of the weld pool close to the weld centerline. When m is high, the radius of the curvature increases, and, consequently, the time during which the metal in the heat affected zone has a temperature close to the melting temperature, increases. The shape of the rear weld pool boundary has a strong influence on the geometry of the crystal axes, especially near the weld centerline, see Figure 5b. It can be seen in the figure, that at the beginning of the crystallization process, all crystals, independent of the shape parameters m and n, grow perpendicular to the fusion line. However, a closer look at the curves shows that the higher the value of m and n, the earlier the curve bends and thus reaches its asymptote, i.e., the weld centerline, at higher $\xi$ values. When the shape of the rear part of the weld pool is close to linear, e.g., $n=1.1$, the trajectory of the crystal axis is close to a straight line and the angle between the crystals growing towards each other near the weld centerline is large. The growth rate of the crystal varies from zero at the fusion boundary to the welding speed near the weld centerline, see Figure 5c. Based on the obtained results, it can be seen that the kinetics of the crystal growth is also greatly influenced by the shape of the rear weld pool boundary. For a nearly linear weld pool boundary, i.e., $m=n=1.1$, the crystal growth rate is constant, except for small marginal areas, i.e., at the beginning and end of the crystallization process. For smoother and closer to ellipse-shaped weld pool boundaries, the growth rate increases linearly as it approaches the weld centerline. During crystals’ growth, the width of the crystal decreases from 1 to 0, as shown in Figure 5d. Thereby, the rate of decrease depends again on the shape of the crystallization front. Nonetheless, the three main crystallization parameters also depend on the length-to-width ratio of the rear weld pool boundary, i.e., the dimensionless parameter $\mathsf{\Lambda }$. Figure 6a shows several crystal axes for ellipse-shaped weld pools, ranging from $\mathsf{\Lambda }=0.2$, i.e., short and wide weld pool, e.g., typical for transverse laser oscillation welding, to $\mathsf{\Lambda }=5$, i.e., long and narrow weld pool, which is typical for high-speed welding. In Figure 6b, the corresponding crystals’ growth rate is shown. As seen, the growth rate increases from 0 at the fusion line, i.e., $\eta =1$, to the welding speed at the weld centerline, i.e., $\eta =0$. On the other hand, in the process of growth, the crystals’ width decreases linearly for weld pools of a round shape, i.e., $\mathsf{\Lambda }=1$, which is similar to the case studied in this paper, see Figure 6c, and decreases sharply at the end of the solidification process for elongated weld pool shapes, i.e., $\mathsf{\Lambda }>1$.

4. Conclusions

In the present paper, a technique for calculating the three main solidification parameters for a two-dimensional columnar crystal growth during complete penetration laser beam keyhole welding of thin steel sheets was developed. Based on the obtained results, the following conclusions were drawn:

• The Lamé curves approximation was successfully utilized for the reconstruction of the rear weld pool boundary and thus for the analysis of the crystallization parameters. It was shown that the reconstruction of the weld pool boundary with Lamé curves provides higher accuracy and flexibility compared to results obtained with elliptical functions.
• General analytical expressions for the main solidification parameters, namely the crystal axis and the corresponding growth rate and cross-sectional area of the crystal were derived.
• Dimensionless analysis of the influence of the size and shape of the rear weld pool boundary on the crystallization parameters was provided. It was shown that sharpened rear weld pool boundaries lead to a higher solidification rate and vice versa. Thus, critical welding parameters can be estimated and adapted accordingly to improve the welding process.
• The derived equations and herewith obtained results were validated and verified by comparing them to known theoretical solutions and experimental measurements, showing a very good correlation.