3D Structural Topology Optimization Using ESO, SESO and SERA: Comparison and an Extension to Flexible Mechanisms
Abstract
1. Introduction
2. Optimization Problem Formulation
2.1. Problem Statement–Minimum Compliance
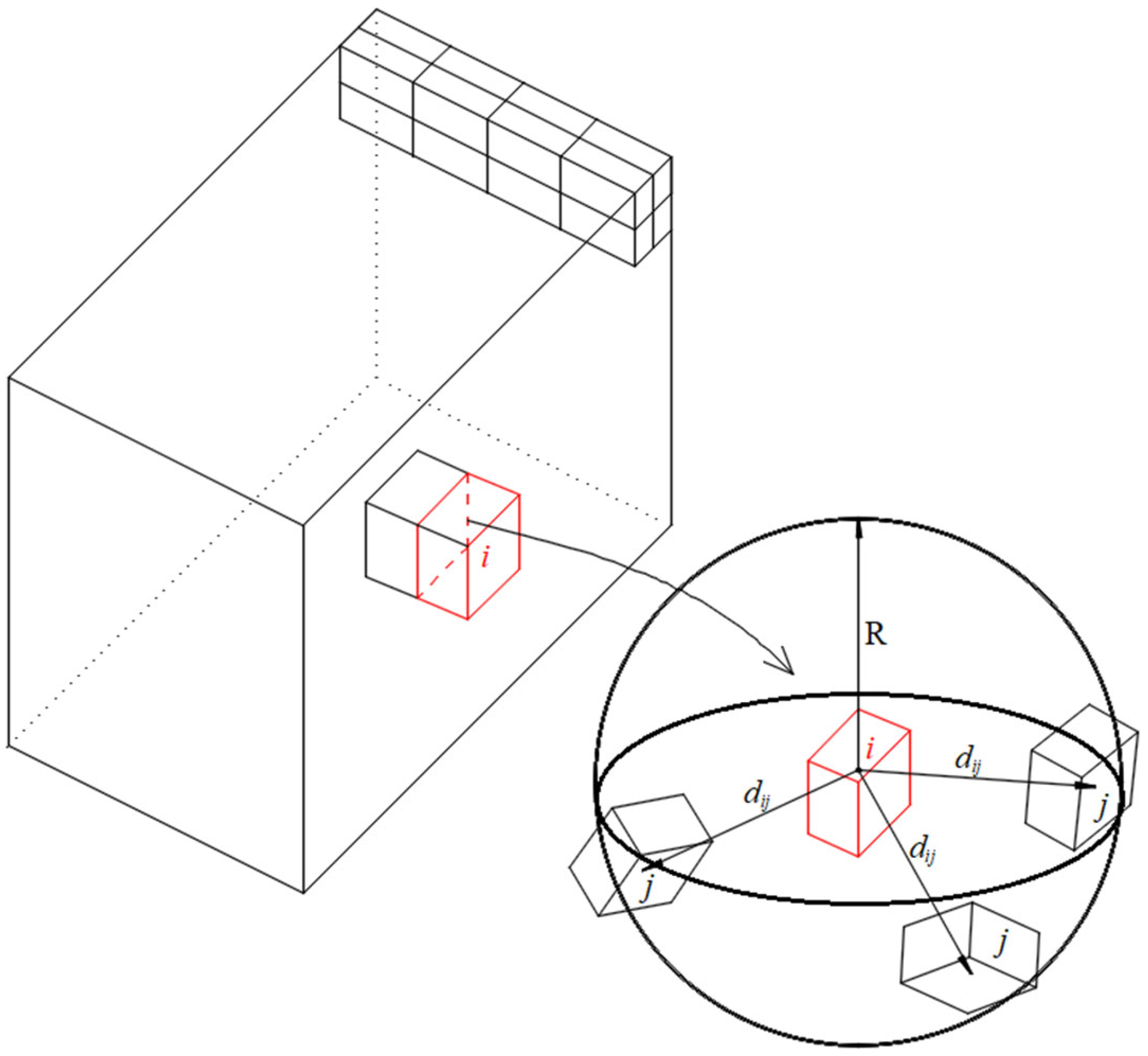
2.2. Sensitivity Analysis
3. Comparing SESO and SERA with Other Topology Optimization Methods
- Step 1:
- Discretize the domain using a refined finite element mesh;
- Step 2:
- Specific the maximum final volume (V*) and the parameters for the desired method. ESO and SESO: rejection rate (RR), evolutionary rate (ER) and the weighted function (η). SERA: total number of iterations (Ntot), progression rate (PR) and smoothing ratio (SR). SIMP: p and
- Step 3:
- Solve the linear elastic problem, applying boundary conditions;
- Step 4:
- Calculate the value of the compliance sensitivity value of each element and update the ratios or thresholds for the method;
- Step 5:
- Remove or introduce elements with the lowest (highest) sensitivity number;
- Step 6:
- Repeat Steps 3 to 5 until the prescribed limit volume has been reached.
3.1. Comparing Topology Optimization Algorithms with a Mesh-Independency Filter
3.2. Comparing Topology Optimization Algorithms without a Mesh-Independency Filter
4. Compliant Mechanism Synthesis
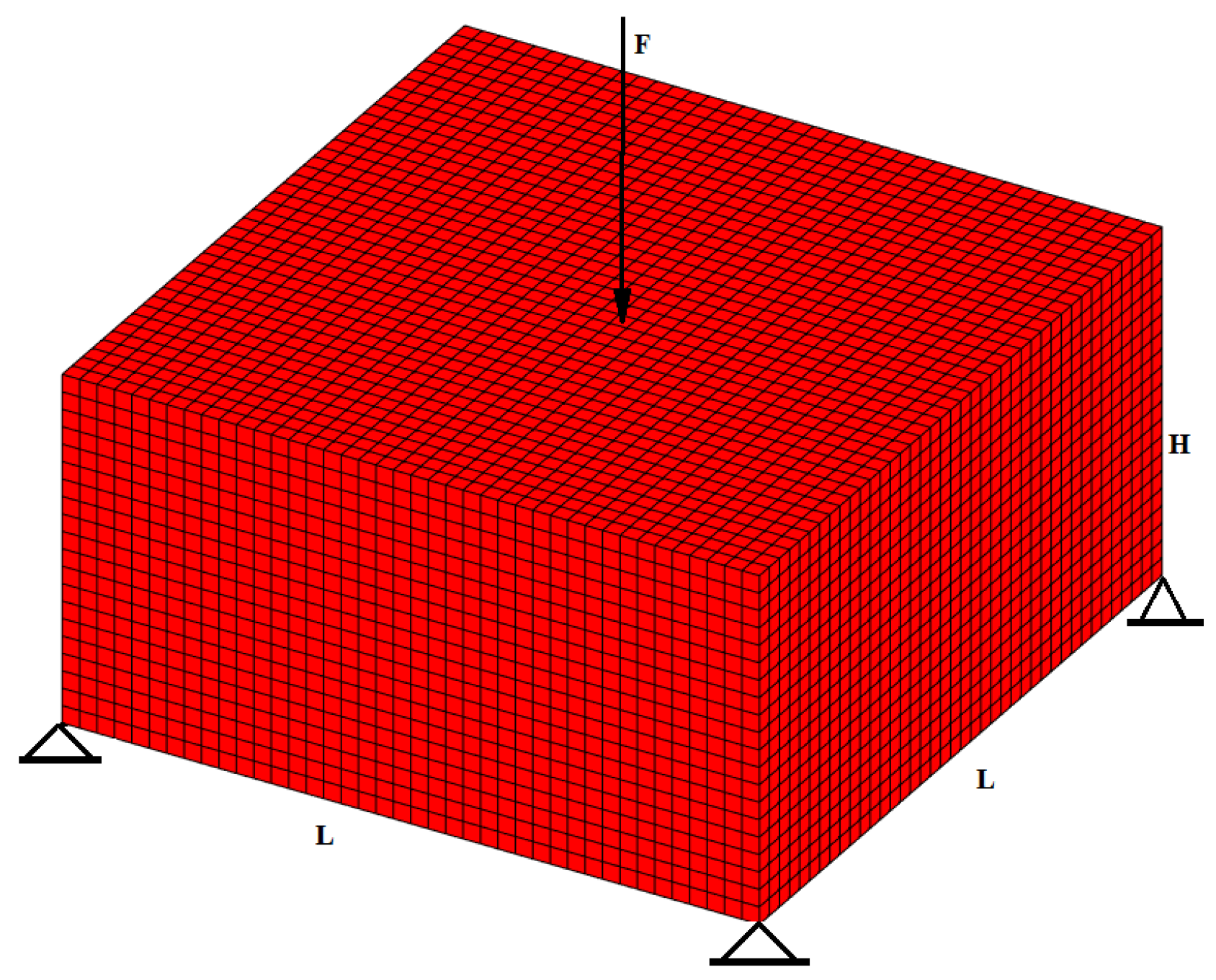
5. Numerical Example
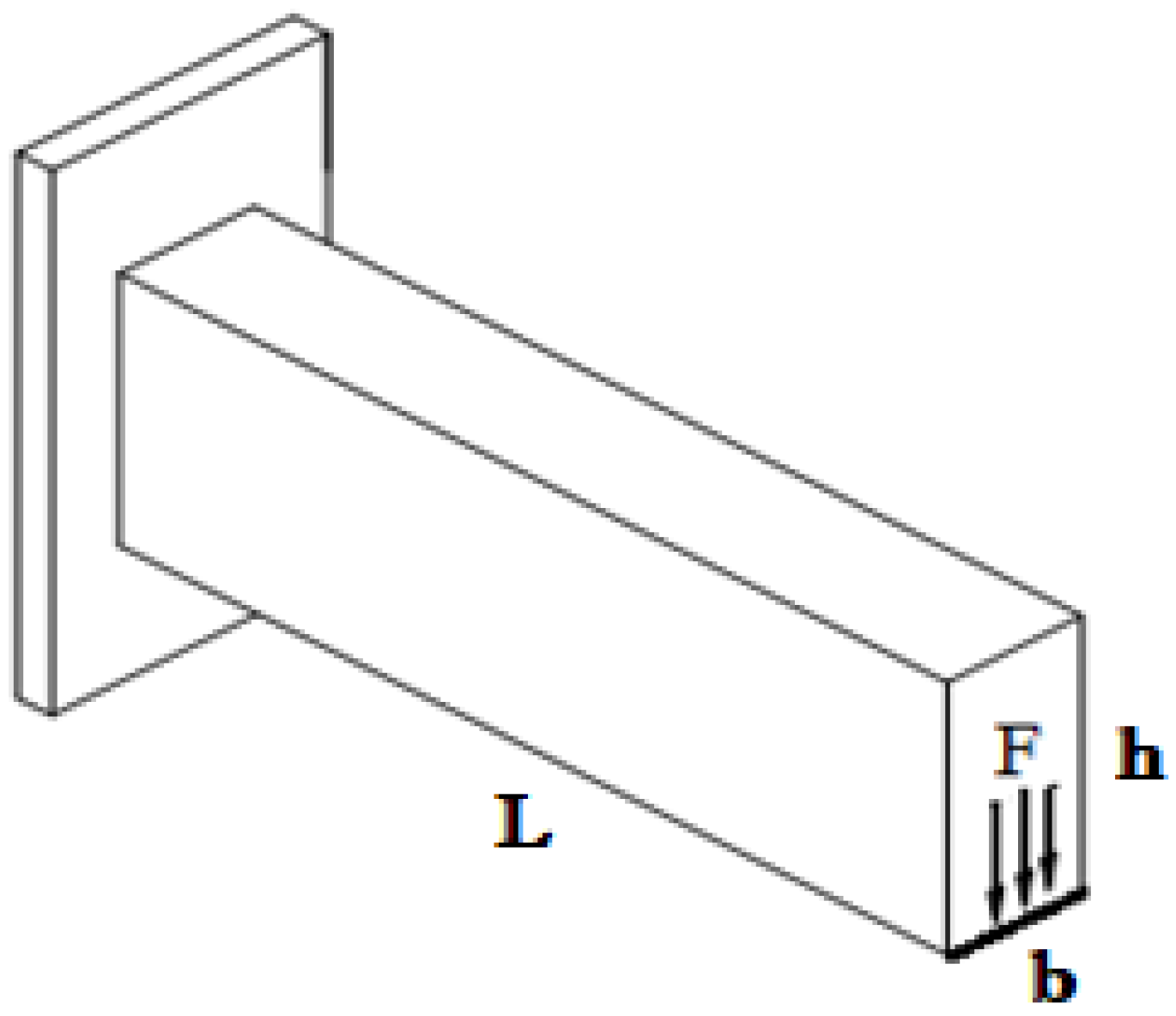
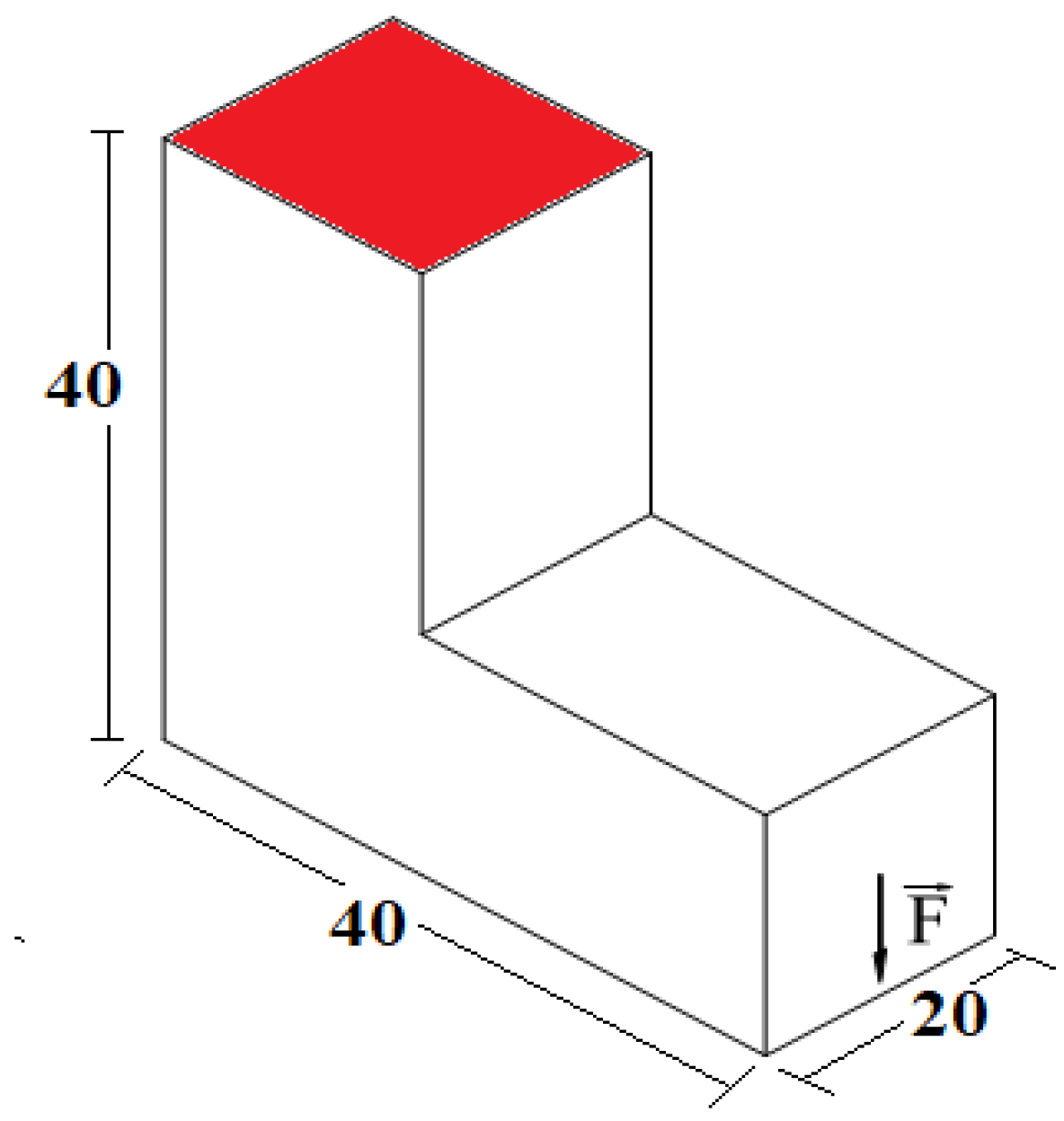
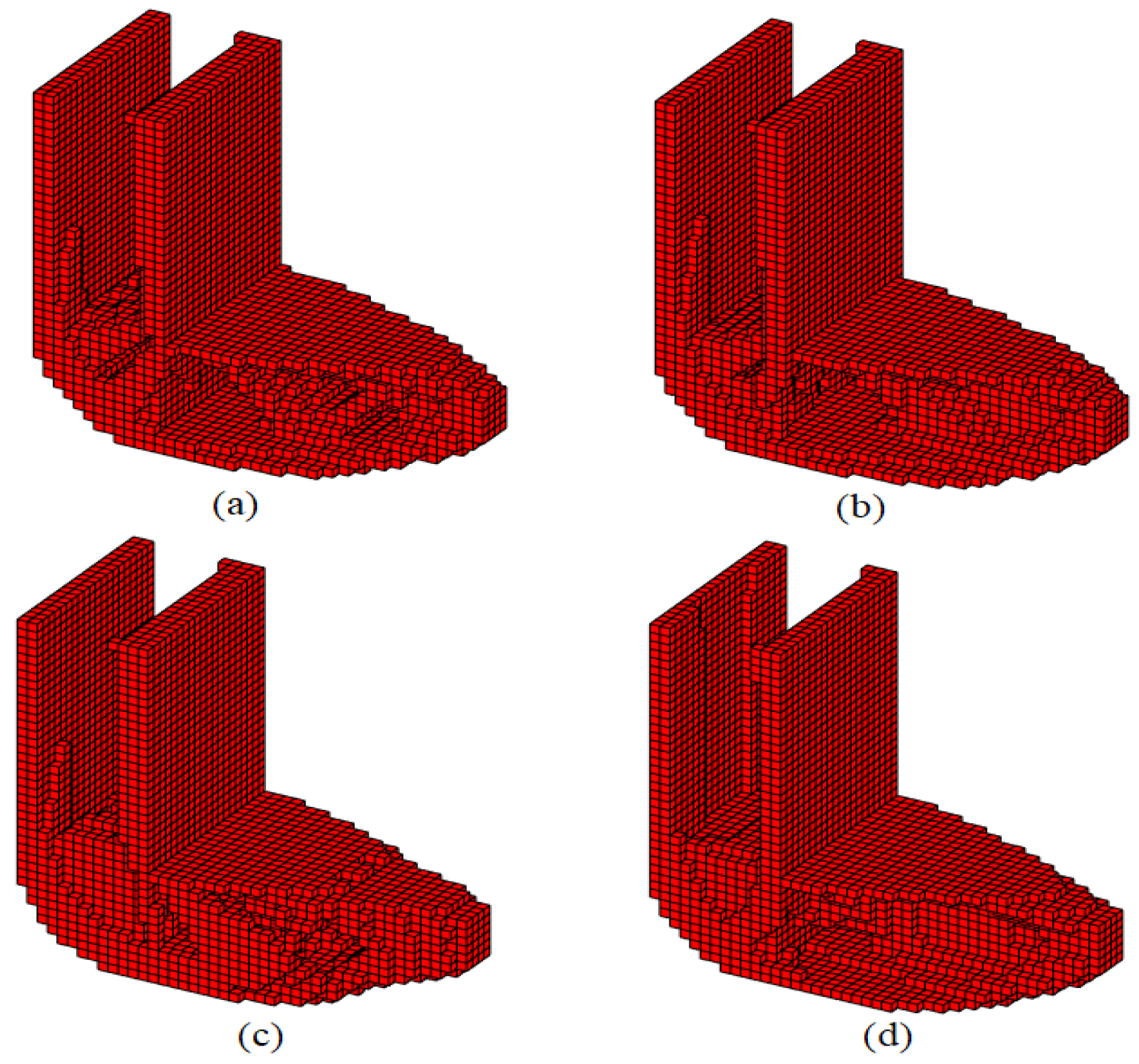
5.1. Example 1—L-Shaped Beam Problem
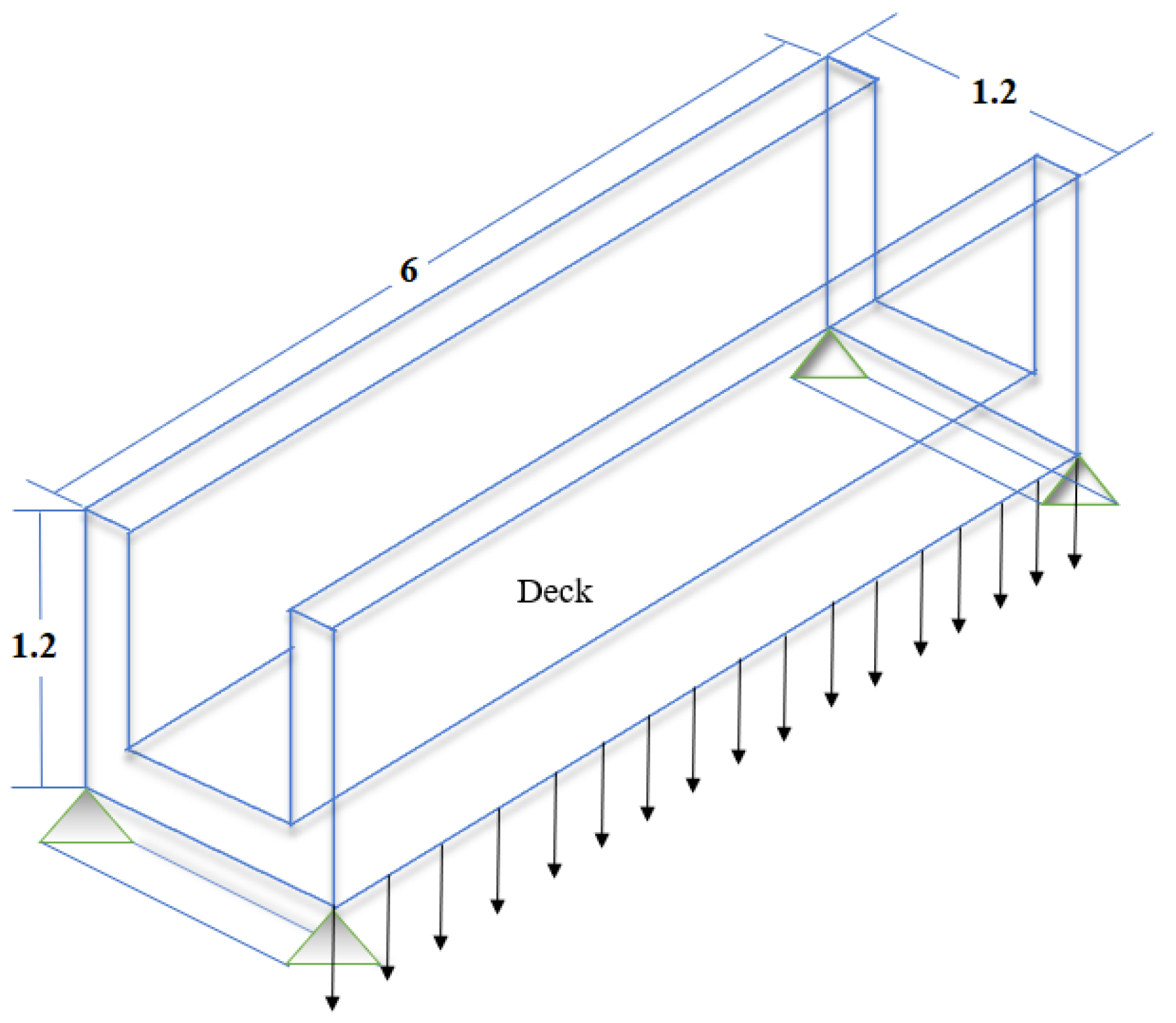
5.2. Example 2—A Channel Beam
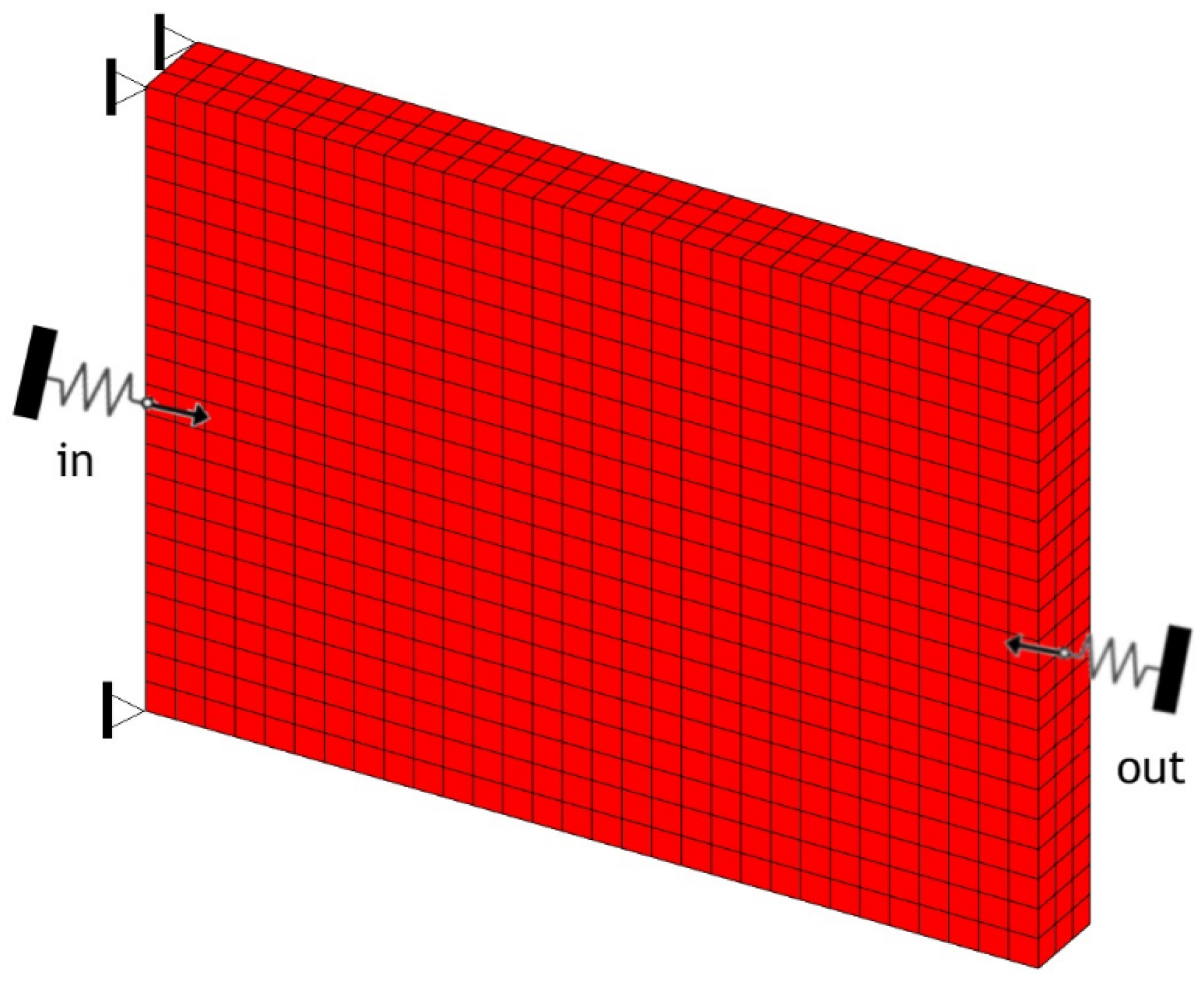
5.3. Example 3—Compliant Mechanism–Mechanical Advantage and Geometrical Advantage
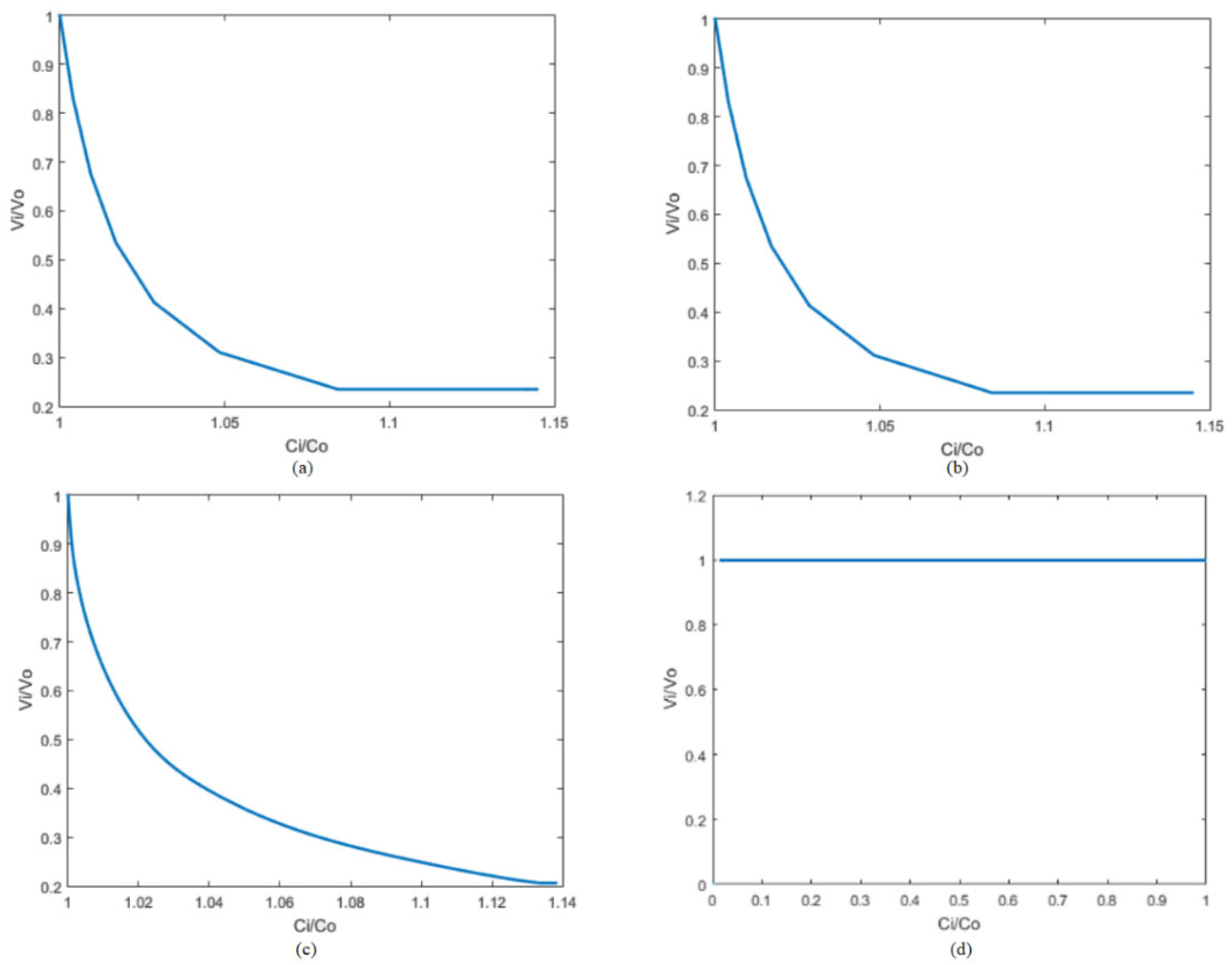
5.4. Example 4—Simply Supported Beam–Performance Characteristic Curve
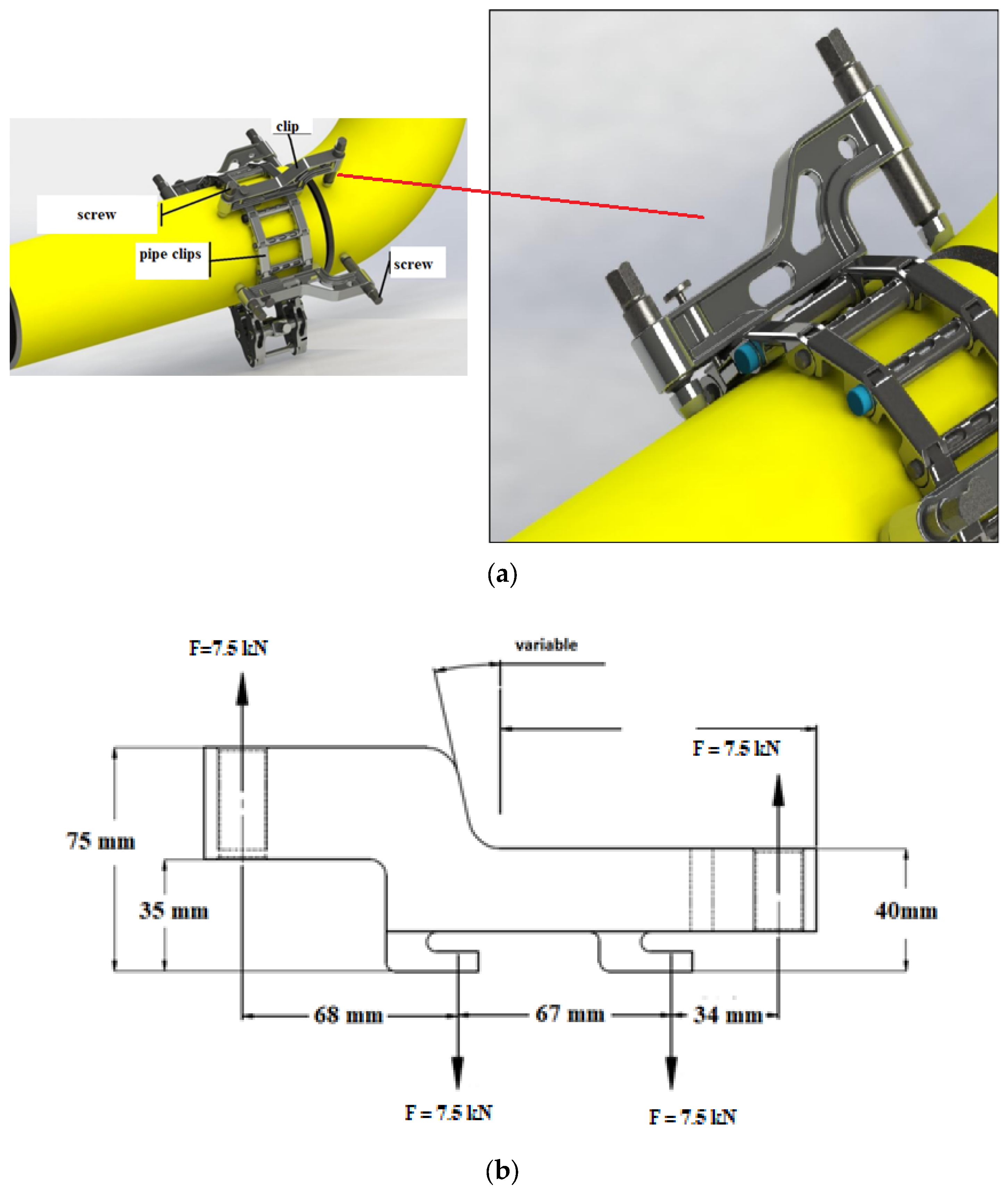
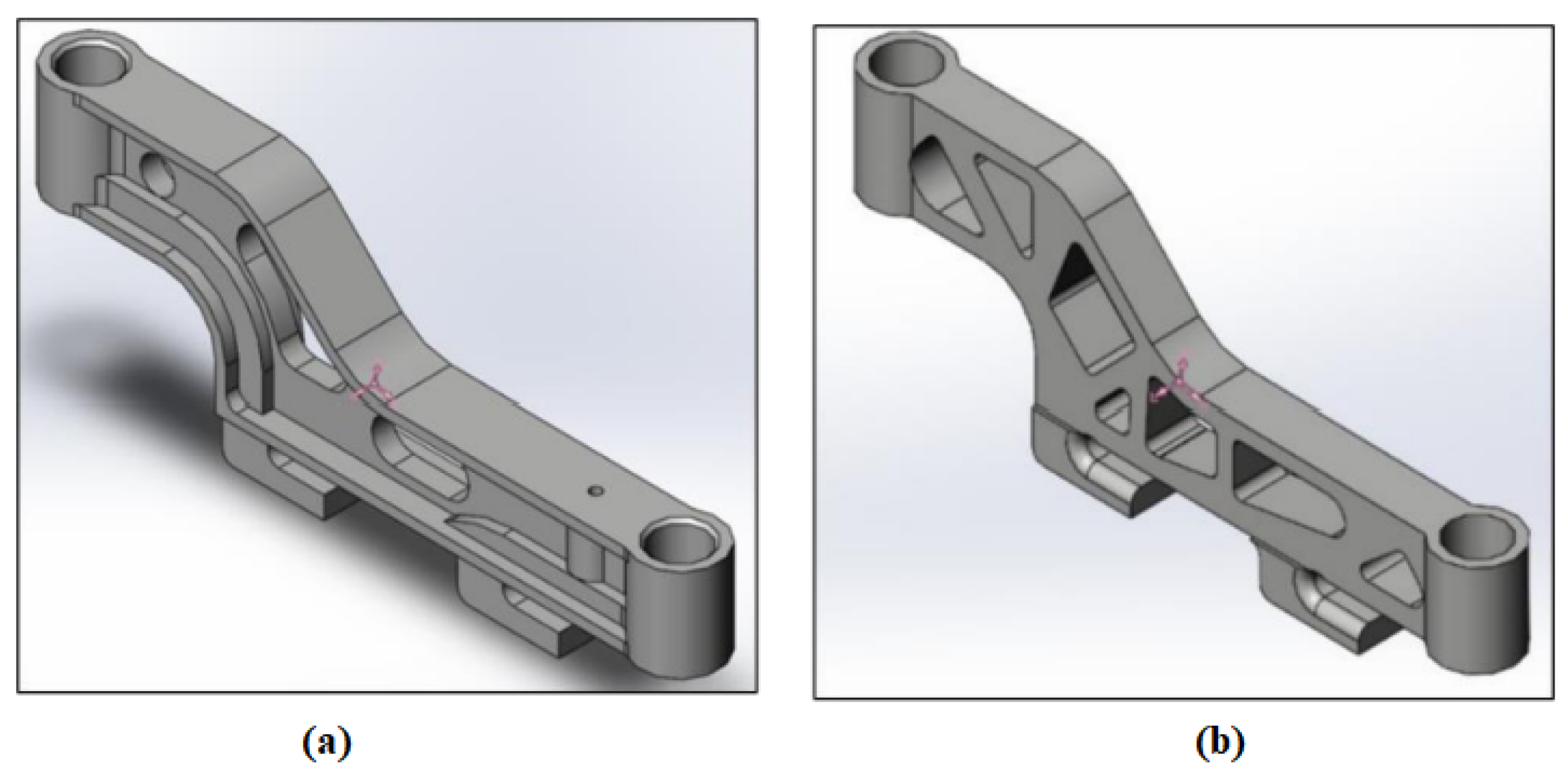
5.5. Example 5—Industrial Application: Flexible Coupler
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sigmund, O. A 99 line topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2001, 21, 120–127. [Google Scholar] [CrossRef]
- Andreassen, E.; Clausen, A.; Schevenels, M.; Lazarov, B.S.; Sigmund, O. Efficient topology optimization in MATLAB using 88 lines of code. Struct. Multidiscip. Optim. 2011, 43, 1–16. [Google Scholar] [CrossRef]
- Challis, V.J. A discrete level-set topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2010, 41, 453–464. [Google Scholar] [CrossRef]
- Huang, X.; Xie, Y.M. Bi-directional evolutionary topology optimization of continuum structures with one or multiple materials. Comput. Mech. 2009, 43, 393–401. [Google Scholar] [CrossRef]
- Ansola Loyola, R.; Querin, O.M.; Garaigordobil Jiménez, A.; Alonso Gordoa, C. A sequential element rejection and admission (SERA) topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2018, 58, 1297–1310. [Google Scholar] [CrossRef]
- Gebremedhen, H.S.; Woldemicahel, D.E.; Hashim, F.M. Three-dimensional stress-based topology optmization using SIMP mehod. Int. J. Simul. Multidiscip. Des. Optim. 2019, 10, A1. [Google Scholar] [CrossRef]
- Liu, K.; Tovar, A. An efficient 3D topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2014, 50, 1175–1196. [Google Scholar] [CrossRef]
- Zegard, T.; Paulino, G.H. GRAND3—Ground structure based topology optimization for arbitrary 3D domains using MATLAB. Struct. Multidiscip. Optim. 2015, 52, 1161–1184. [Google Scholar] [CrossRef]
- Zegard, T.; Paulino, G.H. Bridging topology optimization and additive manufacturing. Struct. Multidiscip. Optim. 2016, 53, 175–192. [Google Scholar] [CrossRef]
- Borrvall, T.; Petersson, J. Large-scale topology optimization in 3D using parallel computing. Comput. Methods Appl. Mech. Eng. 2001, 190, 6201–6229. [Google Scholar] [CrossRef]
- Zuo, Z.H.; Xie, Y.M. A simple and compact Python code for complex 3D topology optimization. Adv. Eng. Softw. 2015, 85, 1–11. [Google Scholar] [CrossRef]
- Langelaar, M. Topology optimization of 3D self-supporting structures for additive manufacturing. Addit. Manuf. 2016, 12, 60–70. [Google Scholar] [CrossRef]
- Chi, H.; Zhang, Y.; Tang, T.L.E.; Mirabella, L.; Dalloro, L.; Song, L.; Paulino, G.H. Universal machine learning for topology optimization. Comput. Methods Appl. Mech. Eng. 2021, 375, 112739. [Google Scholar] [CrossRef]
- Brown, N.K.; Garland, A.P.; Fadel, G.M.; Li, G. Deep reinforcement learning for engineering design through topology optimization of elementally discretized design domains. Mater. Des. 2022, 218, 110672. [Google Scholar] [CrossRef]
- Kollmann, H.T.; Abueidda, D.W.; Koric, S.; Guleryuz, E.; Sobh, N.A. Deep learning for topology optimization of 2D metamaterials. Mater. Des. 2020, 196, 109098. [Google Scholar] [CrossRef]
- Simonetti, H.L.; Almeida, V.S.; Neto, L.O. A smooth evolutionary structural optimization procedure applied to plane stress problem. Eng. Struct. 2014, 75, 248–258. [Google Scholar] [CrossRef]
- Xie, Y.M.; Steven, G.P. A simple evolutionary procedure for structural optimization. Comput. Struct. 1993, 49, 885–896. [Google Scholar] [CrossRef]
- Ghabraie, K. The ESO method revisited. Struct. Multidiscip. Optim. 2015, 51, 1211–1222. [Google Scholar] [CrossRef]
- Ansola, R.; Veguería, E.; Alonso, C.; Querin, O.M. Topology optimization of 3D compliant actuators by a sequential element rejection and admission method. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2016; Volume 108, p. 012035. [Google Scholar] [CrossRef]
- Yang, X.Y.; Xie, Y.M.; Steven, G.P. Evolutionary methods for topology optimisation of continuous structures with design dependent loads. Comput. Struct. 2005, 83, 956–963. [Google Scholar] [CrossRef]
- Sigmund, O.; Petersson, J. Numerical instabilities in topology optimization: A survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Struct. Optim. 1998, 16, 68–75. [Google Scholar] [CrossRef]
- Bruns, T.E.; Tortorelli, D.A. Topology optimization of non-linear elastic structures and compliant mechanisms. Comput. Methods Appl. Mech. Eng. 2001, 190, 3443–3459. [Google Scholar] [CrossRef]
- Wang, M.Y. Mechanical and geometric advantages in compliant mechanism optimization. Front. Mech. Eng. China 2009, 4, 229–241. [Google Scholar] [CrossRef]
- Lau, G.; Du, H.; Lim, M. Convex analysis for topology optimization of compliant mechanisms. Struct. Multidiscip. Optim. 2001, 22, 284–294. [Google Scholar] [CrossRef]
- Simonetti, H.L.; Almeida, V.S.; de Assis das Neves, F.; Del Duca Almeida, V.; de Oliveira Neto, L. Reliability-Based Topology Optimization: An Extension of the SESO and SERA Methods for Three-Dimensional Structures. Appl. Sci. 2022, 12, 4220. [Google Scholar] [CrossRef]
- Ypycom. Ferramentas Especiais. “Fixação com Precisão”. Available online: https://ypycom.com.br (accessed on 13 February 2023). (In Portuguese).
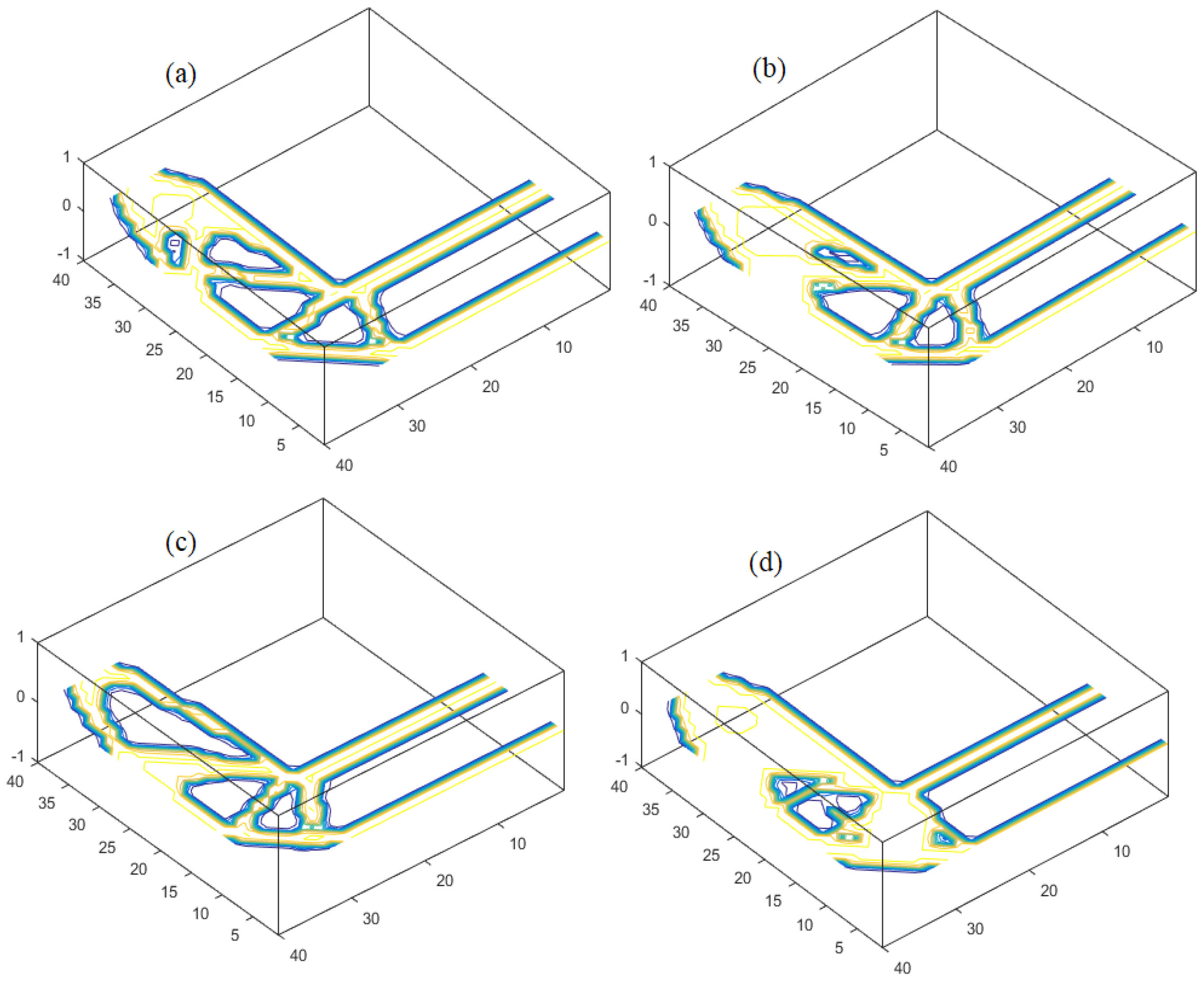

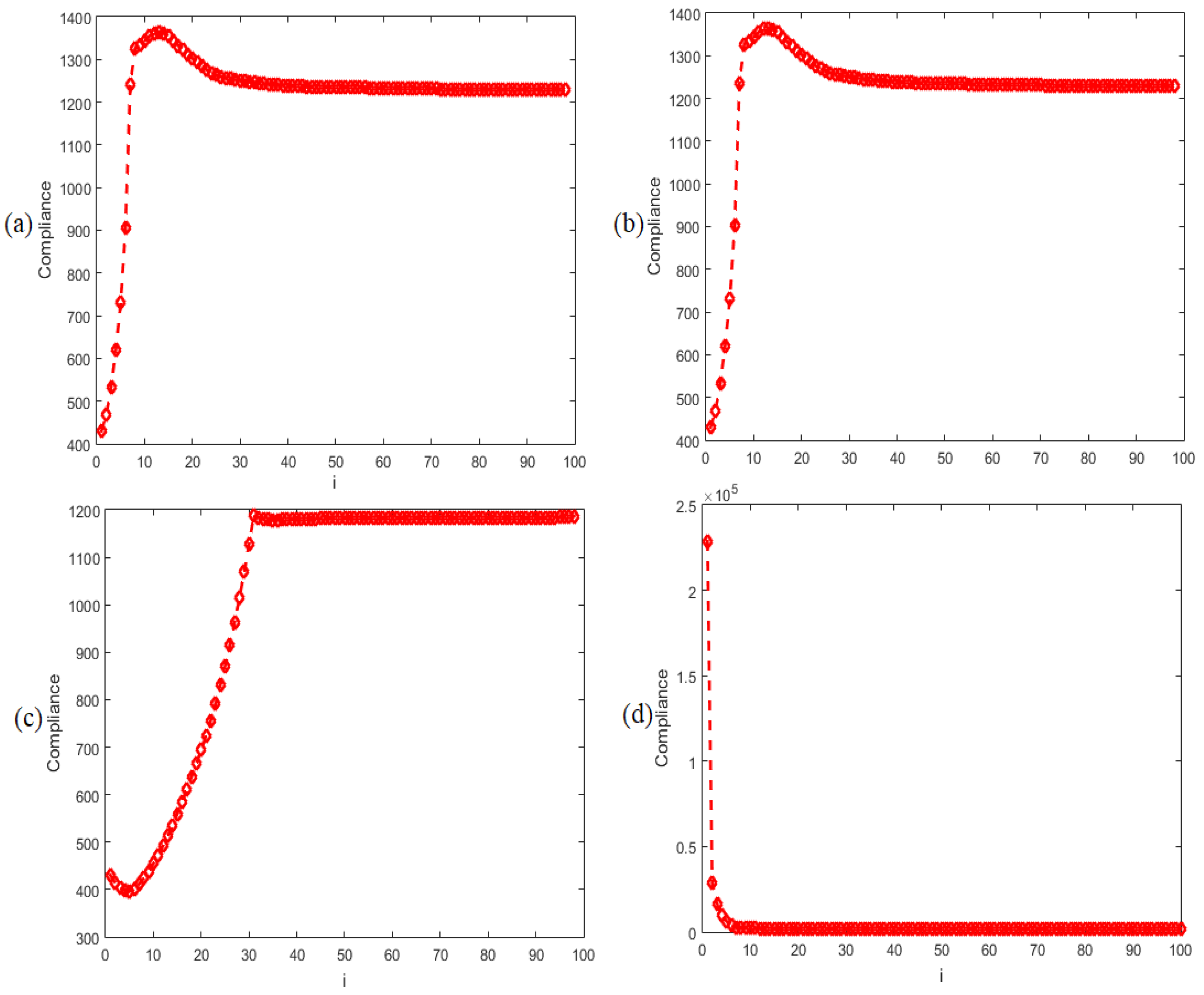
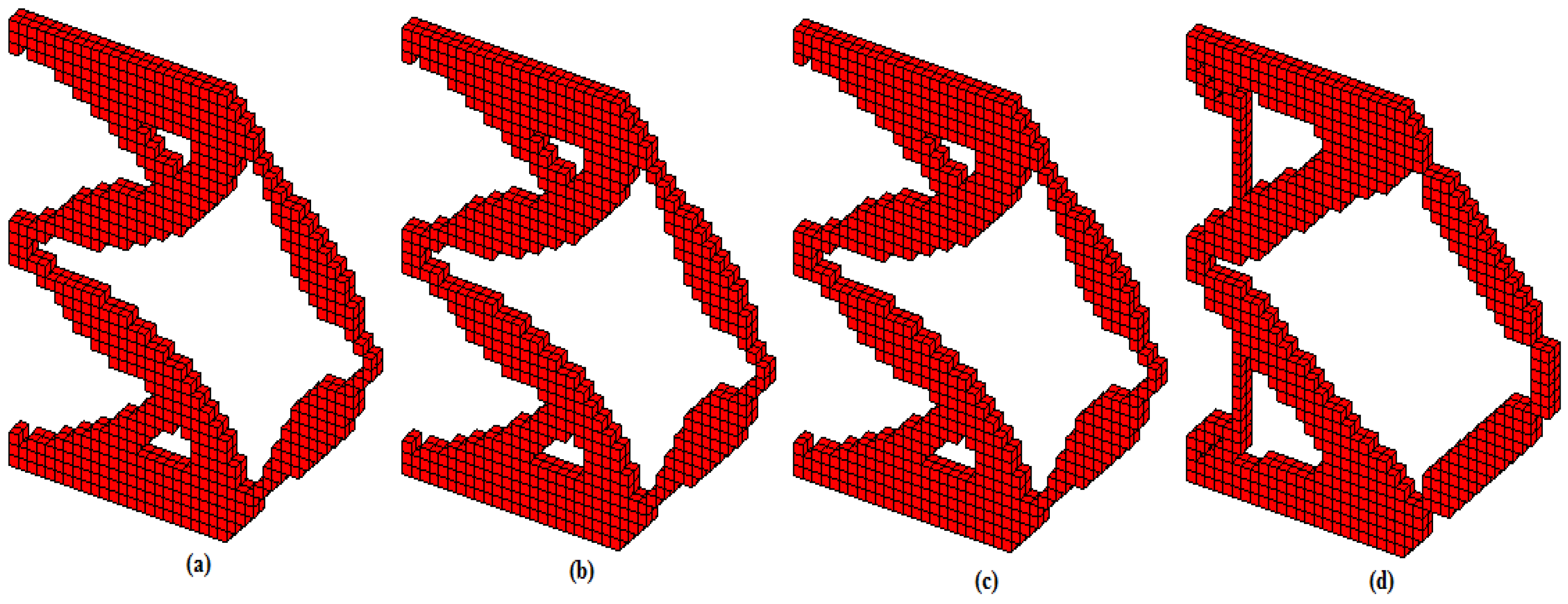
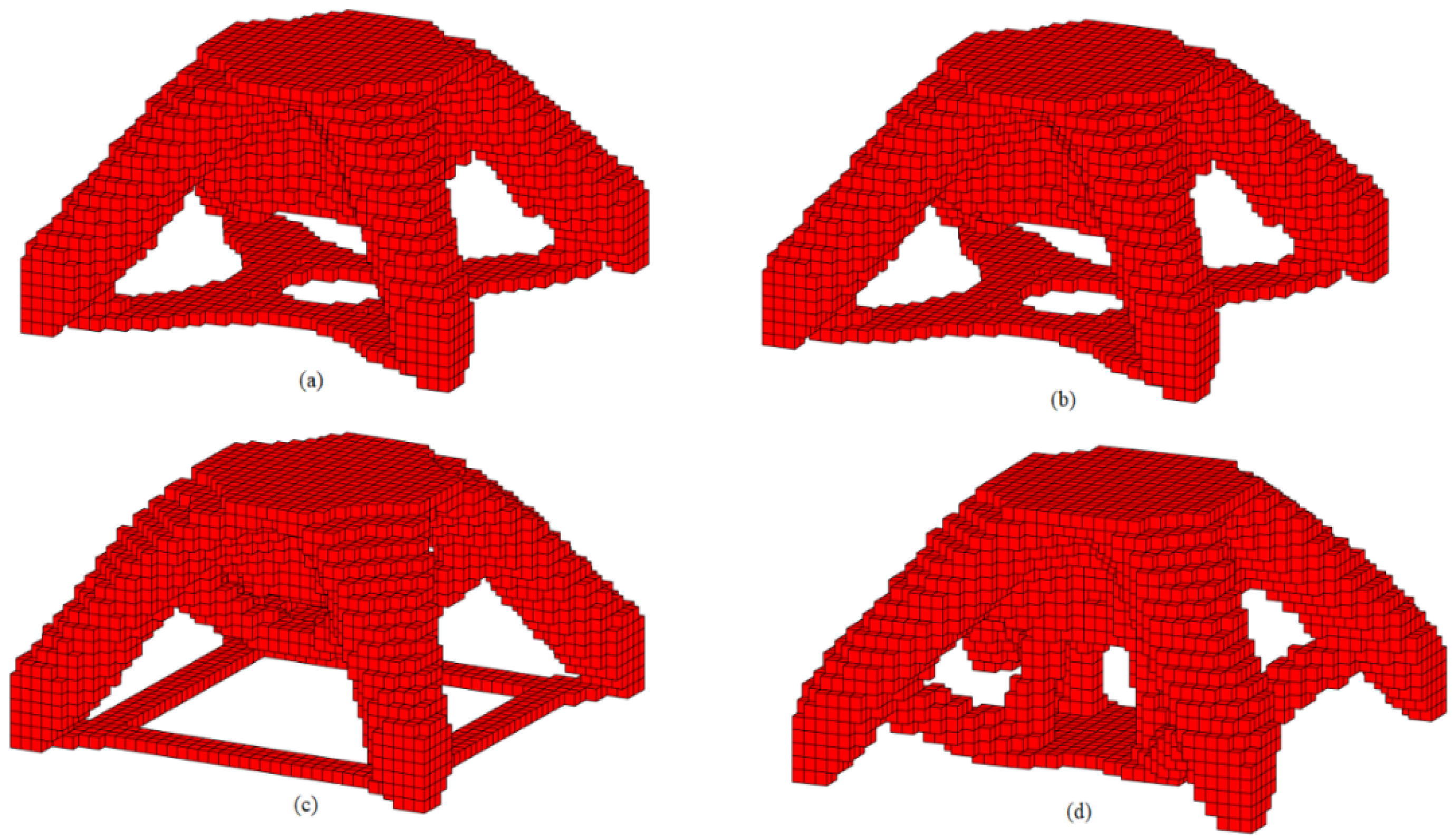
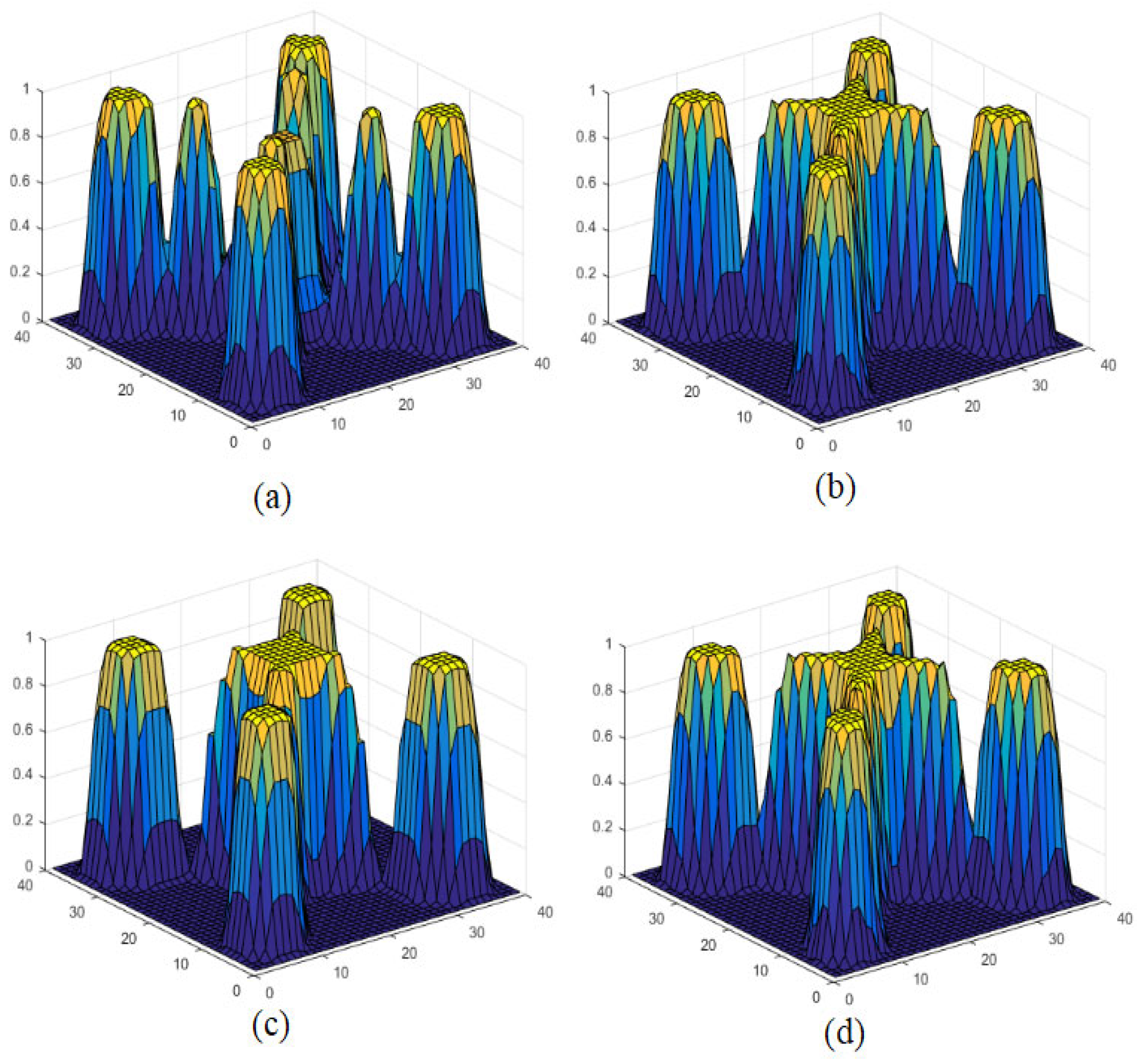

| Methods | Parameters | Number of Iterations/Costs | Optimal Settings/Compliance |
|---|---|---|---|
| ESO |  | ||
| SERA |  | ||
| SESO | 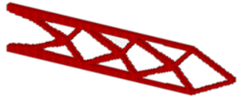 | ||
| SIMP |  |
| Methods | Parameters | Number of Iterations/Costs | Optimal Settings/Compliance |
|---|---|---|---|
| ESO | 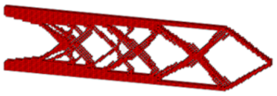 | ||
| SERA | 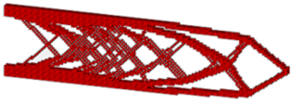 | ||
| SESO | 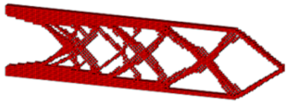 | ||
| SIMP |  |
| Method | Parameters | Number of Iterations | Objective Function | Computational Cost (Minutes) |
|---|---|---|---|---|
| SESO | 100 | 65.74 | 49.72 | |
| ESO | 100 | 65.88 | 49.57 | |
| SERA | 100 | 64.83 | 48.39 | |
| SIMP | 100 | 92.04 | 58.70 |
| Method | SESO | SERA | ESO | SIMP |
|---|---|---|---|---|
| GA |  |  |  |  |
| Time (s) | 19.42 | 19.80 | 19.84 | 25.04 |
| Iteration | 60 | 61 | 61 | 60 |
| Contour graphics |  |  |  |  |
| Objective Function |  |  |  | 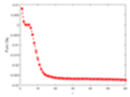 |
| Surface graphics |  |  |  |  |
| Method | SESO | SERA | ESO | SIMP |
|---|---|---|---|---|
| GA |  |  |  |  |
| Time (s) | 19.74 | 19.99 | 20.10 | 21.38 |
| Iteration | 60 | 61 | 61 | 60 |
| Contour graphics |  |  |  |  |
| Objective Function |  |  |  | 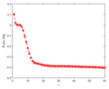 |
| Surface graphics | 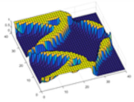 | 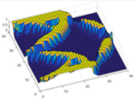 | 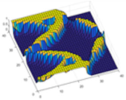 |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simonetti, H.L.; Almeida, V.S.; Neves, F.d.A.d.; Almeida, V.D.D.; Cutrim, M.D.S. 3D Structural Topology Optimization Using ESO, SESO and SERA: Comparison and an Extension to Flexible Mechanisms. Appl. Sci. 2023, 13, 6215. https://doi.org/10.3390/app13106215
Simonetti HL, Almeida VS, Neves FdAd, Almeida VDD, Cutrim MDS. 3D Structural Topology Optimization Using ESO, SESO and SERA: Comparison and an Extension to Flexible Mechanisms. Applied Sciences. 2023; 13(10):6215. https://doi.org/10.3390/app13106215
Chicago/Turabian StyleSimonetti, Hélio Luiz, Valério S. Almeida, Francisco de Assis das Neves, Virgil Del Duca Almeida, and Marlan D. S. Cutrim. 2023. "3D Structural Topology Optimization Using ESO, SESO and SERA: Comparison and an Extension to Flexible Mechanisms" Applied Sciences 13, no. 10: 6215. https://doi.org/10.3390/app13106215
APA StyleSimonetti, H. L., Almeida, V. S., Neves, F. d. A. d., Almeida, V. D. D., & Cutrim, M. D. S. (2023). 3D Structural Topology Optimization Using ESO, SESO and SERA: Comparison and an Extension to Flexible Mechanisms. Applied Sciences, 13(10), 6215. https://doi.org/10.3390/app13106215








