Failure Identification Method and LMI-Based Control System for Small Spacecraft

Abstract

This study aimed to design a linear matrix inequality (LMI)-based robust control system and a failure identification method for small spacecraft. The key feature of the proposed method is its capability to withstand failure in the actuation system by means of the observer and controller gain definition. An effective approach for withstanding failure is required due to the small capabilities of the momentum exchange device (MED) and the system’s sensitivity to external perturbations. Passive fault-tolerant approaches can be included in the design process of the control algorithm. In particular, the main objective of this study was the design of an $H_{\infty }$ controller that started from an LMI formulation and considered the parametric uncertainties and matched failure of the actuation system. In addition, a fault detection method based on sliding mode observers was proposed to include an active disturbance correction algorithm and improve the system robustness and performance during spacecraft stabilization. The closed-loop system was evaluated for different initial conditions, including attitude positions that are far from the desired condition. The effectiveness of the proposed approach was demonstrated using extensive simulations that considered a pyramidal actuation configuration and hardware constraints.

1. Introduction

In the last few years, technological improvements and the resulting miniaturization of processors and electronics have given small satellites new capabilities and better performance. The increased usage of small satellites has led to bigger attention from customers for any kind of failure that can affect the spacecraft at any moment. Particularly, spacecraft attitude, communication, or scientific observation impose strict requirements in terms of attitude stability and accuracy. The attitude accuracy is usually a function of the mission scenario and spacecraft characteristics; some mathematics related to the accuracy evaluation for different missions can be found in [1] and in [2] for a real-time implementation. A pointing stability index, for example, can be evaluated during the most critical maneuver phases, as detailed in [3]. Moreover, the reduced mass causes the spacecraft to be more sensitive to external perturbations, and momentum exchange devices (MEDs) have more limitations due to their smaller dimensions.

For this reason, any kind of failure in the actuation system may critically affect the success of the mission. Generally, over-actuated systems guarantee redundancy in the actuators to withstand failures, but the controller design must also allow for this eventuality. In this context, robust control methods for small satellites have been attracting the attention of the space systems community, which needs effective approaches for withstanding failures. Moreover, robust controllers are generally adopted to deal with bounded plant uncertainties, which guarantees the required performance and stability. A first definition of robustness, although not so rigorous, can be the capability of the control system to work well under sets of parameters that are different from the nominal one. For example, these parameters can be uncertainties within the system that are not known but are bounded. Failures can be considered as a bounded uncertainty of the system, and the controller can be designed to guarantee a robust performance.

Robust controllers can be designed to act as passive fault-tolerant algorithms, as in [4,5]; however, they have limited fault tolerance capabilities, as can be seen in [6,7]. Despite the robustness to failure being verified, some perturbation may eventually lead to instability or loss of performance. This is directly related to the loss of control effectiveness. An active approach would result in a more effective performance, but it requires a fault detection system for the complete awareness of the system in real time, as seen in [8,9] for aerial multirotors. Identifying the failure may allow for the reallocation of the control to between the remaining actuators, which would limit the control action loss.

Among robust control strategies, the H${}_{\infty }$ control method is well established and studied. Referring to this controller makes the designer aware of its closed-loop system properties and performance. Recent studies on the H${}_{\infty }$ controller show the introduction of the suboptimal problem [10,11,12]. As conducted in [13,14], the suboptimal problem is brought back to a linear matrix inequalities (LMIs) problem. Solving the LMI problem using numerical methods allows the design of the controller to follow a theoretical approach; in this way, the controller is already designed to satisfy the system requirements. The LMI design approach is under investigation for different control strategies [15,16,17,18]. With respect to previous work, the current study proposed the inclusion of failure and uncertainties directly into the design process. In this study, the solution of the suboptimal problem in the LMI formulation was addressed to include plant uncertainties related to parameter variation in the design process of the H${}_{\infty }$ controller. Failures were modeled as unknown disturbances acting on the systems and were included as uncertainties in the design process.

In this way, it is possible to design a robust controller that also achieves high performance when failure occurs. However, this design process makes the controller extremely sensitive, making actuators generally work at their maximum or minimum torque. This limitation makes it difficult to design an effective control allocation algorithm to further improve controller performance, as control allocation algorithms are the main solution for achieving an effective failure rejection, as seen in [19,20,21,22]. Instead, a control correction approach was proposed that considers the recovery of disturbances (identified as external disturbances and failure) that are acting on the spacecraft dynamics. First, it is necessary to identify when a failure occurs. For this purpose, nonlinear observer-based methods have been considered.

Failure identification is generally seen as a signal estimation problem. Lately, methods based on observers have been under investigation for failure identification and detection [23]. In particular, sliding mode observers (SMOs) [24,25,26,27] are usually developed as failure estimation methods and are able to identify where a failure occurs.Considering this approach, it is possible to identify the failing actuator system and take advantage of this information to evaluate the effects of the failure and disturbance on the spacecraft dynamics. This study proposed the combination of two SMOs: one for the identification of the failing actuator system, and the second for the estimation of disturbances acting on the spacecraft. Generally, the Kalman filter is the typical algorithm that is used to estimate unknown variables [28,29]. However, in this case, system nonlinearities make it difficult to design an effective corrective strategy based on the Kalman filter technique. An observer-based algorithm better fits the problem formulation and, for this reason, it is preferred to classical approaches.

Finally, a robust controller was combined with an active fault detection and correction method, which was based on the partial recovery of the estimated disturbances. The performance of the H${}_{\infty }$ controller has been evaluated and compared while considering different designing approaches and while including the failure correction algorithm based on failure and disturbance estimation. The effectiveness of the proposed approach was verified by considering extensive simulations with varying initial conditions and external disturbances.

The work proposed in this study was based on the thesis of [30]; this study’s novelty and extension of [30] are mainly related to the design of a sliding mode observer for the identification of the failure. Moreover, additional mission scenarios are included to show the effectiveness of the combination of an observer and robust controller. The novelties of this study are: (i) the design of a fault-tolerant H${}_{\infty }$ controller for small spacecraft using the LMI design method to achieve robustness to system uncertainties that are related to the presence of MEDs as actuators, and failures; (ii) the detection of a failure, the identification of the failing actuator, and the estimation of disturbances acting on a spacecraft with failure through the use of observer-based algorithms; and (iii) the combination of the proposed control strategy with a correction approach that is based on the observer’s output.

This paper is organized as follows. The satellite attitude dynamics are presented in Section 2, including the model of the actuator. Section 3 describes the design process of the $H_{\infty }$ controller; in Section 4, the sliding mode observer is introduced as a failure detection method, including a failure correction approach that was employed to improve controller performance. The simulation results are shown in Section 5. Finally, some concluding remarks are listed in Section 6.

2. System Dynamics

In this section, the satellite mathematical model is described. The considered spacecraft falls within the small satellite definition, and it is equipped with an MED to achieve a high attitude accuracy during maneuvers. The spacecraft’s ability to modify its orientation arises in the use of the MED system, particularly when reaction wheels are considered. These devices apply torque through an electric motor that sets a wheel to rotate while an equal and opposite torque is applied on the spacecraft, which allows the wheel to rotate.

The spacecraft attitude is expressed by means of quaternions and by considering the rotation of the body reference frame with respect to an inertial reference frame. Quaternions were chosen to describe the spatial rotations due to their compact nature, lower computational cost, and lack of singularity, as seen in [31]. In this paper, they are represented through the scalar plus the three-vector representation, as follows

$$q={\{q_0,q_v\}}^T$$

where $q_0\in \mathbb{R}$ and $q_v\in {\mathbb{R}}^3$. The system kinematics are expressed by the evolution of quaternions in time, and it is defined as a function of the system angular velocity

$$\dot{q}=\frac{1}{2}\left[\begin{array}{cccc}0& -{\omega }_1& -{\omega }_2& -{\omega }_3\\ {\omega }_1& 0& -{\omega }_3& {\omega }_2\\ {\omega }_2& {\omega }_3& 0& -{\omega }_1\\ {\omega }_3& -{\omega }_2& {\omega }_1& 0\end{array}\right]q$$

where $\omega ={\{{\omega }_1,{\omega }_2,{\omega }_3\}}^T\in {\mathbb{R}}^3$ is the spacecraft angular velocity expressed in the body reference frame.

Starting from the rigid body dynamics theory, as performed in [31], the spacecraft attitude dynamics is expressed as the conservation of the total angular momentum as the sum of the spacecraft’s elements and MED elements. In the inertial reference frame, the conservation of the angular momentum is given as

$$u_{ext}^I={\dot{h}}^I={\dot{h}}_{s/c}^I+{\dot{h}}_{med}^I$$

where $u_{ext}^I\in {\mathbb{R}}^3$ is the resultant external torque, and $h_{s/c}^I\in {\mathbb{R}}^3$ and $h_{med}^I\in {\mathbb{R}}^3$ are the spacecraft’s and resultant MED elements’ angular momentum, respectively. It is useful to express this relationship in the body reference frame (parameters with no apex are expressed in this reference frame). In this case, the attitude dynamics is expressed by

$$\dot{\omega }=J^{-1}\left(u_{ext}-{\dot{h}}_{med}-\omega \times J\omega \right)$$

(1)

where $J\in {\mathbb{R}}^{3,3}$ is the spacecraft inertia matrix and $h_{med}\in {\mathbb{R}}^3$ is the resultant MED elements’ angular momentum. For each reaction wheel, the applied torque is equal to the variation in time of the angular momentum, expressed in the wheels reference frame as

$$\tau ={\dot{h}}_{med}^w$$

where $\tau ,h_{med}^w\in {\mathbb{R}}^4$. Components${\tau }_i$ and $h_{med,i}^w$ represent the applied torque and angular momentum, respectively, of the i-th reaction wheel.

The definition of a rotation matrix is necessary to move from the wheels reference frame to the body reference frame, and it is properly defined from the geometric configuration. For this application, four reaction wheels are considered and are arranged in a pyramidal configuration. So, the spin axes of the wheels are pointing towards the faces of a pyramid with a square base. This means that the wheels are inclined with a fixed angle with respect to the base of the pyramid, generating torque along the height of the pyramid; the projections of the wheels’ momentum lie in the pyramid base, which generates torque along the last two directions.

Thus, the rotation matrix is defined as

$$Z=\left[\begin{array}{cccc}cos\left(\beta \right)cos\left(\alpha \right)& -cos\left(\beta \right)sin\left(\alpha \right)& -cos\left(\beta \right)cos\left(\alpha \right)& cos\left(\beta \right)sin\left(\alpha \right)\\ cos\left(\beta \right)sin\left(\alpha \right)& cos\left(\beta \right)cos\left(\alpha \right)& -cos\left(\beta \right)sin\left(\alpha \right)& -cos\left(\beta \right)cos\left(\alpha \right)\\ sin\left(\beta \right)& sin\left(\beta \right)& sin\left(\beta \right)& sin\left(\beta \right)\end{array}\right]$$

where $\alpha$ is the angle between the x-axis and the first reaction wheel, and $\beta$ is the angle between the plane xy and each reaction wheel, as shown in Figure 1. For this study, we considered $\alpha =0^{\circ }$ and $\beta ={60}^{\circ }$.

The reaction wheels dynamics can be expressed in the body reference frame including the rotation matrix Z as

$$Z\tau ={\dot{h}}_{med}+\omega \times Z{h}_{med}^w$$

Finally, the attitude dynamics, Equation (1), is combined with MED dynamics, and it is given as

$$\dot{\omega }=J^{-1}\left[u_{ext}-Z\tau -\omega \times \left(J\omega +Z{h}_{med}^w\right)\right]$$

(2)

where $J\in {\mathbb{R}}^{3\times 3}$ is the inertia matrix, $u_{ext}\in {\mathbb{R}}^3$ are the external disturbances, $\omega \in {\mathbb{R}}^3$ is the spacecraft angular velocity, $Z\in {\mathbb{R}}^{3\times 4}$ is the rotational matrix from the wheels to the body reference frames, $\tau \in {\mathbb{R}}^4$ is the torque applied to each reaction wheel, and $h_{med}^w\in {\mathbb{R}}^4$ is the angular momentum of each reaction wheel.

In order to simulate reaction wheels dynamics, a first-order filter is included in the model as a transport delay, as shown in Figure 1. ${\tau }_{cmd}\in {\mathbb{R}}^4$ is the control torque given by the controller and designed as

$${\tau }_{cmd}=Z^{+}u$$

where $Z^{+}\in {\mathbb{R}}^{4\times 3}$ is the pseudo-inverse matrix of Z. Note that, except for the NASA configuration with three RWs, it is necessary to allocate the three-axis control torque to the four wheels assembly. To accomplish this, it is common to use the Moore–Penrose pseudoinverse matrix, $Z^{+}$, as the non-square control allocation matrix $Z\in {\mathbb{R}}^{3\times 4}$ cannot be inverted.

3. Attitude Controller

In this section, the design process of the H${}_{\infty }$ control algorithm is described. First, the bounded real lemma is introduced and described. Then, the state-feedback controller for a small spacecraft equipped with reaction wheels is designed, where the controller gain is evaluated by solving an LMI problem. Finally, failures are introduced in the design process, helping to achieve a fault-tolerant control design.

Consider the continuous linear time-invariant (LTI) dynamical system, given as

$$\left\{\begin{array}{c}\dot{x}=Ax+B_{u}u+B_{w}w\hfill \\ z=C_{z}x+D_{u}u+D_{w}w\hfill \end{array}\right.$$

(3)

where $x={\{q_v,\omega \}}^T\in {\mathbb{R}}^6$ is the vector state, $u\in {\mathbb{R}}^3$ is the control input, $w\in {\mathbb{R}}^3$ is the disturbances vector, and $z\in {\mathbb{R}}^6$ is the system output. Using the state-feedback control policy, it leads to the closed-loop system

$$\left\{\begin{array}{c}\dot{x}=(A-B_{u}K)x+B_{w}w\hfill \\ z=(C_z-D_{u}K)x+D_{w}w\hfill \end{array}\right.$$

of which the corresponding transfer function is

$$\frac{Z\left(s\right)}{W\left(s\right)}=G\left(s\right)=(C_z-D_{u}K){(sI-A+B_{u}K)}^{-1}+D_w$$

The H${}_{\infty }$ norm of the LTI system is the induced energy-to-energy gain, defined as

$${\parallel G\left(s\right)\parallel }_{\infty }=\underset{\omega \in \mathbb{R}}{sup}\overline{\sigma }\left(G\left(j\omega \right)\right)$$

which is physically interpreted as the maximal gain of the frequency response of the system. However, the H${}_{\infty }$ norm cannot be analytically computed, and it has to be solved using numerical methods. In particular, a classification of numerical methods that are used to solve the problem can be found in [13].

According to the bounded real lemma, the closed-loop system is internally stable with

$${\parallel G\left(s\right)\parallel }_{\infty }<\gamma$$

if there is a positive definite symmetric matrix P [14] such that

$$\left[\begin{array}{ccc}{A}^{T}P+PA& PB& C^T\\ B^{T}P& -\gamma I& D^T\\ C& D& -\gamma I\end{array}\right]<0,P>0$$

where $\gamma >0$ is the H${}_{\infty }$ performance specification. The control problem is defined through the H${}_{\infty }$ sub-optimal control problem.

The controller is designed to ensure

$${\parallel G\left(s\right)\parallel }_{\infty }<\gamma$$

where $\gamma$ is pre-specified. However, the equation ruling the attitude dynamics of the spacecraft is not linear; thus, it is necessary to adapt the real system to a simplified mathematical model that is defined through the linearization of the equation in the neighborhood of the equilibrium condition, expressed by

$$x_0={\left\{\begin{array}{c}{q}_v\\ \omega \end{array}\right\}}_0={\{0,0,0,0,0,0\}}^T$$

The matrices A, $B_u$, and $B_w$ have been computed through the linearization of the system dynamics

$$\dot{x}=x_0+{\left(\frac{\partial \dot{x}}{\partial x}\right)}_{x=x_0}x+{\left(\frac{\partial \dot{x}}{\partial u}\right)}_{u=0}u+{\left(\frac{\partial \dot{x}}{\partial w}\right)}_{w=0}w$$

where $A\in {\mathbb{R}}^{6,6}$, $B_u\in {\mathbb{R}}^{3,6}$, and $B_w\in {\mathbb{R}}^{3,6}$ are the Jacobian matrices of $\dot{x}$ computed with respect to x, u, and w, respectively.

$$A=\left[\begin{array}{cccccc}0& 0& 0& \frac{1}{2}& 0& 0\\ 0& 0& 0& 0& \frac{1}{2}& 0\\ 0& 0& 0& 0& 0& \frac{1}{2}\\ 0& 0& 0& 0& \frac{h_{rw,3}}{J_x}& \frac{h_{rw,2}}{J_x}\\ 0& 0& 0& \frac{h_{rw,3}}{J_y}& 0& -\frac{h_{rw,1}}{J_y}\\ 0& 0& 0& -\frac{h_{rw,2}}{J_z}& \frac{h_{rw,1}}{J_z}& 0\end{array}\right]B_u=B_w=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ \frac{1}{J_x}& 0& 0\\ 0& \frac{1}{J_y}& 0\\ 0& 0& \frac{1}{J_z}\end{array}\right]$$

For what concerns $C_z$, $D_u$, and $D_w$, it is possible to follow the same approach of the equation that is used to describe the measurements, but for the purposes of this study, we chose to assume $C_z\in {\mathbb{R}}^{6,6}$ as the identity matrix $I_6$ and $D_u,D_w\in {\mathbb{R}}^{3,6}$ as the null matrices.

Linear controllers also require the system to be controllable and observable. The controllability is expressed by the matrix $\mathcal{C}$, which is defined as

$$\mathcal{C}=\left[\begin{array}{ccccc}B& AB& A^{2}B& \cdots & A^{n-1}B\end{array}\right]$$

where $A\in {\mathbb{R}}^{n,n}$ and $B\in {\mathbb{R}}^{r,n}$. The system is fully controllable if $\mathcal{C}$ is a full row rank

$$rank\left(\mathcal{C}\right)=n$$

The observability is expressed by the matrix $\mathcal{O}$, which is defined as

$$\mathcal{O}=\left[\begin{array}{ccccc}C& CA& C{A}^2& \cdots & C{A}^n\end{array}\right]$$

and the system is fully observable if $\mathcal{O}$ is a full row rank

$$rank\left(\mathcal{O}\right)=n$$

The linearized system is fully controllable and observable, fulfilling all of the requirements for the linear controllers.

3.1. State-Feedback Controller

The proposed control method consists of a state-feedback H${}_{\infty }$ controller that is designed to solve an LMI problem. As already defined in the previous paragraph, a linearized dynamic system (i.e., an LTI system, as in Equation (3)) is considered. The control policy is defined as

$$u=-Kx$$

such that it has

$${\parallel G\left(s\right)\parallel }_{\infty }<\gamma$$

As previously mentioned, applying the bounded real lemma to the closed-loop system is equivalent to solving the following LMI problem

$$\left[\begin{array}{ccc}AQ+Q{A}^T+B_{u}Y+Y^T{B}_u^T& Q{C}_z^T+Y^T{D}_u^T& B_w\\ C_{z}Q+D_{u}Y& -{\gamma }^{2}I& D_w\\ B_w^T& D_w^T& -1\end{array}\right]<0$$

(4)

$$Q>0$$

where the matrix is identified as M, and $Q\in {\mathbb{R}}^{6,6}$, $Y\in {\mathbb{R}}^{3,6}$ and $\gamma >0$ are the problem variables. The solution of these LMIs is processed using a mathematical solver. In particular, Mosek [32] integrated Matlab with the Yalmip [33] package, which is used for the evaluation of the H${}_{\infty }$ suboptimal state-feedback controller; the author defined the gain matrix K.

The matrix A is subjected to uncertainties that are related to the value of reaction wheels’ angular momentum. Considering N values of $h_{rw,i}$ within the working range, it is possible to build different $A_j$ matrices for each $h_{rw,i}$ combination of values. For each $A_j$ matrix, an $M_j$ matrix is built from Equation (4). All of the $M_j$ matrices are included in the LMI problem to achieve a unique state-feedback controller K

$$\begin{array}{c}{M}_1<0\\ M_2<0\\ ⋮\\ M_m<0\\ Q>0\end{array}\to K=Y_{sol}{Q}_{sol}^T$$

(5)

The controller gain K is defined considering a large combination of the reaction wheels’ angular momentum. In this way, the controller guarantees system robustness to the uncertainties regarding the reaction wheels’ angular momentum.

3.2. Uncertainties in the $B_u$ Matrix

The reaction wheels’ failure is considered as uncertainty in the matrix $B_u$. First, the actuator health indicator (AHI) matrix is defined as

$$AHI=\Delta =\left[\begin{array}{cccc}{\delta }_1& 0& 0& 0\\ 0& {\delta }_2& 0& 0\\ 0& 0& {\delta }_3& 0\\ 0& 0& 0& {\delta }_4\end{array}\right]$$

where ${\delta }_i$ indicates the status of the i-th reaction wheel. It is a scalar value between zero and one, where zero represents a failed reaction wheel and one represents a healthy one. It is possible to rewrite the spacecraft attitude dynamics equation to include the AHI

$$J\dot{\omega }=u_{ext}-Z\Delta \tau -\omega \times \left(J\omega +Z{h}_{med}^w\right)$$

In the nominal case, when all of the reaction wheels are working, it is verified that

$$Z\Delta \tau =Z\tau$$

In the case of failure, the ratio between the component of $Z\Delta \tau$ and $Z\tau$ is not equal to one, and it is used to represent the $B_u$ uncertainties. Defining

$$b_i=\frac{{(Z\Delta \tau )}_i}{{\left(Z\tau \right)}_i}$$

where $b\in {\mathbb{R}}^3$ is the actuators’ uncertainty vector, and $B_u$ is corrected as

$${\left(B_u\right)}_{un}=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ b_1/J_x& 0& 0\\ 0& b_2/J_y& 0\\ 0& 0& b_3/J_z\end{array}\right]$$

The operation used for the A matrix uncertainties is applied to each failure case. All of the $M_i$ matrices are included to generate a single state-feedback controller K

$$\begin{array}{c}{M}_1<0\\ M_2<0\\ ⋮\\ M_{5m}<0\\ Q>0\end{array}\to K=Y_{sol}{Q}_{sol}^T$$

(6)

The new design process for K allows the controller to guarantee system robustness to failure.

4. Reaction Wheels Failure Identification and Control Correction

In this section, the observer design for the failure and disturbances estimation is addressed. First, a sliding mode observer is designed to detect and identify the failure in the actuation systems. Then, a second sliding mode observer is designed to estimate the disturbances acting on the spacecraft. Finally, the disturbances are coupled with the control input in order to improve the controller performance.

The problem of fault diagnosis can be seen as the problem of identifying and reconstructing unknown inputs. The identification of the failing reaction wheel can be used to improve the controller’s performance during the maneuver. Considering the following nonlinear system described by

$$x^{\left(n\right)}=g(x,t)$$

where $g(x,t)$ is a nonlinear, uncertain function and $x_1$ is the measurement.

The Slotine’s observer [34] is defined as

$$\left\{\begin{array}{c}{\dot{\widehat{x}}}_1=-{\alpha }_1{e}_1+{\widehat{x}}_2-k_1\mathrm{sign}\left(e_1\right)\hfill \\ {\dot{\widehat{x}}}_2=-{\alpha }_2{e}_1+{\widehat{x}}_3-k_2\mathrm{sign}\left(e_1\right)\hfill \\ \cdots \cdots \hfill \\ {\dot{\widehat{x}}}_n=-{\alpha }_n{e}_1+\widehat{g}-k_n\mathrm{sign}\left(e_1\right)\hfill \end{array}\right.$$

(7)

where ${\alpha }_i$ is chosen to ensure asymptotic error decaying when $k_i=0$; for a Luenberger observer [27,35], $e_1={\widehat{x}}_1-x_1$ is the observer output error, and $\widehat{g}$ is an estimation of $g(x,t)$. The ability to generate a sliding motion between the measured plant output and the output of the observer ensures that a sliding mode observer produces a set of state estimates that are precisely commensurate with the actual output of the plant [36,37,38].

The reaction wheel fault has been estimated while considering a fault model within the reaction wheels dynamics as

$${\dot{h}}_{rw}=\tau +f$$

(8)

where $f\in {\mathbb{R}}^4$ represents the faulty function. The estimation of the faulty function is addressed by the SMO. Considering the angular momentum of each reaction wheel as the observer input, it is possible to identify when a reaction wheel is failing, and it is possible to reconstruct the fault signal.

Starting from Equations (7) and (8), the SMO is designed as

$$\left\{\begin{array}{c}{\dot{\widehat{h}}}_{rw}=\tau +\widehat{f}+k_1\mathrm{sign}(h_{rw}-{\widehat{h}}_{rw})\hfill \\ \dot{\widehat{f}}=k_2\mathrm{sign}(h_{rw}-{\widehat{h}}_{rw})\hfill \end{array}\right.$$

(9)

A secondary observer is designed to estimate the disturbances acting on the spacecraft dynamics. First, the ideal behavior of each reaction wheel is supposed so as to have

$${\dot{h}}_{rw}^{*}=\tau$$

Then, after the failure case is determined from the output of Equation (9), it is included in the reaction wheels model as

$${\dot{h}}_{rw}^{*}=\widehat{\Delta }\tau$$

(10)

The secondary SMO is designed as

$$\left\{\begin{array}{c}\dot{\widehat{\omega }}=J^{-1}\left[-Z\tau +\widehat{d}-\omega \times \left(J\omega +Z{h}_{rw}^{*}\right)\right]+k_3\mathrm{sign}(\omega -\widehat{\omega })\hfill \\ \dot{\widehat{d}}=k_4\mathrm{sign}(\omega -\widehat{\omega })\hfill \end{array}\right.$$

(11)

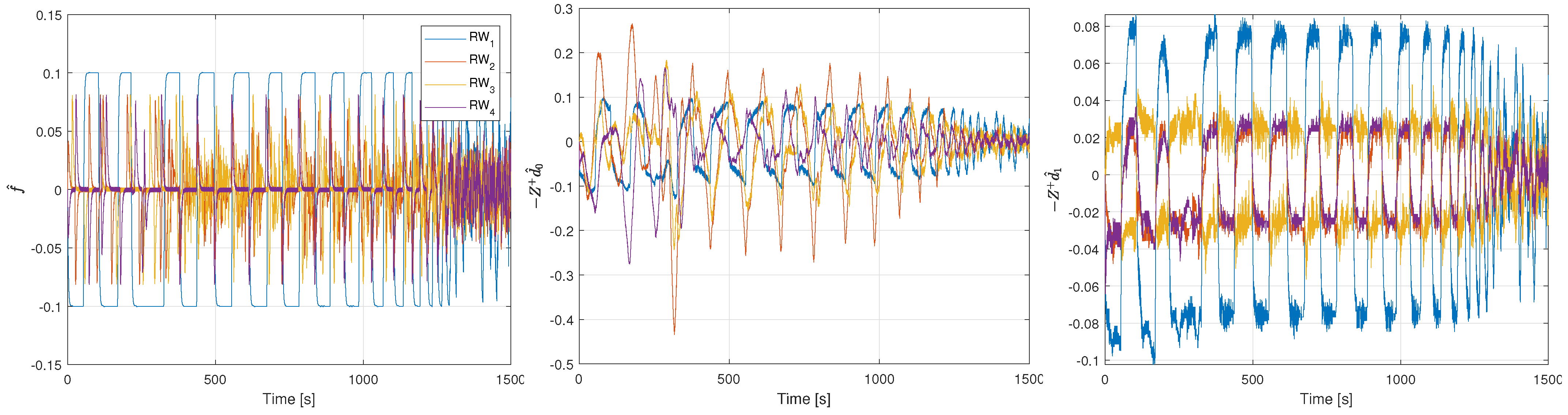
where $\widehat{d}\in {\mathbb{R}}^3$ is the estimation of the disturbances acting on the spacecraft; it takes into account the external disturbances and failure. Considering the ideal case, with $u_{ext}=0$, the disturbances should match the effects of the fault signal $\widehat{f}$, and this is true if Equation (10) matches the correct failure case. Evidence regarding this is provided in Figure 2 where the failure is estimated from $\widehat{d}$ as $-Z^{+}\widehat{d}$ while assuming different failure cases in the observer model.

The left plot from Figure 2 shows the failure estimation from Equation (9) and reports the first reaction wheel failing. The spikes are due to reaction wheels dynamics and the delay generated by the filter between the torque application and angular momentum change. This effect is not present in the other plots, as the observer takes advantage of an ideal reaction wheel model. The center plot shows the failure estimation from Equation (11) assuming no failure, which achieves no matching with the failure case. Finally, the right plot shows the failure estimation from Equation (11) when assuming that the first reaction wheel fails, matching the failure case.

Finally, the disturbances are partially recovered by the remaining reaction wheels by considering

$$\tau =\mathrm{sat}(-\mathrm{sat}\left(Z^{+}{u}_{cmd}\right)-Z^{+}(\widehat{d}-Z\widehat{f}))$$

(12)

where the sat$(·)$ function is the saturation of the control torque according to the maximum and minimum requirements.

5. Simulations Results

In this section, extensive simulations are carried out to evaluate the controller’s performance. The LMI-based robust design was proposed to achieve fault-tolerant controllers for space applications. In particular, small spacecraft equipped with reaction wheels are considered for their sensitivity to failure and external perturbation.

Considering the model of the spacecraft attitude dynamics as expressed by Equation (2), the capability of the controller to stabilize the spacecraft with failure and perform a pointing maneuver was investigated. The attitude controller was defined as a state-feedback controller, taking into account both the rotation and angular velocity of the spacecraft. A sliding mode observer was considered to detect and identify the failure (Equation (9)). Then, considering the failure, a secondary observer, Equation (11), was designed to estimate the disturbances acting on the spacecraft. Disturbances estimation takes into account both the failure recovery and external disturbances, and it was coupled with the controller input to improve its effectiveness.

In order to consider a detailed model, sensors noise that was based on real sensors was also included. The attitude measurement noise was modeled according to [39], where two star-tracker sensors were combined with an IMU, providing the attitude with a 10 arcsec accuracy at 10 Hz. The angular velocity was measured at 50 Hz while considering a gyroscope model based on stim380h [40] (noise power spectral density $0.8462·{10}^{-9}$(rad/s)${}^2$/Hz). For the first observer, the reaction wheels’ angular momentum was assumed to be measured at $10$ Hz with an accuracy of ${10}^{-5}$ kg m${}^2$s${}^{-1}$.

First, the H${}_{\infty }$ state-feedback controllers were compared while considering the formulations from Equations (5) and (6) and with the inclusion of the proposed disturbances correction algorithm Equation (12).

In Figure 3, the spacecraft stabilization from random initial conditions is considered, and a comparison between the design approach is made. The inclusion of the failure in the evaluation of the H${}_{\infty }$ state-feedback controller was mandatory to achieve the desired robustness to the failure of one reaction wheel. In the right plot from Figure 3, with the controller in the state matrix (only A uncertainties), the closed-loop system does not converge to the desired value.

In Figure 3 and Figure 4, a comparison is also made between the H${}_{\infty }$ state-feedback controller with and without the correction algorithm. The proposed approach significantly reduces the time required to accomplish the stabilization, with comparable accuracy for both cases. The simulation results proved that including failures as uncertainties in the controller design allowed us to design a robust, failure-tolerant controller. The proposed corrective algorithm does not affect the system’s capabilities to withstand failures, but it is helpful in the stabilization process by reducing the maneuvering time.

Finally, a simulation campaign was carried out to point out the effectiveness of the augmented controller. The simulation parameters are reported in

Table 1. Simulation parameters.

Parameter	Value/Range
Inertia matrix [kg/m${}^2$]	diag ([25 50 50])
RW inertia [kg/m${}^2$]	0.022
Maximum torque [Nm]	±0.1
External disturbances [Nmm]	[−0.1, 0.1]
Initial attitude [${}^{\circ }$]	[−25, 25]
Initial angular velocity [mrad/s]	[−5, 5]

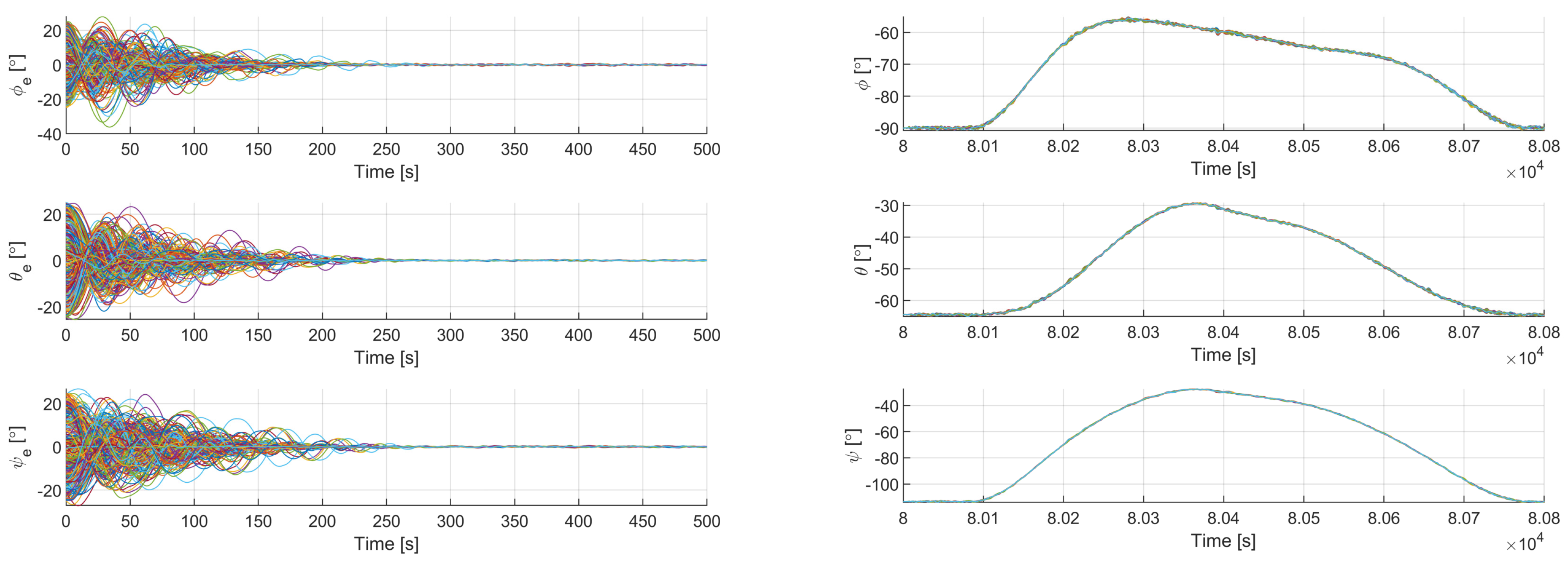
. The considered spacecraft follows in the small spacecraft category, with a mass of $200$ kg. The initial conditions and external disturbances are changed in each simulation while considering random values. In the left plot of Figure 5, the attitude time variation for the spacecraft stabilization of different initial conditions is shown, considering random external disturbances and failure cases. Moreover, to test the reliability and robustness of the controller, a real mission scenario was considered. The Earth observation consisted of an 86,400 s mission, where the attitude was kept in the same configuration for most of the time, and the actual maneuver lasted for 659 s. In the right plot from Figure 5, only the part concerning this maneuver is reported. The maneuver can be described in three phases. Firstly, there is a transitional phase, where the spacecraft moves from the initial configuration to the desired configuration. Then, a scientific phase occurs, in which the spacecraft moves according to the mission-chosen path. Finally, the spacecraft returns to its initial configuration after a second transitional phase. The proposed algorithm was able to accomplish the desired tasks in all of the considered scenarios.

6. Conclusions

In this study, a fault-tolerant robust controller design was addressed for small spacecraft attitude control. Robust controllers are adopted to deal with bounded system uncertainties. In particular, an H${}_{\infty }$ controller was designed as a spacecraft attitude controller and started from the LMI formulation to achieve robustness for bounded plant uncertainties. A spacecraft equipped with four reaction wheels was considered. Failures were modeled and included in the design process as plant uncertainties. The H${}_{\infty }$ suboptimal problem was then solved for the definition of the feedback controller gain. However, despite the controller being robust to the failure when it occurs, the system results are more sensitive to perturbations. For this reason, an active strategy based on failure identification and control correction was included. First, an observer was designed to detect the failure and identify the failing reaction wheel. Then, considering the presence of the failure, the disturbances acting on the spacecraft dynamics were estimated by means of a second observer. The disturbances take into account external disturbances, failure effects, and sensor uncertainties. The controller input was then coupled and corrected with the estimated disturbances, improving controller performance. By means of extensive simulation, the controller performance was investigated by considering random initial conditions and external disturbances.

The simulation results verify the controller robustness, and the proposed control correction shows a significant performance improvement in terms of the amount of time needed to accomplish the maneuver. The accuracy is compromised by the high sensor uncertainties; it could be improved by implementing a navigation algorithm, but that is not the main purpose of this work. However, the controller robustness to sensor uncertainties is verified, which was also verified while considering the controller reliability in an Earth observation mission scenario. The proposed study addresses the design of a simple and low computational cost technique for failure-tolerant attitude control. However, some aspects can be further improved in future studies. The desired controller is able to satisfy the requirements, but this design method makes the tuning process not trivial. Different approaches may be investigated to improve controller tuning according to system requirements. Moreover, failure identification is based on reaction wheel data and can be further improved. More sophisticated techniques may be considered (i.e., machine learning and artificial intelligence) to detect and identify the failure. Finally, robustness to multiple failures may be addressed, evaluating the proposed design approach or possible action plan to avoid complete mission failure.