Featured Application
The algorithm can be used to develop cryptographic protection for data transmission in front and back-end systems. As the algorithm does not require key distribution, it also has applications in the distributed domain.
Abstract
This paper provides a systematic analysis of existing resource platforms, evaluating their advantages and drawbacks with respect to data privacy protection. To address the privacy and security risks associated with resource platform data, we propose a novel privacy protection algorithm based on chunking disorder. Our algorithm exchanges data within a specific range of chunk size for the position and combines the chunked data with the MD5 value in a differential way, thus ensuring data privacy. To ensure the security of the algorithm, we also discuss the importance of preventing client and server decompilation during its implementation. The findings of our experiments are as follows. Our proposed privacy-preserving algorithm is extremely secure and easy to implement. Our algorithm has a significant avalanche effect, maintaining values of 0.61–0.85, with information entropy being maintained at 4.5–4.9. This indicates that our algorithm is highly efficient without compromising data security. Furthermore, our algorithm has strong encryption and decryption time stability. The key length can be up to 594 bits, rendering it challenging to decrypt. Compared with the traditional DES algorithm, our algorithm has better security under the same conditions and approaches the levels of security offered by the AES and RC4 algorithms.
1. Introduction
With the continuous improvement of infrastructure network facilities in universities and the deepening of education reform, the use of information technology as an aid to improve the cross-collaboration of disciplines between colleges and the coordinated development of multiple disciplines has become the general idea of university construction, in which the resource platform has a vital position. Many universities have seriously thought about how to provide students with rich educational resources that suit their needs and are personalized and have developed various resource platforms for this purpose. These resource platforms provide teachers with rich course resources, electronic lesson plans, courseware, and exercise libraries. They also facilitate students’ ability to learn what they are interested in at any time and anywhere.
This paper intends to address the data protection issue in constructing resource platforms. To this end, we propose a chunked and disordered exchange algorithm that has been successfully applied in a resource-sharing platform. Our algorithm ensures high security standards by processing data in chunks and encrypting it according to specific chaotic order rules. As a result, data become more secure and reliable during transmission and storage. The contributions of this paper are shown below:
- A chunked and disordered symmetric encryption algorithm is proposed: This a highly secure algorithm that makes data transmission more secure and reliable by chunking the data and encrypting it according to specific disordered rules.
- It is successfully applied to a resource-sharing platform, and the algorithm provides a more secure data transmission for the platform users.
- A new idea is provided in the field of cryptography that enhances the richness of the variety of encryption algorithms and improves the security of encryption algorithms.
This paper will examine the following aspects.All abbreviations in this document are detailed in Appendix A.
Related Work: This section provides a concise overview of the challenges related to data protection on the current resource platform. An introduction is also given to the current encryption algorithm being utilized, which involves chunking and disordering the data for increased security.
System Architecture: The main focus of this section is on the technical components used in the front and back end of the resource platform and the overall hierarchical call approach. It also covers the system’s operation and the maintenance of the resource platform.
The Encryption Process: This process consists of three parts: internally defined chunking chaos rules, differential bit combinations, and critical information extraction. Among them, two MD5 values are used for double-checking to ensure the validity of the information.
Algorithm Deployment: In this section, the algorithm is packaged into a jar file, imported under the Maven control tool of the resource platform system, and finally called directly into the system.
Experimental Results and Analysis: The avalanche effect of the chunked and garbled encryption algorithm is compared with the DES, AES, and RC4 encryption algorithms for different plaintext encryption lengths. In addition, the security of this chunked chaotic algorithm is also discussed in terms of information entropy and algorithmic attacks.
Algorithm Evaluation: The security of this chunked chaotic algorithm without secret key distribution is discussed, mainly based on the experimental results.
Conclusion and System Evaluation: How the application of the present block disorder algorithm improves the security of the resource platform system is discussed, and future work and directions of improvement for the current algorithm are also proposed.
2. Related Work
A system that was designed for cloud course resource management uses Hadoop’s highly available components for extensive data analysis and application course resource management, improving resource sharing and utilization rate and providing better services for teachers and students [1]. By adopting a cloud platform, colleges can achieve the integration, efficiency, scalability, and interactivity of English resource bases, thus solving problems related to resource utilization [2]. Several learning resource-sharing platforms have been developed to address the problems of the low utilization and high repetition rates of educational resources in universities. One platform used the SSM framework, which facilitates undergraduate students’ access to learning resources [3]. Multimedia and network technologies have been employed to provide students and teachers with the latest technological trends and integrate a variety of high-quality teaching resources on an IT platform to promote common sharing [4]. A video resource management system, which utilizes microgrid technology and ASP.NET, has been designed to meet universities’ teaching needs [5]. Cloud technology has been shown to integrates multimedia resources, such as text, images, and videos, more transparently and vividly [6]. An evaluation index system has been built based on cybernetics principles to divide the platform’s overall network structure and effectively realize sports educational resource sharing [7]. An intelligent cloud service platform for education has been constructed to ensure the fair distribution and high utilization rates of high-cost resources when multiple groups of time-varying resource demands are put forward [8]. Furthermore, a platform that accurately recommends relevant innovation and entrepreneurship resources using SSH2 technology has been designed [9]. A management platform has been designed to develop and utilize power infrastructure resources to achieve agility in business processing and the unified management of resources [10].
In the above literature, the construction of the information security of the resource platform is rarely mentioned. Most of the relevant resources for resource platforms are publicly released on the Internet, so there is a certain degree of security risk. As time goes by, more and more users use the resource platform to obtain relevant teaching materials and hope to obtain more and better resources. Therefore, ensuring that many teaching resources stored on the resource platform can be recovered and protected for various reasons is imperative [11,12,13]. Ensuring the confidentiality, integrity, and availability of the information in resource platforms has become an urgent problem to be solved. At present, many universities have taken measures to protect the security of the resource platform, such as purchasing genuine software, installing anti-virus software, updating patches regularly, and so on. Although this does play a specific role, there are still some things that could be improved. For example, due to the complexity of schools’ intranet environments, there are many kinds of viruses that can easily cause severe consequences if there is a vulnerability. In addition, if everyone downloads the latest version of the software, the server will be overstressed and not function properly. Therefore, finding new ways to secure resource platforms is vital [14,15,16,17].
Encryption algorithms in cryptography are usually divided into two categories: symmetric encryption methods and asymmetric encryption methods [18,19,20,21]. Symmetric encryption algorithms can be divided into public-key encryption (PKE) and private-key encryption (PKE), both of which are effective methods for securing data. When sent to the receiver, the public-key encryption algorithm encrypts plaintext with a public key. The receiver receives the ciphertext and then decrypts it with this key to obtain the original plaintext. On the contrary, a private-key encryption algorithm can only open a file with the corresponding private key. An asymmetric encryption algorithm means the same person does not perform the encryption and decryption processes; the “public key” and “private key” are different.
At present, many scholars have proposed many solutions for information security technologies, such as digital watermarking technology, authentication technology, and access control technology [22,23,24,25,26,27,28,29,30]. However, these technologies all have one thing in common, which is that they need to modify the whole system or redevelop a new system to realize its functions; this, in turn, leads to problems such as high costs or long cycle times. Although these methods can protect the information in the resource platform, all of them have some shortcomings in one way or another. The commonly used information encryption and decryption algorithms have problems related to key distribution, which may cause indelible losses if the key is leaked or the system is accessed by lifting rights in an open and complex network architecture [31,32,33,34,35]. In some scenarios with high-security-factor requirements, multiple DES is usually used, which further increases the algorithm’s complexity by multiple iterations and improves the security of encrypted data to some extent. However, the complexity of its decryption will inevitably consume too many of the system’s arithmetic resources [36]. Among the asymmetric encryption algorithms, RSA still has a tedious public key generation process due to the limitation of large prime number generation technology, which struggles to meet the requirement of “one key at a time” in distributed and open-network environments. Therefore, asymmetric encryption is difficult to use in open and temporary environments.
In order to overcome the shortcomings of the above traditional algorithms, this paper proposes a new algorithm, the chunking disorder algorithm. The main idea of this algorithm is to break up the plaintext into several small segments, then rearrange and combine them into ciphertext, and finally use the corresponding algorithm to complete the decryption work. This algorithm dramatically reduces the computational effort required and avoids the problem of key distribution. At the same time, it does not require additional hardware support but only requires the integration the relevant algorithm on the server side to run. The algorithm has good pervasiveness and can be applied to systems and platforms of any size to provide error-free encryption and decryption services. The proposed chunking disorder algorithm is executed by user-selected iterations, N. The original data are chunked according to a specific chunk size, and the chunked data are randomly selected for execution by one set of location-swapping algorithms. The data after completing one encryption generate a sharing code according to the logic at the time of encryption and then iterate N times to stitch the sharing code and take the MD5 value of the original data and the encrypted data, respectively. The algorithm then combines the MD5 value, the ciphertext, and the sharing code difference to complete the encryption of the plaintext. Due to the uncertainty of the number of iterations, n, and, thus, the length of the sharing code, the encryption mechanism of this algorithm is superior to that of the DES algorithm under the same conditions. This algorithm solves the security problem caused by key distribution, which must ensure that the client and server cannot be decompiled.
In this paper, based on the current research results, we adopt a simple and effective method of deploying the chunked disorderly algorithm to the back-end separately and then combine it to complete the design and implementation of the whole system for a specific project requirement. This method can reduce not only the system’s complexity but also improve the scalability of the system and the ease of maintaining and upgrading it.
3. System Architecture of Resource Platform
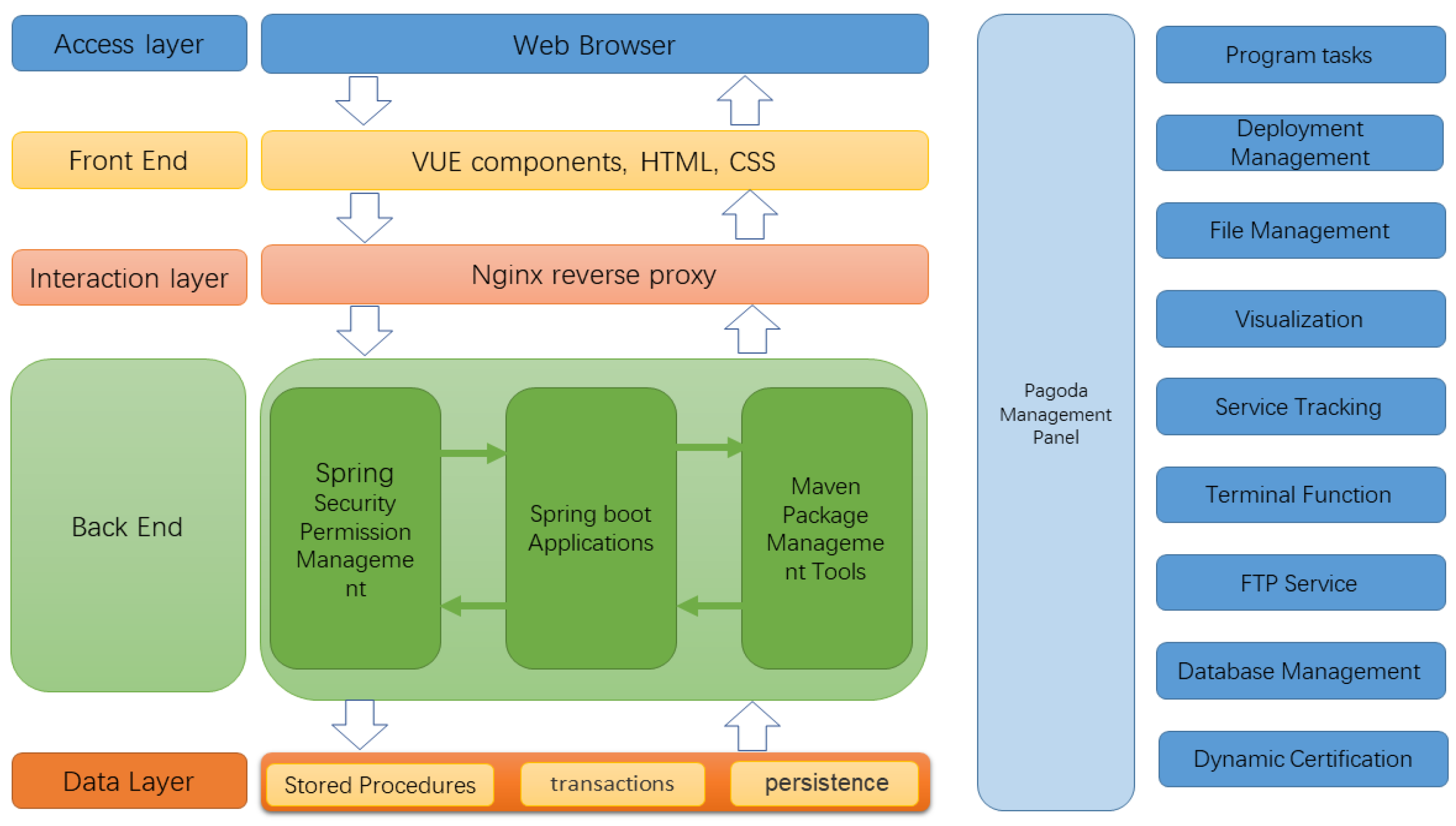
The entire system is divided into five software-level layers, which are, from the bottom to the top, the basic data layer, the back-end, the interaction layer, the front-end, and the access layer. The data layer serves as the persistence support for the whole system, providing relevant data to external services through connection pools. Specifically, it contains relevant stored procedures and predefined transactions. The back-end mainly uses the Spring Security framework to classify access to requests and deploy the Spring application on the server to manipulate various types of data. The interaction layer mainly uses the Nginx server to handle the upper application requests. It accesses the back-end server through interface-routing hops according to the configuration file format to achieve load balancing [37]. The front-end is mainly the display part of the page, developed by Hyper Text Markup Language (HTML), Cascading Style Sheets (CSS) for page rendering, and finally integrated by the Vue front-end tool. The access layer is how users access the resource platform using tools such as browsers. The system uses a front-end and back-end deployment approach, with the front-end using the Vue framework and the back-end using the Spring Boot framework for development [38,39] through the Maven packaging tool for deployment. The data storage uses the MySQL database to store project details and teacher account information for the subsequent release of shared resources. The Spring Security framework is used for the security verification of the website and user authentication. The front- and back-end separation architecture of the system is shown in Figure 1.
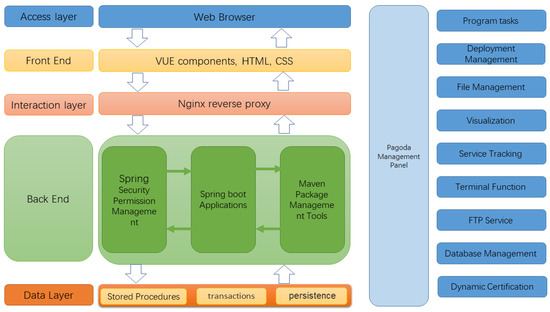
Figure 1.
Resource platform architecture diagram.
4. Encryption Process
The encryption process can be described according to three aspects: the chunking disorder process, the data combination process, and the ciphertext-splitting process.
4.1. Chunking Disorder Process
Upon receiving the number of iterations m, a set of chaotic swapping algorithms is generated within the system, which consists of the following four parts.
In adjacent parity exchange, the first and second blocks of the chunked data are exchanged, the third and fourth blocks are exchanged, and the penultimate block is exchanged with the last block. The head and tail engage in a pattern of decreasing exchange; that is, after chunking, the head and tail of the data block exchange positions until they have exchanged with the middlemost two. The specific position of the first block of data after chunking with the last block must exchange the second block with the penultimate block of data until the exchange between the middlemost two blocks is complete. Adjacent odd blocks are exchanged by swapping each of the two odd bits of data from the beginning. Adjacent even blocks are swapped by swapping each of the two even bits of data from the header.
Moreover, the above algorithm is labeled as One, two, three, and four at a time for the chaotic exchange process, as shown in Table 1 (suppose the plaintext is 123456789 and the chunk size is 2).

Table 1.
Diagram of chunked disorderly exchange.
The pseudo-code of the disordered exchange Algorithms 1–4 is as follows:
| Algorithm 1 Parity of exchange | |
| Require: | ▹ Data to be chunked |
| for to do | |
| ▹ Exchange | |
| end for | |
| Algorithm 2 HeadTail of exchange | |
| Require: | ▹ Data to be chunked |
| while do | |
| ▹ Exchange | |
| end while | |
| Algorithm 3 Odd of exchange | |
| Require: | ▹ Data to be chunked |
| for to do | |
| ▹ Exchange | |
| end for | |
| Algorithm 4 Even of exchange | |
| Require: | ▹ Data to be chunked |
| for to do | |
| ▹ Exchange | |
| end for | |
The data are combined based on the above-mentioned chunking disorder rules in the following way:
- Generate a random integer n as the random chunk size, chunk the plaintext message according to the random chunk size n, record the message length as the length, and obtain the chunk string S.
- If the last chunk length does not satisfy the chunk size n, then the last unsatisfied chunk is treated as a separate chunk, and finally, the number of chunks is counted.
- In the chunking process, the chunk size interval is defined as [2, 9].
- Generate a random integer T as the selected chaotic exchange algorithm number. Select the chaotic exchange algorithm corresponding to this number and perform a chaotic exchange of the current chunk string S according to the corresponding algorithm.
- Splice the chunk size n of the data with the algorithm number T to obtain a sharing code .
- Iterate the above process m times; then, splice the sharing code of the m times chaotic exchange in order to obtain the final sharing code FinalKey and the encrypted data SplitSTR. Record the length of the sharing code FinalKey as K.
- Adopt the 16-bit lowercase in MD5 encryption. Take the MD5 value to the plaintext message to define the data as N, and take the MD5 value to the encrypted data SplitSTR string MD5 value to define the encrypted data as M.
4.2. Data Combination Process
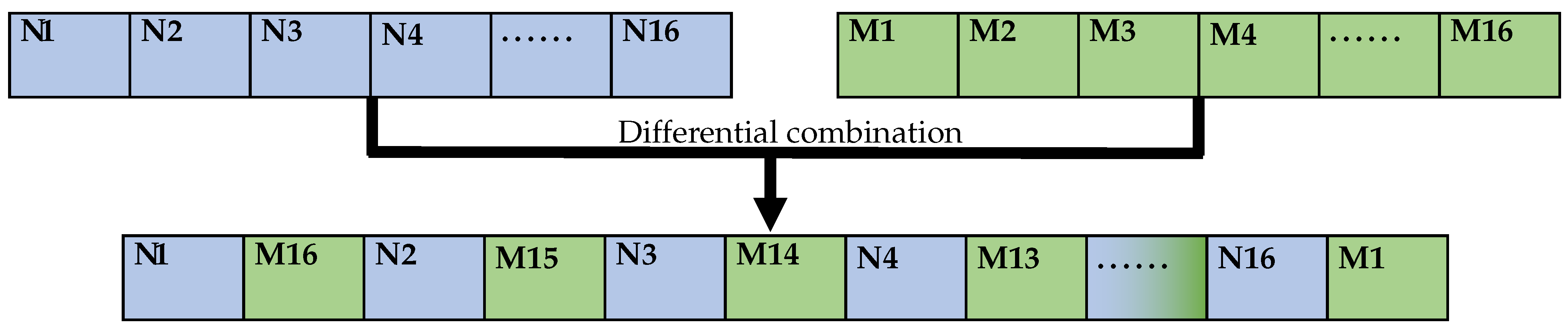
The MD5 value M of the encrypted data SplitSTR is inverted and used as the even bits of the string TS, and the MD5 value N of the plaintext message is used as the odd bits of the string TS, thus completing the combination of the two MD5 values. The combination process is shown in Figure 2.
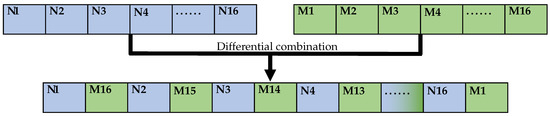
Figure 2.
Combination of MD5 values.
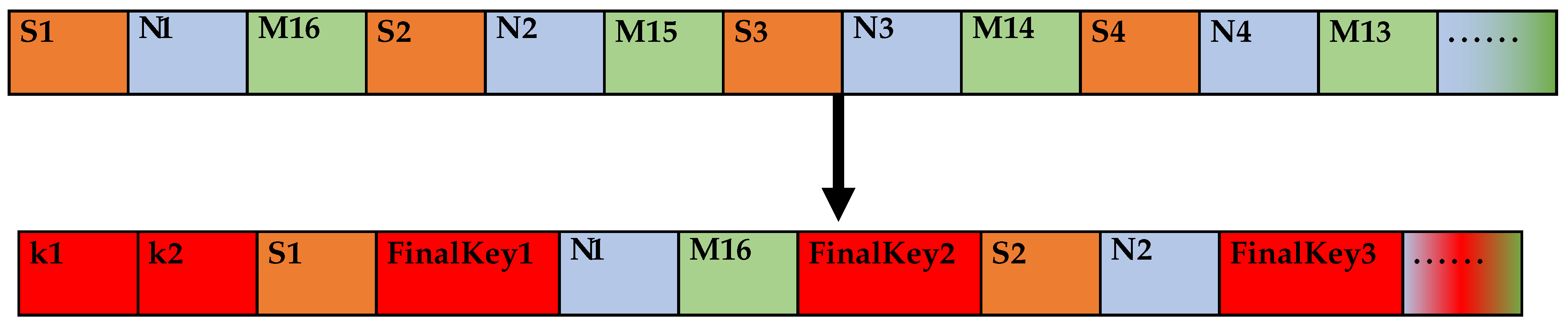
The combined MD5 value is inserted into the encrypted data SplitSTR by taking two intervals at a time.
- One sharing code is inserted in order from the first bit after the interval of 2 bits. If it exceeds the data length, the remaining sharing code is added to the end of the data to generate the final transmission control character.
- The sharing code length K is inserted into the first part of the data. If it is less than 2 bits, a leading 0 is added.
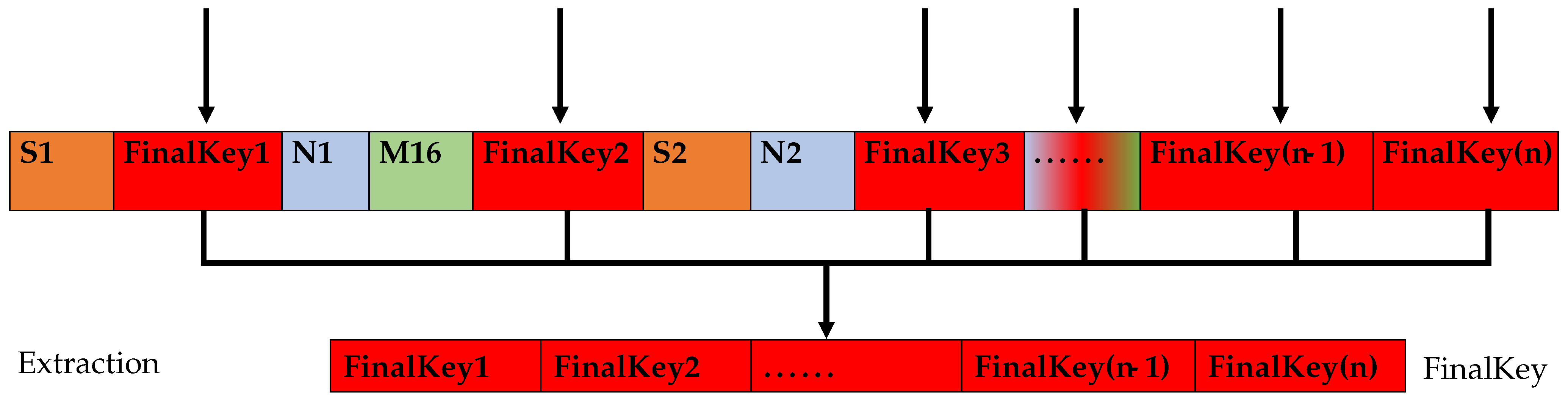
- Finally, the data are generated as the ciphertext FinalSTR. The sharing code insertion process is shown in Figure 3.
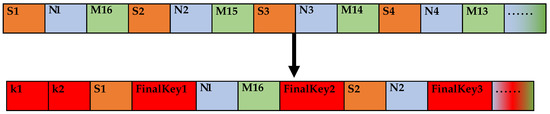 Figure 3. Sharing code insertion process.
Figure 3. Sharing code insertion process. - S1, S2, … denoteindicate the data in the messy encrypted data string SplitSTR.
- N1, N2, … denote the data of the plaintext message with their MD5 values.
- M1, M2, … denote the data of the encrypted data SplitSTR with MD5 values.
- K1, K2, … denote the data regarding the sharing code’s length.
- FinalKey1, FinalKey2, … denote the sharing code’s data.
4.3. Ciphertext Splitting
The relevant information is extracted continuously from the combined data in the following order: the length of the sharing code, the sharing code, the MD5 value, and the remaining chunked and disordered data after extraction.
4.3.1. Take Out the Length of the Sharing Code
The first two bits are extracted from the ciphertext FinalSTR to obtain the sharing code length K. Since the sharing code length is less than 2 bits, a leading 0 will be added, so the final extracted sharing code length will have two bits, which are recorded as k1 and k2.
4.3.2. Take Out the Sharing Code
Calculate the mid-length of the ciphertext FinalSTR.
Calculate and round down to nums, extract the sharing code and the length of the sharing code from the ciphertext FinalSTR so that only the final scrambled encrypted data string and the combination of two MD5s are left in FinalSTR.
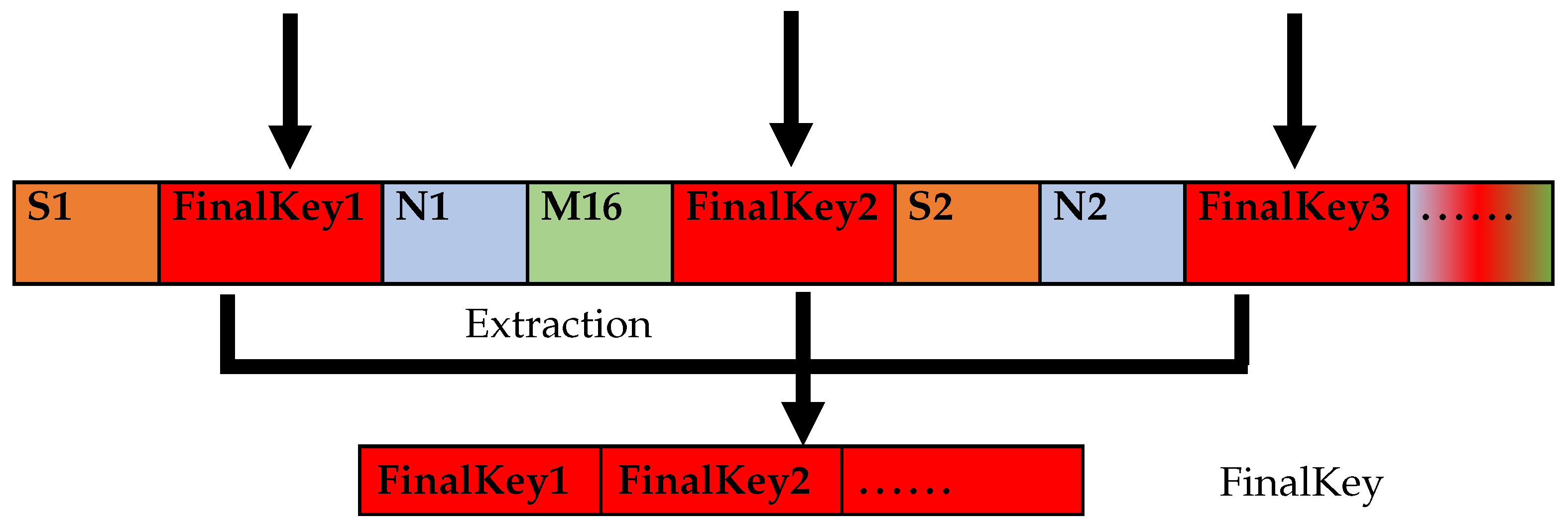
If , all sharing codes can be inserted at intervals of two bits, and the sharing codes are extracted from the third bit of the data transmission string FinalSTR at intervals of two bits to restore the original sharing code FinalKey, as shown in Figure 4.
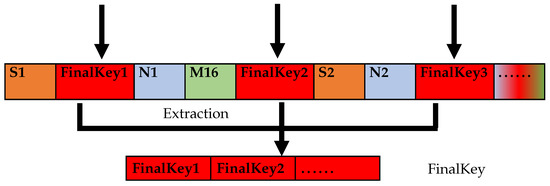
Figure 4.
sharing code extraction format.
If , we cannot insert all the sharing codes in two intervals, and some of the sharing codes are placed at the end of the FinalSTR. Firstly, the sharing code is extracted from the 3rd bit of the FinalSTR, and then the sharing code is combined into a left party with an interval of 2 bits. The number of extraction is , and then the value of is calculated as the right party. Finally, the original sharing code is the sequential combination of the left party and the right party. The operation flow is shown in Figure 5.
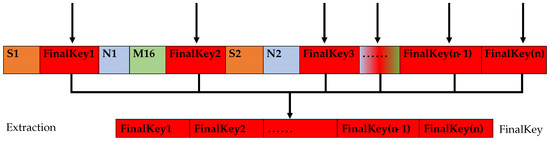
Figure 5.
sharing code extraction format.
4.3.3. Take Out the Two MD5 Values
After the ciphertext FinalSTR extracts the sharing code and the length of the sharing code, only the combination of the encrypted data SplitSTR and two MD5 values (N and M) remains in FinalSTR, as shown in Figure 6.

Figure 6.
Schematic diagram of the ciphertext format after extracting the sharing code.
The length of the data sequence FinalSTR after the sharing code has been extracted is calculated and noted as MNLength. Then, the following specific formula is generated to discern whether the encrypted data SplitSTR can meet the interval insertion MD5 value.
The shortest plaintext message length that can satisfy the full interval insertion is
For FinalSTR, only SplitSTR and the minimum length of the combination of two MD5 values (N and M) is
Since the MD5 values are taken in 16-bit lowercase, the final result of the above formula is .
If , the encrypted data SplitSTR is not able to insert the complete combination of two MD5 values at intervals and restore the original data in the following way.
Extracting the MD5 value N of the original data D.
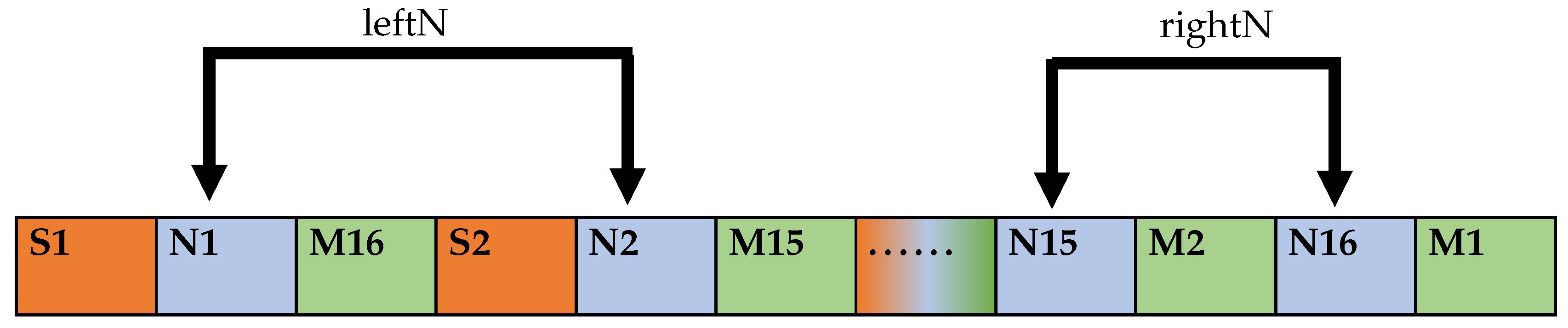
The extraction starts from the first bit of FinalSTR after the sharing code is extracted. The extraction interval is 2 bits, and the extraction times are . The extracted partial MD5 value is defined as leftN. After extraction, the extraction starts from the position of the two bits after the last extraction position interval. In this stage of the extraction process, the extraction interval is 1 bit until the extraction reaches the end of the data sequence FinalSTR. The partial MD5 value of the original data N is defined as rightN. The sequential combination of leftN and rightN is defined as tmpN, and the subsequent judgment is whether the data are changed, i.e., whether they are the MD5 value N of the original data of D. The operation flow is shown in Figure 7.
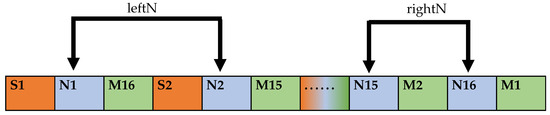
Figure 7.
MD5 value extraction format for plaintext message.
Extract the MD5 value M of a garbled encrypted data string.
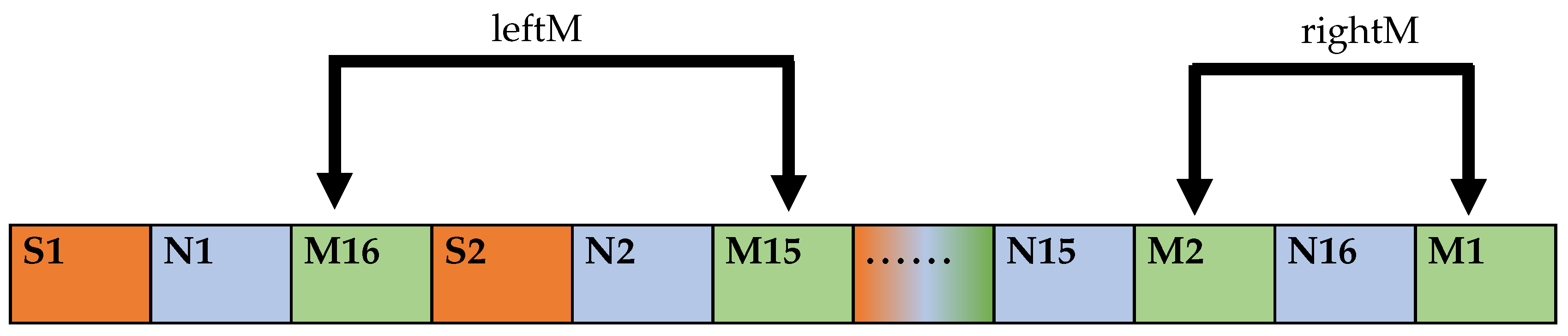
The extraction starts from the 2nd bit of FinalSTR, where the extraction interval is 2 bits, the extraction count is , and the component MD5 value is defined as leftM. After the extraction count is finished, the extraction starts from the position of one bit after the last extraction position interval. Additionally, the extraction interval is one bit in this stage of the extraction process until the extraction reaches the end of the data sequence FinalSTR to acquire part of the MD5 value as rightM. The sequential combination of leftM and rightM is defined as tmpM. The operation flow is shown in Figure 8.
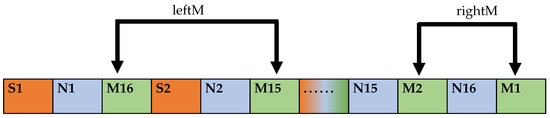
Figure 8.
MD5 value extraction format for plaintext message.
If , the original data D can be spaced to insert the complete combination of two MD5 values and restore the original data as follows.
Take the MD5 value N of the original data D.
As shown in Figure 9, the extraction starts from the first bit of the data sequence FinalSTR, where the extraction interval is 2 bits, the number of extractions is 16, and the final extraction result is the MD5 value of the original data N, defined as tmpN.

Figure 9.
MD5 value extraction format for plaintext message.
Extract the MD5 value of garbled encrypted data M.
The extraction starts from the second bit of FinalSTR; the extraction interval is 2 bits, the number of extractions is 16, and the final extraction result is the MD5 value of the garbled encrypted data, defined as tmpM. The operation flow is shown in Figure 10.

Figure 10.
MD5 value extraction format of data SplitSTR after encryption.
The remaining data sequence FinalSTR is defined as SplitS, i.e., the data after chunking disorder, and the receiving end cooperates with the parsed sharing code FinalKey to restore the original data by decryption algorithm.
5. Decryption Process
Each time two digits are taken out from the end of the sharing code FinalKey, defined as PQ, where P is the size of the chunk and Q is the chunking chaos algorithm used, for SplitS, the last block position that can be used for exchange is calculated as if , indicating that the number of chunks is even. Then, the last block that can participate in the exchange is the penultimate block; if , the number of chunks is odd, and the last block that can participate in the exchange is the penultimate block. Assign the value of Q to T and choose the disordering algorithm according to the value of T.
The pseudo-code for decryption is shown below as Algorithms 5 and 6.
The algorithm is novel in that, unlike traditional key distribution methods, it uses chunking and exchange logic to generate the sharing code. It hides it in the data by interval insertion, thus reducing the hazards associated with key distribution. The sharing code is also extracted in a way that is problematic to break. The use of different disordering algorithms and the fact that multiple encryptions for the same plaintext have different results and different encryption lengths make it challenging to break this algorithm using attacks that build dictionary libraries based on plaintexts and ciphertexts.
| Algorithm 5 Decryption. | |
| Require: | ▹ Data after chunking disorder |
| if then | |
| ▹ Select adjacent parity exchange Algorithm 1 | |
| else if then | |
| ▹ select the head-tail decreasing exchange Algorithm 2 | |
| else if then | |
| ▹ Select adjacent odd block exchange Algorithm 3 | |
| else if then | |
| ▹ Select adjacent even block exchange Algorithm 4 | |
| end if | |
| Algorithm 6 Determining data integrity. | |
| ▹ Take MD5 value | |
| if then | |
| if then | |
| ▹ Accepted data | |
| else | |
| ▹ Discarded data | |
| end if | |
| else | |
| ▹ Discarded data | |
| end if | |
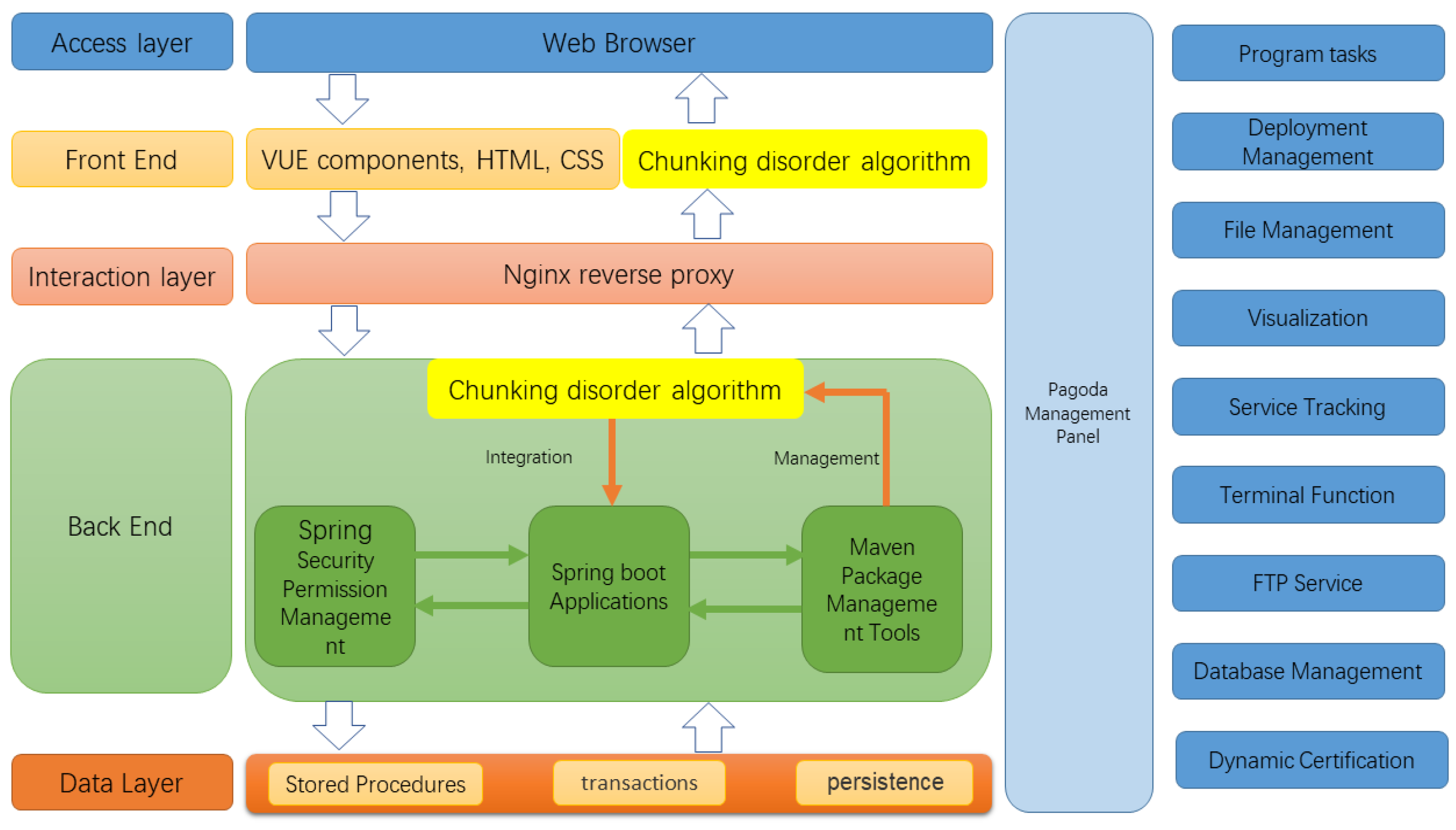
6. Algorithm Deployment
This chunking disorder algorithm was written in the JAVA language and then packaged as a Java Archive File (jar). The jar package was deployed on the server side, and the Spring boot application was introduced using the Maven package management tool.
The system architecture after deployment using the algorithm is shown in Figure 11.
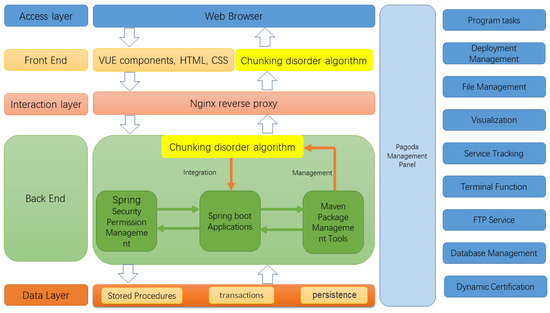
Figure 11.
Blocked and disordered resource platform architecture.
The chunked and disordered algorithm was packaged as a jar with a convenient management effect. This method can add a digital signature to the contents of the jar file so that tools that can identify the signature can selectively authorize the security privileges of the resource platform while also being able to detect whether the code has been tampered with to avoid the harm caused by the implantation of a Trojan horse on the jar.
7. Experimental Results and Analysis
7.1. Encryption Effect Test
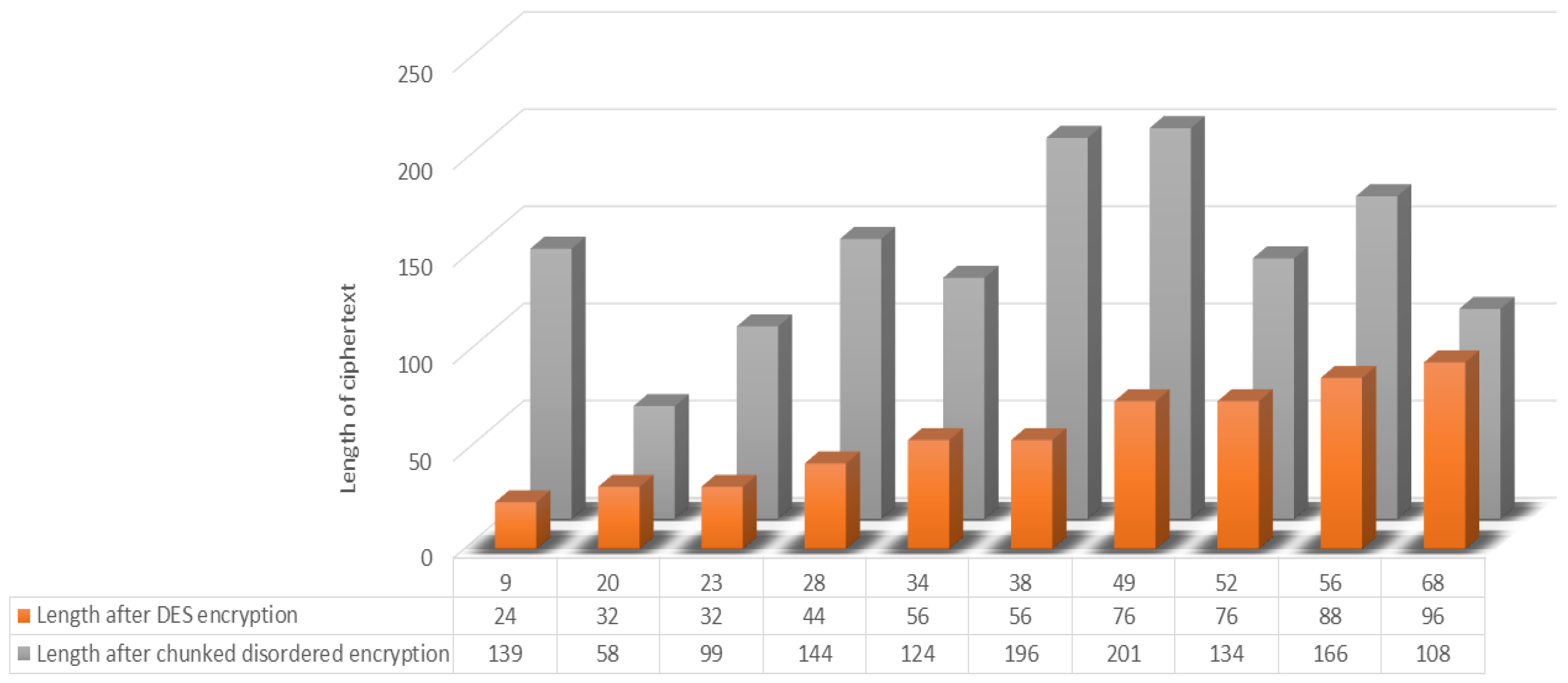
The encryption effect of the algorithm can be judged based on the comparison of the resultant lengths of encryption of plaintexts of different lengths. Therefore, the effect will be illustrated using the traditional DES encryption algorithm and the present chunked and disordered encryption algorithm. First, the traditional DES encryption and the chunked jumbled encryption were utilized for plaintexts of different lengths. It can be seen that the traditional DES encryption algorithm shows a linear growth in the length of the ciphertext as the length of the plaintext increases. The length of the plaintext in this chunked disorder algorithm is independent of the length of the encrypted ciphertext but fluctuates within a certain range. This is because this algorithm uses techniques such as dynamic grouping and disordered mapping, which makes the plaintext generate a random sequence after several iterations, and then realizes disordered arrangement, which improves the encryption efficiency and has a better encryption effect. The ciphertext becomes completely unrecognizable compared with the plaintext and has good security.As shown in the Figure 12.
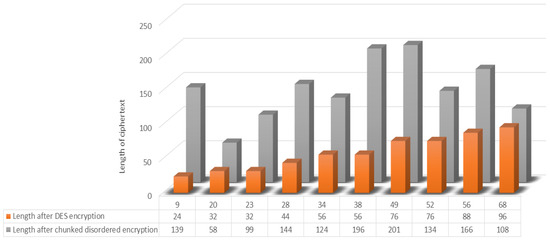
Figure 12.
Encryption length result test.
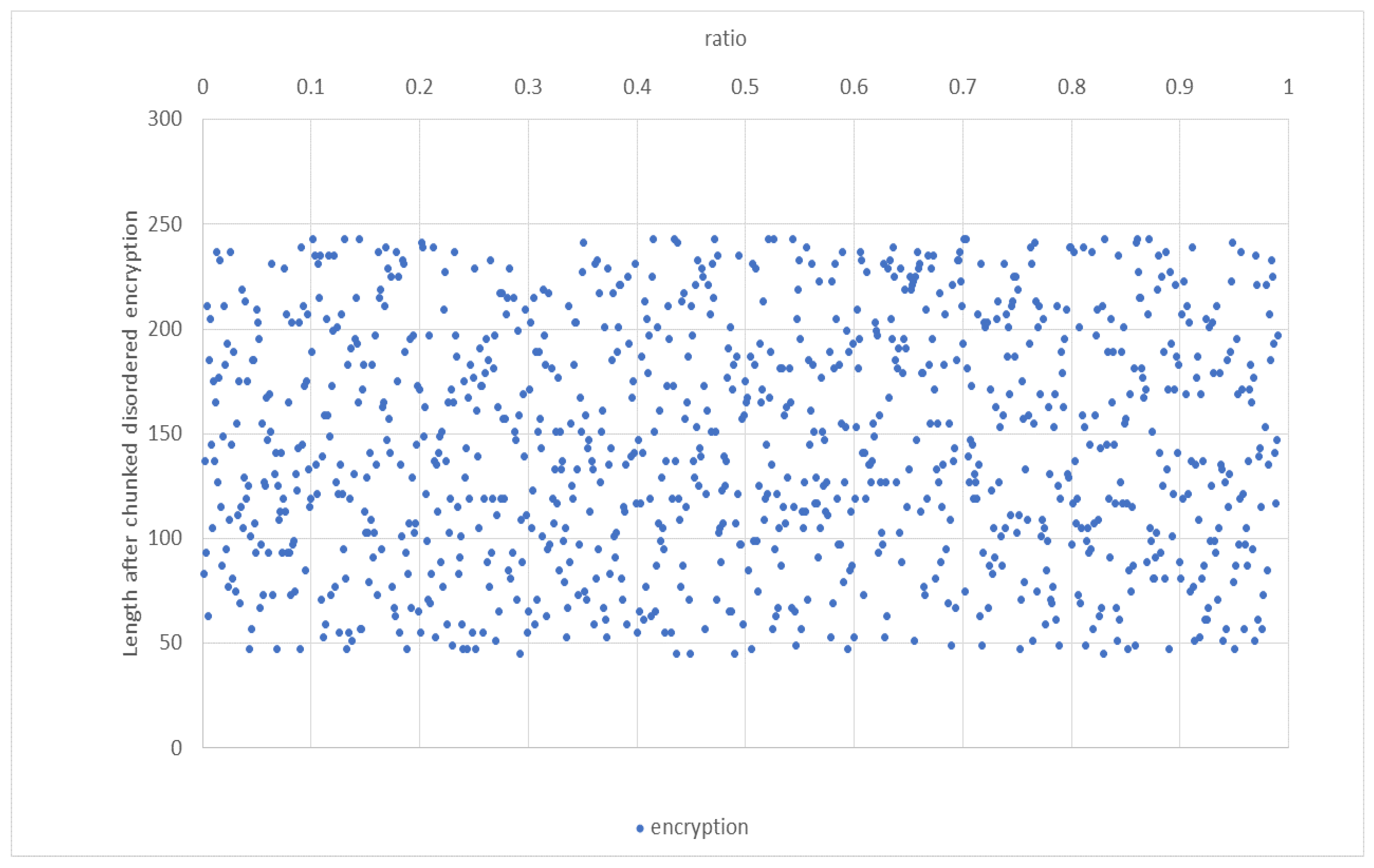
In addition, to avoid experimental chance, the same plaintext “planText123” was encrypted 1 million times using this chunking disorder algorithm, and the ciphertext length distribution had a certain randomness.As shown in the Figure 13.
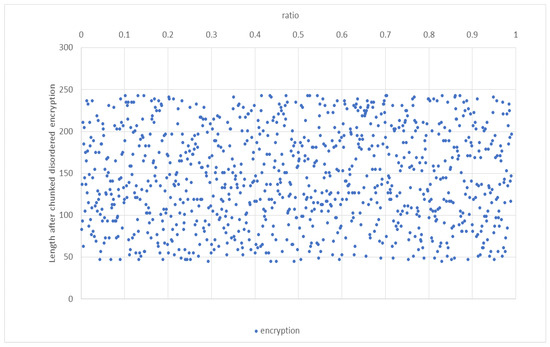
Figure 13.
Distribution of the same encryption length.
7.2. Avalanche Effect Test
The “avalanche effect” describes a state of unstable equilibrium. Changing the plaintext or SK may result in a significant change in the ciphertext. Suppose a block cipher or cryptographic hash function lacks significant avalanche characteristics. In that case, it may result in a lack of good randomness, making it impossible for a cryptanalyst to accurately predict the input information based on the output information. As a result of this situation, the algorithm may be partially or even wholly corrupted. Therefore, it is critical to ensure that the development of cryptographic algorithms and devices can effectively resist the avalanche effect.
An essential research task is establishing a key and sequence that can effectively withstand the avalanche. As technology has evolved, block ciphers and hash functions are no longer limited to products and blocks of data, making both methods of critical importance for securing data. Because of these unique features, even the slightest changes can be quickly captured by the algorithm so that each digit of the output will significantly impact each digit of the input until the algorithm is completed.
Based on this, this paper explains the “avalanche effect” of the traditional DES algorithm and chunking algorithm in terms of changing one plaintext and one key. In the “avalanche effect” experiment, we used a slight difference in the plaintext or secret key to update the position of a piece of data and carefully explained the steps of the experiment and the final results. In addition, by analyzing multiple sets of data, the chance factor in the experiment can be effectively reduced, and the accuracy of the “avalanche effect” algorithm can be improved by changing the position of the plaintext or the key.
7.2.1. Keep the Key Unchanged and Change One Plaintext
We let the plaintext be “planTextabcd”. Then, we kept the key of the conventional DES encryption unchanged, changed only one plaintext, and encrypted the plaintext changed by one bit using conventional DES. There is no key distribution problem for this chunking disorder algorithm, so the ciphertext length is guaranteed to be the same while keeping the number of iterations unchanged. On this basis, only one bit of plaintext was changed for encryption. In addition, in order to avoid experimental chance, it was necessary to ensure that the key of DES was unchanged when traditional DES encryption was used; chunked chaotic order encryption uses the encrypted strong random number generator (RNG) built in Java language to avoid the influence of pseudo-random numbers on the experimental results.
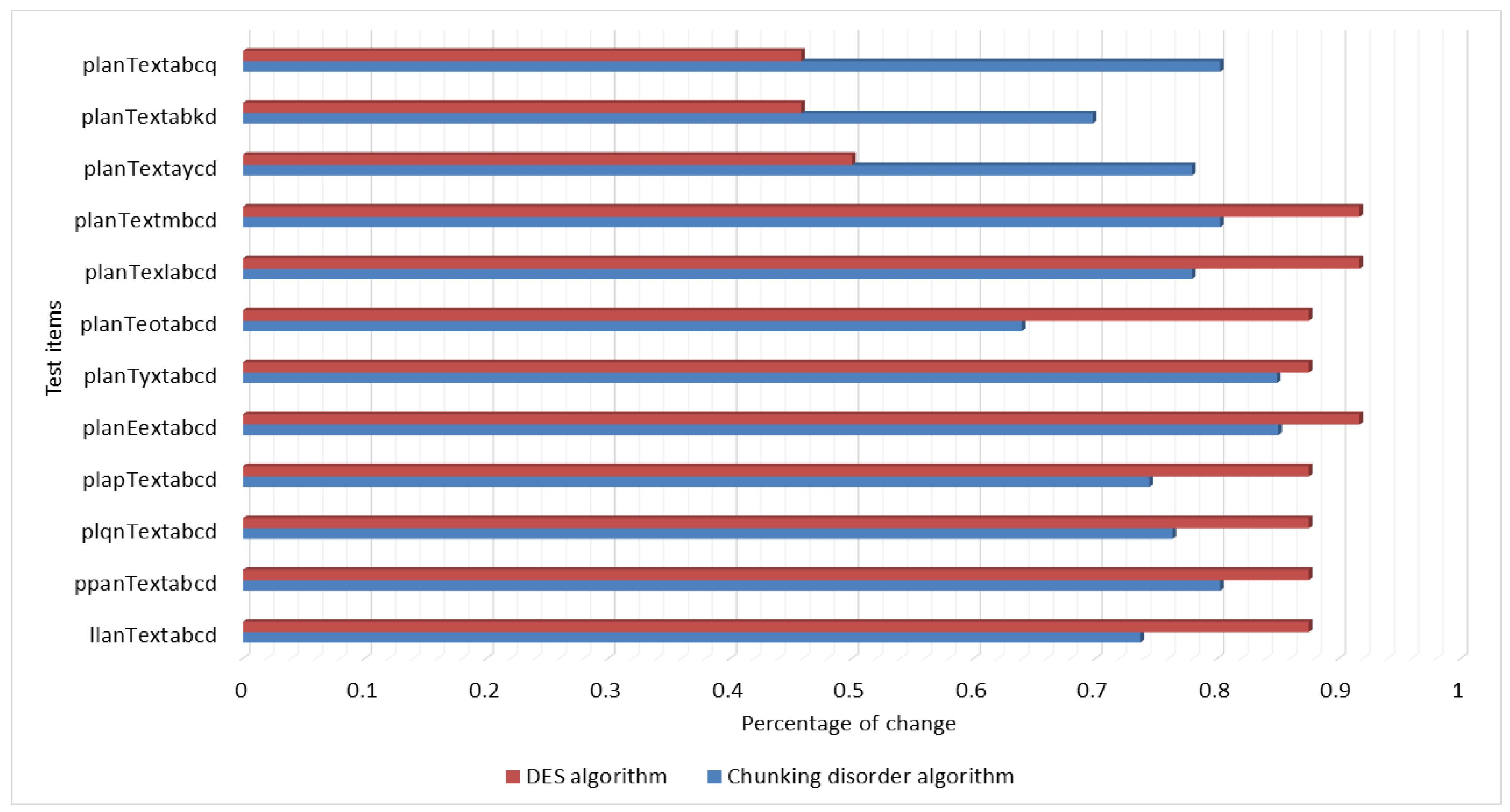
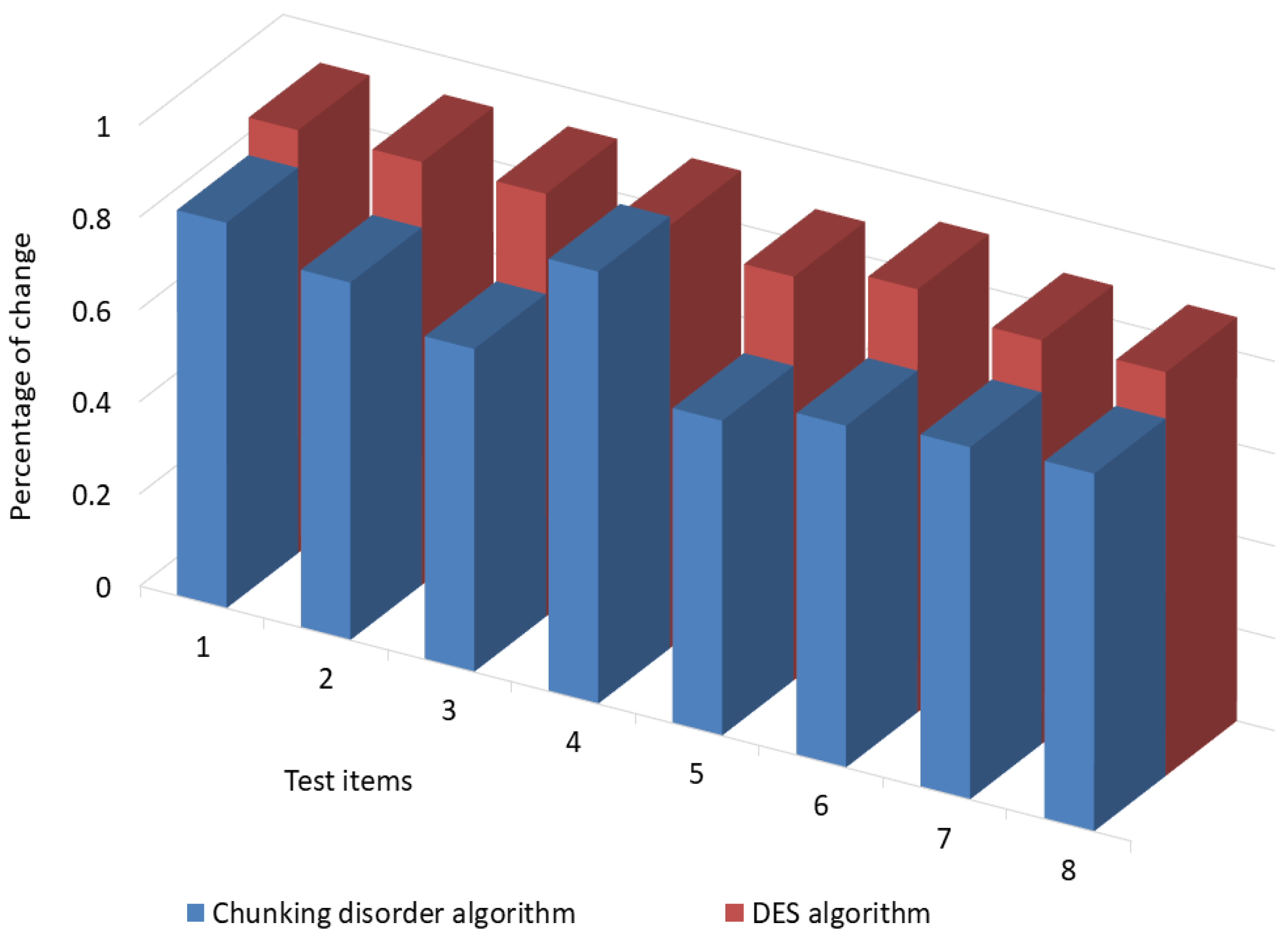
The experimental results show that the traditional DES algorithm has the same “avalanche effect” as the chunking algorithm. When the plaintext is changed by one bit, the ciphertext is changed by more than half of the original ciphertext. The change ratio is basically maintained at 0.61 to 0.85, which has a good “avalanche effect” compared with the original ciphertext. Figure 14 illustrates “avalanche effect” of changing the plaintext test results.
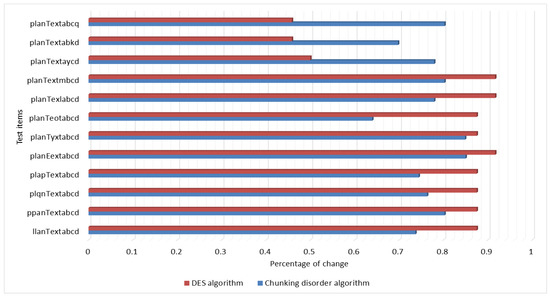
Figure 14.
“Avalanche effect” of changing the plaintext test results.
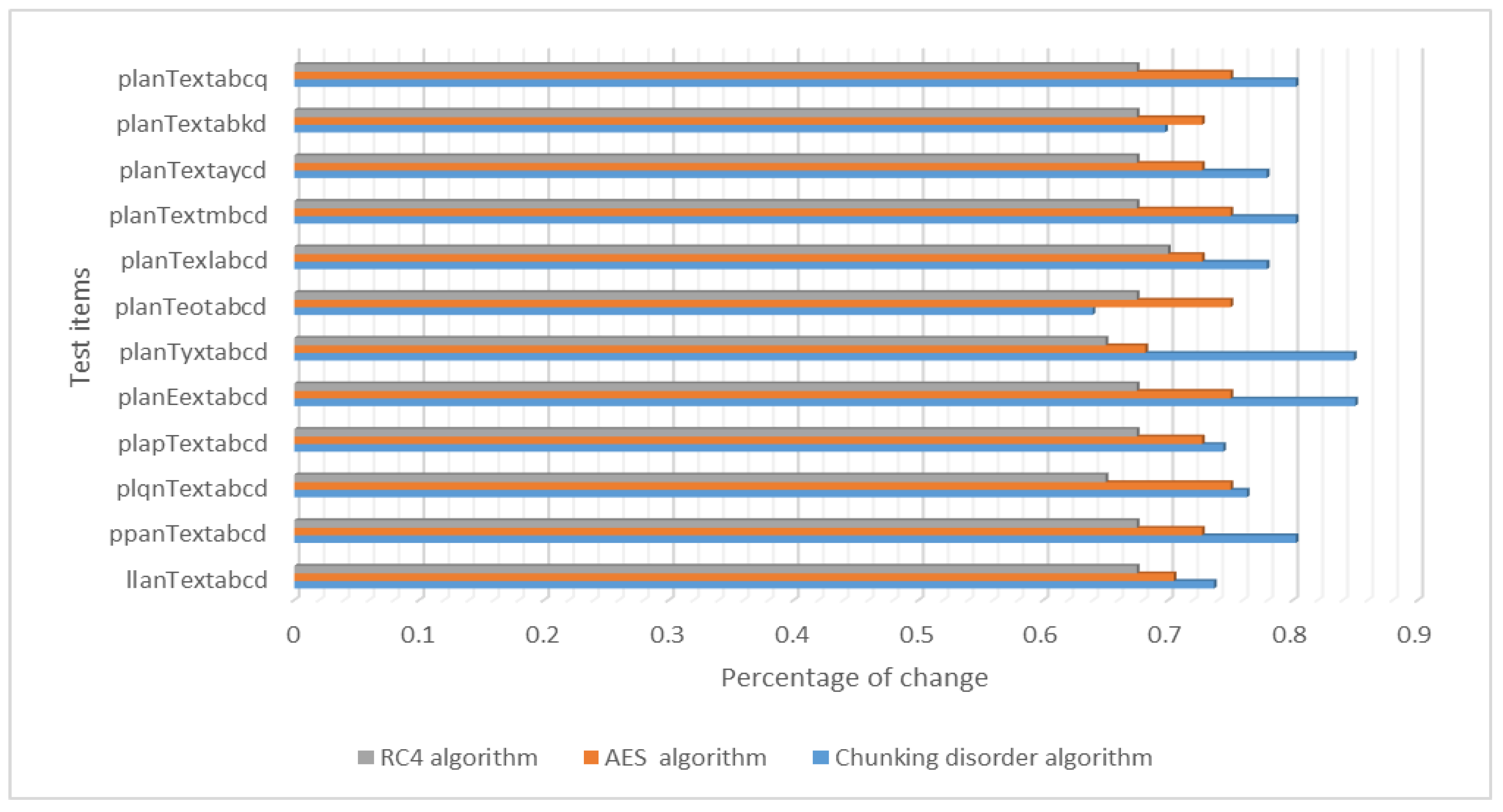
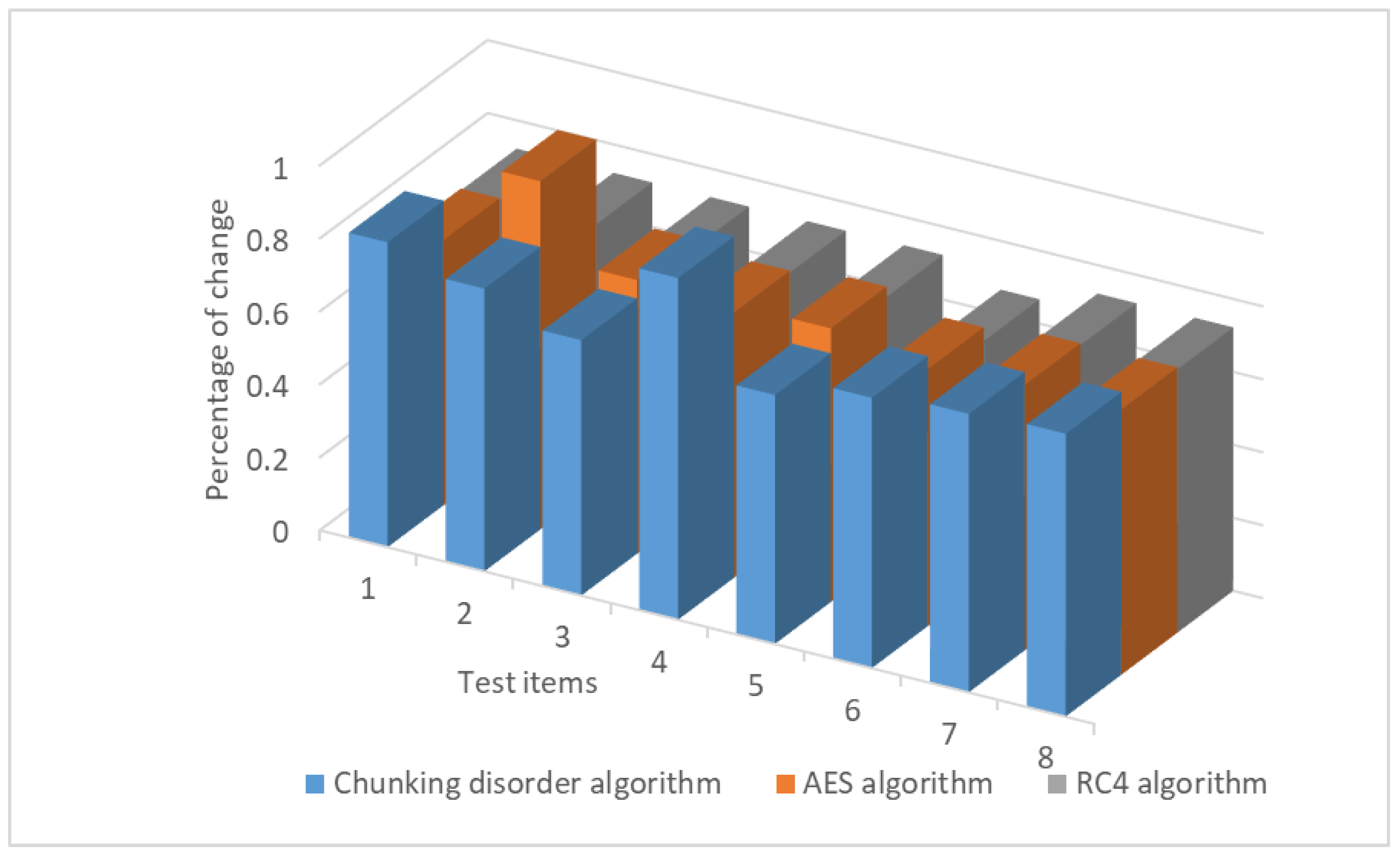
Furthermore, we conducted a comparison with other symmetric encryption algorithms, namely AES and RC4. During the encryption process, these algorithms keep the key unchanged and gradually change one bit of the plaintext, which is then encrypted in the same manner as described above. The experimental results demonstrate that the present chunking algorithm has the same “avalanche effect” as the AES and RC4 symmetric encryption algorithms. That is, when one bit of the plaintext is changed, the number of bits of the ciphertext is altered by more than half of the original ciphertext. The change ratio remains essentially in the range of 0.61–0.85. To some extent, the avalanche effect is more pronounced in this algorithm than in the AES and RC4 encryption algorithms. Figure 15 illustrates “avalanche effect” compared to AES and RC4 algorithm when changing the plaintext test results.
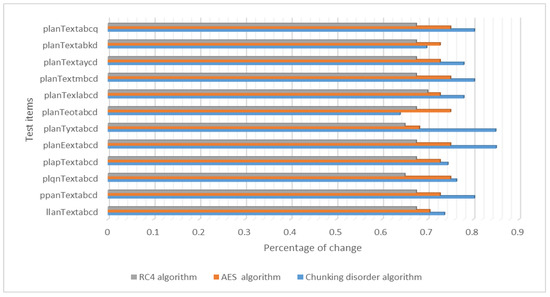
Figure 15.
“Avalanche effect” compared to AES and RC4 algorithm when changing the plaintext test results.
7.2.2. Keep the Plaintext Unchanged and Change One Bit of the Key
We then let the plaintext be “planTextabc”. When encrypting, we kept the plaintext unchanged and changed one bit of the key. The plaintext was encrypted using the conventional DES and chunking disorder algorithms. The chunking disorder algorithm simulated the process by changing the chunk size. In order to avoid experimental chance, the same plaintext “planTextabc” was encrypted with 8 test items that differed by only one bit each, and the chunking disorder algorithm also used a strong cryptographic random number generator (RNG) to avoid the influence of pseudo-random numbers on the experimental results.
The experimental results show that by keeping the plaintext unchanged and changing one bit of the key, the messages are encrypted with the traditional DES algorithm and the chunked disorder algorithm. The traditional DES and chunked disorder algorithms have an excellent “avalanche effect”. By keeping the plaintext unchanged and changing one bit of the key, the ciphertext is changed by more than half of the original ciphertext. The ”avalanche effect” of the chunking algorithm is somewhat similar to the “avalanche effect” of the traditional DES algorithm. Figure 16 illustrates results of “avalanche effect” test with different encryption factors.
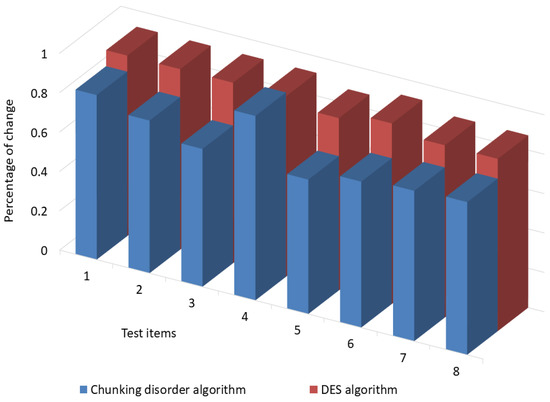
Figure 16.
Results of “avalanche effect” test with different encryption factors.
Furthermore, we conducted a comparison with the AES and RC4 symmetric encryption algorithms. The data were encrypted and compared in the same manner as described above, with a one-bit key change. The experimental results show that the chunking algorithm has the same “avalanche effect” as AES and RC4 when changing one key. That is, when changing one key, the number of bits of the ciphertext is altered by more than half of the original number of bits. The change ratio remains essentially between 0.7 and 0.8, indicating a good avalanche effect. Figure 17 illustrates avalanche effect” compared to AES and RC4 algorithm regarding the secret key test results.
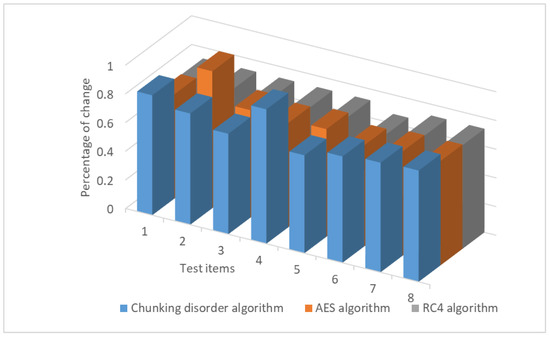
Figure 17.
“Avalanche effect” compared to AES and RC4 algorithm regarding the secret key test results.
7.3. Safety Discussion
7.3.1. Information Entropy Experiment
Information entropy is a mathematical concept used to measure the degree of information chaos. In information theory, information entropy measures uncertainty, the expected value of the information available for all possibilities. If a random variable has more possible values, its entropy will be more significant, and vice versa. The more orderly a system is, the lower the information entropy; conversely, the more chaotic a system is, the higher the information entropy. Therefore, information entropy can be used to measure the degree of orderliness of a system. In cryptography, information entropy can be used to assess the strength and security of a password. The strength of a password depends on its information entropy, i.e., the randomness and unpredictability of the password. If a password’s information entropy is high, it will be tough to crack that password, as the cracker will need to traverse all possible combinations of passwords to find the correct one. Security in cryptography depends on the information entropy of a password, which, in turn, depends on the randomness and unpredictability of the password. The higher the information entropy of a password, the more secure it is, and the more difficult it is to break through guessing or cracking methods. Calculating the information entropy of a ciphertext effectively reflects the degree of confusion of the ciphertext; the higher the degree of confusion, the better the encryption effect. The formula to calculate information entropy is shown above, where represents the probability of event X occurring and is the logarithm with a base of 2.
Using the likelihood of each character, we calculated the information entropy for the present chunked chaotic exchange algorithm, as well as the DES, AES, and RC4 algorithms.
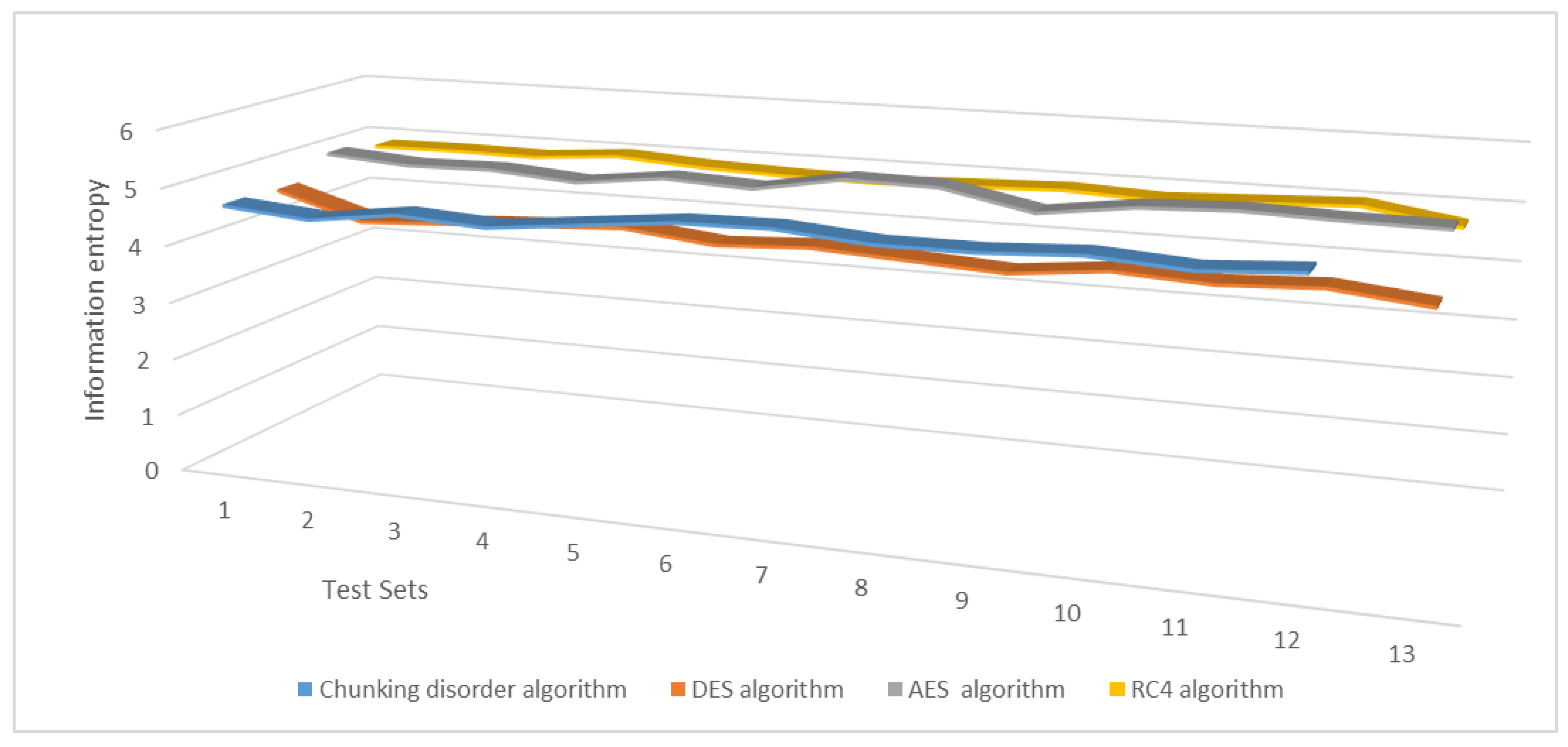
In addition, we conducted experiments to change one bit of plaintext and tested the information entropy of the resulting ciphertext. The experimental results show that the average information entropy of the present chunking disorder algorithm remains primarily in the range of 4.5–4.9, which is essentially higher than the average information entropy of the DES algorithm and is closer to that of the AES and RC4 algorithms. These results indicate that the present chunking disorder algorithm has better encryption effectiveness, more confusion in the ciphertext, and more robust security. Figure 18 illustrates change in the average information entropy of a ciphertext under one plaintext.
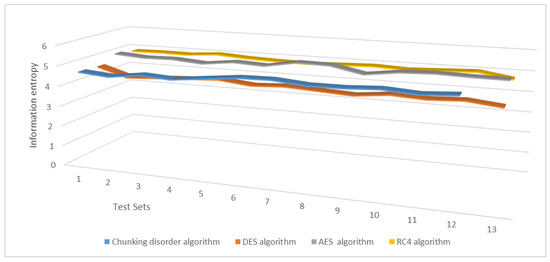
Figure 18.
Change in the average information entropy of a ciphertext under one plaintext.
By changing one bit of the key, we can test the information entropy of the plaintext. Due to the random nature of the chunked jumbled algorithm-sharing code generation, we can perform relevant tests by varying the key length.
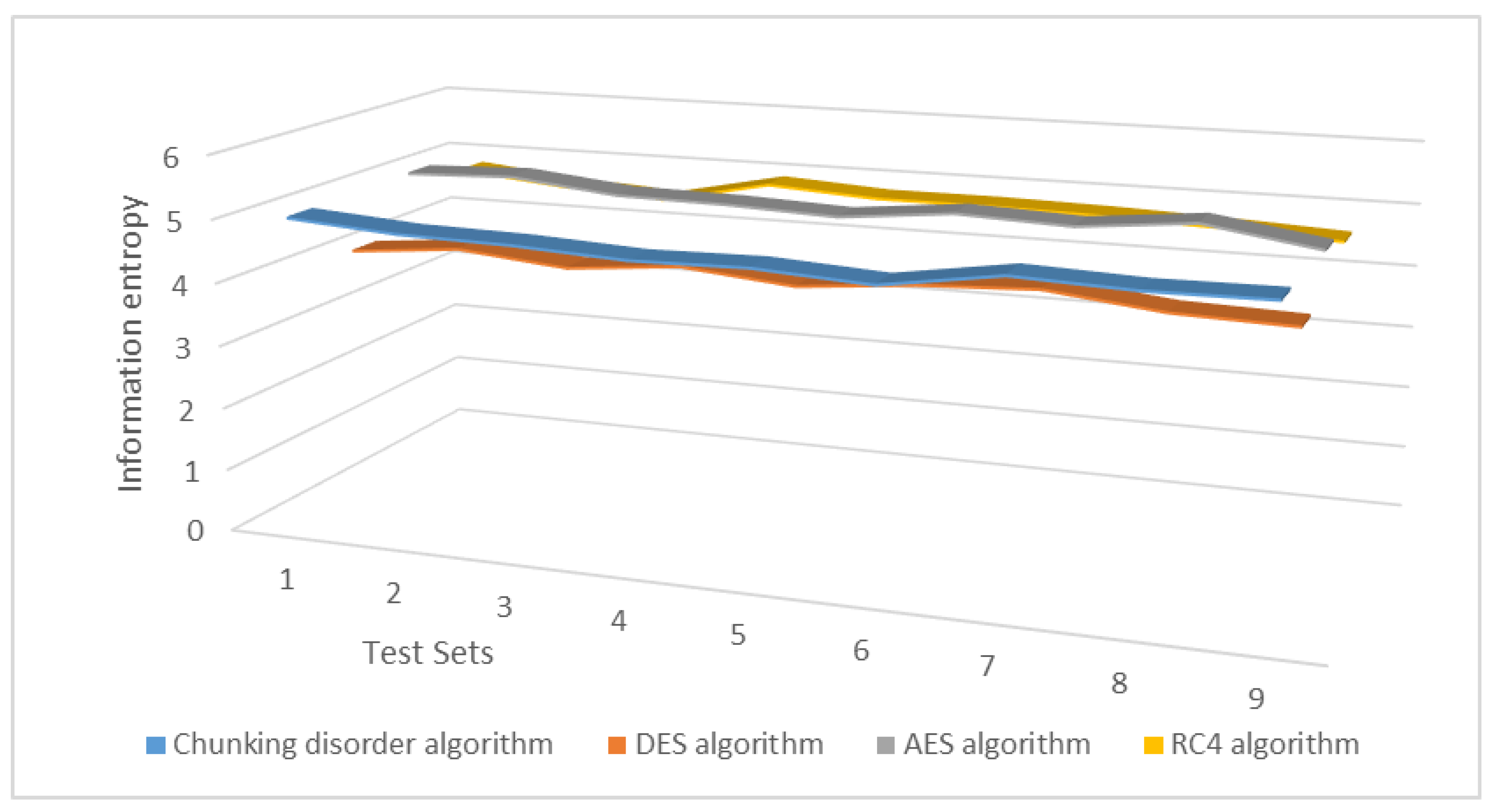
The experimental results demonstrate that the average information entropy of the present chunking disorder algorithm remains primarily in the range of 4.5–4.9, which is better than that of the DES algorithm and, to some extent, closer to that of the AES and RC4 algorithms. These results indicate that the present chunking disorder algorithm has better encryption effectiveness, more confusion in the ciphertext, and more robust security. Figure 19 illustrates change in the average information entropy of the ciphertext under one key.
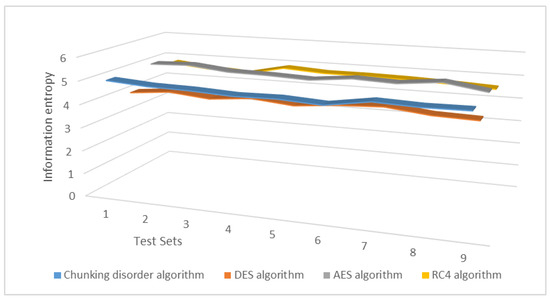
Figure 19.
Change in the average information entropy of the ciphertext under one key.
7.3.2. Brute-Force Cracking Attacks
Brute-force cipher breaking is a method of cracking a cipher by systematically trying all possible keys. The size of a cipher’s secret key space determines its strength, which is the set of all possible keys in a cryptosystem. A larger secret key space makes it more difficult to crack the cipher since more time and computational resources are required to exhaust all possible keys. Therefore, the security of a cipher depends on the size of its secret key space.
For the DES algorithm, the secret key length is 56 bits, which gives possiblesecret keys. This size is relatively small, making cracking difficult.
In contrast, the AES algorithm can have a secret key length of up to 256 bits, which gives possible secret keys, making it highly resistant to attacks. Similarly, RC4 can take a long time and be more difficult to crack.
The present chunking algorithm can use up to 99 sharing codes, with each code occupying 6 bits, resulting in a secret key length of 594 bits and a secret key space of , which surpasses the secret key space of DES and AES. This makes it highly difficult to crack, and as the length of the sharing code increases, the difficulty of cracking increases exponentially.
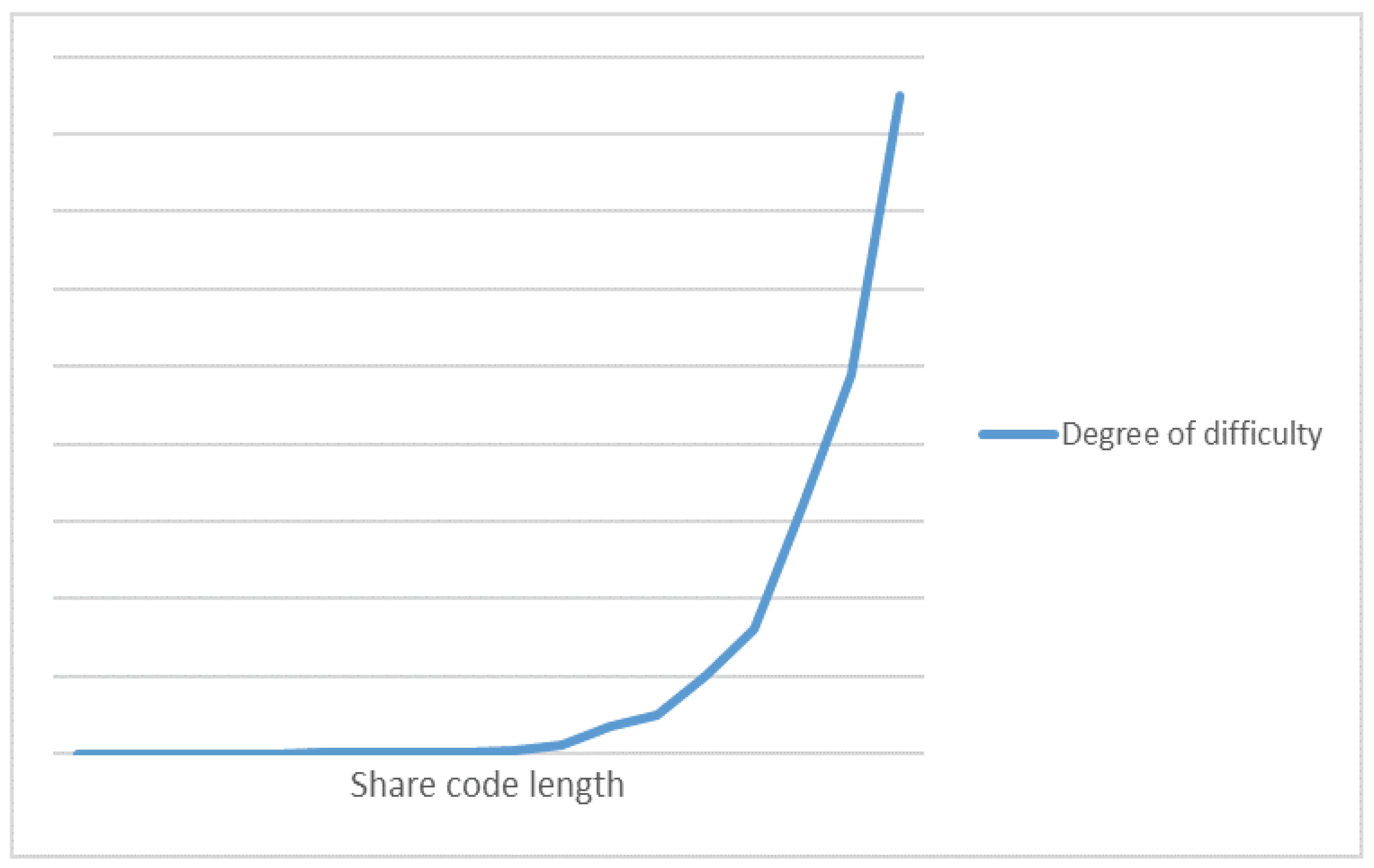
Experimental tests have shown that with only a few sharing codes, a brute-force simulation analysis of this chunking disorder algorithm can decrypt the plaintext in a short time. Due to the small number of sharing codes, a cracker can easily attempt all possible combinations of sharing codes to find the correct one and decrypt the plaintext. However, as the length of the sharing code increases, cracking becomes much more challenging. As the length of the sharing code increases, the number of sharing code combinations grows exponentially. The cracker needs more time and computational resources to try all possible sharing code combinations to find the correct one and decrypt the plaintext. Therefore, the security of this chunking disorder algorithm increases as the length of the sharing code increases. Figure 20 illustrates difficulty of brute-force cracking.
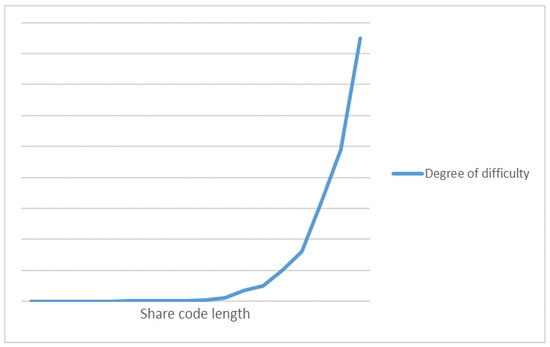
Figure 20.
Difficulty of brute-force cracking.
7.3.3. Side Channel Attacks
A side channel attack is a type of attack that leverages unintentional information leakage in a cryptographic device or implementation to extract secret information, such as keys or plaintexts. These channels can include power consumption, electromagnetic radiation, acoustic emissions, and temporal information. Side channel attacks can be effective against many cryptographic implementations, including both symmetric and public key cryptosystems. One common type of side channel attack is a time-based analysis, in which a certain amount of time is required to encrypt and decrypt data during encryption. This time is dependent on factors such as the encryption algorithm and key length. An attacker can use this time information to infer the key and gain further details about the encrypted data. By analyzing the encryption and decryption times of the algorithm under a large number of different plaintexts, the attacker can analyze the relationship between the plaintext and ciphertext to find features for algorithm cracking.
Cryptographers have taken several countermeasures against edge channel attacks, such as adding noise, increasing randomness, and increasing the algorithm’s complexity. For this chunked disordered encryption algorithm, the randomness of the length of its sharing code and its disorderliness increases the difficulty of the attack in time-consuming analysis to a certain extent. At the same time, we can further verify the algorithm’s security by taking different lengths of sharing codes to test its encryption and decryption time.
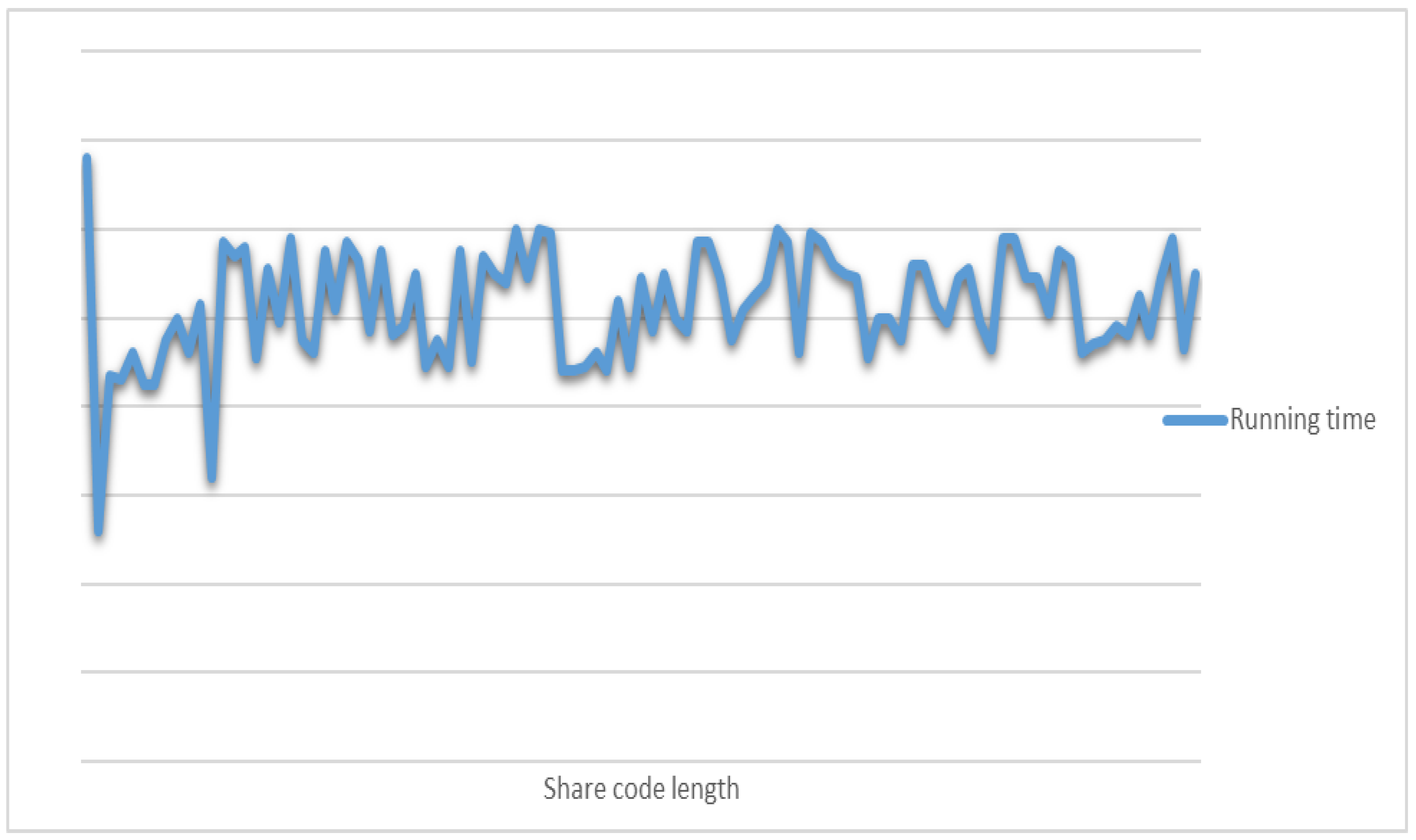
The experimental results show that the encryption and decryption time of this chunking disorder algorithm is weakly correlated with the length of the sharing code, and the encryption and decryption time is random and fluctuates within a specific interval, which means that it is difficult to crack the encryption and decryption time of the algorithm by using time-consuming analysis attacks. Therefore, the present chunking scrambling algorithm strongly resists edge channel attacks. Figure 21 illustrates encryption and decryption times for different lengths of sharing codes.
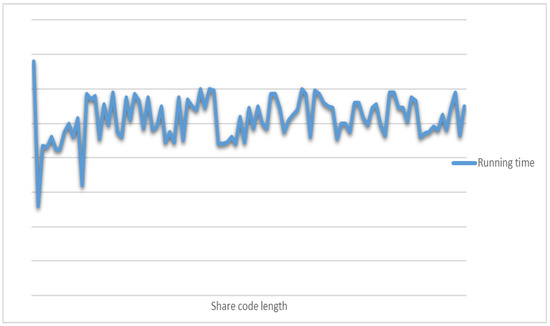
Figure 21.
Encryption and decryption times for different lengths of sharing codes.
7.4. Resource Platform System Requirements
The resource platform system contains a large number of resources and stores user login credentials. The back-end utilizes Spring Boot for data calls and a MySQL database for data storage. User identification and rights management are implemented using Spring Security. The chunking algorithm is packaged as a jar file and deployed in the back-end, where it can be invoked through the Maven management tool. This approach enables the easy and efficient invocation of the chunking algorithm on a highly scalable platform. The entire platform is deployed on an Nginx server, and the environment is monitored using the Pagoda O&M management tool, which enhances the reliability of the resource platform. Ultimately, the server provides an interface to the front-end for relevant invocations. The deployment of the chunking algorithm in the resource platform system dramatically enhances the security of the data transmitted through the platform. The use of jar packages allows the chunking algorithm to be easily and quickly integrated into the system, thus increasing the scalability of the system. In addition, the chunked disorder algorithm can support data encryption scenarios for most functions of the resource platform system, including the encrypted transmission of data such as usernames, passwords, and text resources, further improving the system’s security. Ultimately, the architecture design of the system and the deployment method of the chunked chaotic algorithm fully consider the scalability and security requirements of the system, providing users with a more secure and reliable resource platform service.
8. Algorithm Evaluation
The traditional DES symmetric encryption algorithm needs to distribute keys in advance. However, obtaining a sufficient number of keys in practical application scenarios is often tricky, which limits this algorithm’s wide application. In contrast, the chunked chaotic algorithm does not need to distribute keys in advance and is suitable for systems of all sizes. In addition, the chunked chaos algorithm supports the online upgrade function, and new algorithm modules can be added at any time to meet evolving business needs. For example, more adjustment factors can be added to the rules of chunked chaos to achieve a chaotic effect. The chunked chaotic algorithm inserts the chaotic rules into the generated string in the form of sharing code when generating the ciphertext to achieve the purpose of steganography so that there is no need to distribute the sharing code in advance during the data transmission, which improves the security and applicability of the algorithm. In addition, the MD5 values of the plaintext and post-garbled plaintext are also introduced in the insertion rules for double-checking after the subsequent separation of the post-garbled data by the sharing code to ensure the reliability of data transmission and reduce the probability of success of attackers. As different block sizes and scrambling algorithms are used to reintegrate the plaintext, collisions may occur between the chunking and scrambling processes, resulting in the same data after reintegration. If they happen to be modified during transmission, they may be misclassified as unmodified secure data. Although it is possible to follow the logic of the chunking and disordering algorithm to restore it, data hazards are still involved, thus reducing the algorithm’s security. This chunking algorithm adds two MD5 values to the ciphertext to reduce the chance of collision and misclassification and improve the algorithm’s security. These two MD5 values are obtained by hashing the plaintext and the chunked data. During the decryption process 5,6, the MD5 values are verified to match, and if they do not match, the ciphertext has been tampered with and needs to be processed accordingly. Therefore, increasing the MD5 value can effectively reduce the chance of collision and false positives and improve the algorithm’s security.
9. Conclusions and System Evaluation
In summary, this paper proposes a novel symmetric encryption algorithm that addresses the long-standing challenge of key distribution by eliminating the need for pre-distributed keys. Our algorithm achieves data encryption through multiple iterations of data, with the user specifying the number of iterations to increase the algorithm’s difficulty in breaking. Additionally, each iteration generates a sharing code that builds an exclusive encryption algorithm, which is randomized to avoid the analysis of behavioral tendencies. Since the correspondence between the length of the sharing code and the specific messy encrypted message is not known in the transmitted ciphertext message, the speculation of the encryption logic through network-sniffing malicious attacks [40,41,42] is also avoided to some extent. Experimental simulations demonstrate the algorithm’s superiority and scalability as the sharing code’s length increases exponentially with the number of iterations, substantially enhancing the algorithm’s security. Our proposed algorithm is deployable on both the client and server sides, which must be secured to further improve its security. Our findings provide a practical solution for secure data encryption without the need for pre-shared keys, which can have significant implications for the field of cybersecurity.
However, there are still many shortcomings and improvements that can be made. For example, the chunking algorithm’s security depends on the chunks’ size and the chunking algorithm’s choice. It can be easily broken if not chosen correctly, leading to data leakage and loss. Therefore, we must carefully select the appropriate chunk size and scrambling algorithm and design the algorithm with security in mind.
Secondly, chunking disorder algorithms may be incompatible with other encryption algorithms and protocols, leading to difficulties in integration and application. Therefore, in practical applications, we need to consider compatibility issues with different encryption algorithms and protocols to apply the chunking disorder algorithm better.
In future work, we will continue to improve the chunking disorder algorithm by increasing its performance, improving the chunking and disorder strategies, and optimizing the algorithm execution logic to enhance operational efficiency and security. Additionally, we will consider how to efficiently apply the chunking disorder algorithm in a distributed environment, as the current algorithm is well-suited for standalone environments. We will also work on improving the algorithm’s scalability to meet the needs of large-scale data processing.
Author Contributions
Conceptualization, D.Z. and J.C.; Data curation, D.Z., J.C., C.D., Y.H. and J.L.; Formal analysis, J.C., Y.H., X.L., X.C. and J.L.; Funding acquisition, D.Z.; Investigation, D.Z., X.L. and X.C.; Methodology, J.C., Y.H., X.L., X.C., C.D. and J.L.; Project administration, D.Z. and Y.H.; Resources, D.Z., Y.H., and J.L.; Software, D.Z. and J.L.; Validation, D.Z., Y.H. and X.L.; Visualization, J.C. and J.L.; Writing—original draft, J.C., Y.H. and J.L.; Writing—review & editing, D.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Sichuan Province Department of Education (Grant No. JG2021-464) and the Ya’an Digital Agricultural Engineering Technology Research Center.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data in this study are available on request from the corresponding author.
Acknowledgments
We are very grateful to the Sichuan Province 2021–2023 Higher Education Talent Training Quality and Teaching Reform Project.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Explanationof related words.
DES: Data Encryption Standard.
Vue: It is a set of progressive boxes for building user interfaces.
MD5: A widely used cryptographic hash function that generates a 128-bit (16-byte) hash value to ensure that messages are transmitted consistently. This article uses the 16-bit lowercase format of MD5.
FinalKey: the sequence of all the shared codes in the messy encryption process.
SplitSTR: the plaintext number after the chaotic exchange of data.
M: the data after taking MD5 value for SplitSTR.
N: the data after taking MD5 value for plaintext.
FinalSTR: the final encrypted string information.
partKey: the sharing code inserted by two intervals.
otherKey: the sharing code placed at the end of the string in order.
leftN: the data inserted in the left side of the string with two intervals.
rightN:N inserted at one interval on the right side of the string.
tmpN:the data of the combination of leftN and righN in order.
leftM: the data on the left side of the string with two intervals of M.
rightM: the data on the right side of the string inserted at one interval of N.
tmpM: the data of leftM and rightM combined sequentially.
SplitS: the chunked and disordered data extracted from FinalSTR.
Java Archive File: is a document format for Java, a platform-independent file format that allows multiple files to be combined into a single file.
AES:AES is a symmetric key encryption algorithm used to protect the confidentiality of data.
RC4:RC4 is a Stream Cipher, also a symmetric encryption algorithm.
Appendix B
Data position is calculated from the 0 position. For a data string such as “word" the start position w is defined as position 0.
| 0 | 1 | 2 | 3 |
| w | o | r | d |
References
- Zhao, Y.; Liu, H. Cloud curriculum resource management platform based on Hadoop. Meas. Control 2020, 53, 1782–1790. [Google Scholar] [CrossRef]
- Wang, J.; Li, W. The construction of a digital resource library of English for higher education based on a cloud platform. Sci. Program. 2021, 2021, 4591780. [Google Scholar] [CrossRef]
- Baskaran, S.; Shenbaga, V.; Thenmozhi, D.; Shanmugapriya, S. Resource sharing platform for collaborative cloud campus. In Proceedings of the International Conference on Computation of Power, Energy, Information and Communication (ICCPEIC), Chennai, India, 16–17 April 2014; pp. 473–477. [Google Scholar] [CrossRef]
- Zhang, Y. Analyzing the construction of university ELT resource base using cloud platform. Mob. Inf. Syst. 2022, 2022, 4986923. [Google Scholar] [CrossRef]
- Yan, Q. Design of teaching video resource management system in colleges and universities based on microtechnology. Secur. Commun. Netw. 2021, 2021, 9914048. [Google Scholar] [CrossRef]
- Cui, Y. Development and utilization of college Chinese curriculum resources based on cloud computing resource scheduling algorithm. Math. Probl. Eng. 2022, 2022, 3648678. [Google Scholar] [CrossRef]
- Chu, T. Integration and Application of Online Sports Resources Based on Multidimensional Intelligent Technology and Resource Optimization Architecture. J. Adv. Transp. 2022, 2022, 2333497. [Google Scholar] [CrossRef]
- Feng, J.; Zhang, W.; Tsai, S.B. Construction of a Multimedia-Based University Ideological and Political Big Data Cloud Service Teaching Resource Sharing Model. Math. Probl. Eng. 2021, 2021, 9907630. [Google Scholar] [CrossRef]
- Wu, L.; Feng, L.; Yan, J. Research on University Innovation and Entrepreneurship Resource Database System Based on SSH2. Math. Probl. Eng. 2022, 2022, 1168796. [Google Scholar] [CrossRef]
- Guo, F.; Zha, M.; Tai, Q.; Xue, W.; Zou, Y. Research on Power Base Resource Development and Utilization Management Platform Based on Mid-Platform. In Proceedings of the 5th International Conference on Information Technologies and Electrical Engineering, Changsha, China, 4–6 November 2022; pp. 409–412. [Google Scholar] [CrossRef]
- Abu-Faraj, M.; Al-Hyari, A.; Altaharwa, I.; Alqadi, Z.; Ali, B. Increasing the security of transmitted text messages using chaotic key and image key cryptography. Int. J. Data Netw. Sci. 2023, 7, 809–820. [Google Scholar] [CrossRef]
- Kaur, J.; Kumar, K.R. Key Management using Lagrange Interpolation for Wireless Communications. In Proceedings of the 2nd International Conference on Advance Computing and Innovative Technologies in Engineering (ICACITE), Greater Noida, India, 28–29 April 2022; pp. 2084–2087. [Google Scholar] [CrossRef]
- Sangeetha, S.B.; Sabitha, R.; Dhiyanesh, B.; Kiruthiga, G.; Yuvaraj, N.; Raja, R.; Arshath, R.; Raj, P.; Thirunavukarasu, R. Resource Management Framework Using Deep Neural Networks in Multi-Cloud Environment; Springer International Publishing: Berlin/Heidelberg, Germany, 2022; pp. 89–104. [Google Scholar] [CrossRef]
- Kaur, J.; Kumar, K.R. A Secure Data Transfer Approach With an Efficient Key Management Over Cloud. Int. J. Inf. Technol. Web Eng. (IJITWE) 2022, 17, 1–21. [Google Scholar] [CrossRef]
- Faisal, A.; Zulkernine, M. DKS-PKI: A Distributed Key Server Architecture for Public Key Infrastructure. In Information Systems Security, Proceedings of the 18th International Conference, ICISS 2022, Tirupati, India, 16–20 December 2022; Springer: Cham, Switzerland, 2022; Volume 13784, pp. 23–43. [Google Scholar] [CrossRef]
- Teegala, S.P.; Rao, C.V.G. A Novel Authentication Mechanism for SecureData Access based on Encryption Key Sharing for Cloud Web Application. In Proceedings of the 8th International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, 25–26 March 2022; pp. 1890–1897. [Google Scholar] [CrossRef]
- MacFadden, M.S.; Qiu, M. Performance Impacts of JavaScript-Based Encryption of HTML5 Web Storage for Enhanced Privacy. In Proceedings of the 7th International Conference on Smart Cloud (SmartCloud), Shanghai, China, 8–10 October 2022; pp. 190–196. [Google Scholar] [CrossRef]
- Salmani, K. An Efficient, Verifiable, and Dynamic Searchable Symmetric Encryption with Forward Privacy. In Proceedings of the 19th Annual International Conference on Privacy, Security & Trust (PST), Fredericton, NB, Canada, 22–24 August 2022; pp. 1–10. [Google Scholar] [CrossRef]
- Meraouche, I.; Dutta, S.; Tan, H.; Sakurai, K. Tree Parity Machine-Based Symmetric Encryption: A Hybrid Approach; Springer Nature Singapore: Singapore, 2022; pp. 61–73. [Google Scholar] [CrossRef]
- Uma Maheswari, K.; Sumalatha, V. Cloud Computing based Symmetric Encryption Algorithm (Blueshift). In Proceedings of the International Conference on Augmented Intelligence and Sustainable Systems (ICAISS), Trichy, India, 24–26 November 2022; pp. 904–909. [Google Scholar] [CrossRef]
- Zakaria, A.A.; Ab Halim, A.H.; Ridzuan, F.; Zakaria, N.H.; Daud, M. LAO-3D: A Symmetric Lightweight Block Cipher Based on 3D Permutation for Mobile Encryption Application. Symmetry 2022, 14, 2042. [Google Scholar] [CrossRef]
- Lee, Y.H.; Seo, Y.H.; Kim, D.W. Digital hologram watermarking by embedding Fresnel-diffracted watermark data. Opt. Eng. 2019, 58, 035102. [Google Scholar] [CrossRef]
- Dronyuk, I.; Fedevych, O.; Kryvinska, N. Constructing of digital watermark based on generalized fourier transform. Electronics 2020, 9, 1108. [Google Scholar] [CrossRef]
- Chen, T. Deep Learning-Based Optimization Algorithm for Enterprise Personnel Identity Authentication. Comput. Intell. Neurosci. 2022, 2022, 9662817. [Google Scholar] [CrossRef] [PubMed]
- Parah, S.A.; Sheikh, J.A.; Dey, N.; Bhat, G.M. Realization of a new robust and secure watermarking technique using DC coefficient modification in pixel domain and chaotic encryption. J. Glob. Inf. Manag. (JGIM) 2017, 25, 80–102. [Google Scholar] [CrossRef]
- Naseem, M.T.; Nadeem, M.; Qureshi, I.M.; Hussain, A. Optimal secure information using digital watermarking and fuzzy rule base. Multimed. Tools Appl. 2019, 78, 7691–7712. [Google Scholar] [CrossRef]
- Cai, F.; Zhu, N.; He, J.; Mu, P.; Li, W.; Yu, Y. Survey of access control models and technologies for cloud computing. Clust. Comput. 2019, 22, 6111–6122. [Google Scholar] [CrossRef]
- Hsu, C.H.; Wang, S.; Zhang, D.; Chu, H.C.; Lu, N. Efficient identity authentication and encryption technique for high throughput RFID system. Secur. Commun. Netw. 2016, 9, 2581–2591. [Google Scholar] [CrossRef]
- Zhang, M.; Ma, Z.; Zhang, Y.; Wang, Y. An identity authentication scheme based on cloud computing environment. Multimed. Tools Appl. 2018, 77, 4283–4294. [Google Scholar] [CrossRef]
- Zhao, B.; Xiao, Y.; Huang, Y.; Cui, X. A private user data protection mechanism in trustzone architecture based on identity authentication. Tsinghua Sci. Technol. 2017, 22, 218–225. [Google Scholar] [CrossRef]
- Xue, L.; Liu, D.; Huang, C.; Shen, X.S.; Zhuang, W.; Sun, R.; Ying, B. Secure and Flexible Data Sharing for Distributed Storage with Efficient Key Management. In Proceedings of the ICC 2022—International Conference on Communications, Seoul, Republic of Korea, 16–20 May 2022; pp. 4408–4413. [Google Scholar] [CrossRef]
- Imdad, M.; Ramli, S.N.; Mahdin, H. An Enhanced Key Schedule Algorithm of PRESENT-128 Block Cipher for Random and Non-Random Secret Keys. Symmetry 2022, 14, 604. [Google Scholar] [CrossRef]
- Sasikumar, S.; Sundar, K.; Jayakumar, C.; Obaidat, M.S.; Stephan, T.; Hsiao, K.F. Modeling and simulation of a novel secure quantum key distribution (SQKD) for ensuring data security in cloud environment. Simul. Model. Pract. Theory 2022, 121, 102651. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, F.; Duan, F.; Liu, Z.; Chen, Z. Anonymous Privacy-Preserving Consensus via Mixed Encryption Communication. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3445–3449. [Google Scholar] [CrossRef]
- Yin, L.; Mo, F.; Wu, Q.; Long, Y. Research on Application of Data Encryption in Computer Network Security; Springer Nature Singapore: Singapore, 2022; pp. 697–704. [Google Scholar] [CrossRef]
- Babinkostova, L.; Bowden, A.M.; Kimball, A.M.; Williams, K.J. A Simplified and Generalized Treatment of DES-Related Ciphers. Cryptologia 2015, 39, 3–24. [Google Scholar] [CrossRef]
- Chatterjee, A.; Prinz, A. Applying spring security framework with KeyCloak-based OAuth2 to protect microservice architecture APIs: A case study. Sensors 2022, 22, 1703. [Google Scholar] [CrossRef] [PubMed]
- Gómez, O.S.; Rosero, R.H.; Cortés-Verdín, K. CRUDyLeaf: A DSL for Generating Spring Boot REST APIs from Entity CRUD Operations. Cybern. Inf. Technol. 2020, 20, 3–14. [Google Scholar] [CrossRef]
- Zhang, F.; Sun, G.; Zheng, B.; Dong, L. Design and Implementation of Energy Management System Based on Spring Boot Framework. Information 2021, 12, 457. [Google Scholar] [CrossRef]
- Jakobsson, M.; Stamm, S. Web camouflage: Protecting your clients from browser-sniffing attacks. IEEE Secur. Priv. 2007, 5, 16–24. [Google Scholar] [CrossRef]
- Lichtman, M.; Jover, R.P.; Labib, M.; Rao, R.; Marojevic, V.; Reed, J.H. LTE/LTE-A jamming, spoofing, and sniffing: Threat assessment and mitigation. IEEE Commun. Mag. 2016, 54, 54–61. [Google Scholar] [CrossRef]
- Xu, J.; Gong, S.; Zou, Y.; Liu, W.; Zeng, K.; Niyato, D. Redundant sniffer deployment for multi-channel wireless network forensics with unreliable conditions. IEEE Trans. Cogn. Commun. Netw. 2019, 6, 394–407. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).