Surrogate Method for Suspended Sediment Concentration Monitoring on the Alluvial Reach of the River Danube (Baja, Hungary)

Featured Application

Riverine suspended sediment monitoring.

Abstract

Sediment balance is essential for understanding changes in river morphology and ecosystems and related services depending on them. However, the currently used methods to quantify riverine sediment processes are not adequate enough. We have examined the sediment regime of the Danube River, particularly the suspended sediment yield. This parameter can be calculated based on stage or discharge using a suspended sediment yield rating curve; however, the uncertainty of this method can reach even 150%. The suspended sediment yield of a section does not only depend on processes that take place in the riverbed; thus, it cannot be described by only one easily measurable parameter. An integrated surrogate method based on turbidity registration is tested in order to determine suspended sediment yield on the lower Hungarian (sand-bed alluvial) reach of the Danube River. The near-bank turbidity is converted into suspended sediment concentration and then into suspended sediment yield. The turbidity is measured with a built-in turbidity probe, while the suspended sediment yield is determined with traditional methods (discharge measurement, suspended sediment sampling, laboratory processing, and calculation). The traditional and integrated surrogate methods are compared based on the results of the measurements, and different aspect correlations are established between flow parameters, turbidity, and suspended load. The results achieved with the integrated method are promising, but more measurements are required in order to refine the relationships in a broader interval.

1. Introduction

Knowledge of river sediment transport conditions and sediment balance is essential for river management professionals. Sediment balance is very important for understanding changes in riverine ecosystems, channel morphology, and related habitat resources. That is why it is necessary to know if a certain reach of a river is in a state of sediment equilibrium, accumulation, or deficit [1]. In the case that there are gauging stations along the river where regular sediment monitoring takes place, the changes of the sediment balance over time or the influence of tributaries and floodplains can be observed, which makes it possible to investigate sediment transport processes, deposition, and erosion between the stations. However, in the European Union, operational sediment monitoring is unfortunately not yet well developed. As stipulated by the Common Implementation Strategy (CIS) for the Water Framework Directive (WFD), “sediments provide important ecosystem services, such as balancing riverine and coastline morphology, contributing to the connection between surface water and groundwater, increasing soil fertility, contributing to natural water purification, mitigating the negative effects of extreme flow events, etc., and the importance of properly managing sediment to reach the environmental objectives of the WFD, but also of many other EU policies, has been now well recognised.” Turbidity as one of the surrogate measuerements for suspended sediment concentation determination is recommended [2].

The importance of sediment monitoring, especially along the second largest river of Europe, the Danube River, is also shown by the fact that in the last decade, several renowned European institutions (e.g., the University of Natural Resources and Life Sciences in Vienna, the Budapest University of Technology and Economics, and the Faculty of Water Sciences of the University of Public Service in Baja (UPS FWS)), all situated along the Danube River, have investigated the issue in the frames of different projects (e.g., SEDDON, DanubeSediment) [3,4,5].

Suspended sediment can be described by a couple of parameters, including dry matter content (weight [mg, g] of dry matter in an arbitrary volume of water sample), sediment concentration (mass of sediment in a unit volume of water [mg/L, kg/m³]), and sediment yield (mass of sediment passing through the selected cross-section during a selected period of time [kg/s, t/year]), while turbidity can be defined as the reduced transparency of water caused by the particles in it by scattering and absorbing the passing-through light (in the form of, e.g., NTU—Nephelometric Turbidity Unit, FTU—Formazin Nephelometric Unit or FNU—Formazin Nephelometric Unit). Turbidity is now widely used as a surrogate measurement method to estimate suspended load [6,7,8]. This method is based on the quasi-continuous measurement of turbidity, where the turbidity sensor measurements are calibrated with (traditional) suspended sediment sampling during several flood events [9]. In situ turbidimeters are widely used because of the advantages (quasi-continuous measurement, automatic data transfer) of them. Their main disadvantage is biological fouling, which can be minimized by built-in methods (brush) or by regular maintenance [8].

The principles of sediment transport have long been known; however, quick and efficient measurement and accurate direct or indirect calculation methods require further development. In Hungarian practice, the sediment transport conditions of a river at a cross-section are described by the sediment yield rating curves, which give the sediment yield as the function of the discharge (G = f(Q)). The sediment yield rating curves can be created based on the results of the simultaneous suspended sediment sampling and discharge measurement. The dates of the official sediment measurements are regulated by the measurement plan of the General Directorate of Water Management and the water management directorates. The investigated reach belongs to the Lower Danube-Valley Water Directorate (LDVWD). In recent years, on average, five measurements are made annually at predetermined dates. Depending on the hydrological situation, additional measurements are carried out, so the number of measurements at a gauging station in a year is from 5 to 12.

As a result of the current practice, suspended sediment sampling is regular but rare in Hungary, and it is not well harmonized to flood events. Sampling is done with different pump samplers, and laboratory analyses are subcontracted to different firms. Based on this, the sediment datasets in Hungary are of rather questionable quality [10]. Because of the above, the sediment transport conditions can only be described in an approximate way with the sediment yield rating curve created based on the results.

To illustrate this, the difference between the sediment yield rating curve and the measured points, or even the difference between the measured points at nearly the same stage or discharge, can be significant. For example, at the Dunaújváros station (Danube), at a discharge of approximately 3000 m³/s, 80 kg and 250 kg of suspended sediment can as well be measured.

Due to the above, the sediment yield calculated based on the sediment yield curve is fraught with uncertainties. The identification of the changes in the sediment regime of major rivers is heavily dependent on the availability of reliable data [8]. In the case of major rivers around the world (and on the Danube River as well), only a few sediment samples are collected each year, so the data are usually aggregated over a long time in order to create a suspended sediment yield rating curve for that period [11].

Therefore, it is necessary to have a method that provides more reliable data faster than the currently used one, with less resources (no direct sampling costs, i.e., boat and staff, no laboratory needs) as well as a better temporal resolution. There are many good practices in international literature [12], as well as examples from Hungary [13,14,15], but nothing like that along the alluvial sand-bed reach of the Danube.

Furthermore, in the regular sediment monitoring of the Water Authorities, the Baja gauging station (rkm 1479) was included in the past (1951–1965), but nowadays it is not. Thus, there is no regular sediment sampling, just occasional measurements in the frame of projects at this very important section, and one of the reasons why the current study focuses on this particular place is to re-establish sediment monitoring here. This gauging station is located on the left bank of the Danube at river kilometer 1479 (46°10′37″ N, 18°55′26″ E). The ‘0’ point of the station is 80.99 m above the Baltic Sea’s sea level. The water fluctuation range of the stage is 30–1000 cm, and discharge fluctuation is 900– m³/s. The catchment of the station is 208,282 km².

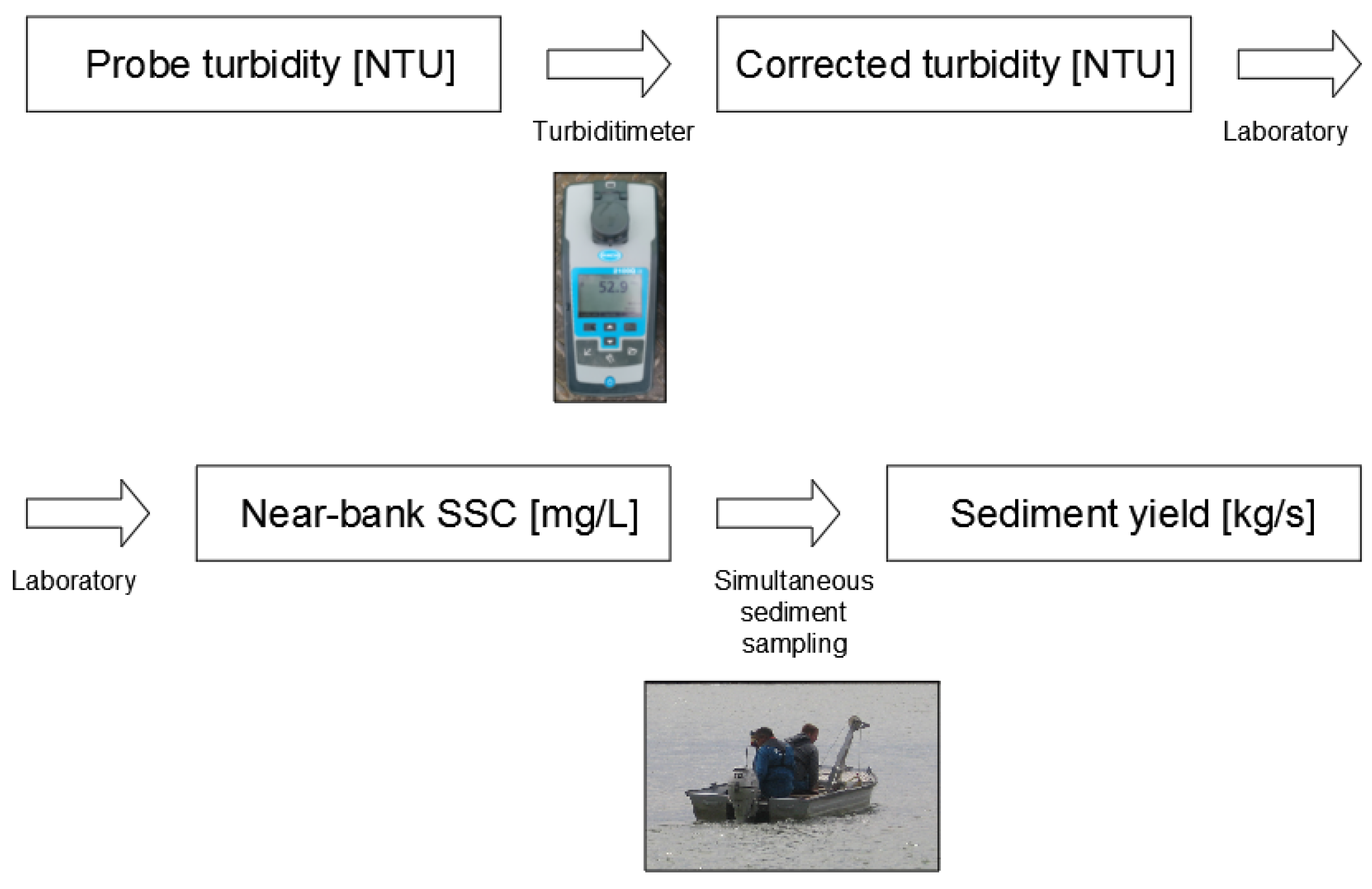
Within the framework of the DanubeSediment Project, a number of scientific articles have been published, recommending good practices applicable to the entire reach of the Danube. An integrated method based on remotely registered turbidity measurement was recommended for the determination of the mass of sediment for the Danube River [4]. The essence of the method is that a sensor installed close to the riverbank continuously registers turbidity, which can be converted into a near-bank suspended sediment concentration using a calibration equation. The sediment concentration measured at a point close to the bank can be converted into a section mean concentration by using another calibration equation. By multiplying the section mean concentration with the discharge, the sediment yield of the entire section can be calculated, which, when integrated over time, results in the mass of the sediment [4,12]. There are some examples already regarding the successful application of the recommended method. The staff of the University of Natural Resources and Life Sciences (Vienna, Austria) have successfully established a multistage relationship between near-bank turbidity and the section mean concentration [12]. In Hungary, the staff of the Budapest University of Technology and Economics has also successfully applied the method on the gravel-bed Danube reach between Sződliget and Ráckeve (rkm 1674, rkm 1604), where a relationship was established between the suspended sediment concentration registered near-bank and the sediment yield of the cross-section [15]. The flowchart of the recommended method is shown in Figure 1.

2. Materials and Methods

2.1. Direct Sampling of Suspended Load

Until recent times, riverine suspended sediment data have been produced by gravimetric analyses performed on water sediment samples collected most of the time manually or, in the U.S., in some sites by automatic samplers. These methods tend to be expensive, difficult, labor intensive, and, under some conditions, e.g., during high floods, hazardous. Specialized equipment and considerable training are prerequisites for obtaining reliable samples and results [8]. However, in Hungary, direct sampling is still an integral part of the sediment monitoring standardization, and it stipulates sampling by a bottle (which is very inexact) or with a pump [16].

During pump sampling, the sample is brought to the surface (on the Danube River, aboard a measuring ship anchored in the vertical) with a pump. In international literature, pump sampling can as well be executed in a different way, when the sample at a monitoring station is taken automatically through a built-in pump. In Hungarian practice, the end of the pump suction tube is lowered into the sampling point using a suitable weight, and the sample of the required volume is sucked up. The disadvantage of the pumping method is that if the sampling velocity does not match the water velocity at the point, the sediment concentration of the sample will not, either. Depending on the relative sampling rate (sampling rate/water velocity), the difference in concentration can be −20–+60%. A deviation is also caused if the end of the intake is not parallel to the flow direction. The effects of divergence in various parameters were studied and published at the University of Iowa, U.S. [17].

Direct sampling methods can be further subdivided according to the number of sampling verticals, and the literature distinguishes between single- and multi-vertical methods. The location of the verticals in the case of the single-vertical method is determined based on different technical considerations (in the middle, at the maximum depth). In the selected vertical, the sampler is lowered and lifted up during the continuous sampling. Among the multi-vertical methods, the international literature recommends three: sampling in lamellae with the same water flow, lamellae of the same width, and lamellae of the same area. Sampling is carried out in a similar way for multi-vertical methods as for the single-vertical method (moving at the same speed); the difference is in the number of verticals. For the lamellae method with the same water flow, a vertical average sample should be taken in between 4 and 9 verticals, and for the method of lamellae of the same width, at least 10 verticals [18]. The Hungarian standard on suspended sediment sampling provides for a multi-vertical method where the lamellae are of equal width, but the average sample for a given vertical is to be prepared by taking 1 L of sample in the vertical at each of the 10 points of different depths, evenly distributed, and then pouring these samples together into one canister to form the vertical average sample with a volume of 10 L. In the case of the Danube, the standard prescribes for seven sampling verticals [16].

As stipulated by the Hungarian standard [16], “during sampling it is very important to ensure that the sampling nozzle faces the flow, the pipe is not bent and to let enough time before taking samples to flush the pipe. Sampling needs to be carried out with care to adjust the revolutions per minute value (RPM) or the discharge of the pump for the velocity through the nozzle V_in should not differ much from the velocity of the flow v at the given point

0.8 v ≤ V_in ≤ 1.5 v

(1)

In case the velocities are outside this range, the RPM of the pump should be accordingly adjusted, or a tap should be installed at the end of the pipe to ensure that intake velocities match. In order to determine intake velocity, the discharge of the pump (q_p) has to be divided by the cross-section area of the nozzle (f_n)

v_in = q_p/f_n

(2)

In practice, sampling is performed with a constant pumping discharge, assigning a fixed intake velocity to different velocity ranges of the flow, keeping the hydraulic coefficient between the values 0.8 and 2.0. This ensures a maximum 20% difference in concentrations, which is acceptable.” [10]

For the purposes of the current study, direct sampling of the suspended sediment load was carried out in accordance with the relevant technical regulations. The method can be used to measure the suspended sediment yield of open watercourses occasionally, but not more than 1–2 times a day (from a boat or bridge). The method is applicable if the vertical mean velocity does not exceed 1.8 m/s and if the water depth at each sampling point is greater than 1 m [16].

Sampling was carried out simultaneously with discharge measurement based on the Doppler principle (using an ADCP instrument) with at least four crossings according to the relevant technical prescription [19]. After the discharge measurement, the same measuring group performed the suspended sediment sampling. As the samples belonging to one vertical are stored in one single container, during the laboratory analyses, the vertical average values of the sediment parameters are given. In some exceptional cases, when we also examined the differences in the sediment concentration/particle size distribution (PSD) within a vertical (e.g., for model calibration), we analyzed all the samples from each vertical individually, but later we averaged the concentration for each vertical in order to get similar results.

2.2. Laboratory Analyses

Before analysis, the samples were left to settle. During and after settling, the samples were stored in a place free of light and frost. After short storage, the turbidity of the samples was measured with a handheld turbidity meter. To measure turbidity, a Hach 2100QIS handheld turbidity meter was used, which determines turbidity based on the standard EPA 180.1. The instrument measures the 90° dispersion of the light transmitted through the sample in NTU. The turbidity meter can measure the turbidity of a 15 mL sample in the range from 0 to 1000 NTU. The correct results of the instrument can be checked regularly with a series of 6-part standard series of known turbidity and, if necessary, easily calibrated with the same series. During turbidity measurement, a sample is taken from the well-stirred vertical average sample with a smaller vessel, and then the instrument’s cuvette is filled with it. After cleaning the cuvette and shaking it, it is inserted it into the instrument and the measurement is started. The turbidity is determined three times per vertical, taking new samples from the stirred vertical average each time. If there is a result significantly different from the average of the three measurements, a supplementary measurement is carried out. The turbidity of the vertical average sample will be the average of the three best measurement results.

After manual turbidity measurement, the sediment samples are settled, withdrawn to a volume of ~1 L, and sent to the laboratory, where their dry matter content and particle size distribution (PSD) curves are determined (PSDs are not discussed in the present study). The method of laboratory processing is regulated by the same [16] technical prescription as the sampling (it is prescribed that the dry matter contents of the samples must be determined after drying the samples at 105 °C for 24 h, and the PSDs of suspended sediments must be determined by a special settling device operating based on Stokes’s law).

2.3. Sediment Yield Calculation

The basic equation for calculating the sediment yield is:

$$G={\displaystyle \sum }_{i=1}^n{q}_i\ast c_i$$

(3)

where:

G—is the suspended sediment yield of the section [g/s]

n—is the number of sediment sampling verticals [pcs]

q_i—is the partial discharge of the sediment sampling lamella [m³/s]

c_i—is the sediment concentration of the sediment sampling vertical [g/m³]

The calculation shall be done for the lamellae of the sediment sampling verticals (bed width belonging to the sediment sampling vertical). A sediment measurement lamella consists of several discharge measurement lamellae; therefore, the discharge of the sediment sampling lamella is the sum of the partial discharges of the discharge measurement lamellae contained therein. The product of the partial discharge of the sediment measurement lamella and the sediment concentration of the sediment sampling vertical gives the sediment yield of the lamella. Summing up the sediment yields per lamellae, one can obtain the suspended sediment yield of the cross section (Figure 2, based on [20]).

2.4. Indirect Measurement of Suspended Load

Sediment concentrations were as well determined indirectly, using in situ turbidity measurement. The turbidity of water expresses its reduced transparency, which is caused by particles in water, by scattering or absorbing light rays passing through water. The instruments used in daily use are based on the laws of nephelometry (nephelometers). Nephelometric measurement measures a 90° scattering of light in the visible or infrared range. Wedges measuring optical reflection measure light rays scattered in 140–165° in the infrared range. Such devices are also suitable for analyzing a sample of small volume (a few cm³). The dispersion of light depends on the size of the particles in the sample, their color, and the shape of the particles [22]. The advantage of this method is that the probe can be fixed in a suitable place and its operation can be automated, which greatly increases the temporal resolution of sediment data. The disadvantage of the method is that turbidity depends on the size, composition, color, and shape of the sediment. The disadvantage of installation is that the accuracy can be greatly reduced by biofilm formation on the probe, so it is necessary to ensure continuous cleaning. Being an indirect method, calibration is required to convert turbidity into sediment concentration.

When using direct methods, data are generated only if the sampling team is physically present on site, takes the samples, and performs the necessary laboratory and processing work. The temporal resolution of data obtained by direct methods should not be arbitrarily low, as they depend on the available human resources and measurement conditions. Indirect methods are based on the use of a physical relationship, so each requires a calibration between the measured and the parameter being sought. An increased number of samplings is required until the calibration is established, after which it is sufficient to check the correctness of the calibration set up by sampling on a regular basis. However, the need for routine calibration is expected to diminish over time [8]. Indirect methods do not give information specific to the entire cross-section, only point information. A separate calibration is required for cross-sectional extension of point information. Another advantage of the indirect methods is that they can be remotely controlled, so they can provide data without on-site presence, at almost any temporal resolution.

To continuously detect turbidity, an OTT Hydrolab HL7 multiparameter probe was used. The parameters measured by the probe can be selected at the time of purchase, and the manufacturer offers a total of 13 sensors for the probe. The probe operated in this specific research measures turbidity, α-chlorophyll, and water temperature. The turbidity sensor can measure turbidity in the range of 0–3000 NTU. Measurement is carried out according to ISO 7027 using light with a wavelength of 880 nm (infrared). Since the measurement accuracy of optical turbidity meters is significantly impaired by the biofilm formed on the sensor, the probe is equipped with a central brush that keeps the instrument clean at all times.

The operation of the turbidity probe and the handheld turbidity meter differ based on the standards used. The probe measures optical reflections of infrared light according to ISO 7027, while the handheld turbidity meter measures 90° dispersion according to EPA 180.1. The analyzed sample is also different, the turbidity probe is in situ, while the handheld turbidity meter analyzes a disturbed sample several times.

The multiparameter probe is fixed and built as a remote registration station. The station was installed on the sand-bed alluvial reach of the Danube River in the ~1479.6 rkm section of the river on a floating pontoon next to the left bank (Figure 3) in January 2020. The support structure, consisting of a protective tube and an instrument box, is mounted on the downstream edge of the pontoon. The placement on the float ensures that the measuring point is always at a depth of ~1.5 m. The subsurface placement provides greater protection from driftwood. The probe is located in a protective basket at the bottom of the protective tube attached to the pontoon. The station consists of a probe, a data logger, additional electronics, and the supporting structure. The probe measures the parameters every hour and sends them to the data logger located in the instrument box, which transmits the data to the LDVWD, where the measured data can be seen with minimal delay. Thanks to the low power consumption of the devices, the installed 50 W solar panel and the 22 Ah buffer battery supply the system with power without problems.

The turbidity measured by the probe is checked by comparative measurements regularly, but at almost every flood wave. During the regular inspection, a sample is taken next to the probe, and then the turbidity of the sample taken is measured also with a hand-held turbidity meter, as described in Section 2.2.

Before carrying out further calculations, the adequacy of the values recorded by the probe was checked. According to the user information, the probe must be calibrated before the first use and at regular intervals. The calibration standard series consists of seven samples (0.1–4000 NTU), of which at least five are required for the Danube River (0.1–1000 NTU).

The probe must therefore be calibrated to improve its measurement accuracy. In order to monitor and improve the measurement accuracy of the probe without the calibration series, water samples are regularly taken from the probe and the turbidity of the sample taken is measured with a handheld turbidimeter. The turbidity of a sample is measured three times and a sample is taken twice from next to the probe.

The correct functioning of the chlorophyll sensor has to be checked with campaign-like measurements as well. During the occasional sampling, the correct registration of chlorophyll content and water temperature is checked, and additional chemical parameters (pH, specific conductivity, dissolved oxygen content, and saturation) are also measured. These parameters are measured and checked for purposes not relevant to this study.

In the used method, the turbidities registered by the installed probe were corrected based on the control measurements made with the handheld turbidity meter. Based on the reliable relationship between the turbidity and the sediment concentration, the corrected turbidity was converted into a near-bank suspended sediment concentration. Using the relationships established based on the simultaneous suspended sediment measurements and near-bank turbidity measurements, the sediment yield along the section was calculated by using a relationship between it and the near-bank sediment concentration (near-bank SSC in Figure 4). A flowchart of the method used is shown in Figure 4.

3. Results

3.1. Turbidity-Suspended Sediment Concentration Relationship

One of the essential steps of this method is to establish the relationship between the turbidity and the suspended sediment concentration. This relationship was set up based on more than 1000 measurements between 2018 and 2022 that were carried out in the frame of regular monitoring at the LDVWA. The measurements were done for four sections on the alluvial reach of the Danube (Dunaújváros, Dombori, Baja, and Mohács). Based on the results, the relationship between the turbidity and the suspended sediment concentration is very strong for each location (R² = 0.92–0.99), and overall, as well (R² = 0.95); furthermore, it was determined that the relationship in those four cases was insensitive for the location. Accepting these results, the turbidity measured by the handheld turbidimeter can be converted into suspended sediment concentration in a reliable way [23]. The suspended sediment concentration as the function of the turbidity can be seen in Figure 5.

3.2. Accuracy of Probe-Recorded Turbidites

Since the installation, 28 control measurements have been carried out, of which 23 have been turbidity comparisons. Based on the measurement results, it can be seen that under 50 NTU turbidimeter turbidity the relative accuracy of the probe is low, as it measures 50–125% of the turbidimeter turbidity. The turbidity range below 50 NTU is in case of low discharge conditions with a low amount of suspended sediment, as well. Because of this, a larger relative error in this range will not cause a significant error in absolute terms. In the turbidity range above 50 NTU, the probe measures 60–90% of the handheld turbidity. The difference between the turbidity measured by the turbidimeter and the probe may be because of the difference between the measurement methods. The difference can also be caused by the fact that the probe is an in situ device, while the turbidimeter analyzes a small volume of sample which is repeatedly disturbed.

In Figure 6, the turbidity measured with the turbidimeter is plotted as a function of the turbidity measured by the probe. Based on the equation of the regression line, the turbidity measured by the probe can be corrected.

The correlation between the turbidity meter and the turbidity probe turbidities can be expressed as follows:

Turbidimeter turbidity = 1.1893 ∗ Probe turbidity + 3.9477

(4)

with a correlation coefficient squared R² = 0.95, which can be considered a rather good correlation.

3.3. Water Level versus Suspended Sediment Concentration

In order to find a relationship between water level (changes) and turbidity, the relationship between the two parameters in the time series was sought. The recorded turbidity as a function of water level was given for the floods listed in

Table 1. Attributes of the analyzed flood waves [23].

Period	Peak Water Level [cm]	Peak Discharge [m3/s]	Peak Turbidity [NTU]
February 2020	639	4450	150
June–July 2020	574	4000	50
June–July 2020	483	3350	25
June–July 2020	400	2800	30
July–September 2021	668	4700	230
July–September 2021	540	3750	70
July–September 2021	496	3450	55
July–September 2021	397	2800	60

.

Several conclusions can be drawn based on the water level and sediment concentration time series, as well as the peak water level and sediment concentration. It is assumed that sediment concentration (similarly to discharge) peaks after the water level. It can be observed in the time series that the water level and sediment concentration do not always peak at the same time. Comparing the water levels and the sediment concentrations, it can be concluded that floods with approximately the same peak water level do not peak with the same sediment concentration. It can be also observed that peak values do not follow each other consistently: the peak water level of 400 cm had a peak concentration of 60 mg/L, but two weeks later the next flood peaked with a lower, 350 cm water level and a higher, 100 mg/L sediment concentration. The examined floods also include ones where there has been no increase in concentration during the entire duration of the flood.

Figure 7 shows the sediment concentration as a function of water level for three periods from Table 1. The three biggest floods peaked with water levels between 570 and 670 cm, but the peak sediment concentrations are not proportional to the peak water level, as they were between 50 and 230 mg/L. In addition, in the case of the two largest flood waves, a hysteresis of sediment concentrations (similar to discharge hysteresis) can be observed. The shape of the curves for each flood wave are different. The hysteresis curve of the 2020 February flood wave has the shape of an asymmetrical 8. The next flood wave, which occurred in June and July 2020, does not have an exact shape nor a significant rise in the suspended sediment concentration, while the flood wave of June and July 2021 has a shape of an open 8. The higher suspended sediment concentrations occurred at the falling limb in the case of these flood waves.

According to [24], the main factors influencing sediment hysteresis in the case of this particular gauging station of the Danube River may be the magnitude and sequence of events, PSD, and sediment source. As in the discussed analysis, these latter two factors were not investigated, and at the moment, no explanation is sought for the described hysteresis phenomena. However, sediment dynamics are complex, and the hysteresis patterns may be linked to many other factors as well.

3.4. Discharge and Sediment Sampling Measurement

The results of the discharge and sediment sampling measurements for the establishment of a relationship between turbidities and the total suspended load can be seen in

Table 2. Discharge and sediment yield.

Date	Water Level [cm]	Discharge [m3/s]	Sediment Yield [kg/s]	Hydrological Condition	Performer
11 February 2020	546	3722	445	Falling	LDVWD
13 May 2020	171	1633	35	Stagnating	LDVWD
12 June 2020	219	1914	30	Rising	LDVWD
23 June 2020	490	3500	161	Rising	LDVWD
29 June 2020	422	2620	194	Falling	UPS FWS
8 July 2020	444	3098	113	Falling	LDVWD
10 August 2020	580	3979	345	Falling	LDVWD
4 February 2021	513	3713	265	Falling	LDVWD
6 May 2021	278	2223	62	Rising	LDVWD
25 May 2021	523	3587	136	Falling	LDVWD
7 September 2021	442	2900	300	Falling	UPS FWS

. The measurements were performed by LDVWD and UPS FWS with standard methods (pump sampling and ADCP discharge measurement) in the relatively low water period of the years 2021–2022, when only a few medium-sized flood waves happened (Figure 7).

In order to provide a picture of the water regime of the Danube River, the hydrograph of the Baja gauging station for the investigated period is provided, with indication of the measurements (Figure 8).

The suspended sediment yield rating curve (suspended sediment yield as the function of the discharge) based on the data above is shown in Figure 8. The fit of the regression to calculate the suspended sediment yield based on the discharge is medium. The correlation coefficient squared is R² = 0.59 for the exponential curve with Equation (5).

Suspended sediment yield = 11.149 ∗ e^{0.0009∗Discharge}

(5)

As a comparison, the suspended sediment yield rating curve based on the old data (1951–1965) is also shown in Figure 9. The correlation coefficient squared is R² = 0.76, which indicates a good relationship between the discharge and the suspended sediment yield.

3.5. Near-Bank Suspended Sediment Concentration versus Suspended Sediment Yield

In the final step of the analysis, a relationship between the near-bank suspended sediment concentration and suspended sediment yield was sought. The near-bank suspended sediment concentration was calculated based on the probe turbidity corrected by the probe-turbidimeter relationship.

Since the installation of the probe, 11 sediment yield measurements have been carried out. Based on the results so far, there is a usable relationship between the two quantities. Based on the literature available [12,15,25], two straight lines were fitted to the measurement results, as the slope of the regression line is significantly decreasing around a sediment concentration of 80 mg/L. The fit of the regression line in the lower range is very strong, R² = 0.90. Due to the low number of measurements (three), the goodness of the fit of the regression line in the higher range is approximate. This approximate fit is very strong as well, R² = 0.85. The regression lines fit well for the rising limb, falling limb, and for the stagnating conditions, as well. The relationship between the near-bank suspended sediment concentration and the suspended sediment yield based on the findings of this study is shown in Figure 10, while the comparison between the correlations with discharge for the old and new data is shown in Figure 9.

4. Discussion

4.1. Water Level versus Sediment Concentration

Based on the analysis of the simultaneous water level and sediment concentration data, it can be concluded that an unequivocal relationship cannot be established between the water level (or discharge) and the sediment concentration. The equivocal relationship can be traced back to a number of reasons, which may be more on a watershed scale. The sediment concentration during a flood wave may depend on the factors triggering it (snowmelt, precipitation). The concentration may also depend on which subbasin the flood wave comes from and the characteristics of this subbasin. In addition to the above, the amount of suspended sediment is also influenced by the level of the flood wave: the flood wave can descend at such a high level that it washes out the silt deposited in the side-branches or by reaching the floodplain, and the deposited silt may be washed into the bed as well. The arriving flood may also increase the amount of sediment being transported by tearing up the bed armor formed between floods. The succession of the floods may also affect the sediment concentration, since the first flood wave can wash out the deposited silt from the side-branches or tear up the bed armor (thus increasing the sediment concentration); subsequent flood waves can no longer do this. Because of these, the sediment regime of a river can usually not be described with the traditional relationship (G = f(Q)) due to its complexity [26].

There is an amount of international literature on the direction of hysteresis of water level and suspended sediment concentration (or discharge and turbidity) [27,28,29]. In the research presented in [27], simultaneous flow and turbidity data of several flood waves were examined in medium-sized river basins, where several hysteresis samples (clockwise, counter-clockwise, eight-shaped, and complex) were distinguished, and the different hysteresis patterns were explained by the factors triggering the flood wave, the number of sediment sources, the distance of sediment sources from the examined cross-section, and the mobility of individual sediment sources.

4.2. Suspended Sediment Yield Rating Curve

The accuracy of the suspended sediment rating curves must be checked, regardless of the regression coefficients. The goodness of them was checked by calculating the difference between the measured value and the value calculated by the usage of the curve equation.

In the case of the 2020–2021 measurement campaign, the average difference between them was 52% in relative terms and 88 kg/s in absolute terms. In half of the cases (6 out of 11), the relative difference was above 50%, and in five cases, the difference was equal to or above 100 kg/s.

By analyzing the historical data, it can be concluded that based on the regression coefficient (R² = 0.76) or the average relative and the average absolute difference (31%, 46 kg/s), this relationship is much more accurate than the one based on the recent measurement. However, the calculation error in the discharge range above 2000 m³/s is higher with an average value of 72 kg/s. About 22% of the differences (13 out of 58) in this range are above 100 kg/s.

Based on these, the accuracy of the suspended sediment yield rating curve is not adequate enough to perform accurate calculations about the annual sediment regime.

4.3. Near-Bank Suspended Sediment Concentration versus Suspended Sediment Yield

Two regression lines were fitted for the simultaneous data of the near-bank suspended sediment concentration and the suspended sediment yield. The accuracy of the relationship between the near-bank suspended sediment concentration and the suspended sediment yield (R² = 0.85–0.90, Figure 9) is better than the suspended sediment yield rating curve based on the discharge either in the case of historical or new data (R² = 0.42–0.57, Figure 8).

The breakpoint of the slope between the two regression lines will be more accurately marked by increasing the number of measurements. In the article [15] published in 2020, the authors defined the breakpoint between the regression lines at around 30 mg/L suspended sediment concentration for the Danube reach between Sződliget and Ráckeve. There is a relatively long distance between these stations and Baja (130–190 km), the PSD of the transported sediment is rather different, and the difference between the breakpoints (breakpoint of Baja is at 80 mg/L) can also be caused by the different geometries of the two cross-sections.

The results so far provide a good starting point; however, 11 measurements are not yet enough to establish reliable relationships covering all ranges. In the future, the measurements will continue in order to refine the relationships. After the establishment of an acceptable relationship which covers all the ranges, this integrated method will be compared with the sediment yield rating curve method by determining and comparing the annual and flood wave sediment regimes. Further tests will be carried out about the suitability of the selected gauging station (Baja), as during the measurements made so far, the water level of the Danube River did not exceed the point of overflowing the banks of the main riverbed (400 m wide), so the effects of the floodplain (7 km wide) on the sediment transport in the case of the integrated method could not yet be detected.

Overall, the prospect of large-scale applications of proven suspended sediment surrogate technologies is a revolutionary concept in fluvial sediment monitoring technologies with important future benefits, providing for safer, more frequent and consistent, arguably more accurate, and ultimately less expensive fluvial sediment data collection [8], which underlines the importance of the presented research.