Analysis of Variables Influencing Scour on Large Sand-Bed Rivers Conducted Using Field Data
Abstract
1. Introduction
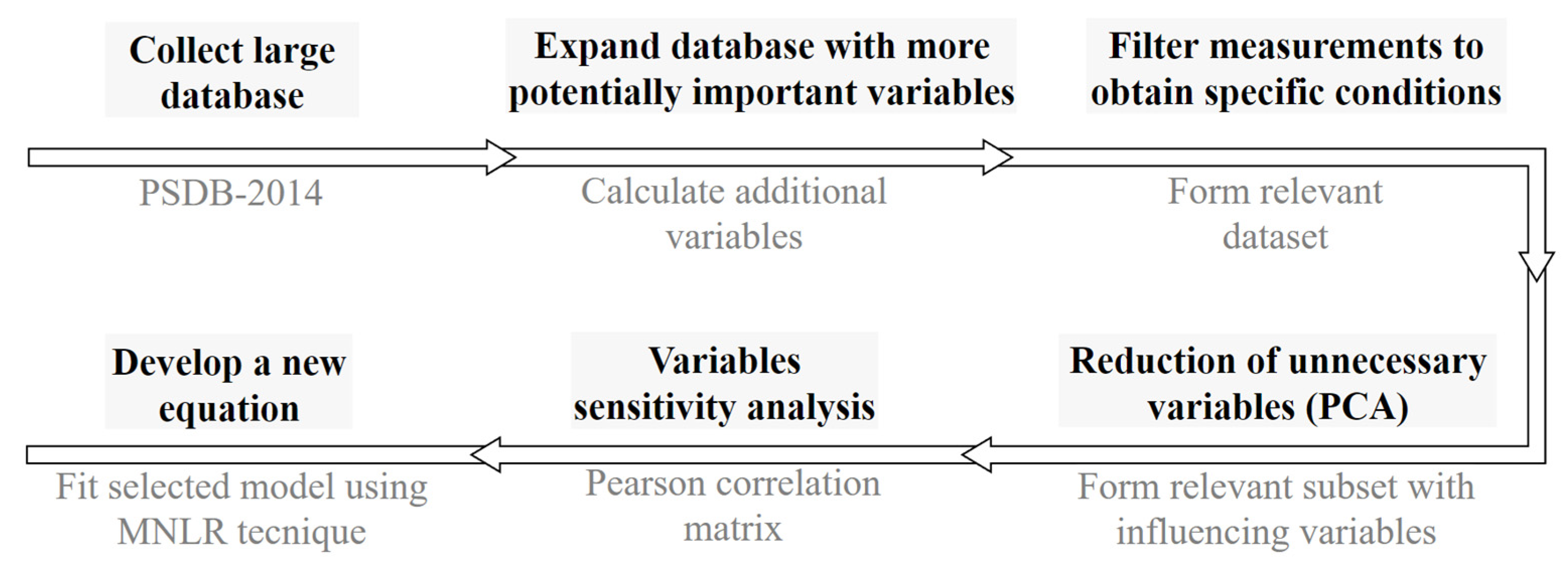
2. Methodology
2.1. Influencing Variables
2.2. Data Filtering
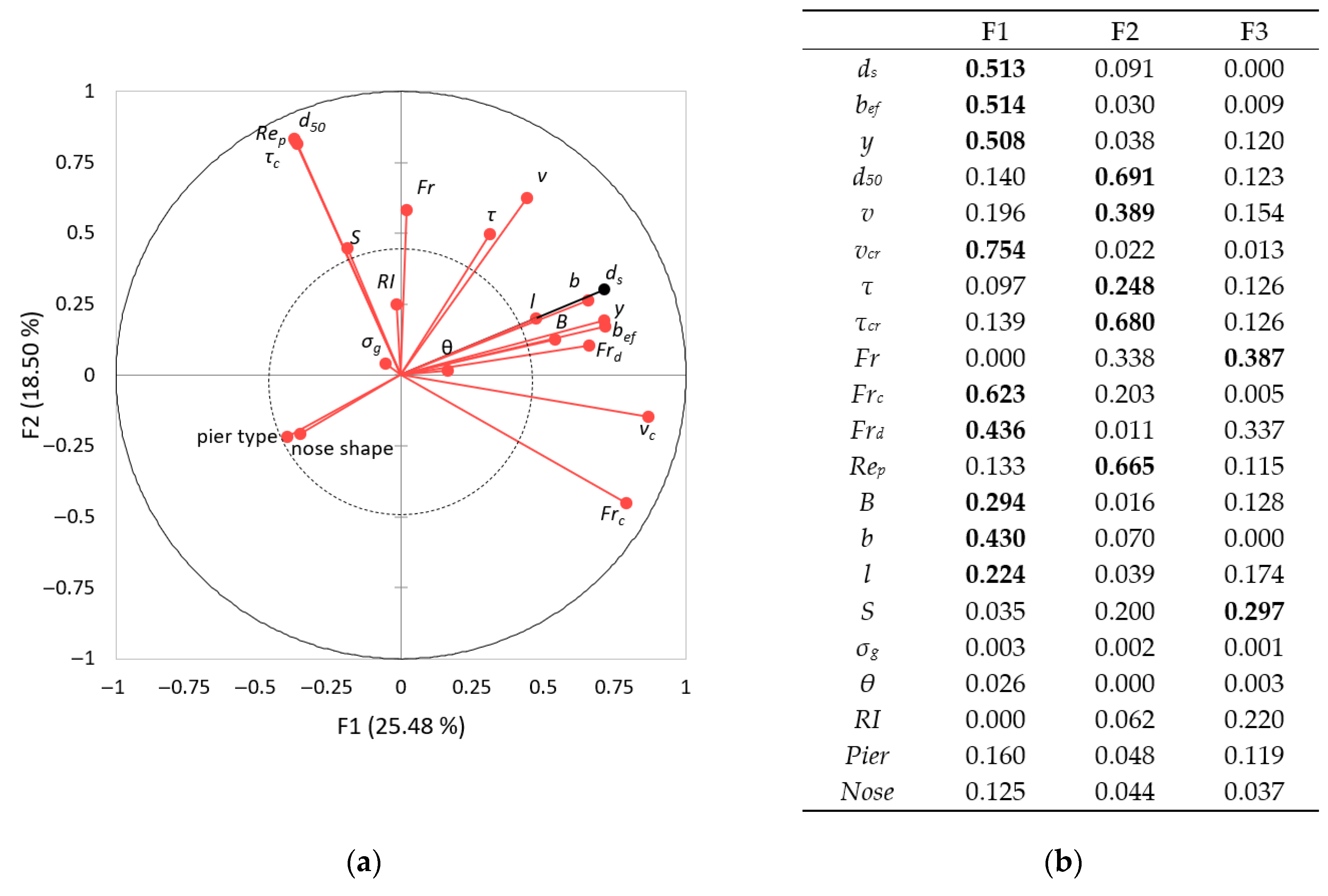
2.3. Variable Reduction
3. Results
3.1. MNLR—Multiple Nonlinear Regression
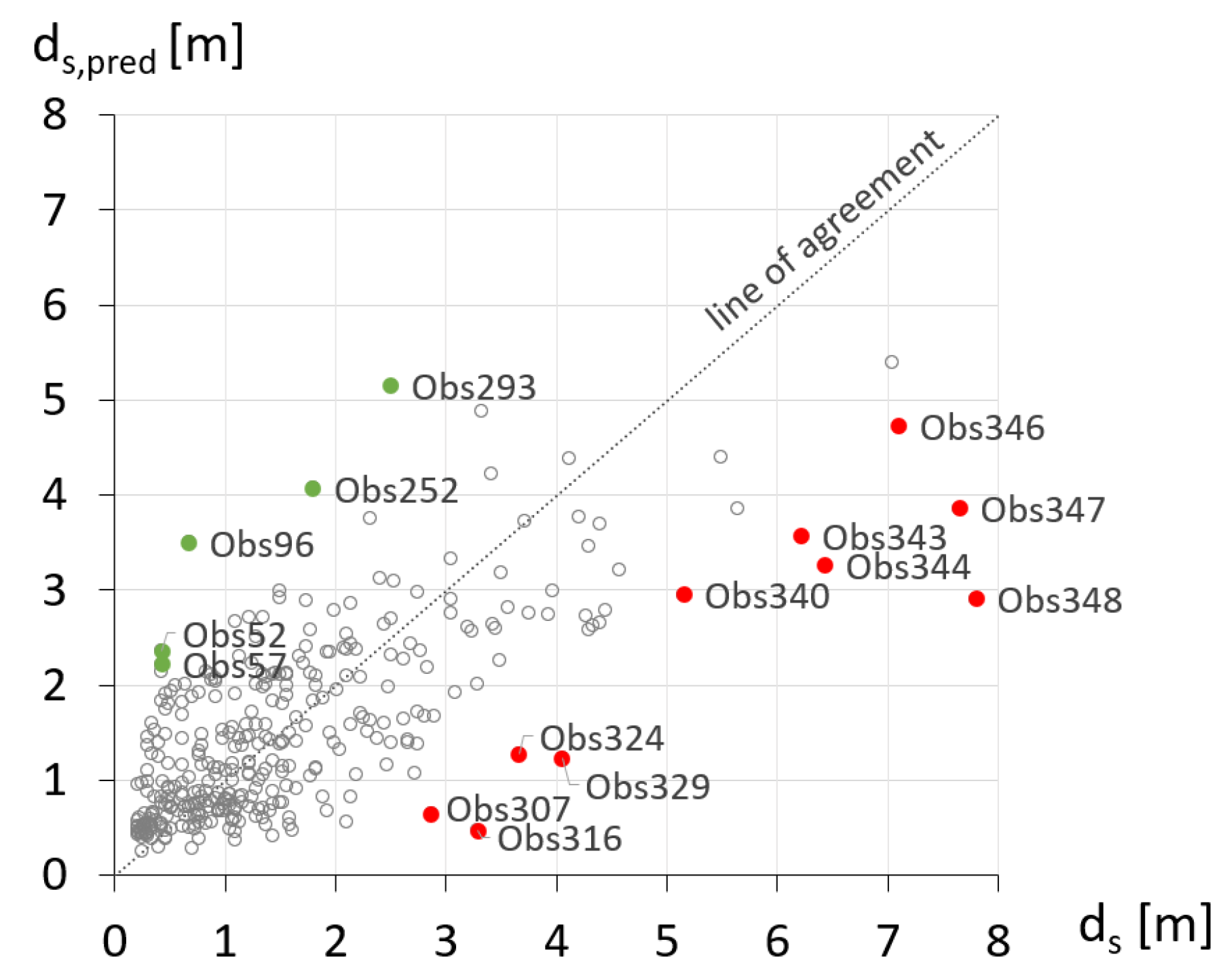
3.2. Comparison with Different Scour Models
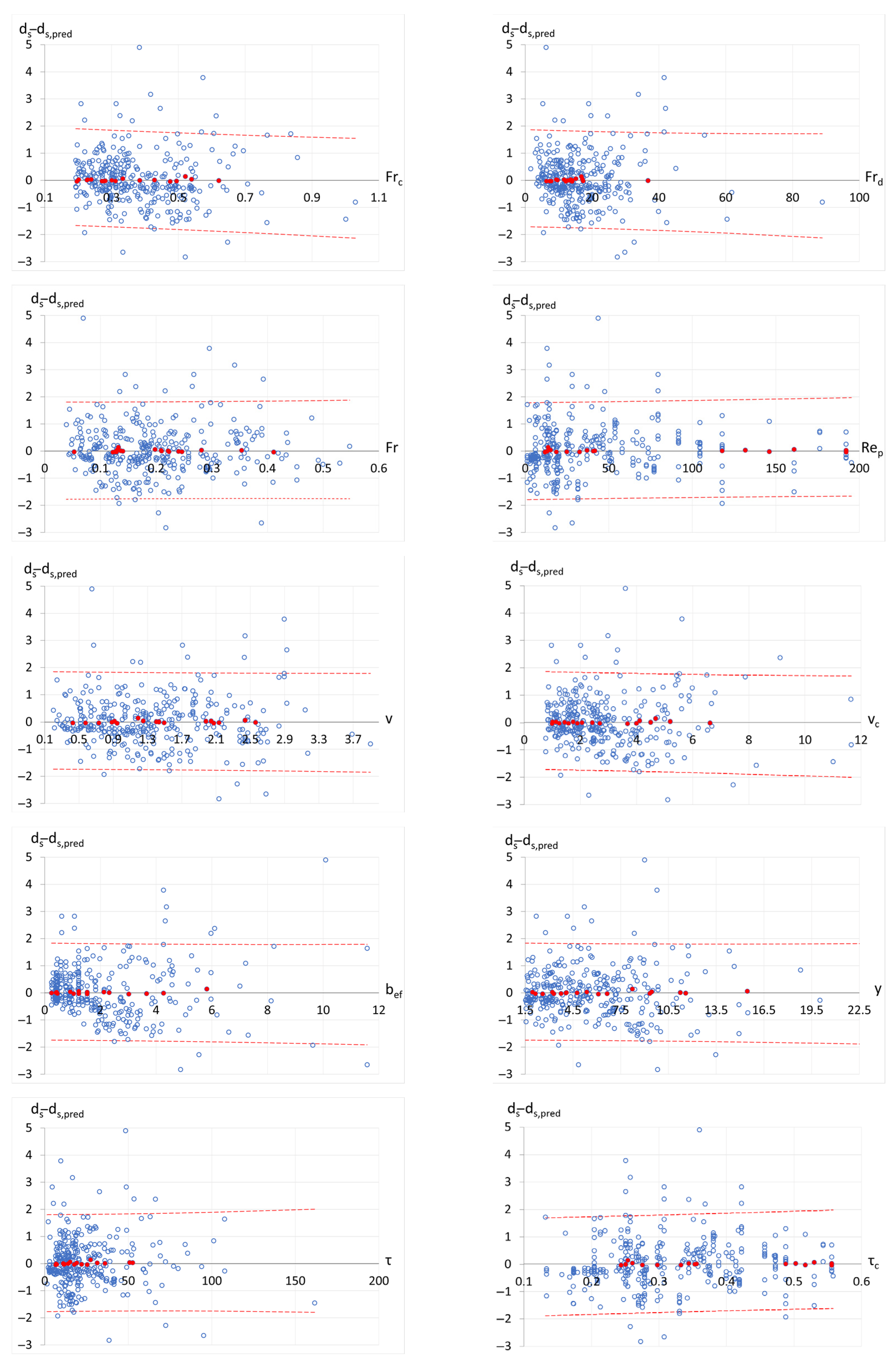
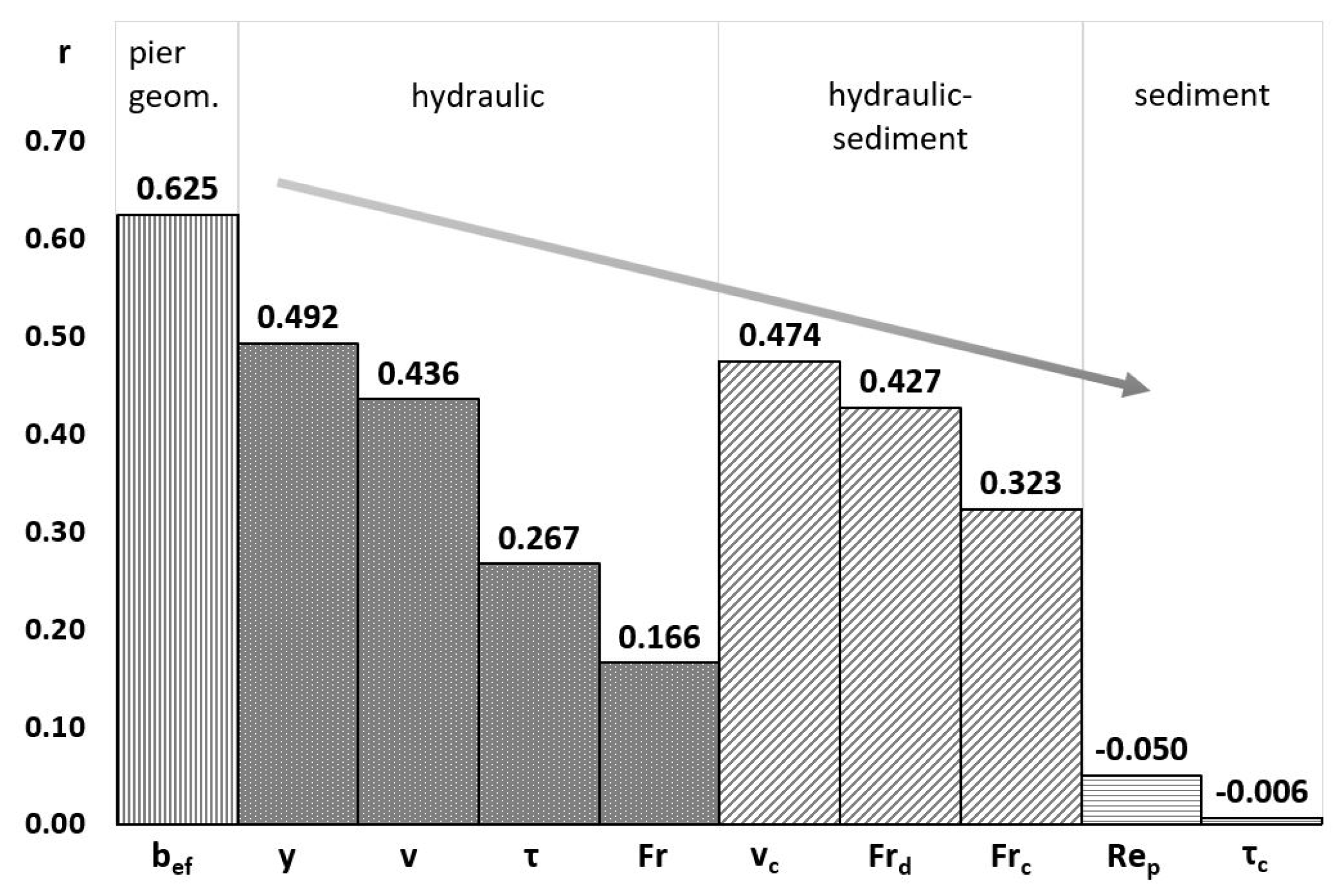
3.3. Variable Sensitivity Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Glossary
| Symbol | Unit | Description |
| ds | [m] | scour depth |
| v | [m/s] | local approach flow velocity (upstream of the pier) |
| vc | [m/s] | critical velocity |
| y | [m] | approach water depth (upstream of the pier) |
| b | [m] | nominal pier width |
| l | [m] | pier length |
| bef | [m] | effective pier width normal to the flow |
| θ | [°] | angle of attack |
| B | [m] | the channel width |
| S | [1] | stream slope |
| τ | [Pa] | local bed shear stress |
| τc | [Pa] | critical bed shear stress |
| Fr | [1] | Froude number |
| Frc | [1] | critical Froude number for incipient motion |
| Frd | [1] | densimetric Froude number |
| Rep | [1] | particle Reynolds number |
| RI | [years] | recurrence interval for measured flow rate |
| g | [m/s2] | gravitational acceleration |
| d50 | [mm] | sediment median grain size |
| d95 | [mm] | the size at which 95% of the sediment particles are smaller |
| σg | [1] | geometrical standard deviation of sediment (measure of non-uniformity) |
| ρrel | [1] | submerged relative mass density of sediment particles (ρrel = [(ρs − ρ)/ρ] − 1 = 1.65) |
| ρs | [kg/m3] | mass density of sediment particles (equal to 2650 kg/m3) |
| ρw | [kg/m3] | mass density of water (equal to 1000 kg/m3) |
| γs | [N/m3] | specific gravity of sediment (equal to 25,996.5 N/m3) |
| γw | [N/m3] | specific gravity of water (equal to 9810 N/m3) |
| K1 | [1] | the live-bed vs. clear-water correction factor |
| K2 | [1] | the pier shape correction factor |
| ν | [m2/s] | kinematic viscosity of fluid (ν = 1.6 × 10−6 m2/s) |
| Φ | [°] | angle of repose for sediments |
| r | [1] | Pearson correlation coefficient |
References
- Grizzetti, B.; Pistocchi, A.; Liquete, C.; Udias, A.; Bouraoui, F.; Van de Bund, W. Human pressures and ecological status of European rivers. Sci. Rep. 2017, 7, 205. [Google Scholar] [CrossRef]
- Sholtes, J.S.; Ubing, C.; Randle, T.J.; Fripp, J.; Cenderelli, D.; Baird, D.C. Managing Infrastructure in the Stream Environment; Advisory Committee on Water Information Subcommittee on Sedimentation: Austin, TX, USA, 2017; p. 65. [Google Scholar]
- Lee, M.; Yoo, M.; Jung, H.-S.; Kim, K.H.; Lee, I.-W. Study on Dynamic Behavior of Bridge Pier by Impact Load Test Considering Scour. Appl. Sci. 2020, 10, 6741. [Google Scholar] [CrossRef]
- Kallias, A.N.; Imam, B. Probabilistic assessment of local scour in bridge piers under changing environmental conditions. Struct. Infrastruct. Eng. 2016, 12, 1228–1241. [Google Scholar] [CrossRef]
- Imhof, D. Risk Assessment of Existing Bridge Structures. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2004. [Google Scholar]
- Schaap, H.S.; Caner, A. Bridge collapses in Turkey: Causes and remedies. Struct. Infrastruct. Eng. 2022, 18, 694–709. [Google Scholar] [CrossRef]
- Yao, C.; Briaud, J.-L.; Gardoni, P. Risk Analysis on Bridge Scour Failure. In Proceedings of the International Foundations Congress and Equipment Expo, San Antonio, TX, USA, 17–21 March 2015; pp. 1936–1945. [Google Scholar]
- Nasr, A.; Björnsson, I.; Honfi, D.; Larsson Ivanov, O.; Johansson, J.; Kjellström, E. A review of the potential impacts of climate change on the safety and performance of bridges. Sustain. Resilient Infrastruct. 2021, 6, 192–212. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Pińskwar, I. Are Pluvial and Fluvial Floods on the Rise? Water 2022, 14, 2612. [Google Scholar] [CrossRef]
- Nemry, F.; Demirel, H. Impacts of Climate Change on Transport: A Focus on Road and Rail Transport Infrastructures; European Commission Joint Research Centre: Luxembourg, 2012. [Google Scholar]
- Badroddin, M.; Chen, Z. Lifetime Resilience Measurement of River-Crossing Bridges with Scour Countermeasures under Multiple Hazards. J. Eng. Mech. 2021, 147, 04021058. [Google Scholar] [CrossRef]
- Tubaldi, E.; White, C.J.; Patelli, E.; Mitoulis, S.A.; de Almeida, G.; Brown, J.; Cranston, M.; Hardman, M.; Koursari, E.; Lamb, R.; et al. Invited perspectives: Challenges and future directions in improving bridge flood resilience. Nat. Hazards Earth Syst. Sci. 2022, 22, 795–812. [Google Scholar] [CrossRef]
- Imam, B.M.; Chryssanthopoulos, M.K. Causes and Consequences of Metallic Bridge Failures. Struct. Eng. Int. 2012, 22, 93–98. [Google Scholar] [CrossRef]
- Borghei, S.M.; Kabiri-Samani, A.; Banihashem, S.A. Influence of unsteady flow hydrograph shape on local scouring around bridge pier. Proc. Inst. Civ. Eng. -Water Manag. 2012, 165, 473–480. [Google Scholar] [CrossRef]
- Hung, C.-C.; Yau, W.-G. Behavior of scoured bridge piers subjected to flood-induced loads. Eng. Struct. 2014, 80, 241–250. [Google Scholar] [CrossRef]
- Lu, J.-Y.; Hong, J.-H.; Su, C.-C.; Wang, C.-Y.; Lai, J.-S. Field Measurements and Simulation of Bridge Scour Depth Variations during Floods. J. Hydraul. Eng. 2008, 134, 810–821. [Google Scholar] [CrossRef]
- Harasti, A.; Gilja, G.; Potočki, K.; Lacko, M. Scour at Bridge Piers Protected by the Riprap Sloping Structure: A Review. Water 2021, 13, 3606. [Google Scholar] [CrossRef]
- Benedict, S.T.; Caldwell, A.W. Upper Bound of Pier Scour in Laboratory and Field Data. Transp. Res. Rec. 2016, 2588, 145–153. [Google Scholar] [CrossRef]
- Annad, M.; Lefkir, A. New Formula for Calculating Local Scour around Bridge Piers. Adv. Eng. Forum 2022, 45, 57–64. [Google Scholar] [CrossRef]
- Gaudio, R.; Grimaldi, C.; Tafarojnoruz, A.; Calomino, F. Comparison of formulae for the prediction of scour depth at piers. In Proceedings of the First European IAHR Congress, Edinburgh, UK, 4–6 May 2010; pp. 6–12. [Google Scholar]
- Zhang, G.; Hsu, S.A.; Guo, T.; Zhao, X.; Augustine, A.D.; Zhang, L. Evaluation of Design Methods to Determine Scour Depths for Bridge Structures; FHWA/LA.11/491; Louisiana State University: Baton Rouge, LA, USA; Federal Highway Administration: Washington, DC, USA, 2013.
- Dong, H.; Sun, Z.; Li, Z.; Chong, L.; Zhou, H. Artificial Intelligence for Predicting Local Scour Depth around Piers Based on Dimensional Analysis. J. Coast. Res. 2020, 111, 21–25. [Google Scholar] [CrossRef]
- Pandey, M.; Zakwan, M.; Sharma, P.K.; Ahmad, Z. Multiple linear regression and genetic algorithm approaches to predict temporal scour depth near circular pier in non-cohesive sediment. ISH J. Hydraul. Eng. 2018, 26, 96–103. [Google Scholar] [CrossRef]
- Rady, R.M.A.E.-H. Prediction of local scour around bridge piers: Artificial-intelligence-based modeling versus conventional regression methods. Appl. Water Sci. 2020, 10, 57. [Google Scholar] [CrossRef]
- Muzzammil, M.; Alama, J.; Danish, M. Scour Prediction at Bridge Piers in Cohesive Bed Using Gene Expression Programming. Aquat. Procedia 2015, 4, 789–796. [Google Scholar] [CrossRef]
- Benedict, S.T.; Caldwell, A.W. A Pier-Scour Database: 2427 Field and Laboratory Measurements of Pier Scour; Data Series 845; U.S. Geological Survey: Reston, VA, USA, 2014; p. 32.
- Benedict, S.T.; Knight, T.P. Use of Laboratory and Field Data to Evaluate the Pier Scour Equation from Hydraulic Engineering Circular 18. Transp. Res. Rec. 2017, 2638, 113–121. [Google Scholar] [CrossRef]
- Rathod, P.; Manekar, V.L. Gene expression programming to predict local scour using laboratory and field data. ISH J. Hydraul. Eng. 2022, 28, 143–151. [Google Scholar] [CrossRef]
- Pandey, M.; Oliveto, G.; Pu, J.H.; Sharma, P.K.; Ojha, C.S.P. Pier Scour Prediction in Non-Uniform Gravel Beds. Water 2020, 12, 1696. [Google Scholar] [CrossRef]
- Ali, A.S.A.; Günal, M. Artificial Neural Network for Estimation of Local Scour Depth Around Bridge Piers. Arch. Hydro-Eng. Environ. Mech. 2021, 68, 87–101. [Google Scholar] [CrossRef]
- Shahriar, A.R.; Ortiz, A.C.; Montoya, B.M.; Gabr, M.A. Bridge Pier Scour: An overview of factors affecting the phenomenon and comparative evaluation of selected models. Transp. Geotech. 2021, 28, 100549. [Google Scholar] [CrossRef]
- Qi, M.; Li, J.; Chen, Q. Comparison of existing equations for local scour at bridge piers: Parameter influence and validation. Nat. Hazards 2016, 82, 2089–2105. [Google Scholar] [CrossRef]
- Guo, J.; Suaznabar, O.; Shan, H.; Shen, J. Pier Scour in Clear-Water Conditions with Non-Uniform Bed Materials; FHWA-HRT-12-022; Federal Highway Administration: Washington, DC, USA, 2012; p. 62.
- Shields, A. Application of Similarity Principles and Turbulence Research to Bed-Load Movement; Hydrodynamics Laboratory: Washington, DC, USA, 1936; p. 47. [Google Scholar]
- Shahmohammadi, R.; Afzalimehr, H.; Sui, J. Assessment of Critical Shear Stress and Threshold Velocity in Shallow Flow with Sand Particles. Water 2021, 13, 994. [Google Scholar] [CrossRef]
- Julien, P.Y. Erosion and Sedimentation; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Azamathulla, H.M.; Ghani Aminuddin, A.; Zakaria Nor, A.; Guven, A. Genetic Programming to Predict Bridge Pier Scour. J. Hydraul. Eng. 2010, 136, 165–169. [Google Scholar] [CrossRef]
- Jain, S.C.; Fischer, E.E. Scour around Circular Bridge Piers at High Froude Numbers; FHWA-RD-79-104; Federal Highway Administration: Washington, DC, USA, 1979; p. 70.
- Dey, S.; Raikar, R.V. Clear-Water Scour at Piers in Sand Beds with an Armor Layer of Gravels. J. Hydraul. Eng. 2007, 133, 703–711. [Google Scholar] [CrossRef]
- Benedict, S.T.; Knight, T.P. Benefits of Compiling and Analyzing Hydraulic-Design Data for Bridges. Transp. Res. Rec. 2021, 2675, 1073–1081. [Google Scholar] [CrossRef]
- Garde, R.C.J.; Kothyari, U.C. Scour around bridge piers. PINSA 64 1998, 4, 569–580. [Google Scholar]
- Subedi, A.S.; Sharma, S.; Islam, A.; Lamichhane, N. Quantification of the Effect of Bridge Pier Encasement on Headwater Elevation Using HEC-RAS. Hydrology 2019, 6, 25. [Google Scholar] [CrossRef]
- Harasti, A.; Gilja, G.; Adžaga, N.; Škreb, K.A. Principal Component Analysis in development of empirical scour formulae. In Proceedings of the 7th IAHR Europe Congress, Athens, Greece, 7–9 September 2022; pp. 271–272. [Google Scholar]
- Zwick, W.R.; Velicer, W.F. Comparison of five rules for determining the number of components to retain. Psychol. Bull. 1986, 99, 432–442. [Google Scholar] [CrossRef]
- Breusers, H.N.C.; Raudkivi, A.J. Scouring, 1st ed.; Taylor and Francis Group: London, UK, 1991; p. 152. [Google Scholar]
- Laursen, E.M. Scour at Bridge Crossings. J. Hydraul. Div. 1960, 86, 39–54. [Google Scholar] [CrossRef]
- Kiraga, M.; Popek, Z. Bed Shear Stress Influence on Local Scour Geometry Properties in Various Flume Development Conditions. Water 2019, 11, 2346. [Google Scholar] [CrossRef]
- Parker, G. Transport of Gravel and Sediment Mixtures. In Sedimentation Engineering; Garcia, M., Ed.; American Society of Civil Engineers: Reston, VA, USA, 2008; pp. 165–251. [Google Scholar]
- Vonkeman, J.K.; Basson, G.R. Evaluation of empirical equations to predict bridge pier scour in a non-cohesive bed under clear-water conditions. J. S. Afr. Inst. Civ. Eng. 2019, 61, 2–20. [Google Scholar] [CrossRef]
- Hassan, W.H.; Jalal, H.K. Prediction of the depth of local scouring at a bridge pier using a gene expression programming method. SN Appl. Sci. 2021, 3, 159. [Google Scholar] [CrossRef]
- Melville, B.W. Local Scour at Bridge Sites; University of Auckland: Auckland, New Zealand, 1975; p. 227. [Google Scholar]
- Melville, B.W.; Sutherland, A.J. Design Method for Local Scour at Bridge Piers. J. Hydraul. Eng. 1988, 114, 1210–1226. [Google Scholar] [CrossRef]
- Richardson, E.V.; Davis, S.R. Evaluating Scour at Bridges, 4th ed.; FHWA NHI 01-001; Hydraulic Engineering Circular No. 18; Federal Highway Administration: Washington, DC, USA, 2001; p. 378.
- Török, G.T.; Józsa, J.; Baranya, S. A Shear Reynolds Number-Based Classification Method of the Nonuniform Bed Load Transport. Water 2019, 11, 73. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Temporal Evolution of Clear-Water Pier and Abutment Scour. J. Hydraul. Eng. 2002, 128, 811–820. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Further Results to Time-Dependent Local Scour at Bridge Elements. J. Hydraul. Eng. 2005, 131, 97–105. [Google Scholar] [CrossRef]
- Tan, S.M.; Lim, S.-Y.; Wei, M.; Cheng, N.-S. Application of Particle Densimetric Froude Number for Evaluating the Maximum Culvert Scour Depth. J. Irrig. Drain. Eng. 2020, 146, 04020020. [Google Scholar] [CrossRef]

| Additional Variable | Equation | |
|---|---|---|
| Froude number | (1) | |
| local shear stress | (2) | |
| critical shear stress [34] | (3) | |
| critical velocity [35] | (4) | |
| critical Froude number | (5) | |
| densimetric Froude number | (6) | |
| particle Reynolds number | (7) |
| Variable | Before Filtering | After Filtering | |||||
|---|---|---|---|---|---|---|---|
| Range | Average | Standard Deviation | Range | Average | Standard Deviation | ||
| Original | ds | 0–10.4 | 1.1 | 1.3 | 0.21–7.8 | 1.5 | 1.3 |
| bef | 0.21–28.7 | 2.3 | 2.5 | 0.24–11.6 | 2.0 | 1.9 | |
| b | 0.21–19.5 | 1.6 | 1.6 | 0.24–11.6 | 1.3 | 1.4 | |
| l | 0.21–39.6 | 6.3 | 5.3 | 0.37–25.3 | 6.3 | 4.7 | |
| θ | 0–85.0 | 6.1 | 10.3 | 0–600 | 6.6 | 9.6 | |
| d50 | 0.001–228.6 | 14.7 | 25.0 | 0.06–1.82 | 0.59 | 0.41 | |
| y | 0–22.5 | 3.9 | 3.2 | 1.5–22.5 | 5.6 | 3.4 | |
| v | 0–5.4 | 1.4 | 0.8 | 0.20–3.9 | 1.4 | 0.71 | |
| RI | 1–500 | 53.6 | 50.9 | 1–500 | 63.1 | 69.4 | |
| σg | 1.2–20.3 | 3.3 | 2.8 | 1.4–20.3 | 3.0 | 1.2 | |
| S | 0.00007–0.02 | 0.00086 | 0.00152 | 0.00007–0.0036 | 0.00052 | 0.00044 | |
| Additional | B | 5.4–692.5 | 71.5 | 67.1 | 10.5–692.5 | 75.3 | 80.7 |
| vc | 0.15–55.7 | 2.4 | 3.2 | 0.76–11.6 | 2.8 | 1.7 | |
| τ | 0–180 | 21.3 | 21.8 | 0.015–1.7 | 0.25 | 0.21 | |
| τc | 0.025–3.9 | 0.87 | 0.77 | 0.13–0.56 | 0.32 | 0.10 | |
| Fr | 0–1.98 | 0.28 | 0.21 | 0.039–0.55 | 0.20 | 0.10 | |
| Frc | 0.19–5.77 | 0.40 | 0.34 | 0.19–1.0 | 0.38 | 0.13 | |
| Frd | 0–629 | 11.1 | 23.4 | 1.6–88.9 | 16.0 | 9.9 | |
| Rep | 0.0025–274,834 | 8222 | 19,074 | 1.2–195.2 | 42.1 | 43.7 | |
| Original | Pier type | Single and group | Not affected | ||||
| Pier nose shape (drag coefficient) [42] | Cylindrical (1.2), Round (1.33), Square (2.0), Sharp (1.0), Triangular (1.72) | ||||||
| Influential variables | bef | y | v | vc | τ | τc | Fr | Frc | Frd | Rep |
| a | b | c | d | e | f | g | h | i | j | k | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| dimensional | 3.29 | 0.49 | 1.19 | −0.91 | −0.99 | −0.011 | 0.019 | 0.38 | 0.26 | 0.97 | −0.44 |
| non-dimensional | 0.002 | 0.48 | −0.90 | −0.047 | −0.33 | −2.50 | 1.16 | −0.094 |
| ID | bef | y | v | vc | τ | τc | Fr | Frc | Frd | Rep | ds | ds,pred | Residuals |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Obs96 | 4.88 | 9.81 | 2.13 | 5.11 | 38.51 | 0.27 | 0.22 | 0.52 | 27.57 | 17.90 | 0.67 | 3.50 | −2.83 |
| Obs293 | 11.58 | 4.85 | 2.68 | 2.30 | 95.08 | 0.31 | 0.39 | 0.33 | 29.82 | 28.11 | 2.50 | 5.15 | −2.65 |
| Obs252 | 5.54 | 13.47 | 2.35 | 7.44 | 72.45 | 0.26 | 0.20 | 0.65 | 32.61 | 14.39 | 1.80 | 4.08 | −2.28 |
| Obs52 | 9.63 | 3.60 | 0.79 | 1.30 | 7.76 | 0.49 | 0.13 | 0.22 | 5.46 | 117.86 | 0.43 | 2.36 | −1.93 |
| Obs57 | 2.50 | 9.33 | 1.55 | 4.09 | 17.38 | 0.33 | 0.16 | 0.43 | 16.63 | 31.55 | 0.43 | 2.22 | −1.79 |
| Obs340 | 5.97 | 8.35 | 1.22 | 3.28 | 11.47 | 0.37 | 0.13 | 0.36 | 11.37 | 47.57 | 5.15 | 2.95 | 2.20 |
| Obs307 | 0.61 | 2.77 | 1.13 | 1.14 | 5.17 | 0.42 | 0.22 | 0.22 | 8.86 | 79.52 | 2.87 | 0.65 | 2.22 |
| Obs346 | 6.10 | 22.52 | 2.43 | 9.11 | 66.29 | 0.34 | 0.16 | 0.61 | 24.65 | 36.96 | 7.10 | 4.73 | 2.37 |
| Obs324 | 1.07 | 4.54 | 1.77 | 2.17 | 53.46 | 0.31 | 0.26 | 0.33 | 19.65 | 28.11 | 3.66 | 1.27 | 2.38 |
| Obs343 | 4.33 | 5.67 | 2.93 | 3.32 | 32.81 | 0.25 | 0.39 | 0.45 | 41.99 | 13.07 | 6.22 | 3.57 | 2.65 |
| Obs329 | 1.07 | 4.15 | 1.71 | 2.00 | 48.80 | 0.31 | 0.27 | 0.31 | 18.97 | 28.11 | 4.05 | 1.23 | 2.82 |
| Obs316 | 0.61 | 2.19 | 0.67 | 0.97 | 4.52 | 0.42 | 0.14 | 0.21 | 5.27 | 79.52 | 3.29 | 0.47 | 2.82 |
| Obs344 | 4.37 | 5.21 | 2.44 | 2.98 | 16.62 | 0.26 | 0.34 | 0.42 | 33.88 | 14.39 | 6.43 | 3.26 | 3.17 |
| Obs347 | 4.27 | 9.78 | 2.90 | 5.62 | 9.60 | 0.25 | 0.30 | 0.57 | 41.55 | 13.07 | 7.65 | 3.86 | 3.79 |
| Obs348 | 10.09 | 9.00 | 0.65 | 3.60 | 48.40 | 0.36 | 0.07 | 0.38 | 6.24 | 43.61 | 7.80 | 2.90 | 4.90 |
| Author | Dataset | Method | Equation | |
|---|---|---|---|---|
| Annad and Lefkir, 2022 [19] | field (PSDB-2014) | MNLR | (11) | |
| Rathod and Manekar, 2022 [28] | field and laboratory (PSDB-2014) | GEP | (12) | |
| Hassan and Jalal, 2021 [50] | numerical on a large scale | GEP | (13) | |
| Jain and Fischer, 1979 [38] | field and laboratory | conventional MNLR | (14) | |
| Azamathulla et al., 2010 [37] | field | MNLR | (15) | |
| Our non-dimensional model | field (PSDB-2014) | MNLR | (16) | |
| Our dimensional model | field (PSDB-2014) | MNLR | (17) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harasti, A.; Gilja, G.; Adžaga, N.; Žic, M. Analysis of Variables Influencing Scour on Large Sand-Bed Rivers Conducted Using Field Data. Appl. Sci. 2023, 13, 5365. https://doi.org/10.3390/app13095365
Harasti A, Gilja G, Adžaga N, Žic M. Analysis of Variables Influencing Scour on Large Sand-Bed Rivers Conducted Using Field Data. Applied Sciences. 2023; 13(9):5365. https://doi.org/10.3390/app13095365
Chicago/Turabian StyleHarasti, Antonija, Gordon Gilja, Nikola Adžaga, and Mark Žic. 2023. "Analysis of Variables Influencing Scour on Large Sand-Bed Rivers Conducted Using Field Data" Applied Sciences 13, no. 9: 5365. https://doi.org/10.3390/app13095365
APA StyleHarasti, A., Gilja, G., Adžaga, N., & Žic, M. (2023). Analysis of Variables Influencing Scour on Large Sand-Bed Rivers Conducted Using Field Data. Applied Sciences, 13(9), 5365. https://doi.org/10.3390/app13095365







