Seismic Performance of a New Assembled Bolt-Connected Concrete Beam–Column Joint: Experimental Test and Finite Element Modeling
Abstract
1. Introduction
2. Experimental Overview
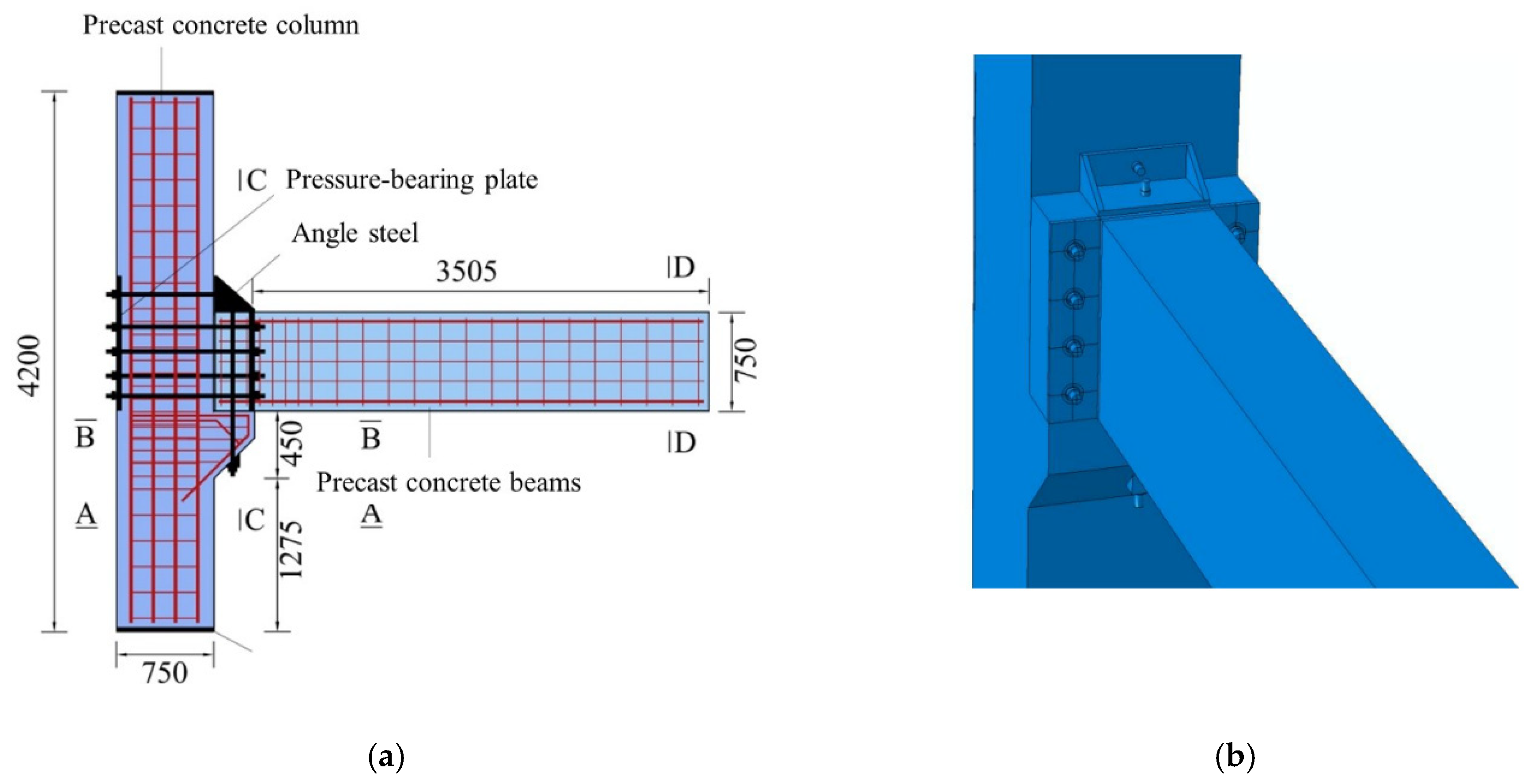
2.1. Test Specimen Design and Fabrication
2.2. Material Properties
2.2.1. Mechanical Properties of Concrete
2.2.2. Mechanical Properties of Steel
2.3. Loading Devices and Loading Regimes
2.4. Measurement Content
3. Experimental Phenomena and Their Analysis
3.1. Main Experimental Phenomena
3.1.1. Crack Development in Specimen J1
3.1.2. Crack Development in Specimen J2
3.2. Analysis of Experimental Phenomena
3.3. Experimental Results
3.3.1. Load-Displacement Curves
- Compared to the hysteresis curves of J1 and J2, the other hysteresis curves are bowed, and the hysteresis curves are generally smooth and full. The area of the hysteresis curve increases with the increase in displacement load, which indicates that both J1 and J2 have a certain plastic deformation capacity and good energy dissipation capacity. At the same time, the loading force and displacement of the two new joints are approximately linear at the beginning of the loading when the joints did not crack; with the increase in force, they gradually became non-linear.
- The hysteresis circle of J2 is significantly larger than that of J1. The ultimate displacements of J2 and J1 are 115.8 mm and 127.6 mm, respectively, and the ultimate displacement of J2 is 10.2% higher than that of J1. This indicates that the deformation of the bolt in the energy dissipation phase of J2 is greater than that of J1, enhancing the energy dissipation performance of the joints. It can be seen that the increase in bolt strength grade will increase the energy dissipation performance of the joints.
- The hysteresis curves of both J1 and J2 are asymmetrical during reciprocating loading. This is due to the corbel limiting the rotation of the precast beam during negative loading, increasing the stiffness of the joints, decreasing the bolt deformation, and reducing the energy dissipation capacity.
3.3.2. Skeleton Curves
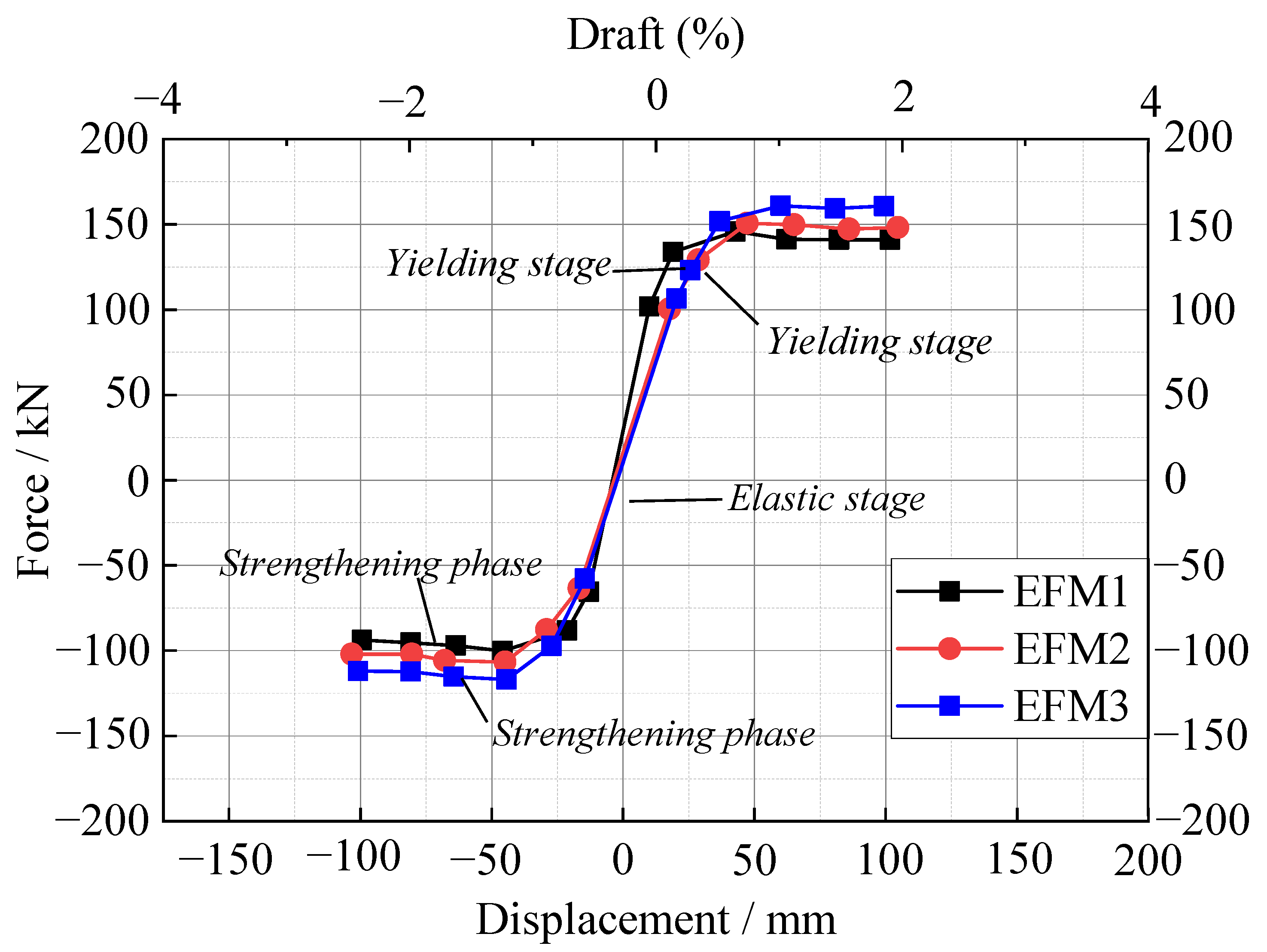
- The two joints in the experimental state go through: the elastic phase, the yield phase, the strengthening phase, and the damage phase. Both maintain good stiffness in the early stages of loading, and the skeleton curves of the specimens all tend to be approximately straight lines, indicating that the components are in the elastic stage with little change in stiffness and displacement. As the load continues to increase, the reinforcement of the precast beam starts to deform and yield and the bolt deformation of specimens J1 and J2 increases. The specimens begin to become elastoplastic, the specimen skeleton curves gradually shift towards the displacement axis and no longer change linearly, and the stiffness of the specimens gradually degrades.
- After J1 and J2 reach the maximum load-bearing capacity, the load-bearing capacity of the beam end continue to increase when the load continues to increase. This indicates that the new joints have stronger structural stiffness under displacement loading and their stiffness degradation trend is smoother, showing that increasing the strength of the bolts can improve the ductility of the joints, which in turn can increase the seismic energy dissipation capacity.
- It can be seen that the J2 yield load is 39.4% higher, the ultimate load is 11.5% higher, and the damage load is 13.2% higher than J1 for the same working conditions. The reason for this is that J2 used stronger bolts, which allowed the fractures of the beam to crack and move back, increasing the stiffness and load-bearing capacity of the expanded end of the precast beam, which increased load-bearing capacity. Therefore, an appropriate increase in bolt strength can improve the energy dissipation capability of the core area of the joint, which can effectively improve the bearing capacity of the specimens. It is suggested that in actual engineering, an appropriate increase in connection bolt strength can be used to improve the bearing capacity of the joints.
- Specimen J1 has a positive peak load of 151 kN and a negative peak load of 113 kN, a difference of 25.2%. Specimen J2 has a positive peak load of 178 kN and a negative peak load of 121 kN, a difference of 32.02%. The corbel acts as a support for the beam and was not subjected to forces, the load capacity being determined by the structure of the beam itself. The final damage to both J1 and J2 was due to the bolts yielding and cracks in the beam end surfaces, but the load-bearing reinforcement did not yield. It can be seen that the energy consumption of the new joints is primarily based on bolts and cracks produced in the core area of the joints; no damage occurred to the corbel and columns, as intended by the new joint design concept.
3.4. Analysis of Experimental Results and Discussion
3.4.1. Joint Corner Displacement Analysis
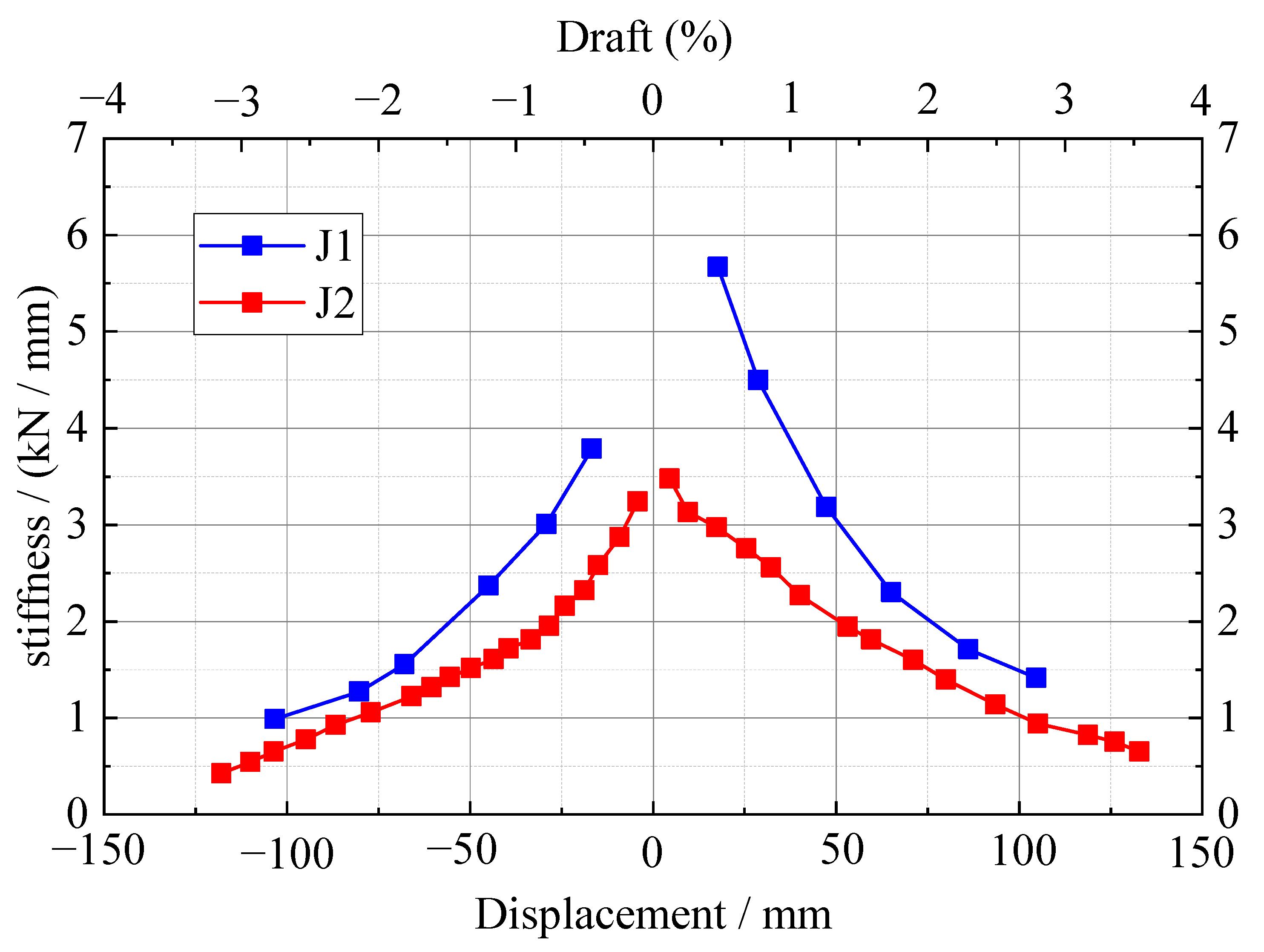
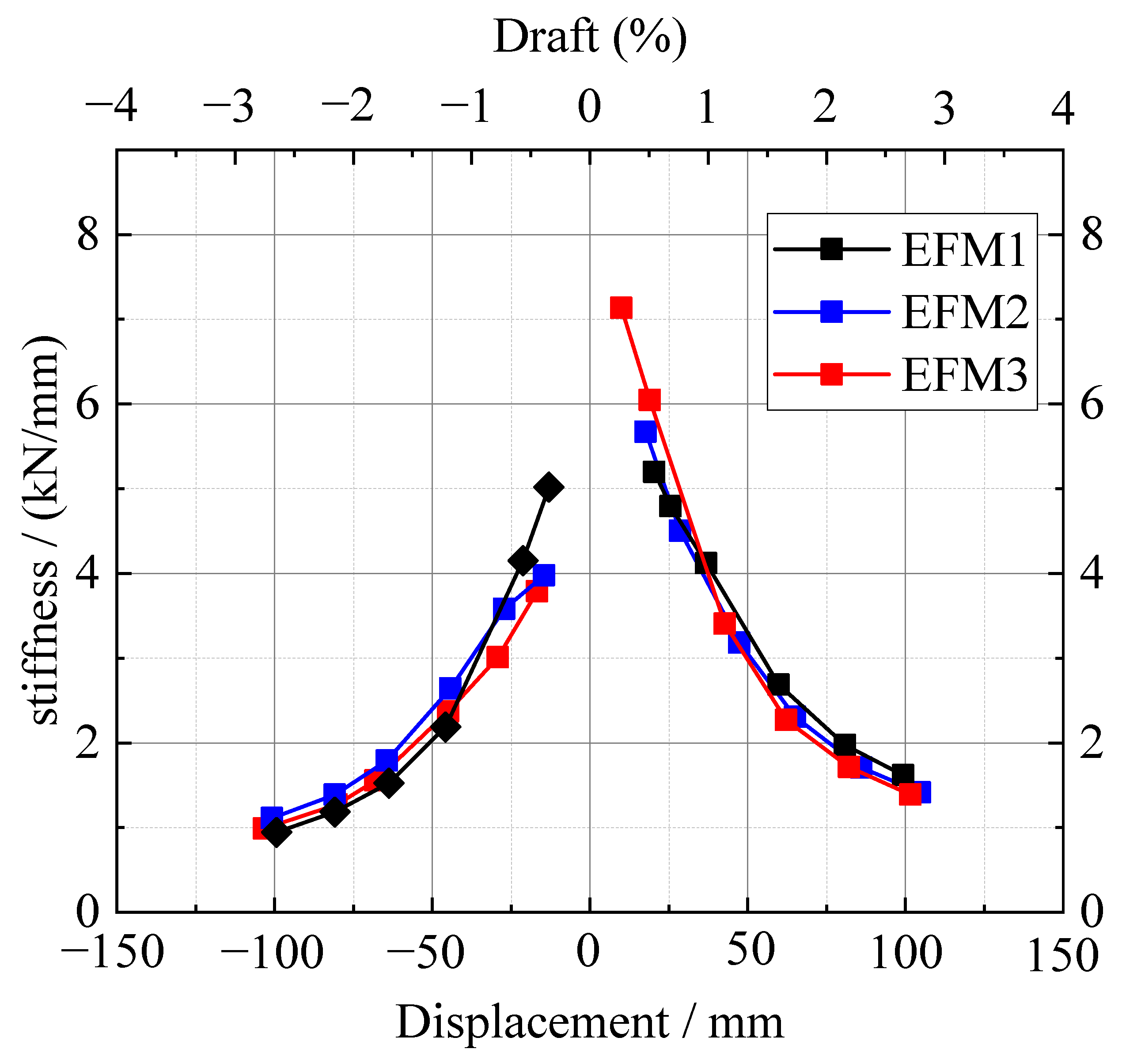
3.4.2. Stiffness Degradation Curves
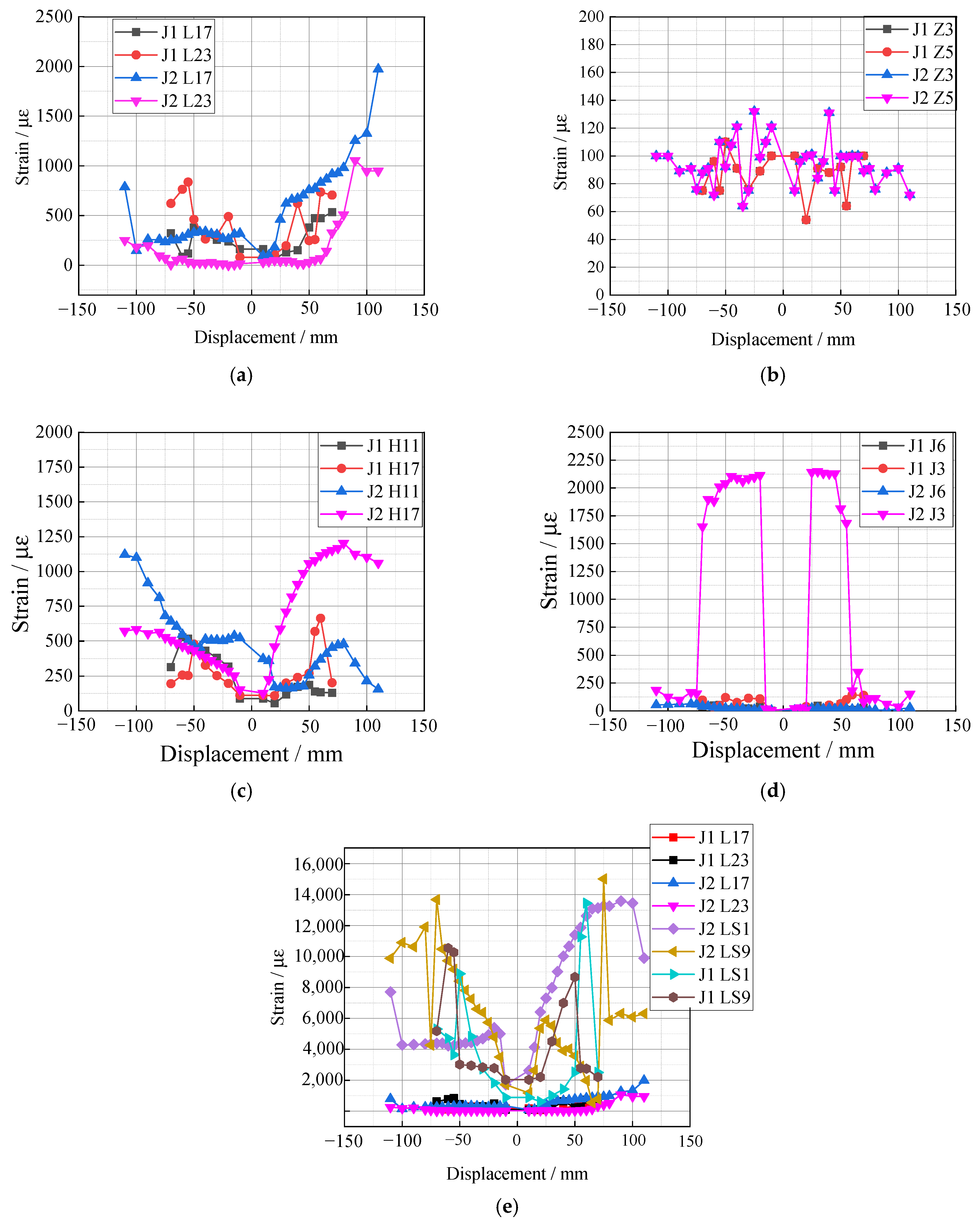
3.4.3. Stress–Strain Analysis
4. Finite Element Numerical Simulation
4.1. Concrete Damage Model Theory
4.1.1. Concrete Material Constitutive Relationships
4.1.2. Hysteresis Rules
4.1.3. Yield Criterion and Law of Flow
4.2. Joint Finite Element Modeling
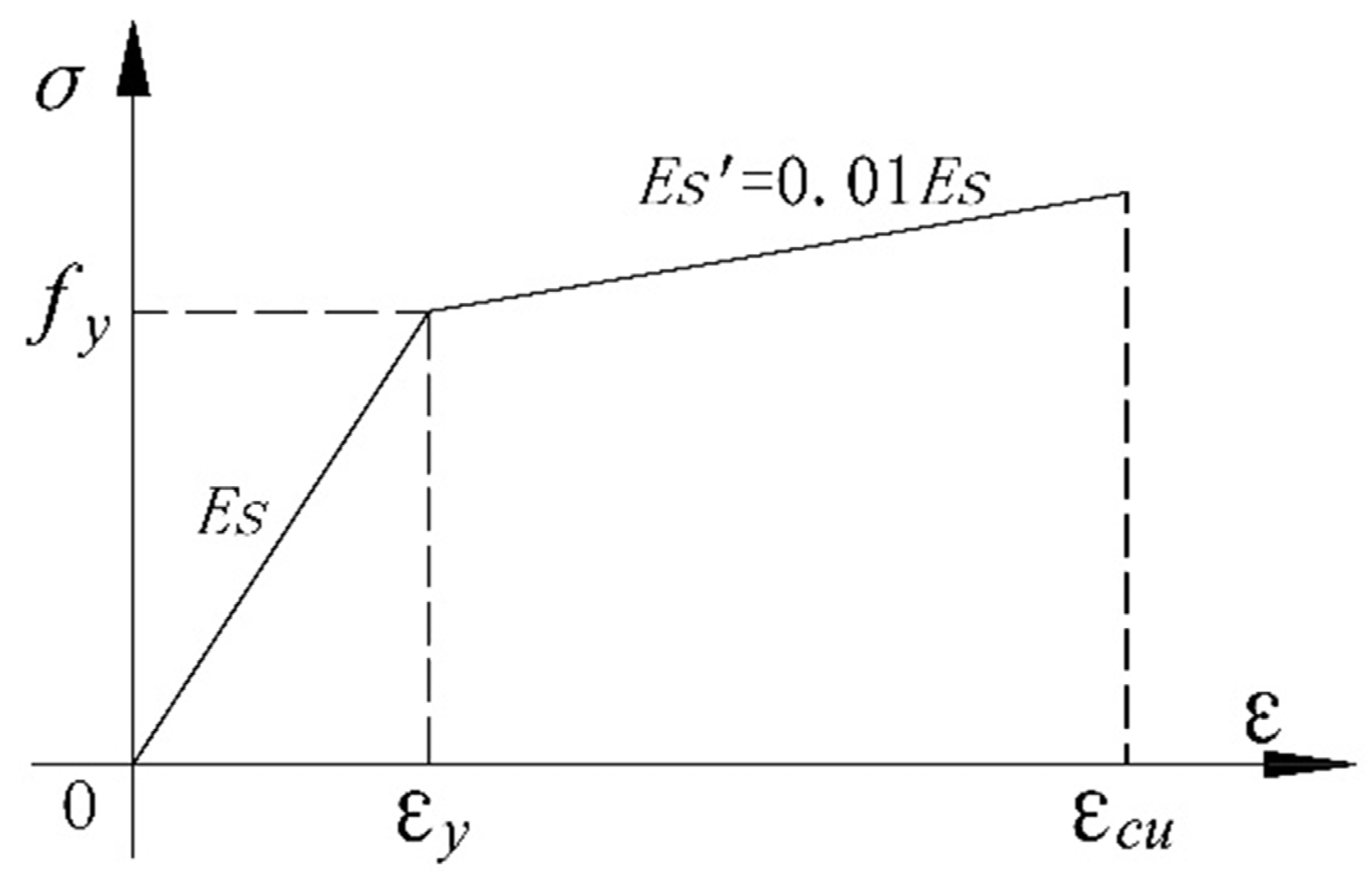
4.2.1. Material Stress–Strain Curves
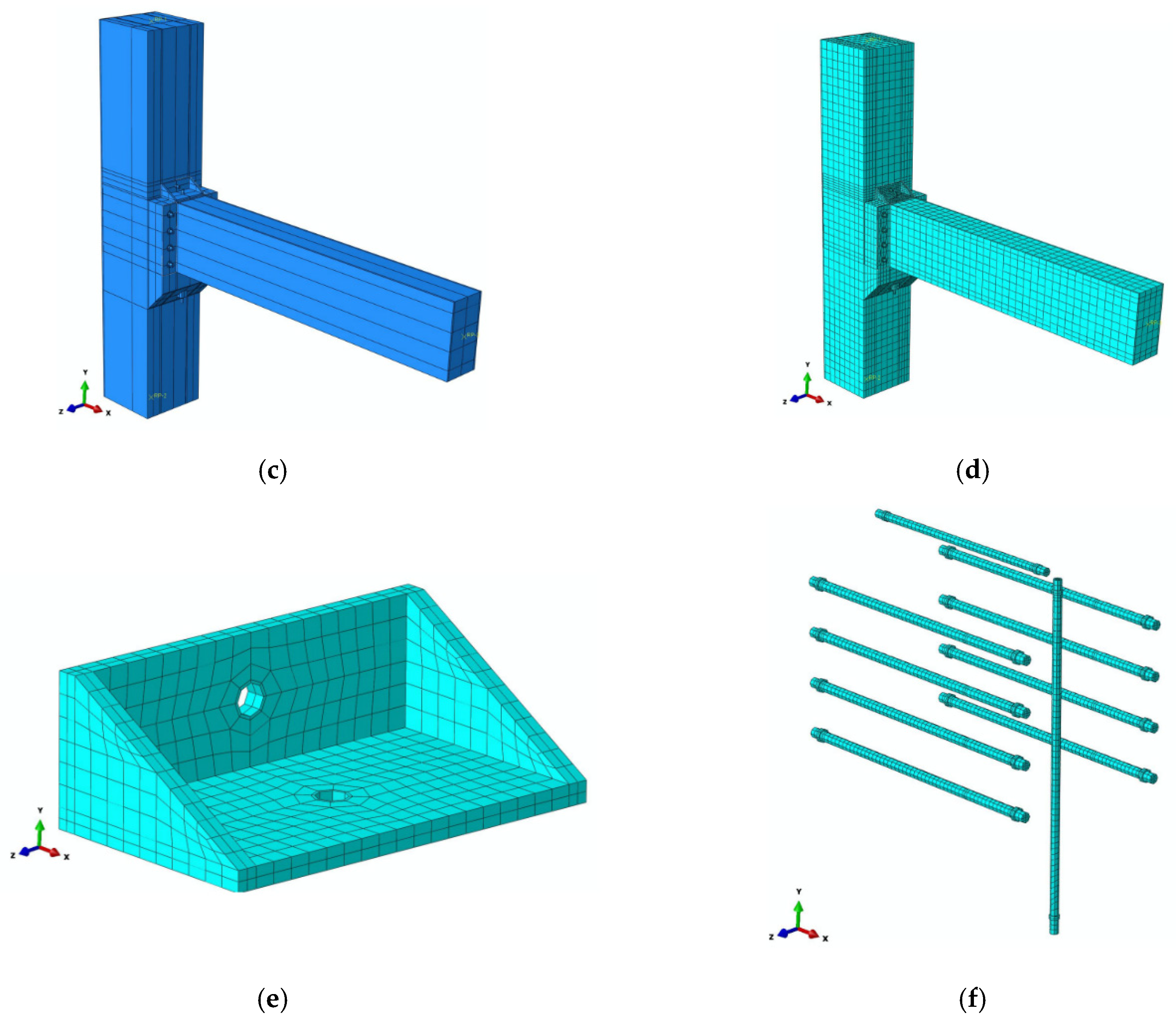
4.2.2. Unit Selection and Division
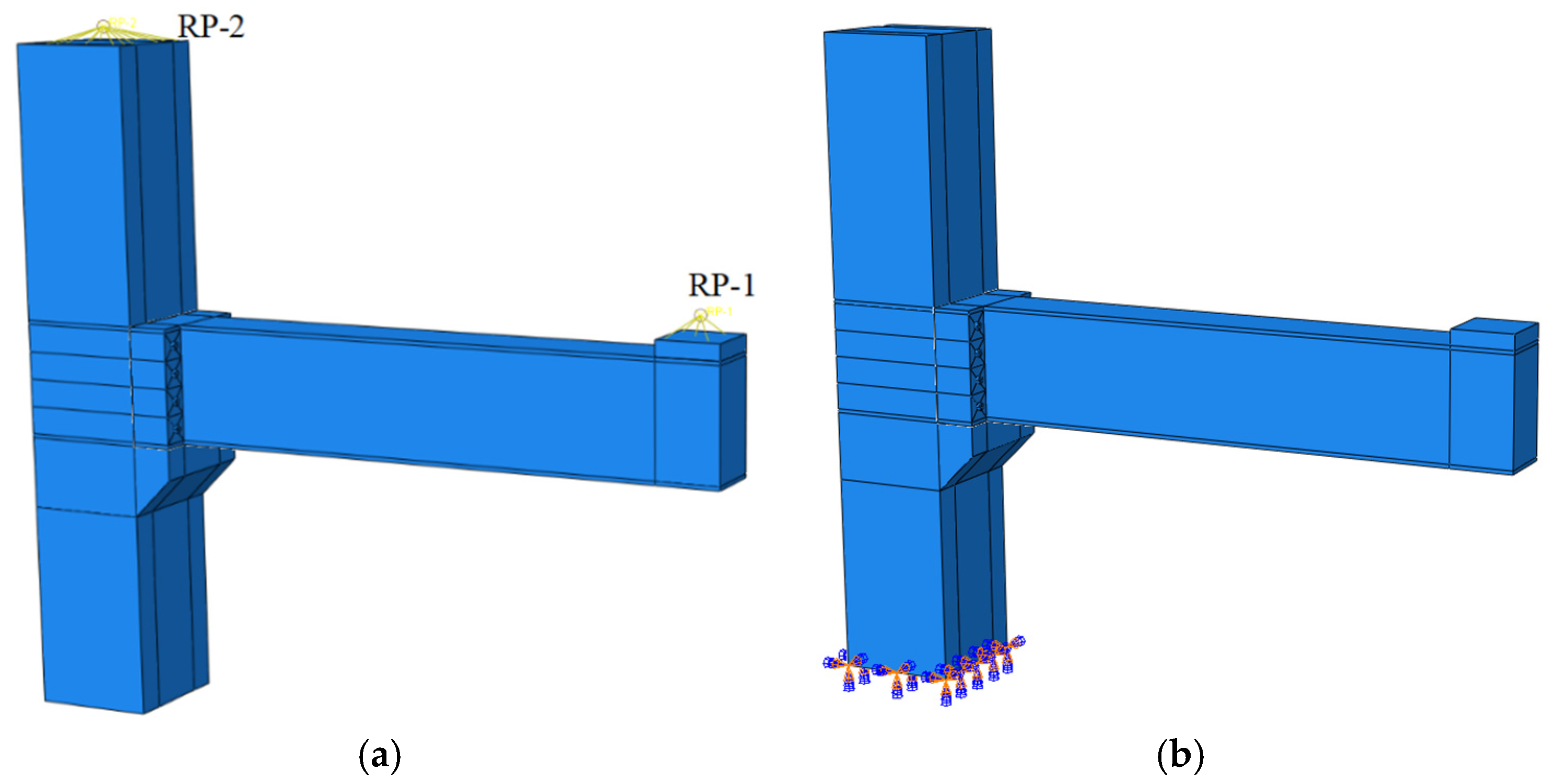
4.2.3. Boundary Conditions and Loading
4.3. Analysis of Calculation Results
4.3.1. Hysteresis Curves
4.3.2. Skeleton Curves
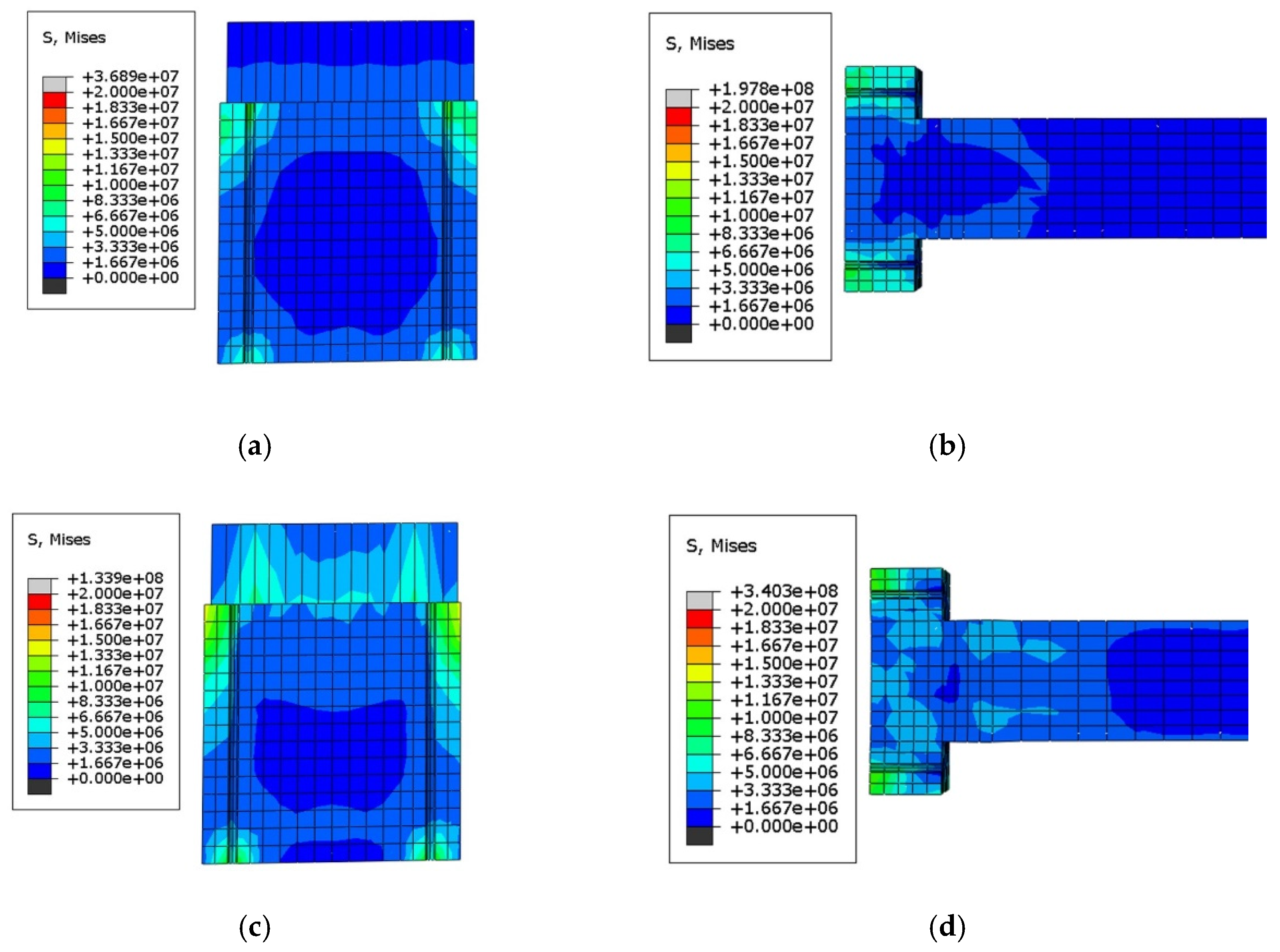
4.4. Stress Clouds
4.4.1. Stress Cloud of J1
4.4.2. Cloud Diagram of Specimen J2
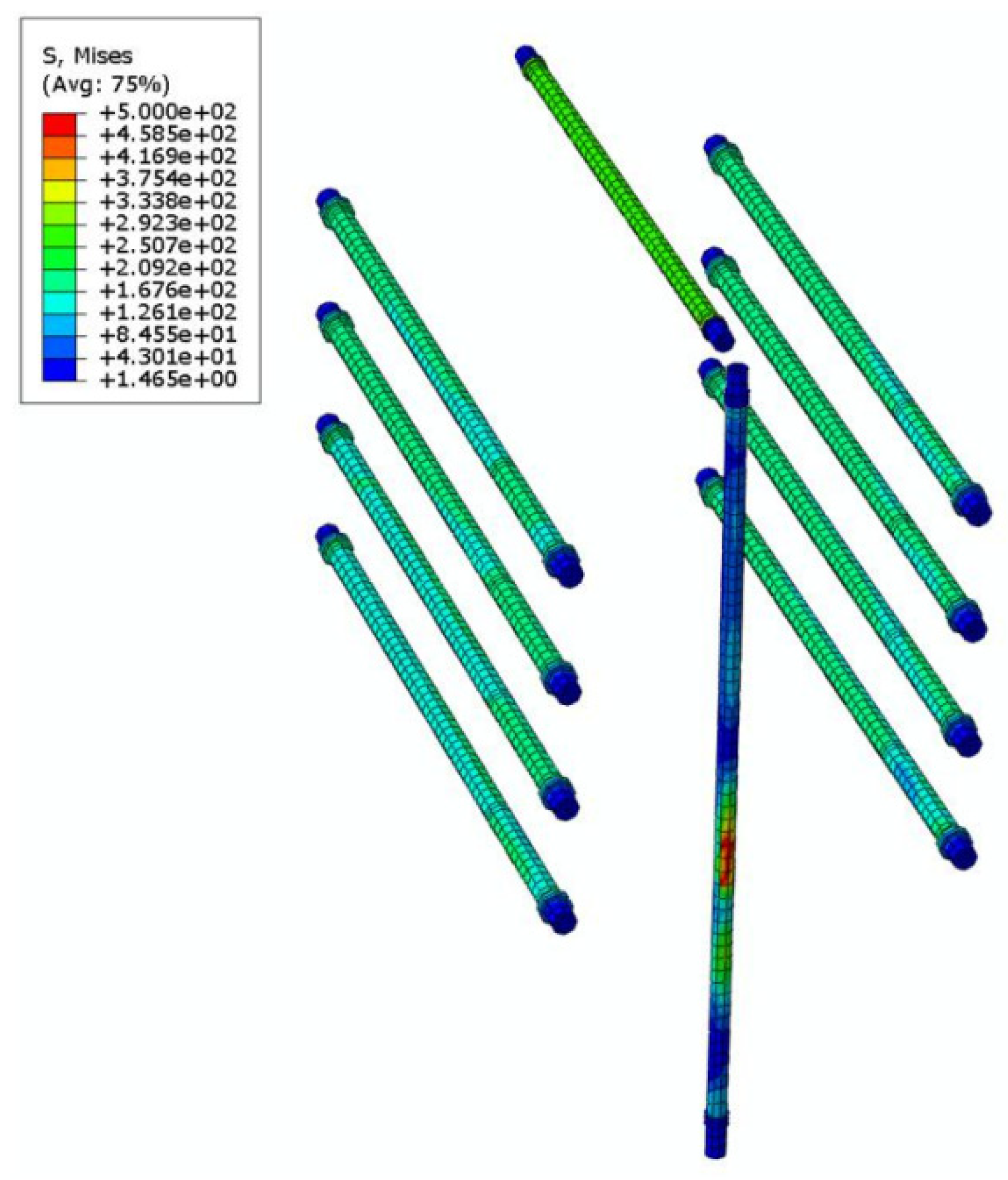
4.4.3. Analysis of Opening Holes in the Joint Core Area and Bolt Stress Cloud Analysis
4.5. Column Axial Pressure Ratio Parameters
4.5.1. Skeleton Curves
4.5.2. Stiffness Degradation Curves
4.6. Optimization of Assembled Semi-Rigid Beam–Column Joints
4.6.1. Joint Design
4.6.2. Finite Element Clouds of Modified Joint
4.6.3. Hysteresis Energy Consumption Performance
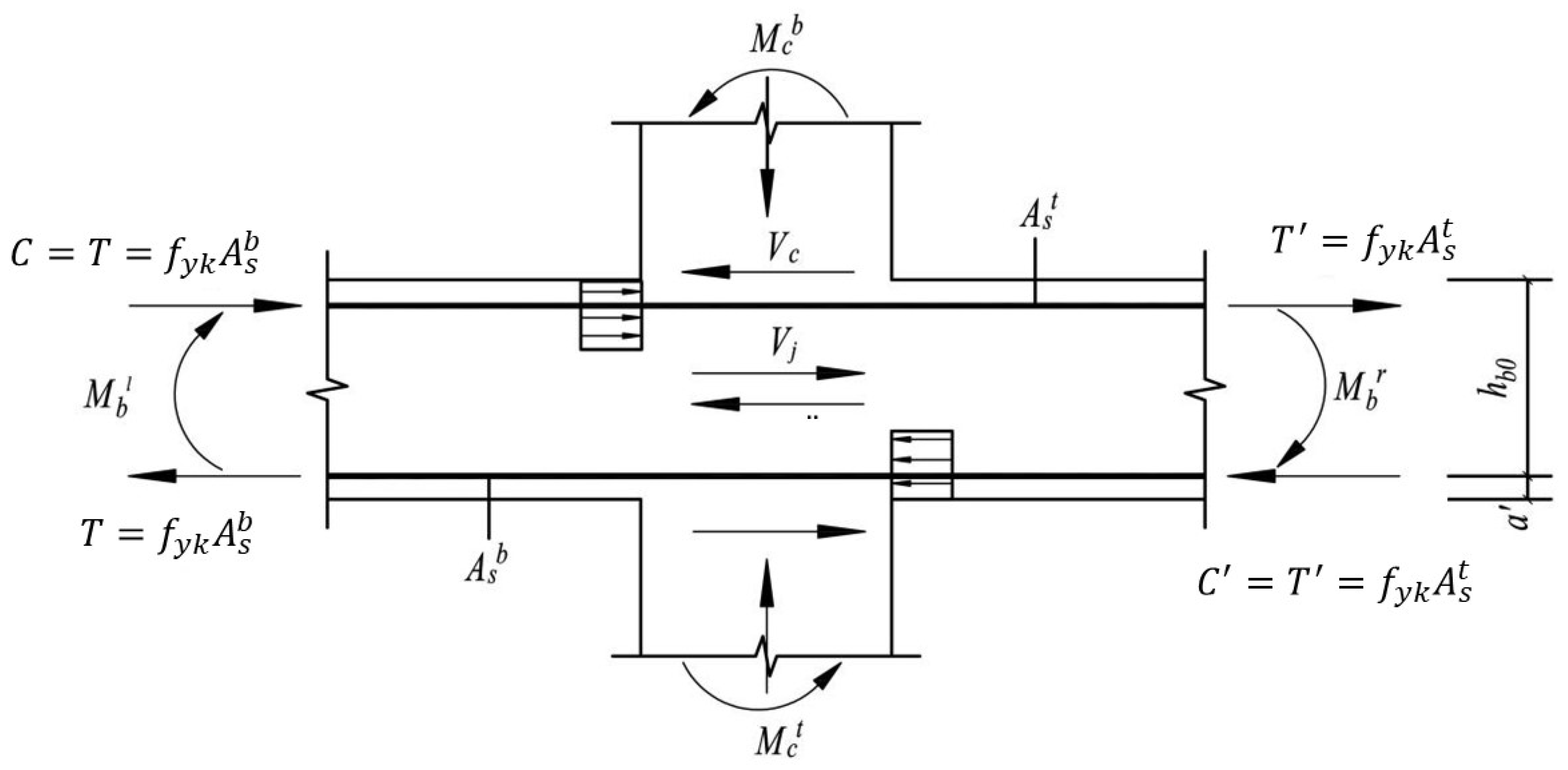
5. Shear Capacity of Joint Core
6. Conclusions
- (1)
- Under the action of low-cycle loading, bolts and precast beams are the main stress components of the new-type joints, and the failure modes are as follows: bolts yield, enlarged ends of precast beams are destroyed, and precast columns and the corbel can still bear the load. Under an earthquake, bolts and precast beams can be replaced to complete the joint repair work, which accords with the new joint design concept.
- (2)
- The hysteresis curves of the two new joints are bow-shaped, and the hysteresis curves are generally smooth and full, with a large hysteresis loop area. The equivalent energy dissipation coefficient is 0.855–1.16, and the equivalent damping coefficient is 0.1–0.25, indicating that the new joints have a strong energy dissipation capacity.
- (3)
- The two new joints have obvious stiffness degradation, and the descending section is relatively gentle. The residual stiffness of J1 and J2 is 1.16 and 0.5, respectively, which indicates that the new joints still have a certain bearing capacity when they are damaged. At the same time, according to the stiffness degradation curve, the stiffness degradation speed of J2 in each displacement stage is slightly smaller than that of specimen J1, and the stiffness of J2 in each displacement stage is higher than that of specimen J1, which indicates that increasing the bolt strength reduces the degradation rate of joint stiffness.
- (4)
- The yield load Py = 98 kN, the ultimate load Pmax = 148 kN, and the ultimate failure load Pu = 151 kN of J1. The yield load Py = 113 kN, the ultimate load Pmax = 165 kN, and the ultimate failure load Pu = 178 kN of J2. Compared with J1, the yield load of J2 is increased by 39.4%, the ultimate load is increased by 11.5%, and the failure load is increased by 13.2%. This shows that when the strength grade of bolts increases, the yield bearing capacity and ultimate bearing capacity of joints will increase. It is suggested that the strength of connecting bolts can be appropriately increased to improve the bearing capacity of joints in practical engineering.
- (5)
- The finite element simulation results are in good agreement with the experimental results. The simulation results showed that the opening cross section of the column in the core of the joint mainly bears the compressive stress along the axial direction of the screw exerted by the bolt in the horizontal direction and forms local concentrated stress in the area of the hole opening but is not subjected to shear stress. The ultimate loads of EMFJ1, EMFJ2, and EMFJ3 are 144 kN, 132 kN, and 167 kN, respectively, indicating that the larger the axial compression ratio, the earlier the damage stage of the concrete and the faster the load-bearing capacity and ductility decrease.
- (6)
- The bolt stress distribution state of the modified and optimized joint J3 is more satisfactory, and this change in the node form can improve the recovery efficiency of the node to a certain extent; the equivalent viscous damping coefficients of J1 are in the range of 0.068–0.197, J2 are in the range of 0.067–0.212, and J3 in the range of 0.024–0.239. The maximum values of the equivalent viscous damping coefficients for J1 are 92.2% and for J2 and J3 are 82.4%. The total energy dissipated by the three groups of components for J1, J2, and J3 is 89.19 kj, 99.43 kj, and 119.52 kj, respectively, with average equivalent damping coefficients of 0.141, 0.148, and 0.154 and energy dissipation coefficients of 0.886, 0.930, and 0.930, respectively. Therefore, J3 has the strongest energy dissipation. This indicates that the addition of the angle construction can improve the seismic energy dissipation capacity of the joint to some extent.
Author Contributions
Funding
Conflicts of Interest
References
- Shu, X.; He, R.; Zhang, Z.; Yao, Y.; Leonard, J. Experimental Study on the Mechanical Properties of a New Long-Span Prefabricated Truss Composite Floor System. Dyna 2019, 94, 189–196. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.Y.; Feng, D.C.; Wang, Z.; Wu, W. Parametric investigation of the assembled bolt-connected buckling-restrained brace and performance evaluation of its application into the structural retrofit. J. Build. Eng. 2022, 48, 103998. [Google Scholar] [CrossRef]
- Yan, Q.S.; Chen, T.Y.; Xie, Z.Y. Seismic experimental study on a precast concrete beam-column connection with grout sleeves. Eng. Struct. 2018, 155, 330–344. [Google Scholar] [CrossRef]
- Xing, G.H.; Wang, Z.M.; Qin, C.J.; Huang, J.; Fan, X. Experimental study on the seismic performance of new assembled concrete frame joints. China Civ. Eng. J. 2022, 3, 1–11. [Google Scholar] [CrossRef]
- Yacine, R.A.; Hicham, B.S.; Badaoui, M. Effect of beam-column joints flexibility on the seismic response of setback RC buildings designed according to the Algerian seismic code. Fract Struct. Integr. 2022, 16, 394–409. [Google Scholar] [CrossRef]
- T/CECS 809-2021; Technical Code for Bolted Multi-Storey Fully Assembled Concrete Wall Panel Structures. China Construction Industry Press: Beijing, China, 2021.
- Torra, B.I.; Mahamid, M. Cyclic behaviour of precast beam-to-column connections: An experimental and numerical investigation. Structures 2022, 35, 939–957. [Google Scholar] [CrossRef]
- Ding, K.W.; Liu, J.H.; Ma, W.; Liu, Y.L. Experimental study on the seismic performance of new assembled semi-rigid joints. China Civ. Eng. J. 2021, 54, 1–7+56. [Google Scholar] [CrossRef]
- Ding, K.W.; Liu, J.H.; Ren, J.W.; Ma, W. Dynamic Responses of Cellular Metal-Filled Steel Beam-Column Joint Under Impact Loading. J. Shanghai Jiaotong Univ. Sci. 2020, 25, 384–393. [Google Scholar] [CrossRef]
- Ding, K.W.; Zong, D.; Liu, Y.L.; He, S.L.; Shen, W.Y. Experimental and Finite Element Analysis of ALC Panel Steel Frames with New Semi-Rigid External Connector. Appl. Sci. 2021, 11, 10990. [Google Scholar] [CrossRef]
- Ding, K.W.; Ye, Y.; Ma, W. Seismic performance of precast concrete beam-column joint based on the bolt connection. Eng. Struct. 2021, 232, 111884. [Google Scholar] [CrossRef]
- Zhang, Y.; Ding, K.W. Study on seismic behavior of fabricated beam-column bolted joint. Struct. Eng. Mech. 2022, 82, 801–812. [Google Scholar] [CrossRef]
- Guan, D.Z.; Tian, W.H.; Chen, Z.X.; Liu, J.B.; Guo, Z.X. Research on the seismic performance of assembled concrete beam-column connections based on UHPC shells. China Civ. Eng. J. 2022, 1–7. [Google Scholar] [CrossRef]
- Fan, W.; Su, H.X.; He, Y.B.; Sun, W.B.; Shao, X.D. Experimental investigation on UHPC-based gravity-type half-grouted sleeve connections under tensile and cyclic loadings. J. Build. Eng. 2022, 61, 105284. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Ding, R.; Nie, X.; Fan, J.S. Seismic performance of a novel interior precast concrete beam-column joint using ultra-high performance concrete. Eng. Struct. 2020, 222, 111145. [Google Scholar] [CrossRef]
- Xiong, X.Y.; Xie, Y.F.; Yao, G.F.; Liu, J.; Yan, L.Z.; He, L. Experimental Study on Seismic Performance of Precast Pretensioned Prestressed Concrete Beam-Column Interior Joints Using UHPC for Connection. Materials 2022, 15, 5791. [Google Scholar] [CrossRef]
- Tang, L.; Tian, W.H.; Guan, D.Z.; Chen, Z.X. Experimental Study of Emulative Precast Concrete Beam-to-Column Connections Locally Reinforced by U-Shaped UHPC Shells. Materials 2022, 15, 4066. [Google Scholar] [CrossRef]
- Choi, H.K.; Choi, Y.C.; Choi, C.S. Development and Testing of Precast Concrete Beam-to-column Connections. Eng. Struct. 2013, 56, 1820–1835. [Google Scholar] [CrossRef]
- Ghayeb, H.H.; Razak, H.A.; Sulong, N.H. Development and testing of hybrid precast concrete beam-to-column connections under cyclic loading. Const. Build. Mater. 2017, 151, 258–278. [Google Scholar] [CrossRef]
- Liu, Y.L.; Zhu, S.T. Finite element analysis on the seismic behavior of side joint of Prefabricated Cage System in a prefabricated concrete frame. Front. Struct. Civ. Eng. 2019, 13, 1095–1104. [Google Scholar] [CrossRef]
- Liu, Y.L.; Liu, C.; Pan, H.; Fu, J.L.; Huang, J.Q.; Hong, J.Q. Experimental and numerical investigation on seismic performance of semi-precast concrete sandwich shear wall. Adv. Struct. Eng. 2022, 25, 2772–2784. [Google Scholar] [CrossRef]
- Liu, Y.L.; Huang, J.Q.; Chong, X.; Ye, X.G. Experimental investigation on flexural performance of semi-precast reinforced concrete one-way slab with joint. Struct. Concr. 2021, 22, 2243–2257. [Google Scholar] [CrossRef]
- Wang, H.S.; Kang, Y.J.; Pan, P. Study on seismic performance of fully assembled self-resetting energy-consuming reinforced concrete frame beam-column joints. J. Build. Struct. 2022, 43, 158–166+176. [Google Scholar]
- Gong, J.W. Seismic Performance Analysis of New Assembled Cross-Type Beam-Column Joints; Hunan University: Changsha, China, 2019. [Google Scholar]
- Wang, S.Y. Research on the Seismic Performance of Flat Steel Tube Concrete Column-H-Beam Joints; Hefei University of Technology: Hefei, China, 2021. [Google Scholar]
- Nzabonimpa, J.D.; Hong, W.K.; Kim, J. Nonlinear finite element model for the novel mechanical beam-column joints of precast concrete-based frame. Comput. Struct. 2017, 189, 31–48. [Google Scholar] [CrossRef]
- Bruno, D.L.; Paolo, N.; Alberto, D.L. Seismic design and performance of dry-assembled precast structures with adaptable joints. Soil Dyn. Earthq. Eng. 2018, 106, 182–195. [Google Scholar] [CrossRef]
- Pan, Z.H.; Si, Q.; Zhou, Z.B.; Zhang, Y.B.; Zhu, Y.Z.; Chen, X.D. Experimental and numerical investigations of seismic performance of hybrid joints with bolted connections. J. Const. Steel Res. 2017, 138, 867–886. [Google Scholar] [CrossRef]
- Wang, H.; Marino, E.M.; Pan, P.; Liu, H.; Nie, X. Experimental Study of a Novel Precast Prestressed ReinforcedConcrete Beam to column Joint. Eng. Struct. 2018, 156, 68–81. [Google Scholar] [CrossRef]
- Kim, S.K.; Kim, J.M.; Hong, W.K. Material Nonlinear Finite Element Analysis of Hybrid Hollow ConcreteBeams Encasing Steel Sections. Structures 2020, 25, 500–519. [Google Scholar] [CrossRef]
- Yang, T.Y.; Dashlejeh, A.A.; Arabzadeh, A.; Hizajir, R. New Model for Prediction of Ultimate Load of Prestressed RC Deep Beams. Structures 2020, 23, 509–517. [Google Scholar] [CrossRef]
- Oliveira, J.L.A.; Araújo, D.L.; El Debs, M.K.; Diógenes, H.J.F. Precast Beam-Column Connection Subjected to Cyclic and Dynamic Loadings. Struct. Eng. Int. 2018, 27, 114–126. [Google Scholar] [CrossRef]
- Dai, E.L.; Jin, G.J.; Dai, S.P. Study on the application of C80 high strength and high performance pumped concrete in practical engineering. Concrete 2013, 1, 97–101+104. (In Chinese) [Google Scholar]
- GB50010-2010; Code for the Design of Concrete Structures. Ministry of Construction of the People’s Republic of China: Beijing, China, 2015. (In Chinese)
- JGJ55-2011; Specification for the Design of Ordinary Concrete Proportions. China Construction Industry Press: Beijing, China, 2011.
- JGJ/T101-2015; Specification for Seismic Testing of Buildings. China Construction Industry Press: Beijing, China, 2015.
- Wu, C.X.; Lai, W.H.; Zhou, Y.; Zhang, C.; Deng, X.S. Experimental study on the seismic performance of new prefabricated assembled energy dissipating and vibration damping concrete frame joints. China Civ. Eng. J. 2015, 48, 23–30. [Google Scholar] [CrossRef]
- Zhuang, Z. ABAQUS Nonlinear Finite Element Analysis with Examples; Science Press: Beijing, China, 2005. [Google Scholar]
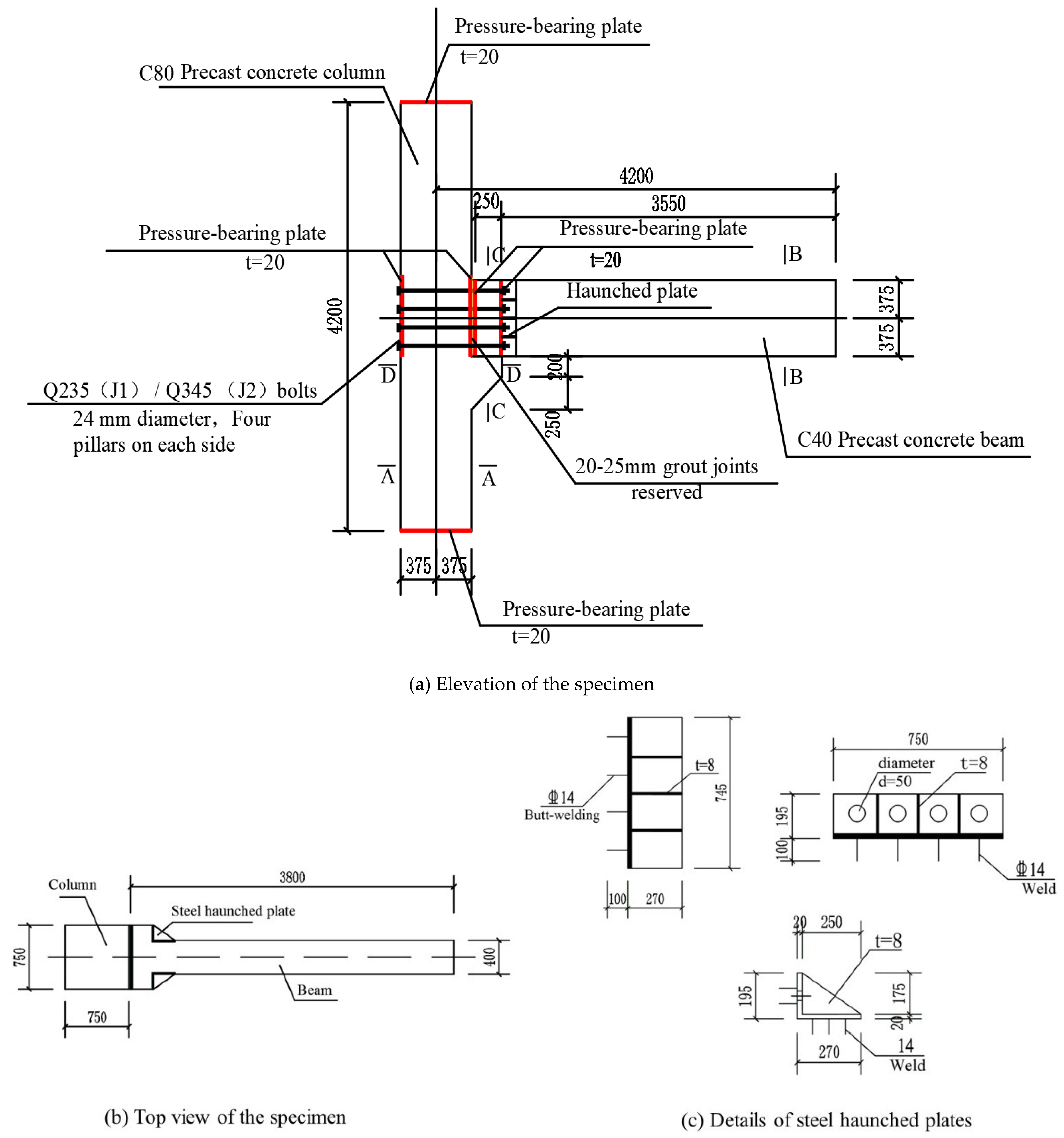
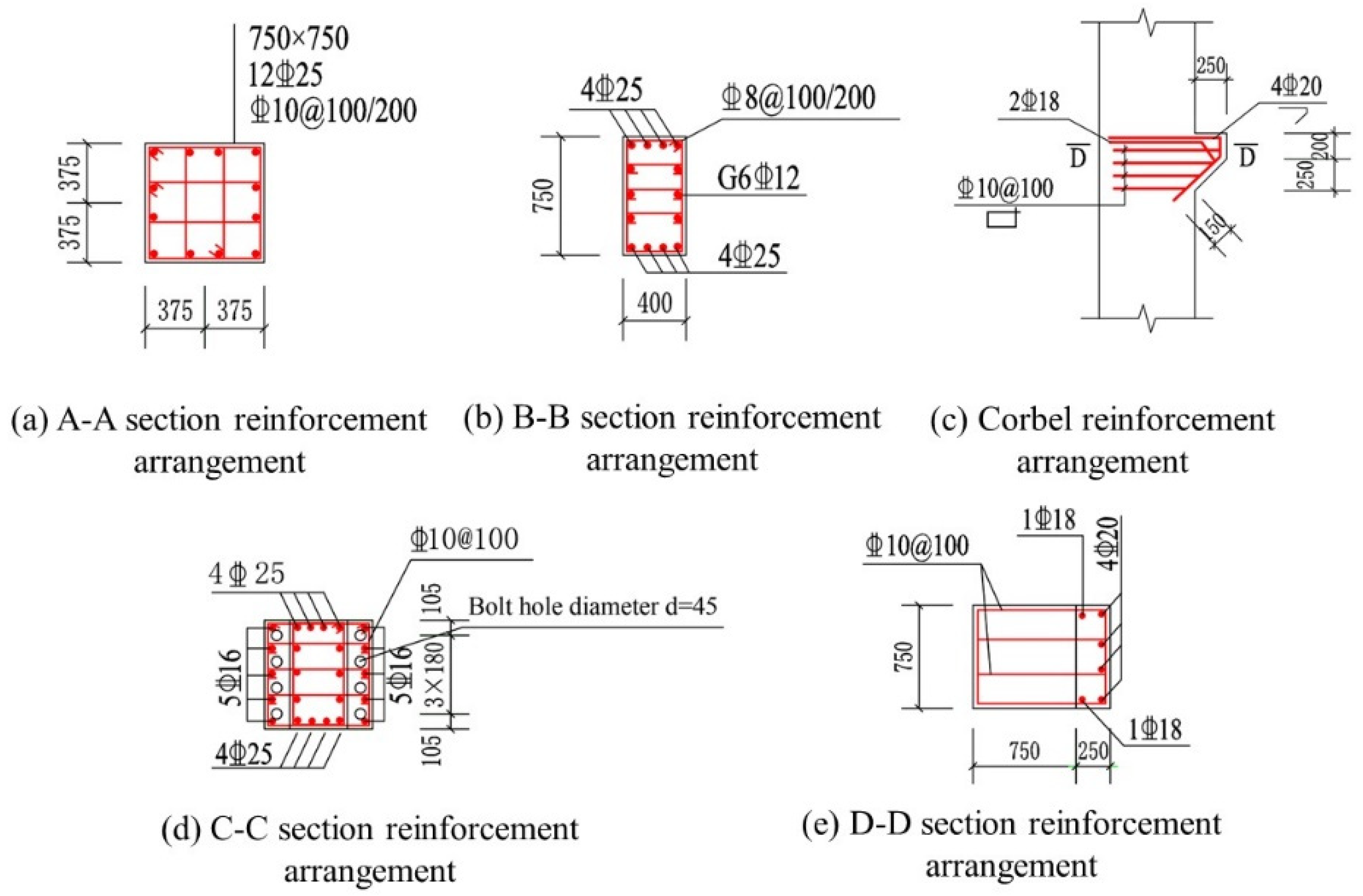




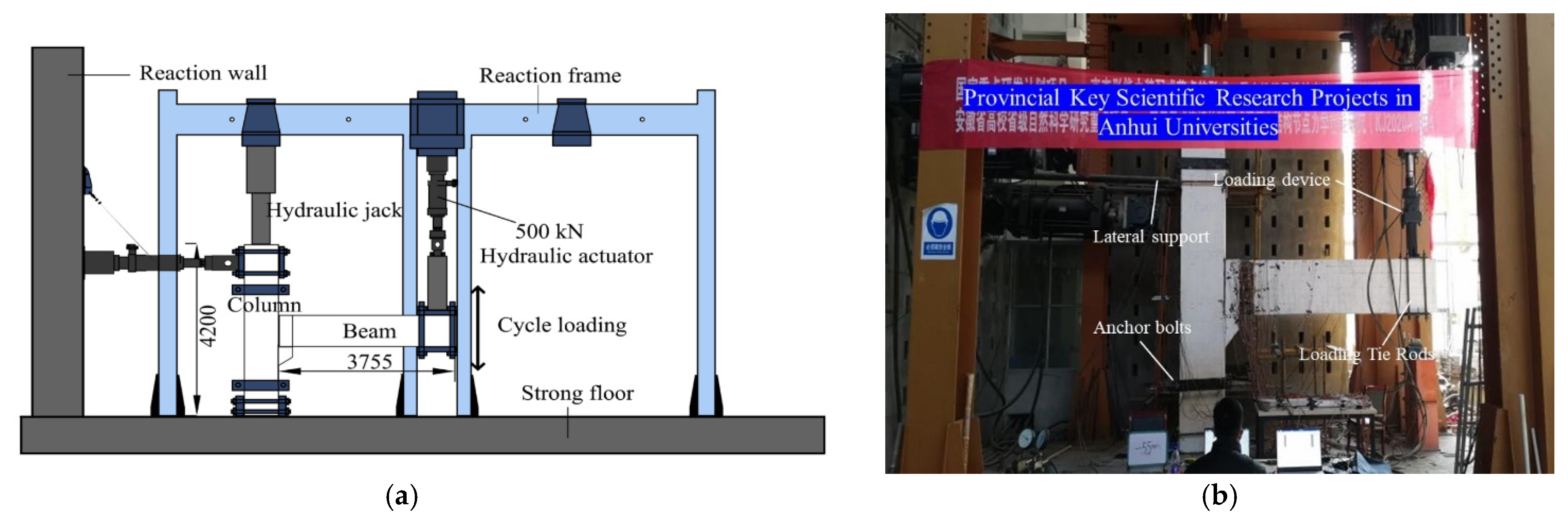
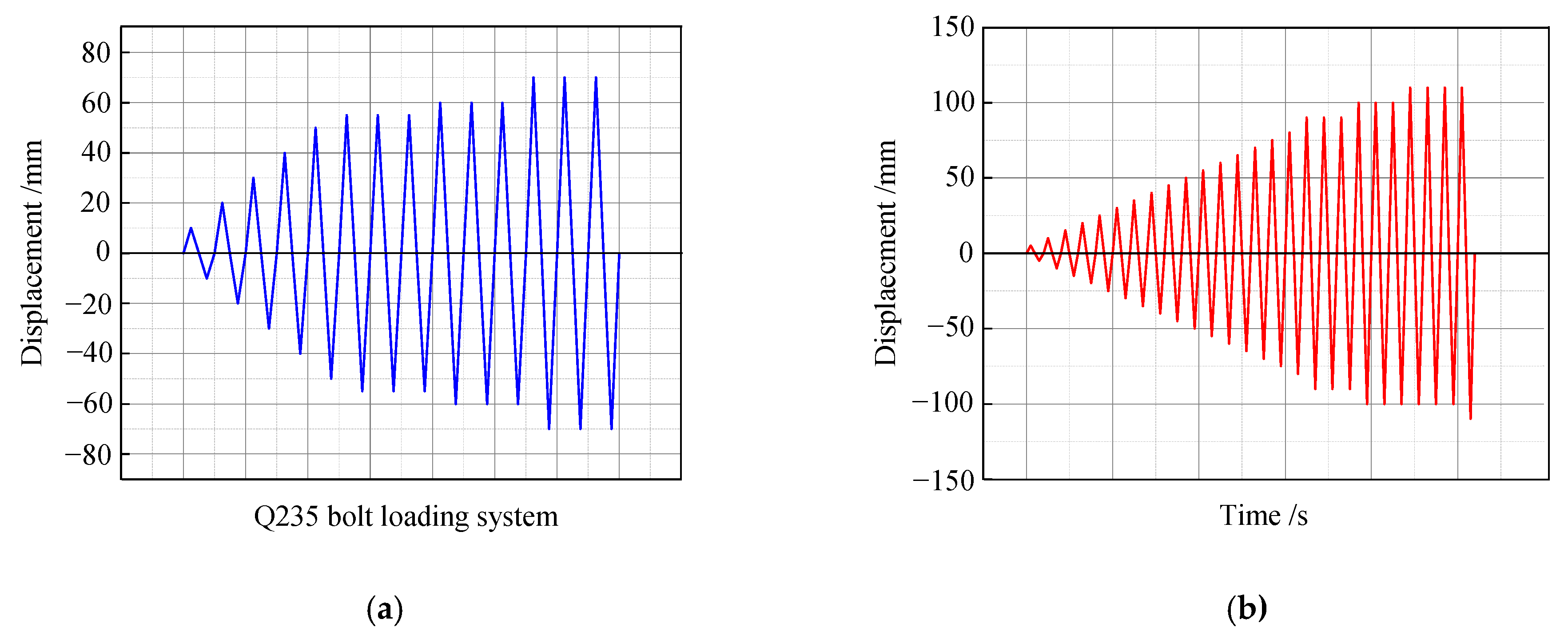
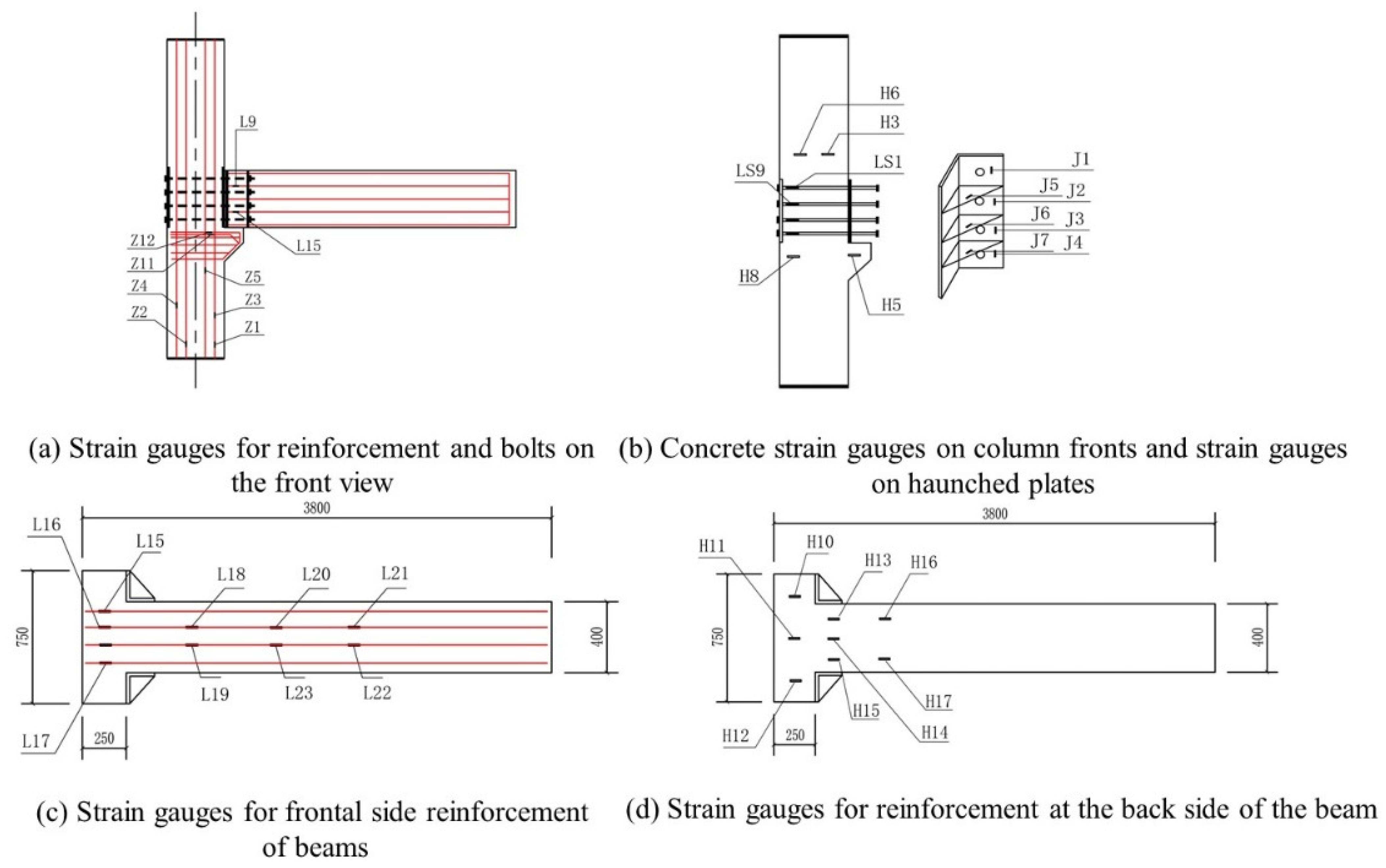
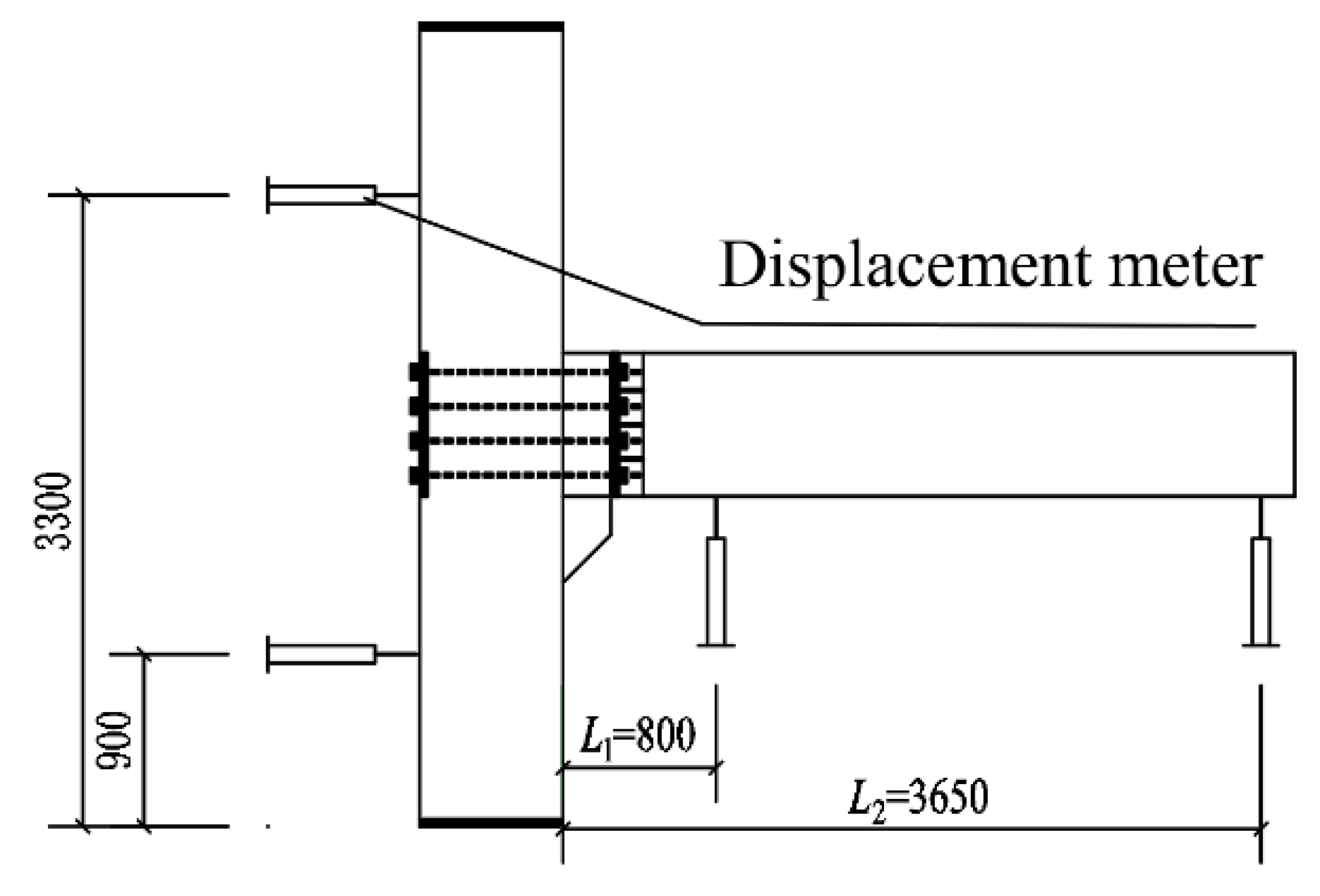

















| Specimen Name | Concrete Grade | The Thickness of the Concrete Protection Layer (mm) | Cross-Sectional Dimensions (mm) | Length (mm) |
|---|---|---|---|---|
| Precast concrete beam | C40 | 25 | 400 × 750 (exlarged end: 750 × 750) | 3800 |
| Precast concrete column | C80 | 25 | 750 × 750 | 4200 |
| Number | Type of Joint Construction | Bolt Grade | Bolt Diameter (mm) |
|---|---|---|---|
| J1 | with haunched plates | Q345 | 24 |
| J2 | with haunched plates | Q235 | 24 |
| Concrete Strength | Cube Compressive Strength (N/mm2) | Standard Values for Axial Compressive Strength (N/mm2) | Modulus of Elasticity (×104 N/mm2) |
|---|---|---|---|
| C40 | 28.28 | 18.34 | 3.25 |
| C40 | 28.68 | 18.25 | 3.25 |
| C40 | 28.13 | 18.32 | 3.25 |
| C80 | 77.30 | 50.20 | 3.80 |
| C80 | 78.20 | 52.30 | 3.80 |
| C80 | 77.90 | 51.40 | 3.80 |
| Category | Diameter (mm) | Yield Strength (N/mm2) | Ultimate Strength (N/mm2) | Modulus of Elasticity (×105 N/mm2) | Elongation/% |
|---|---|---|---|---|---|
| HRB400 | 8 | 427.60 | 637.10 | 2.10 | 16.30 |
| HRB400 | 10 | 437.90 | 568.30 | 2.10 | 15.60 |
| HRB400 | 12 | 465.20 | 577.30 | 2.00 | 16.60 |
| HRB400 | 14 | 447.40 | 547.60 | 2.00 | 16.20 |
| HRB400 | 16 | 437.60 | 640.40 | 2.10 | 23.20 |
| HRB400 | 22 | 487.50 | 635.90 | 2.11 | 21.60 |
| HRB400 | 25 | 456.6 | 605.7 | 2.06 | 17.80 |
| Q345 | 20 (plate thickness) | 425.20 | 570.40 | 2.07 | 31.90 |
| Bolt Grade | Diameter (mm) | Yield Strength (N/mm2) | Ultimate Strength (N/mm2) | Modulus of Elasticity (×105 N/mm2) |
|---|---|---|---|---|
| Q235 | 24 | 326 | 493 | 2.12 |
| Q345 | 24 | 436 | 764 | 2.06 |
| Model | Resistance Value/Ω | Sensitivity Coefficient | Gate Length × Gate Width/mm | Spacer Length × Spacer Width/mm |
|---|---|---|---|---|
| BF120-3AA | 120 ± 0.5 | 2.0 ± 0.01 | 3.0 × 2.0 | 6.9 × 3.6 |
| BX120-100AA | 120 ± 0.5 | 2.08 ± 0.01 | 100 × 3.0 | 106 × 5.5 |
| Position | Test Phenomenon |
|---|---|
| Side of beam | −20 mm: 30 cm from the edge of the column, length of 30 cm, seam width of 0.04 mm |
| −35 mm: 18 cm and 35 cm from the edge of the column, lengths of 13 cm and 20 cm, respectively, both with a seam width of 0.1 mm | |
| −40 mm: 12 cm and 60 cm from the edge of the column, lengths of 20 cm and 25 cm, respectively, both with a seam width of 0.1 mm | |
| −50 mm: at 15 cm, 35 cm, and 45 cm from the edge of the column, lengths of 16 cm, 5 cm, and 24 cm, respectively, seam widths of 0.08 mm, 0.07 mm, and 0.07 mm, respectively | |
| −60 mm: the side of the enlarged end of the beam runs parallel to the face of the bearing plate, length of 73 cm, seam width of 0.13 mm; 45 cm from the edge of the column based on the original crack branch, length of 5 cm, seam width of 0.11 mm | |
| The top surface of the beam | +50 mm: 3 cm, 12 cm, and 25 cm from the edge of the column, lengths of 40 cm, 42 cm, and 40 cm, seam widths of 0.2 mm, 0.11 mm, and 0.22 mm, respectively |
| The bottom surface of the beam | −10 mm: 43 cm and 65 cm from the edge of the column, lengths of 40 cm and 20 cm, respectively, seam widths of 0.13 mm and 0.08 mm, respectively |
| −30 mm at 33 cm from the edge of the column, length of 40 cm, seam width of 0.13 mm | |
| −45 mm: from the bearing plate to the free end of the beam parallel to the long side of the beam, length of 15 cm, seam width of 0.08 mm | |
| −50 mm: at 20 cm, 65 cm, and 88 cm from the edge of the column, lengths of 40 cm, 10 cm, and 18 cm, respectively, seam widths of 0.1 mm, 0.2 mm, and 0.12 mm, respectively |
| Position | Test Phenomenon |
|---|---|
| Side of beam | −50 mm: 35 cm from the edge of the column, length of 8 cm, seam width of 0.07 mm |
| −55 mm: 30 cm from the edge of the column, length of 30 cm, seam width of 0.14 mm; 5 cm from the contact surface of the beam–column joint at the side of the enlarged end of the beam from the bottom up, length of 6 cm, seam width of 0.07 mm | |
| −60 mm: the side of the enlarged end of the beam is carried out parallel to the face of the bearing plate at a distance of 4 cm from the face of the bearing plate, with a length of 74 cm and a seam width of 1.3 mm; at a distance of 45 cm from the edge of the column, with a length of 26 cm and a seam width of 0.1 mm | |
| −70 mm: 58 cm from the edge of the column, length of 25 cm, seam width of 0.1 mm | |
| −75 mm: 35 cm from the edge of the column, length of 20 cm, seam width of 0.1 mm | |
| The top surface of the beam | +35 mm: 25 cm from the edge of the column, length of 20 cm, seam width of 0.9 mm |
| +50 mm: the top surface of the expanded end of the beam, 5 cm, 14 cm, and 23 cm from the edge of the column, length 40 cm, 42 cm, and 40 cm, respectively, seam width 0.2 mm, 0.11 mm, and 0.22 mm, respectively | |
| +55 mm: 35 cm from the edge of the column, length of 15 cm, seam width of 0.12 mm | |
| +60 mm: 65 cm from the edge of the column, length of 13 cm, seam width of 0.1 mm | |
| +70 mm: 65 cm from the edge of the column, length of 20 cm, seam width of 0.09 mm | |
| +80 mm: 56 cm from the edge of the column, length of 18 cm, seam width of 0.07 mm | |
| The bottom surface of the beam | −10 mm: 40 cm and 65 cm from the edge of the column, lengths of 40 cm and 20 cm, respectively, with seam widths of 0.13 mm and 0.08 mm, respectively |
| −30 mm: 32 cm from the edge of the column, length of 40 cm, seam width of 0.1 mm | |
| −50 mm: 20 cm, 65 cm, and 98 cm from the edge of the column, lengths of 30 cm, 10 cm, and 18 cm, respectively, seam widths of 0.1 mm, 0.2 mm, and 0.2 mm, respectively | |
| −55 mm: 3 cm from the edge of the column, length of 10 cm, seam width of 0.1 mm |
| Specimen Condition | (mm) | L (mm) | |
|---|---|---|---|
| Specimen cracking | 4.4 | 550 | 1/125 |
| Specimen yielding | 10.2 | 550 | 1/54 |
| Specimen damage | 19.1 | 550 | 1/42 |
| Specimen Condition | (mm) | L (mm) | |
|---|---|---|---|
| Specimen cracking | 6.4 | 550 | 1/86 |
| Specimen yielding | 12.9 | 550 | 1/43 |
| Specimen damage | 23.3 | 550 | 1/24 |
| Node Number | Total Energy Consumption Energy (kj) | The Average Equivalent Damping Coefficient | Energy Dissipation Coefficient | ||
|---|---|---|---|---|---|
| J1 (+) | 89.19 | 0.136 | 0.141 | 0.855 | 0.886 |
| J1 (−) | 0.142 | 0.892 | |||
| J2 (+) | 99.43 | 0.139 | 0.148 | 0.873 | 0.930 |
| J2 (−) | 0.156 | 0.980 | |||
| J3 (+) | 119.52 | 0.138 | 0.154 | 0.867 | 0.967 |
| J3 (−) | 0.170 | 1.16 | |||
| Specimen Number | Axial Pressure Ratio | Vj Calculation (kN) | Vj Test (kN) | Vj Calculation/Vj Test |
|---|---|---|---|---|
| J1 | 0.05 | 1236 | 1126 | 1.28 |
| J2 | 0.05 | 1452 | 1238 | 1.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Yu, D.; Ding, K.; Liu, Y. Seismic Performance of a New Assembled Bolt-Connected Concrete Beam–Column Joint: Experimental Test and Finite Element Modeling. Appl. Sci. 2023, 13, 73. https://doi.org/10.3390/app13010073
Liu J, Yu D, Ding K, Liu Y. Seismic Performance of a New Assembled Bolt-Connected Concrete Beam–Column Joint: Experimental Test and Finite Element Modeling. Applied Sciences. 2023; 13(1):73. https://doi.org/10.3390/app13010073
Chicago/Turabian StyleLiu, Jianhua, Dehu Yu, Kewei Ding, and Yunlin Liu. 2023. "Seismic Performance of a New Assembled Bolt-Connected Concrete Beam–Column Joint: Experimental Test and Finite Element Modeling" Applied Sciences 13, no. 1: 73. https://doi.org/10.3390/app13010073
APA StyleLiu, J., Yu, D., Ding, K., & Liu, Y. (2023). Seismic Performance of a New Assembled Bolt-Connected Concrete Beam–Column Joint: Experimental Test and Finite Element Modeling. Applied Sciences, 13(1), 73. https://doi.org/10.3390/app13010073






