The Variation of Surface Shape in the Gas Jet Forming
Abstract
1. Introduction
2. Principles of the Gas Jet Forming and Related Inferences
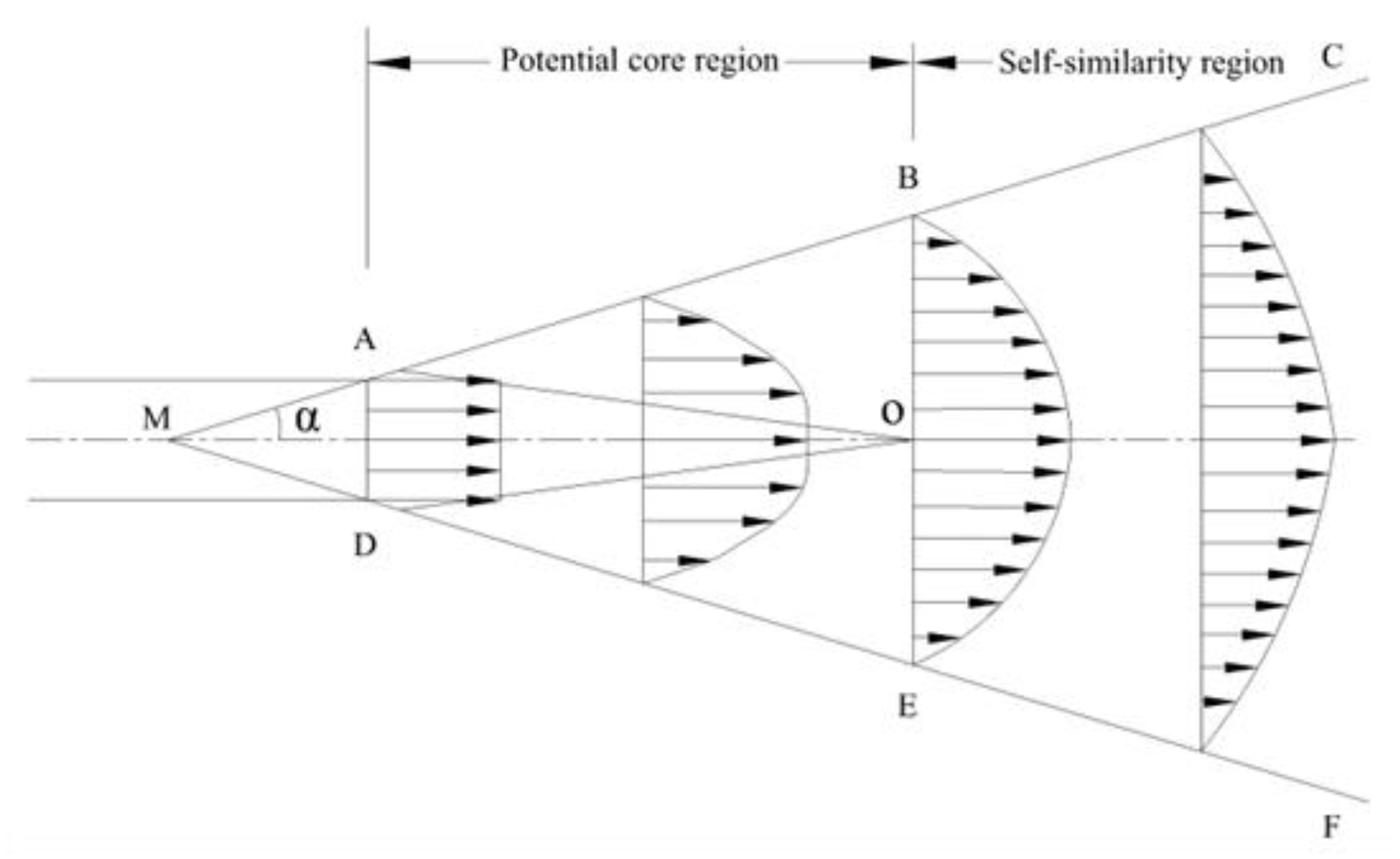
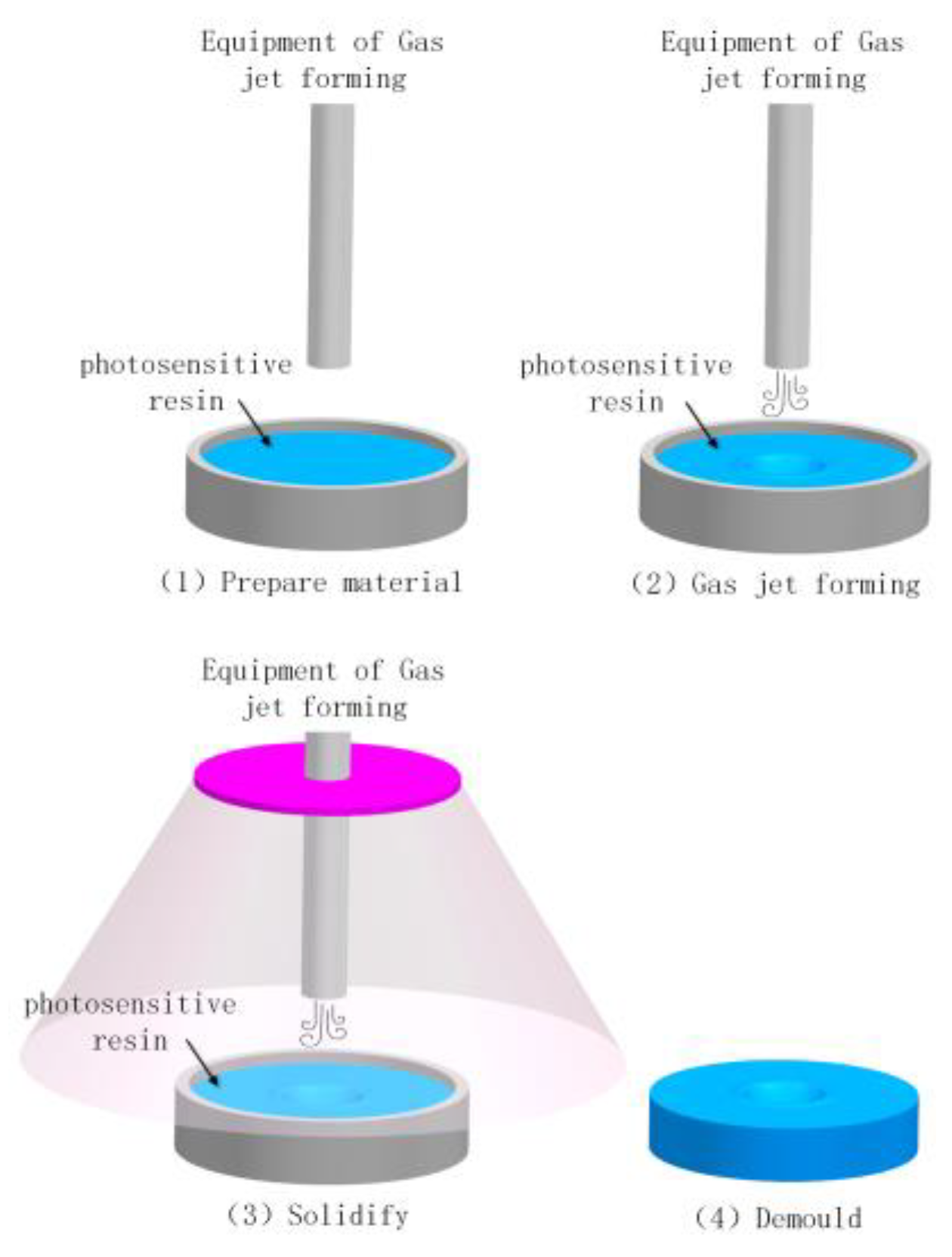
2.1. Principles of the Gas Jet Forming
2.2. Inference of the Relationship between Jet Parameters and Mirror Blank Parameters
3. Numerical Simulation
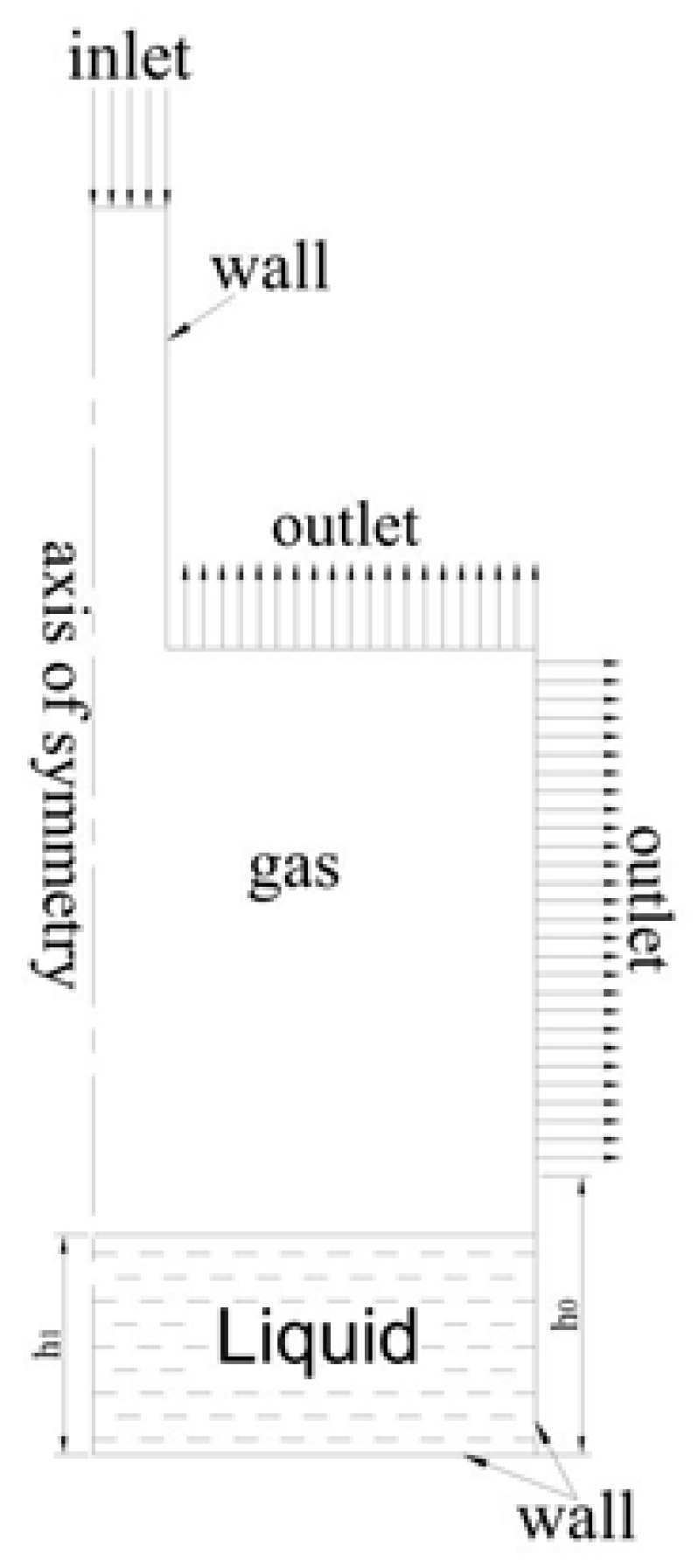
3.1. Establishment of the Model
3.2. Control Equations and Discrete Methods
3.3. Grid Independence Test
3.4. The Setting of the Numerical Simulation Parameters and Analysis of the Results
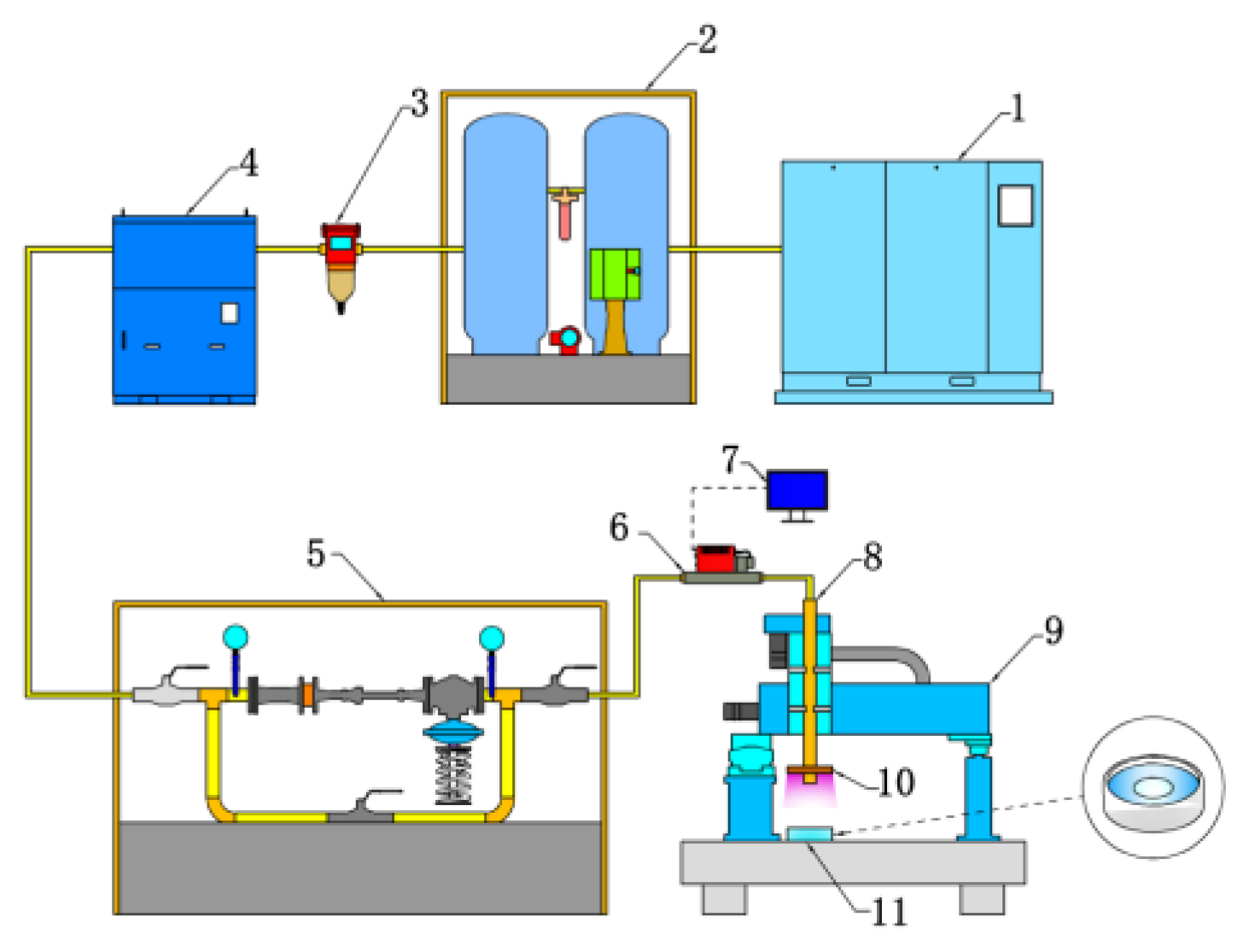
4. Experiments
The Gas Jet Forming Method
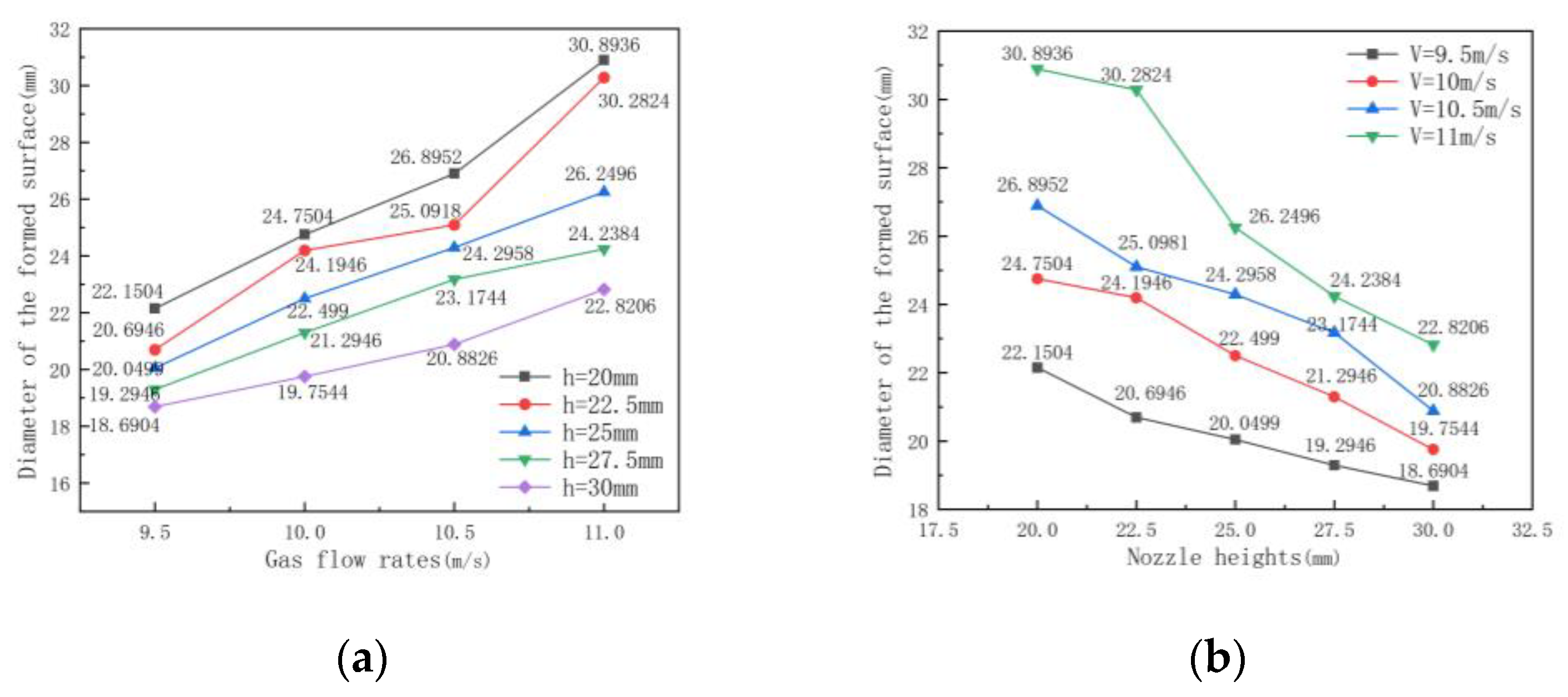
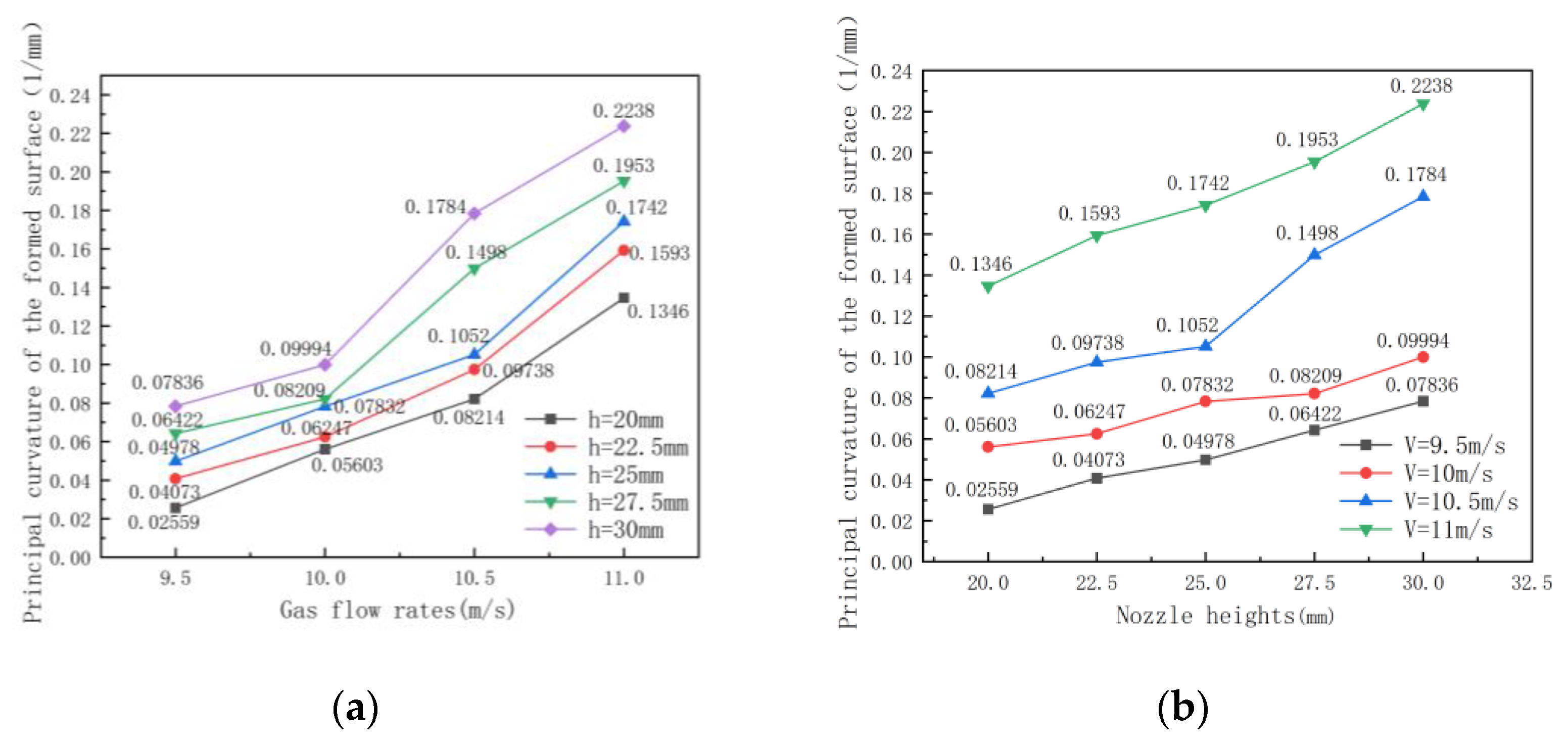
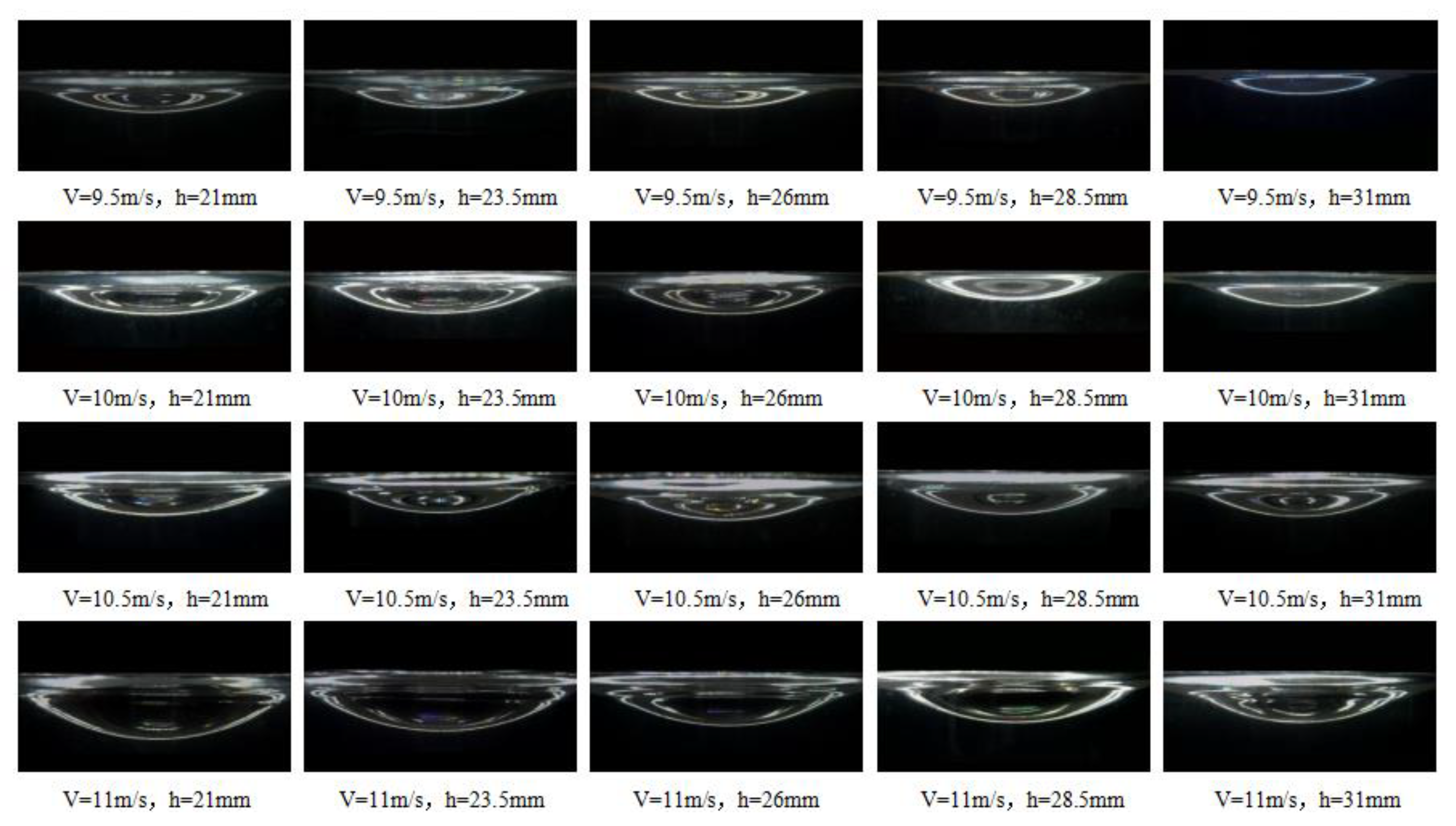
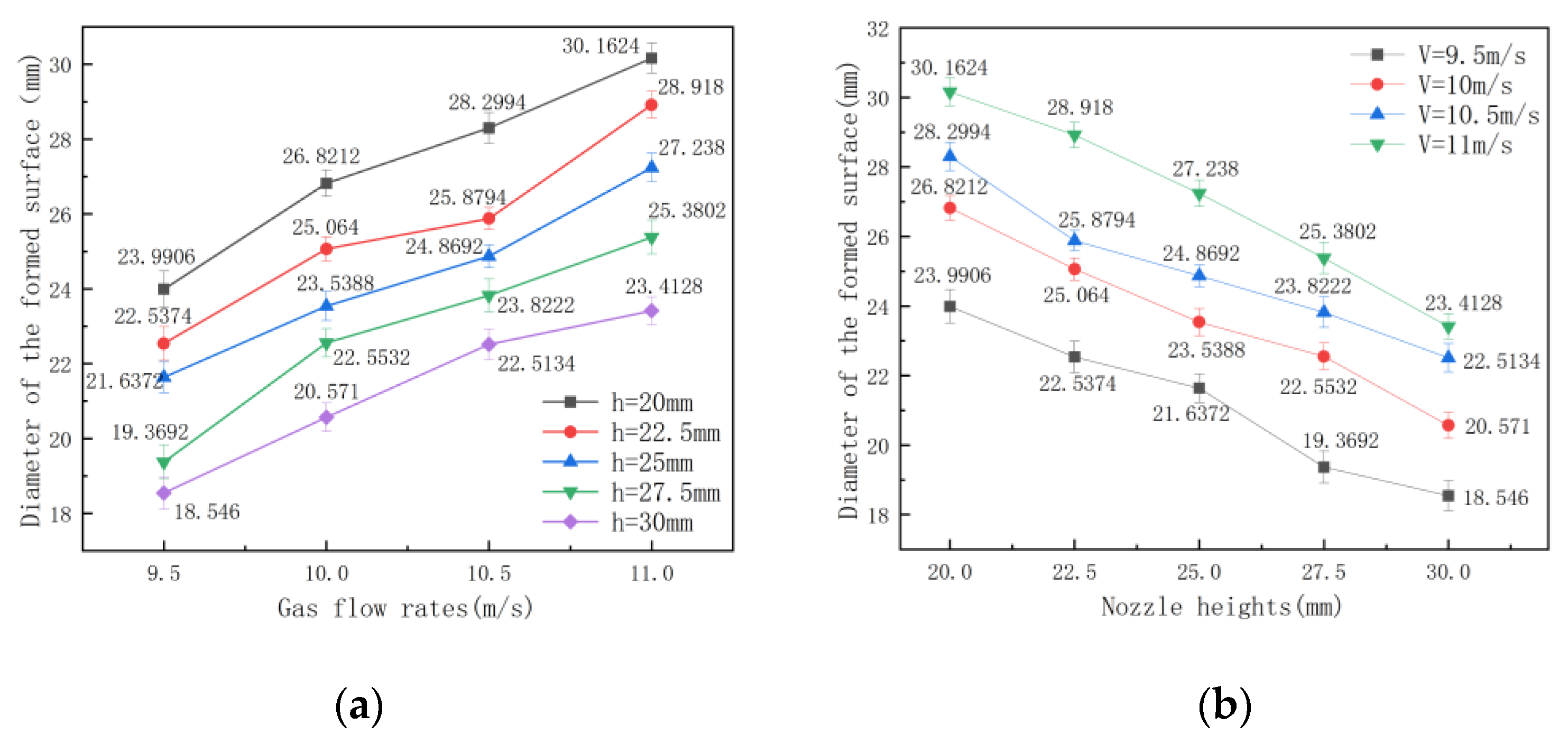
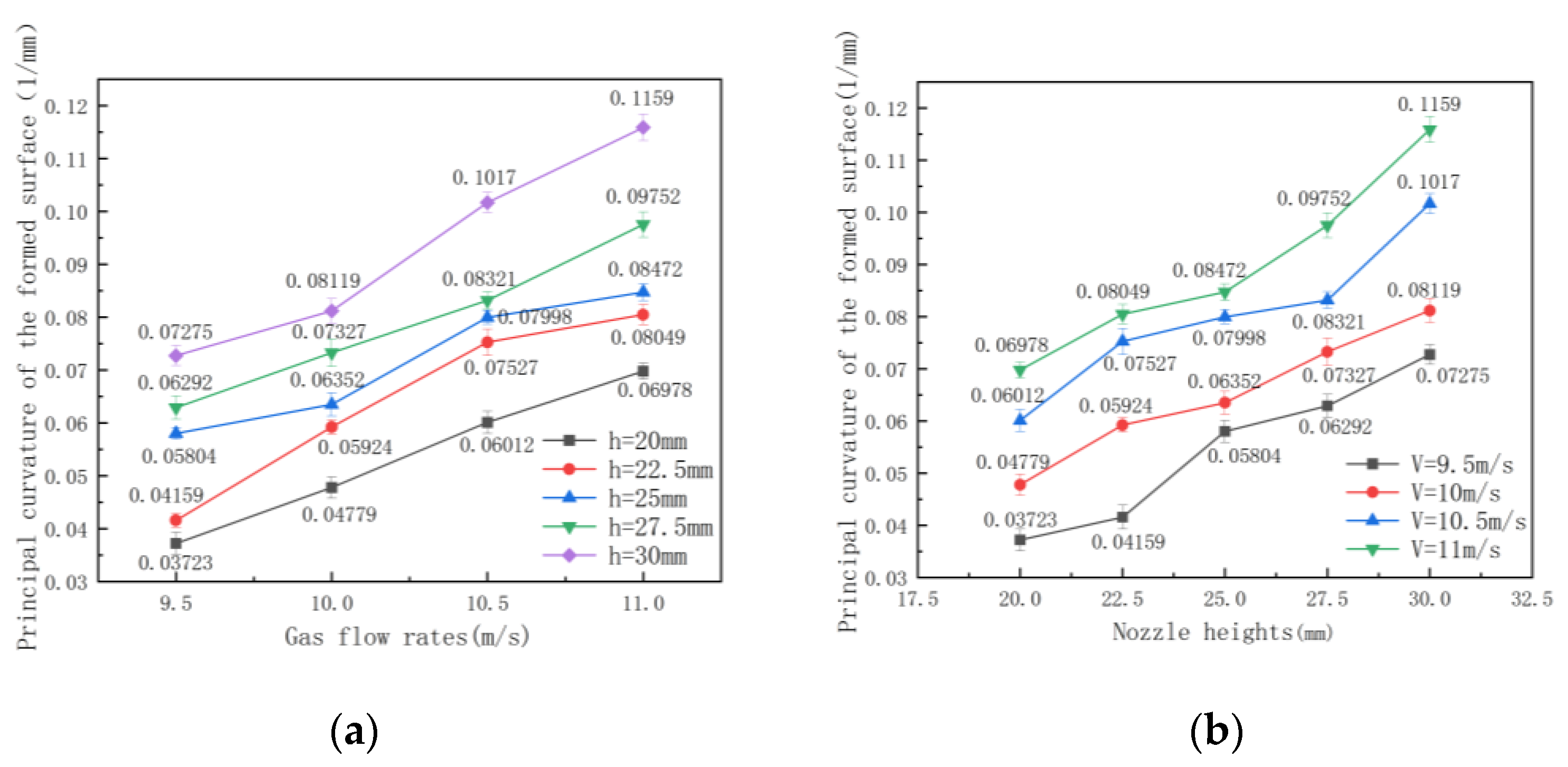
5. Experimental Results
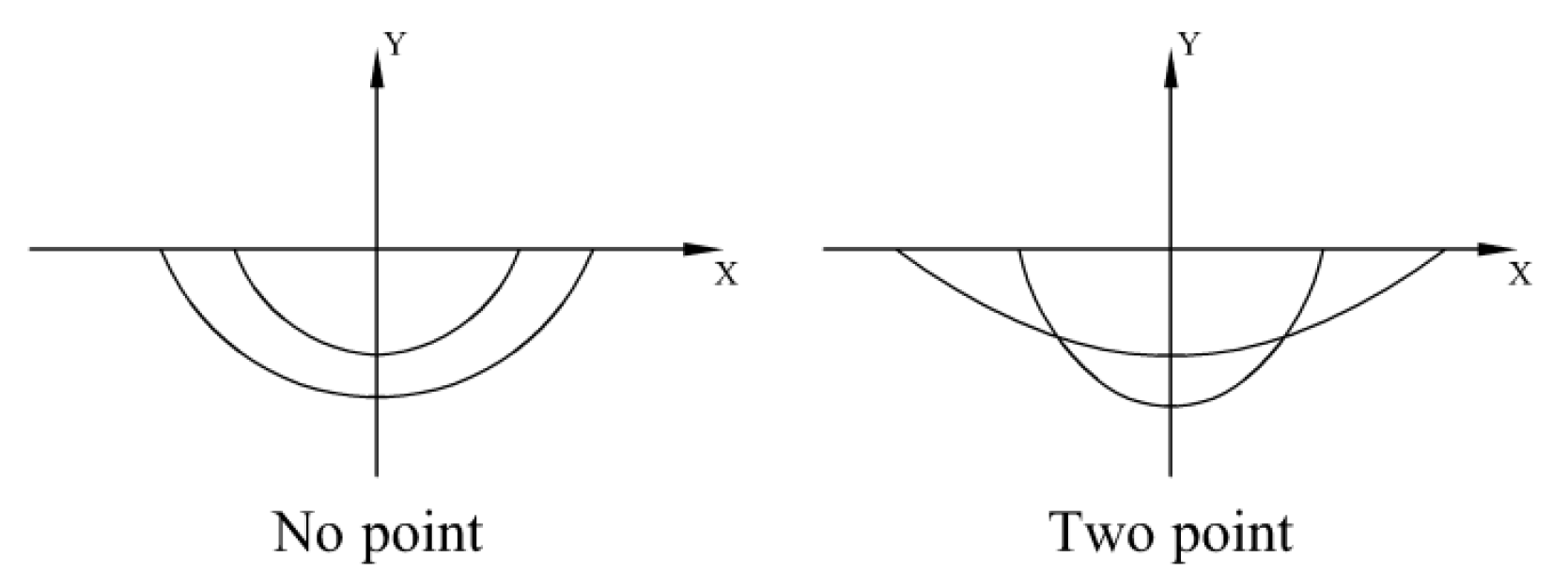
6. Discussion
7. Prediction Modelling of Surface Shape Parameters
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Martin, H.M.; Allen, R.G. Production of 8.4 m segments for the giant magellan telescope. SPIE Astron. Telesc. Instrum. 2012, 8450, 801–815. [Google Scholar]
- Ma, Z.; Peng, L.; Wang, J. Ultra-smooth polishing of high-precision optical surface. Optik 2013, 124, 6586–6589. [Google Scholar] [CrossRef]
- Jedamzik, R.; Werner, T.; Westerhoff, T. Production of the 4.26 m ZERODUR mirror blank for the Advanced Technology Solar telescope (ATST). SPIE Astron. Telesc. Instrum. 2014, 9151, 1012–1020. [Google Scholar] [CrossRef]
- Westerhoff, T.; Schäfer, M.; Thomas, A.; Weissenburger, M.; Werner, T.; Werz, A. Manufacturing of the ZERODUR 1.5-m primary mirror for the solar telescope GREGOR as preparation of light weighting of blanks up to 4-m diameter. SPIE Astron. Telesc. Instrum. 2010, 7739, 206–214. [Google Scholar]
- Hatefi, S.; Abou-El-Hossein, K. Review of single-point diamond turning process in terms of ultra-precision optical surface roughness. Int. J. Adv. Manuf. Technol. 2019, 106, 2167–2187. [Google Scholar] [CrossRef]
- Liu, Y.; Xing, Y.; Yang, C.; Li, C.; Xue, C. Simulation of heat transfer in the progress of precision glass molding with a finite element method for chalcogenide glass. Appl. Opt. 2019, 58, 7311–7318. [Google Scholar] [CrossRef] [PubMed]
- Fu, W.; Zhang, X. Numerical simulation assisted curve compensation in spin casting of optical mirror blank. Optik 2020, 207, 164406. [Google Scholar] [CrossRef]
- Fu, W.; Zhang, X. Experimental and numerical simulation study on gas jet forming of optical mirror blank. Optik 2020, 207, 164451. [Google Scholar] [CrossRef]
- Banks, R.B.; Bhavamai, A. Experimental study of the impingement of a liquid jet on the surface of a heavier liquid. J. Fluid Mech. 1965, 23, 229–240. [Google Scholar] [CrossRef]
- Molloy, N.A. Impinging jet flow in a two-phase system: The basic flow pattern. J. Iron Steel Inst. 1970, 208, 943–950. [Google Scholar]
- Meidani, A.R.N.; Isac, M.; Richardson, A.; Cameron, A.; Guthrie, R.I.L. Modelling Shrouded Supersonic Jets in Metallurgical Reactor Vessels. Iron Steel Inst. Jpn. 2004, 44, 1639–1645. [Google Scholar] [CrossRef]
- Ek, M.; Sichen, D. Study of Penetration Depth and Droplet Behavior in the Case of a Gas Jet Impinging on the Surface of Molten Metal using Liquid Ga–In–Sn. Steel Res. Int. 2012, 83, 678–685. [Google Scholar] [CrossRef]
- Kalifa, R.B.; Mahjoub Saïd, N.; Bournot, H.; Le Palec, G. Numerical Study of a Gas Jet Impinging on a Liquid Surface. In International Conference Design and Modeling of Mechanical Systems; Springer: Cham, Switzerland, 2017; pp. 661–670. [Google Scholar]
- Kofman, N.; Mergui, S.; Ruyer-Quil, C. Characteristics of solitary waves on a falling liquid film sheared by a turbulent counter-current gas flow. Int. J. Multiph. Flow 2017, 95, 22–34. [Google Scholar] [CrossRef]
- Rosler, R.S.; Stewart, G.H. Impingement of gas jets on liquid surfaces. J. Fluid Mech. 1968, 31, 163–174. [Google Scholar] [CrossRef]
- Vouros, A.P.; Panidis, T. Turbulent properties of a low Reynolds number, axisymmetric, pipe jet. Exp. Therm. Fluid Sci. 2013, 44, 42–50. [Google Scholar] [CrossRef]
- Mi, J.; Nobes, D.S.; Nathan, G.J. Influence of jet exit conditions on the passive scalarfield Of an axisymmetric free jet. J. Fluid Mech. 2001, 432, 91–125. [Google Scholar] [CrossRef]
- Banks, R.B.; Chandrasekhara, D.V. Experimental investigation of the penetration of a high-rate gas jet through a liquid surface. J. Fluid Mech. 1963, 15, 13–34. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D.; Romero, N.C. SOLA: A Numerical Solution Algorithm for Transient Fluid Flows. In Energy Research and Development Administration; Energy Research and Devempment Administration: Washington, DC, USA, 1975; pp. 1–19. [Google Scholar]
- Nichols, B.D.; Hirt, C.W.; Hotchkiss, R.S. SOLA-VOF: A Solution Algorithm for Transient Fluid Flow with Multiple Free Boundaries; Los Alamos National Lab: Los Alamos, NM, USA, 1980. [Google Scholar] [CrossRef]
- Ishii, M.; Mishima, K. Two-fluid model and hydrodynamic constitutive relations. Nucl. Eng. Des. 1984, 82, 107–126. [Google Scholar] [CrossRef]
- Brackbill, J.; Kothe, D.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Jeon, S.S.; Kim, S.J.; Park, G.C. CFD Simulation of Condensing Vapor Bubble using VOF Model. World Acad. Sci. Eng. Technol. 2009, 60, 209–215. [Google Scholar]
- Evans, M.R.; Oliver, D.; Shekhar, S.; Harvey, F. Fast and Exact Network Trajectory Similarity Computation: A Case-study on Bicycle Corridor Planning, ACM SIGKDD. In Proceedings of the 2nd ACM SIGKDD International Workshop on Urban Computing, Chicago, IL, USA, 11 August 2013; Association for Computing Machinery: New York, NY, USA, 2013; pp. 1–8. [Google Scholar]
- Fréchet, M.M. Sur Quelques Points du Calcul Fonctionnel. Rend. Del Circ. Mat. Di Palermo 1906, 22, 1–72. [Google Scholar] [CrossRef]
- Chen, L.; Özsu, M.T.; Oria, V. Robust and Fast Similarity Search for Moving Object Trajectories. In Proceedings of the 2005 ACM SIGMOD International Conference on Management of Data, Baltimore, MD, USA, 14–16 June 2005; Association for Computing Machinery: New York, NY, USA, 2005; pp. 491–502. [Google Scholar]
- Schulz, G. Imaging Performance of Aspherices in comparison with Spherical Surfaces. Appl. Opt. 1987, 26, 5118–5142. [Google Scholar] [CrossRef] [PubMed]




| Parameters | Numerical Value |
|---|---|
| Gas flow rate (m/s) | 9.5, 10, 10.5, 11 |
| Nozzle height (mm) | 20, 22.5, 25, 27.5, 31 |
| Air | Photosensitive Resin | |
|---|---|---|
| Density/kg·m−3 | 1.225 | 977 |
| Viscosity/cps | 1.7894 × 10−5 | 2000 |
| Surface tension/mN·m−1 | 37.6 | |
| Parameters | Error | Parameters | Error |
|---|---|---|---|
| V0 = 9.5 m/s, H = 20 mm | 1.8402 | V0 = 10.5 m/s, H = 20 mm | 1.4042 |
| V0 = 9.5 m/s, H = 22.5 mm | 1.8428 | V0 = 10.5 m/s, H = 22.5 mm | 0.7813 |
| V0 = 9.5 m/s, H = 25 mm | 1.5873 | V0 = 10.5 m/s, H = 25 mm | 0.5734 |
| V0 = 9.5 m/s, H = 27.5 mm | 0.0746 | V0 = 10.5 m/s, H = 27.5 mm | 0.6478 |
| V0 = 9.5 m/s, H = 30 mm | 0.1444 | V0 = 10.5 m/s, H = 30 mm | 1.6308 |
| V0 = 10 m/s, H = 20 mm | 2.0708 | V0 = 11 m/s, H = 20 mm | 0.7312 |
| V0 = 10 m/s, H = 22.5 mm | 0.8694 | V0 = 11 m/s, H = 22.5 mm | 1.3644 |
| V0 = 10 m/s, H = 25 mm | 1.0398 | V0 = 11 m/s, H = 25 mm | 0.9884 |
| V0 = 10 m/s, H = 27.5 mm | 1.2586 | V0 = 11 m/s, H = 27.5 mm | 1.1418 |
| V0 = 10 m/s, H = 30 mm | 0.8166 | V0 = 11 m/s, H = 30 mm | 0.5922 |
| Parameters | Error | Parameters | Error |
|---|---|---|---|
| V0 = 9.5 m/s, H = 20 mm | 0.01164 | V0 = 10.5 m/s, H = 20 mm | 0.02202 |
| V0 = 9.5 m/s, H = 22.5 mm | 0.00086 | V0 = 10.5 m/s, H = 22.5 mm | 0.02211 |
| V0 = 9.5 m/s, H = 25 mm | 0.00826 | V0 = 10.5 m/s, H = 25 mm | 0.02522 |
| V0 = 9.5 m/s, H = 27.5 mm | 0.00130 | V0 = 10.5 m/s, H = 27.5 mm | 0.06659 |
| V0 = 9.5 m/s, H = 30 mm | 0.00561 | V0 = 10.5 m/s, H = 30 mm | 0.07670 |
| V0 = 10 m/s, H = 20 mm | 0.00824 | V0 = 11 m/s, H = 20 mm | 0.06482 |
| V0 = 10 m/s, H = 22.5 mm | 0.00323 | V0 = 11 m/s, H = 22.5 mm | 0.07881 |
| V0 = 10 m/s, H = 25 mm | 0.01480 | V0 = 11 m/s, H = 25 mm | 0.08948 |
| V0 = 10 m/s, H = 27.5 mm | 0.00882 | V0 = 11 m/s, H = 27.5 mm | 0.09778 |
| V0 = 10 m/s, H = 30 mm | 0.01875 | V0 = 11 m/s, H = 30 mm | 0.10790 |
| Density/kg·m−3 | 1.225 | 977 |
| −0.49287 | 0.07184 | −0.00231 | 8.28075 | 1.28306 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wang, M.; Fu, W. The Variation of Surface Shape in the Gas Jet Forming. Appl. Sci. 2023, 13, 504. https://doi.org/10.3390/app13010504
Zhang X, Wang M, Fu W. The Variation of Surface Shape in the Gas Jet Forming. Applied Sciences. 2023; 13(1):504. https://doi.org/10.3390/app13010504
Chicago/Turabian StyleZhang, Xinming, Mingwei Wang, and Weijie Fu. 2023. "The Variation of Surface Shape in the Gas Jet Forming" Applied Sciences 13, no. 1: 504. https://doi.org/10.3390/app13010504
APA StyleZhang, X., Wang, M., & Fu, W. (2023). The Variation of Surface Shape in the Gas Jet Forming. Applied Sciences, 13(1), 504. https://doi.org/10.3390/app13010504







