A New Approach to Identifying an Arbitrary Number of Inclusions, Their Geometry and Location in the Structure Using Topological Optimization
Abstract
1. Introduction
2. Materials and Methods
3. Numeric Experiments and Results Discussion
3.1. Problem 1: Investigating the Convergence of a Solution by the FEM Using the COMSOL Multiphysics Software
3.2. Problem 2: Investigation of the Influence of the Boundary Conditions of the Thermal Problem on the Identification of a Large Number of Inclusions in the Form of Rectangles
3.3. Problem 3: Investigation of the Influence of the Boundary Conditions of the Thermal Problem on the Identification of 18 Inclusions in the Form of Rectangles Rotated by 90 Degrees Compared to Problem 2
3.4. Problem 4: Investigation of the Influence of the Boundary Conditions of the Thermal Problem on the Identification of 18 Inclusions in the Form of Rectangles Rotated by 45 Degrees Compared to Problem 3
3.5. Problem 5: Identification of the 18 Rhombuses Inclusions, under the Influence of Temperature and Heat Fluxes
3.6. Problem 6: Identification of the 18 Inclusions in the Form of a Square under the Influence of Temperature and Heat Fluxes
3.7. Problem 7: Identification of Inclusions by Changing Their Location, Number and Size
4. Conclusions
- The best results for determining an arbitrary number of inclusions were obtained when taking into account heat flux from three sides of the boundary conditions (12). Note that, for boundary condition (12), the identification results are not affected by the location of the inclusion and its dimensions.
- The novelty of the proposed approach for inclusion identification allows us to neglect the initial information about the location of inclusions.
- Numerical results in the investigated problems were obtained “practically” as an exact solution. The calculation error does not exceed 0.5% of the exact one.
- The proposed approach and methodology for its implementation are the first step of the analysis of the stress–strain state of fracture of a structure during crack formation.
- A new approach for determining an arbitrary number of inclusions, their geometry and their location can be used to identify inclusions in 3D solids.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gomes, G.F.; Mendez, Y.A.D.; Alexandrino, P.D.S.L.; da Cunha, S.S.; Ancelotti, A.C. A Review of Vibration Based Inverse Methods for Damage Detection and Identification in Mechanical Structures Using Optimization Algorithms and ANN. Arch. Comput. Methods Eng. 2019, 26, 883–897. [Google Scholar] [CrossRef]
- Das, S.; Dhang, N. Damage identification of structures using incomplete mode shape and improved TLBO-PSO with self-controlled multi-stage strategy. Structures 2022, 35, 1101–1124. [Google Scholar] [CrossRef]
- De Assis, F.M.; Gomes, G.F. Crack identification in laminated composites based on modal responses using metaheuristics, artificial neural networks and response surface method: A comparative study. Arch. Appl. Mech. 2021, 91, 4389–4408. [Google Scholar] [CrossRef]
- Hatłas, M.; Beluch, W. Multiscale global identification of porous structures. AIP Conf. Proc. 2018, 1922, 030005. [Google Scholar] [CrossRef]
- Lee, J. Boundary element method based sensitivity analysis of the crack detection in beams. J. Mech. Sci. Technol. 2015, 29, 3627–3634. [Google Scholar] [CrossRef]
- Van Vinh, P.; Van Chinh, N.; Tounsi, A. Static bending and buckling analysis of bi-directional functionally graded porous plates using an improved first-order shear deformation theory and FEM. Eur. J. Mech.-A Solids 2022, 96, 104743. [Google Scholar] [CrossRef]
- Cuong-Le, T.; Nguyen, K.D.; Le-M, H.; Phan-Vu, P.; Nguyen-Trong, P.; Tounsi, A. Nonlinear bending analysis of porous sigmoid FGM nanoplate via IGA and nonlocal strain gradient theory. Adv. Nano Res. 2022, 12, 441–455. [Google Scholar] [CrossRef]
- Mishra, M.; Barman, S.K.; Maity, D.; Maiti, D.K. Performance studies of 10 metaheuristic techniques in determination of damages for large-scale spatial trusses from changes in vibration responses. J. Comput. Civ. Eng. 2020, 34, 04019052. [Google Scholar] [CrossRef]
- Krishnanunni, C.G.; Raj, R.S.; Nandan, D.; Midhun, C.K.; Sajith, A.S.; Ameen, M. Sensitivity-based damage detection algorithm for structures using vibration data. J. Civ. Struct. Health Monit. 2019, 9, 137–151. [Google Scholar] [CrossRef]
- Huang, M.; Li, X.; Lei, Y.; Gu, J. Structural damage identification based on modal frequency strain energy assurance criterion and flexibility using enhanced Moth-Flame optimization. Structures 2020, 28, 1119–1136. [Google Scholar] [CrossRef]
- Sabokrou, M.; Fayyaz, M.; Fathy, M.; Moayed, Z.; Klette, R. Deep-anomaly: Fully convolutional neural network for fast anomaly detection in crowded scenes. Comput. Vis. Image Underst. 2018, 172, 88–97. [Google Scholar] [CrossRef]
- Gomes, G.F.; de Almeida, F.A. Tuning metaheuristic algorithms using mixture design: Application of sunflower optimization for structural damage identification. Adv. Eng. Softw. 2020, 149, 102877. [Google Scholar] [CrossRef]
- Liang, Y.-C.; Sun, Y.-P. Hardware-In-The-Loop Simulations of Hole/Crack Identification in a Composite Plate. Materials 2020, 13, 424. [Google Scholar] [CrossRef] [PubMed]
- Mei, H.; Haider, M.F.; Joseph, R.; Migot, A.; Giurgiutiu, V. Recent Advances in Piezoelectric Wafer Active Sensors for Structural Health Monitoring Applications. Sensors 2019, 19, 383. [Google Scholar] [CrossRef] [PubMed]
- Guemes, A. SHM of Composite structures by fiber optic sensors. In Structural Health Monitoring for Advanced Composite Structures, 1st ed.; Aliabadi, F.M.H., Khodaei, Z.S., Eds.; World Scientific Publishing Europe Ltd.: London, UK, 2018; Chapter 6; pp. 191–213. [Google Scholar] [CrossRef]
- Zhou, S.; Lin, H.; Li, B. Research on HILS Technology Applied on Aircraft Electric Braking System. J. Electr. Comput. Eng. 2017, 2017, 3503870. [Google Scholar] [CrossRef]
- Sokolowski, J.; Zochowski, A. On the topological derivative in shape optimization. SIAM J. Control Optim. 1999, 37, 1251–1272. [Google Scholar] [CrossRef]
- Novotny, A.A.; Sokołowski, J.; Żochowski, A. Studies in Systems, Decision and Control. In Applications of the Topological Derivative Method; Springer Nature Switzerland AG: Cham, Switzerland, 2019; 212p. [Google Scholar] [CrossRef]
- Kefal, A.; Sohouli, A.; Oterkus, E.; Yildiz, M.; Suleman, A. Topology optimization of cracked structures using peridynamics. Contin. Mech. Thermodyn. 2019, 31, 1645–1672. [Google Scholar] [CrossRef]
- Park, W.-K. Topological Derivative for Imaging of Thin Electromagnetic Inhomogeneity: Least Condition of Incident Directions. Adv. Math. Phys. 2018, 2018, 2096058. [Google Scholar] [CrossRef]
- Wahab, A.; Abbas, T.; Ahmed, N.; Zia, Q.M.Z. Detection of electromagnetic inclusions using topological sensitivity. J. Comp. Math. 2017, 35, 642–671. [Google Scholar] [CrossRef]
- Pena, M.; Rapún, M.-L. Detecting Damage in Thin Plates by Processing Infrared Thermographic Data with Topological Derivatives. Adv. Math. Phys. 2019, 2019, 5494795. [Google Scholar] [CrossRef]
- Nowak, M.; Sokołowski, J.; Żochowski, A. Justification of a certain algorithm for shape optimization in 3D elasticity. Struct. Multidiscip. Optim. 2018, 57, 721–734. [Google Scholar] [CrossRef]
- Ferreira, A.; Novotny, A.A. A new non-iterative reconstruction method for the electrical impedance tomography problem. Inverse Probl. 2017, 33, 035005. [Google Scholar] [CrossRef]
- Xavier, M.; Van Goethem, N.; Novotny, A.A. Hydro-mechanical fracture modeling governed by the topological derivatives. Comput. Methods Appl. Mech. Eng. 2020, 365, 112974. [Google Scholar] [CrossRef]
- Fernandez, L.; Novotny, A.A.; Prakash, R.; Sokołowski, J. Pollution Sources Reconstruction Based on the Topological Derivative Method. Appl. Math. Optim. 2021, 84, 1493–1525. [Google Scholar] [CrossRef]
- Fernández, L.; Novotny, A.A.; Prakash, R. Noniterative Reconstruction Method for an Inverse Potential Problem Modeled by a Modified Helmholtz Equation. Numer. Funct. Anal. Optim. 2018, 39, 937–966. [Google Scholar] [CrossRef]
- Xue, Y.; Zhai, Z.J. Inverse identification of multiple outdoor pollutant sources with a mobile sensor. Build. Simul. 2017, 10, 255–263. [Google Scholar] [CrossRef]
- Da Silva, A.A.M.; Novotny, A.A. Damage identification in plate structures based on the topological derivative method. Struct. Multidiscip. Optim. 2022, 65, 7. [Google Scholar] [CrossRef]
- Wei, Z.; Liu, J.; Lu, Z. Structural damage detection using improved particle swarm optimization. Inverse Probl. Sci. Eng. 2018, 26, 792–810. [Google Scholar] [CrossRef]
- Khatir, S.; Wahab, M.A.; Benaissa, B.; Köppen, M. Crack Identification Using eXtended IsoGeometric Analysis and Particle Swarm Optimization. In Lecture Notes in Mechanical Engineering, Proceedings of the 7th International Conference on Fracture Fatigue and Wear, Ghent, Belgium, 9–10 July 2018; Abdel Wahab, M., Ed.; Springer: Singapore, 2019. [Google Scholar] [CrossRef]
- Pereira, J.L.J.; Chuman, M.; Jr, S.S.C.; Gomes, G.F. Lichtenberg optimization algorithm applied to crack tip identification in thin plate-like structures. Eng. Comput. 2021, 38, 151–166. [Google Scholar] [CrossRef]
- Fathi, H.; Vaez, S.H.; Zhang, Q.; Alavi, A.H. A new approach for crack detection in plate structures using an integrated extended finite element and enhanced vibrating particles system optimization methods. Structures 2021, 29, 638–651. [Google Scholar] [CrossRef]
- Hassine, M.; Kallel, I. One-iteration reconstruction algorithm for geometric inverse problems. Appl. Math. E Notes 2018, 18, 43–50. [Google Scholar]
- Machado, T.J.; Angelo, J.S.; Novotny, A.A. A new one-shot pointwise source reconstruction method. Math. Methods Appl. Sci. 2017, 40, 1367–1381. [Google Scholar] [CrossRef]
- Gonçalves, J.F.; Moreira, J.B.D.; Salas, R.A.; Ghorbani, M.M.; Rubio, W.M.; Silva, E.C.N. Identification problem of acoustic media in the frequency domain based on the topology optimization method. Struct. Multidiscip. Optim. 2020, 62, 1041–1059. [Google Scholar] [CrossRef]
- Pena, M.; Rapún, M.L. Application of the topological derivative to post-processing infrared time-harmonic thermograms for defect detection. J. Math. Ind. 2020, 10, 4. [Google Scholar] [CrossRef]
- Burczyński, T.; Kuś, W.; Beluch, W.; Długosz, A.; Poteralski, A.; Szczepanik, M. Intelligent Computing in Inverse Problems. In Intelligent Computing in Optimal Design; Solid Mechanics and Its Applications; Springer: Cham, Switzerland, 2020; Volume 261, pp. 197–236. [Google Scholar] [CrossRef]
- Ben Abda, A.; Méjri, B. Topological sensitivity analysis for identification of voids under Navier’s boundary conditions in linear elasticity. Inverse Probl. 2019, 35, 105003. [Google Scholar] [CrossRef]
- Krysko, A.; Awrejcewicz, J.; Bodyagina, K.; Makseev, A.; Zhigalov, M.; Krysko, V. Identifying inclusions in a non-uniform thermally conductive plate under external flows and internal heat sources using topological optimization. Math. Mech. Solids 2022, 27, 1649–1671. [Google Scholar] [CrossRef]
- Krysko, A.; Awrejcewicz, J.; Pavlov, S.; Bodyagina, K.; Krysko, V. Topological optimization of thermoelastic composites with maximized stiffness and heat transfer. Compos. Part B Eng. 2019, 158, 319–327. [Google Scholar] [CrossRef]
- Krysko, A.V.; Awrejcewicz, J.; Dunchenkin, P.D.; Zhigalov, M.V.; Krysko, V.A. Topological Optimization of Multilayer Structural Elements of MEMS/NEMS Resonators with an Adhesive Layer Subjected to Mechanical Loads. In Recent Approaches in the Theory of Plates and Plate-Like Structures; Springer: Cham, Switzerland, 2022; Volume 151, pp. 155–165. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Pavlov, S.P.; Krysko, A.V.; Zhigalov, M.V.; Bodyagina, K.S.; Krysko, V.A. Decreasing shear stresses of the solder joints for mechanical and thermal loads by topological optimization. Materials 2020, 13, 1862. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Krysko, V.A.; Mitskievich, S.A.; Zhigalov, M.V.; Krysko, A.V. Nonlinear dynamics of heterogeneous shells. Part 1: Statics and dynamics of heterogeneous variable stiffness shells. Int. J. Non-Linear Mech. 2021, 130, 103669. [Google Scholar] [CrossRef]
- Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods and Applications, 2nd ed.; Springer: Berlin, Germany, 2004; 370p. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Krysko, V.A.; Sopenko, A.A.; Zhigalov, M.V.; Kirichenko, A.V.; Krysko, A.V. Mathematical modelling of physically/geometrically non-linear micro-shells with account of coupling of temperature and deformation fields. Chaos Solitons Fractals 2017, 104, 635–654. [Google Scholar] [CrossRef]
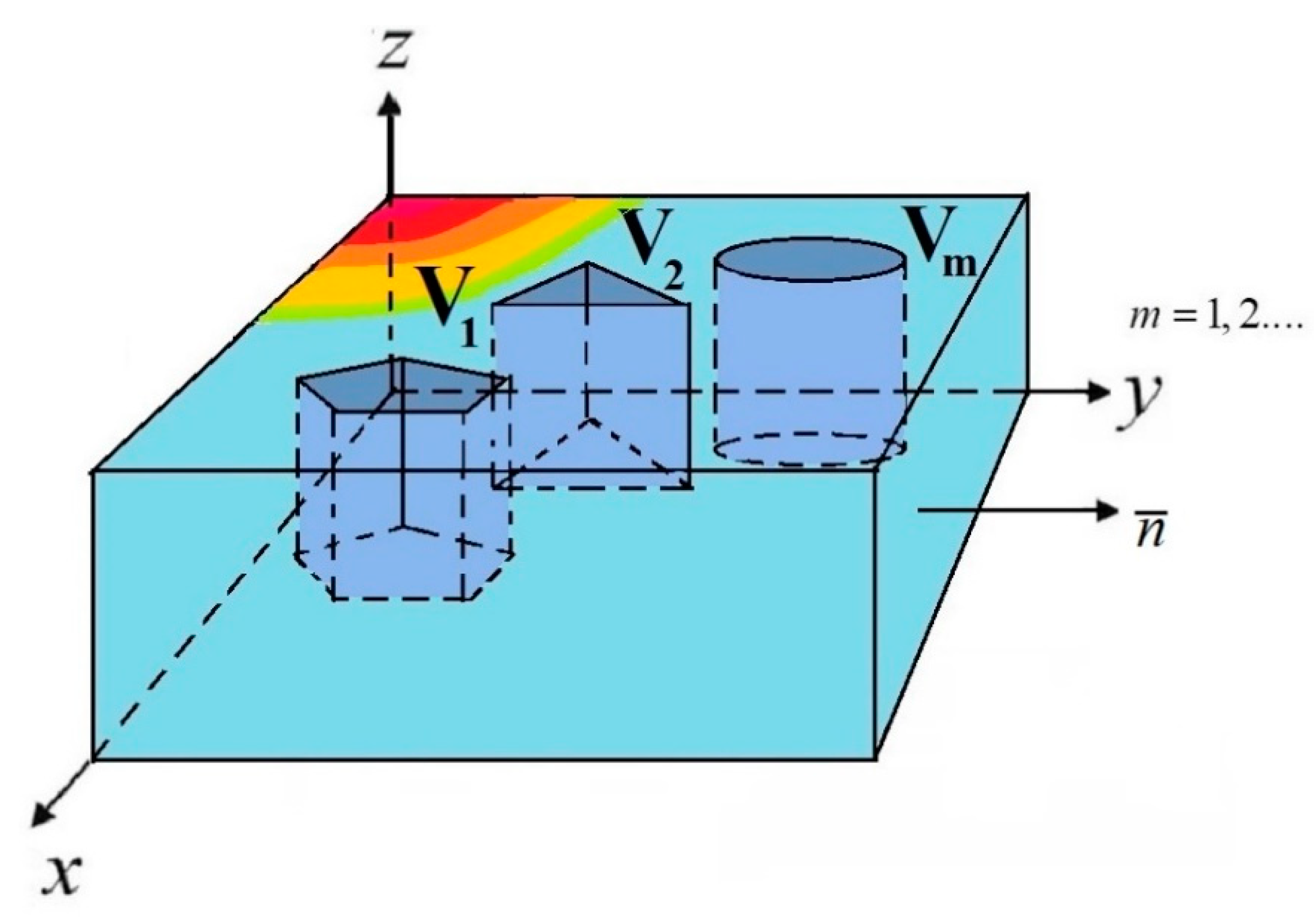
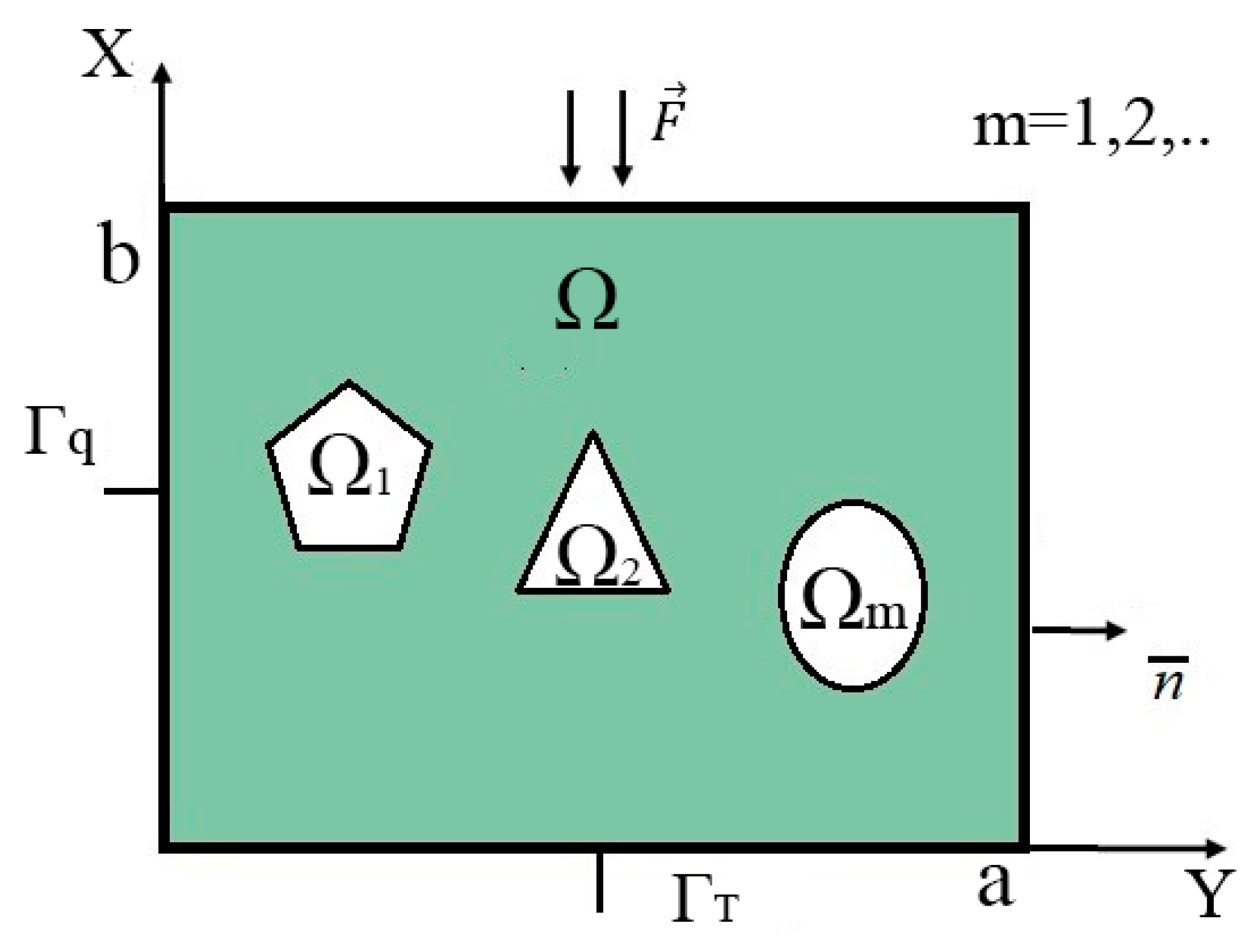
| Coordinates of Location of Centers of Rectangular Inclusions | 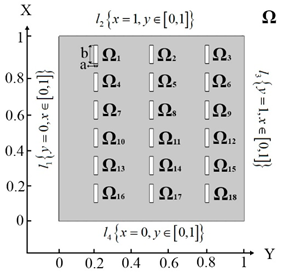 |
| : 1. (0.2, 0.9), 2. (0.5, 0.9), 3. (0.8, 0.9), 4. (0.2, 0.75), 5. (0.5, 0.75), 6. (0.8, 0.75), 7. (0.2, 0.6), 8. (0.5, 0.6), 9. (0.8, 0.6), 10. (0.2, 0.45), 11. (0.5, 0.45), 12. (0.8, 0.45), 13. (0.2, 0.3), 14. (0.5, 0.3), 15. (0.8, 0.3), 16. (0.2, 0.15), 17. (0.5, 0.15), 18. (0.8, 0.15) |
| Geometry and Dimensions Inclusions | 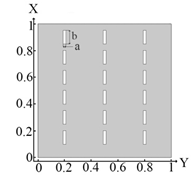 | 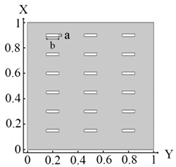 | 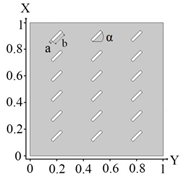 |
| Number FE for | , | , | , |
| Number FE for | , | , | , |
| Type of Boundary Conditions (10)–(12) | Temperature Distribution | Results of the Topological Optimization |
|---|---|---|
| (10) | 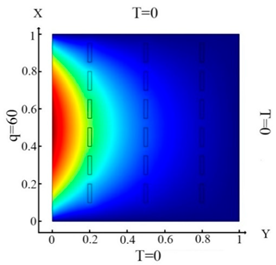 (a) Ωm, m = 1, 2, …18 | 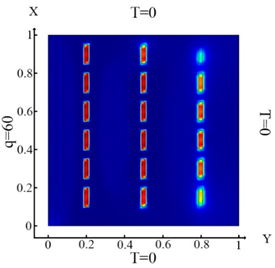 (d) Ωm, m = 1, 2, …18 |
| (11) |  (b) Ωm, m = 1, 2, …18 |  (e) Ωm, m = 1, 2, …18 |
| (12) | 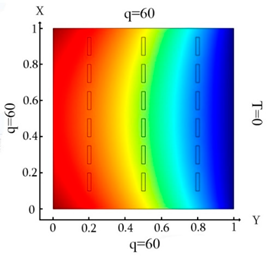 (c) Ωm, m = 1, 2, …18 |  (f) Ωm, m = 1, 2, …18 |
| Type of Boundary Conditions (10)–(12) | Temperature Distribution | Results of the Topological Optimization |
|---|---|---|
| (10) | 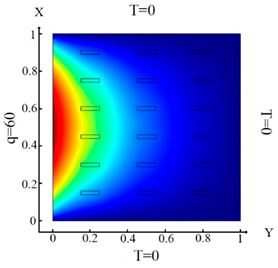 (a) Ωm, m = 1, 2, …18 | 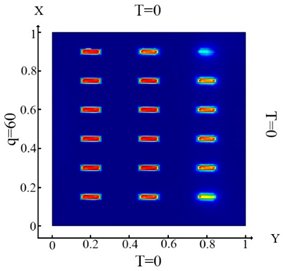 (d) Ωm, m = 1, 2, …18 |
| (11) | 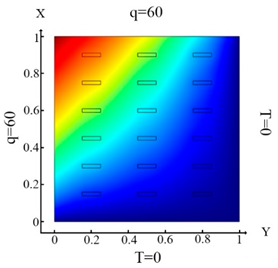 (b) Ωm, m = 1, 2, …18 | 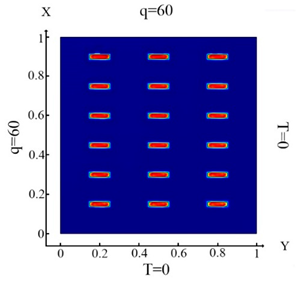 (e) Ωm, m = 1, 2, …18 |
| (12) | 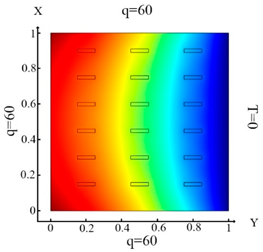 (c) Ωm, m = 1, 2, …18 | 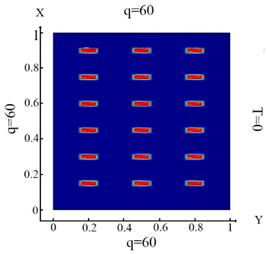 (f) Ωm, m = 1, 2, …18 |
| Type of Boundary Conditions (10)–(12) | Temperature Distribution | Results of the Topological Optimization |
|---|---|---|
| (10) | 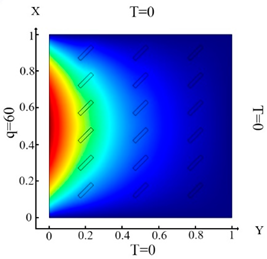 (a) Ωm, m = 1, 2, …18 | 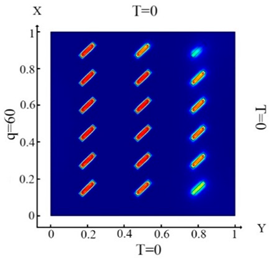 (d) Ωm, m = 1, 2, …18 |
| (11) | 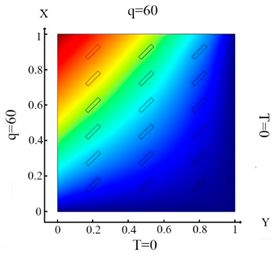 (b) Ωm, m = 1, 2, …18 | 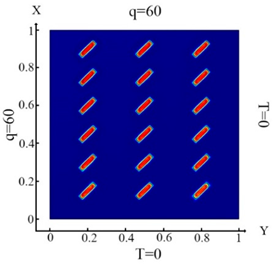 (e) Ωm, m = 1, 2, …18 |
| (12) |  (c) Ωm, m = 1, 2, …18 | 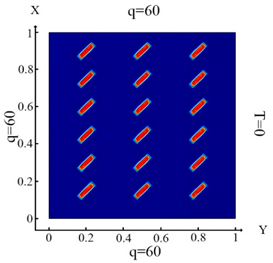 (f) Ωm, m = 1, 2, …18 |
| N FE number | 643 | 1222 |
(in percent) | 1.612 | 0.5142 |
| Type of Boundary Conditions (10)–(12) | Temperature Distribution | Results of the Topological Optimization |
|---|---|---|
| (10) | 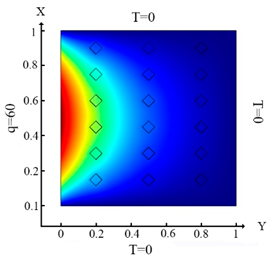 (a) Ωm, m = 1, 2, …18 | 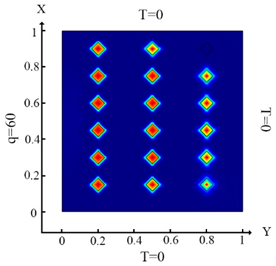 (d) Ωm, m = 1, 2, …18 |
| (11) | 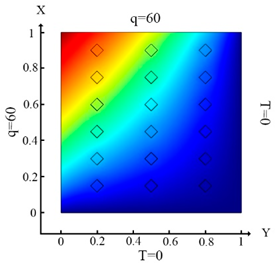 (b) Ωm, m = 1, 2, …18 | 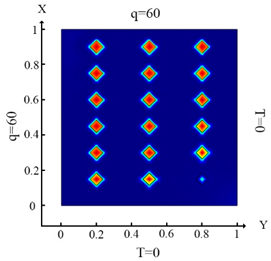 (e) Ωm, m = 1, 2, …18 |
| (12) | 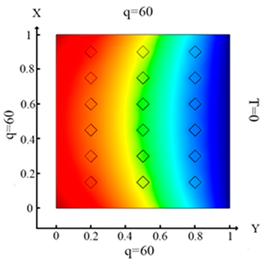 (c) Ωm, m = 1, 2, …18 | 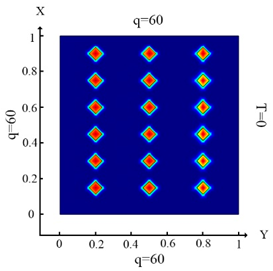 (f) Ωm, m = 1, 2, …18 |
| N FE number | 304 | 1330 |
(in percent) | 1.5863 | 0.5112 |
| Type of Boundary Conditions (10)–(12) | Temperature Distribution | Results of the Topological Optimization |
|---|---|---|
| (10) | 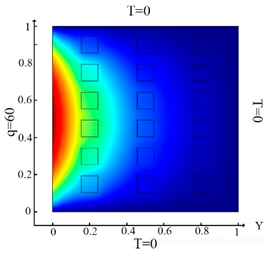 (a) Ωm, m = 1, 2, …18 | 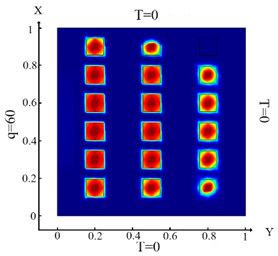 (d) Ωm, m = 1, 2, …18 |
| (11) | 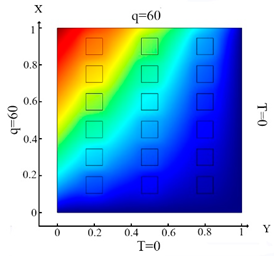 (b) Ωm, m = 1, 2, …18 | 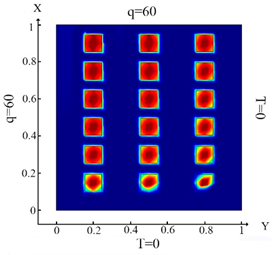 (e) Ωm, m = 1, 2, …18 |
| (12) | 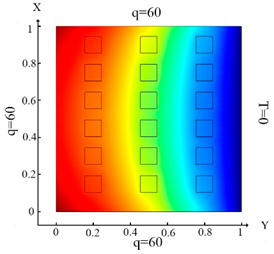 (c) Ωm, m = 1, 2, …18 | 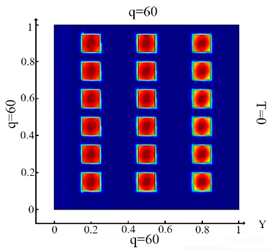 (f) Ωm, m = 1, 2, …18 |
| I. a = 6 · 10−1 m, b = 1 · 10−1 m | II. a = 6 · 10−1 m, b = 2.5 · 10−2 m | ||||
| Coordinates Centers of the Rectangles: A (0.5, 0.35), B (0.5, 0.75) | Coordinates Centers of the Rectangles: A (0.5, 0.9), B (0.1, 0.5), C (0.5, 0.1) | Coordinates Centers of the Rectangles: A (0.5, 0.5), B (0.1, 0.5), C (0.9, 0.5) | |||
 | 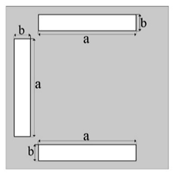 |  | |||
| Boundary condition (10) | Boundary condition (11) | Boundary condition (12) | |||
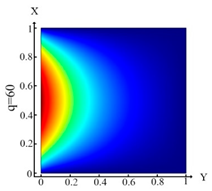 |  | 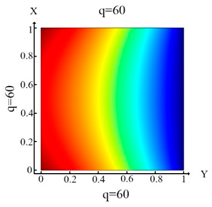 | |||
| I. a = 6 · 10−1 m, b = 1 · 10−2 m | |||
 6488 Fe | 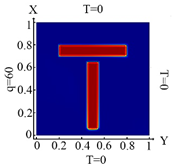 6488 FE Boundary condition (10) | 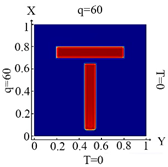 6488 FE Boundary condition (11) | 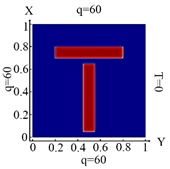 6488 FE Boundary condition (12) |
| II. a = 6 · 10−1 m, b = 2.5 · 10−2 m | |||
 6586 FE | 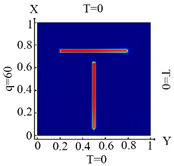 6586 FE Boundary condition (10) |  6586 FE Boundary condition (11) | 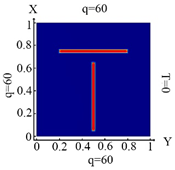 6586 FE Boundary condition (12) |
| I. a = 6 · 10−1 m, b = 1 · 10−1 m | |||
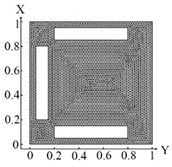 6382 FE | 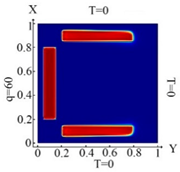 6382 FE Boundary condition (10) | 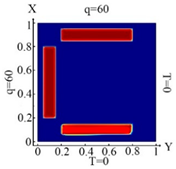 6382 FE Boundary condition (11) | 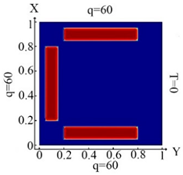 6382 FE Boundary condition (12) |
| II. a = 6 · 10−1 m, b = 2.5 · 10−2 m | |||
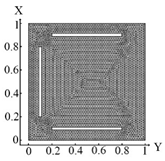 6720 FE | 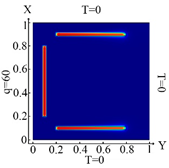 6720 FE Boundary condition (10) | 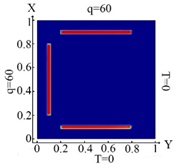 6720 FE Boundary condition (11) | 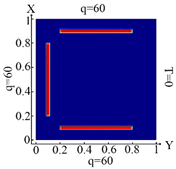 6720 FE Boundary condition (12) |
| I. a = 6 · 10−1 m, b = 1 · 10−1 m | |||
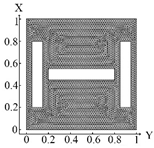 6428 FE | 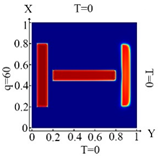 6428 FE Boundary condition (10) | 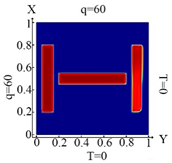 6428 FE Boundary condition (11) | 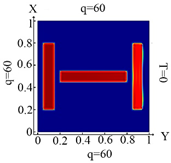 6428 FE Boundary condition (12) |
| II. a = 6 · 10−1 m, b = 2.5 · 10−2 m | |||
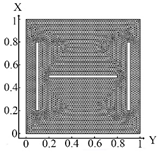 6718 FE | 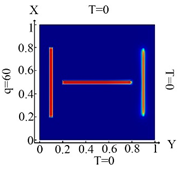 6718 FE Boundary condition (10) | 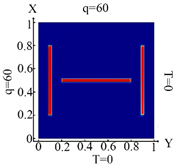 6718 FE Boundary condition (11) | 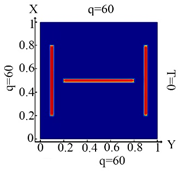 6718 FE Boundary condition (12) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krysko, A.V.; Makseev, A.; Smirnov, A.; Zhigalov, M.V.; Krysko, V.A. A New Approach to Identifying an Arbitrary Number of Inclusions, Their Geometry and Location in the Structure Using Topological Optimization. Appl. Sci. 2023, 13, 49. https://doi.org/10.3390/app13010049
Krysko AV, Makseev A, Smirnov A, Zhigalov MV, Krysko VA. A New Approach to Identifying an Arbitrary Number of Inclusions, Their Geometry and Location in the Structure Using Topological Optimization. Applied Sciences. 2023; 13(1):49. https://doi.org/10.3390/app13010049
Chicago/Turabian StyleKrysko, A. V., Anton Makseev, Anton Smirnov, M. V. Zhigalov, and V. A. Krysko. 2023. "A New Approach to Identifying an Arbitrary Number of Inclusions, Their Geometry and Location in the Structure Using Topological Optimization" Applied Sciences 13, no. 1: 49. https://doi.org/10.3390/app13010049
APA StyleKrysko, A. V., Makseev, A., Smirnov, A., Zhigalov, M. V., & Krysko, V. A. (2023). A New Approach to Identifying an Arbitrary Number of Inclusions, Their Geometry and Location in the Structure Using Topological Optimization. Applied Sciences, 13(1), 49. https://doi.org/10.3390/app13010049






