Computational Acceleration of Topology Optimization Using Deep Learning
Abstract
1. Introduction
1.1. General Knowledge
1.2. Related Works in ML
1.3. Current Work
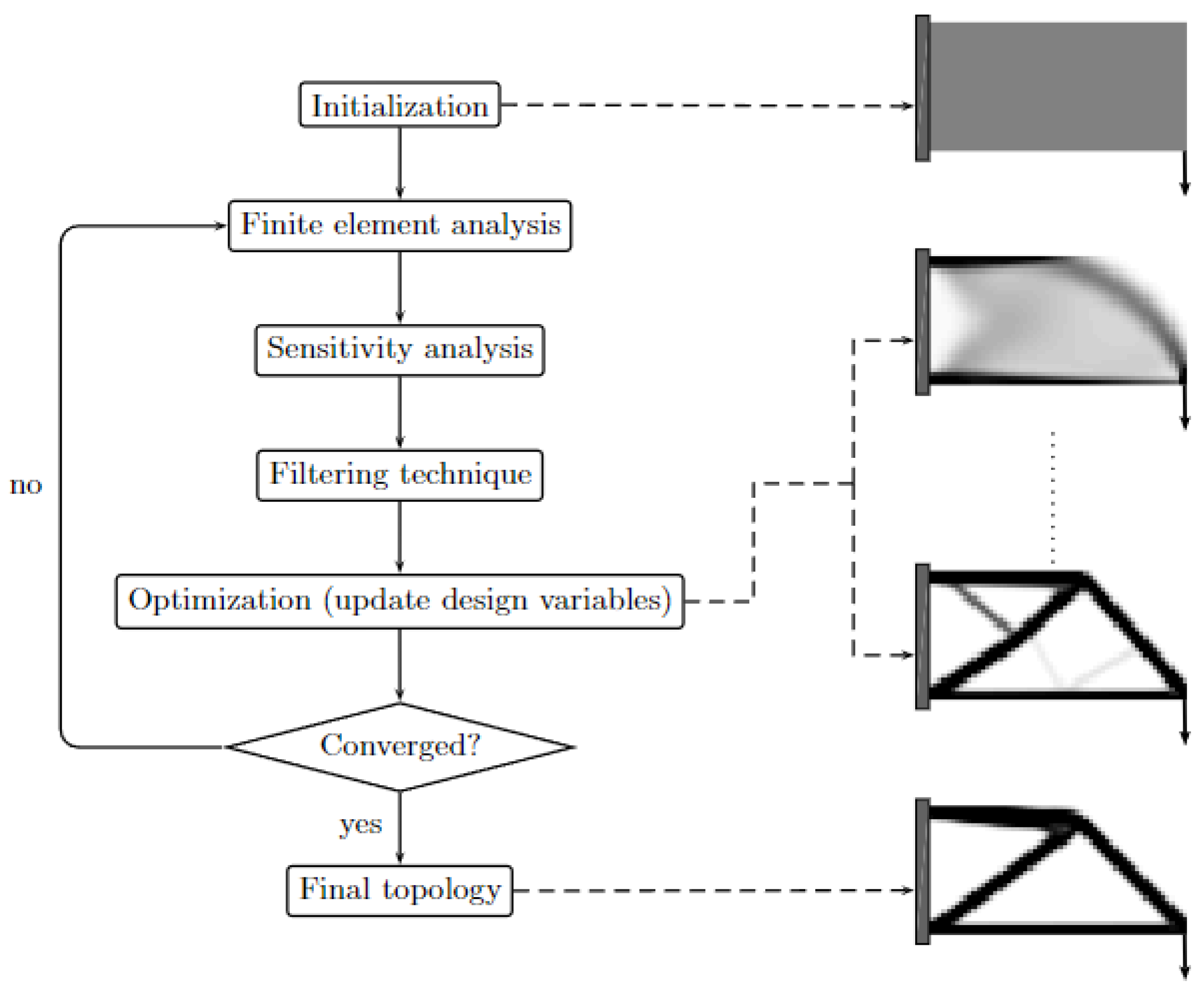
2. Topology Optimization Theory
3. Datasets
3.1. Dataset #1
- The number of nodes with fixed x and y translations and the number of loads are sampled from the Poisson distribution [17]:
- The load values are set to be equal to −1.
- Normal distribution from the equation below was used for the volume fraction sampling.where —mean and —standard deviation.
3.2. Dataset #2
- Volume fraction (VF)—desired volume fraction of the output structure. VF value varies in the range starting from 0.3 to 0.5 with the minimum change equal to 0.02. The volume fraction is represented as a matrix completely filled with the desired volume fraction value. All values of this matrix are the same and equal to the VF value, as shown in Figure 3.
- Displacement boundary conditions (BC) are a 2D matrix with the dimension of 64 × 128, which shows the mounting places of the image. Elements of the matrix are described by 0, 1, 2, or 3 numbers, where:
- ○
- 0—unconstrained;
- ○
- 1—ux is equal to zero;
- ○
- 2—uy is equal to zero;
- ○
- 3—both ux and uy are equal to zero;
where ux, uy are displacement vectors on x and y axis. - Load on x axes—is a 2D matrix with the dimension of 64 × 128 filled with zeros and containing at most one float that is less than or equal to one. Load on x axes—external load acting along the x-axis. Only one cell may have a non-zero value which represents external load magnitude and location.
- Load on y axes—2D matrix with the shape 64 × 128 filled with zeros and containing at most one float that is less than or equal to one. Load on y axes—external load acting along the y-axis. Only one cell may have a non-zero value which represents external load magnitude and location.
- Strain energy density—is a physical field applied to the image and calculated using the following equation:
- Von Mises stress is also a physical field applied to the image and calculated using the following equation:where is strain energy density, is the von Mises stress, are components of the stress tensor. All the above-described features are illustrated in Figure 2.
- BC on x axes—a matrix for showing points that are fixed on x axes. Basically, it is equal to 1 if ux = 0, otherwise it is 0. Alternatively, it is equal to 1 when the cell is on the original BC, which is equal to either 1 or 3.
- BC on y axes—is a matrix for showing points that are fixed on y axes. Basically, it is equal to 1 if uy = 0, otherwise it is 0. Alternatively, it is equal to 1 when the cell is on the original BC, which is equal to either 2 or 3.
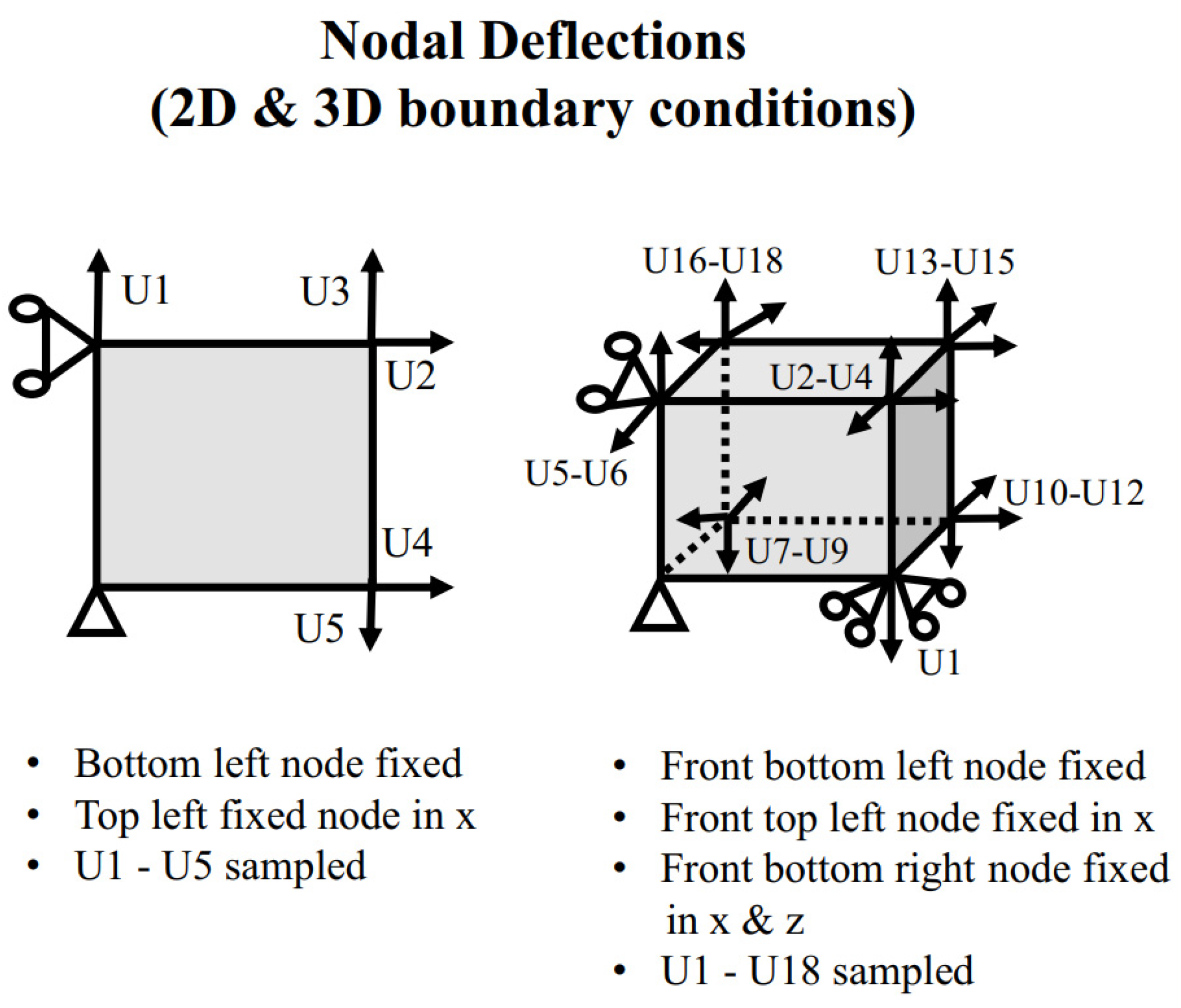
3.3. Dataset #3
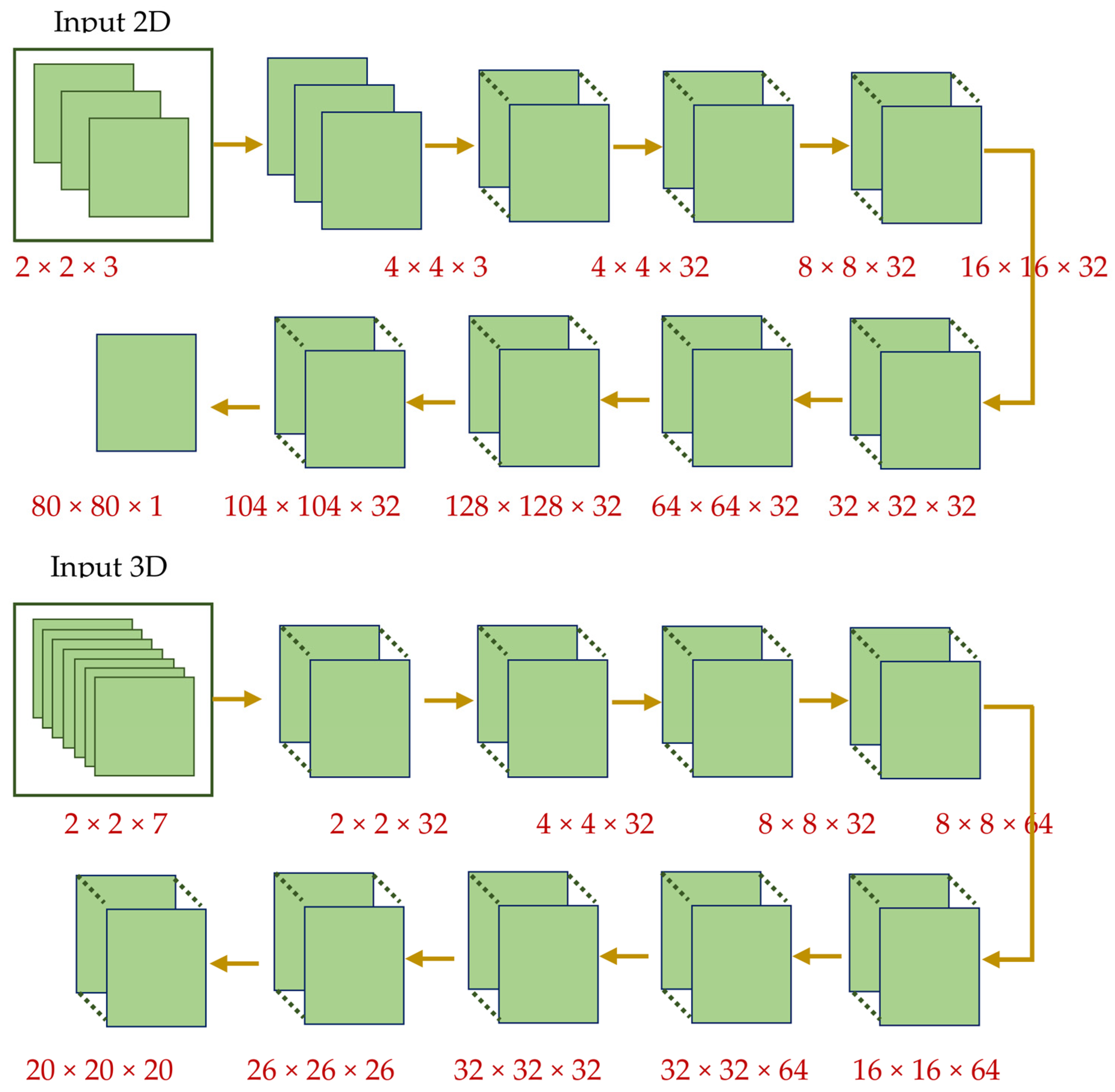
- For 2D objects input vector with [2 × 2 × 3] dimensions:
- For 3D objects input vector with [2 × 2 × 7] dimensions:
4. Model Design
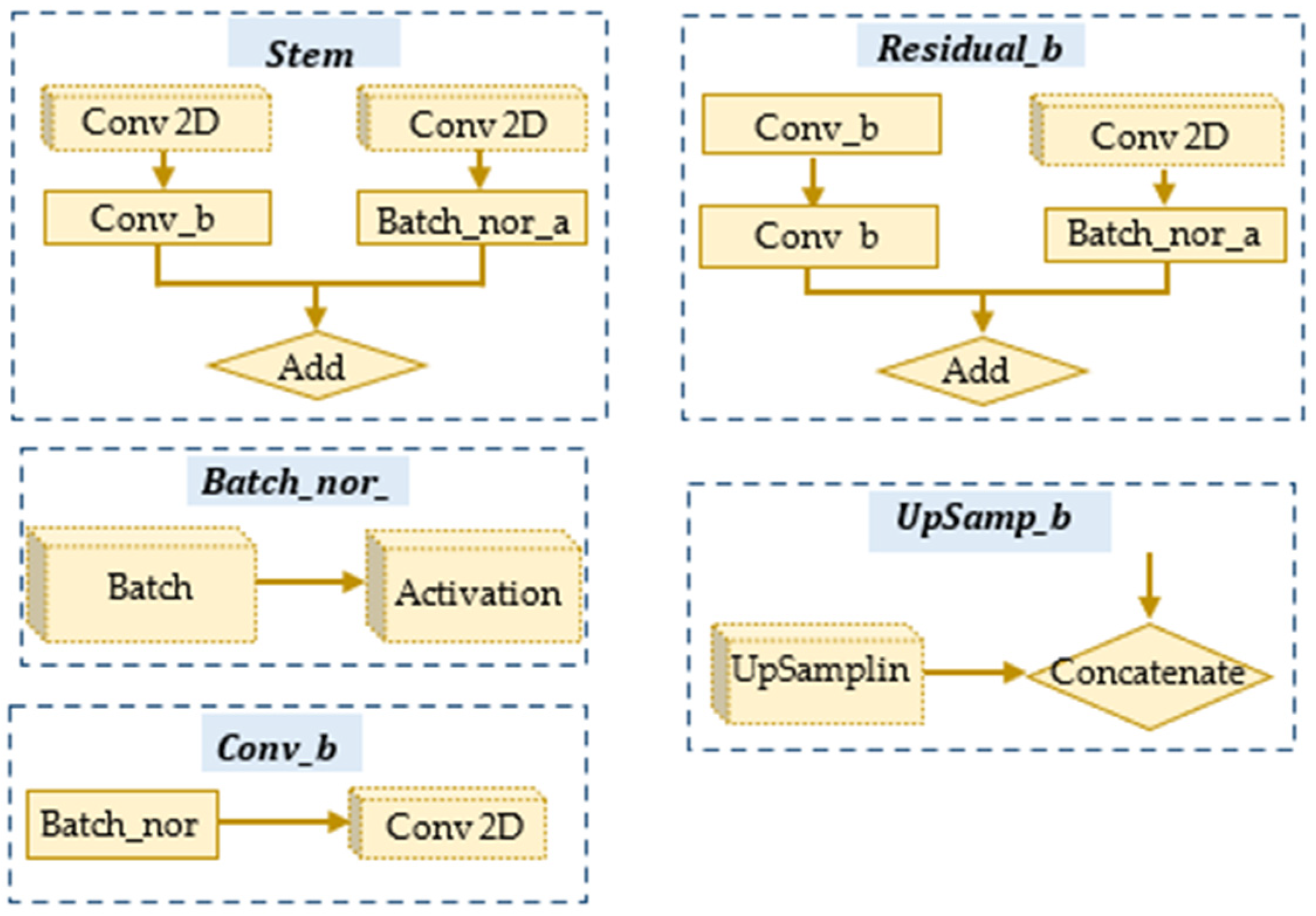
4.1. CNN
4.2. U-Net
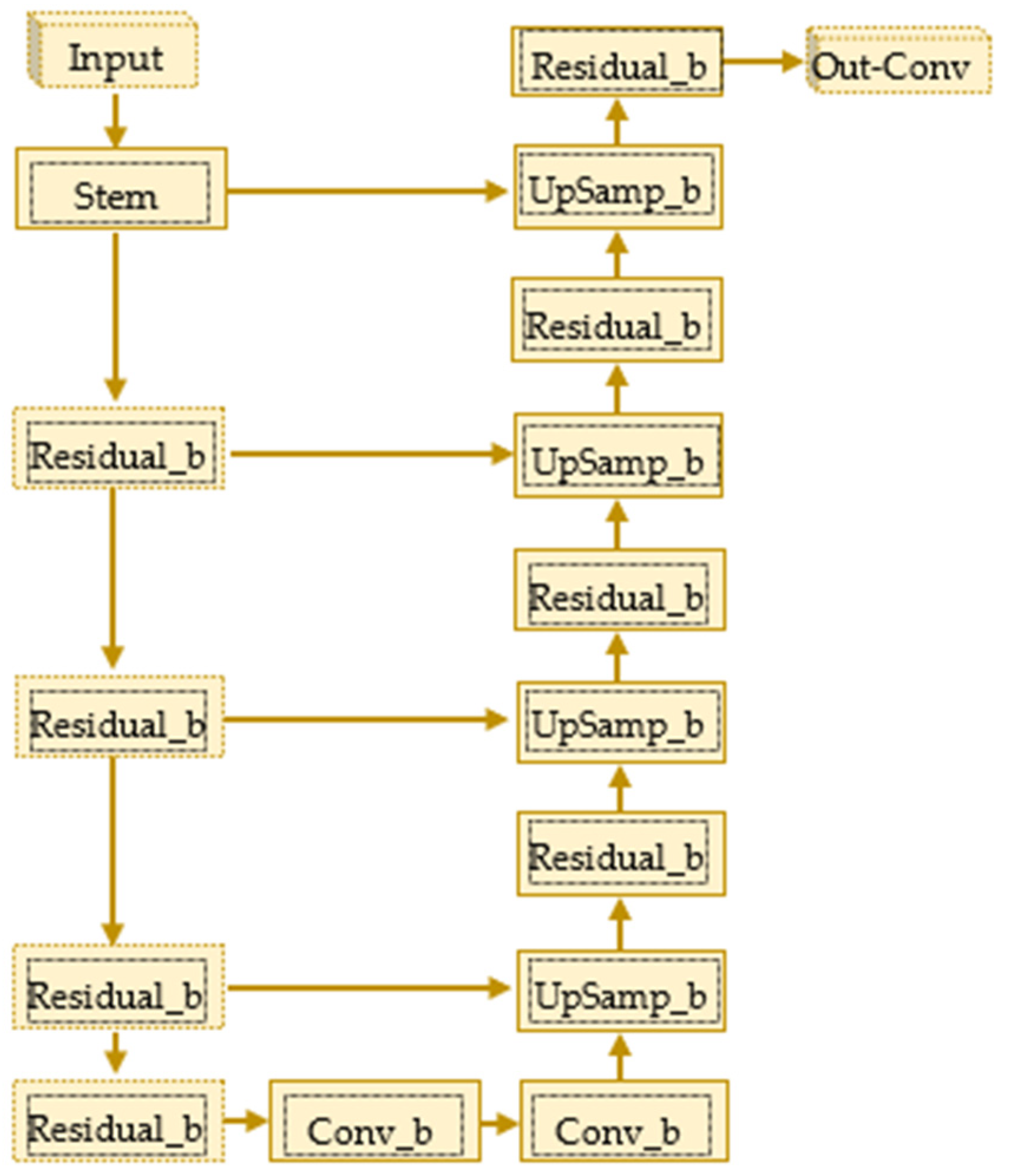
4.3. Res-U-Net
5. Evaluation Metrics
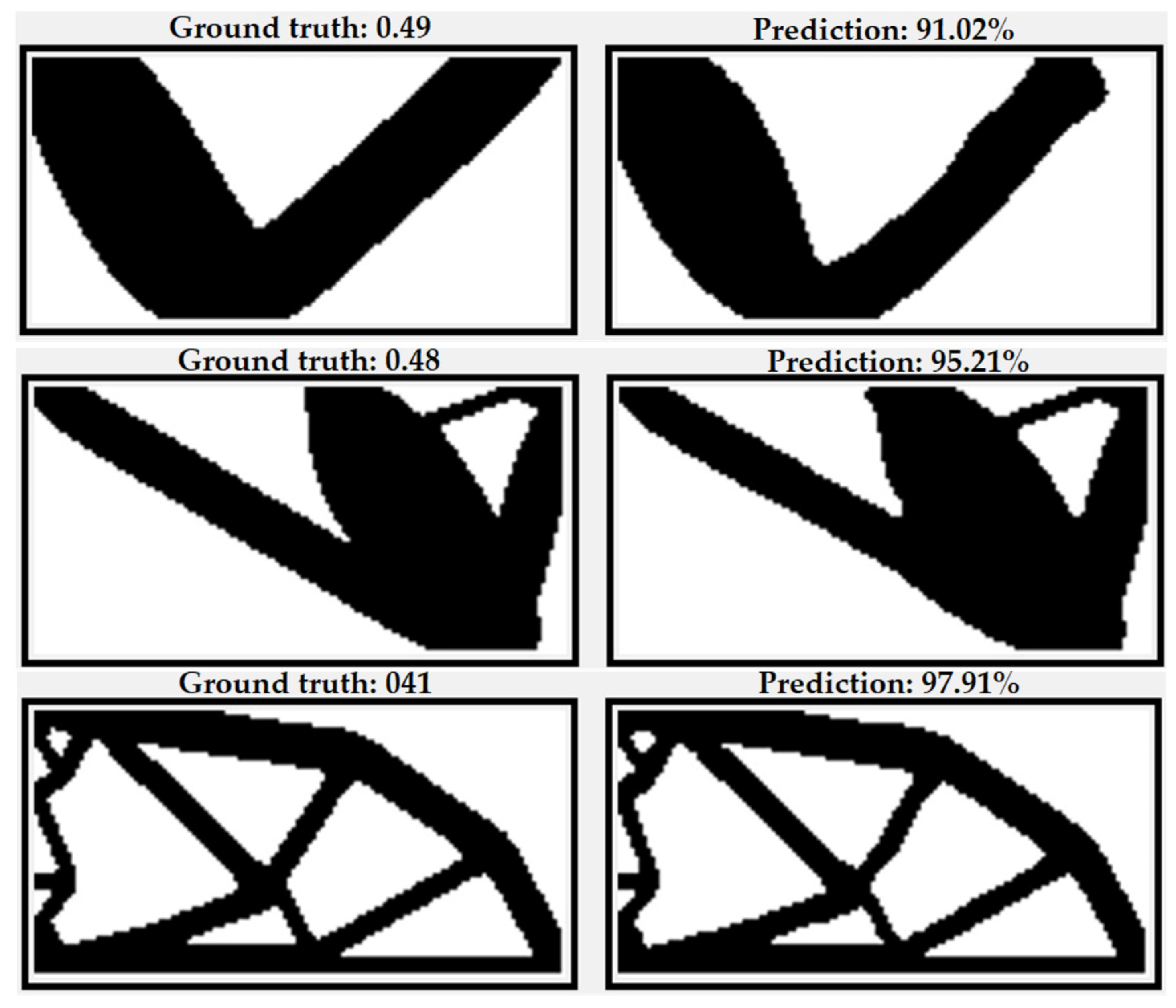
6. Experiments
6.1. Experiments on Dataset #1
6.2. Experiments on Dataset#2
6.3. Experiments on Dataset #3
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Merulla, A.; Gatto, A.; Bassoli, E.; Munteanu, S.I.; Gheorghiu, B.; Pop, M.A.; Bedo, T.; Munteanu, D. Weight reduction by topology optimization of an engine subframe mount, designed for additive manufacturing production. Mater. Today Proc. 2019, 19, 1014–1018. [Google Scholar] [CrossRef]
- Yano, M.; Huang, T.; Zahr, M.J. A globally convergent method to accelerate topology optimization using on-the-fly model reduction. Comput. Methods Appl. Mech. Eng. 2021, 375, 113635. [Google Scholar] [CrossRef]
- Wang, S. Krylov Subscpace Methods for Topology Optimization on Adaptive Meshes. Ph.D. Dissertation, University of Illinois, Champaign, IL, USA, 2007. [Google Scholar]
- Maksum, Y.; Amirli, A.; Amangeldi, A.; Inkarbekov, M.; Ding, Y.; Romagnoli, A.; Rustamov, S.; Akhmetov, B. Computational Acceleration of Topology Optimization Using Parallel Computing and Machine Learning Methods—Analysis of Research Trends. J. Ind. Inf. Integr. 2022, 28, 100352. [Google Scholar] [CrossRef]
- Wang, S.; Sturler, E.; De Paulino, G.H. Large-scale topology optimization using preconditioned Krylov subspace methods with recycling. Int. J. Numer. Methods Eng. 2007, 69, 2441–2468. [Google Scholar] [CrossRef]
- Martínez-Frutos, J.; Herrero-Pérez, D. Large-scale robust topology optimization using multi-GPU systems. Comput Methods Appl. Mech. Eng. 2016, 311, 393–414. [Google Scholar] [CrossRef]
- Dai, W.; Berleant, D. Benchmarking contemporary deep learning hardware and frameworks: A survey of qualitative metrics. In Proceedings of the 2019 IEEE First International Conference on Cognitive Machine Intelligence (CogMI), Los Angeles, CA, USA, 12–14 December 2019; pp. 148–155. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, H.; Li, Y.; Mo, K. Machine Learning based parameter tuning strategy for MMC based topology optimization. Adv. Eng. Softw. 2020, 149, 102841. [Google Scholar] [CrossRef]
- Qiu, C.; Du, S.; Yang, J. A deep learning approach for efficient topology optimization based on the element removal strategy. Mater. Des. 2021, 212, 110179. [Google Scholar] [CrossRef]
- Rade, J.; Balu, A.; Herron, E.; Pathak, J.; Ranade, R.; Sarkar, S.; Krishnamurthy, A. Algorithmically-consistent deep learning frameworks for structural topology optimization. Eng. Appl. Artif. Intell. 2021, 106, 104483. [Google Scholar] [CrossRef]
- Yan, J.; Zhang, Q.; Xu, Q.; Fan, Z.; Li, H.; Sun, W.; Wang, G. Deep learning driven real time topology optimisation based on initial stress learning. Adv. Eng. Inform. 2022, 51, 101472. [Google Scholar] [CrossRef]
- Brown, N.; Garland, A.P.; Fadel, G.M.; Li, G. Deep Reinforcement Learning for Engineering Design Through Topology Optimization of Elementally Discretized Design Domains. Mater. Des. 2022, 218, 110672. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, Y.; Liu, P.; Luo, Y. Topological dimensionality reduction-based machine learning for efficient gradient-free 3D topology optimization. Mater. Des. 2022, 220, 110885. [Google Scholar] [CrossRef]
- Yang, X.; Bao, D.W.; Yan, X. OptiGAN: Topological Optimization in Design Form-Finding with Conditional GANs. In Proceedings of the 27th International Conference of the Association for Computer-Aided Architectural Design Research in Asia (CAADRIA) 2022, Sydney, Australia, 9–15 April 2022. [Google Scholar] [CrossRef]
- Senhora, F.V.; Chi, H.; Zhang, Y.; Mirabella, L.; Tang, T.L.E.; Paulino, G.H. Machine learning for topology optimization: Physics-based learning through an independent training strategy. Comput. Methods Appl. Mech. Eng. 2022, 398, 115116. [Google Scholar] [CrossRef]
- Kai, R.; Chao, T.; Michael, Q.; Wenjing, W. An efficient data generation method for ANN—Based surrogate models. Struct Multidiscip. Optim. 2022, 65, 90. [Google Scholar] [CrossRef]
- Sosnovik, I.; Oseledets, I. Neural networks for topology optimization. Russ. J. Numer. Anal. Math. Model. 2019, 34, 215–223. [Google Scholar] [CrossRef]
- Nie, Z.; Lin, T.; Jiang, H.; Kara, L.B. TopologyGAN: Topology optimization using generative adversarial networks based on physical fields over the initial domain. J. Mech. Des. Trans. ASME 2021, 143, 031715. [Google Scholar] [CrossRef]
- Bielecki, D.; Patel, D.; Rai, R.; Dargush, G.F. Multi-stage deep neural network accelerated topology optimization. Struct. Multidiscip. Optim. 2021, 64, 3473–3487. [Google Scholar] [CrossRef]
- Sigmund, O.; Maute, K. Topology optimization approaches: A comparative review. Struct. Multidiscip. Optim. 2013, 48, 1031–1055. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Sigmund, O. A 99 line topology optimization code written in matlab. Struct. Multidiscip. Optim. 2001, 21, 120–127. [Google Scholar] [CrossRef]
- Neofytou, A.; Yu, F.; Zhang, L.; Kim, H.A. Level Set Topology Optimization for Fluid-Structure Interactions. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; pp. 1–17. [Google Scholar] [CrossRef]
- Rozvany, G.I.N. Aims, scope, methods, history and unified terminology of computer-aided topology optimization in structural mechanics. Struct. Multidiscip. Optim. 2001, 21, 90–108. [Google Scholar] [CrossRef]
- Svanberg, K. The method of moving asymptotes—A new method for structural optimization. Int. J. Numer. Methods Eng. 1987, 24, 359–373. [Google Scholar] [CrossRef]
- Hunter, W. Topy—Topology Optimization with Python 2017. Github. Available online: https://github.com/williamhunter/topy (accessed on 16 October 2022).





| DD | DD | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Uniform | U-Net | 93.59 | 95.44 | 96.23 | 96.68 | 97.20 | 97.59 | 97.77 | 97.97 | 98.08 | 98.22 |
| Res-U-Net | 91.78 | 95.53 | 97.05 | 97.96 | 98.79 | 99.18 | 99.36 | 99.47 | 99.54 | 99.55 | |
| P(5) | U-Net | 94.03 | 95.66 | 96.20 | 96.62 | 96.99 | 97.35 | 97.52 | 97.55 | 97.65 | 97.76 |
| Res-U-Net | 93.79 | 96.73 | 97.23 | 97.58 | 98.06 | 98.36 | 98.58 | 98.74 | 98.86 | 98.95 | |
| P(10) | U-Net | 94.06 | 95.48 | 96.09 | 96.47 | 96.82 | 97.23 | 97.42 | 97.48 | 97.53 | 97.64 |
| Res-U-Net | 92.63 | 96.80 | 97.90 | 98.20 | 98.58 | 98.83 | 99.00 | 99.12 | 99.20 | 99.25 | |
| P(30) | U-Net | 93.88 | 95.96 | 96.85 | 97.19 | 97.61 | 97.83 | 98.00 | 98.19 | 98.28 | 98.42 |
| Res-U-Net | 89.88 | 95.60 | 97.22 | 98.11 | 98.89 | 99.19 | 99.36 | 99.47 | 99.54 | 99.55 |
| Models | Input | BA | MAE | MSE |
|---|---|---|---|---|
| Res-U-Net | Original input | 0.889 | 0.114 | 0.098 |
| Res-U-Net | Modified input | 0.965 | 0.037 | 0.048 |
| U-Net | Modified input | 0.974 | 0.031 | 0.022 |
| Training Parameters | Metrics | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Epoch | Layers | Min.Filters | Features | BA | IOU | MAE | MSE | ||||||||
| Train | Val | Test | Train | Val | Test | Train | Val | Test | Train | Val | Test | ||||
| 100 | 3 | 32 | VF, σ, W | 93.73 | 93.78 | 83.39 | 87.92 | 88.01 | 70.95 | 0.0793 | 0.0789 | 0.1780 | 0.0479 | 0.0478 | 0.1382 |
| 100 | 3 | 32 | VF, BC, σ, W | 93.82 | 93.82 | 83.63 | 88.09 | 88.08 | 71.34 | 0.0314 | 0.0307 | 0.1250 | 0.0194 | 0.0192 | 0.1052 |
| 100 | 3 | 32 | VF, BC, σ, W, L | 93.61 | 93.65 | 83.24 | 87.71 | 87.81 | 70.87 | 0.0587 | 0.0602 | 0.1645 | 0.0358 | 0.0370 | 0.1338 |
| 100 | 6 | 32 | VF, σ, W | 97.43 | 97.49 | 88.01 | 94.87 | 94.98 | 78.10 | 0.0783 | 0.0793 | 0.1779 | 0.0473 | 0.0473 | 0.1341 |
| 100 | 6 | 32 | VF, BC, σ, W | 97.80 | 97.83 | 89.66 | 95.59 | 95.64 | 80.88 | 0.0270 | 0.0267 | 0.1076 | 0.0167 | 0.0167 | 0.0909 |
| 100 | 6 | 32 | VF, BC, σ, W, L | 98.01 | 97.99 | 90.07 | 96.00 | 95.96 | 81.62 | 0.0572 | 0.0630 | 0.1690 | 0.0350 | 0.0383 | 0.1372 |
| 100 | 3 | 64 | VF, σ, W | 95.31 | 95.18 | 84.31 | 90.83 | 90.59 | 72.32 | 0.0810 | 0.0805 | 0.1796 | 0.0489 | 0.0488 | 0.1390 |
| 100 | 3 | 64 | VF, BC, σ, W | 95.43 | 95.00 | 83.93 | 91.05 | 90.25 | 71.81 | 0.0245 | 0.0254 | 0.1027 | 0.0153 | 0.0155 | 0.0881 |
| 100 | 3 | 64 | VF, BC, σ, W, L | 95.69 | 95.47 | 84.32 | 91.53 | 91.11 | 72.32 | 0.0540 | 0.0557 | 0.1655 | 0.0331 | 0.0351 | 0.1329 |
| 300 | 6 | 64 | VF, σ, W | 98.22 | 98.06 | 88.06 | 96.43 | 96.10 | 78.21 | 0.0210 | 0.0229 | 0.1220 | 0.0135 | 0.0149 | 0.1081 |
| 300 | 6 | 64 | VF, BC, σ, W | 98.37 | 98.20 | 89.47 | 96.72 | 96.37 | 80.54 | 0.0194 | 0.0209 | 0.1088 | 0.0125 | 0.0142 | 0.0931 |
| 300 | 6 | 64 | VF, BC, σ, W, L | 98.97 | 98.64 | 89.61 | 97.92 | 97.25 | 80.80 | 0.0124 | 0.0155 | 0.1052 | 0.0080 | 0.0110 | 0.0964 |
| Experiment | Test | Train | Validation | ||||||
|---|---|---|---|---|---|---|---|---|---|
| BA | MAE | MSE | BA | MAE | MSE | BA | MAE | MSE | |
| 2D | 96.67 | 0.0461 | 0.0241 | 96.72 | 0.0449 | 0.0239 | 96.84 | 0.0441 | 0.0229 |
| 3D | 93.22 | 0.0795 | 0.0513 | 94.01 | 0.0733 | 0.0450 | 93.94 | 0.0737 | 0.0457 |
| ID | Data Distribution | Depth | Filters on Each Layer | Accuracy after 5th Iteration of SIMP |
|---|---|---|---|---|
| 1 | Uniform [1–100] | 3 | 16, 32, 64, 64, 32, 16 | 93.59 |
| 2 | Poisson (5) | 3 | 16, 32, 64, 64, 32, 16 | 94.03 |
| 3 | Poisson (10) | 3 | 16, 32, 64, 64, 32, 16 | 94.06 |
| 4 | Poisson (30) | 3 | 16, 32, 64, 64, 32, 16 | 93.88 |
| 5 | Uniform [1–100] | 4 | 16, 32, 64, 128, 128, 64, 32, 16 | 93.78 |
| 6 | Poisson (5) | 4 | 16, 32, 64, 128, 128, 64, 32, 16 | 94.08 |
| 7 | Poisson (10) | 4 | 16, 32, 64, 128, 128, 64, 32, 16 | 93.98 |
| 8 | Poisson (30) | 4 | 16, 32, 64, 128, 128, 64, 32, 16 | 93.53 |
| Experiment # | Depth | Min. Filters | Accuracy |
|---|---|---|---|
| 1 | 3 | 32 | 83.63 |
| 2 | 6 | 32 | 90.07 |
| 3 | 3 | 64 | 84.32 |
| 4 | 6 | 64 | 89.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasulzade, J.; Rustamov, S.; Akhmetov, B.; Maksum, Y.; Nogaibayeva, M. Computational Acceleration of Topology Optimization Using Deep Learning. Appl. Sci. 2023, 13, 479. https://doi.org/10.3390/app13010479
Rasulzade J, Rustamov S, Akhmetov B, Maksum Y, Nogaibayeva M. Computational Acceleration of Topology Optimization Using Deep Learning. Applied Sciences. 2023; 13(1):479. https://doi.org/10.3390/app13010479
Chicago/Turabian StyleRasulzade, Jalal, Samir Rustamov, Bakytzhan Akhmetov, Yelaman Maksum, and Makpal Nogaibayeva. 2023. "Computational Acceleration of Topology Optimization Using Deep Learning" Applied Sciences 13, no. 1: 479. https://doi.org/10.3390/app13010479
APA StyleRasulzade, J., Rustamov, S., Akhmetov, B., Maksum, Y., & Nogaibayeva, M. (2023). Computational Acceleration of Topology Optimization Using Deep Learning. Applied Sciences, 13(1), 479. https://doi.org/10.3390/app13010479






