Parametric Study on Analyzing the Effect of Soil–Cement Strength on the Uplifting Behavior of HSCM Piles Installed in Marine Soft Clay
Abstract
1. Introduction
2. Materials and Methods
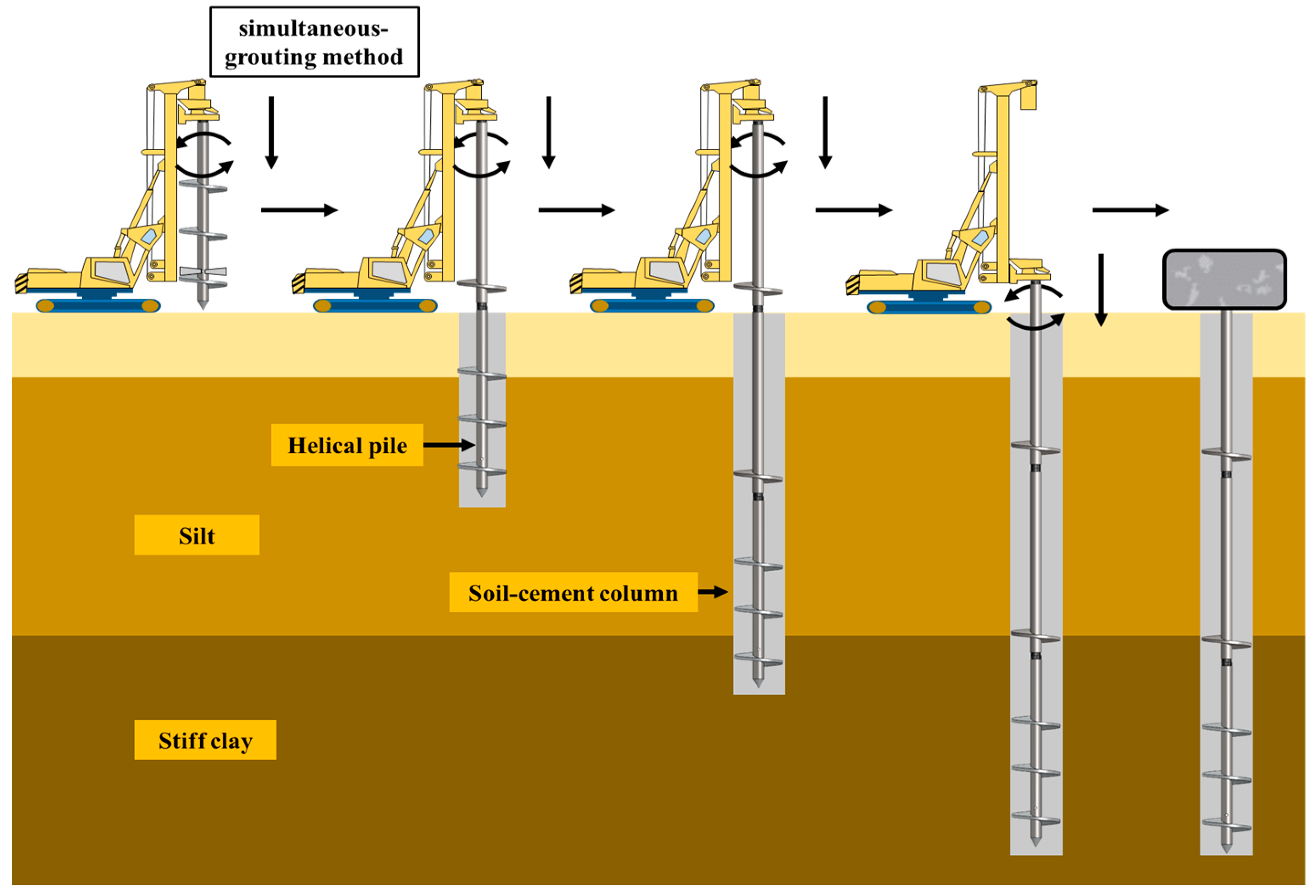
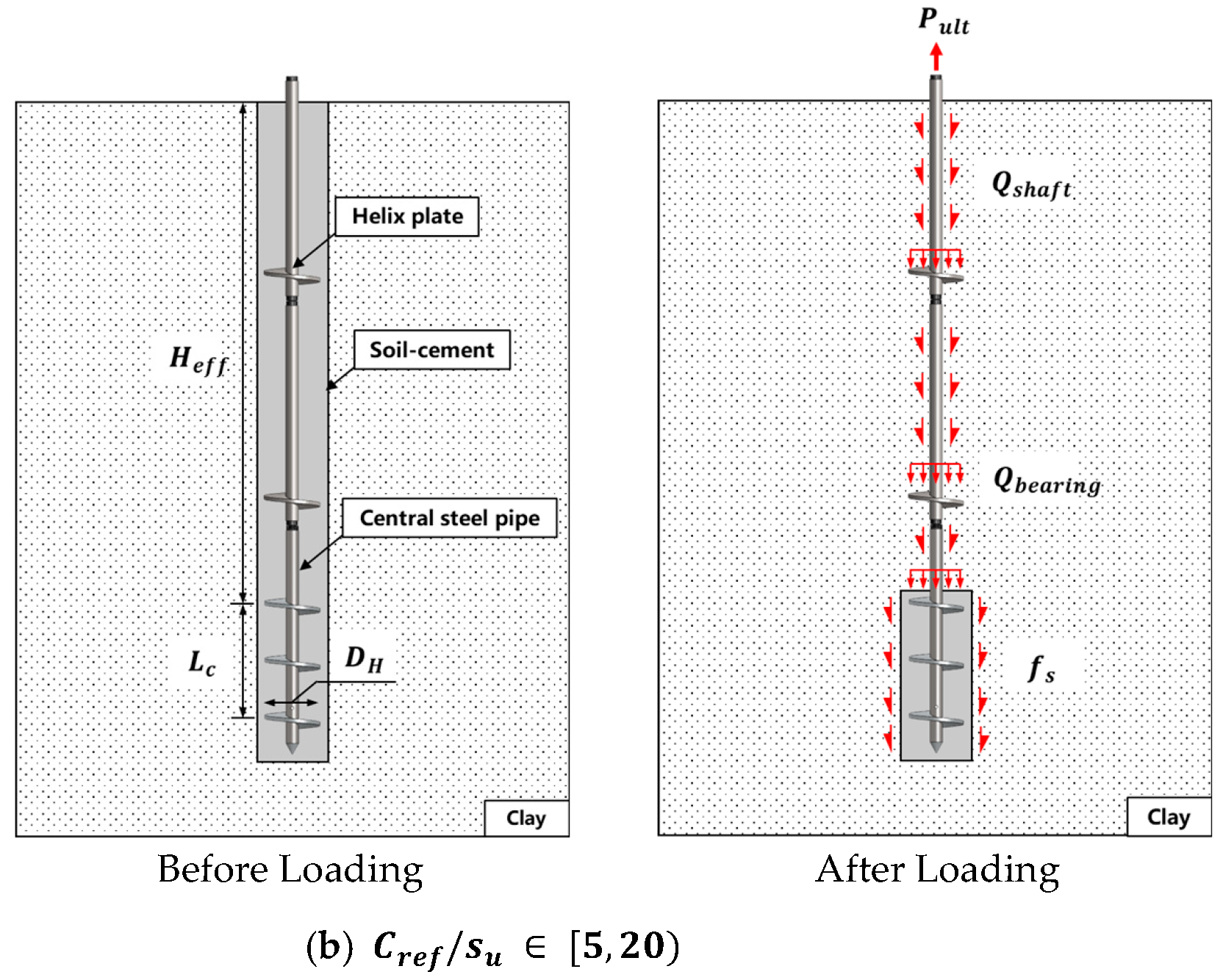
2.1. Experimental Parameters
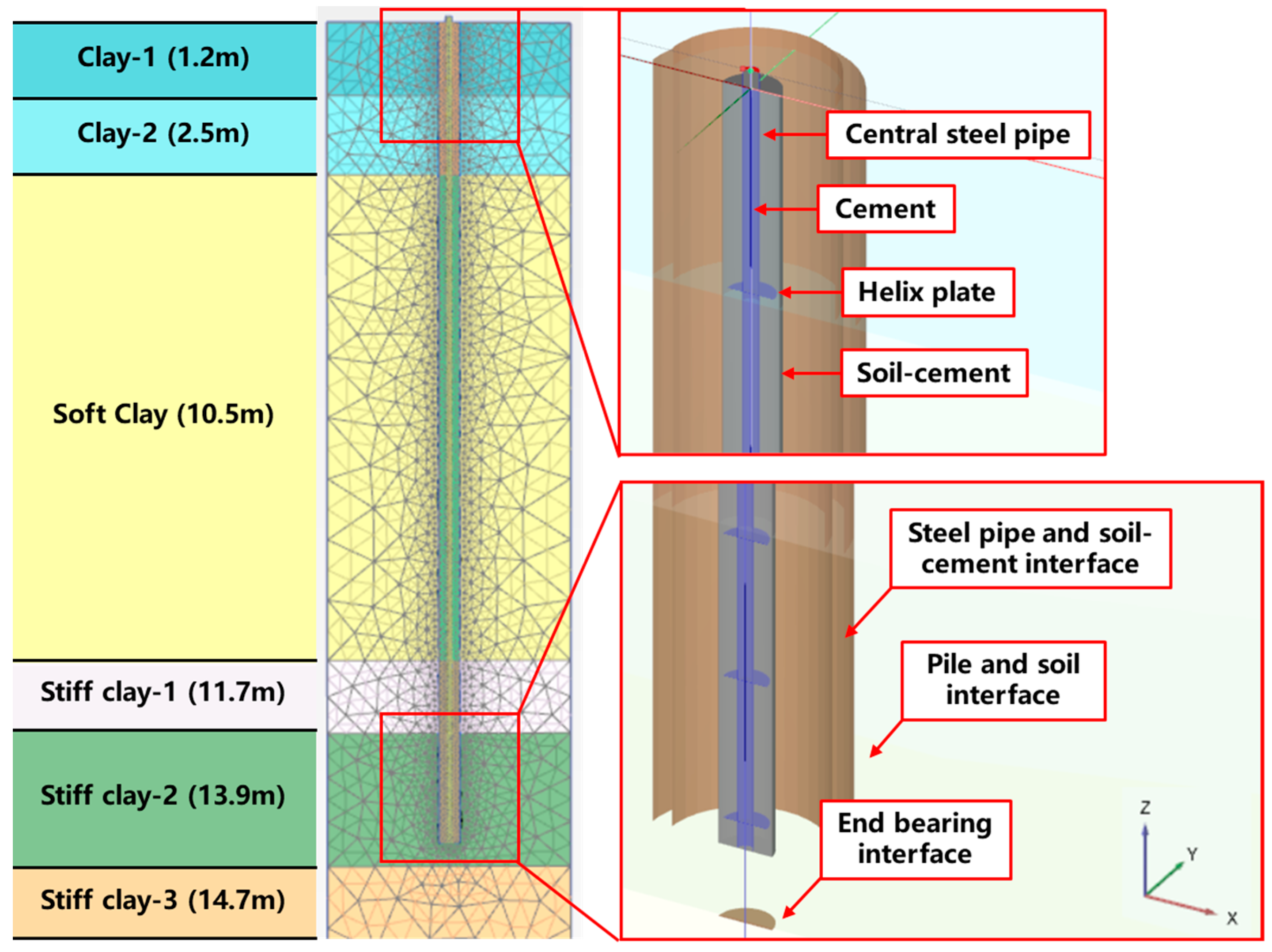
2.2. The FEM Parameters
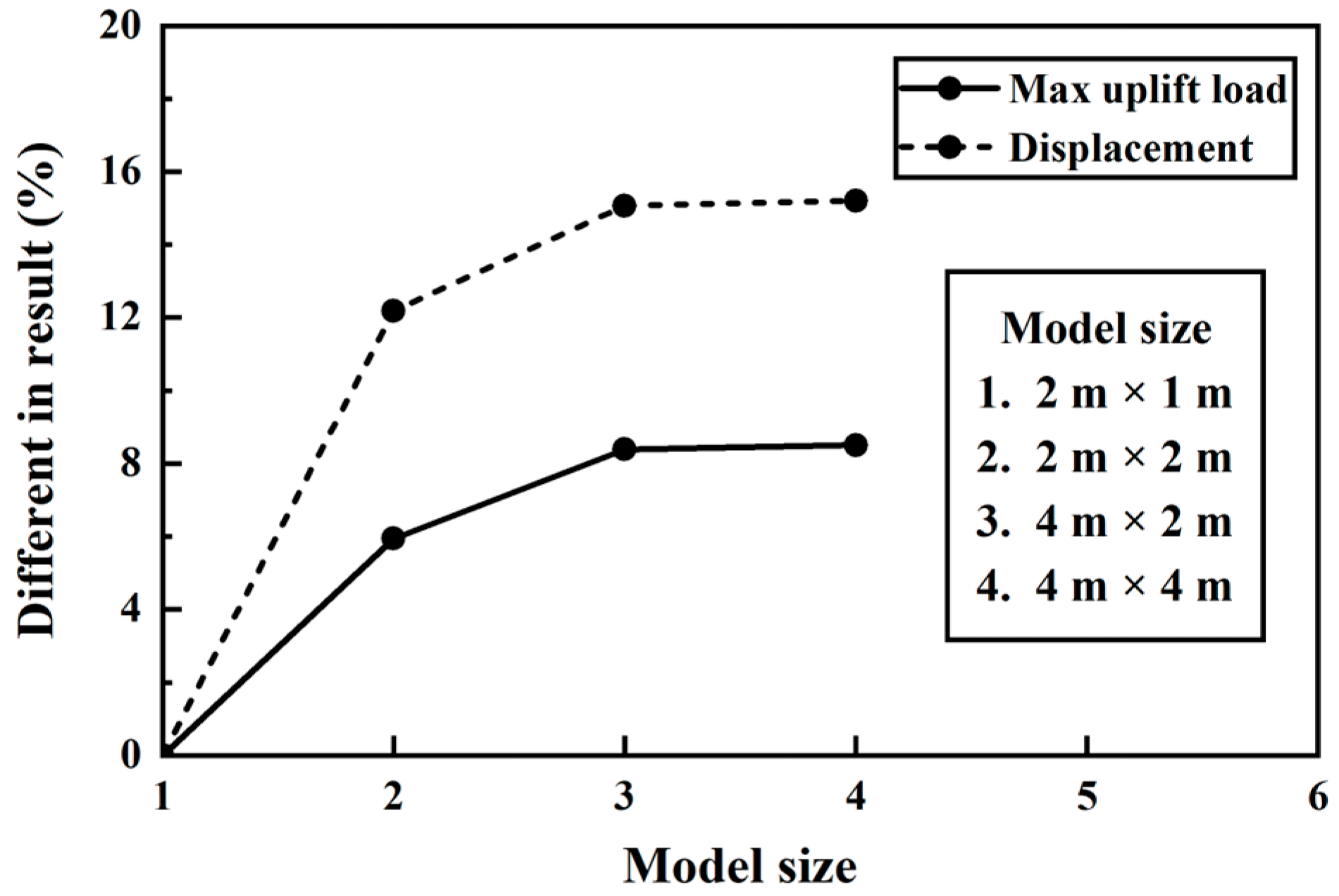
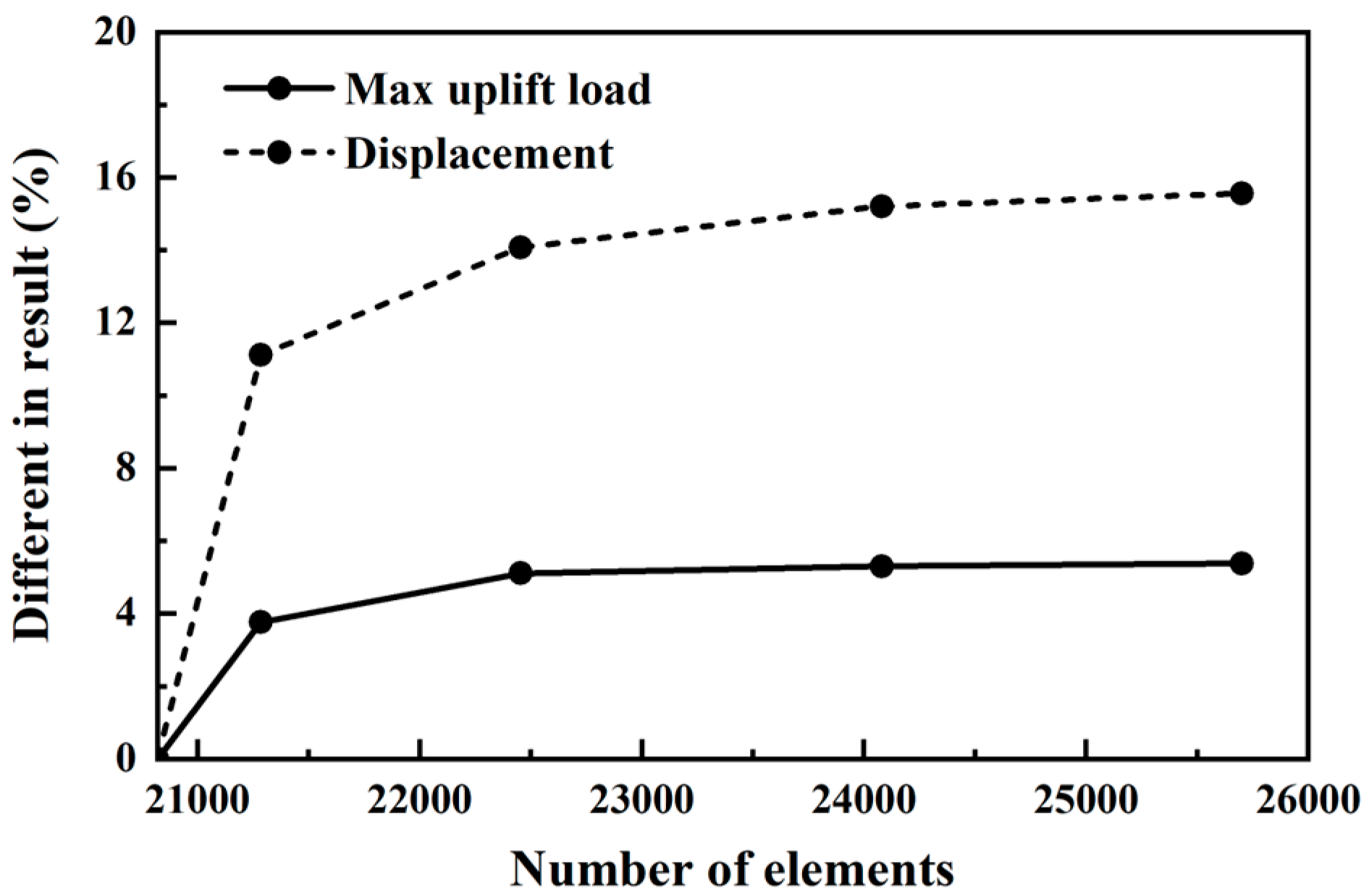
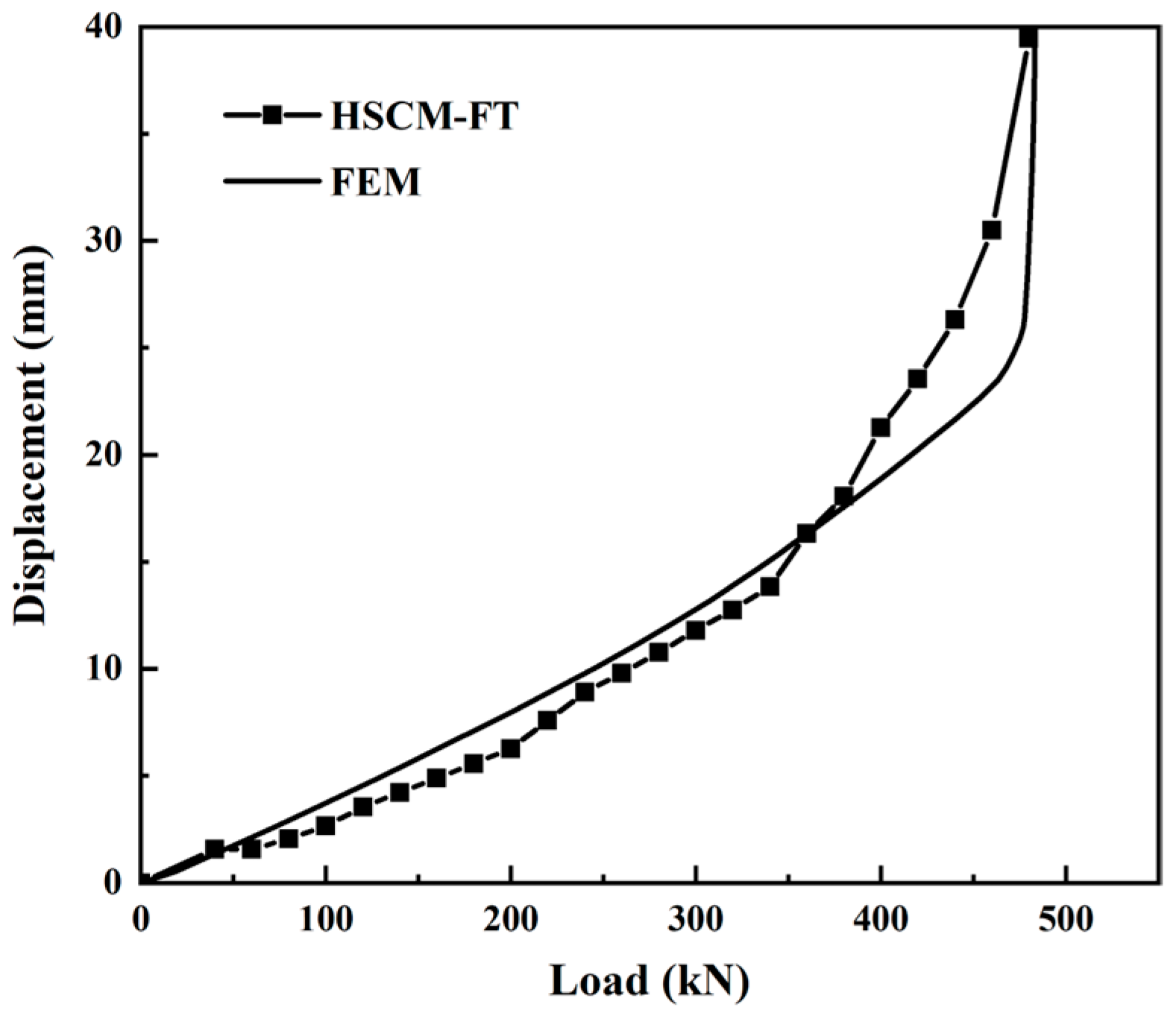
2.3. The FEM Verification
2.4. Numerical Simulation Schemes
3. Results and Discussion
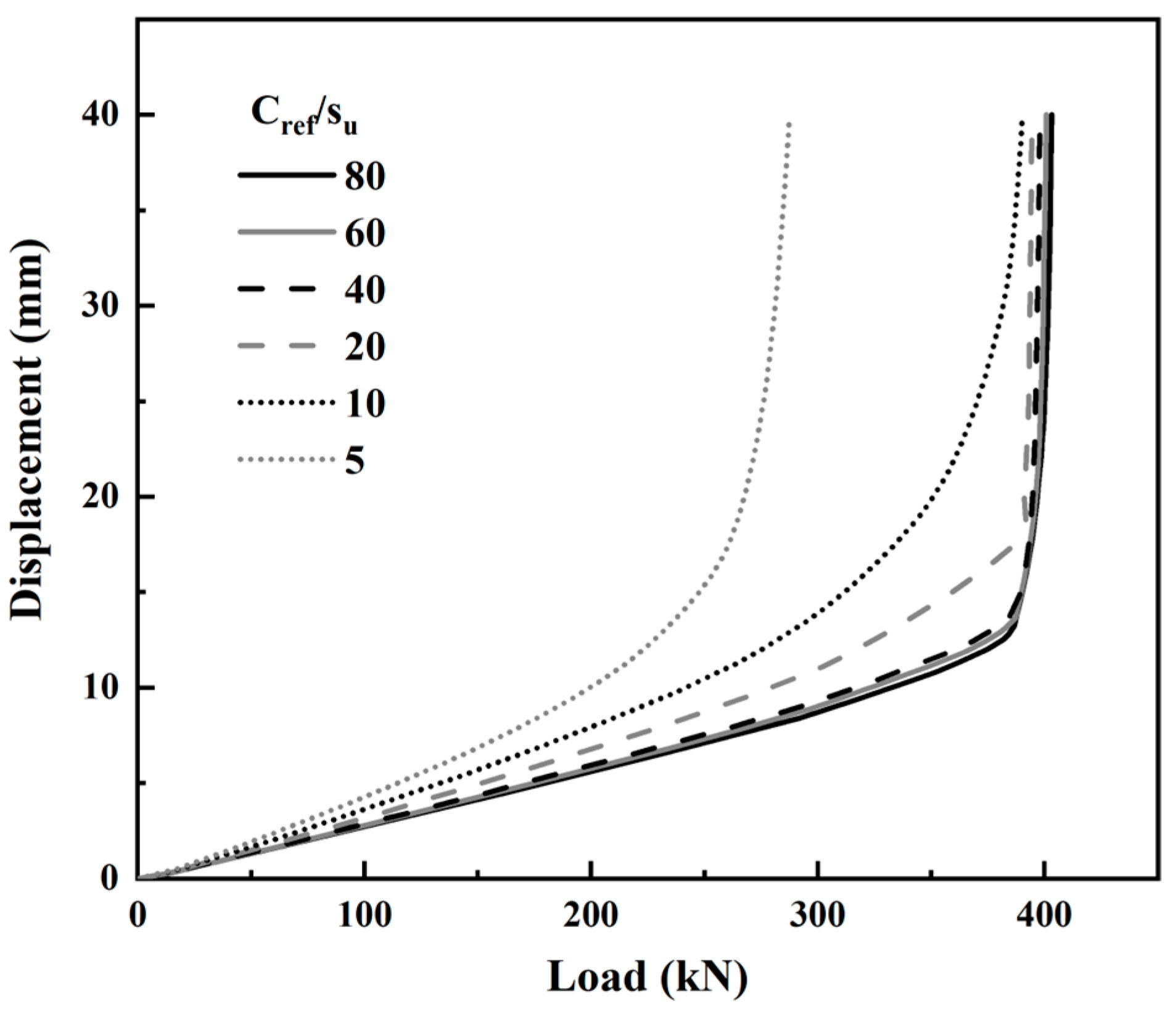
3.1. Load–Settlement Curves
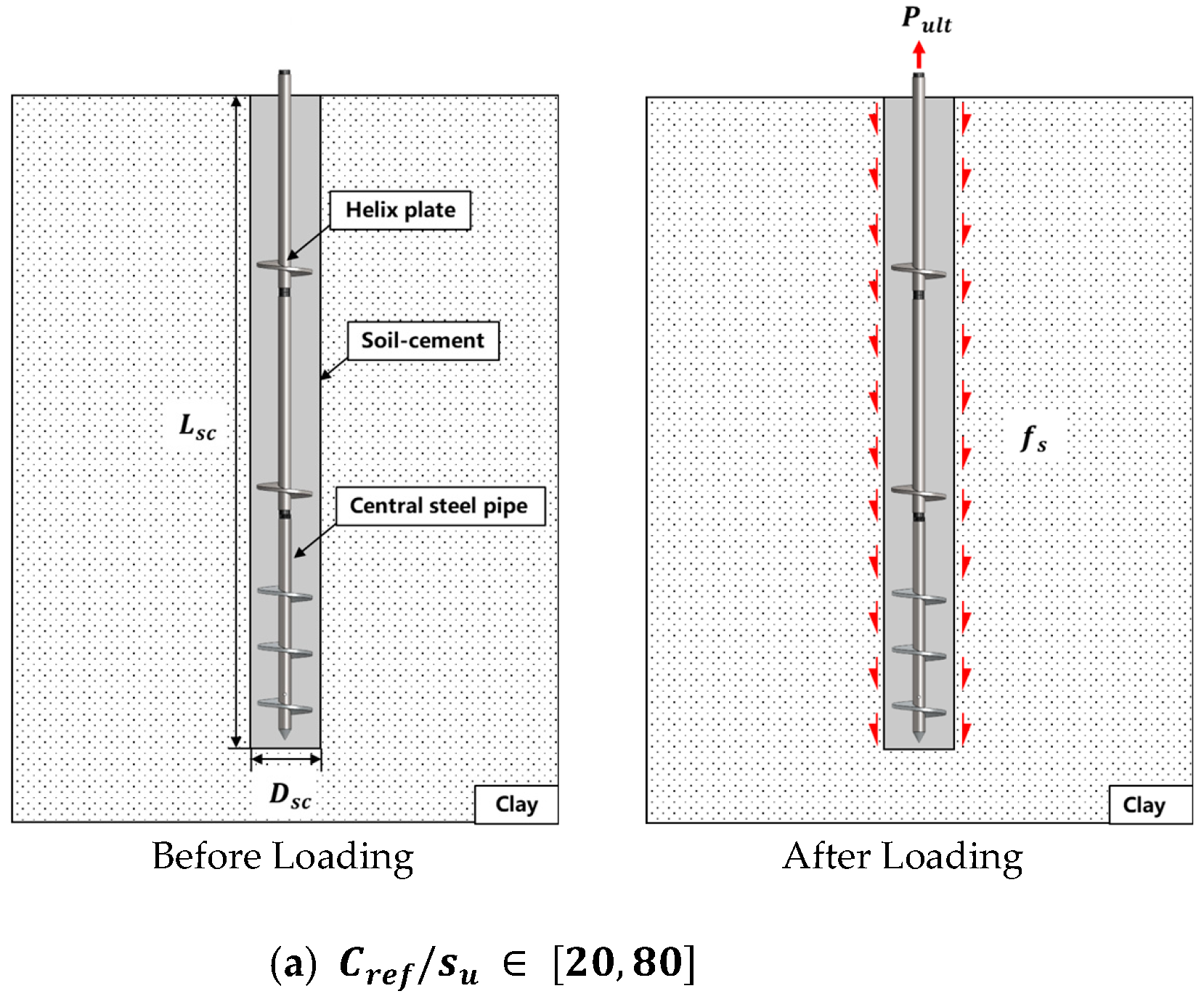
3.2. Pile Failure Mode
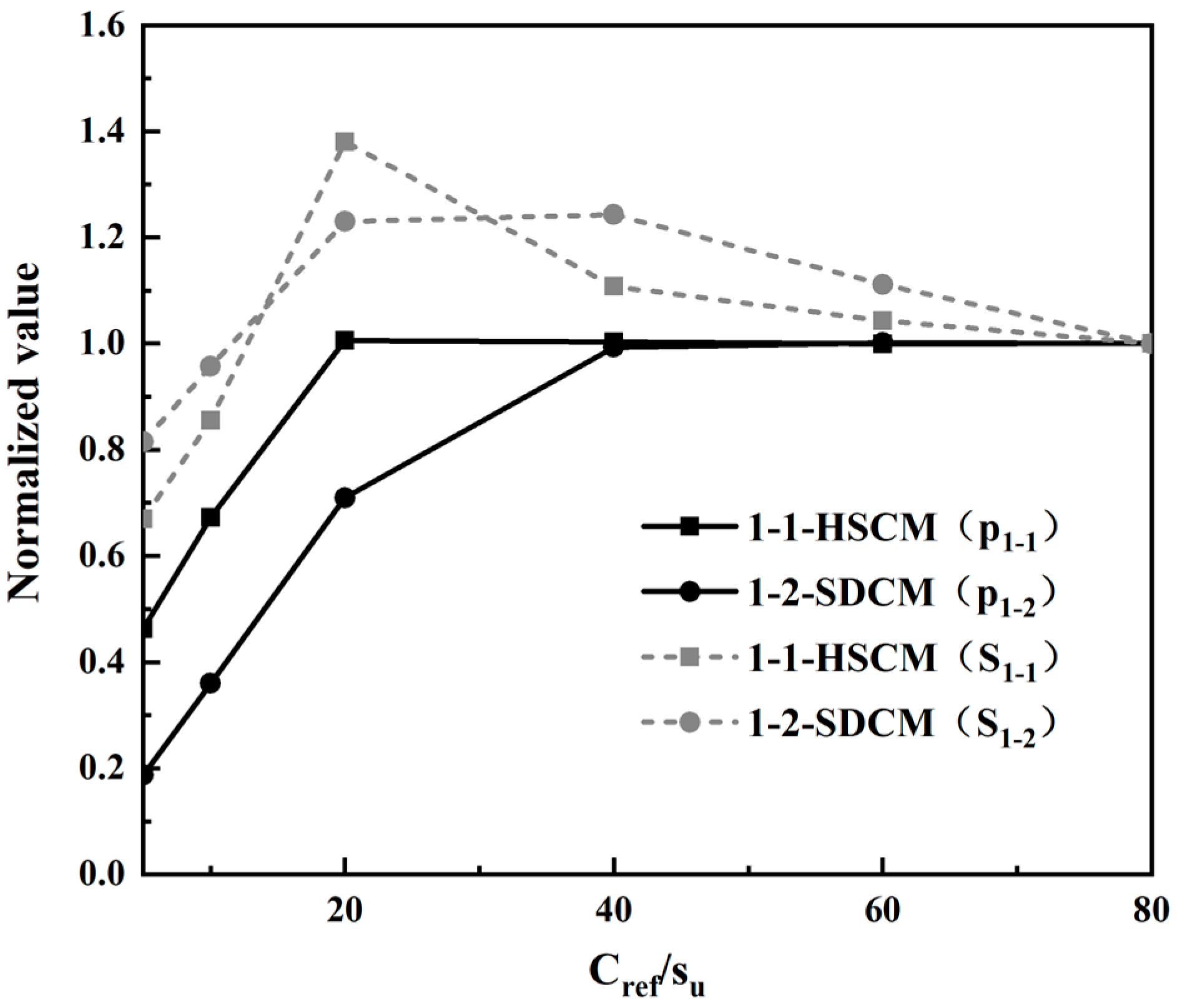
3.3. Patterns of Variation in Ultimate Bearing Capacity
3.4. Theoretical Calculation of the Ultimate Bearing Capacity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhu, S.; Chen, C.; Cai, H.; Mao, F. Analytical modeling for the load-transfer behavior of stiffened deep cement mixing (SDCM) pile with rigid cap in layer soils. Comput. Geotech. 2022, 144, 104618. [Google Scholar] [CrossRef]
- Wonglert, A.; Jongpradist, P.; Jamsawang, P.; Larsson, S. Bearing capacity and failure behaviors of floating stiffened deep cement mixing columns under axial load. Soils Found. 2018, 58, 446–461. [Google Scholar] [CrossRef]
- Voottipruex, P.; Bergado, D.; Suksawat, T.; Jamsawang, P.; Cheang, W. Behavior and simulation of deep cement mixing (DCM) and stiffened deep cement mixing (SDCM) piles under full scale loading. Soils Found. 2011, 51, 307–320. [Google Scholar] [CrossRef]
- Mansour, M.A.; El Naggar, M.H. Optimization of grouting method and axial performance of pressure grouted helical piles. Can. Geotech. J. 2021, 59, 702–714. [Google Scholar] [CrossRef]
- Zhou, J.-J.; Wang, K.-H.; Gong, X.-N.; Zhang, R.-H. Bearing capacity and load transfer mechanism of a static drill rooted nodular pile in soft soil areas. J. Zhejiang Univ. Sci. A 2013, 14, 705–719. [Google Scholar] [CrossRef]
- Vickars, R.A.; Clemence, S.P. Performance of helical piles with grouted shafts. In New Technological and Design Developments in Deep Foundations; Dennis, N.D.J., Castelli, R., O’Neill, M.W., Eds.; American Society of Civil Engineers: Reston, VA, USA, 2000; pp. 327–341. [Google Scholar]
- Khazaei, J.; Eslami, A. Postgrouted helical piles behavior through physical modeling by FCV. Mar. Georesources Geotechnol. 2017, 35, 528–537. [Google Scholar] [CrossRef]
- Mansour, M.A. Performance of Pressure Grouted Helical Piles Under Monotonic Axial and Lateral Loading. Ph.D. Thesis, The University of Western Ontario, London, ON, Canada, 2019. [Google Scholar]
- Shariat, M.; Shariati, M.; Madadi, A.; Wakil, K. Computational Lagrangian Multiplier Method by using for optimization and sensitivity analysis of rectangular reinforced concrete beams. Steel Compos. Struct. 2018, 29, 243–256. [Google Scholar]
- Nabizadeh, F.; Choobbasti, A.J. Field study of capacity helical piles in sand and silty clay. Transp. Infrastruct. Geotechnol. 2017, 4, 3–17. [Google Scholar] [CrossRef]
- Nabizadeh, F.; Choobbasti, A.J. The performance of grouted and un-grouted helical piles in sand. Int. J. Geotech. Eng. 2017, 13, 516–524. [Google Scholar] [CrossRef]
- Zhuang, X.; Zong, Z.; Huang, Y.; Wang, P. Analysis of the installation effect on the axial performance of pressure-grouted helical piles in clay by small-scale model tests. Buildings 2022, 12, 992. [Google Scholar] [CrossRef]
- Srijaroen, C.; Hoy, M.; Horpibulsuk, S.; Rachan, R.; Arulrajah, A. soil–cement screw pile: Alternative pile for low- and medium-rise buildings in soft Bangkok clay. J. Constr. Eng. Manag. 2021, 147, 04020173. [Google Scholar] [CrossRef]
- Madadi, A.; Eskandari-Naddaf, H.; Gharouni-Nik, M. Lightweight ferrocement matrix compressive behavior: Experiments versus finite element analysis. Arab. J. Sci. Eng. 2017, 42, 4001–4013. [Google Scholar] [CrossRef]
- Madadi, A.; Tasdighi, M.; Eskandari-Naddaf, H. Structural response of ferrocement panels incorporating lightweight expanded clay and perlite aggregates: Experimental, theoretical and statistical analysis. Eng. Struct. 2019, 188, 382–393. [Google Scholar] [CrossRef]
- Dong, P.; Qin, R.; Chen, Z. Bearing capacity and settlement of concrete-cored DCM pile in soft ground. Geotech. Geol. Eng. 2004, 22, 105–119. [Google Scholar] [CrossRef]
- Mohajerani, A.; Bosnjak, D.; Bromwich, D. Analysis and design methods of screw piles: A review. Soils Found. 2016, 56, 115–128. [Google Scholar] [CrossRef]
- Spagnoli, G.; de Hollanda Cavalcanti Tsuha, C. A review on the behavior of helical piles as a potential offshore foundation system. Mar. Georesour. Geotechnol. 2020, 38, 1013–1036. [Google Scholar] [CrossRef]
- Bagheri, F.; El Naggar, M. Effects of installation disturbance on behavior of multi-helix piles in structured clays. DFI J.-J. Deep. Found. Inst. 2015, 9, 80–91. [Google Scholar] [CrossRef]
- Lutenegger, A.J. Cylindrical shear or plate bearing?—Uplift behavior of multi-helix screw anchors in clay. In Contemporary Topics in Deep Foundations; American Society of Civil Engineers: Reston, VA, USA, 2009; pp. 456–463. [Google Scholar]
- Huang, Y.; Zhuang, X.; Wang, P.; Zong, Z. Axial behavior of pressure grouted helical piles installed in marine soft clay based on full-scale field tests. Geotech. Geol. Eng. 2022, 40, 5799–5812. [Google Scholar] [CrossRef]
- Zhou, J.; Yu, J.; Gong, X.; El Naggar, M.H.; Zhang, R. The effect of cemented soil strength on the frictional capacity of precast concrete pile–cemented soil interface. Acta Geotech. 2020, 15, 3271–3282. [Google Scholar] [CrossRef]
- Wu, D.; Liu, H.-L.; Kong, G.-Q.; Ng, C.W.W.; Cheng, X.-H. Displacement response of an energy pile in saturated clay. Proc. Inst. Civ. Eng.-Geotech. Eng. 2018, 171, 285–294. [Google Scholar] [CrossRef]




| Soil Layer | Weight kN/m3 | Compression Modulus | Undrained Shear Strength |
|---|---|---|---|
| Clay-1 | 18.40 | 3450 | 26.17 |
| Clay-2 | 19.47 | 5320 | 27.16 |
| Silt | 16.57 | 1790 | 5.68 |
| Stiff clay-1 | 20.47 | 9860 | 102.00 |
| Stiff clay-2 | 20.65 | 10,000 | 114.36 |
| Stiff clay-3 | 20.08 | 9360 | 227.70 |
| Interface | Elastic Modulus | ||
|---|---|---|---|
| Pile and soil-1 | 84.8 × 103 | 424 | 42.4 |
| Pile and soil-2 | 19.2 × 103 | 96 | 9.6 |
| Pile and soil-3 | 34.6 × 104 | 1728 | 172.8 |
| Steel pipe and soil–cement-1 | 84.8 × 103 | 424 | 42.4 |
| Steel pipe and soil–cement-2 | 19.2 × 103 | 96 | 9.6 |
| Steel pipe and soil–cement-3 | 34.6 × 104 | 1728 | 172.8 |
| Pile Type | ID | Dsc (m) | |
|---|---|---|---|
| HSCM | HSCM-1-1 | 5, 10, 20, 40, 60, 80 | 0.32 |
| SDCM | SDCM-1-2 | 5, 10, 20, 40, 60, 80 | 0.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, X.; Zong, Z.; Huang, Y.; Wang, C.; Lin, X. Parametric Study on Analyzing the Effect of Soil–Cement Strength on the Uplifting Behavior of HSCM Piles Installed in Marine Soft Clay. Appl. Sci. 2023, 13, 330. https://doi.org/10.3390/app13010330
Zhuang X, Zong Z, Huang Y, Wang C, Lin X. Parametric Study on Analyzing the Effect of Soil–Cement Strength on the Uplifting Behavior of HSCM Piles Installed in Marine Soft Clay. Applied Sciences. 2023; 13(1):330. https://doi.org/10.3390/app13010330
Chicago/Turabian StyleZhuang, Xiaoxuan, Zhongling Zong, Yunhan Huang, Chushu Wang, and Xiangjun Lin. 2023. "Parametric Study on Analyzing the Effect of Soil–Cement Strength on the Uplifting Behavior of HSCM Piles Installed in Marine Soft Clay" Applied Sciences 13, no. 1: 330. https://doi.org/10.3390/app13010330
APA StyleZhuang, X., Zong, Z., Huang, Y., Wang, C., & Lin, X. (2023). Parametric Study on Analyzing the Effect of Soil–Cement Strength on the Uplifting Behavior of HSCM Piles Installed in Marine Soft Clay. Applied Sciences, 13(1), 330. https://doi.org/10.3390/app13010330







