Study on Mechanical Properties of Simply-Supported Composite Beams Considering Creep and Slip
Abstract
1. Introduction
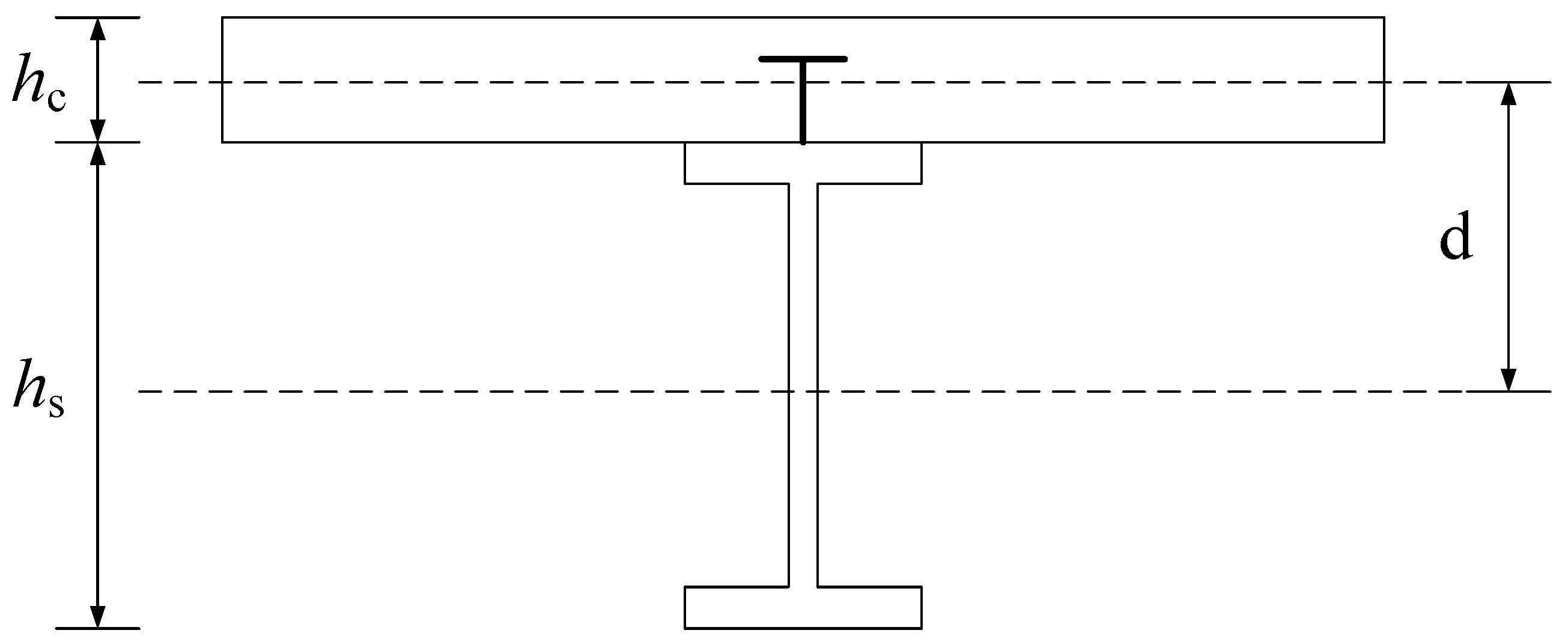
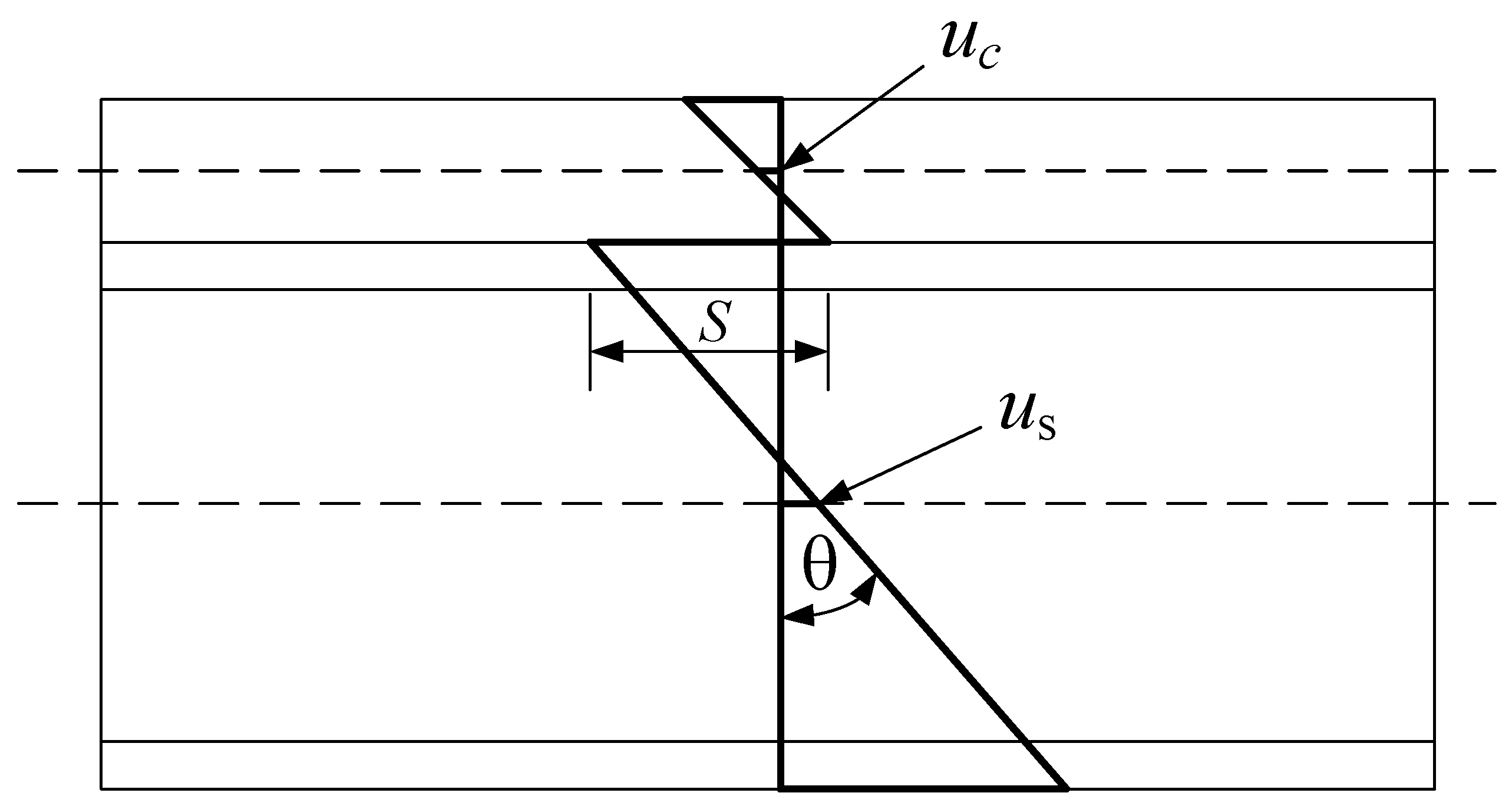
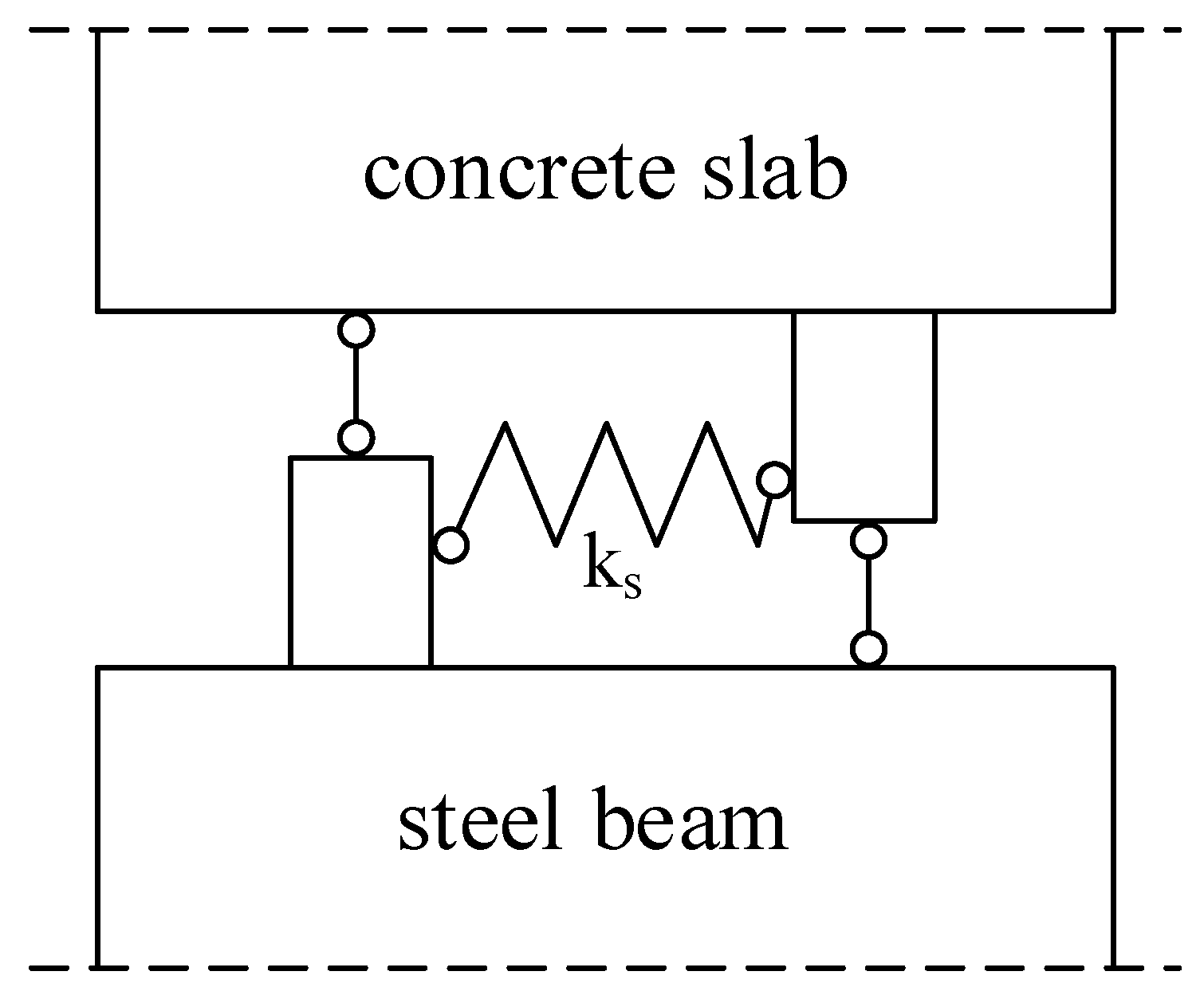
2. Coupling Analysis Considering the Slip and Creep Effect
- The concrete bridge deck and steel beam cross-sections are in accordance with the plane section assumption, and the shear connectors are equivalent to uniform continuous elastic media.
- The stress–strain relationship between the steel beam and concrete in the whole stress stage is linear, and the concrete is not cracked and spalls in the whole stress stage.
- We ignore the steel–concrete composite beam lift phenomenon. Without considering the transverse deformation, the curvatures of the concrete bridge deck and steel beam are equal.
- The influence of the shear-lag effect of the bridge deck on the deflection of the steel-concrete composite beam is ignored.
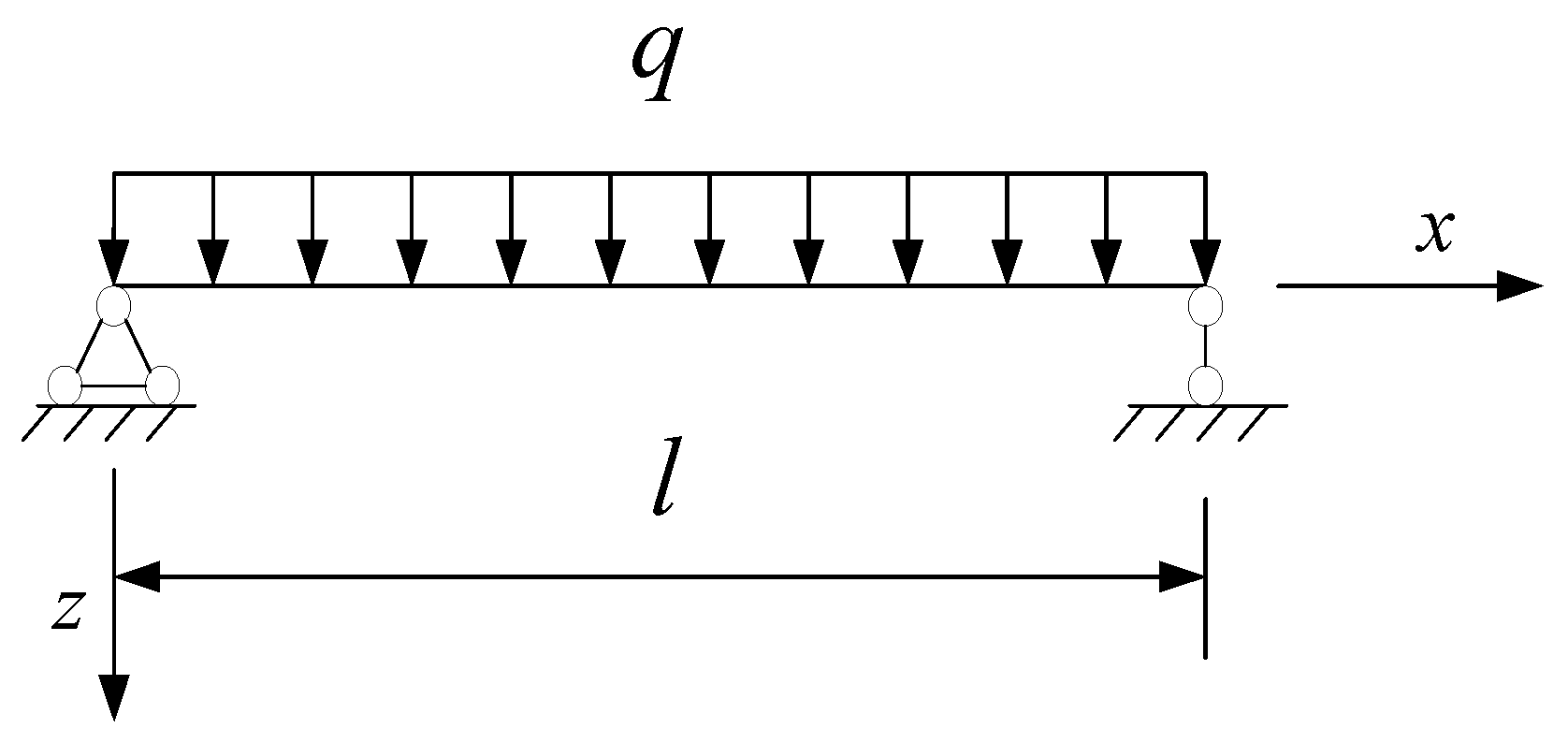
2.1. Analytical Solution of Axial Force
2.2. Analytical Solution of Deflection
2.3. Analytical Solution of Slip
3. ANSYS Finite Element Software Modeling Analysis
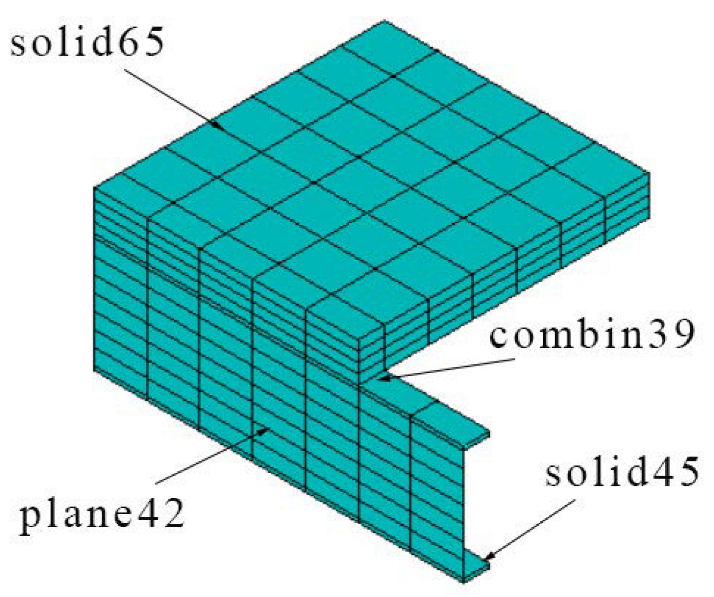
3.1. Selection of Modeling Unit
3.2. Implicit Creep Method
- (1)
- TBOPT = 1 Initial creep equation
- (2)
- TBOPT = 6 Initial creep equation
- (3)
- TBOPT = 11 Initial creep equation + second-order creep equation
4. Analysis of the Result
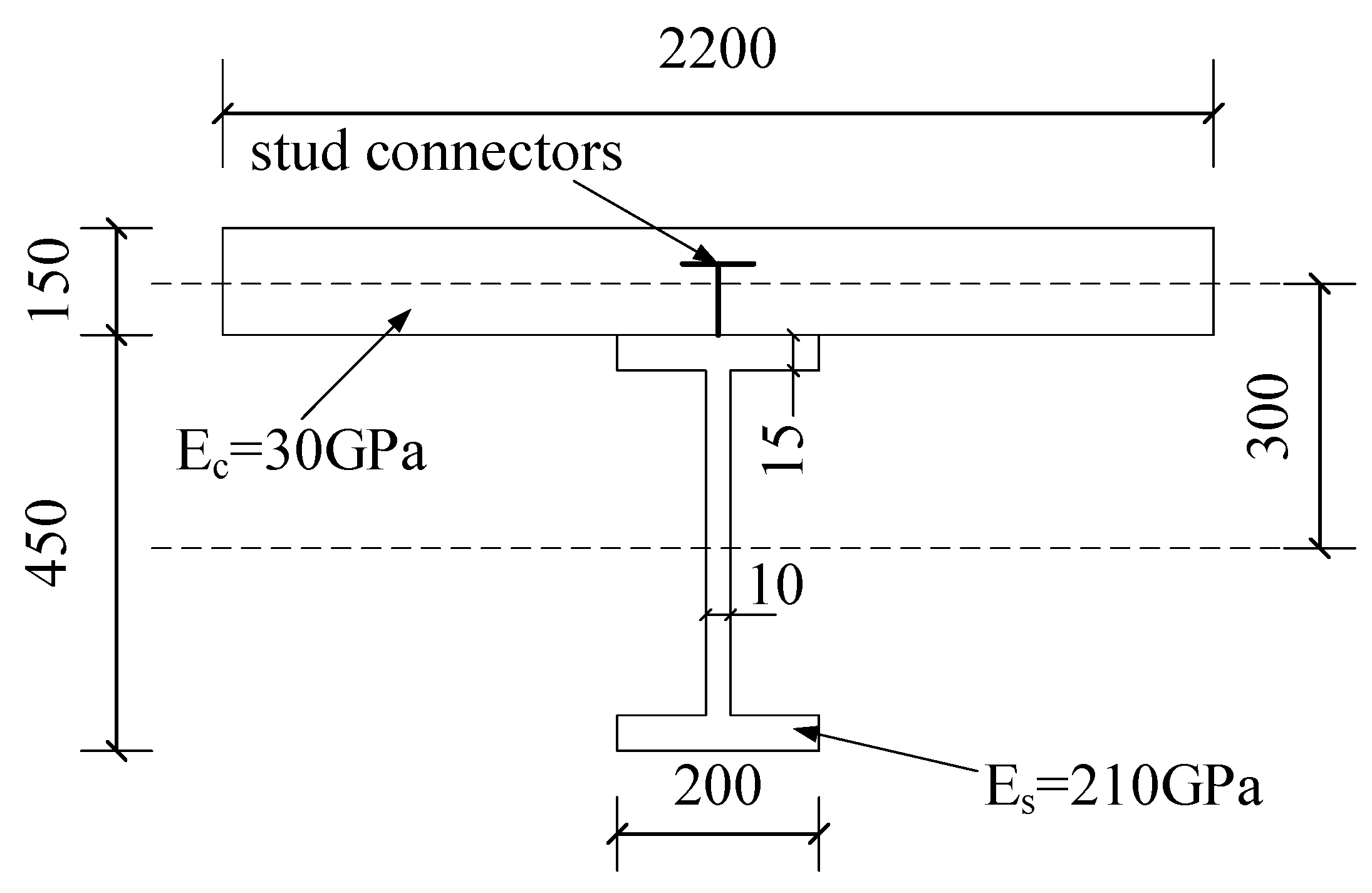
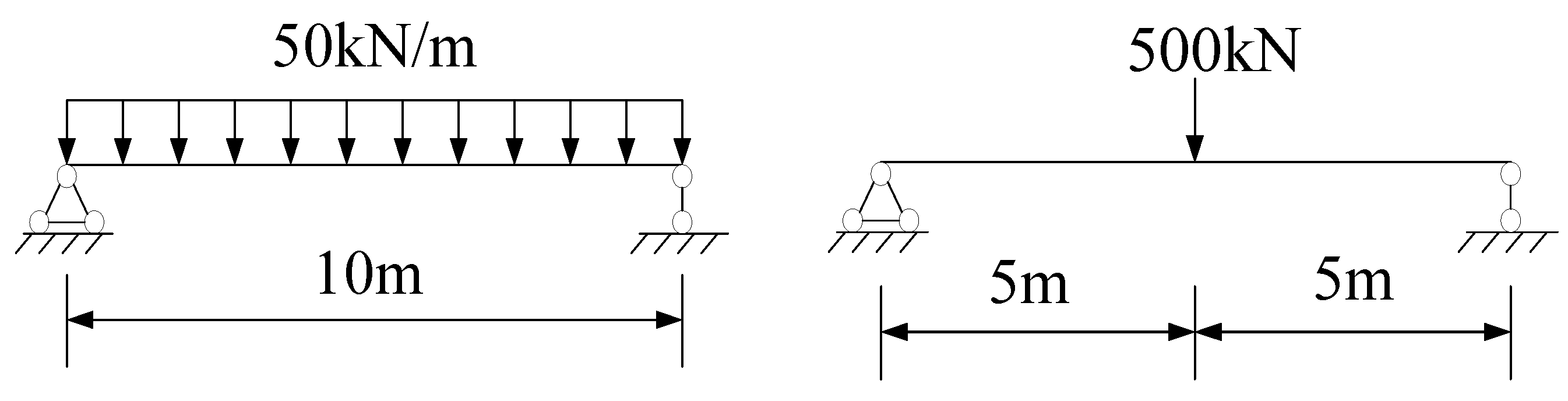
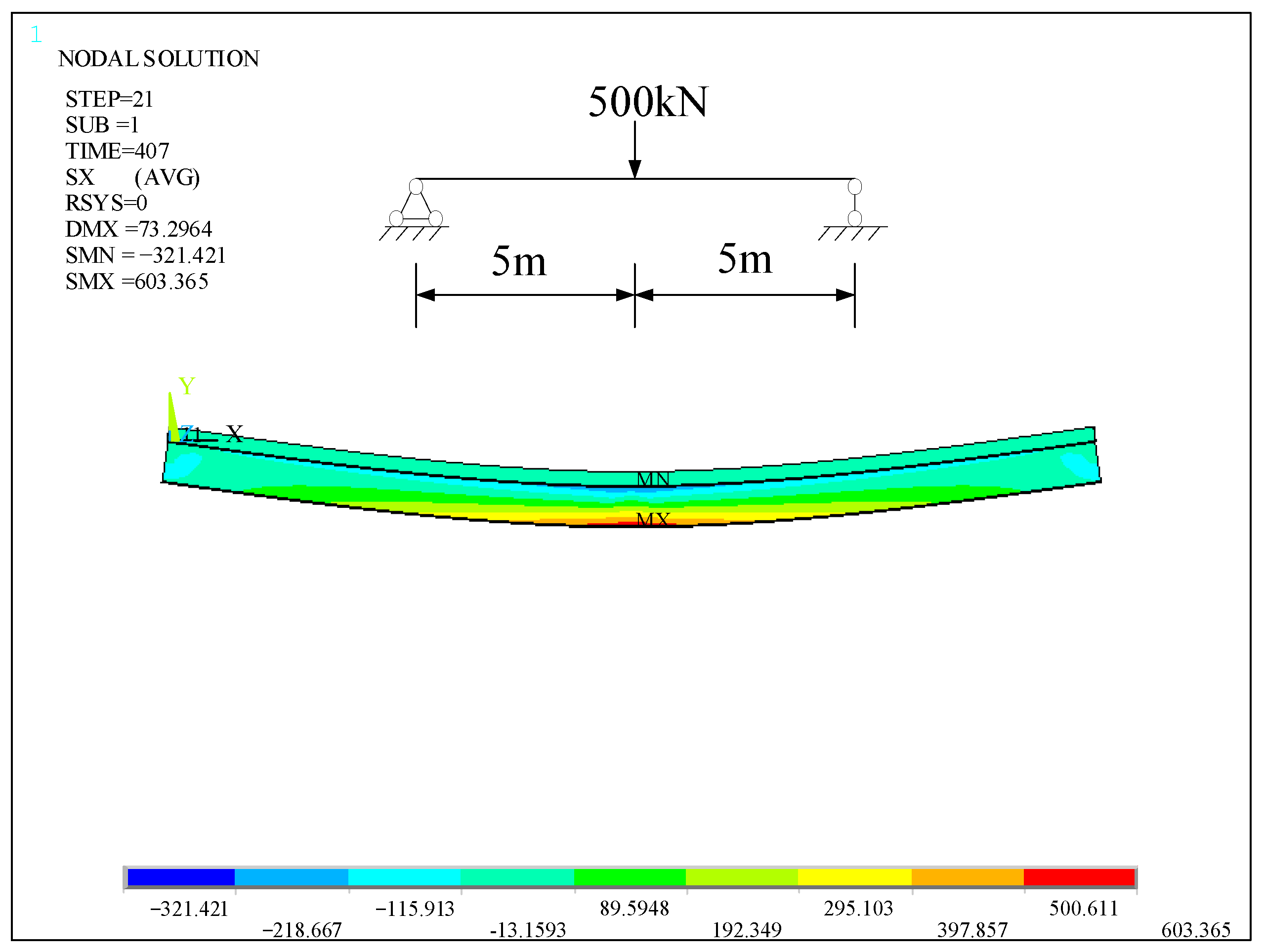
4.1. Example Model
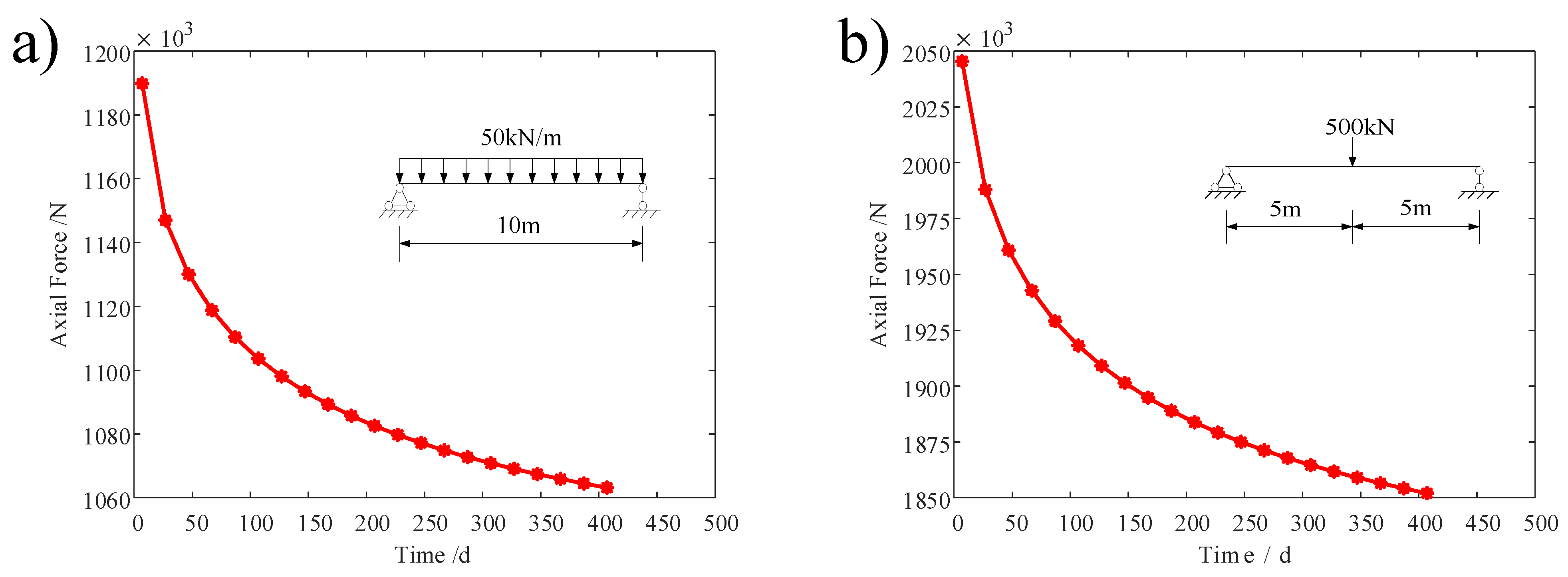
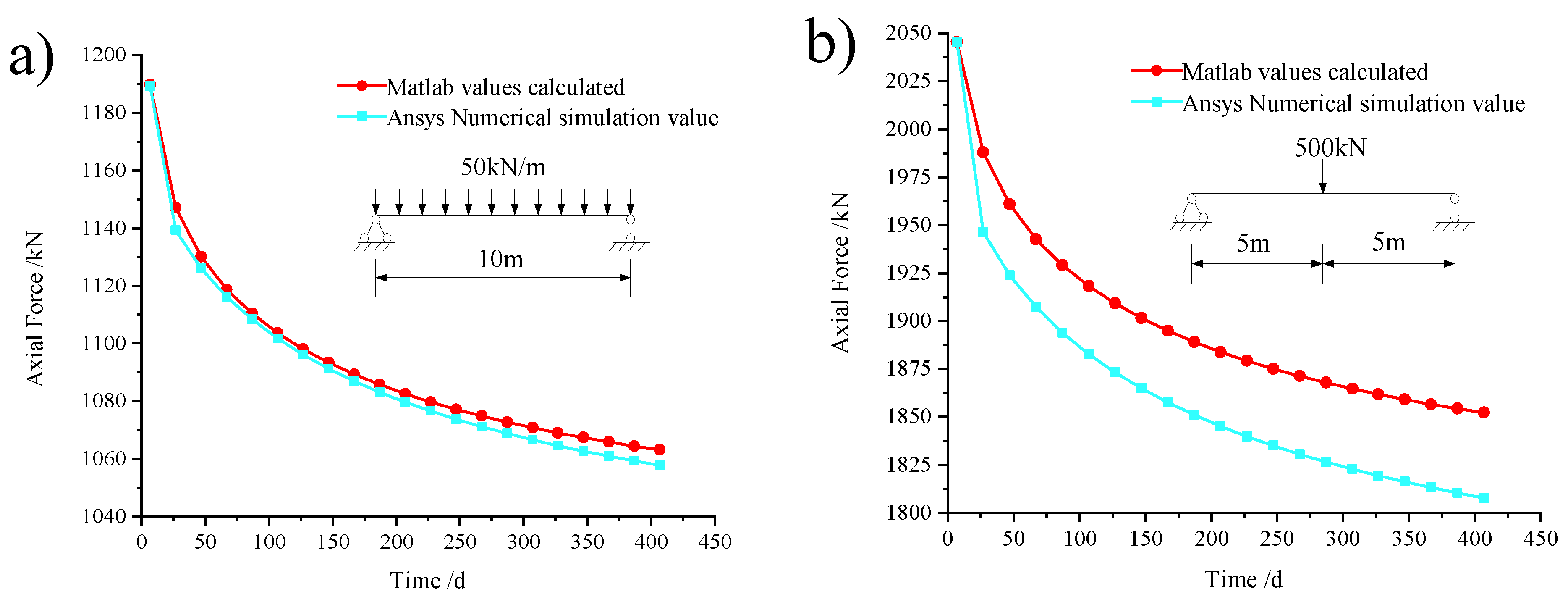
4.2. Comparison of Axial Force under Different Load Situations
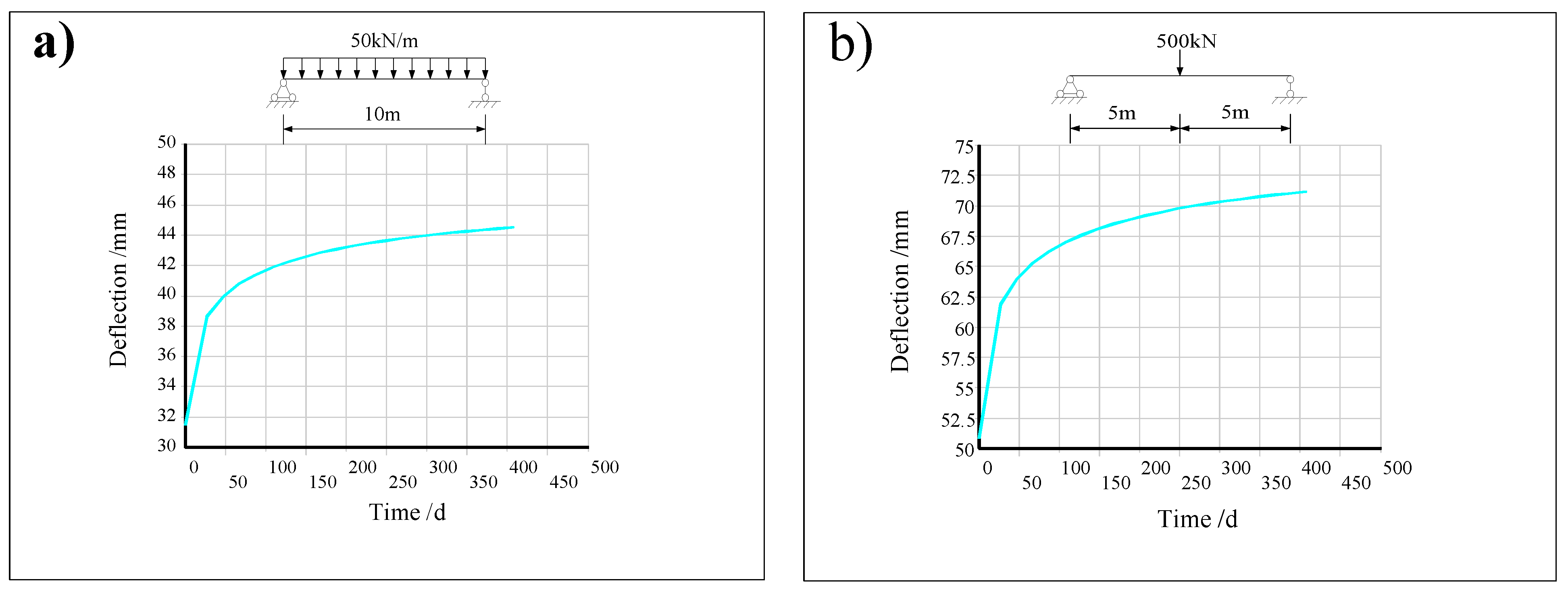
4.3. Comparison of Deflection under Different Load Situations
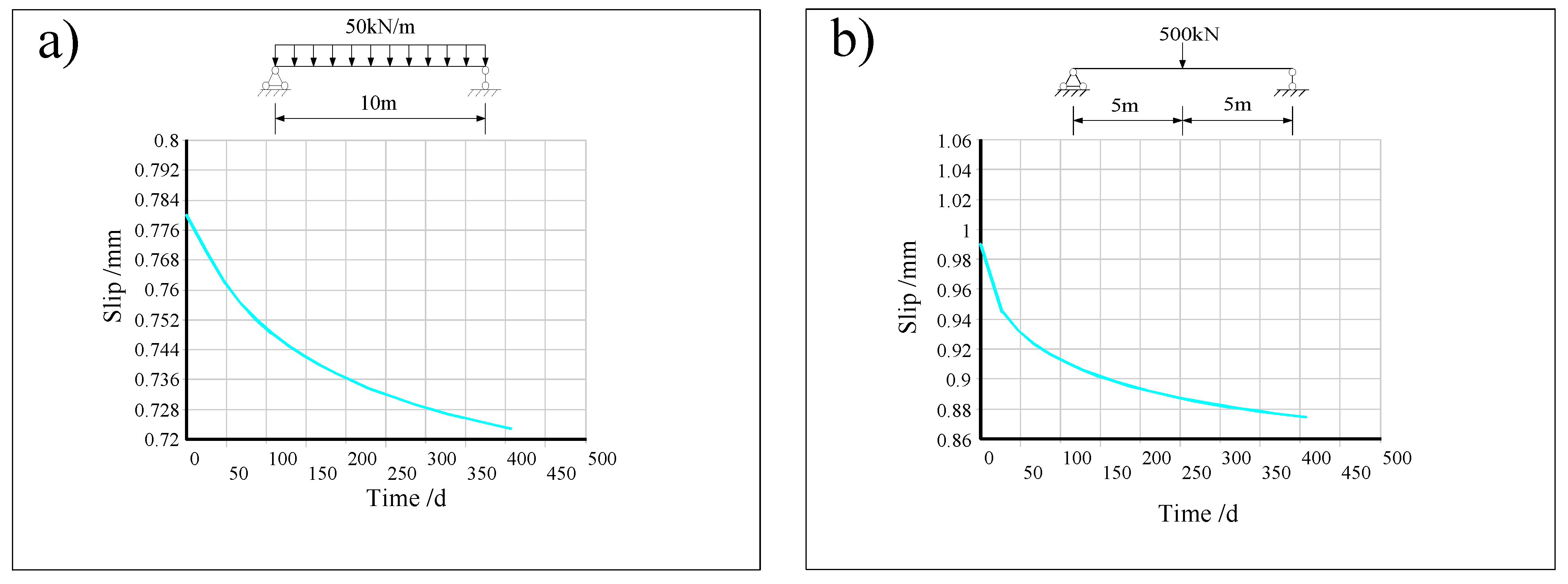
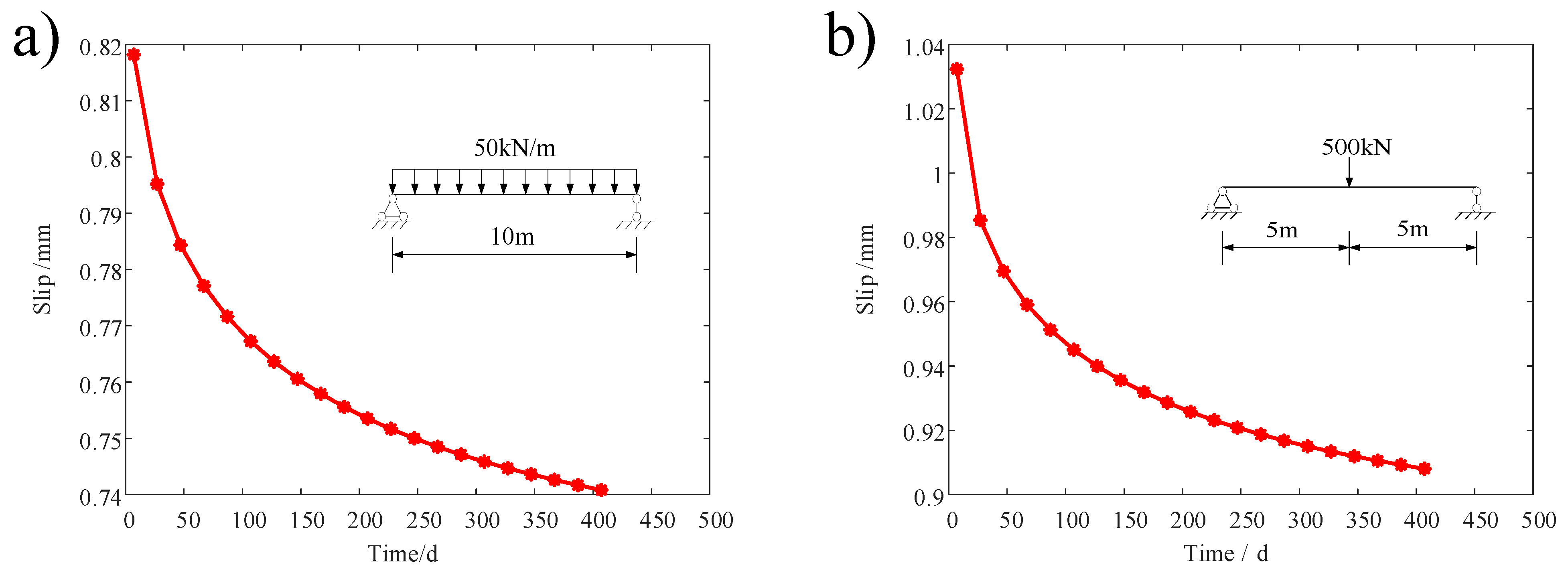
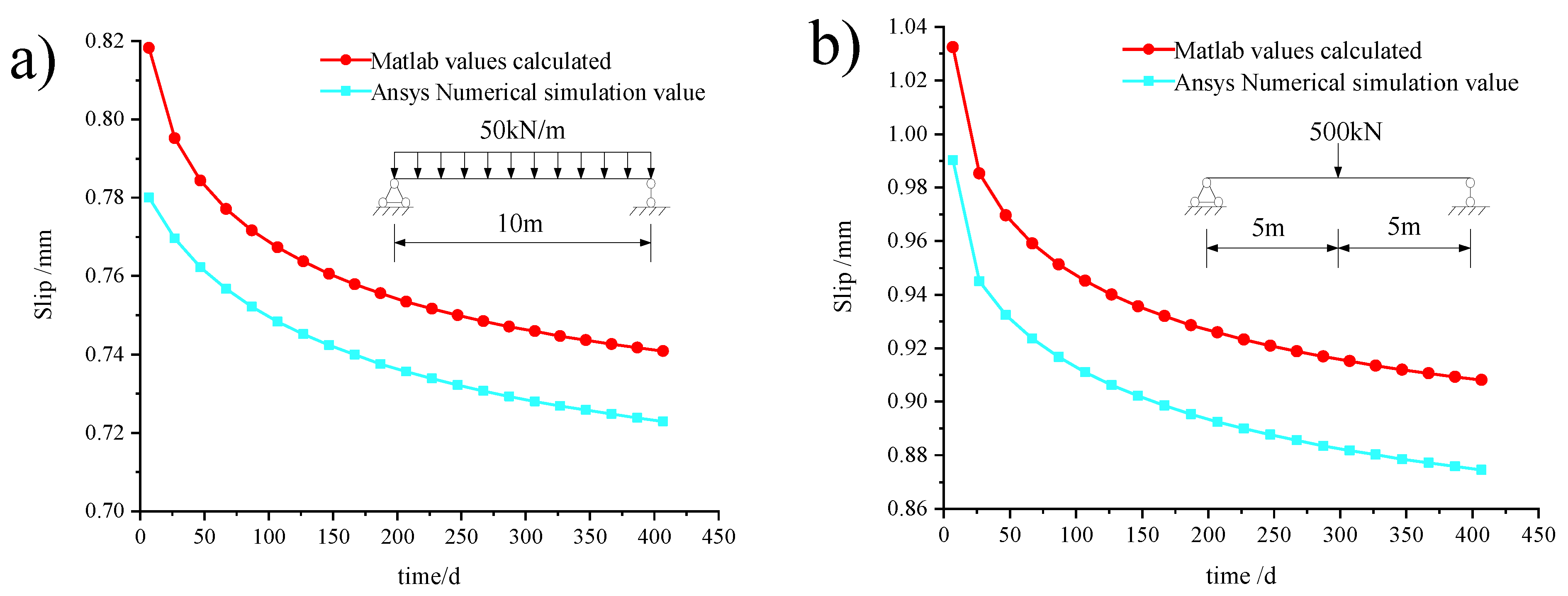
4.4. Comparison of Slip under Different Load Situations
4.5. Comparison of Axial Force, Deflection, and Slip of Composite Beams under Different Stud Stiffness Levels
5. Conclusions
- When considering the creep effect of the combined beam at the same stud stiffness, the axial force of the concrete slab inside the combined beam was reduced by around 11.0–11.6%, and the slip was reduced by 7.32–11.67% at 407 d. However, the deflection of the combined beam increased by 39.91–41.3%, so the concrete creep effect reduces the flexural stiffness of the combined structure, increases the deformation of the combined beam, and adversely affects the combined structure.
- The stud stiffness is an important factor affecting the long-term performance of steel–concrete composite beams. The stud stiffness was varied from 2000 N/mm to 10,000 N/mm, with other parameters unchanged. The change in axial force in the combined beam due to creep variation increased from 7.09% to 12.50%; the change in deflection increased from 31.97% to 46.60%, and the change in slip increased from 4.85% to 10.47% under long-term loading. The results show that the more strongly the studs constrain the concrete slab, the greater the adverse effect of concrete creep on the combined beam.
- By comparing the theoretically derived formulation with the finite element numerical simulation results, the error was around 5%, which proves the validity of the formulation for the calculation of the axial force, deflection, and slip of simply-supported composite beams considering the coupling of creep and slip based on the principle of the energy variational method. The results show that the theoretically derived formulas are applicable to the solution of the axial force, deflection, and slip of simply-supported composite beams under different types of creep and slip coupling.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| age of concrete under loading | |
| calculation of concrete age considering time | |
| strain | |
| instantaneous stress | |
| concrete creep coefficient | |
| nominal creep coefficient | |
| creep coefficient at time | |
| coefficient of creep development with time after loading | |
| average cylinder compressive strength of strength grade C25~C50 concrete at 28 d age, MPa | |
| age of 28 d, with 95% guarantee rate of concrete cube compressive strength standard value, MPa | |
| coefficients related to annual average relative humidity | |
| annual average relative humidity of the environment, % | |
| build theoretical thickness, mm | |
| aging coefficient | |
| , | elastic modulus of the steel beam, elastic modulus of concrete |
| , | cross-section area of the steel beam, cross-sectional area of concrete |
| , | axial horizontal displacement of the steel beam, horizontal displacement of concrete |
| unit beam length slip stiffness |
References
- Xiao, L.; Wei, X.; Wen, Z.; Li, G. State-of-the-art review of steel-concrete composite bridges in 2019. J. Civ. Environ. Eng. 2020, 42, 168–182. (In Chinese) [Google Scholar]
- Newmark, N.M.; Siess, C.P.; Viest, I.M. Tests and analysis of composite beams with incomplete interaction. Proc. Soc. Exp. Stress Anal. 1951, 9, 75–92. [Google Scholar]
- Adekola, A.O. The dependence of shear lag on partial interaction in composite beams. Int. J. Solids. Struct. 1974, 10, 389–400. [Google Scholar] [CrossRef]
- Girhammar, U.A.; Pan, D. Dynamic analysis of composite members with interlayer slip. Int. J. Solids. Struct. 1993, 30, 797–823. [Google Scholar] [CrossRef]
- Oehlers, D.J.; George, S. Composite Beams with Limited-Slip-Capacity Shear Connectors. J. Struct. Eng. 1995, 121, 932–938. [Google Scholar] [CrossRef]
- Fabbrocino, G.; Manfredi, G.; Cosenza, E. Nonlinear analysis of composite beams under positive bending. Comput. Struct. 1999, 70, 77–89. [Google Scholar] [CrossRef]
- Tarantino, A.M.; Dezi, L. Creep effects in composite beam s with flexible shear connectors. J. Struct. Eng. ASCE 1992, 118, 2063–2080. [Google Scholar] [CrossRef]
- Dezi, L.; Tarantino, A.M. Creep in composite continuous beams. I: Theoretical treatment. J. Struct. Eng. 1993, 119, 2095–2111. [Google Scholar] [CrossRef]
- Dezi, L.; Tarantino, A.M. Creep in composite continuous beams. II: Parametric study. J. Struct. Eng. 1993, 119, 2112–2133. [Google Scholar] [CrossRef]
- Gilbert, R.I.; Bradford, M.A. Time-dependent behavior of continuous composite beams at service loads. J. Struct. Eng. 1995, 121, 319–327. [Google Scholar] [CrossRef]
- Dezi, L.; Leoni, G.; Tarantino, A.M. Time-dependent analysis of prestressed composite beams. J. Struct. Eng. 1995, 121, 621–633. [Google Scholar] [CrossRef]
- Dezi, L.; Leoni, G.; Tarantino, A.M. Algebraic method for creep analysis of continuous composite beams. J. Struct. Eng. 1996, 122, 423–430. [Google Scholar] [CrossRef]
- Amadio, C.; Fragiacomo, M. Simplified approach to evaluate creep and shrinkage effects in steel-concrete composite beams. J. Struct. Eng. 1997, 123, 1153–1162. [Google Scholar] [CrossRef]
- Nie, J. Calculation and analysis of long-term deformation of steel-concrete composite beams. Build. Struct. 1997, 1, 42–45. (In Chinese) [Google Scholar] [CrossRef]
- Dezi, L. Time-dependent analysis of shear-lag effect in composite beams. J. Eng. Mech. 2001, 127, 71–79. [Google Scholar] [CrossRef]
- Zhou, L. The stress redistribution in steel-concrete composite girders due to shrinkage and creep of concrete. Bridge Constr. 2001, 2, 1–4. (In Chinese) [Google Scholar]
- Sheng, X.; Yang, J. Redistribution of creep stress in prestressed concrete build-up beam. Bridge Constr. 2003, 4, 11–14. (In Chinese) [Google Scholar]
- Nie, J.; Cai, C. Steel–concrete composite beams considering shear slip effects. J. Struct. Eng. 2003, 129, 495–506. (In Chinese) [Google Scholar] [CrossRef]
- Jiang, L.; Yu, Z.; Li, J. Theoretical analysis of slip and deformation of steel-concrete composite beam under uniform distributed loads. Eng. Mech. 2003, 2, 133–137. (In Chinese) [Google Scholar]
- Wang, J.; Long, P.; Liu, Z. Analysis of creep in composite beams. Highw. Traffic Sci. Technol. 2004, 8, 38–41. (In Chinese) [Google Scholar]
- Qiu, W.; Jiang, M.; Zhang, Z. Finite element analysis for creep and shrinkage of steel-concrete composite beams. Eng. Mech. 2004, 4, 162–166. (In Chinese) [Google Scholar]
- Fan, J.; Nie, J.; Wang, H. Long-term behavior of composite beams with shrinkage, creep and cracking (I)–Experiment and calculation. China. Civ. Eng. J. 2009, 42, 8–15. (In Chinese) [Google Scholar]
- Fan, J.; Nie, X.; Li, Q. Long-term behavior of composite beams with shrinkage, creep and cracking (II)–theoretical analysis. China. Civ. Eng. J. 2009, 42, 16–22. (In Chinese) [Google Scholar]
- Nguyen, Q.H.; Mohammed, H.; Brian, U. Time-dependent analysis of composite beams with continuous shear connection based on a space-exact stiffness matrix. Eng. Struct. 2010, 32, 2902–2911. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Mohammed, H. Nonlinear time-dependent behavior of composite steel-concrete beams. J. Struct. Eng. 2016, 142, 04015175. [Google Scholar] [CrossRef]
- Miao, L.; Chen, D. Closed-form solution of composite beam considering interfacial slip effects. J. Tongji Univ. Nat.Sci. 2011, 39, 1113–1119. (In Chinese) [Google Scholar]
- Ji, W.; Sun, B.; Deng, L.; Zhao, Y.; Lin, P. Calculation and analysis on deflection of steel-concrete continuous composite girder considering effect of multi-factors. J. Hunan Univ. Nat.Sci. 2019, 46, 30–38. (In Chinese) [Google Scholar]
- Oven, V.A.; Burgess, I.W.; Plank, R.J. An analytical model for the analysis of composite beams with partial interaction. Comput. Struct. 1997, 62, 493–504. [Google Scholar] [CrossRef]
- Salari, M.R.; Spacone, E.; Shing, P.B. Nonlinear analysis of composite beams with deformable shear connectors. J. Struct. Eng. 1998, 124, 1148–1158. [Google Scholar] [CrossRef]
- Gattesco, N. Analytical modeling of nonlinear behavior of composite beams with deformable connection. J. Constr. Steel. Res. 1999, 52, 195–218. [Google Scholar] [CrossRef]
- Ayoub, A.; Filippou, F.C. Mixed formulation of nonlinear steel-concrete composite beam element. J. Struct. Eng. 2000, 126, 371–381. [Google Scholar] [CrossRef]
- Qiu, W.; Zhang, Z.; Huang, C. Finite-element method of double-layer beam model for analysis of composite steel-concrete beams. J. Dalian Univ. Technol. 2003, 1, 101–103. (In Chinese) [Google Scholar]
- Fang, K.; Chen, S. Finite element analysis of steel-concrete composite beams with influence of the shear connector stiffness. Ind. Buils. 2003, 9, 75–77. (In Chinese) [Google Scholar]
- Wei, F.; Lv, Z.; Sun, W. Nonlinear finite element analysis of composite steel-concrete beams with partial shear connection. Ind. Build. 2003, 9, 78–79 + 88. (In Chinese) [Google Scholar]
- Miranda, M.P.; Tamayo, J.L.P.; Morsch, I.B. Reassessment of viscoelastic response in steel-concrete composite beams. Struct. Eng. Mech. 2022, 81, 617–631. [Google Scholar] [CrossRef]
- Sarfarazi, V.; Haeri, H.; Shemirani, A.B.; Zhu, Z.; Marji, M.F. Experimental and numerical simulating of the crack separation on the tensile strength of concrete. Struct. Eng. Mech. Int. J. 2018, 66, 569–582. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, J.; Zhang, Y. Analysis and design of long-term responses of simply-supported steel–concrete composite slabs. J. Build. Eng. 2022, 53, 104496. [Google Scholar] [CrossRef]
- Huang, Q.; Li, W.; Wang, B. Analytical method of steel-concrete composite beam based on interface slip and shear deformation. J. Nanjing Univ. Aeronaut. Astronaut. 2018, 50, 131–137. (In Chinese) [Google Scholar]
- JTG 3362-2018; Code for design of highway reinforced concrete and prestressed concrete bridges and culverts. People’s Transportation Publishing House: Beijing, China, 2018. (In Chinese)
- Liu, Y.; Liu, X. Long-term deflection of steel-concrete composite box-beam due to creep. J. Railw. Sci. Eng. 2015, 12, 317–322. (In Chinese) [Google Scholar]
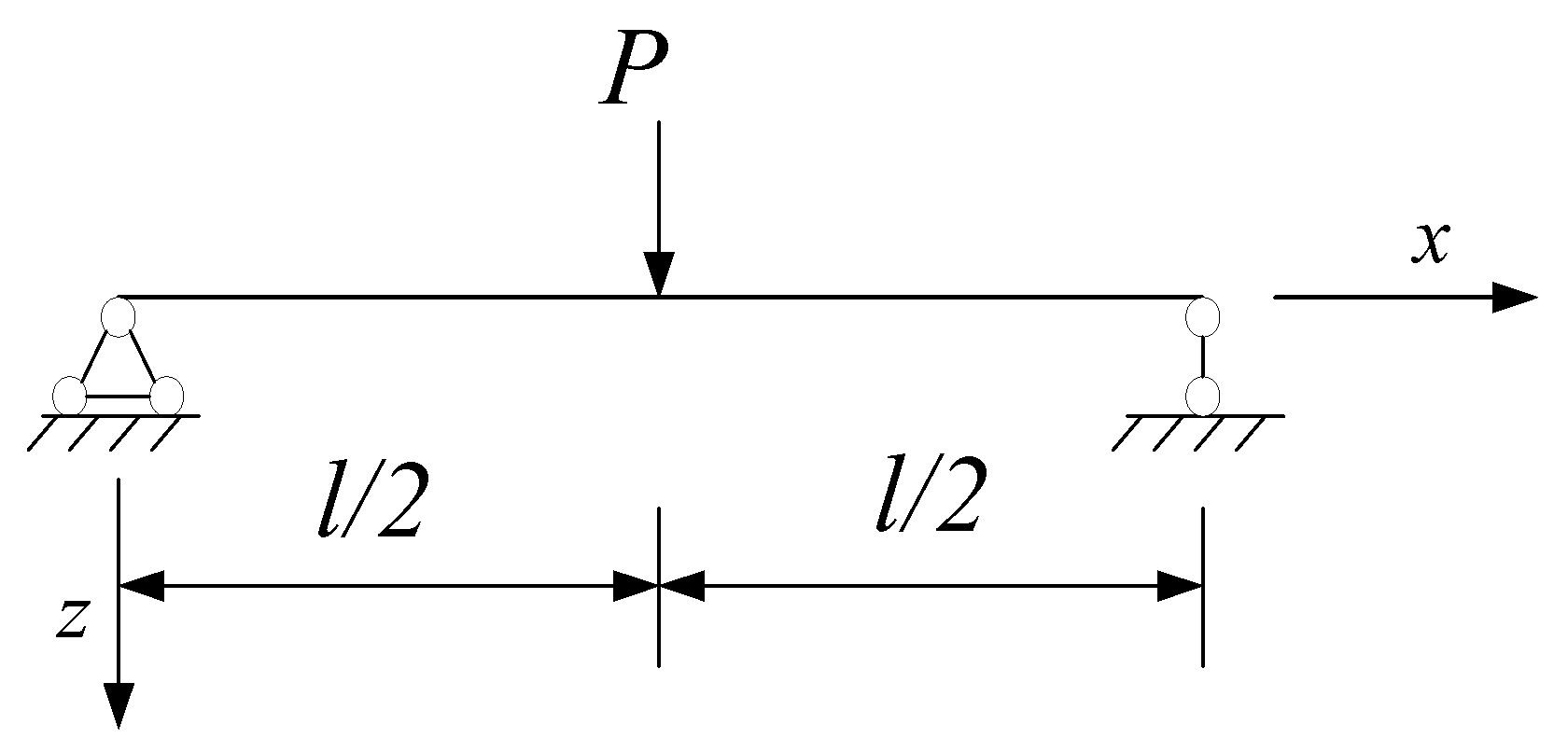

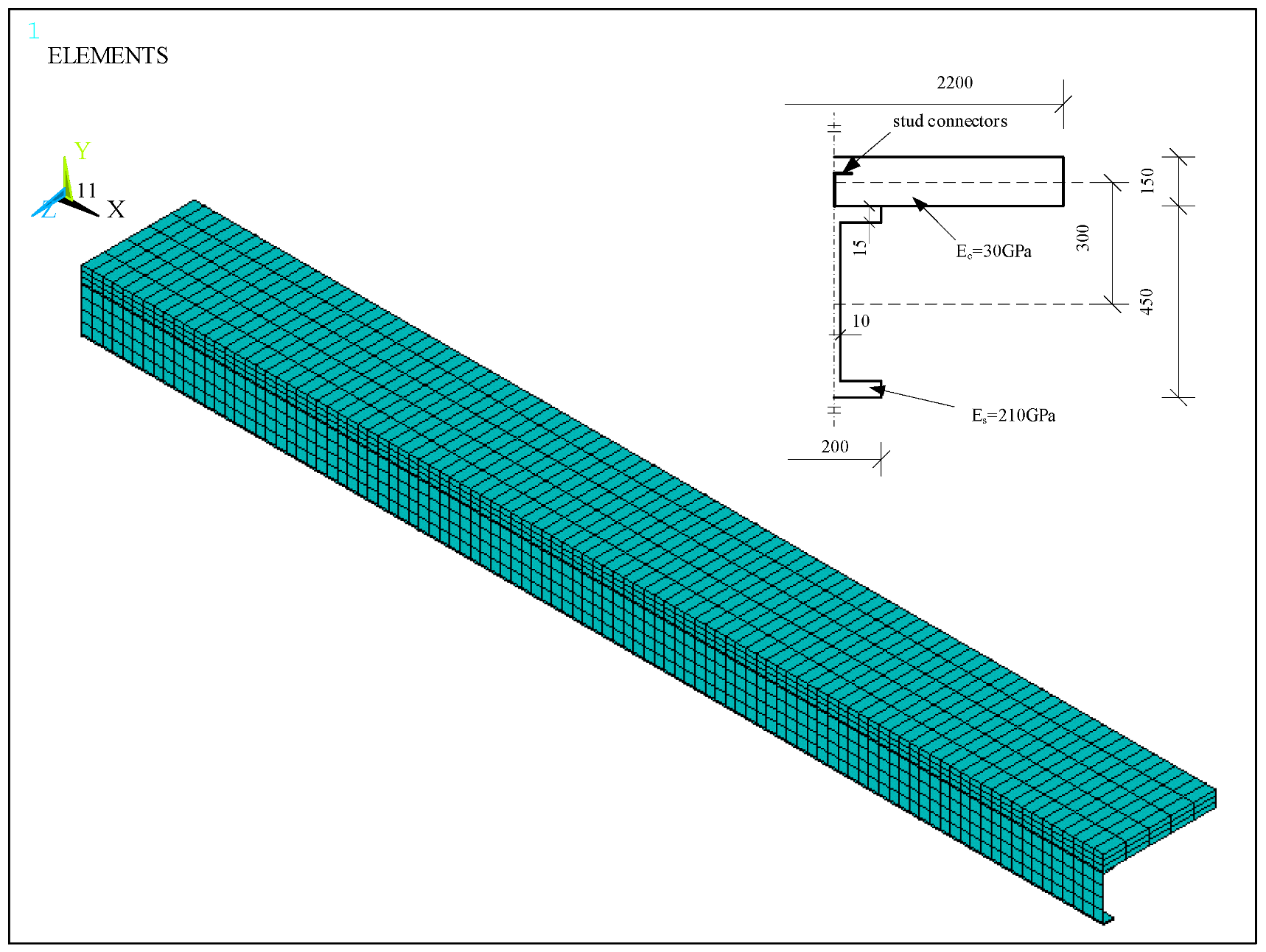
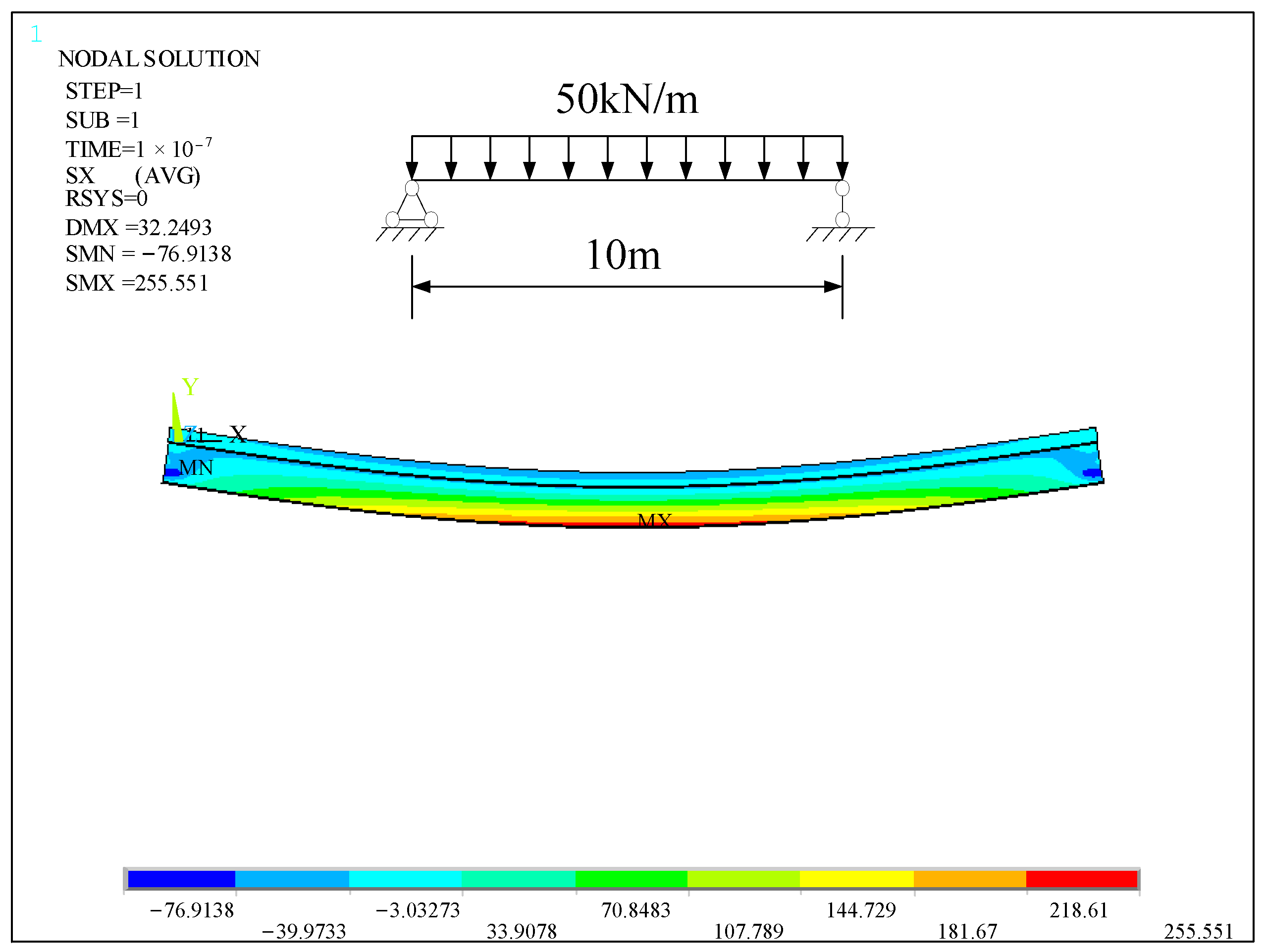
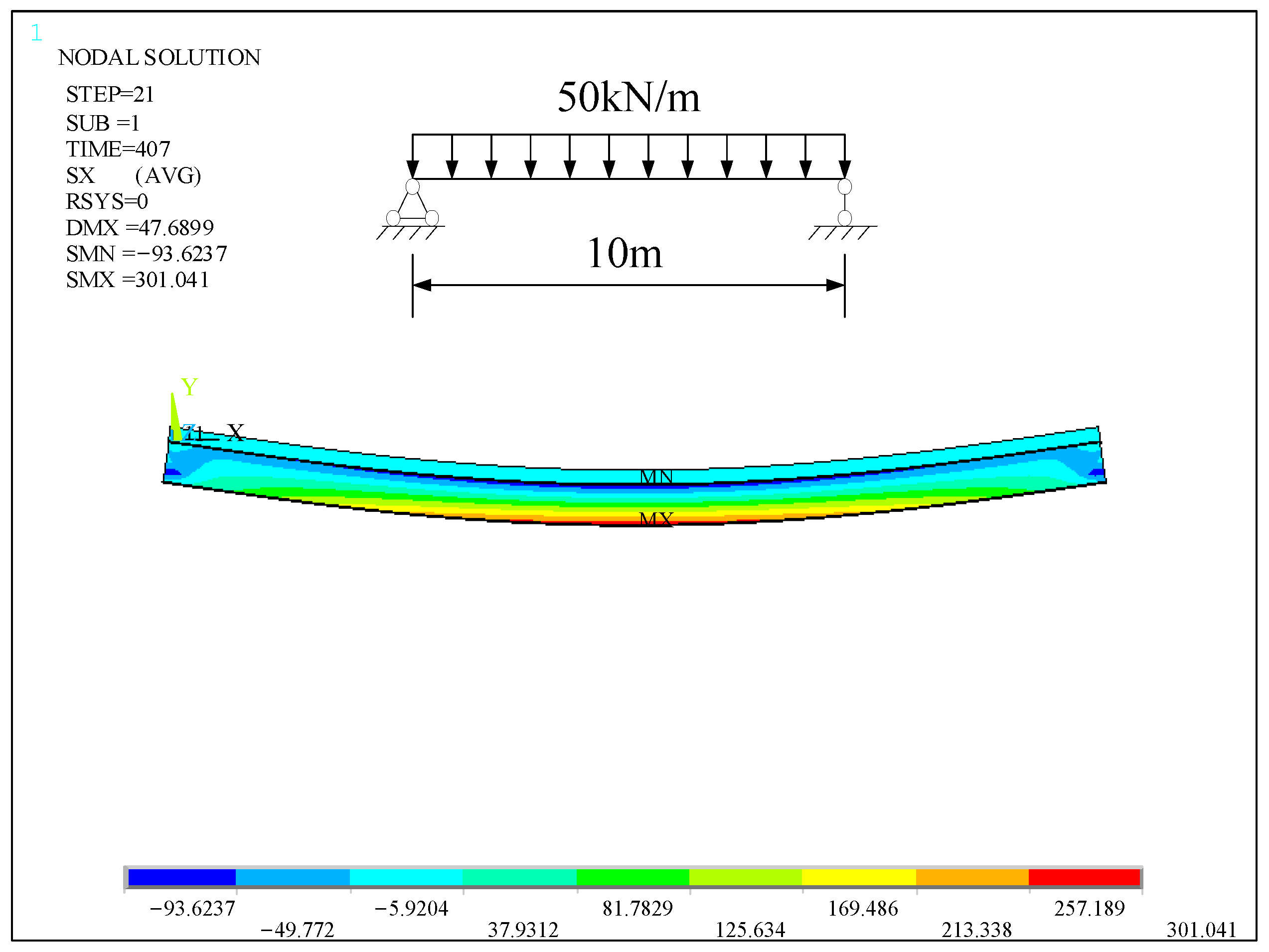
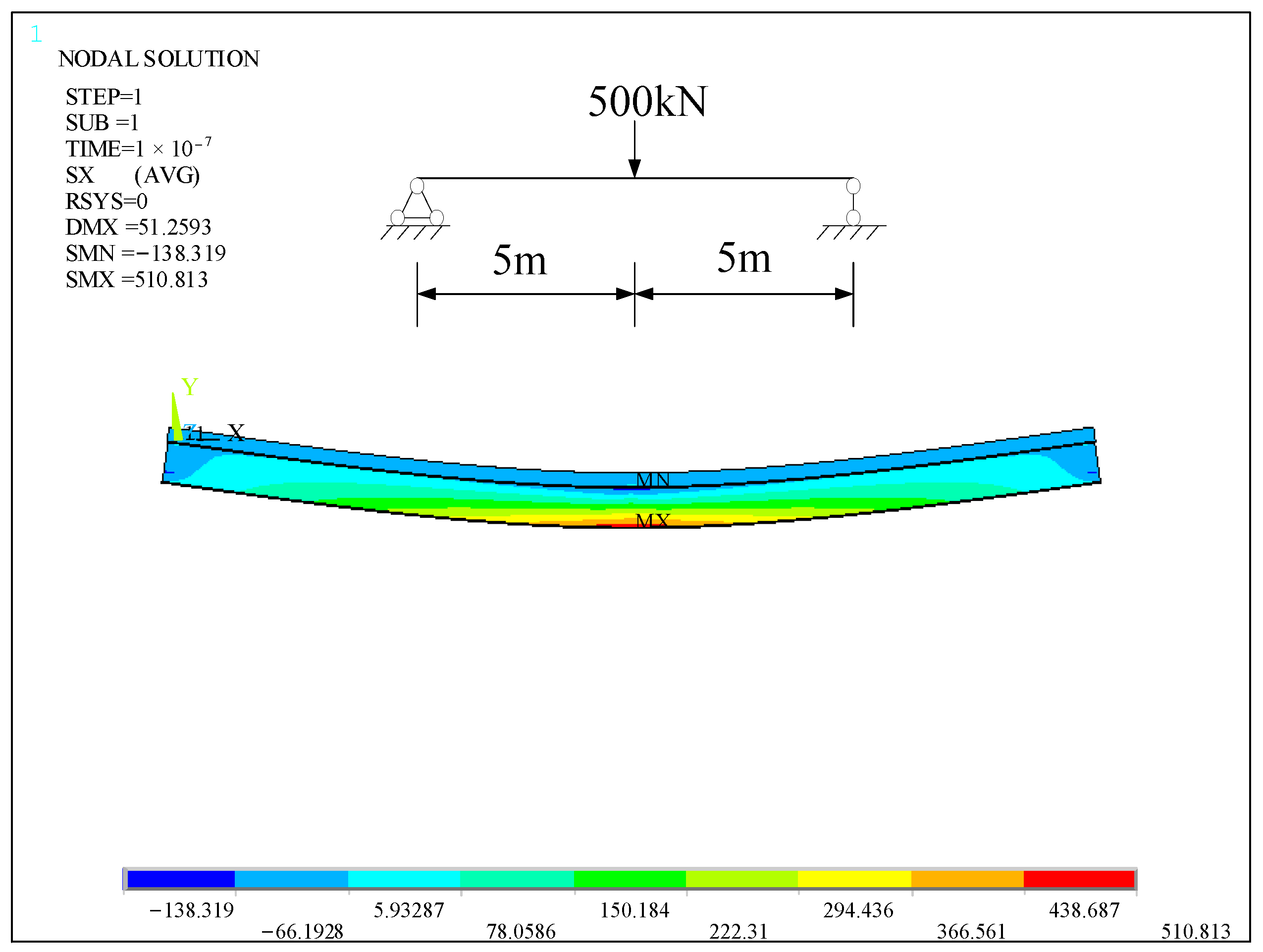



| Time/d | Simulated Calculation Value | Values Calculated | Error 1 | Error 2 | ||
|---|---|---|---|---|---|---|
| Uniformly Distributed Load | Point Load | Uniformly Distributed Load | Point Load | |||
| 7 | 1189.13 | 2045.54 | 1189.85 | 2045.45 | 0.06% | 0.00% |
| 27 | 1139.33 | 1953.53 | 1146.99 | 1988.02 | 0.67% | 2.09% |
| 47 | 1126.02 | 1929.50 | 1130.03 | 1960.89 | 0.35% | 1.89% |
| 67 | 1116.20 | 1911.73 | 1118.80 | 1942.76 | 0.23% | 1.83% |
| 87 | 1108.33 | 1897.53 | 1110.37 | 1929.11 | 0.18% | 1.82% |
| 107 | 1101.76 | 1885.73 | 1103.64 | 1918.20 | 0.17% | 1.85% |
| 127 | 1096.15 | 1875.69 | 1098.09 | 1909.15 | 0.18% | 1.88% |
| 147 | 1091.27 | 1866.97 | 1093.37 | 1901.47 | 0.19% | 1.92% |
| 167 | 1086.96 | 1859.32 | 1089.30 | 1894.83 | 0.21% | 1.97% |
| 187 | 1083.13 | 1852.68 | 1085.73 | 1889.01 | 0.24% | 2.01% |
| 207 | 1079.69 | 1846.55 | 1082.58 | 1883.85 | 0.27% | 2.05% |
| 227 | 1076.57 | 1841.03 | 1079.75 | 1879.23 | 0.29% | 2.10% |
| 247 | 1073.74 | 1836.01 | 1077.21 | 1875.06 | 0.32% | 2.14% |
| 267 | 1071.15 | 1831.42 | 1074.90 | 1871.29 | 0.35% | 2.17% |
| 287 | 1068.77 | 1827.22 | 1072.80 | 1867.84 | 0.38% | 2.21% |
| 307 | 1066.57 | 1823.34 | 1070.87 | 1864.68 | 0.40% | 2.25% |
| 327 | 1064.53 | 1819.75 | 1069.09 | 1861.77 | 0.43% | 2.27% |
| 347 | 1062.72 | 1816.42 | 1067.45 | 1859.08 | 0.44% | 2.31% |
| 367 | 1060.96 | 1813.33 | 1065.93 | 1856.59 | 0.47% | 2.34% |
| 387 | 1059.30 | 1810.43 | 1064.51 | 1854.27 | 0.49% | 2.37% |
| 407 | 1057.76 | 1807.72 | 1063.19 | 1852.10 | 0.51% | 2.40% |
| Time/d | Simulated Calculation Value | Values Calculated | Error 1 | Error 2 | ||
|---|---|---|---|---|---|---|
| Uniformly Distributed Load | Point Load | Uniformly Distributed Load | Point Load | |||
| 7 | 31.5 | 50.86 | 31.11 | 50.38 | 1.24% | 0.95% |
| 27 | 38.62 | 61.86 | 37.50 | 60.62 | 2.98% | 2.05% |
| 47 | 39.95 | 63.96 | 38.55 | 62.28 | 3.64% | 2.70% |
| 67 | 40.78 | 65.27 | 39.20 | 63.31 | 4.04% | 3.10% |
| 87 | 41.38 | 66.22 | 39.67 | 64.06 | 4.31% | 3.37% |
| 107 | 41.84 | 66.96 | 40.04 | 64.65 | 4.50% | 3.58% |
| 127 | 42.22 | 67.56 | 40.34 | 65.12 | 4.66% | 3.74% |
| 147 | 42.54 | 68.06 | 40.59 | 65.52 | 4.80% | 3.87% |
| 167 | 42.81 | 68.49 | 40.81 | 65.87 | 4.90% | 3.98% |
| 187 | 43.05 | 68.86 | 41.00 | 66.17 | 5.01% | 4.07% |
| 207 | 43.26 | 69.19 | 41.16 | 66.43 | 5.10% | 4.16% |
| 227 | 43.44 | 69.48 | 41.31 | 66.66 | 5.16% | 4.23% |
| 247 | 43.61 | 69.75 | 41.44 | 66.87 | 5.24% | 4.31% |
| 267 | 43.76 | 69.98 | 41.56 | 67.06 | 5.30% | 4.36% |
| 287 | 43.89 | 70.2 | 41.67 | 67.23 | 5.33% | 4.42% |
| 307 | 44.02 | 70.39 | 41.77 | 67.39 | 5.40% | 4.46% |
| 327 | 44.13 | 70.57 | 41.86 | 67.53 | 5.43% | 4.50% |
| 347 | 44.23 | 70.73 | 41.94 | 67.66 | 5.46% | 4.53% |
| 367 | 44.33 | 70.89 | 42.02 | 67.79 | 5.50% | 4.58% |
| 387 | 44.42 | 71.03 | 42.09 | 67.90 | 5.54% | 4.61% |
| 407 | 44.51 | 71.16 | 42.16 | 68.01 | 5.58% | 4.64% |
| Time/d | Simulated Calculation Value | Simulated Calculation Value | Error 1 | Error 2 | ||
|---|---|---|---|---|---|---|
| Uniformly Distributed Load | Point Load | Uniformly Distributed Load | Point Load | |||
| 7 | 0.7800 | 0.9901 | 0.8182 | 1.0323 | 4.67% | 4.09% |
| 27 | 0.7696 | 0.9450 | 0.7952 | 0.9853 | 3.22% | 4.09% |
| 47 | 0.7622 | 0.9324 | 0.7844 | 0.9695 | 2.82% | 3.82% |
| 67 | 0.7567 | 0.9236 | 0.7771 | 0.9591 | 2.63% | 3.70% |
| 87 | 0.7522 | 0.9167 | 0.7716 | 0.9513 | 2.52% | 3.63% |
| 107 | 0.7484 | 0.9110 | 0.7673 | 0.9451 | 2.46% | 3.61% |
| 127 | 0.7452 | 0.9062 | 0.7637 | 0.9400 | 2.42% | 3.59% |
| 147 | 0.7424 | 0.9021 | 0.7606 | 0.9356 | 2.39% | 3.58% |
| 167 | 0.7399 | 0.8985 | 0.7579 | 0.9319 | 2.38% | 3.58% |
| 187 | 0.7376 | 0.8953 | 0.7556 | 0.9286 | 2.38% | 3.59% |
| 207 | 0.7356 | 0.8925 | 0.7535 | 0.9258 | 2.38% | 3.59% |
| 227 | 0.7338 | 0.8899 | 0.7517 | 0.9232 | 2.38% | 3.60% |
| 247 | 0.7322 | 0.8876 | 0.7500 | 0.9208 | 2.38% | 3.61% |
| 267 | 0.7307 | 0.8855 | 0.7485 | 0.9187 | 2.38% | 3.62% |
| 287 | 0.7293 | 0.8835 | 0.7471 | 0.9168 | 2.39% | 3.63% |
| 307 | 0.7280 | 0.8817 | 0.7459 | 0.9151 | 2.40% | 3.65% |
| 327 | 0.7269 | 0.8802 | 0.7447 | 0.9134 | 2.39% | 3.64% |
| 347 | 0.7258 | 0.8786 | 0.7436 | 0.9120 | 2.40% | 3.66% |
| 367 | 0.7248 | 0.8772 | 0.7426 | 0.9106 | 2.40% | 3.66% |
| 387 | 0.7238 | 0.8759 | 0.7417 | 0.9093 | 2.41% | 3.67% |
| 407 | 0.7229 | 0.8746 | 0.7408 | 0.9081 | 2.42% | 3.69% |
| Time/d | Simulated Calculation Value | Values Calculated | Error 1 | Error 2 | Error 3 | ||||
|---|---|---|---|---|---|---|---|---|---|
| 7 | 1023.35 | 1189.13 | 1254.24 | 1024.12 | 1189.85 | 1254.84 | 0.08% | 0.06% | 0.05% |
| 407 | 950.79 | 1057.76 | 1097.51 | 949.62 | 1063.19 | 1105.25 | 0.12% | 0.51% | 0.71% |
| value | −72.56 | −131.37 | −156.73 | −74.5 | −126.66 | −149.59 | |||
| Time/d | Simulated Calculation Value | Values Calculated | Error 1 | Error 2 | Error 3 | ||||
|---|---|---|---|---|---|---|---|---|---|
| 7 | 37.29 | 31.50 | 29.12 | 36.91 | 31.11 | 28.73 | 1.02% | 1.24% | 1.34% |
| 407 | 49.21 | 44.51 | 42.69 | 46.97 | 42.16 | 40.28 | 4.55% | 5.28% | 5.65% |
| value | 11.92 | 13.01 | 13.57 | 10.06 | 11.05 | 11.55 | |||
| Time/d | Simulated Calculation Value | Values Calculated | Error 1 | Error 2 | Error 3 | ||||
|---|---|---|---|---|---|---|---|---|---|
| 7 | 1.6644 | 0.7800 | 0.4290 | 1.7038 | 0.8182 | 0.4442 | 2.37% | 4.90% | 3.54% |
| 407 | 1.5836 | 0.7229 | 0.3841 | 1.5959 | 0.7408 | 0.3964 | 0.78% | 2.48% | 3.20% |
| value | −0.0808 | −0.0571 | −0.0249 | −0.1079 | −0.0774 | −0.0478 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, Q.; Wang, P.; Nan, H. Study on Mechanical Properties of Simply-Supported Composite Beams Considering Creep and Slip. Appl. Sci. 2023, 13, 193. https://doi.org/10.3390/app13010193
Lei Q, Wang P, Nan H. Study on Mechanical Properties of Simply-Supported Composite Beams Considering Creep and Slip. Applied Sciences. 2023; 13(1):193. https://doi.org/10.3390/app13010193
Chicago/Turabian StyleLei, Qinan, Peng Wang, and Hongliang Nan. 2023. "Study on Mechanical Properties of Simply-Supported Composite Beams Considering Creep and Slip" Applied Sciences 13, no. 1: 193. https://doi.org/10.3390/app13010193
APA StyleLei, Q., Wang, P., & Nan, H. (2023). Study on Mechanical Properties of Simply-Supported Composite Beams Considering Creep and Slip. Applied Sciences, 13(1), 193. https://doi.org/10.3390/app13010193






