An Efficient Prediction System for Coronary Heart Disease Risk Using Selected Principal Components and Hyperparameter Optimization
Abstract
1. Introduction
1.1. Motivation and Background
1.2. Purpose, Contribution, and Paper Structure
- An accurate coronary heart risk prediction system has been developed based on selected principal components and machine learning algorithms.
- The impact of selecting significant principal components using the CFS technique to improve the prediction results for heart disease diagnosis by reducing the training time has been investigated.
- The performance of the single classifiers such as Decision Tree (DT), Support Vector Machines (SVM), K-Nearest Neighbors (KNN), and ensemble classifiers including AdaBoost M1 (AB), Bagging (BG), and Rotation Forest (RTF) has been examined with and without hyperparameter optimization.
- A performance comparison of state-of-the-art works on coronary heart disease risk prediction with the proposed method has been provided.
2. Related Works
3. Materials and Methods
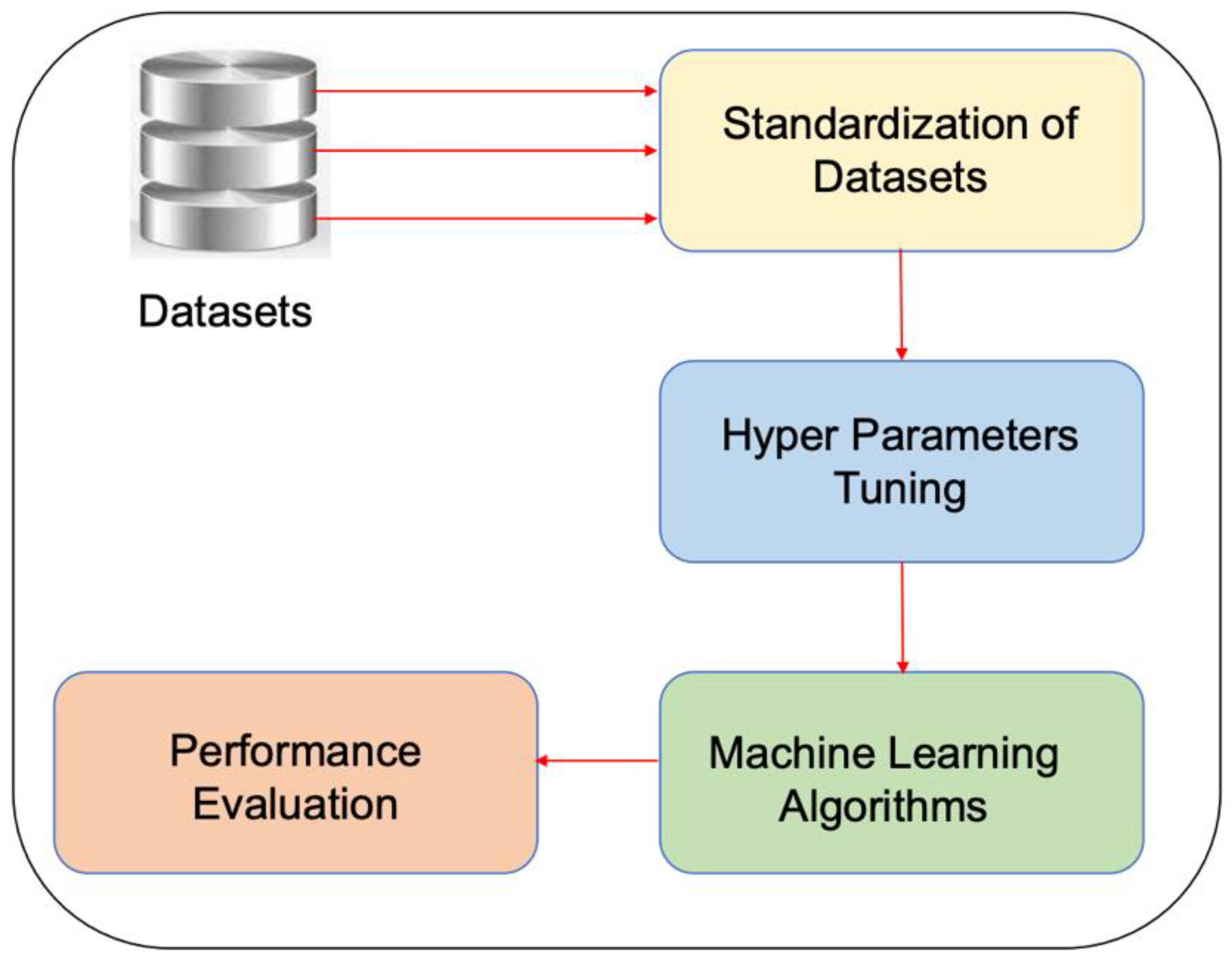
3.1. Proposed Research Methodology
3.2. Dataset Description
3.3. Data Preprocessing
3.4. Feature Extraction
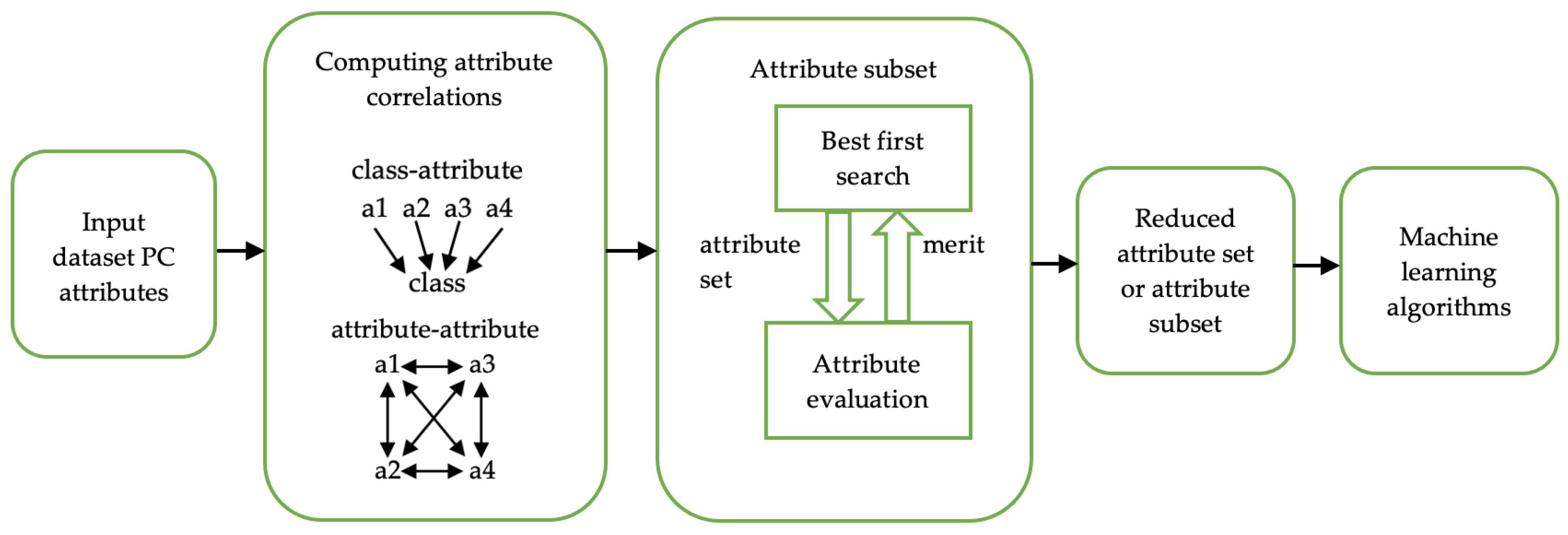
3.5. Feature Selection
3.6. Machine Learning Classifiers
3.6.1. Support Vector Machines
3.6.2. K-Nearest Neighbors
3.6.3. Decision Tree
3.6.4. AdaBoost M1
3.6.5. Bagging
3.6.6. Rotation Forest
3.7. Hyperparameter Optimization
3.8. Performance Metrics
4. Results and Analysis
4.1. Results of Classifiers without Hyperparameter Optimization
4.2. Results of Classifiers with Hyperparameter Optimization
4.2.1. Hyperparameter Optimization of SVM
4.2.2. Hyperparameter Optimization of KNN
4.2.3. Hyperparameter Optimization of J48 DT
4.2.4. Hyperparameter Optimization of AdaBoost M1
4.2.5. Hyperparameter Optimization of Bagging
4.2.6. Hyperparameter Optimization of RTF
5. Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ghiasi, M.M.; Zendehboudi, S.; Mohsenipour, A.A. Decision tree-based diagnosis of coronary artery disease: CART model. Comput. Methods Programs Biomed. 2020, 192, 105400. [Google Scholar] [CrossRef] [PubMed]
- Fitriyani, N.L.; Syafrudin, M.; Alfian, G.; Rhee, J. HDPM: An Effective Heart Disease Prediction Model for a Clinical Decision Support System. IEEE Access 2020, 8, 133034–133050. [Google Scholar] [CrossRef]
- Yadav, D.C.; Pal, S. Prediction of Heart Disease Using Feature Selection and Random Forest Ensemble Method. Int. J. Pharm. Res. 2020, 12, 56–66. [Google Scholar] [CrossRef]
- Shahid, A.H.; Singh, M.P.; Roy, B.; Aadarsh, A. Coronary Artery Disease Diagnosis Using Feature Selection Based Hybrid Extreme Learning Machine. In Proceedings of the 2020 3rd International Conference on Information and Computer Technologies (ICICT), San Jose, CA, USA, 9–12 March 2020; pp. 341–346. [Google Scholar] [CrossRef]
- WHO. 2020. [Online]. Available online: https://www.who.int/health-topics/cardiovascular-diseases/#tab=tab_1 (accessed on 14 October 2021).
- Ryu, H.; Moon, J.; Jung, J. Sex Differences in Cardiovascular Disease Risk by Socioeconomic Status (SES) of Workers Using National Health Information Database. Int. J. Environ. Res. Public Health 2020, 17, 2047. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Garibaldi, J.M. A hybrid model for automatic identification of risk factors for heart disease. J. Biomed. Inform. 2015, 58, S171–S182. [Google Scholar] [CrossRef] [PubMed]
- Sowmiya, C.; Sumitra, P. Analytical study of heart disease diagnosis using classification techniques. In Proceedings of the 2017 IEEE International Conference on Intelligent Techniques in Control, Optimization and Signal Processing (INCOS), Srivilliputtur, India, 23–25 March 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Karthick, D.; Priyadharshini, B. Predicting the chances of occurrence of Cardio Vascular Disease (CVD) in people using classification techniques within fifty years of age. In Proceedings of the 2018 2nd International Conference on Inventive Systems and Control (ICISC), Coimbatore, India, 19–20 January 2018; pp. 1182–1186. [Google Scholar] [CrossRef]
- Dinesh, K.G.; Arumugaraj, K.; Santhosh, K.D.; Mareeswari, V. Prediction of Cardiovascular Disease Using Machine Learning Algorithms. In Proceedings of the 2018 International Conference on Current Trends towards Converging Technologies (ICCTCT), Coimbatore, India, 1–3 March 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Gupta, A.; Kumar, R.; Arora, H.S.; Raman, B. MIFH: A Machine Intelligence Framework for Heart Disease Diagnosis. IEEE Access 2019, 8, 14659–14674. [Google Scholar] [CrossRef]
- Louridi, N.; Amar, M.; El Ouahidi, B. Identification of Cardiovascular Diseases Using Machine Learning. In Proceedings of the 2019 7th Mediterranean Congress of Telecommunications (CMT), Fez, Morocco, 24–25 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Javeed, A.; Rizvi, S.S.; Zhou, S.; Riaz, R.; Khan, S.U.; Kwon, S.J. Heart Risk Failure Prediction Using a Novel Feature Selection Method for Feature Refinement and Neural Network for Classification. Mob. Inf. Syst. 2020, 2020, 8843115. [Google Scholar] [CrossRef]
- Vasant, P.; Ganesan, T.; Elamvazuthi, I.; Webb, J.F. Interactive fuzzy programming for the production planning: The case of textile firm. Int. Rev. Model. Simul. 2011, 4, 961–970. [Google Scholar]
- Ali, Z.; Alsulaiman, M.; Muhammad, G.; Elamvazuthi, I.; Mesallam, T.A. Vocal fold disorder detection based on continuous speech by using MFCC and GMM. In Proceedings of the 2013 7th IEEE GCC Conference and Exhibition (GCC), Doha, Qatar, 17–20 November 2013; pp. 292–297. [Google Scholar] [CrossRef]
- Gupta, R.; Elamvazuthi, I.; Dass, S.C.; Faye, I.; Vasant, P.; George, J.; Izza, F. Curvelet based automatic segmentation of supraspinatus tendon from ultrasound image: A focused assistive diagnostic method. Biomed. Eng. Online 2014, 13, 157. [Google Scholar] [CrossRef]
- Ali, Z.; Alsulaiman, M.; Elamvazuthi, I.; Muhammad, G.; Mesallam, T.A.; Farahat, M.; Malki, K.H. Voice pathology detection based on the modified voice contour and SVM. Biol. Inspired Cogn. Arch. 2016, 15, 10–18. [Google Scholar] [CrossRef]
- Ali, Z.; Elamvazuthi, I.; Alsulaiman, M.; Muhammad, G. Detection of Voice Pathology using Fractal Dimension in a Multiresolution Analysis of Normal and Disordered Speech Signals. J. Med. Syst. 2016, 40, 20. [Google Scholar] [CrossRef] [PubMed]
- Nurhanim, K.; Elamvazuthi, I.; Izhar, L.; Capi, G.; Su, S. EMG Signals Classification on Human Activity Recognition using Machine Learning Algorithm. In Proceedings of the 2021 8th NAFOSTED Conference on Information and Computer Science (NICS), Hanoi, Vietnam, 21–22 December 2021; pp. 369–373. [Google Scholar] [CrossRef]
- Rahim, K.N.K.A.; Elamvazuthi, I.; Izhar, L.I.; Capi, G. Classification of Human Daily Activities Using Ensemble Methods Based on Smartphone Inertial Sensors. Sensors 2018, 18, 4132. [Google Scholar] [CrossRef] [PubMed]
- Sharon, H.; Elamvazuthi, I.; Lu, C.-K.; Parasuraman, S.; Natarajan, E. Development of Rheumatoid Arthritis Classification from Electronic Image Sensor Using Ensemble Method. Sensors 2019, 20, 167. [Google Scholar] [CrossRef] [PubMed]
- Reddy, K.V.V.; Elamvazuthi, I.; Aziz, A.A.; Paramasivam, S.; Na Chua, H.; Pranavanand, S. Rotation Forest Ensemble Classifier to Improve the Cardiovascular Disease Risk Prediction Accuracy. In Proceedings of the 2021 8th NAFOSTED Conference on Information and Computer Science (NICS), Hanoi, Vietnam, 21–22 December 2021; pp. 404–409. [Google Scholar] [CrossRef]
- Reddy, K.V.V.; Elamvazuthi, I.; Aziz, A.A.; Paramasivam, S.; Na Chua, H.; Pranavanand, S. Heart Disease Risk Prediction Using Machine Learning Classifiers with Attribute Evaluators. Appl. Sci. 2021, 11, 8352. [Google Scholar] [CrossRef]
- Maurovich-Horvat, P. Current trends in the use of machine learning for diagnostics and/or risk stratification in cardiovascular disease. Cardiovasc. Res. 2021, 117, e67–e69. [Google Scholar] [CrossRef]
- Gonsalves, A.H.; Thabtah, F.; Mohammad, R.M.A.; Singh, G. Prediction of Coronary Heart Disease using Machine Learning. In Proceedings of the 2019 3rd International Conference on Deep Learning Technologies, Xiamen China, 5–7 July 2019; pp. 51–56. [Google Scholar] [CrossRef]
- Uddin, S.; Khan, A.; Hossain, E.; Moni, M.A. Comparing different supervised machine learning algorithms for disease prediction. BMC Med. Inform. Decis. Mak. 2019, 19, 281. [Google Scholar] [CrossRef]
- Beunza, J.-J.; Puertas, E.; García-Ovejero, E.; Villalba, G.; Condes, E.; Koleva, G.; Hurtado, C.; Landecho, M.F. Comparison of machine learning algorithms for clinical event prediction (risk of coronary heart disease). J. Biomed. Inform. 2019, 97, 103257. [Google Scholar] [CrossRef]
- Le, H.M.; Tran, T.D.; van Tran, L. Automatic heart disease prediction using feature selection and data mining technique. J. Comput. Sci. Cybern. 2018, 34, 33–48. [Google Scholar] [CrossRef]
- Bashir, S.; Khan, Z.S.; Khan, F.H.; Anjum, A.; Bashir, K. Improving Heart Disease Prediction Using Feature Selection Approaches. In Proceedings of the 2019 16th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 8–12 January 2019; pp. 619–623. [Google Scholar] [CrossRef]
- Urbanowicz, R.J.; Meeker, M.; La Cava, W.; Olson, R.S.; Moore, J.H. Relief-based feature selection: Introduction and review. J. Biomed. Inform. 2018, 85, 189–203. [Google Scholar] [CrossRef]
- Javeed, A.; Zhou, S.; Yongjian, L.; Qasim, I.; Noor, A.; Nour, R. An Intelligent Learning System Based on Random Search Algorithm and Optimized Random Forest Model for Improved Heart Disease Detection. IEEE Access 2019, 7, 180235–180243. [Google Scholar] [CrossRef]
- Alam, Z.; Rahman, M.S. A Random Forest based predictor for medical data classification using feature ranking. Inform. Med. Unlocked 2019, 15, 100180. [Google Scholar] [CrossRef]
- Mohamed, A.-A.A.; Hassan, S.; Hemeida, A.; Alkhalaf, S.; Mahmoud, M.; Eldin, A.M.B. Parasitism—Predation algorithm (PPA): A novel approach for feature selection. Ain Shams Eng. J. 2020, 11, 293–308. [Google Scholar] [CrossRef]
- Pasha, S.J.; Mohamed, E.S. Novel Feature Reduction (NFR) Model With Machine Learning and Data Mining Algorithms for Effective Disease Risk Prediction. IEEE Access 2020, 8, 184087–184108. [Google Scholar] [CrossRef]
- Saqlain, S.M.; Sher, M.; Shah, F.A.; Khan, I.; Ashraf, M.U.; Awais, M.; Ghani, A. Fisher score and Matthews correlation coefficient-based feature subset selection for heart disease diagnosis using support vector machines. Knowl. Inf. Syst. 2019, 58, 139–167. [Google Scholar] [CrossRef]
- Bharti, R.; Khamparia, A.; Shabaz, M.; Dhiman, G.; Pande, S.; Singh, P. Prediction of Heart Disease Using a Combination of Machine Learning and Deep Learning. Comput. Intell. Neurosci. 2021, 2021, 8387680. [Google Scholar] [CrossRef]
- Muhammad, Y.; Tahir, M.; Hayat, M.; Chong, K.T. Early and accurate detection and diagnosis of heart disease using intelligent computational model. Sci. Rep. 2020, 10, 19747. [Google Scholar] [CrossRef]
- Ali, L.; Rahman, A.; Khan, A.; Zhou, M.; Javeed, A.; Khan, J.A. An Automated Diagnostic System for Heart Disease Prediction Based on χ2 Statistical Model and Optimally Configured Deep Neural Network. IEEE Access 2019, 7, 34938–34945. [Google Scholar] [CrossRef]
- Kanagarathinam, K.; Sankaran, D.; Manikandan, R. Machine learning-based risk prediction model for cardiovascular disease using a hybrid dataset. Data Knowl. Eng 2022, 140, 102042. [Google Scholar] [CrossRef]
- Gupta, C.; Saha, A.; Reddy, N.V.S.; Acharya, U.D. Cardiac Disease Prediction using Supervised Machine Learning Techniques. J. Phys. Conf. Ser. 2022, 2161, 012013. [Google Scholar] [CrossRef]
- Saboor, A.; Usman, M.; Ali, S.; Samad, A.; Abrar, M.F.; Ullah, N. A Method for Improving Prediction of Human Heart Disease Using Machine Learning Algorithms. Mob. Inf. Syst. 2022, 2022, 1410169. [Google Scholar] [CrossRef]
- Chang, V.; Bhavani, V.R.; Xu, A.Q.; Hossain, M. An artificial intelligence model for heart disease detection using machine learning algorithms. Healthc. Anal. 2022, 2, 100016. [Google Scholar] [CrossRef]
- Krittanawong, C.; Virk, H.U.H.; Bangalore, S.; Wang, Z.; Johnson, K.W.; Pinotti, R.; Zhang, H.; Kaplin, S.; Narasimhan, B.; Kitai, T.; et al. Machine learning prediction in cardiovascular diseases: A meta-analysis. Sci. Rep. 2020, 10, 16057. [Google Scholar] [CrossRef]
- Alaa, A.M.; Bolton, T.; Di Angelantonio, E.; Rudd, J.H.F.; van der Schaar, M. Cardiovascular disease risk prediction using automated machine learning: A prospective study of 423,604 UK Biobank participants. PLoS ONE 2019, 14, e0213653. [Google Scholar] [CrossRef] [PubMed]
- Joloudari, J.H.; Joloudari, E.H.; Saadatfar, H.; Ghasemigol, M.; Razavi, S.M.; Mosavi, A.; Nabipour, N.; Shamshirband, S.; Nadai, L. Coronary Artery Disease Diagnosis; Ranking the Significant Features Using a Random Trees Model. Int. J. Environ. Res. Public Health 2020, 17, 731. [Google Scholar] [CrossRef] [PubMed]
- Baccouche, A.; Garcia-Zapirain, B.; Olea, C.C.; Elmaghraby, A. Ensemble Deep Learning Models for Heart Disease Classification: A Case Study from Mexico. Information 2020, 11, 207. [Google Scholar] [CrossRef]
- Heart Disease Datasets. 2021. Available online: https://archive.ics.uci.edu/ml/datasets/heart+disease (accessed on 24 November 2020).
- Statlog Heart Dataset. Available online: http://archive.ics.uci.edu/ml/datasets/statlog+(heart) (accessed on 24 November 2020).
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Hall, M.A. Correlation-based Feature Selection for Machine Learning. Ph.D. Thesis, The University of Waikato, Hamilton, New Zealand, 1999. [Google Scholar]
- Gazeloglu, C. Prediction of heart disease by classifying with feature selection and machine learning methods. Prog. Nutr. 2020, 22, 660–670. [Google Scholar] [CrossRef]
- Abakar, K.A.A.; Yu, C. Performance of SVM based on PUK kernel in comparison to SVM based on RBF kernel in prediction of yarn tenacity. Indian J. Fibre Text. Res. 2014, 39, 55–59. [Google Scholar]
- Khan, S.R.; Noor, S. Short Term Load Forecasting using SVM based PUK kernel. In Proceedings of the 2020 3rd International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 29–30 January 2020. [Google Scholar] [CrossRef]
- Fan, G.-F.; Guo, Y.-H.; Zheng, J.-M.; Hong, W.-C. Application of the Weighted K-Nearest Neighbor Algorithm for Short-Term Load Forecasting. Energies 2019, 12, 916. [Google Scholar] [CrossRef]
- Sultana, M.; Haider, A.; Uddin, M.S. Analysis of data mining techniques for heart disease prediction. In Proceedings of the 2016 3rd International Conference on Electrical Engineering and Information Communication Technology (ICEEICT), Dhaka, Bangladesh, 22–24 September 2016. [Google Scholar] [CrossRef]
- Dhar, S.; Roy, K.; Dey, T.; Datta, P.; Biswas, A. A Hybrid Machine Learning Approach for Prediction of Heart Diseases. In Proceedings of the 2018 4th International Conference on Computing Communication and Automation (ICCCA), Greater Noida, India, 14–15 December 2018. [Google Scholar] [CrossRef]
- Kang, K.; Michalak, J. Enhanced version of AdaBoostM1 with J48 Tree learning method. arXiv 2018, arXiv:1802.03522. [Google Scholar]
- Freund, Y.; Schapire, R.E. Experiments with a New Boosting Algorithm. In Proceedings of the Thirteenth International Conference on Machine Learning, Bari, Italy, 3–6 July 1996; pp. 148–156. [Google Scholar]
- Kégl, B. The return of ADABOOST.MH: Multi-class Hamming trees. In Proceedings of the 2nd International Conference on Learning and Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Bauer, E.; Kohavi, R. An Empirical Comparison of Voting Classification Algorithms: Bagging, Boosting, and Variants. Mach. Learn. 1999, 36, 105–139. [Google Scholar] [CrossRef]
- Ozcift, A.; Gulten, A. Classifier ensemble construction with rotation forest to improve medical diagnosis performance of machine learning algorithms. Comput. Methods Programs Biomed. 2011, 104, 443–451. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, J.; Kuncheva, L.; Alonso, C. Rotation Forest: A New Classifier Ensemble Method. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1619–1630. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, H.; Younis, E.M.; Hendawi, A.; Ali, A.A. Heart disease identification from patients’ social posts, machine learning solution on Spark. Futur. Gener. Comput. Syst. 2019, 111, 714–722. [Google Scholar] [CrossRef]




| No. | Author(s) & Year | Feature Selection (FS), Classifiers Trained, & Validation Method | Performance Metrics & Software (SW) | Remarks |
|---|---|---|---|---|
| 1. | Javeed et al. [31], 2019 | FS: Random search algorithm Classifiers: RF Hold-out (70:30) validation | Accuracy, sensitivity, specificity, MCC, and ROC-AUC SW: Python programming | Only one classifier has been trained and the dataset samples become fewer when using hold-out validation. |
| 2. | Alam et al. [32], 2019 | FS: InfoGain, GainRatio, Correlation, OneR, and ReliefF Classifiers: RF 10-fold cross-validation (CV) | Accuracy and AUC SW: Weka | One classifier has been utilized and the accuracy achieved was a moderate value. |
| 3. | Mohamed et al. [33], 2019 | FS: Parasitism-predation algorithm Classifiers: KNN with 10-fold CV | Accuracy and execution time SW: Matlab 2017a | Only one classifier has been trained and achieved moderate accuracy. |
| 4. | Pasha et al. [34], 2020 | FS: Novel feature reduction Classifiers: LR, RF, BRT, SGB, and SVM Hold-out (70:30) validation | Accuracy and AUC SW: R programming | Dataset samples were lesser with the 70:30 train-test split resulting in high variance. |
| 5. | Saqlain et al. [35], 2019 | FS: MFSFSA, FFSA, RFSA Classifiers: RBF SVM with 10-fold CV | Accuracy, sensitivity, and specificity SW: not specified | Only one classifier has been trained and the accuracy achieved was poor. |
| 6. | Bharti et al. [36], 2021 | FS: LASSO Classifiers: LR, KNN, SVM, RF, DT, and DL with 10-fold cross-validation | Accuracy, specificity, and sensitivity SW: Python programming | Achieved good accuracy of 94.2%. However, the specificity and sensitivity are poor. |
| 7. | Muhammad et al. [37], 2020 | FS: FCBF, mRMR, LASSO, and Relief Classifiers: KNN, DT, Extra-Tree (ET), RF, LR, NB, ANN, SVM, AdaBoost, and GB with 10-fold cross-validation | Accuracy, Sensitivity, Specificity, AUC, Precision, F1-Score, MCC SW: Python programming | ET classifier provided 92.09% of accuracy with full features, and 94.41% with Relief FS. |
| 8. | Ali et al. [38], 2019 | FS: Chi-square Classifiers: Optimized deep neural network | Accuracy, specificity, sensitivity, MCC, and AUC SW: Python programming | Though sensitivity is 100%, the accuracy is about 7% less than that. |
| 9. | Kanagarathinam et al. [39], 2022 | FS: Pearson’s correlation coefficient Classifiers: NB, XGBoost, k-NN, SVM, MLP, and CatBoost 10-fold cross-validation, 80:20 train-test | Accuracy and AUC SW: Python programming | With the CatBoost classifier achieved 94.34% of accuracy, whereas other classifiers underperformed. |
| 10. | Gupta et al. [40], 2022 | Classifiers: LR, SVM, NB, DT, KNN, and RF 70:30 train-test split | Accuracy, sensitivity, specificity, precision, and F1 score SW: Python programming | No feature selection method was employed. Lesser number of observations for validating the model. |
| 11. | Saboor et al. [41], 2022 | Classifiers: AB, LR, ET, MNB, CART, SVM, LDA, RF, and XGB.10-fold cross-validation | Accuracy, precision, recall, and F measure SW: Python programming | Achieved better accuracy value by performing hyperparameter tuning but no feature selection technique has been applied. |
| 12. | Chang et al. [42], 2022 | FS: Correlation Classifiers: KNN, DT, SVM, RF and LR 10-fold cross-validation | Accuracy SW: Python programming | The achieved accuracy was not up to the level. |
| 13. | Krittanawong (2020), [43] | Classifiers: CNN, SVM, Boosting, RF, DT | AUC, Sensitivity, and Specificity SW: R version 3.2.3 | AUC of 0.93 for CAD with custom-built, and 0.92 for Stroke with SVM. |
| 14. | Alaa et al. (2019), [44] | Ensemble of 3 pipelines using AutoPrognosis with RF, XGBoost, NN etc. | AUC-ROC SW: Python programming | The cholesterol biomarkers were not included. Feature selection has not been employed in this work. |
| 15. | Joloudari et al. (2020), [45] | FS: RTs, DT, CHAID, and SVM Classifier: RTs, DT, CHAID, and SVM with 10-fold CV | Accuracy and AUC SW: IBM Spss Modeler 18.0 | Unbalanced dataset and the methods used for attribute ranking also used for classification task. |
| 16. | Baccouche et al. (2020), [46] | FS: Model-based and Recursive feature elimination Classifiers: Ensemble Deep learning80:20 train-test ratio | Accuracy and F1-Score SW: Python programming | The methodology is computationally expensive and does not validate on benchmark datasets. |
| Ref. | Model | Hyperparameters Tuned |
|---|---|---|
| [31] | RF | Number of decision trees, E depth of each tree, D |
| [36] | Deep learning | Dropout layer |
| [37] | KNN | Number of nearest neighbors, K |
| SVM | Kernel | |
| LR | Regularization strength, C | |
| ANN | Number of hidden neurons | |
| [38] | DNN | Number of neurons in the first hidden layer, N1 Number of neurons in the second hidden layer, N2 |
| [41] | SVM | Complexity parameter, C and Kernel |
| [44] | AutoPrognosis | Weighted ML pipelines with XGBoost ensemble (200 estimators) |
| [46] | Deep learning | Number of epochs, dropout rate, optimizer, learning rate |
| No. | Attribute | Description and Value Range of Attributes |
|---|---|---|
| 1. | age | Age of the patients in years (29 to 77) |
| 2. | sex | Gender of the patients (1 = male, 0 = female) |
| 3. | cp | Chest pain type (1—typical angina, 2—atypical angina, 3—non-angina pain, 4—asymptomatic) |
| 4. | trestbps | Resting blood pressure in mm Hg on admission to the hospital (94 to 200) |
| 5. | chol | Serum cholesterol in mg/dl (126 to 564) |
| 6. | fbs | Fasting blood sugar > 120 mg/dl (1—true, 0—false) |
| 7. | restecg | Resting electrocardiographic results (0—normal, 1—ST-T wave abnormality, 2—definite left ventricular hypertrophy) |
| 8. | thalach | Maximum heart rate achieved (71 to 202) |
| 9. | exang | Exercise induces angina (1—yes, 0—no) |
| 10. | oldpeak | ST depression induced by exercise relative to rest (−2.6 to 6.2) |
| 11. | slope | The slope of the peak exercise ST segment (1—upsloping, 2—flat, 3—downsloping) |
| 12. | ca | Number of major vessels colored by fluoroscopy (0–3) |
| 13. | thal | The heart status (3—normal, 6—fixed defect, 7—reversible defect) |
| 14. | target | Prediction attribute (0—absence of heart disease, 1—presence of heart disease) |
| No. | Principal Components |
|---|---|
| 1. | −0.317slope = 1 − 0.317thal = 3 − 0.302thalach + 0.297oldpeak + 0.292cp = 4… |
| 2. | −0.54restecg = 0 + 0.526restecg = 2 − 0.28thal = 7 + 0.278thal = 3 − 0.24sex = 1… |
| 3. | 0.476ca = 0 − 0.422ca = 1 − 0.364slope = 1 + 0.338slope = 3 + 0.295oldpeak… |
| 4. | 0.37sex = 1 − 0.347slope = 2 + 0.247thal = 7 − 0.271thal = 3 + 0.267thalach… |
| 5. | −0.395fbs = 1 − 0.386cp = 3 + 0.345cp = 4 − 0.289trestbps − 0.278age... |
| 6. | −0.438ca = 2 + 0.368ca = 1 + 0.352cp = 3 + 0.323sex = 1 − 0.253cp = 4... |
| 7. | 0.523thal = 6 + 0.364cp = 1 − 0.333thal = 7 − 0.315cp = 3 − 0.279chol... |
| 8. | −0.488slope = 3 + 0.414slope = 2 − 0.273restecg = 1 − 0.271ca = 1 − 0.242cp = 4... |
| 9. | 0.593ca = 3 + 0.423cp = 2 − 0.337ca = 2 + 0.303thal = 6 − 0.295cp = 1... |
| 10. | 0.381cp = 2 + 0.367ca = 1 − 0.33ca = 2 − 0.285thal = 6 + 0.272cp = 1... |
| 11. | −0.376slope = 3 + 0.355trestbps − 0.344cp = 2 + 0.324thal = 6 − 0.308oldpeak... |
| 12. | −0.494cp = 1 − 0.423ca = 3 + 0.382fbs = 1 + 0.313cp = 2 − 0.233restecg = 1... |
| 13. | 0.642restecg = 1 + 0.36ca = 2 − 0.221fbs = 1 + 0.214thalach − 0.209exang = 1... |
| 14. | −0.625fbs = 1 + 0.429thal = 6 − 0.382restecg = 1 + 0.309chol − 0.217exang = 1... |
| 15. | −0.577chol + 0.425age − 0.305thalach + 0.268trestbps − 0.234cp = 1... |
| 16. | −0.607trestbps + 0.396age − 0.383thalach + 0.294chol + 0.211ca = 0... |
| 17. | 0.592exang = 1 + 0.448sex = 1 − 0.286cp = 4 + 0.225cp = 3 − 0.209fbs = 1... |
| 18. | 0.616sex = 1 − 0.439exang = 1 + 0.256cp = 4 + 0.237thal = 3 − 0.209cp = 1... |
| Classifier | Hyperparameters | Value Range |
|---|---|---|
| SVM | Complexity parameter, C | 1–7 |
| Type of kernel | PolyKernel, PUK, RBF | |
| KNN | Number of neighbors, K | 1, 3, 5, 7 |
| Distance weighting | No distance weighting, 1/distance, 1-distance | |
| J48 | Confidence factor, C | 0.25, 0.50, 0.75 |
| Minimum number of instances per leaf, M | 1–3 | |
| AdaBoostM1 | Base classifier | Decision stump, J48 |
| Number of iterations, I | 10, 20, 30 | |
| Bagging | Base classifier | REPTree, J48 |
| Number of iterations, I | 10, 20, 30 | |
| ROTF | Base classifier | J48, Random Forest |
| Number of iterations, I | 10, 20, 30 | |
| Removed percentage, P | 40, 50 |
| Predicted Class | |||
|---|---|---|---|
| Low Risk (0) | High Risk (1) | ||
| True class | Low risk (0) | True Negative (TN) | False Positive (FP) |
| High risk (1) | False Negative (FN) | True Positive (TP) | |
| On a Complete Set of PCs | On Optimal PCs | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | Acc. | Sen. | Spe. | Pre. | F-mea. | AUC | Cost | Time (ms) | Acc. | Sen. | Spe. | Pre. | F-mea. | AUC | Cost | Time (ms) |
| SVM | 84.82 | 84.82 | 83.62 | 85.00 | 84.91 | 0.842 | 87 | 100 | 84.64 | 84.64 | 83.00 | 85.14 | 84.89 | 0.838 | 88 | 50 |
| KNN | 96.34 | 96.34 | 96.10 | 96.34 | 96.34 | 0.945 | 21 | 0 | 95.81 | 95.81 | 95.73 | 95.81 | 95.81 | 0.963 | 24 | 0 |
| J48 | 92.32 | 92.32 | 92.38 | 92.36 | 92.34 | 0.965 | 44 | 120 | 93.89 | 93.89 | 93.68 | 93.89 | 93.89 | 0.967 | 35 | 10 |
| AB | 81.85 | 81.85 | 80.30 | 82.15 | 82.00 | 0.913 | 104 | 150 | 87.26 | 87.26 | 86.45 | 87.32 | 87.29 | 0.953 | 73 | 30 |
| BG | 89.35 | 89.35 | 88.51 | 89.46 | 89.41 | 0.967 | 61 | 160 | 91.97 | 91.97 | 91.69 | 91.97 | 91.97 | 0.970 | 46 | 40 |
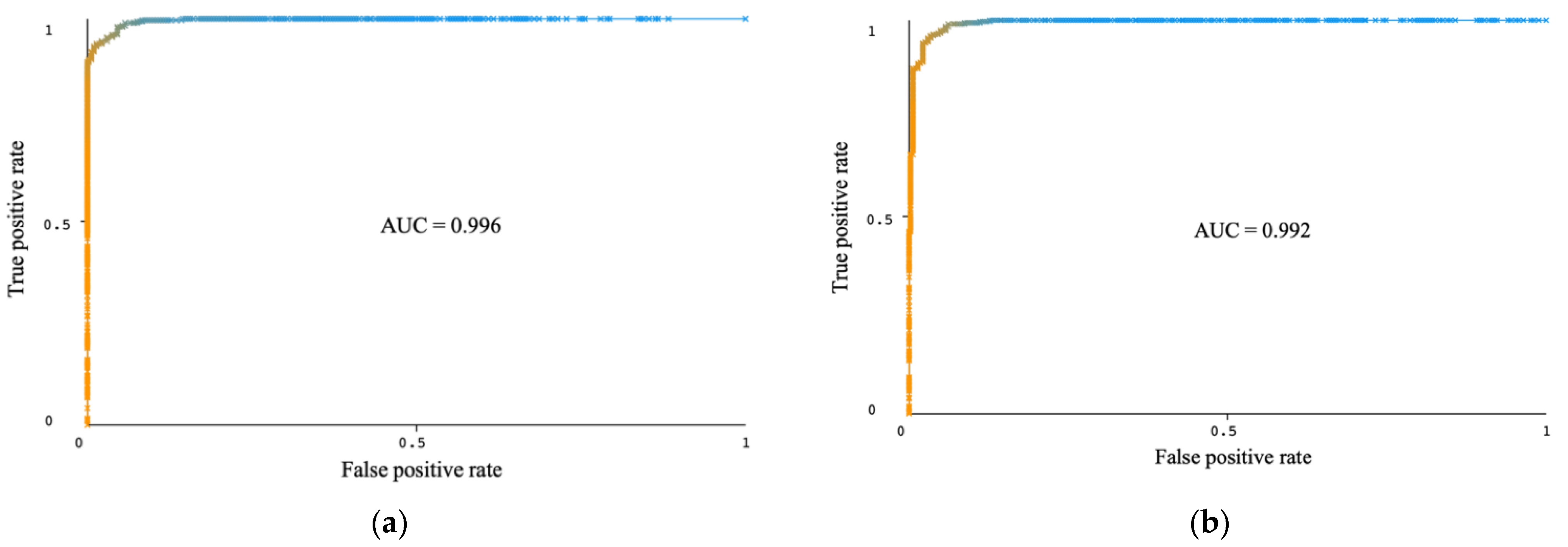
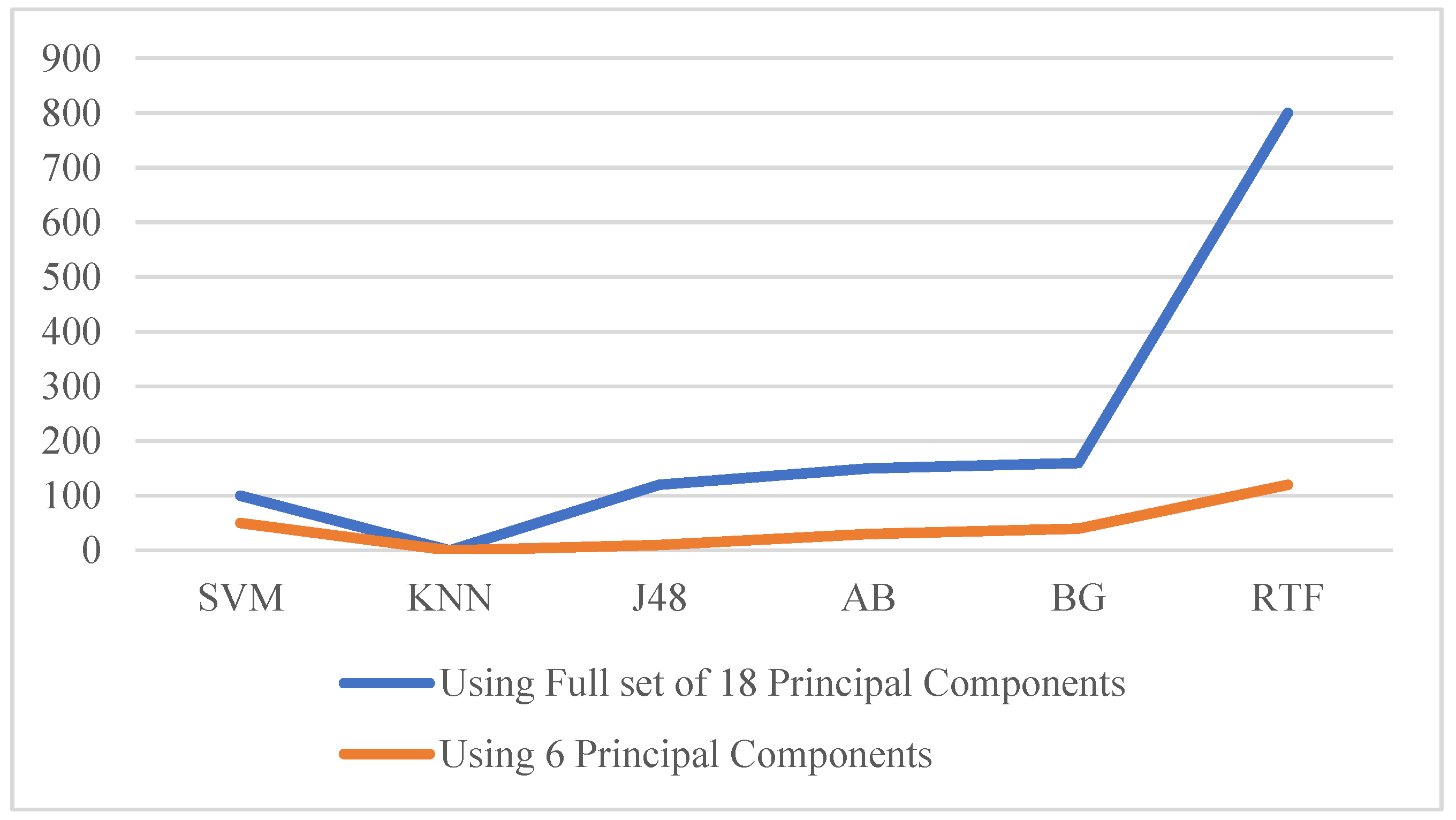
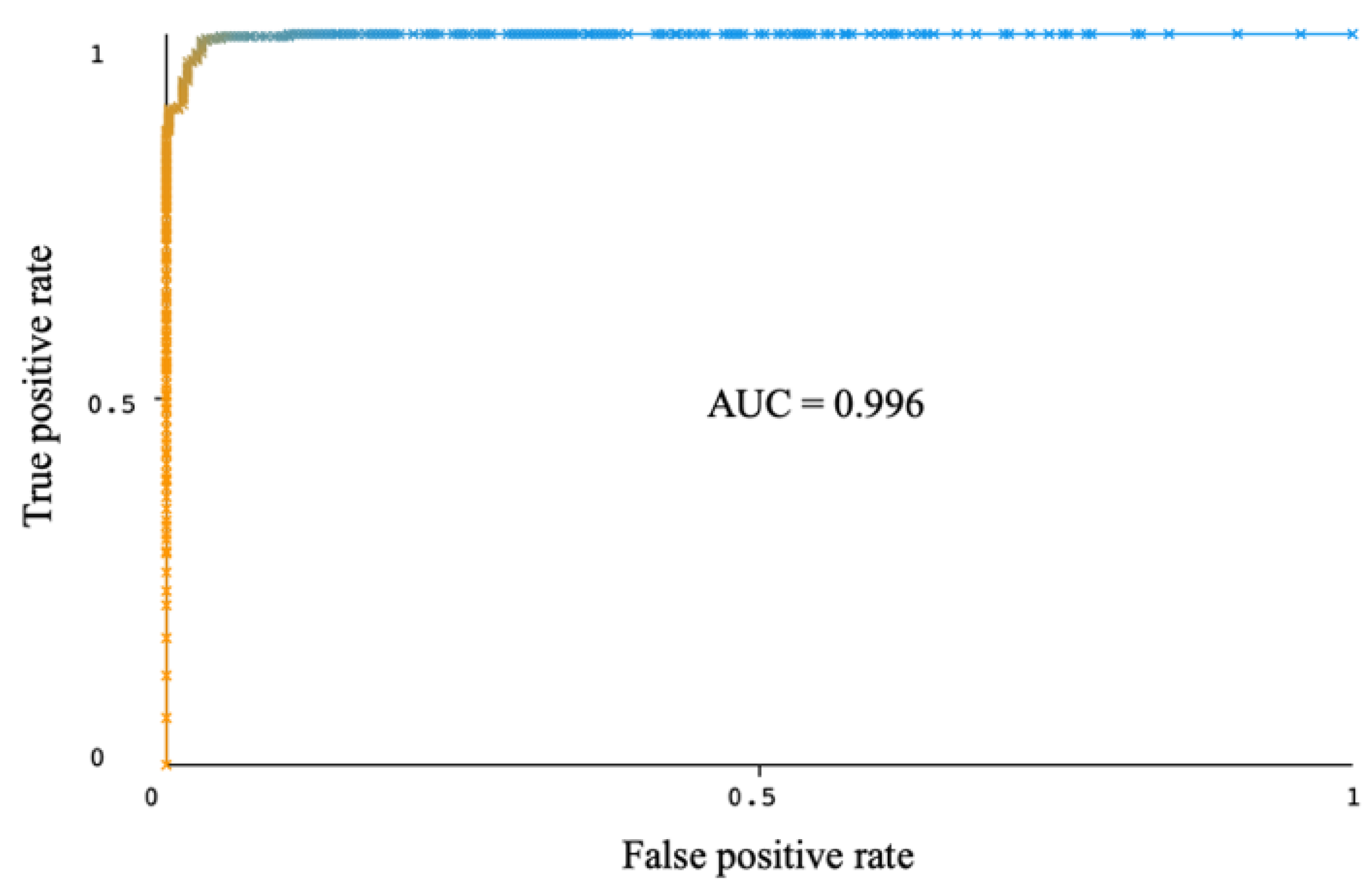
| RTF | 96.16 | 96.16 | 96.02 | 96.16 | 96.16 | 0.996 | 22 | 800 | 95.99 | 95.99 | 95.40 | 96.09 | 96.04 | 0.992 | 23 | 120 |
| Training No. | Complexity Parameter, C | Kernel | Accuracy |
|---|---|---|---|
| 1. | 1 | PolyKernel | 84.6422 |
| 2. | 2 | PolyKernel | 84.8168 |
| 3. | 3 | PolyKernel | 84.6422 |
| 4. | 4 | PolyKernel | 84.8168 |
| 5. | 5 | PolyKernel | 84.9913 |
| 6. | 6 | PolyKernel | 84.9913 |
| 7. | 7 | PolyKernel | 84.8168 |
| 8. | 1 | Pearson VII Universal | 87.2600 |
| 9. | 2 | Pearson VII Universal | 89.8778 |
| 10. | 3 | Pearson VII Universal | 90.4014 |
| 11. | 4 | Pearson VII Universal | 91.2740 |
| 12. | 5 | Pearson VII Universal | 91.7976 |
| 13. | 6 | Pearson VII Universal | 92.6702 |
| 14. | 7 | Pearson VII Universal | 93.1937 |
| 15. | 1 | Radial Basis Function | 69.6335 |
| 16. | 2 | Radial Basis Function | 85.3403 |
| 17. | 3 | Radial Basis Function | 84.2932 |
| 18. | 4 | Radial Basis Function | 83.7696 |
| 19. | 5 | Radial Basis Function | 84.2932 |
| 20. | 6 | Radial Basis Function | 83.7696 |
| 21. | 7 | Radial Basis Function | 83.7696 |
| Training No. | Number of Neighbors, K | Distance Weighting | Accuracy |
|---|---|---|---|
| 1. | 1 | No distance weighting | 95.8115 |
| 2. | 3 | No distance weighting | 89.5288 |
| 3. | 5 | No distance weighting | 85.1658 |
| 4. | 7 | No distance weighting | 84.8168 |
| 5. | 1 | 1/distance | 95.8115 |
| 6. | 3 | 1/distance | 96.6841 |
| 7. | 5 | 1/distance | 97.0332 |
| 8. | 7 | 1/distance | 96.6841 |
| 9. | 1 | 1-distance | 95.8115 |
| 10. | 3 | 1-distance | 90.4014 |
| 11. | 5 | 1-distance | 88.3072 |
| 12. | 7 | 1-distance | 85.3403 |
| Training No. | Confidence Factor, C | Min. Number of Instances per Leaf, M | Accuracy |
|---|---|---|---|
| 1. | 0.25 | 1 | 95.1134 |
| 2. | 0.25 | 2 | 93.8918 |
| 3. | 0.25 | 3 | 93.1937 |
| 4. | 0.50 | 1 | 95.1134 |
| 5. | 0.50 | 2 | 93.8918 |
| 6. | 0.50 | 3 | 93.5428 |
| 7. | 0.75 | 1 | 95.4625 |
| 8. | 0.75 | 2 | 93.8918 |
| 9. | 0.75 | 3 | 92.6702 |
| Training No. | Base Classifier | Number of Iterations, I | Accuracy |
|---|---|---|---|
| 1. | Decision Stump | 10 | 87.2600 |
| 2. | Decision Stump | 20 | 90.0524 |
| 3. | Decision Stump | 30 | 90.9250 |
| 4. | J48 | 10 | 97.2077 |
| 5. | J48 | 20 | 97.0332 |
| 6. | J48 | 30 | 97.3822 |
| Training No. | Base Classifier | Number of Iterations, I | Accuracy |
|---|---|---|---|
| 1. | REPTree | 10 | 91.9721 |
| 2. | REPTree | 20 | 91.6230 |
| 3. | REPTree | 30 | 92.6702 |
| 4. | J48 | 10 | 94.2408 |
| 5. | J48 | 20 | 94.7644 |
| 6. | J48 | 30 | 94.4154 |
| Training No. | Base Classifier | Number of Iterations, I | Removed Percentage, P | Accuracy |
|---|---|---|---|---|
| 1. | J48 | 10 | 50 | 95.9860 |
| 2. | J48 | 20 | 50 | 95.9860 |
| 3. | J48 | 30 | 50 | 96.3351 |
| 4. | J48 | 10 | 40 | 95.2880 |
| 5. | J48 | 20 | 40 | 95.9860 |
| 6. | J48 | 30 | 40 | 95.9860 |
| 7. | RF | 10 | 50 | 97.7312 |
| 8. | RF | 20 | 50 | 97.5567 |
| 9. | RF | 30 | 50 | 97.7312 |
| 10. | RF | 10 | 40 | 97.9058 |
| 11. | RF | 20 | 40 | 97.7312 |
| 12. | RF | 30 | 40 | 97.7312 |
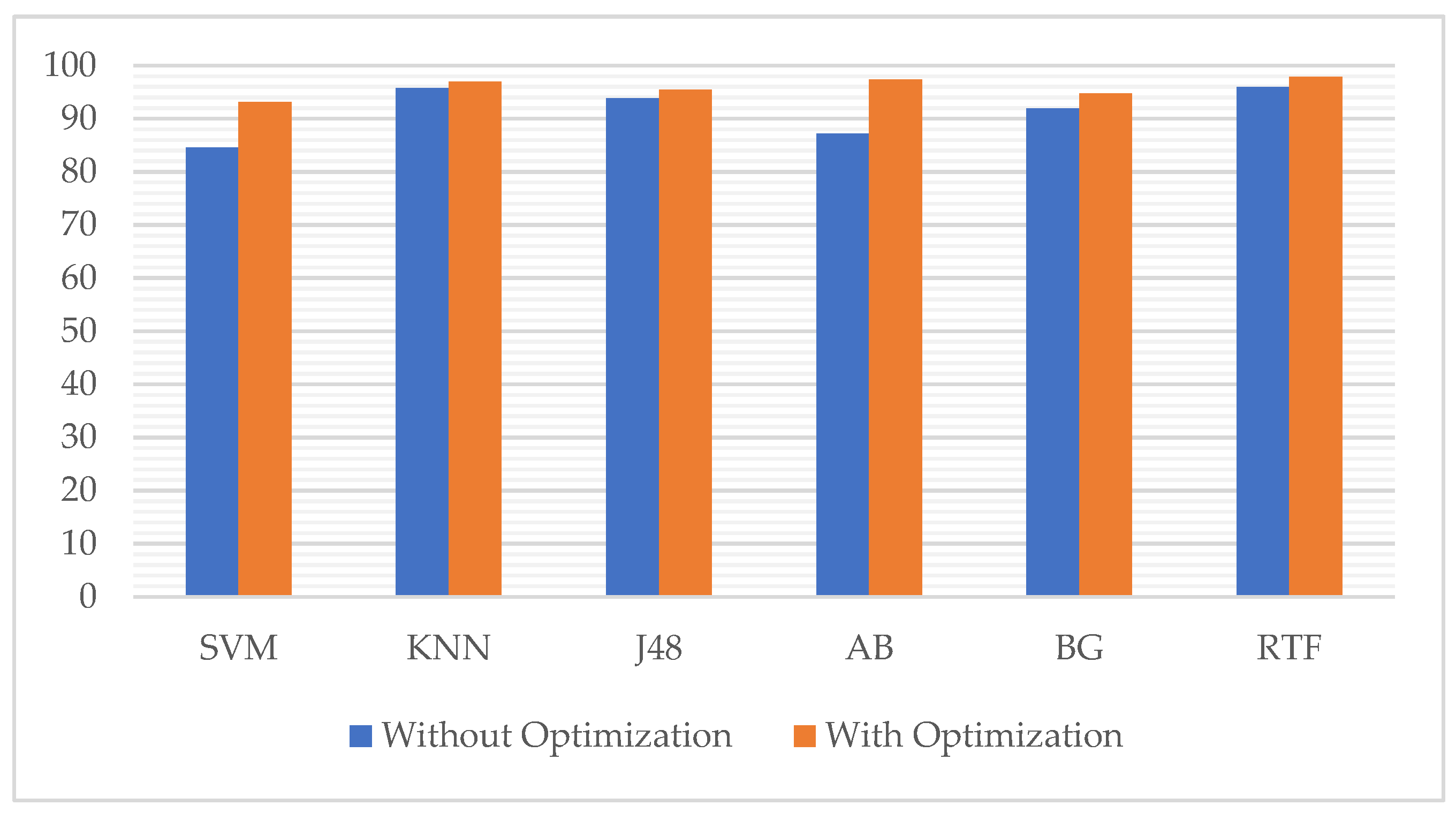
| No. | Classifier | Without Optimization | With Optimization | Improvement |
|---|---|---|---|---|
| 1. | Support Vector Machines | 84.64 | 93.19 | 8.55 |
| 2. | K-Nearest Neighbors | 95.81 | 97.03 | 1.22 |
| 3. | J48 Decision Tree | 93.89 | 95.46 | 1.57 |
| 4. | AdaBoost M1 | 87.26 | 97.38 | 10.12 |
| 5. | Bagging | 91.97 | 94.76 | 2.79 |
| 6. | Rotation Forest | 95.99 | 97.91 | 1.92 |
| On Selected Six Principal Components by the CFS Method | ||||||||
|---|---|---|---|---|---|---|---|---|
| Model | Acc. | Sen. | Spe. | Pre. | F-mea. | AUC | Cost | Best Hyperparameters |
| SVM | 93.19 | 93.19 | 92.56 | 93.28 | 93.24 | 0.929 | 39 | C = 7, PUK kernel |
| KNN | 97.03 | 97.03 | 96.88 | 97.04 | 97.03 | 0.988 | 17 | K = 5, 1/distance weight |
| J48 | 95.46 | 95.46 | 95.24 | 95.5 | 95.46 | 0.969 | 26 | C = 0.75, M = 1 |
| AB | 97.38 | 97.38 | 97.10 | 97.40 | 97.39 | 0.989 | 15 | J48 base classifier, I = 30 |
| BG | 94.76 | 94.76 | 94.46 | 94.77 | 94.77 | 0.987 | 30 | J48 base classifier, I = 20 |
| RTF | 97.91 | 97.91 | 97.66 | 97.92 | 97.91 | 0.996 | 12 | RF base classifier, I = 10, P = 40 |
| No. | Ref. | Year | FS | Classifier | # | Acc. | Sen. | Spe. | Pre. | F-mea. | AUC |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | [31] | 2019 | RSA | RF | 7 | 93.33 | 95.12 | 89.79 | - | - | 0.947 |
| 2. | [32] | 2019 | Relief | RF | 12 | 85.50 | 85.60 | - | 85.50 | 85.50 | 0.915 |
| 3. | [33] | 2020 | PPA | KNN | 4 | 86.17 | - | 85.00 | - | - | - |
| 4. | [34] | 2020 | NFR | LR | 9 | 92.53 | - | - | - | - | 0.926 |
| 5. | [35] | 2019 | FFSA | SVM RBF | 7 | 81.19 | 72.92 | 88.68 | - | - | - |
| 6. | [36] | 2021 | LASSO | DL | 6 | 94.20 | 83.10 | 82.30 | - | - | - |
| 7. | [37] | 2020 | Relief | Extra Tree | 6 | 94.41 | 94.93 | 94.89 | 95.46 | 95.00 | 0.942 |
| 8. | [38] | 2019 | Chi-square | DL | 11 | 93.33 | 85.36 | 100 | - | - | 0.94 |
| 9. | [39] | 2022 | Pearson’s correlation | CatBoost | 10 | 94.34 | - | - | - | - | - |
| 10. | [40] | 2022 | - | LR | 13 | 92.30 | 96.08 | 87.50 | 90.74 | 93.34 | - |
| 11. | [41] | 2022 | - | SVM | 13 | 96.72 | 98.00 | - | 98.00 | 98.00 | - |
| 12. | [42] | 2022 | Correlation | RF | - | 83.00 | - | - | - | - | - |
| 13. | [45] | 2020 | RTs | RTs | 44 | 91.47 | - | - | - | - | 0.967 |
| 14. | [46] | 2020 | Tree-based | BiGRU +CNN | 60 | 96.00 | 92.00 | - | 99.00 | 95.00 | 0.990 |
| 15. | Proposed work | 2022 | PCA + CFS | Rotation Forest | 6 | 97.91 | 97.91 | 97.66 | 97.92 | 97.91 | 0.996 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reddy, K.V.V.; Elamvazuthi, I.; Aziz, A.A.; Paramasivam, S.; Chua, H.N.; Pranavanand, S. An Efficient Prediction System for Coronary Heart Disease Risk Using Selected Principal Components and Hyperparameter Optimization. Appl. Sci. 2023, 13, 118. https://doi.org/10.3390/app13010118
Reddy KVV, Elamvazuthi I, Aziz AA, Paramasivam S, Chua HN, Pranavanand S. An Efficient Prediction System for Coronary Heart Disease Risk Using Selected Principal Components and Hyperparameter Optimization. Applied Sciences. 2023; 13(1):118. https://doi.org/10.3390/app13010118
Chicago/Turabian StyleReddy, Karna Vishnu Vardhana, Irraivan Elamvazuthi, Azrina Abd Aziz, Sivajothi Paramasivam, Hui Na Chua, and Satyamurthy Pranavanand. 2023. "An Efficient Prediction System for Coronary Heart Disease Risk Using Selected Principal Components and Hyperparameter Optimization" Applied Sciences 13, no. 1: 118. https://doi.org/10.3390/app13010118
APA StyleReddy, K. V. V., Elamvazuthi, I., Aziz, A. A., Paramasivam, S., Chua, H. N., & Pranavanand, S. (2023). An Efficient Prediction System for Coronary Heart Disease Risk Using Selected Principal Components and Hyperparameter Optimization. Applied Sciences, 13(1), 118. https://doi.org/10.3390/app13010118







