MARL-Based Dual Reward Model on Segmented Actions for Multiple Mobile Robots in Automated Warehouse Environment
Abstract
:1. Introduction
- A reward model is proposed so that learning can proceed efficiently and stably in an environment where the sparse reward problem of reinforcement learning has become serious.
- The proposed reward model induces and supports reinforcement learning efficiently and stably by using the reward model without modifying the reinforcement learning algorithm or changing the environment.
- It is meaningful as a practical case study that confirms learning efficiently and stably despite the sparse reward problem in a simulation experiment environment similar to an actual automated warehouse.
2. Related Work
2.1. Reinforcement Learning Types
2.1.1. Model-Based vs. Model-Free
2.1.2. Value-Based vs. Policy-Based
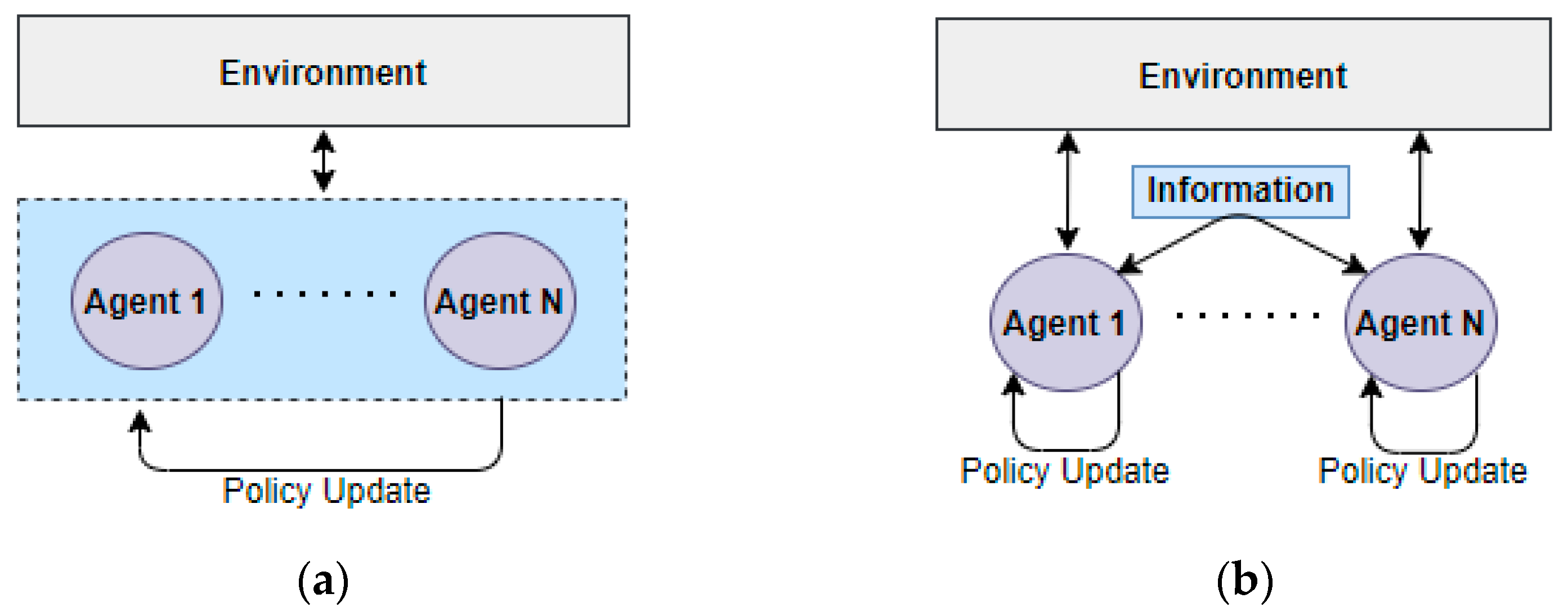
2.2. Multi-Agent Reinforcement Learning (MARL)
2.2.1. Concept of Multi-Agents and MARL Algorithm
2.2.2. MARL Setting Types
- Mixed Type [20]
2.2.3. MARL Learning and Execution Types
- Centralized Training Centralized Execution (CTCE)
- Centralized Training Decentralized Execution (CTDE)
- Distributed Training Decentralized Execution (DTDE)
2.3. Review of Algorithm for Experiment
2.3.1. Deep Q-Networks (DQN)
2.3.2. Double Deep Q-Networks (DDQN)
2.3.3. Independent Q-Learning (IQL)
2.4. Sparse Reward and Improvement Methods
- Reward Shaping
- Transfer Learning
- Curriculum Learning
- Curiosity-Driven Learning
- Hierarchical Reinforcement Learning (HRL)
3. MARL Methodology in a Warehouse Environment
3.1. System Architecture
3.2. Proposed Reward Model
3.2.1. Basic Rules to Define the Proposed Reward Model
- Define Full Actions and Partial Actions
- 2.
- Define the Maximum Reward Value
3.2.2. Define Reward Settings Based on Agent Relationship
- Cooperative Type [20]
- 2.
- Mixed Type [20]
3.2.3. Proposed Reward Model Dual Segmented Reward Model
- Define Segmented Reward Model
- 2.
- Define Dual Reward Model based on Segmented Reward Models
4. Experiment and Results
4.1. Experiment Environment
4.2. Experiment Method
- The mobile robot moves to find the location of the object to be transported.
- When the mobile robot arrives at the location of the object, the operator picks up the object and places it on the transport tray.
- The mobile robot moves to the final destination with the transport tray and delivers the object to the final destination. The operator gets the object from the transport tray.
- The mobile robot returns the transport tray to its initial position.
4.3. Modeling of the Dual Segmented Reward Model
| Algorithm 1: Dual Segmented Reward Model |
| (a) Initialize (b) Loop for Episode: (c) Loop for n Steps: (c-1) Get state (c-2) Take action and next state (c-3) If agent does not complete action in the episode, Get reward value via Reward Model No. 1 with Learning Decay Method Else Get reward value via Reward Model No. 2 (d) Change next state to state |
4.4. Experiment Parameter Values
4.5. Experiment Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Salzman, O.; Stern, R. Research Challenges and Opportunities in Multi-Agent Path Finding and Multi-Agent Pickup and Delivery Problems. In Proceedings of the AAMAS 2020, Auckland, New Zealand, 9–13 May 2020; pp. 1711–1715. [Google Scholar]
- Nguyen, T.T.; Nguyen, N.D.; Nahavandi, S. Deep Reinforcement Learning for Multiagent Systems: A Review of Challenges, Solutions, and Applications. IEEE Trans. Cybern. 2020, 50, 3826–3839. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Christianos, F.; Papoudakis, G.; Rahman, A.; Albrecht, S.V. Scaling Multi-Agent Reinforcement Learning with Selective Parameter Sharing. In Proceedings of the 38th International Conference on Machine Learning (ICML 2021), Virtual, 18–24 July 2021. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Introduction to Reinforcement Learning, 2nd ed.; MIT Press: London, UK, 2018; pp. 1–528. [Google Scholar]
- DAVID SILVER. Available online: https://www.davidsilver.uk/teaching/ (accessed on 2 December 2021).
- OpenAI Spinning Up. Available online: https://spinningup.openai.com/en/latest/index.html (accessed on 6 March 2022).
- Moerland, T.M.; Broekens, J.; Jonker, C.M. Learning Multimodal Transition Dynamics for Model-Based Reinforcement Learning. In Proceedings of the European Machine Learning Conference (ECML), Skopje, Macedonia, 18–22 September 2017. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. In Proceedings of the Neural Information Processing Systems (NIPS), Lake Tahoe, CA, USA, 9 December 2013. [Google Scholar]
- Lv, L.; Zhang, S.; Ding, D.; Wa, Y. Path Planning via an Improved DQN-Based Learning Policy. IEEE Access 2019, 7, 67319–67330. [Google Scholar] [CrossRef]
- van Hasselt, H.; Guez, A.; Silver, D. Deep Reinforcement Learning with Double Q-learning. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence (AAAI-16), San Juan, Puerto Rico, 12–17 February 2016. [Google Scholar]
- Wang, Z.; Schaul, T.; Hessel, M.; van Hasselt, H.; Lanctot, M.; de Freitas, N. Dueling Network Architectures for Deep Reinforcement Learning. In Proceedings of the 33rd International Conference on Machine Learning (ICML-2016), New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Schaul, T.; Quan, J.; Antonoglou, I.; Silver, D. Prioritized Experience Replay. In Proceedings of the International Conference on Learning Representations (ICLR), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Williams, R.J. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach. Learn. 1992, 8, 229–256. [Google Scholar] [CrossRef] [Green Version]
- Sutton, R.S.; McAllester, D.; Singh, S.; Mansour, Y. Policy gradient methods for reinforcement learning with function approximation. In Proceedings of the Neural Information Processing Systems (NIPS), Denver, CO, USA, 29 November–24 June 1999. [Google Scholar]
- Schulman, J.; Levine, S.; Moritz, P.; Jordan, M.I.; Abbeel, P. Trust Region Policy Optimization. In Proceedings of the 32nd International Conference on Machine Learning (ICML-2015), Lille, France, 6–11 July 2015. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.P.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous Methods for Deep Reinforcement Learning. In Proceedings of the 33rd International Conference on Machine Learning (ICML-2016), New York, NY, USA, 19–24 June 2016. [Google Scholar]
- OpenAI. Available online: https://openai.com/blog/baselines-acktr-a2c/ (accessed on 2 December 2021).
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous Control with Deep Reinforcement Learning. In Proceedings of the International Conference on Learning Representations 2016 (ICLR 2016), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Zhang, K.; Yang, Z.; Başar, T. Multi-Agent Reinforcement Learning: A Selective Overview of Theories and Algorithms. arXiv 2019, arXiv:1911.10635. [Google Scholar]
- Littman, M.L. A tutorial on partially observable Markov decision processes. J. Math. Psychol. 2009, 53, 119–125. [Google Scholar] [CrossRef]
- Lee, H.; Jeong, J. Mobile Robot Path Optimization Technique Based on Reinforcement Learning Algorithm in Warehouse Environment. Appl. Sci 2021, 11, 1209. [Google Scholar] [CrossRef]
- Vlontzos, A.; Alansary, A.; Kamnitsas, K.; Rueckert, D.; Kainz, B. Multiple Landmark Detection using Multi-Agent Reinforcement Learning. In Proceedings of the 22nd International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI 2019), Shenzhen, China, 13–17 October 2019. [Google Scholar]
- Papoudakis, G.; Christianos, F.; Schäfer, L.; Albrecht, S.V. Comparative Evaluation of Multi-Agent Deep Reinforcement Learning Algorithms. arXiv 2021, arXiv:2006.07869v1. [Google Scholar]
- Tan, M. Multi-Agent Reinforcement Learning: Independent versus Cooperative Agents. In Proceedings of the 10th International Conference on Machine Learning (ICML 1993), Amherst, MA, USA, 27–29 June 1993; pp. 330–337. [Google Scholar]
- Volodymyr, M.; Koray, K.; David, S.; Andrei, A.R.; Joel, V.; Marc, G.B.; Alex, G.; Martin, R.; Andreas, K.F.; Georg, O.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar]
- Ahilan, S.; Dayan, P. Feudal Multi-Agent Hierarchies for Cooperative Reinforcement Learning. arXiv 2019, arXiv:1901.08492. [Google Scholar]
- Chu, T.; Wang, J.; Codecà, L.; Li, Z. Multi-Agent Deep Reinforcement Learning for Large-scale Traffic Sig-nal Control. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1086–1095. [Google Scholar] [CrossRef] [Green Version]
- Jadid, A.O.; Hajinezhad, D. A Review of Cooperative Multi-Agent Deep Reinforcement Learning. arXiv 2020, arXiv:1908.03963. [Google Scholar]
- Lowe, R.; Wu, Y.; Tamar, A.; Harb, J.; Abbeel, P.; Mordatch, I. Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 6382–6393. [Google Scholar]
- Foerster, J.; Farquhar, G.; Afouras, T.; Nardelli, N.; Whiteson, S. Counterfactual Multi-Agent Policy Gradients. In Proceedings of the 32nd AAAI Conference on Artificial Intelligence (AAAI-18), Long Beach, LA, USA, 2–7 February 2018. [Google Scholar]
- Rashid, T.; Samvelyan, M.; de Witt, C.S.; Farquhar, G.; Foerster, J.; Whiteson, S. QMIX: Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning. In Proceedings of the 35th International Conference on Machine Learning (ICML-2018), Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Christianos, F.; Schäfer, L.; Albrecht, S.V. Shared Experience Actor-Critic for Multi-Agent Reinforcement Learning. In Proceedings of the Advances in Neural Information Processing Systems (NeurIPS), Virtual, 6–12 December 2020. [Google Scholar]
- Tampuu, A.; Matiisen, T.; Kodelja, D.; Kuzovkin, I.; Korjus, K.; Aru, J.; Aru, J.; Vicente, R. Multiagent Cooperation and Competition with Deep Reinforcement Learning. arXiv 2015, arXiv:1511.08779. [Google Scholar] [CrossRef] [PubMed]
- Hoen, P.; Tuyls, K.; Panait, L.; Luke, S.; Poutré, H.L. An Overview of Cooperative and Competitive Multiagent Learning. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems (AAMAS), Utrecht, The Netherlands, 25–29 July 2005. [Google Scholar]
- Gronauer, S.; Diepold, K. Multi-agent deep reinforcement learning: A survey. Artif. Intell. Rev. 2021, 55, 895–943. [Google Scholar] [CrossRef]
- Du, W.; Ding, S. A survey on multi-agent deep reinforcement learning: From the perspective of challenges and applications. Artif. Intell. Rev. 2020, 54, 3215–3238. [Google Scholar] [CrossRef]
- Wen, G.; Fu, J.; Dai, P.; Zhou, J. DTDE: A new cooperative Multi-Agent Reinforcement Learning framework. Innovation 2021, 2, 1209–1226. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Ontañón, S. Action Guidance: Getting the Best of Sparse Rewards and Shaped Rewards for Real-time Strategy Games. arXiv 2020, arXiv:2010.03956. [Google Scholar]
- Gudimella, A.; Story, R.; Shaker, M.; Kong, R.; Brown, M.; Shnayder, V.; Campos, M. Deep Reinforcement Learning for Dexterous Manipulation with Concept Networks. arXiv 2017, arXiv:1709.06977. [Google Scholar]
- Sartoretti, G.; Kerr, J.; Shi, Y.; Wagner, G.; Kumar, T.K.S.; Koenig, S.; Choset, H. PRIMAL: Pathfinding via Reinforcement and Imitation Multi-Agent Learning. IEEE Robot. Autom. Lett. 2019, 4, 2378–2385. [Google Scholar] [CrossRef] [Green Version]
- Foukarakis, M.; Leonidis, A.; Antona, M.; Stephanidis, C. Combining Finite State Machine and Decision-Making Tools for Adaptable Robot Behavior. In Proceedings of the International Conference on Universal Access in Human-Computer Interaction (UAHCI), Crete, Greece, 22–27 June 2014. [Google Scholar]




















| Parameter | Value |
|---|---|
| Learning Rate (α) | 0.00008 |
| Discount Rate (γ) | 0.99 |
| Reward Decay Rate (λ) | 0.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Hong, J.; Jeong, J. MARL-Based Dual Reward Model on Segmented Actions for Multiple Mobile Robots in Automated Warehouse Environment. Appl. Sci. 2022, 12, 4703. https://doi.org/10.3390/app12094703
Lee H, Hong J, Jeong J. MARL-Based Dual Reward Model on Segmented Actions for Multiple Mobile Robots in Automated Warehouse Environment. Applied Sciences. 2022; 12(9):4703. https://doi.org/10.3390/app12094703
Chicago/Turabian StyleLee, Hyeoksoo, Jiwoo Hong, and Jongpil Jeong. 2022. "MARL-Based Dual Reward Model on Segmented Actions for Multiple Mobile Robots in Automated Warehouse Environment" Applied Sciences 12, no. 9: 4703. https://doi.org/10.3390/app12094703
APA StyleLee, H., Hong, J., & Jeong, J. (2022). MARL-Based Dual Reward Model on Segmented Actions for Multiple Mobile Robots in Automated Warehouse Environment. Applied Sciences, 12(9), 4703. https://doi.org/10.3390/app12094703







